МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
ЛАБОРАТОРНАЯ РАБОТА ПО ФИЗИКЕ
«ИЗМЕРЕНИЕ ПЛОТНОСТИ ТЕЛА ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ»
Методические указания к лабораторным работам для студентов всех направлений подготовки
Казань
2014
УДК 535
ББК 22.34 C 31
Методические указания к лабораторным работам по физике для студентов всех направлений подготовки. Лабораторная работа «Измерение плотности тела правильной геометрической формы»/ Сост.: В.И.Сундуков, Казань: КГАСУ, 2014 г. – 12 с.
Печатается по решению Редакционно-издательского совета Казанского государственного архитектурно-строительного университета
В методических указаниях рассматриваются основы теории измерений и обработок ошибок. Подробно приводится метод измерения плотности тела правильной геометрической формы.
Данные методические указания являются составной частью методического обеспечения аудиторной и самостоятельной работы студентов всех направлений подготовки.
Рецензент доцент кафедры теплоэнергетики КазГАСУ
В.Н. Енюшин
УДК 535
ББК 22.34
Казанский государственный архитектурно-строительный университет, 2014 г.
Сундуков В.И., 2014
2
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
Физика имеет дело с физическими величинами, измеряемыми на опыте. Измерение – это определение опытным путем, какой либо физической величины. На эксперименте производится сравнение данной величины с другой, такого же рода величиной, принятой за единицу меры.
Измерения могут быть прямыми и косвенными. Прямое измерение – это непосредственное сравнение измеряемой величины с единицей измерения с помощью приборов и устройств, проградуированных в соответствующих единицах (измерение линейных размеров линейкой, штангенциркулем, измерение времени секундомером).
Косвенно измеряемая величина рассчитывается с помощью некоторой зависимости (формулы) от других величин, полученных прямыми измерениями (определение скорости v=s / t по пути и времени и т.д.).
Любое измерение не дает абсолютно точного значения измеряемой величины из-за неточности приборов, влияния внешних факторов, – поэтому измеренные значения всегда отклоняются от истинного. Эти отклонения называются ошибками или погрешностями измерений. Исключение составляют целочисленные измерения, например, счет предметов, которые могу быть проведены абсолютно точно.
Поэтому, проделав измерения, необходимо оценить точность измерений. Следовательно, задачей измерения является:
1)получение приблизительного значения измеряемой величины,
2)оценка величины погрешности или ошибки.
Различают абсолютные и относительные ошибки. Абсолютной ошибкой называется разница измеренного х и истинного значений Х измеряемой величины.
Абсолютная погрешность является размерной величиной. Она выражается в тех же единицах, что и сама измеряемая величина. Например, абсолютная погрешность измерения длины выражается в метрах. Хотя величина
3

х показывает, насколько измеренное значение отличается от истинного, она не полностью характеризует точность проделанного измерения, поэтому вводят понятие относительной ошибки. Относительная ошибка ε представляет собой отношение модуля абсолютной ошибки к измеряемой величине:
X
Относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно. Поэтому значения х и ε можно лишь оценить, т.е. найти их приближенно с той или иной степенью точности.
Все ошибки можно разделить на случайные, приборные, системати—
ческие и грубые. Систематическая ошибка зависит от точности измерительных приборов и правильности планирования измерений, учёта всех факторов, влияющих на эксперимент, её очень сложно учитывать. При проведении измерений в некоторых случаях постоянно получают разные числа, это обусловлено случайными ошибками. Их название отражает их суть. Если один результат из серии измерений сильно отличается от остальных, то это означает, что имело место грубая ошибка и этот результат следует исключить.
Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как δ х, случайную – как s x.
Способы определения приборных ошибок
Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также класс точности.
Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора.
Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы
Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:
|
К = |
δ х |
100 . |
(3) |
|
П |
4

Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах.
В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из ниже перечисленных способов.
1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись «0,01 мм». Если с помощью этого прибора измеряется, например, диаметр шарика d, то погрешность его измерения δd = 0,01 мм.
2. На приборе указан класс точности. Согласно определению этой величины, из формулы (3) имеем
|
δ x = |
К П |
. |
(4) |
|
100 |
Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения
δ U = 2,5 600 = 15 (В) . 100
3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины δ х.
а) Указатель значения измеряемой величины может принимать только определенные положения, или прибор имеет цифровую шкалу, например, электронные секундомер. Абсолютная погрешность равна цене деления шкалы δ х = Ц или равна единице последнего разряда.
б) Указатель значения измеряемой величины может занимать любое положение на шкале (линейки, термометры). В этом случае абсолютная приборная погрешность равна половине цены деления: δ х = Ц/2.
4. Если какая-либо величина не измеряется в данном опыте, а была измерена независимо и известно лишь ее значение, то она является задан— ным параметром. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если число π=3,14, то его погрешность
δ π = 0,005 мм.
Способы определения случайных ошибок
Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено несколько измерений одной и той же величины и получены различные результаты.
Пусть в результате проделанных измерений получено п значений величины х: х1 , х2 , …, хп . Обозначим через xср среднеарифметическое значение
5
|
1 |
1 |
n |
||||||
|
xcp |
= |
( x1 + x2 |
+ … + xn ) = |
∑xi . |
(5) |
|||
|
n |
n |
|||||||
|
= |
||||||||
|
i 1 |
Доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:
lim xср = X .
n→ ∞
При небольшом числе измерений (п ≤ 10) среднее значение может существенно отличаться от истинного. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью α (0 < α < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина α –
доверительной вероятностью (или коэффициентом надежности). За се-
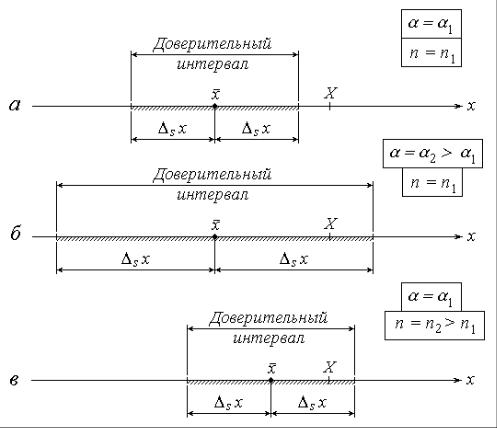
редину интервала принимается среднее значение, рассчитанное по формуле (5). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).
Рис.1. Зависимость доверительного интервала от числа измерений и доверительно вероятности
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка s x) зависит от того, насколько сильно отличаются отдельные измерения величины хi от среднего значения xср. «Разброс» результатов
6

измерений относительно среднего характеризуется среднеквадратичной ошибкой σ , которую находят по формуле
|
1 |
n |
||||
|
σ = |
∑( xi )2 |
, |
(6) |
||
|
n(n −1) |
|||||
|
i =1 |
где xi = xi − xср .
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:
Коэффициент пропорциональности tn,α называется коэффициентом Стьюдента, он зависит от числа опытов п и доверительной вероятности α.
На рис. 1, а, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего (вероятность «накрывания» значения Х более широким интервалом выше). Следовательно, величина tn,α должна быть тем больше, чем выше доверительная вероятность α .
С увеличением количества опытов среднее значение приближается к истинному, поэтому при той же вероятности α доверительный интервал можно взять более узким (см. рис. 1, а,в). Таким образом, с ростом п коэф-
|
фициент Стьюдента должен уменьшаться. |
Таблица значений коэффи- |
|||||||||||
|
циента Стьюдента в зависимости от п и α дана в следующей таблице. |
||||||||||||
|
Таблица1. Значения коэффициента Стьюдента tn,α |
||||||||||||
|
Ч и с л о и з м е р е н и й п |
||||||||||||
|
α |
||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
25 |
||
|
0,90 |
2,92 |
2,35 |
2,13 |
2,02 |
1,94 |
1,90 |
1,86 |
1,83 |
1,76 |
1,73 |
1,71 |
|
|
0,95 |
4,30 |
3,18 |
2,78 |
2,57 |
2,45 |
2,36 |
2,31 |
2,26 |
2,14 |
2,09 |
2,06 |
|
|
0,99 |
9,92 |
5,84 |
4,60 |
4,03 |
3,71 |
3,50 |
3,36 |
3,25 |
2,98 |
2,86 |
2,80 |
|
|
Следует отметить, что доверительная вероятность никак не связана с |
||||||||||||
|
точностью результата измерений. Величиной α задаются заранее, |
исходя |
из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение α принимается равным 0,90.
7

Расчет случайной погрешности измерения величины х проводится в следующем порядке:
1)вычисляется сумма измеренных значений, а затем – среднее значение величины xср по формуле (5),
2)для каждого i-го опыта рассчитываются разность между измерен-
ным и средним значениями xi = xi − xcp , а также квадрат этой разности (отклонения) ( хi)2 ,
3)находится сумма квадратов отклонений, а затем – среднеквадратичная ошибка σ по формуле (6),
4)по заданной доверительной вероятности α и числу проведенных опытов п из таблицы 1 выбирается соответствующее значение коэффици-
ента Стьюдента tn,α и определяется случайная погрешность s x по форму-
ле (7).
Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, столбцы которой заполняются по образцу табл.2.
Пример. Для определения ускорения движения тела измерялось время t прохождения им пути без начальной скорости. Результаты измерения времени приведены во втором столбце таблицы 2. Найдем их сумму, которую запишем под этим столбцом в ячейку « Σ = ». Затем рассчитаем среднее значение tср по формуле (3)
|
tср = |
8,11 |
≈ 2,03 (с). |
|||
|
4 |
|||||
|
Таблица 2. Измерение времени движения. |
|||||
|
Номер |
t, |
t, |
( t)2, |
||
|
опыта |
c |
c |
с2 |
||
|
1 |
2,07 |
0,04 |
0,0016 |
||
|
2 |
1,95 |
-0,08 |
0,0064 |
||
|
3 |
2,13 |
0,10 |
0,0100 |
||
|
4 |
1,96 |
-0,07 |
0,0049 |
||
|
∑= 8,11 |
∑= 0,0229 |
|
Вычитая из каждого значения ti |
среднее, найдем разности ti и зане- |
сем их в третий столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и
8

запишем ее во вторую ячейку « Σ = ». По формуле (4) определим среднеквадратичную погрешность:
|
σ = |
0, 0229 |
≈ 0, 0437(с) . |
|
4(4 − 1) |
Задавшись величиной доверительной вероятности α = 0,95, для числа опытов п = 4 из таблицы 1 выбираем значение коэффициента Стьюдента tn,α = 3,18, с помощью формулы (5) оценим случайную погрешность измерения времени
st = 3,18 0,0437 ≈ 0,14 (с) .
Определения полных ошибок прямых измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями s x и δ х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой x, которая, в зависимости от соотноше-
|
ния между величинами |
s x и δ х, находится следующим образом. |
|
Если одна из погрешностей более чем в три раза превышает другую |
|
|
(например, s x > 3δ х), |
то полная ошибка x принимается равной этой |
большей величине. Если же величины s x и δ х близки между собой, то полная ошибка вычисляется как
|
x = ( |
s |
x)2 |
+ (δx)2 . |
(8) |
На практике чаще всего за ошибку прямых измерений принимается приборная ошибка, если при нескольких измерениях получают одно и то же число. В том случае, если числа разные, то за окончательную ошибку принимают рассчитанную ошибку косвенных измерений, тем самым предполагая, что приборной ошибкой можно пренебречь.
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида
x = xcp ± x
с указанием значения доверительной вероятности α . Величины xcp и вы-
ражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2)Значение полной относительной погрешности
ε= x 100% ,
xcp
9

выраженное в процентах и округленное до десятых долей.
Полная ошибка x округляется до одной значащей цифры. После этого среднее значение хср округляется с той же точностью.
Способы определения ошибок косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин a,b,c,… Расчет проводится по определенной формуле, которую в общем виде можно записать как
В этом случае говорят, что величина и представляет собой результат
косвенного измерения (a,b,c,… являются результатами прямых измерений)
Абсолютная погрешность косвенного измерения и зависит от по-
грешностей прямых измерений a, b, c,… и от вида функции (9). В общем случае, величину u можно оценить по формуле вида
|
u = |
( |
∂u |
a)2 + ( |
∂u |
b)2 + ( |
∂u |
c)2 + … , |
(10) |
||||
|
∂a |
∂b |
∂c |
||||||||||
|
где |
∂u |
, |
∂u |
, |
∂u |
— частные производные функции u, по соответствую- |
||||||
|
∂a ∂b ∂c |
щей переменной.
На практике зависимость (9) чаще всего имеет вид степенной функции
|
u( x, y, z,…) = C a k bm cn …, |
(11) |
показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа, С – постоянный коэффициент. В этом случае абсолютная погрешность u оценивается по формуле
|
u = u |
cp |
(kε |
a |
)2 + (mε |
b |
)2 |
+ (nε |
c |
)2 + … , |
(12) |
|||
|
где ucp – среднее значение величины и, ε a |
= |
a |
, ε b = |
b |
, ε c = |
c |
– от- |
||||||
|
a |
b |
c |
носительные полные погрешности прямых измерений величин a,b,c,… При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, a и a) должны быть выражены в одних и тех же единицах.
10
Соседние файлы в папке новые методички
- #
- #
- #
Физика 7 класс
Лабораторная работа №5
Определение плотности вещества твердого тела
Матвеева Алина Анатольевна,
учитель физики МОУ СОШ 9 г. Надыма
Физика 7 класс
Лабораторная работа №5
Определение плотности вещества твердого тела
Цели урока:
Образовательные:
•введение
понятий: «абсолютная погрешность» и «относительная погрешность»;
•уточнение
понятий «прямое измерение» и «косвенное измерение»; •экспериментальное
определение плотности вещества твердого тела двумя способами: при первом
способе используется оборудование: твердое тело правильной геометрической
формы (параллелепипед), весы, линейка; во втором — твердое тело правильной
геометрической формы(параллелепипед), весы, мензурка.
Развивающие:
•развивать экспериментальные
умения и навыки при обращении с измерительными приборами: определение цены
деления прибора, снятие показаний с приборов, соблюдение техники безопасности;
• развивать
логическое мышление, умение применять теоретические знания на практике;
• сравнение
и анализ полученных результатов.
Воспитательные: воспитание коммуникабельности (работа в малой
группе), аккуратности, ответственности, активности, умение работать по
инструкции.
Здоровьесберегающие:
• создание положительной эмоциональной настроенности;
•использование здоровьесберегающих действий: смена видов деятельности,
физкультминутки для сохранения работоспособности и расширения функциональных
возможностей организма учащихся.
Технологии: проектная,
групповая,
дифференцированная.
Ключевые слова:
плотность, объем, масса, прямое измерение, косвенное измерение, абсолютная
погрешность, относительная погрешность, таблицы плотности твердых тел и
жидкостей.
ХОД УРОКА
Скажи мне, и я забуду.
Покажи мне, и я запомню.
Вовлеки меня , и я научусь.
Китайская мудрость
I.
Организация урока (2мин):
Учитель: Здравствуйте, дорогие ребята. И снова –физика. Послушайте анекдот.
Сын подходит к отцу и
спрашивает:
— Пап, а чем отличаются ум и хитрость?
— Ум позволяет решать сложные проблемы, а хитрость позволяет их обходить.
Сын задумался и снова спрашивает:
— А что полезней?
— Полезней всего — интеллект. Он позволяет выбирать, что лучше: решать,
обходить, или не лезть не в свое дело.(Анекдот). Это –анекдот. Но папа— прав. Человек
прежде всего должен думать о развитии своего интеллекта . Я считаю, что физика
лучше всех других наук помогает ему в этом. Сегодняшний урок не исключение.
На
прошлом уроке мы говорили о плотности тел. Сегодня продолжим эту тему, но
рассмотрим плотность с экспериментальной точки зрения. Когда -то умение
экспериментально определять плотность вещества, принесла славу Архимеду. У нас
в руках, пока еще, не корона и материал— не золото, но это экспериментальное
умение нам нужно в жизни очень часто. Подумайте когда и для чего? Итак, тема
сегодняшнего урока «Лабораторная работа №5 «Определение плотности вещества
твердого тела»». Исходя из темы, сформулируйте цели урока. (Ученики отвечают).
Мы на сегодняшнем уроке должны научиться
оценивать
погрешности прямых и косвенных измерений;
сравнивать
по значению относительной погрешности два способа косвенного определения плотности;
развивать
практические навыки работы с физическими приборами;
развивать
умения целеполаганию, анализа и оценки своей работы и работы одноклассников;
воспитывать
в себе аккуратность, толерантность, взаимопомощь.
Для достижения этих целей мы
должны решить следующие задачи:
•повторение основного материала по теме «Плотность»;
•изучить материал по теме «Теория погрешностей»;
•выполнить лабораторную работу;
•оценить свою деятельность на уроке.
Китайская мудрость гласит: Скажи мне, и я забуду.
Покажи мне, и я запомню.
Вовлеки меня , и я научусь.
Я желаю, чтобы все на уроке получили бесценный багаж знаний. А для
начала –блиц-опрос по определению знаний о плотности. За три верных ответа 1
балл, который будет учитываться при выставлении итоговой оценки за лабораторную
работу.
II. Актуализация опорных
знаний (5мин)
А. Блиц-опрос
1. Что называется плотностью?
2. Какова основная единица измерения плотности? В каких еще единицах
можно измерять плотность?
3. Какие физические величины необходимо знать для определения плотности
тела?
4. Можно ли прямым способом измерить плотность вещества твердого тела?
5-10. По презентации.
II. Выполнение
лабораторной работы
А. Подготовительная часть
Учитель:
Наша
страна нуждается в высококвалифицированных инженерно-технических работниках. Современный
инженер в любой области народного хозяйства должен уметь проводить измерения,
оценивать погрешность результатов измерений с учетом требуемой надежности.
Поэтому при измерениях большое внимание уделяется обработке результатов
измерений. Знакомство с основными методами расчета погрешностей – одна из
главных задач сегодняшнего урока.
Прочитайте
дополнительный материал к уроку «Теория погрешностей» (см. приложение 2) и
ответьте на контрольные вопросы в отчетных листах (см. приложение 1) (10мин),
но читаем медленно, есть такой тренинг по развитию интеллекта «Очень медленное
чтение», при этом необходимо запомнить весь предлагаемый материал при первом
чтении, перечитывать нельзя.
Физкультминутка (2мин):
Мы
очень сильно умственно напряглись при выполнении этого задания, давайте
расслабим немного мозг перед следующим штурмом, а для этого пропитаем весь
наш организм воздухом. (Открываем форточки) Встаем и шумно через нос, протяжно
вдыхаем воздух. Чувствуем, как все тело наполняется воздухом; раз, два, три.
А
теперь сделаем физическое усилие, для этого как можно сильнее нужно
взаимодействовать с землей (полом). Будем надавливать на землю все сильнее и
сильнее.
Садитесь.
Продолжим.
Итак, вначале урока мы решили, что мы будем определять плотность двумя
способами. Следовательно, сформулируйте цель при выполнении лабораторной работы.
( Учащиеся записывают в оценочных листах (см. приложение 1)
Способ 1: У вас имеются
твердое тело правильной
геометрической формы, линейка, … Какие еще приборы вам понадобятся? Возьмите их
из предложенного оборудования. Затем опишите порядок ваших действий на
отчетных листах. Если есть затруднения, загляните в инструкцию по выполнению
лабораторной работы №5 (3 мин). Приступаем к измерениям, обращаю внимание на
правила техники безопасности. А также ваше внимание обращаю ваше внимание на
диагностическую карту по оцениванию лабораторной работы( см. приложение 3) (10
мин).
Переходим ко второму способу. У вас имеются твердое тело правильной
геометрической формы, измерительный цилиндр, …. Какие действия вы будете
выполнять в этом случае? Запишите порядок действий на отчетных листах. Далее
учащиеся проводят измерения, выполняют расчеты, заполняют таблицу.(10мин)
Учитель: Чтобы ощутить себя инженером, необходимо ответить на следующие
контрольные вопросы (3 мин).
Контрольные вопросы:
1. Какой
метод измерения плотности точнее, почему?
2. По
внешнему виду определите, из чего изготовлен цилиндр и сравните полученные
значения с табличными значениями. Совпали ли результаты? Если нет, то почему?
3. Сформулируйте
и запишите вывод о проделанной работе.
Домашнее задание ( на карточках) (см. приложение 4)
Рефлексия деятельности (отвечают письменно на отчетных листах)
Оцените свои
достижения на этом уроке:
n
Все ли у вас получилось?
n
Довольны ли вы своими
результатами?
n
Довелось ли вам в полной
мере реализовать свои возможности, применить полученные знания?
n
Сделайте комплимент себе,
соседу по парте, всему классу …
n
Мне кажется, я заслужил
(а) отметку …
Учитель: Решать загадки можно вечно.
Вселенная ведь
бесконечна.
Спасибо всем вам
за урок,
А главное, чтоб
был он впрок!
Приложение
1
Отчетный лист
по лабораторной работе №5
Определение плотности вещества твёрдого тела
Фамилия, имя, класс
Лабораторная
работа №5 _________
/дата/
Определение плотности вещества твёрдого тела.
Цель работы:
______________________________________________________________________________________________________________________________________________________________________________________________________
Оборудование:1способ: металлический брусок, линейка,—————————————————————-___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2способ: металлический брусок, мензурка—————————————————————_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Правила
техники безопасности.
- Будьте осторожны при работе со стеклянной посудой. Помните, что
стекло хрупкий и опасный материал, легко трескается при ударе. - Будьте внимательны при работе с весами, не теряйте гирьки.
Установите весы на середине стола. - Будьте аккуратны при работе с водой.
Подготовительная часть
Прочитайте информацию «О погрешностях» и
ответьте письменно на вопросы:
- Что значит измерить физическую величину?————————————————————-—
- Почему возникают погрешности измерений?—————————————————————————————————————————————————————————
————————————————————————————————————
- Чему равна абсолютная погрешность прямого
измерения?
- Как определяются абсолютная и относительная
погрешности измерения плотности?
- Сформулируйте правила округления результата
измерения и погрешностей.
Основная часть
А. Опишите порядок ваших действий, при
определении плотности вещества твердого тела первым способом
1._________________________________________________________________
2._________________________________________________________________
3._________________________________________________________________
4._________________________________________________________________
5.____________________________________________________________
Выполнение работы и расчеты:
|
Название вещества |
Масса тела mист,г |
Объем тела Vист, см3 |
Плотность вещества ρист, г/ см3 |
Относительная погрешность измерения ɛ,% |
Все записи выполняйте здесь:
Б. Опишите порядок ваших действий, при
определении плотности вещества твердого тела вторым способом
1._________________________________________________________________
2._________________________________________________________________
3._________________________________________________________________
4._________________________________________________________________
5._________________________________________________________________
|
Название вещества |
Масса тела mист,г |
Объем тела Vист, см3 |
Плотность вещества ρист, г/ см3 |
Относительная погрешность измерения ɛ,% |
Все записи выполняйте здесь:
Контрольные вопросы:
4. Какой
способ измерения плотности точнее, почему?
______________________________________________________________________________________________________________________________________________
5. По
внешнему виду определите из чего изготовлен цилиндр и сравните полученные
значения с табличными значениями. Совпали ли результаты? Если нет, то почему?
______________________________________________________________________________________________________________________________________________
6. Сформулируйте
и запишите вывод о выполненной работе.
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Рефлексия
деятельности:
Оцените свои достижения на этом
уроке:
•Что нового узнали на уроке?
• Довольны ли вы своими
результатами?
• Довелось ли вам в полной мере
реализовать свои возможности, применить полученные знания?
• Я заслужил(а) оценку ….
Фамилия, имя, класс Подпись
Приложение
2
Теория погрешностей
Измерение
физических величин
В
основе точных естественных наук лежат измерения. При измерениях значения
величин выражаются в виде чисел, которые указывают во сколько раз измеренная
величина больше или меньше другой величины, значение которой принято за
единицу.
При
измерениях неизбежно возникают погрешности. Необходимо владеть методами,
применяемыми при обработке результатов, полученных при измерениях. Это позволит
научиться получать из совокупности измерений наиболее близкие к истине результаты,
вовремя заметить несоответствия и ошибки, разумно организовать сами измерения и
правильно оценить точность полученных значений.
Если
измерение заключается в сравнении данной величины с другой, однородной
величиной, принятой за единицу, то измерение в этом случае называется прямым.
Прямые
(непосредственные) измерения
– это такие измерения, при которых мы получаем численное значение измеряемой
величины либо прямым сравнением ее с мерой (эталоном), либо с помощью приборов,
градуированных в единицах измеряемой величины.
Однако
далеко не всегда такое сравнение производится непосредственно. В большинстве
случаев измеряется не сама интересующая нас величина, а другие величины,
связанные с нею теми или иными соотношениями и закономерностями. В этом случае
для измерения необходимой величины приходится предварительно измерить несколько
других величин, по значению которых вычислением определяется значение искомой
величины. Такое измерение называется косвенным.
Косвенные
измерения
состоят из непосредственных измерений одной или нескольких величин, связанных с
определяемой величиной количественной зависимостью, и вычисления по этим данным
определяемой величины.
Современный
инженер должен уметь оценивать погрешность результатов измерений с учетом
требуемой надежности. Поэтому большое внимание уделяется обработке результатов
измерений. Знакомство с основными методами расчета погрешностей – одна из
главных задач при выполнении лабораторных работ.
Почему возникают
погрешности?
Источниками погрешностей при
измерениях являются:
•
неточность самих измерительных приборов;
•
способ снятия показаний с прибора;
•
непостоянство измеряемой величины.
Классификация
погрешностей
Значение
погрешности измерения
некоторой величины принято характеризовать:
1.
Абсолютной погрешностью –
разностью между найденным на опыте (измеренным) и
истинным значением некоторой величины
. (1)
Абсолютная
погрешность показывает, на сколько мы ошибаемся при измерении некоторой
величины Х.
2.
Относительной погрешностью
равной отношению абсолютной погрешности к истинному значению измеряемой
величины Х
100% (2)
Относительная
погрешность показывает, на какую долю от истинного значения величины Х мы
ошибаемся.
Качество результатов измерений какой-то
величины характеризуется относительной
погрешностью . Величина
может
быть выражена в процентах.
При
практических измерениях погрешности не вычисляются, а оцениваются. При оценках
учитываются условия проведения эксперимента, точность методики, качество
приборов и ряд других факторов. Наша задача: научиться строить методику
эксперимента, правильно использовать полученные на опыте данные для нахождения
истинных значений измеряемых величин (или достаточно близких к ним), разумно
оценивать погрешности измерений.
Говоря
о погрешностях измерений, следует, прежде всего, упомянуть о грубых
погрешностях (промахах), возникающих вследствие недосмотра экспериментатора
или неисправности аппаратуры. Грубых ошибок следует избегать. Если установлено,
что они произошли, соответствующие измерения нужно отбрасывать.
Не
связанные с грубыми ошибками погрешности опыта делятся на случайные и
систематические. Но о них в следующий раз.
Расчет
погрешностей прямых измерений
В
наших работах будем считать, что
|
Номинальное |
Пределы |
|
1г |
± 4мг |
|
2г |
± 6мг |
|
5г |
± 8мг |
|
10г |
± 12мг |
|
20г |
± 20мг |
|
50г |
± 30мг |
|
100г |
± 40мг |
·
Абсолютная погрешность
цифровых приборов равна единице минимального разряда.
·
Для всех остальных
приборов абсолютная погрешность принимается равной половине цены деления.
·
Для весов абсолютная погрешность
складывается из погрешностей гирь, использованных при взвешивании данного тела
(см. таб.)
Для простоты расчетов, будем считать, что полная
абсолютная погрешность раавна инструментальной (приборной) погрешности.
Округляется погрешность и результат. Поскольку результат
измерений представляется в виде интервала значений, величину которого
определяет полная абсолютная погрешность, важное значение имеет правильное
округление результата и погрешности.
Округление
начинают с абсолютной погрешности!!! Число значащих цифр (все числа, кроме нулей слева), которое оставляют
в значении погрешности, вообще говоря, зависит от коэффициента надежности и
числа измерений. Однако даже для очень точных измерений не оставляют более двух
значащих цифр. Бóльшее число цифр не имеет смысла, так как определение
погрешности само имеет свою погрешность. В
нашем практикуме сравнительно небольшой коэффициент надежности и малое число измерений. Поэтому при
округлении (с избытком) полной абсолютной погрешности оставляют одну значащую
цифру.
Разряд
значащей цифры абсолоютной погрешности определяет разряд первой сомнительной
цифры в значении результата. Следовательно, само значение результата
нужно округлять (с поправкой) до той значащей цифры, разряд которой совпадает с
разрядом значащей цифры погрешности. Сформулированное правило следует
применять и в тех случаях, когда некоторые из цифр являются нулями.
Затем
вычисляется относительная погрешность .
100%
При округлении относительной погрешности
достаточно оставить две значащие цифры.
результат
серии измерений некоторой физической величины представляют в виде интервала
значений с указанием вероятности попадания истинного значения в данный
интервал, то есть результат
необходимо записать в виде:
;
;
.
Здесь
– полная, округленная до первой значащей
цифры, абсолютная погрешность и – округленное с учетом
уже округленной погрешности среднее значение измеряемой величины. При записи
результата измерений обязательно нужно указать единицу измерения величины.
Итак,
округление абсолютной погрешности производится до первой значащей цифры в
сторону увеличения (с избытком). Среднее значение измеряемой величины
округляется с поправкой до той значащей цифры, разряд которой совпадает с
разрядом значащей цифры погрешности. При округлении относительной погрешности
оставляем две значащие цифры.
Расчет
погрешностей косвенных измерений
Расчет
погрешности косвенных измерений зависит от вида формулы. Поэтому каждый раз
формула для вычисления погрешности будет выглядеть по разному.
Примеры.
1.
Объем
параллелепипеда определяется по формуле:
.
Тогда
абсолютную погрешность определения объема параллелепипеда оцениваем по
формуле
, считая, что абсолютные погрешности
измерений длины a, ширины b, высоты h равны инструментальной
погрешности линейки (половине цены деления линейки). Результат запишется в
виде: Vист= Vизм± ∆V. При
этом относительная погрешность измерения объема равна .
2.
Плотность тела определяется
по формуле ρ=m/V. Абсолютная погрешность измерения плотности
оценивается по формуле . Результат измерения запишется в виде ρист=ρизм±
∆ρ. При этом относительная погрешность измерения плотности∙100%.
Вопросы
и задачи по теории погрешностей:
1. Что
значит измерить физическую величину?
2. Почему
возникают погрешности измерений?
3. Чему
равна абсолютная погрешность прямого измерения?
4. Как
определяются абсолютная и относительная погрешности измерения плотности?
5. Сформулируйте
правила округлений результата и погрешности.
Приложение
3
Инструкция по выполнению лабораторной работы №5
«Определение плотности вещества твердого тела»
Цель работы: научиться определять плотность твердого тела двумя способами: 1) с
помощью весов и линейки и 2) с помощью весов и мензурки с учетом абсолютной и относительной
погрешности;
сравнить полученные значения с табличными
значениями.
Первый способ:
Приборы: рычажные весы, линейка, твердое тело правильной геометрической
формы.
Указание к работе
|
Номинальное значение набора гирь по механике |
Пределы допускаемой основной погрешности |
|
|
± 4мг |
|
2г |
± 6мг |
|
5г |
± 8мг |
|
10г |
± 12мг |
|
20г |
± 20мг |
|
50г |
± 30мг |
|
100г |
± 40мг |
1. Измерить массу тел на весах. Результаты записать в таблицу с учетом
абсолютной погрешности: mист=mизм ± ∆m.
Для определения абсолютной погрешности массы воспользуйтесь
предложенной таблицей.
2. Измерить объем тел с помощью линейки, используя формулу: V=a∙b∙c.
Рассчитать абсолютную погрешность измерения объема по формуле , считая, что абсолютная погрешность
измерения длины a, ширины b, высоты с
равны инструментальной погрешности линейки (половине цены деления линейки).
Результат запишите в виде: Vист= Vизм± ∆V
3. Рассчитать плотность тела ρизм по формуле ρизм=mизм/Vизм. Рассчитать абсолютную погрешность измерения
плотности по формуле . Результат измерения
записать в виде ρист=ρизм± ∆ρ.
4. Рассчитайте относительную погрешность измерения ∙100%
5. Заполнить таблицу измерений
|
Название вещества |
Масса тела mист,г |
Объем тела Vист, см3 |
Плотность |
Относительная |
Примечание: Не забудьте округлить результаты и погрешности!!!
Второй способ:
1. Значение
массы у вас уже известны.
2. Определение
объема тела при помощи мензурки:
а) Определите цену деления измерительного цилиндра
б) Налейте столько воды в цилиндр ,чтобы предложенное тело
могло полностью в нее погрузиться. Запишите объем V1 с учетом
абсолютной погрешности измерения ∆V1.
в) Погрузите тело в воду. Зафиксируйте объем V2 с учетом
абсолютной погрешности измерения ∆V2.
г)Рассчитайте объем тела Vизм= V2— V1. Определите
абсолютную погрешность измерения объема по формуле ∆V=∆V1+∆V2
д)Запишите значение объема в виде Vист= Vизм± ∆V
3. Рассчитать плотность тела ρизм по формуле ρизм=mизм/Vизм. Рассчитать погрешность измерения плотности по
формуле . Результат измерения записать в виде ρист=ρизм±
∆ρ.
4. Рассчитайте относительную погрешность измерения ∙100%
5. Заполнить таблицу измерений
|
Название вещества |
Масса тела mист,г |
Объем тела Vист, см3 |
Плотность |
Относительная |
Приложение 4
Домашнее
задание по теме «Плотность тел»
1. Когда мы, собираясь на каникулы в лагерь, набиваем всё новыми и
новыми вещами и без того уже пухлый чемодан, какие из физических величин мы
изменяем – m, V, r ?

физических величин, характеризующих шарик, изменились – m, V, r ?
3. В воздушный
шарик накачали порцию воздуха. При этом масса возросла в 4 раза, а объём –
вдвое. Во сколько раз возросла плотность воздуха в шарике?
4. Который из
рисунков позволит подсчитать, во сколько раз плотность воды больше плотности
спирта?
5. Найдите ошибку
в рассуждении: плотность 1 м3 керосина 800 кг/м3. Тогда плотность 2 м3 керосина будет 1600 кг/м3.
6. Для измерения
плотности пластилина взяли его кусок массой 100 г. Как изменятся результаты
измерений, если будет взят кусок массой 200 г?
7. Имеются 3 кг
мёда и 3 кг молока. Сравните их объёмы.
8. Чтобы заполнить
банку доверху, потребовалось 4,1 кг меда. Вычислите объём банки.
9. Плотность
золота 19 г/см3. Верно ли, что золотой кубик с объёмом более 10 см3 будет иметь массу
более 100 г?
10. В кастрюлю
объёмом 7,3 л положили 5,7 кг картофеля и доверху залили водой. Ее понадобилось
2,3 л. Найдите плотность картофелины.
Занимательная
задача
Мыло и мыши. Лилипут
отправился мыть руки к ручью, но забыл дома прямоугольный брусочек мыла. Его
длина 0,3 см, ширина составляет 2/3 длины, а высота 1/3 от длины. Брусочек
нашли мыши и половину сгрызли. а) Какова масса оставшегося мыла, если плотность
мыла 1500 кг/м3? б) Сколько процентов мыла мыши измельчили своими острыми зубками?
Экспериментальная
задача
В глубокой древности знаменитый Архимед
смог определить, из чистого ли золота сделана царская корона. Попробуйте
сделать то же самое, изготовив модель короны из пластилина. Оборудование:
модель короны из пластилина, мерный сосуд, весы.
Желаю удачи
Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».
Сначала надо вспомнить основные понятия теории погрешности.
Абсолютная погрешность физической величины ΔА — это
разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:
ΔА = А — Апр .
Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной
погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.
Относительная погрешность измерения
εА равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из
множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.
Зная относительную погрешность, найти абсолютную погрешность измерений можно так:
ΔА = εA· А.
«Правило ничтожных погрешностей»
при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.
Запись результата с указанием погрешности.
Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.
Пример:

Результат записывается в виде:
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм.
При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!
Пример:

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения
Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?
Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за
топливо?

