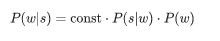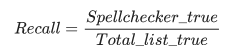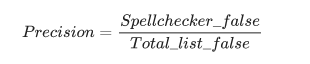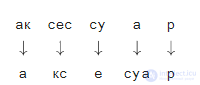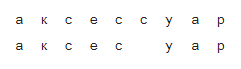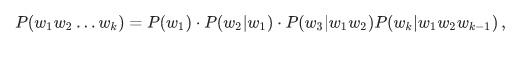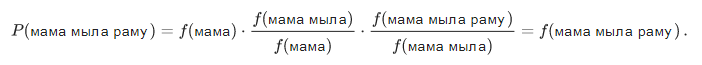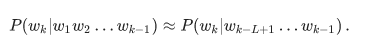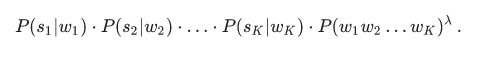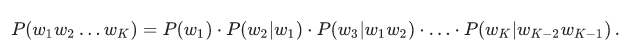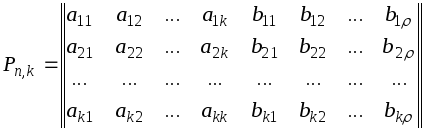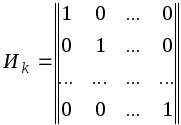Привет, Вы узнаете про алгоритмы исправления опечаток, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
алгоритмы исправления опечаток, исправление опечаток с учётом контекста, исправление опечаток без учёта контекста, модель ошибок, модель языка
, настоятельно рекомендую прочитать все из категории Обработка естественного языка.
Постановка задачи
Итак, нам пришел опечатанный запрос и его надо исправить. Обычно математически задача ставится таким образом:
- дано слово s, переданное нам с ошибками;
- есть словарь Σ правильных слов;
- для всех слов w в словаре есть условные вероятности P(w|s) того, что имелось в виду слово w, при условии, что получили мы слово s;
- нужно найти слово w из словаря с максимальной вероятностью P(w|s).
Эта постановка — самая элементарная — предполагает, что если нам пришел запрос из нескольких слов, то мы исправляем каждое слово по отдельности. В реальности, конечно, мы захотим исправлять всю фразу целиком, учитывая сочетаемость соседних слов; об этом я расскажу ниже, в разделе “Как исправлять фразы”.
Неясных моментов здесь два — где взять словарь и как посчитать P(w|s). Первый вопрос считается простым. В 1990 году словарь собирали из базы утилиты spell и доступных в электронном виде словарей; в 2009 году в Google поступили проще и просто взяли топ самых популярных слов в Интернете (вместе с популярными ошибочными написаниями). Этот подход взял и я для построения своего опечаточника.
Второй вопрос сложнее. Хотя бы потому, что его решение обычно начинается с применения формулы Байеса!
Теперь вместо исходной непонятной вероятности нам нужно оценить две новые, чуть более понятные: P(s|w) — вероятность того, что при наборе слова w можно опечататься и получить s, и P(w) — в принципе вероятность использования пользователем слова w.
Как оценить P(s|w)? Очевидно, что пользователь с большей вероятностью путает А с О, чем Ъ с Ы. А если мы исправляем текст, распознанный с отсканированного документа, то велика вероятность путаницы между rn и m. Так или иначе, нам нужна какая-то модель, описывающая ошибки и их вероятности.
Такая модель называется noisy channel model (модель зашумленного канала; в нашем случае зашумленный канал начинается где-то в центре Брока пользователя и заканчивается по другую сторону его клавиатуры) или более коротко error model —
модель ошибок . Эта модель, которой ниже посвящен отдельный раздел, будет ответственна за учет как орфографических ошибок, так и, собственно, опечаток.
Оценить вероятность использования слова — P(w) — можно по-разному. Самый простой вариант — взять за нее частоту, с которой слово встречается в некотором большом корпусе текстов. Для нашего опечаточника, учитывающего контекст фразы, потребуется, конечно, что-то более сложное — еще одна модель. Эта модель называется language model,
модель языка .
Системы автоматической коррекции орфографии
Мы предоставляем два типа конвейеров для исправления орфографии: levenshtein_corrector использует простое расстояние Дамерау-Левенштейна для поиска кандидатов на исправление, а brillmoore использует для него статистическую модель ошибок. В обоих случаях кандидаты на исправление выбираются на основе контекста с помощью языковой модели кенлм .
Сравнение автоматической коррекции орфографии для русского языка с использованием разлиных алгоритмов:
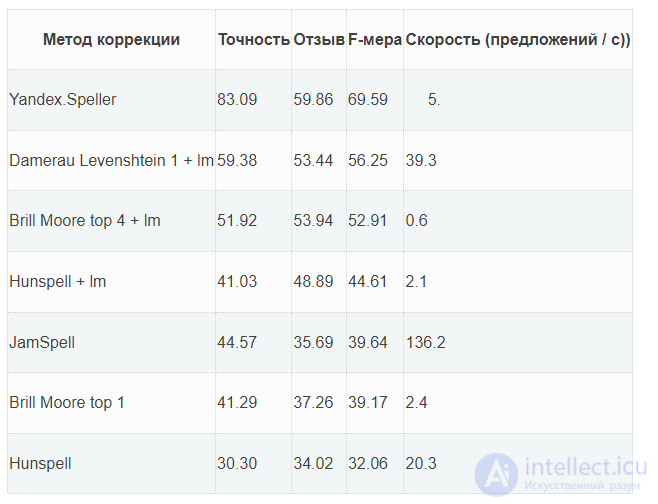
Алгоритмы для исправления опечаток без уета контекста
У каждого пользователя когда-либо были опечатки при написании поисковых запросов. Отсутствие механизмов, которые исправляют опечатки, приводит к выдаче нерелевантных результатов, а то и вовсе к их отсутствию. Поэтому, чтобы поисковая система была более ориентированной на пользователей, в нее встраивают механизмы исправления ошибок.
Задача исправления опечаток, на первый взгляд, кажется довольно несложной. Но если отталкиваться от разнообразия ошибок, реализация решения может оказаться трудной. В целом, исправление опечаток разделяется на контекстно-независимое и контекстно-зависимое (где учитывается словарное окружение). В первом случае ошибки исправляются для каждого слова в отдельности, во втором – с учетом контекста (например, для фразы «она пошле домой» в контекстно-независимом случае исправление происходит для каждого слова в отдельности, где мы можем получить «она пошел домой», а во втором случае правильное исправление выдаст «она пошла домой»).
В поисковых запросах русскоязычного пользователя можно выделить четыре основные группы ошибок только для контекстно-независимого исправления :
1) ошибки в самих словах (пмрвет → привет), к этой категории относятся всевозможные пропуски, вставки и перестановки букв – 63,7%,
2) слитно-раздельное написание слов – 16,9%,
3) искаженная раскладка (ghbdtn → привет) – 9,7 %,
4) транслитерация (privet → привет) – 1,3%,
5) смешанные ошибки – 8,3%.
Пользователи совершают опечатки приблизительно в 10-15% случаях. При этом 83,6% запросов имеют одну ошибку, 11,7% –две, 4,8% – более трех. Контекст важен в 26% случаев.
Эта статистика была составлена на основе случайной выборки из дневного лога Яндекса в далеком 2013 году на основе 10000 запросов. В открытом доступе есть гораздо более ранняя презентация от Яндекса за 2008 год, где показано похожее распределение статистики . Отсюда можно сделать вывод, что распределение разновидностей ошибок для поисковых запросов, в среднем, с течением времени не изменяется.
В общем виде механизм исправления опечаток основывается на двух моделях: модель ошибок и языковая модель. Причем для контекстно-независимого исправления используется только модель ошибок, а в контекстно-зависимом – сразу две. В качестве модели ошибок обычно выступает либо редакционное расстояние (расстояние Левенштейна, Дамерау-Левенштейна, также сюда могут добавляться различные весовые коэффициенты, методы на подобие Soundex и т. д. – в таком случае расстояние называется взвешенным), либо модель Бриля-Мура, которая работает на вероятностях переходов одной строки в другую. Бриль и Мур позиционируют свою модель как более совершенную, однако на одном из последних соревнований SpellRuEval подход Дамерау-Левенштейна показал результат лучше , несмотря на тот факт, что расстояние Дамерау-Левенштейна (уточнение – невзвешенное) не использует априори информацию об опечаточной статистике. Это наблюдение особо показательно в том случае, если для разных реализаций автокорректоров в библиотеке DeepPavlov использовались одинаковые обучающие тексты.
Очевидно, что возможность контекстно-зависимого исправления усложняет построение автокорректора, т. к. дополнительно к модели ошибок добавляется необходимость в языковой модели. Но если обратить внимание на статистику опечаток, то ¾ всех неверно написанных поисковых запросов можно исправлять без контекста. Это говорит о том, что польза как минимум от контекстно-независимого автокорректора может быть весьма существенной.
Также контекстно-зависимое исправление для корректировки опечаток в запросах очень требовательно по ресурсам. Например, в одном из выступлений Яндекса список пар для исправления опечаток (биграмм) слов отличался в 10 раз по сравнению с количеством слов (униграмм), что тогда говорить про триграммы? Очевидно, что это существенно зависит от вариативности запросов. Немного странно выглядит, когда автокорректор занимает половину памяти от предлагаемого продукта компании, целевое назначение которого не ориентировано на решение проблемы правописания. Так что вопрос внедрения контекстно-зависимого исправления в поисковых системах программных продуктов может быть весьма спорным.
На первый взгляд, складывается впечатление, что существует много готовых решений под любой язык программирования, которые можно использовать без особого погружения в подробности работы алгоритмов, в том числе – в коммерческих системах. Но на практике продолжается разработка своих решений. Например, сравнительно недавно в Joom было сделано собственное решение по исправлению опечаток с использованием языковых моделей для поисковых запросов . Действительно ли ситуация непроста с доступностью готовых решений? С этой целью был сделан, по возможности, широкий обзор существующих решений. Перед тем как приступить к обзору, определимся с тем, как проверяется качество работы автокорректора.
Проверка качества работы
Вопрос проверки качества работы автокорректора весьма неоднозначен. Один из простых подходов проверки — через точность (Precision) и полноту (Recall). В соответствии со стандартом ISO, точность и полнота дополняются правильностью (на англ. «corectness»).
Полнота (Recall) рассчитывается следующим образом: список из правильных слов подается автокорректору (Total_list_true), и, количество слов, которое автокорректор считает правильными (Spellchecker_true), разделенное на общее количество правильных слов (Total_list_true), будет считаться полнотой.
Для определения точности (Precision) на вход автокорректора подается список из неправильных слов (Total_list_false), и, количество слов, которое автокорректор считает неправильным (Spell_checker_false), разделенное на общее количество неправильных слов (Total_list_false), определяют как точность.
Насколько вообще эти метрики информативны и как могут быть полезны, каждый определяет самостоятельно. Ведь, фактически, суть данной проверки сводится к тому, что проверяется вхождение слова в обучающий словарь. Более наглядной метрикой можно считать correctness, согласно которой автокорректор для каждого слова из тестового множества неправильных слов формирует список кандидатов-замен, на которые можно исправить это неправильное слово (следует иметь в виду, что здесь могут оказаться слова, которые не содержатся в обучающем словаре). Допустим, размер такого списка кандидатов-замен равен 5. Исходя из того, что размер списка равен 5, будет сформировано 6 групп, в одну из которых мы будем помещать наше каждое исходное неправильное слово по следующему принципу: в 1-ую группу — если в списке кандидатов-замен предполагаемое нами правильное слово стоит 1-ым, во 2-ую если стоит 2-ым и т. д., а в последнюю группу — если предполагаемого правильного слова в списке кандидатов-замен не оказалось. Разумеется, чем больше слов попало в 1-ую группу и чем меньше в 6-ую, тем лучше работает автокорректор.
Рассмотренного выше подхода придерживались авторы в статье , в которой сравнивались контекстно-независимые автокорректоры с уклоном на стандарт ISO. Там же приведены ссылки на другие способы оценки качества.
С одной стороны, такой подход не базируется на опечаточной статистике, в основу которого может быть положена модель ошибок Бриля-Мура , либо модель ошибок взвешенного расстояния Дамерау-Левенштейна.
Для проверки качества работы контекстно-независимого автокорректора был создан собственный генератор опечаток, который генерировал опечатки неверной раскладки и орфографические опечатки исходя из статистики по опечаткам, представленной Яндексом. Для орфографических опечаток генерировались произвольные вставки, замены, удаления, перестановки, а количество ошибок так же варьировалось в соответствии с этой статистикой. Для ошибок искаженной раскладки, правильное слово посимвольно изменялось целиком в соответствии с таблицей перевода символов.
Далее была проведена серия экспериментов для всего списка слов обучающего словаря (слова обучающего словаря исправлялись на неправильные в соответствии с вероятностью возникновения той или иной опечатки). В среднем, автокорректор исправляет слова верно в 75% случаев. Вне всякого сомнения, это количество будет сокращаться при пополнении обучающего словаря близкими по редакционному расстоянию словами, большом многообразии словоформ. Эта проблема может решаться за счет дополнения языковыми моделями, но здесь следует учитывать, что количество требуемых ресурсов ощутимо возрастет.
Модель ошибок
Первые модели ошибок считали P(s|w), подсчитывая вероятности элементарных замен в обучающей выборке: сколько раз вместо Е писали И, сколько раз вместо ТЬ писали Т, вместо Т — ТЬ и так далее . Получалась модель с небольшим числом параметров, способная выучить какие-то локальные эффекты (например, что люди часто путают Е и И).
В наших изысканиях мы остановились на более развитой модели ошибок, предложенной в 2000 году Бриллом и Муром и многократно использованной впоследствии (например, специалистами Google ). Представим, что пользователи мыслят не отдельными символами (спутать Е и И, нажать К вместо У, пропустить мягкий знак), а могут изменять произвольные куски слова на любые другие — например, заменять ТСЯ на ТЬСЯ, У на К, ЩА на ЩЯ, СС на С и так далее. Вероятность того, что пользователь опечатался и вместо ТСЯ написал ТЬСЯ, обозначим P(тся→ться) — это параметр нашей модели. Если для всех возможных фрагментов α,β мы можем посчитать P(α→β), то искомую вероятность P(s|w) набора слова s при попытке набрать слово w в модели Брилла и Мура можно получить следующим образом: разобьем всеми возможными способами слова w и s на более короткие фрагменты так, чтобы фрагментов в двух словах было одинаковое количество. Для каждого разбиения посчитаем произведение вероятностей всех фрагментов w превратиться в соответствующие фрагменты s. Максимум по всем таким разбиениям и примем за значение величины P(s|w):
Давайте посмотрим на пример разбиения, возникающего при вычислении вероятности напечатать «аксесуар» вместо «аксессуар»:
Как вы наверняка заметили, это пример не очень удачного разбиения: видно, что части слов легли друг под другом не так удачно, как могли бы. Если величины P(ак→а) и P(р→р) еще не так плохи, то P(су→е) и P(а→суа), скорее всего, сделают итоговый «счет» этого разбиения совсем печальным. Более удачное разбиение выглядит как-то так:
Здесь все сразу стало на свои места, и видно, что итоговая вероятность будет определяться преимущественно величиной 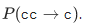
Как вычислить P(s|w)
Несмотря на то, что возможных разбиений для двух слов имеется порядка 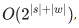
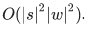
Мы заведем прямоугольную таблицу, строки которой будут соответствовать буквам правильного слова, а столбцы — опечатанного. В ячейке на пересечении строки i и столбца j к концу алгоритма будет лежать в точности вероятность получить s[:j] при попытке напечатать w[:i]. Для того, чтобы ее вычислить, достаточно вычислить значения всех ячеек в предыдущих строках и столбцах и пробежаться по ним, домножая на соответствующие P(α→β). Например, если у нас заполнена таблица
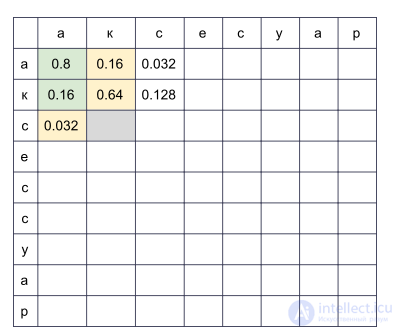
, то для заполнения ячейки в четвертой строке и третьем столбце (серая) нужно взять максимум из величин 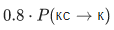
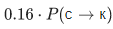
Сложность этого алгоритма, как я уже упомянул выше, составляет 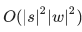
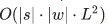
Как максимизировать P(s|w)
Мы научились находить P(s|w) за полиномиальное время — это хорошо. Но нам нужно научиться быстро находить наилучшие слова во всем словаре. Причем наилучшие не по P(s|w), а по P(w|s)! На деле нам достаточно получить какой-то разумный топ (например, лучшие 20) слов по P(s|w), который мы потом отправим в модель языка для выбора наиболее подходящих исправлений (об этом ниже).
Чтобы научиться быстро проходить по всему словарю, заметим, что таблица, представленная выше, будет иметь много общего для двух слов с общими префиксами. Действительно, если мы, исправляя слово «аксесуар», попробуем заполнить ее для двух словарных слов «аксессуар» и «аксессуары», мы заметим, что первые девять строк в них вообще не отличаются! Если мы сможем организовать проход по словарю так, что у двух последующих слов будут достаточно длинные общие префиксы, мы сможем круто сэкономить вычисления.
И мы сможем. Давайте возьмем словарные слова и составим из них trie. Идя по нему поиском в глубину, мы получим желаемое свойство: большинство шагов — это шаги от узла к его потомку, когда у таблицы достаточно дозаполнить несколько последних строк.
Этот алгоритм, при некоторых дополнительных оптимизациях, позволяет нам перебирать словарь типичного европейского языка в 50-100 тысяч слов в пределах сотни миллисекунд . А кэширование результатов сделает процесс еще быстрее.
Как получить P(α→β)
Вычисление P(α→β) для всех рассматриваемых фрагментов — самая интересная и нетривиальная часть построения модели ошибок. Именно от этих величин будет зависеть ее качество.
Подход, использованный в [2, 4], сравнительно прост. Давайте найдем много пар (si,wi), где wi — правильное слово из словаря, а si — его опечатанный вариант. (Как именно их находить — чуть ниже.) Теперь нужно извлечь из этих пар вероятности конкретных опечаток (замен одних фрагментов на другие).
Для каждой пары возьмем составляющие ее w и s и построим соответствие между их буквами, минимизирующее расстояние Левенштейна:
Теперь мы сразу видим замены: а → а, е → и, с → с, с → пустая строка и так далее . Об этом говорит сайт https://intellect.icu . Также мы видим замены двух и более символов: ак → ак, се → си, ес → ис, сс → с, сес → сис, есс → ис и прочая, и прочая. Все эти замены необходимо посчитать, причем каждую столько раз, сколько слово s встречается в корпусе (если мы брали слова из корпуса, что очень вероятно).
После прохода по всем парам (si,wi) за вероятность P(α→β) принимается количество замен α → β, встретившихся в наших парах (с учетом встречаемости соответствующих слов), деленное на количество повторений фрагмента α.
Как найти пары (si,wi)? В предлагается такой подход. Возьмем большой корпус сгенерированного пользователями контента (UGC). В случае Google это были просто тексты сотен миллионов веб-страниц; в нашем — миллионы пользовательских поисковых запросов и отзывов. Предполагается, что обычно правильное слово встречается в корпусе чаще, чем любой из ошибочных вариантов. Так вот, давайте для каждого слова находить близкие к нему по Левенштейну слова из корпуса, которые значительно менее популярны (например, в десять раз). Популярное возьмем за w, менее популярное — за s. Так мы получим пусть и шумный, но зато достаточно большой набор пар, на котором можно будет провести обучение.
Этот алгоритм подбора пар оставляет большое пространство для улучшений. В предлагается только фильтр по встречаемости (w в десять раз популярнее, чем s), но авторы этой статьи пытаются делать опечаточник, не используя какие-либо априорные знания о языке. Если мы рассматриваем только русский язык, мы можем, например, взять набор словарей русских словоформ и оставлять только пары со словом w, найденном в словаре (не лучшая идея, потому что в словаре, скорее всего, не будет специфичной для сервиса лексики) или, наоборот, отбрасывать пары со словом s, найденном в словаре (то есть почти гарантированно не являющимся опечатанным).
Чтобы повысить качество получаемых пар, я написал несложную функцию, определяющую, используют ли пользователи два слова как синонимы. Логика простая: если слова w и s часто встречаются в окружении одних и тех же слов, то они, вероятно, синонимы — что в свете их близости по Левенштейну значит, что менее популярное слово с большой вероятностью является ошибочной версией более популярного. Для этих расчетов я использовал построенную для модели языка ниже статистику встречаемости триграмм (фраз из трех слов).
Модель языка
Итак, теперь для заданного словарного слова w нам нужно вычислить P(w) — вероятность его использования пользователем. Простейшее решение — взять встречаемость слова в каком-то большом корпусе. Вообще, наверное, любая модель языка начинается с собирания большого корпуса текстов и подсчета встречаемости слов в нем. Но ограничиваться этим не стоит: на самом деле при вычислении P(w) мы можем учесть также и фразу, слово в которой мы пытаемся исправить, и любой другой внешний контекст. Задача превращается в задачу вычисления P(w1w2…wk), где одно из wi — слово, в котором мы исправили опечатку и для которого мы теперь рассчитываем P(w), а остальные wi — слова, окружающие исправляемое слово в пользовательском запросе.
Чтобы научиться учитывать их, стоит пройтись по корпусу еще раз и составить статистику n-грамм, последовательностей слов. Обычно берут последовательности ограниченной длины; я ограничился триграммами, чтобы не раздувать индекс, но тут все зависит от вашей силы духа (и размера корпуса — на маленьком корпусе даже статистика по триграммам будет слишком шумной).
Традиционная модель языка на основе n-грамм выглядит так. Для фразы w1w2…wk ее вероятность вычисляется по формуле
где P(w1) — непосредственно частота слова, а P(w3|w1w2) — вероятность слова w3 при условии, что перед ним идут w1w2 — не что иное, как отношение частоты триграммы w1w2w3 к частоте биграммы w1w2. (Заметьте, что эта формула — просто результат многократного применения формулы Байеса.)
Иными словами, если мы захотим вычислить мамамыларамуP(мама мыла раму), обозначив частоту произвольной n-граммы за f, мы получим формулу
Логично? Логично. Однако трудности начинаются, когда фразы становятся длиннее. Что, если пользователь ввел впечатляющий своей подробностью поисковый запрос в десять слов? Мы не хотим держать статистику по всем 10-граммам — это дорого, а данные, скорее всего, будут шумными и не показательными. Мы хотим обойтись n-граммами какой-то ограниченной длины — например, уже предложенной выше длины 3.
Здесь-то и пригождается формула выше. Давайте предположим, что на вероятность слова появиться в конце фразы значительно влияют только несколько слов непосредственно перед ним, то есть что
Положив L=3, для более длинной фразы получим формулу
Обратите внимание: фраза состоит из пяти слов, но в формуле фигурируют n-граммы не длиннее трех. Это как раз то, чего мы добивались.
Остался один тонкий момент. Что, если пользователь ввел совсем странную фразу и соответствующих n-грамм у нас в статистике и нет вовсе? Было бы легко для незнакомых n-грамм положить f=0, если бы на эту величину не надо было делить. Здесь на помощь приходит сглаживание (smoothing), которое можно делать разными способами; однако подробное обсуждение серьезных подходов к сглаживанию вроде Kneser-Ney smoothing выходит далеко за рамки этой статьи.
Как исправлять фразы
Обговорим последний тонкий момент перед тем, как перейти к реализации. Постановка задачи, которую я описал выше, подразумевала, что есть одно слово и его надо исправить. Потом мы уточнили, что это одно слово может быть в середине фразы среди каких-то других слов и их тоже нужно учесть, выбирая наилучшее исправление. Но в реальности пользователи просто присылают нам фразы, не уточняя, какое слово написано с ошибкой; нередко в исправлении нуждается несколько слов или даже все.
Подходов здесь может быть много. Можно, например, учитывать только левый контекст слова в фразе. Тогда, идя по словам слева направо и по мере необходимости исправляя их, мы получим новую фразу какого-то качества. Качество будет низким, если, например, первое слово оказалось похоже на несколько популярных слов и мы выберем неправильный вариант. Вся оставшаяся фраза (возможно, изначально вообще безошибочная) будет подстраиваться нами под неправильное первое слово и мы можем получить на выходе полностью нерелевантный оригиналу текст.
Можно рассматривать слова по отдельности и применять некий классификатор, чтобы понимать, опечатано данное слово или нет, как это предложено в . Классификатор обучается на вероятностях, которые мы уже умеем считать, и ряде других фичей. Если классификатор говорит, что нужно исправлять — исправляем, учитывая имеющийся контекст. Опять-таки, если несколько слов написаны с ошибкой, принимать решение насчет первого из них придется, опираясь на контекст с ошибками, что может приводить к проблемам с качеством.
В реализации нашего опечаточника мы использовали такой подход. Давайте для каждого слова si в нашей фразе найдем с помощью модели ошибок топ-N словарных слов, которые могли иметься в виду, сконкатенируем их во фразы всевозможными способами и для каждой из NK получившихся фраз, где K — количество слов в исходной фразе, посчитаем честно величину
Здесь si — слова, введенные пользователем, wi — подобранные для них исправления (которые мы сейчас перебираем), а λ — коэффициент, определяемый сравнительным качеством модели ошибок и модели языка (большой коэффициент — больше доверяем модели языка, маленький коэффициент — больше доверяем модели ошибок), предложенный в . Итого для каждой фразы мы перемножаем вероятности отдельных слов исправиться в соответствующие словарные варианты и еще домножаем это на вероятность всей фразы в нашем языке. Результат работы алгоритма — фраза из словарных слов, максимизирующая эту величину.
Так, стоп, что? Перебор NK фраз?
К счастью, за счет того, что мы ограничили длину n-грамм, найти максимум по всем фразам можно гораздо быстрее. Вспомните: выше мы упростили формулу для P(w1w2…wK) так, что она стала зависеть только от частот n-грамм длины не выше трех:
Если мы домножим эту величину на 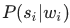
Реализация алгоритма исправления ошибок
Собираем корпус и считаем n-граммы
Сразу оговорюсь: данных в моем распоряжении было не так много, чтобы заводить какой-то сложный MapReduce. Так что я просто собрал все тексты отзывов, комментариев и поисковых запросов на русском языке (описания товаров, увы, приходят на английском, а использование результатов автоперевода скорее ухудшило, чем улучшило результаты) с нашего сервиса в один текстовый файл и поставил сервер на ночь считать триграммы простым скриптом на Python.
В качестве словарных я брал топ слов по частотности так, чтобы получалось порядка ста тысяч слов. Исключались слишком длинные слова (больше 20 символов) и слишком короткие (меньше трех символов, кроме захардкоженных известных русских слов). Отдельно пощадил слова по регулярке r»^[a-z0-9]{2}$» — чтобы уцелели версии айфонов и другие интересные идентификаторы длины 2.
При подсчете биграмм и триграмм во фразе может встретиться несловарное слово. В этом случае это слово я выбрасывал и бил всю фразу на две части (до и после этого слова), с которыми работал отдельно. Так, для фразы «А вы знаете, что такое «абырвалг»? Это… ГЛАВРЫБА, коллега» учтутся триграммы “а вы знаете”, “вы знаете что”, “знаете что такое” и “это главрыба коллега” (если, конечно, слово “главрыба” попадет в словарь…).
Обучаем модель ошибок
Дальше всю обработку данных я проводил в Jupyter. Статистика по n-граммам грузится из JSON, производится постобработка, чтобы быстро находить близкие друг к другу по Левенштейну слова, и для пар в цикле вызывается (довольно громоздкая) функция, выстраивающая слова и извлекающая короткие правки вида сс → с (под спойлером).
Код на Python
короткие правки вида сс → с (под спойлером).
def generate_modifications(intended_word, misspelled_word, max_l=2):
# Выстраиваем буквы слов оптимальным по Левенштейну образом и
# извлекаем модификации ограниченной длины. Чтобы после подсчета
# расстояния восстановить оптимальное расположение букв, будем
# хранить впродолжение следует…
Продолжение:
Часть 1 Алгоритмы исправления опечаток с и без учёта контекста
Часть 2 Результаты — Алгоритмы исправления опечаток с и без учёта контекста
См.также
- Фильтр Блума
- Расстояние Дамерау-Левенштейна
- metaphone , soundex , approximate string matching , fuzzy string searching ,
- инвертированный индекс , расстояние левенштейна , расстояние редактирования , редакционным расстоянием ,
В общем, мой друг ты одолел чтение этой статьи об алгоритмы исправления опечаток. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое алгоритмы исправления опечаток, исправление опечаток с учётом контекста, исправление опечаток без учёта контекста, модель ошибок, модель языка
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Обработка естественного языка
Аннотация: Контроль по четности, CRC, алгоритм Хэмминга. Введение в коды Рида-Соломона: принципы, архитектура и реализация. Метод коррекции ошибок FEC (Forward Error Correction).
Каналы передачи данных ненадежны (шумы, наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных ( М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок ( BER – Bit Error Rate) равна р = 10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p)8 = 7,9 х 10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p)8. Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p)9 – 9p(1 – p)8 = 3,6 x 10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как
для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
В Ethernet вычисление CRC производится аппаратно. На
рис.
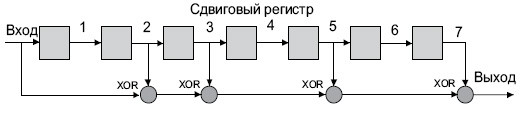
4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x2 + x3 + x5 + x7. В этой схеме входной код приходит слева.
Рис.
4.1.
Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r — степень образующего полинома.
| CRC -12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC -16 | x16 + x15 + x2 + 1 |
| CRC -CCITT | x16 + x12 + x5 + 1 |
4.1. Алгоритмы коррекции ошибок
Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещеных процесса: обнаружение ошибки и определение места (идентификации сообщения и позиции в сообщении). После решения этих двух задач исправление тривиально — надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7), используемыми при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7 + 4 = 11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние Хэмминга 4):
00000000
11110000
00001111
11111111
При получении кода 00000111 нетрудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга.
Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7). Таблица 4.2.
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | * | 0 | 0 | 1 | * | 1 | * | * |
Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XoR (исключающее ИЛИ) над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 05= | 0101 |
| 03= | 0011 |
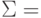 |
1110 |
Таким образом, приемник получит код
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Просуммируем снова коды позиций ненулевых битов и получим нуль;
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 08= | 1000 |
| 05= | 0101 |
| 04= | 0100 |
| 03= | 0011 |
| 02= | 0010 |
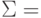 |
0000 |
Ну а теперь рассмотрим два случая ошибок в одном из битов посылки, например в бите 7 (1 вместо 0) и в бите 5 (0 вместо 1). Просуммируем коды позиций ненулевых битов еще раз:
|
|
В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме. Понятно, что если ошибка произойдет при передаче более чем одного бита, код Хэмминга при данной избыточности окажется бесполезен.
В общем случае код имеет N = M + C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М = 4, а N = 7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:
С1 = М1 + М2 + М4 С2 = М1 + М3 + М4 С3 = М2 + М3 + М4
Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):
С11 = С1 + М4 + М2 + М1 С12 = С2 + М4 + М3 + М1 С13 = С3 + М4 + М3 + М2
Результат вычисления интерпретируется следующим образом:
| C11 | C12 | C13 | Значение |
|---|---|---|---|
| 1 | 2 | 4 | Позиция бит |
| 0 | 0 | 0 | Ошибок нет |
| 0 | 0 | 1 | Бит С3 неверен |
| 0 | 1 | 0 | Бит С2 неверен |
| 0 | 1 | 1 | Бит M3 неверен |
| 1 | 0 | 0 | Бит С1 неверен |
| 1 | 0 | 1 | Бит M2 неверен |
| 1 | 1 | 0 | Бит M1 неверен |
| 1 | 1 | 1 | Бит M4 неверен |
Описанная схема легко переносится на любое число n и М.
Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N — число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга ) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более qm.
В теории кодирования существуют следующие оценки максимального числа N n -разрядных кодов с расстоянием D.
| d=1 | n=2n |
| d=2 | n=2n-1 |
| d=3 | N 2n/(1 + n) |
| d = 2q + 1 | (для кода Хэмминга это неравенство превращается в равенство) |
В случае кода Хэмминга первые k разрядов используются в качестве информационных, причем
K = n – log(n + 1), откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.
Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-hocquenghem). Эти коды имеют широкий выбор длин и возможностей исправления ошибок.
Одной из старейших схем коррекции ошибок является двух-и трехмерная позиционная схема (
рис.
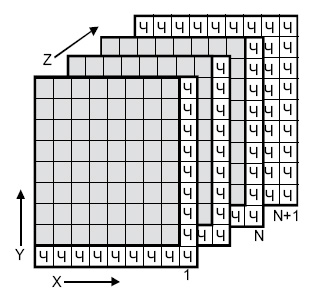
4.2). Для каждого байта вычисляется бит четности (бит <Ч>, направление Х). Для каждого столбца также вычисляется бит четности (направление Y. Производится вычисление битов четности для комбинаций битов с координатами (X,Y) (направление Z, слои с 1 до N ). Если при транспортировке будет искажен один бит, он может быть найден и исправлен по неверным битам четности X и Y. Если же произошло две ошибки в одной из плоскостей, битов четности данной плоскости недостаточно. Здесь поможет плоскость битов четности N+1.
Таким образом, на 512 передаваемых байтов данных пересылается около 200 бит четности.
Рис.
4.2.
Позиционная схема коррекции ошибок
-
Обнаружение и исправление ошибок
-
Общие понятия
-
Для
защиты полезной информации от помех
необходимо в том или ином виде вводить
избыточность: увеличивать число символов
и время их передачи, повторять целые
сообщения, повышать мощность сигнала
— все это ведет к усложнению и удорожанию
аппаратуры. В качестве исследуемой
модели достаточно рассмотреть канал
связи с помехами, потому что к этому
случаю легко сводятся остальные.
Например, запись на диск можно рассматривать
как передачу данных в канал, а чтение с
диска – как прием данных из канала.
Коды
без избыточности обнаружить, а тем более
исправлять
ошибки не могут.
Количество символов, в которых любые
две комбинации кода отличаются друг от
друга, называется кодовым
расстоянием.
Минимальное
количество символов, в которых все
комбинации кода отличаются друг от
друга, называется минимальным
кодовым расстоянием.
Минимальное кодовое расстояние —
параметр, определяющий помехоустойчивость
кода и заложенную в коде избыточность,
т.е. корректирующие свойства кода.
В
общем случае для обнаружения t
ошибок минимальное кодовое расстояние
d0
= t
+ 1.
Минимальное
кодовое расстояние, необходимое для
одновременного обнаружения t
и исправления
ошибок,
d0
= t
+
+ 1.,
Для
кодов, только исправляющих
ошибок,
d0
= 2
+ 1.
Для
того чтобы определить кодовое расстояние
между двумя комбинациями двоичного
кода, достаточно просуммировать эти
комбинации по модулю 2 и подсчитать
число единиц полученной комбинации.
Для
обнаружения и исправления одиночной
ошибки соотношение между числом
информационных разрядив k
и числом корректирующих разрядов
должно удовлетворять следующим условиям:
,
,
при
этом подразумевается, что общая длина
кодовой комбинации
n
= k + ρ
Для
практических расчетов при определении
числа контрольных разрядов кодов с
минимальным кодовым расстоянием d0
= 3 удобно
пользоваться выражениями
ρ1(2)
= [ log2
( n + 1
) ],
если
известна длина полной кодовой комбинации
n,
и
ρ
1(2) =
[log2 {
( k
+ 1 ) + [ log2
(
k + 1) ] } ],
если
при расчетах удобнее исходить из
заданного числа информационных символов
k
.
Для
кодов, обнаруживающих все трехкратные
ошибки (d0
= 4),
ρ
1(3)
1
+ log2
(
n + 1
),
или
ρ
1(3)
1 + log2
[ (
k + 1
) + log2
(
k + 1
) ].
Для
кодов длиной в n
символов, исправляющих одну или две
ошибки (d0
= 5),
ρ
2
log2
(Cn2
+ Cn1
+ 1).
Для практических
расчетов можно пользоваться выражением:
.
Для
кодов, исправляющих 3 ошибки (d0
= 7),
.
-
Линейные групповые коды
Линейными
называются коды, в которых проверочные
символы представляют собой линейные
комбинации информационных символов.
Для
двоичных кодов в качестве линейной
операции используется сложение по
модулю 2.
Последовательность
нулей и единиц, принадлежащих данному
коду, будем называть кодовым
вектором.
Свойство
линейных кодов:
сумма
(разность) кодовых векторов линейного
кода дает вектор, принадлежащий данному
коду.
Линейные
коды образуют алгебраическую группу
по отношению к операции сложения по
модулю 2. В этом смысле они являются
групповыми
кодами.
Свойство
группового кода:
минимальное кодовое
расстояние между кодовыми векторами
группового кода равно минимальному
весу ненулевых кодовых векторов.
Вес
кодового вектора
(кодовой комбинации) равен числу его
ненулевых компонент.
Расстояние
между двумя кодовыми векторами
равно весу вектора, полученного в
результате сложения исходных векторов
по модулю 2. Таким образом, для данного
группового кода
Wmin
=d0.
Групповые
коды удобно задавать матрицами,
размерность которых определяется
параметрами кода k
и .
Число строк матрицы равно k,
число столбцов равно
n
= k +
:
Коды,
порождаемые этими матрицами, известны
как (n,k)-коды,
соответствующие им матрицы называют
порождающими
(производящими, образующими).
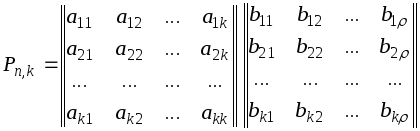
Порождающая
матрица P
может быть представлена двумя матрицами
Uk
и H
(информационной и проверочной). Число
столбцов матрицы H
равно ,
число столбцов матрицы Uk
равно k
Теорией
и практикой установлено, что в качестве
матрицы Uk
удобно брать единичную матрицу в
канонической форме
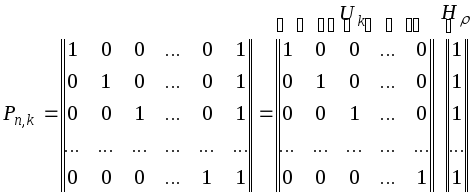
Для
кодов с d0
= 2
производящая матрица P
имеет вид
Во всех комбинациях
кода построенного при помощи такой
матрицы, четное число единиц.
Для
кодов с d0
3 порождающая
матрица не может быть представлена в
форме, общей для всех кодов с данным
d0.
Вид матрицы
зависит от конкретных требований к
порождающему коду. Этими требованиями
могут быть либо минимум корректирующих
разрядов, либо максимальная простота
аппаратуры.
Корректирующие
коды с минимальным количеством избыточных
разрядов называют плотно
упакованными
или
совершенными
кодами.
Для
кодов d0
= 3
соотношения n
и k
следующие: (3; 1), (7; 4),
(15; 11), (31; 26), (63; 57)
и так далее.
Строчки
образующей матрицы P
представляют собой k
комбинаций искомого кода. Остальные
комбинации кода строятся при помощи
образующей матрицы по следующему
правилу: корректирующие символы,
предназначенные для обнаружения и
исправления ошибки в информационной
части кода, находятся путем суммирования
по модулю 2 тех строк матрицы H,
номера которых совпадают с номерами
разрядов, содержащих единицы в кодовом
векторе, представляющем информационную
часть кода. Полученную комбинацию
приписывают справа к информационной
части кода и получают полный вектор
корректирующего кода. Аналогичную
процедуру проделывают со второй, третьей
и последующими информационными кодовыми
комбинациями, пока не будет построен
корректирующий код для передачи всех
символов первичного алфавита.
Алгоритм
образования проверочных символов по
известной информационной части кода
может быть записан следующим образом
или
.
В процессе
декодирования осуществляются проверки,
идея которых в общем виде может быть
представлена следующим образом
Для
каждой конкретной матрицы существует
своя, одна-единственная система проверок.
Проверки производятся по следующему
правилу : в первую проверку вместе с
проверочным рядом b1
входят информационные разряды, которые
соответствуют единицам первого столбца
проверочной матрицы H;
во вторую проверку входит второй
проверочный разряд b2
и информационные
разряды, и т. д. Число проверок равно
числу проверочных разрядов корректирующего
кода .
В
результате осуществления проверок
образуется проверочный
вектор
S1,
S2,
…, S,
который называется синдромом.
Если вес синдрома равен нулю, то принятая
комбинация считается безошибочной.
Если хотя бы один разряд проверочного
вектора содержит единицу, то принятая
комбинация содержит ошибку. Исправление
ошибки производится по виду синдрома,
так как каждому ошибочному разряду
соответствует один единственный
проверочный вектор.
Вид
синдрома для каждой конкретной матрицы
может быть определен при помощи
проверочной матрицы Н’,
которая представляет собой транспонированную
матрицу H,
дополненной единичной матрицей I,
число столбцов которой равно число
проверочных разрядов кода
Н’
= HТI.
Столбцы
такой матрицы представляют собой
значение синдрома для разряда,
соответствующего номеру столбца матрицы
Н’.
Процедура исправления
ошибок в процессе декодирования групповых
кодов сводится к следующему.
Строится
кодовая таблица. В первой строке таблицы
располагаются все кодовые векторы Ai.
В первом столбце второй строки размещается
вектор a1,
вес которого равен 1.
Остальные
позиции второй строки заполняются
векторами, полученными в результате
суммирования по модулю 2 вектора a1
с Аi,
расположенным в соответствующем столбце
первой строки. В первом столбце третьей
строки записывается вектор a2,
вес которого также равен 1, однако , если
вектор a1
содержит единицу в первом разряде, то
a2
— во втором. В остальные позиции третьей
строки записывают суммы Аi
и a2
.
Аналогично
поступают до тех пор, пока не будут
просуммированы с векторами Аi
все векторы
aj
весом 1, с единицей в каждом из n
разрядов. Затем суммируются по модулю
2 векторы aj,
весом 2, с последовательным перекрытием
всех возможных разрядов. Вес вектора
aj
определяет число исправляемых ошибок.
Число векторов aj
определяется возможным числом
неповторяющихся синдромов и равно 2-1
(нулевая комбинация говорит об отсутствии
ошибки). Условие неповторяемости синдрома
позволяет по его виду определять
один-единственный соответствующий ему
вектор aj.
Векторы aj
есть векторы
ошибок, которые могут быть исправлены
данным групповым кодом.
По
виду синдрома принятая комбинация может
быть отнесена к тому или иному смежному
классу, образованному сложением по
модулю 2 кодовой комбинации Аi
с вектором ошибки aj,
т. е. к определенной строке кодовой
таблицы 3.2.1.
Таблица 3.2.1-
Кодовая таблица групповых кодов
|
a |
A1 |
A2 |
… |
A(2k-1) |
|
a1 |
a1A1 |
a2A2 |
… |
a1A(2k-1) |
|
a2 |
a2A1 |
a2A2 |
… |
a2A(2k-1) |
|
… |
… |
… |
… |
… |
|
a(2-1) |
a(2 |
a(2-1)A2 |
… |
a(2-1)A(2k-1) |
Принятая
кодовая комбинация Axn
сравнивается
с векторами, записанными в строке,
соответствующей полученному в результате
проверок синдрому. Истинный код будет
расположен в строке той же колонки
таблицы. Процесс исправления ошибки
заключается в замене на обратное значение
разрядов.
Векторы
a1,
a2,
…,a(2-1)
не должны
быть равными ни одному из векторов А1,
А2,
…, А(2-1),
в противном случае в таблице появились
бы нулевые векторы.
Пример.
Построить
кодовую таблицу, при помощи которой
обнаруживаются и исправляются все
одиночные ошибки и некоторые ошибки
кратностью r
+ 1,
в информационной
части кода (11,7), построенного по матрице
Решение.
Используя
таблицу 3.2.1, строим кодовую таблицу
3.2.2 для кодов, построенных по данной
матрице P,
кодовые комбинации строятся путем
добавления к четырехразрядным комбинациям
натурального двоичного кода корректирующих
разрядов по правилу, описанному выше.
Определяем
систему проверок исходя из матрицы H
Находим
вид синдрома для каждой строки таблицы.
Для этого достаточно произвести проверки
для кодовых комбинаций любого столбца
кодовой таблицы.
Для
нашего примера возьмем столбец A3
.
Таблица 3.2.1 – Пример таблицы
для столбца А3
|
№ |
e |
A1 1000111 |
A2 0100011 |
A3 1100100 |
A4 0010110 |
A5 1010001 |
A6 0110101 |
A7 1110010 |
|
1 2 3 4 5 6 7 |
1000000 0100000 0010000 0001000 1100000 1001000 1010000 |
0000111 1100111 1010111 1001111 0100111 0001111 0010111 |
1100011 0000011 0110011 0101011 1000011 1101011 1110011 |
0100100 1000100 1110100 1101100 0000100 0101100 0110100 |
1010110 0110110 0000110 0011110 1110110 1011110 1000110 |
0010001 1110001 1000001 1011001 0110001 0011001 0000001 |
1110101 0010101 0100101 0111101 1010101 1111101 1100101 |
0110010 1010010 1100010 1111010 0010010 0111010 0100010 |
|
№ |
A8 0001101 |
A9 1001010 |
A10 0101110 |
A11 1101001 |
A12 0011011 |
A13 1011100 |
A14 0111000 |
A15 1111111 |
|
1 2 3 4 5 6 7 |
1001101 0101101 0011101 0000101 1101101 1000101 1011101 |
0001010 1101010 1011010 1000010 0101010 0000010 0011010 |
1101110 0001110 0111110 0100110 1001110 1100110 1111110 |
0101001 1001001 1111001 1100001 0001001 0100001 0111001 |
1011011 0111011 0001011 0010011 1111011 1010011 1001011 |
0011100 1111100 1001100 1010100 0111100 0010100 0001100 |
1111000 0011000 0101000 0110000 1011000 1110000 1101000 |
0111111 1011111 1101111 1110111 0011111 0110111 0101111 |
-
0
1 0 0 1 0 0 -
1
0 0 0 1 0 0 -
1
1 1 0 1 0 0 -
1
1 0 1 1 0 0 -
0
0 0 0 1 0 0 -
0
1 0 1 1 0 0 -
0
1 1 0 1 0 0
Таким
образом вектору ошибки a1
соответствует синдром 1 1 1
“ a2 “ 0
1 1
“ a3 “ 1
1 0
“ a4 “ 1
0 1
“ a5 “ 1
0 0
“ a6 “ 0
1 0
“ a7 “ 0
0 1
Предположим,
приняты комбинации 1011001, 1000101, 0001100,
0000001 и 1010001. Производим проверки
Синдром
первой принятой комбинации — 101, значит
вектор ошибки а4
= 0001000, исправление ошибки производится
заменой символа в четвертом разряде
принятой комбинации на обратный. Истинная
комбинация — А5,
так как принятая комбинация находится
в шестом столбце таблицы в строке,
соответствующей синдрому 101.
Синдром
второй принятой комбинации — 010, находим
ее в шестой строке (010 соответствует а6)
и в девятом столбце. Истинная комбинация
А8
= 0001101, т.е. исправлена двойная ошибка.
Синдром
третьей принятой комбинации — 001
соответствует а7,
истинная комбинация А13.
Синдром
четвертой из принятых комбинаций — 001
также соответствует а7,
но принятую комбинацию мы находим в
шестом столбце таблицы , следовательно,
истинная комбинация — А5.
Синдром шестой
принятой комбинации — 000. Ошибки нет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
To clean up transmission errors introduced by Earth’s atmosphere (left), Goddard scientists applied Reed–Solomon error correction (right), which is commonly used in CDs and DVDs. Typical errors include missing pixels (white) and false signals (black). The white stripe indicates a brief period when transmission was interrupted.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Definitions[edit]
Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.
Error correction is the detection of errors and reconstruction of the original, error-free data.
History[edit]
In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.[5]
The modern development of error correction codes is credited to Richard Hamming in 1947.[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication[7] and was quickly generalized by Marcel J. E. Golay.[8]
Introduction[edit]
All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.
If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Types of error correction[edit]
There are three major types of error correction.[9]
Automatic repeat request[edit]
Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.
Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.
Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.
ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.[10]
For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.
Forward error correction[edit]
Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.[13]
Error-correcting codes are usually distinguished between convolutional codes and block codes:
- Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
- Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.
Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.
The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.
Hybrid schemes[edit]
Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:[10]
- Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
- Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.
The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.
Error detection schemes[edit]
Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).
Minimum distance coding[edit]
A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.
Repetition codes[edit]
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.
A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.[14][15]
Parity bit[edit]
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.
Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.
There are also other bit-grouping techniques.
Checksum[edit]
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy check[edit]
A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.
A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.
The parity bit can be seen as a special-case 1-bit CRC.
Cryptographic hash function[edit]
The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.
Error correction code[edit]
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.
Applications[edit]
Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.
Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.
Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.
Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.
Reliability and inspection engineering also make use of the theory of error-correcting codes.[16]
Internet[edit]
In a typical TCP/IP stack, error control is performed at multiple levels:
- Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
- The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
- The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
- UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
- TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.
Deep-space telecommunications[edit]
The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.
The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.
The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.
The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.
Satellite broadcasting[edit]
The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.
Data storage[edit]
Error detection and correction codes are often used to improve the reliability of data storage media.[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.
Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.
Error-correcting memory[edit]
Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.
Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.[22]
In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.[23][24][25] A few systems[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.
See also[edit]
- Berger code
- Burst error-correcting code
- ECC memory, a type of computer data storage
- Link adaptation
- List of algorithms § Error detection and correction
- List of hash functions
References[edit]
- ^ a b «Masorah». Jewish Encyclopedia.
- ^ Pratico, Gary D.; Pelt, Miles V. Van (2009). Basics of Biblical Hebrew Grammar: Second Edition. Zondervan. ISBN 978-0-310-55882-8.
- ^ Mounce, William D. (2007). Greek for the Rest of Us: Using Greek Tools Without Mastering Biblical Languages. Zondervan. p. 289. ISBN 978-0-310-28289-1.
- ^ Mishneh Torah, Tefillin, Mezuzah, and Sefer Torah, 1:2. Example English translation: Eliyahu Touger. The Rambam’s Mishneh Torah. Moznaim Publishing Corporation.
- ^ Brian M. Fagan (5 December 1996). «Dead Sea Scrolls». The Oxford Companion to Archaeology. Oxford University Press. ISBN 0195076184.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, p. vii, ISBN 0-88385-023-0
- ^ Shannon, C.E. (1948), «A Mathematical Theory of Communication», Bell System Technical Journal, 27 (3): 379–423, doi:10.1002/j.1538-7305.1948.tb01338.x, hdl:10338.dmlcz/101429, PMID 9230594
- ^ Golay, Marcel J. E. (1949), «Notes on Digital Coding», Proc.I.R.E. (I.E.E.E.), 37: 657
- ^ Gupta, Vikas; Verma, Chanderkant (November 2012). «Error Detection and Correction: An Introduction». International Journal of Advanced Research in Computer Science and Software Engineering. 2 (11). S2CID 17499858.
- ^ a b A. J. McAuley, Reliable Broadband Communication Using a Burst Erasure Correcting Code, ACM SIGCOMM, 1990.
- ^ Shah, Pradeep M.; Vyavahare, Prakash D.; Jain, Anjana (September 2015). «Modern error correcting codes for 4G and beyond: Turbo codes and LDPC codes». 2015 Radio and Antenna Days of the Indian Ocean (RADIO): 1–2. doi:10.1109/RADIO.2015.7323369. ISBN 978-9-9903-7339-4. S2CID 28885076. Retrieved 22 May 2022.
- ^ «IEEE SA — IEEE 802.11ac-2013». IEEE Standards Association.
- ^ «Transition to Advanced Format 4K Sector Hard Drives | Seagate US». Seagate.com. Retrieved 22 May 2022.
- ^ Frank van Gerwen. «Numbers (and other mysterious) stations». Archived from the original on 12 July 2017. Retrieved 12 March 2012.
- ^ Gary Cutlack (25 August 2010). «Mysterious Russian ‘Numbers Station’ Changes Broadcast After 20 Years». Gizmodo. Retrieved 12 March 2012.
- ^ Ben-Gal I.; Herer Y.; Raz T. (2003). «Self-correcting inspection procedure under inspection errors» (PDF). IIE Transactions. IIE Transactions on Quality and Reliability, 34(6), pp. 529-540. Archived from the original (PDF) on 2013-10-13. Retrieved 2014-01-10.
- ^ K. Andrews et al., The Development of Turbo and LDPC Codes for Deep-Space Applications, Proceedings of the IEEE, Vol. 95, No. 11, Nov. 2007.
- ^ Huffman, William Cary; Pless, Vera S. (2003). Fundamentals of Error-Correcting Codes. Cambridge University Press. ISBN 978-0-521-78280-7.
- ^ Kurtas, Erozan M.; Vasic, Bane (2018-10-03). Advanced Error Control Techniques for Data Storage Systems. CRC Press. ISBN 978-1-4200-3649-7.[permanent dead link]
- ^ Scott A. Moulton. «My Hard Drive Died». Archived from the original on 2008-02-02.
- ^ Qiao, Zhi; Fu, Song; Chen, Hsing-Bung; Settlemyer, Bradley (2019). «Building Reliable High-Performance Storage Systems: An Empirical and Analytical Study». 2019 IEEE International Conference on Cluster Computing (CLUSTER): 1–10. doi:10.1109/CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite». Tsinghua Space Center, Tsinghua University, Beijing. Archived from the original on 2011-10-02. Retrieved 2009-02-16.
- ^ Jeff Layton. «Error Detection and Correction». Linux Magazine. Retrieved 2014-08-12.
- ^ «EDAC Project». bluesmoke.sourceforge.net. Retrieved 2014-08-12.
- ^ «Documentation/edac.txt». Linux kernel documentation. kernel.org. 2014-06-16. Archived from the original on 2009-09-05. Retrieved 2014-08-12.
Further reading[edit]
- Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
- SoftECC: A System for Software Memory Integrity Checking
- A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
- Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing
External links[edit]
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
- ECC Page — implementations of popular ECC encoding and decoding routines
To clean up transmission errors introduced by Earth’s atmosphere (left), Goddard scientists applied Reed–Solomon error correction (right), which is commonly used in CDs and DVDs. Typical errors include missing pixels (white) and false signals (black). The white stripe indicates a brief period when transmission was interrupted.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Definitions[edit]
Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.
Error correction is the detection of errors and reconstruction of the original, error-free data.
History[edit]
In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.[5]
The modern development of error correction codes is credited to Richard Hamming in 1947.[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication[7] and was quickly generalized by Marcel J. E. Golay.[8]
Introduction[edit]
All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.
If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Types of error correction[edit]
There are three major types of error correction.[9]
Automatic repeat request[edit]
Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.
Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.
Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.
ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.[10]
For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.
Forward error correction[edit]
Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.[13]
Error-correcting codes are usually distinguished between convolutional codes and block codes:
- Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
- Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.
Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.
The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.
Hybrid schemes[edit]
Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:[10]
- Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
- Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.
The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.
Error detection schemes[edit]
Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).
Minimum distance coding[edit]
A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.
Repetition codes[edit]
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.
A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.[14][15]
Parity bit[edit]
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.
Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.
There are also other bit-grouping techniques.
Checksum[edit]
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy check[edit]
A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.
A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.
The parity bit can be seen as a special-case 1-bit CRC.
Cryptographic hash function[edit]
The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.
Error correction code[edit]
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.
Applications[edit]
Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.
Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.
Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.
Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.
Reliability and inspection engineering also make use of the theory of error-correcting codes.[16]
Internet[edit]
In a typical TCP/IP stack, error control is performed at multiple levels:
- Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
- The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
- The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
- UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
- TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.
Deep-space telecommunications[edit]
The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.
The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.
The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.
The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.
Satellite broadcasting[edit]
The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.
Data storage[edit]
Error detection and correction codes are often used to improve the reliability of data storage media.[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.
Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.
Error-correcting memory[edit]
Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.
Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.[22]
In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.[23][24][25] A few systems[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.
See also[edit]
- Berger code
- Burst error-correcting code
- ECC memory, a type of computer data storage
- Link adaptation
- List of algorithms § Error detection and correction
- List of hash functions
References[edit]
- ^ a b «Masorah». Jewish Encyclopedia.
- ^ Pratico, Gary D.; Pelt, Miles V. Van (2009). Basics of Biblical Hebrew Grammar: Second Edition. Zondervan. ISBN 978-0-310-55882-8.
- ^ Mounce, William D. (2007). Greek for the Rest of Us: Using Greek Tools Without Mastering Biblical Languages. Zondervan. p. 289. ISBN 978-0-310-28289-1.
- ^ Mishneh Torah, Tefillin, Mezuzah, and Sefer Torah, 1:2. Example English translation: Eliyahu Touger. The Rambam’s Mishneh Torah. Moznaim Publishing Corporation.
- ^ Brian M. Fagan (5 December 1996). «Dead Sea Scrolls». The Oxford Companion to Archaeology. Oxford University Press. ISBN 0195076184.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, p. vii, ISBN 0-88385-023-0
- ^ Shannon, C.E. (1948), «A Mathematical Theory of Communication», Bell System Technical Journal, 27 (3): 379–423, doi:10.1002/j.1538-7305.1948.tb01338.x, hdl:10338.dmlcz/101429, PMID 9230594
- ^ Golay, Marcel J. E. (1949), «Notes on Digital Coding», Proc.I.R.E. (I.E.E.E.), 37: 657
- ^ Gupta, Vikas; Verma, Chanderkant (November 2012). «Error Detection and Correction: An Introduction». International Journal of Advanced Research in Computer Science and Software Engineering. 2 (11). S2CID 17499858.
- ^ a b A. J. McAuley, Reliable Broadband Communication Using a Burst Erasure Correcting Code, ACM SIGCOMM, 1990.
- ^ Shah, Pradeep M.; Vyavahare, Prakash D.; Jain, Anjana (September 2015). «Modern error correcting codes for 4G and beyond: Turbo codes and LDPC codes». 2015 Radio and Antenna Days of the Indian Ocean (RADIO): 1–2. doi:10.1109/RADIO.2015.7323369. ISBN 978-9-9903-7339-4. S2CID 28885076. Retrieved 22 May 2022.
- ^ «IEEE SA — IEEE 802.11ac-2013». IEEE Standards Association.
- ^ «Transition to Advanced Format 4K Sector Hard Drives | Seagate US». Seagate.com. Retrieved 22 May 2022.
- ^ Frank van Gerwen. «Numbers (and other mysterious) stations». Archived from the original on 12 July 2017. Retrieved 12 March 2012.
- ^ Gary Cutlack (25 August 2010). «Mysterious Russian ‘Numbers Station’ Changes Broadcast After 20 Years». Gizmodo. Retrieved 12 March 2012.
- ^ Ben-Gal I.; Herer Y.; Raz T. (2003). «Self-correcting inspection procedure under inspection errors» (PDF). IIE Transactions. IIE Transactions on Quality and Reliability, 34(6), pp. 529-540. Archived from the original (PDF) on 2013-10-13. Retrieved 2014-01-10.
- ^ K. Andrews et al., The Development of Turbo and LDPC Codes for Deep-Space Applications, Proceedings of the IEEE, Vol. 95, No. 11, Nov. 2007.
- ^ Huffman, William Cary; Pless, Vera S. (2003). Fundamentals of Error-Correcting Codes. Cambridge University Press. ISBN 978-0-521-78280-7.
- ^ Kurtas, Erozan M.; Vasic, Bane (2018-10-03). Advanced Error Control Techniques for Data Storage Systems. CRC Press. ISBN 978-1-4200-3649-7.[permanent dead link]
- ^ Scott A. Moulton. «My Hard Drive Died». Archived from the original on 2008-02-02.
- ^ Qiao, Zhi; Fu, Song; Chen, Hsing-Bung; Settlemyer, Bradley (2019). «Building Reliable High-Performance Storage Systems: An Empirical and Analytical Study». 2019 IEEE International Conference on Cluster Computing (CLUSTER): 1–10. doi:10.1109/CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite». Tsinghua Space Center, Tsinghua University, Beijing. Archived from the original on 2011-10-02. Retrieved 2009-02-16.
- ^ Jeff Layton. «Error Detection and Correction». Linux Magazine. Retrieved 2014-08-12.
- ^ «EDAC Project». bluesmoke.sourceforge.net. Retrieved 2014-08-12.
- ^ «Documentation/edac.txt». Linux kernel documentation. kernel.org. 2014-06-16. Archived from the original on 2009-09-05. Retrieved 2014-08-12.
Further reading[edit]
- Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
- SoftECC: A System for Software Memory Integrity Checking
- A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
- Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing
External links[edit]
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
- ECC Page — implementations of popular ECC encoding and decoding routines