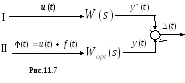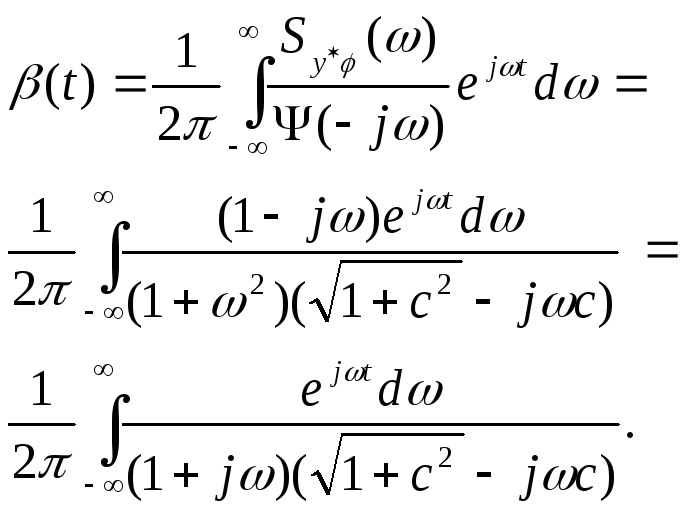In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter.
Motivation[edit]
The term MMSE more specifically refers to estimation in a Bayesian setting with quadratic cost function. The basic idea behind the Bayesian approach to estimation stems from practical situations where we often have some prior information about the parameter to be estimated. For instance, we may have prior information about the range that the parameter can assume; or we may have an old estimate of the parameter that we want to modify when a new observation is made available; or the statistics of an actual random signal such as speech. This is in contrast to the non-Bayesian approach like minimum-variance unbiased estimator (MVUE) where absolutely nothing is assumed to be known about the parameter in advance and which does not account for such situations. In the Bayesian approach, such prior information is captured by the prior probability density function of the parameters; and based directly on Bayes theorem, it allows us to make better posterior estimates as more observations become available. Thus unlike non-Bayesian approach where parameters of interest are assumed to be deterministic, but unknown constants, the Bayesian estimator seeks to estimate a parameter that is itself a random variable. Furthermore, Bayesian estimation can also deal with situations where the sequence of observations are not necessarily independent. Thus Bayesian estimation provides yet another alternative to the MVUE. This is useful when the MVUE does not exist or cannot be found.
Definition[edit]
Let 







where the expectation 




The MMSE estimator is then defined as the estimator achieving minimal MSE:
Properties[edit]
- When the means and variances are finite, the MMSE estimator is uniquely defined[1] and is given by:
-
- In other words, the MMSE estimator is the conditional expectation of
given the known observed value of the measurements. Also, since
is the posterior mean, the error covariance matrix
is equal to the posterior covariance
matrix,
.
- The MMSE estimator is unbiased (under the regularity assumptions mentioned above):
- The MMSE estimator is asymptotically unbiased and it converges in distribution to the normal distribution:
-
- where
is the Fisher information of
. Thus, the MMSE estimator is asymptotically efficient.
-
- for all
in closed, linear subspace
of the measurements. For random vectors, since the MSE for estimation of a random vector is the sum of the MSEs of the coordinates, finding the MMSE estimator of a random vector decomposes into finding the MMSE estimators of the coordinates of X separately:
- for all i and j. More succinctly put, the cross-correlation between the minimum estimation error
and the estimator
should be zero,
Linear MMSE estimator[edit]
In many cases, it is not possible to determine the analytical expression of the MMSE estimator. Two basic numerical approaches to obtain the MMSE estimate depends on either finding the conditional expectation 
One possibility is to abandon the full optimality requirements and seek a technique minimizing the MSE within a particular class of estimators, such as the class of linear estimators. Thus, we postulate that the conditional expectation of 







One advantage of such linear MMSE estimator is that it is not necessary to explicitly calculate the posterior probability density function of 




The expression for optimal 

where 






Thus, the expression for linear MMSE estimator, its mean, and its auto-covariance is given by
where the 


Lastly, the error covariance and minimum mean square error achievable by such estimator is
Univariate case[edit]
For the special case when both 

where 


The above two equations allows us to interpret the correlation coefficient either as normalized slope of linear regression
or as square root of the ratio of two variances
.
When 








Computation[edit]
Standard method like Gauss elimination can be used to solve the matrix equation for 




Linear MMSE estimator for linear observation process[edit]
Let us further model the underlying process of observation as a linear process: 




Thus the expression for the linear MMSE estimator matrix 
Putting everything into the expression for 
Lastly, the error covariance is
The significant difference between the estimation problem treated above and those of least squares and Gauss–Markov estimate is that the number of observations m, (i.e. the dimension of 






Alternative form[edit]
An alternative form of expression can be obtained by using the matrix identity
which can be established by post-multiplying by 

and
Since 



In this form the above expression can be easily compared with weighed least square and Gauss–Markov estimate. In particular, when 







Sequential linear MMSE estimation[edit]
In many real-time applications, observational data is not available in a single batch. Instead the observations are made in a sequence. One possible approach is to use the sequential observations to update an old estimate as additional data becomes available, leading to finer estimates. One crucial difference between batch estimation and sequential estimation is that sequential estimation requires an additional Markov assumption.
In the Bayesian framework, such recursive estimation is easily facilitated using Bayes’ rule. Given 


The 





This is the Markov assumption.
The MMSE estimate 




In the context of linear MMSE estimator, the formula for the estimate will have the same form as before. However, the mean and covariance matrices of 



The mean and covariance matrix of the prior density 

respectively, as per by the property of MMSE estimators.
Similarly, for the linear observation process, the mean and covariance matrix of the likelihood 

.
The difference between the predicted value of 



![{displaystyle mathrm {E} [{tilde {y}}_{k}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7333e06de208be900c7d618273db57bf678fb1f)
.
Hence, in the estimate update formula, we should replace 








Thus, we have the new estimate as
and the new error covariance as
From the point of view of linear algebra, for sequential estimation, if we have an estimate 

The repeated use of the above two equations as more observations become available lead to recursive estimation techniques. The expressions can be more compactly written as
The matrix 
The repetition of these three steps as more data becomes available leads to an iterative estimation algorithm. The generalization of this idea to non-stationary cases gives rise to the Kalman filter. The three update steps outlined above indeed form the update step of the Kalman filter.
Special case: scalar observations[edit]
As an important special case, an easy to use recursive expression can be derived when at each k-th time instant the underlying linear observation process yields a scalar such that 





where 

The 
Here, no matrix inversion is required. Also, the gain factor, 



Alternative approaches: This important special case has also given rise to many other iterative methods (or adaptive filters), such as the least mean squares filter and recursive least squares filter, that directly solves the original MSE optimization problem using stochastic gradient descents. However, since the estimation error 


where 

Examples[edit]
Example 1[edit]
We shall take a linear prediction problem as an example. Let a linear combination of observed scalar random variables 



![{displaystyle z=[z_{1},z_{2},z_{3},z_{4}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45cb1f9123fdf786074088616e42dfbcc1359d07)
then our task is to find the coefficients 

In terms of the terminology developed in the previous sections, for this problem we have the observation vector ![{displaystyle y=[z_{1},z_{2},z_{3}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fdeb8eb600c7a066561d28e2b3f32fb5b1572b9)
![W=[w_{1},w_{2},w_{3}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd8e9343b228a9044dbb8208e9ceeb31270b04c1)


The cross correlation matrix 
We now solve the equation 

So we have 

as the optimal coefficients for 
mean square error then gives ![{displaystyle leftVert erightVert _{min }^{2}=operatorname {E} [z_{4}z_{4}]-WC_{YX}=15-WC_{YX}=.2857}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44558ab7a0b5ead1b9571853096d800773b38877)


Example 2[edit]
Consider a vector 



![1=[1,1,ldots ,1]^{T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43fec89f837a5e8d53869fb49ec95a9e56a788f0)

![[-x_{0},x_{0}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79873ca5ddfd5d6b0168f6373b33c8bc3756c69)


![[-x_{0},x_{0}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79873ca5ddfd5d6b0168f6373b33c8bc3756c69)








Thus, the linear MMSE estimator is given by
We can simplify the expression by using the alternative form for 
where for ![y=[y_{1},y_{2},ldots ,y_{N}]^{T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8317c7045e5b1318cec0c4ee89727a02cdeecafc)

Similarly, the variance of the estimator is
Thus the MMSE of this linear estimator is
For very large 
while the variance will be unaffected by data 
However, the estimator is suboptimal since it is constrained to be linear. Had the random variable 

Example 3[edit]
Consider a variation of the above example: Two candidates are standing for an election. Let the fraction of votes that a candidate will receive on an election day be ![xin [0,1].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c44eb6b4643a03d3c166df0e61c4925b6d4d4f0)


![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)








As with previous example, we have
Here, both the 


where the weights are given by
Here, since the denominator term is constant, the poll with lower error is given higher weight in order to predict the election outcome. Lastly, the variance of 
which makes 

In general, if we have 



Example 4[edit]
Suppose that a musician is playing an instrument and that the sound is received by two microphones, each of them located at two different places. Let the attenuation of sound due to distance at each microphone be 







We can model the sound received by each microphone as
Here both the 
where the i-th weight is given as
See also[edit]
- Bayesian estimator
- Mean squared error
- Least squares
- Minimum-variance unbiased estimator (MVUE)
- Orthogonality principle
- Wiener filter
- Kalman filter
- Linear prediction
- Zero-forcing equalizer
Notes[edit]
- ^ «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 9 May 2017.
- ^ Moon and Stirling.
Further reading[edit]
- Johnson, D. «Minimum Mean Squared Error Estimators». Connexions. Archived from Minimum Mean Squared Error Estimators the original on 25 July 2008. Retrieved 8 January 2013.
- Jaynes, E.T. (2003). Probability Theory: The Logic of Science. Cambridge University Press. ISBN 978-0521592710.
- Bibby, J.; Toutenburg, H. (1977). Prediction and Improved Estimation in Linear Models. Wiley. ISBN 9780471016564.
- Lehmann, E. L.; Casella, G. (1998). «Chapter 4». Theory of Point Estimation (2nd ed.). Springer. ISBN 0-387-98502-6.
- Kay, S. M. (1993). Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall. pp. 344–350. ISBN 0-13-042268-1.
- Luenberger, D.G. (1969). «Chapter 4, Least-squares estimation». Optimization by Vector Space Methods (1st ed.). Wiley. ISBN 978-0471181170.
- Moon, T.K.; Stirling, W.C. (2000). Mathematical Methods and Algorithms for Signal Processing (1st ed.). Prentice Hall. ISBN 978-0201361865.
- Van Trees, H. L. (1968). Detection, Estimation, and Modulation Theory, Part I. New York: Wiley. ISBN 0-471-09517-6.
- Haykin, S.O. (2013). Adaptive Filter Theory (5th ed.). Prentice Hall. ISBN 978-0132671453.
In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter.
Motivation[edit]
The term MMSE more specifically refers to estimation in a Bayesian setting with quadratic cost function. The basic idea behind the Bayesian approach to estimation stems from practical situations where we often have some prior information about the parameter to be estimated. For instance, we may have prior information about the range that the parameter can assume; or we may have an old estimate of the parameter that we want to modify when a new observation is made available; or the statistics of an actual random signal such as speech. This is in contrast to the non-Bayesian approach like minimum-variance unbiased estimator (MVUE) where absolutely nothing is assumed to be known about the parameter in advance and which does not account for such situations. In the Bayesian approach, such prior information is captured by the prior probability density function of the parameters; and based directly on Bayes theorem, it allows us to make better posterior estimates as more observations become available. Thus unlike non-Bayesian approach where parameters of interest are assumed to be deterministic, but unknown constants, the Bayesian estimator seeks to estimate a parameter that is itself a random variable. Furthermore, Bayesian estimation can also deal with situations where the sequence of observations are not necessarily independent. Thus Bayesian estimation provides yet another alternative to the MVUE. This is useful when the MVUE does not exist or cannot be found.
Definition[edit]
Let 







where the expectation 




The MMSE estimator is then defined as the estimator achieving minimal MSE:
Properties[edit]
- When the means and variances are finite, the MMSE estimator is uniquely defined[1] and is given by:
-
- In other words, the MMSE estimator is the conditional expectation of
given the known observed value of the measurements. Also, since
is the posterior mean, the error covariance matrix
is equal to the posterior covariance
matrix,
.
- The MMSE estimator is unbiased (under the regularity assumptions mentioned above):
- The MMSE estimator is asymptotically unbiased and it converges in distribution to the normal distribution:
-
- where
is the Fisher information of
. Thus, the MMSE estimator is asymptotically efficient.
-
- for all
in closed, linear subspace
of the measurements. For random vectors, since the MSE for estimation of a random vector is the sum of the MSEs of the coordinates, finding the MMSE estimator of a random vector decomposes into finding the MMSE estimators of the coordinates of X separately:
- for all i and j. More succinctly put, the cross-correlation between the minimum estimation error
and the estimator
should be zero,
Linear MMSE estimator[edit]
In many cases, it is not possible to determine the analytical expression of the MMSE estimator. Two basic numerical approaches to obtain the MMSE estimate depends on either finding the conditional expectation 
One possibility is to abandon the full optimality requirements and seek a technique minimizing the MSE within a particular class of estimators, such as the class of linear estimators. Thus, we postulate that the conditional expectation of 







One advantage of such linear MMSE estimator is that it is not necessary to explicitly calculate the posterior probability density function of 




The expression for optimal 

where 






Thus, the expression for linear MMSE estimator, its mean, and its auto-covariance is given by
where the 


Lastly, the error covariance and minimum mean square error achievable by such estimator is
Univariate case[edit]
For the special case when both 

where 


The above two equations allows us to interpret the correlation coefficient either as normalized slope of linear regression
or as square root of the ratio of two variances
.
When 








Computation[edit]
Standard method like Gauss elimination can be used to solve the matrix equation for 




Linear MMSE estimator for linear observation process[edit]
Let us further model the underlying process of observation as a linear process: 




Thus the expression for the linear MMSE estimator matrix 
Putting everything into the expression for 
Lastly, the error covariance is
The significant difference between the estimation problem treated above and those of least squares and Gauss–Markov estimate is that the number of observations m, (i.e. the dimension of 






Alternative form[edit]
An alternative form of expression can be obtained by using the matrix identity
which can be established by post-multiplying by 

and
Since 



In this form the above expression can be easily compared with weighed least square and Gauss–Markov estimate. In particular, when 







Sequential linear MMSE estimation[edit]
In many real-time applications, observational data is not available in a single batch. Instead the observations are made in a sequence. One possible approach is to use the sequential observations to update an old estimate as additional data becomes available, leading to finer estimates. One crucial difference between batch estimation and sequential estimation is that sequential estimation requires an additional Markov assumption.
In the Bayesian framework, such recursive estimation is easily facilitated using Bayes’ rule. Given 


The 





This is the Markov assumption.
The MMSE estimate 




In the context of linear MMSE estimator, the formula for the estimate will have the same form as before. However, the mean and covariance matrices of 



The mean and covariance matrix of the prior density 

respectively, as per by the property of MMSE estimators.
Similarly, for the linear observation process, the mean and covariance matrix of the likelihood 

.
The difference between the predicted value of 



![{displaystyle mathrm {E} [{tilde {y}}_{k}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7333e06de208be900c7d618273db57bf678fb1f)
.
Hence, in the estimate update formula, we should replace 








Thus, we have the new estimate as
and the new error covariance as
From the point of view of linear algebra, for sequential estimation, if we have an estimate 

The repeated use of the above two equations as more observations become available lead to recursive estimation techniques. The expressions can be more compactly written as
The matrix 
The repetition of these three steps as more data becomes available leads to an iterative estimation algorithm. The generalization of this idea to non-stationary cases gives rise to the Kalman filter. The three update steps outlined above indeed form the update step of the Kalman filter.
Special case: scalar observations[edit]
As an important special case, an easy to use recursive expression can be derived when at each k-th time instant the underlying linear observation process yields a scalar such that 





where 

The 
Here, no matrix inversion is required. Also, the gain factor, 



Alternative approaches: This important special case has also given rise to many other iterative methods (or adaptive filters), such as the least mean squares filter and recursive least squares filter, that directly solves the original MSE optimization problem using stochastic gradient descents. However, since the estimation error 


where 

Examples[edit]
Example 1[edit]
We shall take a linear prediction problem as an example. Let a linear combination of observed scalar random variables 



![{displaystyle z=[z_{1},z_{2},z_{3},z_{4}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45cb1f9123fdf786074088616e42dfbcc1359d07)
then our task is to find the coefficients 

In terms of the terminology developed in the previous sections, for this problem we have the observation vector ![{displaystyle y=[z_{1},z_{2},z_{3}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fdeb8eb600c7a066561d28e2b3f32fb5b1572b9)
![W=[w_{1},w_{2},w_{3}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd8e9343b228a9044dbb8208e9ceeb31270b04c1)


The cross correlation matrix 
We now solve the equation 

So we have 

as the optimal coefficients for 
mean square error then gives ![{displaystyle leftVert erightVert _{min }^{2}=operatorname {E} [z_{4}z_{4}]-WC_{YX}=15-WC_{YX}=.2857}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44558ab7a0b5ead1b9571853096d800773b38877)


Example 2[edit]
Consider a vector 



![1=[1,1,ldots ,1]^{T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43fec89f837a5e8d53869fb49ec95a9e56a788f0)

![[-x_{0},x_{0}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79873ca5ddfd5d6b0168f6373b33c8bc3756c69)


![[-x_{0},x_{0}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79873ca5ddfd5d6b0168f6373b33c8bc3756c69)








Thus, the linear MMSE estimator is given by
We can simplify the expression by using the alternative form for 
where for ![y=[y_{1},y_{2},ldots ,y_{N}]^{T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8317c7045e5b1318cec0c4ee89727a02cdeecafc)

Similarly, the variance of the estimator is
Thus the MMSE of this linear estimator is
For very large 
while the variance will be unaffected by data 
However, the estimator is suboptimal since it is constrained to be linear. Had the random variable 

Example 3[edit]
Consider a variation of the above example: Two candidates are standing for an election. Let the fraction of votes that a candidate will receive on an election day be ![xin [0,1].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c44eb6b4643a03d3c166df0e61c4925b6d4d4f0)


![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)








As with previous example, we have
Here, both the 


where the weights are given by
Here, since the denominator term is constant, the poll with lower error is given higher weight in order to predict the election outcome. Lastly, the variance of 
which makes 

In general, if we have 



Example 4[edit]
Suppose that a musician is playing an instrument and that the sound is received by two microphones, each of them located at two different places. Let the attenuation of sound due to distance at each microphone be 







We can model the sound received by each microphone as
Here both the 
where the i-th weight is given as
See also[edit]
- Bayesian estimator
- Mean squared error
- Least squares
- Minimum-variance unbiased estimator (MVUE)
- Orthogonality principle
- Wiener filter
- Kalman filter
- Linear prediction
- Zero-forcing equalizer
Notes[edit]
- ^ «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 9 May 2017.
- ^ Moon and Stirling.
Further reading[edit]
- Johnson, D. «Minimum Mean Squared Error Estimators». Connexions. Archived from Minimum Mean Squared Error Estimators the original on 25 July 2008. Retrieved 8 January 2013.
- Jaynes, E.T. (2003). Probability Theory: The Logic of Science. Cambridge University Press. ISBN 978-0521592710.
- Bibby, J.; Toutenburg, H. (1977). Prediction and Improved Estimation in Linear Models. Wiley. ISBN 9780471016564.
- Lehmann, E. L.; Casella, G. (1998). «Chapter 4». Theory of Point Estimation (2nd ed.). Springer. ISBN 0-387-98502-6.
- Kay, S. M. (1993). Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall. pp. 344–350. ISBN 0-13-042268-1.
- Luenberger, D.G. (1969). «Chapter 4, Least-squares estimation». Optimization by Vector Space Methods (1st ed.). Wiley. ISBN 978-0471181170.
- Moon, T.K.; Stirling, W.C. (2000). Mathematical Methods and Algorithms for Signal Processing (1st ed.). Prentice Hall. ISBN 978-0201361865.
- Van Trees, H. L. (1968). Detection, Estimation, and Modulation Theory, Part I. New York: Wiley. ISBN 0-471-09517-6.
- Haykin, S.O. (2013). Adaptive Filter Theory (5th ed.). Prentice Hall. ISBN 978-0132671453.
Во время синтеза
системы может оказаться ситуация, при
которой два сигнала: сигнал управления
и сигналы возмущения, оба имеют случайный
характер. В таком случае принципиальная
задача синтеза системы: определить
параметры системы, доставляющие минимум
средней квадратической ошибки, значение
которой определяется с помощью следующего
выражения:
Можно
обеспечить этот минимум двумя путями:
-
осуществить
параметрический синтез, то-есть,
определить параметры системы, без
изменения её структуры, доставляющие
минимум
-
определить
структуру и параметры системы,
обеспечивающие минимум
(структурно-параметрический синтез).
Параметрический
синтез
осуществляется в следующей
последовательности.
1.Определение
корреляционной функции полезного
сигнала и сигнала возмущения по
практическим экспериментальным данным.
Затем делаем прямое преобразование
Фурье корреляционных функций и приходим
к спектральным плотностям:
Учитывая, что
— функция четная и что
,
получаем
2.
Рассчитываем передаточные функции
системы с обратной связью для ошибки ,
вызванной случайным сигналом управления
и возмущающим воздействием
3. Используя
соответствующие выражения, рассчитываем
спектральную плотность общей ошибки
4. Определяем
дисперсию ошибки по выражению
Парсеваля как
функцию параметров системы
где
,
,
— коэффициенты и постоянные времени
элементов системы.
5. Определяем
числовые значения параметров, решая
систему уравнений
6. Подставляя
числовые значения параметров, определенных
в п.5, в выражение
,
получаем
и
среднеквадратичную ошибку
Если
где
— допустимая ошибка,
означает, что
задача решена. Если неравенство не
выполняется, необходимо приниматься
за структурно-параметрический синтез
системы.
Структурно-параметрический
синтез выполняется
на базе метода оптимальной фильтрации
Винера. Презентация
метода
делается
на
рис.11.7.
Здесь:
канал I
– осуществляет желаемую передачу
входного сигнала
по
следующему выражению:
Второй канал II
– передача, осуществляемая оптимальной
системой
,
в присутствии
В связи с этим ошибка системы
должна удовлетворять критерию
Можно рассматривать
систему
как оптимальный фильтр сигнала
.
Прежде, чем решать
предложенную задачу, рассмотрим
зависимость между корреляционными
функциями сигналов на входе и на выходе
Запишем выражение взаимной корреляционной
функции:
.
Используя выражение
,
приходим к следующей форме :
Или изменяя
последовательность интегрирования,
имеем
.
Полученное выражение
называется уравнением Винера- Хопфа.
Используя
прямое преобразование Фурье, приходим
к замечательному выражению
.
Заметим, что
полученное выражение позволяет определить
частотный образ системы
по реализациям сигналов на входе и на
выходе (результаты пассивного
эксперимента), то-есть, без активного
вмешательства в исследуемый процесс:
.
Определим дисперсию
ошибки, учитывая
:
.
Норберт Винер
доказал , что условием необходимым и
достаточным минимумаявляется
то, что функция веса
должна
быть решением уравнения Винера-Хопфа:
.
Имеем тогда,
Но частотные
характеристики, определенные по этому
выражению
в большинстве практических случаях
имеют нереализуемые свойства, так как
система с
будет неустойчивой.
В этой связи для
отыскания оптимальной функции
,
удовлетворяющей условиям устойчивости,
применяют разложение
на комплексные множители:
Из этого
следует, что
.
Н Винер доказал,
что можно определить оптимальную
передаточную функцию следующим образом:
где
;
Exemple
определения
.
Пусть спектральная
плотность управляющего сигнала
а у помехи типа белого шума
Причем, известно, что
не коррелированны. Необходимо найти
следящей системы.
Решение
Для следящей системы
Поэтому
Учитывая, что
,
можно написать:
принято в рассмотрение
здесь, что
как для сигналов, которые не коррелированны.
Подставляя известные выражения
спектральной плотности, полученные
выше, получаем в нашем случае:
Разложим последнее
выражение на сопряженные множители:
Вычисляем
в соответствии с ранее написанными
выражениями:
Разложив функцию
под знаком интеграла на простые дроби,
получаем
Для вычисления
необходимо взять прямое преобразование
Фурье
которое, в свою очередь, результат
обратного преобразования Фурье выражения,
стоящего в квадратных скобках.
Следовательно,
будет равен этому выражению в квадратных
скобках. Исходя из условий реализуемости
,
отбрасываем слагаемые подынтегральной
функции , имеющей корни в правой
полуплоскости. Тогда
.
Искомая передаточная
функция примет вид
или
,
где
Таким образом,
оптимальный фильтр в данном случае
представляет собой апериодическое
звено первого порядка.
В
заключение заметим, что решение задачи
оптимальной фильтрации может быть также
произведено с помощью фильтра Калмана.
В этом методе предполагается, что на
вход системы поступает аддитивная смесь
управляющего воздействияи
случайного процесса Маркова и помеха
,
представляющая собой гауссовский
«белый» шум. Сигналы
и
не коррелированны. Физически
реализуемый
линейный оператор замкнутой системы,
при котором процесс
на выходе системы является оптимальным
по критерию
минимума
среднеквадратической ошибки, находится
по специально разработанному алгоритму.
Этот алгоритм достаточно громоздок и,
в частности, связан с решением
дифференциального уравнения
Риккатти, для чего,
как правило, требуется применять
численные
методы с использованием
компьютерных технологий. В конечном
итоге, алгоритм
Калмана дает тот же результат, что и
алгоритм
Винера, но в отличие
от последнего, позволяет синтезировать
оптимальные фильтры не только для
установившегося, но и для переходного
режимов, при случайных нестационарных
входных воздействиях.
189
Соседние файлы в папке Лекции по ТАУ-11-мин
- #
- #
- #
- #
- #
- #
Алгоритм минимизации среднеквадратнческой ошибки 18$ где Й,, ‘ — обратная матрица для матрицы корреляции К„. Вектор весовых коэффици- ентов хч, называют Винеровским решением линейной задачи оптимальной фильтрации в честь Норберта Винера (ЯогЬеп %1епег), который внес весомый вющд в ее решение 1434), 11144). Исходя из этого, можно сформулировать следующее утверждение. Дхя эргодического процесса линейный филыпр, построенный по методу наименьших квадратов, асимптотически сходится к фильтру Винера по мере приблиэсения кали- честеа наблюдений к бесконечности. 3.6.
Алгоритм минимизации среднеквадратической ошибки Алгоршпм минимизации среднеквадратической ошибки (!еазпшеап-зцпаге — 1.МБ) основан на использовании дискретных значений функции стоимости: Е(хч) = — ез(п), 2 (3.33) где е(п) — сигнал ошибки, измеренный в момент времени и. Дифференцируя Е(зч) по вектору весов зч, получим: д Е(хч) д е(п) дш дчг = е(п) —. (3.34) Как и в случае линейного фильтра, построенного по методу наименьших квадратов, алгоритм минимизации среднеквадратической ошибки работает с линейным нейроном. Исходя из этого, сигнал ошибки можно записать в следующем виде: е(п) = а(п) — х (п)зч(п). (3.35) Для построения фильтра Винера необходимо знать статистические характеристики второго порядка: матрицу корреляции а„для вектора входного сигнала х(п) и вектора взаимной корреляции г„в между х(п) и желаемым откликом а(п).
Однако эта информация на практике зачастую недоступна. В неизвестной среде можно использовать линейный адаптивный филыпр (11пеаг в1арйче 611ег). Под термином «адаптивность’* понимается возможность настраивать свободные параметры фильтра в соответствии со статистическими вариациями среды. Наиболее популярным алгоритмом такой настройки на непрерывной основе является алгоритм минимизации среднеквадратической ошибки, который самым тесным образом связан с фильтром Винера. 188 Глава 3.
Однослойный лерсвлтрон Следовательно, д е(п) = -х(п), д Е(зч) = — х(п)е(п). Используя полученный результат, можно оценить вектор градиента й(п) = -х(п)е(п). (3.36) И, наконец, используя формулу (3.36) для вектора градиента в методе наискорейшего спуска (3.12), можно сформулировать алгоритм минимизации среднеквадратической ошибки в следующем виде: зв(п + 1) = ч(п) + т1 х(п)е(п), (3.37) где т! — параметр скорости обучения. Контур обратной связи для вектора весов Ф(п) в алгоритме минимизации среднеквадратической ошибки ведет себя как низкочастотный фильтр (1ож-раза Й!гег), передающий низкочастотные компоненты сигнала ошибки и задерживающий его высокочастотные составляющие [434). Усредненная временная константаэтой фильтрации обратно пропорциональнапараметрускорости обучения т).
Следовательно, при малых значениях 11 процесс адаптации будет продвигаться медленно. При этом алгоритм минимизации среднеквадратической ошибки будет запоминать большее количество предшествующих данных, а значит, более точной будет фильтрация. Другими словами, величина, обратная параметру скорости обучения 11, является мерой памяти (шеая~ге о( шепюгу) алгоритма минимизации среднеквадратической ошибки.
В формуле (3.37) вместо зв(п) мы использовали зв(п). Этим подчеркивается тот факт, что алгоритм минимизации среднеквадратической ошибки только оценивает (езйшаге) вектор весовых коэффициентов на основе метода наискорейшего спуска. Следовательно, используя алгоритм минимизации среднеквадратической ошибки, можно пожертвовать одной из отличительных особенностей алгоритма наискорейшего спуска. В последнем вектор весовых коэффициентов и» (и) изменяется по детерминированной траектории в пространстве весов при заранее выбранном параметре 11.
В противоположность этому в алгоритме минимизации среднеквадратической ошибки вектор зг(п) перемещается по случайной траектории. По этой причине алгоритм минимизации среднеквадратической ошибки иногда называют стохастическим градиентным алгоритмом. При стремлении количества итераций в алгоритме 1.МЯ к бесконечности вектор зв(п) выписывает хаотичную траекторию (в соответствии с З.б. Алгоритм минимизации среднеквадратической ошибки 187 ТАБЛИЦА 3.1. Краткое описание алгоритма минимизации среднеквадратической ошибки Вектор входного сигнала = х(п) Желаемый отклик = Н(п) Ч Ф(0) = 0 Для п = 1, 2,…
е(п) = г?(п) — «т(п)х(п), Ф(п + 1) = Ф(п) + з) х(п)е(п) Обучающий пример Выбираемый пользователем параметр Инициализация весов Вычислительная схема Граф передачи сигнала для алгоритма минимизации среднеквадратической ошибки Объединяя формулы (3.35) и (3.37), эволюцию вектора весов в алгоритме минимиза- ции среднеквадратической ошибки можно представить в следуюшсм виде: Ф(п+ 1) = Ф(п) + з? х(п)[г?(п) — хт(п)Ф(п)] = = [1 — з) х(п)хт(п)]Е(п) + з) х(п)д(п), (3.38) где 1 — единичная матрица.
При использовании алгоритма минимизации среднеквад- ратической ошибки (3.39) где х ‘ — оператор единичной задержки, реализующей память алгоритма. Используя выражения (3.38) и (3.39), алгоритм минимизации среднеквадратической ошибки можно представить в виде графа передачи сигнала, показанного на рис. 3.3. На этом графе видно, что алгоритм минимизации среднеквадратической ошибки является всего лишь частным случаем стохастической системы с обратной свзиью (мосйазйс 1еебЬаск зуиеш).
Наличие обратной связи оказывает первостепенное влияние на сходимость алгоритма?.М8. принципами броуновского движения) вокруг Винеровского решения зч,. Важно отметить, что, в отличие от метода наискорейшего спуска, алгоритм минимизации среднеквадратической ошибки не требует знания статистических характеристик окружающей среды. Краткое описание алгоритма минимизации среднеквадратической ошибки представлено в табл. 3.1, из которой ясно видна его простота. Из таблицы видно, что для инициализации (?п?йа?гкайоп) алгоритма достаточно обнулить его начальный вектор весовых коэффициентов.
188 Глава 3. Однослойный персептрон Лк(к й(к) Рис. 3.3. Граф передачи си~нала для апюритма минимизации сред- неквадратической ошибки Лк(к) хт(и) Условия сходимости алгоритма ~МЗ Е[тт(п)] — и, при п — оо, (3.40) где тт, — решение Винера. К сожалению, такой критерий сходимости не имеет большого практичесюго значения, так как последовательность произвольных векторов, имеющих среднее значение О, также будет удовлетворять этому условию.
С практической точки зрения вопрос устойчивости играет роль именно в смысле среднеквадратической сходимосл(и (солтегяепсе ог (1(е теал яоцвге): Е[ез(п)] -+ сопя( при и — оо. (3.41) Из теории управления известно, что устойчивость системы с обратной связью определяется параметрами обратной связи. На рис. 3.3 видно, что нижний контур обратной связи обеспечивает изменение поведения алгоритма минимизации среднеквадратической ошибки. В частности, пропускная способность юнтура обратной связи определяется двумя параметрами: козффициентом сюрости обучения 11 и вектором входного сигнала х(п). Таким образом, можно заключить, что сходимость (и устойчивость) алгоритма минимизации среднеквадратической ошибки зависит от статистических характеристик входного вектора х(п) и значения параметра т).
Другими словами, для каждой среды, из которой поступают входные векторы, следует подбирать собственный параметр скорости обучения (), который обеспечит сходимость алгоритма 1,МБ. Первым критерием сходимости алгоритма минимизации среднеквадратической ошибки является сходимослзь в среднем (сопчегяелсе оГ бте шеал): З.б.
Алюритм минимизации средиеквадратической ошибки 189 К сожалению, детальный анализ сходимости в смысле среднеквадратического значения для алгоритма ЬМЯ чрезвычайно сложен. Чтобы его математически упростить, сделаем следующие предположения. 1. Векторы входных сигналов х(1), х(2),… являются статистически независимыми друг от друга. 2. В момент времени и вектор входного сигнала х(п) является статистически независимым от всех предыдущих желаемых откликов, т.е.
41), д(2),…, И(п — 1). 3. В момент времени п желаемый отклик с1(п) зависит от вектора х(п), ио статистически не зависит от всех предыдущих значений желаемого отклика. 4. Вектор входного сигнала х(п) и желаемый отклик д(п) выбираются из множества, подчиняющегося распределению Гаусса. 2 0<Ч <— )~йЪЗХ (3.42) где 3 — наибольшее собственное значение (1агйез1 е)йепча!ие) матрицы корреляции К,. В типичных приложениях алгоритма ЬМБ значение 3, как правило, не известно. Чтобы обойти эту сложность, в качестве оценки сверху значения Х можно использовать след (пасе) матрицы К,. В этом случае условие (3.42) можно переписать в следующем виде: 2 )’ (3.43) где п[К,) — след матрицы К,. По определению след квадратной матрицы определяется как сумма ее диагональных элементов. Так как каждый из диагональных элементов матрицы корреляции К, является среднеквадратическим значением соответствующего входного сигнала, условие сходимости алгоритма минимизации среднеквадратической ошибки можно сформулировать в виде 2 0<э) < сумма среднеквадратических значений входных сигналов (3.44) Статистический анализ алгоритма минимизации среднеквадратической ошибки при наличии вышеуказанных допущений получил название теории независимости (1пдерепдепсе Гаеогу) [1138).
С учетом допущений теории независимости и достаточно малого значения параметра скорости обучения в [434) показано, что алгоритм минимизации средне- квадратической ошибки сходится в смысле среднеквадратического значения, если з) удовлепюряет условию 190 Глава 3. Однослойный лерселтрон Если параметр скорости обучения удовлетворяет этому условию, то алгоритм минимизации среднеквадратической ошибки сходится также и в смысле среднего значения. Это значит, что сходимость в смысле средиеквадратического значения является достаточным условием сходимости в среднем.









































![{displaystyle C_{X|Y_{1},ldots ,Y_{k-1}}=mathrm {E} [(x-{hat {x}}_{k-1})(x-{hat {x}}_{k-1})^{T}]=C_{e_{k-1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864670362eb4bba0498222e852c5dea705e30bd2)
![{displaystyle {begin{aligned}C_{Y_{k}|X}&=mathrm {E} [(y_{k}-{bar {y}}_{k})(y_{k}-{bar {y}}_{k})^{T}]\&=mathrm {E} [(A(x-{bar {x}}_{k-1})+z)(A(x-{bar {x}}_{k-1})+z)^{T}]\&=AC_{e_{k-1}}A^{T}+C_{Z}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ded2fc5f8faaa6b8d3773dd4eb7a2cd27a457463)

![{displaystyle {begin{aligned}C_{e_{k-1}{tilde {Y}}_{k}}&=mathrm {E} [(x-{hat {x}}_{k-1})(y_{k}-{bar {y}}_{k})^{T}]\&=mathrm {E} [(x-{hat {x}}_{k-1})(A(x-{hat {x}}_{k-1})+z)^{T}]\&=C_{e_{k-1}}A^{T}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e73f96aac3cfb9fa6d74b097374f19dacd8daf7)











![{displaystyle operatorname {cov} (Z)=operatorname {E} [zz^{T}]=left[{begin{array}{cccc}1&2&3&4\2&5&8&9\3&8&6&10\4&9&10&15end{array}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90889a9de7192d317decb8381ca25cda49892b5c)
![{displaystyle C_{Y}=left[{begin{array}{ccc}E[z_{1},z_{1}]&E[z_{2},z_{1}]&E[z_{3},z_{1}]\E[z_{1},z_{2}]&E[z_{2},z_{2}]&E[z_{3},z_{2}]\E[z_{1},z_{3}]&E[z_{2},z_{3}]&E[z_{3},z_{3}]end{array}}right]=left[{begin{array}{ccc}1&2&3\2&5&8\3&8&6end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c0831c4af6cc131c13cd4da73e21ee08aac40c)
![{displaystyle C_{YX}=left[{begin{array}{c}E[z_{4},z_{1}]\E[z_{4},z_{2}]\E[z_{4},z_{3}]end{array}}right]=left[{begin{array}{c}4\9\10end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0b4e00619f85de1c0967817d68b6b154557af03)
![{displaystyle C_{Y}^{-1}C_{YX}=left[{begin{array}{ccc}4.85&-1.71&-0.142\-1.71&0.428&0.2857\-0.142&0.2857&-0.1429end{array}}right]left[{begin{array}{c}4\9\10end{array}}right]=left[{begin{array}{c}2.57\-0.142\0.5714end{array}}right]=W^{T}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f29d9505d5f630feae8a4566c23bae8dd82fd5d)