Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1
vdots
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)
vdots
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$begin{multline*}
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\[0.1cm]
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
end{multline*},$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$begin{multline*}
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
end{multline*}$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$ begin{multline*}
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
end{multline*} $$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
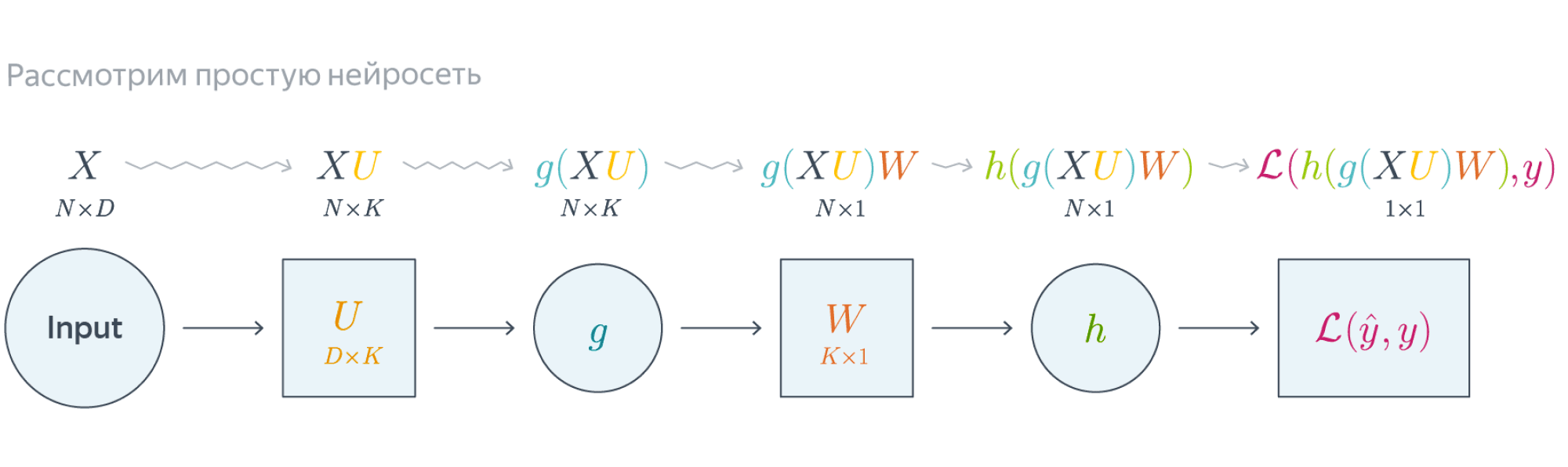
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$)Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
This article is about the computer algorithm. For the biological process, see neural backpropagation.
Backpropagation can also refer to the way the result of a playout is propagated up the search tree in Monte Carlo tree search.
In machine learning, backpropagation (backprop,[1] BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions generally. These classes of algorithms are all referred to generically as «backpropagation».[2] In fitting a neural network, backpropagation computes the gradient of the loss function with respect to the weights of the network for a single input–output example, and does so efficiently, unlike a naive direct computation of the gradient with respect to each weight individually. This efficiency makes it feasible to use gradient methods for training multilayer networks, updating weights to minimize loss; gradient descent, or variants such as stochastic gradient descent, are commonly used. The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight by the chain rule, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this is an example of dynamic programming.[3]
The term backpropagation strictly refers only to the algorithm for computing the gradient, not how the gradient is used; however, the term is often used loosely to refer to the entire learning algorithm, including how the gradient is used, such as by stochastic gradient descent.[4] Backpropagation generalizes the gradient computation in the delta rule, which is the single-layer version of backpropagation, and is in turn generalized by automatic differentiation, where backpropagation is a special case of reverse accumulation (or «reverse mode»).[5] The term backpropagation and its general use in neural networks was announced in Rumelhart, Hinton & Williams (1986a), then elaborated and popularized in Rumelhart, Hinton & Williams (1986b), but the technique was independently rediscovered many times, and had many predecessors dating to the 1960s; see § History.[6] A modern overview is given in the deep learning textbook by Goodfellow, Bengio & Courville (2016).[7]
Overview[edit]
Backpropagation computes the gradient in weight space of a feedforward neural network, with respect to a loss function. Denote:
: input (vector of features)
: target output
- For classification, output will be a vector of class probabilities (e.g.,
, and target output is a specific class, encoded by the one-hot/dummy variable (e.g.,
).
- For classification, output will be a vector of class probabilities (e.g.,
: loss function or «cost function»[a]
- For classification, this is usually cross entropy (XC, log loss), while for regression it is usually squared error loss (SEL).
: the number of layers
: the weights between layer
and
, where
is the weight between the
-th node in layer
and the
-th node in layer
[b]
: activation functions at layer
- For classification the last layer is usually the logistic function for binary classification, and softmax (softargmax) for multi-class classification, while for the hidden layers this was traditionally a sigmoid function (logistic function or others) on each node (coordinate), but today is more varied, with rectifier (ramp, ReLU) being common.
In the derivation of backpropagation, other intermediate quantities are used; they are introduced as needed below. Bias terms are not treated specially, as they correspond to a weight with a fixed input of 1. For the purpose of backpropagation, the specific loss function and activation functions do not matter, as long as they and their derivatives can be evaluated efficiently. Traditional activation functions include but are not limited to sigmoid, tanh, and ReLU. Since, swish,[8] mish,[9] and other activation functions were proposed as well.
The overall network is a combination of function composition and matrix multiplication:
For a training set there will be a set of input–output pairs, 



Note the distinction: during model evaluation, the weights are fixed, while the inputs vary (and the target output may be unknown), and the network ends with the output layer (it does not include the loss function). During model training, the input–output pair is fixed, while the weights vary, and the network ends with the loss function.
Backpropagation computes the gradient for a fixed input–output pair 



Informally, the key point is that since the only way a weight in 






Backpropagation can be expressed for simple feedforward networks in terms of matrix multiplication, or more generally in terms of the adjoint graph.
Matrix multiplication[edit]
For the basic case of a feedforward network, where nodes in each layer are connected only to nodes in the immediate next layer (without skipping any layers), and there is a loss function that computes a scalar loss for the final output, backpropagation can be understood simply by matrix multiplication.[c] Essentially, backpropagation evaluates the expression for the derivative of the cost function as a product of derivatives between each layer from right to left – «backwards» – with the gradient of the weights between each layer being a simple modification of the partial products (the «backwards propagated error»).
Given an input–output pair 
To compute this, one starts with the input 






The derivative of the loss in terms of the inputs is given by the chain rule; note that each term is a total derivative, evaluated at the value of the network (at each node) on the input 
where 
These terms are: the derivative of the loss function;[d] the derivatives of the activation functions;[e] and the matrices of weights:[f]
The gradient 
Backpropagation then consists essentially of evaluating this expression from right to left (equivalently, multiplying the previous expression for the derivative from left to right), computing the gradient at each layer on the way; there is an added step, because the gradient of the weights isn’t just a subexpression: there’s an extra multiplication.
Introducing the auxiliary quantity 


Note that 

The gradient of the weights in layer 
The factor of 




The 
The gradients of the weights can thus be computed using a few matrix multiplications for each level; this is backpropagation.
Compared with naively computing forwards (using the 
there are two key differences with backpropagation:
- Computing
in terms of
avoids the obvious duplicate multiplication of layers
and beyond.
- Multiplying starting from
– propagating the error backwards – means that each step simply multiplies a vector (
) by the matrices of weights
and derivatives of activations
. By contrast, multiplying forwards, starting from the changes at an earlier layer, means that each multiplication multiplies a matrix by a matrix. This is much more expensive, and corresponds to tracking every possible path of a change in one layer
forward to changes in the layer
(for multiplying
by
, with additional multiplications for the derivatives of the activations), which unnecessarily computes the intermediate quantities of how weight changes affect the values of hidden nodes.
Adjoint graph[edit]
|
This section needs expansion. You can help by adding to it. (November 2019) |
For more general graphs, and other advanced variations, backpropagation can be understood in terms of automatic differentiation, where backpropagation is a special case of reverse accumulation (or «reverse mode»).[5]
Intuition[edit]
Motivation[edit]
The goal of any supervised learning algorithm is to find a function that best maps a set of inputs to their correct output. The motivation for backpropagation is to train a multi-layered neural network such that it can learn the appropriate internal representations to allow it to learn any arbitrary mapping of input to output.[10]
Learning as an optimization problem[edit]
To understand the mathematical derivation of the backpropagation algorithm, it helps to first develop some intuition about the relationship between the actual output of a neuron and the correct output for a particular training example. Consider a simple neural network with two input units, one output unit and no hidden units, and in which each neuron uses a linear output (unlike most work on neural networks, in which mapping from inputs to outputs is non-linear)[g] that is the weighted sum of its input.
A simple neural network with two input units (each with a single input) and one output unit (with two inputs)
Initially, before training, the weights will be set randomly. Then the neuron learns from training examples, which in this case consist of a set of tuples 





As an example consider a regression problem using the square error as a loss:
where E is the discrepancy or error.
Consider the network on a single training case: 


Error surface of a linear neuron for a single training case
However, the output of a neuron depends on the weighted sum of all its inputs:
where 

In this example, upon injecting the training data 

Then, the loss function 


One commonly used algorithm to find the set of weights that minimizes the error is gradient descent. By backpropagation, the steepest descent direction is calculated of the loss function versus the present synaptic weights. Then, the weights can be modified along the steepest descent direction, and the error is minimized in an efficient way.
Derivation[edit]
The gradient descent method involves calculating the derivative of the loss function with respect to the weights of the network. This is normally done using backpropagation. Assuming one output neuron,[h] the squared error function is
where
is the loss for the output
and target value
,
is the target output for a training sample, and
is the actual output of the output neuron.
For each neuron 

where the activation function 
which has a convenient derivative of:
The input 







Finding the derivative of the error[edit]
Diagram of an artificial neural network to illustrate the notation used here
Calculating the partial derivative of the error with respect to a weight 
-
(Eq. 1)
In the last factor of the right-hand side of the above, only one term in the sum 

-
(Eq. 2)
If the neuron is in the first layer after the input layer, 

The derivative of the output of neuron 
-
(Eq. 3)
which for the logistic activation function
This is the reason why backpropagation requires the activation function to be differentiable. (Nevertheless, the ReLU activation function, which is non-differentiable at 0, has become quite popular, e.g. in AlexNet)
The first factor is straightforward to evaluate if the neuron is in the output layer, because then 
-
(Eq. 4)
If half of the square error is used as loss function we can rewrite it as
However, if 


Considering 


and taking the total derivative with respect to 
-
(Eq. 5)
Therefore, the derivative with respect to 




Substituting Eq. 2, Eq. 3 Eq.4 and Eq. 5 in Eq. 1 we obtain:
with
if 
To update the weight 
















Second-order gradient descent[edit]
Using a Hessian matrix of second-order derivatives of the error function, the Levenberg-Marquardt algorithm often converges faster than first-order gradient descent, especially when the topology of the error function is complicated.[11][12] It may also find solutions in smaller node counts for which other methods might not converge.[12] The Hessian can be approximated by the Fisher information matrix.[13]
Loss function[edit]
The loss function is a function that maps values of one or more variables onto a real number intuitively representing some «cost» associated with those values. For backpropagation, the loss function calculates the difference between the network output and its expected output, after a training example has propagated through the network.
Assumptions[edit]
The mathematical expression of the loss function must fulfill two conditions in order for it to be possibly used in backpropagation.[14] The first is that it can be written as an average 



Example loss function[edit]
Let 

Select an error function 


The error function over 
Limitations[edit]
Gradient descent may find a local minimum instead of the global minimum.
- Gradient descent with backpropagation is not guaranteed to find the global minimum of the error function, but only a local minimum; also, it has trouble crossing plateaus in the error function landscape. This issue, caused by the non-convexity of error functions in neural networks, was long thought to be a major drawback, but Yann LeCun et al. argue that in many practical problems, it is not.[15]
- Backpropagation learning does not require normalization of input vectors; however, normalization could improve performance.[16]
- Backpropagation requires the derivatives of activation functions to be known at network design time.
History[edit]
The term backpropagation and its general use in neural networks was announced in Rumelhart, Hinton & Williams (1986a), then elaborated and popularized in Rumelhart, Hinton & Williams (1986b), but the technique was independently rediscovered many times, and had many predecessors dating to the 1960s.[6][17]
The basics of continuous backpropagation were derived in the context of control theory by Henry J. Kelley in 1960,[18] and by Arthur E. Bryson in 1961.[19][20][21][22][23] They used principles of dynamic programming. In 1962, Stuart Dreyfus published a simpler derivation based only on the chain rule.[24] Bryson and Ho described it as a multi-stage dynamic system optimization method in 1969.[25][26] Backpropagation was derived by multiple researchers in the early 60’s[22] and implemented to run on computers as early as 1970 by Seppo Linnainmaa.[27][28][29] Paul Werbos was first in the US to propose that it could be used for neural nets after analyzing it in depth in his 1974 dissertation.[30] While not applied to neural networks, in 1970 Linnainmaa published the general method for automatic differentiation (AD).[28][29] Although very controversial, some scientists believe this was actually the first step toward developing a back-propagation algorithm.[22][23][27][31] In 1973 Dreyfus adapts parameters of controllers in proportion to error gradients.[32] In 1974 Werbos mentioned the possibility of applying this principle to artificial neural networks,[30] and in 1982 he applied Linnainmaa’s AD method to non-linear functions.[23][33]
Later the Werbos method was rediscovered and described in 1985 by Parker,[34][35] and in 1986 by Rumelhart, Hinton and Williams.[17][35][36] Rumelhart, Hinton and Williams showed experimentally that this method can generate useful internal representations of incoming data in hidden layers of neural networks.[10][37][38] Yann LeCun proposed the modern form of the back-propagation learning algorithm for neural networks in his PhD thesis in 1987. In 1993, Eric Wan won an international pattern recognition contest through backpropagation.[22][39]
During the 2000s it fell out of favour[citation needed], but returned in the 2010s, benefitting from cheap, powerful GPU-based computing systems. This has been especially so in speech recognition, machine vision, natural language processing, and language structure learning research (in which it has been used to explain a variety of phenomena related to first[40] and second language learning.[41]).
Error backpropagation has been suggested to explain human brain ERP components like the N400 and P600.[42]
See also[edit]
- Artificial neural network
- Neural circuit
- Catastrophic interference
- Ensemble learning
- AdaBoost
- Overfitting
- Neural backpropagation
- Backpropagation through time
Notes[edit]
- ^ Use
for the loss function to allow
to be used for the number of layers
- ^ This follows Nielsen (2015), and means (left) multiplication by the matrix
corresponds to converting output values of layer
to input values of layer
: columns correspond to input coordinates, rows correspond to output coordinates.
- ^ This section largely follows and summarizes Nielsen (2015).
- ^ The derivative of the loss function is a covector, since the loss function is a scalar-valued function of several variables.
- ^ The activation function is applied to each node separately, so the derivative is just the diagonal matrix of the derivative on each node. This is often represented as the Hadamard product with the vector of derivatives, denoted by
, which is mathematically identical but better matches the internal representation of the derivatives as a vector, rather than a diagonal matrix.
- ^ Since matrix multiplication is linear, the derivative of multiplying by a matrix is just the matrix:
.
- ^ One may notice that multi-layer neural networks use non-linear activation functions, so an example with linear neurons seems obscure. However, even though the error surface of multi-layer networks are much more complicated, locally they can be approximated by a paraboloid. Therefore, linear neurons are used for simplicity and easier understanding.
- ^ There can be multiple output neurons, in which case the error is the squared norm of the difference vector.
References[edit]
- ^ Goodfellow, Bengio & Courville 2016, p. 200, «The back-propagation algorithm (Rumelhart et al., 1986a), often simply called backprop, …»
- ^ Goodfellow, Bengio & Courville 2016, p. 200, «Furthermore, back-propagation is often misunderstood as being specific to multi-layer neural networks, but in principle it can compute derivatives of any function»
- ^ Goodfellow, Bengio & Courville 2016, p. 214, «This table-filling strategy is sometimes called dynamic programming.»
- ^ Goodfellow, Bengio & Courville 2016, p. 200, «The term back-propagation is often misunderstood as meaning the whole learning algorithm for multilayer neural networks. Backpropagation refers only to the method for computing the gradient, while other algorithms, such as stochastic gradient descent, is used to perform learning using this gradient.»
- ^ a b Goodfellow, Bengio & Courville (2016, p. 217–218), «The back-propagation algorithm described here is only one approach to automatic differentiation. It is a special case of a broader class of techniques called reverse mode accumulation.»
- ^ a b Goodfellow, Bengio & Courville (2016, p. 221), «Efficient applications of the chain rule based on dynamic programming began to appear in the 1960s and 1970s, mostly for control applications (Kelley, 1960; Bryson and Denham, 1961; Dreyfus, 1962; Bryson and Ho, 1969; Dreyfus, 1973) but also for sensitivity analysis (Linnainmaa, 1976). … The idea was finally developed in practice after being independently rediscovered in different ways (LeCun, 1985; Parker, 1985; Rumelhart et al., 1986a). The book Parallel Distributed Processing presented the results of some of the first successful experiments with back-propagation in a chapter (Rumelhart et al., 1986b) that contributed greatly to the popularization of back-propagation and initiated a very active period of research in multilayer neural networks.»
- ^ Goodfellow, Bengio & Courville (2016, 6.5 Back-Propagation and Other Differentiation Algorithms, pp. 200–220)
- ^ Ramachandran, Prajit; Zoph, Barret; Le, Quoc V. (2017-10-27). «Searching for Activation Functions». arXiv:1710.05941 [cs.NE].
- ^ Misra, Diganta (2019-08-23). «Mish: A Self Regularized Non-Monotonic Activation Function». arXiv:1908.08681 [cs.LG].
- ^ a b Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (1986a). «Learning representations by back-propagating errors». Nature. 323 (6088): 533–536. Bibcode:1986Natur.323..533R. doi:10.1038/323533a0. S2CID 205001834.
- ^ Tan, Hong Hui; Lim, King Han (2019). «Review of second-order optimization techniques in artificial neural networks backpropagation». IOP Conference Series: Materials Science and Engineering. 495 (1): 012003. Bibcode:2019MS&E..495a2003T. doi:10.1088/1757-899X/495/1/012003. S2CID 208124487.
- ^ a b Wiliamowski, Bogdan; Yu, Hao (June 2010). «Improved Computation for Levenberg–Marquardt Training» (PDF). IEEE Transactions on Neural Networks and Learning Systems. 21 (6).
- ^ Martens, James (August 2020). «New Insights and Perspectives on the Natural Gradient Method» (PDF). Journal of Machine Learning Research (21). arXiv:1412.1193.
- ^ Nielsen (2015), «[W]hat assumptions do we need to make about our cost function … in order that backpropagation can be applied? The first assumption we need is that the cost function can be written as an average … over cost functions … for individual training examples … The second assumption we make about the cost is that it can be written as a function of the outputs from the neural network …»
- ^ LeCun, Yann; Bengio, Yoshua; Hinton, Geoffrey (2015). «Deep learning». Nature. 521 (7553): 436–444. Bibcode:2015Natur.521..436L. doi:10.1038/nature14539. PMID 26017442. S2CID 3074096.
- ^ Buckland, Matt; Collins, Mark (2002). AI Techniques for Game Programming. Boston: Premier Press. ISBN 1-931841-08-X.
- ^ a b Rumelhart; Hinton; Williams (1986). «Learning representations by back-propagating errors» (PDF). Nature. 323 (6088): 533–536. Bibcode:1986Natur.323..533R. doi:10.1038/323533a0. S2CID 205001834.
- ^ Kelley, Henry J. (1960). «Gradient theory of optimal flight paths». ARS Journal. 30 (10): 947–954. doi:10.2514/8.5282.
- ^ Bryson, Arthur E. (1962). «A gradient method for optimizing multi-stage allocation processes». Proceedings of the Harvard Univ. Symposium on digital computers and their applications, 3–6 April 1961. Cambridge: Harvard University Press. OCLC 498866871.
- ^ Dreyfus, Stuart E. (1990). «Artificial Neural Networks, Back Propagation, and the Kelley-Bryson Gradient Procedure». Journal of Guidance, Control, and Dynamics. 13 (5): 926–928. Bibcode:1990JGCD…13..926D. doi:10.2514/3.25422.
- ^ Mizutani, Eiji; Dreyfus, Stuart; Nishio, Kenichi (July 2000). «On derivation of MLP backpropagation from the Kelley-Bryson optimal-control gradient formula and its application» (PDF). Proceedings of the IEEE International Joint Conference on Neural Networks.
- ^ a b c d Schmidhuber, Jürgen (2015). «Deep learning in neural networks: An overview». Neural Networks. 61: 85–117. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003. PMID 25462637. S2CID 11715509.
- ^ a b c Schmidhuber, Jürgen (2015). «Deep Learning». Scholarpedia. 10 (11): 32832. Bibcode:2015SchpJ..1032832S. doi:10.4249/scholarpedia.32832.
- ^ Dreyfus, Stuart (1962). «The numerical solution of variational problems». Journal of Mathematical Analysis and Applications. 5 (1): 30–45. doi:10.1016/0022-247x(62)90004-5.
- ^ Russell, Stuart; Norvig, Peter (1995). Artificial Intelligence : A Modern Approach. Englewood Cliffs: Prentice Hall. p. 578. ISBN 0-13-103805-2.
The most popular method for learning in multilayer networks is called Back-propagation. It was first invented in 1969 by Bryson and Ho, but was more or less ignored until the mid-1980s.
- ^ Bryson, Arthur Earl; Ho, Yu-Chi (1969). Applied optimal control: optimization, estimation, and control. Waltham: Blaisdell. OCLC 3801.
- ^ a b Griewank, Andreas (2012). «Who Invented the Reverse Mode of Differentiation?». Optimization Stories. Documenta Matematica, Extra Volume ISMP. pp. 389–400. S2CID 15568746.
- ^ a b Seppo Linnainmaa (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. Master’s Thesis (in Finnish), Univ. Helsinki, 6–7.
- ^ a b Linnainmaa, Seppo (1976). «Taylor expansion of the accumulated rounding error». BIT Numerical Mathematics. 16 (2): 146–160. doi:10.1007/bf01931367. S2CID 122357351.
- ^ a b The thesis, and some supplementary information, can be found in his book, Werbos, Paul J. (1994). The Roots of Backpropagation : From Ordered Derivatives to Neural Networks and Political Forecasting. New York: John Wiley & Sons. ISBN 0-471-59897-6.
- ^ Griewank, Andreas; Walther, Andrea (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition. SIAM. ISBN 978-0-89871-776-1.
- ^ Dreyfus, Stuart (1973). «The computational solution of optimal control problems with time lag». IEEE Transactions on Automatic Control. 18 (4): 383–385. doi:10.1109/tac.1973.1100330.
- ^ Werbos, Paul (1982). «Applications of advances in nonlinear sensitivity analysis» (PDF). System modeling and optimization. Springer. pp. 762–770.
- ^ Parker, D.B. (1985). «Learning Logic». Center for Computational Research in Economics and Management Science. Cambridge MA: Massachusetts Institute of Technology.
- ^ a b Hertz, John (1991). Introduction to the theory of neural computation. Krogh, Anders., Palmer, Richard G. Redwood City, Calif.: Addison-Wesley. p. 8. ISBN 0-201-50395-6. OCLC 21522159.
- ^ Anderson, James Arthur; Rosenfeld, Edward, eds. (1988). Neurocomputing Foundations of research. MIT Press. ISBN 0-262-01097-6. OCLC 489622044.
- ^ Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (1986b). «8. Learning Internal Representations by Error Propagation». In Rumelhart, David E.; McClelland, James L. (eds.). Parallel Distributed Processing : Explorations in the Microstructure of Cognition. Vol. 1 : Foundations. Cambridge: MIT Press. ISBN 0-262-18120-7.
- ^ Alpaydin, Ethem (2010). Introduction to Machine Learning. MIT Press. ISBN 978-0-262-01243-0.
- ^ Wan, Eric A. (1994). «Time Series Prediction by Using a Connectionist Network with Internal Delay Lines». In Weigend, Andreas S.; Gershenfeld, Neil A. (eds.). Time Series Prediction : Forecasting the Future and Understanding the Past. Proceedings of the NATO Advanced Research Workshop on Comparative Time Series Analysis. Vol. 15. Reading: Addison-Wesley. pp. 195–217. ISBN 0-201-62601-2. S2CID 12652643.
- ^ Chang, Franklin; Dell, Gary S.; Bock, Kathryn (2006). «Becoming syntactic». Psychological Review. 113 (2): 234–272. doi:10.1037/0033-295x.113.2.234. PMID 16637761.
- ^ Janciauskas, Marius; Chang, Franklin (2018). «Input and Age-Dependent Variation in Second Language Learning: A Connectionist Account». Cognitive Science. 42: 519–554. doi:10.1111/cogs.12519. PMC 6001481. PMID 28744901.
- ^ Fitz, Hartmut; Chang, Franklin (2019). «Language ERPs reflect learning through prediction error propagation». Cognitive Psychology. 111: 15–52. doi:10.1016/j.cogpsych.2019.03.002. hdl:21.11116/0000-0003-474D-8. PMID 30921626. S2CID 85501792.
Further reading[edit]
- Goodfellow, Ian; Bengio, Yoshua; Courville, Aaron (2016). «6.5 Back-Propagation and Other Differentiation Algorithms». Deep Learning. MIT Press. pp. 200–220. ISBN 9780262035613.
- Nielsen, Michael A. (2015). «How the backpropagation algorithm works». Neural Networks and Deep Learning. Determination Press.
- McCaffrey, James (October 2012). «Neural Network Back-Propagation for Programmers». MSDN Magazine.
- Rojas, Raúl (1996). «The Backpropagation Algorithm» (PDF). Neural Networks : A Systematic Introduction. Berlin: Springer. ISBN 3-540-60505-3.
External links[edit]
- Backpropagation neural network tutorial at the Wikiversity
- Bernacki, Mariusz; Włodarczyk, Przemysław (2004). «Principles of training multi-layer neural network using backpropagation».
- Karpathy, Andrej (2016). «Lecture 4: Backpropagation, Neural Networks 1». CS231n. Stanford University. Archived from the original on 2021-12-12 – via YouTube.
- «What is Backpropagation Really Doing?». 3Blue1Brown. November 3, 2017. Archived from the original on 2021-12-12 – via YouTube.
- Putta, Sudeep Raja (2022). «Yet Another Derivation of Backpropagation in Matrix Form».
This article is about the computer algorithm. For the biological process, see neural backpropagation.
Backpropagation can also refer to the way the result of a playout is propagated up the search tree in Monte Carlo tree search.
In machine learning, backpropagation (backprop,[1] BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions generally. These classes of algorithms are all referred to generically as «backpropagation».[2] In fitting a neural network, backpropagation computes the gradient of the loss function with respect to the weights of the network for a single input–output example, and does so efficiently, unlike a naive direct computation of the gradient with respect to each weight individually. This efficiency makes it feasible to use gradient methods for training multilayer networks, updating weights to minimize loss; gradient descent, or variants such as stochastic gradient descent, are commonly used. The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight by the chain rule, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this is an example of dynamic programming.[3]
The term backpropagation strictly refers only to the algorithm for computing the gradient, not how the gradient is used; however, the term is often used loosely to refer to the entire learning algorithm, including how the gradient is used, such as by stochastic gradient descent.[4] Backpropagation generalizes the gradient computation in the delta rule, which is the single-layer version of backpropagation, and is in turn generalized by automatic differentiation, where backpropagation is a special case of reverse accumulation (or «reverse mode»).[5] The term backpropagation and its general use in neural networks was announced in Rumelhart, Hinton & Williams (1986a), then elaborated and popularized in Rumelhart, Hinton & Williams (1986b), but the technique was independently rediscovered many times, and had many predecessors dating to the 1960s; see § History.[6] A modern overview is given in the deep learning textbook by Goodfellow, Bengio & Courville (2016).[7]
Overview[edit]
Backpropagation computes the gradient in weight space of a feedforward neural network, with respect to a loss function. Denote:
: input (vector of features)
: target output
- For classification, output will be a vector of class probabilities (e.g.,
, and target output is a specific class, encoded by the one-hot/dummy variable (e.g.,
).
- For classification, output will be a vector of class probabilities (e.g.,
: loss function or «cost function»[a]
- For classification, this is usually cross entropy (XC, log loss), while for regression it is usually squared error loss (SEL).
: the number of layers
: the weights between layer
and
, where
is the weight between the
-th node in layer
and the
-th node in layer
[b]
: activation functions at layer
- For classification the last layer is usually the logistic function for binary classification, and softmax (softargmax) for multi-class classification, while for the hidden layers this was traditionally a sigmoid function (logistic function or others) on each node (coordinate), but today is more varied, with rectifier (ramp, ReLU) being common.
In the derivation of backpropagation, other intermediate quantities are used; they are introduced as needed below. Bias terms are not treated specially, as they correspond to a weight with a fixed input of 1. For the purpose of backpropagation, the specific loss function and activation functions do not matter, as long as they and their derivatives can be evaluated efficiently. Traditional activation functions include but are not limited to sigmoid, tanh, and ReLU. Since, swish,[8] mish,[9] and other activation functions were proposed as well.
The overall network is a combination of function composition and matrix multiplication:
For a training set there will be a set of input–output pairs, 



Note the distinction: during model evaluation, the weights are fixed, while the inputs vary (and the target output may be unknown), and the network ends with the output layer (it does not include the loss function). During model training, the input–output pair is fixed, while the weights vary, and the network ends with the loss function.
Backpropagation computes the gradient for a fixed input–output pair 



Informally, the key point is that since the only way a weight in 






Backpropagation can be expressed for simple feedforward networks in terms of matrix multiplication, or more generally in terms of the adjoint graph.
Matrix multiplication[edit]
For the basic case of a feedforward network, where nodes in each layer are connected only to nodes in the immediate next layer (without skipping any layers), and there is a loss function that computes a scalar loss for the final output, backpropagation can be understood simply by matrix multiplication.[c] Essentially, backpropagation evaluates the expression for the derivative of the cost function as a product of derivatives between each layer from right to left – «backwards» – with the gradient of the weights between each layer being a simple modification of the partial products (the «backwards propagated error»).
Given an input–output pair 
To compute this, one starts with the input 






The derivative of the loss in terms of the inputs is given by the chain rule; note that each term is a total derivative, evaluated at the value of the network (at each node) on the input 
where 
These terms are: the derivative of the loss function;[d] the derivatives of the activation functions;[e] and the matrices of weights:[f]
The gradient 
Backpropagation then consists essentially of evaluating this expression from right to left (equivalently, multiplying the previous expression for the derivative from left to right), computing the gradient at each layer on the way; there is an added step, because the gradient of the weights isn’t just a subexpression: there’s an extra multiplication.
Introducing the auxiliary quantity 


Note that 

The gradient of the weights in layer 
The factor of 




The 
The gradients of the weights can thus be computed using a few matrix multiplications for each level; this is backpropagation.
Compared with naively computing forwards (using the 
there are two key differences with backpropagation:
- Computing
in terms of
avoids the obvious duplicate multiplication of layers
and beyond.
- Multiplying starting from
– propagating the error backwards – means that each step simply multiplies a vector (
) by the matrices of weights
and derivatives of activations
. By contrast, multiplying forwards, starting from the changes at an earlier layer, means that each multiplication multiplies a matrix by a matrix. This is much more expensive, and corresponds to tracking every possible path of a change in one layer
forward to changes in the layer
(for multiplying
by
, with additional multiplications for the derivatives of the activations), which unnecessarily computes the intermediate quantities of how weight changes affect the values of hidden nodes.
Adjoint graph[edit]
|
This section needs expansion. You can help by adding to it. (November 2019) |
For more general graphs, and other advanced variations, backpropagation can be understood in terms of automatic differentiation, where backpropagation is a special case of reverse accumulation (or «reverse mode»).[5]
Intuition[edit]
Motivation[edit]
The goal of any supervised learning algorithm is to find a function that best maps a set of inputs to their correct output. The motivation for backpropagation is to train a multi-layered neural network such that it can learn the appropriate internal representations to allow it to learn any arbitrary mapping of input to output.[10]
Learning as an optimization problem[edit]
To understand the mathematical derivation of the backpropagation algorithm, it helps to first develop some intuition about the relationship between the actual output of a neuron and the correct output for a particular training example. Consider a simple neural network with two input units, one output unit and no hidden units, and in which each neuron uses a linear output (unlike most work on neural networks, in which mapping from inputs to outputs is non-linear)[g] that is the weighted sum of its input.
A simple neural network with two input units (each with a single input) and one output unit (with two inputs)
Initially, before training, the weights will be set randomly. Then the neuron learns from training examples, which in this case consist of a set of tuples 





As an example consider a regression problem using the square error as a loss:
where E is the discrepancy or error.
Consider the network on a single training case: 


Error surface of a linear neuron for a single training case
However, the output of a neuron depends on the weighted sum of all its inputs:
where 

In this example, upon injecting the training data 

Then, the loss function 


One commonly used algorithm to find the set of weights that minimizes the error is gradient descent. By backpropagation, the steepest descent direction is calculated of the loss function versus the present synaptic weights. Then, the weights can be modified along the steepest descent direction, and the error is minimized in an efficient way.
Derivation[edit]
The gradient descent method involves calculating the derivative of the loss function with respect to the weights of the network. This is normally done using backpropagation. Assuming one output neuron,[h] the squared error function is
where
is the loss for the output
and target value
,
is the target output for a training sample, and
is the actual output of the output neuron.
For each neuron 

where the activation function 
which has a convenient derivative of:
The input 







Finding the derivative of the error[edit]
Diagram of an artificial neural network to illustrate the notation used here
Calculating the partial derivative of the error with respect to a weight 
-
(Eq. 1)
In the last factor of the right-hand side of the above, only one term in the sum 

-
(Eq. 2)
If the neuron is in the first layer after the input layer, 

The derivative of the output of neuron 
-
(Eq. 3)
which for the logistic activation function
This is the reason why backpropagation requires the activation function to be differentiable. (Nevertheless, the ReLU activation function, which is non-differentiable at 0, has become quite popular, e.g. in AlexNet)
The first factor is straightforward to evaluate if the neuron is in the output layer, because then 
-
(Eq. 4)
If half of the square error is used as loss function we can rewrite it as
However, if 


Considering 


and taking the total derivative with respect to 
-
(Eq. 5)
Therefore, the derivative with respect to 




Substituting Eq. 2, Eq. 3 Eq.4 and Eq. 5 in Eq. 1 we obtain:
with
if 
To update the weight 
















Second-order gradient descent[edit]
Using a Hessian matrix of second-order derivatives of the error function, the Levenberg-Marquardt algorithm often converges faster than first-order gradient descent, especially when the topology of the error function is complicated.[11][12] It may also find solutions in smaller node counts for which other methods might not converge.[12] The Hessian can be approximated by the Fisher information matrix.[13]
Loss function[edit]
The loss function is a function that maps values of one or more variables onto a real number intuitively representing some «cost» associated with those values. For backpropagation, the loss function calculates the difference between the network output and its expected output, after a training example has propagated through the network.
Assumptions[edit]
The mathematical expression of the loss function must fulfill two conditions in order for it to be possibly used in backpropagation.[14] The first is that it can be written as an average 



Example loss function[edit]
Let 

Select an error function 


The error function over 
Limitations[edit]
Gradient descent may find a local minimum instead of the global minimum.
- Gradient descent with backpropagation is not guaranteed to find the global minimum of the error function, but only a local minimum; also, it has trouble crossing plateaus in the error function landscape. This issue, caused by the non-convexity of error functions in neural networks, was long thought to be a major drawback, but Yann LeCun et al. argue that in many practical problems, it is not.[15]
- Backpropagation learning does not require normalization of input vectors; however, normalization could improve performance.[16]
- Backpropagation requires the derivatives of activation functions to be known at network design time.
History[edit]
The term backpropagation and its general use in neural networks was announced in Rumelhart, Hinton & Williams (1986a), then elaborated and popularized in Rumelhart, Hinton & Williams (1986b), but the technique was independently rediscovered many times, and had many predecessors dating to the 1960s.[6][17]
The basics of continuous backpropagation were derived in the context of control theory by Henry J. Kelley in 1960,[18] and by Arthur E. Bryson in 1961.[19][20][21][22][23] They used principles of dynamic programming. In 1962, Stuart Dreyfus published a simpler derivation based only on the chain rule.[24] Bryson and Ho described it as a multi-stage dynamic system optimization method in 1969.[25][26] Backpropagation was derived by multiple researchers in the early 60’s[22] and implemented to run on computers as early as 1970 by Seppo Linnainmaa.[27][28][29] Paul Werbos was first in the US to propose that it could be used for neural nets after analyzing it in depth in his 1974 dissertation.[30] While not applied to neural networks, in 1970 Linnainmaa published the general method for automatic differentiation (AD).[28][29] Although very controversial, some scientists believe this was actually the first step toward developing a back-propagation algorithm.[22][23][27][31] In 1973 Dreyfus adapts parameters of controllers in proportion to error gradients.[32] In 1974 Werbos mentioned the possibility of applying this principle to artificial neural networks,[30] and in 1982 he applied Linnainmaa’s AD method to non-linear functions.[23][33]
Later the Werbos method was rediscovered and described in 1985 by Parker,[34][35] and in 1986 by Rumelhart, Hinton and Williams.[17][35][36] Rumelhart, Hinton and Williams showed experimentally that this method can generate useful internal representations of incoming data in hidden layers of neural networks.[10][37][38] Yann LeCun proposed the modern form of the back-propagation learning algorithm for neural networks in his PhD thesis in 1987. In 1993, Eric Wan won an international pattern recognition contest through backpropagation.[22][39]
During the 2000s it fell out of favour[citation needed], but returned in the 2010s, benefitting from cheap, powerful GPU-based computing systems. This has been especially so in speech recognition, machine vision, natural language processing, and language structure learning research (in which it has been used to explain a variety of phenomena related to first[40] and second language learning.[41]).
Error backpropagation has been suggested to explain human brain ERP components like the N400 and P600.[42]
See also[edit]
- Artificial neural network
- Neural circuit
- Catastrophic interference
- Ensemble learning
- AdaBoost
- Overfitting
- Neural backpropagation
- Backpropagation through time
Notes[edit]
- ^ Use
for the loss function to allow
to be used for the number of layers
- ^ This follows Nielsen (2015), and means (left) multiplication by the matrix
corresponds to converting output values of layer
to input values of layer
: columns correspond to input coordinates, rows correspond to output coordinates.
- ^ This section largely follows and summarizes Nielsen (2015).
- ^ The derivative of the loss function is a covector, since the loss function is a scalar-valued function of several variables.
- ^ The activation function is applied to each node separately, so the derivative is just the diagonal matrix of the derivative on each node. This is often represented as the Hadamard product with the vector of derivatives, denoted by
, which is mathematically identical but better matches the internal representation of the derivatives as a vector, rather than a diagonal matrix.
- ^ Since matrix multiplication is linear, the derivative of multiplying by a matrix is just the matrix:
.
- ^ One may notice that multi-layer neural networks use non-linear activation functions, so an example with linear neurons seems obscure. However, even though the error surface of multi-layer networks are much more complicated, locally they can be approximated by a paraboloid. Therefore, linear neurons are used for simplicity and easier understanding.
- ^ There can be multiple output neurons, in which case the error is the squared norm of the difference vector.
References[edit]
- ^ Goodfellow, Bengio & Courville 2016, p. 200, «The back-propagation algorithm (Rumelhart et al., 1986a), often simply called backprop, …»
- ^ Goodfellow, Bengio & Courville 2016, p. 200, «Furthermore, back-propagation is often misunderstood as being specific to multi-layer neural networks, but in principle it can compute derivatives of any function»
- ^ Goodfellow, Bengio & Courville 2016, p. 214, «This table-filling strategy is sometimes called dynamic programming.»
- ^ Goodfellow, Bengio & Courville 2016, p. 200, «The term back-propagation is often misunderstood as meaning the whole learning algorithm for multilayer neural networks. Backpropagation refers only to the method for computing the gradient, while other algorithms, such as stochastic gradient descent, is used to perform learning using this gradient.»
- ^ a b Goodfellow, Bengio & Courville (2016, p. 217–218), «The back-propagation algorithm described here is only one approach to automatic differentiation. It is a special case of a broader class of techniques called reverse mode accumulation.»
- ^ a b Goodfellow, Bengio & Courville (2016, p. 221), «Efficient applications of the chain rule based on dynamic programming began to appear in the 1960s and 1970s, mostly for control applications (Kelley, 1960; Bryson and Denham, 1961; Dreyfus, 1962; Bryson and Ho, 1969; Dreyfus, 1973) but also for sensitivity analysis (Linnainmaa, 1976). … The idea was finally developed in practice after being independently rediscovered in different ways (LeCun, 1985; Parker, 1985; Rumelhart et al., 1986a). The book Parallel Distributed Processing presented the results of some of the first successful experiments with back-propagation in a chapter (Rumelhart et al., 1986b) that contributed greatly to the popularization of back-propagation and initiated a very active period of research in multilayer neural networks.»
- ^ Goodfellow, Bengio & Courville (2016, 6.5 Back-Propagation and Other Differentiation Algorithms, pp. 200–220)
- ^ Ramachandran, Prajit; Zoph, Barret; Le, Quoc V. (2017-10-27). «Searching for Activation Functions». arXiv:1710.05941 [cs.NE].
- ^ Misra, Diganta (2019-08-23). «Mish: A Self Regularized Non-Monotonic Activation Function». arXiv:1908.08681 [cs.LG].
- ^ a b Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (1986a). «Learning representations by back-propagating errors». Nature. 323 (6088): 533–536. Bibcode:1986Natur.323..533R. doi:10.1038/323533a0. S2CID 205001834.
- ^ Tan, Hong Hui; Lim, King Han (2019). «Review of second-order optimization techniques in artificial neural networks backpropagation». IOP Conference Series: Materials Science and Engineering. 495 (1): 012003. Bibcode:2019MS&E..495a2003T. doi:10.1088/1757-899X/495/1/012003. S2CID 208124487.
- ^ a b Wiliamowski, Bogdan; Yu, Hao (June 2010). «Improved Computation for Levenberg–Marquardt Training» (PDF). IEEE Transactions on Neural Networks and Learning Systems. 21 (6).
- ^ Martens, James (August 2020). «New Insights and Perspectives on the Natural Gradient Method» (PDF). Journal of Machine Learning Research (21). arXiv:1412.1193.
- ^ Nielsen (2015), «[W]hat assumptions do we need to make about our cost function … in order that backpropagation can be applied? The first assumption we need is that the cost function can be written as an average … over cost functions … for individual training examples … The second assumption we make about the cost is that it can be written as a function of the outputs from the neural network …»
- ^ LeCun, Yann; Bengio, Yoshua; Hinton, Geoffrey (2015). «Deep learning». Nature. 521 (7553): 436–444. Bibcode:2015Natur.521..436L. doi:10.1038/nature14539. PMID 26017442. S2CID 3074096.
- ^ Buckland, Matt; Collins, Mark (2002). AI Techniques for Game Programming. Boston: Premier Press. ISBN 1-931841-08-X.
- ^ a b Rumelhart; Hinton; Williams (1986). «Learning representations by back-propagating errors» (PDF). Nature. 323 (6088): 533–536. Bibcode:1986Natur.323..533R. doi:10.1038/323533a0. S2CID 205001834.
- ^ Kelley, Henry J. (1960). «Gradient theory of optimal flight paths». ARS Journal. 30 (10): 947–954. doi:10.2514/8.5282.
- ^ Bryson, Arthur E. (1962). «A gradient method for optimizing multi-stage allocation processes». Proceedings of the Harvard Univ. Symposium on digital computers and their applications, 3–6 April 1961. Cambridge: Harvard University Press. OCLC 498866871.
- ^ Dreyfus, Stuart E. (1990). «Artificial Neural Networks, Back Propagation, and the Kelley-Bryson Gradient Procedure». Journal of Guidance, Control, and Dynamics. 13 (5): 926–928. Bibcode:1990JGCD…13..926D. doi:10.2514/3.25422.
- ^ Mizutani, Eiji; Dreyfus, Stuart; Nishio, Kenichi (July 2000). «On derivation of MLP backpropagation from the Kelley-Bryson optimal-control gradient formula and its application» (PDF). Proceedings of the IEEE International Joint Conference on Neural Networks.
- ^ a b c d Schmidhuber, Jürgen (2015). «Deep learning in neural networks: An overview». Neural Networks. 61: 85–117. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003. PMID 25462637. S2CID 11715509.
- ^ a b c Schmidhuber, Jürgen (2015). «Deep Learning». Scholarpedia. 10 (11): 32832. Bibcode:2015SchpJ..1032832S. doi:10.4249/scholarpedia.32832.
- ^ Dreyfus, Stuart (1962). «The numerical solution of variational problems». Journal of Mathematical Analysis and Applications. 5 (1): 30–45. doi:10.1016/0022-247x(62)90004-5.
- ^ Russell, Stuart; Norvig, Peter (1995). Artificial Intelligence : A Modern Approach. Englewood Cliffs: Prentice Hall. p. 578. ISBN 0-13-103805-2.
The most popular method for learning in multilayer networks is called Back-propagation. It was first invented in 1969 by Bryson and Ho, but was more or less ignored until the mid-1980s.
- ^ Bryson, Arthur Earl; Ho, Yu-Chi (1969). Applied optimal control: optimization, estimation, and control. Waltham: Blaisdell. OCLC 3801.
- ^ a b Griewank, Andreas (2012). «Who Invented the Reverse Mode of Differentiation?». Optimization Stories. Documenta Matematica, Extra Volume ISMP. pp. 389–400. S2CID 15568746.
- ^ a b Seppo Linnainmaa (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. Master’s Thesis (in Finnish), Univ. Helsinki, 6–7.
- ^ a b Linnainmaa, Seppo (1976). «Taylor expansion of the accumulated rounding error». BIT Numerical Mathematics. 16 (2): 146–160. doi:10.1007/bf01931367. S2CID 122357351.
- ^ a b The thesis, and some supplementary information, can be found in his book, Werbos, Paul J. (1994). The Roots of Backpropagation : From Ordered Derivatives to Neural Networks and Political Forecasting. New York: John Wiley & Sons. ISBN 0-471-59897-6.
- ^ Griewank, Andreas; Walther, Andrea (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition. SIAM. ISBN 978-0-89871-776-1.
- ^ Dreyfus, Stuart (1973). «The computational solution of optimal control problems with time lag». IEEE Transactions on Automatic Control. 18 (4): 383–385. doi:10.1109/tac.1973.1100330.
- ^ Werbos, Paul (1982). «Applications of advances in nonlinear sensitivity analysis» (PDF). System modeling and optimization. Springer. pp. 762–770.
- ^ Parker, D.B. (1985). «Learning Logic». Center for Computational Research in Economics and Management Science. Cambridge MA: Massachusetts Institute of Technology.
- ^ a b Hertz, John (1991). Introduction to the theory of neural computation. Krogh, Anders., Palmer, Richard G. Redwood City, Calif.: Addison-Wesley. p. 8. ISBN 0-201-50395-6. OCLC 21522159.
- ^ Anderson, James Arthur; Rosenfeld, Edward, eds. (1988). Neurocomputing Foundations of research. MIT Press. ISBN 0-262-01097-6. OCLC 489622044.
- ^ Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (1986b). «8. Learning Internal Representations by Error Propagation». In Rumelhart, David E.; McClelland, James L. (eds.). Parallel Distributed Processing : Explorations in the Microstructure of Cognition. Vol. 1 : Foundations. Cambridge: MIT Press. ISBN 0-262-18120-7.
- ^ Alpaydin, Ethem (2010). Introduction to Machine Learning. MIT Press. ISBN 978-0-262-01243-0.
- ^ Wan, Eric A. (1994). «Time Series Prediction by Using a Connectionist Network with Internal Delay Lines». In Weigend, Andreas S.; Gershenfeld, Neil A. (eds.). Time Series Prediction : Forecasting the Future and Understanding the Past. Proceedings of the NATO Advanced Research Workshop on Comparative Time Series Analysis. Vol. 15. Reading: Addison-Wesley. pp. 195–217. ISBN 0-201-62601-2. S2CID 12652643.
- ^ Chang, Franklin; Dell, Gary S.; Bock, Kathryn (2006). «Becoming syntactic». Psychological Review. 113 (2): 234–272. doi:10.1037/0033-295x.113.2.234. PMID 16637761.
- ^ Janciauskas, Marius; Chang, Franklin (2018). «Input and Age-Dependent Variation in Second Language Learning: A Connectionist Account». Cognitive Science. 42: 519–554. doi:10.1111/cogs.12519. PMC 6001481. PMID 28744901.
- ^ Fitz, Hartmut; Chang, Franklin (2019). «Language ERPs reflect learning through prediction error propagation». Cognitive Psychology. 111: 15–52. doi:10.1016/j.cogpsych.2019.03.002. hdl:21.11116/0000-0003-474D-8. PMID 30921626. S2CID 85501792.
Further reading[edit]
- Goodfellow, Ian; Bengio, Yoshua; Courville, Aaron (2016). «6.5 Back-Propagation and Other Differentiation Algorithms». Deep Learning. MIT Press. pp. 200–220. ISBN 9780262035613.
- Nielsen, Michael A. (2015). «How the backpropagation algorithm works». Neural Networks and Deep Learning. Determination Press.
- McCaffrey, James (October 2012). «Neural Network Back-Propagation for Programmers». MSDN Magazine.
- Rojas, Raúl (1996). «The Backpropagation Algorithm» (PDF). Neural Networks : A Systematic Introduction. Berlin: Springer. ISBN 3-540-60505-3.
External links[edit]
- Backpropagation neural network tutorial at the Wikiversity
- Bernacki, Mariusz; Włodarczyk, Przemysław (2004). «Principles of training multi-layer neural network using backpropagation».
- Karpathy, Andrej (2016). «Lecture 4: Backpropagation, Neural Networks 1». CS231n. Stanford University. Archived from the original on 2021-12-12 – via YouTube.
- «What is Backpropagation Really Doing?». 3Blue1Brown. November 3, 2017. Archived from the original on 2021-12-12 – via YouTube.
- Putta, Sudeep Raja (2022). «Yet Another Derivation of Backpropagation in Matrix Form».
Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Содержание
- 1 Обучение как задача оптимизации
- 2 Дифференцирование для однослойной сети
- 2.1 Находим производную ошибки
- 3 Алгоритм
- 4 Недостатки алгоритма
- 4.1 Паралич сети
- 4.2 Локальные минимумы
- 5 Примечания
- 6 См. также
- 7 Источники информации
Обучение как задача оптимизации
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:
- где ошибка.
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.
Дифференцирование для однослойной сети
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:
- где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.
Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона , его выходное значение определено как
Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.
Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
у нее удобная производная:
Находим производную ошибки
Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:
Только одно слагаемое в зависит от , так что
Если нейрон в первом слое после входного, то — это просто .
Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и
Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.
Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,
и взять полную производную по , то получим рекурсивное выражение для производной:
Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.
Если собрать все месте:
и
Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:
Алгоритм
- — скорость обучения
- — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
- — обучающее множество
- — количество повторений
- — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
- — количество слоев в сети
- — множество нейронов в слое i
- — множество нейронов в выходном слое
fun BackPropagation:
init
repeat :
for = to :
=
for :
=
for = to :
for :
=
for :
=
=
return
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Примечания
- Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- Neural Nets
- Understanding backpropagation
См. также
- Нейронные сети, перцептрон
- Стохастический градиентный спуск
- Настройка глубокой сети
- Практики реализации нейронных сетей
Источники информации
- https://en.wikipedia.org/wiki/Backpropagation
- https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
Метод обратного распространения ошибки — метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. Полем Дж. Вербосом[1], а также независимо и одновременно А. И. Галушкиным[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[3] и независимо и одновременно С. И. Барцевым и В. А. Охониным (Красноярская группа)[4]. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.[5]
Для возможноcти применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема.
Cигмоидальные функции активации[]
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):

Рациональная сигмоида:
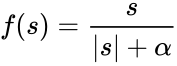
Гиперболический тангенс:
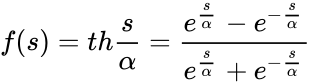
где s — выход сумматора нейрона, 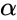
Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активациями, то сигмоиды расчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации — нужно расчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулем). Если считать, что все простейшие операции расчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведенного суммирования (которое займет одинаковое время) будет медленее пороговой функции активации как 1:4.
Функция оценки работы сети[]
В тех случаях, когда удается оценить работу сети обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех ее параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:

где 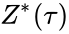
Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок поысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе[6].
Описание алгоритма[]
Файл:Neuro.PNG Архитектура многослойного перцептрона
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть входы 
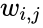
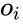
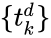
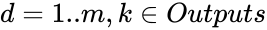

Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого тестового примера. Нам нужно двигаться в сторону, противоположную градиенту, то есть добавлять к каждому весу 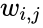
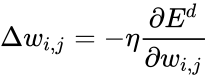
где
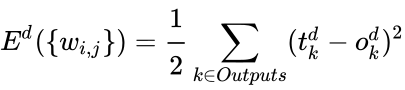
Производная считается следующим образом. Пусть сначала 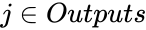
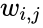
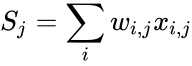

Аналогично, 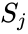
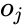
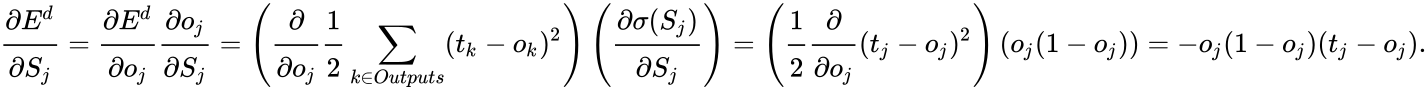
Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае

и

Ну а 
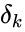
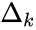
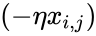
поправок алгоритм называется алгоритмом обратного распространения ошибки (backpropagation). Краткое резюме проделанной работы:
- для узла последнего уровня

- для внутреннего узла сети

- для всех узлов
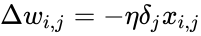
Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм[]
Алгоритм:
BackPropagation 
- Инициализировать
маленькими случайными значениями.
- Повторить NUMBER_OF_STEPS раз:
- Для всех d от 1 до m:
- Подать
на вход сети и подсчитать выходы
каждого узла.
- Для всех
.
- Для каждого уровня l, начиная с предпоследнего:
- Для каждого узла j уровня l вычислить
.
- Для каждого ребра сети {i, j}
.
- Выдать значения
.
Математическая интерпретация обучения нейронной сети[]
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющих обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
Недостатки алгоритма[]
Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Паралич сети[]
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.
Локальные минимумы[]
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Статистические методы обучения могут помочь избежать этой ловушки, но они медленны.
Размер шага[]
Внимательный разбор доказательства сходимости[3] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость. П. Д. Вассерман[7] описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня[8] предложена разветвлённая технология оптимизации обучения.
См. также[]
- Сигмоид
- Многослойный перцептрон
Литература[]
- Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. — М.: «Мир», 1992.
- Хайкин С. Нейронные сети: Полный курс. Пер. с англ. Н. Н. Куссуль, А. Ю. Шелестова. 2-е изд., испр. — М.: Издательский дом Вильямс, 2008, 1103 с.
Внешние ссылки[]
- Копосов А.И., Щербаков И.Б., Кисленко Н.А., Кисленко О.П., Варивода Ю.В. и др. Отчет по научно-исследовательской работе «Создание аналитического обзора информационных источников по применению нейронных сетей для задач газовой технологии». — Москва: ВНИИГАЗ, 1995.
- Миркес Е. М., Нейроинформатика: Учеб. пособие для студентов с программами для выполнения лабораторных работ. Красноярск: ИПЦ КГТУ, 2002, 347 с. Рис. 58, табл. 59, библиогр. 379 наименований. ISBN 5-7636-0477-6
Примечания[]
- ↑ Werbos P. J., Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.
- ↑ Галушкин А. И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.
- ↑ 3,0 3,1 Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318—362. Cambridge, MA, MIT Press. 1986.
- ↑ Барцев С. И., Охонин В. А. Адаптивные сети обработки информации. Красноярск : Ин-т физики СО АН СССР, 1986. Препринт N 59Б. — 20 с.
- ↑ Барцев С. И., Гилев С. Е., Охонин В. А., Принцип двойственности в организации адаптивных сетей обработки информации, В кн.: Динамика химических и биологических систем. — Новосибирск: Наука, 1989. — С. 6-55.
- ↑ Миркес Е. М., — Новосибирск: Наука, Сибирская издательская фирма РАН, 1999. — 337 с. ISBN 5-02-031409-9 Другие копии онлайн: [1]
- ↑ Wasserman P. D. Experiments in translating Chinese characters using backpropagation. Proceedings of the Thirty-Third IEEE Computer Society International Conference.. — Washington: D. C.: Computer Society Press of the IEEE, 1988.
- ↑ Горбань А. Н. Обучение нейронных сетей.. — Москва: СП ПараГраф, 1990.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
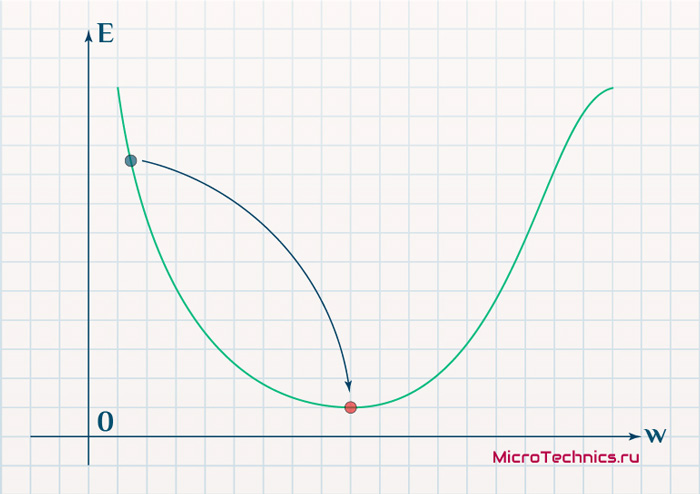
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
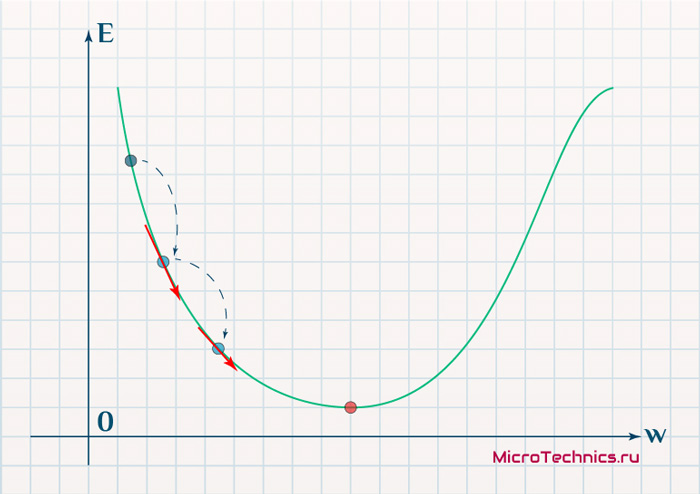
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
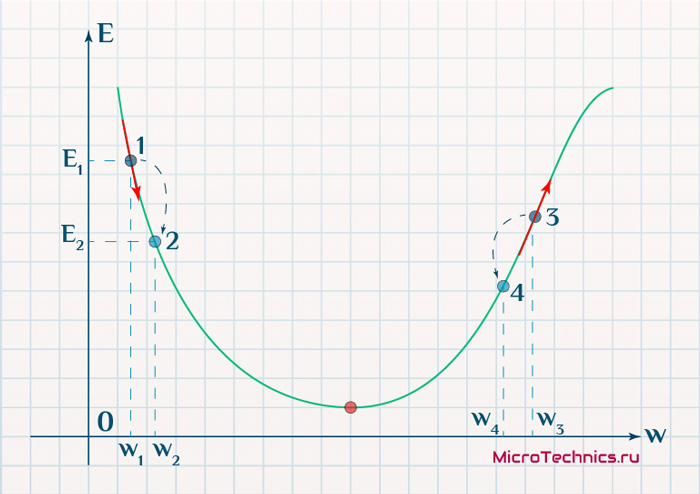
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
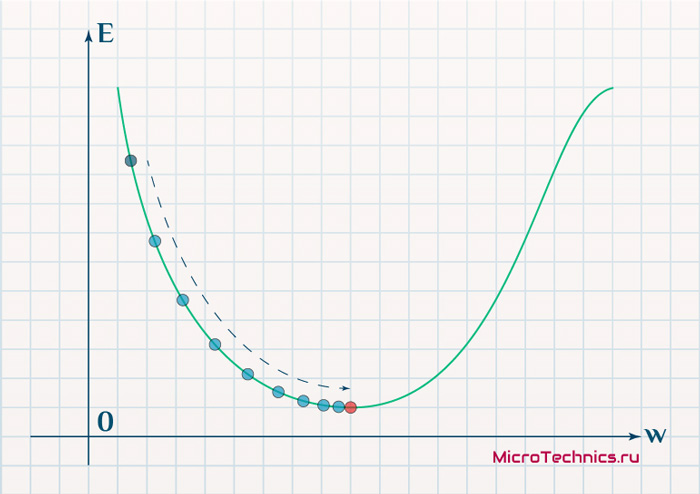
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
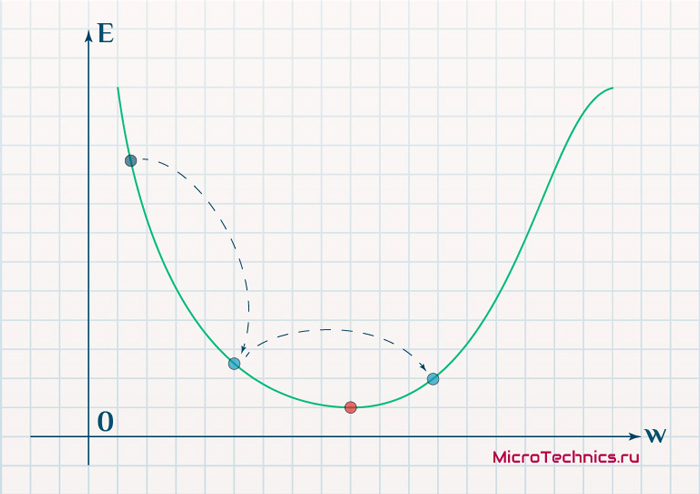
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
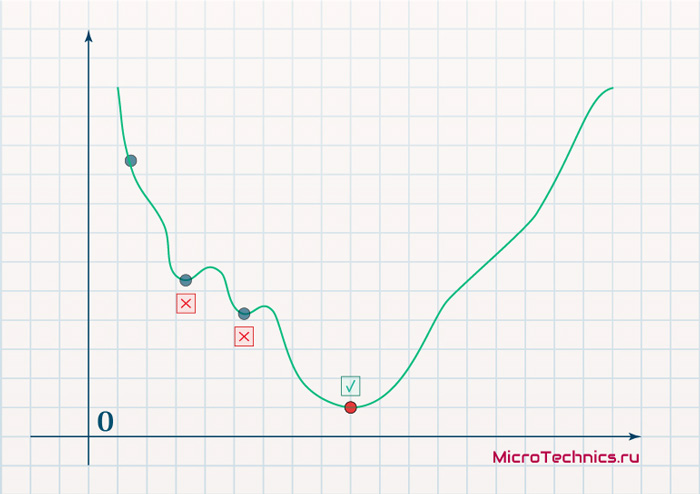
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
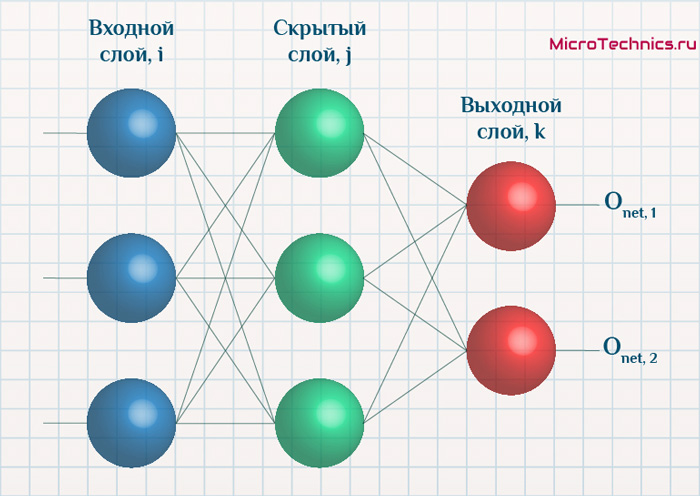
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
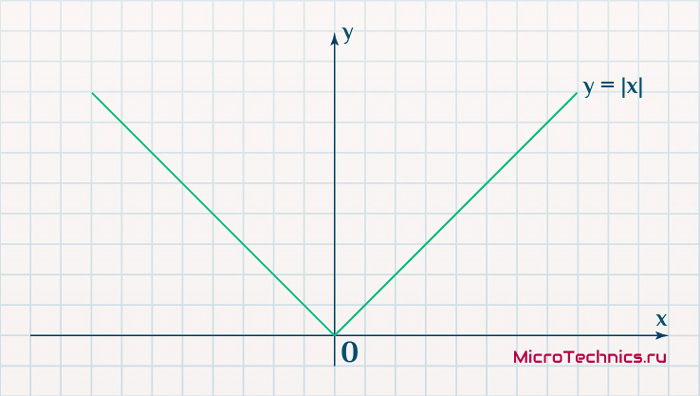
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
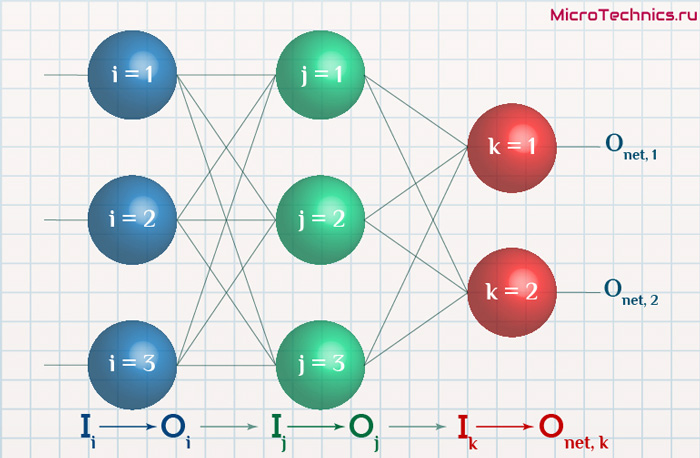
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
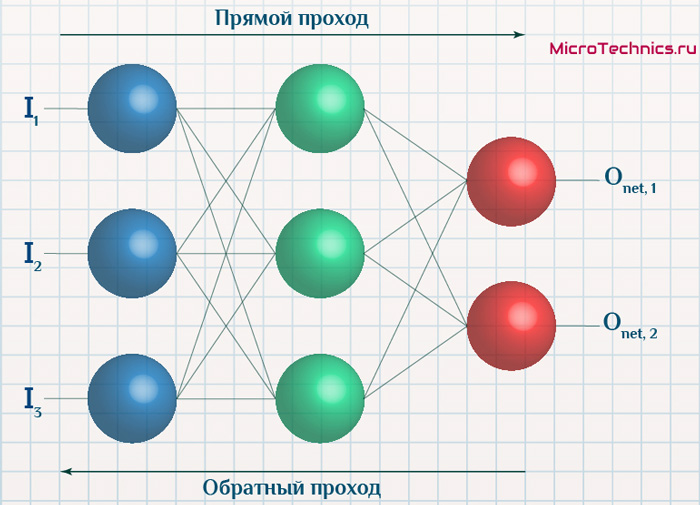
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
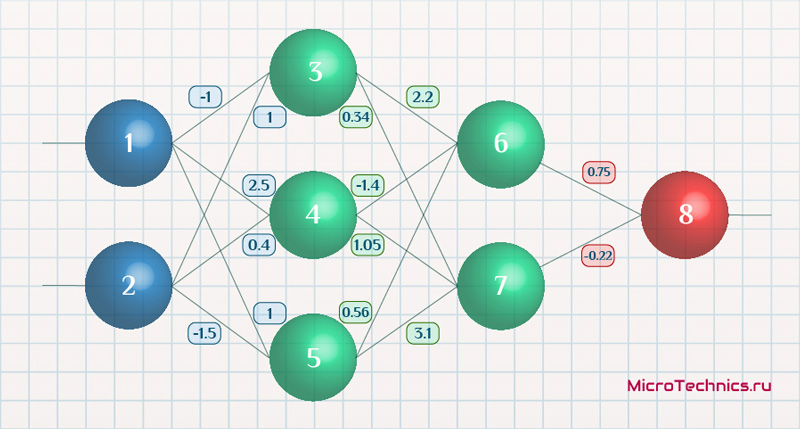
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!

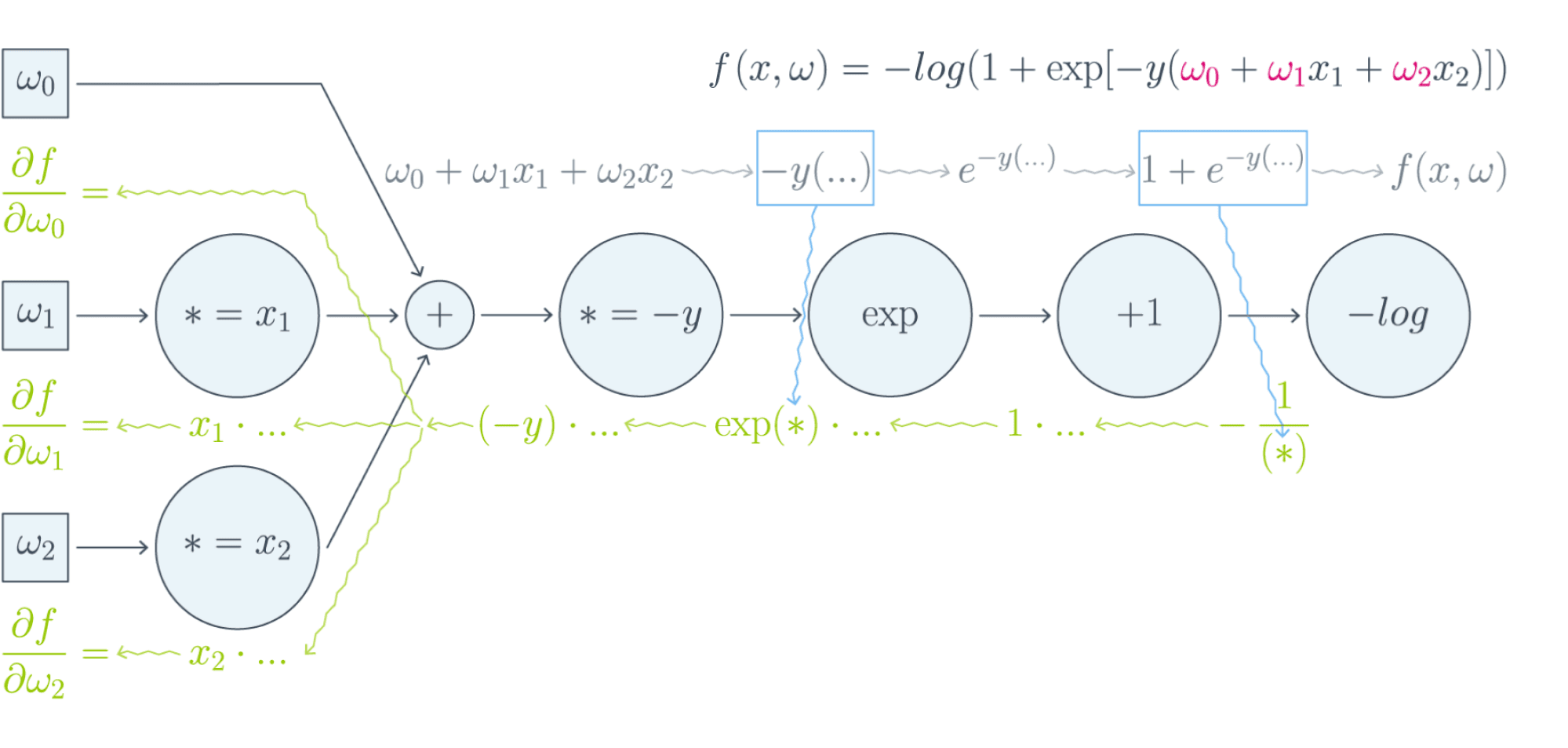
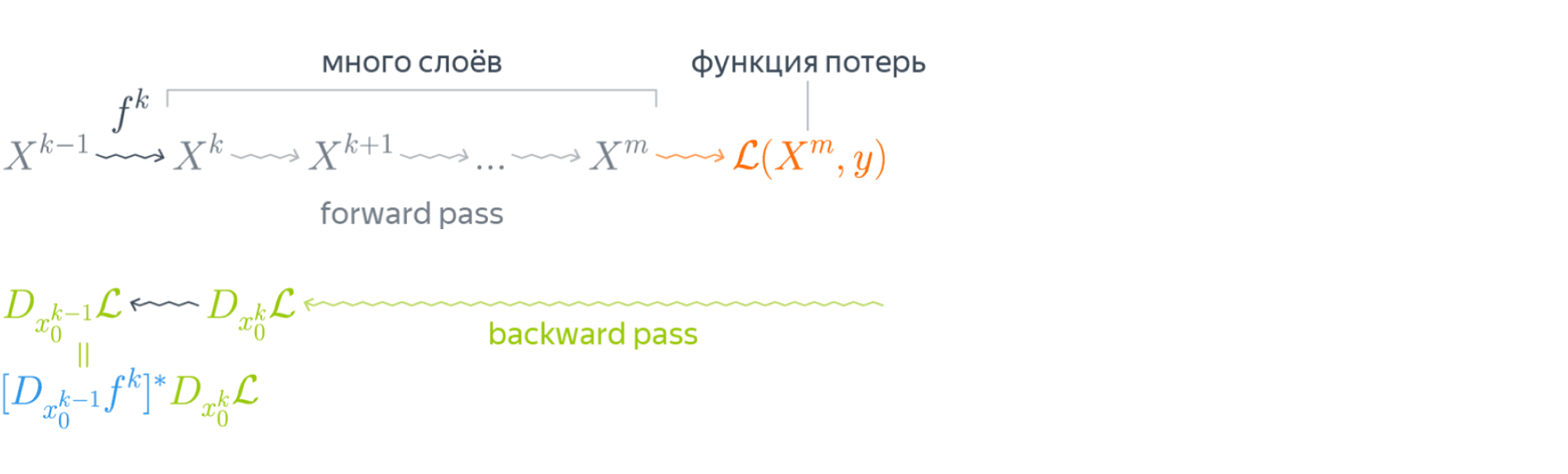
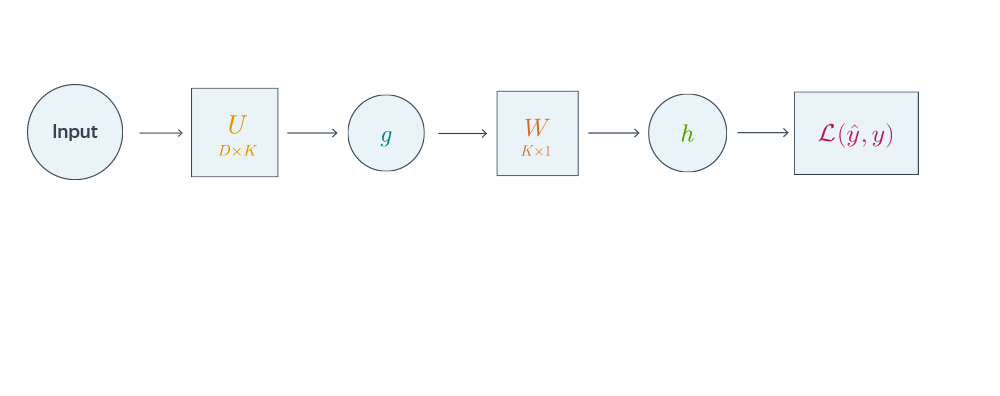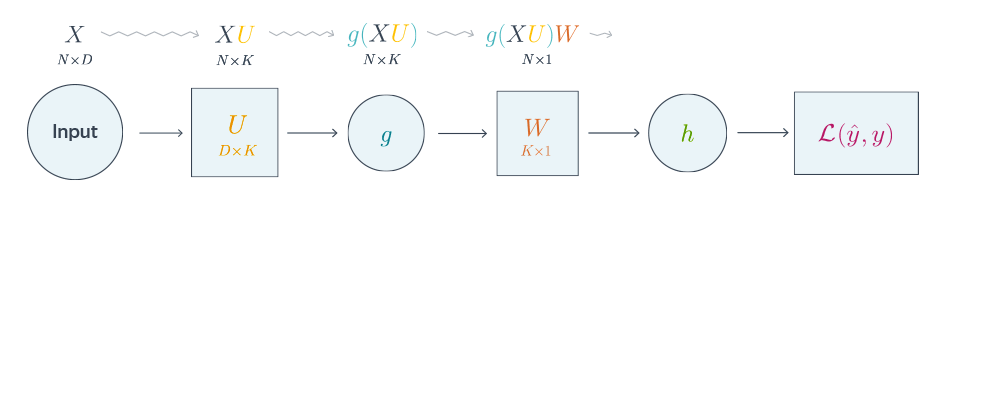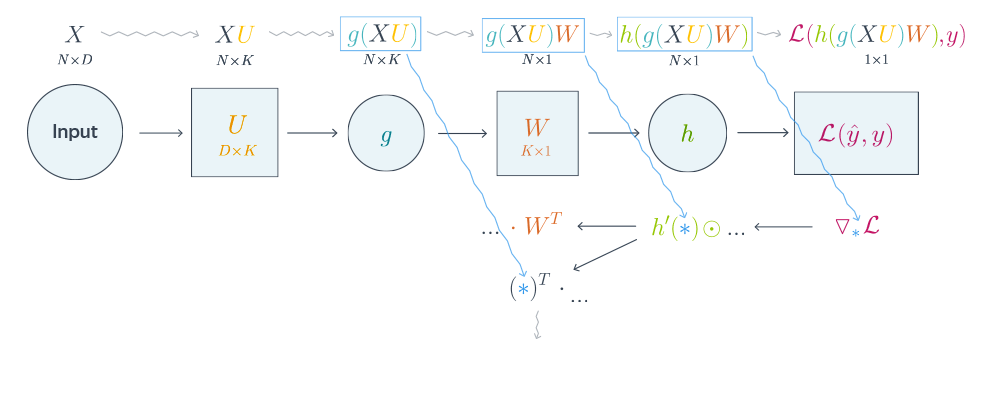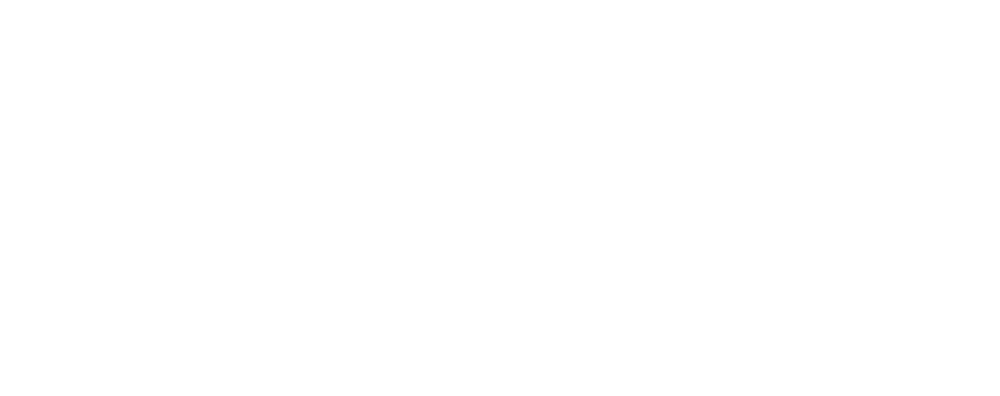

















































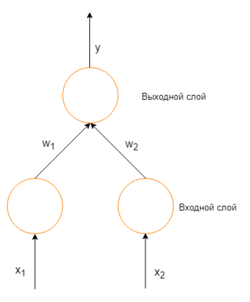
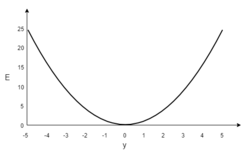
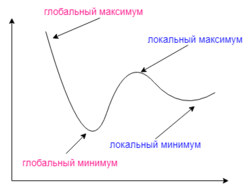
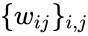 маленькими случайными значениями.
маленькими случайными значениями.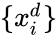 на вход сети и подсчитать выходы
на вход сети и подсчитать выходы 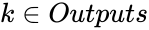
 .
. .
. .
. .
.