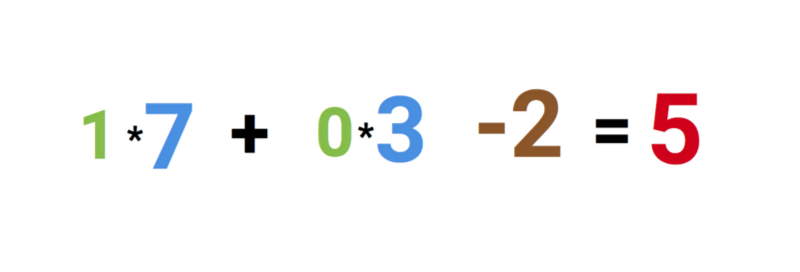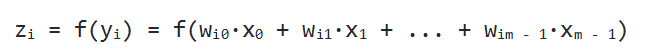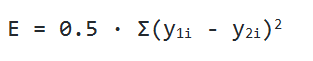Заранее хочу отметить, что тот кто знает как обучается персептрон — в этой статье вряд ли найдет что-то новое. Вы можете смело пропускать ее. Почему я решил это написать — я хотел бы написать цикл статей, связанных с нейронными сетями и применением TensorFlow.js, ввиду этого я не мог опустить общие теоретические выдержки. Поэтому прошу отнестись с большим терпением и пониманием к конечной задумке.
При классическом программировании разработчик описывает на конкретном языке программирования определённый жестко заданный набор правил, который был определен на основании его знаний в конкретной предметной области и который в первом приближении описывает процессы, происходящие в человеческом мозге при решении аналогичной задачи.
Например, может быть запрограммирована стратегия игры в крестики-нолики, шахмат и другое (рисунок 1).
Рисунок 1 – Классический подход решения задач
В то время как алгоритмы машинного обучения могут определять набор правил для решения задач без участия разработчика, а только на базе наличия тренировочного набора данных.
Тренировочный набор — это какой-то набор входных данных ассоциированный с набором ожидаемых результатов (ответами, выходными данными). На каждом шаге обучения, модель за счет изменения внутреннего состояния, будет оптимизировать и уменьшать ошибку между фактическим выходным результатом модели и ожидаемым результатом (рисунок 2).
Рисунок 2 – Машинное обучение
Нейронные сети
Долгое время учёные, вдохновляясь процессами происходящими в нашем мозге, пытались сделать реверс-инжиниринг центральной нервной системы и попробовать сымитировать работу человеческого мозга. Благодаря этому родилось целое направление в машинном обучении — нейронные сети.
На рисунке 3 вы можете увидеть сходство между устройством биологического нейрона и математическим представлением нейрона, используемого в машинном обучении.
Рисунок 3 – Математическое представление нейрона
В биологическом нейроне, нейрон получает электрические сигналы от дендритов, модулирующих электрические сигналы с разной силой, которые могут возбуждать нейрон при достижении некоторого порогового значения, что в свою очередь приведёт к передаче электрического сигнала другим нейронам через синапсы.
Персептрон
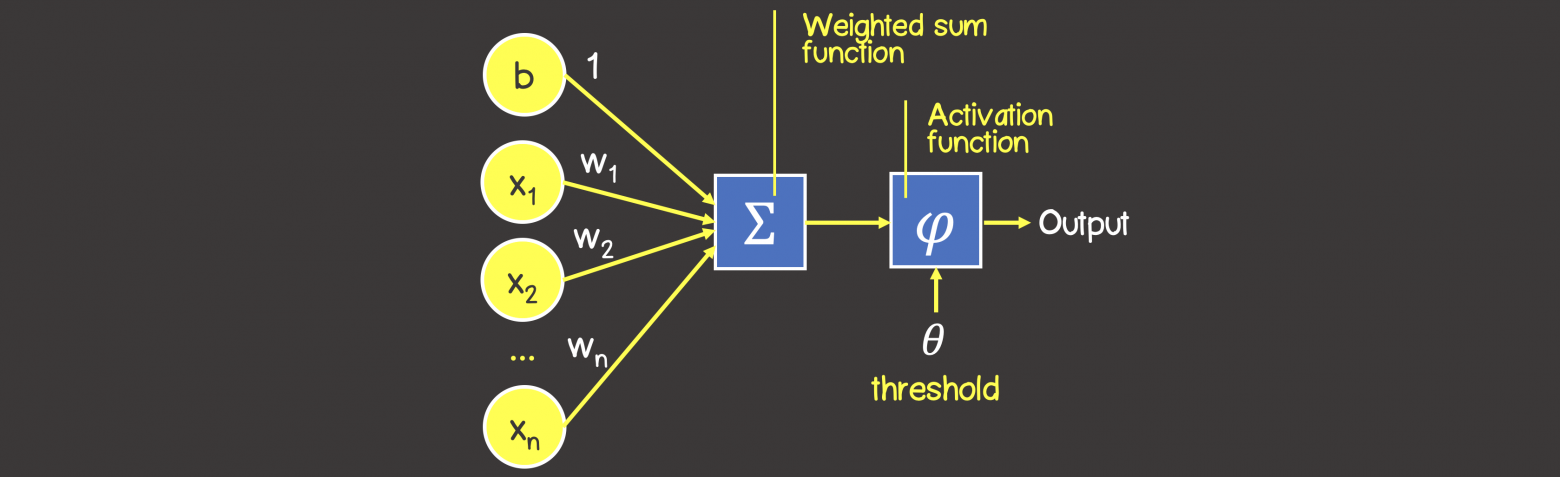
Математическая модель нейронной сети, состоящего из одного нейрона, который выполняет две последовательные операции (рисунок 4):
- вычисляет сумму входных сигналов с учетом их весов (проводимости или сопротивления) связи
- применяет активационную функцию к общей сумме воздействия входных сигналов.
Рисунок 4 – Математическая модель персептрона
В качестве активационной функции может использоваться любая дифференцируемая функция, наиболее часто используемые приведены в таблице 1. Выбор активационной функции ложиться на плечи инженера, и обычно этот выбор основан или на уже имеющемся опыте решения похожих задач, ну или просто методом подбора.
Заметка
Однако есть рекомендация – что если нужна нелинейность в нейронной сети, то в качестве активационной функции лучше всего подходит ReLU функция, которая имеет лучшие показатели сходимости модели во время процесса обучения.
Таблица 1 — Распространенные активационные функции
Процесс обучения персептрона
Процесс обучения состоит из несколько шагов. Для большей наглядности, рассмотрим некую вымышленную задачу, которую мы будем решать нейронной сетью, состоящей из одного нейрона с линейной активационной функции (это по сути персептрон без активационной функции вовсе), также для упрощения задачи – исключим в нейроне узел смещения b (рисунок 5).
Рисунок 5 – Обучающий набор данных и состояние нейронной сети на предыдущем шаге обучения
На данном этапе мы имеем нейронную сеть в некотором состоянии с определенными весами соединений, которые были вычислены на предыдущем этапе обучения модели или если это первая итерация обучения – то значения весов соединений выбраны в произвольном порядке.
Итак, представим, что мы имеем некоторый набор тренировочных данных, значения каждого элемента из набора представлены вектором входных данных (input data), содержащих 2 параметра (feature) . Под
в модели в зависимости от рассматриваемой предметной области может подразумеваться все что угодно: количество комнат в доме, расстояние дома от моря, ну или мы просто пытаемся обучить нейронную сеть логической операции И, или ИЛИ.
Каждый вектор входных данных в тренировочном наборе сопоставлен с вектором ожидаемого результата (expected output). В данном случае вектор выходных данных содержит только один параметр, которые опять же в зависимости от выбранной предметной области может означать все что угодно – цена дома, результат выполнения логической операции И или ИЛИ.
ШАГ 1 — Прямое распространение ошибки (feedforward process)
На данном шаге мы вычисляем сумму входных сигналов с учетом веса каждой связи и применяем активационную функцию (в нашем случае активационной функции нет). Сделаем вычисления для первого элемента в обучающем наборе:
Рисунок 6 – Прямое распространение ошибки
Обратите внимание, что написанная формула выше – это упрощенное математическое уравнение для частного случая операций над тензорами.
Тензор – это по сути контейнер данных, который может иметь N осей и произвольное число элементов вдоль каждой из осей. Большинство с тензорами знакомы с математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строки, колонки).
Формулу можно написать в следующем виде, где вы увидите знакомые матрицы (тензоры) и их перемножение, а также поймете о каком упрощении шла речь выше:
ШАГ 2 — Расчет функции ошибки
Функция ошибка – это метрика, отражающая расхождение между ожидаемыми и полученными выходными данными. Обычно используют следующие функции ошибки:
— среднеквадратичная ошибка (Mean Squared Error, MSE) – данная функция ошибки особенно чувствительна к выбросам в тренировочном наборе, так как используется квадрат от разности фактического и ожидаемого значений (выброс — значение, которое сильно удалено от других значений в наборе данных, которые могут иногда появляться в следствии ошибок данных, таких как смешивание данных с разными единицами измерения или плохие показания датчиков):
— среднеквадратичное отклонение (Root MSE) – по сути это тоже самое что, среднеквадратичная ошибка в контексте нейронных сетей, но может отражать реальную физическую единицу измерения, например, если в нейронной сети выходным параметров нейронной сети является цена дома выраженной в долларах, то единица измерения среднеквадратичной ошибки будет доллар квадратный (), а для среднеквадратичного отклонения это доллар ($), что естественно немного упрощает задачу анализа человеком:
— среднее отклонение (Mean Absolute Error, MAE) -в отличии от двух выше указанных значений, является не столь чувствительной к выбросам:
— перекрестная энтропия (Cross entropy) – использует для задач классификации:
где
– число экземпляров в тренировочном наборе
– число классов при решении задач классификации
— ожидаемое выходное значение
– фактическое выходное значение обучаемой модели
Для нашего конкретного случая воспользуемся MSE:
ШАГ 3 — Обратное распространение ошибки (backpropagation)
Цель обучения нейронной сети проста – это минимизация функции ошибки:
Одним способом найти минимум функции – это на каждом очередном шаге обучения модифицировать веса соединений в направлении противоположным вектору-градиенту – метод градиентного спуска, и это математически выглядит так:
где – k -ая итерация обучения нейронной сети;
– шаг обучения (learning rate) и задается инженером, обычно это может быть 0.1; 0.01 (о том как шаг обучения влияет на процесс сходимости обучения отметить чуть позже)
– градиент функции-ошибки
Для нахождения градиента, используем частные производные по настраиваемым аргументам :
В нашем конкретном случае с учетом всех упрощений, функция ошибки принимает вид:
Памятка формул производных
Напомним некоторые формулы производных, которые пригодятся для вычисления частных производных
Найдем следующие частные производные:
Тогда процесс обратного распространения ошибки – движение по модели от выхода по направлению к входу с модификацией весов модели в направлении обратном вектору градиента. Задавая обучающий шаг 0.1 (learning rate) имеем (рисунок 7):
Рисунок 7 – Обратное распространение ошибки
Таким образом мы завершили k+1 шаг обучения, чтобы убедиться, что ошибка снизилась, а выход от модели с новыми весами стал ближе к ожидаемому выполним процесс прямого распространения ошибки по модели с новыми весами (см. ШАГ 1):
Как видим, выходное значение увеличилось на 0.2 единица в верном направлении к ожидаемому результату – единице (1). Ошибка тогда составит:
Как видим, на предыдущем шаге обучения ошибка составила 0.64, а с новыми весами – 0.36, следовательно мы настроили модель в верном направлении.
Следующая часть статьи:
Машинное обучение. Нейронные сети (часть 2): Моделирование OR; XOR с помощью TensorFlow.js
Машинное обучение. Нейронные сети (часть 3) — Convolutional Network под микроскопом. Изучение АПИ Tensorflow.js
В этой статье мы узнаем о нейронных сетях прямого распространения, также известных как сети с глубокой прямой связью или многослойные персептроны. Они составляют основу многих важных нейронных сетей, используемых в последнее время, таких как сверточные нейронные сетиએ (широко используемые в приложениях компьютерного зрения), рекуррентные нейронные сетиએ (широко используемые для понимания естественного языка и последовательного обучения) и так далее. Мы постараемся понять важные концепции, используя интуитивно понятную игрушку и не будем вдаваясь в математику. Если вы хотите погрузиться в глубокое обучение, но не обладаете достаточным опытом в области статистики и машинного обучения, то эта статья станет идеальной отправной точкой.
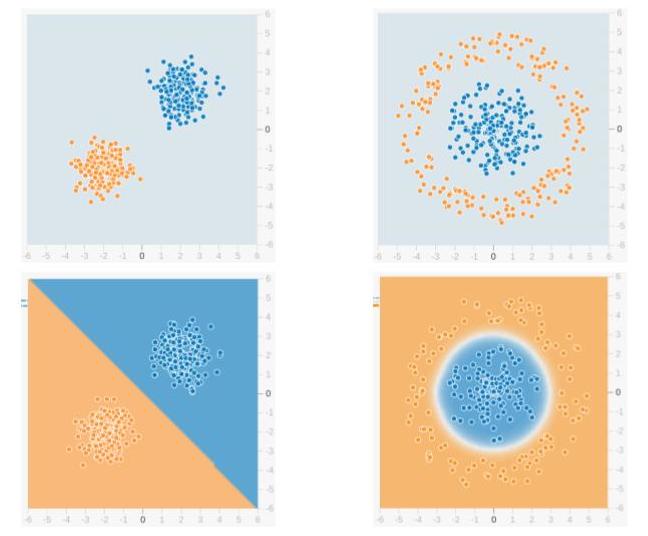
Мы будем использовать сеть прямого распространения для решения задачи двоичной классификации. В машинном обучении классификация — это тип метода контролируемого обучения, в котором задача состоит в том, чтобы разделить образцы данных на заранее определенные группы с помощью функции принятия решений. Когда есть только две группы, это называется двоичной классификацией. На приведенном ниже рисунке показан пример. Точки синего цвета принадлежат одной группе (или классу), а оранжевые точки — другой. Воображаемые линии, разделяющие группы, называются границами принятия решений. Функция принятия решения извлекается из набора помеченных образцов, который называется обучающими данными, а процесс обучения функции принятия решения называется обучением.
В приведенном примере верхняя строка показывает два разных распределения данных, а нижняя строка показывает границу решения. На левом изображении показан пример данных, которые можно разделить линейно. Это означает, что линейная граница (например, прямой линии) достаточно, чтобы разделить данные на группы. С другой стороны, изображение справа показывает пример данных, которые нельзя разделить линейно. Граница решения в этом случае должна быть круговой или многоугольной, как показано на рисунке.
1. Что есть нейронная сеть?
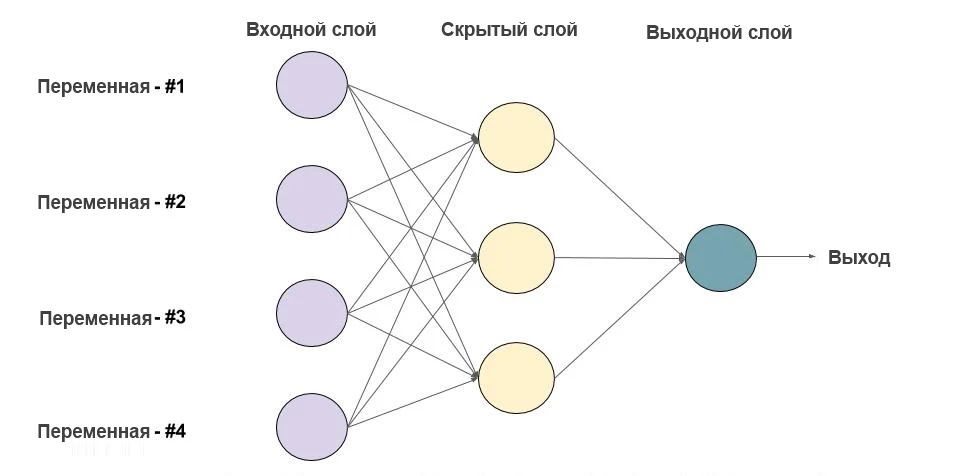
Ниже приведен пример нейронной сети прямого распространения. Это направленный ациклический граф, что означает, что в сети нет обратных связей или петель. У него есть входной слой, выходной слой и скрытый слой. Как правило, может быть несколько скрытых слоев. Каждый узел в слое — нейрон, который можно рассматривать как основной процессор нейронной сети.
1.1. Что есть нейрон?
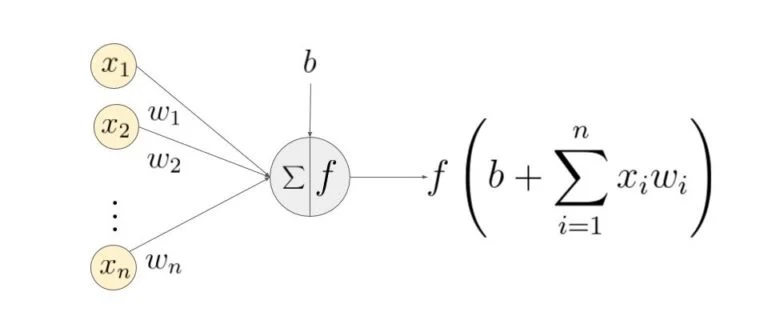
Искусственный нейрон — это основная единица нейронной сети. Принципиальная схема нейрона приведена ниже.
Как видно выше, он работает в два этапа: вычисляет взвешенную сумму своих входных данных, а затем применяет функцию активации для нормализации суммы. Функции активации могут быть линейными или нелинейными. Также, есть веса, связанные с каждым входом нейрона. Это параметры, которые сеть должна приобрести на этапе обучения.
1.2. Функции активации
Функция активацииએ используется как орган принятия решений на выходе нейрона. Нейрон изучает линейные или нелинейные границы принятия решений на основе функции активации. Он также оказывает нормализующее влияние на выход нейронов, что предотвращает выход нейронов после нескольких слоев, чтобы стать очень большим, за счет каскадного эффекта. Есть три наиболее часто используемых функции активации.
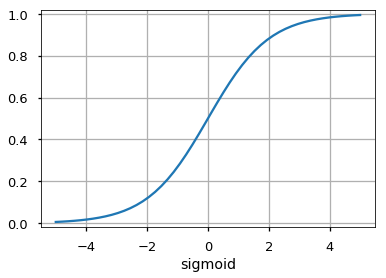
Сигмоидаએ
Он отображает входные данные (ось x) на значения от 0 до 1.
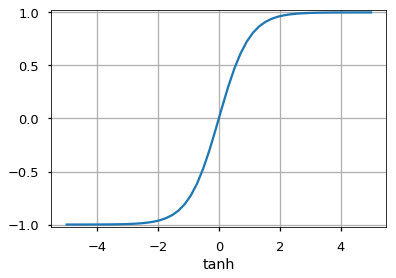
Tanh
Похожа на сигмовидную функцию, но отображает входные данные в значения от -1 до 1.
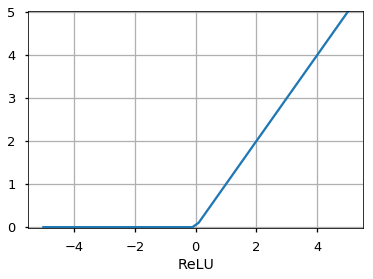
Rectified Linear Unit (ReLU)
Он позволяет проходить через него только положительным значениям. Отрицательные значения отображаются на ноль.
Функция активацииએ может быть другой, например, функция Unit Step, leaky ReLU, Noisy ReLU, Exponential LU и т.д., которые имеют свои плюсы и минусы.
1.3. Входной слой
Это первый слой нейронной сети. Он используется для передачи и приёма входных данных или функций в сеть.
1.4. Выходной слой
Это слой, который выдает прогнозы. Функция активации, используемая на этом уровне, различается для разных задач. Для задачи двоичной классификации мы хотим, чтобы на выходе было либо 0, либо 1. Таким образом, используется сигмовидная функция активации. Для задачи мультиклассовой классификации используется Softmaxએ (воспринимайте это как обобщение сигмоида на несколько классов). Для задачи регрессии, когда результат не является предопределенной категорией, мы можем просто использовать линейную единицу.
1.5. Скрытый слой
Сеть прямого распространения применяет к входу ряд функций. Имея несколько скрытых слоев, мы можем вычислять сложные функции, каскадируя более простые функции. Предположим, мы хотим вычислить седьмую степень числа, но хотим, чтобы вещи были простыми (поскольку их легко понять и реализовать). Вы можете использовать более простые степени, такие как квадрат и куб, для вычисления функций более высокого порядка. Точно так же вы можете вычислять очень сложные функции с помощью этого каскадного эффекта. Наиболее широко используемый скрытый блок — это тот, где функция активацииએ использует выпрямленный линейный блок (ReLU). Выбор скрытых слоёв — очень активная область исследований в машинном обучении. Тип скрытого слоя отличает разные типы нейронных сетей, такие как CNNએ, RNNએ и т.д. Количество скрытых слоев называется глубиной нейронной сети. Вы можете задать вопрос: сколько слоев в сети делают ее глубокой? На это нет правильного ответа. В общем случае, более глубокие сети могут научиться более сложным функциям.
1.6. Как сеть учится?
Обучающие образцы передаются по сети, и выходные данные, полученные от сети, сравниваются с фактическими выходными данными. Эта ошибка используется для изменения веса нейронов таким образом, чтобы ошибка постепенно уменьшалась. Это делается с помощью алгоритма обратного распространения ошибки, также называемого обратным распространением. Итеративная передача пакетов данных по сети и обновление весов для уменьшения ошибки называется стохастический градиентный спускએ (SGD). Величина, на которую изменяются веса, определяется параметром, называемым «Скорость обучения». Подробности SGD и backprop будут описаны в отдельном посте.
2.Зачем использовать скрытые слои?
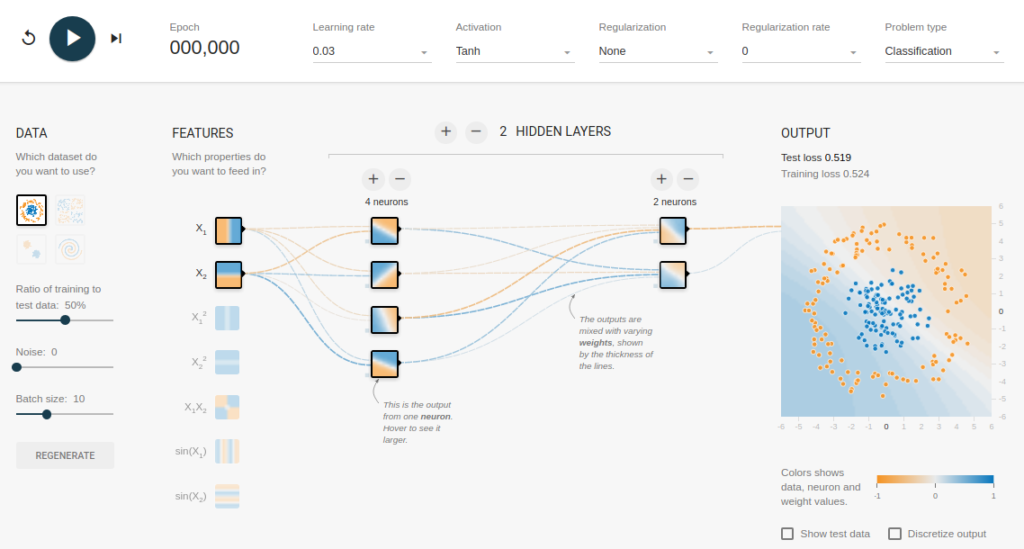
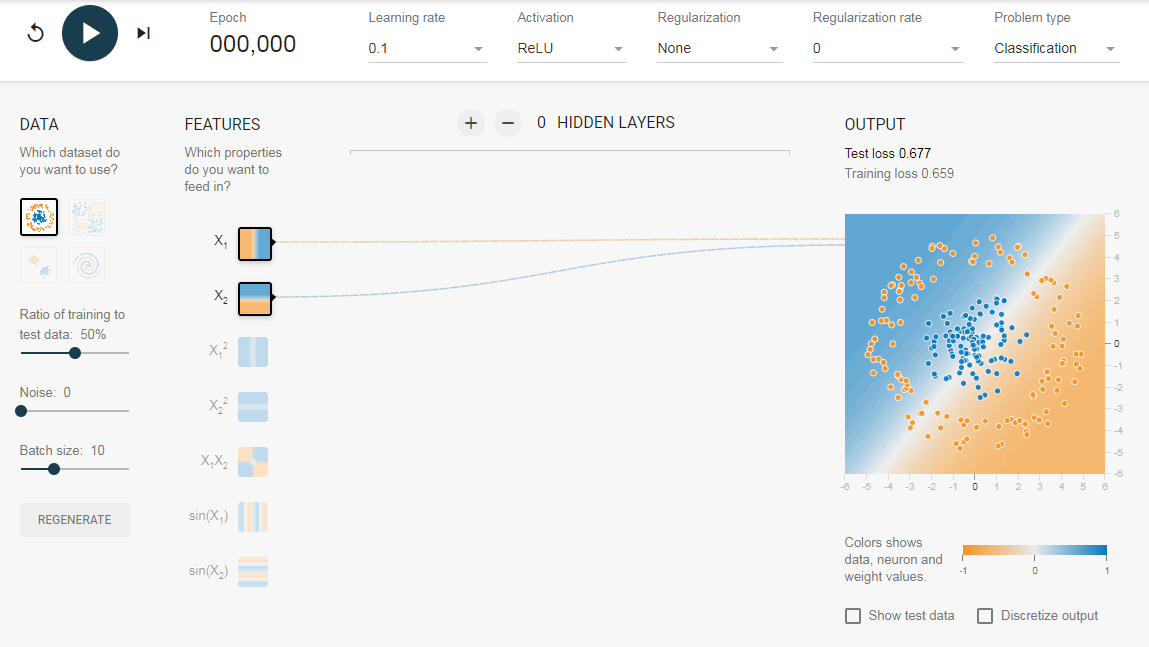
Чтобы понять значение скрытых слоев, мы попытаемся решить проблему двоичной классификации без скрытых слоев. Для этого мы будем использовать интерактивную платформу от Google, plays.tensorflow.org, которая представляет собой веб-приложение, где вы можете создавать простые нейронные сети с прямой связью и видеть эффекты обучения в реальном времени. Вы можете поиграть, изменив количество скрытых слоев, количество нейронов в скрытом слое, тип функции активации, тип данных, скорость обучения, параметры регуляризации и т.д. Выше приведен снимок экрана веб-страницы.
На приведенной выше странице вы можете выбрать данные и нажать кнопку воспроизведения, чтобы начать обучение.
Он покажет вам изученную границу решения и кривые потерь в правом верхнем углу.
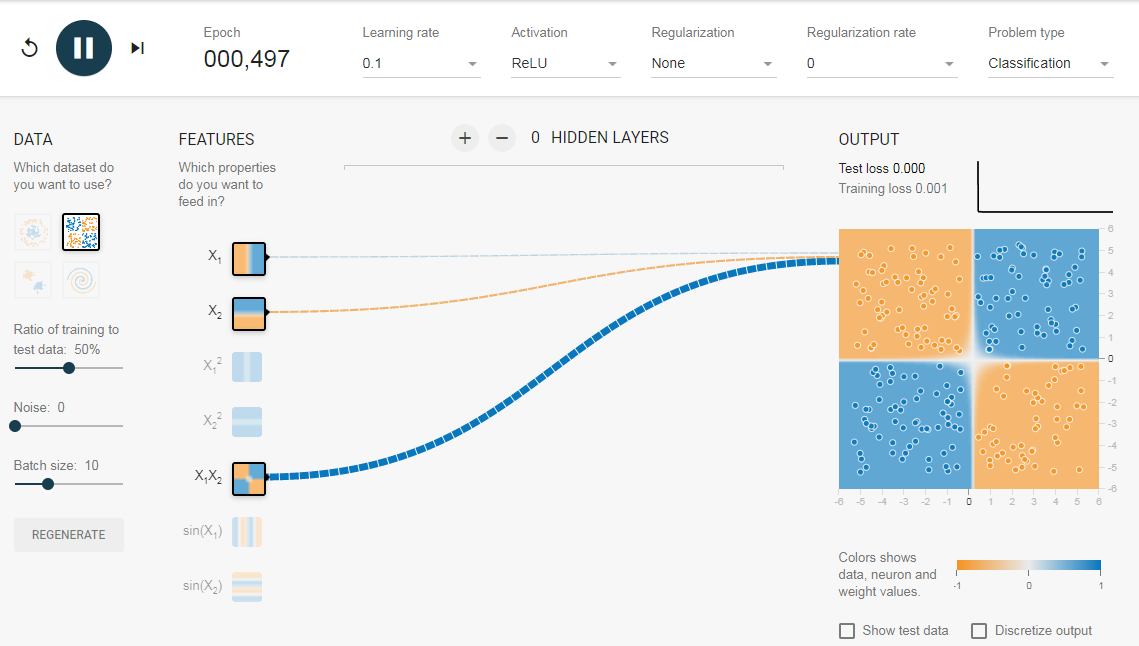
2.1. Без скрытого слоя
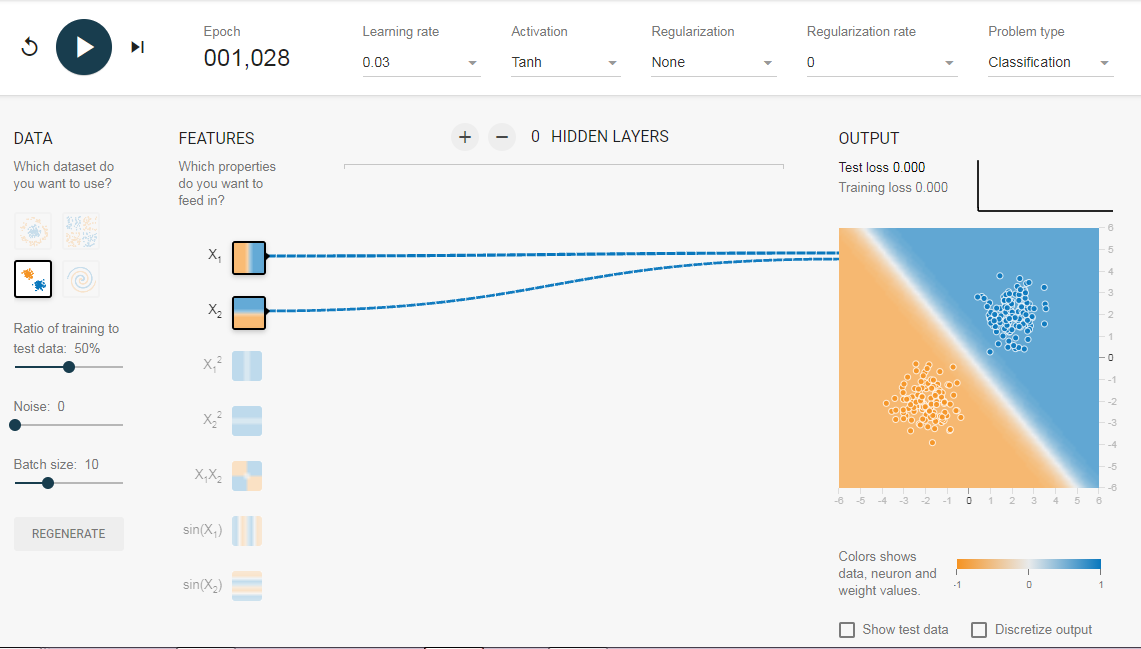
Нам нужна сеть без скрытого слоя, который я создал по этой ссылке. Здесь нет скрытых слоев, поэтому он становится простым нейроном, способным изучать линейную границу принятия решения. Мы можем выбрать тип данных в верхнем левом углу. В случае линейно разделяемых данных (3-й тип), он сможет получить (когда вы нажмете кнопку воспроизведения) линейную границу, как показано ниже.
Однако, если вы выберете первые данные, вы не сможете для них узнать границу кругового решения.
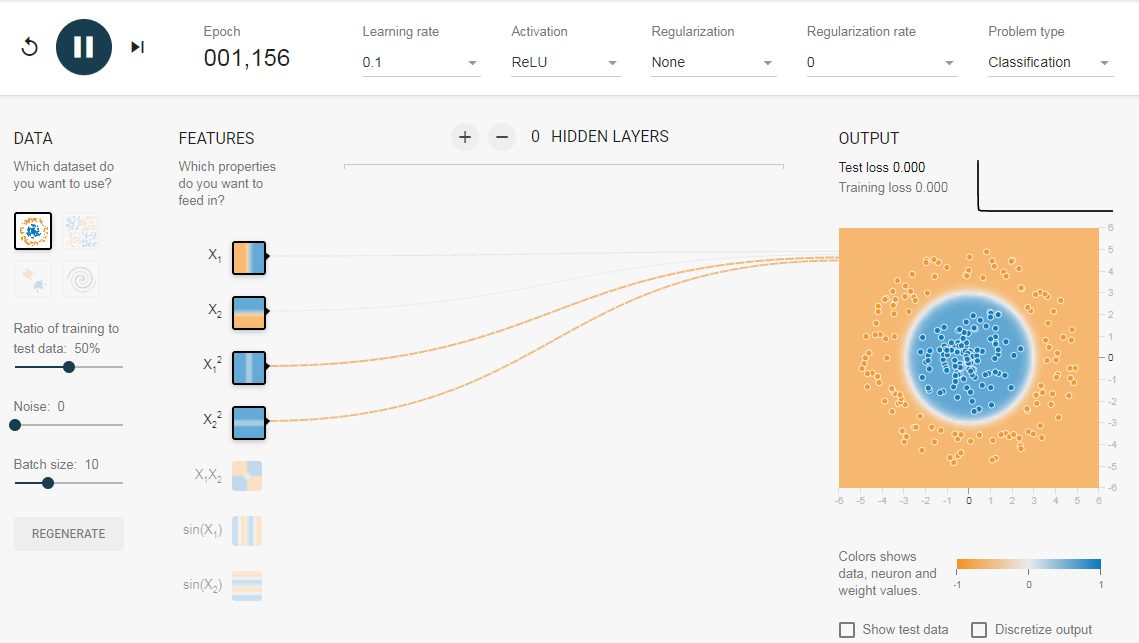
Поскольку данные находятся в круговой области, можно сказать, что использование квадратов значений функций в качестве входных данных может помочь. Оказывается, после обучения нейрон сможет найти круговую границу принятия решения.
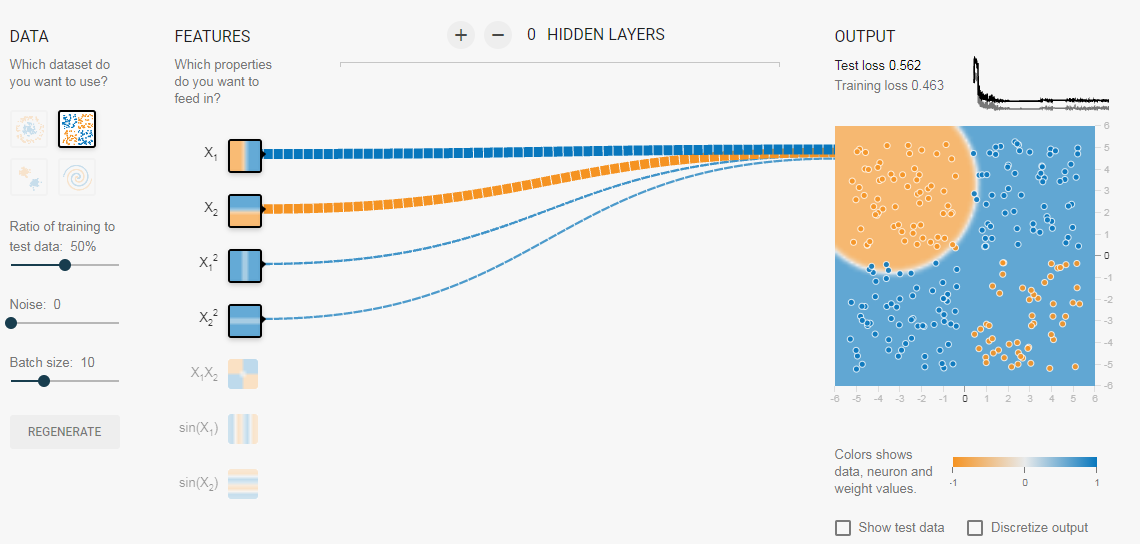
Теперь, если вы выберете 2-е данные, та же конфигурация не сможет узнать соответствующую границу решения.
Опять же интуитивно кажется, что граница решения — это коническое сечение (например, парабола или гипербола). Итак, если мы включим продукт функции (например, X_1 X_2), нейрон сможет узнать желаемую границу принятия решения.
Описанные эксперименты показали:
- Используя один нейрон, мы можем узнать только линейную границу решения.
- Нам пришлось придумать преобразования функций (например, квадрат функций или продукт функций) путем визуализации данных. Этот шаг может быть сложным для данных, которые нелегко визуализировать.
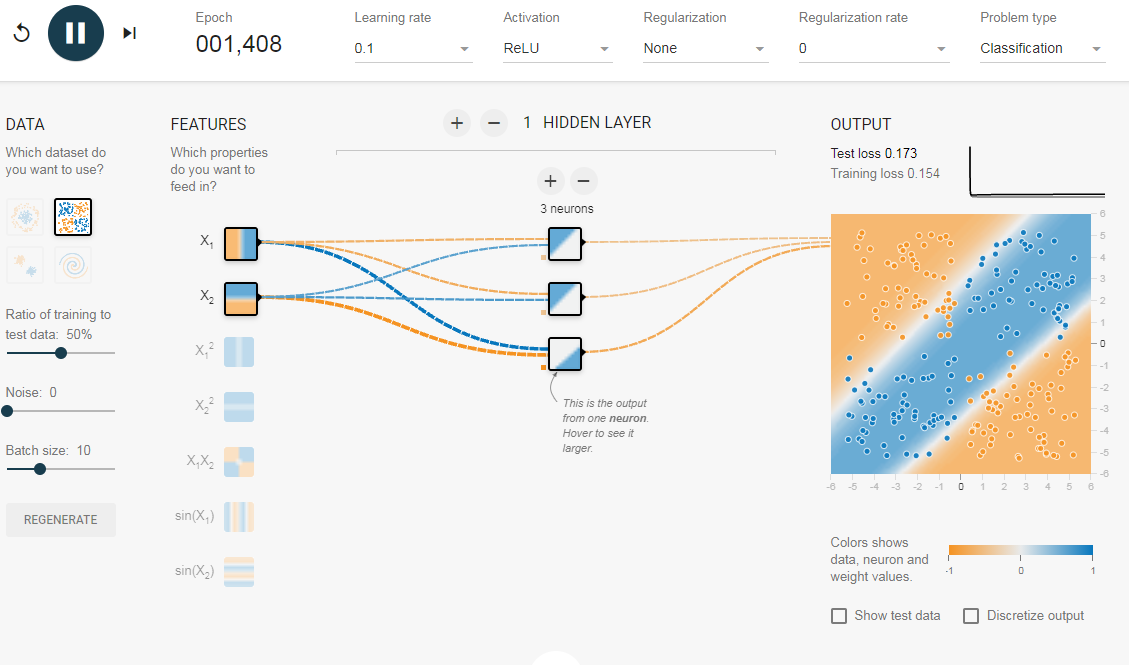
2.2. Добавление скрытого слоя
Добавив скрытый слой, как показано в этой ссылке, мы можем избавиться от этой функции проектирования и получить единую сеть, которая может изучить все три границы принятия решений. Нейронная сеть с одним скрытым слоем с нелинейными функциями активации считается универсальным аппроксиматором функций, теорема Цыбенкоએ (т.е. способной к обучению любой функции). Однако количество единиц в скрытом слое не фиксировано. Результат добавления скрытого слоя всего с 3 нейронами показан ниже:
3. Регуляризация
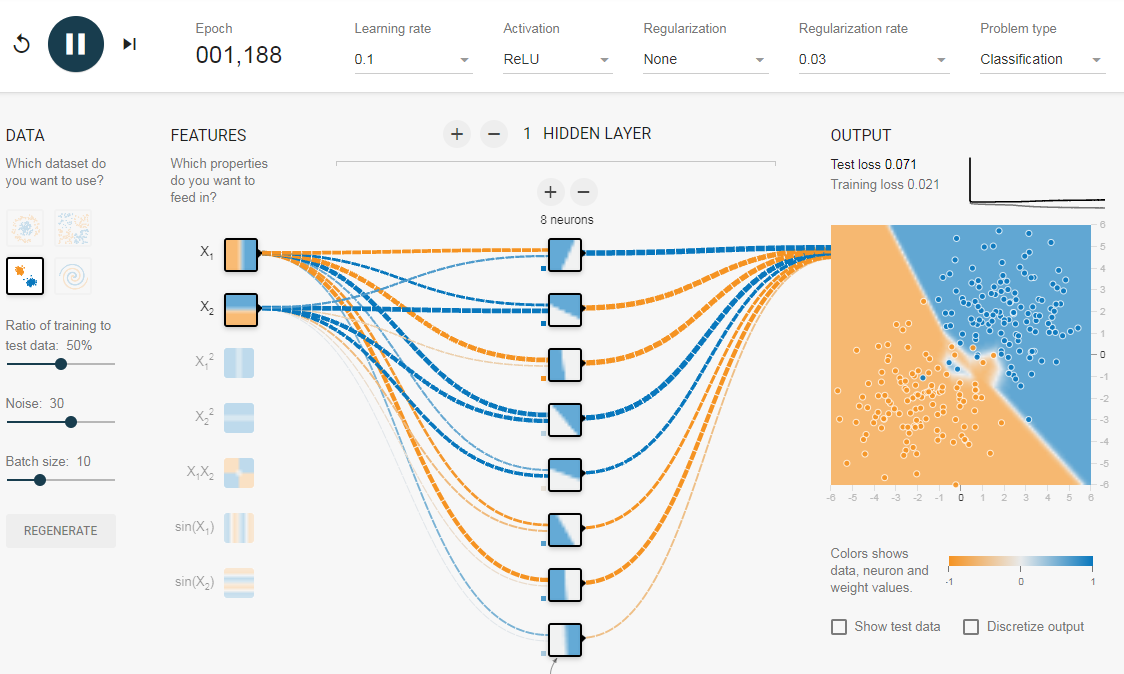
Как мы видели в предыдущем разделе, многослойная сеть может изучать нелинейные границы принятия решений. Однако, если в данных есть шум (что часто бывает), сеть может попытаться изучить нелинейность, вносимую шумом, пытаясь подогнать зашумленные выборки. В таких случаях зашумленные образцы следует рассматривать как выбросы. В этой ссылке я добавил немного шума к линейно разделяемым данным. Также, чтобы продемонстрировать идею, я увеличил количество скрытых нейронов.
На приведенном выше рисунке можно увидеть, что граница принятия решения очень старается приспособить зашумленные выборки, чтобы уменьшить ошибку. Но, как видите, это ошибочно из-за шумных сэмплов. Другими словами, сеть будет неустойчивой при наличии шума. Это явление называется переобучением. В таких случаях, ошибка обучающих данных может уменьшиться, но сеть плохо работает с невидимыми данными. Это видно по кривым потерь в правом верхнем углу.
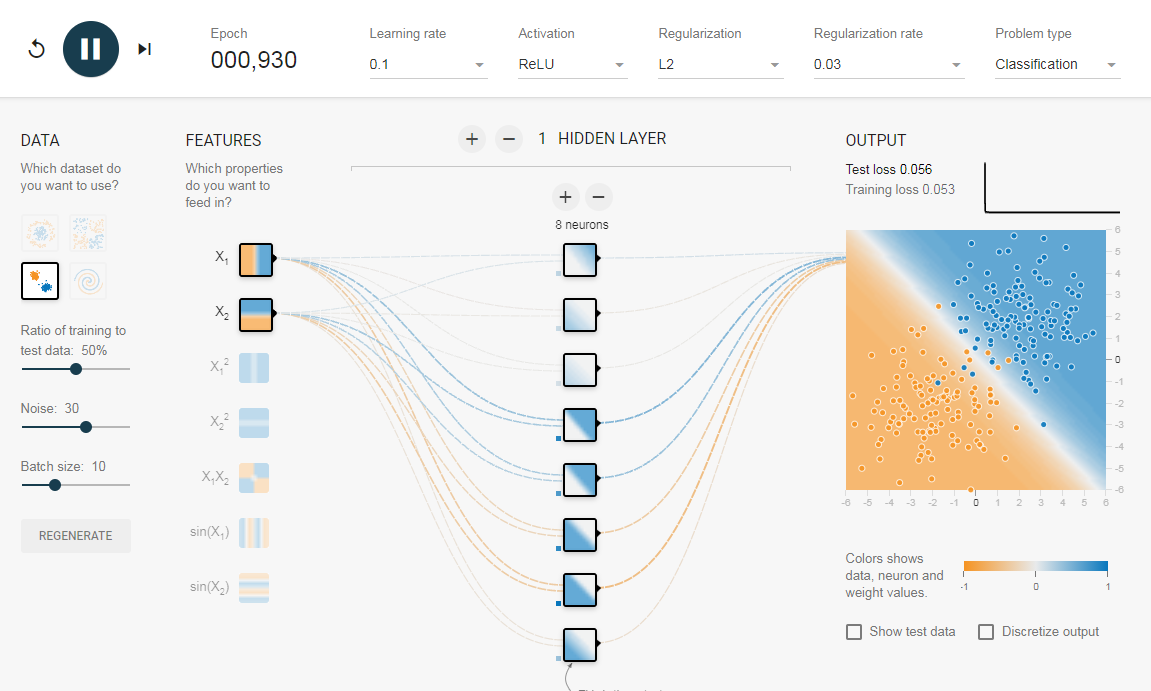
Потери в обучении уменьшаются, но потери в тестах увеличиваются. Также, можно видеть, что некоторые веса стали очень большими (очень толстые соединения или вы можете увидеть веса, если наведете курсор на соединения). Это можно исправить, наложив некоторые ограничения на значения весов (например, не позволяя весам становиться очень высокими). Это называется регуляризацией. Мы накладываем ограничения на остальные параметры сети. В некотором смысле мы не полностью доверяем обучающим данным и хотим, чтобы сеть усвоила «хорошие» границы принятия решений. Я добавил регуляризацию L2 в приведенную выше конфигурацию по этой ссылке, и результат показан ниже.
После включения регуляризации L2 граница принятия решения, изученная сетью, становится более гладкой и аналогичной случаю, когда не было шума. Эффект регуляризации также можно увидеть из кривых потерь и значений весов.
В следующем посте, если он случится мы узнаем, как реализовать нейронную сеть прямого распространения в Keras для решения нескольких проблема классификации и узнайте ещё больше о сетях прямого распространения.
Использованы материалы Understanding Feedforward Neural Networks

Нейросети кажутся людям чем-то очень сложным и запутанным, однако это вовсе не так. Простую нейросеть можно написать менее чем за час с нуля. В нашей статье мы создадим нейронную сеть прямого распространения (также называемую многослойным перцептроном), используя лишь массивы, циклы и условные операторы, а значит этот код легко можно будет перенести на любой язык программирования, предоставляющий эти возможности. А если язык предоставляет библиотеку для матричных и векторных вычислений (как, например, numpy в языке Python, то написание займёт ещё меньше времени).
Что такое нейросеть?
Согласно Википедии, искусственная нейронная сеть (ИНС) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.
Более простыми словами, это некий чёрный ящик, который превращает входные данные в выходные, или, говоря более математическим языком, является отображением пространства входных признаков X в пространство выходных признаков Y: X → Y. То есть мы хотим найти какую-то функцию F, которая сможет выполнять это преобразование. Для начала этой информации нам будет достаточно. Для более подробного ознакомления рекомендуем ознакомиться с этой статьёй на хабре.
Коротко об искусственном нейроне
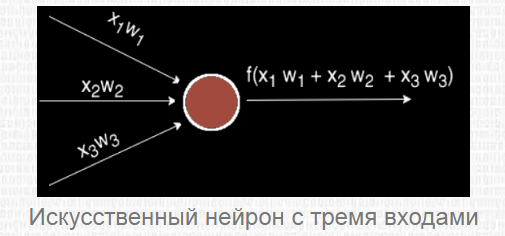
Чаще всего в подобных статьях начинают расписывать про устройство биологического нейрона, связь с его искусственной моделью и прочую лирику. Мы же этого делать не будем, а сразу перейдём к сути. Искусственный нейрон — это всего лишь взвешенная сумма значений входного вектора элементов, которая передаётся на нелинейную функцию активации f: z = f(y), где y = w0·x0 + w1·x1 + ... + wm - 1·xm - 1. Здесь w0, ..., wm - 1 — коэффициенты, веса каждого элемента вектора, x0, ..., xm - 1 — значения входного вектора X, y — взвешенная сумма элементов X, а z — результат применения функции активации. Мы вернёмся к функции активации немного позднее, а пока давайте придумаем, как вместо одного выходного значения получить n.
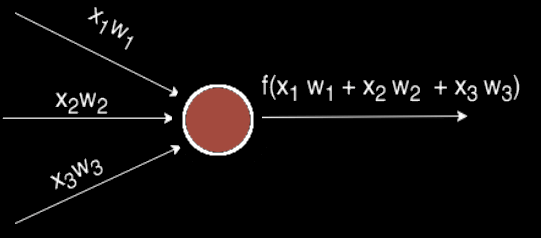
Искусственный нейрон с тремя входами
Нейронный слой
Один нейрон способен входной вектор превратить в одну точку, однако по условию мы хотим получить несколько точек, так как выходной вектор Y может иметь произвольную размерность, определяемую лишь конкретной ситуацией (один выход для XOR, 10 выходов для определения принадлежности к одному из 10 классов и т.д.). Как же нам получить n точек, преобразуя элементы входного вектора X? Оказывается, всё довольно просто: для того, чтобы получить n выходных значений, необходимо использовать не один нейрон, а n. Тогда для каждого из элементов выходного вектора Y будет использовано ровно n различных взвешенных сумм от вектора X. То есть мы получаем, что zi = f(yi) = f(wi0·x0 + wi1·x1 + ... + wim - 1·xm - 1)
Если внимательно посмотреть, то оказывается, что написанная выше формула является определением умножения матрицы на вектор. И действительно, если взять матрицу W размера n на m и умножить её на вектор X размерности m, то получится другой вектор размерности n, то есть ровно то, что нам и нужно. Таким образом, получение выходного вектора по входному для n нейронов можно записать в более удобной матричной форме: Y = W·X, где W — матрица весовых коэффициентов, X — входной вектор и Y — выходной вектор. Однако полученный вектор является неактивированным состоянием (промежуточным, невыходным) всех нейронов, а чтобы получить выходное значение,, необходимо каждое неактивированное значение подать на вход функции активации. Результат её применения и будет выходным значением слоя.
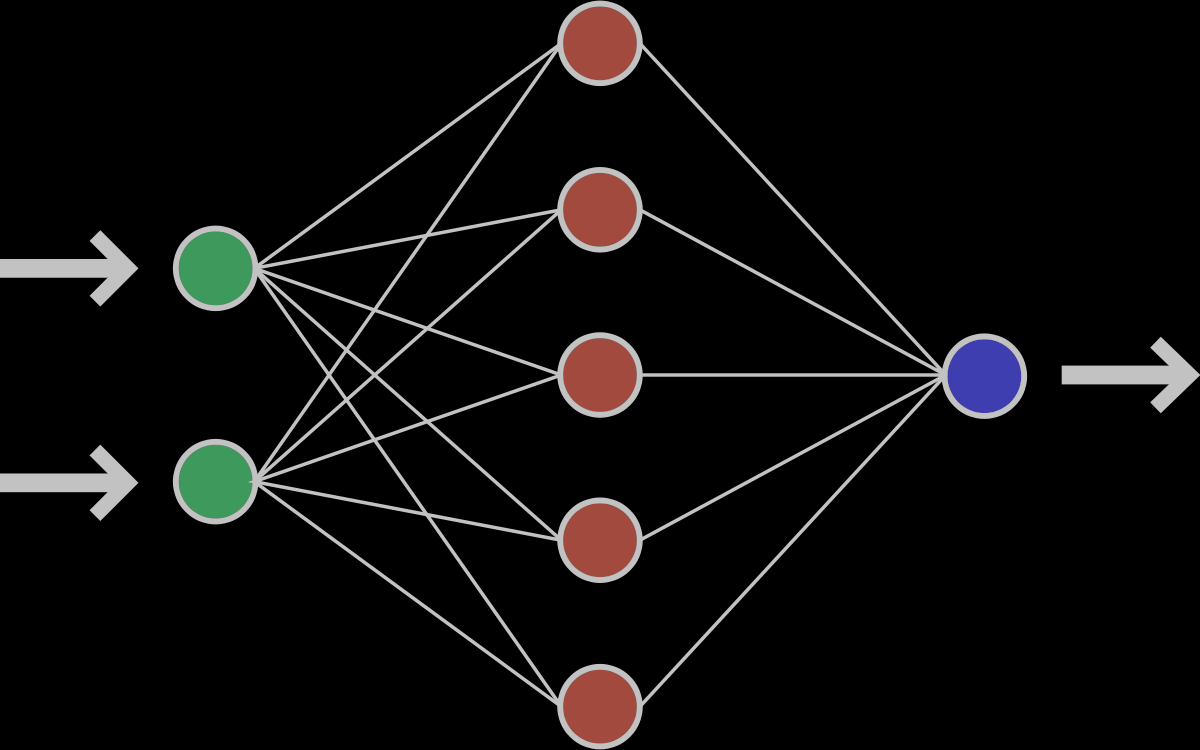
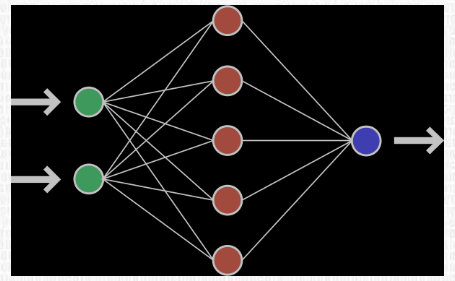
Пример нейронной сети с двумя входами, пятью нейронами в скрытом слое и одним выходом
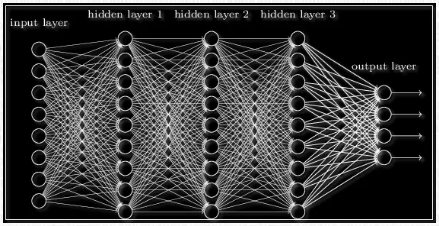
Забегая вперёд скажем о том, что нередко используют последовательность нейронных слоёв для более глубокого обучения сети и большей формализации данных. Поэтому для получения итогового выходного вектора необходимо проделать описанную выше операцию несколько раз подряд от одного слоя к другому. Тогда для первого слоя входным вектором будет X, а для всех последующих входом будет являться выход предыдущего слоя. К примеру, сеть с 3 скрытыми слоями может выглядеть так:
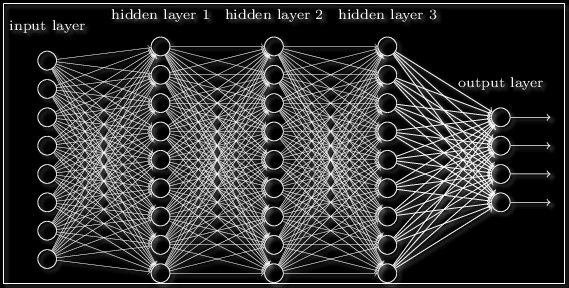
Пример многослойной нейронной сети
Функция активации
Функция активации — это функция, которая добавляет в сеть нелинейность, благодаря чему нейроны могут довольно точно имитировать любую функцию. Наиболее распространёнными функциями активации являются:
- Сигмоида:
f(x) = 1 / (1 + e-x) - Гиперболический тангенс:
f(x) = tanh(x) - ReLU:
f(x) = max(x,0)
У каждой из них есть свои особенности, но об этом лучше почитать в другой статье.
Хватит бла бла, давайте писать код
Теперь нам достаточно знаний, чтобы написать код получения результата нейронной сети. Мы будем писать код на языке C#, однако, уверяем, код будет практически идентичным для других языков программирования. Давайте разберёмся, что нам потребуется для реализации сети прямого распространения:
- Вектор (входные, выходные);
- Матрица (каждый слой содержит матрицу весовых коэффициентов);
- Нейросеть.
1. Вектор:
- Вектор можно создавать из количества элементов (длины);
- Вектор можно создавать из перечисления вещественных чисел;
- Можно получать значения по индексу i.
- Можно изменять значения по индексу i.
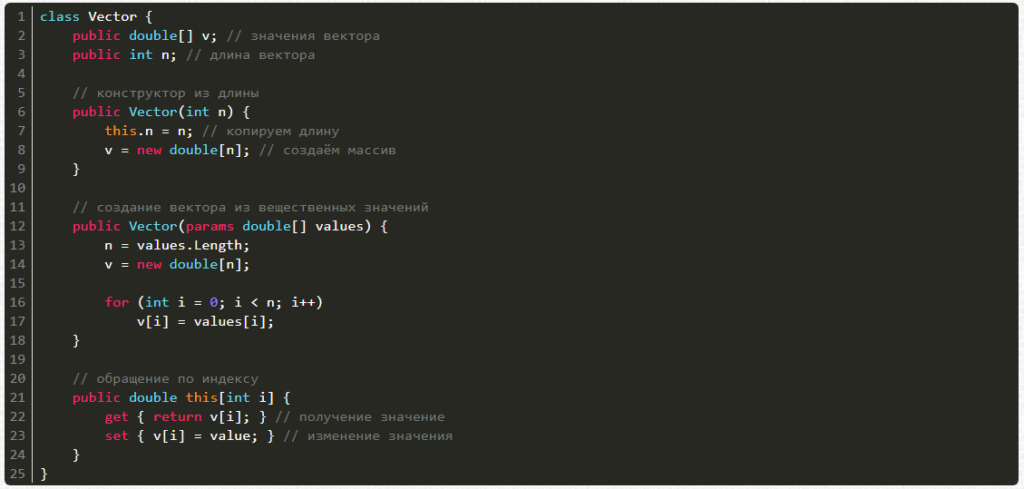
Напишем же это:
class Vector {
public double[] v; // значения вектора
public int n; // длина вектора
// конструктор из длины
public Vector(int n) {
this.n = n; // копируем длину
v = new double[n]; // создаём массив
}
// создание вектора из вещественных значений
public Vector(params double[] values) {
n = values.Length;
v = new double[n];
for (int i = 0; i < n; i++)
v[i] = values[i];
}
// обращение по индексу
public double this[int i] {
get { return v[i]; } // получение значение
set { v[i] = value; } // изменение значения
}
}
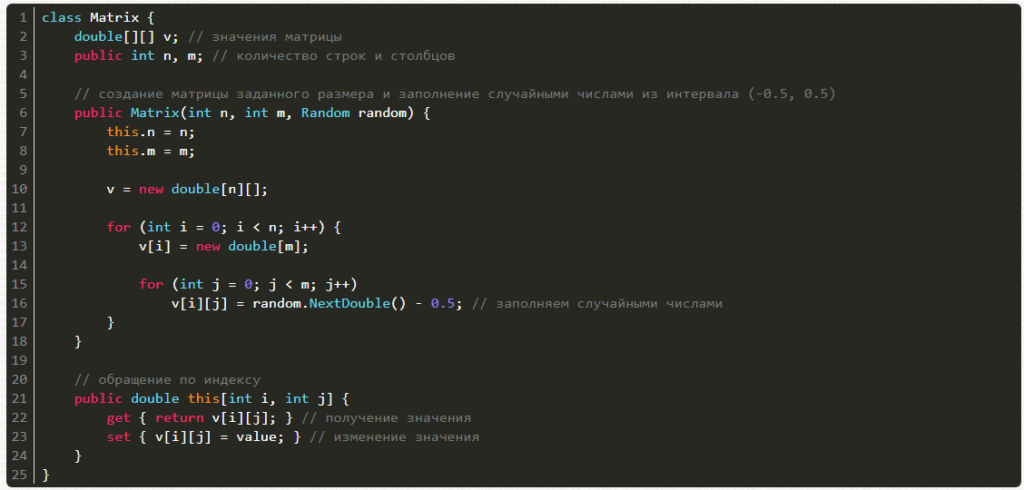
2. Матрица:
- Матрицу можно создавать из числа строк, столбцов и генератора случайных чисел для заполнения случайными значениями;
- Можно получать значения по индексам i и j;
- Можно изменять значения по индексам i и j;
Напишем же это:
class Matrix {
double[][] v; // значения матрицы
public int n, m; // количество строк и столбцов
// создание матрицы заданного размера и заполнение случайными числами из интервала (-0.5, 0.5)
public Matrix(int n, int m, Random random) {
this.n = n;
this.m = m;
v = new double[n][];
for (int i = 0; i < n; i++) {
v[i] = new double[m];
for (int j = 0; j < m; j++)
v[i][j] = random.NextDouble() - 0.5; // заполняем случайными числами
}
}
// обращение по индексу
public double this[int i, int j] {
get { return v[i][j]; } // получение значения
set { v[i][j] = value; } // изменение значения
}
}
3. Сама нейросеть:
class Network {
Matrix[] weights; // матрицы весов слоя
int layersN; // число слоёв
// создание сети из массива количества нейронов в каждом слое
public Network(int[] sizes) {
Random random = new Random(DateTime.Now.Millisecond); // создаём генератор случайных чисел
layersN = sizes.Length - 1; // запоминаем число слоёв
weights = new Matrix[layersN]; // создаём массив матриц
// для каждого слоя создаём матрицы весовых коэффициентов
for (int k = 1; k < sizes.Length; k++) {
weights[k - 1] = new Matrix(sizes[k], sizes[k - 1], random);
}
}
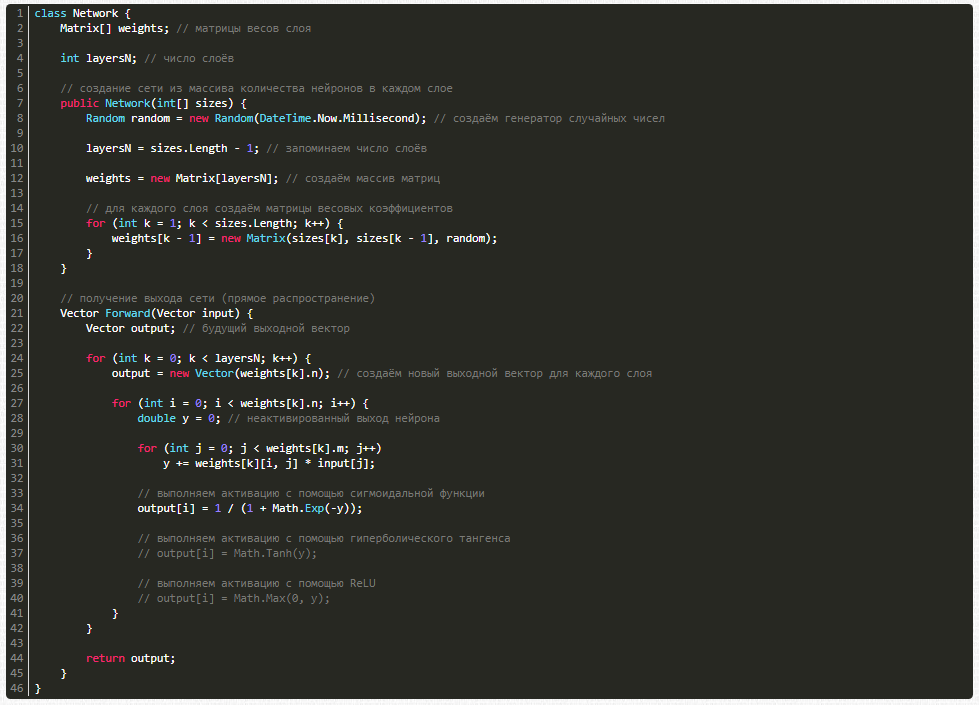
// получение выхода сети (прямое распространение)
Vector Forward(Vector input) {
Vector output; // будущий выходной вектор
for (int k = 0; k < layersN; k++) {
output = new Vector(weights[k].n); // создаём новый выходной вектор для каждого слоя
for (int i = 0; i < weights[k].n; i++) {
double y = 0; // неактивированный выход нейрона
for (int j = 0; j < weights[k].m; j++)
y += weights[k][i, j] * input[j];
// выполняем активацию с помощью сигмоидальной функции
output[i] = 1 / (1 + Math.Exp(-y));
// выполняем активацию с помощью гиперболического тангенса
// output[i] = Math.Tanh(y);
// выполняем активацию с помощью ReLU
// output[i] = Math.Max(0, y);
}
}
return output;
}
}
Сеть есть, но её ответы случайны. Как обучать?
На данный момент мы имеем случайную (необученную) нейронную сеть, которая может по входному вектору input выдать случайный ответ, однако нам требуется ответы, удовлетворяющие конкретной задаче. Чтобы добиться этого нашу сеть необходимо обучить. Для этого нам необходима база тренировочных примеров, то есть множество пар векторов X — Y, на которых будет обучаться сеть. Обучать нейросеть мы будем с помощью алгоритма обратного распространения ошибки. Если кратко, то он работает следующим образом:
- Подать на вход сети обучающий пример (один входной вектор)
- Распространить сигнал по сети вперёд (получить выход сети)
- Вычислить ошибку (разница получившегося и ожидаемого векторов)
- Распространить ошибку на предыдущие слои
- Обновить весовые коэффициенты для уменьшения ошибки
Сам же алгоритм обучения выглядит так:
error = 0 epoch = 1 повторять: Для каждого обучающего примера: Найти ошибку e = f - d Прибавить к error сумму квадратов значений e Распространенить ошибку к первому слою Обновить веса если error < eps выйти если epoch > maxEpoch выйти из-за ограничения на число эпох epoch = epoch + 1
Обучаем нейронную сеть
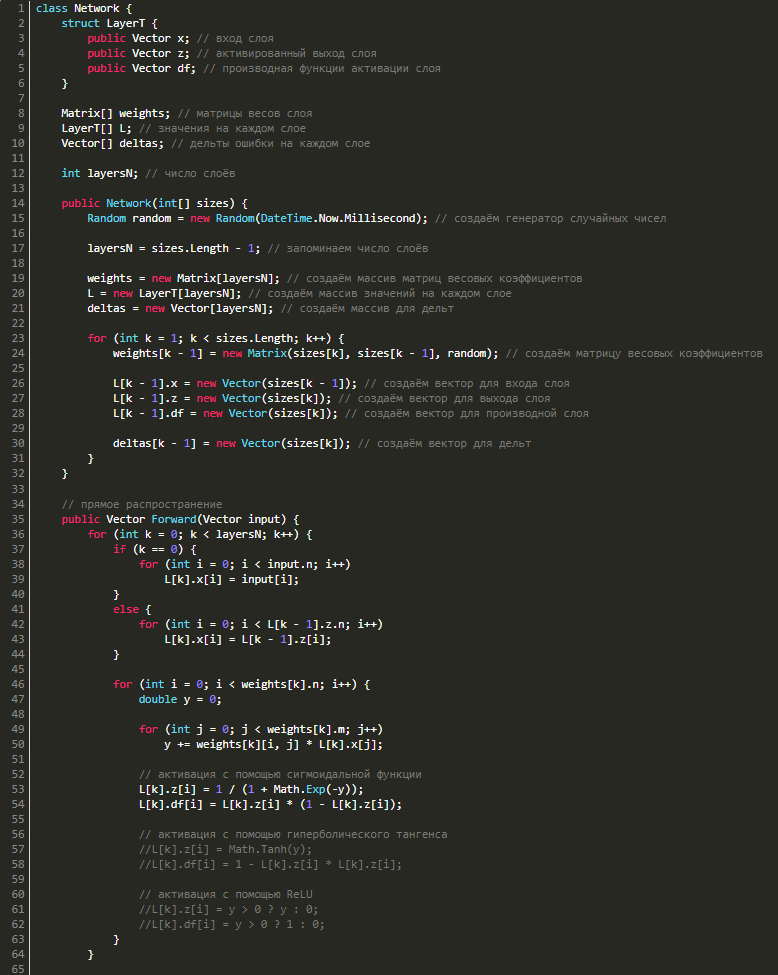
Для обратного распространения ошибки нам потребуется знать значения входов, выходов и значения производных функции активации сети на каждом из слоёв, поэтому создадим структуру LayerT, в которой будет 3 вектора: x — вход слоя, z — выход слоя, df — производная функции активации. Также для каждого слоя потребуются векторы дельт, поэтому добавим в наш класс ещё и их. С учётом вышесказанного наш класс станет выглядеть так:
class Network {
struct LayerT {
public Vector x; // вход слоя
public Vector z; // активированный выход слоя
public Vector df; // производная функции активации слоя
}
Matrix[] weights; // матрицы весов слоя
LayerT[] L; // значения на каждом слое
Vector[] deltas; // дельты ошибки на каждом слое
int layersN; // число слоёв
public Network(int[] sizes) {
Random random = new Random(DateTime.Now.Millisecond); // создаём генератор случайных чисел
layersN = sizes.Length - 1; // запоминаем число слоёв
weights = new Matrix[layersN]; // создаём массив матриц весовых коэффициентов
L = new LayerT[layersN]; // создаём массив значений на каждом слое
deltas = new Vector[layersN]; // создаём массив для дельт
for (int k = 1; k < sizes.Length; k++) {
weights[k - 1] = new Matrix(sizes[k], sizes[k - 1], random); // создаём матрицу весовых коэффициентов
L[k - 1].x = new Vector(sizes[k - 1]); // создаём вектор для входа слоя
L[k - 1].z = new Vector(sizes[k]); // создаём вектор для выхода слоя
L[k - 1].df = new Vector(sizes[k]); // создаём вектор для производной слоя
deltas[k - 1] = new Vector(sizes[k]); // создаём вектор для дельт
}
}
// прямое распространение
public Vector Forward(Vector input) {
for (int k = 0; k < layersN; k++) {
if (k == 0) {
for (int i = 0; i < input.n; i++)
L[k].x[i] = input[i];
}
else {
for (int i = 0; i < L[k - 1].z.n; i++)
L[k].x[i] = L[k - 1].z[i];
}
for (int i = 0; i < weights[k].n; i++) {
double y = 0;
for (int j = 0; j < weights[k].m; j++)
y += weights[k][i, j] * L[k].x[j];
// активация с помощью сигмоидальной функции
L[k].z[i] = 1 / (1 + Math.Exp(-y));
L[k].df[i] = L[k].z[i] * (1 - L[k].z[i]);
// активация с помощью гиперболического тангенса
//L[k].z[i] = Math.Tanh(y);
//L[k].df[i] = 1 - L[k].z[i] * L[k].z[i];
// активация с помощью ReLU
//L[k].z[i] = y > 0 ? y : 0;
//L[k].df[i] = y > 0 ? 1 : 0;
}
}
return L[layersN - 1].z; // возвращаем результат
}
}
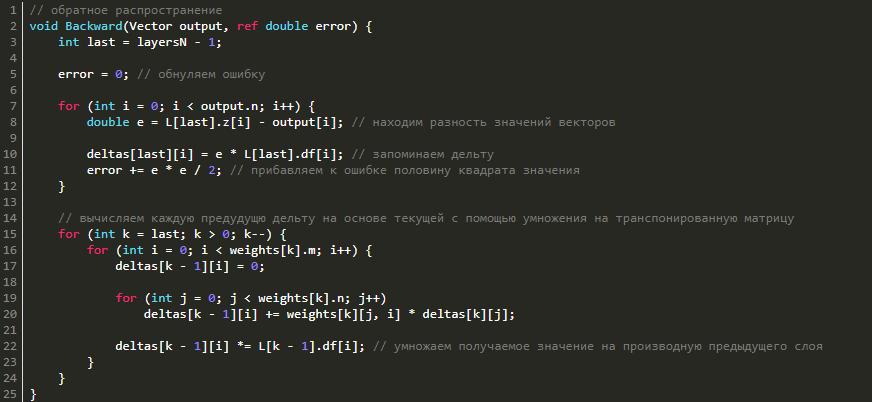
Обратное распространение ошибки
Перейдём к обратному распространению ошибки. В качестве функции оценки сети E(W) возьмём среднее квадратичное отклонение: E = 0.5 · Σ(y1i - y2i)2. Чтобы найти значение ошибки E, нам нужно найти сумму квадратов разности значений вектора, который выдала сеть в качестве ответа, и вектора, который мы ожидаем увидеть при обучении. Также нам потребуется найти дельту для каждого слоя, причём для последнего слоя она будет равна вектору разности полученного и ожидаемого векторов, умноженному (покомпонентно) на вектор значений производных последнего слоя: δlast = (zlast - d)·f'last, где zlast — выход последнего слоя сети, d — ожидаемый вектор сети, f'last — вектор значений производной функции активации последнего слоя.
Теперь, зная дельту последнего слоя, мы можем найти дельты всех предыдущих слоёв. Для этого нужно умножить транспонированную матрицы текущего слоя на дельту текущего слоя и затем умножить полученный вектор на вектор производных функции активации предыдущего слоя: δk-1 = WTk·δk·f'k.
Что ж, давайте реализуем это в коде:
// обратное распространение
void Backward(Vector output, ref double error) {
int last = layersN - 1;
error = 0; // обнуляем ошибку
for (int i = 0; i < output.n; i++) {
double e = L[last].z[i] - output[i]; // находим разность значений векторов
deltas[last][i] = e * L[last].df[i]; // запоминаем дельту
error += e * e / 2; // прибавляем к ошибке половину квадрата значения
}
// вычисляем каждую предудущю дельту на основе текущей с помощью умножения на транспонированную матрицу
for (int k = last; k > 0; k--) {
for (int i = 0; i < weights[k].m; i++) {
deltas[k - 1][i] = 0;
for (int j = 0; j < weights[k].n; j++)
deltas[k - 1][i] += weights[k][j, i] * deltas[k][j];
deltas[k - 1][i] *= L[k - 1].df[i]; // умножаем получаемое значение на производную предыдущего слоя
}
}
}
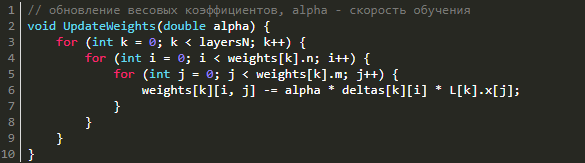
Изменение весов
Для того, чтобы уменьшить ошибку сети нужно изменить весовые коэффициенты каждого слоя. Как же именно нужно менять весовые коэффициенты матриц на каждом слое? Оказывается, всё довольно просто. Для этого используется метод градиентного спуска, а значит нам необходимо вычислить градиент по весам и сделать шаг в отрицательную сторону от этого градиента. На этапе прямого распространения мы зачем-то запоминали входные сигналы, а при обратном распространении ошибки мы вычисляли дельты в каждом слое. Именно их мы и будем сейчас использовать для нахождения градиента! Градиент по весам равен перемножению входного вектора и вектора дельт (не покомпонентно). Поэтому, чтобы обновить весовые коэффициенты и уменьшить тем самым ошибку сети нужно всего лишь вычесть из матрицы весов результат перемножения дельт и входных векторов, умноженный на скорость обучения. Это можно записать в таком виде: Wt+1 = Wt - η·δ·X, где Wt+1 — новая матрица весов, Wt — текущая матрица весов, X — входное значение слоя, δ — дельта этого слоя. Почему именно так с математической точки зрения хорошо описано в этой статье.
// обновление весовых коэффициентов, alpha - скорость обучения
void UpdateWeights(double alpha) {
for (int k = 0; k < layersN; k++) {
for (int i = 0; i < weights[k].n; i++) {
for (int j = 0; j < weights[k].m; j++) {
weights[k][i, j] -= alpha * deltas[k][i] * L[k].x[j];
}
}
}
}
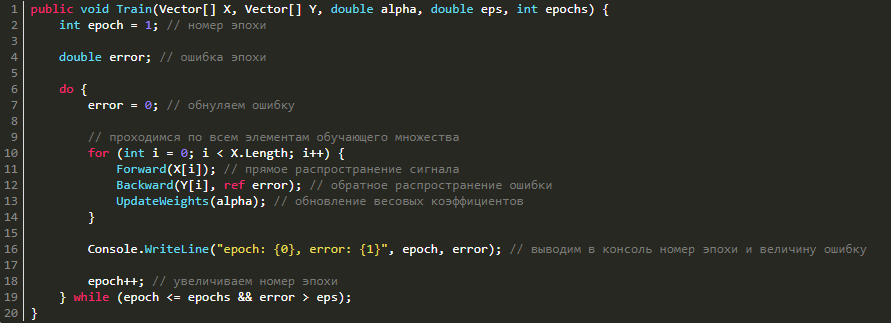
Обучение сети
Теперь, имея методы прямого распространения сигнала, обратного распространения ошибки и изменения весовых коэффициентов, нам остаётся лишь соединить всё вместе в один метод обучения.
public void Train(Vector[] X, Vector[] Y, double alpha, double eps, int epochs) {
int epoch = 1; // номер эпохи
double error; // ошибка эпохи
do {
error = 0; // обнуляем ошибку
// проходимся по всем элементам обучающего множества
for (int i = 0; i < X.Length; i++) {
Forward(X[i]); // прямое распространение сигнала
Backward(Y[i], ref error); // обратное распространение ошибки
UpdateWeights(alpha); // обновление весовых коэффициентов
}
Console.WriteLine("epoch: {0}, error: {1}", epoch, error); // выводим в консоль номер эпохи и величину ошибку
epoch++; // увеличиваем номер эпохи
} while (epoch <= epochs && error > eps);
}
Сеть готова. Давайте же её чему-нибудь научим!
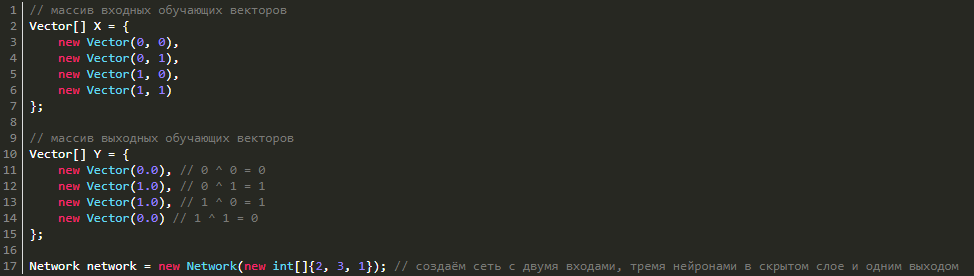
Тренируем нейросеть на функции XOR
Почему функция XOR так интересна? Просто потому, что её невозможно получить одним нейроном: 0 ^ 0 = 0, 0 ^ 1 = 1, 1 ^ 0 = 1, 1 ^ 1 = 0. Однако она легко получается увеличением числа нейронов. Мы же попробуем выполнить обучение сети с 3 нейронами в скрытом слое и 1 выходным (так как выход у нас всего один). Для этого нам необходимо создать массив векторов X и Y с обучающими данными и саму нейросеть:
// массив входных обучающих векторов
Vector[] X = {
new Vector(0, 0),
new Vector(0, 1),
new Vector(1, 0),
new Vector(1, 1)
};
// массив выходных обучающих векторов
Vector[] Y = {
new Vector(0.0), // 0 ^ 0 = 0
new Vector(1.0), // 0 ^ 1 = 1
new Vector(1.0), // 1 ^ 0 = 1
new Vector(0.0) // 1 ^ 1 = 0
};
Network network = new Network(new int[]{2, 3, 1}); // создаём сеть с двумя входами, тремя нейронами в скрытом слое и одним выходом
После чего запустим обучение со следующими параметрами: скорость обучения — 0.5, число эпох — 100000, величина ошибки — 1e-7:
network.Train(X, Y, 0.5, 1e-7, 100000); // запускаем обучение сети
После обучения посмотрим на результаты выполнив прямой проход для всех элементов:
for (int i = 0; i < 4; i++) {
Vector output = network.Forward(X[i]);
Console.WriteLine("X: {0} {1}, Y: {2}, output: {3}", X[i][0], X[i][1], Y[i][0], output[0]);
}
В результате вывод может быть таким:
X: 0 0, Y: 0, output: 0,00503439463431083 X: 0 1, Y: 1, output: 0,996036009216668 X: 1 0, Y: 1, output: 0,996036033202241 X: 1 1, Y: 0, output: 0,00550270947767007
Проверять результаты на тренировочной же выборке довольно скучно, ведь как никак на ней мы сеть обучали, но, увы, для XOR проблемы ничего другого не остаётся. В качестве более серьёзного примера рекомендуем выполнить задачу распознавания картинок с рукописными цифрами MNIST. Это база содержит 60000 картинок написанных от руки цифр размером 28 на 28 пикселей и используется как один из основных датасетов для начала изучения машинного обучения. Не смотря на простоту нашей сети, при грамотном выборе параметров (число нейронов, число слоёв, скорость обучения, число эпох…) можно получить точность распознавания до 98%! Проверить свою сеть вы можете, поучаствовав в соревновании на сайте Kaggle. Нашей команде удалось достичь точности в 98.171%! А вы сможете больше? 
В заключение
Мы написали с вами нейронную сеть прямого распространения и даже обучили её функции XOR. При этом мы позаботились об универсальности, благодаря чему нейросеть может быть обучена на любых данных, главное только подготовить два массива обучающих векторов X и Y, подобрать параметры обучения и запустить само обучение, после чего наблюдать за процессом. Важно помнить, что при использовании сигмоидальной функции активации, выходные значения сети не будут превышать 1, а значит, для обучения данным, которые значительно больше 1 необходимо отнормировать их, то есть привести к отрезку [0, 1].
Возможно, будет интересно: Свёрточная нейронная сеть с нуля. Часть 0. Введение.
Рассказывает Per Harald Borgen
В этот раз я решил изучить нейронные сети. Базовые навыки в этом вопросе я смог получить за лето и осень 2015 года. Под базовыми навыками я имею в виду, что могу сам создать простую нейронную сеть с нуля. Примеры можете найти в моих репозиториях на GitHub. В этой статье я дам несколько разъяснений и поделюсь ресурсами, которые могут пригодиться вам для изучения.
Шаг 1. Нейроны и метод прямого распространения
Так что же такое «нейронная сеть»? Давайте подождём с этим и сперва разберёмся с одним нейроном.
Нейрон похож на функцию: он принимает на вход несколько значений и возвращает одно.
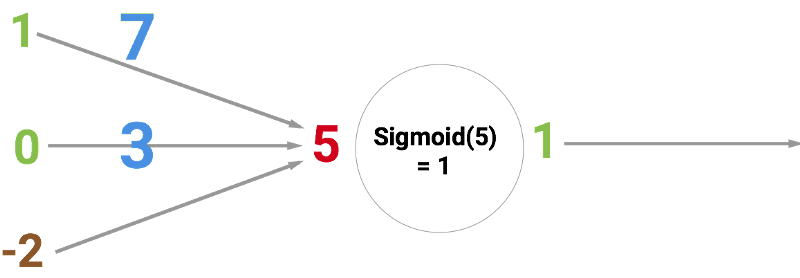
Круг ниже обозначает искусственный нейрон. Он получает 5 и возвращает 1. Ввод — это сумма трёх соединённых с нейроном синапсов (три стрелки слева).
В левой части картинки мы видим 2 входных значения (зелёного цвета) и смещение (выделено коричневым цветом).
Входные данные могут быть численными представлениями двух разных свойств. Например, при создании спам-фильтра они могли бы означать наличие более чем одного слова, написанного ЗАГЛАВНЫМИ БУКВАМИ, и наличие слова «виагра».
Входные значения умножаются на свои так называемые «веса», 7 и 3 (выделено синим).
Теперь мы складываем полученные значения со смещением и получаем число, в нашем случае 5 (выделено красным). Это — ввод нашего искусственного нейрона.
Потом нейрон производит какое-то вычисление и выдает выходное значение. Мы получили 1, т.к. округлённое значение сигмоиды в точке 5 равно 1 (более подробно об этой функции поговорим позже).
Если бы это был спам-фильтр, факт вывода 1 означал бы то, что текст был помечен нейроном как спам.
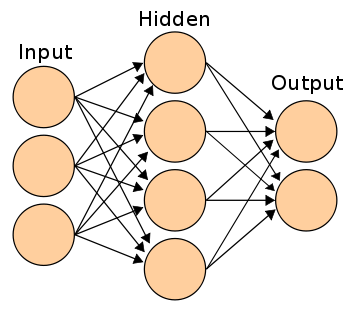
Иллюстрация нейронной сети с Википедии.
Если вы объедините эти нейроны, то получите прямо распространяющуюся нейронную сеть — процесс идёт от ввода к выводу, через нейроны, соединённые синапсами, как на картинке слева.
Я очень рекомендую посмотреть серию видео от Welch Labs для улучшения понимания процесса.
Шаг 2. Сигмоида
После того, как вы посмотрели уроки от Welch Labs, хорошей идеей было бы ознакомиться с четвертой неделей курса по машинному обучению от Coursera, посвящённой нейронным сетям — она поможет разобраться в принципах их работы. Курс сильно углубляется в математику и основан на Octave, а я предпочитаю Python. Из-за этого я пропустил упражнения и почерпнул все необходимые знания из видео.
Сигмоида просто-напросто отображает ваше значение (по горизонтальной оси) на отрезок от 0 до 1.
Первоочередной задачей для меня стало изучение сигмоиды, так как она фигурировала во многих аспектах нейронных сетей. Что-то о ней я уже знал из третьей недели вышеупомянутого курса, поэтому я пересмотрел видео оттуда.
Но на одних видео далеко не уедешь. Для полного понимания я решил закодить её самостоятельно. Поэтому я начал писать реализацию алгоритма логистической регрессии (который использует сигмоиду).
Это заняло целый день, и вряд ли результат получился удовлетворительным. Но это неважно, ведь я разобрался, как всё работает. Код можно увидеть здесь.
Вам необязательно делать это самим, поскольку тут требуются специальные знания — главное, чтобы вы поняли, как устроена сигмоида.
Шаг 3. Метод обратного распространения ошибки
Понять принцип работы нейронной сети от ввода до вывода не так уж и сложно. Гораздо сложнее понять, как нейронная сеть обучается на наборах данных. Использованный мной принцип называется методом обратного распространения ошибки.
Вкратце: вы оцениваете, насколько сеть ошиблась, и изменяете вес входных значений (синие числа на первой картинке).
Процесс идёт от конца к началу, так как мы начинаем с конца сети (смотрим, насколько отклоняется от истины догадка сети) и двигаемся назад, изменяя по пути веса, пока не дойдём до ввода. Для вычисления всего этого вручную потребуются знания матанализа. Khan Academy предоставляет хорошие курсы по матанализу, но я изучал его в университете. Также можно не заморачиваться и воспользоваться библиотеками, которые посчитают весь матан за вас.
Скриншот из руководства Мэтта Мазура по методу обратного распространения ошибки.
Вот три источника, которые помогли мне разобраться в этом методе:
- A Step by Step Backpropagation Example от Matt Mazur;
- Hacker’s guide to Neural Networks от Andrej Karpathy;
- Using neural nets to recognize handwritten digits от Michael Nielsen.
В процессе прочтения первых двух статей вам обязательно нужно кодить самим, это поможет вам в дальнейшем. Да и вообще, в нейронных сетях нельзя как следует разобраться, если пренебречь практикой. Третья статья тоже классная, но это скорее энциклопедия, поскольку она размером с целую книгу. Она содержит подробные объяснения всех важных принципов работы нейронных сетей. Эти статьи также помогут вам изучить такие понятия, как функция стоимости и градиентный спуск.
Шаг 4. Создание своей нейронной сети
При прочтении различных статей и руководств вы так или иначе будете писать маленькие нейронные сети. Рекомендую именно так и делать, поскольку это — очень эффективный метод обучения.
Ещё одной полезной статьёй оказалась A Neural Network in 11 lines of Python от IAmTrask. В ней содержится удивительное количество знаний, сжатых до 11 строк кода.
Скриншот руководства от IAmTrask
После прочтения этой статьи вам следует написать реализацию всех примеров самостоятельно. Это поможет вам закрыть дыры в знаниях, а когда у вас получится, вы почувствуете, будто обрели суперсилу.
Поскольку в примерах частенько встречаются реализации, использующие векторные вычисления, я рекомендую пройти курс по линейной алгебре от Coursera.
После этого можно ознакомиться с руководством Wild ML от Denny Britz, в котором разбираются нейронные сети посложнее.
Скриншот из руководства WildML
Теперь вы можете попробовать написать свою собственную нейронную сеть или поэкспериментировать с уже написанными. Очень забавно найти интересующий вас набор данных и проверить различные предположения при помощи ваших сетей.
Для поиска хороших наборов данных можете посетить мой сайт Datasets.co и выбрать там подходящий.
Так или иначе, теперь вам лучше начать свои эксперименты, чем слушать мои советы. Лично я сейчас изучаю Python-библиотеки для программирования нейронных сетей, такие как Theano, Lasagne и nolearn.
Удачи!
Перевод статьи «Learning How To Code Neural Networks»
- Подробная прямая нейронная сеть и алгоритм BP
- 1. Понятие нейронной сети
- 1.1 Базовая единица искусственной нейронной сети -> Персептрон
- 1.1.1 Объяснение модели персептрона
- 1.1.2 Функция потерь модели персептрона
- 1.1.3 Метод оптимизации функции потерь персептрона и описание алгоритма потока
- 1.1.3.1 Метод оптимизации
- 1.1.3.2 Описание алгоритма
- 1.2 Глубокая нейронная сеть (DNN) и алгоритм прямого распространения
- 1.2.1 Введение в глубокие нейронные сети
- 1.2.2 Алгоритм прямого распространения
- 1.3 Алгоритм обратного распространения BP (обратное распространение)
- 1.3.1 Проблемы, которые необходимо решить путем обратного распространения
- 1.3.2 Основная идея алгоритма обратного распространения
- 1.3.3 Процесс алгоритма обратного распространения DNN
- 1.3.4 Мышление на основе алгоритма обратного распространения DNN
- 1.1 Базовая единица искусственной нейронной сети -> Персептрон
- Во-вторых, практика кодирования прямой нейронной сети на основе TensorFlow
- 2.1 Функции библиотеки TensorFlow участвуют
- 2.2 Подгонка нелинейной регрессии данных
- 2.3 Использование Keras для моделирования непрерывных переменных
- 2.4 Задача мультиклассификации, многоузловой выходной слой
- 1. Понятие нейронной сети
Подробная прямая нейронная сеть и алгоритм BP
1. Понятие нейронной сети
1.1 Базовая единица искусственной нейронной сети -> Персептрон
1.1.1 Объяснение модели персептрона
- Прежде всего, нам необходимо прояснить, что для SVM с функциями ядра или многослойных нейронных сетей с несколькими скрытыми слоями + функциями активации или других моделей, которые могут иметь дело с нелинейной разделимостью, персептроны часто называют нейронами, но Это также можно рассматривать как двухслойную нейронную сеть (То есть только входной слой и выходной слой, нет скрытого слоя ), хотя он может иметь дело только с линейно разделимыми проблемами, он все еще является краеугольным камнем нашего изучения нейронных сетей и глубокого обучения.
- Соответствующие символы на рисунке имеют следующие значения:
- Вход (x1, …, xn)
- Смещение b и синаптические веса (w1, …, wn), обратите внимание, что мы нажимаем ниже, чтобы использовать
θ
i
Вместо wi для вывода формулы. - Комбинированная функция c (·)
- Функция активации а (·)
- Выход у
- На математическом языке, если у нас есть m выборок, каждая выборка соответствует n-мерным элементам и выводу двоичной категории следующим образом:
(
x
1
(
0
)
,
x
2
(
0
)
,
.
.
.
x
n
(
0
)
,
y
0
)
,
(
x
1
(
1
)
,
x
2
(
1
)
,
.
.
.
x
n
(
1
)
,
y
1
)
,
.
.
.
(
x
1
(
m
)
,
x
2
(
m
)
,
.
.
.
x
n
(
m
)
,
y
m
)
- Наша цель — найти гиперплоскость, а именно:
θ
0
+
θ
1
x
1
+
.
.
.
+
θ
n
x
n
=
0
Когда элементы выборки каждой категории приводятся в уравнение, они либо больше 0, либо меньше 0, так что выборки разделяются с обеих сторон гиперплоскости, так что они линейно разделимы. Как правило, если выборка линейно разделима, такая гиперплоскость будет иметь несколько решений, которые не являются уникальными. - Чтобы упростить модель, мы добавляем x0 = 1, делая уравнение гиперплоскости сокращенным
∑
i
=
0
n
θ
i
x
i
=
0
Следующая записываемая векторная форма
θ
∙
x
=
0
среди них
θ
И X оба n * 1 векторов,
∙
Для внутреннего продукта мы будем использовать его для представления гиперплоскости ниже. - Следовательно, модель персептрона может быть определена как
y
=
s
i
g
n
(
θ
∙
x
)
Где знак — это функция активации, которая является функцией знака, также известной как функция шага.
s
i
g
n
(
x
)
=
{
−
1
x
<
0
1
x
≥
0
- В многослойных нейронных сетях мы можем использовать другие функции активации, а именно:
1.1.2 Функция потерь модели персептрона
- Основываясь на приведенном выше анализе, мы будем
θ
∙
x
>
0
Выходное значение категории выборки принимается за 1, а выборка категории менее 0 принимается за -1, поэтому преимущество его определения состоит в том, что нам удобно определять функцию потерь. Из-за вышеупомянутого соглашения правильно классифицированные образцы удовлетворяют:
y
θ
∙
x
>
0
И неправильный образец классификации удовлетворяет
y
θ
∙
x
<
0
, Следовательно, метод оптимизации функции потерь состоит в том, чтобы сделать сумму расстояний до гиперплоскости всех выборок, которые неправильно классифицированы, равными наименьшему (то есть, чтобы неправильно классифицированные выборки постепенно исчезали). - из-за
y
θ
∙
x
<
0
Таким образом, для каждого неправильно классифицированного образца i расстояние до гиперплоскости равно:
−
y
(
i
)
θ
∙
x
(
i
)
/
|
|
θ
|
|
2
- среди них,
|
|
θ
|
|
2
Является ли норма L2. (Если формула расстояния здесь не понята, вы можете самостоятельно проверить расстояние от точки до прямой линии или изучить соответствующие главы машинного обучения) - Далее мы предполагаем, что множество всех ошибочно классифицированных точек равно M, тогда сумма расстояний всех ошибочно классифицированных выборок до гиперплоскости равна:
−
∑
x
i
∈
M
y
(
i
)
θ
∙
x
(
i
)
/
|
|
θ
|
|
2
Таким образом, мы получили функцию потерь предварительной модели персептрона.
- Кроме того, нам также нужно упростить его, мы можем заметить, что как числитель, так и знаменатель имеют
θ
(Т.е. числитель и знаменатель имеют одинаковое увеличение), когда числитель
θ
При увеличении в N раз норма L2 его знаменателя также увеличится в N раз. Поскольку мы изучаем проблему максимизации, мы можем зафиксировать числитель или знаменатель равным 1, затем решить вопрос минимизации оставшегося числителя или обратной величины знаменателя и затем использовать его в качестве функции потерь. Это может упростить нашу функцию потерь и облегчить решение последующих проблем.Примечание. В модели персептрона используется числитель удержания, а фиксированный знаменатель равен 1.То есть функция потерь конечного персептрона равна:
J
(
θ
)
=
−
∑
x
i
∈
M
y
(
i
)
θ
∙
x
(
i
)
В дополнение к нам также необходимо обратить внимание наДля SVM он использует фиксированный числитель 1, а затем решает
1
|
|
θ
|
|
2
Проблема максимизации (Почему проблема максимизации, а не проблема минимизации, это связано с идеей оптимизации SVM, и я не буду ее здесь приводить.)
1.1.3 Метод оптимизации функции потерь персептрона и описание алгоритма потока
1.1.3.1 Метод оптимизации
- После приведенных выше рассуждений, мы получаем функцию потери перцептрона,
J
(
θ
)
=
−
∑
x
i
∈
M
y
(
i
)
θ
∙
x
(
i
)
, Где M — множество всех ошибочно классифицированных точек, и это выпуклая функция, может использовать метод градиентного спуска или квазиньютоновского метода, обычно используемый SGD (случайный градиентный спуск), что означает, что каждый раз необходимо использовать только одну ошибочно классифицированную точку Обновите градиент. Из-за ограничения в нашей функции потерь, только выборки из неправильно классифицированного набора М могут участвовать в оптимизации функции потерь. Следовательно, BGD (пакетный градиентный спуск) нельзя использовать, только SGD или MSGD (небольшой пакетный градиентный спуск). - Функция потери
θ
Частная производная вектора:
∂
∂
θ
J
(
θ
)
=
−
∑
x
i
∈
M
y
(
i
)
x
(
i
)
θ
Формула градиентного спуска:
θ
=
θ
+
α
∑
x
i
∈
M
y
(
i
)
x
(
i
)
- Поскольку мы используем стохастический градиентный спуск, для вычисления градиента за один раз используется только одна неправильно классифицированная выборка. Предполагая, что i-я выборка используется для обновления градиента, упрощенная
θ
Итерационная формула градиентного спуска:
θ
=
θ
+
α
y
(
i
)
x
(
i
)
- Где α — размер шага,
y
(
i
)
Чтобы вывести 1 или -1 для выборки, x (i) является вектором (n + 1) x 1.
1.1.3.2 Описание алгоритма
- Здесь мы подведем итоги вышеприведенного обсуждения и сходимся в алгоритм алгоритма.
- Алгоритм ввода
- Входными данными алгоритма являются m выборок, каждая выборка соответствует n-мерным элементам и выводу двоичной категории 1 или -1 следующим образом:
(
x
1
(
0
)
,
x
2
(
0
)
,
.
.
.
x
n
(
0
)
,
y
0
)
,
(
x
1
(
1
)
,
x
2
(
1
)
,
.
.
.
x
n
(
1
)
,
y
1
)
,
.
.
.
(
x
1
(
m
)
,
x
2
(
m
)
,
.
.
.
x
n
(
m
)
,
y
m
)
- Входными данными алгоритма являются m выборок, каждая выборка соответствует n-мерным элементам и выводу двоичной категории 1 или -1 следующим образом:
- Вывод:
- Модельный коэффициент θ вектора разделяющей гиперплоскости
- Процесс выполнения алгоритма:
- Определить все х0 до 1. Выберите начальное значение вектора θ и начальное значение шага α. Вектор θ может быть установлен на вектор 0, а размер шага установлен на 1. Следует отметить, что, поскольку решение персептрона не является уникальным, два используемых начальных значения будут влиять на конечный результат итерации вектора θ.
- Выберите ошибочно классифицированную точку в тренировочном наборе
(
x
1
(
i
)
,
x
2
(
i
)
,
.
.
.
x
n
(
i
)
,
y
i
)
Выражается в векторах т.е.
(
x
(
i
)
,
y
(
i
)
)
, Этот пункт должен удовлетворять:
y
(
i
)
θ
∙
x
(
i
)
<
0
- Выполните итерацию стохастического градиентного спуска на векторе:
θ
=
θ
+
α
y
(
i
)
x
(
i
)
- Проверьте, есть ли в обучающем наборе все еще неправильно классифицированные точки, в противном случае алгоритм завершается, и вектор θ в это время является окончательным результатом. Если это так, перейдите к шагу 2.
- Наконец, также необходимо упомянуть, что когда алгоритм фактически был реализован в прошлом, мы использовали двойную форму алгоритма персептрона для решения параметров и оптимизации модели, поскольку она может оптимизировать скорость выполнения алгоритма. Читатели могут учиться самостоятельно. Мы все еще сосредоточены на следующем объяснении знаний, связанных с нейронными сетями.
1.2 Глубокая нейронная сеть (DNN) и алгоритм прямого распространения
1.2.1 Введение в глубокие нейронные сети
- С помощью персептрона его можно использовать только для задач двоичной классификации, но он не может решить нелинейные задачи.Нейронные сети сделали много расширений, главным образом отраженных в следующих аспектах:
- Добавлены скрытые слои. Скрытые слои могут иметь несколько слоев, чтобы усилить выразительные возможности модели, поэтому ее сложность также значительно возросла.
- На входном слое имеется более одного нейрона с несколькими выходами. Кроме того, существует полная связь между верхним уровнем и следующим уровнем, и нет связи между нейронами в одном и том же слое, и они не зависят друг от друга. Таким образом, модель может гибко применяться для классификации и регрессии (обычно разница заключается только в функции активации последнего прохода структуры. Если требуется регрессия и требуется непрерывное значение, не используйте стандартизированную функцию сжатия, такую как Sigmoid)
- Функция активации была расширена, чтобы заменить Sign (z) функцией Sigmod или другими функциями активации, tanx, softmax, ReLU и т. Д. Так выглядит следующая картина:
- DNN можно понимать как нейронную сеть с несколькими скрытыми слоями. Кроме того, его иногда называют многослойным персептроном (Multi-Layer Perceptron, MLP). Внутренний уровень нейронной сети делится на три категории: входной слой, скрытый слой и выходной слой. Как показано выше, в целом, первый слой является входным слоем, последний слой является выходным слоем, а все средние слои являются скрытыми слоями. Слои полностью связаны, то есть любой нейрон в слое i должен быть связан с любым нейроном в слое i + 1. Хотя DNN выглядит сложным, маленькая локальная модель остается такой же, как персептрон, то есть линейная зависимость
z
=
∑
w
i
x
i
+
b
Добавьте функцию активации σ (z). Однако с увеличением количества слоев количество линейных соотношений W и смещения b также увеличивается. Определение следующее: -
Сначала давайте взглянем на определение коэффициента линейной зависимости w. На следующем рисунке в качестве примера показан трехслойный DNN. Линейный коэффициент четвертого нейрона во втором слое ко второму нейрону в третьем слое определяется как
w
24
3
Верхний индекс 3 представляет количество слоев, в которых расположен линейный коэффициент w, а нижний индекс соответствует выходному индексу третьего уровня 2 и входному индексу второго уровня 4. Вы можете спросить, почему нет
w
42
3
Вместо
w
24
3
Какой? Это главным образом для облегчения модели для операций матричного представления, если это
w
42
3
И каждый раз, когда выполняется матричная операция
w
T
x
+
b
Нужно транспонировать. Если выходной индекс помещен вперед, вес W не должен быть перемещен в линейной операции. То есть линейные коэффициенты k-го нейрона в слое l-1 до j-го нейрона в слое l определяются как
w
j
k
l
Где входной слой не имеет параметра w.
-
Давайте посмотрим на определение смещения б. На примере этого трехслойного DNN смещение, соответствующее третьему нейрону во втором слое, определяется как
b
3
2
Среди них верхний индекс 2 представляет количество слоев, а нижний индекс 3 представляет индекс нейронов, в которых находится смещение. Таким же образом, смещение первого нейрона в третьем должно быть выражено как
b
1
3
Аналогично, входной слой не имеет параметра смещения b.
1.2.2 Алгоритм прямого распространения
-
Выше мы ввели определение коэффициента линейной зависимости w и смещения b каждого слоя DNN. Предполагая, что выбранная нами функция активации σ (z), выходное значение скрытого слоя и выходного слоя равно a, а затем для трехслойного DNN на следующем рисунке, используя ту же идею, что и персептрон, мы можем использовать выходные данные предыдущего слоя для вычисления Выход первого уровня — это так называемый алгоритм прямого распространения DNN.
- Для вывода второго слоя
a
1
2
,
a
2
2
,
a
3
2
,У нас есть:
a
1
2
=
σ
(
z
1
2
)
=
σ
(
w
11
2
x
1
+
w
12
2
x
2
+
w
13
2
x
3
+
b
1
2
)
a
2
2
=
σ
(
z
2
2
)
=
σ
(
w
21
2
x
1
+
w
22
2
x
2
+
w
23
2
x
3
+
b
2
2
)
a
3
2
=
σ
(
z
3
2
)
=
σ
(
w
31
2
x
1
+
w
32
2
x
2
+
w
33
2
x
3
+
b
3
2
)
- Для вывода третьего слоя
a
1
3
,У нас есть:
a
1
3
=
σ
(
z
1
3
)
=
σ
(
w
11
3
a
1
2
+
w
12
3
a
2
2
+
w
13
3
a
3
2
+
b
1
3
)
- Обобщая вышеприведенный пример, предполагая, что в слое l-1 имеется m нейронов, для вывода j-го нейрона в слое l
a
j
l
,У нас есть:
a
j
l
=
σ
(
z
j
l
)
=
σ
(
∑
k
=
1
m
w
j
k
l
a
k
l
−
1
+
b
j
l
)
- Среди них, если
l
= 2, тогда a_k ^ 1 для входного слоя
x
k
。 - Далее, ключевой момент — матричная запись, потому что алгебраический метод означает, что выходные данные являются сложными, а матричный метод означает, что выходные данные просты. предполагать
l
-1 слой имеет в общей сложности m нейронов, в то время как слой 1 имеет в общей сложности n нейронов, тогда
l
Линейный коэффициент w слоя образует матрицу Wl n × m, первый
l
Смещение b слоя формирует вектор n × 1
b
l
, Раздел
l
Выход a слоя -1 формирует вектор m × 1
a
l
−
1
, Раздел
l
Неактивный линейный выход z слоя формирует вектор n × 1
z
l
, Раздел
l
Выход a слоя формирует вектор n × 1
a
l
, Выражается матричным методом, первым
l
Выход слоя:
a
l
=
σ
(
z
l
)
=
σ
(
W
l
a
l
−
1
+
b
l
)
- Это выражено очень кратко, поэтому последующее обсуждение будет выведено на основе этого матричного метода.
- Описание алгоритма потока:
- Вход: общее количество слоев L, матрица W, соответствующая всем скрытым слоям и выходным слоям, вектор смещения b, вектор входных значений x
- Выход: выходной слой
a
L
- Обработать:
- Initialize
a
1
=x - for
l
=2 to
L
Расчет:
a
l
=
σ
(
z
l
)
=
σ
(
W
l
a
l
−
1
+
b
l
)
- Конечный результат — выход
a
L
- Initialize
- DNN алгоритм прямого распространения, как получить параметры, соответствующие большой матрице W и вектору смещения b? Как получить оптимальную матрицу W и вектор смещения b? Это должно быть решено алгоритмом обратного распространения DNN. Предпосылка понимания алгоритма обратного распространения состоит в том, чтобы понять модель DNN и алгоритм прямого распространения. Далее идет легендарный алгоритм БП.
1.3 Алгоритм обратного распространения BP (обратное распространение)
1.3.1 Проблемы, которые необходимо решить путем обратного распространения
- Прежде, чем понять алгоритм обратного распространения DNN, мы должны сначала знать проблему, которую должен решить алгоритм обратного распространения DNN, то есть, когда нам нужен этот алгоритм обратного распространения?
- Возвращаясь к нашей общей проблеме контролируемого обучения, предположим, что у нас есть m обучающих образцов:
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
m
,
y
m
)
}
Где x — входной вектор, а размерность объекта — n_in, а y — выходной вектор, а размерность объекта — n_out. Нам нужно использовать эти m образцов для обучения модели, когда есть новый тестовый образец (
x
t
e
s
t
?) Когда мы придем, мы можем предсказать
y
t
e
s
t
Векторный вывод. - Если мы примем модель DNN, у нас будет n_in нейронов на входном слое и n_out нейронов на выходном слое. Плюс несколько скрытых слоев, содержащих несколько нейронов. В настоящее время нам нужно найти соответствующую матрицу линейных коэффициентов W и вектор смещения b для всех скрытых слоев и выходных слоев, чтобы выходной сигнал, рассчитанный по всем входным сигналам обучающей выборки, был как можно ближе к выходным данным выборки или близко к ним. Как найти подходящие параметры?
- Вы можете подумать, что вы можете использовать подходящую функцию потерь для измерения выходных потерь обучающей выборки, а затем оптимизировать эту функцию потерь, чтобы минимизировать экстремальное значение. Соответствующий ряд матриц W линейного коэффициента, вектор смещения b является нашей Окончательные результаты. В DNN процесс оптимизации экстремума функции потерь обычно повторяется шаг за шагом по методу градиентного спуска.Конечно, можно использовать и другие итерационные методы, такие как метод Ньютона и квазиньютоновский метод.
- Процесс итеративной оптимизации функции потерь DNN путем градиентного спуска для нахождения минимального значения является нашим алгоритмом обратного распространения.
1.3.2 Основная идея алгоритма обратного распространения
- Перед выполнением алгоритма обратного распространения DNN нам нужно выбрать функцию потерь, чтобы измерить потери между вычисленным выходным значением обучающей выборки и фактическим выходным значением обучающей выборки. Вы можете спросить: как рассчитывается результат на основе обучающей выборки? Эти выходные данные выбираются случайным образом из ряда W, b и вычисляются с использованием алгоритма прямого распространения в нашем предыдущем разделе. То есть с помощью ряда расчетов:
a
l
=
σ
(
z
l
)
=
σ
(
W
l
a
l
−
1
+
b
l
)
, Рассчитать соответствующий L-й слой выходного слоя
a
L
Это выходной сигнал, рассчитанный по алгоритму прямого распространения. — В отличие от функции потерь, существует множество функций потерь, которые DNN может выбрать. Чтобы сосредоточиться на алгоритме, здесь мы используем наиболее распространенную среднеквадратичную ошибку для измерения потерь. То есть для каждого образца мы ожидаем минимизировать следующую формулу:
J
(
W
,
b
,
x
,
y
)
=
1
2
|
|
a
L
−
y
|
|
2
2
- среди них,
a
L
И у — векторы с размерностью объекта n_out, и
|
|
S
|
|
2
Является ли L2 нормой S. - С функцией потерь, теперь мы начинаем использовать градиентный спуск, чтобы итеративно решить W, b для каждого слоя.
- Первый — это L-й слой выходного слоя. Обратите внимание, что W, b в выходном слое удовлетворяет следующей формуле:
a
L
=
σ
(
z
L
)
=
σ
(
W
L
a
L
−
1
+
b
L
)
- Таким образом, для параметров выходного слоя наша функция потерь становится:
J
(
W
,
b
,
x
,
y
)
=
1
2
|
|
a
L
−
y
|
|
2
2
=
1
2
|
|
σ
(
W
L
a
L
−
1
+
b
L
)
−
y
|
|
2
2
- Решить градиент W, b таким образом просто:
∂
J
(
W
,
b
,
x
,
y
)
∂
W
L
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
L
∂
z
L
∂
W
L
=
(
a
L
−
y
)
⊙
σ
′
(
z
L
)
(
a
L
−
1
)
T
∂
J
(
W
,
b
,
x
,
y
)
∂
b
L
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
L
∂
z
L
∂
b
L
=
(
a
L
−
y
)
⊙
σ
′
(
z
L
)
- Обратите внимание, что в приведенной выше формуле есть символ
⊙
, Который представляет произведение Адамара, для двух векторов одного измерения
A
(
a
1
,
a
2
,
.
.
.
a
n
)
T
с участием
B
(
b
1
,
b
2
,
.
.
.
b
n
)
T
, Затем
A
⊙
B
=
(
a
1
b
1
,
a
2
b
2
,
.
.
.
a
n
b
n
)
T
- Мы заметили, что при решении W, b в выходном слое, есть общая часть
∂
J
(
W
,
b
,
x
,
y
)
∂
z
L
Таким образом, мы можем относиться к публичной части как
z
L
Сначала рассчитайте его и запишите как:
δ
L
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
L
=
(
a
L
−
y
)
⊙
σ
′
(
z
L
)
- Теперь, когда мы наконец рассчитали градиент выходного слоя, как рассчитать градиент верхнего слоя L − 1 и верхнего и верхнего слоя L − 2? Здесь нам нужно повторить шаг за шагом, отметив, что для неактивного вывода слоя l
z
l
Его градиент может быть выражен как:
δ
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
L
∂
z
L
∂
z
L
−
1
∂
z
L
−
1
∂
z
L
−
2
.
.
.
∂
z
l
+
1
∂
z
l
- Если мы можем рассчитать первое
l
Многослойные
δ
l
Тогда слой
W
l
,
b
l
Это легко рассчитать? y Поскольку согласно алгоритму прямого распространения, мы имеем:
z
l
=
W
l
a
l
−
1
+
b
l
- Таким образом, согласно приведенной выше формуле мы можем легко вычислить первое
l
Многослойные
W
l
,
b
l
Градиент выглядит следующим образом:
∂
J
(
W
,
b
,
x
,
y
)
∂
W
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
l
∂
z
l
∂
W
l
=
δ
l
(
a
l
−
1
)
T
∂
J
(
W
,
b
,
x
,
y
)
∂
b
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
l
∂
z
l
∂
b
l
=
δ
l
- Тогда ключ к проблеме сейчас заключается в том, чтобы попросить
δ
l
Слишком. Здесь мы используем математическую индукцию, слой L
δ
L
Мы нашли выше, предполагая, что первое
l
+1
δ
l
+
1
Уже
через
нищенство
Вне
Приходить
от
,
который
какой
я
Мы
Такие как
какие
нищенство
Вне
Первый
l
Пол
из
А как насчет δ ^ l $? Мы заметили: (цепное правило)
δ
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
l
+
1
∂
z
l
+
1
∂
z
l
=
δ
l
+
1
∂
z
l
+
1
∂
z
l
- Видимо, рекурсивно по индукции
δ
l
+
1
с участием
δ
l
Ключ должен решить
∂
z
l
+
1
∂
z
l
- Пока
z
l
+
1
с участием
z
l
Отношения на самом деле очень легко найти:
z
l
+
1
=
W
l
+
1
a
l
+
b
l
+
1
=
W
l
+
1
σ
(
z
l
)
+
b
l
+
1
- Это легко найти:
∂
z
l
+
1
∂
z
l
=
(
W
l
+
1
)
T
⊙
(
σ
′
(
z
l
)
,
.
.
,
σ
′
(
z
l
)
)
⏟
n
l
+
1
- Доведите вышеупомянутое до вершины
δ
l
+
1
с участием
δ
l
Мы получили:
δ
l
=
δ
l
+
1
∂
z
l
+
1
∂
z
l
=
(
W
l
+
1
)
T
δ
l
+
1
⊙
σ
′
(
z
l
)
- Теперь мы получили
δ
l
Для рекурсивных отношений требуется только определенный уровень
δ
l
, Решить
W
l
,
b
l
Соответствующий градиент очень прост.
1.3.3 Процесс алгоритма обратного распространения DNN
- Здесь мы обсуждаем пакетный градиентный спуск.На самом деле, Mini-Batch обычно используется в разработке, но алгоритм имеет небольшой эффект.
- Войти:
- Общее количество слоев L и количество нейронов в каждом скрытом слое и выходном слое, функция активации, функция потерь, размер шага итерации α, максимальное количество итераций MAX и порог остановки итерации ϵ, ввод m обучающих выборок.
- Вывод:
- Матрица коэффициентов линейных отношений W и вектор смещения b каждого скрытого слоя и выходного слоя
-
Алгоритм потока:
- (1) Инициализируйте значения матрицы W коэффициента линейного отношения и вектора b смещения каждого скрытого слоя и выходного слоя случайным значением.
- (2) for iter to 1 to MAX:
- (2.1) for i =1 to m:
- (а) Входной DNN
a
1
Установить на Си - (b) для l = 2 до L, для вычисления алгоритма прямого распространения,
a
i
,
l
=
σ
(
z
i
,
l
)
=
σ
(
W
l
a
i
,
l
−
1
+
b
l
)
- (c) Рассчитать выходной слой
δ
i
,
L
- (d) для l = L до 2 выполнить расчет алгоритма обратного распространения
δ
i
,
l
=
(
W
l
+
1
)
T
δ
i
,
l
+
1
⊙
σ
′
(
z
i
,
l
)
- (а) Входной DNN
- (2.2) для l = 2 до L обновите слой 1
W
l
,
b
l
:
W
l
=
W
l
−
α
∑
i
=
1
m
δ
i
,
l
(
a
i
,
l
−
1
)
T
b
l
=
b
l
−
α
∑
i
=
1
m
δ
i
,
l
- (2.3) Если значения изменения всех W, b меньше порога остановки итерации ϵ, то выпрыгните из цикла итерации к шагу 3
- (2.1) for i =1 to m:
- (3) Выведите матрицу коэффициентов линейных отношений W и вектор смещения b каждого скрытого слоя и выходного слоя
-
Если вы видите здесь, вы можете подумать, что вы не понимаете очень глубоко, или если вы думаете, что это слишком теоретически выведено, и нет никакого практического примера, чтобы понять интуитивно, тогда блоггер рекомендует вам изучить эту статью. Он использует яркие изображения Для иллюстрации на примерах, я думаю, это поможет вам понять алгоритм BP.Используйте небольшой пример, чтобы проиллюстрировать алгоритм BP
1.3.4 Мышление на основе алгоритма обратного распространения DNN
- Основываясь на приведенном выше алгоритме вывода, мы знаем, что существует множество параметров DNN, и количество вычислений матрицы также очень велико. При непосредственном использовании возникнут различные проблемы. Каковы проблемы и как попытаться решить эти проблемы и оптимизировать модель и алгоритм DNN.Конечно, многие ученые дали некоторые решения или изучают эти проблемы, и для нас это тоже очень стоящее исследование. Что касается аспектов, ниже кратко обсуждаются эти вопросы без теоретического вывода.
- С точки зрения функции потери и активации:
- Функция активации, которую мы выбрали ранее, является функцией Sigmoid, и, как видно из изображения, приведенного в начале, для Sigmoid, когда значение z становится все больше и больше, кривая функции становится все более плавной, что означает, что в это время Производная σ ′ (z) становится все меньше и меньше. Точно так же, когда значение z становится все меньше и меньше, эта проблема также существует. Только когда значение z составляет около 0, значение производной σ (z) больше. В рассмотренном выше алгоритме обратного распространения среднеквадратичной ошибки + сигмоида каждая прямая рекурсия уровня должна быть умножена на σ (z), чтобы получить значение изменения градиента. Судя по его функциональной кривой изображения, большую часть времени наше значение изменения градиента очень мало, что приводит к более медленной скорости обновления W, b до экстремального значения, то есть скорость сходимости алгоритма ниже.
- Функциональные характеристики сигмоида приводят к проблеме медленной сходимости алгоритма обратного распространения, так как его улучшить? Заменить сигмоид? Это конечно вариант. Другим распространенным вариантом является замена функции среднеквадратичной потери на функцию кросс-энтропийной потери. Давайте сначала обсудим функцию обменных потерь как функцию кросс-энтропии + сигмоидной активации следующим образом:
J
(
W
,
b
,
a
,
y
)
=
−
y
∙
l
n
a
−
(
1
−
y
)
∙
l
n
(
1
−
a
)
- Затем мы рассчитываем выходной слой
δ
L
Ситуация с градиентом, обнаружено, что градиента нет в градиенте
σ
′
(
z
)
Таким образом, даже если обратная функция сигмоида чрезвычайно мала с обеих сторон, это не повлияет на нашу скорость сходимости. - Кроме того, когда мы решаем задачи классификации, мы обычно рассматриваем функцию потери логарифмического правдоподобия и функцию активации softmax. Мы не будем здесь обсуждать причину. Заинтересованные читатели могут изучить ее самостоятельно. Функция активации нейрона определяется следующим образом:
a
i
L
=
e
z
i
L
∑
j
=
1
n
L
e
z
j
L
- Третья проблема заключается в том, что градиент взрыва градиента DNN исчезает, и функция активации ReLU чаще используется для активации исчезновения градиента в CNN с помощью функции активации градиента ReLU. Что такое градиентные взрывы и исчезновения градиентов? Ниже, попробуйте описать это на общем языке, потому что это очень сложно, и может привести к большой книге, поэтому вот краткое описание.
- Проще говоря, в процессе обратного распространения, поскольку мы используем цепное правило матричного дифференцирования (ниже), существует большой ряд умножений. Если число умножений меньше 1 в каждом слое, Затем, чем меньше градиент, тем меньше умножение, и градиент исчезает.Если число умножений больше 1, градиент умножается и градиент взрывается.
δ
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
l
=
∂
J
(
W
,
b
,
x
,
y
)
∂
z
L
∂
z
L
∂
z
L
−
1
∂
z
L
−
1
∂
z
L
−
2
.
.
.
∂
z
l
+
1
∂
z
l
- Обычно используемые в общем машиностроении:
- Для градиентного взрыва это обычно можно решить, отрегулировав параметры инициализации в нашей модели DNN.
- Для проблемы исчезновения градиента, которая не может быть полностью решена, одним из возможных решений проблемы исчезновения градиента является использование функции активации ReLU (выпрямленная линейная единица) ReLU широко используется в CNN. Выражение очень простое: больше или равно 0 останется неизменным, меньше 0 будет равно 0 после активации.
σ
(
z
)
=
m
a
x
(
0
,
z
)
- Кроме того, для решения проблемы переоснащения для регулярности общая регулярность L2 здесь не повторяется, и ее можно использовать как для функции среднеквадратичной ошибки, так и для функции перекрестной энтропии. Кроме того, для регуляризации можно использовать метод интегрированного обучения (Bagging), но из-за дальнейшего увеличения параметров, как правило, производится только 5-10 моделей DNN. Здесь мы обращаем внимание на регуляризацию отсева, которая очень похожа на метод Bagging, но есть некоторые отличия.
- Так называемое выпадение относится к использованию алгоритма прямого распространения и алгоритма обратного распространения для обучения модели DNN.При итерации пакета данных часть нейронов скрытого слоя случайным образом удаляется из полностью подключенной сети DNN. Сеть нейронов с удаленными скрытыми слоями используется, чтобы соответствовать нашей партии обучающих данных. Используйте эту сеть нейронов с удаленным скрытым слоем, чтобы выполнить цикл итераций, обновляя все W, b.В заключениеТаким образом, в каждом цикле итерации градиентного спуска необходимо разделить обучающие данные на несколько пакетов, а затем выполнить итерацию в пакетах. Итеративно обновить W, b. После итеративного обновления каждого пакета данных неполная модель DNN должна быть восстановлена до исходной модели DNN.
- Разница между ним и Bagging, W, b в выпадающей модели — это совокупность. Все итеративные итерации DNN обновляют один и тот же набор W, b, при регуляризации по Бэггингу каждая модель DNN имеет свой уникальный набор параметров W, b, которые не зависят друг от друга. Конечно, они используют наборы пакетных данных на основе исходного набора данных для обучения модели каждый раз, что аналогично.
Во-вторых, практика кодирования прямой нейронной сети на основе TensorFlow
2.1 Функции библиотеки TensorFlow участвуют
-
Функция активации TensorFlow
- стандартная сигмоидная функция tf.sigmoid (x)
- tf.tanh (x) гиперболическая касательная функция
- tf.nn.relu (x) модифицированная линейная функция
-
Другие функции в TensorFlow
- tf.nn.elu (x) экспоненциальная линейная единица: если входное значение меньше 0, оно возвращает exp (x) -1, в противном случае возвращается x
- tf.softsign (x) возвращает x / (abs (x) + 1)
- tf.nn.bias_add (значение, смещение) добавляет смещение к значению
-
Некоторые методы оптимизации потерь Tensorflow
- tf.train.GradientDescentOptimizer (learning_rate, use_locking, name) Оригинальный метод градиентного спуска, единственным параметром является скорость обучения
- tf.train.AdagradOptimizer адаптивно регулирует скорость обучения, в качестве знаменателя используется квадрат накопленного исторического градиента, чтобы предотвратить слишком большое значение градиента в некоторых направлениях, повысить эффективность оптимизации и хорошо справляться с разреженными градиентами
- tf.train.AdadeltaOptimizer Расширенный метод оптимизации AdaGrad накапливает только самое последнее значение градиента и не накапливает градиент во всей истории.
- tf.train.AdamOptimizer Градиентная оценка момента первого порядка и оценка момента второго порядка динамически регулирует скорость обучения каждого параметра.Адам является аббревиатурой для адаптивной оценки момента.
2.2 Подгонка нелинейной регрессии данных
# В этом примере мы вручную генерируем квадратичную функцию плюс набор данных шума, а затем подгоняем ее через простейшую нейронную сеть для достижения цели обучения
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from sklearn.utils import shuffle
from sklearn.metrics import accuracy_score
# Определение размера набора данных
trainsamples = 200
testsamples = 60
# Here we will represent the model,a simple imput,
# a hidden layer of sigmoid activation,
# Определить город ввода, слой вывода и сеть скрытых слоев с 10 узлами
def model(X,hidden_weights1,hidden_bias1,ow):
hidden_layer = tf.nn.sigmoid(tf.matmul(X,hidden_weights1) + hidden_bias1)
return tf.matmul(hidden_layer, ow)
# Создать набор данных
dsX = np.linspace(-1, 1, trainsamples + testsamplt).transpose()
dsY = 0.4 * pow(dsX,2) + 2 * dsX + np.random.randn(*dsX.shape) * 0.22 + 0.8
plt.figure() # create a new figure
plt.title('Origial data')
plt.scatter(dsX,dsY) <matplotlib.collections.PathCollection at 0x114554110>
X = tf.placeholder('float')
Y = tf.placeholder('float')
# create first hidden layer
hw1 = tf.Variable(tf.random_normal([1, 10],stddev=0.01))
# create output connection
ow = tf.Variable(tf.random_normal([10, 1],stddev=0.01))
# create bias
b = tf.Variable(tf.random_normal([10],stddev=0.01))
model_y = model(X,hw1,b,ow)
# cost Function
cost = tf.pow(model_y - Y,2) / (2)
# create train Operator
train_op = tf.train.AdamOptimizer(0.01).minimize(cost)# Launch the graph in a session
with tf.Session() as sess:
tf.initialize_all_variables().run()
# Начать итерацию
for i in range(1,35):
trainX, trainY = dsX[0:trainsamples], dsY[0:trainsamples]
for x1, y1 in zip(trainX,trainY):
sess.run(train_op,feed_dict={X:[[x1]],Y:y1})
testX, testY = dsX[trainsamples:trainsamples + testsamples],dsY[trainsamples:trainsamples+testsamples]
# print testY
cost1 = 0.
for x1, y1 in zip(testX,testY):
cost1 += sess.run(cost,feed_dict={X: [[x1]], Y: y1}) / testsamples
print "Average cost for epoch" + str(i) + ':' + str(cost1)
Average cost for epoch1:[[0.26329115]]
Average cost for epoch2:[[0.22221012]]
Average cost for epoch3:[[0.14709872]]
Average cost for epoch4:[[0.10356887]]
Некоторый контент здесь опущен:
Average cost for epoch29:[[0.02887413]]
Average cost for epoch30:[[0.02915836]]
Average cost for epoch31:[[0.029492]]
Average cost for epoch32:[[0.0298766]]
Average cost for epoch33:[[0.0303134]]
Average cost for epoch34:[[0.03080252]]
2.3 Использование Keras для моделирования непрерывных переменных
%matplotlib inline
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn import datasets, cross_validation,metrics
from sklearn import preprocessing
from tensorflow.contrib import learn
from keras.models import Sequential
from keras.layers import Dense
# Read the original dataset
data = pd.read_csv('mpg.csv',header=0)
print data.describe()
# Convert the displacement column as float
data['displacement'] = data['displacement'].astype(float)
# Игнорировать первый и последний столбец
X = data[data.columns[1:8]]
y = data['mpg']
plt.figure()
f, ax1 = plt.subplots()
for i in range(1,8):
number = 420 + i
ax1.locator_params(bnbins=3)
ax1 = plt.subplot(number)
plt.title(list(data)[i])
ax1.scatter(data[data.columns[i]],y)
plt.tight_layout(pad=0.4,w_pad=0.5,h_pad=1.0) mpg cylinders displacement horsepower weight
count 398.000000 398.000000 398.000000 398.000000 398.000000
mean 23.514573 5.454774 193.425879 102.894472 2970.424623
std 7.815984 1.701004 104.269838 40.269544 846.841774
min 9.000000 3.000000 68.000000 0.000000 1613.000000
25% 17.500000 4.000000 104.250000 75.000000 2223.750000
50% 23.000000 4.000000 148.500000 92.000000 2803.500000
75% 29.000000 8.000000 262.000000 125.000000 3608.000000
max 46.600000 8.000000 455.000000 230.000000 5140.000000
<matplotlib.figure.Figure at 0x11d0fd990>
# Split the datasets
X_train, x_test, y_train, y_test = cross_validation.train_test_split(X,y,test_size=0.25)
# Scale the data for convergency optimization
scaler = preprocessing.StandardScaler()
# set the transform parameters
X_train = scaler.fit_transform(X_train)
# Build a 2 layer fully connected DNN with 10 and 5 units respectively
model = Sequential()
model.add(Dense(10,input_dim=7,init='normal',activation='relu'))
model.add(Dense(5,init='normal',activation='relu'))
# Вывод
model.add(Dense(1,init='normal'))
# Compile the model, which the mean squared error as a loss function
model.compile(loss='mean_squared_error',optimizer='adam')
# Fit the model,in 1000 epochs
# verbose: журналы показывают, что 0 не выводит журнальную информацию о стандартном потоке вывода, 1 - выходные записи индикатора выполнения, а 2 - запись одной строки за эпоху
# epochs: целое число, значение эпохи в конце обучения, обучение остановится, когда будет достигнуто значение эпохи
model.fit(X_train,y_train,nb_epoch=1200,validation_split=0.33,shuffle=True,verbose=2)
Train on 199 samples, validate on 99 samples
Epoch 1/1200
- 0s - loss: 624.4550 - val_loss: 609.7046
Epoch 2/1200
- 0s - loss: 624.0735 - val_loss: 609.3263
Epoch 3/1200
Части здесь опущены ...
Epoch 1197/1200
- 0s - loss: 6.9051 - val_loss: 8.6608
Epoch 1198/1200
- 0s - loss: 6.9028 - val_loss: 8.6282
Epoch 1199/1200
- 0s - loss: 6.8984 - val_loss: 8.6874
Epoch 1200/1200
- 0s - loss: 6.8917 - val_loss: 8.8152
<keras.callbacks.History at 0x11ec65ed0>
2.4 Задача мультиклассификации, многоузловой выходной слой
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from sklearn.utils import shuffle
from sklearn import preprocessing
# Чтение данных
data = pd.read_csv('./wine.csv',header=0)
print (data.describe())
for i in range(1,8):
number = 420 + i
ax1 = plt.subplot(number)
ax1.locator_params(nbins=3)
plt.title(list(data)[i])
ax1.scatter(data[data.columns[i]],data['Wine'])
plt.tight_layout(pad=0.4,w_pad=0.5,h_pad=1.0) Wine Alcohol Malic.acid Ash Acl Mg
count 178.000000 178.000000 178.000000 178.000000 178.000000 178.000000
mean 1.938202 13.000618 2.336348 2.366517 19.494944 99.741573
std 0.775035 0.811827 1.117146 0.274344 3.339564 14.282484
min 1.000000 11.030000 0.740000 1.360000 10.600000 70.000000
25% 1.000000 12.362500 1.602500 2.210000 17.200000 88.000000
50% 2.000000 13.050000 1.865000 2.360000 19.500000 98.000000
75% 3.000000 13.677500 3.082500 2.557500 21.500000 107.000000
max 3.000000 14.830000 5.800000 3.230000 30.000000 162.000000
sess = tf.InteractiveSession()
X = data[data.columns[1:13]].values
# Сами данные начинаются с 1, вычитают отклонение от данных и затем отображают Y в одноразовое кодирование
y = data['Wine'].values - 1
Y = tf.one_hot(indices=y,depth=3,on_value=1.,off_value=0.,axis=1,name='a').eval()
X, Y = shuffle(X, Y)
# Регуляризация тренировочных данных
scaler = preprocessing.StandardScaler()
X = scaler.fit_transform(X)
# Здесь скрытый слой нейронной сети, предназначенный для обучения, выберите соответствующий скрытый слой для сложности модели
# Создайте модель, используйте функцию активации softmax + относительную энтропию в качестве функции потерь, в качестве мультиклассификации
x = tf.placeholder(tf.float32,[None,12]) # Особенности ввода х имеют 12 измерений
W = tf.Variable(tf.zeros([12,3])) # Вес 12 * 3
b = tf.Variable(tf.zeros([3])) # Смещение 1 * 3
y = tf.nn.softmax(tf.matmul(x,W) + b)
# Определяем потери и оптимизатор, функция кросс-энтропии потерь определяется следующим образом:
y_ = tf.placeholder(tf.float32,[None,3])
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y),reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(cross_entropy)
# Train
tf.initialize_all_variables().run() # Инициализировать переменные
for i in range(20):
X, Y = shuffle(X,Y,random_state=1) # Случайно перемешивать данные, чтобы увеличить способность
Xtr = X[0:140,:]
Ytr = Y[0:140,:]
Xt = X[140:178,:]
Yt = Y[140:178,:]
Xtr, Ytr = shuffle(Xtr,Ytr,random_state=0)
batch_xs, batch_ys = Xtr, Ytr
train_step.run({x:batch_xs,y_:batch_ys})
cost = sess.run(cross_entropy,feed_dict={x:batch_xs,y_:batch_ys})
# Test trained model
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
print(accuracy.eval({x:Xt,y_:Yt})) Некоторые вещи здесь опущены ...
0.94736844
0.94736844
0.94736844
0.94736844
0.9736842
1.0
0.9736842
Кодовые слова не легки. Если это поможет вам, пожалуйста, оставьте свои следы или вдохновите меня продолжать.
Примечание: ссылки в этой статье следующие: (Большое спасибо следующим замечательным блоггерам за то, что они позволили мне узнать много полезного)
1、 http://www.cnblogs.com/pinard/p/6472666.html
2、 https://www.jianshu.com/p/964345dddb70
В этой статье поговорим о том, как создавать нейросети и в качестве примера рассмотрим, как сделать нейронную сеть прямого распространения с нуля. Для реализации поставленной задачи воспользуемся языком программирования C#.
Только ленивый не слышал сегодня о существовании и разработке нейронных сетей и такой сфере, как машинное обучение. Для некоторых создание нейросети кажется чем-то очень запутанным, однако на самом деле они создаются не так уж и сложно. Как же их делают? Давайте попробуем самостоятельно создать нейросеть прямого распространения, которую еще называют многослойным перцептроном. В процессе работы будем использовать лишь циклы, массивы и условные операторы. Что означает этот набор данных? Только то, что нам подойдет любой язык программирования, поддерживающий вышеперечисленные возможности. Если же у языка есть библиотеки для векторных и матричных вычислений (вспоминаем NumPy в Python), то реализация с их помощью займет совсем немного времени. Но мы не ищем легких путей и воспользуемся C#, причем полученный код по своей сути будет почти аналогичным и для прочих языков программирования.
Что же такое нейронная сеть?
Под искусственной нейронной сетью (ИНС) понимают математическую модель (включая ее программное либо аппаратное воплощение), которая построена и работает по принципу функционирования биологических нейросетей — речь идет о нейронных сетях нервных клеток живых организмов.
Говоря проще, ИНС можно назвать неким «черным ящиком», превращающим входные данные в выходные данные. Если же посмотреть на это с точки зрения математики, то речь идет о том, чтобы отобразить пространство входных X-признаков в пространство выходных Y-признаков: X → Y. Таким образом, нам надо найти некую F-функцию, которая сможет выполнить данное преобразование. На первом этапе этой информации достаточно в качестве основы.
Какую роль играет искусственный нейрон?
В нашей статье мы не будем вдаваться в лирику и рассказывать об устройстве биологического нейрона в контексте его связи с искусственной моделью. Лучше сразу перейдем к делу.
Искусственный нейрон представляет собой взвешенную сумму векторных значений входных элементов. Эта сумма передается на нелинейную функцию активации f:
Но об активации поговорим после, т. к. сейчас стоит задача узнать, каким образом вместо одного выходного значения можно получить n-значений.
Нейрослой
Один нейрон может превратить в одну точку входной вектор, но по условию мы желаем получить несколько точек, т. к. выходное Y способно иметь произвольную размерность, которая определяется лишь ситуацией (один выход для XOR, десять выходов, чтобы определить принадлежность к одному из десяти классов, и так далее). Каким же образом получить n точек? На деле все просто: для получения n выходных значений, надо задействовать не один нейрон, а n. В результате для каждого элемента выходного Y будет использовано n разных взвешенных сумм от X. В итоге мы придем к следующему соотношению:
Давайте внимательно посмотрим на него. Вышенаписанная формула — это не что иное, как определение умножения матрицы на вектор. И в самом деле, если мы возьмем матрицу W размера n на m и выполним ее умножение на X размерности m, то мы получим другое векторное значение n-размерности, то есть как раз то, что надо.
Таким образом, мы можем записать похожее выражение в более удобной матричной форме:
Но полученный вектор представляет собой неактивированное состояние (промежуточное, невыходное) всех нейронов, а для того, чтобы нам получить выходное значение, нужно каждое неактивированное значение подать на вход вышеупомянутой функции активации. Итогом ее применения и станет выходное значение слоя.
Ниже показан пример нейронной сети, имеющей 2 входа, 5 нейронов и 1 выход:
Последовательность нейрослоев часто применяют для более глубокого обучения нейронной сети и большей формализации имеющихся данных. Именно поэтому, чтобы получить итоговый выходной вектор, нужно проделать вышеописанную операцию пару раз подряд по направлению от одного слоя к другому. В результате для 1-го слоя входным вектором будет являться X, а для последующих входом будет выход предыдущего слоя. То есть нейронная сеть может выглядеть следующим образом:
Функция активации
Речь идет о функции, добавляющей в нейронную сеть нелинейность. В результате нейроны смогут относительно точно сымитировать любую функцию. Широко распространены следующие функции активации:
Каждая из них имеет свои особенности.
Пишем код
Теперь мы знаем достаточно, чтобы создать простую нейронную сеть. Чтобы сделать то, что задумали, нам потребуются:
- Вектор.
- Матрица (каждый слой включает в себя матрицу весовых коэффициентов).
- Нейронная сеть.
Начнем с вектора. Создавать его можно:
- из количества элементов;
- из перечисления вещественных чисел.
Также мы можем получать и менять значения по индексу i.
Пишем код:
Теперь очередь матрицы. Ее можно создавать из числа строк и столбцов, а также генератора случайных чисел, причем есть возможность получать и менять значения по индексам i и j.
А вот и сама нейронная сеть:
Как будем обучать?
Пусть у нас уже есть нейронная сеть, но ведь ее ответы являются случайными, то есть наша нейросеть не обучена. Сейчас она способна лишь по входному вектору input выдавать случайный ответ, но нам нужны ответы, которые удовлетворяют конкретной поставленной задаче. Дабы этого достичь, сеть надо обучить. Здесь потребуется база тренировочных примеров и множество пар X — Y, на которых и будет происходить обучение, причем с использованием известного алгоритма обратного распространения ошибки.
Некоторые особенности работы этого алгоритма:
- на вход сети подается обучающий пример (1 входной вектор);
- сигнал распространяется по нейросети вперед (получаем выход сети);
- вычисляется ошибка (это разница между получившимся и ожидаемым векторами);
- ошибка распространяется на предыдущие слои;
- происходит обновление весовых коэффициентов в целях уменьшения ошибки.
Вот как выглядит алгоритм обучения:
Переходим к обучению
Для обратного распространения ошибки нужно знать значения выходов и входов, а также значения производных функции активации нейросети, причем послойно, следовательно, нужно создать структуру LayerT, где будут три векторных значения:
- x — вход слоя,
- z — выход,
- df — производная функции активации.
Для каждого слоя нам потребуются векторы дельт, в результате чего надо будет добавить в класс еще и их. В итоге класс будет выглядеть следующим образом:
Несколько слов об обратном распространении ошибки
В качестве функции оценки нейросети E(W) мы берем среднее квадратичное отклонение:
Дабы найти значение ошибки E, надо найти сумму квадратов разности векторных значений, которые были выданы нейронной сетью в виде ответа, а также вектора, который ожидается увидеть при обучении. Еще надо будет найти дельту каждого слоя и учесть, что для последнего слоя дельта будет равняться векторной разности фактического и ожидаемого результатов, покомпонентно умноженной на векторное значение производных последнего слоя:
Когда мы узнаем дельту последнего слоя, мы сможем найти дельты и всех предыдущих слоев. Чтобы это сделать, нужно будет лишь перемножить для текущего слоя транспонированную матрицу с дельтой, а потом перемножить результат с вектором производных функции активации предыдущего слоя:
Смотрим реализацию в коде:
Обновление весовых коэффициентов
Для уменьшения ошибки нейронной сети надо поменять весовые коэффициенты, причем послойно. Каким же образом это осуществить? Ничего сложного в этом нет: надо воспользоваться методом градиентного спуска. То есть нам надо рассчитать градиент по весам и сделать шаг от полученного градиента в отрицательную сторону. Давайте вспомним, что на этапе прямого распространения мы запоминали входные сигналы, а во время обратного распространения ошибки вычисляли дельты, причем послойно. Как раз ими и надо воспользоваться в целях нахождения градиента. Градиент по весам будет равняться не по компонентному перемножению дельт и входного вектора. Дабы обновить весовые коэффициенты, снизив таким образом ошибку нейросети, нужно просто вычесть из матрицы весов итог перемножения входных векторов и дельт, помноженный на скорость обучения. Все вышеперечисленное можно записать в следующем виде:
Вот оно, обучение!
Теперь мы имеем все нужные нам методы, поэтому остается лишь всё это вместе соединить, сформировав единый метод обучения.
Наша сеть готова, но мы пока ее еще ничему не научили. Сейчас это исправим.
Тренировка нейронной сети. Функции XOR
Функция XOR интересна тем, что ее нельзя получить одним нейроном:
Но ее легко получить путем увеличения количества нейронов. Давайте попробуем реализовать обучение с тремя нейронами в скрытом слое и одним выходным (выход ведь у нас только один). Чтобы все получилось, создадим массив X и Y, имеющий обучающие данные и саму нейронную сеть:
Теперь запускаем обучение с параметрами ниже:
- скорость обучения — 0.5,
- количество эпох — 100000,
- значение ошибки — 1e-7.
Выполнив обучение, посмотрим итоги, для чего надо будет сделать прямой проход для всех элементов:
В итоге вывод будет следующим:
Результаты
Мы написали нейронную сеть прямого распространения и не только написали, но и обучили ее функции XOR. Также была обеспечена универсальность, поэтому эту нейросеть можно обучать на любых данных — потребуется лишь:
- подготовить 2 векторных обучающих массива векторов X и Y,
- подобрать параметры,
- запустить само обучение,
- наблюдать за процессом.
Однако помните, что если используется сигмоидальная функция активации, выходные числа не будут больше единицы, что означает, что для обучения данным, которые существенно больше единицы, нужно будет нормировать их, приводя к отрезку [0, 1].
Надеемся, что материал был вам полезен и теперь вы знаете, как сделать нейросеть, и какие нюансы разработки стоит учитывать. Если же интересуют более продвинутые знания, обратите внимание на курсы, которые разработала команда Otus:
По материалам: https://programforyou.ru/poleznoe/pishem-neuroset-pryamogo-rasprostraneniya.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
В нашей статье мы создадим нейронную сеть прямого распространения на языке программирования Python. В качестве библиотеки работы с векторами и матрицами будет использоваться библиотека Numpy. Для работы с изображениями потребуется библиотека PLT. Данная работа выполнена в рамках курсового проекта по дисциплине «Machine Learning. Обучающиеся технические системы [1].
Введение
Нейронная сеть — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма [3].
Искусственный нейрон — это всего лишь взвешенная сумма значений входного вектора элементов, которая передаётся на нелинейную функцию активации f: z = f(y), где y = w0·x0 + w1·x1 + … + wm — 1·xm — 1. Здесь w0, …, wm — 1 — коэффициенты, веса каждого элемента вектора, x0, …, xm — 1 — значения входного вектора X, y — взвешенная сумма элементов X, а z— результат применения функции активации.
Функция активации — это функция, которая добавляет в нейронную сеть нелинейность, благодаря чему нейроны могут довольно точно интерполировать произвольную функцию. В настоящее время существует довольно много различных функций активации, но наиболее распространёнными функциями являются следующие:
Сигмоида: f(x) = 1 / (1 + e-x)
Гиперболический тангенс: f(x) = tanh(x)
ReLU: f(x) = max(x, 0)
Написание кода нейронной сети
Для реализации сети прямого назначения нам потребуется:
Вектор (входные, выходные) – из библиотеки Numpy;
Матрица (каждый слой содержит матрицу весовых коэффициентов) – из библиотеки Numpy;
Нейросеть.
Напишем метод, который будет получать выход нейронной сети по заданному входному вектору input:
# инициализация матрицы случайными значениями
def InitWeight(n, m):
w = np.zeros((n, m))
# заполняем матрицу случайными числами из интервала (-0.5, 0.5)
for i in range(n):
for j in range(m):
w[i][j] = random.uniform(-0.5, 0.5)
return w
# инициализация списка матриц весов случайными значениями
def InitWeights(struct):
W = []
# для каждого из весов задаём матрицу
for k in range(1, len(struct)):
w = InitWeight(struct[k], struct[k — 1])
W.append(w)
return W
def Sigmoid(x):
return 1 / (1 + np.exp(-x))
# прямое распространение сигнала по сети
def Forward (weights, input):
z = input;
# проходимся по всем слоям
for k in range(len(weights))
# создаём вектора для текущего слоя
y = weights[k].dot(z) # производим умножения матриц весов на входное значение
z = Sigmoid(y) # применяем сигмоидальную активационную функцию
return z # возвращаем активированный выход последнего слоя
Рис. 1. Код входных значений
Создали нейронную сеть. Теперь необходимо её обучить. Обучать нейросеть мы будем с помощью алгоритма обратного распространения ошибки, который работает следующим образом:
Подать на вход сети обучающий пример (один входной вектор)
Распространить сигнал по сети вперёд (получить выход сети)
Вычислить ошибку (разница получившегося и ожидаемого векторов)
Распространить ошибку на предыдущие слои
Обновить весовые коэффициенты для уменьшения ошибки
Обучаем сеть
Для обратного распространения ошибки нам потребуется знать значения входов, выходов и значения производных функции активации сети на каждом из слоёв, поэтому будем хранить список из структур 3 векторов: x — вход слоя, z — выход слоя, df — производная функции активации. Также для каждого слоя потребуются векторы дельт, поэтому добавим ещё и их. С учётом вышесказанного прямое распространение сигнала по сети будет выглядеть следующим образом:
# инициализация матрицы случайными значениями
def InitWeight(n, m):
w = np.zeros((n, m))
# заполняем матрицу случайными числами из интервала (-0.5, 0.5)
for i in range(n):
for j in range(m):
w[i][j] = random.uniform(-0.5, 0.5)
return w
# инициализация списка матриц весов случайными значениями
def InitWeights(struct):
W = []
# для каждого из весов задаём матрицу
for k in range(1, len(struct)):
w = InitWeight(struct[k], struct[k — 1])
W.append(w)
return W
def Sigmoid(x):
return 1 / (1 + np.exp(-x))
def SigmoidDerivative(y):
return y * (1 — y)
# прямое распространение сигнала по сети
def Forward (weights, input):
X = [] # входные значения слоёв
Z = [] # активированные значения слоёв
D = [] # значения производной функции активации
# проходимся по всем слоям
for k in range(len(weights)):
if k == 0: # если в первом слое, то входом является входной вектор
X.append(np.array(input))
else: # иначе входом является выход предыдущего слоя
X.append(Z[k — 1])
# создаём вектора для текущего слоя
y = weights[k].dot(X[k]) # производим умножения матриц весов на входное значение
z = Sigmoid(y) # применяем сигмоидальную активационную функцию
df = SigmoidDerivative(z) # вычисляем производную функции активации через уже известное значение выхода
Z.append(z)
D.append(df);
return X, Z, D # возвращаем список входов, выходов, активированных выходов и производных
Рис. 2. Код прямого распространения сигнала
Обратное распространение ошибки
В качестве функции оценки сети E(W) возьмём минимальное квадратичное отклонение: E = 0.5 · Σ(y1i — y2i)2. Чтобы найти значение ошибки E, нам нужно найти сумму квадратов разности значений вектора, который выдала сеть в качестве ответа, и вектора, который мы ожидаем увидеть при обучении. Также нам потребуется найти дельту для каждого слоя, причём для последнего слоя она будет равна вектору разности полученного и ожидаемого векторов, умноженному (покомпонентно) на вектор значений производных последнего слоя: δlast = (zlast — d)·f’last, где zlast — выход последнего слоя сети, d — ожидаемый вектор сети, f’last — вектор значений производной функции активации последнего слоя.
Теперь, зная дельту последнего слоя, мы можем найти дельты всех предыдущих слоёв. Для этого нужно умножить транспонированную матрицы текущего слоя на дельту текущего слоя и затем умножить полученный вектор на вектор производных функции активации предыдущего слоя: δk-1 = WTk · δk · f’k. Добавим это в код:
# обратное распространение ошибки
def Backward(weights, Z, df, output):
deltas = []
layersN = len(weights)
last = layersN — 1
error = 0
for k in range(layersN):
deltas.append([])
# расчитываем ошибку на выходном слое
e = Z[last] — output
deltas[last] = np.multiply(e, df[last])
error += np.sum(e**2)
# распространяем ошибку выше по слоям
for k in range(last, 0, -1):
deltas[k — 1] = np.multiply(weights[k].T.dot(deltas[k]), df[k — 1])
return deltas, error # возвращаем дельты и величину ошибки
Рис. 3. Код обратного распространения ошибки
Изменение весов
Для того чтобы уменьшить ошибку сети нужно изменить весовые коэффициенты каждого слоя. Для этого используется метод градиентного спуска. Градиент по весам равен перемножению входного вектора и вектора дельт (не покомпонентно). Поэтому, чтобы обновить весовые коэффициенты и уменьшить тем самым ошибку сети нужно вычесть из матрицы весов результат перемножения дельт и входных векторов, умноженный на скорость обучения. Записываем в виде: Wt+1 = Wt – η · δ · X, где Wt+1 — новая матрица весов, Wt — текущая матрица весов, X — входное значение слоя, δ — дельта этого слоя.
# обновлениевесов
def UpdateWeights(weights, X, deltas, alpha):
for k in range(len(weights)):
weights[k] -= alpha * np.outer(deltas[k], X[k])
Рис. 4. Код изменения весов
Обучение сети
Теперь, имея методы прямого распространения сигнала, обратного распространения ошибки и изменения весовых коэффициентов, нам остаётся лишь соединить всё вместе в один метод обучения.
# обучениесети
def Train(weights, inputData, outputData, alpha, eps, epochs):
print(‘nStart train process:’)
epoch = 1
while True:
error = 0
for i in range(len(inputData)):
X, Z, D = Forward(weights, inputData[i]) # прямое распространение сигнала
deltas, err = Backward(weights, Z, D, outputData[i]) # обратное распространение ошибки
UpdateWeights(weights, X, deltas, alpha) # обновление весовых коэффициентов
error += err / 2
if epoch % 1 == 0:
print(«epoch:», epoch, «alpha:», alpha, «error:», error)
# выходим, если ошибка стала меньше точности
if error < eps:
break;
# выходим, если достигли большого числа эпох
if epoch >= epochs:
print(‘Warning! Max epochs reached’)
break
epoch += 1# увеличиваемчислоэпохна 1
alpha *= 0.999
Рис. 5. Код обучения сети
Тренируем сеть
Создаем массив векторов X и Y с обучающими данными и саму нейросеть:
# массив входных обучающих векторов
X = [
[ 0, 0 ],
[ 0, 1 ],
[ 1, 0 ],
[ 1, 1 ],
];
# массив выходных обучающих векторов
Y = {
[ 0 ], # 0 ^ 0 = 0
[ 1 ], # 0 ^ 1 = 1
[ 1 ], # 1 ^ 0 = 1
[ 0 ] # 1 ^ 1 = 0
}
struct = [ 2, 3, 1 ] # структура сети: 2 входных нейрона, 3 нейрона в скрытом слое, 1 выходной нейрон
W = InitWeights(struct) # матрицы весовых коэффициентов
Рис. 6. Код функции XOR
Запускаем обучение со следующими параметрами: скорость обучения — 0.5, число эпох — 100000, величина ошибки — 1e-7:
Train(W, x, y, 0.5, 1e-7, 100000)
После обучения посмотрим на результаты, выполнив прямой проход для всех элементов:
for i in range(len(X)):
output = Forward(X[i]);
print«X: «, X[i][0], X[i][1], «Y: «, Y[i][0], «output: «, output[0]);
}
В результате вывод может быть таким:
X: 0 0, Y: 0, output: 0,00503439463431083
X: 0 1, Y: 1, output: 0,996036009216668
X: 1 0, Y: 1, output: 0,996036033202241
X: 1 1, Y: 0, output: 0,00550270947767007
Далее будем учить сеть распознавать цифры на картинках с рукописными цифрами из выборки MNIST.
Получаем тренировочную выборку
Файл с тренировочной выборкой train.csv находится по ссылке: http://www.pjreddie.com/media/files/mnist_train.csv [2]
# получение обучающей выборки
def GetTrainData(path, maxLen):
f = open(path, ‘r’)
lines = f.readlines() # считываемстрокифайла
trainInput = []
trainOutput = []
# проходимся по строкам файла, но не более, чем maxLen
for i in range(1, min(maxLen + 1, len(lines))):
splited = lines[i].split(‘,’)
x = []
y = []
# сохраняем нормализованные значения в вектор
for j in range(1, len(splited)):
v = 0.01 + float(splited[j]) / 255 * 0.99
x.append(v)
for j in range(10):
y.append(0);
y[int(splited[0])] = 1 # задаём выходной вектор
# добавляем в обучающую выборку цифру
trainInput.append(x)
trainOutput.append(y)
print(‘nReaded train data:’, len(trainInput), ‘elements’); # выводиминформациюосчитанныхданных
return trainInput, trainOutput
Рис. 7. Код с обучающей выборкой
Получив обучающее множество, состоящее из 42000 примеров, запустим обучений нейронной сети на 20 эпох обучения со скоростью 0.65.
struct = [ 784, 100, 10 ] # структура сети: 784 входных нейрона, 100 в скрытом слое, 10 выходных
W = InitWeights(struct) # матрицы весовых коэффициентов
learningRate = 0.65 # скорость обучения
maxEpoch = 20 # максимальное число эпох
eps = 1e-7 # точность
trainPath = ‘train.csv’ # путь к файлу с обучающей выборкой
testPath = ‘test.csv’ # путь к файлу с тестовой выборкой
answersPath = ‘answers.csv’ # путь к файлу с ответами
print(‘Network structure:’, struct)
print(‘Learning rate (alpha):’, learningRate)
print(‘Max epochs: ‘, maxEpoch)
print(‘Accuracy (eps):’, eps)
x, y = GetTrainData(trainPath, 42000) # считываем обучающую выборку
Train(W, x, y, learningRate, eps, maxEpoch)
Рис. 8. Код запуска обучения
Тестируем сеть
Файл с тестовой выборкой находится по ссылке:
http://www.pjreddie.com/media/files/mnist_test.csv [2]
# проверка точности на обучающей выборке
def Test(weights, testPath, answersPath):
print(‘nStart test process:’);
test = open(testPath, ‘r’)
answers = open(answersPath, ‘r’)
testLine = test.readlines()
answersLine = answers.readlines()
correct = 0
total = 0
# проходимся по всем тестовым строкам кроме первой
for i in range(1, len(testLine)):
splited = testLine[i].split(‘,’) # разбиваем строку по запятым
x = []
# сохраняем нормализованные значения в вектор
for j in range(len(splited)):
v = 0.01 + float(splited[j]) / 255 * 0.99
x.append(v)
d = np.argmax(GetOutput(weights, x)); # получаемцифру, предсказаннуюсетью
y = int(answersLine[i].split(‘,’)[1]) # получаем цифру из ответов
if y == d: # если цифры совпали, увеличиваем на 1 число корректно распознанных
correct += 1
total += 1 # увеличиваем число обработанных строк
if total % 1000 == 0:
print(‘accuracy:’, correct, » / «, total, «: «, (100.0 * correct / total), ‘%’) # выводиминформациюпопредсказаниям
print(‘accuracy:’, correct, » / «, total, «: «, (100.0 * correct / total), ‘%’) # выводим информацию по предсказаниям
Рис. 8. Код с тестовой выборкой
В результате запуска теста мы получили точность около 97%. Таким образом мы научились распознавать изображения.
# предсказание по картинке
def Predict(weights, path):
img = plt.imread(path)
x = 0.01 + img.flatten() * 256 / 255 * 0.99
return GetOutput(weights, x)
while True:
path = input(‘Enter path to image:’);
if path == »:
break;
d = Predict(W, path)
print(‘For image », path, » probably it is’, np.argmax(d))
Рис. 8. Код распознавания
Выводы
Нейронная сеть успешно обучилась функции исключающего ИЛИ (XOR), а также смогла распознавать изображения рукописных цифр с точностью более 97%.
СПИСОК ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
Воронова Л.И., Воронов В.И.. Machine Learning: регрессионные методы интеллектуального анализа данных: учебное пособие / МТУСИ.– М., 2017.- 92с.
Рашид Т. Создаем нейронную сеть.: Пер. с англ. – СПб.: ООО «Диалектика», 2018 – 272 с.: ил. – Парал. тит. англ.
Википедия [Электронный ресурс]. Режим доступа: https://ru.wikipedia.org
В предыдущей части мы учились рассчитывать изменения сигнала при проходе по нейросети. Мы познакомились с матрицами, их произведением и вывели простые формулы для расчетов.
В 6 части перевода выкладываю сразу 4 раздела книги. Все они посвящены одной из самых важных тем в области нейросетей — методу обратного распространения ошибки. Вы научитесь рассчитывать погрешность всех нейронов нейросети основываясь только на итоговой погрешности сети и весах связей.
Материал сложный, так что смело задавайте свои вопросы на форуме.
Вы можете скачать PDF версию перевода.
Приятного чтения!
Оглавление
1 Глава. Как они работают.
- 1.1 Легко для меня, тяжело для тебя
- 1.2 Простая предсказательная машина
- 1.3 Классификация это почти что предсказание
- 1.4 Тренировка простого классификатора
- 1.5 Иногда одного классификатора недостаточно
- 1.6 Нейроны — природные вычислительные машины
- 1.7 Проход сигнала через нейросеть
- 1.8 Умножать матрицы полезно… Серьезно!
- 1.9 Трехслойная нейросеть и произведение матриц
- 1.10 Калибровка весов нескольких связей
- 1.11 Обратное распространение ошибки от выходных нейронов
- 1.12 Обратное распространение ошибки на множество слоев
- 1.13 Обратное распространение ошибки и произведение матриц
1.10 Калибровка весов нескольких связей
Ранее мы настраивали линейный классификатор с помощью изменения постоянного коэффициента уравнения прямой. Мы использовали погрешность, разность между полученным и желаемым результатами, для настройки классификатора.
Все те операции были достаточно простые, так как сама связь между погрешностью и величины, на которую надо было изменить коэффициент прямой оказалось очень простой.
Но как нам калибровать веса связей, когда на получаемый результат, а значит и на погрешность, влияют сразу несколько нейронов? Рисунок ниже демонстрирует проблему:
Очень легко работать с погрешностью, когда вход у нейрона всего один. Но сейчас уже два нейрона подают сигналы на два входа рассматриваемого нейрона. Что же делать с погрешностью?
Нет никакого смысла использовать погрешность целиком для корректировки одного веса, потому что в этом случае мы забываем про второй вес. Ведь оба веса задействованы в создании полученного результата, а значит оба веса виновны в итоговой погрешности.
Конечно, существует очень маленькая вероятность того, что только один вес внес погрешность, а второй был идеально откалиброван. Но даже если мы немного поменяем вес, который и так не вносит погрешность, то в процессе дальнейшего обучения сети он все равно придет в норму, так что ничего страшного.
Можно попытаться разделить погрешность одинаково на все нейроны:
Классная идея. Хотя я никогда не пробовал подобный вариант использования погрешности в реальных нейросетях, я уверен, что результаты вышли бы очень достойными.
Другая идея тоже заключается в разделении погрешности, но не поровну между всеми нейронами. Вместо этого мы кладем большую часть ответственности за погрешность на нейроны с большим весом связи. Почему? Потому что за счет своего большего веса они внесли больший вклад в выход нейрона, а значит и в погрешность.
На рисунке изображены два нейрона, которые подают сигналы третьему, выходному нейрону. Веса связей: ( 3 ) и ( 1 ). Согласно нашей идее о переносе погрешности на нейроны мы используем ( frac{3}{4} ) погрешности на корректировку первого (большего) веса и ( frac{1}{4} ) на корректировку второго (меньшего) веса.
Идею легко развить до любого количества нейронов. Пусть у нас есть 100 нейронов и все они соединены с результирующим нейроном. В таком случае, мы распределяем погрешность на все 100 связей так, чтобы на каждую связь пришлась часть погрешности, соответствующая ее весу.
Как видно, мы используем веса связей для двух задач. Во-первых, мы используем веса в процессе распространения сигнала от входного до выходного слоя. Мы уже разобрались, как это делается. Во-вторых, мы используем веса для распространения ошибки в обратную сторону: от выходного слоя к входному. Из-за этого данный метод использования погрешности называют методом обратного распространения ошибки.
Если у нашей сети 2 нейрона выходного слоя, то нам пришлось бы использовать этот метод еще раз, но уже для связей, которые повлияли на выход второго нейрона выходного слоя. Рассмотрим эту ситуацию подробнее.
1.11 Обратное распространение ошибки от выходных нейронов
На диаграмме ниже изображена нейросеть с двумя нейронами во входном слое, как и в предыдущем примере. Но теперь у сети имеется два нейрона и в выходном слое.
Оба выхода сети могут иметь погрешность, особенно в тех случаях, когда сеть еще не натренирована. Мы должны использовать полученные погрешности для настройки весов связей. Можно использовать метод, который мы получили в предыдущем разделе — больше изменяем те нейроны, которые сделали больший вклад в выход сети.
То, что сейчас у нас больше одного выходного нейрона по сути ни на что не влияет. Мы просто используем наш метод дважды: для первого и второго нейронов. Почему так просто? Потому что связи с конкретным выходным нейроном никак не влияют на остальные выходные нейроны. Их изменение повлияет только на конкретный выходной нейрон. На диаграмме выше изменение весов ( w_{1,2} ) и ( w_{2,2} ) не повлияет на результат ( o_1 ).
Погрешность первого нейрона выходного слоя мы обозначили за ( e_1 ). Погрешность равна разнице между желаемым выходом нейрона ( t_1 ), который мы имеем в обучающей выборке и полученным реальным результатом ( o_1 ).
[ e_1 = t_1 — o_1 ]
Погрешность второго нейрона выходного слоя равна ( e_2 ).
На диаграмме выше погрешность ( e_1 ) разделяется на веса ( w_{1,1} ) и ( w_{2,1} ) соответственно их вкладу в эту погрешность. Аналогично, погрешность ( e_2 ) разделяется на веса ( w_{1,2} ) и ( w_{2,2} ).
Теперь надо определить, какой вес оказал большее влияние на выход нейрона. Например, мы можем определить, какая часть ошибки ( e_1 ) пойдет на исправление веса ( w_{1,1} ):
[ frac{w_{1,1}}{w_{1,1}+w_{2,1}} ]
А вот так находится часть ( e_1 ), которая пойдет на корректировку веса ( w_{2,1} ):
[ frac{w_{2,1}}{w_{1,1} + w_{2,1}} ]
Теперь разберемся, что означают два этих выражения выше. Изначально наша идея заключается в том, что мы хотим сильнее изменить связи с большим весом и слегка изменить связи с меньшим весом.
А как нам понять величину веса относительно всех остальных весов? Для этого мы должны сравнить какой-то конкретный вес (например ( w_{1,1} )) с абстрактной «общей» суммой всех весов, повлиявших на выход нейрона. На выход нейрона повлияли два веса: ( w_{1,1} ) и ( w_{2,1} ). Мы складываем их и смотрим, какая часть от общего вклада приходится на ( w_{1,1} ) с помощью деления этого веса на полученную ранее общую сумму:
[ frac{w_{1,1}}{w_{1,1}+w_{2,1}} ]
Пусть ( w_{1,1} ) в два раза больше, чем ( w_{2,1} ): ( w_{1,1} = 6 ) и ( w_{2,1} = 3 ). Тогда имеем ( 6/(6+3) = 6/9 = 2/3 ), а значит ( 2/3 ) погрешности ( e_1 ) пойдет на корректировку ( w_{1,1} ), а ( 1/3 ) на корректировку ( w_{2,1} ).
В случае, когда оба веса равны, то каждому достанется по половине погрешности. Пусть ( w_{1,1} = 4 ) и ( w_{2,1}=4 ). Тогда имеем ( 4/(4+4)=4/8=1/2 ), а значит на каждый вес пойдет ( 1/2 ) погрешности ( e_1 ).
Прежде чем мы двинемся дальше, давайте на секунду остановимся и посмотрим, чего мы достигли. Нам нужно что-то менять в нейросети для уменьшения получаемой погрешности. Мы решили, что будем менять веса связей между нейронами. Мы также нашли способ, как распределять полученную на выходном слое сети погрешность между весами связей. В этом разделе мы получили формулы для вычисления конкретной части погрешности для каждого веса. Отлично!
Но есть еще одна проблема. Сейчас мы знаем, что делать с весами связей слое, который находится прямо перед выходным слоем сети. А что если наша нейросеть имеет больше 2 слоев? Что делать с весами связей в слоях, которые находятся за предпоследним слоем сети?
1.12 Обратное распространение ошибки на множество слоев
На диаграмме ниже изображена простая трехслойная нейросеть с входным, скрытым и выходным слоями.
Сейчас мы наблюдаем процесс, который обсуждался в разделе выше. Мы используем погрешность выходного слоя для настройки весов связей, которые соединяют предпоследний слой с выходным слоем.
Для простоты обозначения были обобщены. Погрешности нейронов выходного слоя мы в целом назвали ( e_{text{out}} ), а все веса связей между скрытым и выходным слоем обозначили за ( w_{text{ho}} ).
Еще раз повторю, что для корректировки весов ( w_{text{ho}} ) мы распределяем погрешность нейрона выходного слоя по всем весам в зависимости от их вклада в выход нейрона.
Как видно из диаграммы ниже, для корректировки весов связей между входным и скрытым слоем нам надо повторить ту же операцию еще раз. Мы берем погрешности нейронов скрытого слоя ( e_{text{hi}} ) и распределяем их по весам связей между входным и скрытым слоем ( w_{text{ih}} ):
Если бы у нас было бы больше слоев, то мы бы и дальше повторяли этот процесс корректировки, распространяющийся от выходного ко входному слою. И снова вы видите, почему этот способ называется методом обратного распространения ошибки.
Для корректировки связей между предпоследним и выходным слоем мы использовали погрешность выходов сети ( e_{text{out}} ). А чему же равна погрешность выходов нейронов скрытых слоев ( e_{text{hi}} )? Это отличный вопрос потому что сходу на этот вопрос ответить трудно. Когда сигнал распространяется по сети от входного к выходному слою мы точно знаем значения выходных нейронов скрытых слоев. Мы получали эти значения с помощью функции активации, у которой в качестве аргумента использовалась сумма взвешенных сигналов, поступивших на вход нейрона. Но как из выходного значения нейрона скрытого слоя получить его погрешность?
У нас нет никаких ожидаемых или заранее подготовленных правильных ответов для выходов нейронов скрытого слоя. У нас есть готовые правильные ответы только для выходов нейронов выходного слоя. Эти выходы мы сравниваем с заранее правильными ответами из обучающей выборки и получаем погрешность. Давайте вновь проанализируем диаграмму выше.
Мы видим, что из первого нейрона скрытого слоя выходят две связи с двумя нейронами выходного слоя. В предыдущем разделе мы научились распределять погрешность на веса связей. Поэтому мы можем получить две погрешности для обоих весов этих связей, сложить их и получить общую погрешность данного нейрона скрытого слоя. Наглядная демонстрация:
Уже из рисунка можно понять, что делать дальше. Но давайте все-таки еще раз пройдемся по всему алгоритму. Нам нужно получить погрешность выхода нейрона скрытого слоя для того, чтобы скорректировать веса связей между текущим и предыдущим слоями. Назовем эту погрешность ( e_{text{hi}} ). Но мы не можем получить значение погрешности напрямую. Погрешность равна разности между ожидаемым и полученным значениями, но проблема заключается в том, что у нас есть ожидаемые значения только для нейронов выходного слоя нейросети.
В невозможности прямого нахождения погрешности нейронов скрытого слоя и заключается основная сложность.
Но выход есть. Мы умеем распределять погрешность нейронов выходного слоя по весам связей. Значит на каждый вес связи идет часть погрешности. Поэтому мы складываем части погрешностей, которые относятся к весам связей, исходящих из данного скрытого нейрона. Полученная сумма и будем считать за погрешность выхода данного нейрона. На диаграмме выше часть погрешности ( e_{text{out 1}} ) идет на вес ( w_{1,1} ), а часть погрешности ( e_{text{out 2}} ) идет на вес ( w_{1,2} ). Оба этих веса относятся к связям, исходящим из первого нейрона скрытого слоя. А значит мы можем найти его погрешность:
[ e_{text{hi 1}} = text{сумма частей погрешностей для весов } w_{1,1} text{ и } w_{1,2} ]
[ e_{text{hi 1}} = left(e_{text{out 1}}cdotfrac{w_{1,1}}{w_{1,1} + w_{2,1}}right) + left(e_{text{out 2}}cdotfrac{w_{1,2}}{w_{1,2} + w_{2,2}}right) ]
Рассмотрим алгоритм на реальной трехслойной нейросети с двумя нейронами в каждом слое:
Давайте отследим обратное распространение одной ошибки/погрешности. Погрешность второго выходного нейрона равна ( 0.5 ) и она распределяется на два веса. На вес ( w_{12} ) идет погрешность ( 0.1 ), а на вес ( w_{22} ) идет погрешность ( 0.4 ). Дальше у нас идет второй нейрон скрытого слоя. От него отходят две связи с весами ( w_{21} ) и ( w_{22} ). На эти веса связей также распределяется погрешность как от ( e_1 ), так и от ( e_2 ). На вес ( w_{21} ) идет погрешность ( 0.9 ), а на вес ( w_{22} ) идет погрешность ( 0.4 ). Сумма этих погрешностей и дает нам погрешность выхода второго нейрона скрытого слоя: ( 0.4 + 0.9 = 1.3 ).
Но это еще не конец. Теперь надо распределить погрешность нейронов выходного слоя на веса связей между входным и скрытым слоями. Проиллюстрируем этот процесс дальнейшего распространения ошибки:
Ключевые моменты
- Обучение нейросетей заключается в корректировки весов связей. Корректировка зависит от погрешности — разности между ожидаемым ответом из обучающей выборки и реально полученным результатами.
- Погрешность для нейронов выходного слоя рассчитывается как разница между желаемым и полученным результатами.
- Однако, погрешность скрытых нейронов определить напрямую нельзя. Одно из популярных решений — сначала необходимо распределить известную погрешность на все веса связей, а затем сложить те части погрешностей, которые относятся к связям, исходящим из одного нейрона. Сумма этих частей погрешностей и будет являться общей погрешностью этого нейрона.
1.13 Обратное распространение ошибки и произведение матриц
А можно ли использовать матрицы для упрощения всех этих трудных вычислений? Они ведь помогли нам ранее, когда мы рассчитывали проход сигнала по сети от входного к выходному слою.
Если бы мы могли выразить обратное распространение ошибки через произведение матриц, то все наши вычисления разом бы уменьшились, а компьютер бы сделал всю грязную и повторяющуюся работу за нас.
Начинаем мы с самого конца нейросети — с матрицы погрешностей ее выходов. В примере выше у нас имеется две погрешности сети: ( e_1 ) и ( e_2 ).
[ mathbf{E}_{text{out}} = left(begin{matrix}e_1 \ e_2end{matrix}right) ]
Теперь нам надо получить матрицу погрешностей выходов нейронов скрытого слоя. Звучит довольно жутко, поэтому давайте действовать по шагам. Из предыдущего раздела вы помните, что погрешность нейрона скрытого слоя высчитывается как сумма частей погрешностей весов связей, исходящих из этого нейрона.
Сначала рассматриваем первый нейрон скрытого слоя. Как было показано в предыдущем разделе, погрешность этого нейрона высчитывается так:
[ e_{text{hi 1}} = left(e_1cdotfrac{w_{11}}{w_{11} + w_{21}}right) + left(e_2cdotfrac{w_{12}}{w_{12} + w_{22}}right) ]
Погрешность второго нейрона скрытого слоя высчитывается так:
[ e_{text{hi 2}} = left(e_1cdotfrac{w_{21}}{w_{11} + w_{21}}right) + left(e_2cdotfrac{w_{22}}{w_{12} + w_{22}}right) ]
Получаем матрицу погрешностей скрытого слоя:
[ mathbf{E}_{text{hid}} = left(begin{matrix}e_{text{hid 1}} \ e_{text{hid 2}}end{matrix}right) = left(begin{matrix} e_1cdotdfrac{w_{11}}{w_{11} + w_{21}} hspace{5pt} + hspace{5pt} e_2cdotdfrac{w_{12}}{w_{12} + w_{22}} \ e_1cdotdfrac{w_{21}}{w_{11} + w_{21}} hspace{5pt} + hspace{5pt} e_2cdotdfrac{w_{22}}{w_{12} + w_{22}} end{matrix}right) ]
Многие из вас уже заметили произведение матриц:
[ mathbf{E}_{text{hid}} = left(begin{matrix} dfrac{w_{11}}{w_{11} + w_{21}} & dfrac{w_{12}}{w_{12} + w_{22}} \ dfrac{w_{21}}{w_{11} + w_{21}} & dfrac{w_{22}}{w_{12} + w_{22}} end{matrix}right)times left(begin{matrix} e_1 \ e_2 end{matrix}right) ]
Таким образом, мы смогли выразить вычисление матрицы погрешностей нейронов выходного слоя через произведение матриц. Однако выражение выше получилось немного сложнее, чем мне хотелось бы.
В формуле выше мы используем большую и неудобную матрицу, в которой делим каждый вес связи на сумму весов, приходящих в данный нейрон. Мы самостоятельно сконструировали эту матрицу.
Было бы очень удобно записать произведение из уже имеющихся матриц. А имеются у нас только матрицы весов связей, входных сигналов и погрешностей выходного слоя.
К сожалению, формулу выше никак нельзя записать в мега-простом виде, который мы получили для прохода сигнала в предыдущих разделах. Вся проблема заключается в жутких дробях, с которыми трудно что-то поделать.
Но нам очень нужно получить простую формулу для удобного и быстрого расчета матрицы погрешностей.
Пора немного пошалить!
Вновь обратим взор на формулу выше. Можно заметить, что самым главным является умножение погрешности выходного нейрона ( e_n ) на вес связи ( w_{ij} ), которая к этому выходному нейрону подсоединена. Чем больше вес, тем большую погрешность получит нейрон скрытого слоя. Эту важную деталь мы сохраняем. А вот знаменатели дробей служат лишь нормализующим фактором. Если их убрать, то мы лишимся масштабирования ошибки на предыдущие слои, что не так уж и страшно. Таким образом, мы можем избавиться от знаменателей:
[ e_1cdot frac{w_{11}}{w_{11} + w_{21}} hspace{5pt} longrightarrow hspace{5pt} e_1 cdot w_{11} ]
Запишем теперь формулу для получения матрицы погрешностей, но без знаменателей в левой матрице:
[ mathbf{E}_{text{hid}} = left(begin{matrix} w_{11} & w_{12} \ w_{21} & w_{22} end{matrix}right)times left(begin{matrix} e_1 \ e_2 end{matrix}right) ]
Так гораздо лучше!
В разделе по использованию матриц при расчетах прохода сигнала по сети мы использовали следующую матрицу весов:
[ left(begin{matrix} w_{11} & w_{21} \ w_{12} & w_{22} end{matrix}right) ]
Сейчас, для расчета матрицы погрешностей мы используем такую матрицу:
[ left(begin{matrix} w_{11} & w_{12} \ w_{21} & w_{22} end{matrix}right) ]
Можно заметить, что во второй матрице элементы как бы отражены относительно диагонали матрицы, идущей от левого верхнего до правого нижнего края матрицы: ( w_{21} ) и ( w_{12} ) поменялись местами. Такая операция над матрицами существует и называется она textbf{транспонированием} матрицы. Ранее мы использовали матрицу весов ( mathbf{W} ). Транспонированные матрицы имеют специальный значок справа сверху: ( ^intercal ). В расчете матрицы погрешностей мы используем транспонированную матрицу весов: ( mathbf{W}^intercal ).
Вот два примера для иллюстрации транспонирования матриц. Заметьте, что данную операцию можно выполнять даже для матриц, в которых число столбцов и строк различно.
[ left(begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 end{matrix}right)^intercal = left(begin{matrix} 1 & 4 & 7 \ 2 & 5 & 8 \ 3 & 6 & 9 end{matrix}right) ]
[ left(begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 end{matrix}right)^intercal = left(begin{matrix} 1 & 4 \ 2 & 5 \ 3 & 6 end{matrix}right) ]
Мы получили то, что хотели — простую формулу для расчета матрицы погрешностей нейронов скрытого слоя:
[ mathbf{E}_{text{hid}} = mathbf{W}^intercal times mathbf{E}_{text{out}} ]
Это все конечно отлично, но правильно ли мы поступили, просто проигнорировав знаменатели? Да.
Дело в том, что сеть обучается не мгновенно, а проходит через множество шагов обучения. Таким образом она постепенно калибрует и корректирует собственные веса до приемлемого значения. Поэтому способ, с помощью которого мы находим погрешность не так важен. Я уже упоминал ранее, что мы могли бы разделить всю погрешность просто пополам между всеми весами, вносящими вклад в выход нейрона и даже тогда, по окончанию обучения, сеть выдавала бы неплохие результаты.
Безусловно, игнорирование знаменателей повлияет на процесс обучения сети, но рано или поздно, через сотни и тысячи шагов обучения, она дойдет до правильных результатов что со знаменателями, что без них.
Убрав знаменатели, мы сохранили общую суть обратного распространения ошибки — чем больше вес, тем больше его надо скорректировать. Мы просто убрали смягчающий фактор.
Ключевые моменты
- Обратное распространение ошибки может быть выражено через произведение матриц.
- Это позволяет нам удобно и эффективно производить расчеты вне зависимости от размеров нейросети.
- Получается что и прямой проход сигнала по нейросети и обратно распространение ошибки можно выразить через матрицы с помощью очень похожих формул.
Сделайте перерыв. Вы его заслужили. Следующие несколько разделов будут финальными и очень крутыми. Но их надо проходить на свежую голову.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
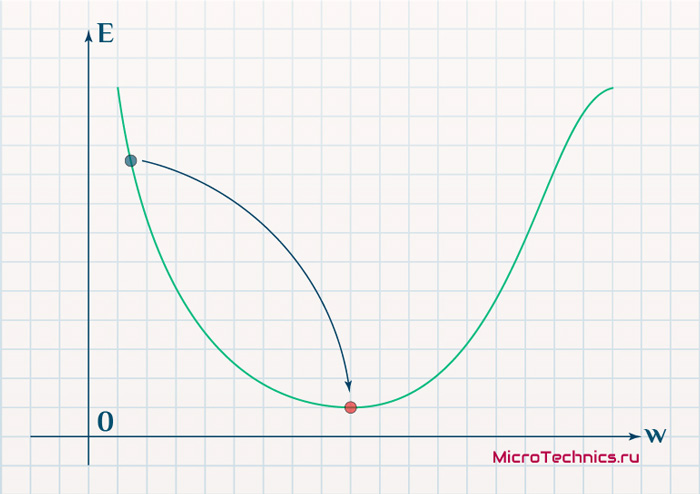
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
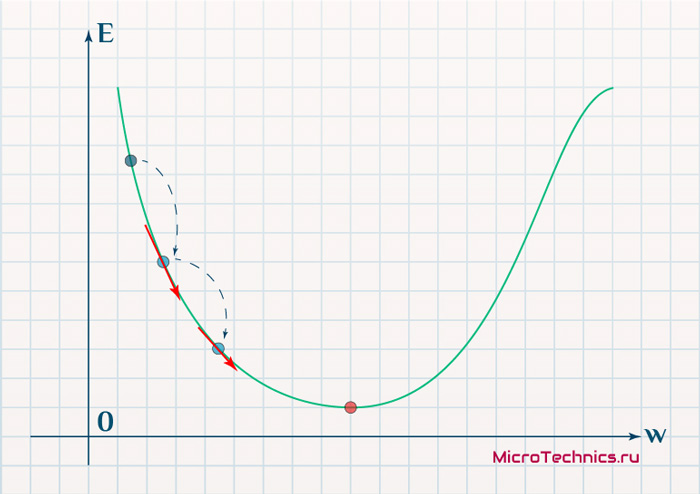
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
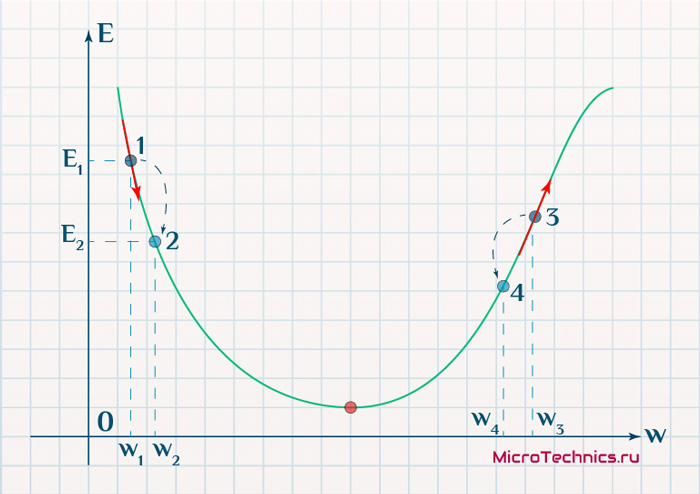
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
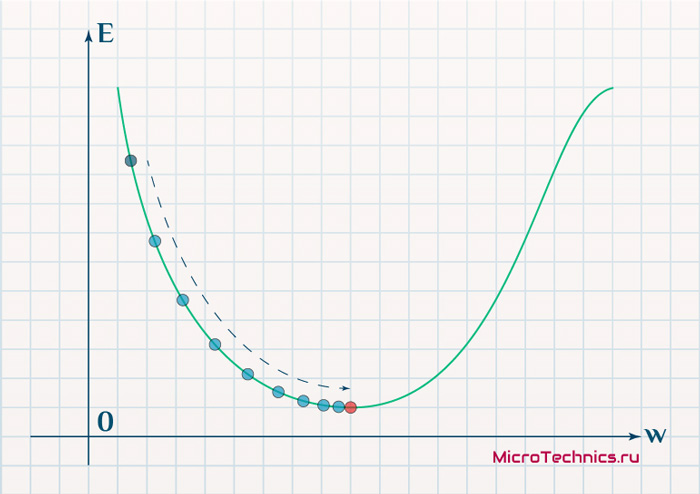
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
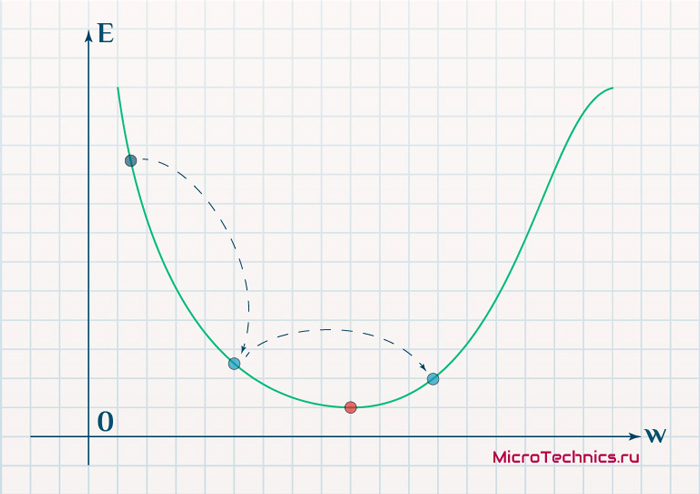
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
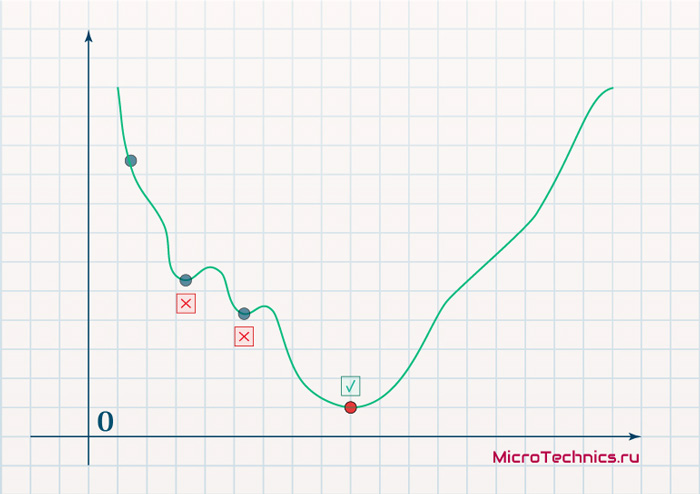
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
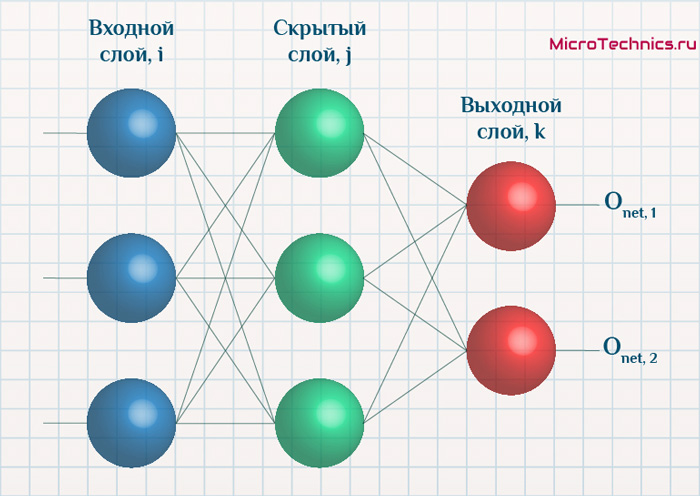
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
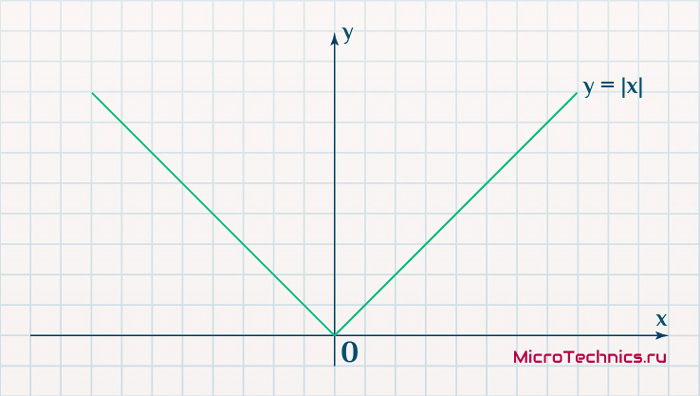
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
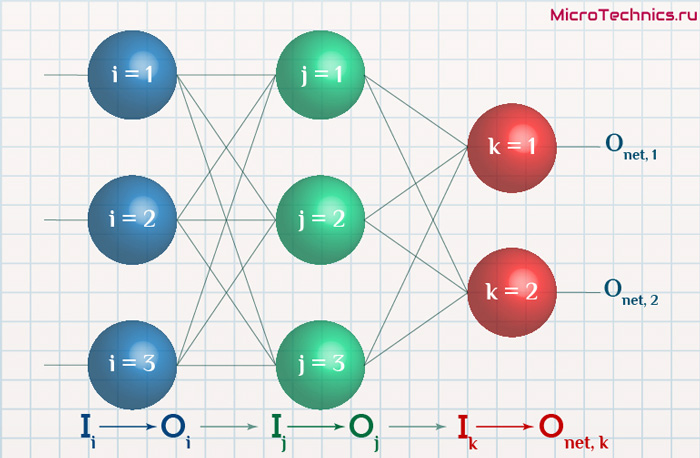
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
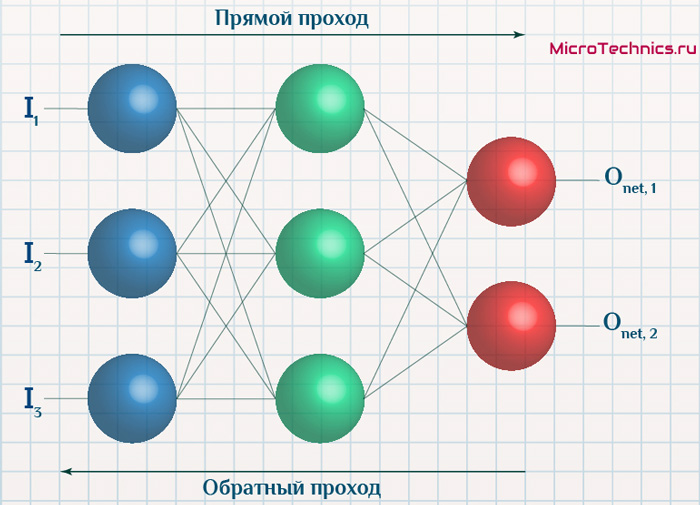
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
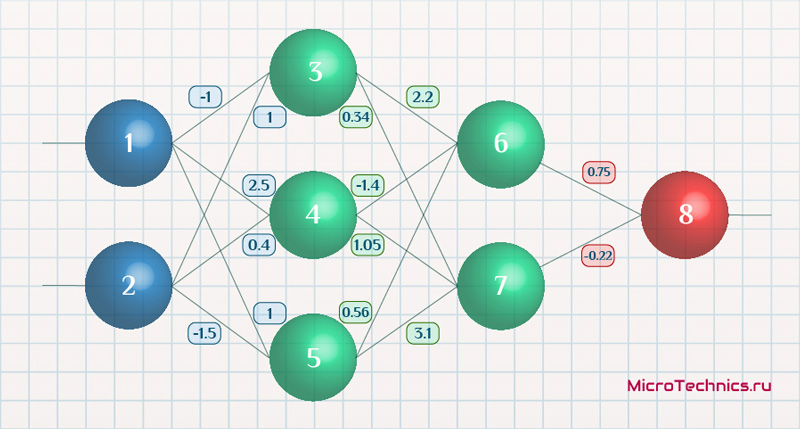
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!