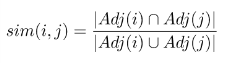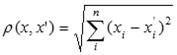Алгоритмы квадратичной ошибки
Задачу кластеризации можно рассматривать
как построение оптимального разбиения
объектов на группы. При этом оптимальность
может быть определена как требование
минимизации среднеквадратической
ошибки разбиения:

где cj — «центр масс» кластера j
(точка со средними значениями характеристик
для данного кластера)
Алгоритмы квадратичной ошибки относятся
к типу плоских алгоритмов. Самым
распространенным алгоритмом этой
категории является метод k-средних. Этот
алгоритм строит заданное число кластеров,
расположенных как можно дальше друг от
друга. Работа алгоритма делится на
несколько этапов:
-
Случайно
выбрать k точек, являющихся начальными
«центрами масс»
кластеров. -
Отнести
каждый объект к кластеру с ближайшим
«центром
масс». -
Пересчитать
«центры масс» кластеров согласно их
текущему
составу. -
Если
критерий остановки алгоритма не
удовлетворен, вернуться к п.
2.
В качестве критерия остановки работы
алгоритма обычно выбирают минимальное
изменение среднеквадратической ошибки.
Так же возможно останавливать работу
алгоритма, если на шаге 2 не было объектов,
переместившихся из кластера в кластер.
К недостаткам данного алгоритма можно
отнести необходимость заранее задавать
количество кластеров для разбиения.
Нечеткие алгоритмы
Наиболее популярным алгоритмом нечеткой
кластеризации является алгоритм
-
средних
(c-means). Он представляет собой модификацию
метода k-средних. Шаги работы алгоритма:-
Выбрать
начальное нечеткое разбиение n объектов
на k кластеров путем
выбора
матрицы принадлежности U размера n x k
( Uij=1,
если i-й
объект
принадлежит j-му кластеру, и Uij=0,
если
нет). -
Используя
матрицу U, найти значение критерия
нечеткой
ошибки:
-
,
где ck — «центр масс»
нечеткого кластера k:
.
-
Перегруппировать
объекты с целью уменьшения этого
значения критерия
нечеткой
ошибки. -
Возвращаться
в п. 2 до тех пор, пока изменения матрицы
U не
станут
незначительными.
Этот алгоритм может не подойти, если
заранее неизвестно число кластеров,
либо необходимо однозначно отнести
каждый объект к одному кластеру.
Существуют алгоритмы, основанные на
теории графов, например такие.
Алгоритм выделения связных компонент
В алгоритме выделения связных компонент
задается входной параметр R и в графе
удаляются все ребра, для которых
«расстояния» больше R. Соединенными
остаются только наиболее близкие пары
объектов. Смысл алгоритма заключается
в том, чтобы подобрать такое значение
R, лежащее в диапазон всех «расстояний»,
при котором граф «развалится» на
несколько связных компонент. Полученные
компоненты и есть кластеры.
Для подбора параметра R обычно
строится гистограмма распределений
попарных расстояний. В задачах с хорошо
выраженной кластерной структурой данных
на гистограмме будет два пика – один
соответствует внутрикластерным
расстояниям, второй – межкластерным
расстояния. Параметр R подбирается
из зоны минимума между этими пиками.
При этом управлять количеством кластеров
при помощи порога расстояния довольно
затруднительно.
Алгоритм минимального покрывающего дерева
Алгоритм минимального покрывающего
дерева сначала строит на графе минимальное
покрывающее дерево, а затем последовательно
удаляет ребра с наибольшим весом.
Приветствую!
В своей дипломной работе я проводил обзор и сравнительный анализ алгоритмов кластеризации данных. Подумал, что уже собранный и проработанный материал может оказаться кому-то интересен и полезен.
О том, что такое кластеризация, рассказал sashaeve в статье «Кластеризация: алгоритмы k-means и c-means». Я частично повторю слова Александра, частично дополню. Также в конце этой статьи интересующиеся могут почитать материалы по ссылкам в списке литературы.
Так же я постарался привести сухой «дипломный» стиль изложения к более публицистическому.
Понятие кластеризации
Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.
Применение кластерного анализа в общем виде сводится к следующим этапам:
- Отбор выборки объектов для кластеризации.
- Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости – нормализация значений переменных.
- Вычисление значений меры сходства между объектами.
- Применение метода кластерного анализа для создания групп сходных объектов (кластеров).
- Представление результатов анализа.
После получения и анализа результатов возможна корректировка выбранной метрики и метода кластеризации до получения оптимального результата.
Меры расстояний
Итак, как же определять «похожесть» объектов? Для начала нужно составить вектор характеристик для каждого объекта — как правило, это набор числовых значений, например, рост-вес человека. Однако существуют также алгоритмы, работающие с качественными (т.н. категорийными) характеристиками.
После того, как мы определили вектор характеристик, можно провести нормализацию, чтобы все компоненты давали одинаковый вклад при расчете «расстояния». В процессе нормализации все значения приводятся к некоторому диапазону, например, [-1, -1] или [0, 1].
Наконец, для каждой пары объектов измеряется «расстояние» между ними — степень похожести. Существует множество метрик, вот лишь основные из них:
- Евклидово расстояние
Наиболее распространенная функция расстояния. Представляет собой геометрическим расстоянием в многомерном пространстве:
- Квадрат евклидова расстояния
Применяется для придания большего веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:
- Расстояние городских кварталов (манхэттенское расстояние)
Это расстояние является средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако для этой меры влияние отдельных больших разностей (выбросов) уменьшается (т.к. они не возводятся в квадрат). Формула для расчета манхэттенского расстояния:
- Расстояние Чебышева
Это расстояние может оказаться полезным, когда нужно определить два объекта как «различные», если они различаются по какой-либо одной координате. Расстояние Чебышева вычисляется по формуле:
- Степенное расстояние
Применяется в случае, когда необходимо увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по следующей формуле:
,
где r и p – параметры, определяемые пользователем. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра – r и p — равны двум, то это расстояние совпадает с расстоянием Евклида.
Выбор метрики полностью лежит на исследователе, поскольку результаты кластеризации могут существенно отличаться при использовании разных мер.
Классификация алгоритмов
Для себя я выделил две основные классификации алгоритмов кластеризации.
- Иерархические и плоские.
Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Т.о. на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера.
Плоские алгоритмы строят одно разбиение объектов на кластеры. - Четкие и нечеткие.
Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру. Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.
Объединение кластеров
В случае использования иерархических алгоритмов встает вопрос, как объединять между собой кластера, как вычислять «расстояния» между ними. Существует несколько метрик:
- Одиночная связь (расстояния ближайшего соседа)
В этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Результирующие кластеры имеют тенденцию объединяться в цепочки. - Полная связь (расстояние наиболее удаленных соседей)
В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. наиболее удаленными соседями). Этот метод обычно работает очень хорошо, когда объекты происходят из отдельных групп. Если же кластеры имеют удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден. - Невзвешенное попарное среднее
В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты формируют различные группы, однако он работает одинаково хорошо и в случаях протяженных («цепочечного» типа) кластеров. - Взвешенное попарное среднее
Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому данный метод должен быть использован, когда предполагаются неравные размеры кластеров. - Невзвешенный центроидный метод
В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. - Взвешенный центроидный метод (медиана)
Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учета разницы между размерами кластеров. Поэтому, если имеются или подозреваются значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
Обзор алгоритмов
Алгоритмы иерархической кластеризации
Среди алгоритмов иерархической кластеризации выделяются два основных типа: восходящие и нисходящие алгоритмы. Нисходящие алгоритмы работают по принципу «сверху-вниз»: в начале все объекты помещаются в один кластер, который затем разбивается на все более мелкие кластеры. Более распространены восходящие алгоритмы, которые в начале работы помещают каждый объект в отдельный кластер, а затем объединяют кластеры во все более крупные, пока все объекты выборки не будут содержаться в одном кластере. Таким образом строится система вложенных разбиений. Результаты таких алгоритмов обычно представляют в виде дерева – дендрограммы. Классический пример такого дерева – классификация животных и растений.
Для вычисления расстояний между кластерами чаще все пользуются двумя расстояниями: одиночной связью или полной связью (см. обзор мер расстояний между кластерами).
К недостатку иерархических алгоритмов можно отнести систему полных разбиений, которая может являться излишней в контексте решаемой задачи.
Алгоритмы квадратичной ошибки
Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения:
где cj — «центр масс» кластера j (точка со средними значениями характеристик для данного кластера).
Алгоритмы квадратичной ошибки относятся к типу плоских алгоритмов. Самым распространенным алгоритмом этой категории является метод k-средних. Этот алгоритм строит заданное число кластеров, расположенных как можно дальше друг от друга. Работа алгоритма делится на несколько этапов:
- Случайно выбрать k точек, являющихся начальными «центрами масс» кластеров.
- Отнести каждый объект к кластеру с ближайшим «центром масс».
- Пересчитать «центры масс» кластеров согласно их текущему составу.
- Если критерий остановки алгоритма не удовлетворен, вернуться к п. 2.
В качестве критерия остановки работы алгоритма обычно выбирают минимальное изменение среднеквадратической ошибки. Так же возможно останавливать работу алгоритма, если на шаге 2 не было объектов, переместившихся из кластера в кластер.
К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.
Нечеткие алгоритмы
Наиболее популярным алгоритмом нечеткой кластеризации является алгоритм c-средних (c-means). Он представляет собой модификацию метода k-средних. Шаги работы алгоритма:
- Выбрать начальное нечеткое разбиение n объектов на k кластеров путем выбора матрицы принадлежности U размера n x k.
- Используя матрицу U, найти значение критерия нечеткой ошибки:
,
где ck — «центр масс» нечеткого кластера k:
.
- Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.
- Возвращаться в п. 2 до тех пор, пока изменения матрицы U не станут незначительными.
Этот алгоритм может не подойти, если заранее неизвестно число кластеров, либо необходимо однозначно отнести каждый объект к одному кластеру.
Алгоритмы, основанные на теории графов
Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа G=(V, E), вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность вносения различных усовершенствований, основанные на геометрических соображениях. Основными алгоритмам являются алгоритм выделения связных компонент, алгоритм построения минимального покрывающего (остовного) дерева и алгоритм послойной кластеризации.
Алгоритм выделения связных компонент
В алгоритме выделения связных компонент задается входной параметр R и в графе удаляются все ребра, для которых «расстояния» больше R. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение R, лежащее в диапазон всех «расстояний», при котором граф «развалится» на несколько связных компонент. Полученные компоненты и есть кластеры.
Для подбора параметра R обычно строится гистограмма распределений попарных расстояний. В задачах с хорошо выраженной кластерной структурой данных на гистограмме будет два пика – один соответствует внутрикластерным расстояниям, второй – межкластерным расстояния. Параметр R подбирается из зоны минимума между этими пиками. При этом управлять количеством кластеров при помощи порога расстояния довольно затруднительно.
Алгоритм минимального покрывающего дерева
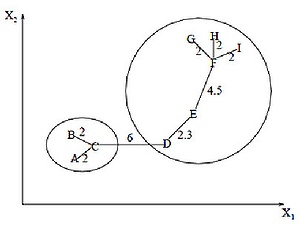
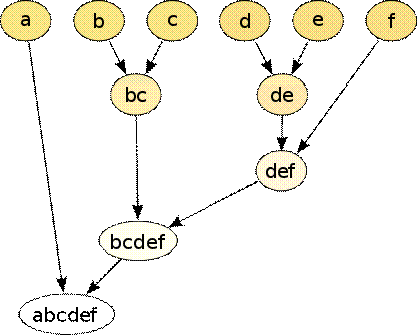
Алгоритм минимального покрывающего дерева сначала строит на графе минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом. На рисунке изображено минимальное покрывающее дерево, полученное для девяти объектов.
Путём удаления связи, помеченной CD, с длиной равной 6 единицам (ребро с максимальным расстоянием), получаем два кластера: {A, B, C} и {D, E, F, G, H, I}. Второй кластер в дальнейшем может быть разделён ещё на два кластера путём удаления ребра EF, которое имеет длину, равную 4,5 единицам.
Послойная кластеризация
Алгоритм послойной кластеризации основан на выделении связных компонент графа на некотором уровне расстояний между объектами (вершинами). Уровень расстояния задается порогом расстояния c. Например, если расстояние между объектами 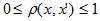
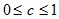
Алгоритм послойной кластеризации формирует последовательность подграфов графа G, которые отражают иерархические связи между кластерами:
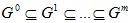
где Gt = (V, Et) — граф на уровне сt,
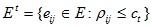
сt – t-ый порог расстояния,
m – количество уровней иерархии,
G0 = (V, o), o – пустое множество ребер графа, получаемое при t0 = 1,
Gm = G, то есть граф объектов без ограничений на расстояние (длину ребер графа), поскольку tm = 1.
Посредством изменения порогов расстояния {с0, …, сm}, где 0 = с0 < с1 < …< сm = 1, возможно контролировать глубину иерархии получаемых кластеров. Таким образом, алгоритм послойной кластеризации способен создавать как плоское разбиение данных, так и иерархическое.
Сравнение алгоритмов
Вычислительная сложность алгоритмов
| Алгоритм кластеризации | Вычислительная сложность |
| Иерархический | O(n2) |
| k-средних | O(nkl), где k – число кластеров, l – число итераций |
|---|---|
| c-средних | |
| Выделение связных компонент | зависит от алгоритма |
| Минимальное покрывающее дерево | O(n2 log n) |
| Послойная кластеризация | O(max(n, m)), где m < n(n-1)/2 |
Сравнительная таблица алгоритмов
| Алгоритм кластеризации | Форма кластеров | Входные данные | Результаты |
| Иерархический | Произвольная | Число кластеров или порог расстояния для усечения иерархии | Бинарное дерево кластеров |
| k-средних | Гиперсфера | Число кластеров | Центры кластеров |
| c-средних | Гиперсфера | Число кластеров, степень нечеткости | Центры кластеров, матрица принадлежности |
| Выделение связных компонент | Произвольная | Порог расстояния R | Древовидная структура кластеров |
| Минимальное покрывающее дерево | Произвольная | Число кластеров или порог расстояния для удаления ребер | Древовидная структура кластеров |
| Послойная кластеризация | Произвольная | Последовательность порогов расстояния | Древовидная структура кластеров с разными уровнями иерархии |
Немного о применении
В своей работе мне нужно было из иерархических структур (деревьев) выделять отдельные области. Т.е. по сути необходимо было разрезать исходное дерево на несколько более мелких деревьев. Поскольку ориентированное дерево – это частный случай графа, то естественным образом подходят алгоритмы, основанными на теории графов.
В отличие от полносвязного графа, в ориентированном дереве не все вершины соединены ребрами, при этом общее количество ребер равно n–1, где n – число вершин. Т.е. применительно к узлам дерева, работа алгоритма выделения связных компонент упростится, поскольку удаление любого количества ребер «развалит» дерево на связные компоненты (отдельные деревья). Алгоритм минимального покрывающего дерева в данном случае будет совпадать с алгоритмом выделения связных компонент – путем удаления самых длинных ребер исходное дерево разбивается на несколько деревьев. При этом очевидно, что фаза построения самого минимального покрывающего дерева пропускается.
В случае использования других алгоритмов в них пришлось бы отдельно учитывать наличие связей между объектами, что усложняет алгоритм.
Отдельно хочу сказать, что для достижения наилучшего результата необходимо экспериментировать с выбором мер расстояний, а иногда даже менять алгоритм. Никакого единого решения не существует.
Список литературы
1. Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. Курс лекций. МГУ, 2007.
2. Jain A., Murty M., Flynn P. Data Clustering: A Review. // ACM Computing Surveys. 1999. Vol. 31, no. 3.
3. Котов А., Красильников Н. Кластеризация данных. 2006.
3. Мандель И. Д. Кластерный анализ. — М.: Финансы и Статистика, 1988.
4. Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин — М.: Финансы и статистика, 1989.
5. Информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных — www.machinelearning.ru
6. Чубукова И.А. Курс лекций «Data Mining», Интернет-университет информационных технологий — www.intuit.ru/department/database/datamining
Анализ и классификация алгоритмов кластеризации
Ершов К.С., Романова Т.Н., МГТУ им. Н.Э. Баумана ersh.konst@gmail.com, rtn51@mail.ru
Аннотация
В статье рассмотрены возможные меры расстояний, используемых в алгоритмах, представлены наиболее популярные алгоритмы кластеризации и их роль в области Data mining. Приведена классификация алгоритмов. Разобраны преимущества и недостатки алгоритмов. Приведено сравнение производительности и формата данных алгоритмов.
1 Введение
Кластеризация — объединение в группы схожих объектов — является одной из фундаментальных задач в области анализа данных и Data Mining. Список прикладных областей, где она применяется, широк: сегментация изображений, маркетинг, борьба с мошенничеством, прогнозирование, анализ текстов и многие другие.
Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель на всех данных.
Далее в статье будут рассмотрены наиболее популярные алгоритмы кластеризации с целью определения наиболее подходящего алгоритма для решения задачи поиска аномалий в данных.
2 Понятие кластеризации
Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами.
Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны.
Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.
Применение кластерного анализа в общем виде сводится к следующим этапам:
1. Отбор выборки объектов для кластеризации.
2. Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости — нормализация значений переменных.
3. Вычисление значений меры сходства между объектами.
4. Применение метода кластерного анализа для создания групп сходных объектов (кластеров).
5. Представление результатов анализа.
После получения и анализа результатов возможна корректировка выбранной метрики и метода кластеризации до получения оптимального результата.
3 Меры расстояний
Чтобы определить однотипность объектов нужно составить вектор характеристик для каждого объекта — как правило, это набор числовых значений, например, рост-вес человека. Однако существуют также алгоритмы, работающие с качественными характеристиками.
После того, как определен вектор характеристик, можно провести нормализацию, чтобы все компоненты давали одинаковый вклад при расчете «расстояния». В процессе нормализации все значения приводятся к некоторому диапазону, например, [-1, -1] или [0, 1].
Для каждой пары объектов измеряется «расстояние» между ними — степень похожести. Существует множество метрик:
1. Евклидово расстояние
Наиболее распространенная функция расстояния. Представляет собой геометрическим расстоянием в многомерном пространстве:
2. Квадрат евклидова расстояния
Применяется для придания большего веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:
и с
3. Расстояние городских кварталов (манхэттенское расстояние)
Это расстояние является средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако для этой меры влияние отдельных больших разностей (выбросов) уменьшается (т.к. они не возводятся в квадрат). Формула для расчета манхэттенского расстояния:
1л:
4. Расстояние Чебышева
Это расстояние может оказаться полезным, когда нужно определить два объекта как «различные», если они различаются по какой-либо одной координате. Расстояние Чебышева вычисляется по формуле:
5. Степенное расстояние
Применяется в случае, когда необходимо
увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по следующей формуле:
где г и р — параметры, определяемые пользователем. Параметр р ответственен за постепенное взвешивание разностей по отдельным координатам, параметр г ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра — г и р — равны двум, то это расстояние совпадает с расстоянием Евклида.
Выбор метрики полностью лежит на исследователе, поскольку результаты кластеризации могут существенно отличаться при использовании разных мер.
4 Классификация алгоритмов
Можно выделить две основные классификации алгоритмов кластеризации
1. Иерархические и плоские.
Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно
разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Т.е. на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера.
Плоские алгоритмы строят одно разбиение объектов на кластеры.
2. Четкие и нечеткие.
Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру. Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.
4.1 Алгоритмы иерархической кластеризации
Среди алгоритмов иерархической кластеризации выделяются два основных типа: восходящие и нисходящие алгоритмы. Нисходящие алгоритмы работают по принципу «сверху-вниз»: в начале все объекты помещаются в один кластер, который затем разбивается на все более мелкие кластеры.
Более распространены восходящие алгоритмы, которые в начале работы помещают каждый объект в отдельный кластер, а затем объединяют кластеры во все более крупные, пока все объекты выборки не будут содержаться в одном кластере.
Таким образом строится система вложенных разбиений. Результаты таких алгоритмов обычно представляют в виде дерева — дендро-граммы. Классический пример такого дерева — классификация животных и растений.
Для вычисления расстояний между кластерами чаще все пользуются двумя расстояниями: одиночной связью или полной связью (см. обзор мер расстояний между кластерами).
К недостатку иерархических алгоритмов можно отнести систему полных разбиений, которая может являться излишней в контексте решаемой задачи.
4.1.1 Объединение кластеров
В случае использования иерархических алгоритмов встает вопрос, как объединять между собой кластера, как вычислять «расстояния» между ними. Существует несколько метрик:
1. Одиночная связь (расстояния ближайшего соседа)
В этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Результирующие кластеры имеют тенденцию объединяться в цепочки.
2. Полная связь (расстояние наиболее удаленных соседей)
В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. наиболее удаленными соседями). Этот метод обычно работает очень хорошо, когда объекты происходят из отдельных групп. Если же кластеры имеют удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.
3. Невзвешенное попарное среднее
В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты формируют различные группы, однако он работает одинаково хорошо и в случаях протяженных («цепочечного» типа) кластеров.
4. Взвешенное попарное среднее
Метод идентичен методу невзвешенного
попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому данный метод должен быть использован, когда предполагаются неравные размеры кластеров.
5. Невзвешенный центроидный метод
В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.
6. Взвешенный центроидный метод (медиана)
Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учета разницы между размерами кластеров. Поэтому, если имеются или подозреваются значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
4.2 Алгоритмы квадратичной ошибки
Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность
СО
Ч — 9
может быть определена как требование минимизации среднеквадратической ошибки разбиения:
е2(Х,1) =
где с} — «центр масс» кластера j (точка со средними значениями характеристик для данного кластера), К — количество кластеров, п -количество точек.
Алгоритмы квадратичной ошибки относятся к типу плоских алгоритмов. Самым распространенным алгоритмом этой категории является метод к-средних. Этот алгоритм строит заданное число кластеров, расположенных как можно дальше друг от друга. Работа алгоритма делится на несколько этапов:
1. Случайно выбрать к точек, являющихся начальными «центрами масс» кластеров.
2. Отнести каждый объект к кластеру с ближайшим «центром масс».
3. Пересчитать «центры масс» кластеров согласно их текущему составу.
4. Если критерий остановки алгоритма не удовлетворен, вернуться к п. 2.
В качестве критерия остановки работы алгоритма обычно выбирают минимальное изменение среднеквадратической ошибки. Так же возможно останавливать работу алгоритма, если на шаге 2 не было объектов, переместившихся из кластера в кластер.
К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.
4.3 Нечеткие алгоритмы
Наиболее популярным алгоритмом нечеткой кластеризации является алгоритм с-средних (с-теа^). Он представляет собой модификацию метода к-средних. Шаги работы алгоритма:
1. Выбрать начальное нечеткое разбиение п объектов на к кластеров путем выбора матрицы принадлежности и размера (п, к).
2. Используя матрицу И, найти значение критерия нечеткой ошибки:
Е2{
Х. Сд.
Нк Ц -1 ¡=1 к=1
где с к — «центр масс» нечеткого кластера к
N
Ск
-1
К — количество кластеров, N — количество точек
3. Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.
4. Возвращаться в п. 2 до тех пор, пока изменения матрицы и не станут незначительными.
Этот алгоритм может не подойти, если заранее неизвестно число кластеров, либо необходимо однозначно отнести каждый объект к одному кластеру.
4.4 Алгоритмы, основанные на теории графов
Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа 0=(У, Е), вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность вносения различных усовершенствований, основанные на геометрических соображениях. Основными алгоритмам являются алгоритм выделения связных компонент, алгоритм построения минимального покрывающего (остовного) дерева и алгоритм послойной кластеризации.
4.5 Алгоритм выделения связных компонент
В алгоритме выделения связных компонент задается входной параметр Я и в графе удаляются все ребра, для которых «расстояния» больше Я. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение Я, лежащее в диапазон всех «расстояний», при котором граф «развалится» на несколько связных компонент. Полученные компоненты и есть кластеры.
Для подбора параметра Я обычно строится гистограмма распределений попарных расстояний. В задачах с хорошо выраженной кластерной структурой данных на гистограмме будет два пика — один соответствует внут-рикластерным расстояниям, второй — межкластерным расстояния. Параметр Я подбирается из зоны минимума между этими пиками. При этом управлять количеством кластеров при помощи порога расстояния довольно затруднительно.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
4.6 Алгоритм минимального покрывающего дерева
Алгоритм минимального покрывающего дерева сначала строит на графе минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом. На рис. 1 изображено минимальное покрывающее дерево, полученное для девяти объектов.
Рис. 1. Покрывающее дерево
Путём удаления связи, помеченной СБ, с длиной равной 6 единицам (ребро с максимальным расстоянием), получаем два кластера: {А, В, С} и {Б, Е, Б, О, Н, I}. Второй кластер в дальнейшем может быть разделён ещё на два кластера путём удаления ребра ЕБ, которое имеет длину, равную 4,5 единицам.
4.7 Послойная кластеризация
Алгоритм послойной кластеризации основан на выделении связных компонент графа на некотором уровне расстояний между объектами (вершинами). Уровень расстояния задается порогом расстояния с. Например, если расстояние между объектами
О < р(х,х») < 1, то 0 < С < 1.
Алгоритм послойной кластеризации формирует последовательность подграфов графа О, которые отражают иерархические связи между кластерами:
<7° с с … с
т — количество уровней иерархии,
= (V, о), о — пустое множество ребер
графа
Посредством изменения порогов расстояния {с°, …, ст}, где
О = с» < с1 <
возможно контролировать глубину иерархии получаемых кластеров. Таким образом, алгоритм послойной кластеризации способен создавать как плоское разбиение данных, так и иерархическое.
В табл. 1 приводится сравнение рассмот- В табл 2 представлена вычислительная ренных алгоритмов. сложность каждого рассмотренного алгорит-
ма
Табл. 1 Сводная таблица
Алгоритм кластеризации Форма кластеров Входные данные Выходные данные
Иерархический Произвольная Число кластеров или порог расстояния для усечения иерархии Бинарное дерево кластеров
к-средних Гиперсфера Число кластеров Центры кластеров
с-средних Гиперсфера Число кластеров, степень нечеткости Центры кластеров, матрица принадлежности
Выделение связных компонент Произвольная Порог расстояния Я Древовидная структура кластеров
Минимальное покрывающее дерево Произвольная Число кластеров или порог расстояния для удаления ребер Древовидная структура кластеров
Послойная кластеризация Произвольная Последовательность порогов расстояния Древовидная структура кластеров с разными уровнями иерархии
Табл. 2 Вычислительная сложность алгоритмов
Алгоритм кластеризации Вычислительная сложность
Иерархический O(n2)
к-средних O(n*k*l), где k — число кластеров, l — число итераций
с-средних
Выделение связных компонент зависит от алгоритма
Минимальное покрывающее дерево O(n2 log n)
Послойная кластеризация O(max(n, m)), где m < n(n-1)/2
Примечание. n — количество точек для кластеризации.
5 Заключение
Парное сравнение объектов между собой в алгоритме k-means есть не что иное, как локальная оптимизация, т. к. на каждой итерации необходимо рассчитывать расстояние от центра кластера до каждого объекта. Это ведет к большим вычислительным затратам. При задании глобальной функции оптимизации добавление новой точки в кластер не требует больших вычислений: оно рассчитывается на основе старого значения, нового объекта и так называемых кластерных характеристик (clusters features). Конкретные кластерные характеристики зависят от того или иного алгоритма. Так появились алгоритмы BIRCH, Largeltem, CLOPE и многие другие.
Таким образом, не существует единого универсального алгоритма кластеризации. При использовании любого алгоритма важно понимать его достоинства и недостатки, учитывать природу данных, с которыми он лучше работает и способность к масштабируемости.
Список литературы
Информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных — www.machinelearning.ru/
Котов А., Красильников Н. Кластеризация данных. 2006.
Мандель И. Д. Кластерный анализ. — М.: Финансы и Статистика, 1988.
Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин — М.: Финансы и статистика, 1989.
Jain A., Murty M., Flynn P. Data Clustering: A Review. // ACM Computing Surveys. 1999. Vol. 31, no. 3.
|
|
Макеты страниц
константами. Таким образом, задача нахождения решения системы линейных неравенств заменяется более строгой, но более понятной задачей определения решения системы линейных уравнений.
Вид системы линейных уравнений упрощается, если ввести матричные обозначения. Пусть 



Тогда наша задача сводится к определению весового вектора а, удовлетворяющего уравнению

Если бы матрица У была невырожденной, то можно было бы записать равенство 



то данный подход будет состоять в минимизации квадрата длины вектора ошибки. Данная операция эквивалентна задаче минимизации функции критерия, выражаемой суммой квадратичных ошибок:

Задача минимизации суммы квадратичных ошибок является классической. Как будет показано в п. 5.8.4, она может быть решена методом градиентного анализа. Простое решение в замкнутой форме можно также получить, образуя градиент

и полагая его равным нулю. Отсюда получается необходимое условие

и задача решения уравнения 




где матрица размера 

называется псевдообращением матрицы У. Заметим, что если матрица У квадратная и невырожденная, псевдообращение совпадаете обычным обращением. Следует также отметить, что 



можно показать, что данный предел всегда существует, и 

Решение с наименьшей квадратичной ошибкой зависит от вектора допуска b, и будет показано, что различные способы выбора b приводят к различным свойствам получаемого решения. Если вектор b задан произвольно, то нет оснований считать, что в случае линейно разделяемых множеств решение с наименьшей квадратичной ошибкой даст разделяющий вектор. Однако можно надеяться, что в случае как разделяемых, так и неразделяемых множеств в результате минимизации функции критерия квадратичной ошибки может быть получена нужная разделяющая функция. Теперь перейдем к исследованию двух свойств решения, подтверждающих данное утверждение.
5.8.2. СВЯЗЬ С ЛИНЕЙНЫМ ДИСКРИМИНАНТОМ ФИШЕРА
В данном пункте будет показано, что при соответствующем выборе вектора b разделяющая функция 













где и является вектор-столбцом из 




и

Можно показать, что при определенном выборе b обнаруживается связь между решением по методу наименьшей квадратичной ошибки и линейным дискриминантом Фишера.
Доказательство начнем, записав соотношение (32) для а с использованием разложенных матриц:

Определяя выборочное среднее 


можно в результате перемножения матриц, входящих в (36), получить следующее выражение:

Полученное выражение может рассматриваться как пара уравнений, причем из первого можно выразить 


где 

Поскольку направление вектора 

следующее выражение:

где a — некоторая скалярная величина. В этом случае соотношение (40) дает

что, за исключением скалярного коэффициента, идентично решению для случая линейного дискриминанта Фишера. Помимо этого, получаем величину порога 



5.8.3. АСИМПТОТИЧЕСКОЕ ПРИБЛИЖЕНИЕ К ОПТИМАЛЬНОМУ ДИСКРИМИНАНТУ
Другое свойство решения по методу наименьшей квадратичной ошибки, говорящее в его пользу, состоит в том, что при условии 


Чтобы продемонстрировать данное утверждение, следует предположить, что выборки взяты независимо в соответствии с вероятностным законом

Решение по методу наименьшей квадратичной ошибки с использованием расширенного вектора у дает разложение в ряд функции 


то нашей задачей будет показать, что величина 

Доказательство упростится при условии сохранения различия между выборками класса 1 и класса 2. Исходя из ненормированных данных, функцию критерия 

Таким образом, в соответствии с законом больших чисел при стремлении 

функции J (а), имеющей вид

где

и

Теперь, если мы из соотношения (42) определим

то получим

Второй член данной суммы не зависит от весового вектора а. Отсюда следует, что а, которое минимизирует 


Данный результат позволяет глубже проникнуть в суть процедуры, обеспечивающей решение по методу наименьшей квадратичной ошибки. Аппроксимируя 







Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Часть I. КЛАССИФИКАЦИЯ ОБРАЗОВ
- 1.2. ПРИМЕР
- 1.3. МОДЕЛЬ КЛАССИФИКАЦИИ
- 1.4. ОПИСАТЕЛЬНЫЙ ПОДХОД
- 1.5. ОБЗОР СОДЕРЖАНИЯ КНИГИ ПО ГЛАВАМ
- 1.6. БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ
- Глава 2. БАЙЕСОВСКАЯ ТЕОРИЯ РЕШЕНИЙ
- 2.2. БАЙЕСОВСКАЯ ТЕОРИЯ РЕШЕНИЙ — НЕПРЕРЫВНЫЙ СЛУЧАЙ
- 2.3. КЛАССИФИКАЦИЯ В СЛУЧАЕ ДВУХ КЛАССОВ
- 2.4. КЛАССИФИКАЦИЯ С МИНИМАЛЬНЫМ УРОВНЕМ ОШИБКИ
- 2.5. КЛАССИФИКАТОРЫ, РАЗДЕЛЯЮЩИЕ ФУНКЦИИ И ПОВЕРХНОСТИ РЕШЕНИЙ
- 2.6. ВЕРОЯТНОСТИ ОШИБОК И ИНТЕГРАЛЫ ОШИБОК
- 2.7. НОРМАЛЬНАЯ ПЛОТНОСТЬ
- 2.8. РАЗДЕЛЯЮЩИЕ ФУНКЦИИ ДЛЯ СЛУЧАЯ НОРМАЛЬНОЙ ПЛОТНОСТИ
- 2.9. БАЙЕСОВСКАЯ ТЕОРИЯ РЕШЕНИЙ — ДИСКРЕТНЫЙ СЛУЧАЙ
- 2.10. НЕЗАВИСИМЫЕ БИНАРНЫЕ ПРИЗНАКИ
- 2.11. СОСТАВНАЯ БАЙЕСОВСКАЯ ЗАДАЧА ПРИНЯТИЯ РЕШЕНИЙ И КОНТЕКСТ
- 2.12. ПРИМЕЧАНИЯ
- 2.13. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ
- Задачи
- Глава 3. ОЦЕНКА ПАРАМЕТРОВ И ОБУЧЕНИЕ С УЧИТЕЛЕМ
- 3.2. ОЦЕНКА ПО МАКСИМУМУ ПРАВДОПОДОБИЯ
- 3.3. БАЙЕСОВСКИЙ КЛАССИФИКАТОР
- 3.4. ОБУЧЕНИЕ ПРИ ВОССТАНОВЛЕНИИ СРЕДНЕГО ЗНАЧЕНИЯ НОРМАЛЬНОЙ ПЛОТНОСТИ
- 3.5. БАЙЕСОВСКОЕ ОБУЧЕНИЕ В ОБЩЕМ СЛУЧАЕ
- 3.6. ДОСТАТОЧНЫЕ СТАТИСТИКИ
- 3.7. ДОСТАТОЧНЫЕ СТАТИСТИКИ И СЕМЕЙСТВО ЭКСПОНЕНЦИАЛЬНЫХ ФУНКЦИЙ
- 3.8. ПРОБЛЕМЫ РАЗМЕРНОСТИ
- 3.9. ОЦЕНКА УРОВНЯ ОШИБКИ
- 3.10. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ
- Задачи
- Глава 4. НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
- 4.2. ОЦЕНКА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
- 4.3. ПАРЗЕНОВСКИЕ ОКНА
- 4.4. ОЦЕНКА МЕТОДОМ БЛИЖАЙШИХ СОСЕДЕЙ
- 4.5. ОЦЕНКА АПОСТЕРИОРНЫХ ВЕРОЯТНОСТЕЙ
- 4.6. ПРАВИЛО БЛИЖАЙШЕГО СОСЕДА
- 4.7. ПРАВИЛО k БЛИЖАЙШИХ СОСЕДЕЙ
- 4.8. АППРОКСИМАЦИИ ПУТЕМ РАЗЛОЖЕНИЯ В РЯД
- 4.9. АППРОКСИМАЦИЯ ДЛЯ БИНАРНОГО СЛУЧАЯ
- 4.10. ЛИНЕЙНЫЙ ДИСКРИМИНАНТ ФИШЕРА
- 4.11. МНОЖЕСТВЕННЫЙ ДИСКРИМИНАНТНЫЙ АНАЛИЗ
- 4.12. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ
- Задача
- Глава 5. ЛИНЕЙНЫЕ РАЗДЕЛЯЮЩИЕ ФУНКЦИИ
- 5.2. ЛИНЕЙНЫЕ РАЗДЕЛЯЮЩИЕ ФУНКЦИИ И ПОВЕРХНОСТИ РЕШЕНИЙ
- 5.3. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ РАЗДЕЛЯЮЩИЕ ФУНКЦИИ
- 5.4. СЛУЧАЙ ДВУХ ЛИНЕЙНО РАЗДЕЛИМЫХ КЛАССОВ
- 5.5. МИНИМИЗАЦИЯ ПЕРСЕПТРОННОЙ ФУНКЦИИ КРИТЕРИЯ
- 5.6. ПРОЦЕДУРЫ РЕЛАКСАЦИЙ
- 5.7. ПОВЕДЕНИЕ ПРОЦЕДУР В СЛУЧАЕ НЕРАЗДЕЛЯЕМЫХ МНОЖЕСТВ
- 5.8. ПРОЦЕДУРЫ МИНИМИЗАЦИИ КВАДРАТИЧНОЙ ОШИБКИ
- 5.8.4. ПРОЦЕДУРА ВИДРОУ — ХОФФА
- 5.9. ПРОЦЕДУРЫ ХО—КАШЬЯПА
- 5.10. ПРОЦЕДУРЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 5.11. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
- 5.12. ОБОБЩЕНИЯ ДЛЯ СЛУЧАЯ МНОГИХ КЛАССОВ
- 5.13. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ
- Задачи
- Глава 6. ОБУЧЕНИЕ БЕЗ УЧИТЕЛЯ И ГРУППИРОВКА
- 6.2. ПЛОТНОСТЬ СМЕСИ И ИДЕНТИФИЦИРУЕМОСТЬ
- 6.3. ОЦЕНКИ ПО МАКСИМУМУ ПРАВДОПОДОБИЯ
- 6.4. ПРИЛОЖЕНИЕ К СЛУЧАЮ НОРМАЛЬНЫХ СМЕСЕЙ
- 6.5. БАЙЕСОВСКОЕ ОБУЧЕНИЕ БЕЗ УЧИТЕЛЯ
- 6.6. ОПИСАНИЕ ДАННЫХ И ГРУППИРОВКА
- 6.7. МЕРЫ ПОДОБИЯ
- 6.8. ФУНКЦИИ КРИТЕРИЕВ ДЛЯ ГРУППИРОВКИ
- 6.9. ИТЕРАТИВНАЯ ОПТИМИЗАЦИЯ
- 6.10. ИЕРАРХИЧЕСКАЯ ГРУППИРОВКА
- 6.11. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ТЕОРИЮ ГРАФОВ
- 6.12. ПРОБЛЕМА ОБОСНОВАННОСТИ
- 6.13. ПРЕДСТАВЛЕНИЕ ДАННЫХ В ПРОСТРАНСТВЕ МЕНЬШЕЙ РАЗМЕРНОСТИ И МНОГОМЕРНОЕ МАСШТАБИРОВАНИЕ
- 6.14. ГРУППИРОВКА И УМЕНЬШЕНИЕ РАЗМЕРНОСТИ
- 6.15. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ
- Задачи
- Часть II. АНАЛИЗ СЦЕН
- Глава 7. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ И ИХ ПЕРВОНАЧАЛЬНЫЕ УПРОЩЕНИЯ
- 7.2. ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ
- 7.3. ПРОСТРАНСТВЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 7.4. ПРОСТРАНСТВЕННОЕ СГЛАЖИВАНИЕ
- 7.5. СРАВНЕНИЕ С ЭТАЛОНОМ
- 7.6. АНАЛИЗ ОБЛАСТЕЙ
- 7.7. ПРОСЛЕЖИВАНИЕ КОНТУРОВ
- 7.8. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- Задачи
- Глава 8. АНАЛИЗ ПРОСТРАНСТВЕННЫХ ЧАСТОТ
- 8.2. ТЕОРЕМА ОТСЧЕТОВ
- 8.3. СРАВНЕНИЕ С ЭТАЛОНОМ И ТЕОРЕМА О СВЕРТКЕ
- 8.4. ПРОСТРАНСТВЕННАЯ ФИЛЬТРАЦИЯ
- 8.5. СРЕДНЕКВАДРАТИЧНАЯ ОЦЕНКА
- 8.6. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- Задачи
- Глава 9. ОПИСАНИЯ ЛИНИИ И ФОРМЫ
- 9.2. ОПИСАНИЕ ЛИНИИ
- 9.3. ОПИСАНИЕ ФОРМЫ
- 9.3.2. ЛИНЕЙНЫЕ СВОЙСТВА
- 9.3.3. МЕТРИЧЕСКИЕ СВОЙСТВА
- 9.3.4. ОПИСАНИЯ, ОСНОВАННЫЕ НА НЕРЕГУЛЯРНОСТЯХ
- 9.3.5. СКЕЛЕТ ОБЪЕКТА
- 9.3.6. АНАЛИТИЧЕСКИЕ ОПИСАНИЯ ФОРМЫ
- 9.3.7. ИНТЕГРАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ ОПИСАНИЯ
- 9.4. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- Задачи
- Глава 10. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 10.2. МОДЕЛИРОВАНИЕ ПРОЦЕССА СЪЕМКИ ИЗОБРАЖЕНИЯ
- 10.3. ПЕРСПЕКТИВНОЕ ПРЕОБРАЗОВАНИЕ В ОДНОРОДНЫХ КООРДИНАТАХ
- 10.3.2. ОБРАТНОЕ ПЕРСПЕКТИВНОЕ ПРЕОБРАЗОВАНИЕ
- 10.4. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ С ДВУМЯ СИСТЕМАМИ ОТСЧЕТА
- 10.5. ПРИМЕРЫ ПРИМЕНЕНИЯ
- 10.5.2. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ОБЪЕКТА
- 10.5.3. ВЕРТИКАЛЬНЫЕ ЛИНИИ: ПЕРСПЕКТИВНОЕ ИСКАЖЕНИЕ
- 10.6. СТЕРЕОСКОПИЧЕСКОЕ ВОСПРИЯТИЕ
- 10.7. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- Задачи
- Глава 11. ПРОЕКТИВНЫЕ ИНВАРИАНТЫ
- 11.2. СЛОЖНОЕ ОТНОШЕНИЕ
- 11.3. ДВУМЕРНЫЕ ПРОЕКТИВНЫЕ КООРДИНАТЫ
- 11.4. ЛИНИЯ, СОЕДИНЯЮЩАЯ ОБЪЕКТИВЫ
- 11.5. АППРОКСИМАЦИЯ ОРТОГОНАЛЬНЫМ ПРОЕКТИРОВАНИЕМ
- 11.6. ВОССТАНОВЛЕНИЕ ОБЪЕКТА
- 11.7. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- Задачи
- Глава 12. МЕТОДЫ СОСТАВЛЕНИЯ И ОБРАБОТКИ ОПИСАНИЙ В АНАЛИЗЕ СЦЕН
- 12.2. ФОРМАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ОПИСАНИЙ
- 12.2.2. ГРАФЫ ОТНОШЕНИЙ
- 12.3. ТРЕХМЕРНЫЕ МОДЕЛИ
- 12.4. АНАЛИЗ МНОГОГРАННИКОВ
- 12.4.2. ОБЪЕДИНЕНИЕ ОБЛАСТЕЙ В ОБЪЕКТЫ
- 12.4.3. МОНОКУЛЯРНОЕ ОПРЕДЕЛЕНИЕ ТРЕХМЕРНОЙ СТРУКТУРЫ
- 12.5. БИБЛИОГРАФИЧЕСКИЕ И ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
Кластерный анализ социальных сетей
Оглавление
Введение
Глава 1. Обзор литературы
.1 Применение кластерного анализа
.2 Особенности кластеризации социальных сетей
.3 Методы распознавания сообществ
.4 Прореживание графа
Выводы по первой главе
Глава 2. Классификация задач, решаемых с помощью кластеризации
.1 Цели и требования
.2 Требования бизнес-задач
Выводы по второй главе
Глава 3. Разработка рекомендаций по выбору метода
кластеризации для выделенных классов задач
.1 Рекомендации по анализу социальных сетей
.2 Современные способы реализации кластерного анализа
Выводы по третьей главе
Глава 4. Практический пример применения кластеризации
.1 Описание проблемы
.2 Входные данные
.3 Анализ данных
.4 Интерпретация результатов
Заключение
Список литературы
Введение
В наше время стремительно развивающихся технологий, растет количество
информации. Вместе с ней не только развиваются возможности старых способов ее
получения, но и появляются новые. Это приводит к накоплению огромного
количества данных, которое необходимо хранить и обрабатывать с целью извлечения
информации. В связи с этим, актуальными стали такие отрасли, как хранение,
обработка и представление данных. В данной работе будет идти речь именно об
обработке, а точнее, об одном из популярных в наше время методе анализа данных,
кластеризации.
Развитие информационных технологий уже упростило коммуникацию между
людьми, и этот процесс не собирается останавливаться. Ежедневно каждый из нас
контактирует с огромным количеством людей, прямо или косвенно. Взаимодействия
между людьми образуют социальную сеть. Термин «социальная сеть» впервые был
введен социологом Джеймсом Барнсом: «социальная сеть — это социальная
структура, состоящая из группы узлов, которыми являются социальные объекты
(люди или организации), и связей между ними (социальных взаимоотношений)». В
настоящее время под этим понятием почти всегда понимается платформа в сети
интернет, хотя алгоритмы, применимые к такого рода сетям не теряют свою
актуальность и при анализе тех, которые не связаны с интернетом. В этом случае
социальная сеть может предоставить довольно большое количество данных о своих
пользователях, что может облегчить процесс кластеризации и повысить его
точность.
Анализ социальных сетей может рассказать многое о характеристиках ее
элементов, а также об их взаимодействии с другими элементами этой сети. Для
кластерного анализа ее необходимо представить в виде графа. Кластеризация графа
социальной сети может быть использована различными компаниями для определения
кластеров клиентов и их характеристик для более таргетированного предоставления
услуг или продажи товаров. Это один из самых эффективных способов получения
информации о клиентах, требующий только определенной вычислительной мощности и
относительно малого количества времени. Для проведения кластерного анализа
нужен также грамотный отбор входных данных, имеющих смысл. Когда речь заходит о
кластеризации именно социальной сети, в набор этих данных обязательно
включаются связи между ее объектами (узлами). На выходе получается информация о
кластерах клиентов, обладающих схожими характеристиками и сравнительно более
тесными связями между объектами, которая может быть использована компанией в
дальнейшем.
Но все вышесказанное уже не ново, так как данная тема была уже довольно
глубоко изучена, несмотря на ее относительно недавний рост популярности. В
данный момент кластерный анализ графов уже знаком многим, и время от времени он
успешно применяется в различных компаниях. Проблема состоит в том, что для
успешного проведения анализа необходимы специалисты, имеющие опыт в этой сфере,
и пока спрос на них значительно превышает предложение. Поэтому, в данный
момент, а, тем более, в дальнейшем, будет пользоваться спросом система,
позволяющая проводить кластерный анализ социальных сетей без глубокого владения
математическим аппаратом. Данная система должна быть основана на выделении
задач/проблем, которые возникают в процессе работы в основные группы и
предлагать оптимальный способ анализа. Именно это и будет сделано в данной
работе.
Объектом данной работы являются социальные сети.
Предметом исследования является применение кластерного анализа социальных
сетей.
Цель работы состоит в том, чтобы выделить основные группы задач в
бизнесе, для решения которых необходима кластеризация, и выделить наиболее
эффективные для них алгоритмы или группы алгоритмов кластерного анализа.
Для достижения цели необходимо будет выполнить следующие задачи:
) провести обзор основных методов кластеризации социальных сетей
) классифицировать бизнес-задачи, решаемые с помощью кластеризации
социальных сетей
) найти наиболее эффективные методы кластерного анализа для
выделенных видов бизнес-задач
) проверить классификацию на реальной задаче
Структура данной работы такова: сначала такой метод анализа, как
кластеризация будет рассмотрен подробнее, с приведением примеров и оценкой их
эффективности, затем будут классифицированы задачи, основанные на выделении
кластеров в социальных сетях, будут выведены рекомендации по использованию
исследованных алгоритмов применительно к выделенным группам задач, а также,
одна из этих рекомендаций будет подтверждена с помощью реально возникшей задачи
из бизнеса.
Расшифровка
терминов
Кластеризация — задача разбиения совокупности элементов на группы,
элементы которых больше похожи и теснее связаны с элементами, принадлежащими
этой группе, чем к элементам других групп. Данные группы называются кластерами.
Алгоритмы кластеризации используют не всем понятную терминологию, которые
требуют объяснения. Ниже приведены некоторые понятия, обязательные для
понимания алгоритмов, использованных в данной работе.
Промежуточность — количество наикратчайших путей между вершинами узлов,
проходящих через данное ребро, при наличии нескольких наикратчайших путей,
ребрам присваивается одинаковая степень промежуточности.
Проведенная кластеризация не будет полностью точна, некоторые элементы
могут быть включены в кластеры, в которых они не должны находиться. И несмотря
на то, что это иногда видно при грамотной визуализации результатов анализа,
необходим способ, позволяющий определять точность кластеризации. Пожалуй, самой
популярной мерой точности кластеризации является модулярность графа. Она была
предложена Гирваном и Ньюманом в ходе разработки метода кластеризации. Формула
представлена ниже:
где A — Матрица смежности графа, Aij — элемент матрицы в строке I, столбце j, di — степень i вершины графа, Ci — сообщество вершины, m —
общее количество ребер в графе. δ(Ci, Cj) — дельта-функция: равна единице, если
Ci = Cj, иначе нулю.
Мера Жаккарда — мера сходства, в кластеризации используется для
определения схожести вершин графа:
где Adj(i) — множество вершин, являющихся соседями вершине i.
Также, в работе будет встречаться такой термин, как центр масс кластера.
В данном контексте он означает точку с координатами, равными средним
координатам всех элементов кластера.
Медоид — элемент, минимально отличающийся от всех остальных элементов
множества (в данном случае кластера). Используется, когда невозможно, либо не
требуется рассчитывать среднее значение всех элементов.
Глава 1.
Обзор литературы
1.1
Применение кластерного анализа
Хотя данная работа посвящена применению кластеризации как метода анализа
данных, для понимания ее потенциала и тех возможностей, которые она
предоставляет, необходимо рассмотреть способы ее применения в различных сферах
жизни общества.
Широкое применение кластерный анализ нашел в биологии. До появления
возможности выделять группы элементов с заранее неизвестными характеристиками,
биология не могла ответить на вопросы, связанные с исследованием характеристик
и взаимодействия большого количества элементов какого-либо множества. Теперь
же, когда с помощью кластеризации, они могут за относительно короткое время
обрабатывать огромное количество параметров, стало появляться все больше исследований
генов, нейронов и клеток, а также их взаимосвязи с функционированием всего
организма. Например, одна из работ [20] посвящена выявлению паттернов реакций
генов с помощью кластерного анализа клеточных массивов опухоли и стенок прямой
кишки. В результате анализа были получены кластеры генов с различной реакцией
на опухоль, а также были найдены те из них, которые увеличивают вероятность
заболевания данным недугом. В другой статье [21], относящейся к области
постгеномных исследований, рассматривается влияние определенных молекул на
клетки организма, в изолированной среде и окруженных другими клетками. Это
позволяет несколько по-другому взглянуть на биологию и, в отдельности,
патологии организмов, с помощью более тщательного понимания взаимодействия системы
клеток на различные молекулы. Еще в одной работе [22] собраны исследования
мозга с помощью кластеризации. Примечательно то, что мозг в таких исследованиях
как правило представляется в виде сети, или графа, т.к. исследуется реакция
всего мозга на раздражители, а следовательно, особое значение имеют связи между
нейронами.
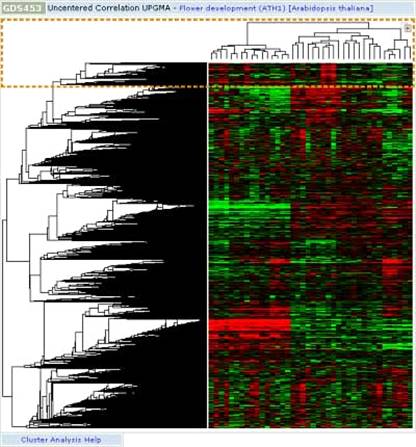
Рис. 1.1. Результаты кластеризации генов по вычислительной активности в
виде дендрограммы
Социология — еще одна наука, значительно раздвинувшая границы своих
возможностей с помощью кластеризации. Суть работы социологов — исследование
взаимодействия индивидов в обществе, отслеживание их реакции на различные
события и т.д. До того, как появилась возможность с помощью кластеризации
отслеживать неочевидные влияния событий и взаимодействий людей между собой,
процесс выделения взаимосвязи имел более низкую точность из-за невозможности
изучить многомиллионные сети индивидов, и поэтому требовал подтверждения
временем. Так как анализ общества немыслим без анализа взаимодействий его
членов, для социологов особенно актуальна кластеризация социальных сетей, или
графов. Например, в одной из работ [23], исследуется теория о том, что
межличностные отношения между членами общества ведут к формированию клик,
подграфов, в которых любые две вершины соединены между собой, а также к
выстраиванию социальной иерархии, основанной на популярности. В статье об
исследовании влияния новостей о самоубийствах на частоту подростковых суицидов
[24] также применяется кластерный анализ. В результате анализа данных о случаях
самоубийств в течение недели после выпусков новостей с сюжетами о суицидах,
исследователи пришли к выводу о том, что среди подростков процент самоубийств
после данных новостей вырастает гораздо больше, чем у взрослых, что может быть
вызвано их желанием к подражанию. Кластерный анализ графов применялся также и в
исследовании явных и неявных пересечений сообществ [25], которое в результате
выделило потребность в непрерывном потоке данных для анализа неявных
пересечений, и дискретных данных для анализа явных.
Пожалуй, больше всего с началом использования кластеризации приобрел
маркетинг. В этой сфере с ее помощью решаются разного рода задачи, например, с
помощью выделения кластеров клиентов с похожим поведением на рынке, становится
возможным персонализировать предложения товаров и/или услуг фирмы ее
покупателям. Кроме того, почти каждая компания работает с определенными
клиентскими сегментами, чьи характеристики, также могут быть исследованы с
помощью кластеризации. Это позволяет определить подход компании по работе с
каждым клиентом, основываясь на том, к какому сегменту он принадлежит. Данная
возможность особенно полезна, т.к. практически невозможно получить всю
необходимую информацию по всем клиентам, а при исследовании большого массива
данных о клиентах, можно примерно понять, какими характеристиками обладает
среднестатистический покупатель, принадлежащий к определенному сегменту, и на
основе этих данных причислять новых клиентов к правильным сегментам, имея
доступ лишь к небольшому количеству информации о нем. Перед фирмами часто стоит
проблема экспансии на другие рынки, или же просто выбора рынка для запуска
продукта. Для этого прекрасно подходит кластерный анализ, т.к. с помощью него
можно понять реакцию потребителей на том или ином рынке на выход нового
продукта, и таким образом, учесть все ошибки и правильные решения.
1.2 Особенности кластеризации социальных сетей
На первый взгляд, кластеризация социальных сетей гораздо сложнее, чем
кластеризация набора несвязанных элементов. Необходимо понять, так ли это.
Социальные сети, как правило, представляются в виде графов. Они могут
быть ориентированными (имеет значение направление связи), а также взвешенными
(каждой связи присваивается свой вес). Таким образом, для анализа социальных
сетей можно применять методы кластеризации, основанные на теории графов.
Однако, если граф нормализовать, т.е. избавиться от его ориентированности с
помощью добавления весов ребер к уже существующим весам, и представить в виде
матрицы, то получится набор данных, ничем не отличающийся от набора
характеристик несвязанных элементов. В таком случае, связь вершины с другой
становится просто ее дополнительной характеристикой, и возможно применять
обычные методы кластеризации, не основанные на теории графов.
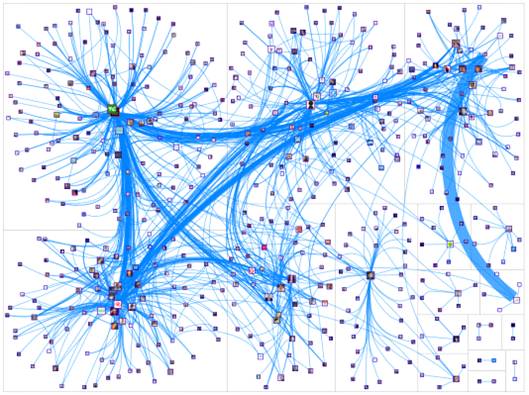
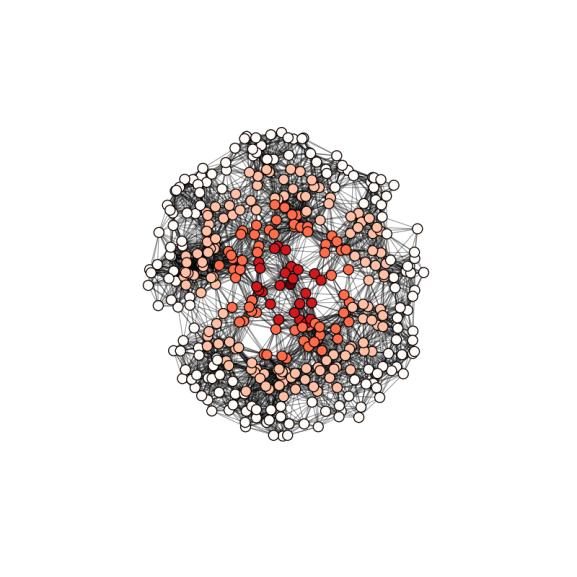
Рис. 1.2. Пример графа социальной сети
Для алгоритмов кластеризации важны качество и тип данных, которые они
обрабатывают. Как правило, используются реляционные базы, хранящие данные в
виде таблиц. Они довольно просты в понимании и универсальны. Но для отображения
связей между записями больше подходят графовые базы данных, являющиеся одним из
NoSQL-подходов к хранению данных. Они не
только открывают возможность к применению стандартных графовых методов, но и
позволяют достичь больше гибкости при хранении не похожих друг на друга
объектов. Некоторые графовые базы данных показали почти десятикратное
превосходство в скорости над реляционными при выполнении таких операций, как
поиск соседей с максимальной степенью и поиск пересечения сообществ соседей
двух вершин.
1.3 Методы распознавания сообществ
Алгоритмы
квадратичной ошибки.
Группа методов квадратичной ошибки основана на минимизации функции расстояния
между элементами кластера и его центром при разбиении объектов на группы. Эта
функция также часто называется «ошибкой». Существует обширное количество мер
расстояний, ниже приведены самые популярные из них:
1) Евклидово расстояние
Данная мера является расстоянием между объектами на геометрической
плоскости:
Часто, когда необходимо увеличить значение большого расстояния между
объектами, используется квадрат Евклидова расстояния.
) Манхэттэнское расстояние (расстояние городских кварталов)
Величина данного расстояния между двумя точками определяется как сумма
модулей разностей их координат:
При применении данной формулы при определении ошибки снижается влияние
отдельных выбросов, т.к. они, в отличие от случая применения Евклидова
расстояния, не возводятся в квадрат.
) Расстояние Чебышева
Это расстояние равно максимальной разнице между одной из двух пар
координат точек:
Пожалуй, самым популярным алгоритмом кластеризации является k-means. Он состоит из следующих шагов:
) Находится количество кластеров k
) Случайным образом выбираются k точек, являющихся центрами будущих кластеров
) Каждая точка присваивается кластеру с ближайшим центром, и
находится расстояние от этой точки до центра кластера
) Для каждого кластера находится новый центр, являющийся «центром
масс» точек этого кластера
) Начиная с п.3 процесс повторяется, пока не будет достигнуто
необходимое разбиение. Чаще всего алгоритм останавливается, когда суммарная
ошибка в каждом кластере снизилась на незначимую величину
Другим примером алгоритмов квадратичной ошибки является k-medoids. Он полностью повторяет алгоритм k-means с тем отличием, что центр находится не как среднее, а
как медоид всех точек.
Также, существует алгоритм FOREL,
действующий по принципу, схожему с k-means. Последовательность его действий
такова:
) Выбирается случайный элемент из выборки
) Выделяем все элементы выборки, находящиеся на расстоянии
меньшем, чем R от первоначально выбранного элемента
) Вычисляется новый центр кластера путем нахождения центра масс
) Шаги 2 и 3 повторяются, пока центр кластера не сдвинется на
незначительную величину
) Элементы найденного кластера удаляются
) Алгоритм повторяется до тех пор, пока каждый элемент не будет
присвоен какому-либо кластеру
Алгоритмы данного вида относительно просты и универсальны, однако, перед
их применением необходимо знать количество кластеров, для чего приходится
прибегать к различным алгоритмам, решающим данную проблему.
Иерархические алгоритмы. Следующий вид алгоритмов, иерархические алгоритмы,
имеет два подвида: восходящие и нисходящие. Изначально восходящие алгоритмы
присваивают каждый элемент отдельному кластеру, таким образом, на первом шаге
количество кластеров равно количеству элементов. Затем данные кластеры
итеративно объединяются до получения устраивающего разбиения. Менее популярные
нисходящие алгоритмы сначала помещают все элементы в один кластер, а затем
разбивают его итеративно не части. На выходе получается дерево разбиений.
Рис. 1.3. Дерево разбиений.
Но объединение или разъединение кластеров проходит не случайным образом.
Очевидно, стоит объединять кластеры, находящиеся ближе друг к другу, чем
остальные. Вопрос лишь состоит в том, как определять расстояние между ними.
Существует ряд методов, позволяющих находить его, ниже приведены некоторые из
них:
) Метод одиночной связи
При данном методе расстояние между кластерами приравнивается расстоянию
между ближайшими их вершинами.
) Метод полной связи
Расстояние между кластерами равно максимальному расстоянию между точками
кластеров. Данный метод непригоден при объединении кластеров, имеющих
продолговатую форму.
) Метод средней связи
Расстояние между кластерами равно среднему расстояний между всеми парами
точек. Различают взвешенный и невзвешенный методы средней связи, в зависимости
от размера кластеров, если они сильно отличаются — применяется весовой
коэффициент, находящийся из размера кластера.
) Центроидный метод
Этот метод основывается на вычислении расстояния между центрами масс
кластеров, также существуют взвешенный и невзвешенный виды этого метода.
) Метод Уорда
Данный метод рассчитывает сумму расстояний между элементами кластера и
его центром до и после присоединения к нему другого кластера и объединяет его с
тем, который обеспечивает минимальный прирост этой ошибки, чем очень похож на
методы квадратичной ошибки.
Алгоритмы иерархической кластеризации позволяют получить разные «уровни»
разбиений, что даст возможность выбрать оптимальное разбиение. Однако, велик
риск выполнения излишних операций, что может быть критично в условиях
ограниченности времени.
Методы,
основанные на теории графов. Данная группа алгоритмов анализирует объекты, представленные
в виде графа, поэтому появляется дополнительная возможность учитывать не только
характеристики объектов, но и связи между ними.
С появлением ребер открывается возможность путем их последовательного
удаления получать несвязанные друг с другом ребрами кластеры. Выбирать ребра
для удаления можно разными способами. Зачастую из графа удаляются все ребра, имеющие
длину больше заданного исследователем значения. Проблема данного подхода
состоит в том, чтобы выбрать это оптимальное значение. Для этого необходимо
найти распределение длин ребер, и найти пиковые значения. Какие-то из этих
значений будут равны средней длине ребер внутри кластеров, какие-то — средней
длине ребер между ними.
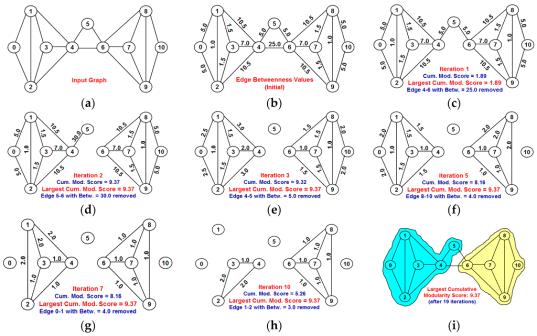
Другой оптимальный способ предложили М. Гирман и М. Ньюман [16]. Они
ввели новый параметр, присущий всем ребрам — меру промежуточности. Она
представляет собой количество наикратчайших путей между всеми вершинами графа,
проходящими между ними. Таким образом, ребра, имеющие наибольшие значения
величины промежуточности, с большей долей вероятности лежат между кластерами,
т.к. являются «мостом-соединителем» элементов этих кластеров. Следуя алгоритму
Гирвана-Ньюмана, из графа удаляются эти ребра до тех пор, пока не уйдут все эти
мосты между кластерами. В итоге получатся группы, элементы которых связаны
между собой внутри них, но не связаны с элементами других групп.
Рис. 1.4. Алгоритм Гирвана-Ньюмана
1.4 Прореживание графа
При анализе графов сетей, имеющих в своем составе миллионы, а то и
миллиарды элементов, проблема скорости работы алгоритма, становится все более
актуальной, тем более, при применении в бизнесе, где важна скорость принятия
решений. Так как алгоритм обрабатывает граф социальной сети, будет разумным
подготовить его к анализу, уменьшив его размер. Это можно сделать с помощью так
называемого локального прореживания (local graph sparsification, или l-spar). Он
позволяет избавиться от ненужных ребер и при этом сохранить, а иногда и лучше
выделить структуру графа. Количество его вершин при этом неизменно. Идея
прореживания состоит в том, чтобы оставить только те ребра, которые с большей долей
вероятности соединяют вершины одного сообщества (кластера). Для этого
используется упомянутая выше мера Жаккарда. Но если из графа удалить все ребра,
мера Жаккарда которых будет ниже определенного значения, можно потерять связи в
кластерах с более низкой полностью, поэтому необходимо задавать не значение
меры Жаккарда, а количество или долю ребер, исходящих из одной вершины и
подлежащих удалению.
Выводы по
первой главе
В данной главе был приведен результат обзора литературы, заключающийся в
примерах применения кластерного анализа в современном мире. Кроме того, были
объяснены особенности, отличающие кластеризацию социальных сетей от
кластеризации массива элементов, не связанных между собой ничем, кроме
характеристик. Была приведена классификация алгоритмов кластеризации социальных
сетей, с объяснением принципов действия каждого из их видов, также для каждого
из них были приведены примеры алгоритмов, с кратким объяснением принципа их
действия. В конце был рассмотрен алгоритм, позволяющий оптимизировать граф
социальной сети перед его кластеризацией путем удаления ребер с низким
значением меры Жаккарда.
Глава 2.
Классификация задач, решаемых с помощью кластеризации
2.1 Цели и
требования
Данная глава посвящена разработке классификации задач, решаемых с помощью
применения кластерного анализа социальных сетей. При ее создании преследовалась
цель создания групп, включающих в себя все возможные задачи.
При классификации необходимо помнить, что множество проблем, решаемых с
помощью кластеризации, настолько огромно, что правильнее будет исходить из
целей, преследуемых исследователями при обращении к алгоритмам кластерного
анализа. Создание классификации преследует цель упрощения выбора алгоритма в
случае возникновения проблемы. Кроме того, следует понимать, что под социальной
сетью в данной работе имеется в виду не интернет-платформа для обмена
информацией, а любая совокупность людей, связанных между собой какими-либо
методами взаимодействия.
Соответственно, исходя из данной цели, к классификации возникают
следующие требования:
) она должна полностью охватывать виды задач, решаемых с помощью
алгоритмов кластеризации
) необходимо учесть возможный контекст задач
) данная классификация должна иметь возможность быть разложенной
на подгруппы задач
2.2
Требования бизнес-задач
Понимание того, каким методом лучше всего решить имеющуюся проблему,
основывается на том, какие требования предъявляются к методам решения этих
проблем, а также, какие входные данные смогут использовать алгоритмы.
Как правило, задачи компании разделяются на следующие группы:
) Неоднородность имеющихся данных.
Многие компании, получая первоначальный набор данных, которые они прежде
не обрабатывали, сталкиваются с проблемой их тщательного анализа. Причем,
сложность состоит не только в размере этих данных, но и в определении степени
их однородности. Метод анализа, примененный ко всей совокупности полученных
данных, может показать в корне неверную информацию.
Чтобы этого избежать, перед анализом данных необходимо понять их
структуру. Сделать это можно с помощью кластеризации. Разделив все данные по
кластерам, будет легче понять, из каких групп они состоят, чтобы в дальнейшем
анализировать каждую из этих групп в отдельности и таким образом увеличить
точность принимаемых решений.
В процесс решения данной задачи большое количество кластеров будет
вносить лишь излишнюю сложность в дальнейший их анализ, поэтому необходимо
выделять небольшое количество кластеров, обычно до 5.
) Оптимизация процесса дальнейшей обработки данных.
Зачастую, когда компания применяет сложные методы анализа, задействующие
большие вычислительные мощности, либо, когда она вынуждена постоянно
присваивать новые объекты уже имеющимся кластерам (например, определять сегмент
новых клиентов для предложения им релевантных товаров и услуг), не имеет смысла
анализировать всю совокупность данных. В таком случае, необходимо сократить их
количество, повысив таким образом скорость получения результатов. Это также
может быть сделано с помощью кластеризации. После получения набора кластеров, в
каждом из них находится наиболее типичный объект, характеризующий весь кластер,
и дальнейший анализ проводится уже не со всеми группами объектов, а только лишь
с несколькими, наиболее типичными из них. Необходимо также учесть, что в
небольших кластерах найденное среднее значение всех параметров их объектов
может сильно отличаться от того среднего значения, которое будет получено при
увеличении размеров кластеров. В таком случае, придется либо разработать
индивидуальный подход к анализу малых кластеров, а также постоянно отслеживать
их состав, для точного определения наиболее типичного представителя.
Из-за того, что результаты кластеризации в этом случае будут
анализироваться в дальнейшем, нужно добиться максимальной схожести объектов
внутри них.
) Необходимо регулярное подтверждение состава кластеров.
Как уже говорилось в предыдущем пункте, проблема проверки состава
имеющихся кластеров всплывает довольно часто. Действительно, компании
необходимо понимать, актуально ли существующее разбиение на кластеры. Для этого
нужно постоянно анализировать поступающие данные и выделять те элементы,
которые нельзя отнести ни к одному из имеющихся кластеров, а также отслеживать
частое появление элементов, сильно отличающихся от средних значений
присваиваемых им кластеров. При возникновении данной проблемы необходимо
сделать акцент на отличии элементов друг от друга, и увеличить вес расстояния
между ними.
К сожалению, приведенная выше классификация задач не является полной. Это
связано с наличием дополнительных требований к выполнению кластеризации. Каждый
алгоритм может быть оценен с помощью следующих параметров: скорость, точность,
надежность и интерпретируемость.
С ростом популярности кластеризация стала использоваться повсеместно для
решения большого количества задач. Почти все они задают алгоритмам ограничение
по времени получения результатов. С дальнейшим развитием и ростом популярности
кластерного анализа, эти требования будут становиться только жестче из-за
растущей конкуренции между компаниями и увеличивающейся важности таких
параметров, как скорость получения информации и принятия решений. Эти параметры
напрямую зависят от того, насколько быстро алгоритм кластеризации сможет
обработать имеющиеся данные. Скорость работы алгоритма зависит от трех
составляющих: мощности ЭВМ, силами которой обрабатывается алгоритм, качества
входных данных, а также сложности и избыточности операций, составляющих
алгоритм. Величина ресурсов ЭВМ, как правило, может быть увеличена либо
количественно, что подразумевает собой дополнительные траты, часто очень
большие, либо же качественно, с помощью оптимизации процесса использования этих
ресурсов.
Следующий, не менее важный параметр каждого алгоритма — точность. Наряду
со скоростью принимаемых решений, также важна и их точность, ведь решение,
принятое быстрее других, но с меньшей точностью, способно принести не только
меньшие прибыли, но и колоссальные убытки. Этот параметр, так же, как и
скорость, зависит от качества данных, а также от сложности и проработанности
алгоритма. Под проработанностью в данном случае понимается наличие в алгоритме
неочевидных необработанных исключений, которые могут выдать ошибку в результате
применения. Как правило, чем алгоритм популярней, тем меньше вероятность того,
что он выдаст ошибку. Под качеством же данных понимается не только отсутствие
пропусков, несоответствий типов, но и то, насколько легко алгоритму будет
определить элементы в кластеры. Для избегания попадания объектов в чужие
кластеры, зачастую необходимо провести предварительную обработку данных, в ходе
которой упрощать данные, например, выделять ключевые свойства объектов, по
которым можно почти однозначно определить их принадлежность кластерам.
Не менее важна и надежность алгоритма. Под надежностью понимается
способность алгоритма анализировать пропущенные или зашумленные данные, а также
его возможности по работе в условиях нарушения каких-либо предпосылок.
Еще одна характеристика, присущая любому алгоритму — интерпретируемость.
Она зависит от того, что получается в результате обработки алгоритма и влияет
на необходимость дальнейшей обработки. Возможность отследить промежуточные
результаты работы алгоритма становится все более востребованной, для
своевременного отслеживания ошибок.
К сожалению, почти невозможно одновременно улучшить все вышеперечисленные
параметры, поэтому, в зависимости от ситуации, приходится идти на компромисс и
выбирать более быстрые и менее точные алгоритмы в условиях нехватки времени,
либо увеличивать точность и интерпретируемость алгоритмов за счет их скорости.
кластеризация
социальный сеть прореживание
Выводы по второй главе
Результатом 2 главы является классификация задач, составленная на основе
основных целей, преследуемых при применении кластеризации, а также контекста
появления этих задач и дополнительных требований к ним.
Проверим соответствие классификации заданным изначально требованиям:
) Выделенные классы с высокой долей вероятности покрывают все
потенциальные бизнес-задачи из-за высокоуровневой группировки целей
кластеризации.
) Учтен контекст задач, а именно — возможные дополнительные
требования к алгоритмам, влияющие на их выбор.
) Вследствие обширности классификации возможно дальнейшее
разбиение в зависимости от дополнительных требований к алгоритмам, а также
отрасли компании и подразделения, в которых возникают эти задачи.
Глава 3.
Разработка рекомендаций по выбору метода кластеризации для выделенных классов
задач
3.1
Рекомендации по анализу социальных сетей
Ниже будут даны рекомендации по выбору алгоритмов кластеризации для
каждого из случаев, когда необходима кластеризация.
) Неоднородность имеющихся данных.
Данная группа задач характерна тем, что о данных известно немногое.
Непонятна структура данных, неизвестно, в какие группы объединяются элементы
графов, а также, насколько эти данные полны, т.е. какая доля данных в среднем
отсутствует у каждого элемента. Особенностью требований к данным задачам также
является наличие небольшого количества кластеров, которых будет достаточно для
понимания дальнейшей структуры графа и его элементов. Задачи этого класса можно
эффективно решать с помощью методов квадратической ошибки. Например, для этого
хорошо подойдет алгоритм k-means, доступный к внедрению для широкого
класса специалистов по причине своей простоты и доступности на языке Python. Для этого лишь необходимо
установить один из пакетов, например, scikit-learn. Если в графе социальной сети нужно
выделить центральный узел, лучше всего подойдет k-medoids, т.к.
данный алгоритм за центр кластера берет только элементы графа, что сэкономит
время на вычисление центрального узла. Кроме того, при наличии вершин в графе,
которые не могут быть точно отнесены вышеприведенными алгоритмами к отдельным
кластерам, либо для мониторинга склонности клиентов менять свой кластер, лучше
всего подойдет c-means. По причине того, что в результате использования
данного алгоритма каждая вершина получает вероятность принадлежности к каждому
кластеру, можно присвоить эту вершину одному из них, на основании малейшего
перевеса в его сторону.
Но так как мы говорим о кластеризации социальных сетей, открыты для
рассмотрения методы, основанные на теории графов. Основная выгода их
использования для решения рассматриваемого класса задач состоит в отсутствии
необходимости задавать количество кластеров, оно будет найдено в процессе
работы алгоритма. Хоть это и сильно не изменит количество кластеров, но может
повлиять на принятие дальнейших решений. При использовании k-means, для экономии времени будет задано, например, 3
кластера, которые в целом действительно легко выделить на общем графе. Но при
дальнейшем увеличении количества вершин в графе, возможно разбиение одного из
существующих кластеров на два и более. Использование методов теории графов дает
шанс избежать этого и получить более точное количество кластеров при сохранении
скорости и точности кластеризации практически на том же уровне. К сожалению,
действие каждого алгоритма должно быть предельно понятно исследователю, в чем
нельзя быть уверенным при применении теории графов в кластеризации. К тому же,
пакеты, необходимые для этого, более специфичны, и могут вызвать проблемы у
исследователей, пытающихся их установить.
) Оптимизация процесса дальнейшей обработки данных.
Алгоритмы, решающие задачи этого типа должны уметь получать несколько
разбиений, т.к. исследователю необходимо решить, насколько крупными должны быть
кластеры. Лучше всего для этого подойдут алгоритмы иерархической кластеризации.
Результатом их применения является дерево разбиений элементов графа, которое
позволит просмотреть несколько вариантов расположения кластеров практически без
траты времени. Основываясь на опыте некоторых исследователей, лучшим критерием
кластеризации является сумма квадратических ошибок, предложенная Уордом. В
таком случае, как правило, получается более визуально понятное разбиение. Стоит
заметить, что чем точнее необходимо определять кластеры в графе, тем меньшее расстояние
между ними должно быть в кластерах, но в тоже время, вырастет риск непопадания
каких-либо вершин в кластеры. Этот недостаток может быть несущественен, когда
необходимо получить небольшие группы элементов с тесными связями между ними, а
все остальные неважны для анализа.
) Необходимо регулярное подтверждение состава кластеров.
Данные задачи характерны жестким набором кластеров, что открывает
возможность использования алгоритмов квадратичной ошибки, главный недостаток
которых (определение числа кластеров), в данном случае пропадает, а,
следовательно, открывается возможность к их применению.
В результате анализа была получена следующая таблица выбора алгоритмов в
зависимости от возникающей задачи:
Таблица 3.1
|
Задача |
Оптимальные алгоритмы |
|
Первичный анализ структуры социальной сети |
Метод минимального покрывающего дерева, метод |
|
Сжатие данных |
Иерархический метод Уорда |
|
Проверка состава кластеров |
k-means, k-medoids, c-means |
3.2
Современные способы реализации кластерного анализа
Выбор
языка. Не менее
важен выбор инструментов, с помощью которых будет реализован алгоритм
кластерного анализа. Они включают в себя язык программирования, среду
разработки и методы визуализации результатов. Ниже будет выбран один их языков
программирования, а также рассмотрены некоторые среды разработки и методы
визуализации.
Кластеризация может быть реализована с помощью различных языков
программирования: C, R, Python и т.д. Для данной работы будет выбран язык Python. Этот выбор сделан неслучайно:
данный язык одновременно прост в освоении (относительно, например, C-языков) и в то же время достаточно
быстр и разнообразен в применении. Python является самым популярным языком для анализа данных в том числе из-за
наличия в свободном доступе огромного количества библиотек, позволяющих
проводить аналитику данных на высшем уровне.
Язык Python почти неразрывно связан с платформой
анализа данных Anaconda. Данная
платформа состоит из интерпретатора языка Python, а также включает в себя около 150 предустановленных
пакетов и более 250 пакетов, готовых к установке. Anaconda включает в себя пакеты, которые
являются основными почти для всех остальных пакетов или библиотек Python.
Среда разработки (или IDE) —
комплекс программного обеспечения, используемого для разработки ПО. Как
правило, они позволяют работать с несколькими языками программирования. Ниже
будут рассмотрены основные IDE,
используемые для написания кода на Python.
1) Jupyter Notebook
Это приложение, позволяющее работать почти с 40 языками, включая
популярные языки анализа данных, такие как Python, R, Julia и Scala. Оно находится в открытом доступе и позволяет
создавать документы и обмениваться ими. Как правило, Jupyter Notebook применяют для анализа данных,
машинного обучения и проверки статистических гипотез и т.д. Его особенностью
является наличие браузерного вида, не требующего установки на локальный
компьютер. Это же свойство, при использовании какой-либо организацией,
позволяет централизованно хранить код и результаты его выполнения.
Рис. 3.1. Домашняя страница Jupyter Notebook
Еще одной особенностью Jupyter Notebook является
возможность просмотра промежуточных результатов выполнения кода. В отличие от
обычных IDE, в Jupyter можно запускать отдельные строчки кода, которые буду
мгновенно выполняться, а результаты запоминаться для дальнейшего кода.
Рис. 3.2. Блочное выполнение кода
2) Eclipse
Эта среда разработки, как и Jupyter Notebook,
находится в открытом доступе. Она позволяет работать со многими языками,
например, с PHP, C/C++, Python и т.д.
Основное преимущество работы с Eclipse — возможность установки большого количества расширений,
включающих в себя как модули языков, так и расширения, позволяющие работать с
базами данных, серверами приложений и т.д.
Рис. 3.3. Eclipse.
3) Spyder
Последняя IDE, описываемая в
данной работе. Данная среда разработки выделяется среди остальных относительно
небольшим весом и легкостью использования. Она была разработана специально для
использования Python, но также поддерживает C/C++ и Fortran.
Рис. 3.4. Среда разработки Spyder.
Методы
визуализации. К
сожалению, возможности языка Python
в представлении графов несколько ограничены, поэтому вариантов визуализации не
так много.
1) Jupyter Notebook
Он имеет встроенные возможности визуализации графов, которых достаточно в
большинстве случаев.
Рис.3.5. Представление графа в Jupyter Notebook
2) NetworkX
Это библиотека языка Python, ползволяющая работать с
визуализацией графов. Она позволяет работать в том числе с ориентированными и
взвешенными графами, с такими их характеристиками, как степени вершин, длины
путей и т.д. Данная библиотека позволяет достичь высокой производительности и
способна обрабатывать графы с несколькими миллионами вершин и десятками
миллионов ребер между ними. Для работы networkX также требуется установленный
Graphviz.
Рис.3.6. Визуализация графа с помощью networkX
Выводы по
третьей главе
В данной главе были выработаны рекомендации по выбору алгоритмов
кластеризации в зависимости от класса возникшей в бизнесе задачи. Они
основывались на характеристиках алгоритмов, рассмотренных в 1 главе. При
написании этих рекомендаций были учтены требования к методам решения проблем,
описанные во 2 главе.
Глава 4.
Практический пример применения кластеризации
4.1
Описание проблемы
Для проверки рекомендаций было решено протестировать их на реальной
задаче из бизнеса, а конкретно, в компании «Альфа-банк». Деятельность банка
очень разносторонняя, поэтому для понимания контекста важно отметить, в каком
подразделении возникла эта задача. В данном случае исследуется задача
исследования характеристик совокупности клиентов, выделенных для проведения
пилотной кампании подразделения вторичных продаж. Ее цель — подтвердить
гипотезу о параметрах имеющихся сегментов клиентов для подтверждения
потенциальной ценности этих клиентов для банка. В случае, если гипотеза
подтвердится, для каждого сегмента будет разработана отдельная стратегия
взаимодействия. Всего сегмента четыре, в зависимости от склонности клиентов к
совершению транзакций и уровня остатков на их счетах. Кроме того, специфика
задачи состоит в связи между клиентами посредством транзакций.
4.2
Входные данные
В ходе решения данной задачи алгоритм будет обрабатывать данные
своеобразной социальной сети, образующей граф, в котором клиенты будут
вершинами, а количество транзакций за последний месяц между ними — ребрами. В
качестве дополнительных параметров также были взяты среднемесячное количество
транзакций за последние полгода, а также среднемесячные остатки на
накопительных, текущих и депозитных счетах также за последние полгода. Ниже,
для понимания, приведена часть таблицы. Количество клиентов в данной таблице —
100 тыс., количество связей между ними — 80 тыс. Данное соотношение количества
ребер и вершин довольно нетипично для графов, однако, в данном случае, это
объясняется тем, что клиенты банка довольно редко делают транзакции друг другу.
Таблица 4.1
|
PIN_EQ |
CN_PURCH_DC |
CN_PURCH_CR |
SS_CUR |
SS_SAVE |
SS_DEP |
|
AAAWXBAB |
68 |
12 |
27495 |
1854 |
0 |
|
AAAWYMAE |
15 |
36 |
267391 |
127849 |
2000000 |
|
AAAWYOCD |
0 |
4 |
3050 |
0 |
0 |
|
AAAWZGGX |
12 |
33504 |
25049 |
253412 |
|
|
AAAWZPLR |
34 |
0 |
7585 |
3403 |
403242 |
4.3 Анализ
данных
Для начала, необходимо понять, к какому из выделенных классов задач
принадлежит данная. Эта задача характеризуется тем, что нам известно количество
кластеров, а также есть примерная гипотеза о том, с какими средними параметрами
должны получиться кластеры. Это позволяет отнести данную задачу к 3 классу, а
именно, к подтверждению состава кластеров. Проверим оправданность рекомендации,
согласно которой, для решения данной задачи оптимальнее всего использовать
метод k-means.
Метод k-means не умеет работать с ребрами графа, поэтому необходимо
привести их к табличному виду. Так как ребра графа были построены на основе
среднего количества транзакций клиентам из отбора, для каждого клиента добавим
в таблицу ID тех, с которым он связан. Результат
данной операции виден в таблице 4.2.
Таблица 4.2
|
PIN_EQ |
CN_PURCH_DC |
CN_PURCH_CR |
SS_CUR |
SS_SAVE |
SS_DEP |
PIN_EQ_TO |
TRAN_CNT |
|
AAAWXBAB |
68 |
12 |
27495 |
1854 |
0 |
AAJDKLSM |
6 |
|
AAAWXBAB |
68 |
12 |
27495 |
1854 |
0 |
AAJASASM |
3 |
|
AAAWYMAE |
15 |
36 |
267391 |
127849 |
2000000 |
ABDSHDJD |
7 |
|
AAAWYOCD |
0 |
4 |
3050 |
0 |
0 |
AADSKDMS |
1 |
Однако, алгоритм все еще не сможет обработать ID клиентов-получателей транзакций, поэтому, необходимо
избавиться от этого поля. Это было сделано посредством агрегации среднего
количества транзакций каждому из клиентов в отборе. В итоге, получилась таблица
4.3., в которой поле TRAN_CNT отображает количество транзакций
клиентам из отбора за последний месяц.
Таблица 4.3
|
PIN_EQ |
CN_PURCH_DC |
CN_PURCH_CR |
SS_CUR |
SS_SAVE |
SS_DEP |
TRAN_CNT |
|
AAAWXBAB |
68 |
12 |
27495 |
1854 |
0 |
9 |
|
AAAWYMAE |
36 |
267391 |
127849 |
2000000 |
7 |
|
|
AAAWYOCD |
0 |
4 |
3050 |
0 |
0 |
1 |
|
AAAWZGGX |
7 |
12 |
33504 |
25049 |
253412 |
2 |
|
AAAWZPLR |
34 |
0 |
7585 |
3403 |
403242 |
1 |
Итак, данные готовы для анализа, теперь необходимо определиться с выбором
среды разработки. В данном случае была использована Jupyter Notebook по причине того, что данное ПО уже
используется в этом банке, поэтому не требуется согласовывать установку
дополнительного оборудования.
Сначала, для увеличения скорости работы алгоритма, данные были
сгруппированы:
Рис. 4.1. Группировка полей
Данное действие допустимо только в случае, если нам неважен тип
транзакций и на каком счете лежат средства.
Получилось так, что элементы сильно разрознены, поэтому модель не может
правильно учесть огромные расстояния между ними. Для этого введем еще несколько
столбцов, которые будут равны прологарифмированным прежним столбцам с числами:
Рис. 4.2. Создание новых столбцов
Теперь необходимо выполнить саму кластеризацию. На текущем этапе данные,
несмотря на их логарифмирование, принадлежат довольно большому диапазону,
поэтому надо их дополнительно нормализовать:
Рис. 4.3. Нормализация данных
Рис. 4.4. Реализация алгоритма k-means
Итак, алгоритм был применен, как видно из (рис. ), было взято 4 кластера,
максимальное количество итераций смены центра масс каждого кластера было равно
300. Процесс реализации занял примерно 5 секунд, учитывая время инициализации
запроса к базе данных. При отсутствии высокой нагрузки на сервера баз данных
результаты могли быть получены быстрее примерно на 1 секунду.
В результате применения алгоритма каждому клиенту был присвоен один из
четырех кластеров. Теперь необходимо понять, подтвердилась ли изначальная
гипотеза, и насколько характеристики кластеров в данном отборе отличаются от
средних характеристик этих кластеров по всей клиентской базе.
Для лучшего понимания получившихся результатов, можно визуально показать
разбиение элементов по кластерам. Так как распределение клиентов по плоскости
равномерное и довольно плотное, вывод всего графа не будет иметь смысл из-за
его нечитабельности. Поэтому, было принято решение о выводе средних значений
параметров элементов кластеров. Ниже приведен код, реализующий вывод средних
значений по каждому параметру в четырех кластерах.
Рис. 4.5. Вывод центров кластеров
Графики ниже отображают значения переменных в центрах кластеров. Чем
дальше значения друг от друга, тем лучше была проведена кластеризация. В данном
случае мы видим, что для каждого параметра два центра кластера имеют почти
одинаковые значения (нельзя забывать, что данные значения нормализованы,
поэтому кажущиеся небольшие различия двух других кластеров на самом деле
гораздо больше).
Рис. 4.6. Центры кластеров
Также, ниже приведены результаты кластеризации в табличном виде.
Таблица 4.4
|
CLUSTER |
CN_PURCH |
CN_PURCH_CR |
CN_PURCH_DC |
SS |
TRAN_CNT |
|
1 |
55,0 |
13,0 |
42,0 |
33626,0 |
5,0 |
|
2 |
5,0 |
2,0 |
3,0 |
104731,0 |
1,0 |
|
3 |
22,0 |
21,0 |
10437,0 |
9,0 |
|
|
4 |
2,0 |
1,0 |
1,0 |
0,0 |
0,0 |
4.4
Интерпретация результатов
Выше приведенные результаты свидетельствуют о том, что изначальная
гипотеза о параметрах кластеров подтвердилась: один из кластеров объединяет
клиентов, держащих небольшое количество остатков на счетах, но активно
пользуясь картами. Этот сегмент прибылен для банка, поэтому с ним будет вестись
работа по удержанию и предложению более выгодных условий, по которым он сможет
использовать карты и счета с максимальной выгодой для себя. Во втором кластере
находятся клиенты, почти не делающие транзакций, но хранящие большие остатки на
счетах. Необходимо отметить, что в рассмотрение включены депозитные счета,
суммы на которых преобладают у клиентов данного сегмента. Скорее всего, они
используют данный банк только в качестве хранителя денег, а делают транзакции и
получают зарплату в другом банке. Необходимо добиться того, чтобы эти
транзакции клиент делал в нашем банке. Поэтому данный тип клиентов должен
обрабатываться банком сильнее, им будут предлагаться карты, которые позволят им
открыть счета для ежедневного пользования. Третий кластер включает зарплатных
клиентов данного банка, выводящих свои средства в другие банки, и оставляющие
небольшие суммы на счетах для оплаты мелких операций. Данным клиентам также
будут делаться предложения карт, но с менее выгодными условиями, т.к. они несут
больше рисков для банка. Последний сегмент объединяет самых «мертвых» клиентов:
они не хранят деньги в банке, и не почти не делают транзакции. С данными
клиентами будет выстроена стратегия коммуникации, направленная на
предотвращение оттока, заключающаяся в предложении акционных продуктов, которые
сохранят свои параметры в случае активного использования счетов и карт
клиентом.
Таким образом, мы действительно убедились, что k-means хорошо
подходит для решения задачи проверки параметров кластеров, следовательно,
гипотеза подтвердилась.
Заключение
Результаты
Результатом данной работы является выполнение задач, поставленных в ее
начале, а именно:
) Был проведен обзор литературы, в ходе которого были изучены
основные виды алгоритмов кластеризации: алгоритмы квадратичной ошибки, иерархические
и графовые алгоритмы. Кроме того, был рассмотрен механизм прореживания графа,
позволяющий повысить эффективность кластеризации.
) Вся группа задач, возникающих в бизнесе, была разбита на
следующие группы: проблемы, связанные с неоднородностью данных, задачи
оптимизации обработки данных, а также задачи, требующие регулярного
подтверждения состава кластеров.
) Для выделенных классов бизнес-проблем были выработаны
рекомендации по выбору оптимальных алгоритмов кластеризации на основе их
параметров.
) Одна из рекомендаций была протестирована на реальной задаче и
была таким образом подтверждена.
Дальнейшие
исследования
В дальнейшем будет необходимо многократно подтвердить рекомендации,
выведенные в этой работе, а также, постоянно проверять новые алгоритмы
кластеризации на предмет эффективности в применении к выделенным классам задач.
Выводы по
результатам
По результатам работы можно сделать следующие выводы:
) Все задачи разделяются только на большие группы, практически
невозможно провести точную классификацию, которая будет работать в 100%
случаев.
) На выбор оптимального алгоритма сильно влияет контекст задачи,
включающий в себя возможность использования дополнительного ПО, возможность
визуализации результатов анализа, потребность в скорости, точности, надежности,
а также интерпретируемости алгоритмов.
) Методы работы с графами на языке Python находятся на начальном уровне развития и имеют
высокий потенциал стать основным способом анализа социальных сетей.
) Анализ социальных сетей имеет высокий потенциал ввиду ориентации
всего мира на коммуникацию и связь между людьми. Кроме того, при дальнейшем
развитии алгоритмов, способных качественно анализировать ориентированные и
взвешенные связи между вершинами графа, существенно вырастут возможности по
принятию компаниями решений исходя из информации о данных связях.
Список
литературы
1. Батура Т.В. (2013). Методы анализа компьютерных
социальных сетей. Новосибирск: Новосибирский Государственный Университет. URL:
<http://nsu.ru/xmlui/handle/nsu/250>
2. Белов Ю.А., Вовчок С.И. (2016). Генерация графа
социальной сети с использованием Apache Spark. Ярославль: Ярославский
государственный университет. URL:
<http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mais&paperid=540&option_lang=rus>
. Бузун Н., Коршунов А. (2012). Выявление
пересекающихся сообществ в социальных сетях. Федеральное государственное
бюджетное учреждение науки Институт системного программирования Российской
академии наук. URL: <http://www.ispras.ru/publications/overlapping_community_detection_in_social_networks.pdf
>
4. Коршунов А., Белобородов И. (2014). Анализ социальных
сетей: методы и приложения. Федеральное государственное бюджетное учреждение
науки Институт системного программирования Российской академии наук. URL: <http://cyberleninka.ru/article/n/analiz-sotsialnyh-setey-metody-i-prilozheniya>
5. Краковецкий А. (2009). Кластеризация: алгоритмы k-means и c-means. URL: <https://habrahabr.ru/post/67078/>
. Пронин А., Веретенник Е., Семенов А. (2014).
Формирование учебных групп в университете с помощью анализа социальных сетей.
Федеральное государственное автономное образовательное учреждение высшего
профессионального образования «Национальный исследовательский
университет» Высшая школа экономики «. URL:
<http://cyberleninka.ru/article/n/formirovanie-uchebnyh-grupp-v-universitete-s-pomoschyu-analiza-sotsialnyh-setey>
7. Сивоголовко Е.В. (2011). Методы обобщающей
кластеризации при анализе социальных сетей. Закрытое акционерное общество
Исследовательский Институт «Центрпрограммсистем». URL: <http://cyberleninka.ru/article/n/metody-obobschayuschey-klasterizatsii-pri-analize-sotsialnyh-setey>
. Целых Ю.А. (2008). — Теоретико-графовые методы
анализа нечетких социальных сетей. Закрытое акционерное общество
Исследовательский Институт «Центрпрограммсистем». URL:
<http://cyberleninka.ru/article/n/teoretiko-grafovye-metody-analiza-nechetkih-sotsialnyh-setey>
. Чихрадзе К.К., Коршунов А.В., Бузун Н.О., Кузюрин
Н.Н. (2014). Иcпользование модели социальной сети с сообществами пользователей
для распределенной генерации случайных социальных графов. Федеральное
государственное бюджетное учреждение науки Институт системного программирования
Российской академии наук. URL:
<http://jmlda.org/papers/doc/2014/no8/Chykhradze2014Communities.pdf>
. Часовских А. (2010). Обзор алгоритмов кластеризации
данных. URL:
<https://habrahabr.ru/post/101338/ >
. Aiello W., Ghung F., Linyuan Lu (2001). A
Random Graph Model for Power Law Graphs. URL:
<http://people.math.sc.edu/lu/papers/power.pdf>
. Bonchi F., Castillo C., Gionis A., Jaimes A.
(2011). Social Network Analysis and Mining for Business Applications.
Barcelona: Yahoo! Research. URL:
<http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.225.9932&rep=rep1&type=pdf>
. Girvan M., Newman M.E.J. (2002). Community
structure in social and biological networks. Santa Fe: The National Academy of
Sciences. URL: <http://www.pnas.org/content/99/12/7821.full>
. Kosorukoff A. (2011). Social networks
analysis: theory and applications. Passmore, D. L. URL:
<https://www.politaktiv.org/documents/10157/29141/SocNet_TheoryApp.pdf >
. Martinez A., Dimitriadis Y., Rubia B., Gomez
E., P. de la Fuente (2003). Combining qualitative evaluation and social network
analysis for the study of classroom social interactions. Elsevier Science Ltd.
URL: <http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.12.8978&rep=rep1&type=pdf>
. Newman M.E.J. (2006). Modularity and
community structure in networks. Department of Physics and Center for the Study
of Complex Systems, University of Michigan, Ann Arbor. URL:
<http://www.pnas.org/content/103/23/8577.full.pdf>
17. Ziv. E., Middendorf M., Wiggins C. (2004). An
Information-Theoretic Approach to Network Modularity. Center for Computational
Biology and Bioinformatics, Columbia University. URL: <https://arxiv.org/abs/q-bio/0411033>
. Venu M. Satuluri. Scalable Clustering of
Modern Networks //Dissertation, The Ohio State University, 2012.
19. Бартенев М.В., Вишняков И.Э. Использование графовых
баз данных в целях оптимизации анализа биллинговой информации. Инженерный
журнал: наука и инновации, 2013, вып. 11. URL:
20. U. Alon, N. Barkai, D. A. Notterman, K. Gish,
S. Ybarra, D. Mack, A. J. Levine. Broad patterns of gene expression revealed by
clustering analysis of tumor and normal colon tissues probed by oligonucleotide
arrays, 1999.
. A.-L.
Barabási1, Z. N. Oltvai. Network biology: understanding the cell’s
functional organization //Nature Reviews Genetics 5, 101-113. 2004.
22. Ed Bullmore, O. Sporns. Complex brain networks:
graph theoretical analysis of structural and functional systems //Nature
Reviews Neuroscience 10, 186-198 (2009).
. James A. Davis. Clustering and Hierarchy in
Interpersonal Relations: Testing Two Graph Theoretical Models on 742
Sociomatrices //American Sociological Review Vol. 35, No. 5, pp. 843-851
(1970).
. D. P. Phillips, L. L. Carstensen. Clustering
of Teenage Suicides after Television News Stories about Suicide //The New
England Journal of Medicine, 1986.
. P. Arabie. Clustering representations of
group overlap. //The Journal of Mathematical Sociology, 1977.

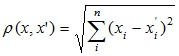
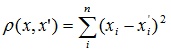
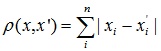
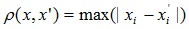
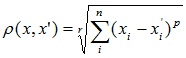 ,
,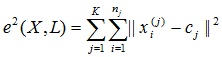
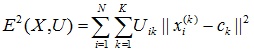 ,
, .
.