Absolute, relative, and percent error are the most common experimental error calculations in science. Grouped together, they are types of approximation error. Basically, the premise is that no matter how carefully you measure something, you’ll always be off a bit due to the limitations of the measuring instrument. For example, you may be only able to measure to the nearest millimeter on a ruler or the nearest milliliter on a graduated cylinder. Here are the definitions, equations, and examples of how to use these types of error calculations.
Absolute Error
Absolute error is the magnitude (size) of the difference between a measured value and a true or exact value.
Absolute Error = |True Value – Measured Value|
Absolute Error Example:
A measurement is 24.54 mm and the true or known value is 26.00 mm. Find the absolute error.
Absolute Error = |26.00 mm – 25.54 mm|= 0.46 mm
Note absolute error retains its units of measurement.
The vertical bars indicate absolute value. In other words, you drop any negative sign you may get. For this reason, it doesn’t actually matter whether you subtract the measured value from the true value or the other way around. You’ll see the formula written both ways in textbooks and both forms are correct.
What matters is that you interpret the error correctly. If you graph error bars, half of the error is higher than the measured value and half is lower. For example, if your error is 0.2 cm, it is the same as saying ±0.1 cm.
The absolute error tells you how big a difference there is between the measured and true values, but this information isn’t very helpful when you want to know if the measured value is close to the real value or not. For example, an absolute error of 0.1 grams is more significant if the true value is 1.4 grams than if the true value is 114 kilograms! This is where relative error and percent error help.
Relative Error
Relative error puts absolute error into perspective because it compares the size of absolute error to the size of the true value. Note that the units drop off in this calculation, so relative error is dimensionless (unitless).
Relative Error = |True Value – Measured Value| / True Value
Relative Error = Absolute Error / True Value
Relative Error Example:
A measurement is 53 and the true or known value is 55. Find the relative error.
Relative Error = |55 – 53| / 55 = 0.034
Note this value maintains two significant digits.
Note: Relative error is undefined when the true value is zero. Also, relative error only makes sense when a measurement scale starts at a true zero. So, it makes sense for the Kelvin temperature scale, but not for Fahrenheit or Celsius!
Percent Error
Percent error is just relative error multiplied by 100%. It tells what percent of a measurement is questionable.
Percent Error = |True Value – Measured Value| / True Value x 100%
Percent Error = Absolute Error / True Value x 100%
Percent Error = Relative Error x 100%
Percent Error Example:
A speedometer says a car is going 70 mph but its real speed is 72 mph. Find the percent error.
Percent Error = |72 – 70| / 72 x 100% = 2.8%
Mean Absolute Error
Absolute error is fine if you’re only taking one measurement, but what about when you collect more data? Then, mean absolute error is useful. Mean absolute error or MAE is the sum of all the absolute errors divided by the number of errors (data points). In other words, it’s the average of the errors. Mean absolute error, like absolute error, retains its units.
Mean Absolute Error Example:
You weigh yourself three times and get values of 126 lbs, 129 lbs, 127 lbs. Your true weight is 127 lbs. What is the mean absolute error of the measurements.
Mean Absolute Error = [|126-127 lbs|+|129-127 lbs|+|127-127 lbs|]/3 = 1 lb
References
- Hazewinkel, Michiel, ed. (2001). “Theory of Errors.” Encyclopedia of Mathematics. Springer Science+Business Media B.V. / Kluwer Academic Publishers. ISBN 978-1-55608-010-4.
- Helfrick, Albert D. (2005). Modern Electronic Instrumentation and Measurement Techniques. ISBN 81-297-0731-4.
- Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, With Special Reference to Biological Sciences. McGraw-Hill.
The absolute error in any one trial (with name or index $k$) is
$$ varepsilon_a^k = widetilde x_k — x_k, $$
where $x_k$ is the true value of the quantity under consideration in trial $k$, and $widetilde x_k$ is the value which is inferred of that quantity in trial $k$, with the techniques and observational data available.
The average of the absolue errors over a set of trials, $k = 1 , … , n$, is accordingly
$$ varepsilon_a = frac{1}{n} , sum_{k = 1}^n varepsilon_a^k = frac{1}{n} left( sum_{k = 1}^n widetilde x_k right) — frac{1}{n} left( sum_{k = 1}^n x_k right).$$
If the quantity under consideration happened to have one particular always equal true value $x$ in all trials of this set, i.e. if for all $k$ holds $x_k = x$, then
$$ varepsilon_a = frac{1}{n} left( sum_{k = 1}^n widetilde x_k right) — x.$$
Concerning relative error, there are various definitions to consider.
One, apparently common definition of «relative error» is setting in any one trial
$$ varepsilon_r^k = frac{varepsilon_a^k}{x_k} = frac{widetilde x_k — x_k}{x_k}, $$
and correspondingly in a set of trials with equal true value $x$:
$$ varepsilon_r = frac{varepsilon_a}{x} = frac{1}{n} left( sum_{k = 1}^n frac{widetilde x_k}{x} right) — 1.$$
The main drawback of this definition is its apparent failure (divergence) if the true value $x$ over the set of trials under consideration happens to be $0$; or when referring only to one trial, if the true value $x_k$ in that trial happens to be $0$.
Another, arguably more robust definition of relative error is based on noting that the inferred values $widetilde x_k$ are necessarily elements of an entire range of values which are «technically admissible»; such as the actual practically usable extent on a dial indicator of a measuring instrument, or the actual range of an engineer’s scale.
This range, which is due to the technique being used to obtain the inferred values $widetilde x_k$, should have some non-zero extend (or in other words: it should have more than one element) because otherwise the result of applying that particular technique would be predetermined and known in advance; counter to the meaning of «measuring» and «finding out in dependence of observational data gathered».
Writing this range therefore as $widetilde x_{max} — widetilde x_{min}$, the relative error can be defined for any one trial as
$$ varepsilon_r^k = frac{varepsilon_a^k}{widetilde x_{max} — widetilde x_{min}} = frac{widetilde x_k — x_k}{widetilde x_{max} — widetilde x_{min}}, $$
and correspondingly in a set of trials with equal true value $x$:
$$ varepsilon_r = frac{varepsilon_a}{widetilde x_{max} — widetilde x_{min}}.$$
Let’s first know some basics about numbers used in floating-point arithmetic or in other words Numerical analysis and how they are calculated.
Basically, all the numbers that we use in Numerical Analysis are of two types as follows.
- Exact Numbers –
Numbers that have their exact quantity, means their value isn’t going to change. For example- 3, 2, 5, 7, 1/3, 4/5, or √2 etc. - Approximate Numbers –
These numbers are represented in decimal numbers. They have some certain degrees of accuracy. Like the value of π is 3.1416 if we want more precise value, we can write 3.14159265, but we can’t write the exact value of π.These digits that we use in any approximate value, or in other way digits which represent the numbers are called Significant Digits.
How to count significant digits in a given number :
For example –
In the normal value of π (3.1416), there are 5 significant digits and when we write more precise value of it (3.14159265) we get 9 significant digits.
Let’s say we have numbers: 0.0123, 1.2300, and 0.10234. Now we have 4, 3, and 5 significant digits respectively.
In the Scientific Representation of numbers –
2.345×107, 8.7456 ×104, 5.4×106 have 4, 5 and 2 significant digits respectively.
Absolute Error :
Let the true value of a quantity be X and the approximate value of that quantity be X1. Hence absolute error has defined the difference between X and X1. Absolute Error is denoted by EA.
Hence EA= X-X1=δX
Relative Error :
It is defined as follow.
ER = EA/X = (Absolute Error)/X
Percentage Error :
It is defined as follow.
EP= 100×EP= 100×EA/X
Let’s say we have a number δX = |X1-X|, It is an upper limit on the magnitude of Absolute Error and known as Absolute Accuracy.
Similarly the quantity δX/ |X| or δX/ |X1| called Relative Accuracy.
Now let’s solve some examples as follows.
- Ex-1 :
We are given an approximate value of π is 22/7 = 3.1428571 and true value is 3.1415926. Calculate absolute, relative and percentage errors?
Solution –We have True value X= 3.1415926, And Approx. value X1= 3.1428571. So now we calculate Absolute error, we know that EA= X - X1=δX Hence EA= 3.1415926- 3.1428571 = -0.0012645 Answer is -0.0012645 Now for Relative error we’ve (absolute error)/(true value of quantity) Hence ER = EA/X = (Absolute Error)/X, EA=(-0.0012645)/3.1415926 = -0.000402ans. Percentage Error, EP= 100 × EA/X = 100 × (-0.000402) = - 0.0402ans.
- Ex-2 :
Let the approximate values of a number 1/3 be 0.30, 0.33, 0.34. Find out the best approximation.
Solution –
Our approach is that we first find the value of Absolute Error, and any value having the least absolute will be best. So, we first calculate the absolute errors in all approx values are given.
<pre
|X-X1| = |1/3 – 0.30| = 1/30
|1/3 – 0.33| = 1/300
|1/3 – 0.34| = 0.02/3 = 1/500Hence, we can say that 0.33 is the most precise value of 1/3;
- Ex-3 :
Finding the difference—
√5.35 - √4.35
Solution –
√5.35 = 2.31300 √4.35 = 2.08566 Hence, √5.35 - √4.35 = 2.31300 – 2.08566 = 0.22734
Here our answer has 5 significant digits we can modify them as per our requirements.
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
- Среднеквадратичная ошибка (Mean Squared Error)
- Корень из среднеквадратичной ошибки (Root Mean Squared Error)
- Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error)
- Cредняя абсолютная ошибка (Mean Absolute Error)
- Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error)
- Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error)
- Средняя абсолютная масштабированная ошибка (Mean absolute scaled error)
- Средняя относительная ошибка (Mean Relative Error)
- Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error
- R-квадрат
- Скорректированный R-квадрат
- Сравнение метрик
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
Absolute and Relative Error Calculation
Brand X Pictures/Getty Images
Updated on October 06, 2019
Absolute error and relative error are two types of experimental error. You’ll need to calculate both types of error in science, so it’s good to understand the difference between them and how to calculate them.
Absolute error is a measure of how far ‘off’ a measurement is from a true value or an indication of the uncertainty in a measurement. For example, if you measure the width of a book using a ruler with millimeter marks, the best you can do is measure the width of the book to the nearest millimeter. You measure the book and find it to be 75 mm. You report the absolute error in the measurement as 75 mm +/- 1 mm. The absolute error is 1 mm. Note that absolute error is reported in the same units as the measurement.
Alternatively, you may have a known or calculated value and you want to use absolute error to express how close your measurement is to the ideal value. Here absolute error is expressed as the difference between the expected and actual values.
Absolute Error = Actual Value — Measured Value
For example, if you know a procedure is supposed to yield 1.0 liters of solution and you obtain 0.9 liters of solution, your absolute error is 1.0 — 0.9 = 0.1 liters.
Relative Error
You first need to determine absolute error to calculate relative error. Relative error expresses how large the absolute error is compared with the total size of the object you are measuring. Relative error is expressed as a fraction or is multiplied by 100 and expressed as a percent.
Relative Error = Absolute Error / Known Value
For example, a driver’s speedometer says his car is going 60 miles per hour (mph) when it’s actually going 62 mph. The absolute error of his speedometer is 62 mph — 60 mph = 2 mph. The relative error of the measurement is 2 mph / 60 mph = 0.033 or 3.3%
Sources
- Hazewinkel, Michiel, ed. (2001). «Theory of Errors.» Encyclopedia of Mathematics. Springer Science+Business Media B.V. / Kluwer Academic Publishers. ISBN 978-1-55608-010-4.
- Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, With Special Reference to Biological Sciences. McGraw-Hill.
Measurement is a major part of scientific calculations. Completely accurate measurement results are absolutely rare. While measuring different parameters, slight errors are common. There are different types of errors, which cause differences in measurement. All the errors can be expressed in mathematical equations. By knowing the errors, we can calculate correctly and find out ways to correct the errors. There are mainly two types of errors – absolute and relative error. In this article, we are going to define absolute error and relative error. Here, we are giving explanations, formulas, and examples of absolute error and relative error along with the definition. The concept of error calculation is essential in measurement.
Define Absolute Error
Absolute error is defined as the difference between the actual value and the measured value of a quantity. The importance of absolute error depends on the quantity that we are measuring. If the quantity is large such as road distance, a small error in centimetres is negligible. While measuring the length of a machine part an error in centimetre is considerable. Though the errors in both cases are in centimetres, the error in the second case is more important.
Absolute Error Formula
The absolute error is calculated by the subtraction of the actual value and the measured value of a quantity. If the actual value is x₀ and the measured value is x, the absolute error is expressed as,
∆x = x₀- x
Here, ∆x is the absolute error.
Absolute Error Example
Here, we are giving an example of the absolute error in real life. Suppose, we are measuring the length of an eraser. The actual length is 35 mm and the measured length is 34.13 mm.
So, The Absolute Error = Actual Length — Measured Length
= (35 — 34.13) mm
= 0.87 mm
Classification Of Absolute Error
-
Absolute accuracy error
Absolute accuracy error is the other name of absolute error. The formula for absolute accuracy error is written as E= E exp – E true, where E is the absolute accuracy error, E exp is the experimental value and E true is the actual value.
-
Mean absolute error
MAE or the mean absolute error is the mean or average of all absolute errors. The formula for Mean Absolute Error is given as,
MAE = [frac{1}{n}] [sum_{i=1}^{n}mid x_{i} -xmid]
-
Absolute Precision Error
It is a standard deviation of a group of numbers. Standard deviation helps to know how much data is spread.
Relative Error Definition
The ratio of absolute error of the measurement and the actual value is called relative error. By calculating the relative error, we can have an idea of how good the measurement is compared to the actual size. From the relative error, we can determine the magnitude of absolute error. If the actual value is not available, the relative error can be calculated in terms of the measured value of the quantity. The relative error is dimensionless and it has no unit. It is written in percentage by multiplying it by 100.
Relative Error Formula
The relative error is calculated by the ratio of absolute error and the actual value of the quantity. If the absolute error of the measurement is ∆x, the actual value is x0, the measured value is x, the relative error is expressed as,
xᵣ = (x₀ — x)/ x₀ = ∆x/x₀
Here, xr is the relative error.
Relative Error Example
Here, we are giving an example of relative error in real life. Suppose, the actual length of an eraser is 35 mm. Now, the absolute error = (35-34.13) mm = 0.87 mm.
So, the relative error = absolute error/actual length
= 0.87/35
= 0.02485
(Image will be Uploaded Soon)
Relative Error as a Measure of Accuracy
In many cases, relative error is a measure of precision. At the same time, it can also be used as a measure of accuracy. Accuracy is the extent of knowing how accurate the value is as compared to the actual or true value. Students can find the RE accuracy only if they know the true value or measurement. For simplicity, we have the formula for calculating the RE accuracy which is given as
RE[_{accuracy}] = Actual error/ true value * 100%
Absolute Error and Relative Error in Numerical Analysis
Numerical analysis of error calculation is a vital part of the measurement. This analysis finds the actual value and the error quantity. The absolute error determines how good or bad the measurement is. In numerical calculation, the errors are caused by round-off error or truncation error.
Absolute and Relative Error Calculation — Examples
1. Find the absolute and relative errors. The actual value is 125.68 mm and the measured value is 119.66 mm.
Solution:
Absolute Error = |125.68 – 119.66| mm
= 6.02 mm
Relative Error = |125.68 – 119.66| / 125.68
= 0.0478
2. Find out the absolute and relative errors, where the actual and measured values are 252.14 mm and 249.02 mm.
Solution:
Absolute Error = |252.14 – 249.02| mm
= 3.12 mm
Relatives Error = 3.12/252.14
= 0.0123
Did You Know?
In different measurements, the quantity is measured more than one time to get an average value of the quantity. Mean absolute error is one of the most important terms in this kind of measurement. The average of all the absolute errors of the collected data is called the MAE ( Mean Absolute Error). It is calculated by dividing the sum of absolute errors by the number of errors. The formula of MAE is –
MAE = [frac{displaystylesumlimits_{i=1}^n mid x_{0}-x mid }{n}]
Here,
n is the number of errors,
x₀ is the actual value,
x is the measured value, and
|x₀-x| is the absolute error.
Part I of a manual on
Uncertainties, Graphing, and the Vernier Caliper
| Copyright July 1, 2000 |
Vern Lindberg |
Contents
1. Systematic versus Random Errors
2. Determining Random Errors (a) Instrument Limit of
Error,
least count (b) Estimation
(c) Average
Deviation
(d) Conflicts (e) Standard
Error in the Mean
3. What does uncertainty tell me? Range of
possible values
4. Relative and Absolute error
5. Propagation of errors
(a) add/subtract
(b) multiply/divide (c) powers (d) mixtures of +-*/
(e) other
functions
6. Rounding answers properly
7. Significant figures
8. Problems to try
9. Glossary of terms (all terms that are
bold
face and underlined)
| In this manual there will be problems for you to try. They are highlighted in yellow. |
| There are also examples highlighted in green. |
1. Systematic and random errors.
No measurement made is ever exact. The accuracy
(correctness) and
precision (number of significant figures) of a measurement
are always
limited by the degree of refinement of the apparatus used, by the skill
of the
observer, and by the basic physics in the experiment. In doing
experiments we
are trying to establish the best values for certain quantities, or trying
to validate
a theory. We must also give a range of possible true values
based
on our limited number of measurements.
Why should repeated measurements of a single quantity give different
values?
Mistakes on the part of the experimenter are possible, but we do not
include
these in our discussion. A careful researcher should not make mistakes!
(Or
at least she or he should recognize them and correct the mistakes.)
We use the synonymous terms uncertainty, error, or
deviation
to represent the variation in measured data. Two types of errors are
possible.
Systematic error is the result of a mis-calibrated
device, or
a measuring technique which always makes the measured value larger (or
smaller)
than the «true» value. An example would be using a steel ruler at
liquid nitrogen
temperature to measure the length of a rod. The ruler will contract at
low temperatures
and therefore overestimate the true length. Careful design of an
experiment
will allow us to eliminate or to correct for systematic errors.
Even when systematic errors are eliminated there will remain a second
type
of variation in measured values of a single quantity. These remaining
deviations
will be classed as random errors, and can be dealt with
in a statistical
manner. This document does not teach statistics in any formal sense,
but it
should help you to develop a working methodology for treating errors.
2. Determining random errors.
How can we estimate the uncertainty of a measured quantity? Several
approaches
can be used, depending on the application.
(a) Instrument Limit of Error (ILE) and Least
Count
-
The least count is the smallest division that is marked
on the
instrument. Thus a meter stick will have a least count of 1.0 mm, a
digital
stop watch might have a least count of 0.01 sec.
The instrument limit of error, ILE for short,
is the
precision to which a measuring device can be read, and is always
equal to
or smaller than the least count. Very good measuring tools are
calibrated
against standards maintained by the National Institute of Standards
and Technology.
The Instrument Limit of Error is generally taken to be the least
count or
some fraction (1/2, 1/5, 1/10) of the least count). You may wonder
which
to choose, the least count or half the least count, or something
else.
No hard and fast rules are possible, instead you must be guided by
common
sense. If the space between the scale divisions is large, you may be
comfortable
in estimating to 1/5 or 1/10 of the least count. If the scale
divisions are
closer together, you may only be able to estimate to the nearest 1/2
of the
least count, and if the scale divisions are very close you may only
be able
to estimate to the least count.
For some devices the ILE is given as a tolerance or a percentage.
Resistors
may be specified as having a tolerance of 5%, meaning that the ILE is
5% of
the resistor’s value.
Problem: For each of the following
scales
(all in centimeters) determine the least count, the ILE, and read
the
length of the gray rod. Answer

(b) Estimated Uncertainty
-
Often other uncertainties are larger than the ILE. We may try to
balance a simple
beam balance with masses that have an ILE of 0.01 grams, but find that
we can
vary the mass on one pan by as much as 3 grams without seeing a change
in the
indicator. We would use half of this as the estimated
uncertainty,
thus getting uncertainty of ±1.5 grams.
Another good example is determining the focal length of a lens by
measuring
the distance from the lens to the screen. The ILE may be 0.1 cm,
however the
depth of field may be such that the image remains in focus while we
move the
screen by 1.6 cm. In this case the estimated uncertainty would be
half the
range or ±0.8 cm.
Problem: I measure your
height while
you are standing by using a tape measure with ILE of 0.5
mm. Estimate
the uncertainty. Include the effects of not knowing whether
you
are «standing straight» or slouching. Solution.
(c) Average Deviation: Estimated Uncertainty by Repeated
Measurements
-
The statistical method for finding a value with its uncertainty is to
repeat
the measurement several times, find the average, and find
either
the average deviation or the standard
deviation.
Suppose we repeat a measurement several times and record the
different values.
We can then find the average value, here denoted by a symbol
between
angle brackets, <t>, and use it as our best estimate of the
reading. How
can we determine the uncertainty? Let us use the following data as an
example.
Column 1 shows a time in seconds.
|
Time, t, sec. |
(t — <t>), sec |
|t — <t>|, sec |
|
|
7.4 |
-0.2 |
0.2 |
0.04 |
|
8.1 |
0.5 |
0.5 |
0.25 |
|
7.9 |
0.3 |
0.3 |
0.09 |
|
7.0 |
-0.6 |
0.6 |
0.36 |
| <t> = 7.6 | <t-<t>>= 0.0 | <|t-<t>|>= 0.4 | Std. dev = 0.50 |
-
A simple average of the times is the sum of all values
(7.4+8.1+7.9+7.0)
divided by the number of readings (4), which is 7.6 sec. We will use
angular
brackets around a symbol to indicate average; an alternate notation
uses a bar
is placed over the symbol.
Column 2 of Table 1 shows the deviation of each time from the
average, (t-<t>).
A simple average of these is zero, and does not give any new
information.
To get a non-zero estimate of deviation we take the average of the
absolute
values of the deviations, as shown in Column 3 of Table 1. We will
call this
the average deviation, Dt.
Column 4 has the squares of the deviations from Column 2, making the
answers
all positive. The sum of the squares is divided by 3, (one less
than
the number of readings), and the square root is taken to produce the
sample
standard deviation. An explanation of why we
divide by
(N-1) rather than N is found in any statistics text. The sample
standard
deviation is slightly different than the average deviation, but
either one
gives a measure of the variation in the data.
If you use a spreadsheet such as Excel there are built-in functions
that
help you to find these quantities. These are the Excel
functions.
| =SUM(A2:A5) | Find the sum of values in the range of cells A2 to A5. |
| =COUNT(A2:A5) | Count the number of numbers in the range of cells A2 to A5. |
| =AVERAGE(A2:A5) | Find the average of the numbers in the range of cells A2 to A5. |
| =AVEDEV(A2:A5) | Find the average deviation of the numbers in the range of cells A2 to A5. |
| =STDEV(A2:A5) | Find the sample standard deviation of the numbers in the range of cells A2 to A5. |
For a second example, consider a measurement of length shown in
Table 2.
The average and average deviation are shown at the bottom of the
table.
|
Length, x, m |
|x- <x>|, m |
|
|
15.4 |
0.06667 |
0.004445 |
|
15.2 |
0.26667 |
0.071112 |
|
15.6 |
0.13333 |
0.017777 |
|
15.7 |
0.23333 |
0.054443 |
|
15.5 |
0.03333 |
0.001111 |
|
15.4 |
0.06667 |
0.004445 |
|
Average 15.46667 m |
±0.133333 m |
St. dev. ±0.17512 |
We round the uncertainty to one or two significant figures (more on
rounding
in Section 7), and round the average to the same number of digits
relative
to the decimal point. Thus the average length with average deviation
is either
(15.47 ± 0.13) m or (15.5 ± 0.1) m. If we use
standard
deviation we report the average length as (15.47±0.18) m or
(15.5±0.2)
m.Follow your instructor’s instructions on whether to use average or
standard
deviation in your reports.Problem
Find
the average, and average deviation for the following data on
the length
of a pen, L. We have 5 measurements,
(12.2, 12.5, 11.9,12.3, 12.2) cm.
SolutionProblem: Find the
average
and the average deviation of the following measurements of a
mass.(4.32, 4.35, 4.31, 4.36, 4.37, 4.34)
grams. Solution
(d) Conflicts in the above
-
In some cases we will get an ILE, an estimated uncertainty, and an
- Choose the largest of (i) ILE, (ii) estimated uncertainty, and
(iii)
average or standard deviation. - Round off the uncertainty to 1 or 2 significant figures.
- Round off the answer so it has the same number of digits before
or after
the decimal point as the answer. - Put the answer and its uncertainty in parentheses, then put the
power
of 10 and unit outside the parentheses.
average deviation
and we will find different values for each of these. We will be
pessimistic
and take the largest of the three values as our uncertainty.
[When you
take a statistics course you should learn a more correct approach
involving
adding the variances.] For example we might measure a mass required to
produce
standing waves in a string with an ILE of 0.01 grams and an estimated
uncertainty
of 2 grams. We use 2 grams as our uncertainty.
The proper way to write the answer is
Problem: I make several
measurements
on the mass of an object. The balance has an ILE of 0.02
grams.
The average mass is 12.14286 grams, the average deviation is
0.07313 grams.
What is the correct way to write the mass of the object including
its
uncertainty? What is the mistake in each incorrect
one?
Answer
- 12.14286 g
- (12.14 ± 0.02) g
- 12.14286 g ± 0.07313
- 12.143 ± 0.073 g
- (12.143 ± 0.073) g
- (12.14 ± 0.07)
- (12.1 ± 0.1) g
- 12.14 g ± 0.07 g
- (12.14 ± 0.07) g
Problem: I measure a length with a meter stick
with a
least count of 1 mm. I measure the length 5 times with results
(in mm)
of 123, 123, 123, 123, 123. What is the average length and the
uncertainty
in length? Answer
(e) Why make many
measurements?
Standard Error in the Mean.We know that by making several measurements
(4 or
5) we should be more likely to get a good average value for what we
are
measuring. Is there any point to measuring a quantity more
often than
this? When you take a statistics course you will learn that the
standard
error in the mean is affected by the number of measurements
made.The standard error in the mean in the
simplest case
is defined as the standard deviation divided by the square root of
the number
of measurements.The following example illustrates this in
its simplest
form. I am measuring the length of an object. Notice that the
average and
standard deviation do not change much as the number of measurements
change,
but that the standard error does dramatically decrease as N
increases.
Finding Standard Error in the Mean
Number of Measurements, N Average Standard Deviation Standard Error 5 15.52 cm 1.33 cm 0.59 cm 25 15.46 cm 1.28 cm 0.26 cm 625 15.49 cm 1.31 cm 0.05 cm 10000 15.49 cm 1.31 cm 0.013 cm For this introductory course we will not
worry about
the standard error, but only use the standard deviation, or
estimates of
the uncertainty.
3. What is the range of possible values?
When you see a number reported as (7.6 ± 0.4) sec your first
thought
might be that all the readings lie between 7.2 sec (=7.6-0.4) and 8.0
sec
(=7.6+0.4). A quick look at the data in the Table 1 shows that this
is not
the case: only 2 of the 4 readings are in this range. Statistically
we expect
68% of the values to lie in the range of <x> ± Dx,
but that 95% lie within <x> ± 2 Dx. In
the first example all the data lie between 6.8 (= 7.6 — 2*0.4) and
8.4 (=
7.6 + 2*0.4) sec. In the second example, 5 of the 6 values lie within
two
deviations of the average. As a rule of thumb for this course we
usually
expect the actual value of a measurement to lie within two deviations
of the
mean. If you take a statistics course you will talk about
confidence
levels.How do we use the uncertainty? Suppose you measure the density of
calcite
as (2.65 ± 0.04).
The textbook value is 2.71.
Do the two values agree? Since the text value is within the range of
two deviations
from the average value you measure you claim that your value agrees
with the
text. If you had measured the density to be (2.65 ±
0.01)
you would be forced to admit your value disagrees with the text
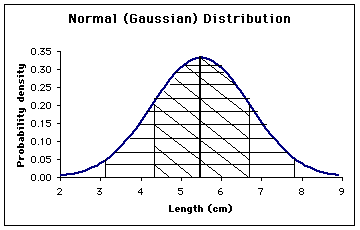
value.The drawing below shows a Normal Distribution (also
called
a Gaussian). The vertical axis represents the
fraction
of measurements that have a given value z. The most likely
value is
the average, in this case <z> = 5.5 cm. The standard
deviation is
s = 1.2. The central shaded region
is the
area under the curve between (<x> — s)
and (x
+ s), and roughly 67% of the time a
measurement
will be in this range. The wider shaded region represents
(<x> —
2s) and (x + 2s),
and 95% of the measurements will be in this range. A statistics
course
will go into much more detail about this.
Problem: You measure a
time to
have a value of (9.22 ± 0.09) s. Your friend
measures the
time to be (9.385 ± 0.002) s. The accepted value
of the
time is 9.37 s. Does your time agree with the
accepted?
Does your friend’s time agree with the accepted? Answer.Problem: Are the following numbers equal within
the
expected range of values? Answer(i) (3.42 ± 0.04) m/s and 3.48 m/s?
(ii) (13.106 ± 0.014) grams and 13.206 grams?
(iii) (2.95 ± 0.03) x
m/s and 3.00 x
m/s

4. Relative and Absolute Errors
The quantity Dz is called the
absolute error
while Dz/z is called the relative
error
or fractional uncertainty. Percentage error is the
fractional
error multiplied by 100%. In practice, either the percentage error or
the
absolute error may be provided. Thus in machining an engine part the
tolerance
is usually given as an absolute error, while electronic components
are usually
given with a percentage tolerance.
Problem: You are given a resistor with a
resistance of
1200 ohms and a tolerance of 5%. What is the absolute error
in the
resistance? Answer.
5. Propagation of Errors, Basic Rules
(a) Addition and
Subtraction:
z = x + y or z = x —
y(b) Multiplication and
Division:
z = x y or z = x/y(c) Products of powers:
.
(d) Mixtures of
multiplication,
division, addition, subtraction, and powers.(e) Other Functions:
e.g..
z = sin x. The simple approach.(f)
Other Functions: Getting formulas using partial
derivatives
6. Rounding off answers
in regular
and scientific notation.7. Significant
Figures8. Problems on
Uncertainties
and Error Propagation.9. Glossary of Important Terms
�
| Term | Brief Definition |
| Absolute error | The actual error in a quantity, having the same units as the quantity. Thus if c = (2.95 ± 0.07) m/s, the absolute error is 0.07 m/s. See Relative Error. |
| Accuracy | How close a measurement is to being correct. For gravitational acceleration near the earth, g = 9.7 m/s2 is more accurate than g = 9.532706 m/s2. See Precision. |
| Average | When several measurements of a quantity are made, the sum of the measurements divided by the number of measurements. |
| Average Deviation | The average of the absolute value of the differences between each measurement and the average. See Standard Deviation. |
| Confidence Level | The fraction of measurements that can be expected to lie within a given range. Thus if m = (15.34 ± 0.18) g, at 67% confidence level, 67% of the measurements lie within (15.34 — 0.18) g and (15.34 + 0.18) g. If we use 2 deviations (±0.36 here) we have a 95% confidence level. |
| Deviation | A measure of range of measurements from the average. Also called error oruncertainty. |
| Error | A measure of range of measurements from the average. Also called deviation or uncertainty. |
| Estimated Uncertainty | An uncertainty estimated by the observer based on his or her knowledge of the experiment and the equipment. This is in contrast to ILE, standard deviation or average deviation. |
| Gaussian Distribution | The familiar bell-shaped distribution. Simple statistics assumes that random errors are distributed in this distribution. Also called Normal Distribution. |
| Independent Variables | Changing the value of one variable has no effect on any of the other variables. Propagation of errors assumes that all variables are independent. |
| Instrument Limit of Error (ILE) |
The smallest reading that an observer can make from an instrument. This is generally smaller than the Least Count. |
| Least Count | The size of the smallest division on a scale. Typically the ILE equals the least count or 1/2 or 1/5 of the least count. |
| Normal Distribution | The familiar bell-shaped distribution. Simple statistics assumes that random errors are distributed in this distribution. Also called Gaussian Distribution. |
| Precision | The number of significant figures in a measurement. For gravitational acceleration near the earth, g = 9.532706 m/s2 is more precise than g = 9.7 m/s2. Greater precision does not mean greater accuracy! See Accuracy. |
| Propagation of Errors | Given independent variables each with an uncertainty, the method of determining an uncertainty in a function of these variables. |
| Random Error | Deviations from the «true value» can be equally likely to be higher or lower than the true value. See Systematic Error. |
| Range of Possible True Values |
Measurements give an average value, <x> and an uncertainty, Dx. At the 67% confidence level the range of possible true values is from <x> — Dx to <x> + Dx. See Confidence Level . |
| Relative Error | The ratio of absolute error to the average, Dx/x. This may also be called percentage error or fractional uncertainty. See Absolute Error. |
| Significant Figures | All non-zero digits plus zeros that do not just hold a place before or after a decimal point. |
| Standard Deviation | The statistical measure of uncertainty. See Average Deviation. |
| Standard Error in the Mean |
An advanced statistical measure of the effect of large numbers of measurements on the range of values expected for the average (or mean). |
| Systematic Error | A situation where all measurements fall above or below the «true value». Recognizing and correcting systematic errors is very difficult. |
| Uncertainty | A measure of range of measurements from the average. Also called deviation or error. |
Definition of Absolute Error
[Click Here for Sample Questions]
Absolute error is defined as the difference between a measured or derived value of a quantity and an actual value.The meaning of the absolute error depends on the quantity to be measured. Absolute errors are not enough because there is no information about the meaning of the error.
- At street distances, such as in large quantities, small errors in centimeters are negligible. When measuring the length of machine parts, the error of centimeters is large.
- In both cases the error is shown in centimeters, but the error in the second case is more important. When measuring distances between cities that are kilometers apart, errors of a few centimeters are negligible and irrelevant.
- Consider another case where the centimeter error when measuring a small mechanical part is a very significant error .Both errors are on the order of centimeters, but the second error is more serious than the first.
Also Read: Linear Approximation Formula
Absolute Error Formula
If x is the actual value of the quantity
x0 is the measured value of the quantity, the absolute error value can be calculated using the following formula:
Δx = x0–x
Here, Δx is called the absolute error.
When considering multiple measurements, the arithmetic mean of the absolute error of each measurement should be the final absolute error.
Example of Absolute Error
Here are some examples of absolute mistakes in real life.
Suppose you want to measure the length of the eraser.
The actual length is 35mm and the measured length is 34.13mm.
Therefore, absolute error = actual length measurement — length = (35 — 34.13) mm = 0.87mm
Classification of Absolute Error
[Click Here for Sample Questions]
Absolute Accuracy Error
Absolute accuracy error is the other name of absolute error.
The formula for absolute accuracy error is written as
E = Eexp – Etrue,
where E is the absolute accuracy error,
Eexp is the experimental value
Etrue is the actual value.
Mean Absolute Error
Mean absolute error is the mean or average of all absolute errors. The formula for Mean Absolute Error is given as,
Mean Absolute Error
Definition of Relative Error
[Click Here for Sample Questions]
Relative error is defined as the ratio of the absolute error of the measured value to the actual measured value.
- Using this method, you can determine the amount of absolute error with respect to the actual size of the measurement. If you don’t know the actual measurement of the object, you can find the relative error from the measurement.
- Relative error indicates how good the measurement is in relation to the size of the object being measured.
- Note that the relative error is dimensionless. When writing relative errors, it is common to multiply the decimal error by 100 and express it as a percentage.
Relative Error Formula
Relative errors are calculated by the absolute error ratio and the actual amount value. If the absolute error is the measurement Δx, the actual value x0 is x and the relative error is —
(x0 — x)/x = (Δx)/x
Here, XR is a relative error.
Example of Relative Error
Here is an example of an actual relative error.
Suppose the actual length of the eraser is 35mm.
Here, the absolute error = (35 – 34.13) mm = 0.87 mm.
Therefore, relative error = absolute error / actual length = 0.87 / 35 = 0.02485
Accuracy of Relative Error Measurement
Relative error is often a measure of accuracy. At the same time, it can be used as a measure of accuracy. Accuracy is the degree of knowledge about how accurate a value is compared to its actual or true value.
Students can only find the accuracy of the RE if they know the true or measured value.
For simplicity, there is an expression that calculates the RE accuracy given as
Accuracy = actual error / true value * 100%.
Things to Remember
- There are two types of errors affected by measuring tool accuracy, absolute error and relative error.
- Formula of absolute error: Δx = x0–x,
- Formula of relative error: (x0 — x)/x = (Δx)/x
- Absolute error indicates the magnitude of the error, and relative error indicates the magnitude of the error for the correct value.
- Mean Absolute Error is the average of all the absolute errors in the collected data. Abbreviated as MAE (Mean Absolute Error).
Read also:
Sample Questions
Ques. The time T, taken for a complete oscillation of a single pendulum with length l , is given by the equation: T = 2π√(l/g), where g is constant. Find the approximate percentage error in the calculated value of T corresponding to an error of 2 percent in the value of 1. (2 Marks)
Ans:
T = 2π√(l/g)
T = 2π(l/g)1/2
log T = log 2π + (1/2) [log l — log g]
(1/T) dT/dl = 0 + (1/2) [(1/l) — 0]
dT/T = (1/2) (1/l) dl
Percentage error = (1/2) (1/l) × 0.02 l × 100
= 1%
Ques. Find the absolute and relative errors. The actual value is 125.68 mm and the measured value is 119.66 mm. (2 Marks)
Ans:
Absolute Error = |125.68 – 119.66| mm= 6.02 mm
Relative Error = |125.68 – 119.66| / 125.68= 0.0478
Ques. Find out the absolute and relative errors, where the actual and measured values are 252.14 mm and 249.02 mm. (2 Marks)
Ans:
Absolute Error = |252.14 – 249.02| mm = 3.12 mm
Relatives Error = 3.12/252.14 = 0.0123
Ques. The radius of a circular plate is measured as 12.65 cm instead of the actual length 12.5 cm. find the following in calculating the area of the circular plate:
(i) Absolute error (ii) Relative error. (5 Marks)
Ans: (i) Absolute error:
Absolute error = Actual value — Approximate value
Actual length = 12.5 cm approximate value = 12.65 cm
Area of circle A(r) = πr2
Actual change in area = π(12.65)2 — π(12.5)2
= π[160.0225 — 156.25]
= π(3.7725)
= 3.7725π —(1)
Approximate change = A'(12.5) x change in radius
= 2π(12.5) x 0.15
= 25π x 0.15
= 3.75π —(2)
(1) — (2)
Absolute error = 3.7725π — 3.75π
= 0.0225π cm2
(ii) Relative error = (Actual value — Approximate value)/Actual value
Relative error = 0.0225π / 3.7725π
= 0.0059 cm2
Ques. Absolute error of a number is 5 and Relative error for the same number is 0.2. Find out the actual value of the number. (3 Marks)
Ans: Relative error = Absolute error/ Actual value
Given, the relative error is 0.2
Absolute error is 5.
So, actual value = 5/0.2
= 25
Hence the actual value is 25.
Ques. If absolute error and actual value of a number are 5, 15. What is the relative error? (2 Marks)
Ans: Relative error = absolute error/ actual value
Absolute Error = 5
Actual Value = 15
Hence,
Relative error = 5/15
= 1/3
Ques. A scale incorrectly measures a value as 6 cm because of some marginal errors. If the real measurement of the value is taken as 10 cm then what will be the percentage of error. (2 Marks)
Ans: Given,
Approximate value/wrong value = 6 cm
Exact value = 10 cm
Percentage Error = (Approximate Value — Exact Value)/Exact Value) × 100
Percentage Error = (10 – 6)/10 × 100
= 40 %
Ques: If the actual value of a shaft diameter is 1.605 inches and the shaft is measured and found to be 1.603 inches, determine the relative and absolute error. (3 Marks)
Ans. We know that, Absolute error = true value — measured value
= 1.605 – 1.603
= 0.002 inches
The relative error = absolute error/ true value × 100
= 0.002 / 1.605 × 100
= 0.1246 %
Ques: The table is 150 cm wide. When measured with a school ruler, it equals to 150.2 cm. Calculate the absolute and relative error. (2 Marks)
Ans: Real value = 150 cm
Measured value = 150.2 cm
Absolute error = real value — measured value
150 — 150.2
= 0.2 cm
Relative error = 0.2150 × 100
= 0.1 %
Also Read: