From Wikipedia, the free encyclopedia
In digital transmission, the number of bit errors is the number of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.[1]
The bit error probability pe is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.
Example[edit]
As an example, assume this transmitted bit sequence:
1 1 0 0 0 1 0 1 1
and the following received bit sequence:
0 1 0 1 0 1 0 0 1,
The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.
Packet error ratio[edit]
The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability pp, which for a data packet length of N bits can be expressed as
,
assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately
Similar measurements can be carried out for the transmission of frames, blocks, or symbols.
The above expression can be rearranged to express the corresponding BER (pe) as a function of the PER (pp) and the data packet length N in bits:
Factors affecting the BER[edit]
In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.
The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.
The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.
Analysis of the BER[edit]
The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.
Examples of simple channel models used in information theory are:
- Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
- Additive white Gaussian noise (AWGN) channel without fading.
A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).
Bit-error rate curves for BPSK, QPSK, 8-PSK and 16-PSK, AWGN channel.
In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).
For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:

People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.
Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.
A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.[3]
Mathematical draft[edit]
The BER is the likelihood of a bit misinterpretation due to electrical noise 





Knowing that the noise has a bilateral spectral density 


and 

Returning to BER, we have the likelihood of a bit misinterpretation 


where 

We can use the average energy of the signal 
±§
Bit error rate test[edit]
BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.
A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.
Common types of BERT stress patterns[edit]
- PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
- QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
- 3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
- 1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
- Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
- All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
- All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
- Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
- 2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
- Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
- Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
- T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.
Bit error rate tester[edit]
A bit error rate tester (BERT), also known as a «bit error ratio tester»[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.
The main building blocks of a BERT are:
- Pattern generator, which transmits a defined test pattern to the DUT or test system
- Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
- Clock signal generator to synchronize the pattern generator and the error detector
- Digital communication analyser is optional to display the transmitted or received signal
- Electrical-optical converter and optical-electrical converter for testing optical communication signals
See also[edit]
- Burst error
- Error correction code
- Errored second
- Pseudo bit error ratio
- Viterbi Error Rate
References[edit]
- ^ Jit Lim (14 December 2010). «Is BER the bit error ratio or the bit error rate?». EDN. Retrieved 2015-02-16.
- ^
Digital Communications, John Proakis, Massoud Salehi, McGraw-Hill Education, Nov 6, 2007 - ^
«Keyboards and Covert Channels»
by Gaurav Shah, Andres Molina, and Matt Blaze (2006?) - ^ «Bit Error Rate Testing: BER Test BERT » Electronics Notes». www.electronics-notes.com. Retrieved 2020-04-11.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).
External links[edit]
- QPSK BER for AWGN channel – online experiment
Качество сетей передачи данных. Транспорт
Время прочтения
8 мин
Просмотры 28K
В предыдущей статье были затронуты базовые метрики качества сетей и систем передачи данных. Также было обещано написать про то, как все работает изнутри. И намеренно не было упомянуто про качество среды передачи данных и ее характеристиках. Надеюсь, что новая статья даст ответы на эти вопросы.
Среда передачи
Начну, пожалуй, с последнего пункта — качества среды передачи. Как уже написано выше, про нее ничего не говорилось в предыдущем повествовании, поскольку само по себе количество сред и их характеристики очень сильно различаются и зависят от просто колоссального множества факторов. Разбираться во всем этом многообразии задача соответствующих специалистов. Всем очевидно использование радио-эфира в качестве среды передачи данных. Я же помню в конце 90-х начале 00-х особой популярностью у операторов связи стали пользоваться такие экзотические способы передачи, как лазерные атмосферные передатчики. 
Соответственно погружаясь в вопрос в результате будем иметь множество сред и ни одной обобщенной характеристики. Тем не менее для нас среда это всего лишь транспорт, передающий информацию из точки А в точку Б. А для транспорта (даже общественного) характеристикой отражающей его качество будет доставка всех битов (ну или пассажиров) без искажений и потерь (не хотелось бы лишиться части тела при перевозке, согласитесь). Т.е. мы приходим к такой обобщенной метрике качества транспорта как количество битовых ошибок, или BER (Bit error rate). В чисто пакетных сетях она практически не используется, поскольку ошибки передачи выявляются на уровне пакета, например подсчетом контрольных сумм: FCS (Frame check sequence) для L2 или сhecksum IP для L3. Если контрольная сумма не совпадает, то пакет целиком отбрасывается как невалидный. Если же рассмотреть гетерогенные сети, те в которых транспортом может служить непакетная сеть, а, например, один из вариантов описанных выше, либо вообще используется транзит через ATM, PDH, SDH и подобное без непосредственной (но с восстановлением) передачи пакета, то битовые ошибки транспорта могут значительно влиять, конечно в зависимости от технологии. Рассмотрим инкапсуляцию и передачу Ethernet-фрейма в HDLC. Другие технологии используют практически такую же технику.
Схема читается слева-направо (взята здесь).
- Какой-то узел сети А отправляет пакет в сторону какого-то узла сети Б
- Транспорт между сетями построен на сети PDH
- Узел на границе выхода сети А вырезает из Ethernet-фрейма область полезной нагрузки (поля от DestinationAddress до FCS включительно), оборачивает в HDLC заголовки, и отправляет на граничный узел входа сети Б
- Граничный узел входа сети Б выделяет область полезной нагрузки и восстанавливает Ethernet-фрейм
- Фрейм с граничного узла отправляется получателю
Как можно видеть, в данном случае контрольная передается корректно и в случае повреждения битового потока в процессе передачи восстановленный пакет с неверной FCS будет отброшен получателем. В данном случае механизм обнаружения ошибки налицо.
Но не всегда используется надстройка инкапсуляции, либо передается вообще не полноценный фрейм, а лишь поле payload. Т.е. вырезается область, оборачивается во внутренний протокол, а на другой стороне восстанавливаются недостающие данные, включая отсутствующие заголовки L2. Соответственно пропадает и FCS — она просто рассчитывается заново. Таким образом получается, если данные были повреждены, а FCS рассчитан на основании “испорченных” данных, то получатель принимает совсем не тот пакет, который ему отправляли. Это довольно часто встречается в спутниковой связи, чтобы повысить полезную утилизацию канала, избегая передачи условно “лишней” информации. Резюмируя, получается что метрика BER может быть интересна в случаях когда:
- необходимо проверить стабильность физического канала, например для оптики это 10E-12 (упоминается в IEEE802.3)
- Ethernet-фреймы упаковывают в SDH(GFP), PDH, ATM и другие транспортные сети.
- используются технологии xHSL, PPP протоколы в которые упаковывают IP пакеты
BER тест
Метрика известна — это отношение количество битовых ошибок к общему числу переданных битов. Методика измерения для сетей TDM известна как спецификация ITU-T G.821. Классически для проверки каналов используется BERT (BER Test) первого уровня, но с учетом специфики работы протоколов инкапсуляции пакетных сетей и самого принципа работы пакетных сетей необходимо иметь возможность проводить тесты на L1-L4. Немного далее будет рассмотрено подробнее. Ну а сейчас следует определиться что проверять и как проверять. На вопрос:” Что проверять?” Отвечает ITU-T 0.150. В его пункте 5 рассмотрены типы ПСП (псевдослучайных последовательностей), из которых просто берутся данные для формирования пакета. Т.е. нужно просто взять и заполнить соответствующий уровень пакета данными выбранной ПСП. У нас в приборах используются следующие ПСП:
- ПСП 2е9 (ITU-T 0.150 пункт 5.1)
- ПСП 2е11 (ITU-T 0.150 пункт 5.2)
- ПСП 2е15 (ITU-T 0.150 пункт 5.3)
- ПСП 2е23 (ITU-T 0.150 пункт 5.6)
- ПСП 2е31 (ITU-T 0.150 пункт 5.8)
- пользовательская последовательность (32 бита)
- все нули
- все единицы
- альтернативная последовательность (01010101)
Пользовательская последовательность введена для совместимости с приборами, которые существуют на рынке, т.е можно задать любую последовательность и проводить совместный тест.
Вопрос как проверять пока что открыт, попробуем разобраться. Допустим мы умеем генерировать определенные пакеты. Если отправить такой пакет на другой конец транспорта, то как понять, что он не изменился (следует абстрагироваться от пакетного принципа, поскольку у нас может не быть FCS и других типов контроля, как описано ранее)? Самый простой вариант — завернуть пакет обратно (в TDM называется “сделать петлю”, в Ethernet — установить шлейф). Заворот, во многих случаях, можно сделать на выходе канала без изменения среды передачи, т.е. реально поставить петлю на выходе E1 и все будет работать. Но т.к. данные проделывают двойной путь, то вероятность возникновения ошибки также возрастает в 2 раза. Да и каналы могут быть асимметричными или однонаправленными. Соответственно идеальным было бы иметь возможность обладать информацией о корректном следовании и сравнивать приходящие пакеты с уже известной информацией. Первый, и наиболее простой вариант, применимый когда оба выхода канала располагаются рядом (например такое возможно при TDM коммутации, или тестировании оптического “кольца”) заключается в том, что один порт прибора генерирует тестовый трафик, а другой порт этого же прибора его получает и сравнивает, а т.к. сравнение происходит в том же узле, что и генерация, то проблем со сравнением данных последовательности не возникает. Второй вариант предполагает восстановление первоначальной последовательности и сравнение ее с приходящими данными. В случае с полностью случайной последовательностью реализовать такое не представляется возможным, а вот если последовательность псевдослучайная, то вполне. Какое-то время затрачивается на синхронизацию в самом начале теста, но затем сравнение не представляет сложности. Поскольку ПСП первого прибора и ПСП второго известны и одинаковы, синхронизация сводится к поиску места начала сравнения в ПСП второго прибора. Таким образом существуют следующие топологии:
- «сам на себя» 1 — один прибор на одном порту, на другом конце транспорта стоит шлейф
- «сам на себя» 2 — один прибор с одного порта своего порта на другой свой порт
- с одного прибора на другой прибор, с синхронизацией
Еще раз стоит отметить, что тест BER не рекомендуется использовать на сетях лишь с пакетной коммутацией. Приведу пример. Допустим, уже идет тестовый поток и приборы синхронизированы (топология 3). В какой-то момент времени происходит следующее:
- формируется Ethernet-фрейм, содержащий данные ПСП
- для такого фрейма рассчитывается FCS и он укладывается в выходной буфер
- фрейм отправляется по сети на другой прибор
- по каким-то причинам происходит изменение всего одного бита внутри пакета
- получатель принимает пакет
- FCS принятого пакета не соответствует содержимому
- пакет отбрасывается (если между отправителем и получателем есть, например, коммутатор, то “кривой” пакет вообще не дойдет до получателя, т.к. будет уничтожен до него)
- отправитель формирует следующий пакет (все начинается с п.1)
В приведенном примере на шаге 8 произойдет срыв синхронизации на стороне получателя. Произойдет это потому, что отправитель возьмет следующий блок ПСП, а получатель будет сравнивать с тем блоком, который потерялся в предыдущем цикле (он ведь ничего не знает о потере). Срыв синхронизации приведет к необоснованно большому росту битовых ошибок, т.к. все вновь идущие блоки абсолютно не совпадают, что приведет к тому, что за один пакет число битовых ошибок будет увеличиваться на размер фрейма. Через какое-то время будет предпринята попытка восстановления синхронизации, но количество накопленных битовых ошибок будет сильно не соответствовать действительности.
А как в железе?
Как у других не знаю, но у наших приборов Беркут (ET, ETX, ETL, B100, а также модуль B5-GBE для MMT) дела обстоят следующим образом. Помня принцип о генерации и анализе трафика как можно ближе к физическому сегменту из первой статьи, все подобные задачи были возложены на FPGA. Упрощенная структурная схема выглядит так:
MAC ядро представлено двумя блоками: один на прием, другой на передачу. Это позволяет независимо принимать и отправлять пакеты, т.е. нет взаимовлияния очереди отправки на очередь приема и наоборот. Также с двух независимых блоков возможно вести общую статистику по полученному и отправленному трафику независимо от типа теста. Данные с блока передачи поступают на трансмиттер и отправляются в сеть, а входящие данные с трансивера поступают в блок приема.
Поскольку для некоторых топологий тестов необходим функционал шлейфа (loopback, петля), то он реализован отдельным блоком. Возможно установить шлейф уровня L1-L4:
- L1 — просто заворачивает трафик обратно (происходит это еще в трансивере)
- L2 — меняет DstMAC<->SrcMAC местами, пересчитывает FCS
- L3 — меняет DstMAC<->SrcMAC и DstIP<->SrcIP местами, пересчитывает FCS
- L4 — меняет DstMAC<->SrcMAC, DstIP<->SrcIP и DstPort<->SrcPort, пересчитывает FCS
Статистика по пакетам ведется и для режима шлейфа тоже, что позволяет грубо оценить соотношение отправленных и принятых пакетов.
Модуль генератора для каждого типа теста свой, для BERT он содержит генератор ПСП всех заявленных типов.
Работает это следующим образом. От генератора ПСП поступают данные на мультиплексор (проще говоря коммутатор), который, если не включен какой-то другой канал в данный момент, направляет поток в MAC tx модуль. MAC tx модуль, в соответствии с настройками теста (уровень BERT, размер пакета, данные полей) формирует из ПСП валидный Ethernet-фрейм и отправляет его в трансивер, который в свою очередь отправляет его в сеть. В зависимости от топологии теста фрейм либо заворачивается удаленной стороной, либо анализируется. В любом случае первичная обработка пакета не отличается. Фрейм попадает на MAC rx ядро, которое отправляет его на мультиплексор. Мультиплексор в зависимости от режима работы прибора направляет пакет либо в Loopback модуль, откуда после обработки он сразу же направляется в MAC tx для отправки, либо в модуль обработки и статистики теста, где, если потребуется, будет проведена попытка синхронизации ПСП и выполнено сравнение исходной последовательности с полученной. Результаты обработки отдаются в модуль вывода статистики.
Использование FPGA или ASIC позволяет все операции проводить параллельно, что не вносит какие либо задержки на обработку и исключает взаимовлияние модулей обработки.
Заключение
Несмотря на всю кажущуюся простоту алгоритмов и методик, за ними стоит много лет серьезных исследований. Огромное число факторов до сих пор влияет как на точность измерений, так и на стоимость приборов (прецизионные элементы, высокоскоростные ПЛИС). Например, приведенный выше BER тест не отличается значительной сложностью в общем алгоритмическом плане, но требует знаний в области математики, информатики и теории информации для разработки жизнеспособной модели. Модификация BER теста для пакетных сетей (поддержка уровней L2-L4) требует глубокого понимания принципов коммутации и маршрутизации. Надеюсь, что подобного рода статьи интересны и приносят пользу. В следующих публикациях планирую написать про сертифицированные тесты, генераторы трафика, фильтры и аналитические комплексы. Ведь как сказал Джон Фицджеральд Кеннеди на выступлении перед гражданами США перед стартом Лунной программы:
“И мы сделаем это. Не потому, что это легко, а потому что трудно.”
PS. Задавайте вопросы и предлагайте темы, в рамках нашей компетенции готовы на все 
Анализатор Greenlee DataScout 1G позволяет выполнить BERT тестирование потока E1 (2048 Кбит/с). Он предоставляет инженеру возможность вставки единичных, непрерывных, а также следующих с заданной частотой кодовых, кадровых, CRC и BPV ошибок. Это дает возможность оператору подтверждать результаты тестов и исследовать обработку ошибок тестируемой системой.
На рисунках 1 и 2 показана типовая установка для тестирования битовых ошибок в режиме шлейфа (Loopback) или в сквозном режиме «точка-точка».
После подключения кабеля Bantam или RJ-45 и настройки анализатора в меню «Настройки», нажмите кнопку «ПУСК» для начала тестирования BERT.
Тестирование битовых ошибок E1 – BERT
С использованием петли или сквозного подключения
- Сетевой коммутатор
Рисунок 1 — Тестирование BERT с закольцовыванием
Рисунок 2 — Сквозное тестирование BERT
При обнаружении ошибок значение на счетчике LOGIC (LGC) ERROR увеличивается.
Светодиодный индикатор Pattern Sync загорится зеленым цветом, если передаваемая последовательность совпадает с принимаемой.
 |
|
|
|
Для просмотра гистограммы выбранного измерения нажмите на соответствующее поле в столбце ERROR (ошибка). Это поле изменит цвет с белого на зеленый, и ниже появится гистограмма.
Если в поле подменю для гистограмм показано ERROR INJECTION SUBMENU (подменю ввода ошибки), нажмите кнопку «Вправо», чтобы его открыть.
Меню ALARM (тревога)
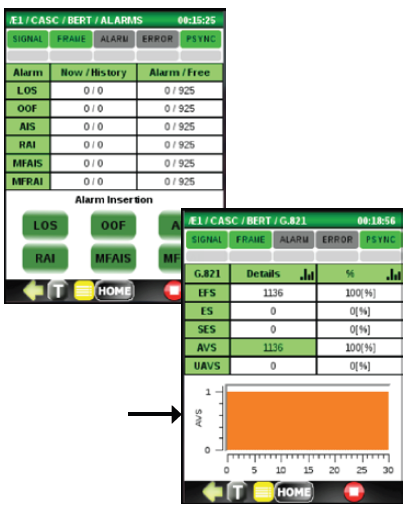
Используйте это меню для:
- Проверки того, какие сигналы тревоги вызвали включение красного светодиодного индикатора ALARM.
- Принудительного использования одного из доступных типов ошибок на передатчике E1:
- LOS (потеря сигнала)
- OOF (выпадение из синхронизации)
- OOMF (выпадение из мультикадровой синхронизации)
- AIS (индикация тревоги для всех единиц)
- REMOTE (индикация удаленной тревоги)
Для выхода нажмите кнопку «Влево».
Меню G.821 ERROR
Чтобы войти в это меню, нажмите в меню ALARM кнопку «Вправо».
Для выхода нажмите кнопку «Влево».
СОДЕРЖАНИЕ:
-
Настройка анализатора Greenlee DataScout 1G
-
Автоматический анализ параметров потока E1
-
Мониторинг потока E1 без прекращения его работы
-
Тестирование битовых ошибок (BERT)
-
Измерение задержки распространения E1 (PDL)
-
Анализ формы импульса E1 (Pulse Shape)
Содержание
- Тестирование битовых ошибок (BERT)
- Меню ALARM (тревога)
- Меню G.821 ERROR
- Bit Errror Rate Test (BERT) explained
- BERT introduction
- Why BERT
- BERT Physical setup and considerations
- Pattern selection options
- Error injecting Options
- Use cases, Best Practices and Conclusion
- Качество сетей передачи данных. Транспорт
- Среда передачи
- BER тест
- А как в железе?
- Заключение
Тестирование битовых ошибок (BERT)
Анализатор Greenlee DataScout 1G позволяет выполнить BERT тестирование потока E1 (2048 Кбит/с). Он предоставляет инженеру возможность вставки единичных, непрерывных, а также следующих с заданной частотой кодовых, кадровых, CRC и BPV ошибок. Это дает возможность оператору подтверждать результаты тестов и исследовать обработку ошибок тестируемой системой.
На рисунках 1 и 2 показана типовая установка для тестирования битовых ошибок в режиме шлейфа (Loopback) или в сквозном режиме «точка-точка».
После подключения кабеля Bantam или RJ-45 и настройки анализатора в меню «Настройки», нажмите кнопку «ПУСК» для начала тестирования BERT.
Тестирование битовых ошибок E1 – BERT
С использованием петли или сквозного подключения
Рисунок 1 — Тестирование BERT с закольцовыванием
Рисунок 2 — Сквозное тестирование BERT
При обнаружении ошибок значение на счетчике LOGIC (LGC) ERROR увеличивается.
Светодиодный индикатор Pattern Sync загорится зеленым цветом, если передаваемая последовательность совпадает с принимаемой.
 |
|
|
|
Для просмотра гистограммы выбранного измерения нажмите на соответствующее поле в столбце ERROR (ошибка). Это поле изменит цвет с белого на зеленый, и ниже появится гистограмма.
Если в поле подменю для гистограмм показано ERROR INJECTION SUBMENU (подменю ввода ошибки), нажмите кнопку «Вправо» , чтобы его открыть.
Меню ALARM (тревога)

Используйте это меню для:
- Проверки того, какие сигналы тревоги вызвали включение красного светодиодного индикатора ALARM.
- Принудительного использования одного из доступных типов ошибок на передатчике E1:
- LOS (потеря сигнала)
- OOF (выпадение из синхронизации)
- OOMF (выпадение из мультикадровой синхронизации)
- AIS (индикация тревоги для всех единиц)
- REMOTE (индикация удаленной тревоги)
Для выхода нажмите кнопку «Влево» .
Меню G.821 ERROR
Чтобы войти в это меню, нажмите в меню ALARM кнопку «Вправо» .
Источник
Bit Errror Rate Test (BERT) explained

BERT introduction
As you can guess from the name this test is really to test physical layer traffic for any anomalies. This is a result from the test origins where T1/E1 circuits have been tested and each bit in each time-slot mattered as the providers were using those up to the limit as bandwidth was scarce. Also as most of the data being transferred were voice calls any pattern alterations had quite serious implications on the quality of service. This also led to the (in)famous reliability of five nines or the 99.999% which basically states that the link/device must be available 99.999% throughout a specified SLA period (normally a month or a year). One must remember that redundancy was rather rare so the requirements for hardware reliability was really high. But by the move away from the circuit-based TDM networks towards the packet-based IP networks the requirements changed. The bandwidth is now in abundance in most places and the wide deployment of advanced Ethernet and IP feature rich devices provides with plenty options for redundancy and QoS with packet-switched voice traffic on rise – one would think it is not really necessary to consider BERT as something one should use as test method but that would be huge mistake.
Why BERT
There are few considerations that can make BERT an interesting choice. I will list some I think are the most interesting.
- It has been designed to run for extended period of time which makes it ideal for acceptance testing which is still often required
- BERT is ideal for testing jitter as it was one of the primary design goals
- The different patters used in BERT can be used for packet optimization testing (I will discuss this later in more detail)
- Most of the BERT tests are smarter than just counting bit errors so the test can be used for other testing
BERT Physical setup and considerations
On Ethernet network you cannot run a simple L1 test unless you test just a piece of cable or potentially a hub as all other devices would require some address processing. This makes the test being different on Ethernet network from unframed E1 as unlike on E1 we need to set framing to Ethernet with the source and destination defined on the tester. Also as Ethernet must be looped on a logical level it is not possible to use simple RJ45 with pair of wires going from TX to RX as you could with E1 and either hardware or software loopback reflector is required. Most tester will actually allow you to specify even layer 3 and 4 for IP addresses and UDP ports. The reason is usually so the management traffic between tester and loopbacks can use this channel for internal communication.
Pattern selection options
As thi s test originates from the telco industry some interesting options are usually presented on the testers. The stream can generate these patterns:
- All zeros or all ones – which are specific patters originated from TDM environment
- 0101 pattern and 1010 pattern – patterns that can be easily compressed
- PRBS – Pseudo Random Bit Sequence – is an deterministic sequence that cannot be compressed/optimized the details and calculation can be found on wikipedia
- Inverted PRBS – the same as above but the calculation function is inversed to counter any “optimization” for the PRBS
The thing to remember is that PRBS will be applied to the payload of the frame/packet/datagram so it there is any sort of optimization present it will have no effect as PRBS is by design not compressible. There are various “strengths” of the pseudo-random pattern the higher the number the less repeating it will include. Normally it is possible to see two main variants: 2^15 which is 32,767 bits long and 2^23 which 8,388,607 bits long. Obviously the longer the pattern the better and more “random” behavior it emulates.
Error injecting Options
As this test originated in telco world injecting errors was a major thing but in Ethernet network it lost its importance. If you inject even a single bit error in an Ethernet frame the CRC should be incorrect and the whole frame should be dropped on first L2 equipment it will be passed through which should always result in alarm LoF(Loss of Frame)/LoP (Loss of Pattern).
Use cases, Best Practices and Conclusion
The most common use case for BERT in nowadays network would be in commissioning new links as you can run a fairly simple test for a long time that will give you a reasonable idea bout it’s quality in terms of frames drops and jitter.
The few recommendations about how to run this test would be as follows:
- Use the largest pattern you can.
- Remember that the line rate and L2 rates will be different because of the overheads.
- Remember that 99.999% of availability results in 0.8s outage in 24 hours (which can be quite a lot of frames)
- PRBS cannot be optimized
Источник
Качество сетей передачи данных. Транспорт

В предыдущей статье были затронуты базовые метрики качества сетей и систем передачи данных. Также было обещано написать про то, как все работает изнутри. И намеренно не было упомянуто про качество среды передачи данных и ее характеристиках. Надеюсь, что новая статья даст ответы на эти вопросы.
Среда передачи
Начну, пожалуй, с последнего пункта — качества среды передачи. Как уже написано выше, про нее ничего не говорилось в предыдущем повествовании, поскольку само по себе количество сред и их характеристики очень сильно различаются и зависят от просто колоссального множества факторов. Разбираться во всем этом многообразии задача соответствующих специалистов. Всем очевидно использование радио-эфира в качестве среды передачи данных. Я же помню в конце 90-х начале 00-х особой популярностью у операторов связи стали пользоваться такие экзотические способы передачи, как лазерные атмосферные передатчики. 
Соответственно погружаясь в вопрос в результате будем иметь множество сред и ни одной обобщенной характеристики. Тем не менее для нас среда это всего лишь транспорт, передающий информацию из точки А в точку Б. А для транспорта (даже общественного) характеристикой отражающей его качество будет доставка всех битов (ну или пассажиров) без искажений и потерь (не хотелось бы лишиться части тела при перевозке, согласитесь). Т.е. мы приходим к такой обобщенной метрике качества транспорта как количество битовых ошибок, или BER (Bit error rate). В чисто пакетных сетях она практически не используется, поскольку ошибки передачи выявляются на уровне пакета, например подсчетом контрольных сумм: FCS (Frame check sequence) для L2 или сhecksum IP для L3. Если контрольная сумма не совпадает, то пакет целиком отбрасывается как невалидный. Если же рассмотреть гетерогенные сети, те в которых транспортом может служить непакетная сеть, а, например, один из вариантов описанных выше, либо вообще используется транзит через ATM, PDH, SDH и подобное без непосредственной (но с восстановлением) передачи пакета, то битовые ошибки транспорта могут значительно влиять, конечно в зависимости от технологии. Рассмотрим инкапсуляцию и передачу Ethernet-фрейма в HDLC. Другие технологии используют практически такую же технику.
Схема читается слева-направо (взята здесь).
- Какой-то узел сети А отправляет пакет в сторону какого-то узла сети Б
- Транспорт между сетями построен на сети PDH
- Узел на границе выхода сети А вырезает из Ethernet-фрейма область полезной нагрузки (поля от DestinationAddress до FCS включительно), оборачивает в HDLC заголовки, и отправляет на граничный узел входа сети Б
- Граничный узел входа сети Б выделяет область полезной нагрузки и восстанавливает Ethernet-фрейм
- Фрейм с граничного узла отправляется получателю
Как можно видеть, в данном случае контрольная передается корректно и в случае повреждения битового потока в процессе передачи восстановленный пакет с неверной FCS будет отброшен получателем. В данном случае механизм обнаружения ошибки налицо.
Но не всегда используется надстройка инкапсуляции, либо передается вообще не полноценный фрейм, а лишь поле payload. Т.е. вырезается область, оборачивается во внутренний протокол, а на другой стороне восстанавливаются недостающие данные, включая отсутствующие заголовки L2. Соответственно пропадает и FCS — она просто рассчитывается заново. Таким образом получается, если данные были повреждены, а FCS рассчитан на основании “испорченных” данных, то получатель принимает совсем не тот пакет, который ему отправляли. Это довольно часто встречается в спутниковой связи, чтобы повысить полезную утилизацию канала, избегая передачи условно “лишней” информации. Резюмируя, получается что метрика BER может быть интересна в случаях когда:
- необходимо проверить стабильность физического канала, например для оптики это 10E-12 (упоминается в IEEE802.3)
- Ethernet-фреймы упаковывают в SDH(GFP), PDH, ATM и другие транспортные сети.
- используются технологии xHSL, PPP протоколы в которые упаковывают IP пакеты
BER тест
Метрика известна — это отношение количество битовых ошибок к общему числу переданных битов. Методика измерения для сетей TDM известна как спецификация ITU-T G.821. Классически для проверки каналов используется BERT (BER Test) первого уровня, но с учетом специфики работы протоколов инкапсуляции пакетных сетей и самого принципа работы пакетных сетей необходимо иметь возможность проводить тесты на L1-L4. Немного далее будет рассмотрено подробнее. Ну а сейчас следует определиться что проверять и как проверять. На вопрос:” Что проверять?” Отвечает ITU-T 0.150. В его пункте 5 рассмотрены типы ПСП (псевдослучайных последовательностей), из которых просто берутся данные для формирования пакета. Т.е. нужно просто взять и заполнить соответствующий уровень пакета данными выбранной ПСП. У нас в приборах используются следующие ПСП:
- ПСП 2е9 (ITU-T 0.150 пункт 5.1)
- ПСП 2е11 (ITU-T 0.150 пункт 5.2)
- ПСП 2е15 (ITU-T 0.150 пункт 5.3)
- ПСП 2е23 (ITU-T 0.150 пункт 5.6)
- ПСП 2е31 (ITU-T 0.150 пункт 5.8)
- пользовательская последовательность (32 бита)
- все нули
- все единицы
- альтернативная последовательность (01010101)
Пользовательская последовательность введена для совместимости с приборами, которые существуют на рынке, т.е можно задать любую последовательность и проводить совместный тест.
Вопрос как проверять пока что открыт, попробуем разобраться. Допустим мы умеем генерировать определенные пакеты. Если отправить такой пакет на другой конец транспорта, то как понять, что он не изменился (следует абстрагироваться от пакетного принципа, поскольку у нас может не быть FCS и других типов контроля, как описано ранее)? Самый простой вариант — завернуть пакет обратно (в TDM называется “сделать петлю”, в Ethernet — установить шлейф). Заворот, во многих случаях, можно сделать на выходе канала без изменения среды передачи, т.е. реально поставить петлю на выходе E1 и все будет работать. Но т.к. данные проделывают двойной путь, то вероятность возникновения ошибки также возрастает в 2 раза. Да и каналы могут быть асимметричными или однонаправленными. Соответственно идеальным было бы иметь возможность обладать информацией о корректном следовании и сравнивать приходящие пакеты с уже известной информацией. Первый, и наиболее простой вариант, применимый когда оба выхода канала располагаются рядом (например такое возможно при TDM коммутации, или тестировании оптического “кольца”) заключается в том, что один порт прибора генерирует тестовый трафик, а другой порт этого же прибора его получает и сравнивает, а т.к. сравнение происходит в том же узле, что и генерация, то проблем со сравнением данных последовательности не возникает. Второй вариант предполагает восстановление первоначальной последовательности и сравнение ее с приходящими данными. В случае с полностью случайной последовательностью реализовать такое не представляется возможным, а вот если последовательность псевдослучайная, то вполне. Какое-то время затрачивается на синхронизацию в самом начале теста, но затем сравнение не представляет сложности. Поскольку ПСП первого прибора и ПСП второго известны и одинаковы, синхронизация сводится к поиску места начала сравнения в ПСП второго прибора. Таким образом существуют следующие топологии:
- «сам на себя» 1 — один прибор на одном порту, на другом конце транспорта стоит шлейф
- «сам на себя» 2 — один прибор с одного порта своего порта на другой свой порт
- с одного прибора на другой прибор, с синхронизацией
Еще раз стоит отметить, что тест BER не рекомендуется использовать на сетях лишь с пакетной коммутацией. Приведу пример. Допустим, уже идет тестовый поток и приборы синхронизированы (топология 3). В какой-то момент времени происходит следующее:
- формируется Ethernet-фрейм, содержащий данные ПСП
- для такого фрейма рассчитывается FCS и он укладывается в выходной буфер
- фрейм отправляется по сети на другой прибор
- по каким-то причинам происходит изменение всего одного бита внутри пакета
- получатель принимает пакет
- FCS принятого пакета не соответствует содержимому
- пакет отбрасывается (если между отправителем и получателем есть, например, коммутатор, то “кривой” пакет вообще не дойдет до получателя, т.к. будет уничтожен до него)
- отправитель формирует следующий пакет (все начинается с п.1)
В приведенном примере на шаге 8 произойдет срыв синхронизации на стороне получателя. Произойдет это потому, что отправитель возьмет следующий блок ПСП, а получатель будет сравнивать с тем блоком, который потерялся в предыдущем цикле (он ведь ничего не знает о потере). Срыв синхронизации приведет к необоснованно большому росту битовых ошибок, т.к. все вновь идущие блоки абсолютно не совпадают, что приведет к тому, что за один пакет число битовых ошибок будет увеличиваться на размер фрейма. Через какое-то время будет предпринята попытка восстановления синхронизации, но количество накопленных битовых ошибок будет сильно не соответствовать действительности.
А как в железе?
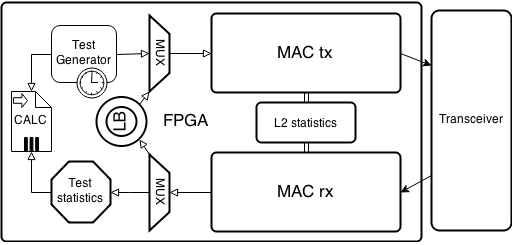
Как у других не знаю, но у наших приборов Беркут (ET, ETX, ETL, B100, а также модуль B5-GBE для MMT) дела обстоят следующим образом. Помня принцип о генерации и анализе трафика как можно ближе к физическому сегменту из первой статьи, все подобные задачи были возложены на FPGA. Упрощенная структурная схема выглядит так:
MAC ядро представлено двумя блоками: один на прием, другой на передачу. Это позволяет независимо принимать и отправлять пакеты, т.е. нет взаимовлияния очереди отправки на очередь приема и наоборот. Также с двух независимых блоков возможно вести общую статистику по полученному и отправленному трафику независимо от типа теста. Данные с блока передачи поступают на трансмиттер и отправляются в сеть, а входящие данные с трансивера поступают в блок приема.
Поскольку для некоторых топологий тестов необходим функционал шлейфа (loopback, петля), то он реализован отдельным блоком. Возможно установить шлейф уровня L1-L4:
- L1 — просто заворачивает трафик обратно (происходит это еще в трансивере)
- L2 — меняет DstMAC SrcMAC местами, пересчитывает FCS
- L3 — меняет DstMAC SrcMAC и DstIP SrcIP местами, пересчитывает FCS
- L4 — меняет DstMAC SrcMAC, DstIP SrcIP и DstPort SrcPort, пересчитывает FCS
Статистика по пакетам ведется и для режима шлейфа тоже, что позволяет грубо оценить соотношение отправленных и принятых пакетов.
Модуль генератора для каждого типа теста свой, для BERT он содержит генератор ПСП всех заявленных типов.
Работает это следующим образом. От генератора ПСП поступают данные на мультиплексор (проще говоря коммутатор), который, если не включен какой-то другой канал в данный момент, направляет поток в MAC tx модуль. MAC tx модуль, в соответствии с настройками теста (уровень BERT, размер пакета, данные полей) формирует из ПСП валидный Ethernet-фрейм и отправляет его в трансивер, который в свою очередь отправляет его в сеть. В зависимости от топологии теста фрейм либо заворачивается удаленной стороной, либо анализируется. В любом случае первичная обработка пакета не отличается. Фрейм попадает на MAC rx ядро, которое отправляет его на мультиплексор. Мультиплексор в зависимости от режима работы прибора направляет пакет либо в Loopback модуль, откуда после обработки он сразу же направляется в MAC tx для отправки, либо в модуль обработки и статистики теста, где, если потребуется, будет проведена попытка синхронизации ПСП и выполнено сравнение исходной последовательности с полученной. Результаты обработки отдаются в модуль вывода статистики.
Использование FPGA или ASIC позволяет все операции проводить параллельно, что не вносит какие либо задержки на обработку и исключает взаимовлияние модулей обработки.
Заключение
“И мы сделаем это. Не потому, что это легко, а потому что трудно.”
PS. Задавайте вопросы и предлагайте темы, в рамках нашей компетенции готовы на все 🙂
Источник
This topic describes how to compute error statistics for various communications
systems.
Computation of Theoretical Error Statistics
The biterr function, discussed in the
Compute SERs and BERs Using Simulated Data section, can help you gather empirical error
statistics, but validating your results by comparing them to the theoretical error
statistics is good practice. For certain types of communications systems,
closed-form expressions exist for the computation of the bit error rate (BER) or an
approximate bound on the BER. The functions listed in this table compute the
closed-form expressions for the BER or a bound on it for the specified types of
communications systems.
| Type of Communications System | Function |
|---|---|
| Uncoded AWGN channel | berawgn
|
| Uncoded Rayleigh and Rician fading channel | berfading
|
| Coded AWGN channel | bercoding |
| Uncoded AWGN channel with imperfect synchronization | bersync
|
The analytical expressions used in these functions are discussed in
Analytical Expressions Used in BER Analysis. The reference pages of these functions also list
references to one or more books containing the closed-form expressions implemented
by the function.
Theoretical Performance Results
-
Plot Theoretical Error Rates
-
Compare Theoretical and Empirical Error Rates
Plot Theoretical Error Rates
This example uses the bercoding function to compute upper bounds on BERs for convolutional coding with a soft-decision decoder.
coderate = 1/4; % Code rate
Create a structure, dspec, with information about the distance spectrum. Define the energy per bit to noise power spectral density ratio (Eb/N0) sweep range and generate the theoretical bound results.
dspec.dfree = 10; % Minimum free distance of code dspec.weight = [1 0 4 0 12 0 32 0 80 0 192 0 448 0 1024 ... 0 2304 0 5120 0]; % Distance spectrum of code EbNo = 3:0.5:8; berbound = bercoding(EbNo,'conv','soft',coderate,dspec);
Plot the theoretical bound results.
semilogy(EbNo,berbound) xlabel('E_b/N_0 (dB)'); ylabel('Upper Bound on BER'); title('Theoretical Bound on BER for Convolutional Coding'); grid on;
Compare Theoretical and Empirical Error Rates
Using the berawgn function, compute the theoretical symbol error rates (SERs) for pulse amplitude modulation (PAM) over a range of Eb/N0 values. Simulate 8 PAM with an AWGN channel, and compute the empirical SERs. Compare the theoretical and then empirical SERs by plotting them on the same set of axes.
Compute and plot the theoretical SER using berawgn.
rng('default') % Set random number seed for repeatability M = 8; EbNo = 0:13; [ber,ser] = berawgn(EbNo,'pam',M); semilogy(EbNo,ser,'r'); legend('Theoretical SER'); title('Theoretical Error Rate'); xlabel('E_b/N_0 (dB)'); ylabel('Symbol Error Rate'); grid on;
Compute the empirical SER by simulating an 8 PAM communications system link. Define simulation parameters and preallocate variables needed for the results. As described in [1], because N0=2×(NVariance)2, add 3 dB to the Eb/N0 value when converting Eb/N0 values to SNR values.
n = 10000; % Number of symbols to process k = log2(M); % Number of bits per symbol snr = EbNo+3+10*log10(k); % In dB ynoisy = zeros(n,length(snr)); z = zeros(n,length(snr)); errVec = zeros(3,length(EbNo));
Create an error rate calculator System object™ to compare decoded symbols to the original transmitted symbols.
errcalc = comm.ErrorRate;
Generate a random data message and apply PAM. Normalize the channel to the signal power. Loop the simulation to generate error rates over the range of SNR values.
x = randi([0 M-1],n,1); % Create message signal y = pammod(x,M); % Modulate signalpower = (real(y)'*real(y))/length(real(y)); for jj = 1:length(snr) reset(errcalc) ynoisy(:,jj) = awgn(real(y),snr(jj),'measured'); % Add AWGN z(:,jj) = pamdemod(complex(ynoisy(:,jj)),M); % Demodulate errVec(:,jj) = errcalc(x,z(:,jj)); % Compute SER from simulation end
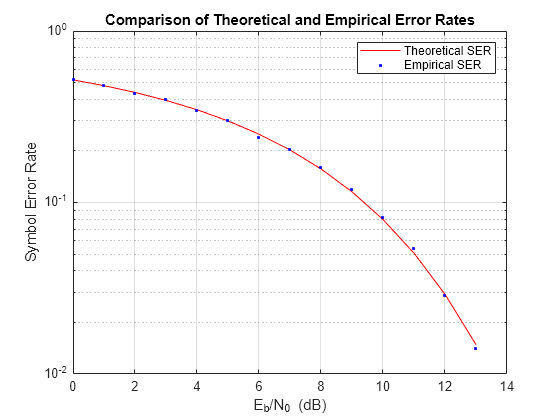
Compare the theoretical and empirical results.
hold on; semilogy(EbNo,errVec(1,:),'b.'); legend('Theoretical SER','Empirical SER'); title('Comparison of Theoretical and Empirical Error Rates'); hold off;
Performance Results via Simulation
-
Section Overview
-
Compute SERs and BERs Using Simulated Data
Section Overview
This section describes how to compare the data messages that enter and leave
a communications system simulation and how to compute error statistics using the
Monte Carlo technique. Simulations can measure system performance by using the
data messages before transmission and after reception to compute the BER or SER
for a communications system. To explore physical layer components used to model
and simulate communications systems, see PHY Components.
Curve fitting can be useful when you have a small or imperfect data set but
want to plot a smooth curve for presentation purposes. To explore the use of
curve fitting when computing performance results via simulation, see the Curve Fitting for Error Rate Plots section.
Compute SERs and BERs Using Simulated Data
The example shows how to compute SERs and BERs using the biterr and symerr functions, respectively. The symerr function compares two sets of data and computes the number of symbol errors and the SER. The biterr function compares two sets of data and computes the number of bit errors and the BER. An error is a discrepancy between corresponding points in the two sets of data.
The two sets of data typically represent messages entering a transmitter and recovered messages leaving a receiver. You can also compare data entering and leaving other parts of your communications system (for example, data entering an encoder and data leaving a decoder).
If your communications system uses several bits to represent one symbol, counting symbol errors is different from counting bit errors. In either the symbol- or bit-counting case, the error rate is the number of errors divided by the total number of transmitted symbols or bits, respectively.
Typically, simulating enough data to produce at least 100 errors provides accurate error rate results. If the error rate is very small (for example, 10-6 or less), using the semianalytic technique might compute the result more quickly than using a simulation-only approach. For more information, see the Performance Results via Semianalytic Technique section.
Compute Error Rates
Use the symerr function to compute the SERs for a noisy linear block code. Apply no digital modulation, so that each symbol contains a single bit. When each symbol is a single bit, the symbol errors and bit errors are the same.
After artificially adding noise to the encoded message, compare the resulting noisy code to the original code. Then, decode and compare the decoded message to the original message.
m = 3; % Set parameters for Hamming code n = 2^m-1; k = n-m; msg = randi([0 1],k*200,1); % Specify 200 messages of k bits each code = encode(msg,n,k,'hamming'); codenoisy = bsc(code,0.95); % Add noise newmsg = decode(codenoisy,n,k,'hamming'); % Decode and correct errors
Compute the SERs.
[~,noisyVec] = symerr(code,codenoisy); [~,decodedVec] = symerr(msg,newmsg);
The error rate decreases after decoding because the Hamming decoder correct errors based on the error-correcting capability of the decoder configuration. Because random number generators produce the message and noise is added, results vary from run to run. Display the SERs.
disp(['SER in the received code: ',num2str(noisyVec(1))])
SER in the received code: 0.94571
disp(['SER after decoding: ',num2str(decodedVec(1))])
SER after decoding: 0.9675
Comparing SER and BER
These commands show the difference between symbol errors and bit errors in various situations.
Create two three-element decimal vectors and show the binary representation. The vector a contains three 2-bit symbols, and the vector b contains three 3-bit symbols.
bpi = 3; % Bits per integer
a = [1 2 3];
b = [1 4 4];
int2bit(a,bpi)
ans = 3×3
0 0 0
0 1 1
1 0 1
ans = 3×3
0 1 1
0 0 0
1 0 0
Compare the binary values of the two vectors and compute the number of errors and the error rate by using the biterr and symerr functions.
format rat % Display fractions instead of decimals [snum,srate] = symerr(a,b)
snum is 2 because the second and third entries have bit differences. srate is 2/3 because the total number of symbols is 3.
[bnum,brate] = biterr(a,b)
bnum is 5 because the second entries differ in two bits, and the third entries differ in three bits. brate is 5/9 because the total number of bits is 9. By definition, the total number of bits is the number of entries in a for symbol error computations or b for bit error computations times the maximum number of bits among all entries of a and b, respectively.
Performance Results via Semianalytic Technique
The technique described in the Performance Results via Simulation
section can work for a large variety of communications systems but can be
prohibitively time-consuming for small error rates (for example,
10-6 or less). The semianalytic technique is an
alternative way to compute error rates. The semianalytic technique can produce
results faster than a nonanalytic method that uses simulated data.
For more information on implementing the semianalytic technique using a
combination of simulation and analysis to determine the error rate of a
communications system, see the semianalytic function.
Error Rate Plots
-
Section Overview
-
Creation of Error Rate Plots Using
semilogy
Function -
Curve Fitting for Error Rate Plots
-
Use Curve Fitting on Error Rate Plot
Section Overview
Error rate plots can be useful when examining the performance of a
communications system and are often included in publications. This section
discusses and demonstrates tools you can use to create error rate plots, modify
them to suit your needs, and perform curve fitting on the error rate data and
the plots.
Creation of Error Rate Plots Using semilogy Function
In many error rate plots, the horizontal axis indicates
Eb/N0
values in dB, and the vertical axis indicates the error rate using a logarithmic
(base 10) scale. For examples that create such a plot using the semilogy function, see Compare Theoretical and Empirical Error Rates and Plot Theoretical Error Rates.
Curve Fitting for Error Rate Plots
Curve fitting can be useful when you have a small or imperfect data set but
want to plot a smooth curve for presentation purposes. The berfit function includes
curve-fitting capabilities that help your analysis when the empirical data
describes error rates at different
Eb/N0
values. This function enables you to:
-
Customize various relevant aspects of the curve-fitting process, such
as a list of selections for the type of closed-form function used to
generate the fit. -
Plot empirical data along with a curve that
berfitfits to the
data. -
Interpolate points on the fitted curve between
Eb/N0
values in your empirical data set to smooth the plot. -
Collect relevant information about the fit, such as the numerical
values of points along the fitted curve and the coefficients of the fit
expression.
Note
The berfit function is
intended for curve fitting or interpolation, not extrapolation.
Extrapolating BER data beyond an order of magnitude below the smallest
empirical BER value is inherently unreliable.
Use Curve Fitting on Error Rate Plot
This example simulates a simple differential binary phase shift keying (DBPSK) communications system and plots error rate data for a series of Eb/N0 values. It uses the berfit and berconfint functions to fit a curve to a set of empirical error rates.
Initialize Simulation Parameters
Specify the input signal message length, modulation order, range of Eb/N0 values to simulate, and the minimum number of errors that must occur before the simulation computes an error rate for a given Eb/N0 value. Preallocate variables for final results and interim results.
Typically, for statistically accurate error rate results, the minimum number of errors must be on the order of 100. This simulation uses a small number of errors to shorten the run time and to illustrate how curve fitting can smooth a set of results.
siglen = 100000; % Number of bits in each trial M = 2; % DBPSK is binary EbN0vec = 0:5; % Vector of EbN0 values minnumerr = 5; % Compute BER after only 5 errors occur numEbN0 = length(EbN0vec); % Number of EbN0 values ber = zeros(1,numEbN0); % Final BER values berVec = zeros(3,numEbN0); % Updated BER values intv = cell(1,numEbN0); % Cell array of confidence intervals
Create an error rate calculator System object™.
errorCalc = comm.ErrorRate;
Loop the Simulation
Simulate the DBPSK-modulated communications system and compute the BER using a for loop to vary the Eb/N0 value. The inner while loop ensures that a minimum number of bit errors occur for each Eb/N0 value. Error rate statistics are saved for each Eb/N0 value and used later in this example when curve fitting and plotting.
for jj = 1:numEbN0 EbN0 = EbN0vec(jj); snr = EbN0; % For binary modulation SNR = EbN0 reset(errorCalc) while (berVec(2,jj) < minnumerr) msg = randi([0,M-1],siglen,1); % Generate message sequence txsig = dpskmod(msg,M); % Modulate rxsig = awgn(txsig,snr,'measured'); % Add noise decodmsg = dpskdemod(rxsig,M); % Demodulate berVec(:,jj) = errorCalc(msg,decodmsg); % Calculate BER end
Use the berconfint function to compute the error rate at a 98% confidence interval for the Eb/N0 values.
[ber(jj),intv1] = berconfint(berVec(2,jj),berVec(3,jj),0.98);
intv{jj} = intv1;
disp(['EbN0 = ' num2str(EbN0) ' dB, ' num2str(berVec(2,jj)) ...
' errors, BER = ' num2str(ber(jj))])
end
EbN0 = 0 dB, 18392 errors, BER = 0.18392 EbN0 = 1 dB, 14307 errors, BER = 0.14307 EbN0 = 2 dB, 10190 errors, BER = 0.1019 EbN0 = 3 dB, 6940 errors, BER = 0.0694 EbN0 = 4 dB, 4151 errors, BER = 0.04151 EbN0 = 5 dB, 2098 errors, BER = 0.02098
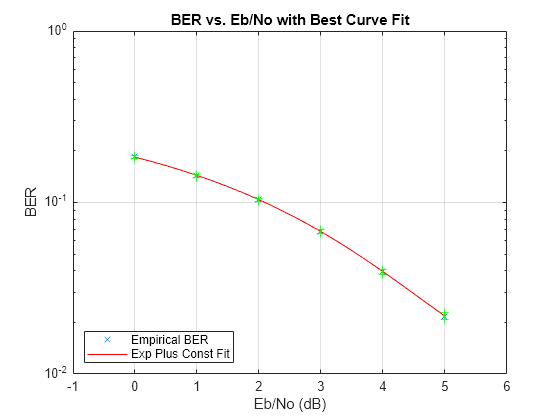
Use the berfit function to plot the best fitted curve, interpolating between BER points to get a smooth plot. Add confidence intervals to the plot.
fitEbN0 = EbN0vec(1):0.25:EbN0vec(end); % Interpolation values berfit(EbN0vec,ber,fitEbN0); hold on; for jj=1:numEbN0 semilogy([EbN0vec(jj) EbN0vec(jj)],intv{jj},'g-+'); end hold off;
See Also
Apps
- Bit Error Rate Analysis
Functions
berawgn|bercoding|berconfint|berfading|berfit|bersync
Related Topics
- Analyze Performance with Bit Error Rate Analysis App
- Analytical Expressions Used in BER Analysis

BERT introduction
As you can guess from the name this test is really to test physical layer traffic for any anomalies. This is a result from the test origins where T1/E1 circuits have been tested and each bit in each time-slot mattered as the providers were using those up to the limit as bandwidth was scarce. Also as most of the data being transferred were voice calls any pattern alterations had quite serious implications on the quality of service. This also led to the (in)famous reliability of five nines or the 99.999% which basically states that the link/device must be available 99.999% throughout a specified SLA period (normally a month or a year). One must remember that redundancy was rather rare so the requirements for hardware reliability was really high. But by the move away from the circuit-based TDM networks towards the packet-based IP networks the requirements changed. The bandwidth is now in abundance in most places and the wide deployment of advanced Ethernet and IP feature rich devices provides with plenty options for redundancy and QoS with packet-switched voice traffic on rise – one would think it is not really necessary to consider BERT as something one should use as test method but that would be huge mistake.
Why BERT
There are few considerations that can make BERT an interesting choice. I will list some I think are the most interesting.
- It has been designed to run for extended period of time which makes it ideal for acceptance testing which is still often required
- BERT is ideal for testing jitter as it was one of the primary design goals
- The different patters used in BERT can be used for packet optimization testing (I will discuss this later in more detail)
- Most of the BERT tests are smarter than just counting bit errors so the test can be used for other testing
BERT Physical setup and considerations
On Ethernet network you cannot run a simple L1 test unless you test just a piece of cable or potentially a hub as all other devices would require some address processing. This makes the test being different on Ethernet network from unframed E1 as unlike on E1 we need to set framing to Ethernet with the source and destination defined on the tester. Also as Ethernet must be looped on a logical level it is not possible to use simple RJ45 with pair of wires going from TX to RX as you could with E1 and either hardware or software loopback reflector is required. Most tester will actually allow you to specify even layer 3 and 4 for IP addresses and UDP ports. The reason is usually so the management traffic between tester and loopbacks can use this channel for internal communication.
Pattern selection options
As this test originates from the telco industry some interesting options are usually presented on the testers. The stream can generate these patterns:
- All zeros or all ones – which are specific patters originated from TDM environment
- 0101 pattern and 1010 pattern – patterns that can be easily compressed
- PRBS – Pseudo Random Bit Sequence – is an deterministic sequence that cannot be compressed/optimized the details and calculation can be found on wikipedia
- Inverted PRBS – the same as above but the calculation function is inversed to counter any “optimization” for the PRBS
The thing to remember is that PRBS will be applied to the payload of the frame/packet/datagram so it there is any sort of optimization present it will have no effect as PRBS is by design not compressible. There are various “strengths” of the pseudo-random pattern the higher the number the less repeating it will include. Normally it is possible to see two main variants: 2^15 which is 32,767 bits long and 2^23 which 8,388,607 bits long. Obviously the longer the pattern the better and more “random” behavior it emulates.
Error injecting Options
As this test originated in telco world injecting errors was a major thing but in Ethernet network it lost its importance. If you inject even a single bit error in an Ethernet frame the CRC should be incorrect and the whole frame should be dropped on first L2 equipment it will be passed through which should always result in alarm LoF(Loss of Frame)/LoP (Loss of Pattern).
Use cases, Best Practices and Conclusion
The most common use case for BERT in nowadays network would be in commissioning new links as you can run a fairly simple test for a long time that will give you a reasonable idea bout it’s quality in terms of frames drops and jitter.
The few recommendations about how to run this test would be as follows:
- Use the largest pattern you can.
- Remember that the line rate and L2 rates will be different because of the overheads.
- Remember that 99.999% of availability results in 0.8s outage in 24 hours (which can be quite a lot of frames)
- PRBS cannot be optimized
So as you can see BERT is rather simple and straight forward test that even though is in many ways deprecated by RFC2544 and others (like Y.156sam) it is still a very good test to know especially if you are in jitter sensitive environment e.g. where VoIP and IPTV is deployed.



![{displaystyle p_{e}=1-{sqrt[{N}]{(1-p_{p})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d380e45b0451c45265e199221fae5bd5b84bf9)