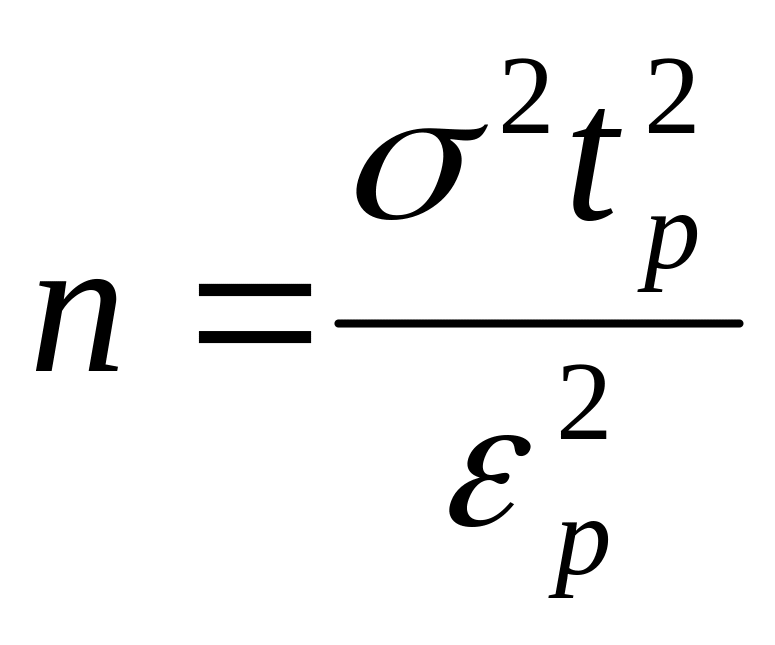Чем меньше колеблемость признака тем величина средней ошибки

Статистическое
наблюдение по полноте охвата совокупности
может быть:

—сплошное,
когда обследованию подвергаются все
единицы генеральной совокупности;

—несплошное,
когда обследованию подвергается часть
единиц.

Одним из
основных видов несплошного наблюдения
является выборочный
метод.

При выборочном
методе статистического наблюдения
обследованию подвергаются не все объекты
генеральной совокупности, а лишь часть
ее – выборочная совокупность.

Причины
использования выборочного метода

1). Повышение
точности данных, уменьшение числа единиц
наблюдения в выборке резко снижает
ошибки регистрации;

2). Экономия
материальных, трудовых, финансовых
ресурсов и времени.

3). Невозможность
сплошного наблюдения. Например, при
обследовании полей на зараженность
невозможно пересчитать все колосья;

4). Экономическая
нецелесообразность сплошного наблюдения.
Например, при определении жирности
молока, всхожести семян продукт
уничтожается.

Основная
задача
выборочного наблюдения заключается в
том, чтобы на основе изучения выборочной
совокупности получить такие выборочные
характеристики, которые как можно более
точно отражали бы характеристики
генеральной совокупности.

Научные условия
организации выборочного наблюдения

1). Случайность
отбора единиц в выборку.

2) Равновозможность
попадания единиц в выборку.

3) Независимость
отбора единиц.

4). Объективность
попадания каждой единицы в выборку.

5). Достаточно
большая численность выборочной
совокупности.

Способы отбора
в выборку

1). Собственно-случайный
отбор. Когда
отбор из единиц генеральной совокупности
производится в случайном порядке.
Случайность отбора заключается в
соблюдении равной возможности для всех
единиц генеральной совокупности попасть
в выборку. Может быть организована по
схеме: а) повторного
отбора, когда
отобранная единица после регистрации
возвращается обратно в генеральную
совокупность и в дальнейшем снова может
попасть в выборку. При таком способе
отбора численность генеральной
совокупности остается неизменной в
ходе всего процесса выборки и поэтому
для всех единиц совокупности обеспечивается
равная вероятность попасть в выборку;

б)
бесповторного
отбора, когда
отобранная один раз единица не возвращается
в генеральную совокупность и из
дальнейшего участия в процессе выборки
исключается и не может быть отобрана
повторно. В связи с этим численность
генеральной совокупности не остается
неизменной, а уменьшается после каждого
отбора. Вероятность попасть в выборку
для оставшихся единиц соответственно
повышается, то есть нарушается принцип
равновозможности.

2). Механический
отбор. Генеральная
совокупность как бы механически
расчленяется на n
равных частей (интервалов) и из каждой
такой части в определенном порядке
отбирается один представитель. Например,
располагают все единицы в определенном
порядке (по алфавиту или др.) и отбирают
из них каждую десятую, пятую, двадцатую
и т.п. Если в первой десятке оказалась
третья единица (выбирается путем жребия),
то отобранными окажутся единице: 13, 23,
33, 43 ……. . Проводится, как правило, по
бесповторной схеме.

3).Типический
отбор. При
этом способе отбора единицы генеральной
совокупности предварительно объединяются
в типические группы по какому-либо
существенному признаку, и непосредственный
отбор единиц производится в пределах
отдельных типических групп.

Под типическими
группами понимаются группы единиц,
объединенные не только каким-либо общим
признаком, но, главное незначительно
отличающиеся друг от друга по количественным
значениям этого признака. Следовательно,
в понятие типической группы включается
понятие однородности
входящих в нее единиц. Группы считаются
однородными, если коэффициент вариации
в группах не превышает 33%. При отборе из
типических групп колеблемость выборочной
средней всегда меньше, чем при отборе
из общей совокупности, и поэтому оценки
показателя получаются более точные.
Отбор единиц из каждой группы проводится
методом случайного отбора. Возможны
два случая: а) равномерная
выборка,
когда из каждой типической группы
отбирается одинаковое число единиц.
Такой подход оправдан лишь при равенстве
численности исходных типических групп;

б) пропорциональная
выборка,
когда численности частных выборок,
взятых из каждой типической группы
пропорциональны либо численностям
типических групп, либо средним
квадратическим отклонениям или
дисперсиям, либо и численностям и
дисперсиям одновременно.

4).Серийный
отбор.
Характер размещения объектов в генеральной
совокупности может быть таким, что они
расположены однородными сериями
(Например, продукция, упакованная в
мешки, ящики). В таких случаях формирование
выборочной совокупности путем отбора
отдельных единиц практически
нецелесообразно. Проще организовать
отбор сериями и провести сплошное
обследование отобранных серий.

Описанные выше
приемы формирования выборочной
совокупности каждый в отдельности в
чистом виде применяется довольно редко.
На практике приходится сочетать различные
формы и виды статистического наблюдения.
Часто одна форма выборки применяется
в сочетании с другой. Например,
типологическая сочетается с механической
и собственно-случайной и т.д. Таким
образом, имеет место комбинированное
статистическое
наблюдение.

Ошибки выборочного
наблюдения

1).Регистрации.
Связаны с неточностью измерительных
приборов, недостаточной квалификацией
наблюдателей, неточностью подсчетов и
т.п.

2). Систематические.
Возникают, когда нарушен принцип
случайности отбора и в выборку попали
единицы, обладающие нехарактерными
свойствами для всех единиц генеральной
совокупности. Нетипичными называются
единицы, которые обладают значениями
некоторого признака существенно
отличающегося от остальных уровней
статистического ряда распределения.
(Нетипичные значения могут быть объективно
таковыми, т.е. достоверными, либо быть
ошибочными вследствие различных причин).

3).Репрезентативности
(представительности).
Обусловлены тем, что даже при тщательном
планировании выборка не может в точности
воспроизвести структуру генеральной
совокупности. Объясняются недостаточно
равномерным представлением в выборке
различных категорий единиц совокупности.
Выделяют три вида ошибок репрезентативности:
а) конкретная
ошибка (
):
это разность
между соответствующими параметрами
генеральной совокупности и выборочной
совокупности. Например, конкретная
ошибка для выборочной средней:

,где

—
средняя в генеральной совокупности,

-средняя
в выборке.

б)
средняя
ошибка(m):
это средняя
квадратическая величина, вычисленная
из всех возможных конкретных ошибок.
Например, средняя ошибка выборочной
средней

,
где n
– численность выборки.

Квадрат средней
ошибки (т.е. дисперсия выборочных средних)
прямо пропорционален средней колеблемости
признака в генеральной совокупности
(
)
и обратно пропорционален численности
выборки (n):

,
откуда

.

Следовательно,
средняя ошибка тем больше, чем выше
колеблемость признака в генеральной
совокупности, и тем меньше, чем больше
численность совокупности.

Доказано, что
соотношение между генеральной и
выборочной дисперсии следующее:

, но
так как при достаточно большой численности
выборки (n)
отношение

стремиться к 1, то

,
а

.

в)
предельная
ошибка (
):
это максимальная
ошибка выборки при заданном уровне
вероятности:

,
где t_p
– коэффициент доверия, зависящий от
вероятности, с которым можно гарантировать
определенные размеры предельной ошибки.
С увеличением вероятности (р),
увеличивается и коэффициент доверия
(t_p),
но увеличивается и предельная ошибка
(
).

Величины t
и p
находят по таблице «Значение интеграла
вероятностей при разных значениях t».

Наиболее часто
используемая вероятность: p=0,95;
0,954; 0,997; 0,999. Вероятность 0,95 показывает,
что в 5 случаях из 100 ошибка может выйти
за установленную границу.

Коэффициент доверия
при указанных уровнях вероятности
составит:

.

Исследования
В.Госсета (псевдоним Стьюдент) показали,
что при выборках численностью менее 30
единиц (малые выборки), среднее
квадратическое отклонение выборки
значительно отличается от среднего
квадратического отклонения генеральной
совокупности, выборочная дисперсия
оказывается значительно смещенной. Для
получения несмещенной оценки дисперсии
по данным малой выборки сумму квадратов
отклонений нужно делить не на n
как в случае большой выборки, а на
величину n
– 1. Эта величина называется числом
степеней свободы вариации (
).
В качестве критерия в малых выборках
используется критерий t
– Стьюдента. Он определяется по таблице
«Значение критерия t
– Стьюдента» при заданном уровне
вероятности суждения и соответствующим
числом степеней свободы.

Организация
выборочного наблюдения и обработка
выборочных данных в целях получения
характеристик генеральной совокупности
ставит 3 основные задачи:

1). Определение
необходимой численности выборки (n).

2). Установление
доверительных пределов генеральной
средней (доли).

3). Определение
вероятности заданного размера ошибки
(p).

Формулы расчета
средней ошибки выборочной средней (m)
и необходимой численности выборки(n)
при различных способах отбора

Способ отбора	m	n
Случайный повторный
Случайный бесповторный	где N – численность генеральной совокупности
Механический
Типический	, где -остаточная дисперсия. Репрезентативность типической выборки зависит от того, насколько точно воспроизводят каждую данную типическую группу те единицы, которые из нее отобраны. Точность типической выборки для всей совокупности в целом зависит от средней из частных дисперсий (остаточной), поэтому при определении ошибки выборки берется не общая дисперсия, а остаточная.
Серийный	,где -межсерийная дисперсия, nc— численность серий в выборке, Nc— число серий в генеральной совокупности. Каждая серия выступает как единица наблюдения, поэтому вариация внутри серии снимается. Средняя и предельная ошибки, следовательно, зависят только от межсерийной дисперсии.

Средняя ошибка
выборочной доли определяется по формуле

, где

—
выборочная доля единиц, обладающих
изучаемым признаком, а

—
дисперсия доли (альтернативного
признака).

При бесповторном
отборе в формулах добавляется множитель

,
то есть

Результатом
осуществления выборочного метода
является статистический вывод, который
может быть двух видов:

1. Статистическая
   оценка;

2. Проверка
   статистических гипотез.

Статистическая
оценка параметров генеральной
совокупности.

При статистической
оценке выводы и обобщения сводятся к
оценке неизвестных параметров генеральной
совокупности. При этом задача оценки
неизвестных параметров может быть
решена двояко: либо неизвестный параметр
характеризуется одним числом (точкой),
либо указывается интервал, в котором с
некоторой вероятностью может находиться
исходный параметр.

В связи с этим
различают два метода статистической
оценки:

1) Точечная
оценка.
Состоит в том, что за наилучшее приближение
к истинному параметру генеральной
совокупности принимается конкретное
числовое значение выборки, оценка
добавляется показателем средней ошибки.

Например, точечная
оценка выборочной средней:

,
с учетом

2)
Интервальная оценка.
Указывается интервал (доверительный),
в котором с некоторой вероятностью
может находиться искомый параметр
генеральной совокупности.

Например, интервальная
оценка выборочной средней: генеральная
средняя будет находиться в пределах:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

---

С этим файлом связано 2 файл(ов). Среди них: Novyj.odt, Новый Vector Paro.doc.
Показать все связанные файлы

---

Подборка по базе: 10. СП 36.13330.2012 Магистральные трубопроводы. Актуализированн, Гайнеева диплом редакция.docx, Положение текущем контроле и промежуточной аттестации Новая реда, КТП ШЮЗ редакция (1).rtf, СП 50.13330.2012«Тепловая защита зданий. Актуализированная редак, 5-сынып ҚМЖ Растрлық суреттерді құру және редакциялау.doc, 5 сын 8.11._Растрлық кескіндерді құру және редакциялау_.pptx, Положение текущем контроле и промежуточной аттестации Новая реда, СП 36.13330.2012 Магистральные трубопроводы. Актуализированная р, Объекты последняя редакция. Учебное пособие.doc

---

Редакция 3 от 04.04.2012г

УДК 614.2.001.12 (075)

ББК 51.1(2)

УМО – 75.07.02.05
Составители:

профессор В. И. Сабанов,

ст. преподаватель, канд. мед. наук Н. П. Багметов,

доцент, канд. мед. наук В. В. Ивашева,

ассистент, канд. мед. наук А. Н. Голубев,

ассистент А. С. Рогова
Рецензенты:

д-р мед. наук, профессор, гл. специалист по общественному

здоровью и здравоохранению ЮФО, зав. кафедрой общественного здоровья и здравоохранения с курсами информатики, истории медицины и культурологи АГМА Сердюков А. Г.,

канд. мед. наук, доцент, зав. кафедрой общественного здоровья
и здравоохранения № 2 факультета повышения
квалификации РГМУ Салатич А. И.
Квалификационные тесты по специальности «Организация здравоохранения и общественное здоровье»: Метод. указания / Сост.: В. И. Сабанов, Н. П. Багметов, В. В. Ивашева,
А. Н. Голубев, А. С. Рогова. — Изд. 3-е, испр. и доп. — Волгоград: Изд-во ВолГМУ, 2009. — 284 с.
Методические указания рекомендуются слушателям факультетов усовершенствования врачей, организаторам здравоохранения всех типов лечебно-профилактических учреждений, специалистам фондов обязательного медицинского страхования и страховых медицинских организаций, преподавателям кафедр общественного здоровья и здравоохранения для подготовки и сдачи экзамена по специальности «Организация здравоохранения и общественное здоровье».

ОГЛАВЛЕНИЕ

РАЗДЕЛ 01.
«МЕДИКО-САНИТАРНАЯ СТАТИСТИКА» 4

РАЗДЕЛ 02.
«МЕДИКО-ДЕМОГРАФИЧЕСКИЕ АСПЕКТЫ
ОРГАНИЗАЦИИ ЗДРАВООХРАНЕНИЯ» 27

РАЗДЕЛ 03.
«ЗАБОЛЕВАЕМОСТЬ.
МЕТОДИКА ЕЕ ИЗУЧЕНИЯ» 48

РАЗДЕЛ 04.
«ОРГАНИЗАЦИЯ ЗДРАВООХРАНЕНИЯ» 69

РАЗДЕЛ 05.
«КАЧЕСТВО МЕДИЦИНСКОЙ ПОМОЩИ» 124

РАЗДЕЛ 06.
«ЭКСПЕРТИЗА ВРЕМЕННОЙ
И СТОЙКОЙ УТРАТЫ ТРУДОСПОСОБНОСТИ» РЕД.04.04.2012г 135

РАЗДЕЛ 07.
«МЕДИЦИНА КАТАСТРОФ» 180

РАЗДЕЛ 08.
«МЕДИЦИНСКОЕ СТРАХОВАНИЕ» 188

РАЗДЕЛ 09.
«ЭКОНОМИКА, ПЛАНИРОВАНИЕ
И УПРАВЛЕНИЕ В ЗДРАВООХРАНЕНИИ» 203

РАЗДЕЛ 10.
«ГРАЖДАНСКОЕ И ТРУДОВОЕ ПРАВО» 240

РАЗДЕЛ 11.
«МЕЖДУНАРОДНЫЕ АСПЕКТЫ ЗДРАВООХРАНЕНИЯ» 264

РАЗДЕЛ 12.
«АСУ В ЗДРАВООХРАНЕНИИ» 271

РАЗДЕЛ 01. «МЕДИКО-САНИТАРНАЯ СТАТИСТИКА

001. Интенсивные показатели принято изображать в виде диаграмм:

а) Столбиковых

б) Секторных

в) Комбинированных

г) Радиальных
002. Динамические показатели характеризуют:

а) Структуру явления

б) Частоту явления в другой среде

в) Изменение величины явления во времени
003. Экстенсивные показатели характеризуют:

а) Структуру явления

б) Частоту явления в другой среде

в) Изменение величины явления во времени
004. Интенсивные показатели характеризуют:

а) Структуру явления

б) Частоту явления в изучаемой среде

в) Частоту явления в другой среде

г) Изменение величины явления во времени
005. Величина, наиболее часто встречающаяся
в вариационном ряду, называется:

а) Медианой (Ме)

б) Средней арифметической (Мср)

в) Модой (Мо)

г) Средним квадратическим отклонением
006. Если в вариационном ряду каждая варианта повторяется несколько раз, то этот ряд:

а) Простой

б) Сложный

в) Сгруппированный

г) Комбинированный
007. Коэффициент вариации, равный 25 %, свидетельствует о разнообразии признака:

а) Сильном

б) Среднем

в) Слабом
008. В городе N в структуре младенческой смертности в 1980 г. на долю инфекций дыхательных путей приходилось 42 %, а кишечных инфекций — 35 %, в 1995 г. — 38 % и 30 % соответственно. Верен ли вывод о снижении младенческой смертности от этих видов патологии:

а) Верен, показатели действительно снизились

б) Не верен, по структуре нельзя судить о частоте явления

в) Не верен, не указана достоверность различия показателей

г) Верен, определяется явная достоверность различия по амплитуде
009. Достоверность различия двух средних величин определяется с помощью:

а) Ошибки репрезентативности

б) Коэффициента вариации

в) Средней арифметической

г) Критерия Стьюдента
010. Доверительный интервал — это:

а) Степень разнообразия единиц по изучаемому признаку

б) Пределы варьирования средней величины при разной степени вероятности

в) Мера колеблемости ряда

г) Мерило изменчивости средней арифметической или относительной величины
011. О наличии сильной положительной корреляционной зависимости можно говорить при значении коэффициента корреляции:

а) Больше или равно 0,6

б) Меньше или равно 0,10

в) Больше или равно 0,9

г) Меньше или равно 0,4

012. Репрезентативность выборки обеспечивается:

а) Соответствующим объемом и случайностью отбора единиц наблюдения

б) Соответствующим объемом и стандартизацией

г) Стандартизацией и нормированием когорт наблюдения
013. Какие из перечисленных ниже пар показателей являются интенсивными:

а) Показатели рождаемости и заболеваемости населения гепатитом

б) Показатель рождаемости и структура причин инвалидности

в) Структура причин инвалидности и заболеваемость населения гепатитом
014. Для графического изображения экстенсивных показателей используются диаграммы:

а) Секторная

б) Столбиковая

в) Динамическая

г) Линейная
015. Для определения структуры заболеваемости, смертности применяется показатель:

а) Экстенсивный

б) Интенсивный

в) Соотношения

г) Наглядности
016. Какой из перечисленных ниже показателей является показателем соотношения:

а) Обеспеченность населения врачами

б) Общая смертность

в) Летальность
017. Если t-критерий (Стьюдента) больше или равен 2, то различия двух средних величин:

а) Достоверны

б) Недостоверны

в) Сравнимы

г) Несравнимы

д) Выборочны
018. Если в вариационном ряду каждая варианта ни разу не повторяется, то этот ряд:

а) Простой

б) Сложный

в) Сгруппированный

г) Комбинированный
019. Мера достоверности средней величины:

а) Амплитуда

б) Ошибка репрезентативности

в) Критерий Стьюдента

г) Варианта

д) Медиана
020. Коэффициент вариации, равный 7 %, свидетельствует о разнообразии признака:

а) Сильного

б) Среднего

в) Слабого
021. Степень представительности выборки оценивается с помощью:

а) Коэффициента корреляции

б) Среднего квадратического отклонения

в) Ошибки репрезентативности
022. Для сравнения показателей, полученных на неоднородных по своему составу совокупностях, используется метод:

а) Корреляции

б) Выравнивания динамических рядов

в) Стандартизации

г) Экстраполяции
023. Статистическое наблюдение может быть:

а) Текущим и единовременным

б) Фактическим и результативным

в) Единовременным и стандартизованным

г) Фактическим и единовременным
024. Какие ошибки, учитываемые статистическими методами, не могут быть полностью устранены:

а) Арифметические

б) Степени точности вычисления

в) Методические

г) Репрезентативности
025. Какой из перечисленных ниже показателей является экстенсивным:

а) Структура причин смерти

б) Младенческая смертность

в) Уровень заболеваемости населения дифтерией
026. Укажите последовательность этапов статистического исследования, обозначенных буквами, выбрав соответствующую комбинацию букв: A) сбор материала и статистическое наблюдение; B) разработка плана и программы исследования; C) анализ результатов исследования; D) разработка материала

а) АВСD

б) DBAC

в) BADC
027. Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные при вероятности безошибочного прогноза, равном и более:

а) 68 %

б) 90 %

в) 92 %

г) 95 %
028. Частоту или распространенность явления характеризует показатель:

а) Экстенсивный

б) Интенсивный

в) Соотношения

г) Корреляции
029. В городе А сердечно-сосудистые заболевания составляют 20 %, а в городе Б — 30 % от всех заболеваний. Можно ли утверждать, что в городе Б эти заболевания встречаются чаще:

1) можно, процент заболеваний в городе Б явно выше; 2) можно, данные показатели характеризуют уровень сердечно-сосудистых заболеваний; 3) можно, данные показатели характеризуют частоту сердечно-сосудистых заболеваний, а в городе Б она выше;
4) нельзя, мы не знаем ошибки данных показателей; 5) нельзя, процент сердечно-сосудистых заболеваний в городе Б может быть выше за счет меньшего удельного веса других заболеваний; по структуре нельзя судить о частоте

а) 1

б) 2

в) 3

г) 4

д) 5
030. Если t-критерий (Стьюдента) меньше 2, то различия двух средних величин:

а) Достоверны

б) Недостоверны

в) Сравнимы

г) Несравнимы

д) Выборочны
031. Коэффициент вариации, равный 35 %, свидетельствует о разнообразии признака:

а) Сильного

б) Среднего

в) Слабого
032. Отражает ли структурное распределение заболеваемости населения такие показатели, как средняя продолжительность лечения и кратность заболеваний в год:

а) Да

б) Нет
033. Уровень общей заболеваемости населения характеризуется коэффициентом:

а) Экстенсивным

б) Соотношения

в) Интенсивным

г) Наглядности
034. Укажите показатели, в которых должны быть представлены результаты исследования при изучении распространенности гипертонической болезни у лиц разного возраста:

а) Интенсивные

б) Экстенсивные

в) Соотношения

г) Наглядности

035. Дайте определение вариационного ряда:
1) однородная в качественном отношении статистическая совокупность, отдельные единицы которой характеризуют количественные различия изучаемого признака или явления; 2) ряд чисел, характеризующих качественно неоднородную совокупность; 3) количественное выражение различных признаков

а) 1

б) 2

в) 3
036. Варианта — это:

а) Числовое выражение признака

б) Средняя величина

в) Относительный показатель

г) Качественная характеристика признака
037. Выберите правильное определение понятия «Единица статистического наблюдения»: 1) составная часть объекта наблюдения, подлежащая изучению и регистрации в соответствии с программой исследования; 2) явление, которое подлежит детальному изучению и все учетные признаки которого могут быть измерены только количественно; 3) явление, которое подлежит детальному изучению и его учетные признаки должны носить только качественный, описательный характер

а) 1

б) 2

в) 3
038. Объект статистического наблюдения — это:
1) статистическая совокупность явлений (предметов), о которых должны быть собраны статистические сведения; 2) каждое отдельное явление, которое подвергается углубленному изучению и регистрации на специальной учетной форме (бланке); 3) место или территория, где осуществляется статистическое наблюдение

а) 1

б) 2

в) 3
039. Для оценки обеспеченности населения врачами используется показатель:

а) Интенсивности

б) Экстенсивности

в) Соотношения

г) Наглядности
040. Показатель наглядности используется для:

а) Определения удельного веса изучаемого признака

б) Характеристики структуры

в) Сравнения явлений в динамике

г) Оценки распространенности явления
041. Репрезентативность — это: 1) соответствие средней арифметической величины выборочной совокупности аналогичному параметру генеральной совокупности; 2) достоверность полученного результата при сплошном исследовании; 3) понятие, характеризующее связь между признаками; 4) характеристика методики исследования

а) 1

б) 2

в) 3

г) 4
042. С увеличением объема наблюдений ошибка репрезентативности:

а) Увеличивается

б) Остается без изменений

в) Уменьшается
043. Предметом изучения медицинской статистики является: 1) здоровье населения; 2) выявление и установление зависимостей между уровнем здоровья и факторами окружающей среды; 3) данные о сети, деятельности, кадрах учреждений здравоохранения;
4) достоверность результатов клинических и экспериментальных исследований; 5) все вышеперечисленное

а) 1

б) 2

в) 3

г) 4

д) 5
044. Коэффициент корреляции между двумя выборками равен 0. Вывод о взаимной независимости выборок можно сделать:

а) В любом случае

б) Если обе выборки имеют одинаковое распределение

в) Если обе выборки имеют нормальное распределение

г) Если хотя бы одна выборка имеет нормальное распределение
045. Коэффициент корреляции между двумя выборками равен 1. Такой результат позволяет предложить наличие взаимосвязи между ними:

а) В любом случае

б) Если обе выборки имеют одинаковое распределение

в) Если обе выборки имеют нормальное распределение

г) Если хотя бы одна выборка имеет нормальное распределение
046. Под статистикой понимают: 1) самостоятельную общественную науку, изучающую количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной; 2) сбор, обработку и хранение информации, характеризующей количественные закономерности общественных явлений; 3) анализ массовых количественных данных с использованием статистических методов; 4) анализ массовых количественных данных с использованием статистическо-математических методов; 5) статистическо-математические методы при сборе, обработке и хранении информации

а) 1

б) 2

в) 3

г) 4

д) 5
047. Под медицинской статистикой понимают:
1) отрасль статистики, изучающую здоровье населения; 2) совокупность статистических методов, необходимых для анализа деятельности ЛПУ; 3) отрасль статистики, изучающую вопросы, связанные с медициной, гигиеной, санитарией и здравоохранением; 4) отрасль статистики, изучающую вопросы, связанные с медициной и социальной гигиеной; 5) отрасль статистики, изучающую вопросы, связанные с социальной гигиеной, планированием и прогнозированием деятельности ЛПУ

а) 1

б) 2

в) 3

г) 4

д) 5
048. Предметом изучения медицинской статистики является информация о:

а) Здоровье населения

б) Влиянии факторов окружающей среды на здоровье человека

в) Кадрах, сети и деятельности учреждений и служб здравоохранения

г) Результатах клинических и экспериментальных исследований в медицине

д) Всем вышеперечисленном
049. Здоровье населения рассматривается (изучается) как: 1) многофакторная проблема, включающая в себя цели и задачи по изучению здоровья населения и влияющих факторов окружающей среды; 2) совокупность показателей, характеризующих здоровье общества как целостного функционирующего организма; 3) все вышеперечисленное

а) 1

б) 2

в) 3
050. Виды относительных величин все, кроме:

а) Интенсивных показателей

б) Экстенсивных показателей

в) Показателей наглядности

г) Показателей соотношения

д) Средних величин
051. Показатель соотношения характеризует:

а) Структуру, состав явления

б) Частоту явления в своей среде

в) Соотношение двух разнородных совокупностей

г) Распределение целого на части
052. В каких показателях должны быть представлены результаты исследования при изучении структуры госпитализированных больных по отделениям стационара:

а) Экстенсивных

б) Интенсивных
053. К интенсивным статистическим показателям относятся:

а) Распределение больных по полу и возрасту

б) Показатели заболеваемости, смертности

в) Структура заболеваний по нозологическим формам
054. Диаграммой, наиболее наглядно характеризующей сезонность заболеваемости, служит:

а) Секторная

б) Радиальная

в) Столбиковая
055. Какой статистический показатель характеризует развитие явления в среде, непосредственно с ним не связанной:

а) Экстенсивный

б) Интенсивный

в) Соотношения

г) Наглядности

д) Средняя арифметическая
056. Какие показатели позволяют демонстрировать сдвиги явления во времени или по территории, не раскрывая истинного уровня этого явления:

а) Экстенсивные

б) Интенсивные

в) Соотношения

г) Наглядности

д) Регрессии
057. Статистическая совокупность как объект статистического исследования включает группу или множество относительно однородных элементов, обладающих признаками:

а) Сходства

б) Различия

в) Сходства и различия
058. Программа статистического исследования — это:

а) Перечень вопросов

б) Совокупность изучаемых признаков

в) Определение масштаба исследования

г) Определение времени исследования
059. Из приведенных ниже примеров характерным для единовременного наблюдения является:

а) Рождаемость

б) Заболеваемость

в) Профилактический осмотр

г) Смертность
060. Выборочное наблюдение — это: 1) наблюдение, охватывающее часть единиц совокупности для характеристики целого; 2) наблюдение, приуроченное к одному какому-либо моменту; 3) наблюдение в порядке текущей регистрации; 4) обследование всех без исключения единиц изучаемой совокупности

а) 1

б) 2

в) 3

г) 4
061. Сплошное наблюдение — это: 1) наблюдение, охватывающее часть единиц совокупности для характеристики целого; 2) наблюдение, приуроченное к одному какому-либо моменту; 3) наблюдение в порядке текущей регистрации; 4) обследование всех без исключения единиц изучаемой совокупности

а) 1

б) 2

в) 3

г) 4
062. Единовременное наблюдение — это: 1) наблюдение, охватывающее часть единиц совокупности для характеристики целого; 2) наблюдение, приуроченное к одному какому-либо моменту; 3) наблюдение в порядке текущей регистрации; 4) обследование всех без исключения единиц изучаемой совокупности

а) 1

б) 2

в) 3

г) 4
063. Текущее наблюдение — это: 1) наблюдение, охватывающее часть единиц совокупности для характеристики целого; 2) наблюдение, приуроченное к одному какому-либо моменту; 3) наблюдение в порядке текущей регистрации; 4) обследование всех без исключения единиц изучаемой совокупности

а) 1

б) 2

в) 3

г) 4
064. Из перечисленных видов статистических таблиц наилучшее представление об исследуемой совокупности дает:

а) Простая таблица

б) Групповая таблица

в) Комбинационная таблица
065. Единица наблюдения — это: 1) первичный элемент объекта статистического наблюдения, являющийся носителем признаков, подлежащих регистрации;
2) массив единиц, являющихся носителем изучаемого признака; 3) наблюдение, приуроченное к какому-либо моменту; 4) определение объема наблюдений

а) 1

б) 2

в) 3

г) 4
066. Вариационный ряд — это:

а) Ряд чисел

б) Совокупность вариантов

в) Ряд чисел, характеризующих определенный признак

г) Варианты, расположенные в определенной последовательности
067. Средняя величина — это:

а) Частота явления

б) Структура явления

в) Обобщающая характеристика варьирующего признака
068. При корреляционном анализе используются коэффициенты:

а) Вариации

б) Регрессии

в) Корреляции

г) Соотношения

д) Все вышеперечисленные
069. При соблюдении каких условий средняя арифметическая наиболее точно характеризует средний уровень варьирующего признака: 1) при условии симметричности совокупности, полном представлении выборочной совокупности специфических особенностей генеральной совокупности; 2) при условии симметричности совокупности, числа наблюдений в ней не менее 100; 3) только в генеральной совокупности;
4) в нормальном распределении при достаточно большом числе наблюдений и однородности изучаемого явления; 5) при достаточно большом числе наблюдений и однородности изучаемого явления

а) 1

б) 2

в) 3

г) 4

д) 5
070. Показатель наглядности — это показатель, который: 1) характеризует отношение между двумя, не связанными друг с другом, совокупностями; 2) указывает, во сколько раз или на сколько процентов произошло увеличение или уменьшение сравниваемых величин; 3) указывает на отношение части к целому;
4) указывает на частоту изучаемого явления в среде

а) 1

б) 2

в) 3

г) 4
071. В каких пределах может колебаться значение коэффициента корреляции:

а) от 0 до 1

б) от 0 до 2

в) от 0,5 до 1

г) от –1 до +1
072. В больнице № 1 показатель больничной летальности составил 2,1 ± 0,4 %, а в больнице № 2 —
1,2 ± 0,3 %. В какой больнице качество лечения лучше, на основании чего сделан вывод: 1) сравнению данные показатели не подлежат; 2) в данном случае для сравнения качества лечения нужно применить метод стандартизации, но данных для этого недостаточно;
3) утверждать, что в больнице № 2 качество лечения лучше, нельзя, т. к. по критерию Стьюдента t < 2, т. е. для окончательного вывода надо увеличить число наблюдений; 4) в больнице № 2 качество лечения выше, чем в больнице № 1, т. к. по критерию Стьюдента t > 2

а) 1

б) 2

в) 3

г) 4
073. Медиана ряда (Ме) — это:

а) Наибольшая по значению варианта

б) Варианта, встречающаяся чаще других

в) Центральная варианта, делящая ряд пополам
074. Назовите крайние варианты вариационного ряда, если известно, что М_ср. = 40,0 кг, s = 3,0 кг:

а) 37 – 43 кг

б) 31 – 49 кг

в) 39 – 42 кг
075. Укажите формулу, по которой рассчитывается отклонение (d):

а) d = V — M_ср.

б) d = M_ср. — V

в) d = M_ср. — s

г) d = s — M_ср.
076. Какая варианта вариационного ряда чаще всего принимается за условную среднюю:

а) Мода

б) Медиана

в) V max

г) V min
077. При сравнении интенсивных показателей, полученных на однородных по своему составу совокупностях, необходимо применять:

а) Оценку показателей соотношения

б) Определение относительной величины

в) Стандартизацию

г) Оценку достоверности разности показателей

д) Все вышеперечисленное
078. Разность между двумя относительными показателями считается достоверной, если превышает свою ошибку:

а) В 2 и более раза

б) Меньше, чем в 2 раза
079. В каких границах возможны случайные колебания средней величины с вероятностью 95,5 %:

а) M ± m

б) M ± 2m

в) M ± 3m
080. Какой степени вероятности соответствует доверительный интервал Р ± 2m:

а) 68,3 %

б) 95,5 %

в) 99,7 %
081. Какой степени вероятности соответствует доверительный интервал М ± 3m:

а) 68,3 %

б) 95,5 %

в) 99,7 %
082. Чем меньше колеблемость признака, тем величина средней ошибки:

а) Меньше

б) Больше

в) Остается неизменной
083. Чтобы уменьшить ошибку выборки, число наблюдений нужно:

а) Увеличить

б) Уменьшить

в) Оставить без изменения
084. Чем меньше число наблюдений, тем величина средней ошибки:

а) Меньше

б) Больше

в) Эти показатели не связаны друг с другом
085. Разница между средними величинами считается достоверной, если:

а) t=1

б) t=2 и больше

в) t<1,5

г) t=1,5
086. Не считается достоверной для научных медико-социальных исследований вероятность:

а) 68,3 %

б) 95,5 %

в) 99,7 %
087. Случайным называют событие, которое:

а) Может произойти при любых заданных условиях

б) При заданных условиях может произойти или не прои-зойти

в) При заданных условиях может произойти

г) Может произойти при не заданных условиях

д) Может не произойти при заданных условиях
088. Средним квадратическим отклонением называется: 1) средняя величина абсолютных отклонений величин признака у членов совокупности от средней арифметической величины данного признака в совокупности; 2) квадратный корень из среднего квадрата отклонения величин признака у членов совокупности от средней арифметической величины данного признака в совокупности; 3) квадратный корень из абсолютных отклонений величины признака у членов совокупности

а) 1

б) 2

в) 3
089. При изучении состояния здоровья населения используются следующие виды относительных показателей:

а) Интенсивные и экстенсивные показатели

б) Показатели соотношения

в) Все вышеперечисленные
090. Интенсивный показатель — это показатель, который: 1) характеризует отношение между двумя, не связанными друг с другом, совокупностями; 2) указывает на отношение части к целому; 3) указывает, во сколько раз или на сколько процентов произошло увеличение или уменьшение сравниваемых величин;
4) указывает на частоту изучаемого явления в среде

а) 1

б) 2

в) 3

г) 4
091. Экстенсивный показатель — это показатель, который: 1) характеризует отношение между двумя, не связанными друг с другом, совокупностями; 2) указывает на отношение части к целому; 3) указывает, во сколько раз или на сколько процентов произошло увеличение или уменьшение сравниваемых величин;
4) указывает на частоту изучаемого явления в среде

а) 1

б) 2

в) 3

г) 4
092. Показатель соотношения — это показатель, который: 1) характеризует отношение между двумя, не связанными друг с другом, совокупностями; 2) указывает на отношение части к целому; 3) указывает, во сколько раз или на сколько процентов произошло увеличение или уменьшение сравниваемых величин;
4) указывает на частоту изучаемого явления в среде

а) 1

б) 2

в) 3

г) 4
093. Общественное здоровье — это:

а) Наука о социологии здоровья

б) Система лечебно-профилактических мероприятий по охране здоровья

в) Наука о социальных проблемах медицины

г) Наука о закономерностях здоровья населения

д) Система социально-экономических мероприятий по охране здоровья
094. Здравоохранение — это:

а) Наука о социологии здоровья

б) Система лечебно-профилактических мероприятий по охране здоровья

в) Наука о социальных проблемах медицины

г) Наука о закономерностях здоровья населения

д) Система социально-экономических мероприятий по охране здоровья
095. Основателем кафедры общественного здоровья и здравоохранения в нашей стране является:

а) Ю. П. Лисицын

б) Н. А. Семашко

в) З. З. Френкель

г) А. В. Петров

д) З. П. Соловьев
096. Общественное здоровье характеризует здоровье:

а) Населения в целом

б) Отдельных возрастно-половых групп населения

в) Каждого жителя страны

г) Каждого жителя региона

д) Больных, страдающих каким-либо хроническим заболеванием

е) Правильные ответы а, б, д

ж) Все ответы правильные

з) Все ответы неправильные
097. Основными группами показателей общественного здоровья являются:

а) Показатели заболеваемости

б) Обращения за медицинской помощью

в) Показатели инвалидности

г) Показатели физического развития

д) Демографические показатели

е) Летальность

ж) Все ответы правильные

з) Верно а, в, г, д
098. К группам факторов, определяющих общественное здоровье, относятся:

а) Биологические

б) Природно-климатические

в) Социально-экономические

г) Образ жизни

д) Уровень организации медицинской помощи

е) Все ответы правильные

ж) Все ответы неправильные

099. Среди факторов, определяющих здоровье населения, лидируют:

а) Экологические

б) Биологические

в) Образ жизни

г) Уровень организации медицинской помощи

д) Качество медицинской помощи
100. Свойство репрезентативности характерно для статистической совокупности:

а) Генеральной

б) Выборочной
101. К средним величинам относятся все величины, кроме:

а) Средней арифметической простой

б) Моды

в) Средней арифметической взвешенной

г) Ошибки средней величины

д) Медианы
102. Для определения достоверности разности двух средних величин необходимо знать:

а) Значения сравниваемых средних величин и их ошибки

б) Величину доверительного коэффициента «t» и объем наблюдения

в) Среднее квадратичное отклонение и ошибки сравниваемых величин
103. Разность показателей является существенной, если величина «t» равна:

а) 0,5

б) 1,0

в) 1,5

г) 2,0

д) 2,5

е) Верно а, г

ж) Верно г, д

з) Верно б, в
104. Оценка коэффициента корреляции производится по следующим параметрам:

а) Характеру (направлению)

б) Стандарту

в) Силе

г) Достоверности

д) Нормативу

е) Верно а, в, г

ж) Верно б, г, д

з) Все ответы неправильные
105. Из применяемых методов стандартизации наиболее точным является:

а) Обратный

б) Косвенный

в) Прямой
106. В медицинских исследованиях малой выборкой называется статистическая совокупность, насчитывающая объем исследования в количестве:

а) До 20 единиц наблюдения

б) До 30 единиц наблюдения

в) До 50 единиц наблюдения

г) До 100 единиц наблюдения
107. К текущим наблюдениям относятся:

а) Перепись населения

б) Регистрация случаев рождения живого ребенка

в) Определение возрастного состава студентов

г) Учет коечного фонда

д) Регистрация случаев смерти

е) Верно б, д

ж) Верно а, в, г

з) Все ответы неправильные
108. Статистические таблицы могут быть:

а) Простыми

б) Комбинационными

в) Контрольными

г) Аналитическими

д) Групповыми

е) Верно а, б, д

ж) Верно в, г, д

з) Верно б, в, г
109. Оптимальным числом взаимосвязанных признаков в комбинационной таблице следует считать:

а) Один–два

б) Три–четыре

в) Пять–шесть

г) Более шести
110. При проведении статистического исследования контрольная группа применяется:

а) Для сравнения с результатами основной группы

б) Для выявления факторов риска

в) Для выявления благоприятных факторов здоровья

г) Все ответы правильные

д) Все ответы неправильные
111. Основными задачами общественного здоровья и здравоохранения в нашей стране являются все, кроме:

а) Разработки мероприятий по сохранению и улучшению здоровья населения

б) Изучения факторов социальной среды, оказывающих влияние на здоровье населения

в) Изучения факторов, способствующих повышению качества медицинской помощи

г) Разработки мероприятий по улучшению жилищных условий населения
ОТВЕТЫ К РАЗДЕЛУ 01

«МЕДИКО-САНИТАРНАЯ СТАТИСТИКА»
001-а 002-в 003-а 004-б 005-в

006-в 007-а 008-б 009-г 010-б

011-в 012-а 013-а 014-а 015-а

016-а 017-а 018-а 019-б 020-в

021-в 022-в 023-а 024-г 025-а

026-в 027-г 028-б 029-д 030-б

031-а 032-б 033-в 034-а 035-а

036-а 037-а 038-а 039-в 040-в

041-а 042-в 043-д 044-в 045-а

046-а 047-в 048-д 049-в 050-д

051-в 052-а 053-б 054-б 055-в

056-г 057-а 058-б 059-в 060-а

061-г 062-б 063-в 064-в 065-а

066-в 067-в 068-в 069-г 070-б

071-г 072-б 073-в 074-б 075-а

076-а 077-г 078-а 079-б 080-б

081-в 082-а 083-а 084-б 085-б

086-а 087-б 088-б 089-а 090-г

091-б 092-а 093-г 094-б 095-б

096-е 097-з 098-е 099-в 100-б

101-г 102-а 103-ж 104-е 105-в

106-б 107-е 108-е 109-б 110-г

111-г

Статистика МФПА Тест с ответами

Правильных ответов не менее 97%

Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)

В Российской Федерации основные вопросы организации статистического учета регулируются …

Правительством Российской Федерации

+Федеральным законом «Об официальном статистическом учете и системе государственной статистики в Российской Федерации»

Президентом Российской Федерации

Данные об организациях, созданных на территории РФ, их местных единицах, индивидуальных предпринимателях, других типах статистических единиц, являющихся объектами федерального статистического наблюдения, отражаются Росстатом …

в статистических отчетах

+ в Статистическом регистре хозяйствующих субъектов

в статистических публикациях

Объектом статистики является изучение …

+статистических совокупностей

взаимосвязи между социально-экономическими явлениями посредством статистических показателей

количественной стороны массовых социально-экономических явлений и процессов

Медианой распределения является …

значение изучаемого признака, повторяющееся с наибольшей частотой

разность между наибольшим и наименьшим значениями варьирующего признака

+ значение признака, приходящееся на середину ранжированной совокупности

При сравнении всех уровней ряда динамики с первым уровнем рассчитанные показатели называют …

+базисными

аналитическими

цепными

Основанием группировки может быть … признак

только качественный

только количественный

+как качественный, так и количественный

Наибольшее значение признака в интервале называется … границей

+верхней

нижней

открытой

Для прогнозирования величины колебания курса доллара на основании изменения цены барреля нефти следует применить … анализ

+регрессионный

вариационный

корреляционный

Признаки, изменяющиеся под воздействием других связанных с ними признаков, называются …

факторными

+результативными

варьирующими

Если число уровней ряда – четное, то показатель времени t методом условного нуля задается как …

t =…, -4, -3, -2, -1, 0, 1, 2, 3, 4,

t = …, -3, -2, -1, 1, 2, 3,

+ t =…, -5, -3, -1, 1, 3, 5,

Показатель «Отношение затрат на оплату труда топ-менеджеров предприятия к объему затрат на основной персонал предприятия» является примером относительного показателя …

реализации планового задания

структуры

+координации

Показатель «Курс рубля по отношению к доллару» является примером относительного показателя …

+сравнения

координации

интенсивности

Расчет среднегодовой численности предприятий по данным за 2007–2013 гг. (на 1 января каждого года) следует производить по формуле средней …

2007 2008 2009 2010 2011 2012 2013

2901 3106 3346 3594 3845 4150 4417

+хронологической простой

хронологической взвешенной

арифметической простой

Если известны коэффициент корреляции, равный -0,603, и построенное методом наименьших квадратов уравнение регрессии Yx=38,2 – 5,3X, то значение Y при X = 5 составит …

-43,2

4,397

+11,7

14,397

Если объем инвестиционных вложений характеризуется следующим рядом динамики, млн руб. по месяцам 2013 г. (см. таблицу), то средний абсолютный прирост объема инвестирования за последние 3 месяца составляет …

Январь Февраль Март Апрель Май Июнь Июль

90,0        92,0        80,0     78,0     86,0   60,0   80,0

-2 млн руб.

+ -3 млн руб.

2 млн руб.

3 млн руб.

Если для исследования соблюдения регламента взаимодействия с клиентами персоналом торгово-сбытовой компании строится 15-процентная выборка, объектами которой становятся сотрудники по работе с клиентами торговых точек компании, отбираемых пропорционально количеству сотрудников компании в соответствующем федеральном округе РФ, то такое построение выборки характерно для …

систематической (механической) выборки

собственно случайной выборки

повторной выборки любого вида выборочного исследования

+стратифицированной (типической) выборки

Если среднемесячная номинальная начисленная заработная плата работников в Российской Федерации в 2011 году составляла 23369,2 руб., то в этом случае с точки зрения статистических категорий показателем является …

среднемесячная номинальная начисленная заработная плата

+23 369,2 руб.

Российская Федерация

Если относительный показатель реализации предприятием плана производства продукции составил 103 %, а объем производства по сравнению с предшествующим периодом вырос на 2 %, значит, план предусматривал … объема производства

+рост

снижение

стабилизацию

В представленном ряду распределения (см. таблицу) модальным является интервал …

Выручка аудиторской фирмы

За I полугодие 2013 года, млн. руб.     Число фирм

До 5                                                            40

5–10                                                             26

10-15                                                           10

15–20                                                           14

20–25                                                            5

25 и  более                                                  5

Итого                                                          100

+ до 5

15–20

5–10

10–15

Размах вариации группировочного признака определяется по формуле …

+ R=x_max – x_min

h= (x_max – x_min)/m

m=1+3,322*lg N

Статистическая совокупность, все единицы которой близки друг к другу по значениям выбранных для исследования признаков, в статистике называется …

+ однородной

симметричной

одноразмерной

При построении интервальной группировки из 6 групп с минимальным значением группировочного признака, равным 130, и максимальным, равным 250, ширина равного интервала составит …

15

+20

31

48

Если зависимость стоимости рекламного объявления (Y, руб.) от численности читательской аудитории (Х, тыс. чел.) описывается уравнением Yх = 1300 + 5Х и численность аудитории достигнет 10 тыс. чел., то стоимость рекламного объявления составит …

50 руб.

1 305 руб.

1 310 руб.

+1 350 руб.

Если в совокупности единиц среднее квадратическое отклонение признака составило 7, а средняя величина этого признака равняется 21, то совокупность единиц по величине данного признака …

+ однородна

равномерна

неоднородна

Среднее квадратическое отклонение можно рассчитать по формуле …

+

Абсолютные показатели отображают …

соотношение значений индивидуальных показателей

разницу между значениями индивидуальных показателей

+размеры и характеристики индивидуальных объектов

Темп роста исчисляется как … уровней ряда

+отношение

разность

сумма

Данные приведенной ниже таблицы представляют собой пример … ряда распределения

Распределение акций по величине курса продажи

Курс акции, руб. Число акций

10                               5

20                              10

40                              12

Итого                        37

интервального вариационного

интервального атрибутивного

+дискретного вариационного

При уменьшении объема выборки величина ее средней ошибки …

уменьшается

остается неизменной

+увеличивается

При анализе товарооборота супермаркета сводный индекс цен продукции составил 104,5 %. – следовательно, стоимость продукции …

+увеличилась на 4,5 %

увеличилась на 104,5 %

снизилась на 4,5 %

Если менеджер по персоналу для исследования показателей квартальной производительности труда менеджеров по работе с физическими лицами корпорации извлек систематическую выборку объемом 30 человек из 150 менеджеров, состоящих в штате, то доля отбора составленной им выборки равна …

50 %

30 %

+20 %

При функциональной зависимости между Х и Y значение коэффициента корреляции …

+равно единице

равно нулю

близко к нулю

близко к единице

Под вариацией понимают изменение …

массовых явлений во времени

состава объектов статистической совокупности

+значений признака у различных единиц совокупности

Расчет средней величины по указанным данным (см. таблицу) следует производить по формуле средней …

Выручка ауд. фирмы      Средняя стоимость контракта  Федеральный округ

за I пол 2013 г., млн. р.   на проведение аудита, млн. р.

36                                                1,5                                        А

34                                                2,0                                        Б

29                                                1,8                                        В

25                                                1,4                                        Г

гармонической простой

арифметической простой

гармонической взвешенной

+арифметической взвешенной

Если активные потребители составляют 10,0 % рынка и тратят в среднем 600 руб. на покупку продукции возглавляемого вами предприятия, пассивные потребители составляют 40,0 % рынка и тратят 400 руб., а остальные потребители в среднем тратят 500 руб., то средний объем трат для всех потребителей составляет …

500 руб.

80 руб.

600 руб.

+470 руб.

Если товарооборот в целом по товарной группе в июне составил 900 тыс. руб., а в мае (при фиксированном объеме реализации на уровне июня) – 850 тыс. руб., это говорит о величине …

+ перерасхода покупателей на 50 тыс. руб. от изменения цен

экономии покупателей на 50 тыс. руб. от изменения себестоимости

перерасхода покупателей на 800 тыс. руб. от изменения цен

Характеристика выборочной совокупности, зависящая от уровня вероятности, с которым гарантируется, что средняя величина признака в генеральной совокупности не выйдет за рассчитанные границы, – это …

+предельная ошибка выборки

ошибка репрезентативности

средняя ошибка выборки

Чтобы получить относительный показатель динамики с переменной базой сравнения для i-го периода, необходимо …

+разделить значение показателя в i-й период на величину показателя в предшествующий i-му период

разделить значение показателя в период i на значение, соответствующее начальному периоду рассматриваемого ряда динамики

разделить значение показателя в период (i – 1) на значение показателя в период i

Если коэффициент вариации возраста слушателей группы составляет 12.5 %. то в среднем возраст каждого слушателя этой группы отличается от общего среднего возраста, равного 24 годам, на …

1,1 года

1,2 года

1,92 года

+3 года

Механическая выборка осуществляется только способом … отбора

группового

комбинированного

+бесповторного

повторного

Доход, находящийся в середине ранжированного ряда распределения населения по доходу, (т.е. половина населения имеет доход ниже этого показателя, а вторая половина — выше), называется …

ранжированный доход

модальный доход

+медианный доход

Средняя гармоническая используется в случае, когда …

числитель исходного соотношения средней величины неизвестен

знаменатель исходного соотношения средней величины известен

+знаменатель исходного соотношения средней величины неизвестен

Перечень признаков (вопросов), подлежащих регистрации в процессе наблюдения, называется ..

статистическим формуляром

+программой наблюдения

отчетностью

Единица наблюдения – это

+первичный элемент статистической совокупности, являющийся носителем признаков

элемент математического множества

признак совокупности

Отдельное значение группировочного признака, положенного в основание ряда распределена, называют…

частотой

частостью

подлежащим

+вариантой

Средняя гармоническая используется в случае, когда …

числитель исходного соотношения средней величины неизвестен

знаменатель исходного соотношения средней величины известен

+знаменатель исходного соотношения средней величины неизвестен

Структурными средними являются …

средняя гармоническая

средняя квадратическая

средняя арифметическая

средняя геометрическая

+мода

+медиана

Если использовать коэффициент вариации для оценки однородности земельных участков по урожайности

Участок Урожайность, ц/га Посевная площадь, га

1                   16                         30

2                   20                         45

3                   21                         120

то доля участков указанных в ряду распределения будет составлять

+8,8%

11,9%

10,6%

1,5%

Абсолютный прирост исчисляется как …

произведение уровней ряда

+разность уровней ряда

отношение уровней ряда

Функциональной называется связь …

+при которой, определенному значению факторного признака соответствует одно значение результативного

между двумя признаками

при которой, определенному значению факторного признака соответствует несколько значений результативного

Коэффициент вариации характеризует:

пределы колеблемости признака

тесноту связи между признаками

диапазон вариации признака

+степень вариации признака

Аналитическое выражение связи определяется с помощью метода анализа

группировок

графического

+регрессионного

корреляционного

Коэффициент вариации признака составил 25%, средняя величина признака –  25. определите среднее квадратическое отклонение признака:

0,8

5

+6,25

25

Абсолютный размер колеблемости признака около средней величины характеризует …

дисперсия

коэффициент вариации

+среднее квадратическое отклонение

размах вариации

Ряд распределения, построенный по качественным признакам, называется …

+атрибутивным

дискретным вариационным

вариационным

Содержание курса лекций «Статистика»

Показатели вариации в анализе взаимосвязей

Для измерения степени колеблемости отдельных значений признака относительно средней исчисляют основные показатели вариации.

---

---

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение.

Так, например, для выявления наиболее стабильно работающего коллектива или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели дают возможность количественно определить размеры устойчивости производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя, как «выполнение работ в срок» имеет важное значение для принятия решений заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Осо­бое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств.

---

---

Основными показателями, характеризующими вариацию, являются:

• размах вариации;
• среднее линейное отклонение;
• дисперсия;
• среднее квадратическое отклонение;
• коэффициент вариации.
  

  ---

  ---

1)  Размах вариации

---

---

2) Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:

---

---

где  –абсолютные значения отклонений отдельных вариантов xi от средней арифметической ;  fi  – частота.

---

---

3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:

---

---

4. Среднее квадратическое отклонение – корень квадратный из дисперсии:

---

---

---

!!!В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака (руб., тыс., млн и т.д.).!!!

---

---

5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:

---

---

Пример. Для иллюстрации расчетов воспользуемся данными нижеприведенной табл. 9.1:

Таблица 9.1 ‑ Данные о продаже основных марок холодильников:

	Модель	Цена ( $ )	Объем продаж (шт.)	xifi
1	Siemens	1000	30	30000
2	Bosch	800	26	20800
3	AEG Santo	900	24	21600
4	Miele KF	1200	30	36000
5	Gorenje	870	20	17400
6	Haier	570	23	13110
7	Samsung	760	30	22800
8	Zanussi	700	20	14000
9	Daewoo	460	20	9200
10	Beko	650	25	16250
11	Candy	480	20	9600
10	Whirpool	470	21	9870
	ИТОГО	8860	289	220630

---

Рассчитаем размах вариации.

R= 1200-460=740$

Пример вычисления размаха вариации

---

Размах вариации служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.

Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака.

---

Этого недостатка лишен другой показатель – дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины.

Между индиви­дуальными отклонениями от средней и колеблемостью признака существует прямая зави­симость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и менее устойчив изучаемый показатель.

Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной

По приведенным выше данным определим средневзвешенную цену холодильника:

---

Далее рассчитаем дисперсию:

---

!!!Следует отметить, что дисперсия еще не дает представления об однородности со­вокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рас­считан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, на­сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак.!!!

---

---

Рассчитаем среднее квадратическое отклонение

---

Вывод: Таким образом, цена каждой марки холодильника отклоняется от средней цены в среднем на 271,1 $

---

---

Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости ка­кого-либо одного признака или для определения однородности совокупности рассчиты­вают относительные показатели.

Эти показатели вычисляются как отношение размаха вариации, среднего линейно­го отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.

---

---

Определим значение  показателя вариации по вышеприведенным данным таблицы

---

Совокупность считается однородной, если V не превышает 33%.

Если V<10%  вариация признака слабая;

10% < V<25% –  вариация средняя;

V>25% – вариация сильная.

Вывод: Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).

---

---

!! Следует отметить, что коэффициент вариации может быть более 100%, что, в част­ности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.

---

Изучая вариацию интересующего нас признака в пределах исследуемой совокупно­сти и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака.

При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подвер­женным влиянию).

---

---

Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации резуль­тативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индиви­дуальных значений признака, используют правило сложения дисперсий.

Общая дисперсия представляет собой сумму средней из виутригрупповой и меж­групповой и дисперсий:

---

 где:

---

Общая дисперсия характеризует вариацию признака по всей совокупности как ре­зультат влияния всех факторов, определяющих индивидуальные различия единиц сово­купности.

---

---

где:

---

---

Межгрупповая дисперсия  характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.

---

где:

---

---

Средняя из внутригрупповых дисперсий отражает ту часть вариации результа­тивного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рас­считывается отдельно по каждой j-ой группе.

---

где:

---

---

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:

---

---

Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:

---

Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении об­щей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчле­нения общей совокупности.

---

---

Теснота связи между факторным и результативным признаками оценивается на ос­нове эмпирического корреляционного отношения:

---

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

---

---

Пример. На следующем условном примере исследуем зависимость объема выполненных ра­бот от формы собственности проектно-изыскательских организаций.

Таблица 9.2. Выполнение работ проектно-изыскательскими организациями разной формы собственности

Форма собственности	Количество предприятий	Объем выполненных работ (млн. руб.)	Итого
Государственная	4	10,30,20,40	100
Негосударственная	6	20, 40, 60, 20, 50, 50	240
Итого	10		340

---

Решение:

1) Определим средний объем работ для предприятий двух форм собственности.

---

2) Определим средний объем работ для каждой формы собственности.

---

3) Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.

---

4) Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета.

Таблица 9.3. – Вспомогательная таблица

Форма собственности	Число предприятий	Средняя по группе	Внутригрупповые дисперсии
Государственная	4	25	125
Негосударственная	6	40	233
Итого	10

---

Пример. Средняя из внутригрупповых дисперсий

---

Пример. Межгрупповая дисперсия

---

---

На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:

Проверка закона сложения дисперсий:  54,0+189,8=243,8

---

Вывод: Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8) х 100%] зависит от фак­тора, положенного в основание группировки, т.е. от формы собственности, а на 78% [(189,8/243,8)х100%)] ‑ от прочих факторов.

---

Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:

Вывод: Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика

---

Содержание курса лекций «Статистика»

---

Контрольные задания

1. Распределение студентов одного из факультетов по возрасту характеризуется следующими данными:

Возраст студентов, лет	17	18	19	20	21	22	23	24	Всего
Число студентов	20	80	90	110	130	170	90	60	750

Вычислить: а) размах вариации; б)среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; относительные показатели вариации возраста студентов.

2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.

Содержание курса лекций «Статистика»