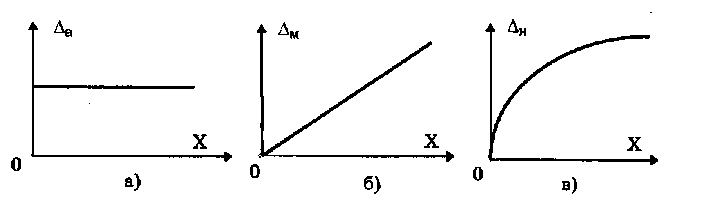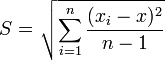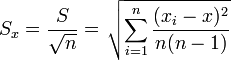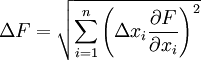Чем отличается ошибка от погрешности измерений метрология - Исправление ошибок и поиск оптимальных решений проблем

Погрешности измерений. Основные понятия и виды погрешностей.

Процедура измерений состоит из следующих
основных этапов:

—принятые модели объекта измерения;

—выбор метода измерений;

—выбор средств измерений;

—проведение эксперимента для
получения численного значения результата
измерения.

Различные недостатки, присуще этим
этапам, приводят к тому, что результат
измерения отличается от истинного
значения измеряемой величины.

Причины возникновения погрешности
могут быть различными.

Измерительные преобразования
осуществляются с использованием
различных физических явлений, на
основании которых можно установить
соотношение между измеряемой величиной
объекта исследования и выходным сигналом
средства измерений, по которому
оценивается результат измерения.

Точно установить это соотношение никогда
не удается вследствие недостаточной
изученности объекта исследования и
неадекватности его принимаемой модели,
невозможности точного учета влияния
внешних факторов, недостаточной
разработанности теории физических
явлений, положенных в основу измерения,
использования простых, но приближенных
аналитических зависимостей вместо
более точных, но сложных и т.д.

Понятие
«погрешность» — одно из центральных
в метрологии, где используются понятия
«погрешность результата измерения»
и «погрешность средства измерения».
Погрешность
результата измерения —
это разница между результатом измерения
X
и истинным
(или действительным) значением Q
измеряемой величины:

Она
указывает границы неопределенности
значения измеряемой величины.
Погрешность
средства измерения —
разность между показанием СИ и
истинным (действительным) значением
измеряемой ФВ. Она характеризует точность
результатов измерений, проводимых
данным средством.

Эти два
понятия во многом близки друг к другу
и классифицируются
по одинаковым признакам.

По
характеру
проявления погрешности
делятся на случайные, систематические,
прогрессирующие и грубые (промахи).

Заметим,
что из приведенного выше определения
погрешности никак
не следует, что она должна состоять из
каких-либо составляющих.
Деление погрешности на составляющие
было введено для удобства обработки
результатов измерений исходя из характера
их проявления.
В процессе формирования метрологии
было обнаружено, что погрешность не
является постоянной величиной. Путем
элементарного анализа установлено,
что одна ее часть проявляется как
постоянная величина, а другая — изменяется
непредсказуемо. Зги части
назвали систематической и случайной
погрешностями.

Как
будет показано в разд. 4.3, изменение
погрешности во времени представляет
собой нестационарный случайный процесс.
Разделение
погрешности на систематическую,
прогрессирующую и случайную
составляющие представляет собой попытку
описать различные участки частотного
спектра этого широкополосного процесса:
инфранизкочастотный, низкочастотный
и высокочастотный.

Случайная
погрешность —
составляющая погрешности измерения,
изменяющаяся случайным образом (по
знаку и значению) в серии
повторных измерений одного и того же
размера ФВ, проведенных
с одинаковой тщательностью в одних и
тех же условиях. В появлении
таких погрешностей не наблюдается
какой-либо
закономерности, они обнаруживаются при
повторных измерениях одной и той же
величины в виде некоторого разброса
получаемых
результатов. Случайные погрешности
неизбежны, неустранимы
и всегда присутствуют в результате
измерения. Описание случайных
погрешностей возможно только на основе
теории случайных
процессов и математической статистики.

В отличие от систематических
случайные погрешности нельзя исключить
из результатов измерений путем введения
поправки, однако
их можно существенно уменьшить путем
увеличения числа наблюдений.
Поэтому для получения результата,
минимально отличающегося
от истинного значения измеряемой
величины, проводят многократные измерения
требуемой величины с последующей
Математической
обработкой экспериментальных данных.

Систематическая
погрешность —
составляющая погрешности измерения,
остающаяся постоянной или закономерно
меняющаяся при
повторных измерениях одной и той же ФВ.
Постоянная и переменная
систематические погрешности показаны
на рис. 4.2. Их отличительный признак
заключается в том, что они могут быть
предсказаны,
обнаружены и благодаря этому почти
полностью устранены
введением соответствующей поправки.

Прогрессирующая
(дрейфовая) погрешность —
это непредсказуемая
погрешность, медленно меняющаяся во
времени. Впервые это
понятие было введено в монографии М.Ф.
Маликова «Основы метрологии»,
изданной в 1949 г. Отличительные особенности
прогрессирующих погрешностей:

они
могут быть скорректированы поправками
только в данный
момент времени, а далее вновь непредсказуемо
изменяются;
изменения
прогрессирующих погрешностей во времени
— нестационарный
случайный процесс, и поэтому в рамках
хорошо разработанной
теории стационарных случайных процессов
они могут
быть
описаны лишь с известными оговорками.

Понятие
прогрессирующей погрешности широко
используется при
исследовании динамики погрешностей СИ
и метрологической
надежности последних.

Грубая погрешность (промах)
— это случайная
погрешность результата
отдельного наблюдения, входящего в ряд
измерений, которая
для данных условий резко отличается от
остальных результатов
этого ряда. Они, как правило, возникают
из-за ошибок или
неправильных действий оператора (его
психофизиологического состояния,
неверного отсчета, ошибок в записях или
вычислениях,
неправильного включения приборов или
сбоев в их работе и др.).
Возможной причиной возникновения
промахов также могут быть
кратковременные резкие изменения
условий проведения измерений.
Если промахи обнаруживаются в процессе
измерений, то результаты, их содержащие,
отбрасывают. Однако чаще всего промахи
выявляют только при окончательной
обработке результатов измерений
с помощью специальных критериев.

По
способу
выражения,
различают
абсолютную, относительную и
приведенную погрешности.

Абсолютная
погрешность описывается
формулой (4.1) и выражается
в единицах измеряемой величины.

Однако
она не может в полной
мере служить показателем точности
измерений, так как одно и то же ее
значение, например, Д = 0,05 мм при X
= 100 мм соответствует достаточно
высокой точности измерений, а при X
= 1 мм — низкой. Поэтому
и вводится понятие относительной
погрешности. Относительная
погрешность —
это отношение абсолютной погрешности
измерения
к истинному значению измеряемой величины:

Эта
наглядная характеристика точности
результата измерения не
годится для нормирования погрешности
СИ, так как при изменении
значений Q
принимает различные значения вплоть
до бесконечности
при Q
= 0. В связи с этим для указания и
нормирования погрешности
СИ используется еще одна разновидность
погрешности
— приведенная.

Приведенная
погрешность — это
относительная погрешность, в
которой абсолютная погрешность СИ
отнесена к условно принятому
,
постоянному во всем диапазоне измерений
или его части:

Условно принятое
значение Q_N
называют нормирующим.
Чаще всего за него
принимают верхний предел измерений
данного СИ, применительно
к которым и используется главным образом
понятие «приведенная
погрешность».

В
зависимости от места
возникновения различают
инструментальные, методические и
субъективные погрешности.

Инструментальная
погрешность обусловлена
погрешностью применяемого
СИ. Иногда эту погрешность называют
аппаратурной.

Методическая,
погрешность измерения
обусловлена:

• отличием
принятой модели объекта измерения от
модели, адекватно описывающей его
свойство, которое определяется путем
измерения;

• влиянием
способов применения СИ. Это имеет место,
например,
при измерении напряжения вольтметром
с конечным значением
внутреннего сопротивления. В данном
случае вольтметр шунтирует
участок цепи, на котором измеряется
напряжение, и оно оказывается
меньше, чем было до присоединения
вольтметра;

влиянием
алгоритмов (формул), по которым
производятся вычисления
результатов измерений;
влиянием
других факторов, не связанных со
свойствами используемых
средств измерения.

Отличительной
особенностью методических погрешностей
является
то, что они не могут быть указаны в
нормативно-технической документации
на используемое СИ, поскольку от него
не зависят, а должны определяться
оператором в каждом конкретном случае.
В связи
с этим оператор должен четко различать
фактически измеряемую
им величину и величину, подлежащую
измерению.

Субъективная
(личная) погрешность измерения
обусловлена погрешностью отсчета
оператором показаний по шкалам СИ,
диаграммам
регистрирующих приборов. Они вызываются
состоянием оператора, его положением
во время работы, несовершенством органов
чувств,
эргономическими свойствами СИ.
Характеристики личной погрешности
определяют на основе нормированной
номинальной цены
деления шкалы измерительного прибора
(или диаграммной бумаги
регистрирующего прибора) с учетом
способности «среднего оператора»
к интерполяции в пределах деления шкалы.

По
зависимости
абсолютной погрешности от значений
измеряемой
величины различают
погрешности (рис. (1).4.):

• аддитивные
,
не зависящие от измеряемой величины;

•
мультипликативные
,
которые прямо пропорциональны измеряемой
величине;

•
нелинейные
,
имеющие нелинейную зависимость от
измеряемой
величины.

Эти
погрешности применяют в основном для
описания метрологических
характеристик СИ. Разделение погрешностей
на аддитивные,
мультипликативные и нелинейные весьма
существенно при решении
вопроса о нормировании и математическом
описании погрешностей СИ.

Примеры
аддитивных погрешностей — от постоянного
груза на чашке
весов, от неточной установки на нуль
стрелки прибора перед измерением, от
термо-ЭДС в цепях постоянного тока.
Причинами возникновения
мультипликативных погрешностей могут
быть: изменение коэффициента усиления
усилителя, изменение жесткости мембраны
датчика манометра или пружины прибора,
изменение опорного
напряжения в цифровом вольтметре.

Рис. (1).4.
Аддитивная (а), мультипликативная (б) и
нелинейная (в)погрешности

По
влиянию
внешних условий различают
основную и дополнительную
погрешности СИ. Основной
называется
погрешность СИ, определяемая в нормальных
условиях его применения. Для каждого
СИ в нормативно-технических документах
оговариваются условия эксплуатации
— совокупность влияющих величин
(температура
окружающей среды, влажность, давление,
напряжение и частота
питающей сети и др.), при которых
нормируется его погрешность.
Дополнительной,
называется
погрешность СИ, возникающая вследствие
отклонения какой-либо из влияющих
величин.

В
зависимости
от влияния характера изменения измеряемых
величин
погрешности
СИ делят на статические и динамические.
Статическая
погрешность —
это погрешность СИ применяемого
для измерения ФВ, принимаемой за
неизменную. Динамической
называется
погрешность СИ, возникающая дополнительно
при измерении
переменной ФВ и обусловленная
несоответствием его реакции
на скорость (частоту) изменения измеряемого
сигнала.

Источник

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».

Содержание

1 Определение погрешности
2 Классификация погрешностей
- 2.1 По форме представления
- 2.2 По причине возникновения
- 2.3 По характеру проявления
- 2.4 По способу измерения
3 См. также
4 Литература

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

$Delta x=frac{x_{max}-x_{min}}{2}$

Средняя квадратическая погрешность:

$S =left. sqrt{sum_{i=1}^{n}frac{(x_i-x)^2}{n-1}} right.$

Средняя квадратическая погрешность среднего арифметического:

$S _x= frac{S} {sqrt{n}} = left. sqrt{sum_{i=1}^{n}frac{(x_i-x)^2}{n(n-1)}} right.$

Классификация погрешностей

По форме представления

Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины X_meas. При этом равенство:

ΔX = | X_true − X_meas | ,

где X_true — истинное значение, а X_meas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина X_meas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

$delta_x =frac{ Delta x}{X}$ .

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

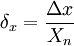
$delta_x =frac{ Delta x}{X_n}$ ,

где X_n — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то X_n определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведенная погрешность — безразмерная величина (может измеряться в процентах).

По причине возникновения

Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.

Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.

По характеру проявления

Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).

По способу измерения

Погрешность прямых измерений
Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если F = F(x₁,x₂…x_n), где x_i — непосредственно измеряемые независимые величины, имеющие погрешность Δx_i, тогда:

$Delta F = sqrt{sum_{i=1}^n left(Delta x_i frac{partial F}{partial x_i}right)^2}$

См. также

Измерение физических величин
Класс точности
Метрология
Система автоматизированного сбора данных со счетчиков по радиоканалу
Методы электроаналитической химии

Литература

Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.

Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.

Wikimedia Foundation.
2010.

Источник

Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Простая и логичная концепция точности, в конце прошлого столетия в ряде зарубежных стран стала подвергаться критике. Основной причиной неудовлетворенности являлся термин «погрешность».

Дело в том, что, в отличие от русского языка, в английском и французском языках понятия «ошибка» (т. е. просчет, неверное действие) и «погрешность» не различаются (the error в английском языке, erreur во французском). По этой причине метрологическая терминология вошла в противоречие с получившей всеобщее признание и повсеместно применяемой в мире идеологией управления качеством товаров и услуг на основе стандартов ИСО серии 9000. Суть этой методологии заключается в обеспечении условий для безошибочного выполнения всех производственных функций и трудовых операций. В то же время такую идеальную картину производства портят ошибки измерений (в русском языке — погрешности, имеющие несколько другой смысл), которых, в отличие от обычных ошибок, нельзя избежать, поскольку они являются неизбежным следствием ограниченных возможностей измерительной техники и сопровождают каждое измерение.
Похожая проблема стояла в 1927 г. перед физиком Вернером Гейзенбергом, когда он готовил к публикации свою знаменитую статью «О наглядном содержании квантово-теоретической кинематики и механики». В этой работе он ввел в физику знаменитые соотношения (3.1), устанавливающие принципиальные ограничения снизу погрешностей измерений импульса силы ?р и координаты ?х, энергии ?Е и импульса ?t:

в которых h= 1,05457266 * 10~34 — постоянная Планка. Автор назвал эти фундаментальные неравенства соотношениями неопределенностей, применив термин «неопределенность» (the uncertainty) как синоним термина «погрешность».
После публикации этой статьи термин «неопределенность» стал часто употребляться в физике. Он был использован в новой концепции оценивания точности измерений, регламентированной в международном документе «Руководство по выражению неопределенности измерения» (далее — Руководство). Этот документ был опубликован в 1993 г. от имени семи авторитетных международных организаций:

Международное бюро мер и весов (МБМВ),
Международная электротехническая комиссия (МЭК),
Международная федерация клинической химии (МФКХ),
Международная организация по стандартизации (ИСО),
Международный союз по чистой и прикладной химии (ИЮПАК),
Международный союз по чистой и прикладной физике (ИЮПАП),
Международная организация законодательной метрологии (МОЗМ).

Руководство фактически приобрело статус международного регламента, обязательного к применению. Оно нацелено, во-первых, на обеспечение потребителей полной информацией о всех составляющих погрешности результатов измерений и, во-вторых, на международную унификацию отчетов об измерениях и оценке их точности, с целью формирования основы для международного сравнения результатов измерений. При этом имеется в виду, что всемирное единство в методах оценки точности измерений обеспечивает правильное использование результатов измерений во всех областях деятельности.
Концепция неопределенности, введенная в Руководстве, заключается в следующем. Базовые понятия классической теории точности: истинное значение, действительное значение и погрешность измерения — не вводятся. Взамен введено понятие неопределенность измерения, понимаемое как сомнение, неполное знание значения измеряемой величины после проведения измерений (трактовка в широком смысле) и как количественное описание этого неполного знания (трактовка в узком смысле). Далее это понятие уточняется: неопределенность — параметр, связанный с результатом измерения и характеризующий рассеяние значений, которые могли бы быть приписаны измеряемой величине. В математической статистике известны два вида параметров, характеризующих рассеяние некоррелированных случайных величин: СКО и доверительный интервал. Они и принимаются в качестве характеристик неопределенности с наименованиями стандартная неопределенность и расширенная неопределенность. При этом, как и следовало ожидать, оказалось, что стандартная неопределенность является полным аналогом СКО погрешности измерений, а расширенная неопределенность — полным аналогом доверительных границ погрешности измерений. И в этом указанная концепция сомкнулась с традиционной постановкой задачи оценивания точности измерений.
Таким образом, в части практических приложений новая концепция оценивания точности измерений оказалась полностью идентичной классической. Более того, эти концепции тесно связаны друг с другом и, в принципе, известны давно.

Можно констатировать, что эти концепции отличаются тем, к какой величине относят дисперсию, характеризующую разброс наблюдаемых значений. При классическом подходе ее относят к истинному значению измеряемой величины X, в другом случае — к результату измерений L. Но это различие не влияет на подведение окончательных результатов, поскольку и в классическом подходе погрешности измерений также приписывают результату измерений. Таким образом, обе концепции дополняют друг друга, сливаясь в единую концепцию оценивания точности результатов измерений. При этом, следуя причинно-следственным связям, целесообразно установить следующую последовательность введения основных понятий теории точности измерений:

истинное значение величины => действительное значение величины => результат измерения => погрешность измерения => неопределенность результата измерения как характеристика этой погрешности.

Таким образом, понятия погрешность и неопределенность могут быть гармонично использованы без их взаимного противопоставления.

Статьи по теме:

Классификация погрешностей
Классификация неопределенностей измерений
Нормируемые метрологические характеристики средств измерений
Методические погрешности измерений
Суммирование погрешностей.
Количественное описание неопределенности в аналитических измерениях.
Нормированные формы представления результатов измерений и оценки неопределенности результатов измерений. Описание результата измерений должно осуществляться в одной из стандартных форм по МИ 1317–86 «Методические указания. ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров». МИ 1317–86 требует включения либо «характеристик погрешности измерений», либо их статистических оценок.
Каталог статей о погрешности и неопределенности

Источник

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

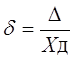
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
вторые — старением элементов средства измерения.

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

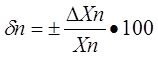
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

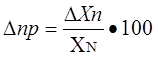
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.

Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Погрешности средств измерений подразделяются также на статические и динамические.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник