Математические диктанты по математике
(6 класс, учебник авт. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир)
Диктант 1 по теме «Делители и кратные»
-
Закончите предложение.
1) Натуральное число a делится нацело на натуральное число b, если … .
2) Число a называют кратным числа b, если … .
3) Если число a делится нацело на число b, то число b называют … .
4) Наименьшим делителем любого натурального числа a является … .
5) Наибольшим делителем любого натурального числа a является … .
6) Среди чисел, кратных числу a, наибольшего … .
7) Среди чисел, кратных числу a, наименьшим является … .

9) Если ни число a, ни число b не делятся нацело на число k, то их сумма a + b … .
10) Если число a делится нацело на число k, а число b не делится нацело на число k, то сумма a + b … .
-
Запишите числа: 1, 2, 3, 4, 5, 6, 7, 10, 12, 15, 20, 25, 40. Подчеркните те их них, которые являются делителями числа 40.
-
Запишите все делители числа 20.
-
Запишите в порядке возрастания шесть первых чисел, кратных 8.
-
Запишите все двузначные числа, кратные 21.
-
Запишите все двузначные числа, являющиеся делителями числа 120.
Диктант 2 по теме «Признаки делимости на 10, на 5 и на 2»
-
Закончите предложение.
1) Натуральное число делится нацело на 10, если его запись … .
2) Натуральное число не делится нацело на 10, если … .
3) Чётными называют натуральные числа, которые … .
4) Нечётными называют натуральные числа, которые … .
5) Чётными называют цифры … .
6) Нечётными называют цифры … .
7) Натуральное число делится нацело на 2, если … .

9) Натуральное число делится нацело на 5, если … .
10) Натуральное число не делится нацело на 5, если … .
-
Запишите какие-либо три трёхзначных числа, кратных 10.
-
Запишите какие-либо три четырёхзначных числа, кратных 2.
-
Запишите какие-либо три трёхзначных числа, кратных 5 и не кратных 2.
-
Запишите все чётные двузначные числа, которые кратны 5 и больше 50.
-
Запишите наименьшее четырёхзначное число, кратное 10.
-
Запишите наибольшее нечётное четырёхзначное число, кратное 5.
Диктант 3 по теме «Признаки делимости на 9 и на 3»
-
Закончите предложение.
1) Натуральное число делится нацело на 9, если … .
2) Натуральное число не делится нацело на 9, если … .
3) Натуральное число делится нацело на 3, если … .
4) Натуральное число не делится нацело на 3, если … .
-
Запишите числа: 219, 378, 1 368, 6 732. Подчеркните те из них, которые кратны 9.
-
Запишите числа: 564, 256, 3 125, 4 707. Подчеркните те их них, которые кратны 3.
-
Запишите наименьшее двузначное число, кратное 9.
-
Запишите наибольшее двузначное число, которое делится нацело на 3 и на 5.
-
Запишите наименьшее чётное трёхзначное число, кратное 3.
-
Запишите наименьшее нечётное трёхзначное число, кратное 9.
-
Запишите наибольшее чётное трёхзначное число, кратное 9.
Диктант 4 по теме «Простые и составные числа»
-
Закончите предложение.
1) Натуральное число называют простым, если … .
2) Наименьшим простым числом является число … .
3) Натуральное число называют составным, если … .
4) Число 1 не относят … .
-
Запишите все простые числа первых двух десятков.
-
Запишите все составные числа третьего и четвёртого десятков.
-
Запишите число 36 в виде произведения:
1) двух различных множителей, отличных от 1 и 36;
2) трёх различных множителей, отличных от 1 и 36;
3) простых множителей.
-
Представьте число 10 в виде суммы:
1) двух различных простых чисел;
2) трёх простых чисел.
-
Представьте число 16 в виде суммы:
1) двух простых чисел;
2) трёх простых чисел.
Диктант 5 по теме «Наибольший общий делитель»
-
Закончите предложение.
1) Наибольшим общим делителем двух натуральных чисел называют … .
2) Два натуральных числа называют взаимно простыми, если … .
3) Если число a — делитель числа b, то наибольший общий делитель чисел a и b
равен … .
-
Запишите все общие делители чисел 12 и 18, подчеркните наибольший из них.
-
Чему равен наибольший общий делитель чисел:
1) 6 и 9; 3) 10 и 20; 5) 6, 12 и 18;
2) 8 и 4; 4) 32 и 48; 6) 8, 24 и 32?
-
Являются ли взаимно простыми числа:
1) 15 и 18; 2) 12 и 35?
-
Запишите какое-либо число a такое, что числа a и 18 взаимно простые.
-
Запишите какие-либо два числа, наибольший общий делитель которых равен 14.
Диктант 6 по теме «Наименьшее общее кратное»
-
Закончите предложение.
1) Наименьшим общим кратным двух натуральных чисел называют … .
2) Если число a — делитель числа b, то наименьшее общее кратное чисел a и b
равно … .
3) Наименьшее общее кратное взаимно простых чисел равно … .
-
Чему равно наименьшее общее кратное чисел:
1) 20 и 50; 3) 6 и 8; 5) 4, 5 и 6?
2) 8 и 24; 4) 8 и 15;
-
Запишите наименьшее общее кратное знаменателей дробей:
1) 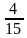
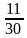
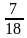
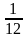
-
Запишите наименьшее общее кратное первых:
1) трёх натуральных чисел;
2) четырёх натуральных чисел.
-
Запишите какие-либо два числа, наименьшее общее кратное которых равно 30.
-
При каком значении a наименьшее общее кратное чисел a и 14 равно 28?
-
Наименьшее общее кратное чисел a и 12 равно 60. Запишите все возможные значения a.
Диктант 7 по теме «Основное свойство дроби»
-
Закончите предложение.
1) Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то … .
2) Если числитель и знаменатель дроби разделить на их общий делитель, то … .
2. Числитель данной дроби умножили на 8. Как надо изменить знаменатель, чтобы получилась дробь, равная данной?
3. Знаменатель данной дроби разделили на 5. Как надо изменить числитель, чтобы получилась дробь, равная данной?
4. Запишите дробь со знаменателем 12, равную дроби 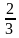
5. Запишите дробь с числителем 16, равную дроби 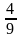
6. Запишите дробь со знаменателем 10, равную дроби 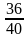
7. Запишите дробь с числителем 6, равную дроби 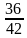
8. Запишите какие-либо три дроби, равные 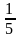
9. Запишите какие-либо три дроби, равные 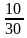
Диктант 8 по теме «Сокращение дробей»
-
Закончите предложение.
1) Деление числителя и знаменателя дроби на их общий делитель, отличный от … .
2) Дробь, числитель и знаменатель которой — взаимно простые числа, называют … .
3) Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получится … .
-
Сократите дробь:
1) 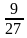
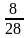
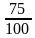
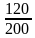
-
Какую часть минуты составляют:
1) 6 с; 2) 12 с; 3) 15 с; 4) 45 с?
Диктант 9 по теме «Приведение дробей к общему знаменателю. Сравнение дробей»
-
Закончите предложение.
1) Общий знаменатель двух дробей — это … .
2) Чтобы сравнить две дроби с разными знаменателями, надо … .
-
Можно ли привести дробь
к знаменателю 54? Ответ обоснуйте.
-
Можно ли привести дробь
к знаменателю 36? Ответ обоснуйте.
-
Приведите к знаменателю 18 дробь:
1) 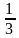
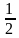
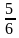
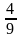
-
Приведите к наименьшему общему знаменателю дроби:
1) 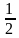
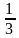
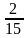
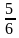
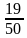
; 4)
и
.
-
Запишите какую-либо дробь, которая больше
и знаменатель которой равен 15.
-
Запишите какую-либо дробь, которая меньше
и знаменатель которой равен 32.
-
Запишите все дроби со знаменателем 16, которые больше
, но меньше
.
Диктант 10 по теме «Сложение и вычитание дробей с разными знаменателями»
-
Найдите сумму дробей
и
.
-
Найдите разность дробей
и
.
-
Найдите сумму чисел:
1) и
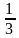
и
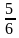
и 2
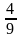
-
Найдите разность чисел:
1) и
; 2)
и
; 3) 9
и 6
.
-
Вычислите значение выражения
Диктант 11 по теме «Умножение дробей»
-
Закончите предложение.
1) Чтобы умножить дробь на натуральное число, надо … .
2) Произведением двух дробей является дробь, числитель которой равен … .
3) Чтобы умножить два смешанных числа, надо … .
-
Найдите произведение дробей
и
.
-
Найдите произведение дробей
и
.
-
Чему равны периметр и площадь квадрата со стороной
м?
-
Найдите произведение чисел:
1) 2 и 5; 2) 3
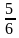
; 3) 2
и 2
; 4) 5
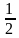
.
Диктант 12 по теме «Нахождение дроби от числа»
-
Закончите предложение.
1) Чтобы найти дробь от числа, можно число … .
2) Чтобы найти проценты от числа, можно представить … .
-
Найдите
от числа 42.
-
Найдите
от числа 18.
-
Найдите 40 % от числа 200.
-
Найдите 12 % от числа 80.
-
Сколько минут содержится:
1) в 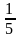
часа; 5) в
часа?
2) в 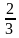
часа;
-
Некоторое число увеличили на 15 %. Во сколько раз увеличилось это число?
-
В бочке было 20 л воды. После дождя количество воды в бочке увеличилось на 20 %. Сколько литров воды стало в бочке?
Диктант 13 по теме «Взаимно обратные числа»
-
Закончите предложение.
1) Два числа называют взаимно обратными, если … .
2) Числом, обратным числу 1, является … .
3) Обратного числа не существует для числа … .
4) Обратным числу является число … .
5) Если n — натуральное число, то обратным ему является число … .
-
Запишите число, обратное числу:
1) 8; 2) 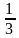
; 4) 1
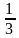
-
Найдите произведение числа
и числа, обратного числу
.
Диктант 14 по теме «Деление дробей»
-
Закончите предложение.
1) Чтобы разделить одну дробь на другую, надо … .
2) В буквенном виде правило деления дробей записывают так: … .
3) Нельзя делить на число … .
-
Найдите частное от деления:
1) 8 на ; 3) 14 на
; 5) 1
на 2
.
2) на 3; 4) 1 на
;
-
Сколько получится частей торта, если торт массой 3 кг разрезать на части:
1) по 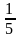
кг?
-
Решите уравнение:
1) 2 x = 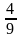
x = 1; 5) 4
: x = 4
.
2) 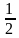
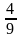
-
Во сколько раз число
больше числа
?
-
Уменьшите число 1
в 18 раз.
-
Запишите выражение и найдите его значение:
1) частное произведения чисел и
и числа
;
2) частное суммы и разности чисел 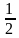
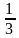
Диктант 15 по теме «Нахождение числа по заданному значению его дроби»
-
Закончите предложение.
1) Чтобы найти число по заданному значению его дроби, можно … .
2) Чтобы найти число по его процентам, можно … .
-
Найдите число, если:
1) его равна 5; 3) 15 % его равны 30;
2) его равны 24; 4) 120 % его равны 360.
-
Маша испекла пирожки, из которых 15 были с мясом, что составляет
всех пирожков. Сколько всего пирожков испекла Маша?
-
Если 16 % пути составляет 48 км, то сколько километров составляет весь путь?
-
Известно, что 70 % сплава составляет медь. Сколько получили килограммов сплава, если для его изготовления взяли 14 кг меди?
Диктант 16 по теме «Преобразование обыкновенной дроби в десятичную»
1. Закончите предложение.
1) Чтобы несократимую дробь преобразовать в десятичную, необходимо привести её к … .
2) Несократимую дробь a b можно преобразовать в десятичную только тогда, когда … .
3) Чтобы преобразовать обыкновенную дробь в десятичную, можно её числитель … .
2. Запишите дроби: ,
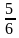
,
,
,
,
. Обведите те из них, которые нельзя преобразовать в десятичные.
3. Преобразуйте в десятичную дробь:
1) ; 2)
; 3)
; 4)
.
Диктант 17 по теме «Бесконечные периодические десятичные дроби»
-
Закончите предложение.
При делении натурального числа на натуральное число можно получить один из трёх результатов: … .
-
Запишите периодическую дробь:
1) нуль целых и два в периоде;
2) одна целая и тридцать пять в периоде;
3) нуль целых две десятых и шесть в периоде;
4) восемь целых четырнадцать сотых и девятнадцать в периоде.
-
Преобразуйте обыкновенную дробь в бесконечную периодическую десятичную дробь:
1) 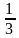
; 3)
; 4)
.
Диктант 18 по теме «Отношения»
-
Закончите предложение.
1) Частное двух чисел a и b, отличных от нуля, называют … .
2) Отношение чисел a и b можно записать двумя способами: … .
3) Отношение не изменится, если его члены … .
4) Отношение чисел a и b показывает … .
-
Чему равно отношение чисел:
1) 24 и 6; 2) 9 и 27?
-
Отношение какого числа к числу 8 равно 6?
-
Отношение числа 36 к числу a равно 3. Чему равно число a?
-
Отношение числа 15 к числу b равно
. Чему равно число b?
-
Замените отношение дробных чисел отношением натуральных чисел:
1) 1 : ; 2)
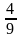
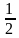
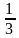
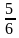
.
Диктант 19 по теме «Пропорции»
-
Закончите предложение.
1) Пропорцией называют … .
2) В записи a : b = c : d крайними членами пропорции называют числа … .
3) В записи a : b = c : d средними членами пропорции называют числа … .
4) Основное свойство пропорции формулируют так: … .
-
Составьте пропорцию из чисел 2, 3, 4 и 6.
-
Решите уравнение, используя основное свойство пропорции:
1) x : 12 = 4 : 3; 2) 8 : x = 16 : 10; 3) .
Диктант 20 по теме «Процентное отношение двух чисел»
-
Закончите предложение.
1) Процентное отношение двух чисел — это … .
2) Процентное отношение двух чисел показывает … .
3) Чтобы найти процентное отношение двух чисел, надо … .
-
Сколько процентов число 19 составляет от числа 100?
-
Сколько процентов число 11 составляет от числа 22?
-
Сколько процентов число 8 составляет от числа 32?
-
Сколько процентов число 24 составляет от числа 300?
-
Из 400 деталей бракованными оказались 4 детали. Сколько процентов всех деталей составляли качественные детали?
-
Футбольная команда шестиклассников, принимая участие в турнире, забила 24 гола, из которых 6 забил её лучший нападающий. Какой процент голов забил этот нападающий?
-
На уроке математики 9 мин проверяли выполнение домашнего задания, а затем 27 мин писали самостоятельную работу. Сколько процентов продолжительности урока заняла проверка домашнего задания и сколько — выполнение самостоятельной работы, если продолжительность урока 45 мин?
-
Какую цифру надо дописать справа к числу, чтобы получить число, составляющее 1000 % данного числа?
Диктант 21 по теме «Прямая и обратная пропорциональные зависимости»
-
Закончите предложение.
1) Две переменные величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая … .
2) Если две переменные величины прямо пропорциональны, то отношение соответствующих значений этих величин равно … .
3) Две переменные величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая … .
4) Если две переменные величины обратно пропорциональны, то произведение соответствующих значений этих величин равно … .
-
Из трёх величин: путь, скорость и время движения — укажите какие-либо две:
1) прямо пропорциональные величины;
2) обратно пропорциональные величины.
-
Из трёх величин: цена единицы товара, количество купленных единиц товара, общая стоимость купленного товара — укажите какие-либо две:
1) прямо пропорциональные величины;
2) обратно пропорциональные величины.
-
Из 50 кг муки получают 70 кг хлеба.
1) Сколько хлеба получают из 150 кг муки?
2) Сколько надо муки, чтобы испечь 14 кг хлеба?
-
В 3 л раствора содержится 12 г соли. Сколько соли содержится в 4,5 л этого раствора?
-
Три одинаковых насоса наполняют бассейн водой за 5 ч. За какое время наполнят этот бассейн шесть таких насосов?
-
За некоторую сумму денег можно купить 28 одинаковых тонких тетрадей. Сколько толстых тетрадей можно купить за эту сумму денег, если каждая толстая тетрадь в 4 раза дороже тонкой тетради?
Диктант 22 по теме «Окружность и круг»
-
Закончите предложение.
1) Все точки окружности удалены на одинаковое расстояние от … .
2) Радиусом окружности называют отрезок, соединяющий … .
3) Хордой называют отрезок … .
4) Диаметром называют … .
5) Диаметр больше радиуса в … .
6) Дугой окружности называют каждую из частей, на которые делят её … .
7) Кругом называют часть … .

9) Сектором называют каждую из частей круга, на которые делят его … .
10) Полукругом называют каждую из … .
-
Запишите, чему равен диаметр окружности, если расстояние от центра окружности до точки, принадлежащей окружности, равно 8 см.
-
Принадлежит ли окружности её центр?
-
Принадлежит ли кругу его центр?
-
Начертите произвольную окружность. Проведите радиус окружности, её диаметр, на котором не лежит проведённый радиус, и хорду, отличную от диаметра.
-
Внутри окружности отметили точку, отличную от её центра. Сколько через эту точку можно провести:
1) диаметров; 2) хорд, отличных от диаметра?
-
На окружности отметили произвольную точку. Сколько можно провести:
1) диаметров с концом в этой точке;
2) хорд, отличных от диаметра, с концом в этой точке?
Диктант 23 по теме «Длина окружности. Площадь круга»
-
Запишите приближённое значение числа π с точностью до сотых.
-
Запишите формулу, по которой вычисляют длину окружности, если известен её диаметр.
-
Запишите формулу, по которой вычисляют длину окружности, если известен её радиус.
-
Как изменится отношение длины окружности к её диаметру, если диаметр увеличить в 5 раз?
-
Вычислите длину окружности, радиус которой равен 5 дм.
-
Чему равен радиус окружности, длина которой — 9π см?
-
Длина окружности равна 18π см. Какой станет длина окружности, если её радиус:
1) уменьшить в 9 раз;
2) увеличить в 6 раз?
-
Запишите формулу, по которой вычисляют площадь круга, если известен его радиус.
-
Вычислите площадь круга, диаметр которого равен 20 мм.
-
Чему равен диаметр круга, площадь которого равна 49π см2?
-
Как изменится площадь круга, если его радиус:
1) увеличить в 4 раза;
2) уменьшить в 10 раз?
Диктант 24 по теме «Случайные события. Вероятность случайного события»
-
Закончите предложение.
1) Событие, которое в одних и тех же условиях может произойти, а может и не произойти, называют … .
2) Науку, которая занимается оценками вероятностей случайных событий, называют … .
3) Вероятность достоверного события равна … .
4) Вероятность невозможного события равна … .
5) Если эксперимент заканчивается одним из n равновозможных исходов, из которых m являются благоприятными для наступления данного события, то вероятность этого события равна … .
-
Известно, что из каждых 1000 лампочек — 5 бракованных. Какова вероятность приобрести бракованную лампочку?
-
Какова вероятность того, что:
1) после субботы настанет воскресенье;
2) после 30 апреля настанет 31 апреля?
-
В ящике лежат 36 карточек, пронумерованных числами от 1 до 36. Какова вероятность того, что номер наугад взятой карточки будет делителем числа 36?
-
Какова вероятность того, что при кидании игрального кубика выпадет число, не кратное 3?
-
Одну грань кубика покрасили в белый цвет, две грани — в жёлтый, а три грани — в синий. Какова вероятность выпадения при кидании кубика:
1) белой грани; 4) красной грани;
2) жёлтой грани; 5) не чёрной грани?
3) синей грани;
Диктант 25 по теме «Координатная прямая»
-
Закончите предложение.
1) Координатной прямой называют прямую, на которой выбрали … .
2) На координатной прямой существуют такие два направления: … .
3) Стрелкой на координатной прямой указывают … .
4) Неотрицательными числами называют … .
5) Неположительными числами называют … .
6) Начало отсчёта имеет координату … .
7) Если точка A имеет координату 12, то это записывают так: … .

-
Начертите координатную прямую и отметьте на ней числа −2, 4, −6, 5, −3.
-
Запишите какие-нибудь три числа, расположенные на координатной прямой:
1) левее числа 0,2;
2) левее числа −4,3;
3) правее числа −10,4;
4) правее числа −0,1;
5) левее числа −6, но правее числа −12;
6) левее числа −4,2, но правее числа −4,5.
-
Длина единичного отрезка координатной прямой равна 2 см. Чему равно расстояние между точками:
1) A (2) и B (7); 2) C (−10) и D (−2); 3) E (−6) и F (3)?
Диктант 26 по теме «Целые числа. Рациональные числа»
-
Закончите предложение.
1) Целыми числами называют … .
2) Натуральные числа ещё называют … .
3) Целые и дробные числа образуют … .
-
Запишите число, противоположное:
1) числу 9; 2) числу −4,3; 3) самому себе; 4) числу −1.
-
Начертите координатную прямую и отметьте на ней числа −6 и 2, а также числа, им противоположные.
-
Найдите значение выражения −m, если m = −3,6.
-
Запишите какие-нибудь четыре числа, являющихся целыми, но не являющихся натуральными.
-
Запишите какие-нибудь четыре числа, являющихся рациональными, но не являющихся целыми.
-
Запишите все целые числа, расположенные на координатной прямой между числами −3 и 2.
-
Сколько целых чисел расположено на координатной прямой между числами:
1) −9,4 и 9,4; 2) −27,8 и 18,1?
-
Ученик записывает целые числа, изображённые на координатной прямой, в таком порядке: −8, −7, −6. Какое следующее число он запишет?
Диктант 27 по теме «Модуль числа»
-
Закончите предложение.
1) Модулем числа a называют расстояние от … .
2) Модуль числа принимает только … .
3) Модуль неотрицательного числа равен … .
4) Модуль отрицательного числа равен … .
5) Модули противоположных чисел … .
-
Запишите в виде равенства утверждение: модуль числа m равен 10.
-
Чему равен модуль числа:
1) 17; 2) −20; 3) 0,4; 4) −0,1?
-
Вычислите значение выражения:
1) |−4| + |4|; 2) |10| − |−10|.
-
Запишите положительное число, модуль которого равен 25.
-
Запишите отрицательное число, модуль которого равен 7,2.
-
Известно, что |x| = 5. Чему равен |−x|?
-
Известно, что |−y| = 7,2. Чему равен |y|?
-
Запишите все целые значения x, при которых верно неравенство |x|
Диктант 28 по теме «Сравнение чисел»
-
Закончите предложение.
1) На координатной прямой из двух чисел большее число расположено … .
2) Любое положительное число больше любого … .
3) Из двух отрицательных чисел меньше то … .
4) Если a a — число … .
5) Если a 0, то a — число … .
-
Сравните числа:
1) 12 и −8; 3) −12 и −8; 5) −14 и 0,1;
2) −12 и 8; 4) −12 и 0; 6) −0,3 и −0,03.
-
Запишите какие-нибудь четыре числа, которые:
1) меньше 0; 3) меньше 2; 5) меньше −6;
2) больше 0; 4) больше −1; 6) больше −6.
-
Запишите в порядке возрастания целые числа:
1) от −5 до 5; 2) от −100 до −90.
-
Запишите в порядке убывания целые числа:
1) от 0 до −10; 2) от −8 до −14.
-
При каких целых значениях m верно неравенство:
1) −2 m ≤ 4; 2) −3 ≤ m ≤ 1,2?
Диктант 29 по теме «Сложение рациональных чисел и его свойства»
-
Найдите сумму чисел:
1) −1 и 0,8; 4) −3 и 3,5; 7) −0,1 и −1; 10) − 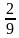
;
2) −3 и 1,3; 5) −0,1 и 1; 
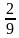
; 11) −
и
;
3) 4,2 и 6; 6) 0,1 и −1; 9) 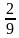
; 12) 0 и −
.
-
Чему равно значение выражения:
1) |−6| + (−10); 2) −6 + |−10|; 3) −6 + |−6|?
-
Запишите в виде равенства утверждение: «Сумма чисел −7 и m равна 11». Каким числом, положительным или отрицательным, является число m?
-
Найдите сумму всех целых чисел, удовлетворяющих неравенству −3 p ≤ 1.
-
Число a — отрицательное, число b — положительное. Сумма этих чисел — число отрицательное. Сравните модули чисел a и b.
-
Запишите в виде суммы двух равных слагаемых число:
1) −2,4; 2) −9.
-
Какое число надо прибавить к числу −16, чтобы сумма была равной 16?
-
Какое число надо прибавить к сумме чисел −8 и 32, чтобы получить в результате число 0?
Диктант 30 по теме «Вычитание рациональных чисел»
-
Закончите предложение.
1) Чтобы найти разность двух чисел, можно … .
2) Чтобы из числа a вычесть число −5, надо к числу a прибавить число … .
3) Чтобы из числа b вычесть число 16, надо к числу b прибавить число … .
4) Если из большего числа вычтем меньшее, то получим число … .
5) Если из меньшего числа вычтем большее, то получим число … .
-
Вычислите разность чисел:
1) 6 и 18; 4) −1,5 и −1,5; 7) 0 и 3 8 ;
2) −7 и −1; 5) −1,5 и 1,5; 
3) 4 и −11; 6) −3,2 и 2,4; 9) −12 и −8.
-
Решите уравнение:
1) x + 5 = 3; 4) x + 0,4 = -0,3;
2) 1,2 − x = 4; 5) 3 − x = −1.
3) −10 − x = 6;
-
Число a — положительное, число b — отрицательное. Положительной или отрицательной является разность a − b?
-
Числа a и b — положительные, разность a − b — отрицательное число. Сравните модули чисел a и b.
Диктант 31 по теме «Умножение рациональных чисел»
-
Закончите предложение.
1) Чтобы умножить два числа с разными знаками, надо … .
2) Чтобы умножить два отрицательных числа, надо … .
3) Если числа a и b имеют одинаковые знаки, то произведение ab … .
4) Если произведение ab положительно, то числа a и b имеют … .
5) Если числа a и b имеют разные знаки, то произведение ab … .
6) Если произведение ab отрицательно, то числа a и b имеют … .
7) Если хотя бы одно из чисел a или b равно нулю, то произведение ab равно … .

9) При умножении числа на –1 получаем число … .
10) При любых значениях x выражение x2 принимает … .
-
Запишите свойство единицы при умножении.
-
Запишите свойство нуля при умножении.
-
Вычислите произведение чисел:
1) −5 и 6; 3) −4 и −0,7; 5) и
; 7) −1
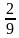
2) −0,8 и 9; 4) −1,2 и 10; 6) −5 и −1;

-
Запишите два противоположных числа, произведение которых равно −9.
-
Решите уравнение x(x + 2) = 0.
-
Запишите три последовательных целых числа, произведение которых равно нулю.
-
Запишите все целые отрицательные значения x, удовлетворяющие неравенству
−3x -
Запишите все целые неотрицательные значения x, удовлетворяющие неравенству
−4x −28. -
Известно, что a 0, b
1) a2b; 2) ab2.
Диктант 32 по теме «Переместительное и сочетательное свойства умножения рациональных чисел. Коэффициент»
-
Сформулируйте переместительное свойство умножения.
-
Сформулируйте сочетательное свойство умножения.
-
Упростите выражение −3a ⋅ (−1,3). Подчеркните его коэффициент.
-
Упростите выражение −0,9 ⋅ (−a) ⋅ 9b. Подчеркните его коэффициент.
-
Упростите выражение −x ⋅ (−2,4) ⋅ (−5y). Подчеркните его коэффициент.
-
Чему равно произведение всех целых чисел, которые больше −10, но меньше 10?
-
Запишите число 240 в виде произведения пяти неравных целых чисел, среди которых есть отрицательные.
-
Запишите число −210 в виде произведения четырёх неравных целых множителей.
Диктант 33 по теме «Деление рациональных чисел»
-
Закончите предложение.
1) Чтобы найти частное двух чисел с разными знаками, надо … .
2) Чтобы найти частное двух отрицательных чисел, надо … .
3) Частное любого рационального числа и единицы равно … .
4) Частное двух равных чисел, отличных от нуля, равно … .
5) Частное двух противоположных чисел равно … .
6) На нуль делить … .
-
Найдите частное чисел:
1) 12 и −3; 3) −28 и −0,7; 5) −3,6 и 4;
2) −2 и −0,5; 4) −54 и −90; 6) 0,96 и −0,012.
-
Можно ли найти частное чисел:
1) 0 и −6; 2) −6 и 0?
-
Решите уравнение:
1) −0,2x = 5; 3) x : ;
2) − 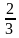
: x = − 1.
Диктант 34 по теме «Перпендикулярные прямые»
-
Закончите предложение.
1) Две прямые называют перпендикулярными, если при их пересечении … .
2) Если прямые a и b перпендикулярны, то это записывают так: … .
3) Два отрезка называют перпендикулярными, если … .
-
Начертите квадрат DEFK, сторона которого равна 3 см. Запишите, используя символ перпендикулярности, каким сторонам квадрата перпендикулярна сторона FK.
-
Проведите прямую m и отметьте точку A, ей не принадлежащую. Проведите через точку A прямую, перпендикулярную прямой m.
-
Проведите прямую b и отметьте точку C, ей принадлежащую. Проведите через точку C прямую, перпендикулярную прямой b.
-
Начертите перпендикулярные луч и отрезок так, чтобы они:
1) пересекались;
2) не имели общих точек.
Диктант 35 по теме «Осевая и центральная симметрии»
-
Закончите предложение.
1) Точки M и N называют симметричными относительно прямой l, если … .
2) Точки A и A1 называют симметричными относительно точки O, если … .
-
Начертите отрезок CD длиной 4 см. Проведите прямую, относительно которой точки C и D будут симметричными.
-
Начертите ломаную BCD и проведите прямую a, её не пересекающую. Постройте ломаную, симметричную ломаной BCD относительно прямой a. Обозначьте полученную ломаную. Запишите пары звеньев ломаных, симметричных относительно прямой a.
-
Начертите отрезок MK длиной 3 см. Отметьте точку, относительно которой точки M и K будут симметричными.
-
Начертите координатную прямую и отметьте на ней точки M (−5), K (3), P (−1). Постройте:
1) точку M1, симметричную точке M относительно начала координат;
2) точку K1, симметричную точке K относительно точки P. Запишите координаты точек M1 и K1.
-
Начертите ломаную MKD и отметьте точку S, ей не принадлежащую. Постройте ломаную, симметричную ломаной MKD относительно точки S. Обозначьте полученную ломаную. Запишите пары звеньев ломаных, симметричных относительно точки S.
Диктант 36 по теме «Параллельные прямые»
-
Закончите предложение.
1) Две прямые на плоскости называют параллельными, если … .
2) Если прямые a и b параллельны, то это записывают так: … .
3) Два отрезка называют параллельными, если … .
4) Если две прямые, лежащие в одной плоскости, перпендикулярны третьей прямой, то … .
-
Начертите квадрат DEFK, сторона которого равна 3 см. Запишите, используя соответствующий символ, параллельные стороны квадрата.
-
Проведите прямую m и отметьте точку K, ей не принадлежащую. Проведите через точку K прямую, параллельную прямой m.
-
Начертите тупой угол ABC. Отметьте между сторонами угла точку D и проведите через эту точку прямые, параллельные сторонам угла.
Диктант 37 по теме «Координатная плоскость»
-
Закончите предложение.
1) Осями координат называют две перпендикулярные координатные прямые, которые … .
2) Точку пересечения осей координат называют … .
3) Горизонтальную ось координат называют осью … .
4) Вертикальную ось координат называют осью … .
5) Вместе оси координат образуют … .
6) Координатной плоскостью называют … .
7) Записывая координаты точки, ординату всегда ставят на … .

9) Если точка лежит на оси абсцисс, то равна нулю её … .
10) Если точка лежит на оси ординат, то равна нулю её … .
11) Две точки с противоположными абсциссами и ординатами симметричны относительно … .
12) Две точки с равными ординатами и противоположными абсциссами симметричны относительно … .
13) Две точки с равными абсциссами и противоположными ординатами симметричны относительно … .
-
Запишите, как обозначают, что точка D имеет абсциссу, равную −3, и ординату, равную 7.
-
На координатной плоскости отметьте точки A (−2; 3), B (3; −2), C (−1; 0), D (0; −1), E (−4; −1).
-
В какой четверти координатной плоскости находится точка:
1) A (2; 8); 3) C (1; −125);
2) B (−6; −2); 4) D (−168; 293)?
-
Принадлежит ли точка координатной оси (в случае утвердительного ответа укажите, какой именно):
1) A (−6; 0); 3) C (0; 4); 5) E (0,1; −0,2);
2) B (3; 1); 4) D (0; −9); 6) F (450; 0)?
-
На координатной плоскости отметьте точку M (−3; −4). Постройте точку M1, симметричную точке M относительно начала координат; точку M2, симметричную точке M относительно оси x; точку M3, симметричную точке M относительно оси y. Запишите координаты точек M1, M2 и M3.
-
На координатной плоскости отметьте точки С (3; 1) и D (−1; −3). Проведите прямую CD. Отметьте на прямой CD точки, ординаты которых равны соответственно 0; −1; −2; 2.
-
- 0
-
Знаменатель данной дроби разделили на 2. Как нужно изменить числитель, чтобы получилась дробь, равная данной?
Запишите дробь с числителем 9, равную дроби .
Числитель данной дроби умножили на 7. Как нужно изменить знаменатель, чтобы получилась дробь, равная данной?
Запишите дробь со знаменателем 16, равную дроби .
Запишите дроби . Подчеркните дроби, которые равны между собой.
-
Комментариев (0)
-
- 0
-
Если знаменатель дроби разделить на 2, то и числитель надо разделить на 2, чтобы получилась дробь равная данной
10/16=5/8
числитель умножили на 7, надо и знаменатель умножить на 7
9/15=63/105
-
Комментариев (0)
Вы можете сохранять ваши расчеты и они будут отображаться здесь.
Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

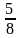 к знаменателю 36? Ответ обоснуйте.
к знаменателю 36? Ответ обоснуйте.