Что характеризует функция потерь ошибку

From Wikipedia, the free encyclopedia

In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) ^[1] is a function that maps an event or values of one or more variables onto a real number intuitively representing some «cost» associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy.

In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century.^[2] In the context of economics, for example, this is usually economic cost or regret. In classification, it is the penalty for an incorrect classification of an example. In actuarial science, it is used in an insurance context to model benefits paid over premiums, particularly since the works of Harald Cramér in the 1920s.^[3] In optimal control, the loss is the penalty for failing to achieve a desired value. In financial risk management, the function is mapped to a monetary loss.

Examples[edit]

Regret[edit]

Leonard J. Savage argued that using non-Bayesian methods such as minimax, the loss function should be based on the idea of regret, i.e., the loss associated with a decision should be the difference between the consequences of the best decision that could have been made had the underlying circumstances been known and the decision that was in fact taken before they were known.

Quadratic loss function[edit]

The use of a quadratic loss function is common, for example when using least squares techniques. It is often more mathematically tractable than other loss functions because of the properties of variances, as well as being symmetric: an error above the target causes the same loss as the same magnitude of error below the target. If the target is t, then a quadratic loss function is

for some constant C; the value of the constant makes no difference to a decision, and can be ignored by setting it equal to 1. This is also known as the squared error loss (SEL). ^[1]

Many common statistics, including t-tests, regression models, design of experiments, and much else, use least squares methods applied using linear regression theory, which is based on the quadratic loss function.

The quadratic loss function is also used in linear-quadratic optimal control problems. In these problems, even in the absence of uncertainty, it may not be possible to achieve the desired values of all target variables. Often loss is expressed as a quadratic form in the deviations of the variables of interest from their desired values; this approach is tractable because it results in linear first-order conditions. In the context of stochastic control, the expected value of the quadratic form is used.

0-1 loss function[edit]

In statistics and decision theory, a frequently used loss function is the 0-1 loss function

where is the indicator function.
Meaning if the input is evaluated to true, then the output is 1. Otherwise, if the input is evaluated to false, then the output will be 0.

Constructing loss and objective functions[edit]

In many applications, objective functions, including loss functions as a particular case, are determined by the problem formulation. In other situations, the decision maker’s preference must be elicited and represented by a scalar-valued function (called also utility function) in a form suitable for optimization — the problem that Ragnar Frisch has highlighted in his Nobel Prize lecture.^[4]
The existing methods for constructing objective functions are collected in the proceedings of two dedicated conferences.^[5][6]
In particular, Andranik Tangian showed that the most usable objective functions — quadratic and additive — are determined by a few indifference points. He used this property in the models for constructing these objective functions from either ordinal or cardinal data that were elicited through computer-assisted interviews with decision makers.^[7][8]
Among other things, he constructed objective functions to optimally distribute budgets for 16 Westfalian universities^[9]
and the European subsidies for equalizing unemployment rates among 271 German regions.^[10]

Expected loss[edit]

In some contexts, the value of the loss function itself is a random quantity because it depends on the outcome of a random variable X.

Statistics[edit]

Both frequentist and Bayesian statistical theory involve making a decision based on the expected value of the loss function; however, this quantity is defined differently under the two paradigms.

Frequentist expected loss[edit]

We first define the expected loss in the frequentist context. It is obtained by taking the expected value with respect to the probability distribution, P_θ, of the observed data, X. This is also referred to as the risk function^{[11][12][13][14]} of the decision rule δ and the parameter θ. Here the decision rule depends on the outcome of X. The risk function is given by:

Here, θ is a fixed but possibly unknown state of nature, X is a vector of observations stochastically drawn from a population, is the expectation over all population values of X, dP_θ is a probability measure over the event space of X (parametrized by θ) and the integral is evaluated over the entire support of X.

Bayesian expected loss[edit]

In a Bayesian approach, the expectation is calculated using the posterior distribution π^* of the parameter θ:

One then should choose the action a^* which minimises the expected loss. Although this will result in choosing the same action as would be chosen using the frequentist risk, the emphasis of the Bayesian approach is that one is only interested in choosing the optimal action under the actual observed data, whereas choosing the actual frequentist optimal decision rule, which is a function of all possible observations, is a much more difficult problem.

Examples in statistics[edit]

• For a scalar parameter θ, a decision function whose output is an estimate of θ, and a quadratic loss function (squared error loss)

  

  the risk function becomes the mean squared error of the estimate,

  

  An Estimator found by minimizing the Mean squared error estimates the Posterior distribution’s mean.

• In density estimation, the unknown parameter is probability density itself. The loss function is typically chosen to be a norm in an appropriate function space. For example, for L² norm,

  

  the risk function becomes the mean integrated squared error

  

Economic choice under uncertainty[edit]

In economics, decision-making under uncertainty is often modelled using the von Neumann–Morgenstern utility function of the uncertain variable of interest, such as end-of-period wealth. Since the value of this variable is uncertain, so is the value of the utility function; it is the expected value of utility that is maximized.

Decision rules[edit]

A decision rule makes a choice using an optimality criterion. Some commonly used criteria are:

• Minimax: Choose the decision rule with the lowest worst loss — that is, minimize the worst-case (maximum possible) loss:

  

• Invariance: Choose the decision rule which satisfies an invariance requirement.
• Choose the decision rule with the lowest average loss (i.e. minimize the expected value of the loss function):

  

Selecting a loss function[edit]

Sound statistical practice requires selecting an estimator consistent with the actual acceptable variation experienced in the context of a particular applied problem. Thus, in the applied use of loss functions, selecting which statistical method to use to model an applied problem depends on knowing the losses that will be experienced from being wrong under the problem’s particular circumstances.^[15]

A common example involves estimating «location». Under typical statistical assumptions, the mean or average is the statistic for estimating location that minimizes the expected loss experienced under the squared-error loss function, while the median is the estimator that minimizes expected loss experienced under the absolute-difference loss function. Still different estimators would be optimal under other, less common circumstances.

In economics, when an agent is risk neutral, the objective function is simply expressed as the expected value of a monetary quantity, such as profit, income, or end-of-period wealth. For risk-averse or risk-loving agents, loss is measured as the negative of a utility function, and the objective function to be optimized is the expected value of utility.

Other measures of cost are possible, for example mortality or morbidity in the field of public health or safety engineering.

For most optimization algorithms, it is desirable to have a loss function that is globally continuous and differentiable.

Two very commonly used loss functions are the squared loss, , and the absolute loss, . However the absolute loss has the disadvantage that it is not differentiable at . The squared loss has the disadvantage that it has the tendency to be dominated by outliers—when summing over a set of ‘s (as in ), the final sum tends to be the result of a few particularly large a-values, rather than an expression of the average a-value.

The choice of a loss function is not arbitrary. It is very restrictive and sometimes the loss function may be characterized by its desirable properties.^[16] Among the choice principles are, for example, the requirement of completeness of the class of symmetric statistics in the case of i.i.d. observations, the principle of complete information, and some others.

W. Edwards Deming and Nassim Nicholas Taleb argue that empirical reality, not nice mathematical properties, should be the sole basis for selecting loss functions, and real losses often are not mathematically nice and are not differentiable, continuous, symmetric, etc. For example, a person who arrives before a plane gate closure can still make the plane, but a person who arrives after can not, a discontinuity and asymmetry which makes arriving slightly late much more costly than arriving slightly early. In drug dosing, the cost of too little drug may be lack of efficacy, while the cost of too much may be tolerable toxicity, another example of asymmetry. Traffic, pipes, beams, ecologies, climates, etc. may tolerate increased load or stress with little noticeable change up to a point, then become backed up or break catastrophically. These situations, Deming and Taleb argue, are common in real-life problems, perhaps more common than classical smooth, continuous, symmetric, differentials cases.^[17]

See also[edit]

• Bayesian regret
• Loss functions for classification
• Discounted maximum loss
• Hinge loss
• Scoring rule
• Statistical risk

References[edit]

Further reading[edit]

• Aretz, Kevin; Bartram, Söhnke M.; Pope, Peter F. (April–June 2011). «Asymmetric Loss Functions and the Rationality of Expected Stock Returns» (PDF). International Journal of Forecasting. 27 (2): 413–437. doi:10.1016/j.ijforecast.2009.10.008. SSRN 889323.
• Berger, James O. (1985). Statistical decision theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. Bibcode:1985sdtb.book…..B. ISBN 978-0-387-96098-2. MR 0804611.

• Cecchetti, S. (2000). «Making monetary policy: Objectives and rules». Oxford Review of Economic Policy. 16 (4): 43–59. doi:10.1093/oxrep/16.4.43.

• Horowitz, Ann R. (1987). «Loss functions and public policy». Journal of Macroeconomics. 9 (4): 489–504. doi:10.1016/0164-0704(87)90016-4.

• Waud, Roger N. (1976). «Asymmetric Policymaker Utility Functions and Optimal Policy under Uncertainty». Econometrica. 44 (1): 53–66. doi:10.2307/1911380. JSTOR 1911380.

From Wikipedia, the free encyclopedia

In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) ^[1] is a function that maps an event or values of one or more variables onto a real number intuitively representing some «cost» associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy.

In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century.^[2] In the context of economics, for example, this is usually economic cost or regret. In classification, it is the penalty for an incorrect classification of an example. In actuarial science, it is used in an insurance context to model benefits paid over premiums, particularly since the works of Harald Cramér in the 1920s.^[3] In optimal control, the loss is the penalty for failing to achieve a desired value. In financial risk management, the function is mapped to a monetary loss.

Examples[edit]

Regret[edit]

Leonard J. Savage argued that using non-Bayesian methods such as minimax, the loss function should be based on the idea of regret, i.e., the loss associated with a decision should be the difference between the consequences of the best decision that could have been made had the underlying circumstances been known and the decision that was in fact taken before they were known.

Quadratic loss function[edit]

The use of a quadratic loss function is common, for example when using least squares techniques. It is often more mathematically tractable than other loss functions because of the properties of variances, as well as being symmetric: an error above the target causes the same loss as the same magnitude of error below the target. If the target is t, then a quadratic loss function is

for some constant C; the value of the constant makes no difference to a decision, and can be ignored by setting it equal to 1. This is also known as the squared error loss (SEL). ^[1]

Many common statistics, including t-tests, regression models, design of experiments, and much else, use least squares methods applied using linear regression theory, which is based on the quadratic loss function.

The quadratic loss function is also used in linear-quadratic optimal control problems. In these problems, even in the absence of uncertainty, it may not be possible to achieve the desired values of all target variables. Often loss is expressed as a quadratic form in the deviations of the variables of interest from their desired values; this approach is tractable because it results in linear first-order conditions. In the context of stochastic control, the expected value of the quadratic form is used.

0-1 loss function[edit]

In statistics and decision theory, a frequently used loss function is the 0-1 loss function

where is the indicator function.
Meaning if the input is evaluated to true, then the output is 1. Otherwise, if the input is evaluated to false, then the output will be 0.

Constructing loss and objective functions[edit]

In many applications, objective functions, including loss functions as a particular case, are determined by the problem formulation. In other situations, the decision maker’s preference must be elicited and represented by a scalar-valued function (called also utility function) in a form suitable for optimization — the problem that Ragnar Frisch has highlighted in his Nobel Prize lecture.^[4]
The existing methods for constructing objective functions are collected in the proceedings of two dedicated conferences.^[5][6]
In particular, Andranik Tangian showed that the most usable objective functions — quadratic and additive — are determined by a few indifference points. He used this property in the models for constructing these objective functions from either ordinal or cardinal data that were elicited through computer-assisted interviews with decision makers.^[7][8]
Among other things, he constructed objective functions to optimally distribute budgets for 16 Westfalian universities^[9]
and the European subsidies for equalizing unemployment rates among 271 German regions.^[10]

Expected loss[edit]

In some contexts, the value of the loss function itself is a random quantity because it depends on the outcome of a random variable X.

Statistics[edit]

Both frequentist and Bayesian statistical theory involve making a decision based on the expected value of the loss function; however, this quantity is defined differently under the two paradigms.

Frequentist expected loss[edit]

We first define the expected loss in the frequentist context. It is obtained by taking the expected value with respect to the probability distribution, P_θ, of the observed data, X. This is also referred to as the risk function^{[11][12][13][14]} of the decision rule δ and the parameter θ. Here the decision rule depends on the outcome of X. The risk function is given by:

Here, θ is a fixed but possibly unknown state of nature, X is a vector of observations stochastically drawn from a population, is the expectation over all population values of X, dP_θ is a probability measure over the event space of X (parametrized by θ) and the integral is evaluated over the entire support of X.

Bayesian expected loss[edit]

In a Bayesian approach, the expectation is calculated using the posterior distribution π^* of the parameter θ:

One then should choose the action a^* which minimises the expected loss. Although this will result in choosing the same action as would be chosen using the frequentist risk, the emphasis of the Bayesian approach is that one is only interested in choosing the optimal action under the actual observed data, whereas choosing the actual frequentist optimal decision rule, which is a function of all possible observations, is a much more difficult problem.

Examples in statistics[edit]

• For a scalar parameter θ, a decision function whose output is an estimate of θ, and a quadratic loss function (squared error loss)

  

  the risk function becomes the mean squared error of the estimate,

  

  An Estimator found by minimizing the Mean squared error estimates the Posterior distribution’s mean.

• In density estimation, the unknown parameter is probability density itself. The loss function is typically chosen to be a norm in an appropriate function space. For example, for L² norm,

  

  the risk function becomes the mean integrated squared error

  

Economic choice under uncertainty[edit]

In economics, decision-making under uncertainty is often modelled using the von Neumann–Morgenstern utility function of the uncertain variable of interest, such as end-of-period wealth. Since the value of this variable is uncertain, so is the value of the utility function; it is the expected value of utility that is maximized.

Decision rules[edit]

A decision rule makes a choice using an optimality criterion. Some commonly used criteria are:

• Minimax: Choose the decision rule with the lowest worst loss — that is, minimize the worst-case (maximum possible) loss:

  

• Invariance: Choose the decision rule which satisfies an invariance requirement.
• Choose the decision rule with the lowest average loss (i.e. minimize the expected value of the loss function):

  

Selecting a loss function[edit]

Sound statistical practice requires selecting an estimator consistent with the actual acceptable variation experienced in the context of a particular applied problem. Thus, in the applied use of loss functions, selecting which statistical method to use to model an applied problem depends on knowing the losses that will be experienced from being wrong under the problem’s particular circumstances.^[15]

A common example involves estimating «location». Under typical statistical assumptions, the mean or average is the statistic for estimating location that minimizes the expected loss experienced under the squared-error loss function, while the median is the estimator that minimizes expected loss experienced under the absolute-difference loss function. Still different estimators would be optimal under other, less common circumstances.

In economics, when an agent is risk neutral, the objective function is simply expressed as the expected value of a monetary quantity, such as profit, income, or end-of-period wealth. For risk-averse or risk-loving agents, loss is measured as the negative of a utility function, and the objective function to be optimized is the expected value of utility.

Other measures of cost are possible, for example mortality or morbidity in the field of public health or safety engineering.

For most optimization algorithms, it is desirable to have a loss function that is globally continuous and differentiable.

Two very commonly used loss functions are the squared loss, , and the absolute loss, . However the absolute loss has the disadvantage that it is not differentiable at . The squared loss has the disadvantage that it has the tendency to be dominated by outliers—when summing over a set of ‘s (as in ), the final sum tends to be the result of a few particularly large a-values, rather than an expression of the average a-value.

The choice of a loss function is not arbitrary. It is very restrictive and sometimes the loss function may be characterized by its desirable properties.^[16] Among the choice principles are, for example, the requirement of completeness of the class of symmetric statistics in the case of i.i.d. observations, the principle of complete information, and some others.

W. Edwards Deming and Nassim Nicholas Taleb argue that empirical reality, not nice mathematical properties, should be the sole basis for selecting loss functions, and real losses often are not mathematically nice and are not differentiable, continuous, symmetric, etc. For example, a person who arrives before a plane gate closure can still make the plane, but a person who arrives after can not, a discontinuity and asymmetry which makes arriving slightly late much more costly than arriving slightly early. In drug dosing, the cost of too little drug may be lack of efficacy, while the cost of too much may be tolerable toxicity, another example of asymmetry. Traffic, pipes, beams, ecologies, climates, etc. may tolerate increased load or stress with little noticeable change up to a point, then become backed up or break catastrophically. These situations, Deming and Taleb argue, are common in real-life problems, perhaps more common than classical smooth, continuous, symmetric, differentials cases.^[17]

See also[edit]

• Bayesian regret
• Loss functions for classification
• Discounted maximum loss
• Hinge loss
• Scoring rule
• Statistical risk

References[edit]

Further reading[edit]

• Aretz, Kevin; Bartram, Söhnke M.; Pope, Peter F. (April–June 2011). «Asymmetric Loss Functions and the Rationality of Expected Stock Returns» (PDF). International Journal of Forecasting. 27 (2): 413–437. doi:10.1016/j.ijforecast.2009.10.008. SSRN 889323.
• Berger, James O. (1985). Statistical decision theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. Bibcode:1985sdtb.book…..B. ISBN 978-0-387-96098-2. MR 0804611.

• Cecchetti, S. (2000). «Making monetary policy: Objectives and rules». Oxford Review of Economic Policy. 16 (4): 43–59. doi:10.1093/oxrep/16.4.43.

• Horowitz, Ann R. (1987). «Loss functions and public policy». Journal of Macroeconomics. 9 (4): 489–504. doi:10.1016/0164-0704(87)90016-4.

• Waud, Roger N. (1976). «Asymmetric Policymaker Utility Functions and Optimal Policy under Uncertainty». Econometrica. 44 (1): 53–66. doi:10.2307/1911380. JSTOR 1911380.

Функция потерь (Loss Function, Cost Function, Error Function; J) – фрагмент программного кода, который используется для оптимизации Алгоритма (Algorithm) Машинного обучения (ML). Значение, вычисленное такой функцией, называется «потерей».

Функция (Function) потерь может дать бо́льшую практическую гибкость вашим Нейронным сетям (Neural Network) и будет определять, как именно выходные данные связаны с исходными.

Нейронные сети могут выполнять несколько задач: от прогнозирования непрерывных значений, таких как ежемесячные расходы, до Бинарной классификации (Binary Classification) на кошек и собак. Для каждой отдельной задачи потребуются разные типы функций, поскольку выходной формат индивидуален.

С очень упрощенной точки зрения Loss Function может быть определена как функция, которая принимает два параметра:

• Прогнозируемые выходные данные
• Истинные выходные данные

Эта функция, по сути, вычислит, насколько хорошо работает наша модель, сравнив то, что модель прогнозирует, с фактическим значением, которое она должна выдает. Если Y_pred очень далеко от Yi, значение потерь будет очень высоким. Однако, если оба значения почти одинаковы, значение потерь будет очень низким. Следовательно, нам нужно сохранить функцию потерь, которая может эффективно наказывать модель, пока та обучается на Тренировочных данных (Train Data).

Этот сценарий в чем-то аналогичен подготовке к экзаменам. Если кто-то плохо сдает экзамен, мы можем сказать, что потеря очень высока, и этому человеку придется многое изменить внутри себя, чтобы в следующий раз получить лучшую оценку. Однако, если экзамен пройдет хорошо, студент может вести себя подобным образом и в следующий раз.

Теперь давайте рассмотрим классификацию как задачу и поймем, как в этом случае работает функция потерь.

Классификационные потери

Когда нейронная сеть пытается предсказать дискретное значение, мы рассматриваем это как модель классификации. Это может быть сеть, пытающаяся предсказать, какое животное присутствует на изображении, или является ли электронное письмо спамом. Сначала давайте посмотрим, как представлены выходные данные классификационной нейронной сети.

Количество узлов выходного слоя будет зависеть от количества классов, присутствующих в данных. Каждый узел будет представлять один класс. Значение каждого выходного узла по существу представляет вероятность того, что этот класс является правильным.

Как только мы получим вероятности всех различных классов, рассмотрим тот,  что имеет наибольшую вероятность. Посмотрим, как выполняется двоичная классификация.

Бинарная классификация

В двоичной классификации на выходном слое будет только один узел. Чтобы получить результат в формате вероятности, нам нужно применить Функцию активации (Activation Function). Поскольку для вероятности требуется значение от 0 до 1, мы будем использовать Сигмоид (Sigmoid), которая приведет любое реальное значение к диапазону значений от 0 до 1.

По мере того, как входные реальные данные становятся больше и стремятся к плюс бесконечности, выходные данные сигмоида будут стремиться к единице. А когда на входе значения становятся меньше и стремятся к отрицательной бесконечности, на выходе числа будут стремиться к нулю. Теперь мы гарантированно получаем значение от 0 до 1, и это именно то, что нам нужно, поскольку нам нужны вероятности.

Если выход выше 0,5 (вероятность 50%), мы будем считать, что он попадает в положительный класс, а если он ниже 0,5, мы будем считать, что он попадает в отрицательный класс. Например, если мы обучаем нейросеть для классификации кошек и собак, мы можем назначить собакам положительный класс, и выходное значение в наборе данных для собак будет равно 1, аналогично кошкам будет назначен отрицательный класс, а выходное значение для кошек будет быть 0.

Функция потерь, которую мы используем для двоичной классификации, называется Двоичной перекрестной энтропией (BCE). Эта функция эффективно наказывает нейронную сеть за Ошибки (Error) двоичной классификации. Давайте посмотрим, как она выглядит.

Как видите, есть две отдельные функции, по одной для каждого значения Y. Когда нам нужно предсказать положительный класс (Y = 1), мы будем использовать следующую формулу:

$$Потеря = -log(Y_{pred})space{,}space{где}$$
$$Jspace{}{–}space{Потеря,}$$
$$Y_predspace{}{–}space{Предсказанные}space{значения}$$

И когда нам нужно предсказать отрицательный класс (Y = 0), мы будем использовать немного трансформированный аналог:

$$Потеря = -log(1 — Y_{pred})space{,}space{где}$$
$$Jspace{}{–}space{Потеря,}$$
$$Y_predspace{}{–}space{Предсказанные}space{значения}$$

Для первой функции, когда Y_pred равно 1, потеря равна 0, что имеет смысл, потому что Y_pred точно такое же, как Y. Когда значение Y_pred становится ближе к 0, мы можем наблюдать, как значение потери сильно увеличивается. Когда же Y_pred становится равным 0, потеря стремится к бесконечности. Это происходит, потому что с точки зрения классификации, 0 и 1 – полярные противоположности: каждый из них представляет совершенно разные классы. Поэтому, когда Y_pred равно 0, а Y равно 1, потери должны быть очень высокими, чтобы сеть могла более эффективно распознавать свои ошибки.

Полиномиальная классификация

Полиномиальная классификация (Multiclass Classification) подходит, когда нам нужно, чтобы наша модель каждый раз предсказывала один возможный класс. Теперь, поскольку мы все еще имеем дело с вероятностями, имеет смысл просто применить сигмоид ко всем выходным узлам, чтобы мы получали значения от 0 до 1 для всех выходных значений, но здесь кроется проблема. Когда мы рассматриваем вероятности для нескольких классов, нам необходимо убедиться, что сумма всех индивидуальных вероятностей равна единице, поскольку именно так определяется вероятность. Применение сигмоида не гарантирует, что сумма всегда равна единице, поэтому нам нужно использовать другую функцию активации.

В данном случае мы используем функцию активации Softmax. Эта функция гарантирует, что все выходные узлы имеют значения от 0 до 1, а сумма всех значений выходных узлов всегда равна 1. Вычисляется с помощью формулы:

$$Softmax(y_i) = frac{e^{y_i}}{sum_{i = 0}^n e^{y_i}}space{,}space{где}$$
$$y_ispace{}{–}space{i-e}space{наблюдение}$$

Пример:

Как видите, мы просто передаем все значения в экспоненциальную функцию. После этого, чтобы убедиться, что все они находятся в диапазоне от 0 до 1 и сумма всех выходных значений равна 1, мы просто делим каждую экспоненту на сумму экспонент.

Итак, почему мы должны передавать каждое значение через экспоненту перед их нормализацией? Почему мы не можем просто нормализовать сами значения? Это связано с тем, что цель Softmax – убедиться, что одно значение очень высокое (близко к 1), а все остальные значения очень низкие (близко к 0). Softmax использует экспоненту, чтобы убедиться, что это произойдет. А затем мы нормализуем результат, потому что нам нужны вероятности.

Теперь, когда наши выходные данные имеют правильный формат, давайте посмотрим, как мы настраиваем для этого функцию потерь. Хорошо то, что функция потерь по сути такая же, как у двоичной классификации. Мы просто применим Логарифмическую потерю (Log Loss) к каждому выходному узлу по отношению к его соответствующему целевому значению, а затем найдем сумму этих значений по всем выходным узлам.

Эта потеря называется категориальной Кросс-энтропией (Cross Entropy). Теперь перейдем к частному случаю классификации, называемому многозначной классификацией.

Классификация по нескольким меткам

Классификация по нескольким меткам (MLC) выполняется, когда нашей модели необходимо предсказать несколько классов в качестве выходных данных. Например, мы тренируем нейронную сеть, чтобы предсказывать ингредиенты, присутствующие на изображении какой-то еды. Нам нужно будет предсказать несколько ингредиентов, поэтому в Y будет несколько единиц.

Для этого мы не можем использовать Softmax, потому что он всегда заставляет только один класс «становиться единицей», а другие классы приводит к нулю. Вместо этого мы можем просто сохранить сигмоид на всех значениях выходных узлов, поскольку пытаемся предсказать индивидуальную вероятность каждого класса.

Что касается потерь, мы можем напрямую использовать логарифмические потери на каждом узле и суммировать их, аналогично тому, что мы делали в мультиклассовой классификации.

Теперь, когда мы рассмотрели классификацию, перейдем к регрессии.

Потеря регрессии

В Регрессии (Regression) наша модель пытается предсказать непрерывное значение, например, цены на жилье или возраст человека. Наша нейронная сеть будет иметь один выходной узел для каждого непрерывного значения, которое мы пытаемся предсказать. Потери регрессии рассчитываются путем прямого сравнения выходного и истинного значения.

Самая популярная функция потерь, которую мы используем для регрессионных моделей, – это Среднеквадратическая ошибка (MSE). Здесь мы просто вычисляем квадрат разницы между Y и Y_Pred и усредняем полученное значение.

Автор оригинальной статьи: deeplearningdemystified.com

Фото: @leni_eleni

Обзор

• Узнайте, что такое функции потерь и как они работают в алгоритмах машинного обучения

• Функция потерь на самом деле является ядром технологии, которую мы часто используем.

• В этой статье представлены различные функции потерь и принципы их работы, а также способы их программирования на Python.

Вступление

Представьте, что вы обучили модель машинного обучения на заданном наборе данных и готовы предоставить ее клиентам. Но как определить, что модель может обеспечить наилучшие результаты? Существуют ли индикаторы или методы, которые помогут быстро оценить модель на наборе данных?

Конечно, есть. Короче говоря, функция потерь в машинном обучении может решить вышеуказанные проблемы.

Функция потерь — это ядро ​​алгоритмов машинного обучения, которые нам нравится использовать. Но большинство новичков и энтузиастов не знают, как и где их использовать.

Их нетрудно понять, но они могут улучшить ваше понимание алгоритмов машинного обучения. Итак, что такое функции потерь и как вы понимаете их значение?

В этой статье я рассмотрю 7 общих функций потерь, используемых в машинном обучении, и объясню, как использовать каждую функцию.

содержание

• Что такое функция потерь?

• Функция потерь регрессии

• Потеря квадратичной ошибки

• Абсолютная потеря ошибок

• Потеря Хубера

• Двухклассовая функция потерь

• Двоичная кросс-энтропия

• Потеря шарнира

• Мультиклассовая функция потерь

• Мультиклассовая кросс-энтропийная потеря

• KL Дивергенция (потеря дивергенции Кульбака-Лейблера)

Что такое функция потерь?

Предположим, вы находитесь на вершине горы и вам нужно спуститься. Как вы решаете, в каком направлении двигаться?

Я хочу сделать следующее:

• Осмотритесь и увидите все возможные пути

• Откажитесь от этих восходящих путей. Это связано с тем, что эти дорожки фактически потребляют больше энергии и усложняют задачу по спуску.

• Наконец, идиЯ думаюПуть с наибольшим уклоном

Что касается моей интуиции, чтобы судить, хорошее или плохое мое решение, это именно то, что может дать функция потерь.

Функция потерь сопоставляет решение с соответствующей стоимостью

Выбор пути в гору потребует нашей энергии и времени. Выбор спуска принесет нам пользу. Поэтому стоимость спуска меньше.

В алгоритме машинного обучения с учителем мы надеемся минимизировать ошибку каждого обучающего примера в процессе обучения. Это делается с помощью некоторых стратегий оптимизации, таких как градиентный спуск. И эта ошибка возникает из-за функции потерь.

В чем разница между функцией потерь (функцией потерь) и функцией стоимости (функцией стоимости)?

Подчеркните здесь этот момент, хотяФункция затратсФункция потерьЯвляются синонимами и могут использоваться как синонимы, но они разные.

Функция потерь используется для одной обучающей выборки. Иногда его называютФункция ошибки(error function). С другой стороны, функция стоимости — это весь набор обучающих данных.Средняя потеря(average function). Стратегия оптимизации направлена ​​на минимизацию функции затрат.

Функция потерь регрессии

На данный момент вы должны быть хорошо знакомы с линейной регрессией. Он включает зависимую переменную Y и несколько независимых переменных.XiСмоделируйте линейную зависимость между. Поэтому мы подгоняем к этим данным в пространстве прямую линию или гиперплоскость.

Y = a0 + a1 * X1 + a2 * X2 + ....+ an * Xn

Мы будем использовать данные точки данных, чтобы найти коэффициенты a0, a1, …, an.

Мы воспользуемся знаменитым Boston Housing Dataset ^ 1, чтобы понять эту концепцию. Для простоты мы будем использовать только одну функцию — среднее количество комнат в резиденции (Average number of rooms per dwelling) (X), чтобы спрогнозировать среднее значение зависимой переменной — цена дома в 1000 долларов (Median Value)(Y)

Мы будем использоватьГрадиентный спуск(Gradient Descent) В качестве стратегии оптимизации для поиска линии регрессии. Я не буду вдаваться в подробности Gradient Descent, но вот напоминание о правилах обновления веса:

Здесь,θjНужно ли обновлять вес,αСкорость обучения,JФункция стоимости. Функция стоимости определяется выражениемθпараметризовать. Наша цель — найти значение θ, которое дает наименьшие общие затраты.

Я определил шаги, которые мы будем выполнять для каждой функции потерь ниже:

1. Напишите выражение функции прогноза f (X) и определите параметры, которые нам нужны, чтобы найти

2. Определите рассчитанные потери для каждой обучающей выборки

3. Найдите выражение функции стоимости (средняя потеря всех выборок)

4. Найдите градиент функции стоимости, связанный с каждым неизвестным параметром

5. Определите скорость обучения и итеративно выполните правило обновления веса фиксированное количество раз.

1. Потеря квадратной ошибки

Квадрат потерь ошибок для каждой обучающей выборки (также называемыйL2 Loss) Является квадратом разницы между фактическим значением и прогнозируемым значением:

Соответствующие функции затрат таковыСредняя квадратичная ошибка(MSE)。

Рекомендуется попробовать рассчитать градиент самостоятельно, цитируя следующий код

def update_weights_MSE(m, b, X, Y, learning_rate):
    m_deriv = 0
    b_deriv = 0
    N = len(X)
    for i in range(N):
Вычислить частную производную как
        # -2x(y - (mx + b))
        m_deriv += -2*X[i] * (Y[i] - (m*X[i] + b))
        # -2(y - (mx + b))
        b_deriv += -2*(Y[i] - (m*X[i] + b))
 # Мы вычитаем, потому что производная указывает на самый крутой подъем
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate

    return m, b

На данных о жилищном строительстве в Бостоне, повторенные 500 раз с разной скоростью обучения, чтобы получить следующую цифру:

Давайте поговорим о функции потерь MSE.Это квадратичная функция (в виде ax ^ 2 + bx + c), и ее значение больше или равно 0. График квадратичной функции показан ниже:

У квадратичной функции есть только глобальный минимум. Поскольку местного минимума нет, мы никогда не попадем в него. Следовательно, можно гарантировать, что градиентный спуск будет сходиться к глобальному минимуму (если он полностью сходится).

Функция потерь MSE штрафует большие ошибки, сделанные моделью, квадратной ошибкой. Если возвести в квадрат большее число, оно станет больше. Но следует отметить, что этот атрибут снижает устойчивость функции стоимости MSE к выбросам.Поэтому, если наши данные подвержены множеству выбросов, их не следует использовать.

2. Абсолютная потеря ошибок

Абсолютная ошибка каждой обучающей выборки — это расстояние между предсказанным значением и фактическим значением, независимо от знака. Абсолютная ошибка также называетсяL1 Loss：

Как я упоминал ранее, стоимость — это среднее значение этих абсолютных ошибок (MAE).

По сравнению с MSE стоимость MAE более устойчива к выбросам. Однако в математических уравнениях непросто иметь дело с абсолютными или модульными операторами. Мы можем рассматривать это как недостаток МАЭ.

Ниже приведен код для веса обновления стоимости MAE.

def update_weights_MAE(m, b, X, Y, learning_rate):
    m_deriv = 0
    b_deriv = 0
    N = len(X)
    for i in range(N):
 # Вычислить частную производную
        # -x(y - (mx + b)) / |mx + b|
        m_deriv += - X[i] * (Y[i] - (m*X[i] + b)) / abs(Y[i] - (m*X[i] + b))
        # -(y - (mx + b)) / |mx + b|
        b_deriv += -(Y[i] - (m*X[i] + b)) / abs(Y[i] - (m*X[i] + b))
 # Мы вычитаем, потому что производная указывает на самый крутой подъем
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m, b

После 500 итераций с разной скоростью обучения мы получим следующий график:

3. Потеря Хубера

Убыток Хубера сочетает в себе лучшие характеристики МСЭ и МАЭ. Для небольших ошибок он квадратичный, в противном случае — линейный (то же самое и для его градиента). Необходимо определить потерю Хубераδпараметр:

def update_weights_Huber(m, b, X, Y, delta, learning_rate):
    m_deriv = 0
    b_deriv = 0
    N = len(X)
    for i in range(N):
 # Вторая производная малого значения, линейная производная большого значения
        if abs(Y[i] - m*X[i] - b) <= delta:
            m_deriv += -X[i] * (Y[i] - (m*X[i] + b))
            b_deriv += - (Y[i] - (m*X[i] + b))
        else:
            m_deriv += delta * X[i] * ((m*X[i] + b) - Y[i]) / abs((m*X[i] + b) - Y[i])
            b_deriv += delta * ((m*X[i] + b) - Y[i]) / abs((m*X[i] + b) - Y[i])
 # Мы вычитаем, потому что производная указывает на самый крутой подъем
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m, b

Мы используем скорость обучения 0,0001δВыполнение 500 итераций обновления веса для различных значений параметров приводит к следующему рисунку:

Потери Хубера сильнее для выбросов, чем для MSE.Он используется для робастной регрессии, M-оценки и аддитивных моделей. Варианты потери Хубера также могут быть использованы для классификации.

Двухклассовая функция потерь

Значение такое же, как и в имени. Вторая классификация относится к отнесению предметов к одной из двух категорий. Классификация основана на правилах, применяемых к входному вектору признаков. Пример двух классификаций, например, классификация электронных писем как спама или не-спама на основе темы электронного письма.

Я проиллюстрирую эти двоичные функции потерь на наборе данных о раке груди ^ 2.Средний радиус，площадь，периметрПо другим признакам опухоль классифицируется как «Злокачественный«или же»Доброкачественный«. Для простоты мы будем использовать только две входные функции (X_1 и X_2), а именно»Худшая область«с»Средняя симметрия«Используется для классификации. Y двоичный, 0 (злокачественный) или 1 (доброкачественный).

Это диаграмма рассеяния наших данных:

1. Бинарная кросс-энтропийная потеря

Начнем с понимания термина «энтропия».. Обычно мы используем энтропию, чтобы выразить беспорядок или неуверенность. Измерьте случайную величину X с распределением вероятностей p (X):

Отрицательный знак используется для того, чтобы окончательный результат был положительным.

Чем больше энтропия вероятностного распределения, тем больше неопределенность распределения. Точно так же меньшее значение представляет более определенное распределение.

Это делает бинарную кросс-энтропию подходящей функцией потерь (Вы хотите минимизировать его ценность). Мы используем модель классификации для вероятности выхода pПотеря двоичной кросс-энтропии。

Вероятность принадлежности элемента к первому классу (или положительному классу) = p
 Вероятность того, что элемент принадлежит к 0 классу (или отрицательному классу) = 1-p

Затем сумма кросс-энтропийных потерь и прогнозируемая вероятность p выходной метки y (которая может принимать значения 0 и 1) определяются как:

Это также называется потерями журнала (Log Loss). Чтобы вычислить вероятность p, мы можем использовать сигмовидную функцию. Здесь z — функция нашей входной функции:

Диапазон сигмовидной функции составляет [0,1], что делает ее пригодной для вычисления вероятностей.

Рекомендуется попробовать рассчитать градиент самостоятельно, цитируя следующий код

def update_weights_BCE(m1, m2, b, X1, X2, Y, learning_rate):
    m1_deriv = 0
    m2_deriv = 0
    b_deriv = 0
    N = len(X1)
    for i in range(N):
        s = 1 / (1 / (1 + math.exp(-m1*X1[i] - m2*X2[i] - b)))
 Вычислить частную производную
        m1_deriv += -X1[i] * (s - Y[i])
        m2_deriv += -X2[i] * (s - Y[i])
        b_deriv += -(s - Y[i])
 # Мы вычитаем, потому что производная указывает на самый крутой подъем
    m1 -= (m1_deriv / float(N)) * learning_rate
    m2 -= (m2_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m1, m2, b

Используя правило обновления веса для 1000 итераций с разными значениями альфа, получается следующий рисунок:

2. Потеря петли

Потеря шарнира в основном используется для машин опорных векторов (SVM) с метками классов -1 и 1.. Поэтому не забудьте изменить метку «злокачественного» класса в наборе данных с 0 на -1.

Потеря петли не только наказывает неправильные прогнозы, но также наказывает неуверенные правильные прогнозы.

Потеря шарнира пары данных (x, y) показана на рисунке:

def update_weights_Hinge(m1, m2, b, X1, X2, Y, learning_rate):

    m1_deriv = 0
    m2_deriv = 0
    b_deriv = 0
    N = len(X1)
    for i in range(N):
 Вычислить частную производную
        if Y[i]*(m1*X1[i] + m2*X2[i] + b) <= 1:
            m1_deriv += -X1[i] * Y[i]
            m2_deriv += -X2[i] * Y[i]
            b_deriv += -Y[i]
 # В противном случае частная производная равна 0
 # Мы вычитаем, потому что производная указывает на самый крутой подъем
    m1 -= (m1_deriv / float(N)) * learning_rate
    m2 -= (m2_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
return m1, m2, b

После запуска функции обновления для 2000 итераций с тремя разными значениями альфа получается следующий рисунок:

Потери на шарнирах упрощают математические операции SVM, увеличивая при этом потери (по сравнению с Log-Loss). Его можно использовать, когда мы хотим принимать решения в реальном времени вместо того, чтобы сосредоточиться на точности.

Мультиклассовая функция потерь

Электронная почта не только классифицируется как спам или спам (это уже не 90-е!). Они делятся на различные другие категории: работа, семья, социальные сети, продвижение по службе и т. Д.

Мы будем использовать набор данных Iris ^ 3, чтобы понять оставшиеся две функции потерь. Мы будем использовать 2 функцииX1Длина чашелистикиИ особенностиX2Ширина лепесткаЧтобы предсказать категорию радужной оболочки (Y) —Сетоса, Версиколор или Вирджиния

Наша задача — реализовать классификатор с использованием модели нейронной сети и оптимизатора Adam, встроенного в Keras. Это связано с тем, что по мере увеличения количества параметров математика и код становятся трудными для понимания.

Это диаграмма рассеяния наших данных:

1. Мультиклассовая кросс-энтропийная потеря

Потеря кросс-энтропии в нескольких классах является обобщением потери кросс-энтропии в двоичной системе. Входной векторXiИ соответствующий целевой вектор горячего кодированияYiУбыток составляет:

Мы используем функцию softmax, чтобы найти вероятностьpij：

«Слой Softmax подключается перед выходным уровнем нейронной сети. Слой Softmax должен иметь такое же количество узлов, что и выходной уровень». Блог разработчика Google

Наконец, наш выход — это категория с наибольшей вероятностью данного входа.

Мы используем входной и выходной слой для построения модели и компиляции с разной скоростью обучения. Задайте функцию потерь как ‘category_crossentropy’ в операторе model.compile ():

# Импортировать пакет
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import adam
 #alpha установлено на 0,001, как показывает параметр lr в оптимизаторе adam.
 # Создать модель
model_alpha1 = Sequential()
model_alpha1.add(Dense(50, input_dim=2, activation='relu'))
model_alpha1.add(Dense(3, activation='softmax'))
 # Скомпилировать модель
opt_alpha1 = adam(lr=0.001)
model_alpha1.compile(loss='categorical_crossentropy', optimizer=opt_alpha1, metrics=['accuracy'])
 # Модель примерки
 # Dummy_Y закодирован в горячем формате
 # History_alpha1 используется для оценки проверки и точности рисунка
history_alpha1 = model_alpha1.fit(dataX, dummy_Y, validation_data=(dataX, dummy_Y), epochs=200, verbose=0)

Диаграммы стоимости и точности после 200 туров обучения при разных скоростях обучения следующие:

2. Расхождение KL

Мера разницы между распределением вероятностей дивергенции KL и другим распределением вероятностей. Нулевая дивергенция KL означает такое же распределение.

Обратите внимание, что функция дивергенции асимметрична. который:

Вот почему расхождение KL нельзя использовать в качестве меры расстояния.

Я опишу основной метод использования дивергенции KL в качестве функции потерь без выполнения математических расчетов. Учитывая некоторое приблизительное распределение Q, мы надеемся аппроксимировать истинное распределение вероятностей P целевой переменной относительно входных характеристик. Благодаря асимметричной дивергенции KL мы можем добиться этого двумя способами:

Первый метод используется для обучения с учителем, а второй метод используется для обучения с подкреплением. Дивергенция KL аналогична мультиклассовой кросс-энтропии по функции, дивергенцию KL также можно назвать относительной энтропией P относительно Q:

Мы указываем ‘kullback_leibler_divergence’ в качестве функции потерь в функции compile (), точно так же, как мы это делали при работе с кросс-энтропийной потерей нескольких классов.

# Импортировать пакет
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import adam
 # Альфа установлена ​​на 0,001, как показано параметром lr в оптимизаторе adam
 # Создать модель
model_alpha1 = Sequential()
model_alpha1.add(Dense(50, input_dim=2, activation='relu'))
model_alpha1.add(Dense(3, activation='softmax'))
 # Скомпилировать модель
opt_alpha1 = adam(lr=0.001)
model_alpha1.compile(loss='kullback_leibler_divergence', optimizer=opt_alpha1, metrics=['accuracy'])
 # Модель примерки
 # Dummy_Y закодирован в горячем формате
 # History_alpha1 используется для оценки проверки и точности рисунка
history_alpha1 = model_alpha1.fit(dataX, dummy_Y, validation_data=(dataX, dummy_Y), epochs=200, verbose=0)

Диаграммы стоимости и точности после 200 туров обучения при разных скоростях обучения следующие:

По сравнению с многоклассовой классификацией дивергенция KL чаще используется для аппроксимации сложных функций. Мы часто используем расхождение KL при использовании моделей генерации глубины, таких как вариационные автоэнкодеры (VAE).

Все курсы > Вводный курс > Занятие 11

Мы уже дважды пытались подобраться к этой теме. Первый раз на втором занятии, когда искали веса для уравнения модели кредитного скоринга. Второй раз — на прошлом занятии, когда моделировали зависимость окружности шеи от роста.

Больше тянуть нельзя. Продолжим с примером модели регрессии. Напомню, какую модель мы построили на прошлом занятии.

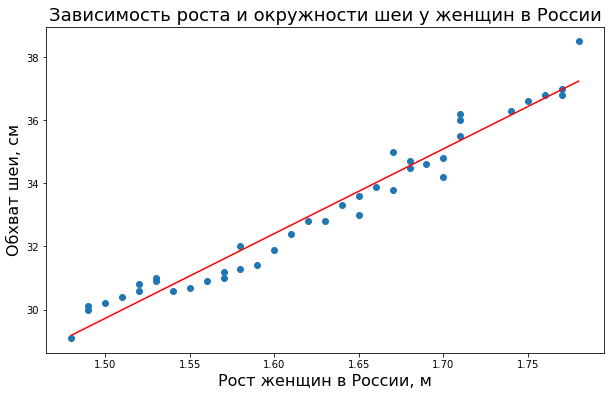
Алгебраически уравнение, задающее линию, выглядит следующим образом:

$$ y = 26.86x-10.57 $$

Посмотрим, как были найдены веса 26.86 и −10.57.

Вначале откроем ноутбук к этому занятию⧉

Функция потерь

Мы уже сказали, что прямую нужно построить так, чтобы общее расстояние всех точек до прямой было минимальным. Вот о каких расстояниях идет речь.

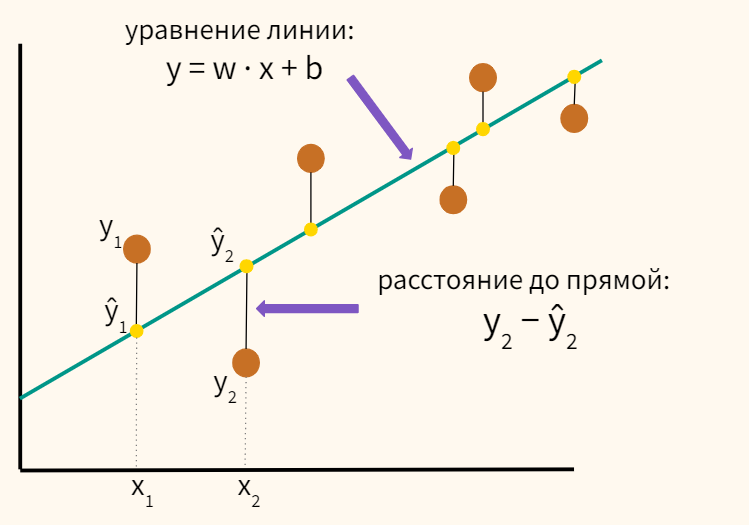
Средняя сумма этих расстояний для всех точек равна:

$$ средняяspaceсуммаspaceрасстояний = frac {sum^{n}_{i=1} (y_i-hat{y}_i) ^2} {n} $$

Мы возвели расстояния в квадрат для того, чтобы избавиться от отрицательных значений. Например, в случае y₂ − ŷ₂, мы получим отрицательное значение, так как y₂ < ŷ₂. Если затем сложить это расстояние с положительным расстоянием y₁ − ŷ₁, то отрицательное и положительное значения взаимно сократятся, и мы получим некорректную среднюю сумму расстояний.

В целом, такое выражение называется функцией потерь (loss или cost function). Считайте, что оно показывает, сколько мы «теряем» из-за невозможности провести прямую ровно через каждую из точек.

Очевидно, лучше «терять» как можно меньше. Значит, задача сводится к поиску минимума функции потерь или ее оптимизации.

Раздел математики, занимающийся поиском минимума функции, называется теорией оптимизации (Optimization Theory).

Как найти минимум функции

Можно использовать компьютер. Он будет поочередно подставлять разные w и e до тех пор, пока функция потерь не выдаст наименьшее значение.

Ещё раз посмотрим на этот процесс графически. Когда мы (1) перемещаем нашу прямую в различные положения

то (2) постепенно изменяем потерю (еще говорят ошибку, error).

Компьютер будет двигать прямую на первом графике до тех пор, пока на втором графике значение функции потерь не окажется минимальным.

То, что на втором графике ошибка неуклонно уменьшается, не просто случайность, веса изменяются согласно определенной логике.

Теперь, когда мы минимизировали потерю, наша прямая наилучшим возможным образом описывает существующие данные. Именно этого мы и добивались.

Создание модели на Питоне с помощью библиотеки Scikit-learn

На прошлом занятии мы построили нашу прямую, проходящую через данные, с помощью несложной функции polyfit библиотеки Numpy. Теперь воспользуемся библиотекой Scikit-learn. Она даст нам большую свободу в выборе, обучении и оценке качества моделей.

Для начала вновь возьмем данные роста и обхвата шеи. Только теперь запишем рост в переменную X, а обхват шеи в переменную y (таким образом, сразу становится понятно, что является независимой переменной, а что — зависимой).

X = [1.48, 1.49, 1.49, 1.50, 1.51, 1.52, 1.52, 1.53, 1.53, 1.54, 1.55, 1.56, 1.57, 1.57, 1.58, 1.58, 1.59, 1.60, 1.61, 1.62, 1.63, 1.64, 1.65, 1.65, 1.66, 1.67, 1.67, 1.68, 1.68,  1.69, 1.70, 1.70, 1.71, 1.71, 1.71, 1.74, 1.75, 1.76, 1.77, 1.77, 1.78] y = [29.1, 30.0, 30.1, 30.2, 30.4, 30.6, 30.8, 30.9, 31.0, 30.6, 30.7, 30.9, 31.0, 31.2, 31.3, 32.0, 31.4, 31.9, 32.4, 32.8, 32.8, 33.3, 33.6, 33.0, 33.9, 33.8, 35.0, 34.5, 34.7, 34.6, 34.2, 34.8, 35.5, 36.0, 36.2, 36.3, 36.6, 36.8, 36.8, 37.0, 38.5]

Теперь подготовим этим данные. Scikit-learn принимает данные X (т.е. независимые переменные, признаки) в формате, так называемого, двумерного массива. Пока я просто покажу код, без детальных объяснений. На последующих курсах мы внимательно его разберем.

# импортируем библиотеку Numpy import numpy as np # преобразуем наш список X сначала в одномерный массив Numpy, а затем добавим второе измерение X = np.array(X).reshape(—1, 1) # список y достаточно преобразовать в одномерный массив Numpy y = np.array(y)

Импортируем необходимые модули и создадим объект класса линейной регрессии.

# из набора линейных моделей библиотеки sklearn импортируем линейную регрессию from sklearn.linear_model import LinearRegression # создадим объект этого класса и запишем в переменную model model = LinearRegression()

Обучим нашу модель. Другими словами, построим нашу прямую таким образом, чтобы минимизировать функцию ошибки. Для этого в библиотеке Scikit-learn используется метод
.fit().

# обучим нашу модель # т.е. найдем те самые веса или наклон и сдвиг прямой с помощью функции потерь model.fit(X, y)

Выведем веса нашей модели:

print(model.coef_, model.intercept_)

[26.86181201] —10.570936299787334

Новые веса, а значит и уравнение идентичны найденным на прошлом занятии.

$$ y = 26.86x-10.57 $$

Это логично, мы использовали одни и те же данные, и одну и ту же функцию потерь для построения модели.

Рассчитаем прогнозные значения, соответствующие нашим исходным данным (X), т.е. найдем значения ŷ_i. Для этого используем метод
.predict().

y_pred = model.predict(X)

Выведем для примера первые пять значений (в этом случае вместо индекса указывается диапазон индексов [от : до, но не включая], например, [ : 5] выведет элемент с нулевого по четвертый).

[29.18454547 29.45316359 29.45316359 29.72178171 29.99039983]

В целом похоже на то, что мы делали в прошлый раз.

Однако библиотека Scikit-learn позволяет нам также вывести уровень потери или ошибку, которую метод
.fit() стремился минимизировать. Этот уровень правильнее называть среднеквадратической ошибкой (Mean Squared Error, MSE). Выведем ее:

# импортируем модуль метрик, то есть измерений качества моделей from sklearn import metrics # выведем среднеквадратическую ошибку print(‘Mean Squared Error (MSE):’, metrics.mean_squared_error(y, y_pred))

Mean Squared Error (MSE): 0.2273395626677337

Чтобы избавиться от квадрата в вычислениях, возьмем квадратный корень из нашей метрики (Root Mean Squared Error, RMSE).

print(‘Root Mean Squared Error:’, np.sqrt(metrics.mean_squared_error(y, y_pred)))

Root Mean Squared Error (RMSE): 0.47680138702371

Для того чтобы оценить много это или мало, мы можем сравнить RMSE со средним арифметическим наших исходных данных обхвата шеи.

Как мы видим, RMSE чрезвычайно мал по сравнению со средним значением обхвата шеи (0,48 против 33,1). Т.е. расстояние от предсказанных точек до прямой действительно минимально.

Алгоритм линейной регрессии неплохо потрудился.

На всякий случай, еще раз уточним термины: функция потерь или ошибка по-русски, и loss function, cost function, error function или, как еще говорят, objective function по-английски — это одно и то же.

Подведем итог

Мы начали с того, что у нас есть исходное уравнение, модель, для которой нужно подобрать веса. В зависимости от того, какие веса мы возьмём, расстояние от прямой до точек данных будет варьироваться. Эту вторую зависимость можно описать функцией потерь.

Задача сводится к тому, чтобы с помощью компьютера минимизировать функцию потерь. Тогда в исходной модели прямая будет наилучшим образом описывать данные.

Вопросы для закрепления

Как называется функция, с помощью которой мы находим оптимальные веса в уравнении (исходной модели)?

Посмотреть правильный ответ

Ответ: функция потерь (loss function).

Какие метрики (критерии) качества модели линейной регрессии мы уже знаем?

Посмотреть правильный ответ

Ответ: (1) средняя квадратическая ошибка (Mean Squared Error, MSE), средняя сумма расстояний от прямой до данных и (2) корень средней квадратической ошибки (Root Mean Squared Error, RMSE)

Дополнительные упражнения⧉ вы найдете в конце ноутбука.

Чего не хватает

Пока что мы рассматривали уравнение, где есть одна независимая переменная и одна зависимая, но конечно в реальности независимых переменных может быть больше. И мы об этом сказали ещё на первом занятии.

На следующем, двенадцатом занятии, мы изучим, как использовать векторы и матрицы для представления таких уравнений (а значит и данных), и как это нам поможет в построении моделей.

---

Ответы на вопросы

Вопрос. В модели линейной регрессии на видео вы используете два двумерных массива для X и для y, а в коде двумерным становится только массив признаков (Х), как правильно?

Ответ. Можно и так, и так. Код, который я использую на видео правильный, но избыточный. Для целевой переменной y достаточно одномерного массива, признакам (X) всегда нужен двумерный массив.

В целом, забегая немного вперед, скажу, что моделям в sklearn можно передавать:

• массивы Numpy (Numpy arrays, 1D и 2D)
• разреженные матрицы (sparse matrices)
• датафреймы (в формате DataFrame для X и Series для y)

---

Вопрос. Возник такой вопрос: в 10 занятии для подбора коэффициентов линии регрессии, которая описывает взаимосвязь роста и окружности шеи, в качестве функции потерь использовалась сумма отклонений прогноза от факта. В этом занятии — сумма квадратов отклонений. Но коэффициенты получились одинаковые. Разве не должны они получится разными?

Ответ. На самом деле, как видно из документации, и функция polyfit()⧉ библиотеки Numpy, которую мы использовали на десятом занятии, и класс LinearRegression⧉ библиотеки sklearn из одиннадцатого занятия минимизируют именно сумму квадратов отклонений прогноза от факта. Так как их алгоритм (для линейной модели) идентичен, то и коэффициенты получились одинаковыми.

На десятом занятии я опять же сознательно не упомянул, что речь идет о квадрате отклонений, потому что не хотел слишком усложнять материал. Более того, «под капотом» и функция polyfit(), и класс LinearRegression используют метод наименьших квадратов (МНК, Least Squares), я же подвожу к алгоритму оптимизации, который называется градиентным спуском (Gradient Descent). Это еще одна сознательная неточность.

Метод наименьших квадратов на этом этапе мне кажется довольно сложным и не интуитивным. Функцию polyfit() и класс LinearRegression я пока использовал как черный ящик, который получает данные и выдает коэффициенты/веса.

Градиентный спуск (т.е. минимизация функции потерь с помощью производной/градиента), наоборот, интуитивно более понятен и широко используется в большинстве алгоритмов машинного обучения. Его мы напишем «с нуля» для линейной регрессии, логистической регресии (решает задачу классификации) и несложной нейросети на курсе по оптимизации.

Одним словом, вводный курс содержит множество упрощений, но все это будет уточнено и расставлено по своим местам на последующих курсах. Пока что я ориентируюсь на тех, кто первый раз сталкивается с решением таких задач.

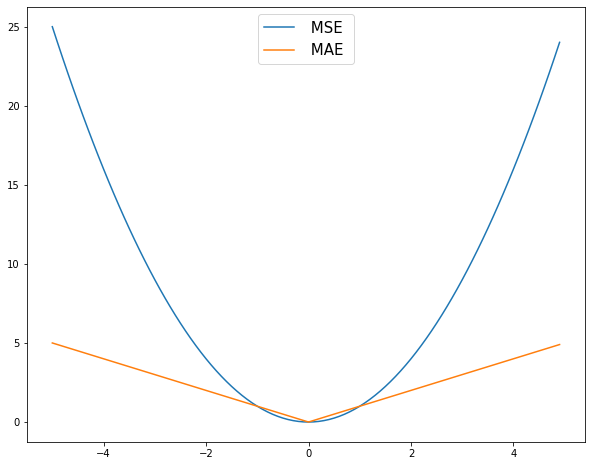
P.S. Также замечу, забегая немного вперед, что напрямую использовать сумму отклонений прогноза от факта в качестве функции потерь мы в любом случае не можем. Если для одного наблюдения отклонение составит 4, а для другого −4, их сумма (то есть общая ошибка) будет равна нулю, что по сути неверно, потому что оба наблюдения отклоняются от прогноза. Чтобы этого избежать, мы либо возводим отклонение в квадрат (Mean Squared Error), либо находим абсолютное значение/модуль отклонения (Mean Absolute Error). Графически это будет парабола и функция модуля соответственно.

Как у MAE, так и у MSE есть достоинства и недостатки, и их можно преодолеть, например, с помощью функции Хьюбера (Huber loss) и других более продвинутых функций потерь.