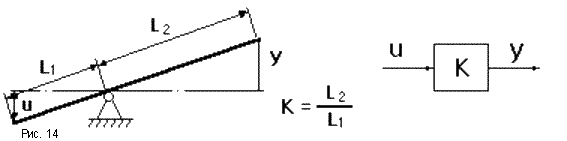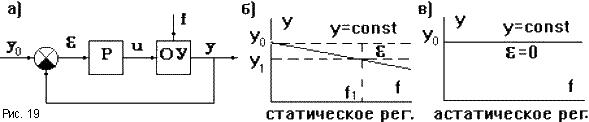Что называется статической ошибкой регулятора как ее уменьшить - Исправление ошибок и поиск оптимальных решений проблем

Режим работы САУ, в котором управляемая
величина и все промежуточные величины
не изменяются во времени, называется
установившимся, илистатическим
режимом. Любое звено и САУ в целом в
данном режиме описываетсяуравнениями
статикивидаy = F(u,f), в которых
отсутствует времяt. Соответствующие
им графики называютсястатическими
характеристиками. Статическая
характеристика звена с одним входом u
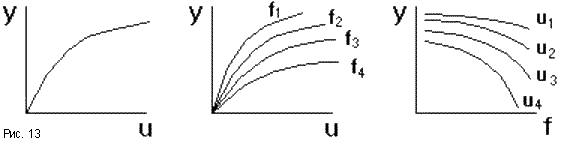
может быть представлена кривойy = F(u)(рис.13). Если звено имеет второй вход по
возмущению f, то статическая
характеристика задается семейством
кривыхy = F(u)при различных значениях
f, илиy = F(f)при различныхu.

Т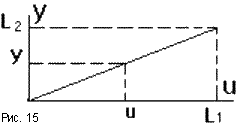ак
примером одного из функциональных
звеньев системы регулирования воды в
баке (см. выше) является обычный рычаг
(рис.14). Уравнение статики для него имеет
видy = Ku. Его можно изобразить звеном,
функцией которого является усиление
(или ослабление) входного сигнала вKраз. Коэффициент K = y/u, равный отношению
выходной величины к входной называетсякоэффициентом усилениязвена. Когда
входная и выходная величины имеют разную
природу, его называюткоэффициентом
передачи.

Статическая характеристика данного
звена имеет вид отрезка прямой линии с
наклоном a = arctg(L₂/L₁)
= arctg(K)(рис.15). Звенья с линейными
статическими характеристиками называютсялинейными. Статические характеристики
реальных звеньев, как правило, нелинейны.
Такие звенья называютсянелинейными.
Для них характерна зависимость
коэффициента передачи от величины
входного сигнала: K =
y/uconst.

Например, статическая характеристика
насыщенного генератора постоянного
тока представлена на рис.16. Обычно
нелинейная характеристика не может
быть выражена какой-либо математической
зависимостью и ее приходится задавать
таблично или графически.

З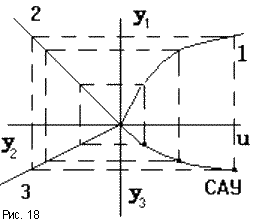ная
статические характеристики отдельных
звеньев, можно построить статическую
характеристику САУ (рис.17, 18). Если все
звенья САУ линейные, то САУ имеет линейную
статическую характеристику и называетсялинейной. Если хотя бы одно звено
нелинейное, то САУнелинейная.

Звенья, для которых можно задать
статическую характеристику в виде
жесткой функциональной зависимости
выходной величины от входной, называются
статическими. Если такая связь
отсутствует и каждому значению входной
величины соответствует множество
значений выходной величины, то такое
звено называетсяастатическим.
Изображать его статическую характеристику
бессмысленно. Примером астатического
звена может служить двигатель, входной
величиной которого является напряжениеU, а выходной — угол поворота вала,
величина которого приU = constможет
принимать любые значения. Выходная
величина астатического звена даже в
установившемся режиме является функцией
времени.

2.3. Статическое и астатическое регулирование

Е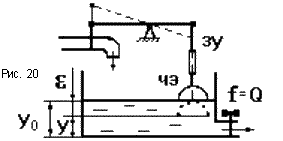сли
на управляемый процесс действует
возмущениеf, то важное значение
имеет статическая характеристика САУ
в формеy = F(f)приy_o
= const. Возможны два характерных вида
этих характеристик (рис.19). В соответствии
с тем, какая из двух характеристик
свойственна для данной САУ, различаютстатическое и астатическое регулирование.

Рассмотрим систему регулирования уровня
воды в баке (рис.20). Возмущающим фактора
является поток Qводы из бака. Пусть
приQ = 0имеемy = y_o,e = 0. ЗУ системы настраивается так,
чтобы вода при этом не поступала. ПриQ0,
уровень воды понижается (e0),
поплавок опускается и открывает заслонку,
в бак начинает поступать вода. Новое
состояние равновесия достигается при
равенстве входящего и выходящего потоков
воды. Но в любом случае приQ0заслонка должна быть обязательно
открыта, что возможно только приe0.
Причем, чем больше Q, тем при больших
значениях e, устанавливается новое
равновесное состояние. Статическая
характеристика САУ имеет характерный
наклон (рис.19б). Это есть примерстатического
регулирования. Для получения
статического регулирование, все звенья
САР должны быть статическими.

С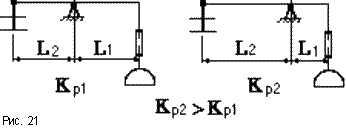татические
регуляторы работают при обязательном
отклоненииeрегулируемой величины
от требуемого значения. Это отклонение
тем больше, чем больше возмущениеf.
Это заложено в принципе действия
регулятора и не является его погрешностью,
поэтому данное отклонение называетсястатической ошибкой регулятора. Из
рис.21 видно, что, чем больше коэффициент
передачи регулятораK_р,
тем на большую величину откроется
заслонка при одних и тех же значенияхe, обеспечив в установившемся режиме
большую величину потокаQ. Это значит,
что на статической характеристике
одинаковым значениямeпри большихK_рбудут соответствовать
большие значения возмущенияQ,
статическая характеристика САУ пойдет
более полого. Поэтому,чтобы уменьшить
статическую ошибку надо увеличивать
коэффициент передачи регулятора.
Того же результата можно добиться,
увеличивая коэффициент передачи объекта
управления, но это дело конструкторов,
проектирующих данный объект, а не
специалистов по автоматике.

Статизмd, САР, характеризует насколько
сильно значение регулируемой величины
отклоняется от требуемого значения при
действии возмущений, и равна тангенсу
угла наклона статической характеристики,
построенной в относительных единицах:d = tg(a) =
(рис.22),
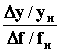
гдеy = y_н,
f = f_н
— точка номинального режима САУ. При
достаточно больших значенияхK_pимеемd
1/K_p.

Внекоторых случаях статическая ошибка
недопустима, тогда переходят кастатическому регулированию, при
котором регулируемая величина в
установившемся режиме принимает точно
требуемое значение независимо от
величины возмущающего фактора. Статическая
характеристика астатической САУ не
имеет наклона (рис.19в). Возможные
неточности относятся к погрешностям
конкретной системы и не являются
закономерными.

Для того, чтобы получить астатическое
регулирование, необходимо в регулятор
включить астатическое звено, например
ИД, между ЧЭ и УО (рис.23).

Если уровень воды понизится, то поплавок
переместит движок потенциометра на
величину
L,
за счет этого появится разность
потенциалов0и ИД начнет поднимать заслонку до тех
пор, покане
уменьшится до нуля, а это возможно только
при y = y_o. При поднятии уровня воды разность
потенциалов сменит знак, и двигатель
будет вращаться в противоположную
сторону, опуская заслонку.

Достоинства и недостатки статического
и астатического регулирования:
статические регуляторы обладают
статической ошибкой; астатические
регуляторы статической ошибки не имеют,
но они более инерционны, сложны
конструктивно и более дороги.

Обеспечение требуемой статической
точности регулирования является первой
основной задачей при расчете элементов
САУ.

Вопросы

Перечислите и дайте краткую характеристику
основных видов САУ?
Что называется статическим режимом
САУ?
Что называется статическими
характеристиками САУ?
Что называется уравнением статики САУ?
Что называется коэффициентом передачи,
в чем отличие от коэффициента усиления?
В чем отличие нелинейных звеньев от
линейных?
Как построить статическую характеристику
нескольких звеньев?
В чем отличие астатических звеньев от
статических?
В чем отличие астатического регулирования
от статического?
Как сделать статическую САР астатической?
Что называется статической ошибкой
регулятора, как ее уменьшить?
Что называется статизмом САР?
Назовите достоинства и недостатки
статического и астатического
регулирования?

Источник

Уменьшение — статическая ошибка

Cтраница 1

Уменьшение статической ошибки осуществляется в результате воздействия астатической части, которая в основном и служит для ликвидации остаточного отклонения. По окончании переходного режима движок реостатного датчика Rn и контактные группы обоих реле приходят в первоначальное среднее положение, соответствующее заданному значению регулируемой величины, а положение рукоятки спаренных сопротивлений Л5 и jR6 ( ручная перестановка) показывает степень открытия регулирующего органа в процентах от полного открытия. Доля участия пропорциональной части в перемещении регулирующего органа зависит от диапазона пропорциональности, а астатической — от величины времени действия астатической части.
[1]

Уменьшение статической ошибки ( а при бесконечно большом коэффициенте усиления усилителя в статике — сведение ее к нулю) в контуре с объектом в виде интегрирующего звена может быть достигнуто путем использования ПИ-регулятора.
[2]

Уменьшение статической ошибки регулирования ( ошибки в установившемся режиме) и увеличение быстродействия системы может быть достигнуто последовательным включением в контур системы автоматического регулирования ( в регулятор, осуществляющий основную обратную связь) безынерционного звена с большим коэффициентом усиления.
[4]

Для уменьшения статической ошибки используют также принцип управления по возмущению в комбинированных САУ. Из множества возмущений выбирается главное, и на основе его измерения воздействуют на объект управления таким образом, чтобы компенсировать естественное влияние данного воздействия на выходную величину системы. Комбинированные системы позволяют значительно снизить статическую ошибку системы без повышения степени ее астатизма.
[5]

Для уменьшения статической ошибки без нарушения устойчивости необходимо в контур ввести первую производную от входного сигнала.
[6]

Для уменьшения статической ошибки следует увеличивать коэффициент усиления системы. До известной степени можно считать, что величина коэффициента усиления определяется требованиями к величине статической ошибки.
[8]

Для уменьшения статической ошибки регулирования иногда рекомендуется установка в приточной камере двух калориферов ( или двух рядов калориферов), соединенных последовательно по воздуху и параллельно по воде. Теплопроизводительность каждого калорифера составляет приблизительно 50 % от общей требуемой. Благодаря этому статическая ошибка выбранного регулятора может быть снижена вдвое, так как регулируется только половина нагрузки. Первый по ходу воздуха калорифер отключается двухпозиционным регулятором, датчик которого установлен на входе наружного воздуха, когда достигается температура, при которой требуется только половина нагрузки — теплопроизводительности. Для определения температуры настройки двухпозиционного регулятора требуется провести дополнительные несложные расчеты.
[9]

Для уменьшения статической ошибки копирования в следящей системе предусмотрено интегрирующее звено по управляющему воздействию.
[10]

Пусть теперь для уменьшения статической ошибки в систему вводится воздействие по производной.
[11]

Например, для уменьшения статической ошибки и улучшения динамических характеристик необходимо увеличивать коэффициент усиления, однако это ухудшает устойчивость системы. Поэтому для усилительной схемы задаются предельные значения / Ста и / тт, при достижении которых возникает отказ.
[13]

Это всегда полезно для уменьшения статической ошибки, ибо в этом случае при изменении нагрузки остаточное отклонение регулируемого параметра будет меньше. Обычно пропорциональные регуляторы применяются с объектами средней емкости при малых запаздываниях и малых изменениях нагрузки.
[14]

Есть, однако, способ уменьшения статической ошибки системы вне зависимости от динамических ее свойств.
[15]

Страницы:

Источник

По наличию статической ошибки — регуляторы статические и астатические. [c.35]

Интегральное регулирование допускает, большие изменения нагрузки и исключает возможность появления статической ошибки. Поэтому такая комбинация дает хорошие результаты почти во всех случаях, за исключением процессов с очень резкими возмущающими воздействиями или очень большими запаздываниями. Регуляторы такого типа иногда называют регуляторами с автоматической обратной перестановкой, так как они автоматически сводят к нулю статическую ошибку, возникающую при пропорциональном регулировании. [c.460]

Введение интеграла (использование ПИ-регулятора) устраняет статическую ошибку, но мало улучшает динамику процесса. Добавление импульса по производной (применение ПИД-регуля-тора) существенно повышает быстродействие системы, но при большом коэффициенте усиления возникает значительное перерегулирование и САР становится более чувствительной к внешним возмущениям. Для устранения этих недостатков возможны два пути усложнение САР (создание многоконтурной системы с дополнительными перекрещивающимися обратными связями) или создание регулятора со специальной характеристикой. При этом передаточная функция регулятора должна иметь вид [21] [c.711]

Величины Xyi, Phi, Ху, и р, — координаты узловых точек реальной статической характеристики регулятора (см. рис. 4.8, б). В качестве примера на рис. 4.10 изображена характеристика статической точности регулирования насоса при Dj, = 6,33, рв = 0,05, Ху1 = 0,555, Рн1 = 0,315, Ху2 = 0,86 и рна = 0.56. В шести точках характеристики относительная ошибка регулирования равна нулю, максимальное вначение ее не превышает 6,2%. [c.297]

Полезно заметить, что при астатическом объекте (vj ф 0), но статическом регуляторе (vj = 0), как показывает формула (5.85), постоянное возмущающее воздействие создает в системе статическую ошибку, которая не возникает, если объект статический (vx = 0), а регулятор астатический (vj Ф 0). [c.158]

Изодромные, или пропорционально-инте-тральные, регуляторы (сокращенно ПИ-регуляторы) объединяют в себе положительные свойства пропорциональных и интегральных регуляторов. Как следует из сказанного выше, наличие отрицательной обратной связи благотворно влияет на переходный процесс регулирования, но приводит к остаточному отклонению. В пропорционально-интегральных регуляторах применяется особая обратная связь — упругая, действие которой постепенно исчезает после осуществления пропорционального воздействия. Благодаря этому возникают дополнительные перемещения регулирующего органа, ликвидирующие статическую ошибку. Устройство упругой обратной связи носит название изодрома, откуда и происходит наименование самого регулятора. [c.42]

Величина отклонения параметра в конце процесса регулирования от заданного значения называется остаточной неравномерностью, или статической ошибкой. Она представляет собой отклонение регулируемого параметра в процентах от заданного значения, вызывающее полный ход исполнительного механизма. Например, если степень неравномерности регулятора равна 10%, то это значит, что изменение параметра на I % от шкалы регулятора вызовет перемещение регулирующего органа на Vio его полного хода из одного крайнего положения в другое. Неравномерность, или статическая ошибка, регулирующего органа с чувствительным элементом определяется жесткостью связи. Чем жестче связь, тем большее изменение задания регулируемого параметра вызывает перемещение регулирующего органа на единицу его полного хода. В данном примере жесткость связи определяется положением точки 4 на рычаге 1. Чем больше расстояние между точками 2 я 4, тем жестче связь и больше статическая ошибка. [c.262]

У астатических регуляторов (рис. 18, д) малейшее отклонение входного параметра X вызывает непрерывное движение РО с определенной скоростью до предельного значения К акс- Регулирующий орган остановится только при X = Хо. Если при этом окажется МрФ Мн,, то снова возникнет рассогласование X — Хо и РО дополнительно переместится, пока не остановится в положении, при котором Мр == Мн. и X = Хо, т. е. когда статическая ошибка равна нулю. Именно поэтому их и называют астатическими. [c.36]

Диапазон пропорциональности и соответственно коэффициент усиления (чувствительность прибора) зависит от жесткости пружины, площади мембраны и обычно не регулируется. В схеме на рис. 19, а коэффициент усиления зависит также от соотношения плеч рычага ОА и ОБ. Перемещая винтом 2 центр О вправо, можно повысить чувствительность прибора. Характеристика 1 — 2 станет круче. Это уменьшит ДП, а следовательно, и статическую ошибку. Однако в реальных регуляторах увеличение чувствительности ухудшает переходные характеристики. [c.39]

Устраняя статическую ошибку, И-регуляторы, однако, ухудшают качество переходного процесса в системе. При малой скорости перемещения РО изменение нагрузки вызывает слишком большие отклонения регулируемого параметра, а при большой скорости РО возникают долго незатухающие колебания. Эти особенности И-регуляторов станут понятнее, когда будет рассмотрена совместная работа регуляторов с объектом (см. рис. 25). [c.41]

С увеличением тепловой нагрузки установившийся режим может наступить только при условии большей подачи жидкости через ТРВ. Из статической характеристики видно, что это возможно лишь при большем перегреве, т. е. испаритель будет заполнен меньше (точка Б на рис. 75, а). С увеличением давления на входе в ТРВ (р ) пропускная способность его увеличивается и требуемая производительность его будет обеспечена при меньшем перегреве (точка Б» на рис. 75,а). Таким образом, ТРВ, как всякий пропорциональный регулятор, неизбежно дает статическую ошибку, однако ошибка эта невелика и практически не ухудшает работу испарителя (см. гл. IV). [c.155]

Более экономичен способ регулирования р водорегулирующим вентилем. При снижении р давление на мембрану регулятора падает и под действием пружины ВРВ уменьшает подачу воды. В пределах статической ошибки ( 1,5 кгс/см ) ВРВ поддерживает р постоянным. [c.220]

Пропорциональные регуляторы неизбежно дают статическую ошибку, поэтому их относят к классу статических регуляторов. Действительно, при больших нагрузках должно возрасти и регулирующее воздействие, т. е. открытие клапана К должно быть больше среднего значения Уц- А, значение Х ст при этом как видно из статической характеристики, должно быть больше, чем Хо, т. е. устанавливается статическая ошибка, равная Ху т — Хц. [c.130]

У статических регуляторов (рис. 18, а) установившееся значение выходного параметра У однозначно ( жестко ) определяется значением входного параметра X. При регулировании они неизбежно дают статическую ошибку (см. рис. 7,б и в). [c.39]

Статическая ошибка регулятора прямого действия существенно зависит от силы, возникающей со стороны регулирующего органа насоса, в частности, наклонной шайбы. Сила трения на регулирующем органе насоса приводит к петлевой статической характеристике регулятора прямого действия. Снизить влияние нагрузки на регулятор можно, увеличив эффективную плоы адь плунжера и соответственно жесткость пружинного блока. Однако из-за этого во многих случаях габаритные размеры регулятора мощности прямого действия значительно увеличиваются. [c.284]

Сиглске [21], анализируя полученные динамические характеристики колпачковой абсорбционной колонны, предположил, что необходимо поддерживать постоянным состав выходящего газа. В результате показано, что по динамике лучше всего воздействовать на состав входящей жидкости (канал состав входящей жидкости—состав выходящего газа является наименее инерционным). Однако из практических соображений удобнее воздействовать на подачу входящей жидкости некоторое ухудшение динамических свойств при этом компенсируется техническими преимуществами. При использовании в этом случае П-регулятора САР устойчива, но передемпфирована она имеет статическую ошибку, и процесс регулирования проходит медленно. [c.711]

На рис. 4.5 показан аксиально-поршневой насос / с валом 2 и регулятором мощности прямого действия. Через отверстия А Б камеру с плунжером 5 поступа<т рабочая жидкость под давлением Рн- Плунжер 5 через промежуточный толкатель 4 поворачивает наклонную шайбу 6, пока сила со стороны пружинного блока 3 не уравновесит силу давления жидкости. Перемещение Ху и поворот шайбы приводят к изменению удельного рабочего объема i7n насоса. Пружинный блок составлен из двух цилиндрических пружин различной длины, поэтому статическая характеристика данного регулятора имеет вид ломаной линии (см. на рис. 4.4, б линию 2). Отклоиеиие ломаной линии 2 от идеальной статической характеристики (линии 1) приводит к появлению статической ошибки регулирования. (Изготовление специальной пружины с заданной нелинейной характеристикой сопряжено со значительными трудностями). [c.283]

Рассматриваемый регулятор имеет дополнительный подвод энергии в виде рабочей жидкости, поступающей от вспомогательного насоса в исполнительный механизм через отверстие Б и уходящей на слив через В. Благодаря вспомогательному следящему приводу, называемому иногда гидроусилителем, нагрузка со стороны регулирующего органа насоса несущественно влияет на статическую характеристику регулятора мощности. Использование в пружинном блоке трех пружин различной жесткости уменьшает статическую ошибку по сравнению с двухпружинным блоком. Демпфирующий поршень снижает колебания регулятора при переходном процессе. [c.285]

Соотношение (5.88) показывает, что при отсутствии в системе интегрирующих звеньев (разомкнутая система — статическая) постоянные воздействия и /о вызывают постоянную установив-щуюся ошибку (,, которую называют статической. Эта ошибка будет тем меньше, чем больше коэффициент-усиления К. системы, причем для уменьшения статической ошибки, вызываемой возмущающим воздействием, следует для увеличения К увеличивать коэффициент /Са регулятора, а не К объекта. [c.158]

Критерий статической ошибки. При использовании статических, регуляторов каждому значению величины статичеокого отклонения возмущающего воздействия соответствует определенное отклонение выходного пара-M Tipa объекта. [c.109]

Отклонение выходного параметра от требуемого значения есть величина статической ошибкй, которая тем меньше, чем меньше коэффициент усиления по дйн-ному каналу, т. е. чем выше коэфф ицие Нт усиления uetiH регулированиями ниже так называемая степень нерав- номерности самого регулятора. [c.109]

Пропорциональные регуляторы не могут поддерживать постоянное значение регулируемой величины, так как перемещение регулирующего органа в таких системах однозначно связано с изменением входной величины, следовательно, всякому новому его положению, необходимому при изменениях нагрузки, отвечает некоторое новое значение регулируемого параметра. Это неизбежное отклонение называют остаточной неравномерностью регулирования или статической ошибкой. Величина остаточной неравномерности тем менЫне, чем больше коэффициент передачи регулятора по прямому тракту. [c.41]

У астатических регуляторов регулирующий орган перемещается со-скоростью, пропорциональной отклонению регулируемого параметра. Преимуществом регуляторов этого типа является то, что установившееся значение регулируемой величины не зависит от нагруз-ки, и статическая ошибка равна нулю. Однако астатические регуляторы можно применять лишь для управления объектами, обладающими самовыравни-ванием в противном случае система будет неустойчивой. [c.543]

У статических регуляторов (рис. 18,г) установившееся значение вырдного параметра У однозначно ( жестко ) определяется величиной входного параметра X. При регулировании они дают статическую ошибку (см рис. 7, в). [c.35]

Сопоставляя переходные характеристики П-регулятора и ПД-регулятора видим, что у ПД-регулятора отклонения регулируемого параметра меньше (более быстрое затухание процесса). Поэтому если колебания параметра в переходном процессе у П-регулятора выходят за допустимые пределы, то следует выбрать ПД-регулятор. Для уменьшения статической ошибки применяют интегральные регуляторы (рис. 25, е). Однако при большой скорости РО они дают долгр не затухающий переходный процесс. При малой скорости РО возникают слишком большие отклонения регулируемого параметра в переходном процессе (показаны пунктиром). Поэтому И-регуляторы целесообразно применять в случаях, когда нагрузка меняется очень редко и решающую роль играет не переходный процесс, а установившееся состояние. [c.51]

Статическая характеристика регуляторов. По установившемуся значению регулируемого параметра различают регуляторы статические (пропорциопальные) и астатические (простые и изодромные). У статич. регулятора имеется монотонная связь между воспринимаемым им установившимся значением регулируемого параметра и положением регулирующего органа. Напр., в регуляторе уровня жидкости (в резервуаре) воспринимающий элемент (поплавок) связан системой рычагов с золотником задвижки на линии подачи жидкости в резервуар. Если изменится нагрузка объекта (расход жидкости из резервуара), то для приведения его к новому установившемуся состоянию нужно в том же направлении и на столько же изменить подачу в резервуар, т. е. нужно соответственно передвинуть золотник задвижки. Когда последний займет новое положение, при к-ром поступление и расход жидкости уравняются, поплавок, связанный рычажной системой с золотником задвижки, окажется уже в новом положении, отличающемся от исходного. Соответственно этому изменится и уровень жидкости в резервуаре. Следовательно, статич. регулятор не может обеспечить постоянства регулируемого параметра на заданном уровне при переменной нагрузке объекта (при этом возникает статич. ошибка регулирования). У астатич. регулятора нет непосредственной постоянной связи между установившимися значениями регулируемого параметра и положением регулирующего органа. Поэтому при изменении нагрузки не возникает статич. ошибка регулирования, и равновесие подобного регулятора имеет место лишь в случае, когда действительное значение [c.285]

Статическая ошибка регулирования (отклонение регулируемого параметра от заданного значения последостижения САР нового установившегося состояния). Возмущающие воздействия могут быть приложены к любому звену САР, но важнейшими являются возмущения, приложенные к входу объекта (изменения нагрузки) или к входу регулятора (его перенастройка). Возмущающее воздействие, приложенное к объекту регулирования, считается положительным, если приводит к увеличению регулируемого параметра. Увеличение нагрузки объекта уменьшает регулируемый параметр и является поэтому отрицательным возмущением снижение нагрузки приводит к увеличению качественного показателя и является положительным возмущением. Если возмущение скачком приложено к входу объекта, то при установке астатич. регулятора статич. ошибка равна пулю (для любых объектов регулирования). Подобная САР наз. астатической относительно возмущения, приложенного к объекту (т.е. по нагрузке). При установке статич. регулятора и возмущениях, приложенных к входу объекта, всегда имеется статич. ошибка. Подобная ( АР наз. статической относительно возмущения, приложенного к объекту. Величина статич. ошибки равна ири статич. объекте регулирования [c.290]

О качестве системы удобно судить по переходному процессу, т. е. по процессу регулирования, вызванному стуиенчатым изые-нениег.1 нагрузки (рис. 69). Примером ступенчатого изменения нагрузки может служить включение лампочек в холодильной камере. Если нагрузки от М о резко возросла до Л4 ь то ДХ начинает увеличиваться. Регулятор увеличивает Мр, причем мол<ет оказаться Мр > М 1. Тогда X станет уменьшаться. Возникает колебательный процесс. При затухании колебаний X принимает новое установившееся значение Хуст- Отклонение этого значения от начального называют статической ошибкой [c.124]

Из статической характеристики И-регулятора (рис. 76, б) видно, что клапан может занять одно из промежуточных значений только при X = Хо. Так, при X > Хо клапан полностью открыт, а при X < Хо полностью закрыт. Отсюда видно, что в установившемся состоянии статическая ошибка АХст = X — Хо равна нулю, т. е. интегральные регуляторы относятся к классу астатических регуляторов. [c.131]

Для улучшения качества регулирования применяют регуляторы с более сложными законами регулирования пропорциональноинтегральные, которые в первый момент времени работают как П-регуляторы, но затем сводят к нулю статическую ошибку пропорционально-дифференциальные, которые реагируют не только на б 131 [c.131]

С увеличением тепловой нагрузки подача жидкости через ТРВ должна быть больше. А это возможно лишь при большем перегреве (точка Б ), т. е. испаритель немного недозаполнен. А с увеличением давления Рк пропускная способность ТРВ увеличивается, и требуемая производительность будет обеспечена при меньшем перегреве (точка Б»). Таким образом, ТРВ, как всякий П-регулятор, дает некоторую статическую ошибку. [c.149]

У регуляторов с высокой чувствительностью (например, с мягкой пружиной) статическая ошибка значительно меньше, но в переходном процессе возникают долго не затухаюш,ие колебания с большими отклонениями параметров в начале процесса. [c.131]

Устройство, монтаж и ремонт холодильных установок Издание 4 (1985) — [

c.129

c.130

c.131

c.132

]

Устройство, монтаж и ремонт холодильных установок Издание 4 (1986) — [

c.129

c.130

c.131

c.132

]

Источник

Справочник /
Лекторий Справочник /
Лекционные и методические материалы по машиностроению /
Управление системами и процессами

pdf

Конспект лекции по дисциплине «Управление системами и процессами»,
pdf

Файл загружается

Благодарим за ожидание, осталось немного.

pdf

Конспект лекции по дисциплине «Управление системами и процессами».
pdf

txt

Конспект лекции по дисциплине «Управление системами и процессами», текстовый формат

Управление системами и процессами
Конспект лекций
1.1. Общие понятия
Управление каким-либо объектом (объект управления будем обозначать ОУ) есть
воздействие на него в целях достижения требуемых состояний или процессов. В
качестве ОУ может служить самолет, станок, электродвигатель и т.п. Управление
объектом с помощью технических средств без участия человека называется
автоматическим управлением. Совокупность ОУ и средств автоматического
управления называется системой автоматического управления (САУ).
Основной задачей автоматического управления является поддержание
определенного закона изменения одной или нескольких физических величин,
характеризующих процессы, протекающие в ОУ, без непосредственного участия
человека. Эти величины называются управляемыми величинами. Если в качестве
ОУ рассматривается хлебопекарная печь, то управляемой величиной будет
температура, которая должна изменяться по заданной программе в соответствии с
требованиями технологического процесса.
1.2. Фундаментальные принципы управления
Принято различать три фундаментальных принципа управления: принцип
разомкнутого управления, принцип компенсации, принцип обратной связи.
1.2.1. Принцип разомкнутого управления
Рассмотрим САУ хлебопекарной печи (рис.1). Ее принципиальная схема показывает
принцип действия данной конкретной САУ, состоящей из конкретных технических
устройств. Принципиальные схемы могут быть электрическими, гидравлическими,
кинематическими и т.п.
Технология выпечки требует изменения температуры в печи по заданной
программе, в частном случае требуется поддержание постоянной температуры. Для
этого надо реостатом регулировать напряжение на нагревательном элементе НЭ.
Подобная часть ОУ, с помощью которой можно изменять параметры управляемого
процесса называется управляющим органом объекта (УО). Это может быть реостат,
вентиль, заслонка и т.п.
Часть ОУ, которая преобразует управляемую величину в пропорциональную ей
величину, удобную для использования в САУ, называют чувствительным
элементом (ЧЭ). Физическую величину на выходе ЧЭ называют выходной
величиной ОУ. Как правило, это электрический сигнал (ток, напряжение) или
механическое перемещение. В качестве ЧЭ могут использоваться термопары,
тахометры, рычаги, электрические мосты, датчики давления, деформации,
положения и т.п. В нашем случае это термопара, на выходе которой формируется
напряжение, пропорциональное температуре в печи, подаваемое на измерительный
прибор ИП для контроля. Физическую величину на входе управляющего органа ОУ
называютвходной величинойОУ.
Управляющее воздействие u(t) — это воздействие, прикладываемое к УО объекта с
целью поддержания требуемых значений управляемой величины. Оно формируется
устройством управления (УУ). Ядром УУ является исполнительный элемент, в
качестве которого может использоваться электрические или поршневые двигатели,
мембраны, электромагниты и т.п.
Задающим устройством (ЗУ) называется устройство, задающее программу
изменения управляющего воздействия, то есть формирующее задающий сигнал
uо(t). В простейшем случае uо(t)=const. ЗУ может быть выполнено в виде
отдельного устройства, быть встроенным в УУ или же вообще отсутствовать. В
качестве ЗУ может выступать кулачковый механизм, магнитофонная лента, маятник
в часах, задающий профиль и т.п. Роль УУ и ЗУ может исполнять человек. Однако
это уже не САУ. В нашем примере УУ является кулачковый механизм,
перемещающий движок реостата согласно программе, которая задается профилем
кулачка.
Рассмотренную САУ можно представить в виде функциональной схемы, элементы
которой называются функциональными звеньями. Эти звенья изображаются
прямоугольниками, в которых записывается функция преобразования входной
величины в выходную (рис.2). Эти величины могут иметь одинаковую или
различную природу, например, входное и выходное электрическое напряжение, или
электрическое напряжение на входе и скорость механического перемещения на
выходе и т.п.
Величина f(t), подаваемая на второй вход звена, называется возмущением. Она
отражает влияние на выходную величину y(t) изменений окружающей среды,
нагрузки и т.п.
В общем случае функциональное звено может иметь несколько входов и выходов
(рис.3). Здесь u1,u2,…,un — входные (управляющие) воздействия; f1,f2,…,fm возмущающие воздействия; y1,y2,…,yk- выходные величины.
Принцип работы функциональных звеньев может быть различным, поэтому
функциональная схема не дает представление о принципе действия конкретной
САУ, а показывает лишь пути прохождения и способы обработки и преобразования
сигналов. Сигнал — это информационное понятие, соответствующее на
принципиальной схеме физическим величинам. Пути его прохождения указываются
направленными отрезками (рис.4). Точки разветвления сигнала называются узлами.
Сигнал определяется лишь формой изменения физической величины, он не имеет
ни массы, ни энергии, поэтому в узлах он не делится, и по всем путям от узла идут
одинаковые сигналы, равные сигналу, входящему в узел. Суммирование сигналов
осуществляется в сумматоре, вычитание — в сравнивающем устройстве.
Рассмотренную САУ хлебопекарной печи можно изобразить функциональной
схемой (рис.5). В данной схеме заложен принцип разомкнутого управления,
сущность которого состоит в том, что программа управления жестко задана ЗУ;
управление не учитывает влияние возмущений на параметры процесса. Примерами
систем, работающих по принципу разомкнутого управления, являются часы,
магнитофон, компьютер и т.п.
1.2.2. Принцип компенсации
Если возмущающий фактор искажает выходную величину до недопустимых
пределов, то применяют принцип компенсации (рис.6, КУ — корректирующее
устройство).
Пусть yо — значение выходной величины, которое требуется обеспечить согласно
программе. На самом деле из-за возмущения f на выходе регистрируется значение
y. Величина e = yо — y называется отклонением от заданной величины. Если
каким-то образом удается измерить величину f, то можно откорректировать
управляющее воздействие u на входе ОУ, суммируя сигнал УУ с корректирующим
воздействием, пропорциональным возмущению f и компенсирующим его влияние.
Примеры систем компенсации: биметаллический маятник в часах, компенсационная
обмотка машины постоянного тока и т.п. На рис.6 в цепи НЭ стоит
термосопротивление Rt, величина которого меняется в зависимости от колебаний
температуры окружающей среды, корректируя напряжение на НЭ.
Достоинство принципа компенсации: быстрота реакции на возмущения. Он более
точен, чем принцип разомкнутого управления. Недостаток: невозможность учета
подобным образом всех возможных возмущений.
1.2.3. Принцип обратной связи
Наибольшее распространение в технике получил принцип обратной связи (рис.7).
Здесь управляющее воздействие корректируется в зависимости от выходной
величины y(t). И уже не важно, какие возмущения действуют на ОУ. Если значение
y(t) отклоняется от требуемого, то происходит корректировка сигнала u(t) с целью
уменьшения данного отклонения. Связь выхода ОУ с его входом называется
главной обратной связью (ОС).
В частном случае (рис.8) ЗУ формирует требуемое значение выходной величины
yо(t), которое сравнивается с действительным значением на выходе САУ y(t).
Отклонение e = yо-y с выхода сравнивающего устройства подается на вход
регулятора Р, объединяющего в себе УУ, УО, ЧЭ.Если e
0, то регулятор
формирует управляющее воздействие u(t), действующее до тех пор, пока не
обеспечится равенство e = 0, или
y = yо. Так как на регулятор подается разность
сигналов, то такая обратная связь называется отрицательной, в отличие от
положительной обратной связи, когда сигналы складываются.
Такое управление в функции отклонения называется регулированием, а подобную
САУ называют системой автоматического регулирования(САР). Так на рис.9
изображена упрощенная схема САР хлебопекарной печи.
Роль ЗУ здесь выполняет потенциометр, напряжение на котором Uз сравнивается с
напряжением на термопаре Uт. Их разность
U через усилитель подается на
исполнительный двигатель ИД, регулирующий через редуктор положение движка
реостата в цепи НЭ. Наличие усилителя говорит о том, что данная САР является
системой непрямого регулирования, так как энергия для функций управления
берется от посторонних источников питания, в отличие от систем прямого
регулирования, в которых энергия берется непосредственно от ОУ, как, например, в
САР уровня воды в баке (рис.10).
Недостатком принципа обратной связи является инерционность системы.
Поэтому часто применяют комбинацию данного принципа с принципом
компенсации, что позволяет объединить достоинства обоих принципов: быстроту
реакции на возмущение принципа компенсации и точность регулирования
независимо от природы возмущений принципа обратной связи.
Вопросы
1. Что называется управлением?
2. Что называется автоматическим управлением?
3. Что называется системой автоматического управления?
4. Что является основной задачей автоматического управления?
5. Что называется объектом управления?
6. Что называется управляемой величиной?
7. Что называется управляющим органом?
8. Что называется чувствительным элементом?
9. Что такое входная и выходная величины?
10. Что называется управляющим воздействием?
11. Что называется возмущением?
12. Что называется отклонением от заданной величины?
13. Что называется управляющим устройством?
14. Что называется задающим устройством?
15. Что называется функциональной схемой и из чего она состоит?
16. В чем отличие сигнала от физической величины?
17. В чем суть принципа разомкнутого управления?
18. В чем суть принципа компенсации?
19. В чем суть принципа обратной связи?
20. Перечислите достоинства и недостатки принципов управления?
21. Какой частный случай управления называется регулированием?
22. В чем отличие систем прямого и непрямого регулирования?
2.1. Основные виды САУ
В зависимости от принципа и закона функционирования ЗУ, задающего программу
изменения выходной величины, различают основные виды САУ: системы стабилизации,
программные, следящие и самонастраивающиеся системы, среди которых можно
выделить экстремальные, оптимальныеи адаптивные системы.
В системах стабилизации (рис.9,10) обеспечивается неизменное значение управляемой
величины при всех видах возмущений, т.е. y(t) = const. ЗУ формирует эталонный сигнал, с
которым сравнивается выходная величина. ЗУ, как правило, допускает настройку
эталонного сигнала, что позволяет менять по желанию значение выходной величины.
В программных системах о
беспечивается изменение управляемой величины в
соответствии с программой, формируемой ЗУ. В качестве ЗУ может использоваться
кулачковый механизм, устройство считывания с перфоленты или магнитной ленты и т.п. К
этому виду САУ можно отнести заводные игрушки, магнитофоны, проигрыватели и т.п.
Различают системы с временной программой (например, рис.1), обеспечивающие y = f(t)
,
и системы с пространственной программой, в которых y = f(x), применяемые там, где на
выходе САУ важно получить требуемую траекторию в пространстве, например, в
копировальном станке (рис.11), закон движения во времени здесь роли не играет.
Следящие системы отличаются от программных лишь тем, что программа y = f(t) или
y=
f(x) заранее неизвестна. В качестве ЗУ выступает устройство, следящее за изменением
какого-либо внешнего параметра. Эти изменения и будут определять изменения выходной
величины САУ. Например, рука робота, повторяющая движения руки человека.
Все три рассмотренные вида САУ могут быть построены по любому из трех
фундаментальных принципов управления. Для них характерно требование совпадения
выходной величины с некоторым предписанным значением на входе САУ, которое само
может меняться. То есть в любой момент времени требуемое значение выходной
величины определено однозначно.
В самонастраивающихся системах ЗУ ищет такое значение управляемой величины,
которое в каком-то смысле является оптимальным.
Так в экстремальных системах (рис.12) требуется, чтобы выходная величина всегда
принимала экстремальное значение из всех возможных, которое заранее не определено и
может непредсказуемо изменяться. Для его поиска система выполняет небольшие
пробные движения и анализирует реакцию выходной величины на эти пробы. После этого
вырабатывается управляющее воздействие, приближающее выходную величину к
экстремальному значению. Процесс повторяется непрерывно. Так как в данных САУ
происходит непрерывная оценка выходного параметра, то они выполняются только в
соответствии с третьим принципом управления: принципом обратной связи.
Оптимальные системы являются более сложным вариантом экстремальных систем.
Здесь происходит, как правило, сложная обработка информации о характере изменения
выходных величин и возмущений, о характере влияния управляющих воздействий на
выходные величины, может быть задействована теоретическая информация, информация
эвристического характера и т.п. Поэтому основным отличием экстремальных систем
является наличие ЭВМ. Эти системы могут работать в соответствии с любым из трех
фундаментальных принципов управления.
В адаптивных системах предусмотрена возможность автоматической перенастройки
параметров или изменения принципиальной схемы САУ с целью приспособления к
изменяющимся
внешним
условиям.
В
соответствии
с
этим
различают
самонастраивающиесяи самоорганизующиеся а
даптивные системы.
Все виды САУ обеспечивают совпадение выходной величины с требуемым значением.
Отличие лишь в программе изменения требуемого значения. Поэтому основы ТАУ
строятся на анализе самых простых систем: систем стабилизации. Научившись
анализировать динамические свойства САУ, мы учтем все особенности более сложных
видов САУ.
2.2. Статические характеристики
Режим работы САУ, в котором управляемая величина и все промежуточные величины не
изменяются во времени, называется установившимся, или статическим режимом.
Любое звено и САУ в целом в данном режиме описывается уравнениями статики вида
y
= F(u,f), в которых отсутствует время t. Соответствующие им графики называются
статическими характеристиками. Статическая характеристика звена с одним входом u
может быть представлена кривой y = F(u) (рис.13). Если звено имеет второй вход по
возмущению f, то статическая характеристика задается семейством кривых y = F(u) при
различных значенияхf, или y = F(f)при различных u.
Так примером одного из функциональных звеньев системы регулирования воды в баке
(см. выше) является обычный рычаг (рис.14). Уравнение статики для него имеет вид
y=
Ku. Его можно изобразить звеном, функцией которого является усиление (или
ослабление) входного сигнала в K раз. Коэффициент K = y/u, равный отношению
выходной величины к входной называется коэффициентом усиления звена. Когда
входная и выходная величины имеют разную природу, его называют коэффициентом
передачи.
Статическая характеристика данного звена имеет вид отрезка прямой линии с наклоном
a
= arctg(L2/L
1) = arctg(K) (рис.15). Звенья с линейными статическими характеристиками
называются линейными. Статические характеристики реальных звеньев, как правило,
нелинейны. Такие звенья называются нелинейными. Для них характерна зависимость
коэффициента передачи от величины входного сигнала:K =
y/
u
const.
Например, статическая характеристика насыщенного генератора постоянного тока
представлена на рис.16. Обычно нелинейная характеристика не может быть выражена
какой-либо математической зависимостью и ее приходится задавать таблично или
графически.
Зная статические характеристики отдельных звеньев, можно построить статическую
характеристику САУ (рис.17, 18). Если все звенья САУ линейные, то САУ имеет линейную
статическую характеристику и называется линейной. Если хотя бы одно звено нелинейное,
то САУ нелинейная.
Звенья, для которых можно задать статическую характеристику в виде жесткой
функциональной
зависимости
выходной
величины
от
входной,
называются
статическими. Если такая связь отсутствует и каждому значению входной величины
соответствует множество значений выходной величины, то такое звено называется
астатическим. Изображать его статическую характеристику бессмысленно. Примером
астатического звена может служить двигатель, входной величиной которого является
напряжение
U, а выходной — угол поворота вала
, величина которого при
U=
const может принимать любые значения. Выходная величина астатического звена даже в
установившемся режиме является функцией времени.
2.3. Статическое и астатическое регулирование
Если на управляемый процесс действует возмущение f, то важное значение имеет
статическая характеристика САУ в форме y = F(f) при yo = const. Возможны два
характерных вида этих характеристик (рис.19). В соответствии с тем, какая из двух
характеристик свойственна для данной САУ, различают статическое и астатическое
регулирование.
Рассмотрим систему регулирования уровня воды в баке (рис.20). Возмущающим фактора
является поток Q воды из бака. Пусть при Q = 0 имеем y = yo , e = 0. ЗУ системы
настраивается так, чтобы вода при этом не поступала. При Q
0, уровень воды
понижается (e
0), поплавок опускается и открывает заслонку, в бак начинает поступать
вода. Новое состояние равновесия достигается при равенстве входящего и выходящего
потоков воды. Но в любом случае при Q
0 заслонка должна быть обязательно открыта,
что возможно только при e
0. Причем, чем больше Q, тем при больших значениях e,
устанавливается новое равновесное состояние. Статическая характеристика САУ имеет
характерный наклон (рис.19б). Это есть пример статического регулирования. Для
получения статического регулирование, все звенья САР должны быть статическими.
Статические регуляторы работают при обязательном отклонении e регулируемой
величины от требуемого значения. Это отклонение тем больше, чем больше возмущение
f. Это заложено в принципе действия регулятора и не является его погрешностью, поэтому
данное отклонение называется статической ошибкой регулятора. Из рис.21 видно, что,
чем больше коэффициент передачи регулятора Kр, тем на большую величину откроется
заслонка при одних и тех же значениях e, обеспечив в установившемся режиме большую
величину потока Q. Это значит, что на статической характеристике одинаковым значениям
e при больших Kр будут соответствовать большие значения возмущения Q, статическая
характеристика САУ пойдет более полого. Поэтому, чтобы уменьшить статическую
ошибку надо увеличивать коэффициент передачи регулятора. Того же результата
можно добиться, увеличивая коэффициент передачи объекта управления, но это дело
конструкторов, проектирующих данный объект, а не специалистов по автоматике.
Статизм d
, САР, характеризует насколько сильно значение регулируемой величины
отклоняется от требуемого значения при действии возмущений, и равна тангенсу угла
наклона статической характеристики, построенной в относительных единицах: d = tg(a) =
(рис.22), где y = y
— точка номинального режима САУ. При достаточно
н, f = f
н
больших значениях Kpимеем d
1/Kp.
В некоторых случаях статическая ошибка недопустима, тогда переходят к астатическому
регулированию, при котором регулируемая величина в установившемся режиме
принимает точно требуемое значение независимо от величины возмущающего фактора.
Статическая характеристика астатической САУ не имеет наклона (рис.19в). Возможные
неточности относятся к погрешностям конкретной системы и не являются закономерными.
Для того, чтобы получить астатическое регулирование, необходимо в регулятор включить
астатическое звено, например ИД, между ЧЭ и УО (рис.23).
Если уровень воды понизится, то поплавок переместит движок потенциометра на
величину
L, за счет этого появится разность потенциалов
0 и ИД начнет
поднимать заслонку до тех пор, пока
не уменьшится до нуля, а это возможно только
при y = yo . При поднятии уровня воды разность потенциалов сменит знак, и двигатель
будет вращаться в противоположную сторону, опуская заслонку.
Достоинства и недостатки статического и астатического регулирования:
статические регуляторы обладают статической ошибкой; астатические регуляторы
статической ошибки не имеют, но они более инерционны, сложны конструктивно и более
дороги.
Обеспечение требуемой статической точности регулирования является первой
основной задачей при расчете элементов САУ.
Вопросы
1.
2.
3.
4.
5.
Перечислите и дайте краткую характеристику основных видов САУ?
Что называется статическим режимом САУ?
Что называется статическими характеристиками САУ?
Что называется уравнением статики САУ?
Что называется коэффициентом передачи, в чем отличие от коэффициента
усиления?
6. В чем отличие нелинейных звеньев от линейных?
7. Как построить статическую характеристику нескольких звеньев?
8. В чем отличие астатических звеньев от статических?
9. В чем отличие астатического регулирования от статического?
10. Как сделать статическую САР астатической?
11. Что называется статической ошибкой регулятора, как ее уменьшить?
12. Что называется статизмом САР?
13. Назовите достоинства и недостатки статического и астатического регулирования?
3.1. Динамический режим САУ.
Уравнение динамики
Установившийся режим не является характерным для САУ. Обычно на управляемый
процесс действуют различные возмущения, отклоняющие управляемый параметр от
заданной величины.
Процесс установления требуемого значения управляемой величины называется
регулированием. Ввиду инерционности звеньев регулирование не может осуществляться
мгновенно.
Рассмотрим САР, находящуюся в установившемся режиме, характеризующемся
значением выходной величины y = y
. Пусть в момент t = 0 на объект воздействовал какой
o
— либо возмущающий фактор, отклонив значение регулируемой величины. Через
некоторое время регулятор вернет САР к первоначальному состоянию (с учетом
статической точности) (рис.24). Если регулируемая величина изменяется во времени по
апериодическому закону, то процесс регулирования называется апериодическим.
При резких возмущениях возможен колебательный затухающий процесс (рис.25а).
Существует и такая вероятность, что после некоторого времени Тр в системе установятся
незатухающие колебания регулируемой величины — незатухающий колебательный
процесс (рис.25б). Последний вид — расходящийся колебательныйпроцесс (рис.25в).
Таким образом, основным режимом работы САУ считается динамический режим,
характеризующийся протеканием в ней переходных процессов. Поэтому второй основной
задачей при разработке САУ является анализ динамических режимов работы САУ.
Поведение САУ или любого ее звена в динамических режимах описывается уравнением
динамики y(t) = F(u,f,t), описывающее изменение величин во времени. Как правило, это
дифференциальное уравнение или система дифференциальных уравнений. Поэтому
основным методом исследования САУ в динамических режимах является метод
решения дифференциальных уравнений. Порядок дифференциальных уравнений может
быть довольно высоким, то есть зависимостью связаны как сами входные и выходные
величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д. Поэтому уравнение
динамики в общем виде можно записать так:
F(y, y’, y”,…, y(n), u, u’, u”,…, u(m), f, f ’, f ”,…, f(k)) = 0.
3.2. Линеаризация уравнения динамики
В общем случае уравнение динамики оказывается нелинейным, так как реальные звенья
САУ обычно нелинейны. В целях упрощения теории нелинейные уравнения заменяют
линейными, которые приблизительно описывают динамические процессы в САУ.
Получаемая при этом точность уравнений оказывается достаточной для технических
задач. Процесс преобразования нелинейных уравнений в линейные называется
линеаризацией уравнений динамики. Рассмотрим сначала геометрическое обоснование
линеаризации.
В нормально функционирующей САУ значение регулируемой и всех промежуточных
величин незначительно отличается от требуемых. В пределах малых отклонений все
нелинейные зависимости между величинами, входящими уравнение динамики, могут быть
приближенно представлены отрезками прямых линий. Например, нелинейная статическая
характеристика звена на участке АВ (рис.26) может быть представлена отрезком
касательной в точке номинального режима А»В». Начало координат переносится в точку
О’, и в уравнениях записываются не абсолютные значения величин y,u,f, а их отклонения
от номинальных значений:
y = y — yн,
u = u — uн,
f = f — fн. Это позволяет получить
нулевые начальные условия, если считать, что при t
0 система находилась в
номинальном режиме в состоянии покоя.
Математическое обоснование линеаризации состоит в том, что если известно значение
f(a) какой — либо функции f(x) в любой точке x = a, а также значения производных от этой
функции в данной точке f’(a), f”(a), …, f(n)(a), то в любой другой достаточно близкой точке
x
+
x значение функции можно определить, разложив ее в окрестности точки a в ряд
Тейлора:
Аналогично можно разложить и функцию нескольких переменных. Для простоты возьмем
упрощенный, но наиболее характерный вариант уравнения динамики САУ: F(y,y’,y»,u,u’) =
f. Здесь производные по времени u’,y’,y» также являются переменными. В точке, близкой к
номинальному режиму: f = f
f и F = Fн +
F. Разложим функцию F в ряд Тейлора в
н +
окрестности точки номинального режима, отбрасывая члены ряда высоких порядков
малости:
.
В номинальном режиме, когда все отклонения и их производные по времени равны нулю,
получаем частное решение уравнения: Fн= fн. Учитывая это и вводя обозначения получим:
ao
Отбрасывая все знаки
y” + a1
y’ + a2
y = bo
u’ + b1
u + co
f.
, получим:
aoy” + a1y’ + a2y = bou’ + b1u + cof.
Отбрасывая все знаки
, получим:
В более общем случае:
aoy(n)+ a1y(n-1)+ … + an — 1y’ + any = bou(m)+ … + bm- 1u’ + bmu + c
f.
o
При этом всегда нужно помнить, что в данном уравнении используются не абсолютные
значения величин y, u, f их производных по времени, а отклонения этих величин от
номинальных значений. Поэтому полученное уравнение будем называть уравнением в
отклонениях.
К линеаризованной САУ можно применить принцип суперпозиции: реакция системы на
несколько одновременно действующих входных воздействий равна сумме реакций на
каждое воздействие в отдельности. Это позволяет звено с двумя входами u и f разложить
на два звена, каждое из которых имеет один вход и один выход (рис.27). Поэтому в
дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом,
уравнение динамики которых имеет вид:
(n-1)
aoy(n)+ a1y
+ … + a
y’ + any = bou(m)+ … + bm- 1u’ + bmu.
n — 1
Это уравнение описывает САУ в динамическом режиме лишь приближенно с той
точностью, которую дает линеаризация. Однако следует помнить, что линеаризация
возможна только при достаточно малых отклонениях величин и при отсутствии разрывов в
функции F в окрестностях интересующей нас точки, которые могут быть созданы
различными выключателями, реле и т.п.
Обычно n
m, так как при n < mСАУ технически нереализуемы.
3.3. Передаточная функция
В ТАУ часто используют операторную форму записи дифференциальных уравнений. При
этом вводится понятие дифференциального оператора p = d/dt так, что, dy/dt = py, а
pn =
dn/dtn. Это лишь другое обозначение операции дифференцирования. Обратная
дифференцированию операция интегрирования записывается как 1/p. В операторной
форме исходное дифференциальное уравнение записывается как алгебраическое:
(n-1)
aop(n)y + a
1p
(n-1)
(n)
y + … + any = (a
op + a
1p
(m-1)
(m)
+ … + an)y = (bop
+ b1p
+ … + bm)u
Не надо путать эту форму записи с операционным исчислением хотя бы потому, что здесь
используются непосредственно функции времени y(t), u(t) (оригиналы), а не их
изображения Y(p), U(p), получаемые из оригиналов по формуле преобразования Лапласа.
Вместе с тем при нулевых начальных условиях с точностью до обозначений записи
действительно очень похожи. Это сходство лежит в природе дифференциальных
уравнений. Поэтому некоторые правила операционного исчисления применимы к
операторной форме записи уравнения динамики. Так оператор p можно рассматривать в
качестве сомножителя без права перестановки, то есть py
скобки и т.п.
yp. Его можно выносить за
Поэтому уравнение динамики можно записать также в виде:
Дифференциальный оператор W(p) называют передаточной функцией. Она определяет
отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t)
,
поэтому ее еще называют динамическим коэффициентом усиления. В установившемся
режиме d/dt = 0, то есть p = 0
, поэтому передаточная функция превращается в
коэффициент передачи звена K = bm/an.
Знаменатель передаточной функции D(p) = aopn + a1pn — 1 + a2pn — 2 + … + an называют
характеристическим полиномом. Его корни, то есть значения p, при которых знаменатель
D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами
передаточной функции.
m — 1
Числитель K(p) = bopm + b
+ … + bm называют операторным коэффициентом
1p
передачи. Его корни, при которых K(p) = 0 и W(p) = 0, называются нулями передаточной
функции.
Звено САУ с известной передаточной функцией называется динамическим звеном. Оно
изображается прямоугольником, внутри которого записывается выражение передаточной
функции. То есть это обычное функциональное звено, функция которого задана
математической зависимостью выходной величины от входной в динамическом режиме.
Для звена с двумя входами и одним выходом должны быть записаны две передаточные
функции по каждому из входов. Передаточная функция является основной
характеристикой звена в динамическом режиме, из которой можно получить все
остальные характеристики. Она определяется только параметрами системы и не зависит
от входных и выходных величин. Например, одним из динамических звеньев является
интегратор. Его передаточная функция Wи
(p) = 1/p. Схема САУ, составленная из
динамических звеньев, называется структурной.
3.4. Элементарные динамические звенья
Динамика большинства функциональных элементов САУ независимо от исполнения
может быть описана одинаковыми по форме дифференциальными уравнениями не более
второго порядка. Такие элементы называют элементарными динамическими звеньями.
Передаточная функция элементарного звена в общем виде задается отношением двух
полиномов не более чем второй степени:
Wэ(p) =
.
Известно также, что любой полином произвольного порядка можно разложить на простые
сомножители не более, чем второго порядка. Так по теореме Виета можно записать
n — 1
D(p) = aopn+ a1p
+ a
pn — 2+ … + an= ao(p — p1)(p — p2)…(p — pn),
2
где p1, p2, …, pn- корни полинома D(p)
. Аналогично
K(p) = bopm+ b1pm — 1+ … + bm= bo(p — p~1)(p — p~2)…(p — p~m),
где p~
1, p~
2, …, p~
m- корни полинома
K(p). То есть
Корни любого полинома могут быть либо вещественными pi = ai , либо комплексными
попарно сопряженными pi = a
± j i . Любому вещественному корню при разложении
i
полинома соответствует сомножитель (p — ai ). Любая пара комплексно сопряженных
корней соответствует полиному второй степени, так как
(p — ai+ j
То есть
)(p — a
-j
i
i
2
) = (p — ai)
+
i
2
= p
— 2pai+ (ai2
+
2
i
).
2
i
Поэтому любую сложную передаточную функцию линеаризованной САУ можно
представить как произведение передаточных функций элементарных звеньев. Каждому
такому звену в реальной САУ, как правило, соответствует какой — то отдельный узел. Зная
свойства отдельных звеньев можно судить о динамики САУ в целом.
В теории удобно ограничиться рассмотрением типовых звеньев, передаточные функции
которых имеют числитель или знаменатель, равный единице, то есть W(p) =
,
W(p) =
, W(p) = 1/p, W(p) = p, W(p) = Tp + 1, W(p) = k. Из них могут
быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя
больше порядка полинома знаменателя, технически нереализуемы.
Вопросы
1. Какой режим САУ называется динамическим?
2. Что называется регулированием?
3. Назовите возможные виды переходных процессов в САУ. Какие из них являются
допустимыми для нормальной работы САУ?
4. Что называется уравнением динамики? Каков его вид?
5. Как провести теоретическое исследование динамики САУ?
6. Что называется линеаризацией?
7. В чем геометрический смысл линеаризации?
8. В чем состоит математическое обоснование линеаризации?
9. Почему уравнение динамики САУ называется уравнением в отклонениях?
10. Справедлив ли для уравнения динамики САУ принцип суперпозиции? Почему?
11. Как звено с двумя и более входами представить схемой, состоящей из звеньев с
одним входом?
12. Запишите линеаризованное уравнение динамики в обычной и в операторной
формах?
13. В чем смысл и какими свойствами обладает дифференциальный оператор p?
14. Что называется передаточной функцией звена?
15. Запишите линеаризованное уравнение динамики с использованием передаточной
функции. Справедлива ли эта запись при ненулевых начальных условиях? Почему?
16. Напишите выражение для передаточной функции звена по известному
линеаризованному уравнению динамики: (0.1p + 1)py(t) = 100u(t).
17. Что называется динамическим коэффициентом усиления звена?
18. Что называется характеристическим полиномом звена?
19. Что называется нулями и полюсами передаточной функции?
20. Что называется динамическим звеном?
21. Что называется структурной схемой САУ?
22. Что называется элементарными и типовыми динамическими звеньями?
23. Как сложную передаточную функцию разложить на передаточные функции
типовых звеньев?
4.1. Эквивалентные преобразования структурных схем
Структурная схема САУ в простейшем случае строится из элементарных динамических
звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со
сложной передаточной функцией. Для этого существуют правила эквивалентного
преобразования структурных схем. Рассмотрим возможные способы преобразований.
1. Последовательное соединение (рис.28) — выходная величина предшествующего звена
подается на вход последующего. При этом можно записать:
y1= W
; …; yn= Wn yn — 1= >
1 y
o; y
2= W
2 y
1
yn= W
…..Wn.yo= Wэкв yo,
1 W
2
где
.
То есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное
звено с передаточной функцией, равной произведению передаточных функций отдельных
звеньев.
2. Параллельно — согласное соединение (рис.29) — на вход каждого звена подается один и
тот же сигнал, а выходные сигналы складываются. Тогда:
y = y1+ y2+ … + yn= (W1+ W2+ … + W3)yo= Wэкв yo,
где
.
То есть цепочка звеньев, соединенных параллельно — согласно, преобразуется в звено с
передаточной функцией, равной сумме передаточных функций отдельных звеньев.
3. Параллельно — встречное соединение (рис. 30а) — звено охвачено положительной или
отрицательной обратной связью. Участок цепи, по которому сигнал идет в противоположном
направлении по отношению к системе в целом (то есть с выхода на вход) называется цепью
обратной связис передаточной функцией Wос. При этом для отрицательной ОС:
y = W
u; y1= Wосy; u = yo- y1,
п
следовательно
y = Wпyo- Wпy1= Wпyo- WпWocy = >
y(1 + WпWoc) = Wпyo= > y = Wэквyo,
где
Аналогично:
.
— для положительной ОС.
Если Woc= 1, то обратная связь называется единичной (рис.30б), тогда Wэкв= Wп/(1 ± W
).
п
Замкнутую систему называют одноконтурной, если при ее размыкании в какой либо точке
получают цепочку из последовательно соединенных элементов (рис.31а). Участок цепи,
состоящий из последовательно соединенных звеньев, соединяющий точку приложения
входного сигнала с точкой съема выходного сигнала называется прямой ц
епью (рис.31б,
передаточная функция прямой цепи Wп = Wo W1 W2). Цепь из последовательно
соединенных звеньев, входящих в замкнутый контур называют разомкнутой цепью (рис.46в,
передаточная функция разомкнутой цепи Wp = W1 W2 W3 W4). Исходя из приведенных
выше способов эквивалентного преобразования структурных схем, одноконтурная система
может быть представлена одним звеном с передаточной функцией: Wэкв = Wп/(1 ± W
) p
передаточная функция одноконтурной замкнутой системы с отрицательной ОС равна
передаточной функции прямой цепи, деленной на единицу плюс передаточная функция
разомкнутой цепи. Для положительной ОС в знаменателе знак минус. Если сменить точку
снятия выходного сигнала, то меняется вид прямой цепи. Так, если считать выходным
сигнал y1 на выходе звена W1, то Wp = Wo W1. Выражение для передаточной функции
разомкнутой цепи не зависит от точки снятия выходного сигнала.
Замкнутые системы бывают одноконтурными и
многоконтурной (рис.32).Чтобы найти
эквивалентную передаточную функцию для данной схемы нужно сначала осуществить
преобразование отдельных участков.
Если многоконтурная система имеет перекрещивающиеся связи (рис.33), то для вычисления
эквивалентной передаточной функции нужны дополнительные правила:
4. При переносе сумматора через звено по ходу сигнала необходимо добавить звено с
передаточной функцией того звена, через которое переносится сумматор. Если сумматор
переносится против хода сигнала, то добавляется звено с передаточной функцией,
обратной передаточной функции звена, через которое переносим сумматор (рис.34).
Так с выхода системы на рис.34а снимается сигнал
y2= (f + yoW1)W2.
Такой же сигнал должен сниматься с выходов систем на рис.34б:
y2= fW
W1W2= (f + yoW1)W2,
2+ y
o
и на рис.34в:
y2= (f(1/W1) + yo)W1W2= (f + yoW1)W2.
При подобных преобразованиях могут возникать неэквивалентные участки линии связи (на
рисунках они заштрихованы).
5. При переносе узла через звено по ходу сигнала добавляется звено с передаточной
функцией, обратной передаточной функции звена, через которое переносим узел. Если узел
переносится против хода сигнала, то добавляется звено с передаточной функцией звена,
через которое переносится узел (рис.35). Так с выхода системы на рис.35а снимается сигнал
y1= yoW1.
Такой же сигнал снимается с выходов рис.35б:
y1= yoW1W2/W2= yoW1
и рис.35в:
y1= yoW1.
6. Возможны взаимные перестановки узлов и сумматоров: узлы можно менять местами (рис.
36а); сумматоры тоже можно менять местами (рис.36б); при переносе узла через сумматор
необходимо добавить сравнивающий элемент (рис.36в: y = y1 + f1 = > y1 = y — f1) или
сумматор (рис.36г: y = y1+ f1).
Во всех случаях переноса элементов структурной схемы возникают неэквивалентные
участкилинии связи, поэтому надо быть осторожным в местах съема выходного сигнала.
При эквивалентных преобразованиях одной и той же структурной схемы могут быть
получены различные передаточные функции системы по разным входам и выходам. Так на
рис.48 имеется два входа: по управляющему воздействию u и возмущению f при одном
выходе y. Такая схема может быть преобразована к одному звену с двумя передаточными
функциями Wuy
и Wfy
.
4.2. САР напряжения генератора постоянного тока
Для примера рассмотрим схему САР напряжения генератора постоянного тока (рис.37).
Выведем дифференциальное уравнение исполнительного двигателя постоянного тока. Его
схема замещения изображена на рис. 38.
Для якорной цепи справедливо уравнение
.
Если принять, что
, гдеj
– угол поворота вала двигателя, то
,
то есть
,
где
– постоянная времени якорной цепи;
пропорциональнсти.
,
– коэффициенты
Если учесть, что
, где J – момент инерции якоря,
M электромагнитный момент, Мс
– момент сторонних сил, то получим
.
Следовательно
=>
=>
=>
=>
=>
.
Здесь
– электромеханическая постоянная времени;
;
;
;
,
по напряжению и моменту сторонних сил.
– коэффициенты пропорциональности;
– передаточные функции
Структурная схема двигателя постоянного тока показана на рис.39.
Аналогичным образом выводится передаточная функция генератора постоянного тока,
которая с учетом пренебрежения индуктивностью обмотки якоря имеет вид, показанный на
рис.40, где
.
Усилитель можно представить пропорциональным звеном с коэффициентом усиления
K
.В
у
окончательном виде структурная схема САР напряжения генератора постоянного тока
показана на рис.41.
Вопросы
1. Перечислите типичные схемы соединения звеньев САУ?
2. Как преобразовать цепь последовательно соединенных звеньев к одному звену?
3. Как преобразовать цепь параллельно соединенных звеньев к одному звену?
4. Как преобразовать обратную связь к одному звену?
5. Что называется прямой цепью САУ?
6. Что называется разомкнутой цепью САУ?
7. Как перенести сумматор через звено по ходу и против движения сигнала?
8. Как перенести узел через звено по ходу и против движения сигнала?
9. Как перенести узел через узел по ходу и против движения сигнала?
10. Как перенести сумматор через сумматор по ходу и против движения сигнала?
11. Как перенести узел через сумматор и сумматор через узел по ходу и против
движения сигнала?
12. Что называется неэквивалентными участками линий связи в структурных схемах?
13. Каково назначение САР напряжения генератора постоянного тока?
5.1. Понятие временных характеристик
Для оценки динамических свойств системы и отдельных звеньев принято исследовать их
реакцию на типовые входные воздействия, которые наиболее полно отражают
особенности реальных возмущений. Во — первых, это позволяет сравнивать отдельные
элементы между собой с точки зрения их динамических свойств. Во — вторых, зная реакцию
системы на типовые воздействия, можно судить о том, как она будет вести себя при
сложных изменениях входной величины.
Наиболее распространенными типовыми воздействиями являются: ступенчатое,
импульсное и гармоническое воздействия. Любой сигнал u(t), имеющий сложную форму,
можно разложить на сумму типовых воздействий ui(t) и исследовать реакцию системы на
каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить
результирующее изменение выходной величины y(t) суммируя полученные таким образом
составляющие выходного сигнала yi(t)
.
Особенно важное значение в ТАУ придают ступенчатому воздействию 1(t) =
.
Все остальные воздействия могут быть сведены к нему. Так, например, реальный
импульсный сигнал может быть представлен двумя ступенчатыми сигналами одинаковой
величины, но противоположными по знаку, поданными один за другим через интервал
времени
t(рис.42).
Зависимость изменения выходной величины системы от времени при подаче на ее вход
единичного ступенчатого воздействия при нулевых начальных условиях называется
переходной характеристикойи обозначается h(t).
Не менее важное значение в ТАУ уделяется импульсной переходной характеристике,
которая описывает реакцию системы на единичное импульсное воздействие при нулевых
начальных условиях, обозначают
(t). Единичный импульс физически представляет из
себя очень узкий импульс, ширина которого стремится к нулю, а высота — к бесконечности,
ограничивающий единичную площадь. Математически он описывается дельта — функцией
d(t) = 1’(t).
Переходная и импульсная переходная характеристики называются временными
характеристиками. Каждая из них является исчерпывающей характеристиками системы и
любого ее звена при нулевых начальных условиях. По ним можно однозначно определить
выходную величину при произвольном входном воздействии.
Зная передаточную функцию W(p) = K(p)/D(p), выражение для переходной функции можно
найти из формулы Хевисайда:
, где pk — корни
характеристического уравнения D(p) = 0. Взяв производную от переходной функции можно
получить выражение для импульсной переходной функции
(t) = h’(t).
5.2. Переходные характеристики элементарных звеньев
Здесь мы рассмотрим только самые основные звенья.
5.2.1. Безынерционное (пропорциональное, усилительное) звено
Это звено, для которого в любой момент времени выходная величина пропорциональна
входной.
Его уравнение: y(t) = k u(t).
Передаточная функция: W(p) = k.
Переходная характеристика: h(t) = k 1(t).
В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает
величины в k раз большей, чем на входе и сохраняет это значение (рис.43). При k = 1 звено
никак себя не проявляет, а приk = — 1- инвертирует входной сигнал.
Любое реальное звено обладает инерционностью, но с определенной точностью некоторые
реальные звенья могут рассматриваться как безынерционные, например, жесткий
механический рычаг, редуктор, потенциометр, электронный усилитель и т.п.
5.2.2. Интегрирующее (астатическое) звено
Его уравнение
, или
, или py = ku.
Передаточная функция: W(p) = k/p.
Переходная характеристика:
(рис.44).
При k = 1 звено представляет собой “чистый” интегратор W(p) = 1/p. Интегрирующее звено
неограниченно «накапливает» входное воздействие. Примеры интегрирующих звеньев:
электродвигатель, поршневой гидравлический двигатель, емкость и т.п. Введение его в САУ
превращает систему в астатическую, то есть ликвидирует статическую ошибку.
5.2.3. Инерционное звено первого порядка (апериодическое)
Уравнение динамики:
, или Tpy + y = ku.
Передаточная функция: W(p) =
.
Переходная характеристика может быть получена с помощью формулы Хевисайда:
,
где p1= — 1/T- корень уравнения D(p) = Tp + 1 = 0; D’(p1) = T.
Переходная характеристика имеет вид экспоненты (рис.45), по которой можно определить
передаточный коэффициент k, равный установившемуся значению h(t), и постоянную
времени Т по времени t, соответствующему точке пересечения касательной к кривой в
начале координат с ее асимптотой. При достаточно больших Т звено на начальном участке
может рассматриваться как интегрирующее, при малых Т звено приближенно можно
рассматривать как безынерционное. Примеры апериодического звена: термопара,
электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и
индуктивности.
5.2.4. Инерционные звенья второго порядка
Его уравнение: T12p2y + T2py + y = ku.
Передаточная функция:W(p) =
.
Решение уравнения зависит от соотношения постоянных времени T1 и T2, которое
определяет коэффициент затухания r =
где T = T1.
. Можно записать W(p) =
,
Если r
1, то знаменатель W(p) имеет два вещественных корня p1 и p2 и раскладывается
на два сомножителя:
2
T2p
+ 2rTp + 1 = T2 (p — p1).(p — p2).
Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно
не является элементарным.
При r<1 корни полинома знаменателя W(p) комплексно сопряженные: p1,2 =
± j .
Переходная характеристика представляет собой выражение, характеризующее затухающий
колебательный процесс с затуханием
и частотой
(рис.46). Такое звено называется
колебательным. При r = 0 колебания носят незатухающий характер. Такое звено является
частным случаем колебательного звена и называется консервативным. Примерами
колебательного звена могут служить пружина, имеющая успокоительное устройство,
электрический колебательный контур с активным сопротивлением и т.п. Зная
характеристики реального устройства можно определить его параметры как колебательного
звена. Передаточный коэффициент k равен установившемуся значению переходной
функции.
5.2.5. Дифференцирующее звено
Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики
идеального звена: y(t) =
, или y = kpu. Здесь выходная величина пропорциональна
скорости изменения входной величины. Передаточная функция: W(p) = kp. При k = 1 звено
осуществляет чистое дифференцирование W(p) = p. Переходная характеристика: h(t) = k
1’(t) = d(t).
Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска
выходной величины при подаче на вход единичного ступенчатого воздействия всегда
ограничена.
На
практике
используют
реальные
дифференцирующие
звенья,
осуществляющие приближенное дифференцирование входного сигнала.
Его уравнение: Tpy + y = kTpu.
Передаточная функция: W(p) =
.
При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходную
характеристики можно вывести с помощью формулы Хевисайда:
,
здесь p1 = — 1/T - корень характеристического уравнения D(p) = Tp + 1 = 0; кроме того, D’(p
)
1
= T.
При подаче на вход единичного ступенчатого воздействия выходная величина оказывается
ограничена по величине и растянута во времени (рис.47). По переходной характеристике,
имеющей вид экспоненты, можно определить передаточный коэффициент k и постоянную
времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и
емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья
являются главным средством, применяемым для улучшения динамических свойств САУ.
Кроме рассмотренных имеется еще ряд звеньев, на которых подробно останавливаться не
будем. К ним можно отнести идеальное форсирующее звено (W(p) = Tp + 1, практически не
реализуемо), реальное форсирующее звено (W(p) =
, при T1 >>
T2),

T
— p
запаздывающее звено (W(p) = e ), воспроизводящее входное воздействие с
запаздыванием по времени и другие.
Вопросы
1. Что называется и какие Вы знаете типовые входные воздействия? Для чего они
нужны?
2. Что называется переходной характеристикой?
3. Что называется импульсной переходной характеристикой?
4. Что называется временными характеристиками?
5. Для чего служит формула Хевисайда?
6. Как получить кривую переходного процесса при сложной форме входного
воздействия, если известна переходная характеристика звена?
7. Что называется безынерционным звеном, его уравнение динамики, передаточная
функция, вид переходной характеристики?
8. Что называется интегрирующим звеном, его уравнение динамики, передаточная
функция, вид переходной характеристики?
9. Что называется апериодическим звеном, его уравнение динамики, передаточная
функция, вид переходной характеристики?
10. Что называется колебательным звеном, его уравнение динамики, передаточная
функция, вид переходной характеристики?
11. Что называется консервативным звеном, его уравнение динамики, передаточная
функция, вид переходной характеристики?
12. Почему не являются элементарными инерционные звенья второго порядка с
коэффициентом затухания большим или равным единице?
13. Что называется идеальным дифференцирующим звеном? Почему его нельзя
реализовать?
14. Что называется реальным дифференцирующим звеном, его уравнение динамики,
передаточная функция, вид переходной характеристики?
6.1. Понятие частотных характеристик
Если подать на вход системы с передаточной функцией W(p) гармонический сигнал
то после завершения переходного процесса на выходе установится гармонические
колебания
с той же частотой
, но иными амплитудой и фазой, зависящими от частоты
возмущающего воздействия. По ним можно судить о динамических свойствах системы.
Зависимости, связывающие амплитуду и фазу выходного сигнала с частотой входного
сигнала, называются частотными характеристиками (ЧХ). Анализ ЧХ системы с целью
исследования ее динамических свойств называется частотным анализом.
Подставим выражения для u(t)и y(t)в уравнение динамики
n-2
(aоpn
+ a1pn — 1 + a2p
+ … + an)y = (bоpm
+ b1pm-1+ … + bm)u.
Учтем, что
а значит
pnu = pnUmejwt = Um(jw)nejwt = (jw)nu.
Аналогичные соотношения можно записать и для левой части уравнения. Получим:
По аналогии с передаточной функцией можно записать:
.
W(j ), равная отношению выходного сигнала к входному при изменении входного сигнала
по гармоническому закону, называется частотной передаточной функцией. Легко
заметить, что она может быть получена путем простой замены p на j
W(j
) есть комплексная функция, поэтому:
в выражении W(p).
где P(
) — вещественная ЧХ (ВЧХ); Q(
) — мнимая ЧХ (МЧХ); А(
) — амплитудная ЧХ
(АЧХ):
( ) — фазовая ЧХ (ФЧХ). АЧХ дает отношение амплитуд выходного и входного
сигналов, ФЧХ — сдвиг по фазе выходной величины относительно входной:
;
Если W(j
) изобразить вектором на комплексной плоскости, то при изменении
его конец будет вычерчивать кривую, называемую годографом вектораW(j
амплитудно — фазовую частотную характеристику (АФЧХ)(рис.48).
от 0 до +
), или
Ветвь АФЧХ при изменении
от до 0 можно получить зеркальным отображением
данной кривой относительно вещественной оси.
В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.49):
логарифмическая амплитудная ЧХ (ЛАЧХ) L(
(
) и логарифмическая фазовая ЧХ (ЛФЧХ)
). Они получаются путем логарифмирования передаточной функции:
ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования
умножается на 20, и используют не натуральный логарифм, а десятичный, то есть L(
)=
20lgA( ). Величина L( ) откладывается по оси ординат в децибелах. Изменение уровня
сигнала на 10 дб соответствует изменению его мощности в 10 раз. Так как мощность
гармонического сигнала Р пропорциональна квадрату его амплитуды А, то изменению
сигнала в 10 раз соответствует изменение его уровня на 20дб,так как
lg(P2/P1) = lg(A22/A12) = 20lg(A2/A1).
По оси абсцисс откладывается частота w в логарифмическом масштабе. То есть единичным
промежуткам по оси абсцисс соответствует изменение w в 10 раз. Такой интервал
называется декадой. Так как lg(0) = — , то ось ординат проводят произвольно.
ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси
Величина
(
.
) откладывается по оси ординат в градусах или радианах. Для
элементарных звеньев она не выходит за пределы: —
+
.
ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно
восстановить ее передаточную функцию и определить параметры.
6.2. Частотные характеристики типовых звеньев
Зная передаточную функцию звена W(p) легко получить все его частотные характеристики.
Для этого необходимо подставить в нее j
выразить из нее ВЧХ P(
) и МЧХ (Q(
форму и получают АЧХ A(
20lgA(
) и ФЧХ
вместо p, получим АФЧХ W(j
). Затем надо
). После этого преобразуют АФЧХ в показательную
(
), а затем определяют выражение ЛАЧХ L(w) =
) (ЛФЧХ отличается от ФЧХ только масштабом оси абсцисс).
6.2.1. Безынерционное звено
Передаточная функция:
W(p) = k.
АФЧХ: W(j
) = k.
ВЧХ: P(
) = k.
МЧХ: Q(
) = 0.
АЧХ: A(
) = k.
ФЧХ:
(
ЛАЧХ: L(
) = 0.
) = 20lgk.
Некоторые ЧХ показаны на рис.50. Звено пропускает все частоты одинаково c увеличением
амплитуды в k раз и без сдвига по фазе.
6.2.2. Интегрирующее звено
Передаточная функция:
W(p) = k/p.
Рассмотрим частный случай, когда k = 1, то есть
W(p) = 1/p.
АФЧХ: W(j
)=
ВЧХ: P(
) = 0.
МЧХ: Q(
) = — 1/
АЧХ: A(
) = 1/
ФЧХ:
(
ЛАЧХ: L(
)=-
.
.
.
/2.
) = 20lg(1/
) = — 20lg(
).
о
ЧХ показаны на рис.51. Все частоты звено пропускает с запаздыванием по фазе на 90
.
Амплитуда выходного сигнала увеличивается при уменьшении частоты, и уменьшается до
нуля при росте частоты (звено «заваливает» высокие частоты). ЛАЧХ представляет собой
прямую, проходящую через точку L( ) = 0 при
= 1. При увеличении частоты на декаду
ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен — 20 дб/дек (децибел на
декаду).
6.2.3. Апериодическое звено
При k = 1 получаем следующие выражения ЧХ:
W(p) =
;
;
;
;
(
)=
1-
2 = — arctg(
T);
;
L(
) = 20lg(A(
)) = — 10lg(1 + (
T)2).
Здесь A1 и A2 — амплитуды числителя и знаменателя ЛФЧХ;
числителя и знаменателя. ЛФЧХ:
1 и
2 — аргументы
ЧХ показаны на рис.52. АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2.
При построении асимптотической ЛАЧХ считают, что при
T)2 выражении для L(
), то есть L(
)
<
1
= 1/T можно пренебречь (
— 10lg1 = 0.. При
>
1
пренебрегают
единицей в выражении в скобках, то есть L(w)
— 20lg(wT). Поэтому ЛАЧХ проходит вдоль
оси абсцисс до сопрягающей частоты, затем — под наклоном — 20 дб/дек. Частота w1
называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от
асимптотических не превышает 3 дб при
=
.
1
ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота,
тем меньше искажения сигнала по фазе) и к —
/2 при возрастании
до бесконечности.
Перегиб в точке
=
( ) = — /4. ЛФЧХ всех апериодических звеньев имеют
1 при
одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом
вдоль оси частот.
6.2.4. Инерционные звенья второго порядка
При k = 1 передаточная функция звена: W(p) =
.
В виду сложности вывода выражений для частотных характеристик рассмотрим их без
доказательства, они показаны на рис.53.
Асимптотическая ЛАЧХ колебательного звена до сопрягающей частоты
1 = 1/T
1 совпадает
с осью абсцисс, при дальнейшем увеличении частоты идет с наклоном — 40 дб/дек. То есть
высокие частоты колебательное звено «заваливает» сильнее, чем апериодическое звено.
Реальная ЛАЧХ при
1значительно отличается от асимптотической. Это отличие тем
существенней, чем меньше коэффициент демпфирования . Точную кривую можно
построить, воспользовавшись кривыми отклонений, которые приводятся в справочниках. В
предельном случае = 0 получаем консервативное звено, у которого при
амплитуда выходных колебаний стремится к бесконечности (рис.54).
1
ЛФЧХ при малых частотах асимтотически стремится к нулю. При увеличении частоты до
бесконечности выходной сигнал поворачивается по фазе относительно входного на угол,
стремящийся в пределе к — 180о. ЛФЧХ можно построить с помощью шаблона, но для этого
нужен набор шаблонов для разных коэффициентов демпфирования. При уменьшении
коэффициента демпфирования АФЧХ приближается к оси абсцисс и в пределе у
консервативного звена она вырождается в два луча по оси абсцисс, при этом фаза
выходных колебаний скачком меняется от нуля до — 180о при переходе через сопрягающую
частоту (рис.54).
6.2.5. Правила построения ЧХ элементарных звеньев
При построении ЧХ некоторых звеньев можно использовать “правило зеркала”: при k = 1
ЛАЧХ и ЛФЧХ звеньев с обратными передаточными функциями зеркальны относительно
горизонтальной оси. Так на рис.55 изображены ЧХ идеального дифференцирующего и
идеального форсирующего звеньев.
Если k
1, то передаточную функцию звена можно рассматривать как произведение W =
k.W1, где W1 — передаточная функция с k = 1. При этом амплитуда вектора АФЧХ W(j
) при
всех значениях
должна быть увеличена в k раз, то есть A( ) = kA1( ). Поэтому,
например, центр полуокружности АФЧХ апериодического звена будет находиться не в точке
P = 1/2, а в точке k/2. ЛАЧХ также изменится: L(
20lgA1(
формы
) = 20lgA(
) = 20lgkA1(
) = 20lgk +
). Поэтому при k
1 ЛАЧХ звена нужно поднять по оси ординат не меняя ее
на
20lgk.
На
ЛФЧХ
изменение
k
никак
не
отразится.
Для примера на рис.56 приведены частотные
характеристики апериодического звена при k = 10 и T = 1c. При этом ЛАЧХ апериодического
звена с k = 1 поднята вверх на 20lg10 = 20.
Вопросы
1. Что называется частотными характеристиками?
2. Как получить частотные характеристики опытным путем?
3. Как получить частотные характеристики теоретическим путем по известной
передаточной функции звена?
4. Что такое и как получить АФЧХ?
5. Что такое и как получить ВЧХ?
6. Что такое и как получить МЧХ?
7. Что такое и как получить АЧХ?
8. Что такое и как получить ФЧХ?
9. Что такое и как получить ЛАЧХ?
10. Что такое и как получить ЛФЧХ?
11. Как построить годограф АФЧХ?
12. Постройте АФЧХ, ЛАЧХ и ЛФЧХ безынерционного звена.
13. Постройте АФЧХ, ЛАЧХ и ЛФЧХ интегрирующего звена.
14. Постройте АФЧХ, ЛАЧХ и ЛФЧХ апериодического звена.
15. Постройте АФЧХ, ЛАЧХ и ЛФЧХ колебательного звена.
16. Постройте АФЧХ, ЛАЧХ и ЛФЧХ консервативного звена.
17. Постройте ЛАЧХ и ЛФЧХ идеального дифференцирующего звена.
18. Постройте ЛАЧХ и ЛФЧХ идеального форсирующего звена.
19. Как изменятся ЛАЧХ и ЛФЧХ звена, если коэффициент усиления возрастет в 100
раз?
20. Для чего служит правило зеркала.
7.2. Законы регулирования
Пусть задана какая-то САР (рис.59).
Законом регулирования называется математическая зависимость, в соответствии с которой
управляющее воздействие на объект вырабатывалось бы безынерционным регулятором.
Простейшим из них является пропорциональный закон регулирования, при котором
u(t) = Ke(t) (рис.60а),
где u(t)- это управляющее воздействие, формируемое регулятором, e(t)- отклонение
регулируемой величины от требуемого значения, K- коэффициент пропорциональности
регулятора Р.
То есть для создания управляющего воздействия необходимо наличие ошибки
регулирования и чтобы величина этой ошибки была пропорциональна возмущающему
воздействию f(t). Другими словами САУ в целом должна быть статической.
Такие регуляторы называют П-регуляторами.
Так как при воздействии возмущения на объект управления отклонение регулируемой
величины от требуемого значения происходит с конечной скоростью (рис.60б), то в
начальный момент на вход регулятора подается очень малая величина e , вызывая при этом
слабые управляющие воздействия u. Для повышения быстродействия системы желательно
форсировать процесс управления.
Для этого в регулятор вводят звенья, формирующие на выходе сигнал, пропорциональный
производной от входной величины, то есть дифференцирующие или форсирующие звенья.
Такой закон регулирования называется пропорционально — дифференциальным:
u(t) = K1e(t) + K2 de(t)/dt.
В соответствии с ним работают ПД-регуляторы.
Чем быстрее нарастает отклонение регулируемой величины от требуемого значения, тем
интенсивнее работает ПД-регулятор, что препятствует дальнейшему нарастанию данного
отклонения. Кроме того при увеличении отклонения (de(t)/dt > 0) управляющий сигнал u
будет больше, чем при уменьшении (de(t)/dt < 0), что также играет положительную роль,
снижая колебательность процеса управления.
Добавление в регулятор двух дифференцирующих звеньев позволяет формировать
управляющее воздействие по второй производной отклонения e, такой регулятор
называется ПДД-регулятором.
Интегральный закон регулированияреализуется И-регулятором, его формулировка:
.
Этот регулятор наращивает управляющее воздействие до тех пор пока управляемая
величина отличается от требуемого значения, то есть пока e(t)
0.
И-регулятор обеспечивает астатическое регулирование.
При малых eуправляющее воздействие изменяется с малой скоростью, поэтому данный
регулятор очень инерционный.
Чтобы увеличить быстродействие обычно последовательно с ним включают усилитель, это
дает пропорционально-интегральный закон регулирования (ПИ-регулятор), его формула:
.
Первое слагаемое обеспечивает быстродействие, второе — астатичность, то есть точность
регулирования.
Еще большее быстродействие обеспечивается при добавлении слагаемого,
пропорционального производной от отклонения управляемой величины de/dt, такой закон
регулирования обеспечивается ПИД-регулятором, его формула:
.
Вопросы
1. Что представляет собой разомкнутая одноконтурная САУ?
2. Почему для построения ЧХ разомкнутых одноконтурных САУ удобно пользоваться
логарифмическими характеристиками?
3. Чем отличается ЛФЧХ от ФЧХ?
4. Постройте ЛАЧХ и ЛФЧХ разомкнутой одноконтурной САУ с передаточной функцией
W(p) =
.
5. Постройте ЛАЧХ и ЛФЧХ разомкнутой одноконтурной САУ с передаточной функцией
W(p) =
.
6. Как изменится ЛАЧХ и ЛФЧХ разомкнутой одноконтурной САУ, если коэффициент
усиления увеличить в 10 раз?
7. Чем отличается реальная ЛАЧХ от асимптотической?
8. Как определить уравнение динамики реального звена, если не известен его
механизм, но известно как задать входное воздействие и как померить выходное?
9. Что называется законом регулирования?
10. Как реализовать пропорциональный закон регулирования?
11. Зачем в регулятор добавляют дифференцирующие и форсирующие звенья?
12. Зачем в регулятор добавляют интегрирующие звенья?
8.1. Понятие устойчивости системы
Под устойчивостью системы понимается способность ее возвращаться к состоянию
установившегося равновесия после снятия возмущения, нарушившего это равновесие.
Неустойчивая система н
епрерывно удаляется от равновесного состояния или совершает
вокруг него колебания с возрастающей амплитудой.
Устойчивость линейной системы определяется не характером возмущения, а структурой
самой системы (рис.61). Говорят, что система устойчива «в малом», если определен факт
наличия устойчивости, но не определены ее границы. Система устойчива «в большом»,
когда определены границы устойчивости и то, что реальные отклонения не выходят за эти
границы.
В соответствии с классическим методом решение дифференциального уравнения ищется в
виде:
y(t) = yвын(t) + yсв(t).
Здесь yсв(t) — общее решение однородного дифференциального уравнения, то есть
уравнения с нулевой правой частью:
(n)
aoy
+ a1y(n-1)+ … + a(n-1)y’ + a(n)y = 0.
Физически это означает, что все внешние воздействия сняты и система абсолютно
свободна, ее движения определяются лишь собственной структурой. Поэтому решение
данного уравнения называется свободной составляющей общего решения. yвын
(t) — частное
решение неоднородного дифференциального уравнения, под которым понимается
уравнение с ненулевой правой частью. Физически это означает, что к системе приложено
внешнее воздействие u(t). Поэтому вторая составляющая общего решения называется
вынужденный. Она определяет вынужденный установившийся режим работы системы после
окончания переходного процесса.
Можно провести аналогию между САУ и пружиной, колебания которой описываются
аналогичным дифференциальным уравнением (рис.62). Оттянем пружину, а затем отпустим,
предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной
составляющей решения уравнения, то есть характер колебаний будет определяться только
структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на
свободные колебания наложится внешняя сила Р. После затухания колебаний,
описываемых только свободной составляющей общего решения, система перейдет в новый
установившийся режим, характеризуемый вынужденной составляющей yвын = y(t
)
.
Если внешнее воздействие само будет изменяться по синусоидальному закону P = Posin(
+
t
), то после затухания переходного процесса система будет совершать вынужденные
колебания с той же частотой, что и вынуждающая сила, то есть yвын= ymaxsin(
t + y).
Каждая составляющая общего решения уравнения динамики ищется отдельно.
Вынужденная составляющая ищется на основе решения уравнения статики для данной
системы для времени t
. Свободная составляющая представляет собой сумму из n
отдельных составляющих:
, где pi корни характеристического
уравнения D(p) = a0pn + a1pn-1 + a
. Корни могут быть либо вещественными p
2p
n-2 + … + a
n = 0
i
= ai, либо попарно комплексно сопряженными pi = ai ± j i. Постоянные интегрирования
А
i
определяются исходя из начальных и конечных условий, подставляя в общее решение
значения u, yи их производные в моменты времениt = 0иt
.
Каждому отрицательному вещественному корню соответствует экспоненциально
затухающая во времени составляющая yсв(t)i, каждому положительному — экспоненциально
расходящаяся, каждому нулевому корню соответствует yсв(t)
i = const (рис.63). Пара
комплексно сопряженных корней с отрицательной вещественной частью определяет
затухающие колебания с частотой
, при положительной вещественной части i
расходящиеся колебания, при нулевой — незатухающие (рис.64).
Так как после снятия возмущения yвын(t) = 0, то устойчивость системы определяется только
характером свободной составляющей yсв(t). zПоэтому условие устойчивости систем по
Ляпунову формулируется так: в устойчивой системе свободная составляющая решения
уравнения динамики, записанному в отклонениях, должна стремиться к нулю, то есть
затухать.
Исходя из расположения на комплексной плоскости корни с отрицательными
вещественными частями называются
левыми, с положительными — правыми (рис.65).
Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом:
для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее
характеристического уравнения были левыми. Если хотя бы один корень правый, то система
неустойчива. Если один из корней равен нулю (в системах, где an = 0), а остальные левые,
то система находится на границе апериодической устойчивости. Если равны нулю
вещественные части одной или нескольких пар комплексно сопряженных корней, то система
находится на границе колебательной устойчивости.
Правила, позволяющие судить о знаках корней характеристического уравнения без его
решения, называются критериями устойчивости. Их можно разделить на алгебраические
(основаны на составлении по данному характеристическому уравнению по определенным
правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и
частотные(основаны на исследовании частотных характеристик).
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Характеристическое уравнение системы с помощью теоремы Виета может быть записано в
виде
n-1
D(p) = aopn+ a1p
+ a2pn-2+ … + an= ao(p-p1)(p-p2)…(p-pn) = 0,
где p1, p2, …, pn — корни этого уравнения. Если система устойчива, значит все корни левые, то
есть вещественные части всех корней
отрицательны, что можно записать какai= -|ai| < 0. Подставим их в уравнение:
a0 (p + |a1|) (p + |a2| — j
2) (p + |a2| + j
2) … = 0.
Перемножая комплексно сопряженные выражения, получим:
a0 (p + |a
|)2 + (
1|) ((p + |a
2
2)2) … = 0.
После раскрытия скобок должно получиться выражение
n
a0 p
+ a1 pn-1+ a2 pn-2 + … + an= 0.
Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов
a0,a1,…,an не будет отрицательным. Поэтому необходимым условием устойчивости САУ
является положительность всех коэффициентов характеристического уравнения: a0 > 0, a
>
1
0, … , an > 0. В дальнейшем будем рассматривать только уравнения, где a0 > 0. В противном
случае уравнение домножается на -1.
Рассмотренное условие является необходиным, но не достаточным условием.
Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.
8.2.1. Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется
специальная таблица с использованием коэффициентов характеристического уравнения:
1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке
их возрастания;
2) во второй строке — с нечетными;
3) остальные элементы таблицы определяется по формуле: ck,i = ck+ 1,i — 2 — ri ck + 1,i — 1, где ri =
c1,i — 2/c1,i — 1, i
3- номер строки, k- номер столбца.
4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Ri
ik
1
2
3
4
—
1
c11= a0
c21= a2
c31= a4
…
—
2
c12= a1
c22= a3
c32= a5
…
r3= c11/cc12
3
c13= c21-r3c
22
c23= c31-r3c
32
c33= c41-r3c42
…
r3= c11/c12
4
c14= c22-r3c
23
c24= c32-r4c
33
c34= c42-r4c43
…
…
…
…
…
…
…
Критерий Рауса: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы
коэффициенты первого столбца таблицы Рауса c11, c12, c13,… были положительными. Если
это не выполняется, то система неустойчива, а количество правых корней равно числу
перемен знака в первом столбце.
Достоинство
критерий
прост
в
использовании
независимо
от
порядка
характеристического уравнения. Он удобен для использования на ЭВМ. Его недостаток малая наглядность, трудно судить о степени устойчивости системы, на сколько далеко
отстоит она от границы устойчивости.
8.2.2. Критерий Гурвица
Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического
уравнения строится определитель Гурвица
по алгоритму:
1) по главной диагонали слева направо
характеристического уравнения от a1до an;
выставляются
все
коэффициенты
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так,
чтобы индексы убывали сверху вниз;
3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.
Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы
все n диагональных миноров определителя Гурвица были положительны. Эти миноры
называются определителями Гурвица.
Рассмотрим примеры применения критерия Гурвица:
1) n = 1 => уравнение динамики: a0
p + a1 = 0. Определитель Гурвица:
> 0, то есть условиие устойчивости:a0> 0, a1 >
;
0
=
1
= a1 > 0 при
a
2) n = 2 => уравнение динамики: a0
p2 + a1p + a2 = 0. Определители Гурвица:
1 = a
1 > 0, D
2 =
a1a2 - a0a3 = a1a2 > 0, так как a3 = 0, то есть условие устойчивости: a0> 0, a1
> 0, a2 > 0;
3) n = 3 => уравнение динамики: a0
p3 + a1p2 + a2p + a3 =
. Определители Гурвица:
0
0,
,
2 = a
1a
2 — a
0a
3 > 0
a0a3 >
0
;

3 = a3
1
= a
1 >
> 0, условие устойчивости: a0 > 0, a1 > 0, a2 > 0, a3 > 0, a
a
1
2
2
Таким образом при n 2 положительность коэффициентов характеристического уравнения
является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются
дополнительные условия.
Критерий Гурвица применяют при n
4. При больших порядках возрастает число
определителей и процесс становится трудоемким. Имеется ряд модификаций данного
критерия, расширяющие его возможности.
Недостаток критерия Гурвица — малая наглядность. Достоинство — удобен для
реализации на ЭВМ. Его часто используют для определения влияния одного из
параметров САУ на ее устойчивость. Так равенство нулю главного определителя
n = a
n
a
n-1 = 0 говорит о том, что система находится на границе устойчивости. При этом либо
n = 0 при выполнении остальных условий система находится на границе апериодической
устойчивости, либо предпоследний минор
n-1 = 0 — при положительности всех остальных
миноров система находится на границе колебательной устойчивости. Параметры САУ
определяют значения коэффициентов уравнения динамики, следовательно изменение
любого параметра Ki влияет на значение определителя
. Исследуя это влияние можно
n-1
найти, при каком значении Ki определитель
станет равен нулю, а потом n-1
отрицательным (рис.67). Это и будет предельное значение исследуемого параметра, после
которого система становится неустойчивой.
Вопросы
1. Что понимают под устойчивостью САУ в малом и в большом?
2. Какой вид имеет решение уравнения динамики САУ?
3. Как найти вынужденную составляющую решения уравнения динамики САУ?
4. Какой вид имеет свободная составляющая решения уравнения динамики САУ?
5. Что такое характеристическое уравнение?
6. Какой вид имеют корни характеристического уравнения?
7. Чем отличаются правые и левые корни характеристического уравнения?
8. Сформулируйте условие устойчивости систем по Ляпунову.
9. Что такое граница устойчивости?
10. Что такое критерии устойчивости?
11. Сформулируйте необходимое условие устойчивости САУ.
12. Сформулируйте критерий Рауса.
13. Сформулируйте критерий Гурвица.
14. В чем достоинства и недостатки алгебраических критериев устойчивости?
Частотные критерии устойчивости
Это графоаналитические методы, позволяющие по виду частотных характеристик САУ
судить об их устойчивости. Их общее достоинствов простой геометрической
интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального
уравнения.
9.1. Принцип аргумента
Запишем характеристический полином САУ в виде
D(p) = a0 (p — p1) (p — p2) … (p — pn) = 0.
Его корни
pi=
где arg(pi) = arctg(
i/ai) + k
i
+j
i = |pi|ejarg(pi),
,
.
Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда
разность p — piизобразится разностью векторов (рис.68б), где p - любое число.
Еcли менять значение p произвольным образом, то конец вектора p — piбудет перемещаться
по комплексно плоскости, а его начало будет оставаться неподвижным, так как pi- это
конкретное неизменное значение.
В частном случае, если на вход системы подавать гармонические колебания с различной
частотой
, то p = j
, а характеристический полином принимает вид:
D(j
При этом концы векторов j
) = a0 (j
— p1) (j
— p2) … (j
— pn).
— piбудут находиться на мнимой оси (рис.68в). Если менять
от до + , то каждый вектор j
— piбудет поворачиваться относительно своего начала
p
на
угол
+p
для
левых
и

p
для
правых
корней (рис.68г).
i
Характеристический полином можно представить в виде
D(j
где
|D(j
arg(D(j
)| = a0 |j
)) = arg(j
— p1| |j
) = |D(j
— p2|…|j
— p1) + arg(j
)|ejarg(D(j
),
)
— pn|,
— p2) + .. + arg(j
— pn).
Пусть из n корней m- правые, а n — m- левые, тогда угол поворота вектора D(j
изменении
от -
до +
равен
= (n — m)
или при изменении
от 0до +
получаем
= (n — 2m) (
/2).
-m
,
)при
Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты
до + равно разности между числом левых и правых корней уравнения D(p) = 0,
умноженному на
/2.
, а при изменении частоты
от 0до +
от —
эта разность умножается на
Это и есть принцип аргумента. Он положен в основе всех частотных критериев
устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий
Михайлова и критерий Найквиста.
9.2. Критерий устойчивости Михайлова
Так как для устойчивой САУ число правых корней m = 0, то угол поворота вектора D(j
составит
=n
То есть САУ будет устойчива, если вектор D(j
повернется на угол n
)
/2.
)при изменении частоты
от 0 до +
/2.
При этом конец вектора опишет кривую, называемую годографом Михайлова. Она
начинается на положительной полуоси, так как D(0) = an, и последовательно проходит
против часовой стрелки n квадрантов комплексной плоскости, уход в бесконечность в n- ом
квадранте (рис.69а).
Если это правило нарушается (например, число проходимых кривой квадрантов не равно
n
,
или нарушается последовательность прохождения квадрантов (рис.69б)), то такая САУ
неустойчива — это и есть необходимое и достаточное условие критерия Михайлова.
Достоинства. Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи
начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим
критерием удобно пользоваться, если известно уравнение замкнутой САУ.
Для облегчения построения годографа Михайлова выражение для D(j
суммой вещественной и мнимой составляющих:
)представляют
D(j
)= a0(j
— p1)(j
— p2)…(j
— p
) = a0(j
n
)n+ a1(j
)n — 1+ … + an= ReD(j
) + jImD(j
),
где
ReD(j
) = a
n- a
n-2
ImD(j
) = an — 1
2
+ an- 4
— an — 3
3
4
— …,
+ an- 5
5
— ….
Меняя
от
0до
по этим формулам находят координаты точек годографа, которые
соединяют плавной линией.
9.3. Критерий устойчивости Найквиста
Этот критерий позволяет судить об устойчивости замкнутой САУ по виду АФЧХ разомкнутой
САУ (рис.70). Исследование разомкнутой САУ проще, чем замкнутой. Его можно
производить экспериментально, поэтому часто оказывается, что АФЧХ разомкнутой САУ мы
имеем или можем получить.
Передаточная функция разомкнутой САУ:
Wp(p) = Wp(p)/Dp(p)= > уравнение динамики: y(t) =
e(t),
или
Dp(p) y(t) = Kp(p) e(t).
Здесь Dp(p)- характеристический полином разомкнутой САУ. То есть по виду корней
уравнения Dp(p) = 0можно судить об устойчивости разомкнутой САУ. Но это пока ничего не
говорит об устойчивости замкнутой САУ.
Для того, чтобы получить уравнение динамики замкнутой САУ при свободном движении,
считаем, что внешнее воздействие u = 0, тогда на вход первого звена САУ подается сигнал
e(t) = u(t) — y(t) = — y(t).
То есть
Dp(p) y(t) = Kp(p) ( — y(t)),
следовательно уравнение замкнутой САУ:
(Dp(p) + Kp(p)) y(t) = 0.
Таким образом, характеристическое уравнение замкнутой САУ:
Dз(p) = Dp(p) + Kp(p) = 0.
По виду его корней уже можно судить об устойчивости замкнутой САУ.
Воспользуемся вспомогательной функцией:
F(j
) = 1 + Wр(j
)=
.
По сути дела она представляет собой АФЧХ разомкнутой САУ, сдвинутую на единицу
вправо. Степени полиномов Dз(j
p
pi, то есть можно записать:
F(jw) =
)и
Dp(j
) равны n.Эти полиномы имеют свои корни
p
зiи
.
Каждую разность в скобках можно представить вектором на комплексной плоскости, конец
которого скользит по мнимой оси
векторов j
правый.
(рис.63в). При изменении
от —
до +
каждый из
— piбудет поворачиваться на угол +p, если корень левый и -p, если корень
Пусть полином Dз(jw) имеет mправых корней и n — mлевых, а полином Dp(j
)имеетg
правых корней и n — gлевых. Тогда суммарный угол поворота вектора функции F(j
изменении частоты
от —
до +
)при
:
p[(n — m) — m)] — p[(n
— g) — g] = 2p(g — m).
Если замкнутая САУ устойчива, то m = 0, тогда суммарный поворот вектора F(j
изменении
составит 2
от —
до +
должен быть равен 2

g, а при изменении
) при
от 0до +
он
g/2.
Отсюда можно сформулировать критерий устойчивости Найквиста: если разомкнутая
САУ неустойчива и имеетgправых корней, то для того, чтобы замкнутая САУ была
устойчива необходимо и достаточно, чтобы вектор F(j )при изменении
от 0 до +
охватывал начало координат в положительном направлении g/2раз, то есть АФЧХ
разомкнутой САУ должна охватвать g/2раз точку ( — 1, j0).
На рис.71а приведены АФЧХ разомкнутых САУ, устойчивых в замкнутом состоянии, на
рис.71б — замкнутая САУ неустойчива.
На рис.71в и 71г показаны АФЧХ разомкнутых астатических САУ, соответственно
устойчивых и неустойчивых в замкнутом состоянии. Их особенность в том, что АФЧХ при
0уходит в бесконечность.
В этом случае при использовании критерия Найквиста ее мысленно замыкают на
вещественную ось по дуге окружности бесконечно большого радиуса.
Достоинство. Критерий Найквиста очень нагляден. Он позволяет не только выявить,
устойчива ли САУ, но и, в случае, если она неустойчива, наметить меры по достижению
устойчивости.
Вопросы
1.
2.
3.
4.
5.
Что называется частотными критериями устойчивости САУ?
В чем преимущество частотных критериев устойчивости перед алгебраическими:
Сформулируйте принцип аргумента.
Сформулируйте критерий устойчивости Михайлова.
Поясните каждый из годографов на рис.69. Как вы судите об устойчивости
соответствующих САУ?
6. Как из годографов на рис.69 соответствуют САУ, находящимся на границе
устойчивости?
7. Сформулируйте критерий устойчивости Найквиста.
8. Поясните, являются ли устойчивыми САУ, АФЧХ которых в разомкнутом состоянии
представлены на рис.71. Почему?
9. В чем особенность использования критерия Найквиста для астатических САУ?
10. Как из годографов на рис.71 соответствуют САУ, находящимся на границе
устойчивости?
10.1. Понятие структурной устойчивости. АФЧХ астатических САУ
САУ может быть неустойчивой по двум причинам: неподходящий состав динамических
звеньев и неподходящие значения параметров звеньев.
САУ, неустойчивые по первой причине называются структурно неустойчивыми. Это
означает, что изменением параметров САУ нельзя добиться ее устойчивости, нужно менять
ее структуру.
Например, если САУ состоит из любого количества инерционных и колебательных звеньев,
она имеет вид, показанный на рис.72
.
При увеличении коэффициента усиления САУ K каждая точка ее АФЧХ удаляется от начала
координат, пока при некотором значении KкритАФЧХ не пересечет точку (-1, j0). При
дальнейшем увеличении K, САУ будет неустойчива. И наоборот, при уменьшении Kтакую
САУ в принципе возможно сделать устойчивой, поэтому ее называют структурно
устойчивой.
Если САУ астатическая, то при ее размыкании характеристическое уравнение можно
представить в виде: p D1p(p) = 0, гдеn- порядок астатизма, равный количеству
последовательно включенных интеграторов. Это уравнение имеет нулевые корни, поэтому
при
здесь
0, АФЧХ стремится к (рис.71в и 71г). Например, пусть Wр(p) =
= 1, тогда АФЧХ разомкнутой САУ:
W(j
)=
Так как порядок знаменателя больше порядка числителя, то при
, Q(
)
-j
. Подобная АФЧХ представлена на рис.73.
= P(
) + jQ(
,
).
0имеем P(
)
—
Так как АФЧХ терпит разрыв, трудно сказать, охватывает ли она точку (-1,j0). В этом случае
пользуются следующим приемом: если АФЧХ терпит разрыв, уходя в бесконечность при
0, ее дополняют мысленно полуокружностью бесконечного радиуса, начинающейся на
положительной вещественной полуоси и продолжающейся до АФЧХ в отрицательном
направлении. После этого можно применить критерий Найквиста. Как видно из рисунка, САУ,
имеющая одно интегрирующее звено, является структурно устойчивой.
Если САУ имеет два интегрирующих звена (порядок астатизма
бесконечность во втором квадранте (рис.74).
Например, пусть Wр(p) =
W(j
)=
= 2), ее АФЧХ уходит в
, тогда АФЧХ САУ:
= P(
) + jQ(
).
При
0 имеем P( )
— , Q( )
+ j .Такая САУ не будет устойчива ни при
каких значениях параметров, то есть она структурно неустойчива.
Структурно неустойчивую САУ можно сделать устойчивой, включив в нее корректирующие
звенья (например, дифференцирующие или форсирующие) или изменив структуру САУ,
например, с помощью местных обратных связей.
10.2. Понятие запаса устойчивости
В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в
определенных пределах (старение, температурные колебания и т.п.). Эти колебания
параметров могут привести к потере устойчивости системы, если она работает вблизи
границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала
вдали от границы устойчивости. Степень этого удаления называютзапасом устойчивости.
Согласно критерия Найквиста, чем дальше АФЧХ от критической точки (-1, j0), тем больше
запас устойчивости. Различают запасы устойчивости по модулю и по фазе.
Запас устойчивости по модулюхарактеризует удаление годографа АФЧХ разомкнутой САУ
от критической точки в направлении вещественной оси и определяется расстояниемhот
критической точки до точки пересечения годографом оси абсцисс (рис.75).
Запас устойчивости по фазе характеризует удаление годографа от критической точки по
дуге окружности единичного радиуса и определяется углом
между отрицательным
направлением вещественной полуоси и лучом, проведенным из начала координат в точку
пересечения годографа с единичной окружностью.
Как уже отмечалось, с ростом коэффициента передачи разомкнутой САУ растет модуль
каждой точки АФЧХ и при некотором значении K = KкрАФЧХ пройдет через критическую
точку (рис.76) и попадет на границу устойчивости, а при K > Kкрзамкнутая САУ станет
неустойчива. Однако в случае “клювообразных” АФЧХ (получаются из-за наличия
внутренних обратных связей) не только увеличение, но и уменьшение Kможет привести к
потере устойчивости замкнутых САУ (рис.77). В этом случае запас устойчивости
определяется двумя отрезками h1
и h2
, заключенными между критической точкой и АФЧХ.
Обычно при создании САУ задаются требуемыми запасами устойчивости hи
, за пределы
которых она выходить не должна. Эти пределы выставляются в виде сектора,
вычерчиваемого вокруг критической точки, в который АФЧХ разомкнутой САУ входить не
должна (рис.78).
10.3. Анализ устойчивости по ЛЧХ
Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой
САУ. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и
ЛФЧХ.
Пусть известны частотные характеристики двух разомкнутых САУ (1 и 2), отличающихся друг
от друга только коэффициентом передачи K1< K2. Пусть первая САУ устойчива в замкнутом
состоянии, вторая нет.(рис.79).
Если W1(p)- передаточная функция первой САУ, то передаточная функция второй САУ
W2(p) = K W
, где K = K2/K1. Вторую САУ можно представить последовательной цепочкой
1(p)
из двух звеньев с передаточными функциями K (безынерционное звено) и W1(p), поэтому
результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев.
Поэтому ЛАЧХ второй САУ: L2(
а ЛФЧХ:
(
2
)=
(
1
) = 20lgK + L1(
),
).
Пересечениям АФЧХ вещественной оси соответствует значение фазы
соответствует точке пересечения ЛФЧХ
видно на АФЧХ, амплитуды A1(
) = 20lgA1(
) < 0 и L2(
) < 1, A2(
=-
=-
. Это
линии координатной сетки. При этом, как
) > 1, что соответствует на САЧХ значениям
L
(
1
) > 0.
Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет
устойчива, если значению ЛФЧХ
= — будут соответствовать отрицательные значения
ЛАЧХ и наоборот. Запасам устойчивости по модулю h1и h2, определенным по АФЧХ
соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где
логарифмическом масштабе.
=-
, но в
Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты
c1
и
, при которых это происходит называют частотами среза.
c2
В точках пересечения A(
) = 1 = > L(
) = 0- ЛАЧХ пересекает горизонтальную ось. Если
при частоте среза фаза АФЧХ
(рис.79а кривая 1), то замкнутая САУ устойчива. На
c1 >рис.79б это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка
ЛФЧХ, расположенная выше линии
(рис.79а кривая 2)
Угол
1
=
-(-
c1
=-
< - , поэтому при
c2
. И наоборот для неустойчивой замкнутой САУ
=
c2
ЛФЧХ проходит ниже линии
=-
.
)является запасом устойчивости по фазе. Этот угол соответствует
расстоянию от линии
=-
до ЛФЧХ.
Исходя из сказанного, критерий устойчивости Наквиста по логарифмическимЧХ, в
случаях, когда АФЧХ только один раз пересекает отрезок вещественной оси [- ;-1], можно
сформулировать так: для того, чтобы замкнутая САУ была устойчива необходимо и
достаточно, чтобы частота, при которой ЛФЧХ пересекает линию
частоты среза.
=-
, была больше
Если АФЧХ разомкнутой САУ имеет сложный вид (рис.80), то ЛФЧХ может несколько раз
пересекать линию
= — . В этом случае применение критерия Найквиста несколько
усложняется. Однако во многих случаях данной формулировки критерия Найквиста
оказывается достаточно.
Вопросы
1. Какие САУ считаются структурно устойчивыми и структурно неустойчивыми?
2. В каком квадранте уходит в бесконечность АФЧХ разомкнутой САУ если порядок
астатизма равен трем? Является ли такая САУ структурно устойчивой в замкнутом
состоянии:
3. Как сделать устойчивой структурно неустойчивую САУ?
4. Что называется запасом устойчивости по модулю?
5. Что называется запасом устойчивости по фазе?
6. В чем особенность определения запасов устойчивости для клювообразных САУ?
7. Как влияет коэффициент усиления САУ на запасы устойчивости?
8. Чему соответствуют на АФЧХ пересечение ЛАЧХ оси w?
9. Чему соответствуют на АФЧХ пересечение ЛФЧХ значения j = -p?
10. Что называется частотой среза?
11. Сформулируйте критерий Найквиста для логарифмических характеристик.
12. В чем особенность логарифмических характеристик, если АФЧХ имеет
клювообразный характер?

Смотреть все

Поделись лекцией и получи скидку!

Заполни поля, отправь лекцию и мы вышлем тебе скидку-промокод на Автор24

Предмет

Название лекции

Авторы

Описание

Другие Технические предметы

Высшая математика
Электроника, электротехника, радиотехника
Программирование
Информационные технологии
Информатика
Физика
Архитектура и строительство
Теория вероятностей
Метрология
Машиностроение
Теплоэнергетика и теплотехника
Автоматизация технологических процессов
Автоматика и управление
Гидравлика
Транспортные средства
Металлургия
Сопротивление материалов
Технологические машины и оборудование
Информационная безопасность
Материаловедение

Источник

Статическая и динамическая ошибки регулирования. Качество регулирования сау

Главная задача систем регулирования состоит в том, чтобы стабилизировать параметры процесса на заданном уровне при воздействии внешних возмущающих воздействий, действующих на объект управления. Этим занимаются системы автоматической стабилизации. Другой не менее важной задачей является задача обеспечения программного перехода на новые режимы работы. Решение этой проблемы осуществляется с помощью той же системы стабилизации, задание которой изменяется от программного задатчика.

Структурная схема одноконтурной системы АР объектом управления приведена на рис.1. Основными элементами ее являются: АР — автоматический регулятор, УМ — усилитель мощности, ИМ — исполнительный механизм, РО — регулируемый орган, СОУ — собственно объект управления, Д — датчик, НП — нормирующий преобразователь, ЗД — задатчик, ЭС — элемент сравнения.

Переменные: Yз — задающий сигнал, e — ошибка регулирования, U P — выходной сигнал регулятора, U y — управляющее напряжение, h — перемещение регулирующего органа, Q r — расход вещества или энергии, F — возмущающее воздействие, T — регулируемый параметр, Y ОС — сигнал обратной связи (выходное напряжение или ток преобразователя).

Нормирующий преобразователь выполняет следующие функции:

преобразует нестандартный сигнал датчика в стандартный выходной сигнал;
осуществляет фильтрацию сигнала;
осуществляет линеаризацию статической характеристики датчика с целью получения линейного диапазона.

Для расчетных целей исходную схему упрощают до схемы, показанной на рис.2, где АР — регулятор, ОУ — объект управления.

Выбор канала регулирования

Одним и тем ж выходным параметром объекта можно управлять по разным входным каналам.

При выборе нужного канала управления исходят из следующих соображений:

Из всех возможных регулирующих воздействий выбирают такой поток вещества или энергии, подаваемый в объект или отводимый из него, минимальное изменение которого вызывает максимальное изменение регулируемой величины, то есть коэффициент усиления по выбранному каналу должен быть, по возможности, максимальным. Тогда, по данному каналу можно обеспечить наиболее точное регулирование.
Диапазон допустимого изменения управляющего сигнала должен быть достаточен для полной компенсации максимально возможных возмущений, возникающих в данном процессе, то есть должен быть обеспечен запас по мощности управления в данном канале.
Выбранный канал должен иметь благоприятные динамические свойства, то есть запаздывание t
0 и отношение t
0 /T 0 , где T 0 — постоянная времени объекта, должны быть как можно меньшими. Кроме того, изменение статических и динамических параметров объекта по выбранному каналу при изменении нагрузки или во времени должны быть незначительными.

Основные показатели качества регулирования

К автоматическим системам регулирования предъявляются требования не только по устойчивости процессов регулирования во всем диапазоне нагрузок на объект, но и по обеспечению определенных качественных показателей процесса автоматического регулирования.Ими являются:

Ошибка регулирования (статистическая или среднеквадратическая составляющие).
Время регулирования.
Перерегулирование.
Показатель колебательности.

Динамический коэффициент регулирования R d , который определяется из формулы

где смысл величин Y 0 и Y 1 ясен из рис.3.

Величина R d характеризует степень воздействия регулятора на процесс, то есть степень снижения динамического отклонения в системе с регулятором и без него.

Величина перерегулирования зависит от вида отрабатываемого сигнала. При отработке ступенчатого воздействия по сигналу задания величина перерегулирования определяется по формуле

где значения величин X m и X y показаны на рис.4.

При отработке возмущающего воздействия величина перерегулирования определяется из соотношения

где значения величин X m и X y показаны на рис.5

Время регулирования
— это время, за которое регулируемая величина в переходном процессе начинает отличаться от установившегося значения менее, чем на заранее заданное значение b
, гдеb
— точность регулирования. Настройки регулятора выбираются так, чтобы обеспечить либо минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.

В некоторых системах АР наблюдается ошибка, которая не исчезает даж по истечении длительного интервала времени — это статическая ошибка регулирования
-e
с.

У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретически равны нулю, но практически незначительные ошибки могут существовать из-за наличия зон нечувствительности в элементах системы.

Показатель колебательности M
характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса)и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на графике рис.6.

Условно считается,что значение М=1,5ё
1,6 является оптимальным для промышленных систем, так как в этом случае s
обеспечивается в пределах от 20 до 40%. При увеличении M колебательность в системе возрастает.

В некоторых случаях нормируется полоса пропускания системы w
п, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.

При настройке регуляторов можно получить достаточно большое число переходных процессов, удовлетворяющих заданным требованиям. Таким образом, появляется некоторая неопределенность в выборе конкретных значений параметров настройки регулятора. С целью ликвидации этой неопределенности и облегчения расчета настроек вводится понятие оптимальных типовых процессов регулирования.

Выделяют три типовых процесса:

где e — ошибка регулирования.

К достоинствам этого процесса можно отнести высокое быстродействие (1-й полуволны) при довольно значительной колебательности. Кроме этого, оптимизация этого критерия по параметрам настройки регулятора может быть выполнена аналитически, численно или путем моделирования (на АВМ).

Типовая структурная схема регулятора

Автоматический регулятор (рис.10) состоит из: ЗУ — задающего устройства, СУ — сравнивающего устройства, УПУ — усилительно-преобразующего устройства, БН — блока настроек.

Задающее устройство должно вырабатывать высокостабильный сигнал задания (установку регулятора) либо изменять его по определенной программе. Сравнивающее устройство позволяет сопоставлять сигнал задания с сигналом обратной связи и тем самым сформировать величину ошибки регулирования e p . Усилительно-преобразующее устройство состоит из блока формирования алгоритма регулирования, блока настройки параметров этого алгоритма и усилителя мощности.

Классиффикация регуляторов

Автоматические регуляторы классифицируются по назначению, принципу действия, конструктивным особенностям, виду используемой энергии, характеру изменения регулирующего воздействия и т.п.

По принципу действия они подразделяются на регуляторы прямого и непрямого действия. Регуляторы прямого действия не используют внешнюю энергию для процессов управления, а используют энергию самого объекта управления (регулируемой среды). Примером таких регуляторов являются регуляторы давления. В автоматических регуляторах непрямого действия для его работы требуется внешний источник энергии.

По роду действия регуляторы делятся на непрерывные и дискретные. Дискретные регуляторы, в свою очередь, подразделяются на релейные, цифровые и импульсные.

По виду используемой энергии они подразделяются на электронные, пневматические, гидравлические, механические и комбинированные. Выбор регулятора по виду используемой энергии определяется характером объекта регулирования и особенностями автоматической системы.

По закону регулирования они делятся на двух-и трехпозиционные регуляторы, типовые регуляторы (интегральные, пропорциональные, пропорционально-дифференциальные, пропорционально- интегральные и пропорционально- интегрально- дифференциальные регуляторы — сокращенно И, П, ПД, ПИ и ПИД-регуляторы), регуляторы с переменной структурой, адаптивные (самонастраивающиеся) и оптимальные регуляторы. Двухпозиционные регуляторы нашли широкое распространение благодаря своей простоте и малой стоимости.

По виду выполняемых функций регуляторы подразделяются на регуляторы автоматической стабилизации, программные, корректирующие, регуляторы соотношения параметров и другие.

Выбор типа регулятора

Задача проектировщика состоит в выборе такого типа регулятора, который при минимальной стоимости и максимальной надёжности обеспечивал бы заданное качество регулирования.

Для того чтобы выбрать тип регулятора и определить его настройки, необходимо знать:

Статические и динамические характеристики объекта управления.
Требования к качеству процесса регулирования.
Показатели качества регулирования для серийных регуляторов.
Характер возмущений,действующих на процесс регулирования.

Выбор типа регулятора обычно начинается с простейших двухпозиционных регуляторов и может заканчиваться самонастраивающимися микропроцессорными регуляторами.

Рассмотрим показатели качества серийных регуляторов. В качестве серийных предполагаются непрерывные регуляторы, реализующие законы управления И, П, ПИ и ПИД.

Теоретически, с усложнением закона регулирования качество работы системы улучшается. Известно, что на динамику регулирования наибольшее влияние оказывает величина отношения запаздывания к постоянной времени объекта с. Эффективность компенсации ступенчатого возмущения регулятором достаточно точно может характеризоваться величиной динамического коэффициента регулирования R d , а быстродействие — величиной времени регулирования. Теоретически, в системе с запаздыванием минимальное время регулирования t pvin =2/.

Минимально возможное время регулирования для различных типов регуляторов при оптимальной их настройке определяется таблицей 1.

Таблица 1

Руководствуясь таблицей, можно утверждать, что наибольшее быстродействие обеспечивает закон управления П. Однако, если коэффициент усиления П-регулятора KP мал (чаще всего это наблюдается в системах с запаздыванием), то такой регулятор не обеспечивает высокой точности регулирования, так как в этом случае велика величина статической ошибки. Если KP имеет величину равную 10 и более, то П-регулятор приемлем, а если KP<10 то требуется введение в закон управления интегральной составляющей.

Наиболее распространенным на практик является ПИ-регулятор, который обладает следующими достоинствами:

Обеспечивает нулевую статическую ошибку регулирования.
Достаточно прост в настройке, так как настраиваются только два параметра, а именно коэффициент усиления K P и постоянная интегрирования T i . В таком регуляторе имеется возможность оптимизации K p /T i >max, что обеспечивает управление с минимально возможной среднеквадратичной ошибкой регулирования.
Обладает малой чувствительностью к шумам в канале измерения (в отличие от ПИД-регулятора).

Для наиболее ответственных контуров можно рекомендовать использование ПИД-регулятора, обеспечивающего наиболее высокое быстродействие в системе. Однако следует учитывать, что это условие выполняется только при его оптимальных настройках (настраиваются три параметра). С увеличением запаздывания в системе резко возрастают отрицательные фазовые сдвиги, что снижает эффект действия дифференциальной составляющей регулятора. Поэтому качество работы ПИД-регулятора для систем с большим запаздыванием становится сравнимо с качеством работы ПИ-регулятора. Кроме этого, наличие шумов в канале измерения в системе с ПИД-регулятором приводит к значительным случайным колебаниям управляющего сигнала регулятора,что увеличивает дисперсию ошибки регулирования. Таким образом, ПИД-регулятор следует выбирать для систем регулирования с относительно малым уровнем шумов и величиной запаздывания в объекте управления. Примерами таких систем являются системы регулирования температуры.

При выборе типа регулятора рекомендуется ориентироваться на величину отношения запаздывания к постоянной времени в объекте t
/T. Если t
/T< 0,2, то можно выбрать релейный, непрерывный или цифровой регуляторы. Если 0,2 < t
/T< 1, то должен быть выбран непрерывный или цифровой, ПИ или ПИД-регулятор. Если t
/T >1, то выбирают специальный цифровой регулятор с упредителем, который компенсирует запаздывание в контуре управления. Однако этот ж регулятор рекомендуется применять и при меньших отношениях t
/T.

Формульный метод определения настроек регулятора

Метод используется для быстрой приближенной оценки значений параметров настройки регулятора для трех видов оптимальных типовых процессов регулирования.

Метод применим как для статических объектов с самовыравниванием (таблица 2), так и для объектов без самовыравнивания (таблица 3).

Примечание:T,t
,K оу — постоянная времени, запаздывание и коэффициент усиления объекта.

В этих формулах предполагается, что настраивается регулятор с зависимыми настройками, передаточная функция которого имеет вид:

где:
K p — коэффициент усиления регулятора;
T i -время изодрома (постоянная интегрирования регулятора);
T d -время предварения (постоянная дифференцирования).

Расчёт настроек по частотным характеристикам объекта

Существует специальная аппаратура для экспериментального определения амплитуднофазовой характеристики (АФХ) объекта управления: Эту характеристику можно использовать для расчета настроек ПИ-регулятора, гд главным критерием является обеспечение заданных запасов устойчивости в системе.

Запасы устойчивости удобно характеризовать показателем колебательности системы M, величина которого в системе с ПИ-регулятором совпадает с максимумом амплитудно-частотной характеристики замкнутой системы. Для того чтобы этот максимум не превышал заданной величины, АФХ разомкнутой системы не должна заходить внутрь окружности с центром P 0 и радиусом R, где

Можно доказать, что оптимальными по минимуму среднеквадратичной ошибки регулирования настройками будут такие, при которых система с показателем колебательности MЈ
M 1 будет иметь наибольший коэффициент при интегральной составляющей, чему соответствует условие K p /T i >min.

В связи с этим расчет оптимальных настроек состоит из двух этапов:

Нахождение в плоскости параметров K p и T i , границы области, в которой система обладает заданным показателем колебательности M 1 .
Определением на границе области точки, удовлетворяющей требованию K p /T i .

Расчёт настроек по частотным характеристикам объекта. Методика расчёта настроек ПИ регулятора по АФХ объекта

Экспериментальные методы настройки регулятора

Для значительного числа промышленных объектов управления отсутствуют достаточно точные математические модели, описывающие их статические и динамические характеристики. В то ж время проведение экспериментов по снятию этих характеристик весьма дорого и трудоемко.

Экспериментальный метод настройки регуляторов не требуют знания математической модели объекта. Однако предполагается, что система смонтирована и может быть запущена в работу, а также существует возможность изменения настроек регулятора. Таким образом, можно проводить некоторые эксперименты по анализу влияния изменения настроек на динамику системы. В конечном итоге гарантируется получение хороших настроек для данной системы регулирования.

Существуют два метода настройки — метод незатухающих колебаний и метод затухающих колебаний.

Метод незатухающих колебаний

В работающей системе выключаются интегральная и дифференциальная составляющие регулятора (T i =Ґ
,T d =0), то есть система переводится в закон регулирования П.

Путем последовательного увеличения K p с одновременной подачей небольшого скачкообразного сигнала задания добиваются возникновения в системе незатухающих колебаний с периодом T kp . Это соответствует выведению системы на границу колебательной устойчивости. При возникновении данного режима работы фиксируются значения критического коэффициента усиления регулятора K kp и периода критических колебаний в системе T kp . При появлении критических колебаний ни одна переменная системы не должна выходить на уровень ограничения.

По значениям T kp и K kp рассчитываются параметры настройки регулятора:

П-регулятор: K p =0,55 K kp ;
ПИ-регулятор: K p =0,45 K kp ; T i =T kp /1,2;
ПИД-регулятор: K p =0,6 K kp ; T i =T kp /2; T d =T kp /8.

Расчет настроек регулятора можно производить по критической частоте собственно объекта управления w
п. Учитывая, что собственная частота Ґ
п ОУ совпадает с критической частотой колебаний замкнутой системы с П-регулятором, величины T kp и K kp могут быть определены по амплитуд и периоду критических колебаний собственно объекта управления.

При выведении замкнутой системы на границу колебательной устойчивости, амплитуда колебаний может превысить допустимое значение, что в свою очередь приведет к возникновению аварийной ситуации на объекте или к выпуску бракованной продукции. Поэтому не все системы управления промышленными объектами могут выводиться на критический режим работы.

Метод затухающих колебаний

Применение этого метода позволяет настраивать регуляторы без выведения системы на критические режимы работы. Так же, как и в предыдущем методе, для замкнутой системы с П-регулятором путем последовательного увеличения KP добиваются переходного процесса отработки прямоугольного импульса по сигналу задания или возмущения с декрементом затухания D=1/4. Далее определяется период этих колебаний T k и значения постоянных интегрирования и дифференцирования регуляторов T i ,T d .

Для ПИ-регулятора:T i =T k /6;
Для ПИД-регулятора:T i =T k /6;T d =T k /1,5.

После установки вычисленных значений T i и T d на регуляторе необходимо экспериментально уточнить величину K P для получения декремента затухания D=1/4. С этой целью производится дополнительная подстройка K P для выбранного закона регулирования, что обычно приводит к уменьшению K P на 20 –30%. Большинство промышленных систем регулирования считаются качественно настроенными, если их декремент затухания D равен 1/4 или 1/5.

Регулирование при наличии шумов

Наличие высокочастотных шумовых составляющих в измерительном сигнале приводит к случайным колебаниям исполнительного механизма системы, что увеличивает дисперсию ошибки регулирования и снижает точность регулирования. В некоторых случаях сильные шумовые составляющие могут привести систему к неустойчивому режиму работы (стохастическая неустойчивость).

В промышленных системах в измерительных цепях часто присутствуют шумы, связанные с частотой питающей сети. В связи с этим важной задачей является правильная фильтрация измерительного сигнала, а также выбор нужного алгоритма и параметров работы регулятора. Для этого используются фильтры низкой частоты высокого порядка (5 –7), имеющие большую крутизну спада. Их иногда встраивают в нормирующие преобразователи.

Таким образом, главной задачей регулятора является компенсация низкочастотных возмущений. При этом, с целью получения минимальной дисперсии ошибки регулирования, высокочастотные помехи должны быть отфильтрованы. Однако, в общем случае, эта задача противоречивая, так как спектры возмущения и шума могут накладываться друг на друга. Это противоречие разрешается с помощью теории оптимального стохастического управления, которая позволяет добиться хорошего быстрод йствия в системе при минимально возможной дисперсии ошибки регулирования. Для уменьшения влияния помех в практических ситуациях применяются два способа, основанных на:

уменьшении коэффициента усиления регулятора K p , то есть, фактически, переход на интегральный закон регулирования, который малочувствителен к шумам;
фильтрации измеряемого сигнала.

Методы настройки двухсвязных систем регулирования

Из общего числа систем регулирования около 15% составляют двухсвязные системы регулирования (рис.11). В таких системах даже при наличии устойчивой автономной работы двух регуляторов вся система может стать неустойчивой за счет действия перекрестной связи в объекте управления.

Объект управления в двухсвязной системе представлен в Р-канонической форме. Удобство такого представления заключается в том, что путем активного эксперимента можно определить все передаточные функции по соответствующим каналам. Промежуточные сигналы x 1 , x 2 , x 3 , x 4 обычно недоступны для измерения, поэтому управление ведется по вектору выхода Y:

На практике довольно большое число систем являются двухсвязными. Для объективной настройки регуляторов двухсвязных систем формируется критерий качества вида:

где y 1 и y 2 — коэффициенты веса (штрафа), J1 и J 2 — критерии качества первого и второго контуров.

Путем перераспределения коэффициентов веса y 1 и y 2 можно выделить более важный контур, качество процессов управления в котором должно быть более высоким. Например, если первый контур должен обеспечивать более высокую точность работы, то y 1 требуется увеличить.

Задача настройки регулятора состоит в том, чтобы при заданных y 1 и y 2 обеспечить минимальное значение J 0 системы, где

Рассмотрим различные методы настройки регуляторов в двухсвязных системах.

Метод автономной настройки регуляторов

В этом случае настройка регуляторов Р 1 и Р 2 производится последовательно, без учета взаимных влияний контуров. Процедура настройки осуществляется следующим образом:

регулятор Р 2 переводится в ручной режим работы;
настраивается регулятор Р 1 так, чтобы критерий J 1 был минимален;
отключается настроенный регулятор Р 1 и включается регулятор Р 2 ;
настраивается Р 2 , обеспечивая минимум J 2 ;
оба регулятора включаются в работу.

наблюдается малое взаимное влияние контуров;
быстродействие одного контура значительно выше другого (контуры разнесены по частотам);
в перекрестных связях одна из передаточных функций имеет коэффициент передачи значительно меньше, чем другая, то есть наблюдается одностороннее влияние.

Метод итеративной настройки регуляторов

Этот метода аналогичен предыдущему, но здесь осуществляется многократная настройка регуляторов Р 1 и Р 2 (последовательная подстройка) с целью обеспечения минимального значения критерия качества J 0 всей системы.

Следует учитывать, что только метод итеративной настройки регуляторов обеспечивает качественную работу двухсвязной системы даж при наличии сильных перекрестных связей. Это объясняется тем, что оптимизация критерия качества J 0 системы происходит при включенных Р 1 и Р 2 .

Данный метод часто применяется при аналоговом и цифровом моделировании двухсвязных систем, так как в реальных условиях он весьма трудоемок.

Метод аналитического конструирования регуляторов

Этот метод позволяет синтезировать многомерный регулятор, учитывающий в своей структуре взаимосвязь переменных в объекте управления. Синтез ведется с помощью методов теории оптимального или модального управления при описании объекта в пространстве состояний.

Структурная схема оптимального регулятора состояния, содержащего наблюдающее устройство, приведена на рис.12. Схема содержит следующие элементы: Н — наблюдатель, ОУ — объект управления, МОУ — модуль объекта управления, ОРС — оптимальный регулятор состояния, Е Н — ошибка наблюдения, X М — вектор состояния модели, X зад.- вектор задания, U — вектор входа ОУ, Y — вектор выхода ОУ, Y М — вектор выхода модели.

Оптимальный регулятор состояния, являясь наиболее совершенным типом регулятора, требует измерения всех компонентов вектора состояния объекта. Для получения их оценок (x) используется динамическая модель объекта (цифровая или аналоговая), подключенная параллельно исходному ОУ. Для обеспечения равенства движений в реальном объекте и модели используется наблюдатель, который, сравнивая движения векторов Y и Y М, обеспечивает их равенство (E H >0). Параметры регулятора состояния рассчитываются методамианалитического конструирования регуляторов путем минимизации интегрального квадратичного критерия качества

где Q и R — матрицы штрафов (весов) на компоненты вектора состояния и вектора управления.

За основу публикации взят курс лекций, читаемый профессоромВ.М.Мазуровым на каферде АТМ Тульского государственного университета

Входной сигнал x
(t
)=
X
=
const
и изображением его является.
В соответствии с (1.56) статическую ошибкуε
СТ
следует вычислять по
формуле

(1.57)

1). Пусть в (1.57) значение порядка ν
астатизма САУ равно нулю:ν=0
. Такая
САУ называется статической. Тогда
статическая ошибкаε
СТ
будет равна

В статической САУ имеется статическая
ошибка ε
СТ
, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияК
разомкнутой САУ, но обратить в ноль ее
нельзя.

2). Пусть в (1.57) значение порядка ν
астатизма САУ равно 1:ν=1
. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаε
СТ
будет равна

В астатической САУ 1-го порядка статическая
ошибка ε
СТ
равна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1
, статическая ошибка регулирования
всегда будет нулевой.

Расчеты скоростной ошибки εСт регулирования

Входной сигнал x
(t
)=
Vt
и изображением его является
.
В соответствии с (1.56) скоростную ошибкуε
СК
следует вычислять по
формуле

(1.58)

1). Пусть в (1.58) значение порядка ν
астатизма САУ равно нулю:ν=0
. Такая
САУ называется статической. Тогда
скоростная ошибкаε
СК
будет равна

В статической САУ скоростная ошибка
ε
СК
бесконечно большая
и, поэтому, такая САУ неработоспособна.

2). Пусть в (1.58) значение порядка ν
астатизма САУ равно 1:ν=1
. Такая САУ
называется астатической 1-го порядка.
Тогда скоростная ошибкаε
СК
будет равна

В астатической САУ 1-го порядка имеется
скоростная ошибка ε
СК
,
которую можно только уменьшить путем
увеличения общего коэффициента усиленияК
разомкнутой САУ, но обратить в
ноль ее нельзя.

3). Пусть в (1.58) значение порядка ν
астатизма САУ равно 2:ν=2
. Такая САУ
называется астатической 2-го порядка.
Тогда скоростная ошибкаε
СК
будет равна

В астатической САУ 2-го порядка скоростная
ошибка ε
СК
равна нулю,
т.е САУ является абсолютно точной.

Выводы по расчетам статической и скоростной ошибок регулирования:

1. Ошибки регулирования могут быть
уменьшены путем увеличения общего
коэффициента усиления К
и порядка
астатизмаν
разомкнутой САУ.

2. При увеличении К
ошибки регулирования
только уменьшаются. но не обращаются в
ноль.

3. При увеличении ν
САУ становится
абсолютно точной — ошибка регулирования
становится нулевой.

Косвенные
показатели качества САУ и их связь с
прямыми показателями качества.
Использование ЛАЧХ для оценки качества
САУ

Невозможность получения формул для
расчета динамических показателей
качества (рис.1.42), а также требования
задач синтеза САУ, обусловило разработки
комплексных показателей качества.
Косвенные показатели качества, в
большинстве своем, являются частотными,
которые определяются из ЧХ, АЧХ, ФЧХ и
ЛАЧХ. Косвенные показатели качества
должны удовлетворять следующим
требованиям:

1. Косвенные показатели должны просто
вычисляться или определяться из частотных
характеристик разомкнутой САУ.

2. Погрешность определения значений
прямых показателей качества через
значения косвенных показателей качества
должна быть мала.

3. Косвенные показатели должны быть
приспособлены для эффективного решения
задач синтеза САУ.

4
.
Косвенные показатели должны давать
возможность просто анализировать
влияние параметров настроек регуляторов
САУ и характеристик любых других звеньев
САУ на прямые показатели качества.

Косвенных показателей качества или их
наборов разработано достаточно много.
Каждый косвенный показатель качества
или их набор вводятся для эффективного
решения конкретных типов задач
автоматического управления и, поэтому,
универсальных косвенных показателей
качества не существует в принципе. По
сути, косвенные показатели упрощают
анализ и синтез САУ, но прямые показатели
качества определяются через косвенные
всегда неточно.

Прежде всего рассмотрим набор косвенных
показателей качества, полученных из
построений Найквиста (см. тему 1.12):
частоту среза ω
СР
и запас
по фазеγ
. Частота срезаω
СР
просто определяется из ЛАЧХ (рис.1.41).
Запас по фазеγ
рассчитывается по
выражению ФЧХφ
(ω
) только при
одном значении частотыω
СР
:γ=φ
(ω
СР

).

Основой применения косвенных показателей
качества — частоты среза ω
СР
и запаса по фазеγ
— являются
графические зависимости (рис.14.1) между
косвенными и прямыми показателями
качества — перерегулированиемσ
,
временем первой установкиt
1
и временем переходного процессаt
ПП
.

По оси ординат отложены значения
перерегулирования σ
, в процентах
от установившегося значенияh
ycm
(рис.1.42). По оси временt
1
иt
ПП
записаны
формулы, по которым рассчитываютсяt
1
иt
ПП
в
зависимости от частоты срезаω
СР
.
Если из частотных характеристик
определены значения запаса по фазеγ
и частоты срезаω
СР
, то по
графикам можно определить значения
перерегулированияσ
, времени первой
установкиt
1
и времени переходного процессаt
ПП
.
Например, пусть заданы значенияγ=30
о
иω
СР
=1,5 с
-1
.
Тогда, согласно приведенным на рис.1.44
построениям, получим:

σ=19 %,

Найденные значения σ,
t
1
иt
ПП
не
являются точными. Этот факт, отражен на
рис.1.44 как «размытость» графиков.

По этим значениям σ
,t
1
иt
ПП
можно
построить примерный график переходного
процесса (рис.1.45). Как принято, косвенные
показатели качества выбираются такими,
чтобы найденные с их помощью оценки
прямых показателей качества имели бы
погрешность не более 10 %. Это вполне
приемлемо в инженерной практике.

Графические зависимости между косвенными
γ
иω
СР
и прямымиσ
,t
1
иt
ПП
показателями качества САУ, приведенные
на рис.1.44, можно описать в виде следующих
зависимостей пропорционального типа

Важная в практике эксплуатации САУ
задача определения влияния типовых
законов регулирования (пропорционального,
интегрального и дифференциального) на
прямые показатели качества чрезвычайно
эффективно решается с помощью введенных
косвенных показателей γ
иω
СР
.

Ч
астотный
метод синтеза следящей САУ (см. тему
1.23) основан на использовании косвенного
показателя качества – показателя
колебательностиМ
. Показателем
колебательностиМ
называется
величина, численно равная максимуму
нормированной АЧХ (рис.1.46). По значению
показателя колебательностиМ
можно
оценить величину перерегулированияσ
(рис.1.47).

Значение показателя колебательности
М
может быть найдено графически,
без вычислений АЧХ, при использовании
только годографа частотной характеристикиW
раз
(p
)
и, соответственно, ЛАЧХ разомкнутой
САУ. Именно такие построения положены
в основу расчета среднечастотного
участка желаемой ЛАЧХ при упомянутом
выше частотном синтезе следящей САУ.

Требования

САУ рулевого устройства.

привод должен обеспечивать перекладку
от -35˚ до +30˚ за 28с.

При полном ходе в течение 1 часа привод
должен обеспечить 350 перекладок.

Посты управления должны снабжаться
аксиометрами с точностью до 1º в ДП и
1,5º при α = ± 5º. При больших углах ± 2,5º

Требования к СЭЭС:

А) статические требования:

Ошибка регулирования частоты- менее 5%

Ошибка регулирования напряжения – от
-10 до +6%

Неравномерность распределения нагрузки
параллельно работающих генераторов:
не более 10% от мощности наибольшего
генератора или не более 25% от мощности
наименьшего генератора. Из двух вариантов
или выбирается меньший.

Б) динамические показатели

Заброс/провал частоты – не более 10% в
течение 5сек

Заброс/провал напряжения – не более
20% в течение 1,5сек

Требования ДАУ ГД

Регулятор
частоты должен быть всережимным,
допустимая регулировка частоты в
пределах от 40 до 115%

Не
должно быть временной задержки между
перемещением рукоятки на мостике и
началом разворота лопастей и частоты
вращения дизеля

Точность
поддержания частоты не хуже 1,5%

Должно
быть реализовано несколько постов
управления ГД и ВРШ, а именно с разных
постов, при наборе и сбросе хода, при
реверсе, при управлении ВГ, когда он
включен в судовую сеть

Пуск
реверсивной характеристики ГД должны
быть соизмеримы с квалифицированным
ручным управлением

Перечислите
типовые позиционные, интегрирующие и
дифференцирующие звенья САУ и приведите
их примеры из судовых систем автоматики.
Укажите передаточные функции и
переходные характеристики этих звеньев.

Виды типовых позиционных звеньев:

1. Безинерционное (пропорциональное)
звено
имеет передаточную функцию и
описывается алгебраическим уравнением,
соответственно, вида
W
(p
)=
k
,

y
=
kx

Примерами безинерционных звеньев служат
рычажная передача (рис.1.10а),
потенциометрический датчик перемещения
(рис.1.10б).

В этих звеньях выходной сигнал у
повторяет без задержки по форме входной
сигналх
.

Выражение переходного процесса y
=
kx

2. Апериодическое (инерционное) звено
1-го порядка
имеет передаточную функцию
и описывается уравнением вида

где k
, Т —
коэффициент
передачи и постоянная времени звена.

Примерами этого звена служат интегрирующая
RC
—
цепь (рис.1.11а),
«электродвигатель, обмотки которого
разогреваются во время работы (рис.1.11б).

Выполним вывод передаточной функции
для RC
—
цепи. Используя
закон Ома, получим

Переходный процесс описывается
выражением

где вместо x
=1(t
)
,
как должно быть для переходного процесса,
принято фактическое значение сигналаx
, благодаря чему
рассчитывается реакция звена на скачок
произвольной величины.

График переходного процесса приведён
на рис.1.11в. Установившееся значение
y
уст
, равноеkx
, достигается на
бесконечности:t

.
Время переходного процессаt
пп
,
определяемое по моменту окончательного
вхождения графика в 5% зону допуска оту
уст
, составляет3
T
.
Звено обладаетсамовыравниванием
.
Свойство самовыравнивания состоит в
том, что звено самостоятельно без
применения дополнительного регулирования
приходит к постоянному по величине
установившемуся значению.

3
.
Инерционное звено 2-го порядка
имеет
передаточную функцию

Особенность звена в том, что его
характеристическое уравнение имеет
действительные корни.

Примерами этого звена служит RLC
-цепь
(рис.1.13а) при большом сопротивленииR
резистора
,
электропривод, приводящий во вращение
нагрузку с большим моментом инерцииJ
(рис.6.4б).

Переходный процесс описывается выражением

где с
1

и с
2

— постоянные интегрирования.

Г
рафик
переходного процесса (рис.1.14а) имеет
точку перегиба. Время переходного
процессаt
пп
можно определить только графически.

4. Колебательное звено
имеет
передаточную функцию

где T
— период свободных
(незатухающих) колебаний;

ξ
— параметр затухания,
принимающий значения0<
ξ
<1.

Особенность звена в том, что его
характеристическое уравнение имеет
комплексно сопряженные корни.

Примерами этого звена служит RLC
-цепь
(рис.1.13а) при малом сопротивленииR
резистора
,
электропривод, приводящий во вращение
нагрузку с малым моментом инерцииJ
(рис.1.13б). Переходный процесс описывается
выражением

где

— резонансная частота с учётом затухания
колебаний.

График переходного процесса приведён
на рис.1.14б. Чем меньше значение параметра
ξ
, тем медленнее
затухает переходный процесс. Время
переходного процесса можно определить
только графически.

Статическая ошибка относится к состоянию покоя системы. Она складывается из ошибки в сель-синной связи, ошибки из-за наличия внутренних моментов сопротивления в сельсине-приемнике и гидроусилителе, от перестановочных усилий, прилагаемых к золотникам и промежуточным усилителям, люфтов и и деформаций рычажной системы передач и внешних моментов сил сопротивлений, связанных с трением в направляющем аппарате турбины.
Статическая ошибка зависит как от коэффициента усиления контура регулирования положения, так и от жесткости статических механических характеристик системы при разомкнутой связи по положению. В рассматриваемой системе, оптимизированной методом последовательной коррекции, жесткость р ам зависит от отношения рГм / йсСтТ, поэтому уменьшение ап, ас и ат снижает статическую ошибку как за счет возрастания коэффициента усиления, так и за счет увеличения жесткости Рзам — В соответствии с (11 — 32) статическая ошибка может быть полностью устранена использованием двукратноинтегри-рующего контура регулирования скорости при ИП-регу-ляторе скорости.
Статическая ошибка — отклонение регулируемого давления от заданного при установившемся режиме, также называют неравномерностью регулирования.
Газоанализатор инфракрасного поглощения ГИГ1 — 7М. Статическая ошибка — разность между истинной величиной регулируемого параметра и показаниями датчика — должна быть не больше допустимой.
Статическая ошибка пропорциональна значению постоянного внешнего воздействия.
Статическая ошибка будет равна нулю, если система будет астатической относительно задающего воздействия и возмущения. А для этого нужно, чтобы регулятор содержал интегрирующее звено.
Статическая ошибка будет равна нулю, если система будет астатической.
Статическая ошибка уменьшается с ростом коэффициента усиления регулятора КР Kj. Формулы (2.2) и (2.3) справедливы для статического объекта с П — или ПД — регулятором.
Пропорциональный регулятор давления прямого действия. [ IMAGE ] — 4. Статическая характеристика П — регулятора. Статическая ошибка у серийных промышленных регуляторов составляет 5 — 15 % и зависит от величины настроечного параметра / Ср. Наличие статической ошибки (остаточной неравномерности) является существенным недостатком пропорциональных регуляторов, который ограничивает область их применения, несмотря на хорошие показатели качества регулирования. На рис. 15 — 5 показаны графики процесса регулирования в АСР давления, состоящей из П — регулятора прямого действия (рис. 15 — 3) и трубопровода, который можно рассматривать как статический объект первого порядка.
Статическая ошибка, вследствие наличия зоны нечувствительности, здесь имеется, несмотря на то, что по отношению к возмущающему воздействию, как видно из уравнения (34.7), система является астатической.
Пропорциональный регулятор. а — структурная схема, б — переходные процессы в замкнутой системе с П — регулятором. Статическая ошибка — отличительная особенность П — регуляторов и главный их недостаток, так как в реальных условиях при частых изменениях нагрузок и других возмущениях система с П — регулятором не выдерживает точно заданной величины.
Интегральный регулятор.
Статическая ошибка является отличительной особенностью П — ре-гуляторов и главным их недостатком, так как в реальных условиях при частых изменениях нагрузок и других возмущениях система с П — регулятором не выдерживает точно заданной величины, хотя и близка к заданному значению.
Статические ошибки, сеточный ток в первом каскаде усилителя, дрейф нуля, неточные величины сопротивлений входной цепи и цепи обратной связи также оказывают существенное влияние на работу усилителя.
Статическая ошибка не превышает 0 013 мм. Устройство управления имеет 250 электронных ламп и 175 электромеханических реле. Для привода рабочих органов станка применены электродвигатели мощностью 0 55 кет.
Статическая ошибка определяется как среднее значение регулируемого параметра за весь цикл.
Статическая ошибка в незамкнутых системах регулирования дозаторов при соответствии фактических характеристик материала и дозатора расчетным может возникать из-за несоответствия Wp (0) и W0, в (0) на большей или меньшей части рабочей характеристики.
Статическая ошибка является отличительной особенностью П — ре-гуляторов и главным их недостатком, так как в реальных условиях при частых изменениях нагрузок и других возмущениях система с П — ре-гулятором не выдерживает точно заданной величины, хотя и близка к заданному значению.
Статические ошибки от неточности изготовления сельсинов обусловлены, также как и у ВТ, асимметрией магнитопровода, наличием короткозамкнутых витков, эксцентриситетом, неравенством параметров фаз обмотки синхронизации.
Статическая ошибка таких систем определяется зоной нечувствительности. Диапазоны изменений параметров настройки систем весьма ограничены. Зона нечувствительности ограничена допустимой статической ошибкой; скорость перемещения регулирующего органа меняется ступенчато и определяется конструктивными параметрами (табл. 2 — 1) исполнительного механизма и регулирующего органа регулятора.
Статическая ошибка слагается из двух составляющих. Основная составляющая — неравномерность регулирования, зависящая от величины нагрузки в статической системе и равная нулю 6 — 1 График, иллюстрирующий в астатической.
Статическая ошибка обусловлена наличием трения в подвижных частях системы и люфтами. Динамическая ошибка Один определяется углом рассогласования при повороте датчика на ограниченный угол или при его вращении. Динамическая ошибка возникает как результат действия сил инерции и в значительной мере зависит от скорости задания входной величины — угла поворота. Чем быстрее изменяется входная величина, тем больше динамическая ошибка.
Переходные функции силы тока, частоты вращения двигателя и приращения длины петли при изменении. Статическая ошибка при ступенчатом изменении скорости секции / (vj и сигнала, задающего скорость линии (v3), равна: 6vl 8V3 0 при ПИ-регуляторе и Svl 8V3 2тп при П — регуляторе.
Эллиптичность в расточке статора.| Влияние ко-роткозамкнутого витка в магнитопроводе на погрешности трансформаторной синхронной передачи. Статические ошибки из-за неточности изготовления сельсинов обусловлены: асимметрией магнитопровода, наличием коротко-замкнутых витков, эксцентриситетом, неравенством параметров фаз обмотки синхронизации.
Статическая ошибка 8ст в реальных системах увеличи вается с ростом статического момента на валу двигател.

Статическая ошибка, равная AU, характеризует чувствительность блока сравнения. Оценка динамических свойств блока сравнения зависит от режима его работы.
Статическая ошибка ест х — ууст, где х — входная величина. Время достижения первого максимума tM определяется по графику. Время tp соответствует последней точке пересечения y (t) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать допустимого отклонения от установившегося значения. Обычно допустимое отклонение принимается равным 5 % от установившегося значения: А 5 % ууст.
Статическая ошибка равна статизму только при номинальной нагрузке.
Статическая ошибка САР с И-регулятором теоретически равна нулю. Использование их в объектах без самовыравнивания приводит к структурно неустойчивым системам.
Статическая ошибка едоо О, если система обладает астатиз-мом 1-го порядка (у 1) относительно задающего воздействия.
Статическая ошибка привода, возникающая при отказе канала, не превышает текущего рассогласования между каналами.
Статическая ошибка сельсинов может быть разложена на несколько пространственных гармоник. Она вызывается главным образом эллиптичностью статора. Другой общей гармоникой магнитного потока в пространстве является шестая гармоника, обусловливаемая распределением трех фаз обмоток — неравными полными сопротивлениями обмоток и проводов, соединяющих сельсины. Следующая имеющаяся гармоника равна числу пазов в роторе или в статоре, или двойному числу пазов, и вызывается несинусоидальным распределением потока вследствие неравномерности магнитного сопротивления пазов, а также изменяющегося активного или магнитного сопротивлений самих обмоток.
Зависимости AcoiM. lKC. Здесь статическая ошибка равна нулю, но максимум динамической ошибки, отнесенной к статической ошибке в однократнопнтегрпрующей системе, оказывается постоянно близким к единице.
Статическая ошибка следящей системы складывается из двух составляющих, обусловленных действием iWCT и Д1 / с. Каждая из этих составляющих должна равняться такой величине ошибки, при которой достигается компенсация соответствующего внешнего воздействия.
Аксиально-поршневой насос с регулятором мощности прямого действия.| Автоматический регулятор мощности насоса непрямого действия 284. Статическая ошибка регулятора прямого действия существенно зависит от силы, возникающей со стороны регулирующего органа насоса, в частности, наклонной шайбы. Сила трения на регулирующем органе нассса приводит к петлевой статической характеристике регулятора прямого действия. Снизить влияние нагрузки на регулятор можно, увеличив эффективную площадь плунжера и соответственно жесткость пружинного блока. Однако из-за этого во многих случаях габаритные размеры регулятора мощности прямого действия значительно увеличиваются.
Статическую ошибку при постоянном возмущении у получают, предполагая, что на линейную систему при нулевых начальных условиях действует возмущающий момент в виде единичного скачка.
Статической ошибкой называется отклонение заданного значения регулируемой величины в установившемся режиме в связи с изменением величины нагрузки. Регуляторы, не устраняющие такой ошибки, называются статическими.
Статической ошибкой называют угол рассогласования оси ротора нагруженного ЩД в режиме фиксированного останова под током по отношению к направлению вектора МДС, который может быть в пределе равен отрицательной части зоны Эсу.

Статической ошибкой САР называется значение отклонения регулируемой величины (или ее среднего значения) от заданного значения в установившемся режиме.
Характеристика астатического регулирования.| Характеристика статического регулирования. Абсолютной статической ошибкой называют разность между каким-либо установившимся значением регулируемой величины и ее номинальным значением.
Чтобы статическая ошибка была равна нулю при действии возмущения, регулятор должен включать одно интегрирующее звено.
Термин статическая ошибка, применявшийся в начале для следящих систем по положению, был затем распространен на более широкий класс систем управления.
Хотя статическая ошибка имеет главенствующее значение, следует учитывать и динамические ошибки сельсинов. Они вызываются тем, что магнитные потоки, создающиеся в сельсинах, пересекаются обмоткой ротора. Если соединить сельсин-датчик с сельсин-трансформатором при нулевом положении и возбудить сельсин-датчик от источника переменного тока обычным образом, то выходная величина сельсин-трансформатора будет равна нулю, при отсутствии статической ошибки и остаточного напряжения в машинах. Это будет справедливо для любого углового положения соединенных валов.
Если статическая ошибка Дл: 0 во всей зоне регулирования, то такие регуляторы называются астатическими, если Д О, то статическими. Следовательно, астатическими регуляторами называются такие, у которых при различных постоянных значениях внешнего воздействия на объект (например, изменение нагрузки) отклонение регулируемой величины от заданного значения по окончании процесса регулирования становится равным нулю.
Если статическая ошибка САР в состоянии покоя равна пулю для любых внешних возмущений, то система называется астатической. К астатическим системам мы также отнесем системы, в которых статическая ошибка меньше некоторой наперед заданной величины зоны нечувствительности и не зависит от величин приложенных возмущений. Если статическая погрешность САР в состоянии покоя отлична от нуля и зависит от величины внешних воздействий, то система называется статической.
Когда статическая ошибка магнитного компаса заведомо велика, азимутальную коррекцию по магнитной стрелке целесообразно отключать. Например, при использовании прибора на самолете азимутальную коррекцию при длительных виражах самолета отключают и определяют курс непосредственно по гироскопу направления. В качестве магнитного компаса в авиационных гиромагнитных компасах широко применяются феррозондовые датчики магнитного поля, рассмотренные выше.
Форма регулирующего периодического. Если статическая ошибка исследуемых цепей САР равна нулю, то регулируемые величины р2 и фз (рис. 4 — 5 а) будут совершать колебания около тех уровней, которые регуляторы 2 и 3 стремятся поддерживать при отсутствии гармонических колебаний. Это облегчает стабилизацию системы и в случае объектов без самовыравнивания позволяет построить частотные характеристики без нарушения технологического процесса.
Ввиду статической ошибки и наличия ограничений теряет смысл выбор параметров настроек П — регулято-ра с точки зрения минимальной среднеквадратичной ошибки, получения переходного процесса заданной формы или минимального времени регулирования.
Величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
Снятие статической ошибки, имеющей место в процессе регулирования пропорциональными регуляторами, достигается механизмом изодрома, который сообщает регулирующему органу дополнительное перемещение во времени.

К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления
.

Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику . Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).

Классификация показателей качества
состоит из нескольких групп:

прямые
— определяемые непосредственно по процесса,
корневые
— определяемые по корням характеристического полинома,
частотные
— по частотным характеристикам,
интегральные
— получаемые путем интегрирования функций.

Прямыми показателями качества процесса управления, определяемые непосредственно по
являются:

Yуст
,
Степень затухания ?
,
Время достижения первого максимума tmax
,
Ошибка регулирования Ест
(статистическая или среднеквадратическая составляющие),
Динамический коэффициент регулирования Rd
,

Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.

Рисунок 1 — Определение показателей качества по переходной характеристике

Установившееся значение выходной величины Yуст

Установившееся значение выходной величины Yуст
определяется по переходной характеристике,представленной на рис.1.

Степень затухания ?

Степень затухания ?
определяется по формуле:

где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.

Время достижения первого максимума tmax

Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.

Время регулирования tp

Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.

В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.

Качество любой системы регулирования в большой степени определяется величиной ошибки регулирования, равной разности между управляющим воздействием и регулируемой величиной Знание мгновенных значений ошибки в течении всего времени работы объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако на этапах проектирования таких знаний недостаточно. Поэтому разработаны другие критерии,

позволяющие оценивать показатели качества системы и более того обеспечивать необходимые свойства системе в процессе проектирования.

Все критерии и условно разделены на несколько групп:

К первой группе отнесены критерии, использующие для оценки качества величину статической ошибки

в различных типовых режимах.

Ко второй группе относятся критерии, определяющие величину запаса устойчивости

. Эти критерии позволяют почувствовать, как далеко от границы устойчивости находится система регулирования. Наиболее опасной для системы является колебательная граница устойчивости, когда пара комплексных корней характеристического уравнения попадает на мнимую ось комплексной плоскости. Это возникает в случае чрезмерного увеличения коэффициента усиления разомкнутой системы;

Третья группа критериев определяет быстродействие

систем регулирования. Под быстродействием понимается время реагирования системы на появление внешних воздействий. Быстродействие обычно оценивается по времени затухания переходного процесса в системе. Существуют и др. группы критериев .

8.1. Статическая точность систем регулирования

Статическая точность определяется на установившемся режиме, который наступает при времени t → ∞. Ошибка регулирования в этом случае называется статической и состоит из двух составляющих:

(1.113)

где − часть статической ошибки, определяемая управляющим воздействием g(t);

− часть статической ошибки, определяемая возмущающим воздействием f(t), рис.1.50.

Выполним анализ зависимостей величин статических ошибок для различных режимов изменения управляющего воздействия g(t) при наличии и отсутствия возмущения f(t):

1. В качестве первого типового режима рассмотрим установившееся состояние при постоянных значениях управляющего и возмущающего воздействий.

Пусть управляющее воздействие g(t) = g 0 , а возмущение f(t) = 0. Для расчета ошибки воспользуемся выражением для передаточной функции системы по ошибке

, (1.114)

где − передаточная функция разомкнутой системы.

. (1.115)

Рассмотрим пример.
Пусть регулятор и объект управления являются позиционными звеньями и имеют следующие передаточные функции:

, (1.116)

С учетом передаточных функций выражение (1.115) принимает вид

(1.117)

где − коэффициент передачи разомкнутой системы.

Из выражения (1.117) следует, что величина рассматриваемой ошибки зависит от коэффициента передачи . Для уменьшения ошибки необходимо увеличивать этот коэффициент. Однако необходимо помнить, что с увеличением коэффициента система приближается к границе устойчивости.

Если регулятор имеет передаточную функцию интегрирующего типа , (1.118)

то выражение (1.115) примет вид

Видно, что ошибка . Аналогичный результат получается и в случае, когда передаточная функция объекта управления представляется интегрирующим звеном.

Теперь рассмотрим случай, когда управляющее воздействие g(t) = 0, а возмущение f(t) = f 0 .

Для расчета ошибки воспользуемся выражением для передаточной функции системы, определяющей связь между ошибкой регулирования и действующим возмущением

. (1.119)

Для установившегося состояния можно записать

(1.120)

Опять рассмотрим пример.
Пусть регулятор и объект регулирования имеют передаточные функции, соответствующие выражениям (1.116). С учетом этого выражение (1.120) принимает вид

. (1.121)

Видно, что статическая ошибка больше нуля. Величина ошибки, как и в ранее рассмотренном примере (1.116) зависит в основном от коэффициента передачи разомкнутой системы.

Если применить регулятор интегрирующего типа (1.118), то из выражения (1.121) нетрудно понять, что в этом случае статическая ошибка равна нулю.

Из рассмотренных примеров следует, что статическая ошибка характерна для систем регулирования, у которых регулятор в своем составе не имеет интегрирующих звеньев. Далее можно записать полное выражение для статической ошибки (1.113)

2. В качестве второго типового режима для САР рассмотрим изменение управляющего воздействия с постоянной скоростью

g(t) = v*t, (1.122)

где v − постоянный коэффициент.

Этот режим применяется только в следящих системах и в системах программного регулирования.

Примем, что возмущения в системе отсутствуют, т. е. .

С учетом (1.122) выражение для расчета ошибки (1.115) запишется в виде

Применяя изображение Карсона − Хевисайда , можем записать окончательный вид выражения для расчета статической ошибки

Рассмотрим пример.
Пусть передаточные функции регулятора и объекта регулирования соответствуют выражениям (1.116). Тогда выражение для составляющей статической ошибки будет иметь вид

Видно, что составляющая ошибки стремится к бесконечности.

Если в качестве регулятора применить интегрирующее звено, то величина статической ошибки будет конечной:

где коэффициент называется добротностью системы по скорости.

Видно, что имеет место конечная величина ошибки, равная отношению заданной скорости к добротности системы. Данная ошибка называется скоростной. Системы регулирования, у которых регулятор и объект регулирования представлены позиционными звеньями, называют статическими. Если в качестве регулятора применяются интегрирующие звенья, то САР называют астатическими первого или второго порядка, в зависимости от количества интегрирующих звеньев в регуляторе.

Выполненный анализ показывает, что режим движения с постоянной скоростью не должен применяться к статическим системам, так как в установившемся состоянии величина статической ошибки стремится к бесконечности. Этот режим движения применим только к астатическим системам, которые имеют конечную величину статической ошибки, зависящей от добротности системы по скорости.

Случай, когда , а ранее рассматривался. Было показано, что, если регулятор системы содержит интегрирующее звено, то составляющая статической ошибки . Следовательно, в рассматриваемых астатических САР эта составляющая не формирует статическую ошибку.

3. Третьим типовым режимом, применяемым в САР, является движение по гармоническому закону:

G(t) = g max sin(ω k t),

где g max − максимальная величина управляющего воздействия g(t),

ω к − частота гармонического закона.

В данном анализе возмущающие воздействия могут отсутствовать или иметь постоянные значения. Случай постоянства возмущений приводит, как и в рассмотренных выше первом и втором типовых режимах, к появлению некоторой постоянной составляющей ошибки .

Запишем уже известное выражение для ошибки

В линеаризованной системе при гармоническом управляющем воздействии ошибка в установившемся режиме будет также изменяться по гармоническому закону с частотой ω = ω к, т.е.

Sin(ω k t+ψ).

Поэтому точность САР в этом режиме оценивается по амплитуде ошибки, которая может быть найдена по выражению

Так как предполагается, что х max << g max , то >> 1. Следовательно, можно записать, что

(1.123)

где − модуль частотной передаточной функции разомкнутой системы при частоте ω = ω k .

Формула (1.123) позволяет вычислить амплитуду ошибки в установившемся режиме. Для этого необходимо иметь либо аналитическое выражение для передаточной функции разомкнутой системы, либо экспериментальную амплитудно-частотную характеристику.

Выражение (1.123) позволяет сформулировать требования к АЧХ, которые необходимо выполнить при расчете систем регулирования для обеспечения заданной точности. Для этого по заданному значению амплитуды управляющего воздействия g max и допустимой амплитуде ошибки вычисляется требуемое значение А к = . Далее необходимо величину А к отложить на графике АЧХ при частоте ω = ω к. Полученная точка А к называется контрольной точкой. Для того, чтобы амплитуда ошибки в системе не превосходила допустимого значения линия АЧХ должна проходить не ниже контрольной точки А к.

8.2. Оценка запаса устойчивости и быстродействия САР

Оценку запаса устойчивости и быстродействия САР можно выполнить по виду кривой переходного процесса (рис.1.51), возникшего в результате приложения к системе типового внешнего воздействия.

В качестве такого воздействия обычно рассматривается единичный скачок. В этом случае кривую переходного процесса называют переходной характеристикой системы.

Переходная характеристика может строиться для регулируемой величины или для ошибки регулирования .

Склонность системы к колебаниям и запас устойчивости могут быть охарактеризованы величиной перерегулирования

σ % = / y(∞)*100% ,

где у(∞) − установившееся значение регулируемой величины, после завершения переходного процесса.

Считается, что запас устойчивости достаточен, если величина перерегулирования не превышает 10 ¸ 30 %. Быстродействие системы может определяться по длительности переходного процесса .

Рис.1.51. Кривая переходного процесса

Длительность переходного процесса определяется как время, протекающее от момента приложения на вход единичного скачка до момента, после которого имеет место неравенство

| y(t) − y(∞)| £ ∆,

где ∆ − заданная малая постоянная величина, представляющая собой допустимую ошибку, ∆ (.01 ¸ .05) у(∞) .

Иногда в дополнение к величине перерегулирования задается допустимое число колебаний, которое может наблюдаться в течение времени переходного процесса. Количество колебаний должно составлять 1¸3.

Необходимый запас устойчивости, и быстродействие системы достигается в процессе расчета САР. Для расчета широко применяются частотные и корневые критерии и показатели качества регулирования.

Под частотными критериями
понимают такие критерии, которые для оценки качества САР не опираются на формы переходных процессов, а используют для этого некоторые частотные свойства системы.

Частотные критерии наиболее разработаны для оценки запаса устойчивости. Запас устойчивости предлагается определять по удалению амплитудно-фазовой частотной характеристики разомкнутой системы (рис.1.52) от точки (− 1, 0). Для этого вводятся понятия запаса устойчивости поамплитуде (модулю) и запаса устойчивости по фазе.

Для общего случая условной устойчивости, изображенного на рис.1.52, запас устойчивости по амплитуде определяется расположением на вещественной оси комплексной плоскости точек и :

20 lg ; = 20 lg .

Запас устойчивости по амплитуде тем больше, чем больше и . В хорошо демпфированных системах величины и находятся в диапазоне 6 ¸ 20 дб. В случае абсолютной устойчивости имеет смысл только величина .

Запас устойчивости по фазе (Рис.1.52) характеризует удаление АФЧХ по дуге окружности единичного радиуса от точки с координатами (−1,j,0) и соответствует углу μ между отрицательным направлением действительной оси и лучом, проведенным через начало координат и точку пересечения годографа характеристики с окружностью единичного радиуса. Величина запаса устойчивости по фазе определяется по выражению μ = 180˚ + ψ, где ψ − аргумент (смещение, сдвиг по фазе) частотной передаточной функции разомкнутой системы, соответствующий амплитуде равной единице (точка b на рис.1.52).

В хорошо демпфированных системах запас по фазе составляет 30¸60˚.

Недостатком рассмотренного частотного критерия является то, что для определения запаса устойчивости необходимо задавать два числа: μ и .

Более удобно запас устойчивости определять по показателю колебательности

. Показателем колебательности называется максимальное значение ординаты М мах амплитудно — частотной характеристики замкнутой системы (рис.1.53) при начальной ординате, равной единице, т. е. относительная высота резонансного пика.

Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Допустимое значение для показателя колебательности определяется на основании опыта эксплуатации систем регулирования. Считается, что в хорошо демпфированных системах регулирования показатель колебательности не должен быть больше 1.1¸1.5. Однако, в отдельных случаях допускается величина М мах =2¸2.5 .

Корневые критерии качества
опираются на существующую связь характера и качества переходных процессов в системе автоматического регулирования от расположения корней характеристического уравнения на комплексной плоскости. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы посредством наложения условий на расположение корней характеристического уравнения. Заметим, что влиять на расположение корней можно только через коэффициенты характеристического уравнения:

Решение данного уравнения содержит — корней: Уже известно, что корни могут быть вещественными и комплексными типа = − α ± jb. Колебания в системе будут наблюдаться, если в решении характеристического уравнения будет присутствовать хотя бы один комплексный корень. Склонность системы к колебаниям может характеризоваться отношением мнимой части корня к его вещественной части Это отношение называют колебательностью

μ= . (1.125)

Если в решении характеристического уравнения присутствует несколько комплексных корней, то для определения колебательности системы

необходимо брать отношение (1.125) для тех корней, для которых это отношение наибольшее.

Колебательность системы связана с другим корневым показателем запаса устойчивости − затуханием. Рассмотрим эту связь. Комплексные сопряженные корни дают в выражении для переходного процесса, например для ошибки регулирования, член вида

x(t) = Ce – αt sin (bt+ψ).

Найдем затухание амплитуды синусоидального колебания за один период. При некотором времени t = t 1 эта амплитуда равна С 1 = Сe –α t . Через один период Т = 2π/b амплитуда С 2 = Сe – α (t 1 + 2π / b) = C 1 e — 2π α/ b = C 1 e -2π /μ .

Затуханием за период
называют величину

x =

Эта величина обычно выражается в процентах. Поставляя значение амплитуды С 2 , получаем x =1 − e −2 π / μ или μ = 2π / ln .

Обычно в системах автоматического регулирования допускается затухание за период не менее чем 90 ¸ 98 %. Так, например, если x = 98 %, то колебательность при этом составит

μ = 2π / ln 50 ≈ π/2 = 1.57.

Если x =90 %, то колебательность μ ≈ 2.72 .

Для оценки быстродействия

системы может использоваться показатель, называемый степенью устойчивости. Под степенью устойчивости

ή понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис.1.54).

Корни характеристического уравнения, расположенные ближе к мнимой оси дают в переходном процессе (1.102) составляющие, которые затухают наиболее медленно, так как эти корни имеют наименьшую по абсолютной величине вещественную часть. В большинстве случаев переходный процесс можно считать завершенным после затухания составляющей, соответствующей ближайшему к мнимой оси корню. Если ближайшим является вещественный корень, то составляющая в переходном процессе, определяемая этим корнем будет иметь вид = C e – t . Приняв в конце переходного процесса = ΔC , где Δ = 0.01 ¸ 0.05, можно получить приближенную зависимость между степенью устойчивостью и временем переходного процесса:

t n ≈ ln Δ −1 . (1.126)

Так, например, если принять Δ = .05, то время переходного процесса t n ≈ ln2 = 3 . (1.127)

Если ближайшими к мнимой оси является пара комплексных корней , то составляющая в переходном процессе, определяемая этими корнями будет = sin(bt + ψ). Несмотря на присутствие в этой составляющей гармонической функции формула, устанавливающая связь между степенью устойчивости и временем переходного процесса практически будет совпадать с выражением (1.127).

Для систем невысокого порядка степень устойчивости можно найти без вычисления корней характеристического уравнения. С этой целью в уравнении (1.124) необходимо перейти к новой переменной . Подставив в уравнение (1.124) , получим так называемое смещенное уравнение

Раскрывая скобки и группируя члены по степеням переменной , получаем

Это уравнение соответствует смещению осей на плоскости корней влево на величину (рис.1.54). В результате один (рис.1.54,а) или два (рис.1.54,б) корня попадают на ось мнимых, что соответствует границе устойчивости.

Для вычисления степени устойчивости необходимо применить к смещенному уравнению (1.128) любой критерий устойчивости и определить, при каком значении = получается граница устойчивости. Однако, если характеристическое уравнение имеет порядок выше второго, то задача расчета степени устойчивости оказывается не менее сложной, чем расчет корней характеристического уравнения. Например, если в уравнении (1.128) принять , то смещенное уравнение принимает вид:

Видно, что для вычисления степени устойчивости (как и для вычисления корней исходного характеристического уравнения) необходимо решать алгебраическое уравнение третьей степени. Если характеристическое уравнение будет иметь пятый порядок, то для расчета степени устойчивости необходимо будет решать алгебраическое уравнение пятого порядка и т.д. В связи со сложностью решения алгебраических уравнений применение формулы (1.127) для расчета времени переходного процесса оказывается проблематичным.

Однако, применение степени устойчивости оказывается перспективным в задаче обеспечения требуемого быстродействия, возникающей при проектирования системы.

Пусть смещенное уравнение (1.128) относится к проектируемой системе. Этап проектирования соответствует расчету области устойчивости. Для придания системе требуемого быстродействия необходимо выполнить следующее:

Задать требуемое время переходного процесса и по формуле (1.127) вычислить величину . ;

Изменяя переменные параметры, в плоскости которых строилась область устойчивости, необходимо переместить рабочую точку на границу устойчивости.

После выполнения указанных действий полученная система регулирования будет иметь время переходного процесса равное и соответствующие значения переменных параметров.

Диаграмма Вышнеградского (рис.1.55)
позволяет существенно облегчить процесс проектирования систем управления. Несмотря на то, что диаграмма разработана для систем, имеющих характеристическое уравнение третьего порядка, ее применение может существенно облегчить расчет показателей качества и для систем более высокого порядка.

Рассмотрим характеристическое уравнение третьего порядка

Данное уравнение приводится к нормированному виду,

называются параметрами Вышнеградского,
а − это новая переменная, введенная в уравнение (1.130), вместо переменной .

Диаграмма расположена в плоскости параметров А и В (рис.1.55) и содержит несколько основных кривых линий. Первая линия − граница устойчивости (колебательная). Уравнение границы: АВ = 1, при А > 0 и В > 0. Это равнобокая гипербола, для которой оси координат служат асимптотами.


	Рис. 1.55. Диаграмма Вышнеградского

Источник