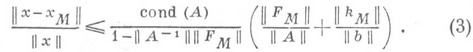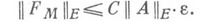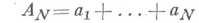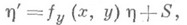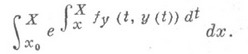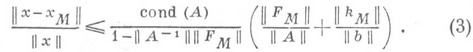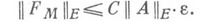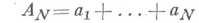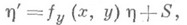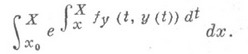при численном решении алгебраических уравнений — суммарное влияние округлений, сделанных на отдельных шагах вычислительного процесса, на точность полученного решения линейной алгебраич. системы. Наиболее распространенным способом априорной оценки суммарного влияния ошибок округления в численных методах линейной алгебры является схема т. н. обратного анализа. В применении к решению системы линейных алгебраич. уравнений
схема обратного анализа заключается в следующем. Вычисленное прямым методом Мрешение хуи не удовлетворяет (1), но может быть представлено как точное решение возмущенной системы
Качество прямого метода оценивается по наилучшей априорной оценке, к-рую можно дать для норм матрицы 



Если оценки для 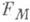
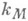

Здесь 
В действительности оценка для 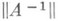

В этой оценке 
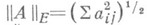
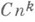
В случае методов типа Гаусса в правую часть оценки (4) входит еще множитель 
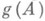
Для квадратного корня метода, к-рый применяется обычно в случае положительно определенной матрицы А, получена наиболее сильная оценка
Существуют прямые методы (Жордана, окаймления, сопряженных градиентов), для к-рых непосредственное применение схемы обратного анализа не приводит к эффективным оценкам. В этих случаях при исследовании Н. п. применяются и иные соображения (см. [6] — [9]).
Лит.:[1] Givens W., «TJ. S. Atomic Energy Commiss. Repts. Ser. OR NL», 1954, № 1574; [2] Wilkinson J. H., Rounding errors in algebraic processes, L., 1963; [3] Уилкинсон Д ж. <Х., Алгебраическая проблема собственных значений, пер. с англ., М., 1970; [4] Воеводин В. В., Ошибки округления и устойчивость в прямых методах линейной алгебры, М., 1969; [5] его же, Вычислительные основы линейной алгебры, М., 1977; [6] Peters G., Wilkinsоn J. H., «Communs Assoc. Comput. Math.», 1975, v. 18, № 1, p. 20-24; [7] Вrоуden C. G., «J. Inst. Math, and Appl.», 1974, v. 14, № 2, p. 131-40; [8] Reid J. К., в кн.: Large Sparse Sets of Linear Equations, L.- N. Y., 1971, p. 231 — 254; [9] Икрамов Х. Д., «Ж. вычисл. матем. и матем. физики», 1978, т. 18, № 3, с. 531-45.
X. Д. Икрамов.
Н. п. округления или погрешности метода возникает при решении задач, где решение является результатом большого числа последовательно выполняемых арифметич. операций.
Значительная часть таких задач связана с решением алгебраич. задач, линейных или нелинейных (см. выше). В свою очередь среди алгебраич. задач наиболее распространены задачи, возникающие при аппроксимации дифференциальных уравнений. Этим задачам свойственны нек-рые специфич. особенности.
Н. п. метода решения задачи происходит по тем же или по более простым законам, что и Н. п. вычислительной погрешности; Н. ,п. метода исследуется при оценке метода решения задачи.
При исследовании накопления вычислительной погрешности различают два подхода. В первом случае считают, что вычислительные погрешности на каждом шаге вносятся самым неблагоприятным образом и получают мажорантную оценку погрешности. Во втором случае считают, что эти погрешности случайны с определенным законом распределения.
Характер Н. п. зависит от решаемой задачи, метода решения и ряда других факторов, на первый взгляд могущих показаться несущественными; сюда относятся форма записи чисел в ЭВМ (с фиксированной запятой или с плавающей запятой), порядок выполнения арифметич. операций и т. д. Напр., в задаче вычисления суммы Nчисел
существенен порядок выполнения операций. Пусть вычисления производятся на машине с плавающей запятой с tдвоичными разрядами и все числа лежат в пределах 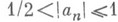
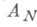
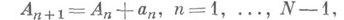
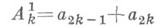


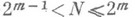
получают 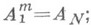
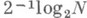
В типичных задачах величины а т вычисляются по формулам, в частности рекуррентным, или поступают последовательно в оперативную память ЭВМ; в этих случаях применение описанного приема приводит к увеличению загрузки памяти ЭВМ. Однако можно организовать последовательность вычислений так, что загрузка оперативной памяти не будет превосходить -log2N ячеек.
При численном решении дифференциальных уравнений возможны следующие случаи. При стремлении шага сетки hк нулю погрешность растет как 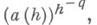
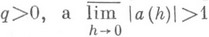
Для устойчивых методов характерен рост погрешности как 
В более сложных случаях применяется метод эквивалентных возмущений (см. [1], [4]), развитый в отношении задачи исследования накопления вычислительной погрешности при решении дифференциальных уравнений (см. [3], [5], [6]). Вычисления по нек-рой расчетной схеме с округлениями рассматриваются как вычисления без округлений, но для уравнения с возмущенными коэффициентами. Сравнивая решение исходного сеточного уравнения с решением уравнения с возмущенными коэффициентами получают оценку погрешности.
Уделяется существенное внимание выбору метода по возможности с меньшими значениями qи A(h). При фиксированном методе решения задачи расчетные формулы обычно удается преобразовать к виду, где 
Величина (h)может сильно расти с ростом промежутка интегрирования. Поэтому стараются применять методы по возможности с меньшим значением A(h). В случае задачи Коши ошибка округления на каждом конкретном шаге по отношению к последующим шагам может рассматриваться как ошибка в начальном условии. Поэтому нижняя грань (h)зависит от характеристики расхождения близких решений дифференциального уравнения, определяемого уравнением в вариациях.
В случае численного решения обыкновенного дифференциального уравнения 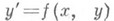
и потому при решении задачи на отрезке ( х 0 , X )нельзя рассчитывать на константу A(h)в мажорантной оценке вычислительной погрешности существенно лучшую, чем
Поэтому при решении этой задачи наиболее употребительны однощаговые методы типа Рунге — Кутта или методы типа Адамса (см. [3], [7]), где Н. п. в основном определяется решением уравнения в вариациях.
Для ряда методов главный член погрешности метода накапливается по подобному закону, в то время как вычислительная погрешность накапливается существенно быстрее (см. [3]). Область практич. применимости таких методов оказывается существенно уже.
Накопление вычислительной погрешности существенно зависит от метода, применяемого для решения сеточной задачи. Напр., при решении сеточных краевых задач, соответствующих обыкновенным дифференциальным уравнениям, методами стрельбы и прогонки Н. п. имеет характер A(h)h-q, где qодно и то же. Значения A(h)у этих методов могут отличаться настолько, что в определенной ситуации один из методов становится неприменимым. При решении методом пристрелки сеточной краевой задачи для уравнения Лапласа Н. п. имеет характер с 1/h, с>1, а в случае метода прогонки Ah-q. При вероятностном подходе к исследованию Н. п. в одних случаях априорно предполагают какой-то закон распределения погрешности (см. [2]), в других случаях вводят меру на пространстве рассматриваемых задач и, исходя из этой меры, получают закон распределения погрешностей округления (см. [8], [9]).
При умеренной точности решения задачи мажорантные и вероятностные подходы к оценке накопления вычислительной погрешности обычно дают качественно одинаковые результаты: или в обоих случаях Н. п. происходит в допустимых пределах, или в обоих случаях Н. п. превосходит такие пределы.
Лит.:[1] Воеводин В. В., Вычислительные основы линейной алгебры, М., 1977; [2] Шура-Бура М. Р., «Прикл. матем. и механ.», 1952, т. 16, № 5, с. 575-88; [3] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [4] Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер. с англ., М.. 1970; [5] Бахвалов Н. С, в кн.: Вычислительные методы и программирование, в. 1, М., 1962, с, 69-79; [6] Годунов С. К., Рябенький В. С, Разностные схемы, 2 изд., М., 1977; [7] Бахвалов Н. С, «Докл. АН СССР», 1955, т. 104, № 5, с. 683-86; [8] его же, «Ж. вычислит, матем. и матем. физики», 1964; т. 4, № 3, с. 399- 404; [9] Лапшин Е. А., там же, 1971, т. 11, № 6, с.1425-36.
Н. С. Бахвалов.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
-
Отладка по – классификация ошибок: ошибки компиляции, компоновки, выполнения; причины ошибок выполнения.
Отладка-это
процесс локализации и исправления
ошибок, обнаруженных при тестировании
программного обеспечения. Локализацией
называют
процесс определения оператора программы,
выполнение которого вызвало нарушение
нормального вычислительного процесса.
До исправления ошибки необходимо
определить ее причину,
т. е. определить оператор или фрагмент,
содержащие ошибку. Причины ошибок могут
быть как очевидны, так и очень глубоко
скрыты.
В целом сложность
отладки обусловлена следующими причинами:
• требует от
программиста глубоких знаний специфики
управления используемыми техническими
средствами, операционной системы, среды
и языка программирования, реализуемых
процессов, природы и специфики различных
ошибок, методик отладки и соответствующих
программных средств;
• психологически
дискомфортна, так как необходимо искать
собственные ошибки и, как правило, в
условиях ограниченного времени;
• возможно
взаимовлияние ошибок в разных частях
программы, например, за счет затирания
области памяти одного модуля другим
из-за ошибок адресации;
• отсутствуют
четко сформулированные методики отладки.
В соответствии с
этапом обработки, на котором проявляются
ошибки, различаю:
• синтаксические
ошибки —
ошибки, фиксируемые компилятором
(транслятором, интерпретатором) при
выполнении синтаксического и частично
семантического анализа программы;
•ошибки компоновки
— ошибки,
обнаруженные компоновщиком (редактором
связей) при объединении модулей программы;
•ошибки выполнения
— ошибки,
обнаруженные операционной системой,
аппаратными средствами или пользователем
при выполнении программы.
Синтаксические
ошибки. Синтаксические
ошибки относят к группе самых простых,
так как синтаксис языка, как правило,
строго формализован, и ошибки сопровождаются
развернутым комментарием с указанием
ее местоположения. Определение причин
таких ошибок, как правило, труда не
составляет, и даже при нечетком знании
правил языка за несколько прогонов
удается удалить все ошибки данного
типа.
Следует иметь в
виду, что чем лучше формализованы правила
синтаксиса языка, тем больше ошибок из
общего количества может обнаружить
компилятор и, соответственно, меньше
ошибок будет обнаруживаться на следующих
этапах. В связи с этим говорят о языках
программирования с защищенным синтаксисом
и с незащищенным синтаксисом. К первым,
безусловно, можно отнести Pascal, имеющий
очень простой и четко определенный
синтаксис, хорошо проверяемый при
компиляции программы, ко вторым — Си со
всеми его модификациями. Чего стоит
хотя бы возможность выполнения
присваивания в условном операторе в
Си, например: if (c = n) x = 0; /* в данном случае
не проверятся равенство с и n, а выполняется
присваивание с значения n, после чего
результат операции сравнивается с
нулем, если программист хотел выполнить
не присваивание, а сравнение, то эта
ошибка будет обнаружена только на этапе
выполнения при получении результатов,
отличающихся от ожидаемых */
Ошибки компоновки.
Ошибки
компоновки, как следует из названия,
связаны с проблемами,
обнаруженными при
разрешении внешних ссылок. Например,
предусмотрено обращение к подпрограмме
другого модуля, а при объединении модулей
данная подпрограмма не найдена или не
стыкуются списки параметров. В большинстве
случаев ошибки такого рода также удается
быстро локализовать и устранить.
Ошибки выполнения.
К самой
непредсказуемой группе относятся ошибки
выполнения. Прежде всего они могут иметь
разную природу, и соответственно
по-разному проявляться. Часть ошибок
обнаруживается и документируется
операционной системой. Выделяют четыре
способа проявления таких ошибок:
• появление
сообщения об ошибке, зафиксированной
схемами контроля выполнения машинных
команд, например, переполнении разрядной
сетки, ситуации «деление на ноль»,
нарушении адресации и т. п.;
• появление
сообщения об ошибке, обнаруженной
операционной системой, например,
нарушении защиты памяти, попытке записи
на устройства, защищенные от записи,
отсутствии файла с заданным именем и
т. п.;
• «зависание»
компьютера, как простое, когда удается
завершить программу без перезагрузки
операционной системы, так и «тяжелое»,
когда для продолжения работы необходима
перезагрузка;
• несовпадение
полученных результатов с ожидаемыми.
Причины ошибок
выполнения очень разнообразны, а потому
и локализация может оказаться крайне
сложной. Все возможные причины ошибок
можно разделить на следующие группы:
• неверное
определение исходных данных,
• логические
ошибки,
• накопление
погрешностей результатов вычислений.
Неверное
определение исходных данных
происходит, если возникают любые ошибки
при выполнении операций ввода-вывода:
ошибки передачи, ошибки преобразования,
ошибки перезаписи и ошибки данных.
Причем использование специальных
технических средств и программирование
с защитой от ошибок позволяет обнаружить
и предотвратить только часть этих
ошибок, о чем безусловно не следует
забывать.
Логические ошибки
имеют разную природу. Так они могут
следовать из ошибок, допущенных при
проектировании, например, при выборе
методов, разработке алгоритмов или
определении структуры классов, а могут
быть непосредственно внесены при
кодировании модуля.
К последней группе
относят:
• ошибки
некорректного использования переменных,
например, неудачный выбор типов данных,
использование переменных до их
инициализации, использование индексов,
выходящих за границы определения
массивов, нарушения соответствия типов
данных при использовании явного или
неявного переопределения типа данных,
расположенных в памяти при использовании
нетипизированных переменных, открытых
массивов, объединений, динамической
памяти, адресной арифметики и т. п.;
• ошибки
вычислений,
например, некорректные вычисления над
неарифметическими переменными,
некорректное использование целочисленной
арифметики, некорректное преобразование
типов данных в процессе вычислений,
ошибки, связанные с незнанием приоритетов
выполнения операций для арифметических
и логических выражений, и т. п.;
•ошибки
межмодульного интерфейса,
например, игнорирование системных
соглашений, нарушение типов и
последовательности при передачи
параметров, несоблюдение единства
единиц измерения формальных и фактических
параметров, нарушение области действия
локальных и глобальных переменных;
• другие ошибки
кодирования,
например, неправильная реализация
логики программы при кодировании,
игнорирование особенностей или
ограничений конкретного языка
программирования.
Накопление
погрешностей
результатов числовых вычислений
возникает, например, при некорректном
отбрасывании дробных цифр чисел,
некорректном использовании приближенных
методов вычислений, игнорировании
ограничения разрядной сетки представления
вещественных чисел в ЭВМ и т. п.
Все указанные выше
причины возникновения ошибок следует
иметь в виду в процессе отладки. Кроме
того, сложность отладки увеличивается
также вследствие влияния следующих
факторов:
• опосредованного
проявления ошибок;
• возможности
взаимовлияния ошибок;
• возможности
получения внешне одинаковых проявлений
разных ошибок;
• отсутствия
повторяемости проявлений некоторых
ошибок от запуска к запуску – так
называемые стохастические ошибки;
• возможности
устранения внешних проявлений ошибок
в исследуемой ситуации при внесении
некоторых изменений в программу,
например, при включении в программу
диагностических фрагментов может
аннулироваться или измениться внешнее
проявление ошибок;
• написания
отдельных частей программы разными
программистами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Отладка программы — один их самых сложных этапов разработки программного обеспечения, требующий глубокого знания:
•специфики управления используемыми техническими средствами,
•операционной системы,
•среды и языка программирования,
•реализуемых процессов,
•природы и специфики различных ошибок,
•методик отладки и соответствующих программных средств.
Отладка — это процесс локализации и исправления ошибок, обнаруженных при тестировании программного обеспечения. Локализацией называют процесс определения оператора программы, выполнение которого вызвало нарушение нормального вычислительного процесса. Доя исправления ошибки необходимо определить ее причину, т. е. определить оператор или фрагмент, содержащие ошибку. Причины ошибок могут быть как очевидны, так и очень глубоко скрыты.
Вцелом сложность отладки обусловлена следующими причинами:
•требует от программиста глубоких знаний специфики управления используемыми техническими средствами, операционной системы, среды и языка программирования, реализуемых процессов, природы и специфики различных ошибок, методик отладки и соответствующих программных средств;
•психологически дискомфортна, так как необходимо искать собственные ошибки и, как правило, в условиях ограниченного времени;
•возможно взаимовлияние ошибок в разных частях программы, например, за счет затирания области памяти одного модуля другим из-за ошибок адресации;
•отсутствуют четко сформулированные методики отладки.
Всоответствии с этапом обработки, на котором проявляются ошибки, различают (рис. 10.1):
синтаксические ошибки — ошибки, фиксируемые компилятором (транслятором, интерпретатором) при выполнении синтаксического и частично семантического анализа программы; ошибки компоновки — ошибки, обнаруженные компоновщиком (редактором связей) при объединении модулей программы;
ошибки выполнения — ошибки, обнаруженные операционной системой, аппаратными средствами или пользователем при выполнении программы.
Синтаксические ошибки. Синтаксические ошибки относят к группе самых простых, так как синтаксис языка, как правило, строго формализован, и ошибки сопровождаются развернутым комментарием с указанием ее местоположения. Определение причин таких ошибок, как правило, труда не составляет, и даже при нечетком знании правил языка за несколько прогонов удается удалить все ошибки данного типа.
Следует иметь в виду, что чем лучше формализованы правила синтаксиса языка, тем больше ошибок из общего количества может обнаружить компилятор и, соответственно, меньше ошибок будет обнаруживаться на следующих этапах. В связи с этим говорят о языках программирования с защищенным синтаксисом и с незащищенным синтаксисом. К первым, безусловно, можно отнести Pascal, имеющий очень простой и четко определенный синтаксис, хорошо проверяемый при компиляции программы, ко вторым — Си со всеми его модификациями. Чего стоит хотя бы возможность выполнения присваивания в условном операторе в Си, например:
if (c = n) x = 0; /* в данном случае не проверятся равенство с и n, а выполняется присваивание с значения n, после чего результат операции сравнивается с нулем, если программист хотел выполнить не присваивание, а сравнение, то эта ошибка будет обнаружена только на этапе выполнения при получении результатов, отличающихся от ожидаемых */
Ошибки компоновки. Ошибки компоновки, как следует из названия, связаны с проблемами,
обнаруженными при разрешении внешних ссылок. Например, предусмотрено обращение к подпрограмме другого модуля, а при объединении модулей данная подпрограмма не найдена или не стыкуются списки параметров. В большинстве случаев ошибки такого рода также удается быстро локализовать и устранить.
Ошибки выполнения. К самой непредсказуемой группе относятся ошибки выполнения. Прежде всего они могут иметь разную природу, и соответственно по-разному проявляться. Часть ошибок обнаруживается и документируется операционной системой. Выделяют четыре способа проявления таких ошибок:
• появление сообщения об ошибке, зафиксированной схемами контроля выполнения машинных команд, например, переполнении разрядной сетки, ситуации «деление на ноль», нарушении адресации и т. п.;
•появление сообщения об ошибке, обнаруженной операционной системой, например, нарушении защиты памяти, попытке записи на устройства, защищенные от записи, отсутствии файла с заданным именем и т. п.;
•«зависание» компьютера, как простое, когда удается завершить программу без перезагрузки операционной системы, так и «тяжелое», когда для продолжения работы необходима перезагрузка;
•несовпадение полученных результатов с ожидаемыми.
Примечание. Отметим, что, если ошибки этапа выполнения обнаруживает пользователь, то в двух первых случаях, получив соответствующее сообщение, пользователь в зависимости от своего характера, степени необходимости и опыта работы за компьютером, либо попробует понять, что произошло, ища свою вину, либо обратится за помощью, либо постарается никогда больше не иметь дела с этим продуктом. При «зависании» компьютера пользователь может даже не сразу понять, что происходит что-то не то, хотя его печальный опыт и заставляет волноваться каждый раз, когда компьютер не выдает быстрой реакции на введенную команду, что также целесообразно иметь в виду. Также опасны могут быть ситуации, при которых пользователь получает неправильные результаты и использует их в своей работе.
Причины ошибок выполнения очень разнообразны, а потому и локализация может оказаться крайне сложной. Все возможные причины ошибок можно разделить на следующие группы:
•неверное определение исходных данных,
•логические ошибки,
•накопление погрешностей результатов вычислений (рис. 10.2).
Н е в е р н о е о п р е д е л е н и е и с х о д н ы х д а н н ы х происходит, если возникают любые ошибки при выполнении операций ввода-вывода: ошибки передачи, ошибки преобразования, ошибки перезаписи и ошибки данных. Причем использование специальных технических средств и программирование с защитой от ошибок (см.§ 2.7) позволяет обнаружить и предотвратить только часть этих ошибок, о чем безусловно не следует забывать.
Л о г и ч е с к и е о ш и б к и имеют разную природу. Так они могут следовать из ошибок, допущенных при проектировании, например, при выборе методов, разработке алгоритмов или определении структуры классов, а могут быть непосредственно внесены при кодировании модуля.
Кпоследней группе относят:
ошибки некорректного использования переменных, например, неудачный выбор типов данных, использование переменных до их инициализации, использование индексов, выходящих за границы определения массивов, нарушения соответствия типов данных при использовании явного или неявного переопределения типа данных, расположенных в памяти при использовании нетипизированных переменных, открытых массивов, объединений, динамической памяти, адресной арифметики и т. п.;
ошибки вычислений, например, некорректные вычисления над неарифметическими переменными, некорректное использование целочисленной арифметики, некорректное преобразование типов данных в процессе вычислений, ошибки, связанные с незнанием приоритетов выполнения операций для арифметических и логических выражений, и т. п.;
ошибки межмодульного интерфейса, например, игнорирование системных соглашений, нарушение типов и последовательности при передачи параметров, несоблюдение единства единиц измерения формальных и фактических параметров, нарушение области действия локальных и глобальных переменных;
другие ошибки кодирования, например, неправильная реализация логики программы при кодировании, игнорирование особенностей или ограничений конкретного языка программирования.
На к о п л е н и е п о г р е ш н о с т е й результатов числовых вычислений возникает, например, при некорректном отбрасывании дробных цифр чисел, некорректном использовании приближенных методов вычислений, игнорировании ограничения разрядной сетки представления вещественных чисел в ЭВМ и т. п.
Все указанные выше причины возникновения ошибок следует иметь в виду в процессе отладки. Кроме того, сложность отладки увеличивается также вследствие влияния следующих факторов:
опосредованного проявления ошибок;
возможности взаимовлияния ошибок;
возможности получения внешне одинаковых проявлений разных ошибок;
отсутствия повторяемости проявлений некоторых ошибок от запуска к запуску – так называемые стохастические ошибки;
возможности устранения внешних проявлений ошибок в исследуемой ситуации при внесении некоторых изменений в программу, например, при включении в программу диагностических фрагментов может аннулироваться или измениться внешнее проявление ошибок;
написания отдельных частей программы разными программистами.
Методы отладки программного обеспечения
Отладка программы в любом случае предполагает обдумывание и логическое осмысление всей имеющейся информации об ошибке. Большинство ошибок можно обнаружить по косвенным признакам посредством тщательного анализа текстов программ и результатов тестирования без получения дополнительной информации. При этом используют различные методы:
ручного тестирования;
индукции;
дедукции;
обратного прослеживания.
Метод ручного тестирования. Это — самый простой и естественный способ данной группы. При обнаружении ошибки необходимо выполнить тестируемую программу вручную, используя тестовый набор, при работе с которым была обнаружена ошибка.
Метод очень эффективен, но не применим для больших программ, программ со сложными вычислениями и в тех случаях, когда ошибка связана с неверным представлением программиста о выполнении некоторых операций.
Данный метод часто используют как составную часть других методов отладки.
Метод индукции. Метод основан на тщательном анализе симптомов ошибки, которые могут проявляться как неверные результаты вычислений или как сообщение об ошибке. Если компьютер просто «зависает», то фрагмент проявления ошибки вычисляют, исходя из последних полученных результатов и действий пользователя. Полученную таким образом информацию организуют и тщательно изучают, просматривая соответствующий фрагмент программы. В результате этих действий выдвигают гипотезы об ошибках, каждую из которых проверяют. Если гипотеза верна, то детализируют информацию об ошибке, иначе — выдвигают другую гипотезу. Последовательность выполнения отладки методом индукции показана на рис. 10.3 в виде схемы алгоритма.
Самый ответственный этап — выявление симптомов ошибки. Организуя данные об ошибке, целесообразно записать все, что известно о ее проявлениях, причем фиксируют, как ситуации, в которых фрагмент с ошибкой выполняется нормально, так и ситуации, в которых ошибка проявляется. Если в результате изучения данных никаких гипотез не появляется, то необходима дополнительная информация об ошибке. Дополнительную информацию можно получить, например, в результате выполнения схожих тестов.
В процессе доказательства пытаются выяснить, все ли проявления ошибки объясняет данная гипотеза, если не все, то либо гипотеза не верна, либо ошибок несколько.
Метод дедукции. По методу дедукции вначале формируют множество причин, которые могли бы вызвать данное проявление ошибки. Затем анализируя причины, исключают те, которые противоречат имеющимся данным. Если все причины исключены, то следует выполнить дополнительное тестирование исследуемого фрагмента. В противном случае наиболее вероятную гипотезу пытаются доказать. Если гипотеза объясняет полученные признаки ошибки, то ошибка найдена, иначе — проверяют следующую причину (рис. 10.4).
Метод обратного прослеживания. Для небольших программ эффективно применение метода обратного прослеживания. Начинают с точки вывода неправильного результата. Для этой точки строится гипотеза о значениях основных переменных, которые могли бы привести к получению имеющегося результата. Далее, исходя из этой гипотезы, делают предложения о значениях переменных в предыдущей точке. Процесс продолжают, пока не обнаружат причину ошибки.
Накопление — ошибка
Cтраница 1
Накопление ошибки от шага к шагу не только увеличивает систематические отклонения между x ( t) и ее дискретным аналогом, но и создает возрастающую погрешность смещения фазы и запаздывание. Поэтому вычисленные значения x ( tk) обычно корректируются путем предсказания ( прогноза) будущих значений x ( t) на основании настоящих и прошлых.
[1]
Накопление ошибок 20 Нижний пояс 47 Новожилов И.В. 9, 191, 227, 376 Ньютон И.
[2]
Накопление антиэкологических ошибок более недопустимо.
[3]
Накопление ошибки счета — В процессе шагового расчета накапливаются ошибки счета, которые, если не принимать специальных мер, могут привести к существенному искажению или даже к полностью неверным результатам. Накопление ошибки связано с рядом причин. Составляющими ошибки счета являются погрешности аппроксимации при решении интегральных задач. Если при рассмотрении стационарного процесса, расчете дисков с использованием конечных соотношений упругости и деформационных теорий пластичности и ползучести задание определенной точности решения дает удовлетворительные результаты при сходящемся процессе, то при повторении этих погрешностей на расчетных этапах и последующем суммировании результатов при шаговом расчете нестационарного процесса накапливается существенная погрешность.
[4]
Вследствие накопления ошибки при развертывании определителя восьмой корень получается близкий к нулю, но не нулевой.
[5]
Чтобы избежать накопления ошибок при откладывании делений, прибегают к следующим приемам.
[6]
Чтобы избежать накопления ошибок при откладывании делений, прибегают к следующим приемам.
[8]
Чтобы избежать накопления ошибок, измерения проводят сериями по 10 — 12 точек в каждой. Первая серия носит разведочный характер.
[10]
Однако при накоплении ошибок в процессе вычислений, выражения, которые алгебраически равны, могут оказаться равными неточно.
[11]
Для избежания такого накопления ошибок в данной работе мы предлагаем пожертвовать мягким корректным учетом вкладов флуктуации разных масштабов и жестко разделить кулонов-ское взаимодействие на Vi и У % — потенциалы, соответствующие ближнему и дальнему вкладам, причем разбиение выполнить таким образом, чтобы носители функций Vi и / 2 не перекрывались.
[12]
В результате такого накопления ошибок вместо предсказанного теорией 10 — 12-кратного выигрыша в точности был получен выигрыш лишь в 4 — 5 раз [ 78, с.
[13]
Существенное влияние на накопление ошибки оказывает погрешность определения величины Аг / при у — — 0, которая при ограниченности экспериментальных данных может оказаться очень значительной.
[14]
Страницы:
1
2
3
4
»
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАКОПЛЕНИЕ ПОГРЕШНОСТИ
Значение НАКОПЛЕНИЕ ПОГРЕШНОСТИ в математической энциклопедии:
при численном решении алгебраических уравнений — суммарное влияние округлений, сделанных на отдельных шагах вычислительного процесса, на точность полученного решения линейной алгебраич. системы. Наиболее распространенным способом априорной оценки суммарного влияния ошибок округления в численных методах линейной алгебры является схема т. н. обратного анализа. В применении к решению системы линейных алгебраич. уравнений
схема обратного анализа заключается в следующем. Вычисленное прямым методом Мрешение хуи не удовлетворяет (1), но может быть представлено как точное решение возмущенной системы
Качество прямого метода оценивается по наилучшей априорной оценке, к-рую можно дать для норм матрицы 



Если оценки для 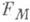
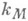

Здесь 
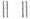
В действительности оценка для 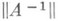

В этой оценке 
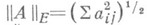
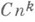
В случае методов типа Гаусса в правую часть оценки (4) входит еще множитель 
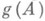
Для квадратного корня метода, к-рый применяется обычно в случае положительно определенной матрицы А, получена наиболее сильная оценка
Существуют прямые методы (Жордана, окаймления, сопряженных градиентов), для к-рых непосредственное применение схемы обратного анализа не приводит к эффективным оценкам. В этих случаях при исследовании Н. п. применяются и иные соображения (см. [6] — [9]).
Лит.:[1] Givens W., «TJ. S. Atomic Energy Commiss. Repts. Ser. OR NL», 1954, № 1574; [2] Wilkinson J. H., Rounding errors in algebraic processes, L., 1963; [3] Уилкинсон Д ж. <Х., Алгебраическая проблема собственных значений, пер. с англ., М., 1970; [4] Воеводин В. В., Ошибки округления и устойчивость в прямых методах линейной алгебры, М., 1969; [5] его же, Вычислительные основы линейной алгебры, М., 1977; [6] Peters G., Wilkinsоn J. H., «Communs Assoc. Comput. Math.», 1975, v. 18, № 1, p. 20-24; [7] Вrоуden C. G., «J. Inst. Math, and Appl.», 1974, v. 14, № 2, p. 131-40; [8] Reid J. К., в кн.: Large Sparse Sets of Linear Equations, L.- N. Y., 1971, p. 231 — 254; [9] Икрамов Х. Д., «Ж. вычисл. матем. и матем. физики», 1978, т. 18, № 3, с. 531-45.
X. Д. Икрамов.
Н. п. округления или погрешности метода возникает при решении задач, где решение является результатом большого числа последовательно выполняемых арифметич. операций.
Значительная часть таких задач связана с решением алгебраич. задач, линейных или нелинейных (см. выше). В свою очередь среди алгебраич. задач наиболее распространены задачи, возникающие при аппроксимации дифференциальных уравнений. Этим задачам свойственны нек-рые специфич. особенности.
Н. п. метода решения задачи происходит по тем же или по более простым законам, что и Н. п. вычислительной погрешности; Н. ,п. метода исследуется при оценке метода решения задачи.
При исследовании накопления вычислительной погрешности различают два подхода. В первом случае считают, что вычислительные погрешности на каждом шаге вносятся самым неблагоприятным образом и получают мажорантную оценку погрешности. Во втором случае считают, что эти погрешности случайны с определенным законом распределения.
Характер Н. п. зависит от решаемой задачи, метода решения и ряда других факторов, на первый взгляд могущих показаться несущественными; сюда относятся форма записи чисел в ЭВМ (с фиксированной запятой или с плавающей запятой), порядок выполнения арифметич. операций и т. д. Напр., в задаче вычисления суммы Nчисел
существенен порядок выполнения операций. Пусть вычисления производятся на машине с плавающей запятой с tдвоичными разрядами и все числа лежат в пределах 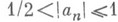
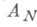
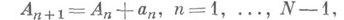
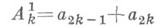


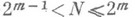
получают 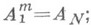
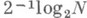
В типичных задачах величины а т вычисляются по формулам, в частности рекуррентным, или поступают последовательно в оперативную память ЭВМ; в этих случаях применение описанного приема приводит к увеличению загрузки памяти ЭВМ. Однако можно организовать последовательность вычислений так, что загрузка оперативной памяти не будет превосходить -log2N ячеек.
При численном решении дифференциальных уравнений возможны следующие случаи. При стремлении шага сетки hк нулю погрешность растет как 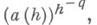
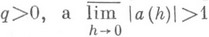
Для устойчивых методов характерен рост погрешности как 
В более сложных случаях применяется метод эквивалентных возмущений (см. [1], [4]), развитый в отношении задачи исследования накопления вычислительной погрешности при решении дифференциальных уравнений (см. [3], [5], [6]). Вычисления по нек-рой расчетной схеме с округлениями рассматриваются как вычисления без округлений, но для уравнения с возмущенными коэффициентами. Сравнивая решение исходного сеточного уравнения с решением уравнения с возмущенными коэффициентами получают оценку погрешности.
Уделяется существенное внимание выбору метода по возможности с меньшими значениями qи A(h). При фиксированном методе решения задачи расчетные формулы обычно удается преобразовать к виду, где 
Величина (h)может сильно расти с ростом промежутка интегрирования. Поэтому стараются применять методы по возможности с меньшим значением A(h). В случае задачи Коши ошибка округления на каждом конкретном шаге по отношению к последующим шагам может рассматриваться как ошибка в начальном условии. Поэтому нижняя грань (h)зависит от характеристики расхождения близких решений дифференциального уравнения, определяемого уравнением в вариациях.
В случае численного решения обыкновенного дифференциального уравнения 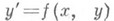
и потому при решении задачи на отрезке ( х 0 , X )нельзя рассчитывать на константу A(h)в мажорантной оценке вычислительной погрешности существенно лучшую, чем
Поэтому при решении этой задачи наиболее употребительны однощаговые методы типа Рунге — Кутта или методы типа Адамса (см. [3], [7]), где Н. п. в основном определяется решением уравнения в вариациях.
Для ряда методов главный член погрешности метода накапливается по подобному закону, в то время как вычислительная погрешность накапливается существенно быстрее (см. [3]). Область практич. применимости таких методов оказывается существенно уже.
Накопление вычислительной погрешности существенно зависит от метода, применяемого для решения сеточной задачи. Напр., при решении сеточных краевых задач, соответствующих обыкновенным дифференциальным уравнениям, методами стрельбы и прогонки Н. п. имеет характер A(h)h-q, где qодно и то же. Значения A(h)у этих методов могут отличаться настолько, что в определенной ситуации один из методов становится неприменимым. При решении методом пристрелки сеточной краевой задачи для уравнения Лапласа Н. п. имеет характер с 1/h, с>1, а в случае метода прогонки Ah-q. При вероятностном подходе к исследованию Н. п. в одних случаях априорно предполагают какой-то закон распределения погрешности (см. [2]), в других случаях вводят меру на пространстве рассматриваемых задач и, исходя из этой меры, получают закон распределения погрешностей округления (см. [8], [9]).
При умеренной точности решения задачи мажорантные и вероятностные подходы к оценке накопления вычислительной погрешности обычно дают качественно одинаковые результаты: или в обоих случаях Н. п. происходит в допустимых пределах, или в обоих случаях Н. п. превосходит такие пределы.
Лит.:[1] Воеводин В. В., Вычислительные основы линейной алгебры, М., 1977; [2] Шура-Бура М. Р., «Прикл. матем. и механ.», 1952, т. 16, № 5, с. 575-88; [3] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [4] Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер. с англ., М.. 1970; [5] Бахвалов Н. С, в кн.: Вычислительные методы и программирование, в. 1, М., 1962, с, 69-79; [6] Годунов С. К., Рябенький В. С, Разностные схемы, 2 изд., М., 1977; [7] Бахвалов Н. С, «Докл. АН СССР», 1955, т. 104, № 5, с. 683-86; [8] его же, «Ж. вычислит, матем. и матем. физики», 1964; т. 4, № 3, с. 399- 404; [9] Лапшин Е. А., там же, 1971, т. 11, № 6, с.1425-36.
Н. С. Бахвалов.