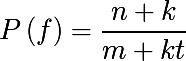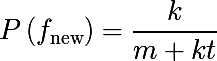Что такое автоматический контроль ошибок

В теория информации и теория кодирования с приложениями в Информатика и телекоммуникации, обнаружение и исправление ошибок или же контроль ошибок методы, которые обеспечивают надежную доставку цифровые данные чрезмерно ненадежный каналы связи. Многие каналы связи подлежат канальный шум, и, таким образом, ошибки могут быть внесены во время передачи от источника к приемнику. Методы обнаружения ошибок позволяют обнаруживать такие ошибки, а исправление ошибок во многих случаях позволяет восстановить исходные данные.

Определения

Обнаружение ошибок это обнаружение ошибок, вызванных шумом или другими помехами во время передачи от передатчика к приемнику. Исправление ошибки это обнаружение ошибок и восстановление исходных безошибочных данных.

История

Современное развитие коды исправления ошибок зачисляется на Ричард Хэмминг в 1947 г.^[1] Описание Код Хэмминга появился в Клод Шеннон с Математическая теория коммуникации^[2] и был быстро обобщен Марсель Дж. Э. Голей.^[3]

Вступление

Все схемы обнаружения и исправления ошибок добавляют избыточность (т.е. некоторые дополнительные данные) к сообщению, которые получатели могут использовать для проверки согласованности доставленного сообщения и для восстановления данных, которые были определены как поврежденные. Схемы обнаружения и исправления ошибок могут быть либо систематический или несистематический. В систематической схеме передатчик отправляет исходные данные и прикрепляет фиксированное количество проверить биты (или же данные о четности), которые получены из битов данных некоторыми детерминированный алгоритм. Если требуется только обнаружение ошибок, приемник может просто применить тот же алгоритм к полученным битам данных и сравнить свой вывод с полученными контрольными битами; если значения не совпадают, в какой-то момент во время передачи произошла ошибка. В системе, которая использует несистематический код, исходное сообщение преобразуется в закодированное сообщение, несущее ту же информацию и имеющее по крайней мере такое же количество битов, как и исходное сообщение.

Хорошая эффективность контроля ошибок требует, чтобы схема была выбрана на основе характеристик канала связи. Общий модели каналов включают без памяти модели, в которых ошибки возникают случайно и с определенной вероятностью, и динамические модели, в которых ошибки возникают в основном в всплески. Следовательно, коды обнаружения и исправления ошибок можно в целом различать между обнаружение / исправление случайных ошибок и обнаружение / исправление пакетных ошибок. Некоторые коды также могут подходить для сочетания случайных ошибок и пакетных ошибок.

Если характеристики канала не могут быть определены или сильно варьируются, схему обнаружения ошибок можно комбинировать с системой для повторных передач ошибочных данных. Это известно как автоматический повторный запрос (ARQ), и наиболее часто используется в Интернете. Альтернативный подход к контролю ошибок: гибридный автоматический запрос на повторение (HARQ), который представляет собой комбинацию ARQ и кодирования с исправлением ошибок.

Виды исправления ошибок

Есть три основных типа исправления ошибок.^[4]

Автоматический повторный запрос (ARQ)

Автоматический повторный запрос (ARQ) — это метод контроля ошибок для передачи данных, который использует коды обнаружения ошибок, сообщения подтверждения и / или отрицательного подтверждения, и таймауты для достижения надежной передачи данных. An подтверждение это сообщение, отправленное получателем, чтобы указать, что он правильно получил кадр данных.

Обычно, когда передатчик не получает подтверждения до истечения тайм-аута (т. Е. В течение разумного промежутка времени после отправки кадра данных), он повторно передает кадр до тех пор, пока он не будет либо правильно принят, либо ошибка сохранится сверх заранее определенного количества повторных передач. .

Есть три типа протоколов ARQ. Остановка и ожидание ARQ, Go-Back-N ARQ, и Селективный повторный ARQ.

ARQ подходит, если канал связи имеет изменяющийся или неизвестный емкость, например, в Интернете. Однако ARQ требует наличия задний канал, приводит к возможному увеличению задержка из-за повторных передач и требует обслуживания буферов и таймеров для повторных передач, что в случае перегрузка сети может вызвать нагрузку на сервер и общую пропускную способность сети.^[5]

Например, ARQ используется на коротковолновых радиоканалах в виде ARQ-E, или в сочетании с мультиплексированием как ARQ-M.

Прямое исправление ошибок

Прямое исправление ошибок (FEC) — это процесс добавления избыточный данные, такие как код исправления ошибок (ECC) в сообщение, чтобы оно могло быть восстановлено получателем, даже если было внесено несколько ошибок (в зависимости от возможностей используемого кода) либо в процессе передачи, либо при хранении. Поскольку получатель не должен запрашивать у отправителя повторную передачу данных, обратный канал не требуется при упреждающем исправлении ошибок и поэтому подходит для симплексная связь Такие как вещание. Коды с исправлением ошибок часто используются в нижний слой коммуникации, а также для надежного хранения на таких носителях, как Компакт-диски, DVD, жесткие диски, и баран.

Коды с исправлением ошибок обычно различают между сверточные коды и блочные коды:

• Сверточные коды обрабатываются побитно. Они особенно подходят для аппаратной реализации, а Декодер Витерби позволяет оптимальное декодирование.
• Коды блокировки обрабатываются на блок за блоком основание. Ранние примеры блочных кодов: коды повторения, Коды Хэмминга и многомерные коды проверки на четность. За ними последовал ряд эффективных кодов, Коды Рида – Соломона являются наиболее заметными из-за их широкого распространения в настоящее время. Турбо коды и коды с низкой плотностью проверки четности (LDPC) — относительно новые конструкции, которые могут обеспечить почти оптимальная эффективность.

Теорема Шеннона является важной теоремой для прямого исправления ошибок и описывает максимальную скорость передачи информации при котором возможна надежная связь по каналу с определенной вероятностью ошибки или соотношение сигнал шум (SNR). Этот строгий верхний предел выражается в терминах пропускная способность канала. В частности, теорема утверждает, что существуют такие коды, что с увеличением длины кодирования вероятность ошибки на дискретный канал без памяти можно сделать сколь угодно малым при условии, что кодовая скорость меньше пропускной способности канала. Кодовая скорость определяется как доля к / п из k исходные символы и п закодированные символы.

Фактическая максимальная допустимая кодовая скорость зависит от используемого кода исправления ошибок и может быть ниже. Это связано с тем, что доказательство Шеннона носило исключительно экзистенциальный характер и не показало, как построить коды, которые одновременно являются оптимальными и имеют эффективный алгоритмы кодирования и декодирования.

Гибридные схемы

Гибридный ARQ представляет собой комбинацию ARQ и прямого исправления ошибок. Есть два основных подхода:^[5]

• Сообщения всегда передаются с данными четности FEC (и избыточностью обнаружения ошибок). Приемник декодирует сообщение, используя информацию о четности, и запрашивает повторную передачу с использованием ARQ только в том случае, если данных четности было недостаточно для успешного декодирования (идентифицированного посредством неудачной проверки целостности).
• Сообщения передаются без данных четности (только с информацией об обнаружении ошибок). Если приемник обнаруживает ошибку, он запрашивает информацию FEC от передатчика с помощью ARQ и использует ее для восстановления исходного сообщения.

Последний подход особенно привлекателен на канал стирания при использовании код бесскоростного стирания.

Схемы обнаружения ошибок

Обнаружение ошибок чаще всего осуществляется с помощью подходящего хеш-функция (или, в частности, контрольная сумма, циклическая проверка избыточности или другой алгоритм). Хеш-функция добавляет фиксированную длину тег в сообщение, что позволяет получателям проверять доставленное сообщение путем пересчета тега и сравнения его с предоставленным.

Существует огромное количество различных конструкций хеш-функций. Однако некоторые из них особенно широко используются из-за их простоты или их пригодности для обнаружения определенных видов ошибок (например, производительность циклического контроля избыточности при обнаружении пакетные ошибки ).

Кодирование минимального расстояния

Код с исправлением случайных ошибок, основанный на кодирование минимального расстояния может предоставить строгую гарантию количества обнаруживаемых ошибок, но не может защитить от атака на прообраз.

Коды повторения

А код повторения представляет собой схему кодирования, которая повторяет биты по каналу для достижения безошибочной связи. Учитывая поток данных, которые необходимо передать, данные разделяются на блоки битов. Каждый блок передается определенное количество раз. Например, чтобы отправить битовую комбинацию «1011», четырехбитовый блок можно повторить три раза, таким образом получая «1011 1011 1011». Если этот двенадцатибитовый шаблон был получен как «1010 1011 1011» — где первый блок не похож на два других, — произошла ошибка.

Код повторения очень неэффективен и может быть подвержен проблемам, если ошибка возникает в одном и том же месте для каждой группы (например, «1010 1010 1010» в предыдущем примере будет обнаружено как правильное). Преимущество кодов повторения состоит в том, что они чрезвычайно просты и фактически используются в некоторых передачах номера станций.^[6][7]

Бит четности

А бит четности — это бит, который добавляется к группе исходных битов, чтобы гарантировать, что количество установленных битов (то есть битов со значением 1) в результате будет четным или нечетным. Это очень простая схема, которую можно использовать для обнаружения одного или любого другого нечетного числа (т. Е. Трех, пяти и т. Д.) Ошибок в выводе. Четное число перевернутых битов сделает бит четности правильным, даже если данные ошибочны.

Расширения и варианты механизма битов четности продольный контроль избыточности, поперечный контроль избыточности и аналогичные методы группировки битов.

Контрольная сумма

А контрольная сумма сообщения — это модульная арифметика сумма кодовых слов сообщения фиксированной длины слова (например, байтовых значений). Сумма может быть отменена с помощью дополнение операция перед передачей для обнаружения непреднамеренных сообщений с нулевым значением.

Схемы контрольной суммы включают биты четности, проверить цифры, и продольный контроль избыточности. Некоторые схемы контрольных сумм, такие как Алгоритм дамма, то Алгоритм Луна, а Алгоритм Верхоффа, специально разработаны для обнаружения ошибок, обычно вносимых людьми при записи или запоминании идентификационных номеров.

Циклическая проверка избыточности

А циклическая проверка избыточности (CRC) небезопасный хеш-функция предназначен для обнаружения случайных изменений цифровых данных в компьютерных сетях. Он не подходит для обнаружения злонамеренно внесенных ошибок. Характеризуется спецификацией порождающий полином, который используется как делитель в полиномиальное деление в столбик через конечное поле, принимая входные данные как дивиденд. В остаток становится результатом.

CRC имеет свойства, которые делают его хорошо подходящим для обнаружения пакетные ошибки. CRC особенно легко реализовать на оборудовании и поэтому обычно используются в компьютерная сеть и устройства хранения, такие как жесткие диски.

Бит четности можно рассматривать как 1-битную CRC особого случая.

Криптографическая хеш-функция

Выход криптографическая хеш-функция, также известный как Дайджест сообщения, может дать твердую уверенность в целостность данных независимо от того, являются ли изменения данных случайными (например, из-за ошибок передачи) или намеренно внесены. Любая модификация данных, скорее всего, будет обнаружена по несоответствию хеш-значения. Кроме того, с учетом некоторого хэш-значения, как правило, невозможно найти некоторые входные данные (кроме заданных), которые дадут такое же хеш-значение. Если злоумышленник может изменить не только сообщение, но и значение хеш-функции, то ключевой хеш или же код аутентификации сообщения (MAC) можно использовать для дополнительной безопасности. Не зная ключа, злоумышленник не может легко или удобно вычислить правильное ключевое значение хеш-функции для измененного сообщения.

Код исправления ошибок

Для обнаружения ошибок можно использовать любой код исправления ошибок. Код с минимум Расстояние Хэмминга, d, может обнаруживать до d — 1 ошибка в кодовом слове. Использование кодов с коррекцией ошибок на основе минимального расстояния для обнаружения ошибок может быть подходящим, если требуется строгое ограничение на минимальное количество обнаруживаемых ошибок.

Коды с минимальным расстоянием Хэмминга d = 2 являются вырожденными случаями кодов с исправлением ошибок и могут использоваться для обнаружения одиночных ошибок. Бит четности является примером кода обнаружения одиночной ошибки.

Приложения

Приложения, требующие малой задержки (например, телефонные разговоры), не могут использовать автоматический повторный запрос (ARQ); они должны использовать упреждающее исправление ошибок (FEC). К тому времени, когда система ARQ обнаружит ошибку и повторно передаст ее, повторно отправленные данные прибудут слишком поздно, чтобы их можно было использовать.

Приложения, в которых передатчик сразу же забывает информацию, как только она отправляется (например, большинство телекамер), не могут использовать ARQ; они должны использовать FEC, потому что при возникновении ошибки исходные данные больше не доступны.

Приложения, использующие ARQ, должны иметь обратный канал; приложения, не имеющие обратного канала, не могут использовать ARQ.

Приложения, требующие крайне низкого уровня ошибок (например, цифровые денежные переводы), должны использовать ARQ из-за возможности неисправимых ошибок с помощью FEC.

Техника обеспечения надежности и контроля также использует теорию кодов с исправлением ошибок.^[8]

Интернет

В типичном TCP / IP стек, контроль ошибок выполняется на нескольких уровнях:

• Каждый Кадр Ethernet использует CRC-32 обнаружение ошибок. Кадры с обнаруженными ошибками отбрасываются аппаратурой приемника.
• В IPv4 заголовок содержит контрольная сумма защита содержимого заголовка. Пакеты с неверными контрольными суммами сбрасываются в сети или на приемнике.
• Контрольная сумма не указана в IPv6 заголовок, чтобы минимизировать затраты на обработку в сетевая маршрутизация и потому что текущий уровень связи предполагается, что технология обеспечивает достаточное обнаружение ошибок (см. также RFC 3819 ).
• UDP имеет необязательную контрольную сумму, покрывающую полезную нагрузку и адресную информацию в заголовках UDP и IP. Пакеты с неверными контрольными суммами отбрасываются Сетевой стек. Контрольная сумма не является обязательной для IPv4 и требуется для IPv6. Если этот параметр опущен, предполагается, что уровень канала передачи данных обеспечивает желаемый уровень защиты от ошибок.
• TCP предоставляет контрольную сумму для защиты полезной нагрузки и адресной информации в заголовках TCP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком и в конечном итоге повторно передаются с использованием ARQ либо явно (например, через тройной удар ) или неявно из-за тайм-аут.

Телекоммуникации в дальнем космосе

Разработка кодов исправления ошибок была тесно связана с историей полетов в дальний космос из-за чрезмерного ослабления мощности сигнала на межпланетных расстояниях и ограниченной доступной мощности на борту космических зондов. В то время как ранние миссии отправляли свои данные в незашифрованном виде, начиная с 1968 года, цифровое исправление ошибок было реализовано в форме (субоптимально декодированные) сверточные коды и Коды Рида – Маллера.^[9] Код Рида-Мюллера хорошо подходил к шуму, которому подвергался космический корабль (приблизительно соответствуя кривая колокола ), и был реализован для космического корабля Mariner и использовался в миссиях с 1969 по 1977 год.

В Вояджер 1 и Вояджер 2 миссии, начатые в 1977 году, были предназначены для доставки цветных изображений и научной информации из Юпитер и Сатурн.^[10] Это привело к повышенным требованиям к кодированию, и, таким образом, космический аппарат поддерживался (оптимально Витерби-декодированный ) сверточные коды, которые могут быть соединенный с внешним Код Голая (24,12,8). Корабль «Вояджер-2» дополнительно поддерживал реализацию Код Рида – Соломона. Конкатенированный код Рида – Соломона – Витерби (RSV) позволил произвести очень мощную коррекцию ошибок и позволил космическому аппарату совершить длительный путь к Уран и Нептун. После модернизации системы ECC в 1989 году оба корабля использовали кодирование V2 RSV.

В Консультативный комитет по системам космических данных в настоящее время рекомендует использовать коды исправления ошибок с производительностью, как минимум, аналогичной коду Voyager 2 RSV. Составные коды все больше теряют популярность в космических миссиях и заменяются более мощными кодами, такими как Турбо коды или же Коды LDPC.

Различные виды дальних космических и орбитальных миссий предполагают, что попытка найти универсальную систему исправления ошибок будет постоянной проблемой. Для миссий, близких к Земле, характер шум в канал связи отличается от того, что испытывает космический корабль в межпланетной миссии. Кроме того, по мере того как космический корабль удаляется от Земли, проблема коррекции шума становится все более сложной.

Спутниковое вещание

Спрос на спутник транспондер пропускная способность продолжает расти, чему способствует желание предоставлять телевидение (включая новые каналы и телевидение высокой четкости ) и данные IP. Доступность транспондеров и ограничения полосы пропускания ограничили этот рост. Емкость транспондера определяется выбранным модуляция схема и доля мощности, потребляемой ТЭК.

Хранилище данных

Коды обнаружения и исправления ошибок часто используются для повышения надежности носителей данных.^[11] «Трек паритета» присутствовал на первом хранение данных на магнитной ленте в 1951 г. «Оптимальный прямоугольный код», использованный в групповая кодированная запись ленты не только обнаруживают, но и исправляют однобитовые ошибки. Немного форматы файлов, особенно форматы архивов, включить контрольную сумму (чаще всего CRC32 ) для обнаружения повреждения и усечения и может использовать избыточность и / или файлы четности для восстановления частей поврежденных данных. Коды Рида-Соломона используются в компакт-диски для исправления ошибок, вызванных царапинами.

Современные жесткие диски используют коды CRC для обнаружения и коды Рида – Соломона для исправления незначительных ошибок при чтении секторов, а также для восстановления данных из «испорченных» секторов и сохранения этих данных в резервных секторах.^[12] RAID системы используют различные методы исправления ошибок для исправления ошибок, когда жесткий диск полностью выходит из строя. Файловые системы, такие как ZFS или же Btrfs, а также некоторые RAID внедрения, поддержка очистка данных и повторное обновление, которое позволяет обнаруживать и (надеюсь) восстанавливать плохие блоки перед их использованием.^[13] Восстановленные данные могут быть перезаписаны точно в том же физическом месте, чтобы освободить блоки в другом месте на том же оборудовании, или данные могут быть перезаписаны на заменяющее оборудование.

Память с исправлением ошибок

DRAM память может обеспечить более надежную защиту от мягкие ошибки полагаясь на коды исправления ошибок.^[14] Такой исправляющая память, известный как ECC или же EDAC-защищенный память, особенно желательна для критически важных приложений, таких как научные вычисления, финансы, медицина и т. д., а также для приложений дальнего космоса из-за увеличения радиация в космосе.

Контроллеры памяти с исправлением ошибок традиционно используют Коды Хэмминга, хотя некоторые используют тройное модульное резервирование.

Чередование позволяет распределить эффект одного космического луча, потенциально нарушающего несколько физически соседних битов по множеству слов, путем связывания соседних битов с разными словами. Пока одно событие расстроено (SEU) не превышает порог ошибки (например, одиночная ошибка) в любом конкретном слове между обращениями, это может быть исправлено (например, с помощью однобитового кода исправления ошибок), и иллюзия безошибочной системы памяти может быть сохранен.^[15]

Помимо оборудования, обеспечивающего функции, необходимые для работы памяти ECC, операционные системы обычно содержат соответствующие средства отчетности, которые используются для предоставления уведомлений о прозрачном восстановлении мягких ошибок. Увеличение количества мягких ошибок может указывать на то, что DIMM модуль нуждается в замене, и такая обратная связь не была бы легко доступна без соответствующих возможностей отчетности. Одним из примеров является Ядро Linux с EDAC подсистема (ранее известная как Bluesmoke), который собирает данные от компонентов компьютерной системы с включенной функцией проверки ошибок; Помимо сбора и отправки отчетов о событиях, связанных с памятью ECC, он также поддерживает другие ошибки контрольной суммы, в том числе обнаруженные на Шина PCI.^[16][17][18]

Некоторые системы также поддерживают очистка памяти.

Смотрите также

• Код Бергера
• Пакетный код исправления ошибок
• Плевать будильник
• Память ECC, тип компьютерного хранилища данных
• Запрещенный ввод
• Адаптация ссылки
• Список алгоритмов обнаружения и исправления ошибок
• Список кодов исправления ошибок
• Список хеш-функций
• Надежность (компьютерные сети)

Рекомендации

дальнейшее чтение

• Шу Линь; Дэниел Дж. Костелло-младший (1983). Кодирование с контролем ошибок: основы и приложения. Prentice Hall. ISBN  0-13-283796-X.

внешняя ссылка

• Он-лайн учебник: теория информации, выводы и алгоритмы обучения, к Дэвид Дж. К. Маккей, содержит главы, посвященные элементарным кодам, исправляющим ошибки; о теоретических пределах исправления ошибок; и на последних современных кодах исправления ошибок, в том числе коды с низкой плотностью проверки четности, турбокоды, и коды фонтанов.
• Вычислить параметры линейных кодов — интерактивный интерфейс для генерации и вычисления параметров (например, минимальное расстояние, радиус покрытия ) из линейные коды исправления ошибок.
• Страница ECC
• SoftECC: система проверки целостности программной памяти
• Настраиваемая программная библиотека обнаружения и исправления ошибок DRAM для HPC
• Обнаружение и исправление скрытых искажений данных для крупномасштабных высокопроизводительных вычислений

In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.

Definitions[edit]

Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.

Error correction is the detection of errors and reconstruction of the original, error-free data.

History[edit]

In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.^[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.^[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.^[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.^[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.^[5]

The modern development of error correction codes is credited to Richard Hamming in 1947.^[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication^[7] and was quickly generalized by Marcel J. E. Golay.^[8]

Introduction[edit]

All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.

Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.

If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.

Types of error correction[edit]

There are three major types of error correction.^[9]

Automatic repeat request[edit]

Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.

Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.

Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.

ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.^[10]

For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.

Forward error correction[edit]

Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,^[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.^[13]

Error-correcting codes are usually distinguished between convolutional codes and block codes:

• Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
• Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.

Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.

The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.

Hybrid schemes[edit]

Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:^[10]

• Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
• Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.

The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.

Error detection schemes[edit]

Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.

There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).

Minimum distance coding[edit]

A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.

Repetition codes[edit]

A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.

A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.^[14][15]

Parity bit[edit]

A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.

Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.

There are also other bit-grouping techniques.

Checksum[edit]

A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.

Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.

Cyclic redundancy check[edit]

A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.

A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.

The parity bit can be seen as a special-case 1-bit CRC.

Cryptographic hash function[edit]

The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.

Error correction code[edit]

Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.

Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.

Applications[edit]

Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.

Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.

Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.

Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.

Reliability and inspection engineering also make use of the theory of error-correcting codes.^[16]

Internet[edit]

In a typical TCP/IP stack, error control is performed at multiple levels:

• Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
• The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
• The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
• UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
• TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.

Deep-space telecommunications[edit]

The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.^[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.

The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.^[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.

The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.

The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.

Satellite broadcasting[edit]

The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.

Data storage[edit]

Error detection and correction codes are often used to improve the reliability of data storage media.^[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.

Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.^[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.^[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.

Error-correcting memory[edit]

Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.

Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.^[22]

In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.^[23][24][25] A few systems^[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.

See also[edit]

• Berger code
• Burst error-correcting code
• ECC memory, a type of computer data storage
• Link adaptation
• List of algorithms § Error detection and correction
• List of hash functions

References[edit]

Further reading[edit]

• Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
• SoftECC: A System for Software Memory Integrity Checking
• A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
• Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing

External links[edit]

• The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
• ECC Page — implementations of popular ECC encoding and decoding routines

In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.

Definitions[edit]

Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.

Error correction is the detection of errors and reconstruction of the original, error-free data.

History[edit]

In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.^[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.^[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.^[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.^[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.^[5]

The modern development of error correction codes is credited to Richard Hamming in 1947.^[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication^[7] and was quickly generalized by Marcel J. E. Golay.^[8]

Introduction[edit]

All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.

Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.

If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.

Types of error correction[edit]

There are three major types of error correction.^[9]

Automatic repeat request[edit]

Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.

Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.

Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.

ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.^[10]

For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.

Forward error correction[edit]

Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,^[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.^[13]

Error-correcting codes are usually distinguished between convolutional codes and block codes:

• Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
• Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.

Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.

The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.

Hybrid schemes[edit]

Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:^[10]

• Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
• Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.

The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.

Error detection schemes[edit]

Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.

There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).

Minimum distance coding[edit]

A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.

Repetition codes[edit]

A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.

A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.^[14][15]

Parity bit[edit]

A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.

Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.

There are also other bit-grouping techniques.

Checksum[edit]

A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.

Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.

Cyclic redundancy check[edit]

A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.

A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.

The parity bit can be seen as a special-case 1-bit CRC.

Cryptographic hash function[edit]

The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.

Error correction code[edit]

Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.

Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.

Applications[edit]

Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.

Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.

Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.

Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.

Reliability and inspection engineering also make use of the theory of error-correcting codes.^[16]

Internet[edit]

In a typical TCP/IP stack, error control is performed at multiple levels:

• Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
• The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
• The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
• UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
• TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.

Deep-space telecommunications[edit]

The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.^[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.

The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.^[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.

The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.

The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.

Satellite broadcasting[edit]

The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.

Data storage[edit]

Error detection and correction codes are often used to improve the reliability of data storage media.^[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.

Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.^[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.^[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.

Error-correcting memory[edit]

Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.

Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.^[22]

In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.^[23][24][25] A few systems^[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.

See also[edit]

• Berger code
• Burst error-correcting code
• ECC memory, a type of computer data storage
• Link adaptation
• List of algorithms § Error detection and correction
• List of hash functions

References[edit]

Further reading[edit]

• Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
• SoftECC: A System for Software Memory Integrity Checking
• A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
• Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing

External links[edit]

• The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
• ECC Page — implementations of popular ECC encoding and decoding routines

Программы для исправления ошибок бывают необходимы во многих случаях: когда нужно проверить документ большого объема или быстро устранить опечатки в тексте. Часто пользователи жалуются на то, что вычитывают текст по нескольку раз, но все равно пропускают ряд ошибок, списывая это на собственную невнимательность. В чем бы ни заключалась проблема, без программ для исправления ошибок работать действительно сложно — даже тем, у кого с внимательностью нет никаких проблем. В этой статье мы расскажем, какими программами для исправления ошибок пользуются юзеры сети и почему.

Доброго времени суток. На днях у меня возникла задача по реализации алгоритма пост-обработки результатов оптического распознавания текста. Для решения этой проблемы не плохо подошла одна из моделей для проверки орфографии в тексте, хотя конечно слегка модифицированная под контекст задачи. Этот пост будет посвящен модели Noisy Channel, которая позволяет осуществлять автоматическую проверку орфографии, мы изучим математическую модель, напишем на c# немного кода, обучим модель на базе Питера Норвига, и под конец протестируем то что у нас получится.

Математическая модель — 1

Для начала постановка задачи. Итак вы хотите написать некоторое слово w состоящее из m букв, но каким то неведомым вам способом на бумаге выходит слово x состоящее из n букв. Кстати вы как раз и есть тот самый noisy channel, канал передачи информации с шумами, который исказил правильное слово w (из вселенной правильных слов) до не правильного x (множества всех написанных слов).

Мы хотим найти такое слово, которое вы наиболее вероятно подразумевали при написании слова x. Запишем эту мысль математически, модель по своей идее похожа на модель наивного байесовского классификатора, хотя даже проще:

• V — список всех слов естественного языка.

Далее используя теорему Байеса развернем причину и следствие, полную вероятность x мы можем убрать из знаменателя, т.к. он при argmax не зависит от w:

• P(w) — априорная вероятность слова w в языке; этот член представляет из себя статистическую модель естественного языка (language model), мы будем использовать модель unigram, хотя конечно вы в праве использовать и более сложные модели; так же заметим, что значение этого члена легко вычисляется из базы слов языка;
• P(x | w) — вероятность того, что правильное слово w было ошибочно написано как x, этот член называется channel model; в принципе обладая достаточно большой базой, которая содержит все способы ошибиться при написании каждого слова языка, то вычисление этого члена не вызвало бы трудностей, но к сожалению такой большой базы нет, но есть похожие базы меньшего размера, так что придется как то выкручиваться (например здесь находится база из 333333 слов английского языка, и только для 7481 есть слова с ошибками).

Вычисление значения вероятности P(x | w)

Тут к нам на помощь приходит расстояние Дамерау-Левенштейна — это мера между двумя последовательностями символов, определяемая как минимальное количество операций вставки, удаления, замены и перестановки соседних символов для приведения строки source к строке target. Мы же далее будем использовать расстояние Левенштейна, которое отличается тем, что не поддерживает операцию перестановки соседних символов, так будет проще. Оба эти алгоритма с примерами хорошо описаны в тут, так что я повторяться не буду, а сразу приведу код:

public static int LevenshteinDistance(string s, string t)
{
    int[,] d = new int[s.Length + 1, t.Length + 1];
    for (int i = 0; i < s.Length + 1; i++)
    {
        d[i, 0] = i;
    }
    for (int j = 1; j < t.Length + 1; j++)
    {
        d[0, j] = j;
    }

    for (int i = 1; i <= s.Length; i++)
    {
        for (int j = 1; j <= t.Length; j++)
        {
            d[i, j] = (new int[]
            {
                d[i - 1, j] + 1, // del
                d[i, j - 1] + 1, // ins
                d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub
            }).Min();
        }
    }
    return d[s.Length, t.Length];
}

Эта функция сообщает нам сколько операций удаления, вставки и замены нужно произвести для приведения одного слова к другому, но нам этого не достаточно, а хотелось бы получить так же список этих самых операций, назовем это backtrace алгоритма. Нам необходим модифицировать приведенный код таким образом, что бы при вычислении матрицы расстояний d, так же записывалась матрица операций b. Рассмотрим пример для слов ca и abc:

Как вы помните, значение ячейки (i,j) в матрице расстояний d вычисляется следующим образом:

d[i, j] = (new int[]
{
    d[i - 1, j] + 1, // del - 0
    d[i, j - 1] + 1, // ins - 1
    d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub - 2
}).Min();

Нам остается в ячейку (i,j) матрицы операций b записывать индекс операции (0 для удаления, 1 для вставки и 2 для замены), соответственно этот кусок кода преобразуется следующим образом:

IList<int> vals = new List<int>()
{
    d[i - 1, j] + 1, // del
    d[i, j - 1] + 1, // ins
    d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub
};
d[i, j] = vals.Min();
int idx = vals.IndexOf(d[i, j]);
b[i, j] = idx;

Как только обе матрицы заполнены, не составит труда вычислить backtrace (стрелочки на картинках выше). Это путь из правой нижней ячейки матрицы операций, по пути наименьшей стоимости матрицы расстояний. Опишем алгоритм:

1. обозначим правую нижнюю ячейку как текущую
2. делаем одно из следующих действий
   • если удаление, то записываем удаленный символ, и сдвигаем текущую ячейку вверх (красная стрелка)
   • если вставка, то записываем вставленный символ и сдвигаем текущую ячейку влево (красная стрелка)
   • если замена, а так же заменяемые символы не равны, то записываем заменяемые символы и сдвигаем текущую ячейку налево и вверх (красная стрелка)
   • если замена, но заменяемые символы равны, то только сдвигаем текущую ячейку налево и вверх (синяя стрелка)

3. если количество записанных операций не равно расстоянию Левенштейна, то на пункт назад, иначе стоп

В итоге получим следующую функцию, вычисляющую расстояние Левенштейна, а так же backtrace:

//del - 0, ins - 1, sub - 2 
public static Tuple<int, IList<Tuple<int, string>>> LevenshteinDistanceWithBacktrace(string s, string t)
{
    int[,] d = new int[s.Length + 1, t.Length + 1];
    int[,] b = new int[s.Length + 1, t.Length + 1];
    for (int i = 0; i < s.Length + 1; i++)
    {
        d[i, 0] = i;
    }
    for (int j = 1; j < t.Length + 1; j++)
    {
        d[0, j] = j;
        b[0, j] = 1;
    }

    for (int i = 1; i <= s.Length; i++)
    {
        for (int j = 1; j <= t.Length; j++)
        {
            IList<int> vals = new List<int>()
            {
                d[i - 1, j] + 1, // del
                d[i, j - 1] + 1, // ins
                d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub
            };
            d[i, j] = vals.Min();
            int idx = vals.IndexOf(d[i, j]);
            b[i, j] = idx;
        }
    }

    List<Tuple<int, string>> bt = new List<Tuple<int, string>>();
    int x = s.Length;
    int y = t.Length;
    while (bt.Count != d[s.Length, t.Length])
    {
        switch (b[x, y])
        {
            case 0:
                x--;
                bt.Add(new Tuple<int, string>(0, s[x].ToString()));
                break;
            case 1:
                y--;
                bt.Add(new Tuple<int, string>(1, t[y].ToString()));
                break;
            case 2:
                x--;
                y--;
                if (s[x] != t[y])
                {
                    bt.Add(new Tuple<int, string>(2, s[x] + "" + t[y]));
                }
                break;
        }
    }
    bt.Reverse();

    return new Tuple<int, IList<Tuple<int, string>>>(d[s.Length, t.Length], bt);
}

Эта функция возвращает кортеж, в первом элементе которого записано расстояние Левенштейна, а во втором список пар <id операции, строка>, строка состоит из одного символа для операций удаления и вставки, и из двух символов для операции замены (подразумевается замена первого символа на второй).

PS: внимательный читатель заметит, что из правой нижней ячейки часто существует несколько способов движения по пути наименьшей стоимости, это один из способов увеличить выборку, но мы его для простоты так же опустим.

Математическая модель — 2

Теперь опишем полученный выше результат на языке формул. Для двух слов x и w мы можем вычислить список операций необходимых для приведений первого слова ко второму, обозначим список операции буквой f, тогда вероятность написать слово x как w будет равна вероятности произвести весь список ошибок f при условии, что мы писали именно x, а подразумевали w:

Вот тут начинаются упрощения, похожие на те что были в наивном байесовском классификаторе:

• порядок следования операций ошибки не имеет значения
• ошибка не будет зависеть от того какое слово мы написали и от того что подразумевали

Теперь для того что бы вычислить вероятности ошибок (независимо от того в каких словах они были сделаны) достаточно иметь на руках любую базу слов с их ошибочным написанием. Запишем финальную формулу, во избежание работы с числами близкими к нулю, будем работать в log space:

Итак, что же мы имеем? Если у нас на руках есть достаточный набор текстов мы можем вычислить априорные вероятности слов в языке; так же имея на руках базу слов с их ошибочным написанием, мы можем вычислить вероятности ошибок, этих двух баз достаточно что бы реализовать модель.

Размытие вероятностей ошибок

При пробеге по все базе слов при argmax, мы ни разу не наткнемся на слова с нулевой вероятностью. Но вот при вычислении операций редактирования для приведения слова x к слову w могут возникнуть такие операции, которые не встречались в нашей базе ошибок. В этом случае нам поможет additive smoothing или размытие по Лапласу (оно так же использовалось в наивном байесовском классификаторе). Напомню формулу, в контексте текущей задачи. Если некоторая операция коррекции f встречается в базе n раз, при том что всего ошибок в базе m, а типов коррекции t (например для замены, не то сколько раз встречается замена «a на b«, а сколько всего уникальных пар «* на *»), то размытая вероятность выглядит следующим образом, где k — коэффициент размытия:

Тогда вероятность операции которая ни разу не встречалась в обучающей базе (n = 0) будет равна:

Скорость

Возникает естественный вопрос, а как быть со скоростью работы алгоритма, ведь нам придется пробегать по всей базе слов, а это сотни тысяч вызовов функции вычисления расстояния Левенштейна с backtrace’ом, а так же вычислять для всех слов вероятности ошибки (сумма чисел, если хранить в базе предвычисленные логарифмы). Тут приходит на помощь следующий статистический факт:

• 80% всех печатных ошибок находятся в пределах 1 операции редактирования, т.е. расстояния Левенштейна равным единице
• почти все печатные ошибки находятся в пределах 2 операций редактирования

Ну а далее вы можете придумывать различные алгоритмические трюки. Я использовал очевидный и очень простой способ ускорить работу алгоритма. Очевидно, что если мне требуются только слова не более чем в t операций редактирования от текущего слова, то их длина отличается от текущего не более чем на t. При инициализации класса, я создаю хэш-таблицу, в которой ключами является длины слов, а значениями — множества слов этой длины, это позволяет значительно сокращать пространство поиска.

Код

Приведу код класса NoisyChannel который у меня получился:

public class NoisyChannel
{

    #region vars

    private string[] _words = null;
    private double[] _wLogPriors = null;        
    private IDictionary<int, IList<int>> _wordLengthDictionary = null; //length of word - word indices 
    private IDictionary<int, IDictionary<string, double>> _mistakeLogProbs = null;
    private double _lf = 1d;
    private IDictionary<int, int> _mNorms = null;

    #endregion

    #region ctor

    public NoisyChannel(string[] words, long[] wordFrequency, 
                        IDictionary<int, IDictionary<string, int>> mistakeFrequency, 
                        int mistakeProbSmoothing = 1)
    {
        _words = words;
        _wLogPriors = new double[_words.Length];
        _wordLengthDictionary = new SortedDictionary<int, IList<int>>();
        double wNorm = wordFrequency.Sum();
        for (int i = 0; i < _words.Length; i++)
        {
            _wLogPriors[i] = Math.Log((wordFrequency[i] + 0d)/wNorm);

            int wl = _words[i].Length;
            if (!_wordLengthDictionary.ContainsKey(wl))
            {
                _wordLengthDictionary.Add(wl, new List<int>());
            }
            _wordLengthDictionary[wl].Add(i);
        }

        _lf = mistakeProbSmoothing;
        _mistakeLogProbs = new Dictionary<int, IDictionary<string, double>>();
        _mNorms = new Dictionary<int, int>();
        foreach (int mType in mistakeFrequency.Keys)
        {
            int mNorm = mistakeFrequency[mType].Sum(m => m.Value);
            _mNorms.Add(mType, mNorm);
            int mUnique = mistakeFrequency[mType].Count;
            _mistakeLogProbs.Add(mType, new Dictionary<string, double>());
            foreach (string m in mistakeFrequency[mType].Keys)
            {
                _mistakeLogProbs[mType].Add(m,
                        Math.Log((mistakeFrequency[mType][m] + _lf)/
                                    (mNorm + _lf*mUnique))
                    );
            }
        }
    }

    #endregion

    #region correction

    public IDictionary<string, double> GetCandidates(string s, int maxEditDistance = 2)
    {
        IDictionary<string, double> candidates = new Dictionary<string, double>();
        IList<int> dists = new List<int>();
        for (int i = s.Length - maxEditDistance; i <= s.Length + maxEditDistance; i++)
        {
            if (i >= 0)
            {
                dists.Add(i);
            }
        }
        foreach (int dist in dists)
        {
            foreach (int tIdx in _wordLengthDictionary[dist])
            {
                string t = _words[tIdx];
                Tuple<int, IList<Tuple<int, string>>> d = LevenshteinDistanceWithBacktrace(s, t);
                if (d.Item1 > maxEditDistance)
                {
                    continue;
                }

                double p = _wLogPriors[tIdx];
                foreach (Tuple<int, string> m in d.Item2)
                {
                    if (!_mistakeLogProbs[m.Item1].ContainsKey(m.Item2))
                    {
                        p += _lf/(_mNorms[m.Item1] + _lf*_mistakeLogProbs[m.Item1].Count);
                    }
                    else
                    {
                        p += _mistakeLogProbs[m.Item1][m.Item2];
                    }
                }
                candidates.Add(_words[tIdx], p);
            }
        }
        candidates = candidates.OrderByDescending(c => c.Value).ToDictionary(c => c.Key, c => c.Value);
        return candidates;
    }

    #endregion

    #region static helper

    //del - 0, ins - 1, sub - 2 
    public static Tuple<int, IList<Tuple<int, string>>> LevenshteinDistanceWithBacktrace(string s, string t)
    {
        int[,] d = new int[s.Length + 1, t.Length + 1];
        int[,] b = new int[s.Length + 1, t.Length + 1];
        for (int i = 0; i < s.Length + 1; i++)
        {
            d[i, 0] = i;
        }
        for (int j = 1; j < t.Length + 1; j++)
        {
            d[0, j] = j;
            b[0, j] = 1;
        }

        for (int i = 1; i <= s.Length; i++)
        {
            for (int j = 1; j <= t.Length; j++)
            {
                IList<int> vals = new List<int>()
                {
                    d[i - 1, j] + 1, // del
                    d[i, j - 1] + 1, // ins
                    d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub
                };
                d[i, j] = vals.Min();
                int idx = vals.IndexOf(d[i, j]);
                b[i, j] = idx;
            }
        }

        List<Tuple<int, string>> bt = new List<Tuple<int, string>>();
        int x = s.Length;
        int y = t.Length;
        while (bt.Count != d[s.Length, t.Length])
        {
            switch (b[x, y])
            {
                case 0:
                    x--;
                    bt.Add(new Tuple<int, string>(0, s[x].ToString()));
                    break;
                case 1:
                    y--;
                    bt.Add(new Tuple<int, string>(1, t[y].ToString()));
                    break;
                case 2:
                    x--;
                    y--;
                    if (s[x] != t[y])
                    {
                        bt.Add(new Tuple<int, string>(2, s[x] + "" + t[y]));
                    }
                    break;
            }
        }
        bt.Reverse();

        return new Tuple<int, IList<Tuple<int, string>>>(d[s.Length, t.Length], bt);
    }

        public static int LevenshteinDistance(string s, string t)
        {
            int[,] d = new int[s.Length + 1, t.Length + 1];
            for (int i = 0; i < s.Length + 1; i++)
            {
                d[i, 0] = i;
            }
            for (int j = 1; j < t.Length + 1; j++)
            {
                d[0, j] = j;
            }

            for (int i = 1; i <= s.Length; i++)
            {
                for (int j = 1; j <= t.Length; j++)
                {
                    d[i, j] = (new int[]
                    {
                        d[i - 1, j] + 1, // del
                        d[i, j - 1] + 1, // ins
                        d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub
                    }).Min();
                }
            }
            return d[s.Length, t.Length];
        }

    #endregion

}

Инициализируется класс следующими параметрами:

• string[] words — список слов языка;
• long[] wordFrequency — частота слов;
• IDictionary<int, IDictionary<string, int>> mistakeFrequency
• int mistakeProbSmoothing = 1 — коэффициент размытия частоты ошибок

Тестирование

Для тестирования используем базу Питера Норвига, в которой содержится 333333 слов с частотами, а также 7481 слово с ошибочными написаниями. Следующий код используется для вычисления значений необходимых для ининциализации класса NoisyChannel:

string[] words = null;
long[] wordFrequency = null;

#region read priors

if (!File.Exists("../../../Data/words.bin") || !File.Exists("../../../Data/wordFrequency.bin"))
{
    IDictionary<string, long> wf = new Dictionary<string, long>();
    Console.Write("Reading data:");
    using (StreamReader sr = new StreamReader("../../../Data/count_1w.txt"))
    {
        string line = sr.ReadLine();
        while (line != null)
        {
            string[] parts = line.Split('t');
            wf.Add(parts[0].Trim(), Convert.ToInt64(parts[1]));
            line = sr.ReadLine();
            Console.Write(".");
        }
        sr.Close();
    }
    Console.WriteLine("Done!");
    words = wf.Keys.ToArray();
    wordFrequency = wf.Values.ToArray();

    using (FileStream fs = File.Create("../../../Data/words.bin"))
    {
        BinaryFormatter bf = new BinaryFormatter();
        bf.Serialize(fs, words);
        fs.Flush();
        fs.Close();
    }

    using (FileStream fs = File.Create("../../../Data/wordFrequency.bin"))
    {
        BinaryFormatter bf = new BinaryFormatter();
        bf.Serialize(fs, wordFrequency);
        fs.Flush();
        fs.Close();
    }
}
else
{
    using (FileStream fs = File.OpenRead("../../../Data/words.bin"))
    {
        BinaryFormatter bf = new BinaryFormatter();
        words = bf.Deserialize(fs) as string[];
        fs.Close();
    }

    using (FileStream fs = File.OpenRead("../../../Data/wordFrequency.bin"))
    {
        BinaryFormatter bf = new BinaryFormatter();
        wordFrequency = bf.Deserialize(fs) as long[];
        fs.Close();
    }
}

#endregion


//del - 0, ins - 1, sub - 2 
IDictionary<int, IDictionary<string, int>> mistakeFrequency = new Dictionary<int, IDictionary<string, int>>();

#region read mistakes

IDictionary<string, IList<string>> misspelledWords = new SortedDictionary<string, IList<string>>();
using (StreamReader sr = new StreamReader("../../../Data/spell-errors.txt"))
{
    string line = sr.ReadLine();
    while (line != null)
    {
        string[] parts = line.Split(':');
        string wt = parts[0].Trim();
        misspelledWords.Add(wt, parts[1].Split(',').Select(w => w.Trim()).ToList());
        line = sr.ReadLine();
    }
    sr.Close();
}
            
mistakeFrequency.Add(0, new Dictionary<string, int>());
mistakeFrequency.Add(1, new Dictionary<string, int>());
mistakeFrequency.Add(2, new Dictionary<string, int>());
foreach (string s in misspelledWords.Keys)
{
    foreach (string t in misspelledWords[s])
    {
        var d = NoisyChannel.LevenshteinDistanceWithBacktrace(s, t);
        foreach (Tuple<int, string> ml in d.Item2)
        {
            if (!mistakeFrequency[ml.Item1].ContainsKey(ml.Item2))
            {
                mistakeFrequency[ml.Item1].Add(ml.Item2, 0);
            }
            mistakeFrequency[ml.Item1][ml.Item2]++;
        }
    }
}

#endregion

Следующий код инициализирует модель и выполняет поиск правильных слов для слова «he;;o» (конечно подразумевается hello, точка-с-запятой находятся справа от l и легко было ошибиться при печати, в базе в списке ошибочных написания слова hello нет слова he;;o) на расстоянии не более 2, с засечением времени:

NoisyChannel nc = new NoisyChannel(words, wordFrequency, mistakeFrequency, 1);

Stopwatch timer = new Stopwatch();
timer.Start();
IDictionary<string, double> c = nc.GetCandidates("he;;o", 2);
timer.Stop();
TimeSpan ts = timer.Elapsed;
Console.WriteLine(ts.ToString());

У меня такое вычисление занимает в среднем чуть менее 1 секунды, хотя конечно процесс оптимизации не исчерпывается приведенными способами, а наоборот, только начинается с них. Взглянем на варианты замены и их вероятности:

Ссылки

• курс Natural Language Processing на курсере
• Natural Language Corpus Data: Beautiful Data
• годное описание алгоритмов Левенштейна и Домерау-Левенштейна

Архив с кодом можно слить от сюда.

По умолчанию Microsoft Word внесен в каталог как основной текстовый процессор, используемый в мире , благодаря своему замечательному историческому времени и большому количеству пользователей, которые он имеет в настоящее время. Принимая во внимание факт что он включен в знаменитый офисный пакет Microsoft .

В этом смысле Word относится к наиболее часто используемым программам для создавать, редактировать, персонализировать и управлять электронными письмами любого типа . Учитывая тот факт, что им управляют как студенты, так и профессионалы из разных сред, благодаря оптимальные инструменты, которые он предлагает для обогащения документов .

Один из них это средство проверки орфографии и грамматики, которое есть в этой программе для более легкого обнаружения слов с ошибками в тексте. Чтобы узнать больше об этой функции и как это использовать , читать дальше.

Прежде чем указывать некоторую интересующую информацию о том, что следует учитывать при использовании этой функции и как вы можете включить или настроить ее в текстовом процессоре, полезно указать в что конкретно делает проверка орфографии в Word .

В этом смысле компьютерную проверку орфографии можно определить как программное приложение, которое позволяет анализировать тексты, чтобы находить и обнаруживать орфографические ошибки , чтобы перейти к их ручному или автоматическому исправлению. Следовательно, в случае Word, это функция, встроенная в программу для облегчить управление документами .

Таким образом, проверка орфографии Microsoft Word служит в основном для того, чтобы помочь пользователю обогатить написание своего текста . Принимая это во внимание, это достигается путем сравнения слов текста со словами словаря и, следовательно, если их нет, они не будут приняты. Следовательно, вы немедленно предоставить аналогичные условия, чтобы заменить их в документе .

Это означает, что его основная функция — редактировать любой текст для убрать письменные ошибки, грамматические ошибки и лексические неточности , чтобы очистить его и убедиться, что читатель может понять весь открытый контент. Поскольку цель проверки орфографии — обеспечить заполнение документов без ошибок или несоответствий при печати .

О чем следует помнить при использовании средства проверки орфографии и грамматики Word?

Несмотря на то, что эта функция работает в Word почти автоматически, правда в том, что есть некоторые предпосылки, которые пользователь должен учитывать при активации и использовании проверки орфографии и грамматики в указанной программе. С, от них вы сможете быстро получить управление указанной утилитой .

Так что, в основном, это интересно ориентироваться на выбранный диалект . Что ж, если вы посмотрите на языковой раздел внизу главного окна Word, вы увидите, что они предлагаем несколько видов «испанского» , например: Аргентина, Колумбия, Испания, Мексика, Венесуэла и многие другие. Что полностью повлияет при проверке и исправлении слов в тексте. Поэтому важно, чтобы вы в этом случае выберите правильный регион .

К этому добавляются и другие аспекты, представляющие большой интерес, которые необходимо понять, прежде чем использовать добавленную грамматику и средство проверки орфографии в Word. Вот самый важный :

• Эта особенность не имеет возможности изменять или переписывать исходную историю, созданную автором , как полагают многие. С тех пор он сосредоточился исключительно на улучшении структуры письма и его представления по отношению к выражениям.
• Его задача — не только дать общую оценку аспектов, которые необходимо исправить в документе, но он также отвечает за предлагать рекомендации и руководить писателями по оптимизации их текстов .
• Проверка орфографии не диктует свой личный стиль , потому что он знает, как важно всегда иметь мнение автора. Следовательно, он не будет вносить никаких изменений в текст без вашего согласия и, что ж, он только предоставляет идеи для улучшения указанного письма на лексическом, грамматическом и синтаксическом уровнях.

Узнайте, как включить и настроить проверку орфографии и грамматики в Microsoft Word.

Ввиду превосходных преимуществ, предлагаемых этой утилитой Word, важно, чтобы все пользователи программы знать, как его активировать и настроить , в соответствии с их потребностями при управлении любой цифровой записью.

Поэтому ниже мы объясним каждый из Шаги по правильному использованию средства проверки орфографии и грамматики в Word :

комментарии

Первое, что вы можете сделать с помощью средства проверки орфографии этой программы для Windows, — это вносить исправления во всем документе . Либо текст в целом, либо только его выделенная часть, в зависимости от того, что вы хотите. Мы упоминаем здесь шаги, которые необходимо выполнить, чтобы активировать эту функцию :

• Для начала вы должны найдите и введите документ, который нужно отредактировать таким образом .
• Как только это будет сделано, перейдите на ленту Word и щелкните вкладку с надписью «Редакция» .
• Затем в группе «Редакция» нажмите на опцию «Орфография и грамматика» .
• Теперь, если программа обнаружит орфографические ошибки, она перейдут к их автоматическому выбору а с правой стороны появится диалоговое окно с первым словом с ошибкой, обнаруженным функцией проверки орфографии и грамматики.
• Наконец он вам просто нужно решить, как исправить эту ошибку , согласно предложенным альтернативам (опустить, изменить или добавить в словарь программы) и, таким образом, Word перейдет к следующему слову или ошибочному выражению.

С другой стороны, если вы хотите быстро запустить проверку орфографии и грамматики документа Microsoft Word, не выполняя все предыдущие шаги; Вы можете просто нажать клавишу F7 и автоматически программа отобразит первую обнаруженную неисправность.

исправления

Среди других альтернатив, связанных со средством проверки орфографии и грамматики в Word, возможно, что та же система мгновенно вносит исправления . Ввиду этого этот инструмент еще называют «автокоррекция» .

Эта функция, соответствующая грамматической проверке орфографии, позволяет вам устанавливать определенные ошибки, чтобы они по умолчанию изменяются средством проверки Word, если пользователь вводит их . Также можно проверить другие полезные функции автокоррекции.

Здесь мы покажем вам, как легко получить доступ к этому разделу, чтобы предусмотреть и записать исправления или «автоматические исправления» что ты хочешь Word автоматически выполняет:

• Находится в рассматриваемом документе, щелкните вкладку «Файл» в панель параметров программы.
• Затем на левой боковой панели нажмите «Параметры» и при этом откроется новое окно, содержащее различные варианты выбора.
• Позже, нажмите «Редакция» а точнее в раздел «Параметры автоматической коррекции» , нажмите кнопку с указанием этого имени, чтобы задать нужные вам термины.
• Enfin, нажмите на обе кнопки ОК , чтобы сохранить внесенные изменения, и при этом вы уже установили автоматическое исправление по умолчанию для Word.

Уведомление на другом языке

Хотя это правда, испанский язык будет использоваться по умолчанию в вашем документе Microsoft Word. Но, если вам нужно написать текст на другом языке и правильно его исправить, есть возможность вносить правки на другом языке без каких-либо осложнений .

В этом случае пошагово следовать следующее :

• Как и в предыдущих случаях, начнем с найти и войти в документ Word в котором вы хотите выполнить проверку орфографии и грамматики на другом языке.
• Тогда пора выберите вкладку «Редакция» на панели параметров главного окна.
• Затем перейдите в поле «Язык» и нажмите стрелку вниз на опции «Язык» . Между двумя отображаемыми вариантами, нажмите «Языковые настройки …» .

• Наконец, откроется новое окно и в указанном разделе для выбора языков редактирования, добавить дополнительные языки, чтобы упростить пересмотр . Другими словами, если ваш текст, например, на немецком языке, вы должны добавить к нему этот язык.

Список лучших инструментов для исправления грамматики и орфографии вне Microsoft Word

Если по какой-то причине вы предпочитаете использовать инструменты, отличные от средства проверки орфографии и грамматики Word, даже при создании текстов из этой программы; есть возможность их делать. С того времени, несколько внешних инструментов были созданы для этой программы, которая легко исправляет орфографию и грамматику .

Поэтому в заключение этой статьи мы остановимся на 5 абсолютно оптимальных бесплатных инструментов для улучшения орфографии и грамматики любого цифрового документа :

CorrectorOnline.es

В первую очередь мы размещаем этот онлайн-инструмент, который используется для находить и выделять основные, орфографические, грамматические и стилистические ошибки в любом цифровом тексте . Как только эти дефекты будут обнаружены, он предложит исправления, чтобы легко обогатить ваш документ. Который, помимо вспомогательных текстов на испанском языке, также имеет другие версии, позволяющие вносить изменения для других языков, например: Английский, португальский, французский, немецкий, итальянский и русский языки .

Со своей стороны, что касается его работы, мы ограничиваем то, что вы должны просто скопируйте и вставьте текст для изменения в указанное поле и если вы установите флажок «Автоматическое исправление», инструмент отобразит страницу результатов со списком, в котором будут указаны все обнаруженные ошибки. Это, когда-то вы нажали кнопку «Отправить» .

Copywritely.com

Еще одним из наиболее известных инструментов для проверки и исправления текстов на предмет возможных орфографических и грамматических ошибок является платформа, которая характеризуется тем, что является одним из наиболее полных для этого . Поскольку, помимо просмотра содержания и рекомендаций по качественному редактированию, он завод также как онлайн-редактор и средство проверки предложений .

К этому добавляется подробное описание процесса использования этого инструмента: вставьте текст, который хотите просмотреть, или его URL-адрес найти орфографические и грамматические ошибки. Позже вы получите рекомендации, как исправить найденные ошибки, а также выполнит переписать текст с помощью онлайн-редактора , затем вы получит обновленный текст .

languagetool.org

Он состоит из еще одной онлайн-проверки орфографии, которая отлично подходит для быстрой и простой проверки ошибок без использования Word и просто путем доступа к Интернету. Оценивая это, бесплатный инструмент (также с некоторыми планами платежей), в котором есть возможность редактировать тексты на нескольких языках (Испанский, английский, французский, немецкий и т. Д.) И не имеет ограничений по длине письма .

Со своей стороны допускает до 20000 знаков на каждую проверку, это оптимальный механизм для изменить стиль, грамматику и орфографию , в дополнение к способности обнаруживать до более чем 2500 XNUMX дополнительных ошибок за короткое время. Чтобы начать обзор, все, что вам нужно сделать, это вставить текст, выбрать правильный язык и нажмите «Проверить текст» . Следует отметить, что предлагает расширение для браузера Google Chrome .

Mystilus.com

Это платный онлайн-инструмент который предлагает своим пользователям два плана подписки и благодаря большому количеству инструментов в его распоряжении, это средство, используемое многими профессионалами при управлении своими цифровыми текстами. Итак, во всех самолетах Стилус обеспечивает чеки грамматика, орфография и стиль, лингвистические инструменты, аудиторские отчеты в различных форматах (PDF, TXT, DOC или HTML), а также гарантирует индивидуальные языковые настройки.

Кроме того, он имеет расширения для Word в Windows, а также для WordPress , учитывая, что он отлично интегрируется, чтобы упростить процесс редактирования. Среди прочего, это предлагает интерактивную коррекцию через Интернет , его лексическая база постоянно обновляется и имеет многоязычный пользовательский интерфейс. Il обеспечивает то же самое обновленные предложения с дидактическими пояснениями и библиографией .

Плагиат.net

Наконец, мы выделяем эту другую онлайн-проверку, которая, несмотря на непривлекательный дизайн страницы и менее известна, чем другие подробные альтернативы, считается хорошим инструментом для проверить орфографию и грамматику любого текста , особенно потому, что это поддерживает несколько языков и среди них кастильский / испанский. Кроме того, следует отметить, что бесплатно и легко использовать .

Как только вы зайдете на соответствующий веб-сайт, паста Simplement запись в соответствующее пустое поле , затем выберите язык указанного текста и нажмите кнопку «Правильное написание» , с помощью которого инструмент выполнит указанную коррекцию. Кроме того, у него есть несколько вариантов редактировать рассматриваемый документ (полужирный, курсив, подчеркивание, размер шрифта, размер и формат и т. д.).

Если у вас есть какие-либо вопросы, оставляйте их в комментариях, мы свяжемся с вами как можно скорее, и это будет большим подспорьем для большего числа участников сообщества. Je Vous remercie!

Инструмент проверки текста на орфографические и грамматические ошибки онлайн, позволит исправить
самые громоздкие
ошибки, с высокой степенью точности и скорости, а
также улучшить свой письменный русский язык.

Если возможно несколько исправлений, вам будет предложено выбрать одно из них.
Слова в которых допущены ошибки выделяются разными цветами, можно кликнуть на подсвеченное слово,
посмотреть описание ошибки
и выбрать исправленный вариант.

Инструмент поддерживает 8 языков.

Орфография

Написать текст без каких-либо орфографических или пунктуационных ошибок достаточно сложно даже
специалистам.
Наша автоматическая проверка
орфографии
может помочь профессионалам, студентам, владельцам веб-сайтов, блогерам и авторам получать текст
практически без ошибок. Это не только поможет им исправить текст, но и
получить информацию о том, почему использование слова неправильно в данном контексте.

Что входит в проверку текста?

• грамматические ошибки;
• стиль;
• логические ошибки;
• проверка заглавных/строчных букв;
• типографика;
• проверка пунктуации;
• общие правила правописания;
• дополнительные правила;

Грамматика

Для поиска грамматических ошибок инструмент содержит более 130 правил.

• Деепричастие и предлог
• Деепричастие и предлог
• «Не» с прилагательными/причастиями
• «Не» с наречиями
• Числительные «оба/обе»
• Согласование прилагательного с существительным
• Число глагола при однородных членах
• И другие

Грамматические ошибки вида: «Идя по улице, у меня развязался шнурок»

• Грамматическая ошибка: Идя по улице, у меня…

• Правильно выражаться: Когда я шёл по улице, у меня развязался шнурок.

Пунктуация

Чтобы найти пунктуационные ошибки и правильно расставить запятые в тексте, инструмент содержит более
60 самых важных правил.

• Пунктуация перед союзами
• Слова не являющиеся вводными
• Сложные союзы не разделяются «тогда как», «словно как»
• Союзы «а», «но»
• Устойчивое выражение
• Цельные выражения
• Пробелы перед знаками препинания
• И другие

Разберем предложение, где пропущена запятая «Парень понял как мальчик сделал эту модель»

• Пунктуационная ошибка, пропущена запятая: Парень понял,

• «Парень понял, как мальчик сделал эту модель»

Какие языки поддерживает инструмент?

Для поиска ошибок вы можете вводить текст не только на Русском
языке, инструмент поддерживает проверку орфографии на Английском, Немецком и Французском

Приложение доступно в Google Play

Никто не застрахован от всевозможных ошибок при написании текста. Более того, рано или поздно каждый сталкивается с ситуацией, когда необходимо создать грамотный текстовый документ для служебных целей. Есть ряд специальных программ, которые помогут с этой задачей, о которых пойдет речь в этой статье.

Key Switcher

Key Switcher — удобный и многофункциональный инструмент, предназначенный для автоматического обнаружения и исправления различных типов ошибок при наборе текста в любой программе, которая, в принципе, имеет поле ввода. Это приложение скрыто и может распознавать более 80 различных языков и диалектов. В список его функций также входит функция распознавания ошибочно включенного макета и его автоматическая модификация. Благодаря «Хранилищу паролей» вам не нужно беспокоиться о том, что при вводе приложение изменит макет и окажется некорректным.

В заключение хотелось бы отметить наличие функции «Автокоррекция», благодаря которой можно настроить автоматическую замену различных сокращений на нужный вариант. Правда, для этого пользователю придется предварительно заполнить эту базу своими словами. Так, например, нельзя изменить раскладку ввода «PS», а написать «shl», после чего Key Switcher автоматически выполнит замену. Это относится к любой другой замене, подобной этой.

Punto Switcher

Punto Switcher — программа, очень похожая по функциональности на предыдущую версию. Он также скрыт в трее и работает в фоновом режиме независимо от конкретного текстового редактора. Кроме того, Punto Switcher может автоматически изменять раскладку клавиатуры или исправлять пользователя, когда он делает опечатку в слове. Основные возможности — транслитерация, замена чисел текстом и изменение регистра орфографии. Punto Switcher также предоставляет функцию сохранения паролей и текстов шаблонов.

Что касается самого исправления ошибок, то здесь есть как общие правила (как исправлять сокращения, две заглавные буквы в начале слова), так и встроенный в базу словарь. Как и в предыдущем программном обеспечении, здесь есть функция «Автозамена», которая упрощает набор часто используемых фраз (например, набор «chd» будет автоматически заменен на «что необходимо доказать») и части предложения, требующие разные макеты. Кроме того, здесь вы можете настроить программы исключения, в рамках которых Punto Switcher не будет работать, а также включить дневник (сохранение набранных текстов в любом приложении), что поможет избежать потери важных писем и документов.

LanguageTool

LanguageTool отличается от других программ, упомянутых в этой статье, главным образом тем, что он предназначен для проверки орфографии уже созданного текста, который был скопирован в буфер обмена. Он содержит правила орфографии для более чем сорока языков, что, в свою очередь, позволяет выполнять проверки высокого качества. Если пользователь замечает отсутствие каких-либо правил, LanguageTool предлагает возможность загрузить их.

Его главная особенность — поддержка N-граммов, которые вычисляют вероятность повторения слов и фраз. Это также должно быть дополнено наличием морфологического анализа контролируемого текста. Также приятно, что программное обеспечение постоянно обновляется, улучшаются словари, что обеспечивает правильное написание не только на родном языке, но и на некоторых иностранных. Кстати, LanguageTool можно установить не только как отдельную программу, но и как надстройку для текстового редактора Microsoft Word, Libre Office, Open Office, Google Docs, расширений для Google Chrome и Mozilla Firefox. К недостаткам можно отнести большой размер дистрибутива (более 150 МБ) и необходимость установки Java для работы.

AfterScan Express

AfterScan Express был создан с целью автоматического исправления ошибок, допущенных при распознавании отсканированного текста сторонним программным обеспечением. Он предлагает пользователю несколько вариантов редактирования, предоставляет отчет о ходе работы и позволяет вносить окончательные исправления. Сам процесс сканирования OCR настраивается и состоит из трех этапов. Попутно вы сможете обрабатывать незнакомые слова, убирать знаки препинания, отступы, «барахло» в соответствии с правилами типографики. Полученный результат можно дополнительно скорректировать: неизвестные слова выделяются красным цветом, и для каждого из них предлагаются любые замены, которые можно вводить с помощью предложенной комбинации клавиш.

Кроме того, есть «Переформатирование», в результате которого будут удалены разрывы строк, сами строки будут склеены, лишние пробелы будут удалены, а другие параметры будут исправлены. Пользователь может настроить форматирование в соответствии со своими потребностями. Поддерживает пакетную обработку текстов, создание собственного словаря. Программа платная и, купив лицензию, пользователь получает дополнительные функции. К ним относятся пакетная обработка документов, настраиваемый словарь и возможность защиты файла от изменений.

Orfo Switcher

Orfo Switcher — еще одна программа, предназначенная для автоматического изменения текста при написании. Он полностью бесплатен, не привязан к конкретному редактору и после установки помещается в системный трей. Программа автоматически изменяет раскладку клавиатуры и предлагает варианты исправления слов с ошибками. Orfo Switcher также предоставляет пользователю возможность составлять словари неограниченного размера, которые содержат исключающие слова (например, пароль) и комбинации букв, необходимые для изменения раскладки клавиатуры. Как и в другом подобном программном обеспечении, здесь вы можете добавить определенные приложения в исключения, чтобы ввод текста в них не проверялся.

Spell Checker

Эта удобная маленькая программа сразу же предупреждает пользователя об опечатке одним словом. Он также может визуально отображать текст, скопированный в буфер обмена, и доступны расширенные параметры визуализации. Но при этом функциональность проверки орфографии распространяется только на английские и русские слова.

Среди дополнительных функций предлагается возможность указать, в каких процессах программа должна работать, а в каких — нет. Также вы можете скачать словари. Главный недостаток Sang Checker в том, что после его установки для работы также необходимо скачать словарь.

ОРФО

Последней в списке будет совсем не программа: ORFO — это надстройка для текстового редактора Microsoft Word. Тот, кто привык создавать документы в этом приложении, но не был удовлетворен базовыми правилами проверки орфографии, оценит возможности ORFO. Он выполняет не только грамматические, но и стилистические проверки, используя более 40 наборов правил и 23 000 шаблонов, которые включают проверку на разных уровнях: строгой, коммерческой или обычной переписке. У каждой найденной ошибки есть описание и объяснение того, почему следует применить то или иное исправление. Кроме того, здесь можно выполнить орфографию согласно стилю газеты и книги. Функция «Тезаурус» обеспечивает поиск и устранение тавтологии (повторения слов) путем поиска синонимов, соответствующих смыслу. Для этих целей в программе есть словарь, содержащий более 60 000 слов, некоторые из которых являются синонимами, антонимами и родственными им.

ORFO состоит из нескольких словарей одновременно, которые вместе обеспечивают высочайший контроль слов и грамматики. Он поддерживает удобную замену определенного слова во всех его словоформах, отображая все доступные формы интересующего слова. Сразу стоит отметить, что расширение платное, но именно здесь программа действительно стоит своих денег. Для работы с ним необходимо установить Word 2016 и более поздние версии, а сама программа выбирается не только по ее версии (есть несколько наборов: Professional, Professional Plus, Maximum, 2 версии для Mac OS), но и в в соответствии с разрядностью самого слова (32/64 бит). В настоящее время разработчик готовит крупное обновление, и, несмотря на то, что сайт выглядит заброшенным, техническая поддержка по электронной почте продолжает активно работать.

В этой статье описаны программы проверки орфографии и пунктуации, которые избавят вас от неграмотного написания текста. После установки одного из них вы можете быть уверены, что все введенные вами слова будут правильными и предложения будут соответствовать правилам орфографии. Однако не забывайте, что даже самое умное программное обеспечение не сможет найти абсолютно все ошибки любого уровня сложности, поэтому не поленитесь перечитать свои тексты и прояснить спорные моменты вручную. Кроме того, отметим, что практически популярные текстовые редакторы имеют встроенную функцию проверки орфографии и пунктуации, а также существуют различные онлайн-сервисы, проверяющие не хуже многих приложений, перечисленных в материале.

Читайте также:
Текстовый редактор для Windows / Linux
Проверьте правописание онлайн