Раскладываем по полочкам параметры АЦП
Время прочтения
10 мин
Просмотры 47K
Привет, Хабр! Многие разработчики систем довольно часто сталкиваются с обработкой аналоговых сигналов. Не все манипуляции с сигналами можно осуществить в аналоговой форме, поэтому требуется переводить аналог в цифровой мир для дальнейшей постобработки. Возникает вопрос: на какие параметры стоит обратить внимание при выборе микроконтроллера или дискретного АЦП? Что все эти параметры означают? В этой статье постараемся детально рассмотреть основные характеристики АЦП и разобраться на что стоит обратить внимание при выборе преобразователя.
Введение
Начать бы хотелось с интересного философского вопроса: если аналоговый сигнал — это бесконечность, теряем ли мы при оцифровке сигнала бесконечное количество информации? Если это так, тогда какой смысл существования такого неэффективного преобразования?
Для того, чтобы ответить на этот вопрос, разберемся с тем, что такое аналого-цифровое преобразование сигнала. Основной график, который отражает работу АЦП – передаточная характеристика преобразования. В идеальном мире это была бы прямая линия, то есть у каждого аналогового уровня сигнала имелся бы единственный цифровой эквивалент.
Рис. 1: Идеальная характеристика АЦП
Однако из-за наличия различных видов шума, мы не можем увеличивать разрядность АЦП до бесконечности. То есть существует предел, который ограничивает минимальную цену деления шкалы. Другими словами, уменьшая деление шкалы мы рано или поздно «упремся» в шум. Да, конечно, можно сделать хоть 100-битный АЦП, однако большинство бит данного АЦП не будут нести полезную информацию. Именно поэтому характеристика АЦП имеет ступенчатую форму, что равносильно наличию конечной разрядности АЦП.
Проектируя систему необходимо выбирать АЦП, который бы обеспечил отсутствие потери информации при оцифровке. Для того, чтобы выбрать преобразователь, необходимо понять, какие параметры его характеризуют.
Параметры АЦП можно разделить на 2 группы:
- Статические — характеризуют АЦП при постоянном или очень медленно изменяющемся входном сигнале. К данным параметрам можно отнести: максимальное и минимальное допустимое значение входного сигнала, разрядность, интегральную и дифференциальную нелинейности, температурную нестабильность параметров преобразования и др.
- Динамические — определяют максимальную скорость преобразования, предельную частоту входного сигнала, шумы и нелинейности.
Статические параметры
- Максимальный (Vref) и минимальный (обычно 0) уровни входного сигнала — устанавливают диапазон шкалы преобразования, относительно которой будет оцениваться входной сигнал (рис. 1). Также этот параметр может обозначаться как FS — full scale. Для дифференциального АЦП шкала определяется от -Vref до +Vref, однако для упрощения далее будем рассматривать только single-ended шкалы.
- Разрядность (N) — разрядность выходного кода, характеризующая количество дискретных значений (
), которые преобразователь может выдать на выходе (рис. 1).
- Ток потребления (Idd) — сильно зависит от частоты преобразования, поэтому информацию об этом параметре лучше искать на соответствующем графике.
- МЗР (LSB) – младший значащий разряд (Least Significant Bit) — минимальное входное напряжение, разрешаемое АЦП (по сути единичный шаг в шкале преобразования). Определяется формулой:
(рис. 1).
- Ошибка смещения (offset error) – определяется как отклонение фактической передаточной характеристики АЦП от передаточной характеристики идеального АЦП в начальной точке шкалы. Измеряется в долях LSB. При ошибке смещения переход выходного кода от 0 в 1 происходит при входном напряжении отличном от 0.5LSB (рис. 2).
Рис. 2: Ошибка смещения
Существует и другой вариант квантователя, когда переход осуществляется при целых значения LSB (характеристика у него будет смещена относительно первого варианта, который представлен на рисунке 2). Оба этих квантователя равноправны, и для простоты далее будем рассматривать только первый вариант. - Ошибка усиления (gain error) – определяется как отклонение средней точки последнего шага преобразования (которому соответствует входное напряжение Vref) реального АЦП от средней точки последнего шага преобразования идеального АЦП после компенсации ошибки смещения (рис. 3).
Рис. 3: Ошибка усиления
- Дифференциальная нелинейность (DNL — Differential nonlinearity) – отклонение ширины ступеньки на передаточной характеристике реального АЦП от номинальной ширины ступеньки у идеального преобразователя. Из-за дифференциальной нелинейности шаги квантования имеют различную ширину (рис. 4).
Рис. 4: Дифференциальная нелинейность
Для 3-х битного АЦП с рисунка 4:
- Интегральная нелинейность ( INL — Integral nonlinearity) – разница по вертикали между реальной и идеальной характеристикой преобразования (рис. 5). INL можно интерпретировать как сумму DNL. Отрицательная INL указывает на то, что реальная характеристика находится ниже идеальной в данной точке шкалы. Для положительной INL реальная характеристика находится выше идеальной. Распределение DNL определяет интегральную нелинейность АЦП.
Рис. 5: Интегральная нелинейность
- Общая нескорректированная ошибка ( TUE — Total Unadjusted Error) – абсолютная ошибка, включающая в себя следующие ошибки: квантования, смещения, усиления и нелинейности. Другими словами, это максимальное отклонение между реальной и идеальной характеристикой преобразования. Для идеального АЦП TUE = 0.5LSB, обусловлена ошибкой квантования (или шум квантования — возникает из-за округления значения аналогового сигнала, которое соответствует цифровому коду). Ошибки усиления и смещения обычно вносят наиболее весомый вклад в абсолютную ошибку. Однако с точки зрения динамических параметров (см. ниже) ошибки смещения и усиления ничтожны, так как они не порождают нелинейных искажений.
Динамические параметры
- Частота дискретизации (fs — sampling frequency) — частота, при которой происходит преобразование в АЦП (ну или 1/Ts, где Ts — период выборки). Измеряется числом выборок в секунду. Обычно под данным обозначением подразумевают максимальную частоту дискретизации, при которой специфицированы параметры преобразователя (рис. 6).
Рис. 6: Процесс преобразования АЦП
- Отношение сигнал/шум (SNR — Signal-to-Noise Ratio) — определяется как отношение мощности обрабатываемого сигнала к мощности шума, добавляемого в процессе преобразования. SNR обычно выражается в децибелах (дБ) и рассчитывается по следующей формуле:
Наглядно данное выражение продемонстрированно на рисунке 7.
Рис. 7: Отношение сигнал/шум
Для оценки SNR АЦП при разработке системы можно воспользоваться следующей формулой:
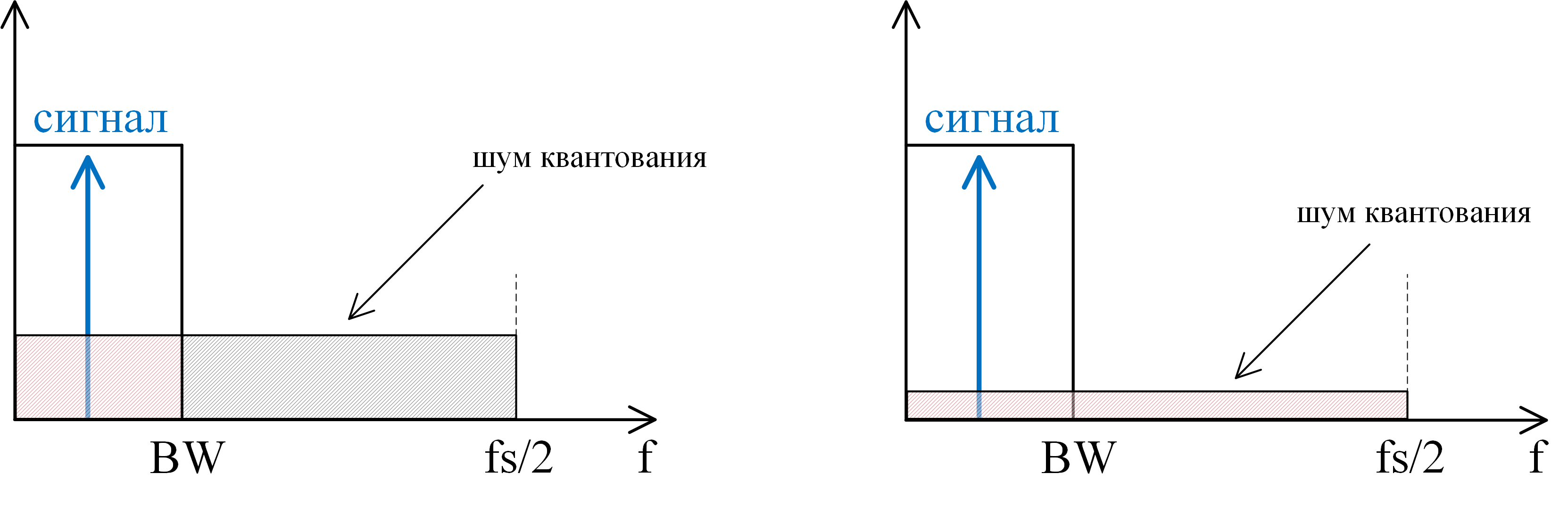
Первые 2 слагаемых учитывают уровень сигнала и ошибку квантования (нужно понимать, что формула верна для сигнала размаха полной шкалы). Третье слагаемое учитывает эффект передискретизации (выигрыш по обработке или processing gain): если полоса обрабатываемого сигнала (BW < fs/2), то, применив цифровой фильтр низких частот (либо полосовой, тут зависит все от полосы и несущей) к результату преобразования, можно вырезать часть шума АЦП, а оставшаяся часть будет распределена от 0 до BW (рис. 8). Если шум АЦП равномерно распределен по всем частотам (т.н. «белый» шум) интегральный шум после фильтрации уменьшится в fs/2 / BW раз, что и отражает третий член формулы.
Рис. 8: Увеличение SNR за счет передискретизации
- Общие нелинейные искажения (THD — total harmonic distortion). Прежде, чем сигнал преобразовывается в цифровой код, он проходит через нелинейные блоки, которые искажают сигнал. К примеру, пусть есть сигнал с частотой f. Пройдя через нелинейный блок к нему добавятся компоненты с частотами 2f, 3f, 4f … — 2-я, 3-я, 4-я и т.д. гармоники входного сигнала. Если дискретизированный сигнал разложить в спектр с помощью ДПФ (Дискретного Преобразования Фурье), мы увидим, что все эти гармоники «перенеслись» в первую зону Найквиста (от 0 до fs/2) (рис. 9).
Рис. 9: Нелинейные искажения
Побочные гармоники искажают обрабатываемый сигнал, что ухудшает производительность системы. Этот эффект можно измерить, используя характеристику общие нелинейные искажения. THD определяется как отношение суммарной мощности гармонических частотных составляющих к мощности основной (исходной) частотной составляющей (в некоторых документациях выражается в дБ):
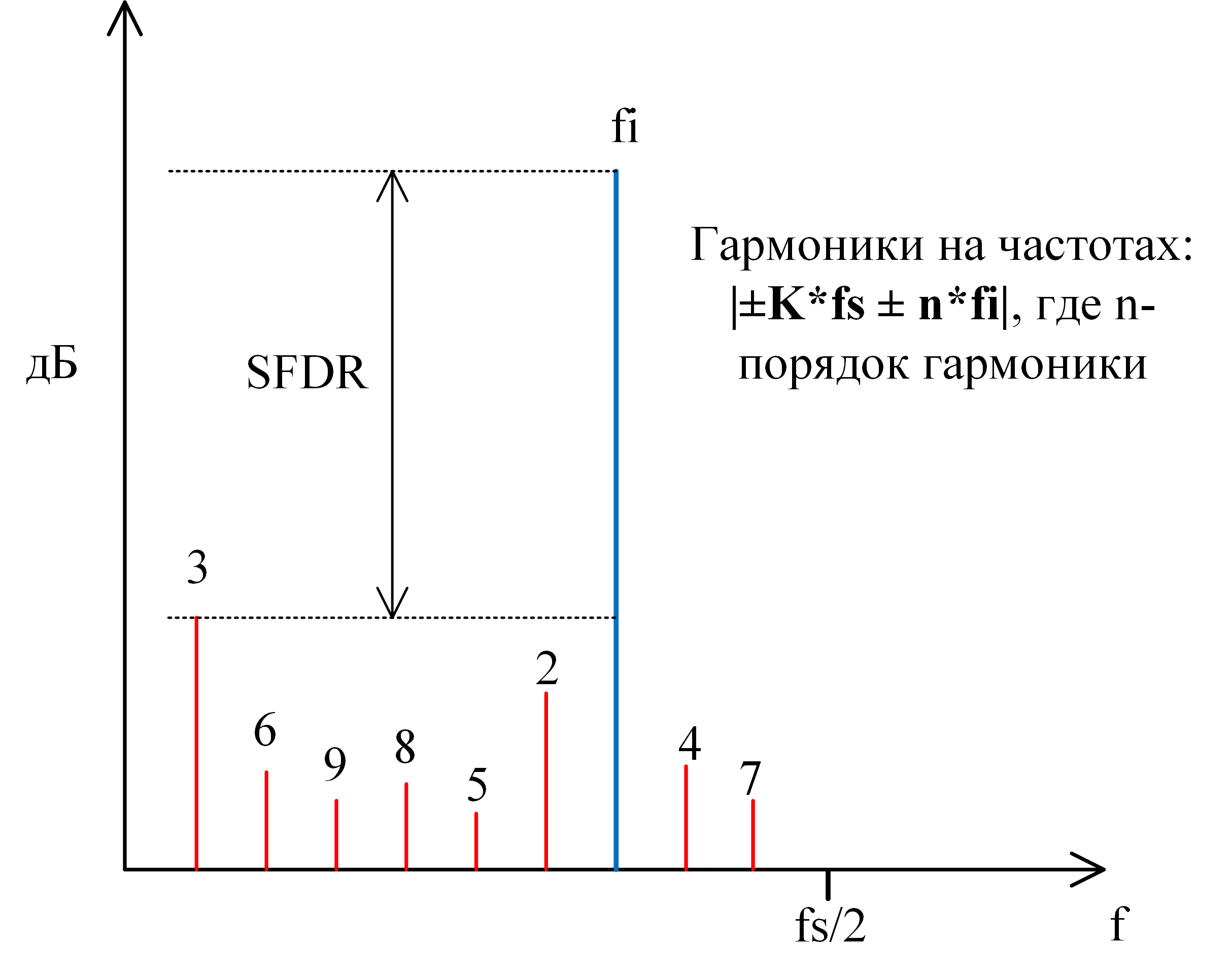
- Динамический диапазон, свободный от гармоник (SFDR — Spurious-Free Dynamic Range). Является отношением мощности полезного сигнала к мощности наибольшего «спура» (любая паразитная составляющая в спектре, не обязательно гармонического происхождения), присутствующего в спектре (рис. 9).
- Отношение сигнал / шум и нелинейные искажения (SINAD — signal-to-noise and distortion ratio). Аналогичен SNR, но помимо шума учитывает все виды помех и искажений, возникающих при аналого-цифровом преобразовании. SINAD является одним из ключевых параметром, характеризующим АЦП (в некоторых источниках обозначается как SNDR):
- Эффективное число бит (ENOB — effective number of bits) – некая абстрактная характеристика, показывающая сколько на самом деле бит в выходном коде АЦП несет в себе полезную информацию. Может принимать дробные значения.
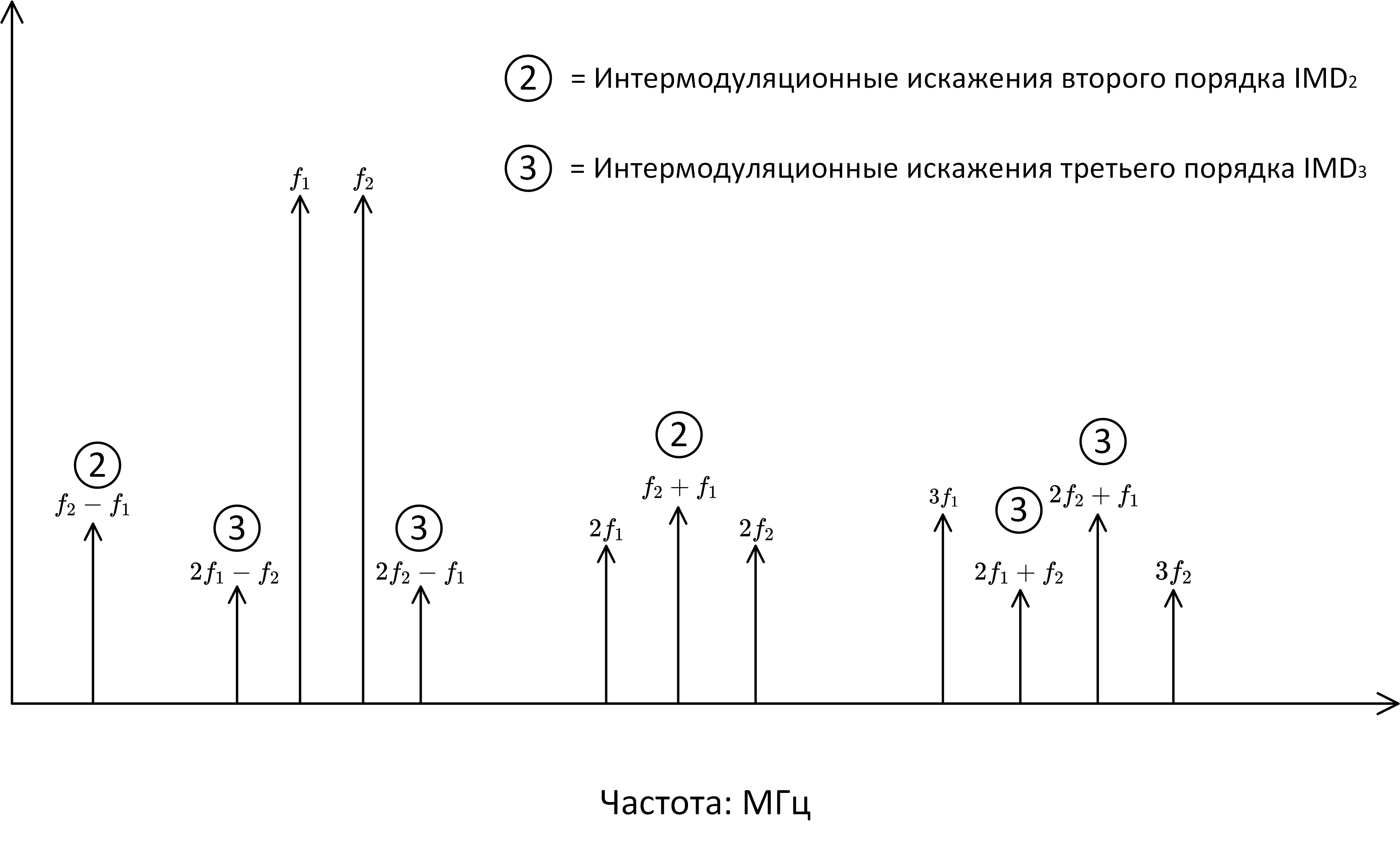
- Интермодуляционные искажения (IMD — intermodulation distortion). Рассмотренные прежде динамические параметры измеряются, когда на вход подается однотональный гармонический сигнал. Такие однотональные тесты хороши, когда АЦП обрабатывает широкополосные сигналы. В этом случае гармоники, располагающиеся выше fs/2 отражаются в первую зону Найквиста и, следовательно, всегда учитываются в расчете параметров. Однако, имея дело с узкополосными сигналами или АЦП с передискретизацией, даже гармоники низкого порядка (2-я, 3-я) могут иметь достаточно высокую частоту, чтобы выйти из рассматриваемого частотного диапазона (или не отразиться в этот диапазон в случае выхода за fs/2). В этом случае эти гармоники не будут учтены, что приведёт к ошибочному завышению динамических параметров.
Для решения этой проблемы используются бигармонические тесты. На вход подают две спектрально чистых синусоиды одинаковой мощности с частотамии
, которые находятся на близком расстоянии друг от друга. Нелинейность преобразователя порождает дополнительные тоны в спектре (их называют интермодуляционными искажениями) на частотах
, где
– произвольные целые числа.
Полезность бигармонического теста в том, что некоторые из интермодуляционных продуктов располагаются в спектре очень близко к исходному сигналу и, следовательно, дают полную информацию о нелинейности АЦП. В частности, интермодуляционные искажения 3-го порядка находятся на частотахи
(рис. 10).
Рис. 10: интермодуляционные искажения
При построении РЧ систем могут быть интересны так же продукты 2-го и более высокого порядка. Параметр АЦП, характеризующий его интермодуляционные искажения n-го порядка, определяется формулой:
[dBc], где
– мощность идентичных синусоид на входе,
– мощность одного из продуктов. Например
– отношение мощности на
к мощности на
Полоса пропускания АЦП и субдискретизация (undersamling/sub-sampling)
Полоса пропускания преобразователя (FPBW — Full Power (Analog) Bandwidth). Обычно ширина полосы преобразователя составляет несколько зон Найквиста. Этот параметр должен быть в спецификации, но, если его нет, можно попробовать самостоятельно оценить минимально возможное значение полосы пропускания для данного АЦП. За период выборки емкость УВХ должна зарядиться с точностью 1 LSB. Если период выборки равен , то ошибка выборки сигнала полной шкалы равна:
Решив относительно t, получаем:
Положив, что , определим минимальную полосу АЦП (для
):
Например, для 16 битного АЦП с частотой дискретизации 80 Мвыб/c и шкалой 2 В ограничение снизу для полосы пропускания, рассчитанное по этой формуле, составит FPBW = 282 МГц.
Analog Bandwidth является очень важным параметром при построении систем, которые работают в режиме субдискретизации (“undersampling”). Объясним это подробнее.
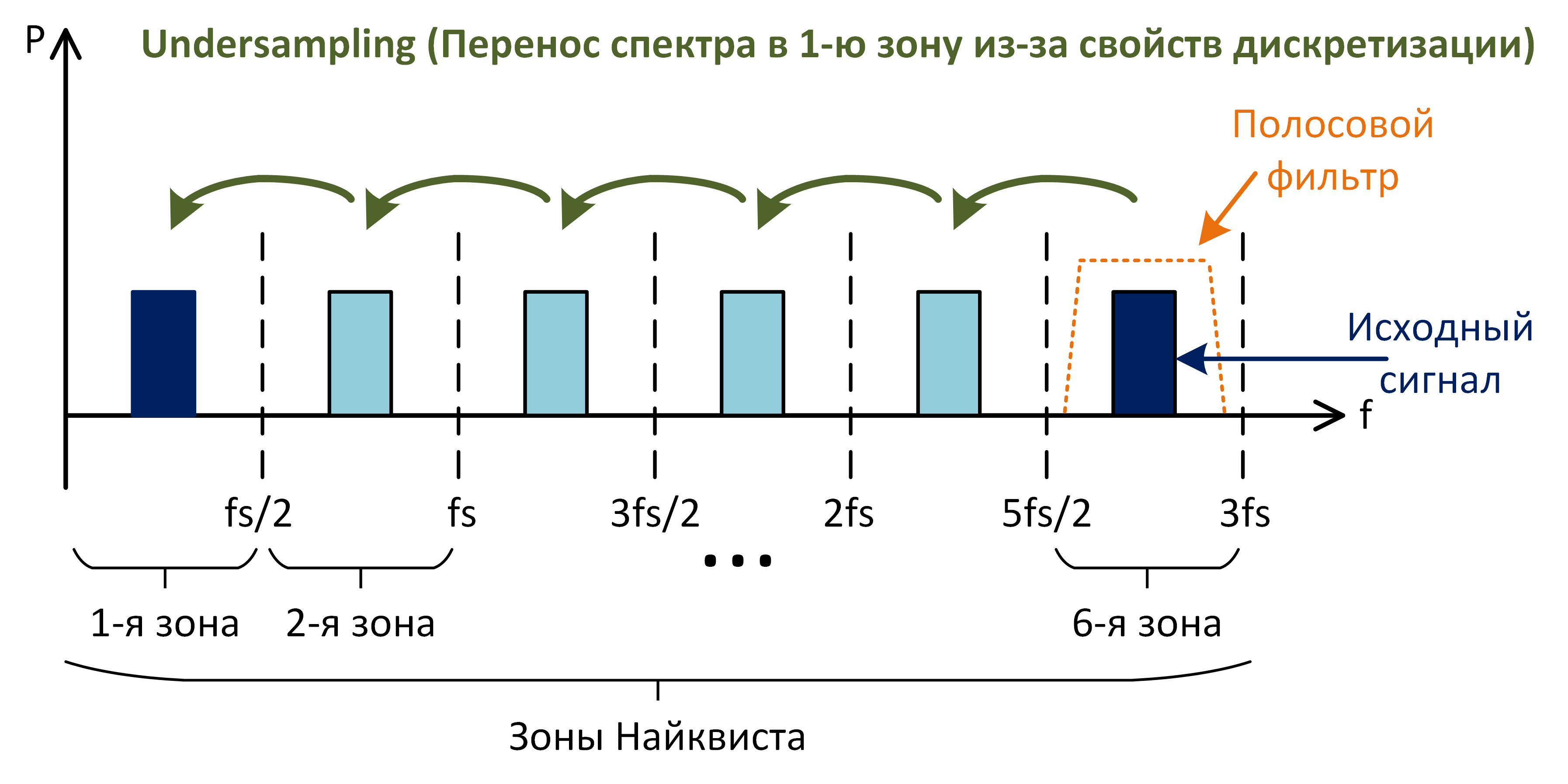
Согласно критерию Найквиста, ширина спектра обрабатываемого сигнала должна быть как минимум в 2 раза меньше частоты дискретизации, чтобы избежать элайзинга. Здесь важно, что именно ширина полосы, а не просто максимальная частота сигнала. Например, сигнал, спектр которого расположен целиком в 6-й зоне Найквиста может быть теоретически дискретизован без потери информации (рис. 11). Ограничив спектр этого сигнала антиэлайзинговым фильтром, его можно подавать на дискретизатор с частотой fs. В результате сигнал отразится в каждой зоне.
Рис. 11: undersampling
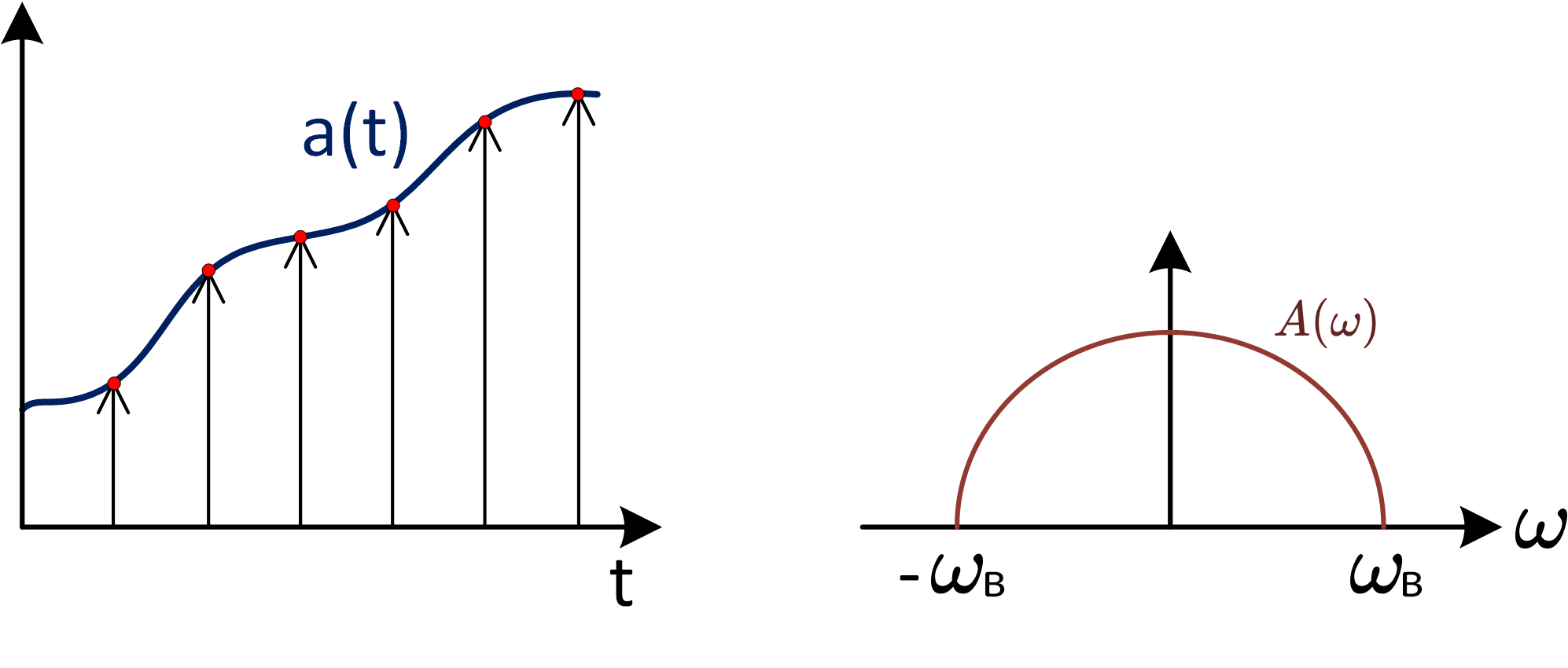
Свойство переноса спектра при дискретизации
Undersampling или sub-sampling имеет место быть из-за свойств дискретизации. Рассмотрим на примере, пусть имеется сигнал a(t) и его спектральная плотность (рис. 12). Необходимо найти спектральную плотность
сигнала после дискретизации сигнала
.
Рис 12: дискретизация непрерывного сигнала
По фильтрующему свойству дельта-функции:
После дискретизации :
где
С помощью формулы Релея вычислим спектр:
Из этого выражения следует что спектр сигнала будет повторяться во всех зонах Найквиста.
Итак, если есть хороший антиэлайзинговый фильтр, то соблюдая критерий Найквиста, можно оцифровывать сигнал с частотой дискретизации намного ниже полосы АЦП. Но использовать субдискретизацию нужно осторожно. Следует учитывать, что динамические параметры АЦП деградируют (иногда очень сильно) с ростом частоты входного сигнала, поэтому оцифровать сигнал из 6-й зоны так же «чисто», как из 1-й не получится.
Несмотря на это субдискритезация активно используется. Например, для обработки узкополосных сигналов, когда не хочется тратиться на дорогой широкополосный быстродействующий АЦП, который вдобавок имеет высокое потребление. Другой пример – выборка ПЧ (IF-sampling) в РЧ системах. Там благодаря undersampling можно исключить из радиоприемного тракта лишнее аналоговое звено — смеситель (который переносит сигнал на более низкую несущую или на 0).
Сравним архитектуры
На данный момент в мире существует множество различных архитектур АЦП. У каждой из них есть свои преимущества и недостатки. Не существует архитектуры, которая бы достигала максимальных значений всех, описанных выше параметров. Проанализируем какие максимальные параметры скорости и разрешения смогли достичь компании, выпускающие АЦП. Также оценим достоинства и недостатки каждой архитектуры (более подробно о различных архитектурах можно прочитать в статье на хабр).
Таблица сравнения архитектур
Информацию для таблицы брал на сайте arrow, поэтому если что-то упустил поправляйте в комментариях.
Заключение
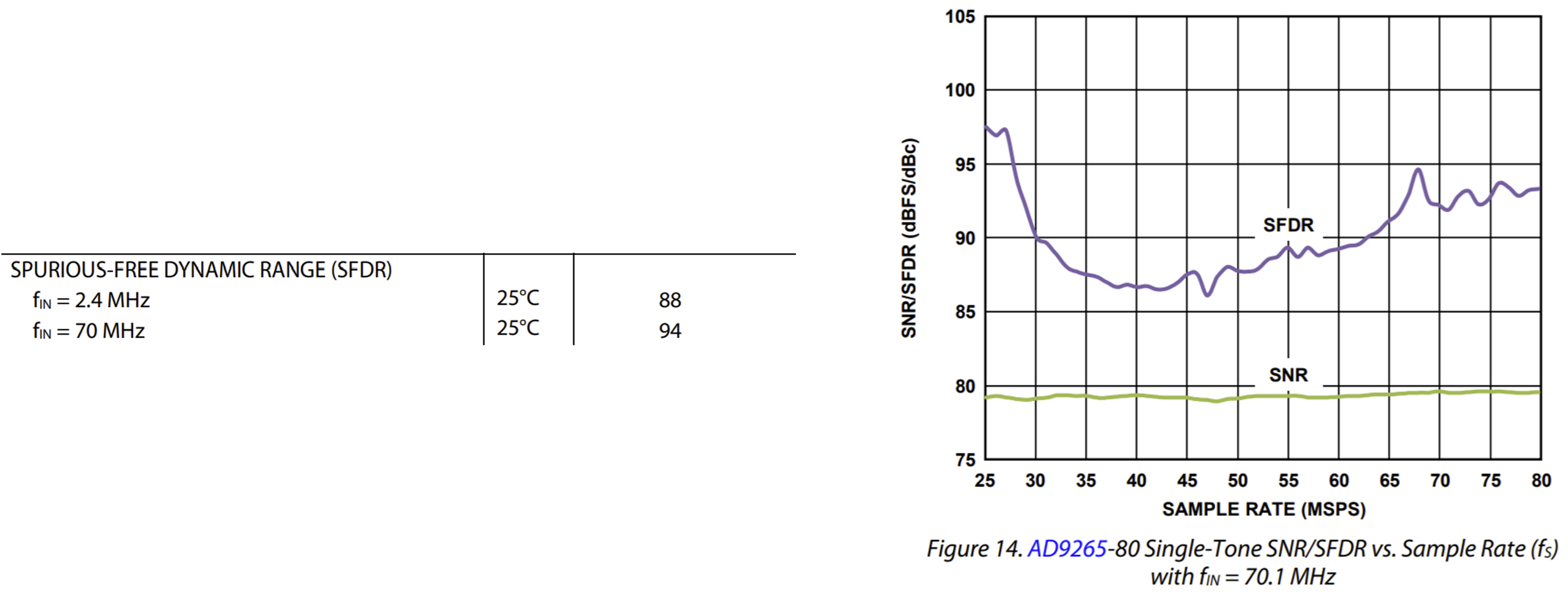
Описав параметры разрабатываемой вами системы, можно понять, какие характеристики АЦП для вас являются критичными. Однако не стоит забывать, что динамические параметры преобразователей сильно зависят от многих факторов (частота дискретизации, частота входного сигнала, амплитуда входного сигнала и тд.) Зачастую в таблицах параметров в документации указывают только «красивые» (с точки зрения маркетинга) цифры. Приведу пример, возьмем АЦП ad9265 и рассмотрим его параметр SFDR при частоте входного сигнала 70 МГц:
Таблица показывает значение SFDR при максимальных значениях частоты дискретизации, однако если вы будете использовать частоту ниже (к примеру 40 МГц), вы не получите этих «хороших» значений. Поэтому советую анализировать характеристики АЦП по графикам, чтобы примерно понимать, сможет ли данная микросхема обеспечить нужную вам точность преобразования.
Содержание
- Раскладываем по полочкам параметры АЦП
- Введение
- Статические параметры
- Динамические параметры
- Сравним архитектуры
- Раскладываем по полочкам параметры АЦП
- Введение
- Статические параметры
- Динамические параметры
- Сравним архитектуры
Раскладываем по полочкам параметры АЦП
Привет, Хабр! Многие разработчики систем довольно часто сталкиваются с обработкой аналоговых сигналов. Не все манипуляции с сигналами можно осуществить в аналоговой форме, поэтому требуется переводить аналог в цифровой мир для дальнейшей постобработки. Возникает вопрос: на какие параметры стоит обратить внимание при выборе микроконтроллера или дискретного АЦП? Что все эти параметры означают? В этой статье постараемся детально рассмотреть основные характеристики АЦП и разобраться на что стоит обратить внимание при выборе преобразователя.
Введение
Рис. 1: Идеальная характеристика АЦП
Однако из-за наличия различных видов шума, мы не можем увеличивать разрядность АЦП до бесконечности. То есть существует предел, который ограничивает минимальную цену деления шкалы. Другими словами, уменьшая деление шкалы мы рано или поздно «упремся» в шум. Да, конечно, можно сделать хоть 100-битный АЦП, однако большинство бит данного АЦП не будут нести полезную информацию. Именно поэтому характеристика АЦП имеет ступенчатую форму, что равносильно наличию конечной разрядности АЦП.
Проектируя систему необходимо выбирать АЦП, который бы обеспечил отсутствие потери информации при оцифровке. Для того, чтобы выбрать преобразователь, необходимо понять, какие параметры его характеризуют.
Параметры АЦП можно разделить на 2 группы:
- Статические — характеризуют АЦП при постоянном или очень медленно изменяющемся входном сигнале. К данным параметрам можно отнести: максимальное и минимальное допустимое значение входного сигнала, разрядность, интегральную и дифференциальную нелинейности, температурную нестабильность параметров преобразования и др.
- Динамические — определяют максимальную скорость преобразования, предельную частоту входного сигнала, шумы и нелинейности.
Статические параметры
Рис. 4: Дифференциальная нелинейность
Для 3-х битного АЦП с рисунка 4:
Интегральная нелинейность ( INL — Integral nonlinearity) – разница по вертикали между реальной и идеальной характеристикой преобразования (рис. 5). INL можно интерпретировать как сумму DNL. Отрицательная INL указывает на то, что реальная характеристика находится ниже идеальной в данной точке шкалы. Для положительной INL реальная характеристика находится выше идеальной. Распределение DNL определяет интегральную нелинейность АЦП.
Рис. 5: Интегральная нелинейность
Динамические параметры
Наглядно данное выражение продемонстрированно на рисунке 7.
Рис. 7: Отношение сигнал/шум
Для оценки SNR АЦП при разработке системы можно воспользоваться следующей формулой:
Первые 2 слагаемых учитывают уровень сигнала и ошибку квантования (нужно понимать что формула верна для сигнала размаха полной шкалы). Третье слагаемое учитывает эффект передискретизации (выигрыш по обработке или processing gain): если полоса обрабатываемого сигнала (BW
Эффективное число бит (ENOB — effective number of bits) – некая абстрактная характеристика, показывающая сколько на самом деле бит в выходном коде АЦП, несет в себе полезную информацию. Может принимать дробные значения.
Сравним архитектуры
На данный момент в мире существует множество различных архитектур АЦП. У каждой из них есть свои преимущества и недостатки. Не существует архитектуры, которая бы достигала максимальных значений всех, описанных выше параметров. Проанализируем какие максимальные параметры скорости и разрешения смогли достичь компании, выпускающие АЦП. Также оценим достоинства и недостатки каждой архитектуры (более подробно о различных архитектурах можно прочитать в статье на хабр).
| Тип архитектуры | Преимущества | Недостатки | Максимальное разрешение | Максимальная частота дискретизации |
| flash | Быстрый преобразователь. Преобразование осуществляется в один такт. | Высокое энергопотребление. Ограниченное разрешение. Требует большой площади кристалла ( |
14 бит 128 КВыб/с AD679 | 3 бит 26 ГВыб/с HMCAD5831 |
| folding-interpolated | Быстрый преобразователь. Преобразование осуществляется в один такт. Требует меньшее число компараторов благодаря предварительной «свёртке» всего диапазона обработки в некоторый более узкий диапазон. Занимает меньше площади. |
Ошибки, связанные с нелинейностью блока свёртки. Задержка на установление уровней в блоке свёртки, которая уменьшает максимальную fs. Среднее разрешение. |
12 бит 6.4 ГВыб/с ADC12DL3200 | 12 бит 6.4 ГВыб/с ADC12DL3200 |
| SAR | Высокая точность. Низкое энергопотребление. Легка в использовании. |
Ограниченная скорость. | 32 бит 1 МВыб/с LTC2500 | 10 бит 40 МВыб/с XRD64L43 |
| pipeline | Быстрый преобразователь. Самая высокая точность среди быстрых АЦП. Не занимает большую площадь. Имеет меньшее потребления, среди аналогичных быстрых преобразователей. |
Конвейерная задержка. | 24 бит 192 КВыб/с AK5386 | 12 бит 10.25 ГВыб/с AD9213 |
| dual-slope | Средняя точность преобразования. Простота конструкции. Низкое потребление. Устойчивость к изменениям факторов внешней среды. |
Обрабатывает низкочастотные Сигналы (низкая fs). Посредственное разрешение. |
12+знаковый бит 10 Выб/с TC7109 | 5+знак бит 200 КВыб/с HI3-7159 |
| ∑-Δ | Самая высокая точность пре- Образования благодаря эффекту «Noise shaping» (спецефическая фильтрация шума квантования) и передискретизации. |
Не может работать с широкополосным сигналом. | 32 бита 769 КВыб/с AK5554 | 16 бит 640МВыб/с AD9267 |
Информацию для таблицы брал на сайте arrow, поэтому если что-то упустил поправляйте в комментариях.
Источник
Раскладываем по полочкам параметры АЦП
Привет, Хабр! Многие разработчики систем довольно часто сталкиваются с обработкой аналоговых сигналов. Не все манипуляции с сигналами можно осуществить в аналоговой форме, поэтому требуется переводить аналог в цифровой мир для дальнейшей постобработки. Возникает вопрос: на какие параметры стоит обратить внимание при выборе микроконтроллера или дискретного АЦП? Что все эти параметры означают? В этой статье постараемся детально рассмотреть основные характеристики АЦП и разобраться на что стоит обратить внимание при выборе преобразователя.
Введение
Рис. 1: Идеальная характеристика АЦП
Однако из-за наличия различных видов шума, мы не можем увеличивать разрядность АЦП до бесконечности. То есть существует предел, который ограничивает минимальную цену деления шкалы. Другими словами, уменьшая деление шкалы мы рано или поздно «упремся» в шум. Да, конечно, можно сделать хоть 100-битный АЦП, однако большинство бит данного АЦП не будут нести полезную информацию. Именно поэтому характеристика АЦП имеет ступенчатую форму, что равносильно наличию конечной разрядности АЦП.
Проектируя систему необходимо выбирать АЦП, который бы обеспечил отсутствие потери информации при оцифровке. Для того, чтобы выбрать преобразователь, необходимо понять, какие параметры его характеризуют.
Параметры АЦП можно разделить на 2 группы:
- Статические — характеризуют АЦП при постоянном или очень медленно изменяющемся входном сигнале. К данным параметрам можно отнести: максимальное и минимальное допустимое значение входного сигнала, разрядность, интегральную и дифференциальную нелинейности, температурную нестабильность параметров преобразования и др.
- Динамические — определяют максимальную скорость преобразования, предельную частоту входного сигнала, шумы и нелинейности.
Статические параметры
Рис. 4: Дифференциальная нелинейность
Для 3-х битного АЦП с рисунка 4:
Интегральная нелинейность ( INL — Integral nonlinearity) – разница по вертикали между реальной и идеальной характеристикой преобразования (рис. 5). INL можно интерпретировать как сумму DNL. Отрицательная INL указывает на то, что реальная характеристика находится ниже идеальной в данной точке шкалы. Для положительной INL реальная характеристика находится выше идеальной. Распределение DNL определяет интегральную нелинейность АЦП.
Рис. 5: Интегральная нелинейность
Динамические параметры
Наглядно данное выражение продемонстрированно на рисунке 7.
Рис. 7: Отношение сигнал/шум
Для оценки SNR АЦП при разработке системы можно воспользоваться следующей формулой:
Первые 2 слагаемых учитывают уровень сигнала и ошибку квантования (нужно понимать, что формула верна для сигнала размаха полной шкалы). Третье слагаемое учитывает эффект передискретизации (выигрыш по обработке или processing gain): если полоса обрабатываемого сигнала (BW Свойство переноса спектра при дискретизации
Рис 12: дискретизация непрерывного сигнала
По фильтрующему свойству дельта-функции:
После дискретизации :
где
С помощью формулы Релея вычислим спектр:
Из этого выражения следует что спектр сигнала будет повторяться во всех зонах Найквиста.
Итак, если есть хороший антиэлайзинговый фильтр, то соблюдая критерий Найквиста, можно оцифровывать сигнал с частотой дискретизации намного ниже полосы АЦП. Но использовать субдискретизацию нужно осторожно. Следует учитывать, что динамические параметры АЦП деградируют (иногда очень сильно) с ростом частоты входного сигнала, поэтому оцифровать сигнал из 6-й зоны так же «чисто», как из 1-й не получится.
Несмотря на это субдискритезация активно используется. Например, для обработки узкополосных сигналов, когда не хочется тратиться на дорогой широкополосный быстродействующий АЦП, который вдобавок имеет высокое потребление. Другой пример – выборка ПЧ (IF-sampling) в РЧ системах. Там благодаря undersampling можно исключить из радиоприемного тракта лишнее аналоговое звено — смеситель (который переносит сигнал на более низкую несущую или на 0).
Сравним архитектуры
На данный момент в мире существует множество различных архитектур АЦП. У каждой из них есть свои преимущества и недостатки. Не существует архитектуры, которая бы достигала максимальных значений всех, описанных выше параметров. Проанализируем какие максимальные параметры скорости и разрешения смогли достичь компании, выпускающие АЦП. Также оценим достоинства и недостатки каждой архитектуры (более подробно о различных архитектурах можно прочитать в статье на хабр).
| Тип архитектуры | Преимущества | Недостатки | Максимальное разрешение | Максимальная частота дискретизации |
| flash | Быстрый преобразователь. Преобразование осуществляется в один такт. | Высокое энергопотребление. Ограниченное разрешение. Требует большой площади кристалла ( |
14 бит 128 КВыб/с AD679 | 3 бит 26 ГВыб/с HMCAD5831 |
| folding-interpolated | Быстрый преобразователь. Преобразование осуществляется в один такт. Требует меньшее число компараторов благодаря предварительной «свёртке» всего диапазона обработки в некоторый более узкий диапазон. Занимает меньше площади. |
Ошибки, связанные с нелинейностью блока свёртки. Задержка на установление уровней в блоке свёртки, которая уменьшает максимальную fs. Среднее разрешение. |
12 бит 6.4 ГВыб/с ADC12DL3200 | 12 бит 6.4 ГВыб/с ADC12DL3200 |
| SAR | Высокая точность. Низкое энергопотребление. Легка в использовании. |
Ограниченная скорость. | 32 бит 1 МВыб/с LTC2500 | 10 бит 40 МВыб/с XRD64L43 |
| pipeline | Быстрый преобразователь. Самая высокая точность среди быстрых АЦП. Не занимает большую площадь. Имеет меньшее потребления, среди аналогичных быстрых преобразователей. |
Конвейерная задержка. | 24 бит 192 КВыб/с AK5386 | 12 бит 10.25 ГВыб/с AD9213 |
| dual-slope | Средняя точность преобразования. Простота конструкции. Низкое потребление. Устойчивость к изменениям факторов внешней среды. |
Обрабатывает низкочастотные Сигналы (низкая fs). Посредственное разрешение. |
12+знаковый бит 10 Выб/с TC7109 | 5+знак бит 200 КВыб/с HI3-7159 |
| ∑-Δ | Самая высокая точность пре- Образования благодаря эффекту «Noise shaping» (специфическая фильтрация шума квантования) и передискретизации. |
Не может работать с широкополосным сигналом. | 32 бита 769 КВыб/с AK5554 | 12 бит 200МВыб/с ADRV9009 |
Информацию для таблицы брал на сайте arrow, поэтому если что-то упустил поправляйте в комментариях.
Источник
Раскладываем по полочкам параметры АЦП +39
Электроника для начинающих, Схемотехника, Инженерные системы, Блог компании Миландр
Рекомендация: подборка платных и бесплатных курсов Java — https://katalog-kursov.ru/
Привет, Хабр! Многие разработчики систем довольно часто сталкиваются с обработкой аналоговых сигналов. Не все манипуляции с сигналами можно осуществить в аналоговой форме, поэтому требуется переводить аналог в цифровой мир для дальнейшей постобработки. Возникает вопрос: на какие параметры стоит обратить внимание при выборе микроконтроллера или дискретного АЦП? Что все эти параметры означают? В этой статье постараемся детально рассмотреть основные характеристики АЦП и разобраться на что стоит обратить внимание при выборе преобразователя.
Введение
Начать бы хотелось с интересного философского вопроса: если аналоговый сигнал — это бесконечность, теряем ли мы при оцифровке сигнала бесконечное количество информации? Если это так, тогда какой смысл существования такого неэффективного преобразования?
Для того, чтобы ответить на этот вопрос, разберемся с тем, что такое аналого-цифровое преобразование сигнала. Основной график, который отражает работу АЦП – передаточная характеристика преобразования. В идеальном мире это была бы прямая линия, то есть у каждого аналогового уровня сигнала имелся бы единственный цифровой эквивалент.
Рис. 1: Идеальная характеристика АЦП
Однако из-за наличия различных видов шума, мы не можем увеличивать разрядность АЦП до бесконечности. То есть существует предел, который ограничивает минимальную цену деления шкалы. Другими словами, уменьшая деление шкалы мы рано или поздно «упремся» в шум. Да, конечно, можно сделать хоть 100-битный АЦП, однако большинство бит данного АЦП не будут нести полезную информацию. Именно поэтому характеристика АЦП имеет ступенчатую форму, что равносильно наличию конечной разрядности АЦП.
Проектируя систему необходимо выбирать АЦП, который бы обеспечил отсутствие потери информации при оцифровке. Для того, чтобы выбрать преобразователь, необходимо понять, какие параметры его характеризуют.
Параметры АЦП можно разделить на 2 группы:
- Статические — характеризуют АЦП при постоянном или очень медленно изменяющемся входном сигнале. К данным параметрам можно отнести: максимальное и минимальное допустимое значение входного сигнала, разрядность, интегральную и дифференциальную нелинейности, температурную нестабильность параметров преобразования и др.
- Динамические — определяют максимальную скорость преобразования, предельную частоту входного сигнала, шумы и нелинейности.
Статические параметры
- Максимальный (Vref) и минимальный (обычно 0) уровни входного сигнала — устанавливают диапазон шкалы преобразования, относительно которой будет оцениваться входной сигнал (рис. 1). Также этот параметр может обозначаться как FS — full scale. Для дифференциального АЦП шкала определяется от -Vref до +Vref, однако для упрощения далее будем рассматривать только single-ended шкалы.
- Разрядность (N) — разрядность выходного кода, характеризующая количество дискретных значений (
), которые преобразователь может выдать на выходе (рис. 1).
- Ток потребления (Idd) — сильно зависит от частоты преобразования, поэтому информацию об этом параметре лучше искать на соответствующем графике.
- МЗР (LSB) – младший значащий разряд (Least Significant Bit) — минимальное входное напряжение, разрешаемое АЦП (по сути единичный шаг в шкале преобразования). Определяется формулой:
(рис. 1).
- Ошибка смещения (offset error) – определяется как отклонение фактической передаточной характеристики АЦП от передаточной характеристики идеального АЦП в начальной точке шкалы. Измеряется в долях LSB. При ошибке смещения переход выходного кода от 0 в 1 происходит при входном напряжении отличном от 0.5LSB (рис. 2).
Рис. 2: Ошибка смещения
Существует и другой вариант квантователя, когда переход осуществляется при целых значения LSB (характеристика у него будет смещена относительно первого варианта, который представлен на рисунке 2). Оба этих квантователя равноправны, и для простоты далее будем рассматривать только первый вариант. - Ошибка усиления (gain error) – определяется как отклонение средней точки последнего шага преобразования (которому соответствует входное напряжение Vref) реального АЦП от средней точки последнего шага преобразования идеального АЦП после компенсации ошибки смещения (рис. 3).
Рис. 3: Ошибка усиления
- Дифференциальная нелинейность (DNL — Differential nonlinearity) – отклонение ширины ступеньки на передаточной характеристике реального АЦП от номинальной ширины ступеньки у идеального преобразователя. Из-за дифференциальной нелинейности шаги квантования имеют различную ширину (рис. 4).
Рис. 4: Дифференциальная нелинейность
Для 3-х битного АЦП с рисунка 4:
- Интегральная нелинейность ( INL — Integral nonlinearity) – разница по вертикали между реальной и идеальной характеристикой преобразования (рис. 5). INL можно интерпретировать как сумму DNL. Отрицательная INL указывает на то, что реальная характеристика находится ниже идеальной в данной точке шкалы. Для положительной INL реальная характеристика находится выше идеальной. Распределение DNL определяет интегральную нелинейность АЦП.
Рис. 5: Интегральная нелинейность
- Общая нескорректированная ошибка ( TUE — Total Unadjusted Error) – абсолютная ошибка, включающая в себя следующие ошибки: квантования, смещения, усиления и нелинейности. Другими словами, это максимальное отклонение между реальной и идеальной характеристикой преобразования. Для идеального АЦП TUE = 0.5LSB, обусловлена ошибкой квантования (или шум квантования — возникает из-за округления значения аналогового сигнала, которое соответствует цифровому коду). Ошибки усиления и смещения обычно вносят наиболее весомый вклад в абсолютную ошибку. Однако с точки зрения динамических параметров (см. ниже) ошибки смещения и усиления ничтожны, так как они не порождают нелинейных искажений.
Динамические параметры
- Частота дискретизации (fs — sampling frequency) — частота, при которой происходит преобразование в АЦП (ну или 1/Ts, где Ts — период выборки). Измеряется числом выборок в секунду. Обычно под данным обозначением подразумевают максимальную частоту дискретизации, при которой специфицированы параметры преобразователя (рис. 6).
Рис. 6: Процесс преобразования АЦП
- Отношение сигнал/шум (SNR — Signal-to-Noise Ratio) — определяется как отношение мощности обрабатываемого сигнала к мощности шума, добавляемого в процессе преобразования. SNR обычно выражается в децибелах (дБ) и рассчитывается по следующей формуле:
Наглядно данное выражение продемонстрированно на рисунке 7.
Рис. 7: Отношение сигнал/шум
Для оценки SNR АЦП при разработке системы можно воспользоваться следующей формулой:
Первые 2 слагаемых учитывают уровень сигнала и ошибку квантования (нужно понимать, что формула верна для сигнала размаха полной шкалы). Третье слагаемое учитывает эффект передискретизации (выигрыш по обработке или processing gain): если полоса обрабатываемого сигнала (BW < fs/2), то, применив цифровой фильтр низких частот (либо полосовой, тут зависит все от полосы и несущей) к результату преобразования, можно вырезать часть шума АЦП, а оставшаяся часть будет распределена от 0 до BW (рис. 8). Если шум АЦП равномерно распределен по всем частотам (т.н. «белый» шум) интегральный шум после фильтрации уменьшится в fs/2 / BW раз, что и отражает третий член формулы.
Рис. 8: Увеличение SNR за счет передискретизации
- Общие нелинейные искажения (THD — total harmonic distortion). Прежде, чем сигнал преобразовывается в цифровой код, он проходит через нелинейные блоки, которые искажают сигнал. К примеру, пусть есть сигнал с частотой f. Пройдя через нелинейный блок к нему добавятся компоненты с частотами 2f, 3f, 4f … — 2-я, 3-я, 4-я и т.д. гармоники входного сигнала. Если дискретизированный сигнал разложить в спектр с помощью ДПФ (Дискретного Преобразования Фурье), мы увидим, что все эти гармоники «перенеслись» в первую зону Найквиста (от 0 до fs/2) (рис. 9).
Рис. 9: Нелинейные искажения
Побочные гармоники искажают обрабатываемый сигнал, что ухудшает производительность системы. Этот эффект можно измерить, используя характеристику общие нелинейные искажения. THD определяется как отношение суммарной мощности гармонических частотных составляющих к мощности основной (исходной) частотной составляющей (в некоторых документациях выражается в дБ):
- Динамический диапазон, свободный от гармоник (SFDR — Spurious-Free Dynamic Range). Является отношением мощности полезного сигнала к мощности наибольшего «спура» (любая паразитная составляющая в спектре, не обязательно гармонического происхождения), присутствующего в спектре (рис. 9).
- Отношение сигнал / шум и нелинейные искажения (SINAD — signal-to-noise and distortion ratio). Аналогичен SNR, но помимо шума учитывает все виды помех и искажений, возникающих при аналого-цифровом преобразовании. SINAD является одним из ключевых параметром, характеризующим АЦП (в некоторых источниках обозначается как SNDR):
- Эффективное число бит (ENOB — effective number of bits) – некая абстрактная характеристика, показывающая сколько на самом деле бит в выходном коде АЦП несет в себе полезную информацию. Может принимать дробные значения.
- Интермодуляционные искажения (IMD — intermodulation distortion). Рассмотренные прежде динамические параметры измеряются, когда на вход подается однотональный гармонический сигнал. Такие однотональные тесты хороши, когда АЦП обрабатывает широкополосные сигналы. В этом случае гармоники, располагающиеся выше fs/2 отражаются в первую зону Найквиста и, следовательно, всегда учитываются в расчете параметров. Однако, имея дело с узкополосными сигналами или АЦП с передискретизацией, даже гармоники низкого порядка (2-я, 3-я) могут иметь достаточно высокую частоту, чтобы выйти из рассматриваемого частотного диапазона (или не отразиться в этот диапазон в случае выхода за fs/2). В этом случае эти гармоники не будут учтены, что приведёт к ошибочному завышению динамических параметров.
Для решения этой проблемы используются бигармонические тесты. На вход подают две спектрально чистых синусоиды одинаковой мощности с частотамии
, которые находятся на близком расстоянии друг от друга. Нелинейность преобразователя порождает дополнительные тоны в спектре (их называют интермодуляционными искажениями) на частотах
, где
– произвольные целые числа.
Полезность бигармонического теста в том, что некоторые из интермодуляционных продуктов располагаются в спектре очень близко к исходному сигналу и, следовательно, дают полную информацию о нелинейности АЦП. В частности, интермодуляционные искажения 3-го порядка находятся на частотахи
(рис. 10).
Рис. 10: интермодуляционные искажения
При построении РЧ систем могут быть интересны так же продукты 2-го и более высокого порядка. Параметр АЦП, характеризующий его интермодуляционные искажения n-го порядка, определяется формулой:
[dBc], где
– мощность идентичных синусоид на входе,
– мощность одного из продуктов. Например
– отношение мощности на
к мощности на
Полоса пропускания АЦП и субдискретизация (undersamling/sub-sampling)
Полоса пропускания преобразователя (FPBW — Full Power (Analog) Bandwidth). Обычно ширина полосы преобразователя составляет несколько зон Найквиста. Этот параметр должен быть в спецификации, но, если его нет, можно попробовать самостоятельно оценить минимально возможное значение полосы пропускания для данного АЦП. За период выборки емкость УВХ должна зарядиться с точностью 1 LSB. Если период выборки равен
, то ошибка выборки сигнала полной шкалы равна:
Решив относительно t, получаем:
Положив, что
, определим минимальную полосу АЦП (для
):
Например, для 16 битного АЦП с частотой дискретизации 80 Мвыб/c и шкалой 2 В ограничение снизу для полосы пропускания, рассчитанное по этой формуле, составит FPBW = 282 МГц.
Analog Bandwidth является очень важным параметром при построении систем, которые работают в режиме субдискретизации (“undersampling”). Объясним это подробнее.
Согласно критерию Найквиста, ширина спектра обрабатываемого сигнала должна быть как минимум в 2 раза меньше частоты дискретизации, чтобы избежать элайзинга. Здесь важно, что именно ширина полосы, а не просто максимальная частота сигнала. Например, сигнал, спектр которого расположен целиком в 6-й зоне Найквиста может быть теоретически дискретизован без потери информации (рис. 11). Ограничив спектр этого сигнала антиэлайзинговым фильтром, его можно подавать на дискретизатор с частотой fs. В результате сигнал отразится в каждой зоне.
Рис. 11: undersampling
Свойство переноса спектра при дискретизации
Undersampling или sub-sampling имеет место быть из-за свойств дискретизации. Рассмотрим на примере, пусть имеется сигнал a(t) и его спектральная плотность
(рис. 12). Необходимо найти спектральную плотность
сигнала после дискретизации сигнала
.
Рис 12: дискретизация непрерывного сигнала
По фильтрующему свойству дельта-функции:
После дискретизации
:
где
С помощью формулы Релея вычислим спектр:
Из этого выражения следует что спектр сигнала будет повторяться во всех зонах Найквиста.
Итак, если есть хороший антиэлайзинговый фильтр, то соблюдая критерий Найквиста, можно оцифровывать сигнал с частотой дискретизации намного ниже полосы АЦП. Но использовать субдискретизацию нужно осторожно. Следует учитывать, что динамические параметры АЦП деградируют (иногда очень сильно) с ростом частоты входного сигнала, поэтому оцифровать сигнал из 6-й зоны так же «чисто», как из 1-й не получится.
Несмотря на это субдискритезация активно используется. Например, для обработки узкополосных сигналов, когда не хочется тратиться на дорогой широкополосный быстродействующий АЦП, который вдобавок имеет высокое потребление. Другой пример – выборка ПЧ (IF-sampling) в РЧ системах. Там благодаря undersampling можно исключить из радиоприемного тракта лишнее аналоговое звено — смеситель (который переносит сигнал на более низкую несущую или на 0).
Сравним архитектуры
На данный момент в мире существует множество различных архитектур АЦП. У каждой из них есть свои преимущества и недостатки. Не существует архитектуры, которая бы достигала максимальных значений всех, описанных выше параметров. Проанализируем какие максимальные параметры скорости и разрешения смогли достичь компании, выпускающие АЦП. Также оценим достоинства и недостатки каждой архитектуры (более подробно о различных архитектурах можно прочитать в статье на хабр).
Таблица сравнения архитектур
Информацию для таблицы брал на сайте arrow, поэтому если что-то упустил поправляйте в комментариях.
Заключение
Описав параметры разрабатываемой вами системы, можно понять, какие характеристики АЦП для вас являются критичными. Однако не стоит забывать, что динамические параметры преобразователей сильно зависят от многих факторов (частота дискретизации, частота входного сигнала, амплитуда входного сигнала и тд.) Зачастую в таблицах параметров в документации указывают только «красивые» (с точки зрения маркетинга) цифры. Приведу пример, возьмем АЦП ad9265 и рассмотрим его параметр SFDR при частоте входного сигнала 70 МГц:
Таблица показывает значение SFDR при максимальных значениях частоты дискретизации, однако если вы будете использовать частоту ниже (к примеру 40 МГц), вы не получите этих «хороших» значений. Поэтому советую анализировать характеристики АЦП по графикам, чтобы примерно понимать, сможет ли данная микросхема обеспечить нужную вам точность преобразования.
Main Content
This example shows how offset error and gain error are calculated and how each affects the transfer curve of an ADC. Offset error and gain error characterize part of the linearity error in an ADC.
Offset error is the difference between the center of the least significant code and the center of the same code on an ideal ADC with the same number of bits. Offset error is usually reported in units of the least significant bit (LSB) of the converter. One LSB is equivalent to the converter’s quantization interval.
Gain error in LSB is the difference between the center of the most significant code after offset error correction and the center of the same code on an ideal ADC with the same number of bits.
Due to the difficulty in determining the precise location of the center of a code with a non finite boundary, these values are most commonly measured with respect to the first and last threshold of the converter, respectively.
Units for Offset Error and Gain Error
The unit 
Thus, an error in 

where 

Linearity errors are also commonly reported in normalized units with respect to the full scale range:
Another unit sometimes used for linearity errors used is percent full scale. Percent full scale is defined as normalized units multiplied by 100:
Calculate Offset Error and Gain Error
Use a 3-bit ADC with dynamic range [-1 1]. Define an offset error of 1 LSB and a gain error of 1 LSB.
Nbits = 3;
Range = [-1 1]; % ADC Full Scale Range
OffsetError = 1;
GainError = 1;
LSB = (max(Range) - min(Range)) / (2^Nbits - 1);
The digital codes from the ideal ADC are identical to those from the experimental ADCs.
[TC0Analog, TC0Digital] = og2tc(Nbits, Range, 0, 0); % Ideal ADC Transfer Curve TC1Analog = og2tc(Nbits, Range, OffsetError, 0); % Offset Error Only TC2Analog = og2tc(Nbits, Range, 0, GainError); % Gain Error Only TC3Analog = og2tc(Nbits, Range, OffsetError, GainError); % Both Offset Error and Gain Error plotAdcTcForExample(TC0Digital, TC0Analog, TC1Analog, TC2Analog, TC3Analog, Nbits);
The sum of offset error and gain error is known as full-scale error. In monopolar converters zero error, essentially offset error defined at analog level 0, is identical to regular offset error. In bipolar converters such as those above, offset error and zero error are different quantities.
Use of Linearity Errors as Impairments
Compare a flash ADC with offset and gain error to one with no impairments.
model = 'OffsetGainExample'; open_system(model); open_system([model '/Time Scope']); sim(model);
The ADC DC Measurement block confirms the values of the impairments to within a margin of error determined by the sample rate of the system. The offset error and gain error were both entered as 1 LSB. Offset error was measured as 1.08 LSB and gain error was measured as 0.97 LSB. Errors in these measurements are due to the converter not sampling exactly at its threshold values. The maximum expected error in LSB is:
where 

See Also
Flash ADC | ADC DC Measurement
- Trial Software
- Trial Software
- Product Updates
- Product Updates
Main Content
This example shows how offset error and gain error are calculated and how each affects the transfer curve of an ADC. Offset error and gain error characterize part of the linearity error in an ADC.
Offset error is the difference between the center of the least significant code and the center of the same code on an ideal ADC with the same number of bits. Offset error is usually reported in units of the least significant bit (LSB) of the converter. One LSB is equivalent to the converter’s quantization interval.
Gain error in LSB is the difference between the center of the most significant code after offset error correction and the center of the same code on an ideal ADC with the same number of bits.
Due to the difficulty in determining the precise location of the center of a code with a non finite boundary, these values are most commonly measured with respect to the first and last threshold of the converter, respectively.
Units for Offset Error and Gain Error
The unit 
Thus, an error in 

where 

Linearity errors are also commonly reported in normalized units with respect to the full scale range:
Another unit sometimes used for linearity errors used is percent full scale. Percent full scale is defined as normalized units multiplied by 100:
Calculate Offset Error and Gain Error
Use a 3-bit ADC with dynamic range [-1 1]. Define an offset error of 1 LSB and a gain error of 1 LSB.
Nbits = 3;
Range = [-1 1]; % ADC Full Scale Range
OffsetError = 1;
GainError = 1;
LSB = (max(Range) - min(Range)) / (2^Nbits - 1);
The digital codes from the ideal ADC are identical to those from the experimental ADCs.
[TC0Analog, TC0Digital] = og2tc(Nbits, Range, 0, 0); % Ideal ADC Transfer Curve TC1Analog = og2tc(Nbits, Range, OffsetError, 0); % Offset Error Only TC2Analog = og2tc(Nbits, Range, 0, GainError); % Gain Error Only TC3Analog = og2tc(Nbits, Range, OffsetError, GainError); % Both Offset Error and Gain Error plotAdcTcForExample(TC0Digital, TC0Analog, TC1Analog, TC2Analog, TC3Analog, Nbits);
The sum of offset error and gain error is known as full-scale error. In monopolar converters zero error, essentially offset error defined at analog level 0, is identical to regular offset error. In bipolar converters such as those above, offset error and zero error are different quantities.
Use of Linearity Errors as Impairments
Compare a flash ADC with offset and gain error to one with no impairments.
model = 'OffsetGainExample'; open_system(model); open_system([model '/Time Scope']); sim(model);
The ADC DC Measurement block confirms the values of the impairments to within a margin of error determined by the sample rate of the system. The offset error and gain error were both entered as 1 LSB. Offset error was measured as 1.08 LSB and gain error was measured as 0.97 LSB. Errors in these measurements are due to the converter not sampling exactly at its threshold values. The maximum expected error in LSB is:
where 

See Also
Flash ADC | ADC DC Measurement
- Trial Software
- Trial Software
- Product Updates
- Product Updates
Main Content
This example shows how offset error and gain error are calculated and how each affects the transfer curve of an ADC. Offset error and gain error characterize part of the linearity error in an ADC.
Offset error is the difference between the center of the least significant code and the center of the same code on an ideal ADC with the same number of bits. Offset error is usually reported in units of the least significant bit (LSB) of the converter. One LSB is equivalent to the converter’s quantization interval.
Gain error in LSB is the difference between the center of the most significant code after offset error correction and the center of the same code on an ideal ADC with the same number of bits.
Due to the difficulty in determining the precise location of the center of a code with a non finite boundary, these values are most commonly measured with respect to the first and last threshold of the converter, respectively.
Units for Offset Error and Gain Error
The unit 
Thus, an error in 

where 

Linearity errors are also commonly reported in normalized units with respect to the full scale range:
Another unit sometimes used for linearity errors used is percent full scale. Percent full scale is defined as normalized units multiplied by 100:
Calculate Offset Error and Gain Error
Use a 3-bit ADC with dynamic range [-1 1]. Define an offset error of 1 LSB and a gain error of 1 LSB.
Nbits = 3;
Range = [-1 1]; % ADC Full Scale Range
OffsetError = 1;
GainError = 1;
LSB = (max(Range) - min(Range)) / (2^Nbits - 1);
The digital codes from the ideal ADC are identical to those from the experimental ADCs.
[TC0Analog, TC0Digital] = og2tc(Nbits, Range, 0, 0); % Ideal ADC Transfer Curve TC1Analog = og2tc(Nbits, Range, OffsetError, 0); % Offset Error Only TC2Analog = og2tc(Nbits, Range, 0, GainError); % Gain Error Only TC3Analog = og2tc(Nbits, Range, OffsetError, GainError); % Both Offset Error and Gain Error plotAdcTcForExample(TC0Digital, TC0Analog, TC1Analog, TC2Analog, TC3Analog, Nbits);
The sum of offset error and gain error is known as full-scale error. In monopolar converters zero error, essentially offset error defined at analog level 0, is identical to regular offset error. In bipolar converters such as those above, offset error and zero error are different quantities.
Use of Linearity Errors as Impairments
Compare a flash ADC with offset and gain error to one with no impairments.
model = 'OffsetGainExample'; open_system(model); open_system([model '/Time Scope']); sim(model);
The ADC DC Measurement block confirms the values of the impairments to within a margin of error determined by the sample rate of the system. The offset error and gain error were both entered as 1 LSB. Offset error was measured as 1.08 LSB and gain error was measured as 0.97 LSB. Errors in these measurements are due to the converter not sampling exactly at its threshold values. The maximum expected error in LSB is:
where 

See Also
Flash ADC | ADC DC Measurement
- Trial Software
- Trial Software
- Product Updates
- Product Updates


 Рис. 2: Ошибка смещения
Рис. 2: Ошибка смещения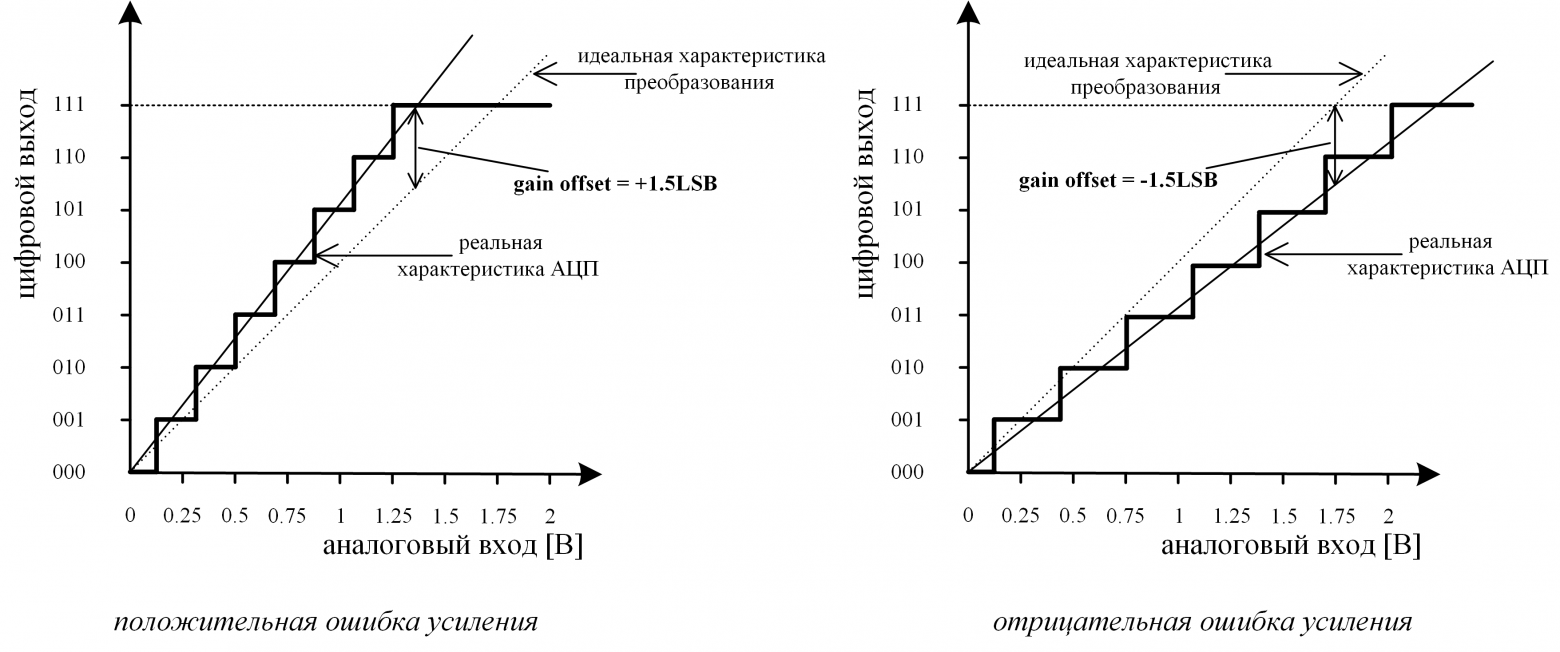 Рис. 3: Ошибка усиления
Рис. 3: Ошибка усиления
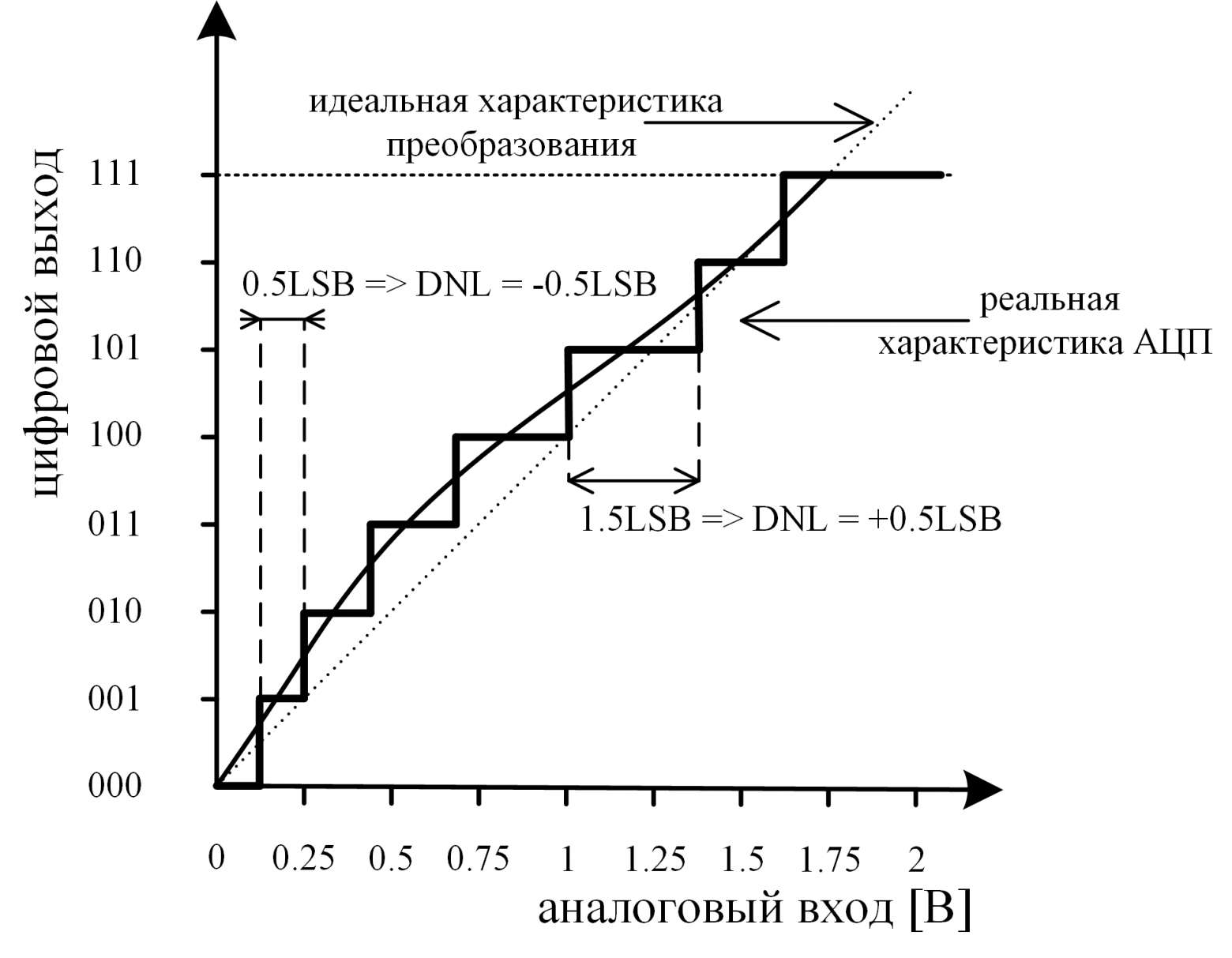
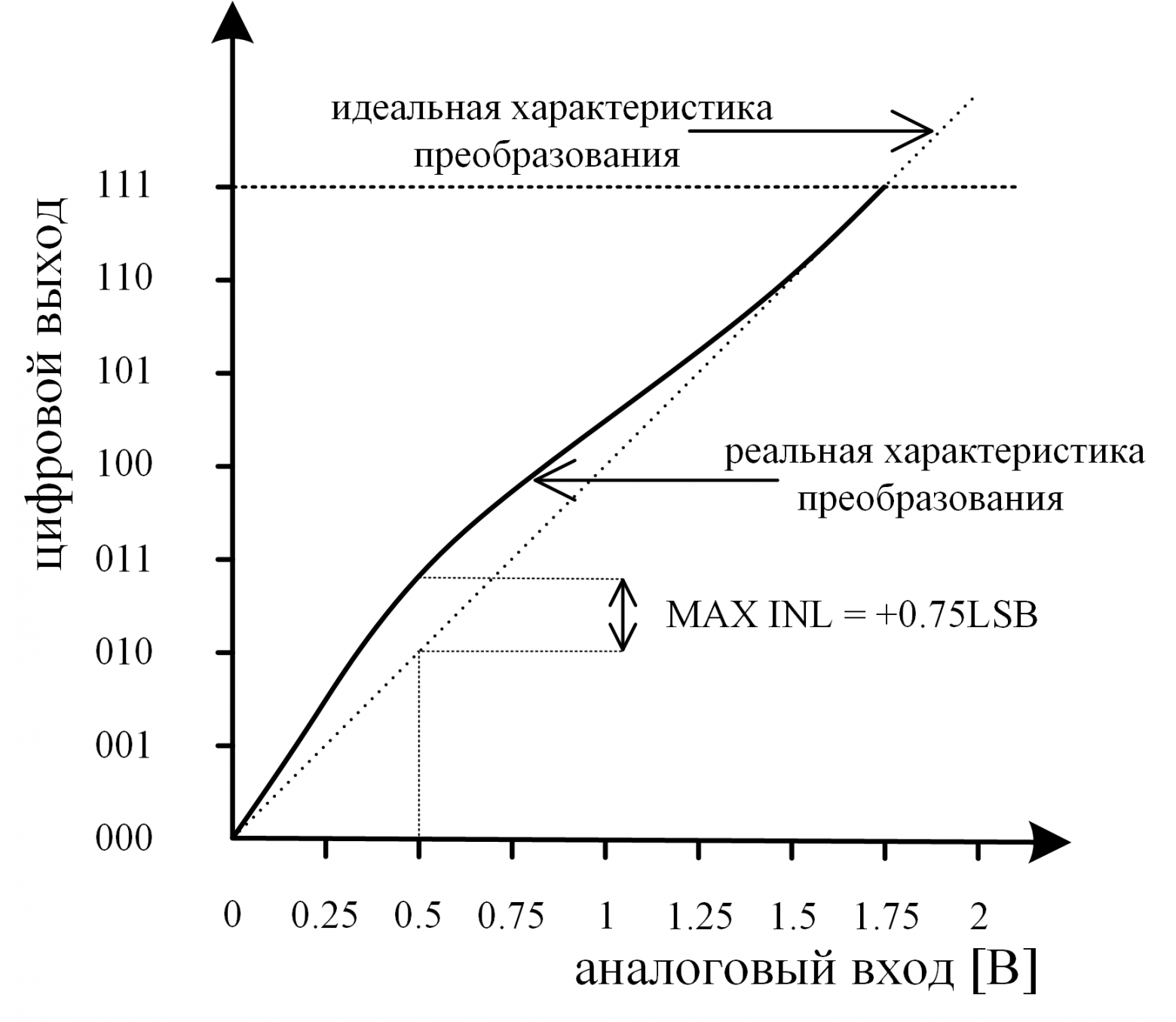

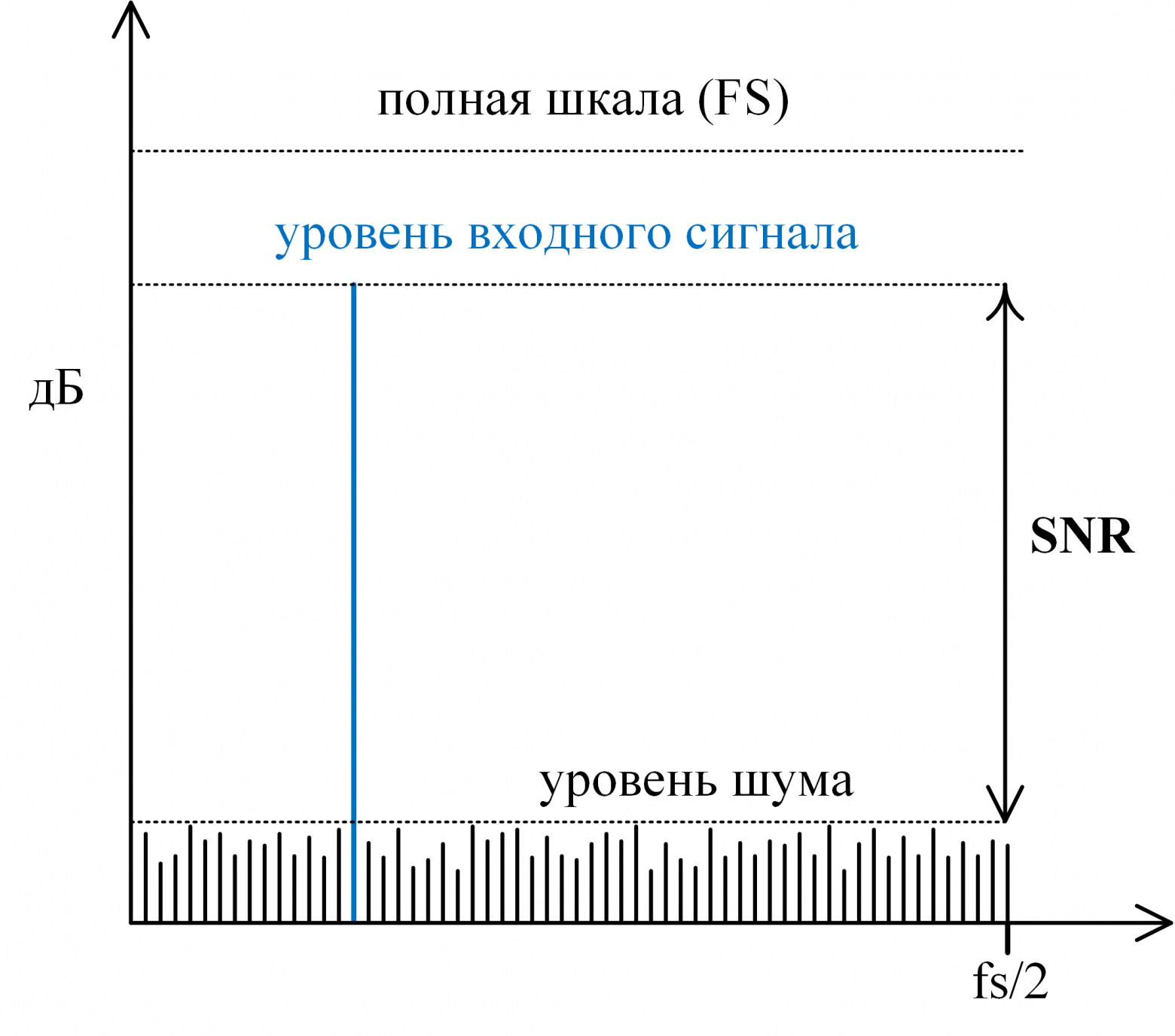

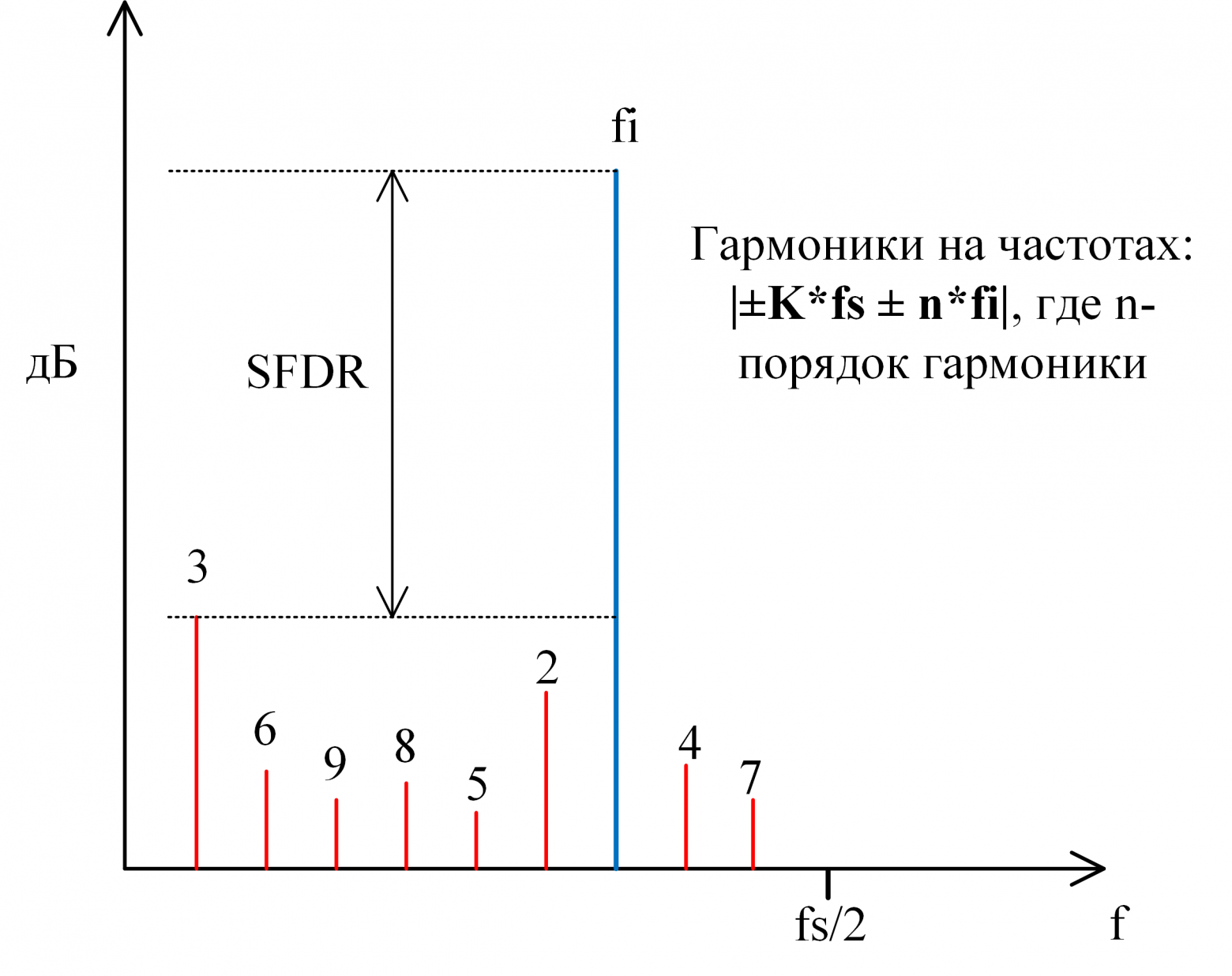

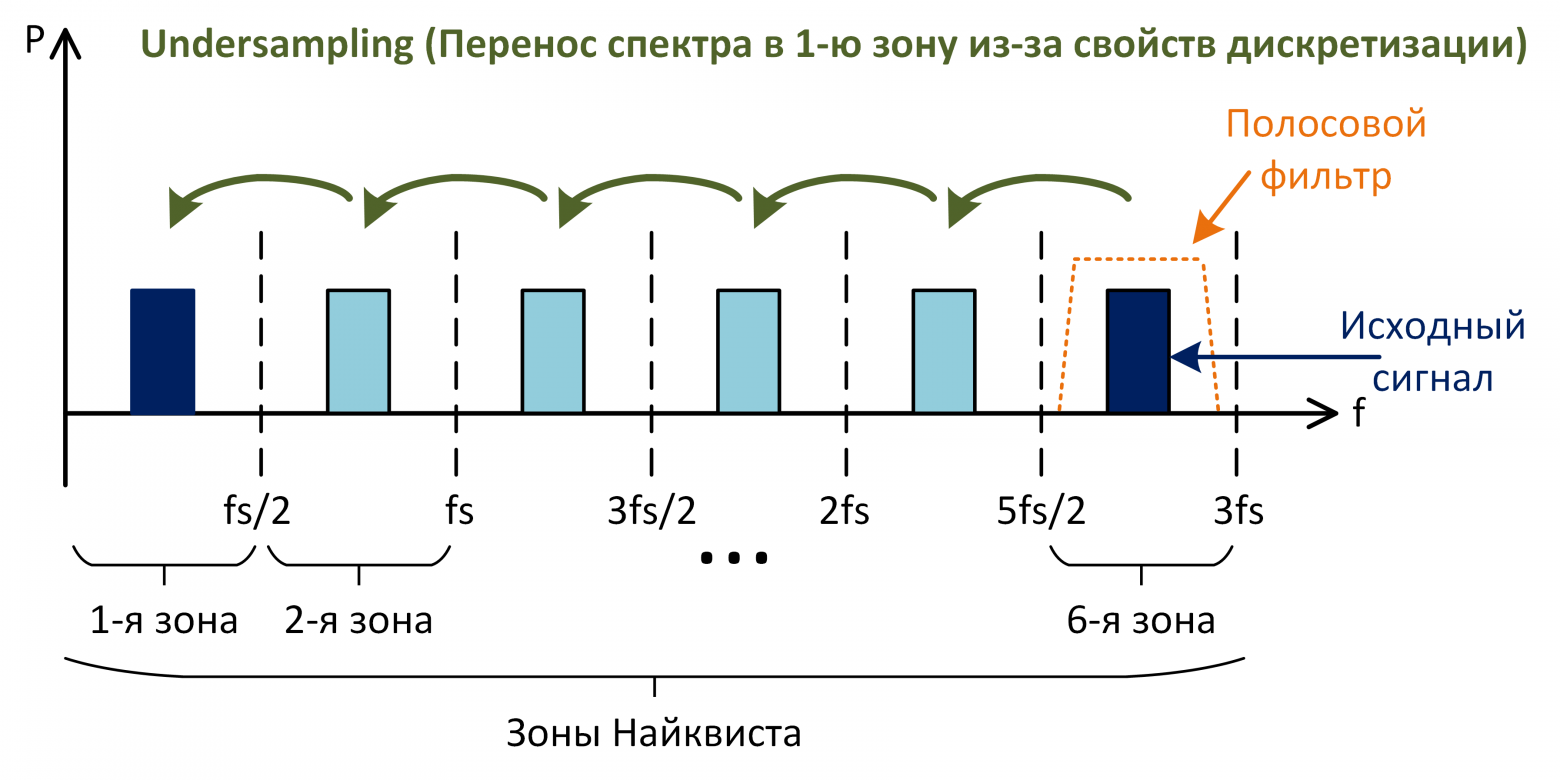
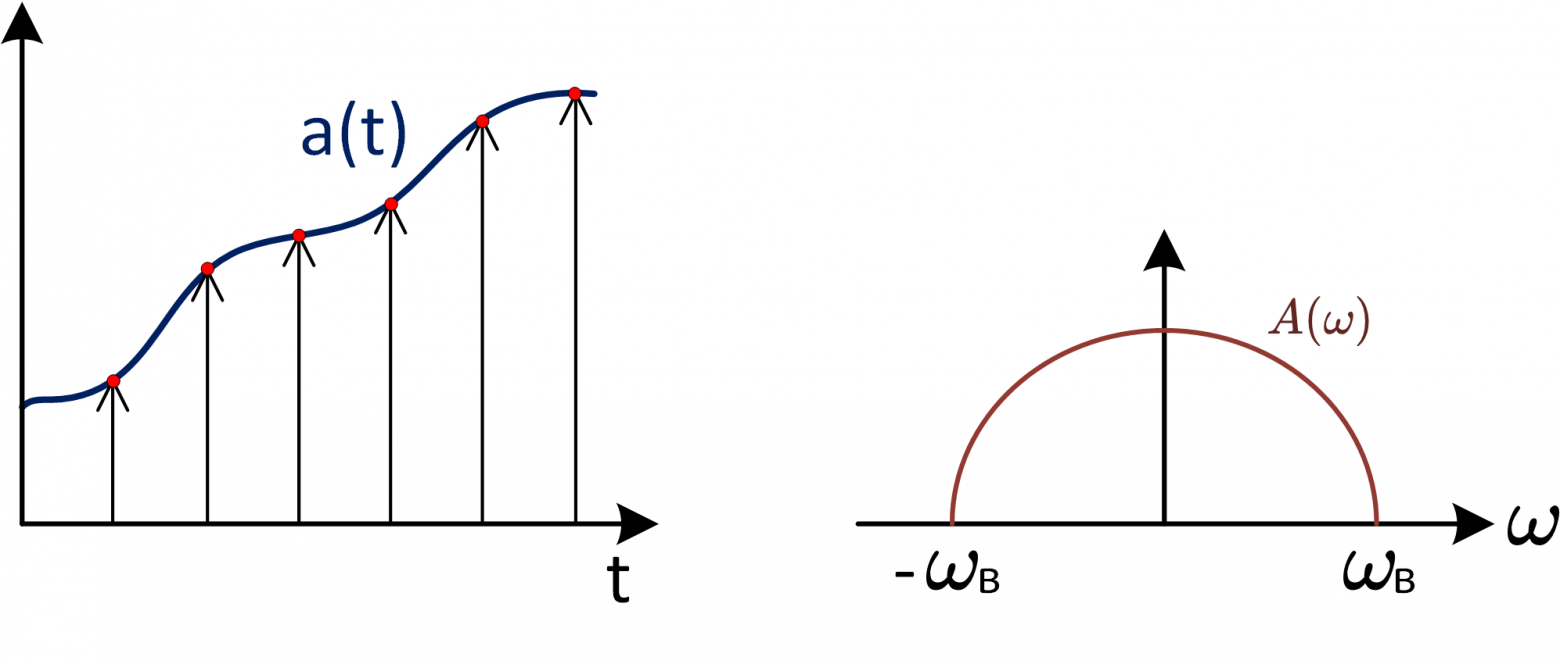
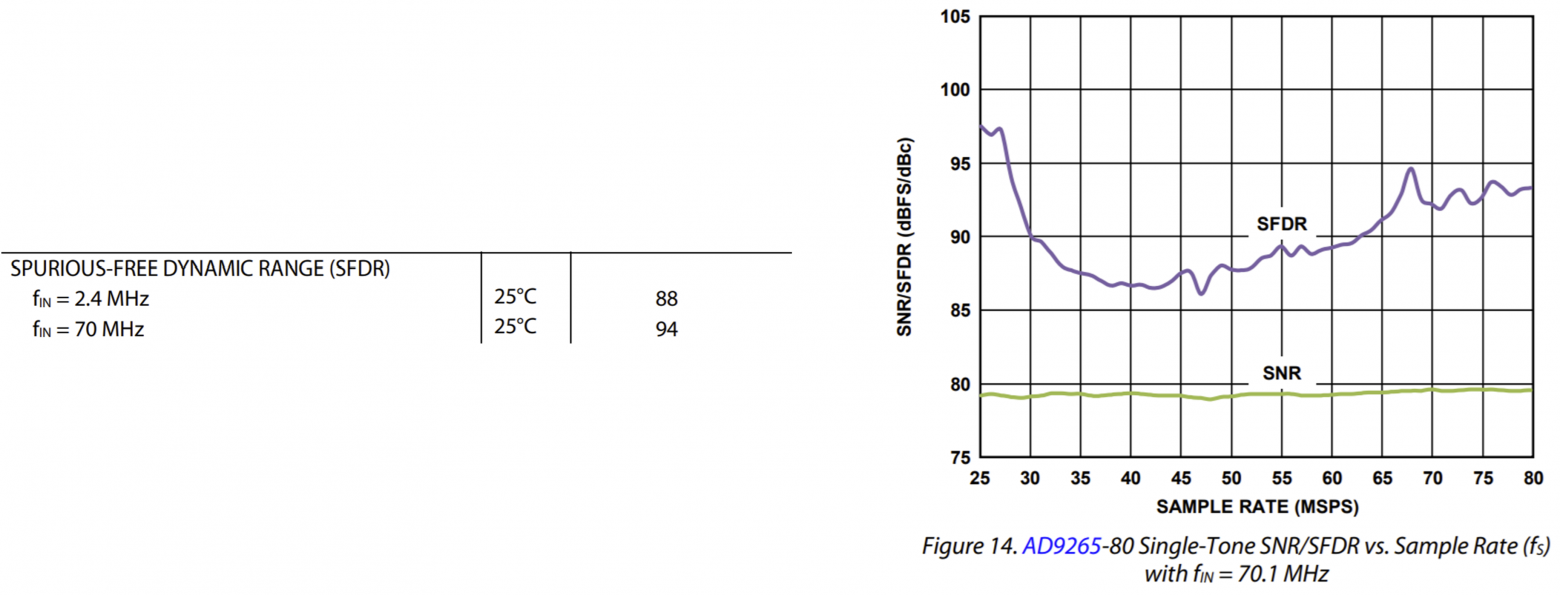
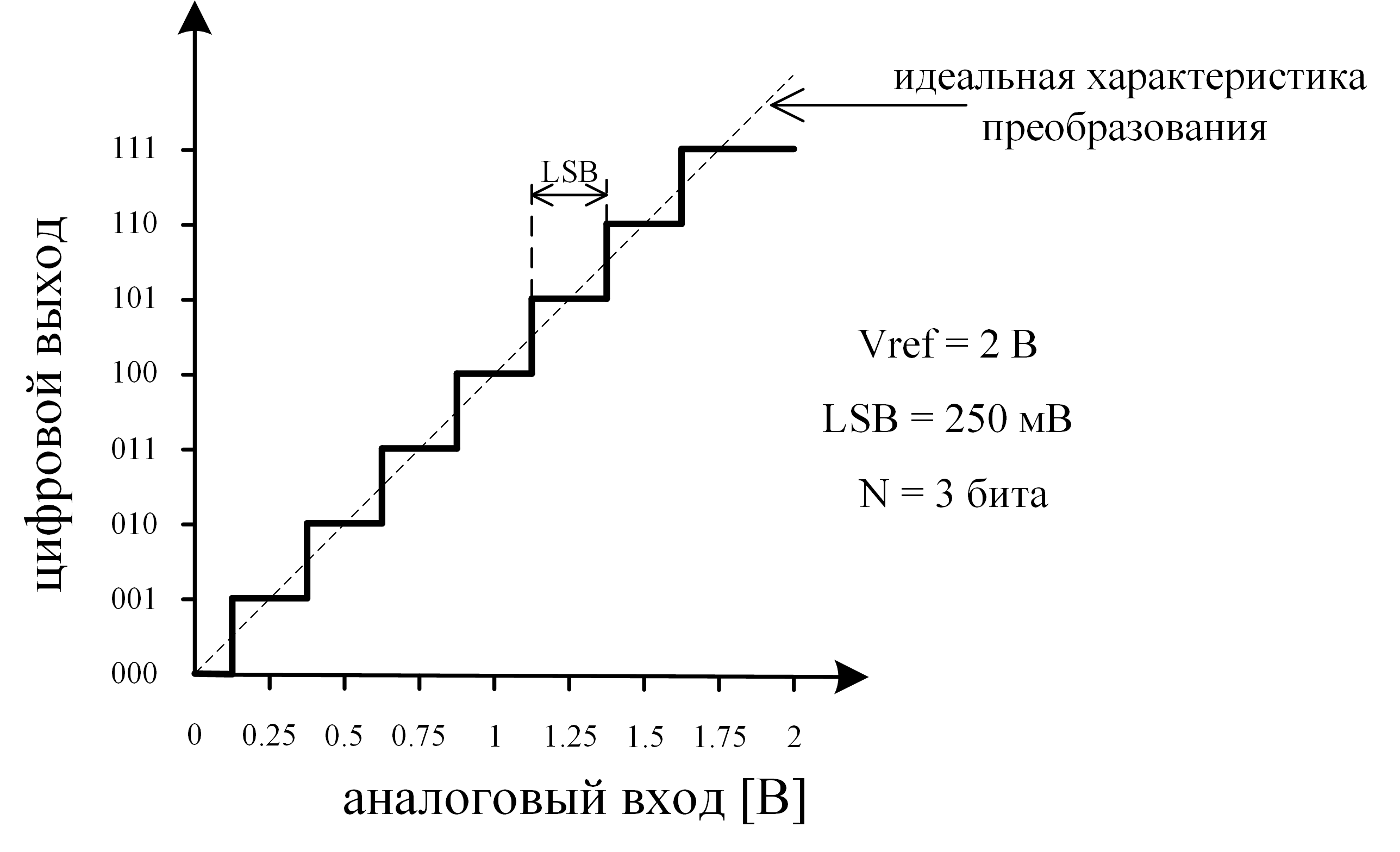
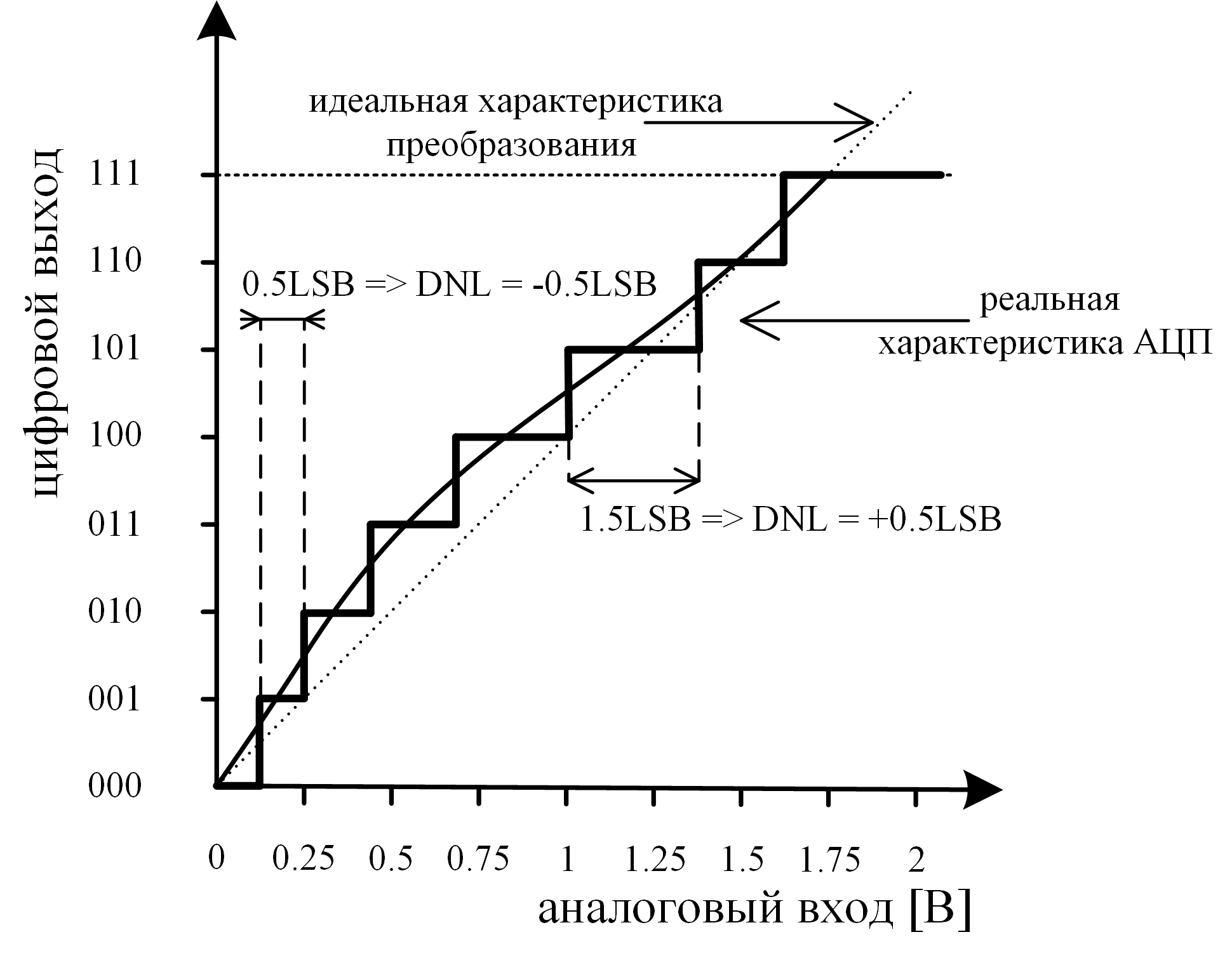

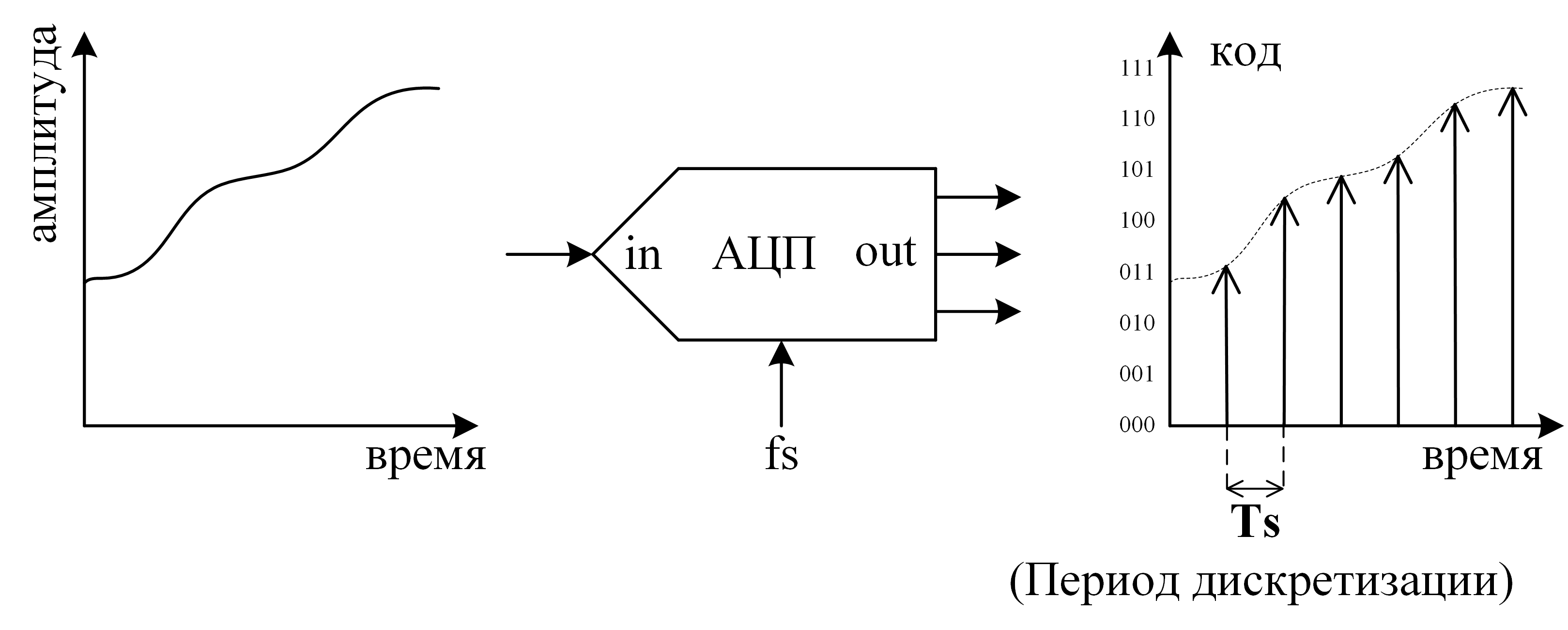

 Рис. 2: Ошибка смещения
Рис. 2: Ошибка смещения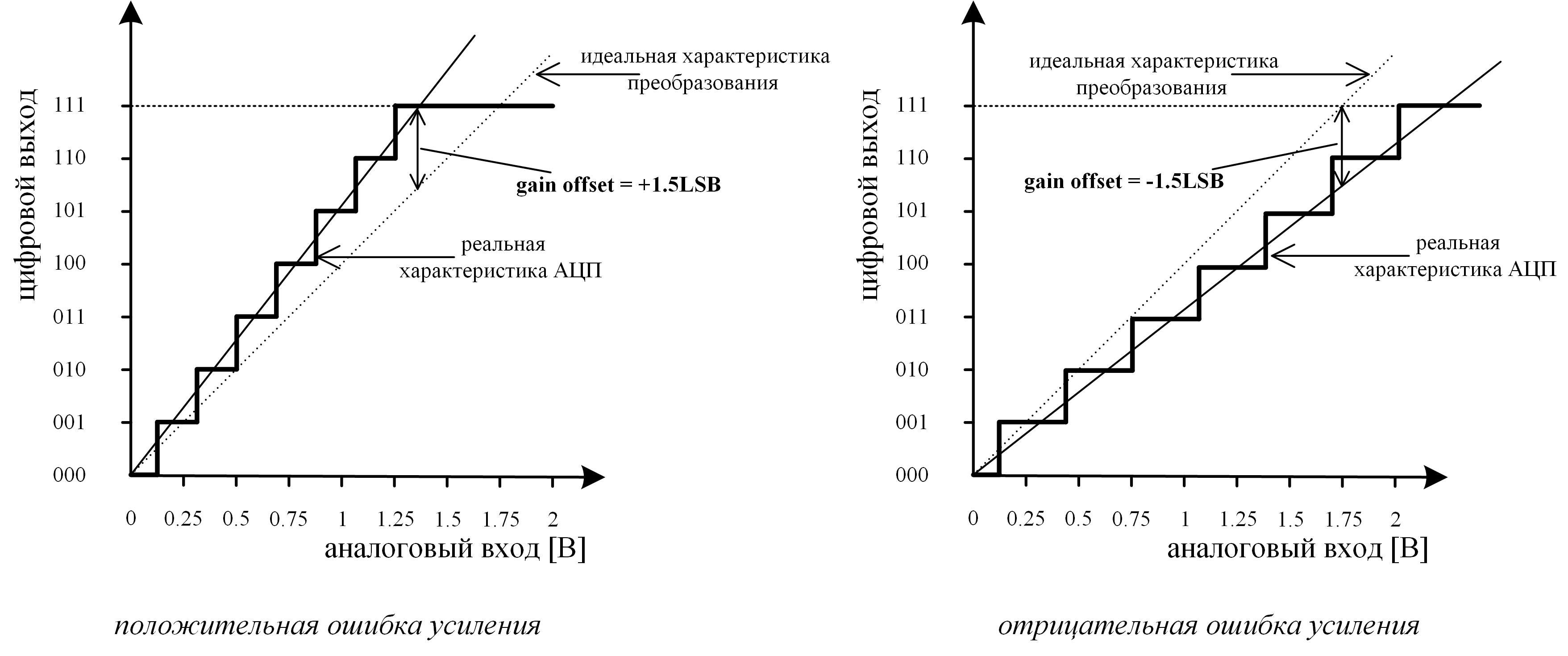 Рис. 3: Ошибка усиления
Рис. 3: Ошибка усиления