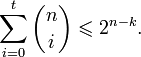Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Содержание
- 1 Способы борьбы с ошибками
- 2 Коды обнаружения и исправления ошибок
- 2.1 Блоковые коды
- 2.1.1 Линейные коды общего вида
- 2.1.1.1 Минимальное расстояние и корректирующая способность
- 2.1.1.2 Коды Хемминга
- 2.1.1.3 Общий метод декодирования линейных кодов
- 2.1.2 Линейные циклические коды
- 2.1.2.1 Порождающий (генераторный) полином
- 2.1.2.2 Коды CRC
- 2.1.2.3 Коды БЧХ
- 2.1.2.4 Коды коррекции ошибок Рида — Соломона
- 2.1.3 Преимущества и недостатки блоковых кодов
- 2.1.1 Линейные коды общего вида
- 2.2 Свёрточные коды
- 2.2.1 Преимущества и недостатки свёрточных кодов
- 2.3 Каскадное кодирование. Итеративное декодирование
- 2.4 Оценка эффективности кодов
- 2.4.1 Граница Хемминга и совершенные коды
- 2.4.2 Энергетический выигрыш
- 2.5 Применение кодов, исправляющих ошибки
- 2.1 Блоковые коды
- 3 Автоматический запрос повторной передачи
- 3.1 Запрос ARQ с остановками (stop-and-wait ARQ)
- 3.2 Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
- 3.3 Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
- 4 См. также
- 5 Литература
- 6 Ссылки
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (forward error correction) применяется на физическом уровне.
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовые слова длиной n бит. Тогда соответствующий блоковый код обычно обозначают 
Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код называется систематическим, иначе несистематическим.
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:
- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида
Линейный блоковый код — такой код, что множество его кодовых слов образует k-мерное линейное подпространство (назовём его C) в n-мерном линейном пространстве, изоморфное пространству k-битных векторов.
Это значит, что операция кодирования соответствует умножению исходного k-битного вектора на невырожденную матрицу G, называемую порождающей матрицей.
Пусть 
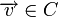
Минимальное расстояние и корректирующая способность
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 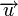

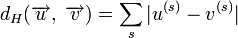
Минимальное расстояние Хемминга 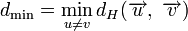
, округляем «вниз», так чтобы 2t < dmin.
Корректирующая способность определяет, сколько ошибок передачи кода (типа 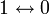
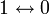

Таким образом получив искажённый код из At декодер принимает решение, что был исходный код A, исправляя тем самым не более t ошибок.
Поясним на примере. Предположим, что есть два кодовых слова A и B, расстояние Хемминга между ними равно 3. Если было передано слово A, и канал внёс ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову A, чем к любому другому, и в частности к B. Но если каналом были внесены ошибки в двух битах (в которых A отличалось от B) то результат ошибочной передачи A окажется ближе к B, чем A, и декодер примет решение что передавалось слово B.
Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 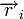

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 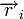
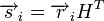
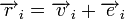
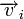
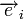

Линейные циклические коды
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 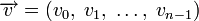
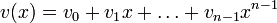
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 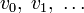
Порождающий (генераторный) полином
Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному g(x). Порождающий полином является делителем xn − 1.
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
- несистематическое кодирование осуществляется путём умножения кодируемого вектора на g(x): v(x) = u(x)g(x);
- систематическое кодирование осуществляется путём «дописывания» к кодируемому слову остатка от деления xn − ku(x) на g(x), то есть
.
Коды CRC
Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления xn − ku(x) на g(x). Ввиду того, что исправление ошибок не требуется, проверка правильности передачи может производиться точно так же.
Таким образом, вид полинома g(x) задаёт конкретный код CRC. Примеры наиболее популярных полиномов:
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | x12 + x11 + x3 + x2 + x + 1 |
| CRC-16 | 16 | x16 + x15 + x2 + 1 |
| CRC-x16 + x12 + x5 + 1 | ||
| CRC-32 | 32 | x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1 |
Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома g(x) на множители в поле Галуа.
Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
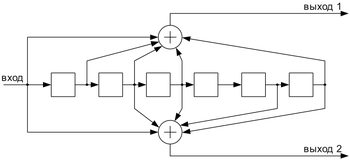
Свёрточные коды
Свёрточный кодер (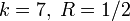
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
Пусть имеется двоичный блоковый (n,k) код с корректирующей способностью t. Тогда справедливо неравенство (называемое границей Хемминга):
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также
- Цифровая связь
- Линейный код
- Циклический код
- Код Боуза — Чоудхури — Хоквингема
- Код Рида — Соломона
- LDPC
- Свёрточный код
- Турбо-код
Литература
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. — ISBN 5-94836-035-0
Ссылки
- Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006.
Wikimedia Foundation.
2010.
To clean up transmission errors introduced by Earth’s atmosphere (left), Goddard scientists applied Reed–Solomon error correction (right), which is commonly used in CDs and DVDs. Typical errors include missing pixels (white) and false signals (black). The white stripe indicates a brief period when transmission was interrupted.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Definitions[edit]
Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.
Error correction is the detection of errors and reconstruction of the original, error-free data.
History[edit]
In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.[5]
The modern development of error correction codes is credited to Richard Hamming in 1947.[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication[7] and was quickly generalized by Marcel J. E. Golay.[8]
Introduction[edit]
All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.
If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Types of error correction[edit]
There are three major types of error correction.[9]
Automatic repeat request[edit]
Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.
Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.
Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.
ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.[10]
For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.
Forward error correction[edit]
Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.[13]
Error-correcting codes are usually distinguished between convolutional codes and block codes:
- Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
- Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.
Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.
The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.
Hybrid schemes[edit]
Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:[10]
- Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
- Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.
The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.
Error detection schemes[edit]
Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).
Minimum distance coding[edit]
A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.
Repetition codes[edit]
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.
A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.[14][15]
Parity bit[edit]
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.
Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.
There are also other bit-grouping techniques.
Checksum[edit]
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy check[edit]
A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.
A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.
The parity bit can be seen as a special-case 1-bit CRC.
Cryptographic hash function[edit]
The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.
Error correction code[edit]
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.
Applications[edit]
Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.
Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.
Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.
Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.
Reliability and inspection engineering also make use of the theory of error-correcting codes.[16]
Internet[edit]
In a typical TCP/IP stack, error control is performed at multiple levels:
- Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
- The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
- The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
- UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
- TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.
Deep-space telecommunications[edit]
The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.
The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.
The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.
The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.
Satellite broadcasting[edit]
The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.
Data storage[edit]
Error detection and correction codes are often used to improve the reliability of data storage media.[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.
Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.
Error-correcting memory[edit]
Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.
Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.[22]
In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.[23][24][25] A few systems[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.
See also[edit]
- Berger code
- Burst error-correcting code
- ECC memory, a type of computer data storage
- Link adaptation
- List of algorithms § Error detection and correction
- List of hash functions
References[edit]
- ^ a b «Masorah». Jewish Encyclopedia.
- ^ Pratico, Gary D.; Pelt, Miles V. Van (2009). Basics of Biblical Hebrew Grammar: Second Edition. Zondervan. ISBN 978-0-310-55882-8.
- ^ Mounce, William D. (2007). Greek for the Rest of Us: Using Greek Tools Without Mastering Biblical Languages. Zondervan. p. 289. ISBN 978-0-310-28289-1.
- ^ Mishneh Torah, Tefillin, Mezuzah, and Sefer Torah, 1:2. Example English translation: Eliyahu Touger. The Rambam’s Mishneh Torah. Moznaim Publishing Corporation.
- ^ Brian M. Fagan (5 December 1996). «Dead Sea Scrolls». The Oxford Companion to Archaeology. Oxford University Press. ISBN 0195076184.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, p. vii, ISBN 0-88385-023-0
- ^ Shannon, C.E. (1948), «A Mathematical Theory of Communication», Bell System Technical Journal, 27 (3): 379–423, doi:10.1002/j.1538-7305.1948.tb01338.x, hdl:10338.dmlcz/101429, PMID 9230594
- ^ Golay, Marcel J. E. (1949), «Notes on Digital Coding», Proc.I.R.E. (I.E.E.E.), 37: 657
- ^ Gupta, Vikas; Verma, Chanderkant (November 2012). «Error Detection and Correction: An Introduction». International Journal of Advanced Research in Computer Science and Software Engineering. 2 (11). S2CID 17499858.
- ^ a b A. J. McAuley, Reliable Broadband Communication Using a Burst Erasure Correcting Code, ACM SIGCOMM, 1990.
- ^ Shah, Pradeep M.; Vyavahare, Prakash D.; Jain, Anjana (September 2015). «Modern error correcting codes for 4G and beyond: Turbo codes and LDPC codes». 2015 Radio and Antenna Days of the Indian Ocean (RADIO): 1–2. doi:10.1109/RADIO.2015.7323369. ISBN 978-9-9903-7339-4. S2CID 28885076. Retrieved 22 May 2022.
- ^ «IEEE SA — IEEE 802.11ac-2013». IEEE Standards Association.
- ^ «Transition to Advanced Format 4K Sector Hard Drives | Seagate US». Seagate.com. Retrieved 22 May 2022.
- ^ Frank van Gerwen. «Numbers (and other mysterious) stations». Archived from the original on 12 July 2017. Retrieved 12 March 2012.
- ^ Gary Cutlack (25 August 2010). «Mysterious Russian ‘Numbers Station’ Changes Broadcast After 20 Years». Gizmodo. Retrieved 12 March 2012.
- ^ Ben-Gal I.; Herer Y.; Raz T. (2003). «Self-correcting inspection procedure under inspection errors» (PDF). IIE Transactions. IIE Transactions on Quality and Reliability, 34(6), pp. 529-540. Archived from the original (PDF) on 2013-10-13. Retrieved 2014-01-10.
- ^ K. Andrews et al., The Development of Turbo and LDPC Codes for Deep-Space Applications, Proceedings of the IEEE, Vol. 95, No. 11, Nov. 2007.
- ^ Huffman, William Cary; Pless, Vera S. (2003). Fundamentals of Error-Correcting Codes. Cambridge University Press. ISBN 978-0-521-78280-7.
- ^ Kurtas, Erozan M.; Vasic, Bane (2018-10-03). Advanced Error Control Techniques for Data Storage Systems. CRC Press. ISBN 978-1-4200-3649-7.[permanent dead link]
- ^ Scott A. Moulton. «My Hard Drive Died». Archived from the original on 2008-02-02.
- ^ Qiao, Zhi; Fu, Song; Chen, Hsing-Bung; Settlemyer, Bradley (2019). «Building Reliable High-Performance Storage Systems: An Empirical and Analytical Study». 2019 IEEE International Conference on Cluster Computing (CLUSTER): 1–10. doi:10.1109/CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite». Tsinghua Space Center, Tsinghua University, Beijing. Archived from the original on 2011-10-02. Retrieved 2009-02-16.
- ^ Jeff Layton. «Error Detection and Correction». Linux Magazine. Retrieved 2014-08-12.
- ^ «EDAC Project». bluesmoke.sourceforge.net. Retrieved 2014-08-12.
- ^ «Documentation/edac.txt». Linux kernel documentation. kernel.org. 2014-06-16. Archived from the original on 2009-09-05. Retrieved 2014-08-12.
Further reading[edit]
- Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
- SoftECC: A System for Software Memory Integrity Checking
- A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
- Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing
External links[edit]
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
- ECC Page — implementations of popular ECC encoding and decoding routines
To clean up transmission errors introduced by Earth’s atmosphere (left), Goddard scientists applied Reed–Solomon error correction (right), which is commonly used in CDs and DVDs. Typical errors include missing pixels (white) and false signals (black). The white stripe indicates a brief period when transmission was interrupted.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Definitions[edit]
Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.
Error correction is the detection of errors and reconstruction of the original, error-free data.
History[edit]
In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.[5]
The modern development of error correction codes is credited to Richard Hamming in 1947.[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication[7] and was quickly generalized by Marcel J. E. Golay.[8]
Introduction[edit]
All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.
If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Types of error correction[edit]
There are three major types of error correction.[9]
Automatic repeat request[edit]
Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.
Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.
Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.
ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.[10]
For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.
Forward error correction[edit]
Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.[13]
Error-correcting codes are usually distinguished between convolutional codes and block codes:
- Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
- Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.
Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.
The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.
Hybrid schemes[edit]
Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:[10]
- Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
- Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.
The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.
Error detection schemes[edit]
Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).
Minimum distance coding[edit]
A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.
Repetition codes[edit]
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.
A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.[14][15]
Parity bit[edit]
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.
Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.
There are also other bit-grouping techniques.
Checksum[edit]
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy check[edit]
A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.
A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.
The parity bit can be seen as a special-case 1-bit CRC.
Cryptographic hash function[edit]
The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.
Error correction code[edit]
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.
Applications[edit]
Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.
Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.
Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.
Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.
Reliability and inspection engineering also make use of the theory of error-correcting codes.[16]
Internet[edit]
In a typical TCP/IP stack, error control is performed at multiple levels:
- Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
- The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
- The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
- UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
- TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.
Deep-space telecommunications[edit]
The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.
The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.
The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.
The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.
Satellite broadcasting[edit]
The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.
Data storage[edit]
Error detection and correction codes are often used to improve the reliability of data storage media.[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.
Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.
Error-correcting memory[edit]
Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.
Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.[22]
In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.[23][24][25] A few systems[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.
See also[edit]
- Berger code
- Burst error-correcting code
- ECC memory, a type of computer data storage
- Link adaptation
- List of algorithms § Error detection and correction
- List of hash functions
References[edit]
- ^ a b «Masorah». Jewish Encyclopedia.
- ^ Pratico, Gary D.; Pelt, Miles V. Van (2009). Basics of Biblical Hebrew Grammar: Second Edition. Zondervan. ISBN 978-0-310-55882-8.
- ^ Mounce, William D. (2007). Greek for the Rest of Us: Using Greek Tools Without Mastering Biblical Languages. Zondervan. p. 289. ISBN 978-0-310-28289-1.
- ^ Mishneh Torah, Tefillin, Mezuzah, and Sefer Torah, 1:2. Example English translation: Eliyahu Touger. The Rambam’s Mishneh Torah. Moznaim Publishing Corporation.
- ^ Brian M. Fagan (5 December 1996). «Dead Sea Scrolls». The Oxford Companion to Archaeology. Oxford University Press. ISBN 0195076184.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, p. vii, ISBN 0-88385-023-0
- ^ Shannon, C.E. (1948), «A Mathematical Theory of Communication», Bell System Technical Journal, 27 (3): 379–423, doi:10.1002/j.1538-7305.1948.tb01338.x, hdl:10338.dmlcz/101429, PMID 9230594
- ^ Golay, Marcel J. E. (1949), «Notes on Digital Coding», Proc.I.R.E. (I.E.E.E.), 37: 657
- ^ Gupta, Vikas; Verma, Chanderkant (November 2012). «Error Detection and Correction: An Introduction». International Journal of Advanced Research in Computer Science and Software Engineering. 2 (11). S2CID 17499858.
- ^ a b A. J. McAuley, Reliable Broadband Communication Using a Burst Erasure Correcting Code, ACM SIGCOMM, 1990.
- ^ Shah, Pradeep M.; Vyavahare, Prakash D.; Jain, Anjana (September 2015). «Modern error correcting codes for 4G and beyond: Turbo codes and LDPC codes». 2015 Radio and Antenna Days of the Indian Ocean (RADIO): 1–2. doi:10.1109/RADIO.2015.7323369. ISBN 978-9-9903-7339-4. S2CID 28885076. Retrieved 22 May 2022.
- ^ «IEEE SA — IEEE 802.11ac-2013». IEEE Standards Association.
- ^ «Transition to Advanced Format 4K Sector Hard Drives | Seagate US». Seagate.com. Retrieved 22 May 2022.
- ^ Frank van Gerwen. «Numbers (and other mysterious) stations». Archived from the original on 12 July 2017. Retrieved 12 March 2012.
- ^ Gary Cutlack (25 August 2010). «Mysterious Russian ‘Numbers Station’ Changes Broadcast After 20 Years». Gizmodo. Retrieved 12 March 2012.
- ^ Ben-Gal I.; Herer Y.; Raz T. (2003). «Self-correcting inspection procedure under inspection errors» (PDF). IIE Transactions. IIE Transactions on Quality and Reliability, 34(6), pp. 529-540. Archived from the original (PDF) on 2013-10-13. Retrieved 2014-01-10.
- ^ K. Andrews et al., The Development of Turbo and LDPC Codes for Deep-Space Applications, Proceedings of the IEEE, Vol. 95, No. 11, Nov. 2007.
- ^ Huffman, William Cary; Pless, Vera S. (2003). Fundamentals of Error-Correcting Codes. Cambridge University Press. ISBN 978-0-521-78280-7.
- ^ Kurtas, Erozan M.; Vasic, Bane (2018-10-03). Advanced Error Control Techniques for Data Storage Systems. CRC Press. ISBN 978-1-4200-3649-7.[permanent dead link]
- ^ Scott A. Moulton. «My Hard Drive Died». Archived from the original on 2008-02-02.
- ^ Qiao, Zhi; Fu, Song; Chen, Hsing-Bung; Settlemyer, Bradley (2019). «Building Reliable High-Performance Storage Systems: An Empirical and Analytical Study». 2019 IEEE International Conference on Cluster Computing (CLUSTER): 1–10. doi:10.1109/CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite». Tsinghua Space Center, Tsinghua University, Beijing. Archived from the original on 2011-10-02. Retrieved 2009-02-16.
- ^ Jeff Layton. «Error Detection and Correction». Linux Magazine. Retrieved 2014-08-12.
- ^ «EDAC Project». bluesmoke.sourceforge.net. Retrieved 2014-08-12.
- ^ «Documentation/edac.txt». Linux kernel documentation. kernel.org. 2014-06-16. Archived from the original on 2009-09-05. Retrieved 2014-08-12.
Further reading[edit]
- Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
- SoftECC: A System for Software Memory Integrity Checking
- A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
- Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing
External links[edit]
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
- ECC Page — implementations of popular ECC encoding and decoding routines
Универсальная система коррекции ошибок — как она устроена
Время прочтения
3 мин
Просмотры 3.9K
Инженеры MIT представили чип, способный работать с любым типом данных, передаваемых по сети. Под катом обсуждаем возможности и перспективы разработки, а также альтернативные решения для квантовых компьютеров.
О чем, собственно, речь
Коды коррекции ошибок при передаче данных используют с 1940-х годов. Каждый такой код разрабатывают в паре с уникальным алгоритмом декодирования и аппаратным обеспечением для его реализации. Но в начале сентября инженеры из Массачусетского технического института (MIT), Бостонского университета и Университета Мейнут в Ирландии предложили альтернативный подход.
Они представили кремниевый чип, способный исправить ошибки при передаче данных любого типа. В основу технологии положили универсальный алгоритм под названием GRAND — Guessing Random Additive Noise Decoding. Классические алгоритмы декодирования работают с кодовой книгой и хэшами, чтобы восстановить исходные данные. В GRAND применен иной механизм — система пытается угадать природу и структуру шума. Так, чип генерирует серию шумовых последовательностей и вычитает их из полученного сигнала. Алгоритм сверяет результат с кодовой книгой — процесс повторяют до тех пор, пока сообщение не будет восстановлено.
Что касается аппаратной части, то чип имеет трёхуровневую структуру. Уровни работают независимо и анализируют шумовые паттерны (от простых к сложным). Чип содержит две микросхемы статической памяти с произвольным доступом (SRAM). Одна отвечает за поиск кодовых слов, а другая — за загрузку кодовых книг.
Каковы перспективы
Новое устройство способно обработать избыточный код длиной до 128 бит с задержкой в одну микросекунду. Авторы говорят, что их решение найдет применение в сетях 5G, IoT-устройствах и системах дополненной и виртуальной реальности — там, где необходима обработка больших объемов данных. Однако все имеет свою цену — платформа потребляет достаточно много энергии, что в перспективе может ограничить её применимость. Хотя инженеры MIT планируют переработать структуру кремниевого чипа, чтобы повысить энергоэффективность (стр.19).
Можно предположить, что GRAND откроет новые возможности в сфере сетевого кодирования и увеличит пропускную способность каналов за счет комбинирования передаваемых пакетов. Авторы также отмечают, что их решение можно использовать для развития других алгоритмов декодирования — например, превратить циклические избыточные коды (CRC) в инструмент коррекции ошибок [обычно CRC используют только для нахождения контрольных сумм и проверки целостности данных].
Аналогичные разработки для кубитов
Механизмы коррекции ошибок разрабатывают и для квантовых компьютеров. Такие алгоритмы необходимы, поскольку базовые элементы квантовых вычислительных машин — кубиты — не идеальны сами по себе. Они крайне хрупкие, могут разрушаться и переходить в неправильное состояние.
Летом этого года новое решение для коррекции ошибок предложили в Google — его реализовали за счет избыточных кубитов, не участвующих в вычислениях. Инженеры соединили кубиты с четырьмя соседними и разместили их в форме решетки. Примерно пятая часть элементов — контрольные. С их помощью оценивают состояние связанных элементов и корректируют данные.
Подобные технологии играют важную роль в создании квантового интернета. Разработками в этой области уже занимаются специалисты из США, Швейцарии, Китая и России. Можно ожидать, что спектр проектов в этой области будет увеличиваться, а инновации вроде GRAND станут источником свежих идей.
Свежие материалы в нашем блоге на Хабре:
-
Компиляция без предупреждений — что случилось в Linux-сообществе
-
QUIC стал RFC, но как дела с перспективами — обсуждаем мнения
-
Что ждет Wi-Fi: три новых стандарта до 2024-го
Больше о протоколах и алгоритмах — в корпоративном блоге VAS Experts:
-
Технологии шифрования нового поколения: как они работают
-
P2P-протокол Dat — как работает и кем используется
-
Пять причин, почему переход на IPv6 идет так долго
Чем занимается корректор? А редактор?
Чем занимается корректор? А редактор?
Корректура текста — это устранение пунктуационных, типографических, орфографических ошибок и опечаток. В переводе с латинского языка слово «corrector» означает «исправитель».
Чем отличается редактура от корректуры
Редактура и корректура существенно отличаются друг от друга. Редакторская правка материала предусматривает мониторинг:
Профессиональный редактор обнаруживает неоднозначные трактовки, проверяет правильность употребления цитат, терминологии. Этот специалист отслеживает логику повествования в художественном тексте, исправляет стилистические погрешности. Одна из задач редактора – проверка информативности контента.
Издательская корректура не предусматривает правку стиля и изменение структуры текста. Специалист устраняет грамматические ошибки, расставляет недостающие знаки препинания и т. д. Корректорской правке предшествует редакторская. Изначально устраняются все недочеты материала: ошибки и стилистические погрешности. После внесения в чистовик правок корректор вычитывает текст.
Иногда задачи корректора и редактора выполняет один и тот же человек. Но в большинстве случаев предусмотрен другой подход к шлифовке материала. Над контентом приходится трудиться целой бригаде редакторов, авторов, контент-специалистов. Это позволяет получить результат, который максимально приближен к идеалу.
Содержание
- Основные составляющие корректуры текста
- Каковы основные задачи корректора
- Этапы корректуры
- Основные составляющие редактуры текста
- Что нужно учитывать при самостоятельном редактировании написанного?
- Стоит ли доверять компьютерным программам?
- Где можно заказать корректуру и редактуру текста
- Книги по редактуре
Основные составляющие корректуры текста
Корректорская правка требуется перед публикацией разнообразного контента:
-
художественного произведения;
Процесс внесения корректорских правок довольно сложен. Он требует внимательного, скрупулезного подхода. Корректору довольно часто приходится вносить синтаксические исправления. К их числу следует отнести:
исправление недочетов в построении фраз;
некорректное употребление деепричастных, причастных оборотов.
В рукописях художественных произведений нередко встречаются и морфологические ошибки. Одна из них — неверное употребление падежей, кратких форм слова, степеней сравнения.
Каковы основные задачи корректора
Корректор — специалист, выполняющий следующие задачи:
исправление неправильных обозначений, сокращений;
проверка соответствия художественного текста основным языковым нормам (в частности, устранение грамматических, словообразовательных ошибок);
финальная вычитка материала, которая осуществляется перед его публикацией.
Обратите внимание! На литературного корректора возложена и такая задача, как обеспечение единства издательского оформления материала (ссылок, сносок, сокращений).
Этапы корректуры
Первой корректурой называют вычитку материала до его передачи в верстку. Она включает в себя:
исправление недочетов стилистического характера;
устранение пунктуационных и орфографических ошибок;
унификация использованных в тексте единиц измерения, сокращений, символов;
проверка полноты библиографического описания, правильности оформления перечней, таблиц и т. д.
Под повторной корректурой понимается итоговая вычитка сверстанного текста. Она может выполняться в PDF-файле либо другом электронном формате. Такая корректорская правка текста призвана устранить недочеты, допущенные при верстке контента (проверка правильности размещения рисунков, колонтитулов, удаление «висячих» строк).
Виды корректуры
Существуют 2 основных вида корректуры: типографская и издательская. Основная задача последней – обнаружение стилистических, смысловых и прочих ошибок, допущенных автором.
Типографская
Корректура в типографии предполагает:
-
сличение оттиска с авторской рукописью;
-
указание имеющихся неточностей, пропусков;
-
наличие неправильных концевых полос.
Обратите внимание! Типографский корректор работает с ошибками в выделении фрагментов текста, нумерации страниц.
Издательская
К основным задачам издательской корректуры принадлежат:
-
проверка единства стиля и терминологии;
-
устранение ошибок, которые не были замечены типографским корректором;
-
определение правильности транскрипции иностранных слов, написания условных сокращений.
Основные составляющие редактуры текста
Литературное редактирование предусматривает:
-
исправление морфологических, лексических ошибок;
-
создание послесловия, предисловия;
-
написание книжной аннотации.
Смысловое редактирование предполагает композиционный анализ художественного текста. На этой стадии происходит подбор более логичных и четких формулировок, уделяется пристальное внимание логике изложения текста. Научное редактирование предусматривает проверку таблиц, формул, графиков. В итоге все данные должны соответствовать международным и отечественным стандартам. Стилистическое редактирование не менее важно. Оно подразумевает приведение авторского текста к единому стилю.
Что нужно учитывать при самостоятельном редактировании написанного?
Начинающему автору, который делает первые шаги на писательском поприще, стоит оценивать свой текст с позиции строгого критика. При самостоятельном внесении правок в небольшие рассказы стоит обращать внимание на:
последовательность изложения. Порой автор излагает материал не по порядку, не выстраивает четкую цепочку событий. Чтобы рассказ не казался читателям несвязным, при его написании рекомендуется придерживаться заранее составленного письменного плана;
стилевые особенности. Не во всех текстах уместны просторечия, сленг. Не стоит использовать не понятные целевой аудитории речевые обороты;
ритм художественного текста. Длинные сложноподчиненные предложения стоит разбить на более короткие: для упрощения восприятия написанного;
благозвучность слога. Начинающему писателю стоит проявлять безжалостность к канцеляризмам, делающим текст излишне громоздким, речевым штампам.
Разумеется, профессиональная корректорская вычитка контента не идет ни в какое сравнение с внесением онлайн-правок в компьютерных программах. Электронное устройство не учитывает множество особенностей русского языка. Компьютерным программам неведомы тонкие нюансы употребления словесных оборотов. Они не способны и отличить прямую речь от косвенной. Следовательно, ни одной компьютерной программе не под силу заменить опытного, высококвалифицированного специалиста.
Стоит ли доверять компьютерным программам?
В настоящее время существует множество сервисов, проверяющих орфографию, стилистику, прочие аспекты правописания. При их использовании нет 100% гарантии в правильности данного компьютерной программой совета. Если орфографические ошибки такие сайты распознают, то проблемы с пунктуацией часто не замечают. А о том, что программы смогут заменить вам редактора, не стоит даже мечтать. Логику повествования, фактические ошибки они не способны оценить.
Поэтому не стоит слишком полагаться на рекомендации таких сервисов. В противном случае использование подобных ресурсов подарит вам излишнюю уверенность, а потом выяснится, что часть ошибок осталась.
Где можно заказать корректуру и редактуру текста
В издательских сервисах ЛитРес можно заказать услуги профессионального корректора. Сроки их выполнения зависят от объема литературного произведения. В большинстве случаев на корректирование текста отводится от 7 до 14 рабочих дней. Если рукопись объёмная (более 8−9 авторских листов), сроки могут быть увеличены. Стоимость корректуры определяется в индивидуальном порядке.
Литературный редактор платформы «ЛитРес. Самиздат» помогает сделать контент более информативным, легким для восприятия читателя. В случае необходимости специалист корректирует неоднозначные сцены или сюжетные повороты, прописанные в книге.
Редактура vs корректура
Рассказываем подробнее об услугах ЛитРес
Книги по редактуре
Основам литературной и лингвистической правки текста посвящены эти книги:
-
Жарков И. А., «Чтение как средство редакторского анализа». (Вестник Московского государственного университета печати им. Ивана Фёдорова).
-
Голуб И. Б., «Конспект лекций по литературному редактированию» (учебное пособие).
-
Мильчин, А. Э. «Культура издания, или как не надо и как надо делать книги: практическое руководство».
-
Голуб И. Б., «Литературное редактирование: учебное пособие».
Была ли данная статья полезна для Вас?
Другие статьи в нашем блоге:
Онлайн проверка орфографии Advego — это сервис по проверке текста на ошибки. Оценивайте грамотность и правописание статей бесплатно! Мультиязычная проверка ошибок в тексте орфо онлайн! Корректировка текста онлайн — ваш инструмент и ежедневный помощник!
Язык: по умолчанию — русский
| Текст: обязательно | длина текста, символов: 0 |
Напишите текст для проверки орфографии и нажмите кнопку «Проверить»
Максимальная длина текста — 100 000 символов.
Проверьте грамотность текста онлайн, чтобы исправить все орфографические ошибки. Сервис проверки правописания Адвего работает на 20 языках совершенно бесплатно и без регистрации.
Какие ошибки исправляет проверка орфографии и корректор текста?
- Орфографические ошибки — несовпадение с мультиязычным словарем.
- Опечатки, пропущенные или лишние буквы.
- Пропущенные пробелы между словами.
- Грамматические и морфологические ошибки
Разместите текст в поле «Текст» и нажмите кнопку «Проверить» — система покажет найденные предположительные ошибки и выделит их в тексте подчеркиванием и цветом.
На каком языке проверяется правописание и ошибки?
По умолчанию грамотность текста анализируется на русском языке.
Для проверки орфографии на другом языке выберите его из выпадающего меню: английский, немецкий, испанский, французский, китайский, украинский, японский, португальский, польский, итальянский, турецкий, арабский, вьетнамский, корейский, урду, персидский, хинди, голландский, финский.
Пример отчета проверки орфографии и грамматики онлайн
Какой объем текста можно проверить на орфографию?
Максимальный объем текста для одной проверки — 100 000 символов с пробелами. Чтобы проверить статью или документ большего размера, разбейте его на фрагменты и проверьте их по очереди.
Вы можете проверить неограниченное количество текстов бесплатно и без регистрации во время коррекции.
Проверка пунктуации онлайн — исправление ошибок в тексте от Адвего
Сервис Адвего поможет не только найти плагиат онлайн бесплатно и определить уникальность текста, но и сможет провести проверку пунктуации с указанием опечаток в знаках препинания и указать наличие орфографических ошибок онлайн.
Адвего рекомендует проверить орфографию и пунктуацию онлайн на русском, украинском, английском и еще более чем 20 языках в своем качественном мультиязычном сервисе орфо онлайн!
просто сказать, что второй блок совпадает с первым, — ему все равно придется послать еще раз те же данные, так как сжимать информацию позволяется только в пределах одного блока.
Обнаружение и коррекция ошибок
Все мы знаем, что такое плохая телефонная связь, когда из за шума и треска трудно бывает расслышать голос собеседника. Правда, поскольку человеческий голос представляет собой анало говый сигнал, он допускает довольно сильные искажения без по тери информации. И все же, если качество связи слишком плохое, мы вынуждены применять некоторые методы коррекции ошибок. Модему же, который обязан абсолютно точно передать каждый бит, приходится прибегать к этим методам гораздо чаще.
Что мы делаем, когда голос в трубке едва слышен? Во первых, если мы не расслышали какое то слово, мы просим собе седника его повторить. Так же поступает, и модем. Он передает информацию не сплошным потоком^ а разделяя на блоки, и после передачи каждого такого блока ждет ответа от модема на другом конце линии — все ли понято правильно. Если принимающий модем не смог расслышать очередной блок, он просит его повторить. Вот почему при плохой связи скорость передачи снижается — часть информации приходится посылать по нескольку раз. Такой принцип коррекции ошибок называется ARQ (Automatic Repeat reQuest, автоматический запрос на повторение).
Во вторых, можно попросить собеседника говорить погромче. Модем не может говорить громче или тише1, но зато он может менять скорость передачи — снижение темпа речи помогает разобрать слова даже эффективнее, чем увеличение громкости. Поэтому почти все протоколы связи (их мы будем подробно рассматривать ниже) отслеживают количество ошибок и, если оно превышает некоторую величину, предлагают модему собеседнику перейти на более низкую скорость или уменьшить размер блоков (т. е. «говорить по буквам»).
Вы можете спросить, как же принимающий модем узнает, что информация передана с ошибкой? Ведь он, в отличие от человека, не может решать, есть ли смысл в том, что он слышит,
— для него это просто последовательность битов.
Чтобы можно было без долгих размышлений придти к вы воду, что информация передана верно, передающий модем добавляет к каждому блоку информации своего рода «опись
содержимого» — некое число, полученное с помощью ариф метических действий над всеми битами блока. Алгоритм получения этого числа выбирается так, чтобы при изменении даже одного единственного бита в передаваемом блоке результат (его называют контрольной суммой) тоже был другим.
Принимающий модем знает этот алгоритм и, получив очередной блок, сам вычисляет контрольную сумму и сравнивает ее с полученной. Если эти две контрольные суммы совпадают, блок считается переданным правильно. Если же совпадения нет, приемник решает, что при передаче произошла ошибка, и просит прислать этот блок еще раз.
Конечно, ошибка может произойти и при передаче контроль ной суммы, а не самого блока информации. В этом случае по вторная пересылка блока, понятно, не обязательна — но, конечно, лучше перестраховаться. Более того, может случиться так, что и сам блок информации, и его контрольная сумма будут содержать ошибки. Но вероятность того, что испорченная контрольная сумма будет соответствовать испорченным данным, практически равна нулю. Поэтому метод контрольной суммы обеспечивает почти стопроцентное обнаружение ошибок.
У семи нянек…
Как показывает опыт, наибольшую путаницу в умах неискушенных пользователей вызывает не сам принцип коррекции ошибок, а то, как и когда эта коррекция работает при передаче данных.
Дело в том, что коррекция ошибок может осуществляться как минимум в двух местах — в коммуникационной программе, которая реализует какой то протокол передачи файлов (например, Xmodem), и в самом модеме, если в нем встроен аппаратный протокол коррекции ошибок (например, V.42). Друг другу эти две коррекции не мешают (хотя одна из них, если активна другая, явно лишняя), но пользователя они могут запутать довольно основательно.
Не меньшая путаница порождается и сжатием данных, о котором мы говорили выше. На сей раз есть уже три действующих лица, которые горят желанием сжать передаваемые данные, — кроме протокола передачи файлов и аппаратного протокола сжатия данных (например, V.42bis), сам пользователь тоже зачастую архивирует файлы перед посылкой! Понятно, что после программ архиваторов (например, arj или zip) другим компрессорам делать уже нечего — но так ли это очевидно для свежеиспеченного владельца модема?
Режимы работы модема
Подключенный к компьютеру модем может находиться в одном из двух режимов — в режиме передачи данных или в режиме ко*
манд. Если вы работали когда нибудь с принтерами, то помните, что у них обычно есть кнопка (и лампочка) под названием «online». Когда эта лампочка горит, принтер не поддается ручному управлению: чтобы загрузить лист бумаги или настроить параметры печати с панели управления, нужно сначала вы ключить режим online.
Режим передачи данных модема напоминает режим online принтера (собственно, по английски это так и называется — «mo dem is online»). В этом режиме все, что посылает ему компьютер, модем воспринимает как данные, которые нужно преобразовать в аналоговый сигнал и послать по телефонной линии. Как говорят, модем в режиме передачи «прозрачен для данных».
Второй режим — режим команд — предназначен для управ ления модемом. Поскольку никаких кнопок на модеме обычно не делают (если не считать тумблера включения у внешних моде мов), то для управления модемом применяются специальные ко манды, посылаемые с компьютера. Модем в этом режиме работает как маленький самостоятельный компьютер: получив строку символов, он пытается интерпретировать ее как команду. Если ему это удается, то он выполняет эту команду, а если нет — выдает сообщение об ошибке.
Разновидность режима команд — режим ожидания звонка, в котором модем ждет звонка, готовый сразу же снять трубку и свя заться с модемом на другом конце линии. В этом режиме модем выполняет любые команды пользователя, но при звонке само стоятельно переходит в режим передачи.
Система команд модема
Набор команд модема, вообще говоря, зависит от его фирмы производителя, модели, года выпуска и других характеристик. Тем не менее немало команд, предназначенных для выполнения основных операций, являются общими для всех модемов.
Любой модем понимает команды снятия трубки, набора номера, установки режимов работы. Специальными командами можно протестировать работу модема, изменить параметры настройки (например, громкость встроенного динамика), получить информацию о состоянии модема и т. п.
Сразу после включения модем находится в режиме команд, а переход в режим передачи данных осуществляется по команде снятия трубки и набора номера. Существует специальная команда (так называемая escape*последовательность), которая воспринимается модемом как команда и в режиме передачи данных — она как раз и служит для перехода обратно в режим команд. Это порождает специфическую проблему: если в самих данных, пред
назначенных для передачи, есть что то похожее на escape после довательность, коммуникационной программе приходится принимать меры, чтобы модем не решил, что к нему обращаются.
Ныне широко распространенный стандарт на систему команд модема был разработан фирмой Hayes, которая первой стала выпускать модемы для компьютеров IBM PC. Другие производители модемов, чтобы не отставать от лидера, вынуждены были встраивать в свои модемы такой же набор команд, и сейчас практически любой модем понимает команды модема Hayes (иначе говоря, является Науеа*совместимым). Даже модемы, у которых есть свой собственный набор команд, обязательно поддерживают и стандарт Hayes (хотя некоторые модемы понимают не все команды этого стандарта, а другие, наоборот, имеют дополнительные).
АТ:команды
Большинство команд стандарта Hayes представляют собой строки символов, начинающиеся с двух букв AT (от англ. attention
— «внимание») и заканчивающиеся символом перевода каретки (клавиша Enter). Поэтому команды стандарта Hayes часто назы вают «АТ командами». Список стандартных АТ команд приведен
вприложении 2 на стр. 293.
Ксчастью, еще один язык команд учить совсем не обяза тельно. В принципе возможно управлять модемом средствами од ной лишь DOS, набирая AT команды с клавиатуры. Но сущест вует огромное количество коммуникационных программ с удоб ным современным интерфейсом, которые возьмут на себя все взаимодействие с модемом. Типы коммуникационных программ и принципы их работы мы рассмотрим в главе 4.
Протоколы
Житейское употребление слова «протокол» (например, «протокол допроса») довольно точно отражает тот смысл, который в него вкладывается в мире телекоммуникаций. Разница лишь в том, что если протокол допроса пишется во время (или после) самого допроса, то протокол связи должен быть известен сторонам заранее — иначе связь будет невозможна.
Если бы наш паралитик из начала этой главы был бы для чистоты эксперимента еще и глухим, то, чтобы передать нам какую то информацию, не слыша вопросов, он должен был бы заранее знать, какие вопросы и в каком порядке мы будем ему задавать. Иными словами, он должен быть осведомлен о
протоколе связи.
Как вы понимаете, договориться об этом на ходу, обмениваясь лишь потоками битов, довольно затруднительно, ибо с самого начала неясно, как эти биты интерпретировать.
Неопытных пользователей протоколы часто повергают в беспросветное отчаяние. Дело в том, что их очень много, а различия между ними редко когда просты и очевидны. И все же самые запутанные вещи всегда можно изложить доступно — что я и постараюсь сделать здесь, пользуясь всем тем, что вы уже знаете.
Итак, в этом разделе мы рассмотрим:
•телекоммуникационные стандарты вообще — кто, как и зачем их устанавливает;
•коммуникационные параметры — стартовые и стоповые биты, контроль четности, управление потоком (стандарт V.14);
•протоколы ^модемной связи — стандарты ITU T V.21, V.22, V.22bis, V.32, V.32bis, V.34, а также фирменные протоколы PEP, HST, V.FC, x2, K56Flex;
•протоколы факсимильной связи;
•протоколы коррекции ошибок и сжатия данных — MNP1 MNP5, V.42, V.42bis;
•протоколы передачи файлов — Xmodem, Kermit, Zmodem и другие;
•параметры эмуляции терминала.
Определимся с терминологией
Слово «протокол» в применении к модемам часто употребляют для обозначения трех совершенно разных вещей — протоколов связи (например, V.22), протоколов коррекции ошибок (например, MNP4) и протоколов сжатия данных (например, V.42bis). Помимо этого, существуют еще и протоколы высокого уровня, реализованные уже не в модеме, а в тех программах, которые с ним работают (в этой главе мы познакомимся только с одной их разновидностью — с протоколами передачи файлов, такими как Zmodem). Читатель должен хорошо понимать разницу между разными типами протоколов и не смешивать, скажем, сжатие данных в аппаратных протоколах сжатия и в протоколах передачи файлов. В тех местах, где вероятность запутаться наиболее велика, я буду обращать ваше внимание на эти различия.
Кроме того, здесь вы найдете сведения о других характеристиках связи, таких как коммуникационные параметры (стартовые и стоповые биты, контроль четности) и эмуляция терминала. Они не относятся к протоколам в узком смысле слова, но по логике вещей самое для них подходящее место — именно в этом разделе. Попросту говоря, я пользуюсь здесь чисто практическим определе
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Методы, обеспечивающие надежную доставку цифровых данных по ненадежным каналам связи 
В теории информации и теории кодирования с приложениями в информатике и телекоммуникациях, обнаружение и исправление ошибок или контроль ошибок — это методы, которые обеспечивают надежную доставку цифровых данных по ненадежным каналам связи. Многие каналы связи подвержены канальному шуму, и поэтому во время передачи от источника к приемнику могут возникать ошибки. Методы обнаружения ошибок позволяют обнаруживать такие ошибки, а исправление ошибок во многих случаях позволяет восстановить исходные данные.
Содержание
- 1 Определения
- 2 История
- 3 Введение
- 4 Типы исправления ошибок
- 4.1 Автоматический повторный запрос (ARQ)
- 4.2 Прямое исправление ошибок
- 4.3 Гибридные схемы
- 5 Схемы обнаружения ошибок
- 5.1 Кодирование на минимальном расстоянии
- 5.2 Коды повторения
- 5.3 Бит четности
- 5.4 Контрольная сумма
- 5.5 Циклическая проверка избыточности
- 5.6 Криптографическая хеш-функция
- 5.7 Ошибка код исправления
- 6 Приложения
- 6.1 Интернет
- 6.2 Связь в дальнем космосе
- 6.3 Спутниковое вещание
- 6.4 Хранение данных
- 6.5 Память с исправлением ошибок
- 7 См. также
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Определения
Обнаружение ошибок — это обнаружение ошибок, вызванных шумом или другими помехами во время передачи от передатчика к приемнику. Исправление ошибок — это обнаружение ошибок и восстановление исходных безошибочных данных.
История
Современная разработка кодов исправления ошибок приписывается Ричарду Хэммингу в 1947 году. Описание кода Хэмминга появилось в Математической теории коммуникации Клода Шеннона и было быстро обобщено Марселем Дж. Э. Голэем.
Введение
Все схемы обнаружения и исправления ошибок добавляют некоторые избыточность (т. е. некоторые дополнительные данные) сообщения, которые получатели могут использовать для проверки согласованности доставленного сообщения и для восстановления данных, которые были определены как поврежденные. Схемы обнаружения и исправления ошибок могут быть систематическими или несистематическими. В систематической схеме передатчик отправляет исходные данные и присоединяет фиксированное количество контрольных битов (или данных четности), которые выводятся из битов данных некоторым детерминированным алгоритмом. Если требуется только обнаружение ошибок, приемник может просто применить тот же алгоритм к полученным битам данных и сравнить свой вывод с полученными контрольными битами; если значения не совпадают, в какой-то момент во время передачи произошла ошибка. В системе, которая использует несистематический код, исходное сообщение преобразуется в закодированное сообщение, несущее ту же информацию и имеющее по крайней мере такое же количество битов, как и исходное сообщение.
Хорошие характеристики контроля ошибок требуют, чтобы схема была выбрана на основе характеристик канала связи. Распространенные модели каналов включают в себя модели без памяти, в которых ошибки возникают случайно и с определенной вероятностью, и динамические модели, в которых ошибки возникают в основном в пакетах . Следовательно, коды обнаружения и исправления ошибок можно в целом различать между обнаружением / исправлением случайных ошибок и обнаружением / исправлением пакетов ошибок. Некоторые коды также могут подходить для сочетания случайных ошибок и пакетных ошибок.
Если характеристики канала не могут быть определены или сильно изменяются, схема обнаружения ошибок может быть объединена с системой для повторных передач ошибочных данных. Это известно как автоматический запрос на повторение (ARQ) и наиболее широко используется в Интернете. Альтернативный подход для контроля ошибок — это гибридный автоматический запрос на повторение (HARQ), который представляет собой комбинацию ARQ и кодирования с исправлением ошибок.
Типы исправления ошибок
Существует три основных типа исправления ошибок.
Автоматический повторный запрос (ARQ)
Автоматический повторный запрос (ARQ) — это метод контроля ошибок для передачи данных, который использует коды обнаружения ошибок, сообщения подтверждения и / или отрицательного подтверждения и тайм-ауты для обеспечения надежной передачи данных. Подтверждение — это сообщение, отправленное получателем, чтобы указать, что он правильно получил кадр данных.
Обычно, когда передатчик не получает подтверждения до истечения тайм-аута (т. Е. В течение разумного периода времени после отправки фрейм данных), он повторно передает фрейм до тех пор, пока он либо не будет правильно принят, либо пока ошибка не останется сверх заранее определенного количества повторных передач.
Три типа протоколов ARQ: Stop-and-wait ARQ, Go-Back-N ARQ и Selective Repeat ARQ.
ARQ is подходит, если канал связи имеет переменную или неизвестную пропускную способность, например, в случае с Интернетом. Однако ARQ требует наличия обратного канала, что приводит к возможному увеличению задержки из-за повторных передач и требует обслуживания буферов и таймеров для повторных передач, что в случае перегрузка сети может вызвать нагрузку на сервер и общую пропускную способность сети.
Например, ARQ используется на коротковолновых радиоканалах в форме ARQ-E, или в сочетании с мультиплексированием как ARQ-M.
Прямое исправление ошибок
Прямое исправление ошибок (FEC) — это процесс добавления избыточных данных, таких как исправление ошибок code (ECC) в сообщение, чтобы оно могло быть восстановлено получателем, даже если в процессе передачи или при хранении был внесен ряд ошибок (в зависимости от возможностей используемого кода). Так как получатель не должен запрашивать у отправителя повторную передачу данных, обратный канал не требуется при прямом исправлении ошибок, и поэтому он подходит для симплексной связи, например вещание. Коды с исправлением ошибок часто используются в нижнем уровне связи, а также для надежного хранения на таких носителях, как CD, DVD, жесткие диски и RAM.
Коды с исправлением ошибок обычно различают между сверточными кодами и блочными кодами. :
- Сверточные коды обрабатываются побитно. Они особенно подходят для аппаратной реализации, а декодер Витерби обеспечивает оптимальное декодирование.
- Блочные коды обрабатываются на поблочной основе. Ранними примерами блочных кодов являются коды повторения, коды Хэмминга и многомерные коды контроля четности. За ними последовал ряд эффективных кодов, из которых коды Рида – Соломона являются наиболее известными из-за их широкого распространения в настоящее время. Турбокоды и коды с низкой плотностью проверки четности (LDPC) — это относительно новые конструкции, которые могут обеспечить почти оптимальную эффективность.
Теорема Шеннона — важная теорема при прямом исправлении ошибок и описывает максимальную информационную скорость, на которой возможна надежная связь по каналу, имеющему определенную вероятность ошибки или отношение сигнал / шум (SNR). Этот строгий верхний предел выражается в единицах пропускной способности канала . Более конкретно, в теореме говорится, что существуют такие коды, что с увеличением длины кодирования вероятность ошибки на дискретном канале без памяти может быть сделана сколь угодно малой при условии, что кодовая скорость меньше чем емкость канала. Кодовая скорость определяется как доля k / n из k исходных символов и n кодированных символов.
Фактическая максимальная разрешенная кодовая скорость зависит от используемого кода исправления ошибок и может быть ниже. Это связано с тем, что доказательство Шеннона носило только экзистенциальный характер и не показало, как создавать коды, которые одновременно являются оптимальными и имеют эффективные алгоритмы кодирования и декодирования.
Гибридные схемы
Гибридный ARQ — это комбинация ARQ и прямого исправления ошибок. Существует два основных подхода:
- Сообщения всегда передаются с данными четности FEC (и избыточностью для обнаружения ошибок). Получатель декодирует сообщение, используя информацию о четности, и запрашивает повторную передачу с использованием ARQ только в том случае, если данных четности было недостаточно для успешного декодирования (идентифицировано посредством неудачной проверки целостности).
- Сообщения передаются без данных четности (только с информация об обнаружении ошибок). Если приемник обнаруживает ошибку, он запрашивает информацию FEC от передатчика с помощью ARQ и использует ее для восстановления исходного сообщения.
Последний подход особенно привлекателен для канала стирания при использовании код бесскоростного стирания.
.
Схемы обнаружения ошибок
Обнаружение ошибок чаще всего реализуется с использованием подходящей хэш-функции (или, в частности, контрольной суммы, циклической проверка избыточности или другой алгоритм). Хеш-функция добавляет к сообщению тег фиксированной длины, который позволяет получателям проверять доставленное сообщение, повторно вычисляя тег и сравнивая его с предоставленным.
Существует огромное количество различных конструкций хеш-функций. Однако некоторые из них имеют особенно широкое распространение из-за их простоты или их пригодности для обнаружения определенных видов ошибок (например, производительности циклического контроля избыточности при обнаружении пакетных ошибок ).
Кодирование с минимальным расстоянием
Код с исправлением случайных ошибок на основе кодирования с минимальным расстоянием может обеспечить строгую гарантию количества обнаруживаемых ошибок, но может не защитить против атаки прообразом.
Коды повторения
A код повторения — это схема кодирования, которая повторяет биты по каналу для достижения безошибочной связи. Учитывая поток данных, которые необходимо передать, данные делятся на блоки битов. Каждый блок передается определенное количество раз. Например, чтобы отправить битовую комбинацию «1011», четырехбитовый блок можно повторить три раза, таким образом получая «1011 1011 1011». Если этот двенадцатибитовый шаблон был получен как «1010 1011 1011» — где первый блок не похож на два других, — произошла ошибка.
Код повторения очень неэффективен и может быть подвержен проблемам, если ошибка возникает в одном и том же месте для каждой группы (например, «1010 1010 1010» в предыдущем примере будет определено как правильное). Преимущество кодов повторения состоит в том, что они чрезвычайно просты и фактически используются в некоторых передачах номеров станций.
Бит четности
Бит четности — это бит, который добавляется к группе исходные биты, чтобы гарантировать, что количество установленных битов (т. е. битов со значением 1) в результате будет четным или нечетным. Это очень простая схема, которую можно использовать для обнаружения одного или любого другого нечетного числа (т. Е. Трех, пяти и т. Д.) Ошибок в выводе. Четное количество перевернутых битов сделает бит четности правильным, даже если данные ошибочны.
Расширениями и вариантами механизма битов четности являются проверки с продольным избыточным кодом, проверки с поперечным избыточным кодом и аналогичные методы группирования битов.
Контрольная сумма
Контрольная сумма сообщения — это модульная арифметическая сумма кодовых слов сообщения фиксированной длины слова (например, байтовых значений). Сумма может быть инвертирована посредством операции дополнения до единиц перед передачей для обнаружения непреднамеренных сообщений с нулевым значением.
Схемы контрольных сумм включают биты четности, контрольные цифры и проверки продольным избыточным кодом. Некоторые схемы контрольных сумм, такие как алгоритм Дамма, алгоритм Луна и алгоритм Верхоффа, специально разработаны для обнаружения ошибок, обычно вносимых людьми при записи или запоминание идентификационных номеров.
Проверка циклическим избыточным кодом
Проверка циклическим избыточным кодом (CRC) — это незащищенная хэш-функция, предназначенная для обнаружения случайных изменений цифровых данных в компьютерных сетях. Он не подходит для обнаружения злонамеренно внесенных ошибок. Он характеризуется указанием порождающего полинома, который используется в качестве делителя в полиномиальном делении над конечным полем, принимая входные данные в качестве дивиденд. остаток становится результатом.
CRC имеет свойства, которые делают его хорошо подходящим для обнаружения пакетных ошибок. CRC особенно легко реализовать на оборудовании и поэтому обычно используются в компьютерных сетях и устройствах хранения, таких как жесткие диски.
. Бит четности может рассматриваться как 1-битный частный случай. CRC.
Криптографическая хеш-функция
Выходные данные криптографической хеш-функции, также известные как дайджест сообщения, могут обеспечить надежную гарантию целостности данных, независимо от того, происходят ли изменения данных случайно (например, из-за ошибок передачи) или злонамеренно. Любая модификация данных, скорее всего, будет обнаружена по несоответствию хеш-значения. Кроме того, с учетом некоторого хэш-значения, как правило, невозможно найти некоторые входные данные (кроме заданных), которые дадут такое же хеш-значение. Если злоумышленник может изменить не только сообщение, но и значение хеш-функции, то для дополнительной безопасности можно использовать хэш-код с ключом или код аутентификации сообщения (MAC). Не зная ключа, злоумышленник не может легко или удобно вычислить правильное ключевое значение хеш-функции для измененного сообщения.
Код исправления ошибок
Для обнаружения ошибок можно использовать любой код исправления ошибок. Код с минимальным расстоянием Хэмминга, d, может обнаруживать до d — 1 ошибок в кодовом слове. Использование кодов с коррекцией ошибок на основе минимального расстояния для обнаружения ошибок может быть подходящим, если требуется строгое ограничение на минимальное количество обнаруживаемых ошибок.
Коды с минимальным расстоянием Хэмминга d = 2 являются вырожденными случаями кодов с исправлением ошибок и могут использоваться для обнаружения одиночных ошибок. Бит четности является примером кода обнаружения одиночной ошибки.
Приложения
Приложения, которым требуется низкая задержка (например, телефонные разговоры), не могут использовать автоматический запрос на повторение (ARQ); они должны использовать прямое исправление ошибок (FEC). К тому времени, когда система ARQ обнаружит ошибку и повторно передаст ее, повторно отправленные данные прибудут слишком поздно, чтобы их можно было использовать.
Приложения, в которых передатчик сразу же забывает информацию, как только она отправляется (например, большинство телекамер), не могут использовать ARQ; они должны использовать FEC, потому что при возникновении ошибки исходные данные больше не доступны.
Приложения, использующие ARQ, должны иметь канал возврата ; приложения, не имеющие обратного канала, не могут использовать ARQ.
Приложения, требующие чрезвычайно низкого уровня ошибок (например, цифровые денежные переводы), должны использовать ARQ из-за возможности неисправимых ошибок с помощью FEC.
Надежность и инженерная проверка также используют теорию кодов исправления ошибок.
Интернет
В типичном стеке TCP / IP ошибка управление осуществляется на нескольких уровнях:
- Каждый кадр Ethernet использует CRC-32 обнаружение ошибок. Фреймы с обнаруженными ошибками отбрасываются оборудованием приемника.
- Заголовок IPv4 содержит контрольную сумму , защищающую содержимое заголовка. Пакеты с неверными контрольными суммами отбрасываются в сети или на приемнике.
- Контрольная сумма не указана в заголовке IPv6, чтобы минимизировать затраты на обработку в сетевой маршрутизации и поскольку предполагается, что текущая технология канального уровня обеспечивает достаточное обнаружение ошибок (см. также RFC 3819 ).
- UDP, имеет дополнительную контрольную сумму, покрывающую полезную нагрузку и информацию об адресации в заголовки UDP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком . Контрольная сумма не является обязательной для IPv4 и требуется для IPv6. Если не указано, предполагается, что уровень канала передачи данных обеспечивает желаемый уровень защиты от ошибок.
- TCP обеспечивает контрольную сумму для защиты полезной нагрузки и адресной информации в заголовках TCP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком и в конечном итоге повторно передаются с использованием ARQ либо явно (например, как через тройное подтверждение ) или неявно из-за тайм-аута .
Телекоммуникации в дальнем космосе
Разработка кодов исправления ошибок была тесно связана с историей полетов в дальний космос из-за сильного ослабления мощности сигнала на межпланетных расстояниях и ограниченной мощности на борту космических зондов. В то время как ранние миссии отправляли свои данные в незашифрованном виде, начиная с 1968 года, цифровая коррекция ошибок была реализована в форме (субоптимально декодированных) сверточных кодов и кодов Рида – Маллера. Код Рида-Мюллера хорошо подходил к шуму, которому подвергался космический корабль (примерно соответствуя кривой ), и был реализован для космического корабля Mariner и использовался в миссиях между 1969 и 1977 годами.
Миссии «Вояджер-1 » и «Вояджер-2 «, начатые в 1977 году, были разработаны для доставки цветных изображений и научной информации с Юпитера и Сатурна. Это привело к повышенным требованиям к кодированию, и, таким образом, космический аппарат поддерживался (оптимально Витерби-декодированный ) сверточными кодами, которые могли быть сцеплены с внешним Голеем (24,12, 
Консультативный комитет по космическим информационным системам в настоящее время рекомендует использовать коды исправления ошибок, как минимум, аналогичные RSV-коду Voyager 2. Составные коды все больше теряют популярность в космических миссиях и заменяются более мощными кодами, такими как Турбо-коды или LDPC-коды.
Различные виды выполняемых космических и орбитальных миссий. предполагают, что попытки найти универсальную систему исправления ошибок будут постоянной проблемой. Для полетов вблизи Земли характер шума в канале связи отличается от того, который испытывает космический корабль в межпланетной миссии. Кроме того, по мере того как космический корабль удаляется от Земли, проблема коррекции шума становится все более сложной.
Спутниковое вещание
Спрос на пропускную способность спутникового транспондера продолжает расти, чему способствует желание предоставлять телевидение (включая новые каналы и телевидение высокой четкости ) и данные IP. Доступность транспондеров и ограничения полосы пропускания ограничили этот рост. Емкость транспондера определяется выбранной схемой модуляции и долей мощности, потребляемой FEC.
Хранение данных
Коды обнаружения и исправления ошибок часто используются для повышения надежности носителей данных. «Дорожка четности» присутствовала на первом устройстве хранения данных на магнитной ленте в 1951 году. «Оптимальный прямоугольный код», используемый в записи с групповым кодированием, не только обнаруживает, но и корректирует однобитовые записи. ошибки. Некоторые форматы файлов, особенно архивные форматы, включают контрольную сумму (чаще всего CRC32 ) для обнаружения повреждений и усечения и могут использовать избыточность и / или четность files для восстановления поврежденных данных. Коды Рида-Соломона используются в компакт-дисках для исправления ошибок, вызванных царапинами.
Современные жесткие диски используют коды CRC для обнаружения и коды Рида – Соломона для исправления незначительных ошибок при чтении секторов, а также для восстановления данных из секторов, которые «испортились», и сохранения этих данных в резервных секторах. Системы RAID используют различные методы исправления ошибок для исправления ошибок, когда жесткий диск полностью выходит из строя. Файловые системы, такие как ZFS или Btrfs, а также некоторые реализации RAID, поддерживают очистку данных и восстановление обновлений, что позволяет удалять поврежденные блоки. обнаружены и (надеюсь) восстановлены, прежде чем они будут использованы. Восстановленные данные могут быть перезаписаны точно в том же физическом месте, чтобы освободить блоки в другом месте на том же оборудовании, или данные могут быть перезаписаны на заменяющее оборудование.
Память с исправлением ошибок
Память DRAM может обеспечить более надежную защиту от программных ошибок, полагаясь на коды исправления ошибок. Такая память с исправлением ошибок, известная как память с защитой ECC или EDAC, особенно желательна для критически важных приложений, таких как научные вычисления, финансы, медицина и т. Д., А также для приложений дальнего космоса из-за повышенное излучение в космосе.
Контроллеры памяти с исправлением ошибок традиционно используют коды Хэмминга, хотя некоторые используют тройную модульную избыточность.
Чередование позволяет распределить эффект одного космического луча, потенциально нарушающего множество физически соседние биты в нескольких словах путем связывания соседних битов с разными словами. До тех пор, пока нарушение единичного события (SEU) не превышает пороговое значение ошибки (например, одиночная ошибка) в любом конкретном слове между доступами, оно может быть исправлено (например, путем исправления однобитовой ошибки code), и может сохраняться иллюзия безошибочной системы памяти.
Помимо оборудования, обеспечивающего функции, необходимые для работы памяти ECC, операционные системы обычно содержат соответствующие средства отчетности, которые используются для предоставления уведомлений при прозрачном восстановлении программных ошибок. Увеличение количества программных ошибок может указывать на то, что модуль DIMM нуждается в замене, и такая обратная связь не была бы легко доступна без соответствующих возможностей отчетности. Одним из примеров является подсистема EDAC ядра Linux (ранее известная как Bluesmoke), которая собирает данные из компонентов компьютерной системы, поддерживающих проверку ошибок; Помимо сбора и отправки отчетов о событиях, связанных с памятью ECC, он также поддерживает другие ошибки контрольного суммирования, в том числе обнаруженные на шине PCI.
Некоторые системы также поддерживают очистку памяти.
См. также
- Код Бергера
- Пакетный код коррекции ошибок
- Неважный сигнал тревоги
- ECC-память, тип хранения компьютерных данных
- Запрещенный ввод
- Адаптация связи
- Список алгоритмов для обнаружение и исправление ошибок
- Список кодов исправления ошибок
- Список хэш-функций
- Надежность (компьютерные сети)
Ссылки
Дополнительная литература
- Шу Линь; Дэниел Дж. Костелло младший (1983). Кодирование с контролем ошибок: основы и приложения. Прентис Холл. ISBN 0-13-283796-X.
Внешние ссылки
- Он-лайн учебник: Теория информации, выводы и алгоритмы обучения, Дэвид Дж. К. Маккей, содержит главы по элементарным кодам исправления ошибок; о теоретических пределах исправления ошибок; и на последних современных кодах исправления ошибок, включая коды проверки четности с низкой плотностью, турбокоды и фонтанные коды.
- Compute параметры линейных кодов — оперативный интерфейс для генерации и вычисления параметров (например, минимальное расстояние, радиус покрытия ) линейных кодов с исправлением ошибок.
- Страница ECC
- SoftECC: Система для проверки целостности памяти программного обеспечения
- Настраиваемая программная библиотека обнаружения и исправления ошибок DRAM для HPC
- Обнаружение и исправление скрытого искажения данных для крупномасштабных высокопроизводительных вычислений


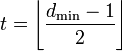 , округляем «вниз», так чтобы
, округляем «вниз», так чтобы  , где
, где 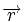 — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.![v(x)=x^{n-k}u(x)+[x^{n-k}u(x),bmod,g(x)]](https://dic.academic.ru/pictures/wiki/files/97/ab852c2832864dffc1acf3cbd9eff59e.png) .
.