Что такое ошибка дискретности

1. Погрешность измерения частоты методом дискретного счета

Предел
основной погрешности измерения частоты
методом дискретного
счета включает две составляющие:
погрешность
частоты кварцевого генератора
δ_кв
=
±Δf_кв/f_кв
и погрешность
дискретности счета
δ_Д:
δ_f
=
(δ_кв
+
δ_Д).

Первая
составляющая является погрешностью
меры частоты и определяется нестабильностью
частоты кварцевого генератора, а также
погрешностью его калибровки. Типовые
значения нестабильности генератора
ЭСЧ составляют ±(2.5·10^–6…7·10^–9)
при изменении температуры в пределах
0 –
50° и долговременная нестабильность
частоты (старение) в пределах ±(3· 10^–7…5·
10^–8)
за месяц.
Погрешность дискретности возникает
из-за того, что длительность временных
ворот T_сч
в общем случае
не совпадает с целым числом периодов
измеряемого сигнала.

На
рис. 3 приведены крайние ситуации,
когда во временные
ворота попадают 9 импульсов (верхний
график) или 7 импульсов (нижний график),
что может реально произойти из-за
нестабильности срабатывания
временного селектора.

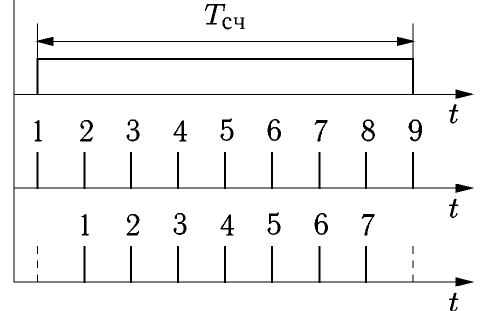
Рис.
3. Образование погрешности дискретности

Между
тем число периодов входного сигнала,
укладывающегося во временные ворота,
равно 8. Таким образом, максимальная
ошибка при подсчете
импульсов составляет ±1 импульс, что
соответствует единице
последнего разряда счетчика. Это дает
абсолютную погрешность дискретности
при измерении частоты ±1/T_сч.
Выбор длительности временных ворот
определяет
разрешающую
способность ЭСЧ
(возможность
различать близко расположенные
значения измеряемой
частоты). Так, для Т_сч
=1 с разрешающая способность равна 1 Гц
(цена деления правого разряда индикатора).
Разрешающая способность не зависит от
частоты входного сигнала. Относительная
погрешность дискретности при этом
обратно
пропорциональна измеряемой
частоте и равна

δ_Д
= ±1/(f_xТ_сч)
=
±1/N. (2)

На
низких частотах
δ_Д
является основной составляющей,
определяющей
точность измерений
частоты методом дискретного счета.

Уменьшение
погрешности дискретности
осуществляют несколькими путями.
Наиболее очевидный –
увеличение
длительности временных ворот T_сч
–приводит
к росту времени
измерения. На практике редко применяют
время счета более 10 с. Другой
способ –
умножение частоты входного сигнала в
целое число раз –
требует
применения дополнительных устройств
(умножителей частоты).
Более удобен способ измерению
периода. Структурная схема измерениия
привндена на рис.4.

Р

Рис.
4. Структурная схема ЭСЧ в режиме
измерения периода

ис.4. Структурная схема
измерения периода

Измерение
периода осуществляют следующим образом.
Временные
ворота образуют из исследуемого сигнала,
который подают на вход Б частотомера.
Формирующим устройством
его преобразуют в последовательность
коротких импульсов U₁
с
периодом Т_х
(рис.
5). Длительность временных ворот T_сч
образуют
делением частоты входного сигнала в m
раз (что эквивалентно увеличению периода)
T_сч
= тТ_х.
Коэффициент деления делают кратным 10
(m
= 10^r,
r
= 0,1,2…).

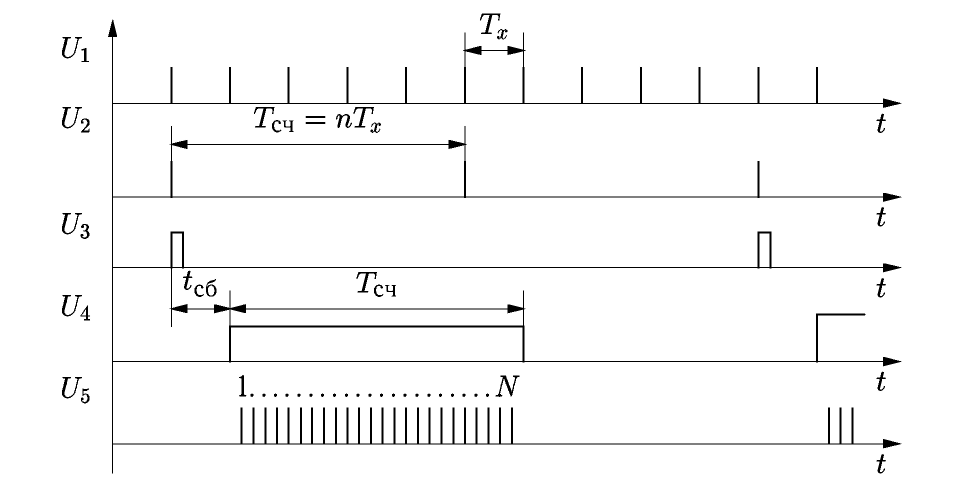
Рис.
5.
Осциллограммы сигналов ЭСЧ в режиме
измерения периода

Счетные
импульсы формируют делением частоты
кварцевого генератора
f_кв
в n
раз. Их период Т_м
кратен 10 и является мерой временного
интервала.
Поэтому длительность Т_м
называют меткой
времени:

Т_M
= n/f_кв
= nT_кв
= 10^-s,

где
s
= 7,6,5…. Минимально возможная метка
времени связана с быстродействием
счетчика и обычно составляет 10… 100 нc.
Таким образом, на счетчик поступают
импульсы U₅,
прошедшие через временной селектор за
время счета T_сч
=
mТ_x,
N≈T_сч/T_М
=
T_x10^(r—s).

На
цифровом табло ЭСЧ предусматривают
индикацию знака десятичной точки,
положение
которой (а также указатель размерности
— с, мс, мкс) связано с регулировками
делителей частоты. При этом прибор дает
прямые показания
измеренного периода.

Погрешность
измерения периода содержит составляющую
δ_кв,
определяемую
нестабильностью кварцевого генератора
(погрешность установки
метки времени), и погрешность дискретности
δ_д.
Абсолютная величина
погрешности дискретности равна ±Т_М
(не превышает по модулю периода счетных
импульсов). Разрешающая способность
ЭСЧ в режиме измерения периода определяется
выбором метки времени. Максимальная
относительная погрешность дискретности
в данном случае равна

δ_д
= ±Т_м/Т_х
= ±1/N, (3)

что
совпадает с погрешностью (2) измерения
частоты. С
ростом измеряемого периода Т_х
число
импульсов N
растет
и относительная погрешность
снижается. В режиме измерения частоты
все происходит наоборот. Следовательно,
измерение периода дает малую погрешность
на низких частотах,
а измерение частоты — на высоких.

При
измерении периода следует учитывать
дополнительные источники
погрешности, связанные с нестабильностью
порога срабатывания формирующего
устройства и со сдвигом фронта и среза
временных ворот из-за
наложения на сигнал внешних шумов. Это
требует по сравнению с
режимом измерения частоты более
тщательной настройки входного устройства
частотомера и фильтрации входного
сигнала.

Погрешность
дискретности по своей природе случайна,
и выражение
(3) определяет ее максимальное значение.
Для
оценки среднеквадратической погрешности
необходимо знать закон распределения
плотности вероятности погрешности. Это
позволяет произвести интервальную
оценку среднеквадратической погрешности
измерения частоты и периода с заданной
доверительной вероятностью.

Рассмотрим
закон распределения погрешности
дискретности при измерении
периода Т_х.
Как
следует из рис. 6, начало измеряемого
интервала Т_х
(временные
ворота) в общем случае не синхронизировано
с метками времени.

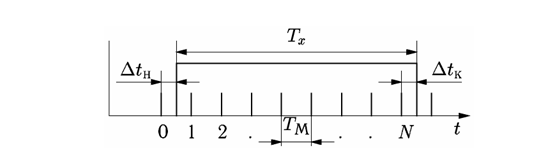
Рис.
6.
Погрешность дискретности при измерении
периода

Результат
измерения
включает два временных интервала, Δt_Н
и Δt_к:

Т_х
= NT_M
— Δt_н
+ Δt_к
=
NT_M
— Δt_д,

где
Δt_д
– общая абсолютная погрешность измерения
периода Т_х.

Начало
временных ворот может с одинаковой
вероятностью попасть в
интервал времени от нулевого до первого
счетного импульса. Эта по грешность
подчинена равномерному закону с
предельными значениями –T_м
и 0. Конец временных ворот с одинаковой
вероятностью может по пасть
в любую точку между двумя счетными
импульсами в пределах 0..
. Т_м.
Таким образом, общая

погрешность
порождается двумя случайными
погрешностями с равномерными законами
распределения р(Δt_н)
и р(Δt_к)
(рис. 7).

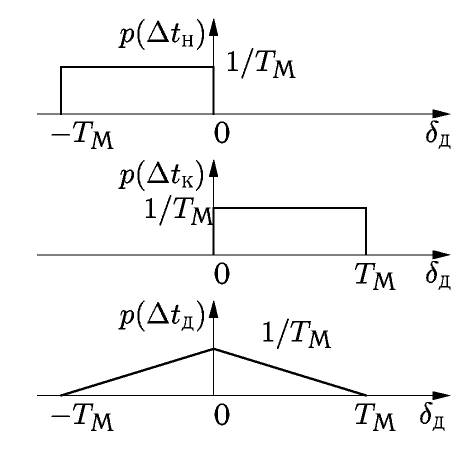
Рис.7.
Закон распределения погрешности
дискретности

Если
интервал Т_х
неизвестен,
то эти случайные погрешности независимы.
Как следует
из теории вероятности,
закон распределения общей
погрешности р(Δt_д)
определяется
сверткой законов
распределения р(Δt_Н)
и
р(Δt_к).
В результате получается
треугольная форма зависимости
(закон распределения
Симпсона) с предельными значениями ±T_М
(см. рис. 7):

Среднеквадратическое
отклонение (СКО) для треугольного закона
распределения
равно Т_м/√6,
поэтому относительная среднеквадратическая
погрешность
дискретности:

При
экспериментальном определении закона
на основе многократных измерений (не
менее 15-20 опытов) строят
гистограмму — графическое изображение
распределения погрешностей.
Она представляет собой ряд смежных
прямоугольников (карманы
гистограммы) (рис. 8).
Ширина
кармана равна заранее выбранному шагу
значений погрешности, высота – числу
опытных данных, попавших в данный
интервал. Огибающая гистограммы дает
форму экспериментального закона
распределения погрешности дискретности.

Ш

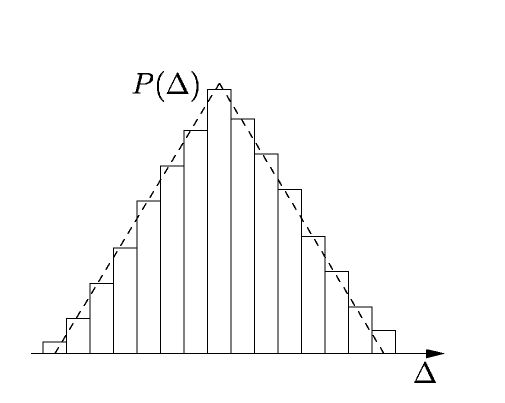
Рис.8.
Гистограмма
треугольного
закона распределения
погрешности

ирина кармана равна заранее
выбранному шагу значений погрешности,
высота – числу опытных данных, попавших
в данный интервал. После нормирования
к общему числу опытов высота равна
относительной частоте – то есть оценке
вероятности попадания погрешности в
карман. Огибающая гистограммы дает
форму экспериментального закона
распределения погрешности дискретности.

В
современных вычислительных частотомерах
для определения частоты используют оба
описанных выше варианта схем – а)
измерение периода путем подсчета
тактовых импульсов кварцевого генератора
и дальнейшее вычисление частоты по
формуле fВХ
= 1/TВХ
(рис.9 а), б) прямой метод — путем подсчета
входных импульсов в течение выбранного
временного окна (рис. 9.б). Как показано
выше, первый метод дает хорошую точность
для низких частот fВХ
(то есть для больших TВХ).
Второй метод дает хорошую точность
только для больших частот fВХ
или в случае большого временного окна.
В первом случае для увеличения точности
необходимо увеличивать тактовую частоту,
во втором – увеличивать длительность
временного окна. Время измерения по
первому методу составляет TВХ.
Для второго метода оно постоянно и равно
длительности временного окна.
Комбинированный способ косвенного
измерения частоты (reciprocal
counting)
позволяет сочетать оба способа.

С

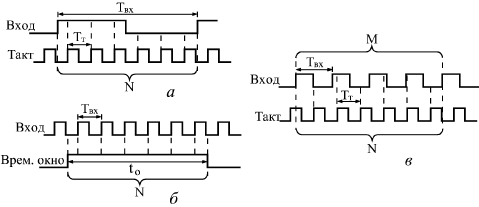
Рис.
9.
Сравнение основных методов измерения
частоты: через период (а), прямой (б) и
комбинированный (в)

уть его – измерение периода
входного сигнала, умноженного в М раз
(рис.9,в). При данном методе импульсы
тактовой частоты подсчитываются в
течение М полных периодов входного
сигнала. При этом количество сосчитанных
импульсов N
определяет точность измерения
(относительная погрешность не превышает
1/N).
Значит, необходимо обеспечить, чтобы N
было достаточно большим, например, при
N>100
относительная погрешность не превысит
1%, а при N
> 1000 она будет меньше 0,1%. Обеспечить
достаточную величину N
можно простым выбором числа М. В
вычислительных ЭСЧ задается требуемое
время измерения (временные ворота Тсч)
и подсчитывается количество периодов
входного сигнала М, укладывающееся в
этот интервал. Затем подсчитывается
количество тактовых импульсов,
укладывающееся в интервал MTx.
Измеренное значение частоты вычисляется
микропроцессором по соотношению fВХ
= M/(NTм).
Достоинством такого подхода является
свободный выбор времени измерения ( не
обязательно кратный 10) и постоянная
относительная погрешность измерения,
не зависящая от входной частоты.

Действительно,
погрешность измерения длительности
интервала MTX
равна длительности метки времени
(периоду тактовых импульсов). Относительная
погрешность измерения частоты примерно
равна этой погрешности

(4)

Таким
образом, относительная погрешность
дискретности зависит от выбранного
времени измерения и тактовой частоты
меток времени и постоянна во всем
диапазоне измерения. Поэтому разрешающую
способность таких частотомеров указывают
не в единицах частоты (Гц), а в количестве
десятичных знаков результата для времени
счета 1 сек. Так, для тактовой частоты
100 МГц погрешность измерения будет
составлять 10-8, а число знаков в результате
– 8 знаков/сек. Однако необходимо помнить,
что данный метод измеряет средний за
Тсч период входного сигнала.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Справочник /

Термины /

Приборостроение и оптотехника /

Погрешность дискретности

Научные статьи на тему «Погрешность дискретности»

1.

Методы обработки данных и численные методы

с непрерывным аргументом на функции, обладающие дискретным аргументом….
При осуществлении перехода к дискретным моделям возникают погрешности аппроксимации изначальных функций…
операций при заданной погрешности….
Причём дискретную функцию тоже можно рассматривать как линейную комбинацию полиномов….
Чтобы оценить погрешности в расчётах могут использоваться следующие методики:

Оценка абсолютной погрешности

Статья от экспертов

2.

Расчет погрешности дискретного уровнемера

3.

Вычислительные методы в экономике

Во время перехода к дискретной модели может появиться погрешность аппроксимации, а в процессе реализации…
погрешности и устойчивости вычислительных алгоритмов….
аргумента на функции дискретного аргумента….
и критериев роста погрешности….
погрешности.

Статья от экспертов

4.

Анализ погрешностей интерполяции случайных полей по дискретным отсчётам

Рассмотрены алгоритмы интерполяции случайных полей по неполным наблюдениям, позволяющие существенно снизить вычислительные затраты при незначительном снижении точности оценивания

Погрешность — дискретность

Cтраница 1

Погрешность дискретности по всей природе случайна и поэтому о ее максимальном значении, разумеется, можно говорить только в вероятностном смысле. Погрешность дискретности складывается из двух составляющих.
 [1]

Погрешность дискретности — это погрешность, обусловленная возможным несовпадением импульсов генератора с фронтом и спадом временных ворот.
 [2]

Погрешность дискретности а обычно полагают равной плюс-минус единице наименьшего разряда. Наличие этой погрешности приводит к тому, что одним и тем же относительным погрешностям при всех прочих равных условиях, но различном удельном весе погрешности дискретности могут соответствовать различные значения абсолютной погрешности.
 [3]

Погрешность дискретности присуща ЦИП и отсутствует у аналоговых приборов. Однако эта погрешность не является препятствием для увеличения точности прибора, так как соответствующим — выбором числа уровней квантования погрешность дискретности-можно сделать сколь угодно малой.
 [5]

Погрешность дискретности возникает в результате квантования непрерывного сигнала по уровню. Динамическая возникает как в результате изменения преобразуемого сигнала X ( t) в процессе его квантования по уровню, так и вследствие инерционности элементов преобразователя. Если преобразуемый сигнал в течение времени квантования по уровню остается неизменным, то динамическая погрешность отсутствует.
 [6]

Погрешность дискретности зависит от соотношения частот исследуемых напряжений и частоты стабилизированного генератора, причем величина погрешности повышается одновременно с увеличением частоты входных напряжений. Допустимое значение суммарной погрешности первого дискретного преобразования при заданной частоте стабилизированного генератора определяется верхней границей полосы частот исследуемых напряжений. Погрешность дискретности второго преобразования из-за некратности частоты исследуемых напряжений определяется величиной, обратной времени измерения, а также несинфазностью начала времени измерения с моментом поступления считываемых пачек импульсов на счетчик. Пачка, целиком не укладывающаяся в пределы времени измерения, дробится с дискретностью, равной одному импульсу стабильной частоты.
 [7]

Погрешность дискретности возрастает с уменьшением частоты исследуемых напряжений и может быть снижена путем увеличения времени измерения. Допустимое значение этой погрешности при заданном времени измерения определяется нижней полосой частот исследуемых напряжений. Время измерения и частота стабилизированного генератора являются постоянными цифрового фазометра с калиброванным временем измерения, определяющими величину его основной погрешности и, следовательно, диапазон частот исследуемых напряжений. Погрешность цифрового фазометра может быть снижена до 0 5 — 0 1 % от предела измеряемой фазы.
 [8]

Погрешность дискретности зависит от соотнощения частот исследуемых напряжений и частоты стабилизированного генератора, причем величина погрешности увеличивается одновременно с увеличением частоты входных напряжений.
 [9]

Погрешность дискретности возрастает с уменьшением частоты исследуемых напряжений и может быть уменьшена путем увеличения времени измерения. Допустимое значение этой погрешности при заданном времени измерения определяется нижней полосой частот исследуемых напряжений. Время измерения и частота стабилизированного генератора являются постоянными цифрового фазометра с калиброванным временем измерения, определяющим величину его основной погрешности и, соответственно, диапазон частот исследуемых напряжений.
 [10]

Погрешность дискретности 1 для низких частот относительно велика, поэтому в цифровых частотомерах нередко предусматривается возможность измерения не только частоты fx, но и периода Тх. В этом случае напряжение достаточно низкой частоты Fx подается на вход Б прибора.
 [11]

Погрешность дискретности получается во много раз меньшей, чем при измерении частоты.
 [12]

Погрешность дискретности, присущая время-импульсным методам измерения напряжения, имеет ту же природу, что п при измерении интервала времени. Ее максимальная величина составляет 1 младшего разряда счета.
 [13]

Погрешность дискретности присуща ЦИП и отсутствует у аналоговых приборов. Однако эта погрешность не является препятствием для увеличения точности прибора, так как соответствующим выбором числа уровней квантования погрешность дискретности можно сделать сколь угодно малой.
 [15]

Страницы:  

   1

   2

   3

   4

ошибка дискретизации

Адаптивное построение сетки состоит в том, что после создания расчетной модели и задания граничных условий генерируется конечно-элементная сетка, затем выполняется анализ, оценивается ошибка дискретизации сетки, после чего меняется размер сетки. Процесс протекает до тех пор, пока значение погрешности не станет меньше заданного, или число итераций не достигнет допустимого значения.
 [c.67]

Ошибки дискретизации являются результатом замены реальной теплопроводящей среды дискретными электрическими ячейками. При этом следует иметь в виду, что ошибки в основном возникают в результате ири-менения сосредоточенных емкостей и индуктивностей. Ошибки, связанные с дискретизацией области, определяются шагом сетки и зависят от характера температурного поля. Это может быть легко продемонстрировано с помощью разложения в ряд Тейлора температуры в некоторой точке области. Ошибка дискретизации координат определяется зависимостью
 [c.359]

Шаг сетки Ах явно входит в выражение для ошибки. Если его уменьшить, то ошибка также уменьшится. При Дл —>»0 ошибка также стремится к нулю. Полагая, что члены, включающие производные выше четвертого порядка, пренебрежимо малы, определим ошибку дискретизации области  [c.359]

Эксперименты показывают, что для многих теплотехнических задач разбиение области в направлении одной координаты иа 8—10 элементарных слоев приводит к существенному уменьшению ошибки дискретизации. Это значит, что если (Д л /б) s O,l, то ошибка дискретизации оказывается настолько малой, что ее в ряде случаев можно не учитывать, так как она стремится к нулю.
 [c.359]

Ошибки дискретизации могут быть уменьшены использованием более мелких элементов или расположением криволинейных элементов около границ и, во всяком случае, стремятся к нулю по мере стремления к нулю размера элемента. Ошибки пробной функции не обязательно уменьшаются по мере уменьшения размера элементов и могут поэтому мешать сходимости к точному решению нли даже приводить к расходимости,
 [c.169]

Мы хотим предложить объяснение этого чуда, основанное на нашем наблюдении, что обычное измерение числа обусловленности для этих матриц неестественно. В вычислительных целях мы будем рассматривать эти матрицы как преобразования евклидова пространства (дискретного Ж°) в себя и потому возьмем одну и ту же норму для невязки уравнения и для результирующей ошибки в решении. Это целиком противоположно тому, что делается в дифференциальной задаче, или тому, что происходит при оценке ошибки дискретизации / измеряется в норме пространства Л1 и ее ошибка — в ш и ее ошибка — в Ж. (В вариационной задаче соответственно и Ж .) В самом деле, оператор I = с каким-либо обычным краевым условием вполне обусловлен как преобразование из Ж в Ж°. Ограниченность операторов I и была существенным моментом в разд. 1.2. Можно показать, что это верно и для разностного оператора б , а также для любого приемлемого аналога в методе конечных элементов, если только эти естественные нормы сохраняются. Следовательно, должен быть алгоритм решения уравнения КО, = Р, отражающий это свойство, и тогда чудо развеялось бы ошибки в Л1 и ш соответствовали бы их положению.
 [c.147]

Важный вывод ошибка округления не зависит сильно от степени полиномиального элемента. Главным образом она зависит от h, от порядка рассматриваемой задачи и от основного собственного значения непрерывной задачи. Поэтому при наличии ошибок округления достичь численную точность можно, увеличивая степень пробных функций. Число обусловленности для кубических элементов лишь немного хуже, чем для линейных, так что ошибки округления в этих случаях для заданного значения h сравнимы. Однако ошибка дискретизации для кубических элементов на порядок меньше. Поэтому в переходный момент, когда округления не позволяют получать более точные результаты за счет уменьшения h, с помощью кубического элемента этого можно достичь. Особенно это относится к вычислению напряжений, где дифференцирование (или взятие разностей) перемещений вводит в численную ошибку дополнительный множитель Л». Даже в задачах второго порядка ошибка округления становится значительной и наилучший выход из положения — увеличить степень пробных функций.
 [c.250]

Ошибки дискретизации возникают прн замене реальной конструкции ограниченны числом конечных элементов (с учетом их формы и размеров).
 [c.28]

В (15.3.1-8) не дается никаких оценок ошибки аппроксимации. Для неравномерной сетки (х. Фх , yj Фу 1) ошибка дискретизации уменьшается почти линейно с уменьшением шага. Некоторые идеи, касающиеся выбора подходящего шага с целью существенного ограничения этой ошибки, даются в п. 15.3.1.4. Кроме того, более полно этот вопрос рассмотрен в классической математической литературе [15.58, 15.47].
 [c.406]

Построение разностной сетки. Для того чтобы затраты времени счета и памяти ЭВМ оставались в разумных пределах, необходимо ограничить число узлов сетки. Соответствующий компромисс между точностью и стоимостью вычислительных ресурсов можно найти, оценив ошибки аппроксимации. В критических областях, с большими ошибками дискретизации, шаг сетки должен быть мелким, в то время как в областях, где ошибки невелики, его можно увеличить. Из этих соображений очевидно, что равномерная сетка непригодна, поскольку в этом случае шаг сетки должен был бы подстраиваться под критические области, и число узлов стало бы очень большим.
 [c.409]

Так как ошибки дискретизации зависят от распределения величин ф, п, р, то прием-
 [c.409]

Как уже обсуждалось ранее, скорость ионизации очень чувствительна к напряженности электрического поля. Следовательно, скорость генерации будет иметь в области отсечки канала сильный пик, который можно правильно рассчитать лишь используя очень мелкую сетку. Интеграл от генерационного члена по всей области дает ток через поверхность, и, следовательно, ошибка дискретизации пропорциональна ошибке в вычислении этого тока. Если мы рассмотрим лишь первую производную электрического поля
 [c.411]

Для снижения методической погрешности при использовании моделей средних значений важно осуществить рациональное условное деление конструкции ЭМУ на отдельные элементы, либо увеличить число таких разбиений. Но в последнем случае метод приближается к методу сеток и становится громоздким, в то время как практически важно получение высокой точности расчетов при ограниченной дискретизации. При умелом применении схем замещения методическая ошибка в сравнении с методом сеток составляет обычно не более 5 % даже при ограниченной степени дискретизации. По крайней мере, это заметно меньше, чем погрешности от неточности задания входной информации. При выборе числа разбиений важен и характер решаемой задачи. При грубой оценке показателей поля возможна упрощенная схема замещения с пятью-шестью укрупненными телами (ротора в целом, объединенных обмотки и пакета статора и т.д.). Если необходим анализ изменения осевой нагрузки на подшипники, то особо подробно должны быть представлены тела, входящие в замкнутую размерную цепь их установки, а остальные элементы могут рассматриваться укрупненно. При анализе относительных температурных деформаций требуется наиболее детальная дискретизация ЭМУ, особенно для элементов, имеющих различные коэффициенты линейного расширения. Здесь ТС, например, должна содержать не менее 15—20 тел.
 [c.127]

При получении совмеш,енных изображений в соответствии с уровнем обработки S остаточная среднеквадратическая ошибка регистрации не должна превышать 50% шага дискретизации. Значение этого параметра зависит главным образом от точности работы системы ориентации спутника.
 [c.98]

Поверхность тела представляется при помощи четырехугольных и треугольных элементов с квадратичным изменением формы и линейным, квадратичным или кубическим изменением перемещения и вектора напряжений относительно внутренней системы координат. Тело разбивается на подобласти производится дискретизация интегрального уравнения для каждой подобласти, и получается система уравнений ленточного типа. Для вычисления интегралов используется квадратурная формула Гаусса, число узлов в которой выбирается на основании верхней оценки для ошибки, определенной по значениям производных от подынтегральных выражений. Масштаб коэффициентов в уравнениях выбирается таким образом, чтобы получить устойчивую при счете систему, разрешимую методом исключения без итерации остатков. Поблочное решение уравнений позволяет рассматривать большие задачи. В программе используется большое число процедур, осуществляющих контроль и автоматическое формирование данных. Результаты решения задачи о фланце трубопровода и характеристики выполнения программы сравниваются с результатами, полученными методом конечных элементов, и экспериментальными результатами.
 [c.111]

Здесь штрихом обозначены измеряемые величины, символом 5 — ошибки измерений. Функции Wf t), Wh t) — импульсные переходные функции стационарных линейных фильтров, применяемых при формировании измерений СНС и гравиметра, — оператор свертки фильтра (указанные фильтры необходимы, в частности, для подавления сигнала вне интервала частот Найквиста, с целью исключения явления маскировки частот при дискретизации измерений). Заметим, что в общем случае измерения в (5) проводятся с разной частотой дискретизации.
 [c.136]

При этом следует соблюдать определенную осторожность. Если нестационарные конечно-разностные уравнения сходятся к устойчивому стационарному решению, то еше нельзя считать, что соответствующие дифференциальные уравнения в частных производных имеют устойчивое стационарное решение. Как мы уже видели, дискретизация иногда приводит к появлению схемной вязкости. Эта и другие ошибки аппроксимации могут привести к тому, что конечно-разностные уравнения окажутся более устойчивыми, чем дифференциальные уравнения в частных производных. Выяснение отличия гидродинамической устойчивости от завышенной численной устойчивости представляет трудную задачу (см. разд. 6.5).
 [c.165]

Заметим, что ошибка в г з, обусловленная дискретизацией, приводит к возникновению ошибки при вычислении толщины вытеснения б (Шлихтинг [1968]), если последнюю определять по формуле
 [c.236]

Вычислить локальную ошибку отсеченИя , или дискретизации, с помощью разложения в ряд Тейлора.
 [c.28]

Исследуем ошибки округления двумя способами. Рассмотрим свободно опертую балку с и и М, равными нулю на обоих концах. Тогда уравнения М» = / и гю» = М можно решить отдельно, сначала для М, а затем для ш, применяя для этого либо конечные разности, либо конечные элементы. Предположим, что приближенное решение задачи М» = / содержит ошибку округления еь обычно порядка для ЭВМ с длиной слова 1. Тогда приближенное решение задачи т» = —/ будет прежде всего содержать свою собственную ошибку округления е2 того же порядка и, кроме того, унаследованную ошибку ез. Последняя удовлетворяет равенству ез = Ъх, или, скорее, точно удовлетворяет используемой дискретизации этого уравнения, и потому порядок ошибки ез также равен Ошибки округления не объединяются в
 [c.146]

При втором способе получаются правильные величины скоростей, но в результате дискретизации вносится ошибка в величины г )1,/. Очевидно, что оба эти способа сходятся при Ау- 0. Поскольку наибольшее влияние на динамику течения оказывает и, а не г1), второй способ, заключающийся в задании во входном сечении потока профиля для и при допущении ошибок в величинах г , кажется предпочтительнее.
 [c.236]

Требования к отношению сигнал-помеха в канале передачи ИКМ сигнала (канала записи — воспроизведения) невысоки, поскольку необходимо передать лишь два уровня сигнала — О и 1. Нелинейные искажения, возникающие в этом канале, практически не оказывают существенного влияния на восстановленный сигнал. Точность передачи сигналов с ИКМ зависит от параметров аналого-цифрового преобразования (АЦП)— частоты дискретизации и шага квантования. Для неискаженной передачи частота дискретизации /д в соответствии с теоремой Котельникова должна по крайней мере вдвое превышать высшую частоту Fb передаваемого аналогового сигнала. Шаг квантования определяет максимальную погрешность восстановленного сигнала и характеризует ошибки квантования, которые проявляются как шум квантования . Шаг квантования связан с числом уровней
 [c.21]

Ошибки могут возникать на различных стадиях конечно-элементного анализа пр постановке задачи, дискретизации (построении модели), численном решении.
 [c.28]

Адаптивное построение сетки. Адаптивное построение сетки состоит в том, что после создания модели и задания граничных условий программа генерирует конечноэлементную сетку, выполняет расчет, оценивает ошибку за счет сеточной дискретизации и меняет размер сетки от решения к решению до тех пор, пока расчетная погрешность не станет меньше некоторой наперед заданной величины (или пока не будет достигнуто установленное число итераций).
 [c.92]

Для каналов первого класса принята частота дискретизации 21 1/3 кГц, второго класса — 14 2/9 кГц, высшего класса — 32 кГц. В каналах высшего класса применено 10-разрядное кодирование с мгновенным компандированием, в каналах первого и второго классов — 9-разрядное. Таким образом, скорость цифрового потока при организации канала высшего класса составляет 320 Кбит/с, первого класса — 192 Кбит/с и второго класса — 128 Кбит/с. В первичном цифровом потоке 2048 Кбит/с в системе Орбита-Рв передаются 10 каналов первого класса, либо 15 каналов второго класса, либо 6 каналов высшего класса. Всего для сигналов ЗВ выделяются два потока по 2048 Кбит/с. В системе использовано помехоустойчивое кодирование, обеспечивающее допустимую при цифровой передаче вероятность ошибки poш=10- .
 [c.314]

При применении прямых методов получение достаточно точных решений связано с решением больших систем уравнений, решение которых затруднено из-за ограниченных возможностей вычислительных машин (память, быстродействие, ошибки округления). Поэтому при составлении программ решения больших систем линейных алгебраических уравнений, полученных при дискретизации вариационных задач, стремятся учесть особый вид магриц таких систем например, их малую заполненность, ленточную структуру и т. д. Такие системы можно решать на ЭВМ точными методами (Гаусса, Жордана), если использовать внешние запоминающие устройства и применять специальные приемы, направленные на экономию памяти и времени счета, например блочный метод Гаусса.
 [c.180]

Штриховая кривая 1 на жс. 4.6 соответствует интегрированию уравнений продолжения модифицированным методом Эйлера с шагом АХ по параметру X, который на начальном участке деформирования при малых Р соответствовал приращению относительного прогиба w(0)/i = 0,005. Штрихпунктирная кривая 2 совтветствует тому же методу, но с шагом w(0)/R = 0/)( 5. Сплошная кривая 3 получена прт комбинировании двух шагов w 0)fR = 0,005 модифицированного метода Эйлера с одним шагом по неявной схеме дискретного продолжения, описанной в ЗА. Эта кривая практически соответствует точному решению задачи (4.3.2), (4.3.3) (конечно, в пределах принятой дискретизации). Как видно из жс. 4.6, модифицированный метод Эйлера дает накопление ошибки, особенно существенное в тех областях параметра, где решение претерпевает значительные изменения. В то же время расход машинного времени при получении кривых 2 и 3 практически одинаков (даже для кривой 5 он был несколько меньшим). Поэтому для всех дальнейших расчетов бьша использована именно такая комбинация непрерывного и дискретного продолжения.
 [c.120]

Для вычисления ДПФР, кроме матрицы bi k, I), определяющей комплексную амплитуду поля на объекте, необходимо еще задаться и величинами и и v, характеризующими относительные размеры объекта, наблюдаемого из воображаемой точки регистрации голограммы. При их выборе следует руководствоваться условиями (1.46) малости ошибки при дискретизации фазовых множителей.
 [c.21]

Численные эксперименты показали, что скорость сходимости итерационного процесса в смешанных задачах слабо зависит от степени дискретизации. Рассматривалась, например, следующа краевая задача [121] для единичного куба на центральной части граней куба, размером 0,8X0,8, задавались перемещения, а на остальной части куба — усилия, соответствующие гидростатическому сжатию. Граничная поверхность разбивалась на 96, 216 н 600 граничных элементов. Исследовался стационарный итерационный процесс (4,2) для дискретного уравнения (2,31) при р=1 и Р = 2, Для первой дискретизации при р=1 отклонение искомы поверхностных сил от точного решения на первой итерации составило 65%, на шестой — 7,5%, на одиннадцатой — 0,9%, Для остальных дискретизаций (216 и 600 граничных элементов) ошибка в 1 % была достигнута соответственно на тринадцатой и четырнадцатой итерациях. При р = 2 итерационный процесс (4,2) сходился значительно быстрее для первой дискретизации (96 гра ничных элементов) отклонение искомых поверхностных сил от точного решения на первой итерации составило 31, %, на второй-— 9%, на третьей —2,6 %, на четвертой — 0,86 % для остальньис дискретизаций (216 и 600 граничных элементов) ошибка в 1 % была достигнута соответственно на пятой и шестой итерациях.
 [c.239]

Базис Каруиепа — Лоэва не отвечает требованиям универсальности (т. е. применимости для достаточно широкого класса сигналов), устойчивости к ошибкам задания статистических характеристик сигнала и требует больших вычислительных затрат при реализации. Поэтому имеет смысл ставить задачу выбора не формально оптимального, а рационального базиса в (1.21), (1.22), удовлетворяющего указанным требованиям. Однако удовлетворить всем требованиям одновременно невозможно. На практике используются различные виды дискретизации [12]. Из них рассмотрим наиболее часто используемые при обработке сигналов аналитических приборов.
 [c.20]

Максимум ошибки всегда достигается на конце большой полуоси эллипса. Поэтому возникла гипотеза, что большая часть ошибки описывается геометрическими причинами — тем, что последовательность точек дискретизации, равномерная в стандартной координате на эллипсе, описывает эллипс неточно (с точки зрения вычислительного метода). Была найдена геометрическая характеристика, с которой ошибка хорошо коррел-лировала. Это отношение кривизны эллипса в вершине к кривизне окружности, проведенной через нее и еще две соседние точки дискретизации. Так, при отношении, близком к двум, ошибка достигала 16%, к трем — 19%. Наличие геометрического описания ошибок позволяет надеяться, что при более удачной расстановке точек на контуре трещины можно ожидать значительного уменьшения ошибок. Действительно, удалось найти геометрический критерий расстановки точек на контурах, позволяющий минимизировать ошибки вычислений (точнее максимум ошибки в точках контура трещины). Точнее, если расстановка точек удовлетворяла этому критерию, то соответствующая ошибка не более чем в 1,5 раза превышала минимально возможную. Опишем здесь результат оптимизации метода.
 [c.195]

Погрешности реконструкции в основном обусловлены неидеальностью используемых аппроксимаций алгоритма реконструкции. Среди наиболее существенных источников пофешностей реконструкции следует указать ошибки, возникающие из-за недостаточно малого интервала дискретизации по углу, пофешности неоптимальной интерполяции и двумерной дискретизации томофаммы, чрезмерный уровень низкочастотной фильтрации реконструированных структур из-за попытки компенсации отмеченных пофешностей снижением высокочастотных компонент ядра свертки или двумерной фильтрацией реконструированных томофамм.
 [c.150]

Общая идея постановки граничных условий, отвечающих бесконечности на наиболее удаленной границе разностной сетки, была предложена Ричардсоном [1910]. Кавагути [1965], Фридман [1970], а также Ли и Фын [1970] в выходном сечении брали, например, профиль Пуазейля. Заметим, что асимптотическое решение, используемое в качестве граничного условия, должно рассматриваться в переменных задачи-, например, если конечно-разностные уравнения записаны в переменных г]) и то и решение Пуазейля должно быть записано для ф и Если и задается по имеющемуся решению дифференциальных уравнений, а ф находится при помощи квадратур, то при этом возникает ошибка в результатах, обусловленная дискретизацией (аналогичная ситуация возникает и в случае постановки условий на входной границе потока см. предыдущий раздел). Для течений более общего вида, например таких, как асимптотическое течение в пограничном слое, решение дифференциальных уравнений будет отличаться от асимптотического конечно-разностного решения по всем переменным. На выходной границе предпочтительнее брать конечно-разностное решение асимптотического обыкновенного дифференциального уравнения (Кавагути [1965]).
 [c.237]

Заметим, что вычисление аппроксимации Ритца предполагалось непрерывньш по времени-, до сих пор лишь дискретизация заменяла все допустимое пространство его подпространством 5 . Это соответствует изложению задачи Коши в гл. 7, где ошибки метода» Ритца отделены от ошибок метода конечных. разностей (или другого метода) по временному направлению. Для нелинейной задачи большие дискуссии вызвал наилучший метод приращений , но мы полагаем, что все основные возможности сходятся в одном. Они просто вносят новую ошибку, пропорциональную степени приращения в случае разностного уравнения.
 [c.138]

В практических задачах времт тоже должно быть дискретизировано, что предполагает применение метода конечных разностей. Например, схема- Кранка — Николсона симметрична относительно п+1/2 при вычислении uf tn+ ) через и потому имеет точность порядка At . Таким образом, окончательно вычисленное приближение содержит эту ошибку, как и ошибку метода Галёркина, вызванную дискретизацией по х. Последнюю из них мы проанализируем подробно и покажем, что при к 2т ее оптимальный порядок для 5-й производной тоже р -вен Этот результат применяется к уравнениям параболического типа, например к уравнению теплопроводности Ь — эллиптический оператор того же типа, что и в стационарных задачах. В случае гиперболических уравнений, не содержащих диссипативных членов, возможности метода конечных элементов несколько меньше трудности в сравнении с явными разностными методами- могут оказаться слишком большими. Тем не менее даже в этом случае достигнуты значительные результаты исследование границ можно проводить почти автоматически в гл. 7 включен набросок теории метода конечных элементов для гиперболического случая.
 [c.139]

Естественно спросить почему конечные элементы не используются также и по временной переменной Конечно, можно было бы попытаться применить их, но это не даст особого успеха. С математической точки зрения вполне разумно изучить дискретизацию в два этапа сначала исследовать ошибку метода конечных элементов и(х, i) —u (x, t], а затем ошибку в возникающую при решении обыкновенных дифференциальных уравнений. По временной переменной геометрия области не вызывает трудностей, которые надо было бы преодолевать с помощью метода конечных элементов, и на самом деле непосредственное применение принципа Галёркина может связать все временные слои и уничтожить главное свойство распространения вперед по. времени. Мы не видим причин отказываться от этой дополнительной гибкости конечных разностей.
 [c.282]

Моделирование позволило отметить некоторые особенности аналогового вычисления суммарного изображения Это, прежде всего, отсутствие регистрации проекций, которое позволяет избежать погрешностей их съема и ввода в ЭВМ, т. е в этом случае восстанов тение искомого распределения осуществляется в отсутствие шумов При моделировании указанная особенность томографической Интерферометрии учитывалась Однако при реализации некоторых математических операций в оптических системах с преобразованием волнового фронта возможно их неточное выполнение из-за аберраций оптических элементов и погрешности юстировки. В томографическом интерферометре искажения, обусловленные аберрациями, устранялись голографической регистрацией волнового фронта. Возможная ошибка ( 30 ) из-за неточности согласования углов зондирования и поворота волнового фронта была равна погрешности из-за дискретизации проекций при цифровом вычислении суммарного изображения на сетке 51X51 отсчетов
 [c.138]

Форматы кодов у устройств разного назначения существенно различны, поскольку у них не совпадают законы кодирования, способы защиты от ощибок, число звуковых каналов, характер и объем дополнительной информации. Так, у студийной аппаратуры определяющими факторами являются высокое качество передачи и возможность введения дополнительной служебной информации (адресно-временного кода для монтажа программ, режиссерских комментариев и т. д.). Результирующая скорость цифрового потока больщой роли не играет, поскольку специфика работы студийной аппаратуры не связана с передачей этих потоков по каналам связи. Поэтому в таких устройствах применяют равномерное квантование с числом разрядов не менее 16 (в пультах и устройствах шумоподавления число разрядов на отсчет доходит до 24) и высокую частоту дискретизации (48 кГц). Избыточность, вводимая для борьбы с ошибками, достигает 33%, а управляющие сигналы, осуществляющие перестройку системы обработки сигнала, и адресно-временной код передаются совместно со звуковыми.
 [c.238]

---