Что такое ошибка опыта

ошибка опыта

Изучение
всех влияющих на исследуемый объект
факторов одновременно провести
невозможно, поэтому в эксперименте
рассматривается их ограниченное число.
Остальные активные факторы стабилизируются,
т.е. устанавливаются на каких-то одинаковых
для всех опытов уровнях.

Некоторые
факторы не могут быть обеспечены
системами стабилизации (например,
погодные условия, самочувствие оператора
и т.д.), другие же стабилизируются с
какой-то погрешностью (например,
содержание какого-либо компонента в
среде зависит от ошибки при взятии
навески и приготовления раствора).
Учитывая также, что измерение
параметра у осуществляется
прибором, обладающим какой-то погрешностью,
зависящей от класса точности прибора,
можно прийти к выводу, что результаты
повторностей одного и того же опыта у_к будут
приближенными и должны отличаться один
от другого и от истинного значения
выхода процесса. Неконтролируемое,
случайное изменение и множества других
влияющих на процесс факторов
вызывает случайныеотклонения
измеряемой величины у_к от
ее истинного значения — ошибку опыта.

Каждый
эксперимент содержит элемент
неопределенности вследствие ограниченности
экспериментального материала. Постановка
повторных (или параллельных) опытов не
дает полностью совпадающих результатов,
потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту
ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится
по возможности в одинаковых условиях
несколько раз и затем берется среднее
арифметическое всех результатов. Среднее
арифметическое у равно сумме всех n
отдельных результатов, деленной на
количество параллельных опытов n:

Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность y₂— ,
где y₂ —
результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.

Дисперсией
называется среднее значение квадрата
отклонений величины от ее среднего
значения. Дисперсия обозначается s² и
выражается формулой:

где
(n-1) — число степеней свободы, равное
количеству опытов минус единица. Одна
степень свободы использована для
вычисления среднего.

Корень
квадратный из дисперсии, взятый с
положительным знаком, называется средним
квадратическим отклонением, стандартом
или квадратичной ошибкой:

Ошибка
опыта является суммарной величиной,
результатом многих ошибок: ошибок
измерений факторов, ошибок измерений
параметра оптимизации и др. Каждую из
этих ошибок можно, в свою очередь,
разделить на составляющие.

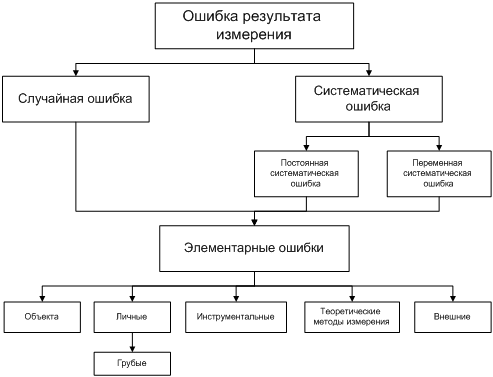
Все
ошибки принято разделять на два класса:
систематические и случайные (рисунок
1).

Систематические
ошибки порождаются причинами, действующими
регулярно, в определенном направлении.
Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая
ошибка —
это ошибка, которая остаётся постоянно
или закономерно изменяется при повторных
измерениях одной и той же величины. Эти
ошибки появляются вследствие неисправности
приборов, неточности метода измерения,
какого либо упущения экспериментатора,
либо использования для вычисления
неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих
случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка
всех измерительных приборов и безусловное
выполнение выработанных практикой
правил экспериментальных работ. Если
систематические ошибки вызваны известными
причинами, то их можно определить.
Подобные погрешности можно устранить
введением поправок.

Систематические
ошибки находят, калибруя измерительные
приборы и сопоставляя опытные данные
с изменяющимися внешними условиями
(например, при градуировке термопары
по реперным точкам, при сравнении с
эталонным прибором). Если систематические
ошибки вызываются внешними условиями
(переменной температуры, сырья и т.д.),
следует компенсировать их влияние.

Случайными ошибками
называются те, которые появляются
нерегулярно, причины, возникновения
которых неизвестны и которые невозможно
учесть заранее. Случайные ошибки
вызываются и объективными причинами и
субъективными. Например, несовершенством
приборов, их освещением, расположением,
изменением температуры в процессе
измерений, загрязнением реактивов,
изменением электрического тока в цепи.
Когда случайная ошибка больше величины
погрешности прибора, необходимо
многократно повторить одно и тоже
измерение. Это позволяет сделать
случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше
погрешности прибора, то уменьшать её
нет смысла. Такие ошибки имеют значение,
которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми
для измерений сделанных даже в одинаковых
условиях. Поскольку причины, приводящие
к случайным ошибкам неодинаковы в каждом
эксперименте, и не могут быть учтены,
поэтому исключить случайные ошибки
нельзя, можно лишь оценить их значения.
При многократном определении какого-либо
показателя могут встречаться результаты,
которые значительно отличаются от
других результатов той же серии. Они
могут быть следствием грубой ошибки,
которая вызвана невнимательностью
экспериментатора.

Систематические
и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы
исключать инструментальные ошибки,
следует проверять приборы перед опытом,
иногда в течение опыта и обязательно
после опыта. Ошибки при проведении
самого опыта возникают вследствие
неравномерного нагрева реакционной
среды, разного способа перемешивания
и т.п.

При
повторении опытов такие ошибки могут
вызвать большой разброс экспериментальных
результатов.

Очень
важно исключить из экспериментальных
данных грубые ошибки, так называемый
брак при повторных опытах. Грубые
ошибки легко
обнаружить. Для выявления ошибок
необходимо произвести измерения в
других условиях или повторить измерения
через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность
в записях, тщательность в работе и записи
результатов эксперимента. Грубая ошибка
должна быть исключена из экспериментальных
данных. Для отброса ошибочных данных
существуют определённые правила.

Например,
используют критерий Стьюдента t (Р; f):
Опыт считается бракованным, если
экспериментальное значение критерия
t по модулю больше табличного значения
t (Р; f).

Если
в распоряжении исследователя имеется
экспериментальная оценка дисперсии
S²(y_k)
с небольшим конечным числом степеней
свободы, то доверительные ошибки
рассчитываются с помощью критерий
Стьюдента t (Р; f):

?()
= t (Р; f)* S(y_k)/=
t (Р; f)* S()

?(y_k)
= t (Р; f)* S(y_k)

6.
Результат прямого измерения — случайная
величина, подчиняющаяся нормальному
закону распределения

Результаты,
которые получаются при экспериментальном
исследовании какого-либо технологического
процесса, зависят от целого ряда факторов.
Поэтому результат исследования является
случайной величиной, распределённой
по нормальному закону распределения.
Оно названо нормальным, т. к. именно
это распределение для случайной величины
является обычным и
называется гаусовским или лапласским. Под распределением
случайной величиныпонимают
совокупность всех возможных значений
случайной величины и соответствующих
им вероятностей.

Законом
распределения случайной величины называется
всякое соотношение, устанавливающее
связь между возможными значениями
случайной величины и соответствующим
им вероятностям.

При
экспериментальном исследовании
какого-либо технологического процесса
измеряемый результат последнего является
случайной величиной, на которую оказывает
влияние огромное число факторов
(изменение погодных условий, самочувствие
оператора, неоднородность сырья, влияние
износа измерительной и стабилизирующей
аппаратуры и т.д. и т.п.). Именно поэтому
результат исследования является
случайной величиной, распределенной
по нормальному закону. Однако если
исследователь какой-либо активный
фактор не заметил или отнес его к
неактивным, а неконтролируемое изменение
этого фактора может вызвать несоразмерно
большое изменение эффективности процесса
и параметра, характеризующего эту
эффективность, то распределение
вероятности последнего может нормальному
закону не подчиниться.

Точно
так же приведет к нарушению нормальности
закона распределения наличие в массиве
экспериментальных данных грубых ошибок.
Именно поэтому в первую очередь проводят
анализ на наличие в экспериментальных
данных грубых ошибок с принятой
доверительной вероятностью.

Случайная
величина будет распределена по нормальному
закону, если она представляет собой
сумму очень большого числа взаимно
зависимых случайных величин, влияния
каждой из которых ничтожно мало. Если
измерения искомой величины y проведены
много раз, то результат можно наглядно
представить, построив диаграмму, которая
показывала бы, как часто получались те
или иные значения. Такая диаграмма
называется гистограммой. Что
бы построить гистограмму нужно разбить
весь диапазон измеренных значений на
равные интервалы. И посчитать сколько
раз каждая величина попадает в каждый
интервал.

Если
измерения продолжать до тех пор, пока
число измеренных значений n не станет
очень большим, то ширину интервала можно
сделать очень малой. Гистограмма перейдёт
в непрерывную прямую, которая
называется кривой
распределения.

В
основе теории случайных ошибок лежат
два предположения:

1.
при большом числе измерений случайные
погрешности одинаково велики, но с
разными знаками встречаются одинаково
часто;

2.
большие (по абсолютной величине)
погрешности встречаются реже, чем малые.
Т. е. вероятность появления погрешности
уменьшается с ростом её величины.

Согласно
закону больших чисел при бесконечно
большом числе измерений n, истинное
значение измеряемой величины y равно
среднеарифметическому значению всех
результатов измерений ?

Для
всех m-повторностей можно записать:

Разделив
это уравнение на число повторностей m,
получим после подстановки:

За
экспериментальную оценку истинного
значения (математического ожидания)
критерия оптимальности у принимается среднеарифметическая
оценкарезультатов
всех т повторностей:

Если
число m велико (m>?), то будет справедливо
равенство:

Таким
образом, при бесконечно большом числе
измерений истинное значение измеряемой
величины y равно среднеарифметическому
значению ? всех результатов произведённых
измерений: y=?, при m>?.

При
ограниченном числе измерений (m??)
среднеарифметическое значение y будет
отличаться от истинного значения, т.е.
равенство y=? будет неточным, а приближённым:
y?? и величину этого расхождения необходимо
оценить.

Если
в распоряжении исследователя имеется
только единичный результат измерения
y_k,
то оценка истинного значения измеряемой
величины будет менее точной. чем
среднеарифметическая оценка при любом
числе повторностей: |y-?|<|y-yk|.

Появление
того или иного значения yk в процессе
измерения является случайным событием.
Функция плотности нормального
распределения случайной величины
характеризуется двумя параметрами:

·
истинным значением y;

·
среднеквадратичным отклонением ?.

а)
б)

Рисунок
— 1а — кривая плотности нормального
распределения; 1б — кривая плотности
вероятности нормально распределенной
случайной величины при различных
дисперсиях

Плотность
нормального распределения (рис. 1а)
симметрична относительно y и достигает
максимального значения при yk= y, стремится
к 0 при увеличении.

Квадрат
среднеквадратичного отклонения
называется дисперсией случайной величины
и является количественной характеристикой
разброса результатов вокруг истинного
значения y. Мера рассеяния результатов
отдельных измерений yk от среднего
значения ? должна выражаться в тех же
единицах, то и значения измеряемой
величины. В связи с этим в качестве
показателя разброса гораздо чаще
используют величину ?:

Значения
этой величины определяют форму кривой
распределения py. Площади под тремя
кривыми одинаковы, но при малых значения
? кривые идут более круто и имеют большее
значение py. С увеличением ? значение py
уменьшается и кривая распределения
растягивается вдоль оси y. Т.о. кривая 1
характеризует плотность распределения
случайной величины, воспроизводимость
которой в повторных измерениях лучше,
чем воспроизводимость случайных величин
имеющих плотность распределения 2, 4. На
практике не возможно произвести слишком
много замеров. Поэтому нельзя построить
нормальное распределение, чтобы точно
определить истинное значение y. В этом
случае хорошим приближением к истинному
значению можно считать ?, а достаточно
точной оценкой ошибки выборочную
дисперсию ??n, вытекающую из закона
распределения, но относящуюся к конечному
числу измерения. Такое название величины
??n объясняется тем, что из всего множества
возможных значений yk, т.е. из генеральной
совокупности выбирают лишь конечное
число значений равное m, называемых
выборкой, которая характеризуется
выборочным средним значением и выборочной
дисперсией.

Соседние файлы в папке planirovanie

• #
• #
• #
• #
• #
• #

Проведение
эксперимента

Познакомимся с
вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.

Ошибки параллельных
опытов

Каждый
эксперимент содержит элемент неопределен­ности вследствие ограниченности
экспериментального ма­териала. Постановка повторных (или параллельных) опытов
не дает полностью совпадающих результатов, потому что всегда существует ошибка
опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным
опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях
несколько раз и затем бе­рется среднее арифметическое всех результатов. Среднее
арифметическое  равно сумме всех п отдельных резуль­татов, деленной на количество
параллельных опытов п

.

Отклонение
результата любого опыта от среднего арифметического можно представить как
разность  где  – результат отдельного опыта. Наличие
откло­нения свидетельствует об изменчивости, вариации значе­ний повторных
опытов. Для измерения этой изменчи­вости чаще всего используют дисперсию.
Диспер­сией называется среднее значение квадрата отклонений величины от ее
среднего значения. Дисперсия обозна­чается s² и
выражается формулой

.

где (n – 1) – число
степеней свободы, равное количе­ству опытов минус единица. Одна степень свободы
исполь­зована для вычисления среднего.

Корень квадратный из
дисперсии, взятый с положи­тельным знаком, называется средним квадратическим от­клонением,
стандартом или квадратичной ошибкой

Стандарт имеет
размерность той величины, для кото­рой он вычислен. Дисперсия и стандарт – это
меры рассеяния, изменчивости. Чем больше дисперсия и стан­дарт, тем больше
рассеяны значения параллельных опы­тов около среднего значения.

Ошибка опыта являемся
суммарной величиной, результатом многих ошибок: ошибок измерений факторов,
ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою
очередь, разделить на состав­ляющие.

Вопрос о классификации ошибок
довольно сложный и вызывает много дискуссий. В качестве примера одной из
возможных схем классификации мы приведем схему из книги Ю. В. Кельница «Теория
ошибок измере­ний» (М., изд-во «Недра», 1967).

Все ошибки принято разделять
на два класса: система­тические и случайные.

Систематические ошибки
порождаются причинами, действующими регулярно, в определенном направлении. Чаще
всего эти ошибки можно изучить и определить количественно.

Систематические ошибки
находят, калибруя измери­тельные приборы и сопоставляя опытные данные с изме­няющимися
внешними условиями (например, при градуи­ровке термопары по реперным точкам,
при сравнении с эта­лонным прибором).

Если систематические ошибки
вызываются внешними условиями (переменной температуры, сырья и т. д.), следу­ет
компенсировать их влияние. Как это делать, будет показано ниже.

Случайными ошибками называются
те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и
которые невозможно учесть заранее.

Систематические и случайные
ошибки состоят из мно­жества элементарных ошибок. Для того, чтобы исключать инструментальные
ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно
после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного
нагрева реакционной среды, раз­ного способа перемешивания и т.п. При повторении
опытов такие ошибки могут вызвать большой разброс эксперимен­тальных
результатов.

Очень важно исключить из экспе­риментальных
данных грубые ошибки, так называемый брак при повторных опытах. Для отброса оши­бочных
опытов существуют правила. Для определения брака используют, например, кри­терий
Стьюдента

.

Значение t берут из таблицы t-распределения Стьюдента. Опыт считается
бракованным, если эксперименталь­ное значение критерия t по модулю больше табличного значения.

Дисперсия параметра
оптимизации

Дисперсия всего эксперимента
получается в результате усреднения дисперсий всех опытов. По терми­нологии,
принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра
оптимизации  или, что то же самое, дисперсии воспроизводимости эксперимента

При подсчете дисперсии
параметра оптимизации квад­рат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просумми­ровать по числу опытов в
матрице N, а затем разделить на N(n — 1):

,

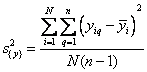
Где i = 1, 2, …, N;      q = 1, 2, …, n.

Такой формулой можно
пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.

Дисперсию воспроизводимости
проще всего рассчиты­вать, когда соблюдается равенство числа повторных опы­тов
во всех экспериментальных точках. На практике весь­ма часто приходится
сталкиваться со случаями, когда число повторных опытов различно. Это происходит
вследствие отброса грубых наблюдений, неуверенности экспе­риментатора в
правильности некоторых результатов (в таких случаях возникает желание еще и еще
раз повторить опыт) и т.п.

Тогда при усреднении
дисперсий приходится пользо­ваться средним взвешенным значением дисперсий,
взятым с учетом числа степеней свободы

,

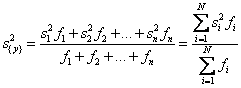
где

– дисперсия i-го опыта;

 – число степеней свободы i-м опыте, равное числу параллельных опытов
n_i минус 1.

Число степеней
свободы средней дисперсии принима­ется равным сумме чисел степеней свободы
дисперсий, из которых она вычислена.

Случай с неравным числом
наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности
матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов,
приведенные ранее. Этот вопрос будет рассмотрен ниже.

Экспериментатору не следует
забывать о про­верке однородности дисперсий, неоднородные дисперсии усреднять
нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в
однородности суммируемых дисперсий.

Проверка
однородности дисперсий

Проверка однородности
дисперсий производится с помощью различных статистических критериев. Простей­шим
из них является критерий Фишера, предназначенный для сравнения двух дисперсий.
Критерий Фишера (F—критерий)
представляет собою отношение большей дисперсии к меньшей. Полученная величина
сравнивается с таблич­ной величиной F-критерия.

Если полученное значение
дисперсионного отно­шения больше приведенного в таблице для соответствую­щих
степеней свободы и выбранного уровня значимости, это означает, что дисперсии
значимо отличаются друг от друга, т. е. что они неоднородны.

Если сравниваемое количество
дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться
критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках
имеется одина­ковое число повторных опытов. При этом подсчитывается дисперсия в
каждой горизонтальной строке матрицы

,

а затем из
всех дисперсий находится наибольшая  ко­торая делится на сумму всех дисперсий. Критерий Кохрена – это
отношение максимальной дисперсии к сумме всех дисперсий

.

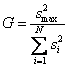
Гипотеза
об однородности дисперсий подтверждается, если экспериментальное значение
критерия Кохрена не превы­шает табличного значения. Тогда можно усреднять дис­персии
и пользоваться формулой

.

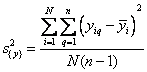
Если возникает предположение
о наличии неодно­родности дисперсий для случая, когда число повторных опытов неодина­ково
во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой
формуле подсчитывается дисперсия воспроизводимости

.

Далее
находится величина

,

где

.

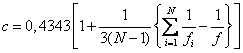
Здесь число
степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании экспе­римента типа
2^k это число равно числу опытов в матрице.

Бартлет показал, что величина
 приближенно подчиняется  – распределению с (N–1) степенями свободы. Значимость критерия
Бартлета проверяется обычным способом.

Критерий Бартлета базируется
на нормальном распре­делении. Если имеются отклонения от нормального распре­деления,
то проверка неоднородности дисперсий может привести к ошибочным результатам.

Можно предложить
использование F-критерия даже в тех случаях, когда число
дисперсий больше двух. Делается это следующим образом. Из всех дисперсий
выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между
собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо,
то диспер­сии, имеющие промежуточные значения, также не могут значимо
отличаться друг от друга. Тогда всю группу дис­персий можно считать
принадлежащей к единой совокуп­ности. В таких случаях нет надобности применять
кри­терий Бартлета.

Рандомизация

Чтобы исключить влияние
систематических ошибок, вызванных внешними условиями (переменой температуры,
сырья, лаборанта и т. д.), рекомендуется случайная пос­ледовательность при
постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать
во времени. Термин «рандомизация» происходит от английского слова random – случайный.

Если экспериментатор
располагает сведениями о пред­стоящих изменениях внешней среды, сырья,
аппаратуры и т. п., то целесообразно планировать эксперимент таким образом,
чтобы эффект влияния внешних условий был сме­шан с определенным
взаимодействием, которое не жалко потерять. Так, при наличии двух партий сырья
матрицу 2³ можно разбить на два блока таким образом, чтобы эффект
сырья сказался на величине трехфакторного взаимодейст­вия. Тогда все линейные
коэффициенты и парные взаимо­действия будут освобождены от влияния
неоднородности сырья.

В этой матрице при
составлении блока 1 отобраны все строки, для которых , а при составления бло­ка 2 – все строки,
для которых . Различие в сырье можно рассматривать как
новый фактор . Тогда матрица 2³, разбитая на
два блока, представляет собой полуреплику 2^4-1 с определяющим
контрастом .

,                 ;

,                ;

,               ;

,                  ;

,                 ;

,              ;

,              ;

,                ;

Эффект сырья
отразился на подсчете свободного члена b₀ и
эффекта взаимодействия второго порядка b₁₂₃.

Аналогично можно разбить на
два блока любой экспе­римент типа 2³. Главное – правильно выбрать
взаимодей­ствие, которым можно безболезненно пожертвовать. При отсутствии
априорных сведений выбирают взаимодействие самого высокого порядка: x₁x₂x₃ для 2³, x₁x₂x₃х₄ для 2⁴, x₁x₂x₃x₄x₅ 2⁵ и т. д. Но если
экспериментатору известно, что одно из парных взаимодействий лишено, например,
физико-химического смысла, то можно пожертвовать парным взаимодействием.

Матрицу типа 2^k можно разбить на количество блоков 2ⁿ (n – степень
двойки) при . Так, матрица 2³
разбивается на два блока по четыре опыта в каждом и на четыре блока по
два опыта в каждом. Матрица 2⁴ – на два блока по 8 опытов в каждом,
на четыре блока по четыре опыта и на восемь блоков по два опыта и т.д.

Сколько раз я сталкивался на консультациях с этой темой — «я боюсь ошибиться». Дальше все развивается, как правило, по одной и той же схеме: человек пытается просчитать варианты, все время прикидывает, думает, анализирует и…. ничего не делает. Потому что как ни прокручивай возможные варианты развития событий, возможность ошибки так или иначе будет заключена в любом из них.

Усугубляет ситуацию и то, что само понятие ошибки — понятие с резко отрицательным значением. Ошибся — значит, неудачник. Ошибся — значит, не умен. Ошибся — значит, недостаточно ловок или силен, и многое другое «недостаточно».

Но существуют ли ошибки вообще? И как мы это оцениваем?

Вообще-то ошибки в чистом виде существуют только там, где есть эталон, четко выверенный. Скажем, вам показалось, что прошел час. А на деле прошло полтора. Вы ошиблись? — да. Потому что есть конкретный эталон часа, минуты и секунды, он общезначим и абсолютно конкретен. Или, если вы сказали, что от стола до двери два метра, но измерив рулеткой, вы выяснили, что их два с половиной — вы тоже ошиблись, потому что есть конкретный эталон метра.

Но есть ли подобные эталоны поступков? Жизни? Суждений, мировоззрения? Вряд ли такое можно сказать с уверенностью. Даже моральные максимы можно толковать весьма относительно, в зависимости от обстоятельств. «Не убий» — казалось бы, куда конкретнее? Но ведь веками в человеческой морали оправдано убийство из самообороны. А что говорить о войнах, под которых подводились самые разные основания, и участники их становились героями?

Давайте начнём с простых ошибок.

Вы не выучили урок в школе и неправильно написали слово или решили неправильно уравнение. Вы ошиблись? С точки зрения русского языка и математики — да. С точки зрения жизни — нет. Вы получили бесценный опыт на тему «что бывает, если не выучить урок».

Ваше отношение к этому может быть разным, но многое зависит здесь от позиции родителей. «Все мы родом из детства» — эту максиму психологи повторяют на все лады, и от нее действительно никуда не денешься. Одни родители могут сказать: «ну что ж, ошибся, давай поможем тебе исправить, ты запомнишь этот опыт и постараешься его не повторять». Но этот случай — довольно редкий.

Чаще всего родители занимают позицию осуждения: «Как ты мог принести двойку? Не будешь хорошо учиться — пойдешь в дворники/лишим тебя мороженого/будешь сидеть дома все выходные».

Ребенок прочно запоминает после нескольких повторений подобной ситуации, что ошибка — это страшно, что за нее следует неизбежное наказание. Причем понятие ошибки распространяется таким образом не только на формальную ошибку в написании слова или решении уравнения, а вообще на то, что что-то в жизни пошло «не идеально», не «как положено».

Вот так, чаще всего, и возникают пресловутые эталоны жизни, опыт перестает восприниматься как опыт, из опыта уже сложно сделать правильные выводы, а вместо них происходит нагнетание страха перед любой ошибкой.

Человек привыкает общаться сам с собой с позиции мамы или папы: «ошибся — плохо», и ругает себя сам. Меж тем полезная информация, которая могла бы быть извлечена из этого опыта, просто теряется, потому что сознание человека привыкает заниматься не работой над ошибкой, а самобичеванием.

Если мы возьмем более сложную ошибку, например, выбор неподходящего партнера для брака, то тут разворачивается целое поле вариантов: как можно было бы поступить с этой ошибкой, если вообще ее так называть. Но эталон жизни готов уже заранее — большинству из нас с детства рассказали «как должно быть».

Причем чаще всего, примера того, как хорошо и комфортно жить в семье, многие не имеют — родители таких детей сами часто жили «так себе», и не преподали ребенку настоящего урока счастливой семейной жизни. И именно в результате этого родители, анализируя свои ошибки, стараются объяснить ребенку, что и как он должен в будущем делать, чтобы избежать ошибок родителей.

Казалось бы, доброе побуждение — передать опыт, научить. А на деле выходит все наоборот — ребенок усваивает шаблон, но он, вероятно, годился для самого родителя, и следует из конкретного жизненного опыта и конкретных обстоятельств.

А вот годится ли этот шаблон для ребенка — спорный вопрос, потому что ребенок — человек с другим характером, другим психотипом и, возможно, даже совсем другими целями в жизни, другим предназначением, и обстоятельства его жизни будут наверняка тоже совсем другими.

Напуганный перспективой ошибки, ребенок старается действовать по шаблону — и чаще всего проигрывает. Во-первых, потому, что действовать по шаблону не удается, ведь опыт, который усваивается прочнее — это реальный жизненный опыт, а из реального опыта у ребенка есть только родительская семья, в которой жили «так себе». И чаще всего, неосознанно, ребенка все равно заносит в тот же сценарий, который проживали и его родители.

Во-вторых, он может проиграть еще и потому, что, пытаясь действовать по шаблону, он не учитывает своих особенностей, своих настоящих желаний и своих ценностей, которые к моменту взросления уже так или иначе формируются.

И в-третьих, потому, что родители не учли возраст ребенка. Могут ли быть в 25 лет те же ценности, что в 50? Вряд ли. И поэтому передача родителями своего опыта с позиции пятидесятилетних все равно не подойдет ребенку, которому едва за двадцать. А свой реальный опыт переживаний в двадцать лет родители редко помнят, увы.

Усложняется все это той же схемой, что была и в школе: «Ошибся? А ведь мы тебе говорили!….» — следует негативная оценка и осуждение. И уже взрослый ребенок вместо извлечения опыта из ошибки идет тем же путем — самобичевания и самообесценивания.

Бывает и так, что человек сам жалеет о своих ошибках, на тему которых ему, предположим, не строили шаблонов. Причиной служит боль и другие негативные эмоции, которые он пережил. Например, сделал ошибку в работе — последовало увольнение. А работа очень нравилась, и найти такую же пока оказалось сложно. Человек мучается тем, что он «мог бы сделать так-то и так-то», и избежать последствий. Да, жалко — никто не спорит.

Но опять энергия уходит не на попытку сделать выводы о том, как больше такого не допустить, а на самобичевание, и причиной этого, скорее всего, тоже служит некий эталон, который человек мог сам себе построить — «жизнь должна проходить без неприятностей».

Мы давно уже забыли, что боль, горечь, досада и обида — в общем-то нормальные эмоции, которые человек может и должен испытывать в жизни. Боль помогает запомнить какой-то опыт. Досада помогает найти выход. Нежелание переживать горечь и вообще негативные эмоции — нормальный двигатель к тому, чтобы найти адекватное решение.

А представьте себе: вы совершили некий поступок, который привел не к тому результату, что вы себе наметили. Но вам от этого никак. Ни горячо ни холодно. Станете ли вы искать другое решение? Да нет, зачем. И вы снова наступите на те же грабли и снова вам будет «никак».

Это вообще похоже на развитие, которое есть суть жизни? Станете ли вы укреплять здоровье, если никогда не болеете? Станете ли вы строить отношения, если вы не испытываете в них никаких эмоций? Зачем, если «все хорошо», а точнее — никак, потому что «плохо» мы познаем в сравнении с «хорошо».

Другое дело, что можно испытывать негативные эмоции, а потом относительно быстро переключаться на выводы и поиск решений, а можно застревать в негативных эмоциях надолго. Как правило, именно это и происходит, и именно этого чаще всего боятся. Причиной застревания служит то, что мы привыкли все контролировать умом.

Ум строит план «как должно быть», мы стремимся к плану, а когда происходит нестыковка — то мы страшно расстраиваемся. Что с одной стороны нормально.

С другой — большинству сложно увидеть в новом развороте событий как опыт, так и возможности. Ум продолжает генерировать мысли в духе «а что я мог бы сделать тогда-то, чтобы не допустить то-то», и в итоге происходит то самое застревание в прошлом и в переживаниях. Меж тем у нас есть наше настоящее. В котором можно задать себе два простых вопроса:

Какой опыт я могу извлечь из этой ситуации, что полезного я могу почерпнуть? Какие возможности может открыть мне новый поворот событий?

Любой, даже самый грустный поворот событий может открыть возможности. Для того, чтобы их увидеть, надо сначала пережить чувства, которые вызвала ситуация — не ругать себя, не подавлять их, а принять.

Принять, что есть боль, горечь, обида или досада, тоска или отчаяние. И проживать их. Осознавать, что они есть, как они называются и выражать их. О том как выражать — мы с вами говорили в статье про эмоциональный кризис. А потом, когда пар будет выпущен — самое время задать себе те вопросы.

И всеми силами удержаться от самокопаний в ключе «ах вот если бы я тогда сказала/сделал/решилась/отказался….» Тогда было тогда. И тогда вы приняли именно то решение, которое могли принять с учетом тех реалий, того состояния души, той информации, что была и тех людей, что вас окружали. Если бы вы действительно могли бы принять другое — вы бы его приняли. Но тогда, коль скоро вы выбрали именно то решение — оно и было тем оптимальным и единственно возможным.

Один знакомый мне хирург, специализировавшийся на очень сложных операциях в области трансплантологии, выбрал своим девизом фразу «все поправимо», хотя вещи, с которыми к нему обращались пациенты, уж точно не относились к категории легко исправимых.

В жизни человека, на уровне поступков, событий и мыслей поправимо практически все. Единственное что мы не может исправить — это уход из жизни близких. Но это — то горе, которое нужно просто переживать. И жить дальше. А касательно всего остального — нет такой ситуации, из которой нельзя было бы извлечь урок, и нет таких катастроф, которые не вызвали бы новый виток развития.

Проблема лишь в нашем уме, который способен годами вызывать сокрушение по поводу того, что что-то пошло не по плану и «не идеально». И, застревая в самобичевании, многие лишают себя возможностей, опыта и конструктивных решений. Как относиться к себе и своим ошибкам — выбор каждого. Но стоит помнить:

Пока мы живы, можно всё исправить,
Всё осознать, раскаяться, простить.
Врагам не мстить, любимым не лукавить,
Друзей, что оттолкнули, возвратить.

Пока мы живы, можно оглянуться,
Увидеть путь, с которого сошли.
От страшных снов очнувшись, оттолкнуться
От пропасти, к которой подошли….

Эдуард Асадов

«Ошибка или опыт?»

https://ZerkaloDushi.org/oshibka-ili-opyt/