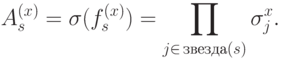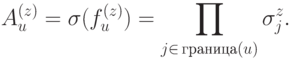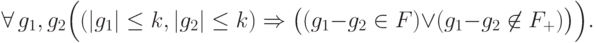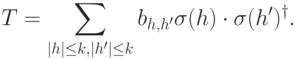Что такое синдром ошибки - Исправление ошибок и поиск оптимальных решений проблем

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ( $A$ , $B$ , $C$ , …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$ . В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$begin{aligned} A &to 0,\ B &to 1. end{aligned}$

Передача по каналу, в котором возникла ошибка будет записана так:

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$ .

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$begin{aligned} A &to 00,\ B &to 11. end{aligned}$

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

Какие выводы мы можем сделать, когда получили $01$ ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$ . А может, во втором, и была передана $A$ .

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Проверим в деле:

Получили $010$ . Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$ . Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$ .

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$ , а получили $001$ . Видно, что эта цепочка больше похожа на исходные $000$ , чем на $111$ . А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$ . Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, , так как все цифры в соответствующих позициях равны, а вот .

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
Расстояние в обе стороны одинаково.
Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$ ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$ , мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$ . Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$d_{min} geqslant 2k+1.$

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned}$

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

	A	B	C	D
A	—	3	3	4
B	3	—	4	3
C	3	4	—	3
D	4	3	3	—

Минимальное расстояние $d_{min}=3$ , а значит , откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned}$

Минимальное расстояние получилось для символа $A$ , значит вероятнее всего передавался именно он:

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned}$

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

Это свойство прямо следует из определения.

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

Математически равенство всех трёх цифр можно записать как систему:

$left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right.$

Или, если воспользоваться свойствами сложения в GF(2), получаем

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Или

$left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right.$

В матричном виде эта система будет иметь вид

где

$H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}.$

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$ ) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}.$

Соответствующая система имеет вид:

$left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right.$

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right.$

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned}$

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$a_1 x^{(1)}+a_2 x^{(2)},$

где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$(a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG.$

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned}$

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0.$

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$ , а было отправлено кодовое слово $v$ . Тогда вектор ошибки по определению

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$begin{aligned} v &= x + e,\ x &= v + e. end{aligned}$

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то . Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

И заметим следующее

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100).$

Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Торические коды.

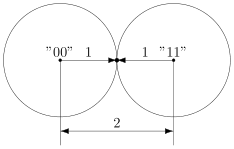
Приведем важный пример симплектического кода. Он строится так. Пусть есть квадратная решетка размера на торе. Сопоставим каждому ее ребру по q-биту. Таким образом, всего имеется n=r^2 q-битов. Проверочные операторы будут двух типов.

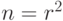
Рис.
14.1.

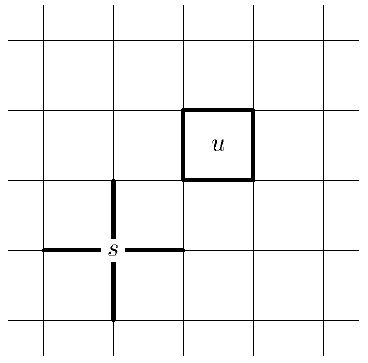
Тип I задается вершинами. Выберем некоторую вершину и сопоставим ей проверочный оператор

$A^{(x)}_s=sigma(f^{(x)}_s)=prod_{jin,mathrm {text{звезда}}(s)}^{} sigma^x_j.$

Тип II задается гранями. Выберем некоторую грань и сопоставим ей проверочный оператор

$A^{(z)}_u=sigma(f^{(z)}_u)=prod_{jin, mathrm {text{граница}}(u)}^{} sigma^z_j.$

Операторы $A^{(x)}_s$ и $A^{(z)}_u$ коммутируют, поскольку граница и звезда всегда пересекаются по четному числу ребер. (Перестановочность оператор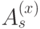ов одного типа очевидна.)

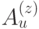
Хотя мы указали 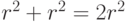проверочных операторов (по одному на грань и на вершину), между ними есть соотношения. Произведение всех $A^{(x)}$ -операторов, как и произведение всех $A^{(z)}$ -операторов, равны тождественному. Можно показать, что других соотношений нет. Поэтому , а . Поэтому торический код позволяет закодировать два q-бита. Посмотрим, чему равно кодовое расстояние для торического кода.

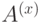
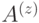
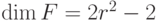
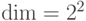
Для торического кода имеются естественные разложения

$F=F^{(x)}oplus F^{(z)},qquad F_+=F_+^{(x)}oplus F_+^{(z)}$

на подпространства, соответствующие проверочным операторам, состоящим только из 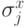, либо только из . Такие коды называются CSS кодами (по фамилиям авторов, впервые рассмотревших этот класс кодов [25, 44]). В случае торического кода элементы подпространств $F^{(z)}$ , $F_+^{(z)}$ имеют вид ; им можно сопоставить 1-цепи, т.е. формальные линейные комбинации ребер с коэффициентами . 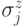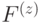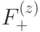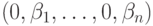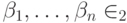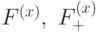Элементам подпространств $F^{(x)}_{ms}, F_+^{(x)}$ сопоставляются 1-коцепи. Рассмотрим вектор $f^{(z)}_uin F^{(z)}_{ms}$ , отвечающий грани с номером . Ему будет сопоставлена 1-цепь, являющаяся границей этой грани. Легко видеть, что пространство $F^{(z)}$ состоит из всех 1-границ. Аналогично, векторам $f_s^{(x)}$ будут сопоставляться 1-кограницы, порождающие все пространство 1-кограниц.

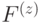
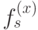
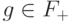
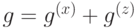
Возьмем произвольный элемент gin F_+ , $g=g^{(x)}+g^{(z)}$ . Условия коммутирования запишутся следующим образом:

$begin{multiline} omega(f_s^{(x)},g)=0quad Longleftrightarrowquad omega(f_s^{(x)},g^{(z)})=0, \ omega(f_u^{(z)},g)=0quad Longleftrightarrowquad omega(f_u^{(z)},g^{(x)})=0. end{multiline}$

Чтобы выполнялось 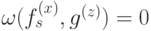$omega(f_s^{(x)},g^{(z)}_{ms})=0$ , нужно, чтобы в любой звезде было четное число ребер с ненулевыми весами из $g^{(z)}$ . Другими словами, $g^{(z)}$ — это 1-цикл (с коэффициентами в ZZ_2 ). Аналогично, $g^{(x)}$ должен быть 1-коциклом.

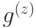
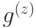
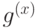
Итак, пространства 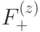$F_+^{(z)}$ , $F_+^{(x)}$ состоят из 1-циклов и 1-коциклов, а пространства $F^{(z)}$ , $F^{(x)}$ состоят из 1-границ и 1-кограниц. Следовательно, кодовое расстояние есть минимальная мощность (количество ненулевых коэффициентов) по циклам, не являющимся границами, и коциклам, не являющимся кограницами. Легко видеть, что этот минимум равен (нужны либо цикл, либо разрез, не гомологичные 0). Это означает, что торический код исправляет ошибок.

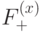
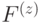
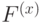
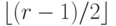
Будем обозначать коды описанного вида через TOR(r) .

Замечание. Торические коды являются очень важным примером, обладающим рядом замечательных свойств. В частности, это коды с локальными проверками. Последовательность кодов называется кодами с локальными проверками, если выполнены следующие условия:

каждый проверочный оператор действует на ограниченное константой число q-битов;
каждый q-бит входит в ограниченное константой число проверочных операторов;
кодовое расстояние неограниченно возрастает.

Такие коды представляют интерес для задачи построения вычислительных схем, устойчивых к ошибкам. При исправлении ошибок могут происходить новые ошибки. Но для кодов с локальными проверками схемы исправления ошибок имеют фиксированную глубину, поэтому одна ошибка при работе такой схемы портит ограниченное число q-битов.

Процедура исправления ошибок.

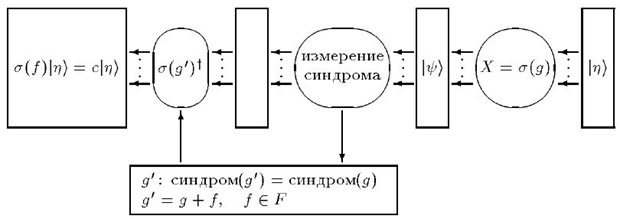
Определение 14.6 и теорема 14.2 указывают только на принципиальную возможность восстановить исходное состояние системы после действия ошибки. На примере симплектических кодов покажем, как реализовать процедуру исправления ошибки.

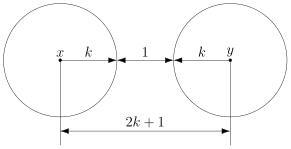
Рассмотрим частный случай, к которому все сводится. Пусть имеются две ошибки, заданные операторами , . Тогда ( |c|=1 ). Назовем синдромом ошибки g_1 вектор (для g_2 — аналогично).

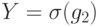
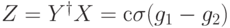
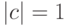
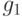
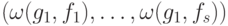
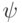
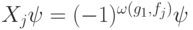
Возьмем вектор . Обозначим . Проверочные операторы действуют на ketpsi так: $X_jketpsi=(-1)^{omega(g_1,f_j)}ketpsi$ . Поэтому, измеряя собственные числа X_j на состоянии , можно измерить синдром.

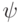
Рис.
14.2.

Если кодовое расстояние равно , то выполнено

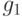
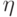
Условие означает эквивалентность ошибок g_1 и g_2 , т.е. для любого вектора keteta из кодового подпространства. Условие равносильно тому, что синдромы ошибок g_1 и g_2 не совпадают. Итак, либо ошибки эквивалентны, либо их можно различить по синдрому. Следовательно, по синдрому можно определить ошибку с точностью до эквивалентности, т.е. по модулю подпространства .

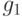
Теперь ясно, как нужно исправлять ошибку. После того как определен синдром, применим оператор, обратный к оператору восстановленной по синдрому ошибки. Получим состояние, отличающееся от исходного лишь на фазовый множитель. Вся процедура изображена на рис. 14.2.

Выше рассмотрен случай ошибки типа 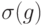. На самом деле ошибка состоит в действии преобразования матриц плотности вида

$T=sum_{|h|leq k,|h'|leq k}^{} b_{h,h'} sigma(h)cdotsigma(h')^dagger.$

В качестве упражнения читателю предлагается проверить, как работает приведенная выше схема в случае такого общего преобразования матриц плотности.

Задача 14.6. Постройте полиномиальный алгоритм определения ошибки по синдрому для торического кода.

Источник

Возможно, вы только что узнали о своей беременности. Врач говорит, что скоро нужно будет пройти какой-то скрининг, а еще давным-давно вы читали статью о том, что на свете есть особые дети, и вот именно сейчас в сердце закралась тревога.
А может быть, вы уже сделали скрининг, и врач говорит, что у малыша, скорее всего, синдром Дауна. Что делать дальше? Какие еще исследования пройти?
Или же вы только планируете беременность и вас растревожили сообщениями о том, что есть такая «болезнь» – синдром Дауна. Поневоле возникают мысли: вдруг и у нас будет такой малыш?
Кто бы вы ни были, эта статья – для вас. Надеемся, она поможет вам сориентироваться в вопросах пренатальной диагностики и даст понимание, куда двигаться дальше.

Что такое пренатальная диагностика?

Во время беременности каждой женщине предлагают пройти комплексную диагностику. С ее помощью можно определить, могут ли у будущего малыша быть проблемы со здоровьем или генетические отклонения, в том числе синдром Дауна. Эти исследования дают информацию, которая помогает семье принять взвешенное решение о судьбе своего будущего ребенка.
Очень важно вовремя встать на учет по беременности, для того чтобы не пропустить важные исследования, так как все они проводятся на определенных сроках беременности.
Выделяют два типа пренатальной диагностики: скрининговую и подтверждающую. Само слово «скрининг» переводится как «просеивание», потому что это массовое исследование – все беременные женщины могут пройти его бесплатно, в рамках финансирования ОМС.
Скрининговые тесты помогают определить группу будущих мам, у которых есть высокая вероятность развития хромосомных отклонений у плода, – в этом случае назначаются дополнительные подтверждающие исследования.
Одновременно с этим анализы выявляют те беременности, для которых повышенной угрозы нет. В этом случае их результаты отрицательные, и необходимости в дополнительных исследованиях (кроме скринингов, проводимых 1 раз в триместр) – нет.
Первый скрининг при беременности проводят между 11 и 13 неделями. Исследование включает в себя УЗИ и анализ крови.
Второй скрининг при беременности проводят на сроке 18–20 недель. В него включены те же два этапа – УЗИ и анализ крови, однако последний сдается только в том случае, если женщина не делала первый скрининг.
Третий скрининг при беременности проводят на 30–34 неделе. Основа третьего скрининга – УЗИ, основная цель которого – определить стратегию родов.
По результатам скринингов в случае необходимости могут назначаться дополнительные исследования.

Как понять, возможен ли у будущего ребенка синдром Дауна?

Есть несколько методов пренатальной диагностики, которые могут дать ответ, родится малыш с синдромом Дауна или нет. Они бывают неинвазивными и инвазивными. Анализ крови и УЗИ – это неинвазивные методы, т.к. их проведение не требует особого вмешательства в организм матери. Никакого риска для будущего ребенка они не несут. Но их результатам далеко не всегда можно доверять. Если вам по результатам УЗИ сказали, что у малыша возможен синдром Дауна, – не воспринимайте это как окончательный диагноз. Это лишь сигнал, что желательно провести дополнительные инвазивные исследования. Их смысл – получить для исследования клетки самого плода. Врачи-генетики, рассматривая эти клетки в микроскоп, смогут увидеть в них лишнюю хромосому и тогда уже поставить точный диагноз – есть ли у будущего малыша синдром Дауна или нет.
Как получить клетки эмбриона? Они есть в околоплодных водах. Чтобы их исследовать, нужно сделать прокол оболочки околоплодного пузыря. Такая медицинская процедура, к сожалению, бывает довольно дискомфортна для мамы, а кроме того, она может быть опасной и для малыша, ведь в результате ее проведения возрастает вероятность выкидыша.
Дальше мы подробнее ответим на вопросы о каждом методе пренатальной диагностики.
Первый скрининг предлагают пройти в первом триместре, в период с 11 до 13 недель и 6 дней беременности. У будущей мамы берут кровь для анализа (измеряют уровень определенных биологических маркеров) и делают УЗИ (оценивают анатомию плода). В результате врач может понять, есть ли у плода риск каких-то болезней и отклонений, в том числе синдрома Дауна. Обратите внимание: результат первого скрининга – это только оценка рисков, а ни в коем случае не окончательный диагноз! Это лишь первое предположение, что, возможно, что-то может пойти не так. По статистике, ребенок с синдромом Дауна появляется лишь в одном из 150 случаев «беременности высокого риска».

Что оценивает врач в процессе первого скрининга, чтобы не пропустить синдром Дауна?

Врач во время УЗИ визуально оценивает некоторые показатели: в первую очередь, есть ли у плода увеличенная воротниковая зона и гипоплазия (укороченность, недоразвитие) носовой кости. Подробнее про определение толщины воротникового пространства вы можете прочитать по ссылке. Если коротко, то на задней поверхности шеи любого малыша есть скопление подкожной жидкости, но у многих детей с синдромом Дауна ее количество сильно увеличено. Понятно, что этот показатель не может говорить о точном диагнозе «синдром Дауна», – он лишь помогает определить, нужно ли назначить более глубокие исследования. Что касается гипоплазии носовой кости (уменьшение размеров косточки носа), то этот показатель тоже выступает лишь сигналом о возможных проблемах.
Кроме УЗИ плода, скрининг включает в себя и анализ крови матери. Врач обращает внимание на значения белков материнской сыворотки. При этом он также учитывает такие факторы, как возраст матери (чем она старше, тем риск больше) и историю беременностей (если таковые уже были). Результаты УЗИ и анализа крови врач анализирует комплексно – так результаты будут точнее.

Если первый скрининг показал, что повышен риск рождения ребенка с синдромом Дауна, – что делать дальше?

Может оказаться, что беременная женщина по результатам скрининга попадает в так называемую группу риска. Это сигнал, что желательно провести дальнейшие исследования, чтобы точно установить диагноз. На данном этапе важно, какую позицию занимает консультирующий врач. Именно он должен объяснить женщине и ее семье ситуацию и риски, правильно сориентировать и помочь выбрать тактику дальнейших действий. Кто-то из беременных этой группы предпочитает оставить всё как есть, не проводить дополнительных исследований и ожидать рождения малыша, а кто-то соглашается на инвазивную процедуру.

Что такое инвазивная процедура? Это опасно?

Инвазивная процедура – это метод, позволяющий с высокой степенью точности ответить на вопрос: есть у малыша синдром Дауна или нет. Инвазивные тесты позволяют практически в 99 % случаев выявить хромосомные аномалии у плода.
Существует несколько инвазивных процедур, из которых самые распространенные – биопсия ворсин хориона и амниоцентез. Подробно о каждом из них вы можете прочитать по ссылкам ниже, а здесь мы обозначим их сущность вкратце.
Для проведения амниоцентеза
из матки женщины берется для исследования образец околоплодной жидкости. Зачем это делается? Дело в том, что в этой жидкости находятся клетки эмбриона, т.е. врач через микроскоп видит клетки будущего ребенка и может определить, есть ли в них дополнительная хромосома, которая говорит о наличии синдрома Дауна.
Биопсия ворсин хориона (БВХ) – это анализ эмбриональной ткани (хориона). Процедура похожа на амниоцентез и тоже предполагает прокол стенки матки. В отличие от амниоцентеза, биопсию хориона проводят несколько раньше по срокам.
Решение о том, делать ли инвазивные исследования, могут принять только сами будущие родители, т.к. эти процедуры сопровождаются риском выкидыша.

Что такое «тест на синдром Дауна по крови»?

Так иногда называют новый метод неинвазивного пренатального тестирования (НИПТ). Это анализ крови матери, но не тот, который делают при обычном скрининге. Дело в том, что в конце XX века ученые обнаружили, что в крови беременной женщины обязательно есть фрагменты ДНК ее будущего ребенка – так называемая внеклеточная ДНК. Суть НИПТа проста – эта внеклеточная ДНК выделяется из крови матери и затем «читается» с помощью сложных компьютерных программ. Этот метод тестирования сейчас активно развивается, и у него очень высокая точность – до 99 % и даже более.

Если этот анализ дает такой точный результат, почему его не делают всем?

Основная причина в том, что НИПТ – довольно дорогостоящий анализ. Кроме того, одни лаборатории имеют необходимое для него оборудование (сложное и очень дорогостоящее), а другие выступают как посредники, которые отсылают биоматериал для проведения анализа за границу.
К тому же НИПТ является скрининговым методом, и в случае выявления высокого риска хромосомной патологии у плода всё равно потребуется проведение уточняющей инвазивной диагностики.

Если я сделаю НИПТ, какие возможны варианты действий дальше?

Ситуации возможны разные.
Если у женщины отрицательный результат по НИПТ, это говорит о низких рисках с вероятностью до 97 %, но не исключает синдром Дауна полностью. Поскольку НИПТ – это неинвазивный тест (для него не используют ни биопсию ворсин хориона, ни амниоцентез), то, несмотря на статистическую точность, следует иметь в виду, что это всё-таки расчетные, а не объективные данные.
Если по предыдущим неинвазивным скринингам риск наличия синдрома Дауна выше, чем 1:100, НИПТ не показан, поскольку в этом случае также не стоит надеяться на расчетные данные. Велика вероятность ошибки: возможны не только ложноотрицательные, но и ложноположительные результаты, что повлечет за собой опасность избавиться от здорового плода.
Еще одна сложность при использовании НИПТ заключается в следующем: если тест проводился после 12 недель беременности и показывает положительный результат – это не будет считаться основанием для перывания беременности. В таком случае для принятия решения всё-таки придется сделать инвазивный тест.
С другой стороны, результаты НИПТ достаточно точные, и в тех случаях, когда предыдущие неинвазивные тесты показывают риск ниже, чем 1:100, женщина для собственного спокойствия может пройти это исследование.

Можно ли отказаться от всех скринингов и исследований?

Да, можно. Будущей маме лишь рекомендуется сделать скрининг – обязанности у нее нет. Врач не может заставить вас делать те или иные тесты и анализы.

Зачем мне заранее знать, будет ли у моего ребенка синдром Дауна или нет?

Все решения, которые касаются судьбы будущего ребенка, принимают исключительно его родители. Ни ваш гинеколог, ни генетик, ни родственники – никто не имеет права склонять вас к тому или иному решению. Но при этом семье очень важно владеть достоверной информацией. Зная, что у будущего малыша, вероятнее всего, синдром Дауна, родители могут поступить по-разному. Кто-то принимает решение о прерывании беременности. Кто-то старается узнать побольше о синдроме, чтобы подготовиться к рождению особого малыша и сразу оказать ему необходимую помощь – и медицинскую, если это нужно, и педагогическую. Кто-то ищет и находит семьи, в которых растут дети с синдромом Дауна, знакомится с ними, общается, заранее занимается поиском профильных организаций и получает там полезную информацию и поддержку. В таком случае рождение особого ребенка не становится для семьи неожиданным ударом, а остается запланированным и таким же долгожданным событием, как рождение любого ребенка, – просто уже с учетом его особенности. Знание о диагнозе малыша помогает будущим родителям перестать жить в пассивной тревоге и отчаянии: ведь когда ты знаешь, чего ожидать, ты можешь начать действовать.

У кого больше всего вероятность родить ребенка с синдромом Дауна?

Ребенок с синдромом Дауна может появиться в любой семье. В данном случае не имеют значения ни социальное положение родителей, ни их состояние здоровья, ни экономическое благополучие, ни национальность, ни место проживания, ни что-либо другое. Единственное, что считается фактором риска для рождения ребенка с синдромом Дауна, – это возраст матери. Чем старше женщина, тем выше вероятность, что у нее может появиться ребенок с синдромом Дауна. Поэтому женщинам старше 35 лет настоятельно рекомендуется проходить пренатальную диагностику. Впрочем, не стоит забывать о том, что дети с синдромом Дауна рождаются у женщин любого возраста.

Можно ли еще до наступления беременности узнать, есть ли вероятность генетических нарушений у будущего ребенка?

В подавляющем большинстве случаев синдром Дауна – это генетическая случайность, но бывают случаи сбалансированной хромосомной перестройки (транслокация, инверсия) или мозаичный кариотип (наличие клеточного клона с аномальным числом хромосом) у кого-либо из родителей. Их поможет обнаружить генетическое исследование

Врач предлагает мне сделать аборт, потому что у малыша синдром Дауна. Он прав?

Еще раз подчеркнем, что решение о судьбе будущего ребенка могут принимать только его родители. Никто не имеет права склонять вас к прерыванию беременности. Единственная задача специалистов, будь то гинеколог, генетик, психолог и т.д., – дать вам достоверную информацию: рассказать обо всех возможных трудностях и радостях жизни с особым ребенком и показать возможные пути действий – ведь у родителей всегда есть возможность выбора. К сожалению, до сих пор многие врачи не могут избежать оценочных высказываний; в ряде случаев они могут навязывать будущим родителям свою точку зрения, рассказывая о жизни с ребенком с синдромом Дауна только с негативной стороны. Знайте, что такие врачи нарушают этические нормы своей профессии! В целом ряде российских регионов существуют официальные протоколы сообщения диагноза ребенка будущим родителям, которые запрещают врачам склонять семью к проведению аборта и оказывать психологическое давление. Если врач убеждает вас сделать аборт, а вы этому сопротивляетесь, – смело меняйте врача!
Мы надеемся, что эта краткая информация в форме ответов на самые частые вопросы, которые задают родители, поможет вам разобраться в тех тестах, которые вы уже прошли или только собираетесь пройти.

Источник

Раньше навыки письма формировались в начальной школе, сейчас – с пяти-шести лет. Если к третьему классу ребенок до сих пор не овладел письменной речью, диагностируется дисграфия. Мы выясним, что это такое, почему возникает и как помочь малышу справиться с этим нарушением.

Что такое дисграфия

Этим термином обозначают расстройство навыков письма, обусловленное недостаточной сформированностью высших психических функций. Ребенку трудно соотнести звуки устной речи с начертанием букв.

Нередко одновременно с дисграфией диагностируется дислексия – нарушение способностей к приобретению навыков чтения.

Проблемы с письмом – это не вина малыша, хотя взрослые из-за недостатка информации списывают это на лень или баловство. Причина всегда кроется в неврологических отклонениях, следовательно, не зависит от воли пациента.

Дисграфия может проявиться в любом возрасте. Разница – в том, врожденная она или приобретенная. В первом случае у человека от рождения нарушены навыки чтения, и их нужно формировать буквально с нуля. Во втором такие навыки в детстве достаточно развились, но после поражения головного мозга были утрачены.

Классификация

Логопеды-дефектологи и неврологи предлагают различные классификации. Чаще всего формы дисграфии выделяют на основе характера и природы ошибок, которые делает ребенок или взрослый:

Артикулярно-акустическая. За неправильным написанием стоит неправильное произношение.
Оптическая. Вызвана расстройством зрительного восприятия начертания букв.
Базирующаяся на нарушениях фонемного распознавания. Больной не может распознать буквы на слух.
Связанная с нарушением функция языкового анализа. Пациент не различает, где заканчивается одно слово и начинается другое.
Аграмматическая. Связана с недостаточным владением лексическими конструкциями (согласованием падежей, спряжений).

Нередко при обследовании выявляются признаки сразу нескольких форм. Такую дисграфию определяют как смешанную.

Стадии развития

Расстройство навыков письменной речи не всегда проявляется в полной мере. Сначала близкие замечают незначительные ошибки, потом они становятся все более существенными. На первой стадии человек заменяет буквы, сходными по звучанию (глухие – звонкими и наоборот), пропускает мягкие знаки. Нарушение легко спутать с недостатком орфографических знаний.

На средней стадии отклонения становятся более очевидными:

подменяемые буквы более ощутимо отличаются друг от друга по звучанию;
больной пропускает отдельные буквы, которые невозможно не услышать;
некоторые слова сливаются воедино.

На последней стадии замена букв логически не объяснима. Нарушается их порядок, появляются лишние гласные, опускаются служебные части речи.

Причины дисграфии

Такие отклонения, как дисграфия и дислексия, не являются результатом низкого интеллекта. Известны случаи, когда взрослые, имеющие подобные нарушения, добивались успеха в разных областях.

Основными причинами неовладения письменной речью в младшем школьном возрасте являются:

внутриутробные инфекции;
родовые травмы;
кислородное голодание;
соматические заболевания, повлекшие неоднородность развития мозговых центров;
неравномерное развитие психических функций.

Дисграфия и дислексия у взрослых обычно провоцируются очаговым поражением речевых зон. Оно, в свою очередь, вызывается черепно-мозговыми травмами, хирургическими вмешательствами, перенесенными инсультами, опухолевыми процессами.

Единственная причина, напрямую не связанная не неврологическими отклонениями – это билингвизм. Ребенок путается в двух различных языковых системах и подменяет элементы. Такая дисграфия чаще всего бывает смешанной.

Причины, связанные с вовлечением анализаторов в процесс письма

Другой подход к обоснованию природы нарушения навыков письма основан на выявлении дисфункций задействованных анализаторов. Повлиять могут следующие группы:

Зрительно-пространственные. Человек не способен правильно воспринимать образы букв. Это заметно по плохому почерку, не связанному с нарушением моторики, и отсутствию минимальных навыков рисования.
Акустические. Нарушен процесс переработки слухоречевой речи. Дополнительный признак – неразличение интонаций.
Моторные. Функционирование нервной системы не синхронизировано с двигательной активностью. Человек пишет медленно, неразборчиво, не способен быстро постукивать пальцами.

Встречается также регуляторная дисграфия. В этом случае действия человека становятся инертными, не соответствующими заданной программе. Ему сложно провести серию движений по написанию фрагмента текста.

Симптомы

Симптомы различаются в зависимости от формы нарушения. Каждой из них присущи особые виды ошибок.

Форма дисграфии	Ошибки-симптомы
Артикулярно-акустическая	невыговаривание отдельных звуков; замена их более простыми на письме; пропуск букв, обозначающих труднопроизносимые звуки.
Оптическая	пропуск целых букв или их отдельных элементов; зеркальное начертание; невозможность визуально определить количество букв.
Базирующаяся на нарушениях фонемного распознавания	письмо по услышанному; неразличение звонких и глухих, твердых и мягких согласных; отсутствие мягких знаков.
Связанная с нарушением функция языкового анализа	раздельное написание частей слова; слитное написание нескольких слов; добавление лишних букв; многократное повторение слогов.
Аграмматическая	трудности со словообразованием; неправильное употребление падежей и спряжений; трудности с подбором окончаний слов.

Диагностика

Первичная диагностика у детей проводится школьным логопедом, который, в свою очередь, получает сигнал от учителей или родителей. Его задача – оценить, как протекают фонематические процессы:

различаются ли звуки на слух;
восприимчив ли ребенок к близким по звучанию словам;
воспринимаются ли им последовательности звуков;
способен ли он подсчитать количество звуков в слове;
имеются ли у него звуковые образы слов.

Обязательно нужно посетить окулиста и отоларинголога. Они помогут разграничить расстройства восприятия от нарушений зрения и слуха.

Окончательный диагноз ставит невролог. Он выясняет, какого рода отклонения послужили причинами дисграфии, и предлагает подходящую схему их коррекции.

Лечение

Дисграфия у детей школьного возраста непосредственному лечению не поддается. Исходные причины устранить невозможно. Однако коррекция симптомов вполне реальна. Программы занятий составляет логопед или нейропсихолог. Они могут дополняться:

Медикаментозной поддержкой. Ноотропные препараты стимулируют мозговую активность, в частности улучшают память и активизируют пораженные речевые зоны.
Физиотерапией. Транскраниальная микрополяризация помогает наладить взаимодействие между участками мозга, участвующими в речевой деятельности.
Остеопатическим лечением. Эффективно при оптической дисграфии, вызванной родовой травмой.

У взрослых причины расстройства навыков письма отличаются. Поэтому коррекция проводится в рамках общей программы реабилитации. Конкретные методы зависят от особенностей поражения мозга.

Упражнения для коррекции

Известно много инструментов для отработки нарушенных навыков письма в условиях поражения мозга. Для каждой формы дисграфии есть свои программы. Отдельно разрабатываются схемы для случаев, когда она сочетается с дислексией.

Упражнения могут быть направлены на:

фонемное распознавание звуков, слогов, слов;
узнавание сходных элементов букв;
поиск различий в начертании букв;
постановку правильного произношения звуков;
отработку навыков языкового анализа и синтеза;
развитие связности речи.

Если проблемы оптического характера, занятия в большей степени ориентированы на формирование зрительного восприятия слов, букв и их элементов, если акустического – на восприятие и распознавание звуков. В случае, когда затруднения в начертании букв вызвано нарушением мелкомоторной координации, полезны упражнения на ее развитие.

Как помочь ребенку с дисграфией адаптироваться в школе

В младшем школьном возрасте трудности с письмом вызывают у ребенка значительное психическое напряжение. Учителей необходимо предупредить об этой особенности во избежание усиления давления.

Для облегчения процесса обучения стоит разработать индивидуальный образовательный маршрут, который может предполагать:

увеличение времени на выполнение письменных заданий;
разбивку больших текстов на несколько маленьких;
отсутствие строгих требований к почерку;
возможность давать ответы устно.

Если школьник занимается по общей программе, ему понадобятся некоторые послабления. Таковым может стать разрешение не записывать материал урока полностью. Родителям на этот случай придется купить диктофон, чтобы ребенок не отставал.

Профилактика

Никто не застрахован от родовой травмы или кислородного голодания. Однако степень развитости высших психических функций ребенка во многом зависит от стараний родителей. Первые меры принимаются задолго до того, как малыш начнет писать:

развитие мелкой моторики;
тренировки памяти и внимания;
отработка навыков пространственного мышления;
расширение словарного запаса.

Крайне важно общение. Гаджеты не заменят малышу живого разговора. Совместное времяпрепровождение за словесными играми, чтением или интересными историями лучше всего способствует формированию речевых навыков.

Внимательные родители замечают отклонения на начальной стадии. Не стоит откладывать посещение логопеда. Чем раньше начнется коррекция, тем больше у малыша шансов приспособиться к своим особенностям и научиться писать. В этом помогут книги О.В. Чистяковой, О.И. Азовой, Е.В. Мазановой и других специалистов.

Источник