From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
Систематическая ошибка
- Систематическая ошибка
-
Систематическая ошибка [systematic error] — понятие математической статистики: ошибка, которая постоянно либо преувеличивает, либо преуменьшает результаты измерений (оценок наблюдаемых величин) вследствие воздействия определенных факторов, систематически влияющих на эти измерения и изменяющих их в одном направлении (например., в отличие от случайных ошибок). Оценки, лишенные систематических ошибок, называются несмещенными оценками.
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело.
.
2003.
Смотреть что такое «Систематическая ошибка» в других словарях:
-
систематическая ошибка — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] систематическая ошибка Понятие математической статистики: ошибка, которая постоянно либо преувеличивает, либо преуменьшает результаты измерений (оценок наблюдаемых величин)… … Справочник технического переводчика
-
систематическая ошибка — Systematic Error Систематическая ошибка Систематическая ошибка измерения это ошибка (погрешность) всегда только преувеличивающая или всегда только преуменьшающая результат измерения, стабильно, устойчиво искажающая его истинные значения.… … Толковый англо-русский словарь по нанотехнологии. — М.
-
Систематическая ошибка отбора — статистическое понятие, показывающее, что выводы, сделанные применительно к какой либо группе, могут оказаться неточными вследствие неправильного отбора в эту группу. Содержание 1 Ошибки отбора результатов 2 … Википедия
-
Систематическая ошибка выжившего — (англ. survivorship bias) разновидность систематической ошибки отбора, когда по одной группе («выжившим») есть много данных, а по другой («погибшим») практически нет. Поэтому исследователи пытаются искать общие черты среди… … Википедия
-
систематическая ошибка (измерения) — вносить систематическую ошибку — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы вносить систематическую ошибку EN bias … Справочник технического переводчика
-
систематическая ошибка смещения — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN bias error … Справочник технического переводчика
-
Систематическая ошибка измерений, вызванная влиянием пола (sex bias in measurement) — С. о. и. имеет место в тех случаях, когда группы реагируют по разному на задания в тестах достижений, интеллекта или способностей, либо в др. измерительных инструментах, таких как опросники интересов. С. о. и., вызванная влиянием пола, имеет… … Психологическая энциклопедия
-
Систематическая ошибка тестов, обусловленная культурными факторами (cultural bias in tests) — Между разными соц. и расовыми группами наблюдаются существенные различия в средних значениях оценок по стандартизованным тестам умственных способностей, широко применяемым при приеме в школы и колледжи, наборе в вооруженные силы и найме на работу … Психологическая энциклопедия
-
систематическая ошибка результата (проверки) — 3.10. систематическая ошибка результата (проверки) Компонент ошибки результата, который остается постоянным или закономерно изменяется в ходе получения результатов проверки для одного признака. Примечание Систематические ошибки и их причины могут … Словарь-справочник терминов нормативно-технической документации
-
СИСТЕМАТИЧЕСКАЯ ОШИБКА — См. постоянная ошибка. СИСТЕМАТИЧЕСКИЙ. 1. Характеризующийся отражением структуры и организационной целостности системы (1). 2. Определяемый конкретной теоретической системой (2). 3. В более широком смысле – организованный, предсказуемый,… … Толковый словарь по психологии
Систематические
ошибки — это ошибки, постоянные для всего
ряда измерений или изменяющиеся по
определенному закону. Влияние их на
результаты эксперимента определяется
и исключается опытным путем на основе
установленных знаний их природы и
способа учета. Эксперимент здесь играет
решающую роль, в отличие от оценки
случайных ошибок, к изучению которых
мы подходим статистически, когда
эксперимент служит для набора совокупности
таких ошибок, по которой составляем
статистические оценки.
2.9.1. Классификация систематических ошибок
По
источнику происхождения систематические
ошибки можно разделить на следующие:
а)
приборные ошибки (см. рис.2.3),
б)
ошибки установки аппаратуры,
в)
личные ошибки, вызванные личными
особенностями наблюдателя,
г)
ошибки метода, вызванные неполным
знанием объекта измерения и условий
наблюдений, а также принятой теоретической
моделью.
По
характеру влияния систематические
ошибки подразделяются на два класса:
постоянные и переменные.
Переменные
в свою очередь подразделяются на
прогрессивные, периодические ошибки и
ошибки, изменяющиеся по сложному закону.
Постоянные
ошибки суть систематические ошибки,
сохраняющие свой знак и значение в
течение всего процесса измерения
(например, ошибка МО при измерении снимка
на СК).
Прогрессивные
ошибки — это такие ошибки, которые при
измерениях изменяются по линейному
закону, в зависимости от размера величины
и влияния фактора. Например, температурное
влияние на измерительный винт СК:
L = l (1 +t
)
мм. Отсюда ошибка
= l
t,
где
l
— отсчет,
-коэффициент линейного расширения,
t.-
изменение температуры.
v
Q
l
l0
L
t
Рис.
2.1. Истинная
и вероятная v ошибки
t
1
2
a
b
Рис.2.2.
Случайная и систематическая ошибка
значение
порога
реагирования
mV
20
10
времяhtvz
1
2
Рис.2.4.
Влияние чувствительности
приемника
шкала
x
шкала
y
измеряемый
отрезок
Рис.2.5.
Суть принципа Аббе
`S
A
P
f
Рис.
2.6. Влияние скорости носителя АФА
1
2
глаз
объект
марка
а
f(Q)
f0(Q)
(Q)
Q
f0(Q)
f0(Q)
f0(Q)
f(Q)
f(Q)
f(Q)
f(Q)
а
а
а
а
а
а
г
в
ба
(Q)
млт
адд
д
Q
Q
Q
Q
об.хд
стат
f(Q)
f(Q)
Рис.2.3.
Составляющие систематической ошибки
СИ
p
p
p=1
. p=1
.30
. 30
____
.25
. 20 ____
____
.
. . 15 ____
____
.10
. . p1 p2
p3 p4 p5
__________________________
_____________________________
1
2 3 4 5 1 2 3
4 5
Рис.3.1.
Графики распределения вероятностей:
а- многоугольник
распределения;
б — гистограмма
p
F(x)
1
. . . . . . . . .. ___ 1.00
____
____
.85 ____
p1+p2+p3
_____ .65 _____
p1+p2
_____ .35 _____
p1
_____ .15_____
___________________________
___________________________
1
2 3 4 5 1 2 3 4 5
Рис.3.2.
Графики распределения кумулятивной
вероятности (функции
распределения):
а — дискретной СВ, б — непрерывной СВ
f(xj)
f(x)
_________________________
___________________________
1
2 3 4 5 1 2 3 4
5
распределения):
а — дискретной СВ, б — непрерывной СВ
f(xj)
f(x)
_________________________
___________________________
1
2 3 4 5 1 2 3 4 5
Рис.3.3.
Графики функций плотности вероятности:
а — дискретной СВ
(не
используется), б — непрерывной СВ
Соседние файлы в папке Коршунов
- #
26.04.201531.23 Кб14NORMDIS.XLS
- #
26.04.201542.5 Кб14АнализИдемпотМТР к МО1Анализ.xls
- #
- #
- #
- #
- #
- #
Справочник /
Термины /
Механика /
Систематические ошибки
Термин и определение
Систематические ошибки
Опубликовано:
viktoriia.semenova.88
Предмет:
Механика
👍 Проверено Автор24
ошибки, сохраняющиеся при повторных измерениях; причины их различны: а) погрешность прибора (например, стрелка амперметра не стоит на нуле при отсутствии тока); б) отсутствие учета влияния внешних факторов (например, взвешивание тела без учета действия на него выталкивающей силы воздуха); систематические ошибки учитывают поправками.
Научные статьи на тему «Систематические ошибки»
1.
Статистические характеристики
Классификация ошибок:
За характером ошибки различают:
случайные ошибки, те которые вызываются любыми…
Случайные ошибки не особо влияют на весь результат;
систематические ошибки, искажают явление только в…
одну из сторон более опасные и, иногда, вызывают действие систематического фактора….
За стадией возникновения:
ошибки при регистрации;
ошибки во время подготовки данных к обработке;
ошибки…
Все специальные ошибки являются систематическими.
Статья от экспертов
2.
О систематических ошибках повторных измерений
Рассмотрен вопрос обнаружения систематических ошибок путем сравнения результатов оценки точности измерений до уравнивания, по разностям двойных измерений и после уравнивания с использованием доверительного оценивания.
3.
Содержательные выборочные методы определения ожидаемой ошибки в аудите
Методы определения ожидаемой ошибки в аудите
Определение 1
Ожидаемая ошибка выборки — это значение…
ошибки в бухгалтерском учете, которое аудитор еще до начала аудиторской проверки хочет обнаружить в…
совокупностей со случайными и равновозможными ошибками….
Систематические ошибки – это ошибки, которые произошли неслучайно, т.е. ошибки которые появились в связи…
На появление систематических ошибок влияют 2 причины.
Статья от экспертов
4.
Алгоритм обработки измерений, устойчивый к систематическим ошибкам
Рассматривается задача оценивания характеристик случайного процесса по дискретным измерениям. Полагается, что измерения содержат кусочно-непрерывные помехи, имеющие конечное число разрывов первого рода на всем отрезке наблюдения и описываемые на интервалах непрерывности степенными полиномами со случайными коэффициентами.
Повышай знания с онлайн-тренажером от Автор24!
- 📝 Напиши термин
- ✍️ Выбери определение из предложенных или загрузи свое
-
🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных
карточек
Когда исследователи рассматривают вопросы, представляющие интерес для аналитиков или портфельных менеджеров, они могут исключить из анализа определенные акции, облигации, портфели, или периоды времени, по разным причинам — возможно, из-за недоступности данных.
Когда недоступность данных приводит к исключению из анализа определенных активов, мы называем эту проблему систематической ошибкой или смещением выборки (англ. ‘sample selection bias’ или ‘sampling bias’).
Например, вы можете сделать выборку из базы данных, которая отслеживает только компании, существующие в настоящее время. Например, многие базы данных взаимных фондов предоставляют историческую информацию только о тех фондах, которые существуют в настоящее время.
Базы данных, в которых хранятся балансовые отчеты и отчеты о прибылях и убытках страдают от той же систематической ошибки, что и базы данных фондов: в них нет фондов или компаний, которые прекратили деятельность.
Исследование, которое использует подобные базы данных, подвержено разновидности систематической ошибки выборки, известной как систематическая ошибка выжившего (англ. ‘survivorship bias’).
Исследователи Димсон, Марш и Стонтон (Dimson, Marsh, and Staunton, 2002) подняли вопрос о систематической ошибке выжившего в международных финансовых индексах:
Известной проблемой является влияние выживания рынков на долгосрочную оценку доходности. Рынки могут испытывать не только разочаровывающие результаты, но и полную потерю стоимости за счет конфискации, гиперинфляции, национализации и кризисов.
При оценке результатов рынков, которые выживают в течение длительных интервалов времени, мы сделали выводы о том, чем обусловлено выживание. Тем не менее, как отметили в исследовании Браун, Готцман и Росс (Brown, Goetzmann, и Ross) в 1995 г. и Готцман и Джорион (Goetzmann and Jorion) в 1999 г., человек не способен заранее определить, какие рынки выживут, а какие нет. (стр. 41)
Систематическая ошибка выжившего иногда появляется, когда мы используем совместно цены акций и данные бухгалтерского учета.
Например, многие исследования в области финансов использовали соотношение рыночной стоимости компании к бухгалтерской стоимости компании на одну акцию (т.е. коэффициент котировки акций, англ. P/B, от ‘price-to-book ratio’ или ‘market-to-book ratio’) и обнаружили, что коэффициент P/B обратно пропорционален доходности компании (см. Fama and French 1992, 1993).
Коэффициент P/B также используется для многих популярных индексов стоимости и роста.
Если база данных, которую мы используем для сбора данных бухгалтерского учета, исключает обанкротившиеся компании, это может привести к систематической ошибке выжившего.
Котхари, Шанкен и Слоун (Kothari, Shanken, and Sloan) в 1995 г. исследовали именно этот вопрос, и оспорили то, что акциям обанкротившихся компаний свойственна самая низкая доходность и коэффициент P/B.
Если мы исключаем из выборки акции обанкротившихся компаний, то акции с низким P/B, которые включены в выборку, будут иметь в среднем более высокую доходность, по сравнению со средней доходностью при включении в выборку всех акций с низким P/B. Котхари, Шанкен и Слоун предположили, что эта систематическая ошибка привела к выводу об обратной связи между средней доходностью и P/B.
См. Fama and French (1996, стр. 80) о интеллектуальном анализе данных и систематической ошибке выжившего в их тестах.
Единственный совет, который мы можем предложить в этой ситуации, — это быть в курсе каких-либо смещений, потенциально присущих в выборке. Очевидно, что смещения выборки могут затуманить результаты любого исследования.
Выборка также может быть смещена из-за удаления (или делистинга) акций компании.
Делистинг (англ. ‘delisting’), т.е. исключение акций компании из котировального списка биржи, может происходить по разным причинам: слияние, банкротство, ликвидация, или переход на другую биржу.
Например, Центр исследований котировок ценных бумаг (CRSP, от англ. Center for Research in Security Prices) в Университете Чикаго является основным поставщиком данных о доходности, используемых в научных исследованиях. Когда происходит делистинг, CRSP пытается собрать данные о доходности исключенной компании, но во многих случаях он не может сделать этого из-за связанных с делистингом трудностях. CRSP вынужден просто указать значение доходности исключенной компании как отсутствующее.
Исследование, опубликованное в Финансовом журнале (см. The Journal of Finance) Шумвеем и Вортером (Shumway and Warther) в 1999 году, задокументировало смещение данных доходности NASDAQ в CRSP, вызванное делистингом.
Авторы показали, что делистинг, связанный с плохой работой компании (например, банкротством) исключается из данных чаще, чем делистинг, связанный с хорошей или нейтральной эффективностью компании (например, слиянием или перемещением на другой рынок). Кроме того, делистинг чаще происходит с небольшими компаниями.
Систематическая ошибка выборки встречается даже на рынках, где качество и согласованность данных весьма высоки. Новые классы активов, такие как хедж-фонды могут представлять еще большие проблемы смещения выборки.
Хедж-фонды (англ. ‘hedge funds’) представляют собой гетерогенную группу инвестиционных инструментов, как правило, организованных таким образом, чтобы быть свободными от регулирующего контроля. В целом, хедж-фонды не обязаны публично раскрывать свою эффективность (в отличие, скажем, от взаимных фондов). Хедж-фонды сами решают, нужно ли им включаться в какую-либо базу данных хедж-фондов.
Хедж фонды с плохой репутацией явно не желают, чтобы их результаты публиковались в базе данных, создавая проблему смещения самовыборки (англ. ‘self-selection bias’) в базах данных хедж-фондов.
Кроме того, как отметили Фанг и Хсие (Fung and Hsieh) в исследовании 2002 г., поскольку только хедж-фонды с хорошими показателями добровольно попадают в базу данных, в целом, историческая эффективность отрасли хедж-фондов имеет тенденцию казаться лучше, чем она есть на самом деле.
Кроме того, многие базы данных хедж-фондов исключают фонды, которые выходят из бизнеса, создавая в базе данных систематическую ошибку выжившего. Даже если база данных не удаляет несуществующие хедж-фонды, в попытке устранить ошибку выжившего, остается проблема хедж-фондов, которые перестают отчитываться об эффективности из-за плохих результатов.
См. Fung and Hsieh (2002) и Horst and Verbeek (2007) для более подробной информации о проблемах интерпретации эффективности хедж-фондов.
Обратите внимание, что систематическая ошибка также возможна, когда успешные фонды перестают отчитываться об эффективности, поскольку они больше не нуждаются в новых потоках денежных средств.
Систематическая ошибка опережения.
Процесс тестирования также подвержен систематической ошибке опережения (англ. ‘look-ahead bias’), если он использует информацию, которая не была доступна на момент тестирования.
Например, тесты правил биржевой торговли, которые используют ставки доходности фондового рынка и данные бухгалтерских балансов должны учитывать систематическую ошибку опережения.
В таких тестах, балансовая стоимость компании на акцию обычно используются для расчета коэффициента P/B.
Хотя рыночная цена акции доступна для всех участников рынка на заданный момент времени, балансовая стоимость на акцию на конец финансового года может стать общедоступной только в будущем — когда-то в следующем квартале.
Систематическая ошибка временного периода.
Тесты также подвержены систематической ошибке или смещению временного периода (англ. ‘time-period bias’), если они основаны на временном периоде, для которого результаты тестирования будут специфичными (т.е., характерными только для данного периода).
Ряды коротких временных периодов, скорее всего, дадут результаты, специфичные для определенного периода, которые могут не отражать более длительный период.
Ряды длительных временных периодов могут дать более точную картину истинной эффективности инвестиций. Недостаток длительных периодов заключается в потенциальных структурных изменениях, происходящих в течение периода, что приведет к двум различным распределениям доходности.
В этой ситуации, распределение, отражающее условия до изменений, будет отличаться от распределения, которые описывают условия после изменений.
Пример (7) систематических ошибок в инвестиционных исследованиях.
Финансовый аналитик рассматривает эмпирические данные об исторической доходности акций США.
Она выясняет, что недооцененные акции (то есть, акции с низким P/B) превзошли по эффективности растущие акции (то есть, акции с высоким P/B) в некоторых последних периодах времени.
После изучения американского рынка, аналитик задается вопросом, могут ли недооцененные акции быть привлекательными в Великобритании. Она исследует эффективность недооцененных и растущих акций на британском рынке за 14-летний период с января 2000 года по декабрь 2013 года.
Для проведения этого исследования, аналитик делает следующее:
- Получает текущий состав компаний Индекса всех акций FTSE (Financial Times Stock Exchange All Share Index), который является взвешенным индексом рыночной капитализации;
- Исключает несколько компаний, у которых финансовый год не заканчивается в декабре;
- Использует балансовую и рыночную стоимость компаний на конец года, чтобы ранжировать остальные пространство компаний по коэффициенту P/B на конец года;
- На основе этих рейтингов, она делит пространство ценных бумаг на 10 портфелей, каждый из которых содержит одинаковое количество акций;
- Вычисляет равновзвешенную доходность каждого портфеля и доходность FTSE All Share Index за 12 месяцев после даты расчета каждого рейтинга; а также
- Вычитает доходность FTSE из доходности каждого портфеля, чтобы получить избыточную доходность для каждого портфеля.
Опишите и обсудите каждую из следующих систематических ошибок, которым подвержен план исследований аналитика:
- систематическую ошибку выжившего;
- систематическую ошибку опережения; а также
- систематическую ошибку временного периода.
Систематическая ошибка выжившего.
План тестирования подвержен систематической ошибке выжившего, если он не принимает в расчет обанкротившиеся компании, слившиеся компании, а также компании, иным образом покинувшие базу.
В этом примере, аналитик использовала текущий список акций FTSE, а не фактический список акций на начало каждого года. В той степени, в которой расчет доходности не учитывает компании, исключенные из индекса, эффективность портфелей с наименьшим P/B подвершена систематической ошибке выжившего и, соответственно, может быть завышена.
В какой-то момент периода тестирования, эти ныне не существующие компании, были исключены из тестирования. У них, вероятно, были низкие цены на акции (и низкий P/ B) и плохая доходность.
Систематическая ошибка опережения.
План тестирования подвержен систематической ошибке опережения, если он использует информацию, недоступную на момент тестирования.
В этом примере, аналитик провела тест, сделав допущение о том, что необходимая бухгалтерская информация была доступна в конце финансового года.
Например, аналитик предположила, что балансовая стоимость на акцию за 2 000 финансовый года был известна на 31 декабря 2000 года. Поскольку эта информация, как правило, не публикуется в течение нескольких месяцев после завершения финансового года, тест, возможно, содержал систематическую ошибку опережения.
Эта ошибка может привести к стратегии, которая окажется успешной, но при этом потребуется идеальная способность прогнозировать бухгалтерские результаты.
Систематическая ошибка временного периода.
План тестирования подвержен систематической ошибке временного периода, если он основан на периоде, для которого результаты будут специфичны.
Хотя тестирование охватывает период более 10 лет, этот период может оказаться слишком коротким для тестирования аномалии.
В идеале, аналитик должна протестировать рыночные аномалии в течение нескольких бизнес-циклов, чтобы гарантировать, что результаты не являются специфичными для рассматриваемого периода.
Эта систематическая ошибка может способствовать предлагаемой стратегии, если выбрать временной период, благоприятный для стратегии.
Разница между случайной ошибкой и систематической ошибкой
Ошибка определяется как разница между фактическим или истинным значением и измеренным значением. Измерение количества или стоимости основано на каком-то стандарте. Измерение любого количества осуществляется путем сравнения его с производным стандартом, который не является полностью точным. Чтобы понять ошибки в измерении, следует понимать два термина, которые определяют ошибку, и они являются истинным значением и измеренным значением. Истинное значение невозможно выяснить, оно может быть определено по среднему значению бесконечного числа. Измеренное значение определяется как оценочное значение истинного значения путем взятия нескольких измеренных значений. Ошибка не должна быть перепутана с ошибкой, ошибки можно избежать, но ошибки не избежать, но их можно минимизировать. Так что ошибка не является ошибкой его части измерительной обработки. Измерение — это разница между измеренным значением количества и его истинным значением. мы обсудим случайную ошибку и систематическую ошибку. Погрешности измерения делятся на два обширных класса ошибок.
- Случайная ошибка
- Систематическая ошибка
Случайная ошибка:
Случайная ошибка — это не что иное, как колебания в измерении, которые в основном наблюдаются путем проведения нескольких испытаний данного измерения. Как следует из названия, эта ошибка происходит совершенно случайно. Они непредсказуемы и не могут быть воспроизведены путем повторения эксперимента снова. Так что каждый раз это дает разные результаты. Случайная ошибка варьируется от наблюдения к другому. При случайной ошибке колебание может быть как отрицательным, так и положительным. Не всегда возможно определить источник случайной ошибки. Случайная ошибка происходит из-за фактора, который не может или не будет контролироваться. Случайная ошибка влияет на достоверность результатов. Некоторые из возможных источников или причин случайных ошибок перечислены ниже.
- Наблюдение: ошибка в суждении наблюдателя.
- Небольшие помехи: Небольшие помехи могут привести к ошибкам измерения, например
- Колеблющиеся условия: Некоторое изменение температуры во времени или в окружающей среде может привести к ошибке в измерении.
- Качество: Некоторое время, когда качество объекта, измерение которого должно быть выполнено, не определено должным образом, приводит к ошибке.
Ошибка может быть уменьшена, если взять число чтений, а затем найти среднее или среднее значение чтения.
Систематическая ошибка:
Систематическая ошибка — это когда одна и та же ошибка присутствует во всех показаниях. Систематическая ошибка предсказуема и обычно постоянна или пропорциональна истинному значению. Таким образом, систематическая ошибка повторяется каждый раз, и это приводит к ошибкам согласованности. Если мы повторим эксперимент, мы получим одну и ту же ошибку каждый раз. Систематические ошибки возникают из-за неправильной калибровки прибора. Систематическая ошибка влияет на точность результата. Систематическая ошибка также называется нулевой ошибкой, положительной или отрицательной ошибкой. Некоторые из возможных источников или причин систематической ошибки перечислены ниже.
- Инструментальная ошибка: оборудование, используемое для измерения объекта, может быть не совсем точным.
- Экологическая ошибка: ошибка возникает из-за изменений условий окружающей среды, таких как влажность, давление, температура и т. Д.
- Наблюдательная ошибка: ошибка в записи данных, также называемая человеческими ошибками. После выявления систематической ошибки она может быть в некоторой степени уменьшена. Систематическая ошибка может быть сведена к минимуму путем регулярной калибровки оборудования, использования элементов управления и сравнения значений со стандартным значением.
Сравнение между случайными ошибками и значением систематической ошибки (инфографика)
Ниже приведено 8 основных различий между случайной ошибкой и систематической ошибкой
Ключевые различия между случайной ошибкой и систематической ошибкой
Давайте обсудим некоторые основные различия между случайной ошибкой и систематической ошибкой
- Случайная ошибка непредсказуема и возникает из-за неизвестных источников, тогда как систематическая ошибка является предсказуемой и возникает из-за дефекта прибора, который используется для измерения.
- Случайная ошибка возникает в обоих направлениях, тогда как систематическая ошибка возникает только в одном направлении.
- Случайная ошибка не может быть устранена, но большинство систематических ошибок может быть уменьшено.
- Случайная ошибка является уникальной и не имеет определенного типа, тогда как систематическая ошибка имеет 3 типа, как указано в таблице выше.
- Систематическую ошибку трудно обнаружить, это происходит из-за одних и тех же результатов каждый раз и не осознает, что проблема вообще существует, тогда как случайную ошибку легко обнаружить из-за разных результатов каждый раз.
Сравнительная таблица случайных ошибок и систематических ошибок
Ниже приведено 8 лучших сравнений между случайной ошибкой и систематической ошибкой.
| Основное сравнение между случайной ошибкой и систематической ошибкой | Случайная ошибка | Систематическая ошибка |
| Определение | Это происходит из-за неопределенных изменений в окружающей среде и колеблется каждый раз при измерении. | Это постоянная ошибка и остается неизменной для всех измерений. |
| Свести к минимуму | Путем многократного взятия показаний и расчета среднего или среднего из повторных показаний. | Сравнивая значение со стандартным значением и улучшая структуру оборудования. |
| Величина ошибки | Каждый раз дают другой результат, который меняется каждый раз. | Результат остается неизменным или постоянным каждый раз. |
| Направление ошибки | Это происходит в обоих направлениях. | Это происходит в том же направлении. |
|
Подтип ошибки |
Нет подтипов | Подтипы Инструмент, Среда и Систематическая Ошибка. |
| воспроизводимый | Невоспроизводимый. | Воспроизводимые. |
| Значение | Цена представляет собой сочетание стоимости. | Затраты снижаются, когда они сравниваются со стоимостью в стоимостном выражении. |
| Пример ошибки | Время реакции, погрешность измерения из-за недостаточной точности, погрешность параллакса (если каждый раз смотреть под случайным углом) | Ошибка шкалы, ошибка нуля, ошибка параллакса (если диск виден под тем же углом) |
Выводы
Таким образом, случайная ошибка в основном возникает из-за каких-либо возмущений в окружающей среде, таких как колебания или различия в давлении, температуре или из-за наблюдателя, который может принять неправильные показания, в то время как систематическая ошибка возникает из-за механической структуры прибора. Случайная ошибка не может быть предотвращена, в то время как систематическая ошибка может быть предотвращена. Полное устранение обеих ошибок невозможно. Основное различие между случайными ошибками и систематическими ошибками заключается в том, что случайная ошибка в основном приводит к колебаниям, тогда как систематические ошибки приводят к предсказуемому и последовательному результату. При работе с промышленными приборами важно, чтобы оператор тщательно следил за экспериментом, чтобы погрешность измерения могла быть уменьшена.
Рекомендуемые статьи
Это было руководство к разнице между случайной ошибкой и систематической ошибкой. Здесь мы также обсудим различия между случайной ошибкой и систематической ошибкой с помощью инфографики и сравнительной таблицы. Вы также можете взглянуть на следующие статьи, чтобы узнать больше.
- Экономический рост против экономического развития
- Бухгалтерский учет и финансовый менеджмент
- Покупка активов против покупки акций
- Ангел Инвестор против Венчурного Капитала
Истории чужого успеха вселяют уверенность: если получилось у одного, получится и у других. За этой убежденностью скрывается систематическая «ошибка выжившего». Рассказываем, что это такое и как избежать этой ловушки
Что такое ошибка выжившего
Систематическая ошибка выжившего — это тип смещения выборки, возникающий, если при принятии решения человек опирается только на примеры «выживших» (тех, кто добился успеха), но не учитывает статистику по «погибшим» (тех, у кого не получилось прийти к такому же результату), поскольку данных по ним мало или они отсутствуют.
Подобные ошибки замечали еще древние греки. В трактате «О природе богов» Марк Туллий Цицерон (106 год до н. э. — 43 год до н. э.) рассказывает историю о философе и знаменитом «безбожнике» Диагоре Мелосском. Друг привел Диагора в храм на эгейском острове Самофракия и задал вопрос: «Вот ты считаешь, что боги пренебрегают людьми. Но разве ты не обратил внимания, как много [в храме] табличек с изображениями и с надписями, из которых следует, что они были пожертвованы по обету людьми, счастливо избежавшими гибели во время бури на море и благополучно прибывшими в гавань?»
«Так-то оно так, — ответил Диагор, — только здесь нет изображений тех, чьи корабли буря потопила, и они сами погибли в море».
Как ошибка выжившего искажает восприятие
Ошибка выжившего — это распространенное когнитивное искажение, в основе которого лежит непонимание причины и следствия. Человек находит закономерность в наборе данных, но не учитывает вероятность простого совпадения. Например, то, что некоторые основатели известных компаний бросили учебу в университете и стали успешны, является совпадением, поскольку не обязательно этот факт привел их к такому результату.
Самира Анохина, клинический психолог высшей категории, действительный член Российского психологического общества:
«С точки зрения психологии, когда мы говорим о феномене «ошибки выжившего», речь идет о двух процессах: перцепции (восприятии) и когниции (осмыслении, оценке, переработке) информации. Если анализировать перцептивный контекст, можно увидеть, что тот, кто совершает такую ошибку, воспринимает только часть ситуации или часть информации, имеющей отношение к этой ситуации.
В качестве примера можно привести двойные картинки, на которых можно последовательно видеть вазу и два профиля, утку либо кролика, портрет молодой девушки либо старухи. Причем увидеть оба изображения одновременно невозможно, как ни старайся. Для того чтобы видеть то или иное «закодированное» изображение, нужно переключать внимание на разные детали картинок. Этот процесс можно сравнить с работой прожектора, который, поворачиваясь, освещает разные участки местности.
Примерно то же происходит и на уровне когнитивной оценки ситуации, когда предположения и выводы делаются на основе информации, отражающей лишь определенную сторону события, при этом та часть информации, которая находится за пределами «когнитивного прожектора», не воспринимается».
Где мы с этим сталкиваемся: примеры в жизни и бизнесе
Люди подвергаются этому когнитивному искажению в разных ситуациях: при принятии решений в повседневной жизни, финансовом планировании, в научных исследованиях, бизнесе.
Как все начиналось: сбитые самолеты Второй мировой войны
Хрестоматийным примером «ошибки выжившего» является открытие математика Абрахама Вальда во время Второй мировой войны. Американская армия теряла много самолетов в боях. Чтобы решить проблему и уменьшить потери, командование поставило перед Вальдом задачу: придумать, как укрепить конструкцию. Полностью забронировать машины было нельзя, иначе они бы просто не полетели, поэтому нужно было определить самые уязвимые места.
Военные инженеры изучили повреждения машин, вернувшихся с поля боя, и предположили, что нужно укреплять наиболее поврежденные части. Однако Абрахам Вальд отметил, что если самолет смог вернуться на базу, то попадания в эти части не критические. Важнее обратить внимание на те повреждения, с которыми самолеты не возвращались. То есть бронировать нужно те места, где у «выживших» машин не было пробоин. Это помогло снизить потери американской авиации и сохранить жизни многих летчиков.
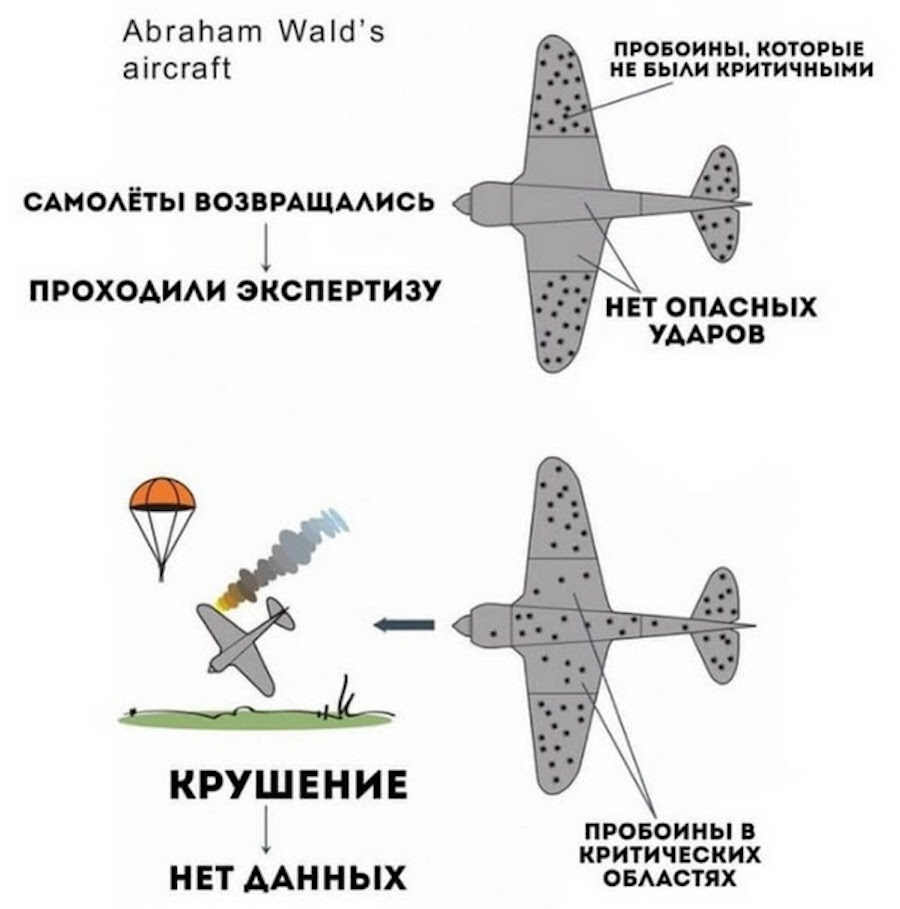
Иллюстрация картины критических и некритических повреждений на бомбардировщике по Абрахаму Вальду
«Ошибка выжившего» сегодня: как проявляется в повседневной жизни
- Если где-то произошло крушение самолета или врачи совершили ошибку, которая привела к летальному исходу, то в СМИ появляется статья об этом. Хотя, по статистике, большинство самолетов успешно приземляется, а врачи чаще совершают правильные действия, инфоповодами становятся в основном негативные сюжеты. Из-за такого перекоса у некоторых людей складывается впечатление, что летать опасно, а все врачи некомпетентны.
- Убеждение в том, что дельфины спасают людей, — еще один пример «ошибки выжившего». Известны случаи, когда они действительно помогали тонущим добраться до берега. Такие истории попадают в СМИ и создают впечатление, что дельфины — спасатели. На самом деле эти млекопитающие могут проявлять агрессивное поведение по отношению к людям, наносить серьезные травмы и даже топить. Те, кому повезло, рассказывают о чудесном спасении, а те, кто стал жертвой дельфинов, по очевидным причинам не расскажут ничего.
- «Ошибка выжившего» обнаруживается и в медицинских исследованиях. Например, когда ученые определяют показатели выживаемости для какого-либо заболевания, в статистику попадают только те пациенты, которым успели поставить диагноз. Те пациенты, которые умирают до постановки диагноза, не попадают в выборку. Это приводит к искажению реальных результатов.
- В условиях пандемии COVID-19 показательный пример «ошибки выжившего» — ковид-диссиденты.
Дмитрий Ковпак, врач-психотерапевт, к. м. н., доцент кафедры психотерапии, медицинской психологии и сексологии Северо-Западного государственного медицинского университета им. И. И. Мечникова, президент Ассоциации когнитивно-поведенческой психотерапии:
«Пандемия ярко показывает, как «ошибка выжившего» искажает восприятие и к чему она приводит. Люди верили в заговоры правительств и транснациональных корпораций, выдвигали конспирологические теории происходящего, а в некоторых странах все доходило до абсурда: граждане, отрицавшие существование нового коронавируса, приводящего к заболеванию COVID-19, демонстративно лизали дверные ручки, лишь бы показать, что этого вируса не существует. И если они не заразились после этого, то преподносили это как доказательство своей теории. Другие люди смотрели на все это и верили в то, что вируса действительно не существует. А потом оказывались в больницах.
В этом случае «ошибка выжившего» — это опасно и больно. Потому что когда человек верит в отсутствие проблемы, а потом сталкивается с ней лицом к лицу, это становится двойным ударом. Помимо того, что он оказывается в тяжелой жизненной ситуации, он еще поражен тем, что случилось то, чего в его картине мира быть просто не могло. Такие серьезные кризисы могут формировать посттравматические расстройства, кризис доверия себе и миру, выученную беспомощность и депрессию».
«Ошибка выжившего» в бизнесе: как она влияет на принятие решений
«Ошибка выжившего» часто встречается в сфере бизнеса. Никто не говорит о компаниях, которые потерпели неудачу на ранней стадии и больше не существуют, зато успехи нескольких десятков компаний, которые «выстрелили», превозносятся десятилетиями. Это искажает статистику и убеждает многих, что положительный исход более вероятен, чем есть на самом деле. Например, несмотря на то, что по статистике 90% стартапов терпят неудачу, начинающие предприниматели уверены, что они смогут попасть в число победителей.

Истории чужого успеха и карьерная стратегия
Яркий пример «ошибки выжившего» — культ историй успеха. Многие черпают вдохновение из рассказов о предпринимателях-миллиардерах и при этом неверно понимают причины и следствие. Например: «Стив Джобс бросил колледж и стал миллионером. Значит, секрет успеха — это уйти из университета и посвятить все время своей идее». На деле это не работает, и миллиардеры без высшего образования встречаются реже, чем кажется: из 362 самых богатых людей Америки только 12,2% бросили университет.
Те, кто стремится повторить историю успеха компании или конкретного человека, часто игнорируют роль времени, удачи, связей и социально-экономического фона. Многие из известных предпринимателей добились успеха, несмотря на свой необычный выбор, а не благодаря ему.
Как не стать жертвой ошибки выжившего
Дмитрий Ковпак:
«Когнитивным искажениям подвержены в той или иной степени все люди. Это систематические отклонения в восприятии, мышлении и поведении, тесно связанные с предубеждениями или так называемыми ограничивающими убеждениями, ошибочными стереотипами. Чаще всего они не осознаются самим носителем и требуют специальных навыков для их обнаружения и коррекции. Если человек думает, что никакого из когнитивных искажений у него нет, то это тоже своего рода когнитивное искажение.
Что касается «ошибки выжившего», то больше всего им подвержены люди, которые живут и действуют на автомате, не задумываются, что из их мыслей, предположений и ожиданий верно, а что нет, не анализируют и не проверяют факты, то есть редко пользуются критическим мышлением, логикой и анализом опыта».
Когда человек знает об «ошибке выжившего», ему гораздо проще не попасться в эту когнитивную ловушку. Кроме этого, избежать последствий влияния этой ошибки можно, если подходить к принятию решения критически.

Копайте глубже
Не доверяйте поверхностным суждениям и скоропалительным выводам, убедитесь, что у вас достаточно информации для принятия решения. Задавайте вопросы, которые помогут увидеть картину целиком. Например:
- Откуда я это знаю?
- Вся ли это информация по теме?
- Какие данные подтверждают эту версию/гипотезу?
- При каких условиях были собраны данные?
- Могу ли я отделить факты от субъективного мнения и впечатлений?
- Та информация, которая есть, составляет полную картину или только ее часть?
Изучайте разные точки зрения
Воспринимайте любую историю успеха как одну из версий развития событий, а не как истину в последней инстанции. Найдите неудачную статистику или истории провала и посмотрите, что в них пошло не так.
Дмитрий Ковпак:
«Многие любят публичные выступления людей, которые преодолели превратности судьбы и выжили всему вопреки. Книги наподобие «Секретов успеха от Джона Смита» также страдают «ошибкой выжившего»: это значит лишь то, что дело Джона Смита не разорилось. Куда полезнее было бы узнать, какие ошибки допустили его разорившиеся конкуренты.
Если вам пришла идея открыть ресторан в своем городе исходя из факта, что здесь много прибыльных ресторанов, вы проигнорировали то, что видите только уцелевшие и ставшие успешными точки общепита, победившие в конкурентной борьбе. Может быть, 90% всех открытых заведений в вашем городе разорились за первые два года. Но вы этого не знаете, потому что для вас они не существуют. Как писал Нассим Талеб в своей книге «Черный лебедь», на кладбище закрытых ресторанов очень тихо».