Содержание
- Ошибка домена математики Python (как исправить эту глупую ошибку)
- Ошибка домена математики Python SQRT
- Журнал ошибки домена Python Math
- Ошибка ошибки домена математики Python ACOS
- Ошибка домена Math Python Asin
- Ошибка ошибки домена Python Math POW POW
- Ошибка numpy математический домен – np.log (x)
- Куда пойти отсюда?
- Методом математической индукции доказать, что: (1*3+2*5+. +n(2n+1)=frac)
- Лучший ответ
- [Math Processing Error] #1032
- Comments
- Обратная пропорциональность. Гипербола
- Обратная пропорциональность – коротко о главном
- График обратной пропорциональности
- На что влияют коэффициенты
Ошибка домена математики Python (как исправить эту глупую ошибку)
Вы можете столкнуться с специальной ValueError при работе с математическим модулем Python. ValueError: Ошибка Math Domain Python поднимает эту ошибку, когда вы пытаетесь сделать что-то, что не является математически возможным или математически определенным. Чтобы понять эту ошибку, посмотрите на определение домена: «Домен функции является полной … ошибка домена Python Math (как исправить эту глупую ошибку) Подробнее»
Автор: Chris
Дата записи
Автор оригинала: Chris.
Вы можете столкнуться с специальными ValueError При работе с Python’s Математический модуль Отказ
Python поднимает эту ошибку, когда вы пытаетесь сделать то, что не математически возможно или математически определяется.
Чтобы понять эту ошибку, посмотрите на определение домен :
« Домен функции – это полный набор возможных значений независимой переменной. Грубо говоря, домен это набор всех возможных (входных) X-значений, который приводит к действительному (выводу) Y-значению. ” ( Источник )
Домен функции – это набор всех возможных входных значений. Если Python бросает ValueError: Ошибка математического домена Вы пропустили неопределенный ввод в Математика функция. Исправьте ошибку, передавая действительный вход, для которого функция может рассчитать числовой выход.
Вот несколько примеров:
Ошибка домена математики Python SQRT
Ошибка по математике домена появляется, если вы передаете отрицательный аргумент в math.sqrt () функция. Математически невозможно рассчитать квадратный корень отрицательного числа без использования сложных чисел. Python не получает это и бросает ValueError: Ошибка математического домена Отказ
Вот минимальный пример:
Вы можете исправить ошибку математической домена, используя CMATH Пакет, который позволяет создавать комплексные числа:
Журнал ошибки домена Python Math
Ошибка математической домена для math.log () Появится функция, если вы проходите нулевое значение в него – логарифм не определен для значения 0.
Вот код на входном значении за пределами домена функции логарифма:
Выходной выход – это ошибка домена математики:
Вы можете исправить эту ошибку, передавая действительное входное значение в math.log () Функция:
Эта ошибка иногда может появиться, если вы пройдете очень небольшое число в IT-Python, который не может выразить все номера. Чтобы пройти значение «Близки к 0», используйте Десятичная Модуль с более высокой точностью или пройти очень маленький входной аргумент, такой как:
Ошибка ошибки домена математики Python ACOS
Ошибка математической домена для math.acos () Появится функция, если вы передаете значение для него, для которого он не определен-ARCCO, определяется только значениями между -1 и 1.
Вот неверный код:
Выходной выход – это ошибка домена математики:
Вы можете исправить эту ошибку, передавая действительное входное значение между [-1,1] в math.acos () Функция:
Ошибка домена Math Python Asin
Ошибка математической домена для math.asin () Функция появляется, если вы передаете значение в него, для которого он не определен – Arcsin определяется только значениями между -1 и 1.
Вот ошибочный код:
Выходной выход – это ошибка домена математики:
Вы можете исправить эту ошибку, передавая действительное входное значение между [-1,1] в math.asin () Функция:
Ошибка ошибки домена Python Math POW POW
Ошибка математической домена для math.pow (a, b) Функция для расчета A ** B, по-видимому, если вы передаете негативное базовое значение, и попытайтесь вычислить негативную мощность. Причина этого не определена, состоит в том, что любое отрицательное число к мощности 0,5 будет квадратным числом – и, таким образом, комплексное число. Но комплексные числа не определены по умолчанию в Python!
Выходной выход – это ошибка домена математики:
Если вам нужен комплекс номер, A B должен быть переписан в E B ln a Отказ Например:
Видите ли, это сложный номер!
Ошибка numpy математический домен – np.log (x)
Это график log (x) . Не волнуйтесь, если вы не понимаете код, что важнее, является следующим точком. Вы можете видеть, что журнал (X) имеет тенденцию к отрицательной бесконечности, когда X имеет тенденцию к 0. Таким образом, математически бессмысленно рассчитать журнал отрицательного числа. Если вы попытаетесь сделать это, Python поднимает ошибку математической домена.
Куда пойти отсюда?
Достаточно теории, давайте познакомимся!
Чтобы стать успешным в кодировке, вам нужно выйти туда и решать реальные проблемы для реальных людей. Вот как вы можете легко стать шестифункциональным тренером. И вот как вы польские навыки, которые вам действительно нужны на практике. В конце концов, что такое использование теории обучения, что никто никогда не нуждается?
Практические проекты – это то, как вы обостряете вашу пилу в кодировке!
Вы хотите стать мастером кода, сосредоточившись на практических кодовых проектах, которые фактически зарабатывают вам деньги и решают проблемы для людей?
Затем станьте питоном независимым разработчиком! Это лучший способ приближения к задаче улучшения ваших навыков Python – даже если вы являетесь полным новичком.
Присоединяйтесь к моему бесплатным вебинаре «Как создать свой навык высокого дохода Python» и посмотреть, как я вырос на моем кодированном бизнесе в Интернете и как вы можете, слишком от комфорта вашего собственного дома.
Присоединяйтесь к свободному вебинару сейчас!
Работая в качестве исследователя в распределенных системах, доктор Кристиан Майер нашел свою любовь к учению студентов компьютерных наук.
Чтобы помочь студентам достичь более высоких уровней успеха Python, он основал сайт программирования образования Finxter.com Отказ Он автор популярной книги программирования Python одноклассники (Nostarch 2020), Coauthor of Кофе-брейк Python Серия самооставленных книг, энтузиаста компьютерных наук, Фрилансера и владелец одного из лучших 10 крупнейших Питон блоги по всему миру.
Его страсти пишут, чтение и кодирование. Но его величайшая страсть состоит в том, чтобы служить стремлению кодер через Finxter и помогать им повысить свои навыки. Вы можете присоединиться к его бесплатной академии электронной почты здесь.
Источник
Методом математической индукции доказать, что: (1*3+2*5+. +n(2n+1)=frac<6>)
| Posted Январь 13, 2014 by Агутина Вероника | ||||||||||||||||||||
| Категория: Алгебра | ||||||||||||||||||||
| Всего просмотров: 3248 | ||||||||||||||||||||
|
Методом математической индукции доказать, что: (1*3+2*5+. +n(2n+1)=frac<6>) Лучший ответДокажем методом математической индукции, что $$1*3+2*5+. +n(2n+1)=frac<6>$$ Доказательство методом математической индукции состоит из 3-х шагов. 1 -й шаг. Проверяем истинность утверждения при (n = 1). Подставляем в нашу формулу (n= 1) и убедимся в этом $$1*(2*1+1)=frac<1*(1+1)(4*1+5)> <6>=> 3 = 3$$Т.е. получили истинное равенство (3 = 3). Для проверки можно подставить (n=2) . Подставляем (n=2) в формулу (3+2*(2*2+1)=frac<2*(2+1)(4*2+5)> <6>=> 13 = 13). Опять получили истинное равенство (так и должно было быть, мы же доказываем истинность для любого (n)). Теперь пора переходить ко второму шагу. 2 — й шаг. Предположим (будем считать), что равенство истинно при (n = n), т.е. (1*3+2*5+. +n(2n+1)=frac<6>) — истинно. 3-й шаг. Необходимо доказать истинность равенства при (n = n+1). Если мы докажем истинность этого равенства, то это будет означать истинность для любого (n). Подставим (n = n+1) в нашу формулу $$1*3+2*5+. +n(2n+1) + (n+1)(2(n+1)+1)=frac<(n+1)(n+1+1)(4(n+1)+5)> <6>=> $$$$ 1*3+2*5+. +n(2n+1) + (n+1)(2n+3)=frac<(n+1)(n+2)(4n+9)> <6>quad (1)$$ Докажем истинность равенства (1). Доказывать будем следующим образом. Рассмотрим левую часть равенства $$ 1*3+2*5+. +n(2n+1) + (n+1)(2n+3) = quad (2)$$ и преобразуем ее к правой части. Первые n — членов ряда, согласно п.2 равны (1*3+2*5+. +n(2n+1)=frac <6>) подставим в формулу (2), получаем $$ = frac <6>+ (n+1)(2n+3)= frac<6>(n(4n+5)+6(2n+3))=$$$$ = frac<6>(4n^2+5n+12n+18))= frac<6>(4n^2+17n+18))= $$ найдем корни квадратного уравнения $$ = frac<6>4*(x+2)(x+frac<9><4>)= frac<(n+1)(x+2)(4x+9)> <6>$$ Путем преобразований левой части (2) получили правую часть. Источник [Math Processing Error] #1032The below math has rendered perfectly in firefox and chrome yesterday, but today we are getting ‘Math processing error’. We are unable to find the issue behind this. Could you please shed light on this? Looking forward to hear from you. The text was updated successfully, but these errors were encountered: Please provide a live sample page (e.g., using jsbin etc) that exhibits the problem. But a wild guess would be that you are using the CDN’s latest branch and given yesterday’s release of 2.5 you now have mixed versions of MathJax in your browser cache. See if it disappears when you clear your browser cache. We’ve just started facing this in the past 12 hours as well. I was able to reproduce it when I first opened the page, but when I refreshed, everything started displaying correctly. Not everyone who experiences this will know to do this though. We’re pointing to: The MathML you site also renders for me. I suspect Peter is right, that it is a caching issue causing you to get a mixture of files from 2.4 and 2.5. Clearing your browser cache and restarting the browser should clear that up. If not, can you temporarily change the URL where you load MathJax to //cdn.mathjax.org/mathjax/2.5-latest and see if that helps? @dpvc re the OP. I could reproduce an issue which seems to happen with the Fast Preview enabled but not without it. The error reported is Error: I is null — see http://codepen.io/pkra/pen/ZYXYmE. @pkra, OK, if I use the CommonHTML output, I do get that result. The problem is that the original MathML is malformed. For example, it contains: But the children of should be not . If you add in the missing and in both tables used for the labels at the top, then CommonHTML will display it properly. I will look into how best to resolve the situation. Источник Обратная пропорциональность. ГиперболаСейчас мы будем говорить об обратной пропорциональности, или другими словами об обратной зависимости, как о функции. Мы закрепим понятие функции и научимся работать с коэффициентами и графиками. А еще мы разберем несколько примеров построения графика функции – гиперболы. Обратная пропорциональность – коротко о главномОпределение:
По-другому эту функцию называют обратной зависимостью. Область определения и область значений функции: ( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или, что то же самое, ( Dleft( y right)=mathbbbackslash left< 0 right>) ( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbbbackslash left< 0 right>). График обратной пропорциональности (зависимости) – гипербола. Коэффициент ( displaystyle k)
Знак коэффициента ( displaystyle k) влияет на то, в каких четвертях расположен график:
если ( displaystyle k Коэффициент ( displaystyle a) Если внимательно посмотреть на знаменатель, видим, что ( displaystyle a) – это такое число, которому не может равняться ( displaystyle x).
Коэффициент ( b) Число ( b) отвечает за смещение графика функции вверх на величину ( b), если ( b>0), и смещение вниз, если ( b
Пример 2 Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»). Напомню, что для этого надо найти корни соответствующего квадратного уравнения: ( displaystyle <^<2>>+4-5=0). Я найду их устно с помощью теоремы Виета: ( displaystyle <_<1>>=-5), ( displaystyle <_<2>>=1). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения». Итак, получаем: ( displaystyle <^<2>>+4-5=left( x+5 right)left( x-1 right)), следовательно: Пример 3 Ты уже попробовал решить сам? В чем загвоздка? Наверняка в том, что в числителе у нас ( displaystyle 2x), а в знаменателе – просто ( displaystyle x). Это не беда. Нам нужно будет сократить на ( displaystyle left( x+2 right)), поэтому в числителе следует вынести ( displaystyle 2) за скобки (чтобы в скобках ( displaystyle x) получился уже без коэффициента): Ответ: ( displaystyle y=2-frac<5>). График обратной пропорциональностиКак всегда, начнем с самого простого случая: ( displaystyle y=frac<1>). Таблица обратной пропорциональности (зависимости)
Нарисуем точки на координатной плоскости: Теперь их надо плавно соединить, но как? Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть. Это график гиперболы и выглядит он так: Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом. Каждая из них стремится своими концами приблизиться к осям ( displaystyle Ox) и ( displaystyle Oy), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина: Оно и понятно: так как ( displaystyle xne 0), график не может пересекать ось ( displaystyle Oy). Но и ( displaystyle yne 0), так что график никогда не коснется и оси ( displaystyle Ox). Ну что же, теперь посмотрим на что влияют коэффициенты. На что влияют коэффициентыРассмотрим такие функции: Ух ты, какая красота! Все графики построены разными цветами, чтобы легче было их друг от друга отличать. Итак, на что обратим внимание в первую очередь? Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси ( displaystyle Ox). Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат. А что, если функция выглядит сложнее, например, ( displaystyle y=frac<1>+2)? В этом случае гипербола будет точно такой же, как обычная ( displaystyle y=frac<1>), только она немного сместится. Давай думать, куда? Чему теперь не может быть равен ( x)? Правильно, ( xne 1). Значит, график никогда не достигнет прямой ( x=1). А чему не может быть равен ( y)? Теперь ( yne 2). Значит, теперь график будет стремиться к прямой ( y=2), но никогда ее не пересечет. Итак, теперь прямые ( x=1) и ( y=2) выполняют ту же роль, которую выполняют координатные оси для функции ( displaystyle y=frac<1>). Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их): Более подробно о том, как строятся такие графики, мы выучим чуть позже. А теперь попробуй решить несколько примеров для закрепления. Примеры 1. На рисунке изображен график функции ( displaystyle y=frac). Определите ( k). 2. На рисунке изображен график функции ( displaystyle y=frac). Определите ( k) 3. На рисунке изображен график функции ( displaystyle y=frac<1>). Определите ( a). 4. На рисунке изображен график функции ( displaystyle y=frac<1>+a). Определите ( a). 5. На рисунке приведены графики функций ( displaystyle y=frac,text< >y=frac) и ( y=frac).
Источник Adblock |
Автор оригинала: Chris.
Вы можете столкнуться с специальными ValueError При работе с Python’s Математический модуль Отказ
ValueError: math domain error
Python поднимает эту ошибку, когда вы пытаетесь сделать то, что не математически возможно или математически определяется.
Чтобы понять эту ошибку, посмотрите на определение домен :
« Домен функции – это полный набор возможных значений независимой переменной. Грубо говоря, домен это набор всех возможных (входных) X-значений, который приводит к действительному (выводу) Y-значению. ” ( Источник )
Домен функции – это набор всех возможных входных значений. Если Python бросает ValueError: Ошибка математического домена Вы пропустили неопределенный ввод в Математика функция. Исправьте ошибку, передавая действительный вход, для которого функция может рассчитать числовой выход.
Вот несколько примеров:
Ошибка домена математики Python SQRT
Ошибка по математике домена появляется, если вы передаете отрицательный аргумент в math.sqrt () функция. Математически невозможно рассчитать квадратный корень отрицательного числа без использования сложных чисел. Python не получает это и бросает ValueError: Ошибка математического домена Отказ
Вот минимальный пример:
from math import sqrt
print(sqrt(-1))
'''
Traceback (most recent call last):
File "C:UsersxcentDesktopFinxterBlogcode.py", line 2, in
print(sqrt(-1))
ValueError: math domain error
'''
Вы можете исправить ошибку математической домена, используя CMATH Пакет, который позволяет создавать комплексные числа:
from cmath import sqrt print(sqrt(-1)) # 1j
Журнал ошибки домена Python Math
Ошибка математической домена для math.log () Появится функция, если вы проходите нулевое значение в него – логарифм не определен для значения 0.
Вот код на входном значении за пределами домена функции логарифма:
from math import log print(log(0))
Выходной выход – это ошибка домена математики:
Traceback (most recent call last):
File "C:UsersxcentDesktopFinxterBlogcode.py", line 3, in
print(log(0))
ValueError: math domain error
Вы можете исправить эту ошибку, передавая действительное входное значение в math.log () Функция:
from math import log print(log(0.000001)) # -13.815510557964274
Эта ошибка иногда может появиться, если вы пройдете очень небольшое число в IT-Python, который не может выразить все номера. Чтобы пройти значение «Близки к 0», используйте Десятичная Модуль с более высокой точностью или пройти очень маленький входной аргумент, такой как:
math.log(sys.float_info.min)
Ошибка ошибки домена математики Python ACOS
Ошибка математической домена для math.acos () Появится функция, если вы передаете значение для него, для которого он не определен-ARCCO, определяется только значениями между -1 и 1.
Вот неверный код:
import math print(math.acos(2))
Выходной выход – это ошибка домена математики:
Traceback (most recent call last):
File "C:UsersxcentDesktopFinxterBlogcode.py", line 3, in
print(math.acos(2))
ValueError: math domain error
Вы можете исправить эту ошибку, передавая действительное входное значение между [-1,1] в math.acos () Функция:
import math print(math.acos(0.5)) # 1.0471975511965979
Ошибка домена Math Python Asin
Ошибка математической домена для math.asin () Функция появляется, если вы передаете значение в него, для которого он не определен – Arcsin определяется только значениями между -1 и 1.
Вот ошибочный код:
import math print(math.asin(2))
Выходной выход – это ошибка домена математики:
Traceback (most recent call last):
File "C:UsersxcentDesktopFinxterBlogcode.py", line 3, in
print(math.asin(2))
ValueError: math domain error
Вы можете исправить эту ошибку, передавая действительное входное значение между [-1,1] в math.asin () Функция:
import math print(math.asin(0.5)) # 0.5235987755982989
Ошибка ошибки домена Python Math POW POW
Ошибка математической домена для math.pow (a, b) Функция для расчета A ** B, по-видимому, если вы передаете негативное базовое значение, и попытайтесь вычислить негативную мощность. Причина этого не определена, состоит в том, что любое отрицательное число к мощности 0,5 будет квадратным числом – и, таким образом, комплексное число. Но комплексные числа не определены по умолчанию в Python!
import math print(math.pow(-2, 0.5))
Выходной выход – это ошибка домена математики:
Traceback (most recent call last):
File "C:UsersxcentDesktopFinxterBlogcode.py", line 3, in
print(math.pow(-2, 0.5))
ValueError: math domain error
Если вам нужен комплекс номер, A B должен быть переписан в E B ln a Отказ Например:
import cmath print(cmath.exp(0.5 * cmath.log(-2))) # (8.659560562354932e-17+1.414213562373095j)
Видите ли, это сложный номер!
Ошибка numpy математический домен – np.log (x)
import numpy as np import matplotlib.pyplot as plt # Plotting y = log(x) fig, ax = plt.subplots() ax.set(xlim=(-5, 20), ylim=(-4, 4), title='log(x)', ylabel='y', xlabel='x') x = np.linspace(-10, 20, num=1000) y = np.log(x) plt.plot(x, y)
Это график log (x) . Не волнуйтесь, если вы не понимаете код, что важнее, является следующим точком. Вы можете видеть, что журнал (X) имеет тенденцию к отрицательной бесконечности, когда X имеет тенденцию к 0. Таким образом, математически бессмысленно рассчитать журнал отрицательного числа. Если вы попытаетесь сделать это, Python поднимает ошибку математической домена.
>>> math.log(-10) Traceback (most recent call last): File "", line 1, in ValueError: math domain error
Куда пойти отсюда?
Достаточно теории, давайте познакомимся!
Чтобы стать успешным в кодировке, вам нужно выйти туда и решать реальные проблемы для реальных людей. Вот как вы можете легко стать шестифункциональным тренером. И вот как вы польские навыки, которые вам действительно нужны на практике. В конце концов, что такое использование теории обучения, что никто никогда не нуждается?
Практические проекты – это то, как вы обостряете вашу пилу в кодировке!
Вы хотите стать мастером кода, сосредоточившись на практических кодовых проектах, которые фактически зарабатывают вам деньги и решают проблемы для людей?
Затем станьте питоном независимым разработчиком! Это лучший способ приближения к задаче улучшения ваших навыков Python – даже если вы являетесь полным новичком.
Присоединяйтесь к моему бесплатным вебинаре «Как создать свой навык высокого дохода Python» и посмотреть, как я вырос на моем кодированном бизнесе в Интернете и как вы можете, слишком от комфорта вашего собственного дома.
Присоединяйтесь к свободному вебинару сейчас!
Работая в качестве исследователя в распределенных системах, доктор Кристиан Майер нашел свою любовь к учению студентов компьютерных наук.
Чтобы помочь студентам достичь более высоких уровней успеха Python, он основал сайт программирования образования Finxter.com Отказ Он автор популярной книги программирования Python одноклассники (Nostarch 2020), Coauthor of Кофе-брейк Python Серия самооставленных книг, энтузиаста компьютерных наук, Фрилансера и владелец одного из лучших 10 крупнейших Питон блоги по всему миру.
Его страсти пишут, чтение и кодирование. Но его величайшая страсть состоит в том, чтобы служить стремлению кодер через Finxter и помогать им повысить свои навыки. Вы можете присоединиться к его бесплатной академии электронной почты здесь.
Оригинал: “https://blog.finxter.com/python-math-domain-error/”
Матрицы и действия с ними, определители
Определение ранга матрицы
Рассмотрим матрицу (A) типа ((m,n)). Пусть, для определенности, (m leq n). Возьмем (m) строк и выберем (m) столбцов матрицы (A), на пересечении этих строк и столбцов получится квадратная матрица порядка (m), определитель которой называют минором порядка (m) матрицы (A). Если этот минор отличен от 0, его называют базисным минором и говорят, что ранг матрицы (A) равен (m). Если же этот определитель равен 0, то выбирают другие (m) столбцов, на их пересечении стоят элементы, образующие другой минор порядка (m). Если минор равен 0, продолжаем процедуру. Если среди всех возможных миноров порядка (m) нет отличных от нуля, мы выбираем (m-1) cтрок и столбцов из матрицы (A), на их пересечении возникает квадратная матрица порядка (m-1), ее определитель называется минором порядка (m-1) исходной матрицы. Продолжая процедуру, ищем ненулевой минор, перебирая все возможные миноры, понижая их порядок.
Определение.
Ненулевой минор данной матрицы наивысшего порядка называется базисным минором исходной матрицы, его порядок называется рангом матрицы (A), строки и столбцы, на пересечении которых находится базисный минор, называются базисныи строками и столбцами. Ранг матрицы обозначается (rang(A)).
Из этого определения следуют простые свойства ранга матрицы: это целое число, причем ранг ненулевой матрицы удовлетворяет неравенствам: (1 leq rang(A) leq min(m,n)).
Как изменится ранг матрицы, если вычеркнуть какую-нибудь строку? Добавить какую-нибудь строку?
1) Ранг может уменьшиться на 1.
2) Ранг может увеличиться на 1.
Линейная зависимость и линейная независимость столбцов матрицы
Пусть (A) — матрица типа ((m,n)). Рассмотрим столбцы матрицы (A) — это столбцы из (m) чисел каждый. Обозначим их (A_1,A_2,…,A_n). Пусть (c_1,c_2,…,c_n) — какие-то числа.
Определение.
Столбец
[
D=c_1A_1+c_2A_2+…+c_nA_n = sum _{m=1}^nc_mA_m
]
называется линейной комбинацией столбцов (A_1,A_2,…,A_n), числа (c_1,c_2,…,c_n) называются коэффициентами этой линейной комбинации.
Определение.
Пусть дано (p) столбцов (A_1, A_2, …, A_p). Если существуют такие числа (c_1,c_2,…,c_p), что
1. не все эти числа равны нулю,
2. линейная комбинация (c_1A_1+c_2A_2+…+c_pA_p =sum _{m=1}^pc_mA_m) равна нулевому столбцу (т.е. столбцу, все элементы которого нули),
то говорят, что столбцы (A_1, A_2, …, A_p) линейно зависимы. Если для данного набора столбцов таких чисел (c_1,c_2,…,c_n) не существует, столбцы называются линейно независимыми.
Пример. Рассмотрим 2-столбцы
[
A_1=left( begin{array}{c} 1 \ 0 end{array} right), A_2=left( begin{array}{c} 0 \ 1 end{array} right),
]
тогда для любых чисел (c_1,c_2) имеем:
[
c_1A_1+c_2A_2=c_1left( begin{array}{c} 1 \ 0 end{array} right)+c_2left( begin{array}{c} 0 \ 1 end{array} right)=left( begin{array}{c} c_1 \ c_2 end{array} right).
]
Эта линейная комбинация равна нулевому столбцу тогда и только тогда, когда оба числа (c_1,c_2) равны нулю. Таким образом, эти столбцы линейно независимы.
Утверждение. Для того, чтобы столбцы были линейно зависимы, необходимо и достаточно, чтобы один из них был линейной комбинацией остальных.
Пусть столбцы (A_1,A_2,…,A_m) линейно зависимы, т.е. для некоторых констант (lambda _1, lambda _2,…,lambda _m), не все из которых равны 0, выполняется:
[
sum _{k=1}^mlambda _kA_k=0
]
(в правой части — нулевой столбец). Пусть, например, (lambda _1 neq 0). Тогда
[
A_1=sum _{k=2}^mc_kA_k, quad c_k=-lambda _k/lambda _1, quad quad (15)
]
т.е. первый столбец — линейная комбинация остальных.
Теорема о базисном миноре
Теорема.
Для любой ненулевой матрицы (A) справедливо следующее:
1. Базисные столбцы линейно независимы.
2. Любой столбец матрицы является линейной комбинацией его базисных столбцов.
(Аналогичное верно и для строк).
Пусть, для определенности, ((m,n)) — тип матрицы (A), (rang(A)=r leq n) и базисный минор расположен в первых (r) строках и столбцах матрицы (A). Пусть (s) — любое число между 1 и (m), (k) — любое число между 1 и (n). Рассмотрим минор следующего вида:
[
D=left| begin{array}{ccccc} a_{11} & a_{12} & ldots & a_{1r} & a_{1s} \
a_{21} & a_{22} & ldots & a_{2r} & a_{2s} \
dots &ldots & ldots & ldots & ldots \
a_{r1} & a_{r2} & ldots & a_{rr} & a_{rs} \
a_{k1} & a_{k2} & ldots & a_{kr} & a_{ks} \
end{array} right| ,
]
т.е. мы к базисному минору приписали (s-)ый столбец и (k-)ую строку. По определению ранга матрицы этот определитель равен нулю (если мы выбрали (sleq r) или (k leq r) , значит в этом миноре 2 одинаковых столбца или 2 одинаковых строки, если (s>r) и (k>r) — по определению ранга минор размера больше (r) обращается в ноль). Разложим этот определитель по последней строке, получим:
[
a_{k1}A_{k1}+a_{k2}A_{k2}+….+a_{kr}A_{kr}+a_{ks}A_{ks}=0. quad quad(16)
]
Здесь числа (A_{kp}) — алгебраические дополнения элементов из нижней строки (D). Их величины не зависят от (k), т.к. образуются с помощью элементов из первых (r) строк. При этом величина (A_{ks}) — это базисный минор, отличный от 0. Обозначим (A_{k1}=c_1,A_{k2}=c_2,…,A_{ks}=c_s neq 0). Перепишем в новых обозначениях (16):
[
c_1a_{k1}+c_2a_{k2}+…+c_ra_{kr}+c_sa_{ks}=0,
]
или, разделив на (c_s),
[
a_{ks}=lambda_1a_{k1}+lambda_2a_{k2}+…+lambda_ra_{kr}, quad lambda _p=-c_p/c_s.
]
Это равенство справедливо для любого значения (k), так что
[
a_{1s}=lambda_1a_{11}+lambda_2a_{12}+…+lambda_ra_{1r},
]
[
a_{2s}=lambda_1a_{21}+lambda_2a_{22}+…+lambda_ra_{2r},
]
[
………………………………………………..
]
[
a_{ms}=lambda_1a_{m1}+lambda_2a_{m2}+…+lambda_ra_{mr}.
]
Итак, (s-)ый столбец является линейной комбинацией первых (r) столбцов. Теорема доказана.
Замечание.
Из теоремы о базисном миноре следует, что ранг матрицы равен числу ее линейно независимых столбцов (которое равно числу линейно независимых строк).
Следствие 1.
Если определитель равен нулю, то у него есть столбец, который является линейной комбинацией остальных столбцов.
Следствие 2.
Если ранг матрицы меньше числа столбцов, то столбцы матрицы линейно зависимы.
Вычисление ранга матрицы и нахождение базисного минора
Некоторые преобразования матрицы не меняют ее ранг. Такие преобразования можно назвать элементарными. Соответствующие факты нетрудно проверить с помощью свойств определителей и определения ранга матрицы.
1. Перестановка столбцов.
2. Умножение элементов какого-нибудь столбца на ненулевой множитель.
3. Прибавление к столбцу любого другого столбца, умноженного на произвольное число.
4. Вычеркивание нулевого столбца.
Аналогичное верно и для строк.
С помощью этих преобразований матрицу можно преобразовать к так называемой «трапециевидной» форме — матрице, под главной диагональю которой располагаются только нули. Для «трапециевидной» матрицы ранг — это число ненулевых элементов на главной диагонали, и базисный минор — минор, диагональ которого совпадает с набором ненулевых элементов на главной диагонали преобразованной матрицы.
Пример.
Рассмотрим матрицу
[
A=left(
begin{array}{cccc}
2 &1 & 11 & 2 \
1 & 0 & 4 & -1 \
11 & 4 & 56 & 5 \
2 & -1 & 5 & -6
end{array}
right).
]
Будем преобразовывать ее с помощью указанных выше преобразований.
[
A=left( begin{array}{cccc} 2 &1 & 11 & 2 \ 1 & 0 & 4 & -1 \ 11 & 4 & 56 & 5 \ 2 & -1 & 5 & -6 end{array} right) mapsto
left( begin{array}{cccc} 1 & 0 & 4 & -1 \ 2 & 1 & 11 & 2 \ 11 & 4 & 56 & 5 \ 2 & -1 & 5 & -6 end{array} right)
mapsto
left( begin{array}{cccc} 1 & 0 & 4 & -1 \ 0 & 1 & 3 & 4 \ 0 & 4 & 12 & 16 \ 0 & -1 & -3 & -4 end{array} right) mapsto
]
[
left( begin{array}{cccc} 1 & 0 & 4 & -1 \ 0 & 1 & 3 & 4 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end{array} right)mapsto
left( begin{array}{cccc} 1 & 0 & 4 & -1 \ 0 & 1 & 3 & 4 end{array}right).
]
Здесь мы последовательно делаем следующие шаги: 1) переставляем вторую строку наверх, 2) вычитаем первую строку из остальных с подходящим множителем, 3) вычитаем вторую строку из третьей 4 раза, прибавляем вторую строку к четвертой, 4) вычеркиваем нулевые строки — третью и четвертую. Наша итоговая матрица прибрела желаемую форму: на главной диагонали стоят ненулевые числа, под главной диагональю — нули. После этого процедура останавливается и число ненулевых элементов на главной диагонали равно рангу матрицы. Базисный минор при этом — две первые строки и два первых столбца. На их пересечении стоит матрица порядка 2 с ненулевым определителем. При этом, возвращаясь по цепочке преобразований в обратную сторону, можно проследить, откуда возникла та или иная строка (тот или иной столбец) в конечной матрице, т.е. определить базисные строки и столбцы в исходной матрице. В данном случае первые две строки и первые два столбца образуют базисный минор.
Пусть (A) — матрица типа ((m,n)) ранга (r_1), (B) — матрица типа ((p,n)) ранга (r_2). Объединим их строки — получим матрицу (C). Можно ли дать двустороннюю оценку ранга матрицы (C)?
(max(r_1, r_2) leq rang(C) leq min(n, r_1 + r_2))
1. Вычислить ранг матрицы
а)
[
left( begin{array}{cccc} 1 &2 &1 & 1 \ 2& 4 & 2 & 2\ 3 & 6& 3& 5 end{array} right) .
]
б)
[
left( begin{array}{cccc} 1 &7 &7 & 9 \ 7& 5 & 1 & -1\ 4 & 2& -1& -3 \ -1 & 1 & 3 &5 end{array} right) .
]
в)
[
left( begin{array}{cccc} 2 & 1 &11 & 2 \ 1& 0 & 4 & -1\ 11 & 4& 56& 5 \ 2 & -1 & 5 &- 6 end{array} right) .
]
г)
[
left( begin{array}{cccc} 5 & 4 & 1 & 3 \ 2& 1 & 1 & 4\ 3 & 2& 1& 1 \ 1 & 3 & -2 & 2 end{array} right) .
]
2. Доказать равенство (rang(A)=rang(A^T)).
3. Пусть (A) и (B) — матрицы с одинаковым числом строк. Доказать, что
[
rangleft( begin{array}{cc} A & B\ 2A & 3B end{array} right)=rang(A)+rang(B).
]
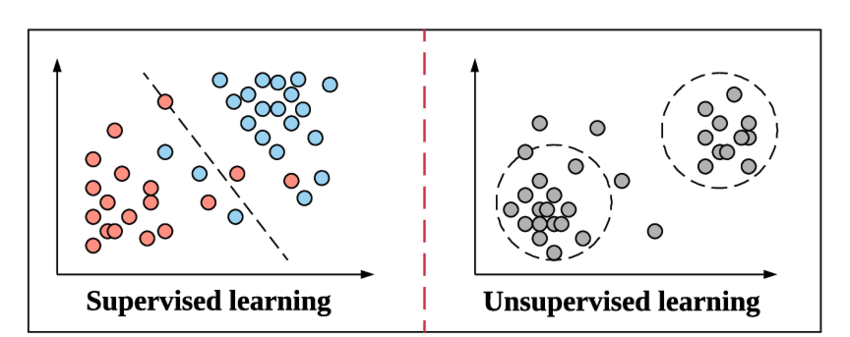
Обучение без учителя
Ранее мы рассматривали в основном только задачи, где у части данных (тренировочной) была размечена целевая функция (таргет), а для другой части данных (тестовой) таргета нет, и мы хотели его восстановить. Такие задачи (классификация, регрессия, ранжирование), как вы помните, называются обучением с учителем (supervised learning).
Давайте посмотрим теперь на задачи, в которых таргета не дано — но все же что-то сопоставить каждому элементу надо. Такие задачи называются обучением без учителя (unsupervised learning).
Примеры таких задач:
- кластеризация
- уменьшение размерности
- визуализация
- вложение в пространство
Одна из особенностей обучения без учителя — нам не нужны тренировочная и тестовая выборка. Нет таргета — нет проблем с переобучением.
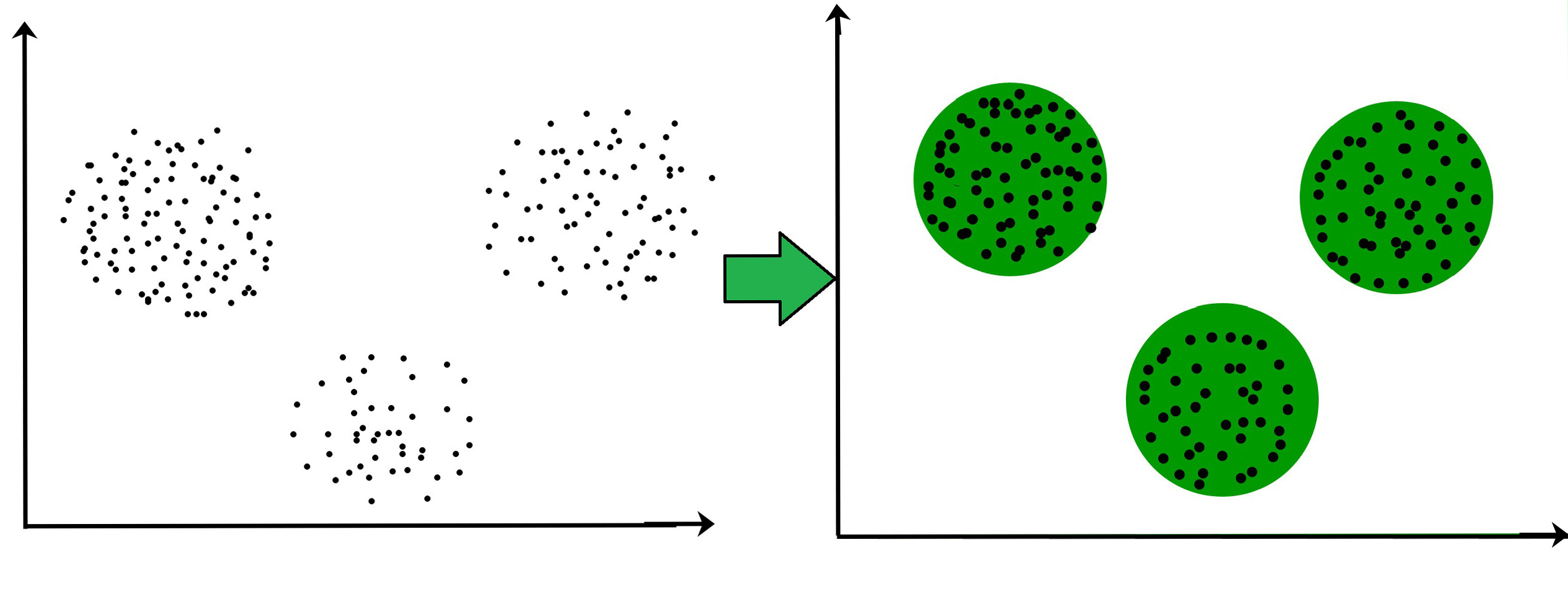
Задачу кластеризации вы знаете: она состоит в разделении точек в пространстве на кластеры близко расположенных.
Рассмотрим несколько известных алгоритмов кластеризации.
Алгоритм K-Means
Визуализация.
Нужно в начале выбрать KK центров кластеров (KK — константа, которую надо самому выбрать).
Далее итеративно выполняются 22 шага, пока обновления не перестанут происходить:
- Обновить кластеры, приписав каждой точке кластер самого близкого к ней центра
- Обновить центр каждого кластера как центр масс его точек
Плюсы:
- простой и понятный
Минусы:
- нужно знать KK
- слишком простая модель, кластер = выпуклая околокруглая штука, так как это по сути диаграмма Вороного (если вы знаете, что это такое)
- если плохо выбрать начальные центры, может сойтись к плохому результату
Поэтому обычно K-Means запускают несколько раз и выбирают лучший результат.
Метрика качества кластеризации
Как и для задач обучения с учителем, хочется уметь понимать, хорошо ли мы решили задачу — нужно научиться измерять качество кластеризации. Так, например, даже не зная число кластеров, можно перебрать KK в K-Means и выбрать гиперпараметр с лучшим качеством.
Одним из примеров метрики может быть метрика силуэт. Для одного элемента xx она считается так:
S(x)=b(x)−a(x)max(a(x),b(x))S(x) = frac{b(x) — a(x)}{max{(a(x), b(x))}}
a(x)a(x) — среднее расстояние от xx до точек внутри того же кластера
b(x)b(x) — среднее расстояние от xx до точек внутри ближайшего кластера
Значение метрики силуэт лежит в диапазоне значений [0.0,1.0][0.0, 1.0], и ее можно посчитать для каждого примера и для кластера.
Значение силуэта для кластера равно среднему значению S(x)S(x) от каждого элемента. Чем он больше тем лучше кластер отделим от других кластеров.
Примеры из выборки можно отсортировать по значению силуэта для каждого примера и по присвоенной метке кластера. Такое представление позволяет отфильтровать шумные примеры (у которых силуэт меньше некоторого порога).
DBSCAN
Визуализация.
DBSCAN строит столько кластеров, сколько получится, причем многие вершины могут не войти ни в один кластер, они называются выбросами.
DBSCAN опирается на два гиперпараметра:
- eps — означает расстояние, на котором две вершины считаются соседями
- min_samples — означает сколько нужно соседей из кластера, чтобы считать вершину коренной вершиной кластера
Сам алгоритм состоит из таких шагов:
- Выбрать соседей для каждой вершины на расстоянии до eps
- Найти компоненты связности коренных вершин — добавляем вершину в компоненту коренных, если у нее хотя бы min_samples соседей лежат в этой компоненте
- Добавить оставшиеся вершины в самый популярный кластер соседей, если есть соседи
- Оставшиеся вершины — это выбросы
Плюсы:
- сам подберет число кластеров
- опирается на плотность точек, кластеры могут быть вытянутыми и даже невыпуклыми
Минусы:
- нужно подбирать два других параметра
- алгоритм считает, что в разных частях данных плотности должны быть примерно одинаковыми
Агломеративная кластеризация
Интуиция у алгоритма очень простая:
- Начинаем с того, что высыпаем на каждую точку свой кластер
- Сортируем попарные расстояния между центрами кластеров по возрастанию
- Берём пару ближайших кластеров, склеиваем их в один и пересчитываем центр кластера
- Повторяем п. 2 и 3 до тех пор, пока все данные не склеятся в один кластер
Чтобы найти пару ближайших кластеров берут не только расстояние между центрами, бывают и такие метрики:
- Single linkage — минимум попарных расстояний между точками из двух кластеров
- Complete linkage — максимум попарных расстояний между точками из двух кластеров
- Average linkage — среднее попарных расстояний между точками из двух кластеров
- Centroid linkage — расстояние между центроидами двух кластеров
По итогам выполнения такого алгоритма строится дерево склеивания кластеров. Глядя на него можно определить, на каком этапе оптимальнее всего остановить алгоритм.
Уменьшение размерности и визуализации
Обе эти задачи состоят в сжатии выборки: нужно перевести точки из NN-мерного пространства в MM-мерное пространство, где M<NM<N, причем так, чтобы близкие точки остались близкими. То есть хочется значительно уменьшить число признаков, не сильно потеряв (или даже улучшив) их качество.
Для примеров мы будем чаще всего переводить в 22-мерное пространство — это заодно и хороший способ визуализировать датасет. Помимо визуализации уменьшение размерности очень часто используют для отбора признаков. Вместо 6464 малозначащих признаков мы хотим оставить 22, в которых лежит как можно больше информации. Заметьте, что это слабый способ отбора признаков: мы никак не используем значение таргета.
SVD — используем матрицы
В этом методе уменьшения размерности применяется SVD-разложение матрицы признаков.
Что это такое? Это единственное представление матрицы в виде произведения трех других:
A=UΣVA=U Sigma V
где AA — прямоугольная матрица признаков, ΣSigma — прямоугольная диагональная, причём числа на диагонали неотрицательны и убывают, U,VU, V квадратные и унитарные (не важно, что это значит, но по смыслу это что-то вроде поворота пространства). Нас больше всего будет интересовать матрица ΣSigma.
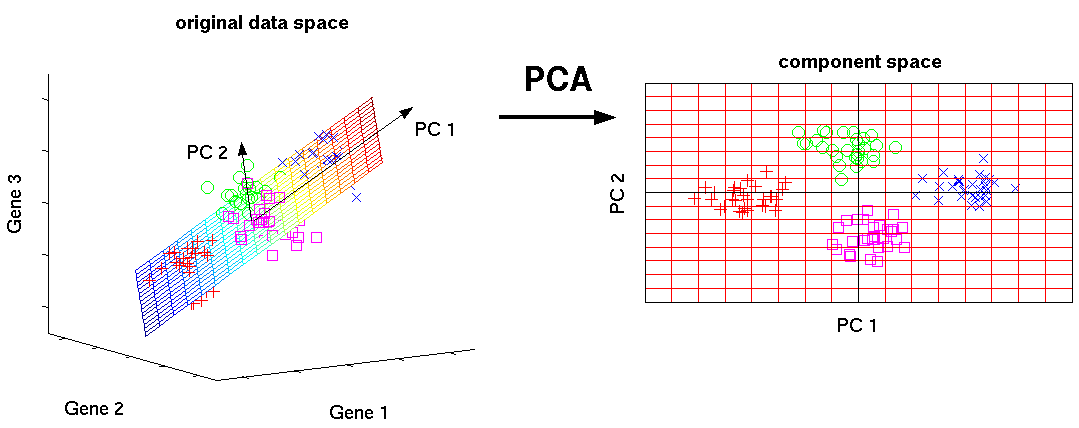
PCA — метод главных компонент
Визуализация выделения первой и второй главных компонент методом PCA.
Метод PCA заключается в том, чтобы найти в NN-мерном пространстве такое KK-мерное пространство, что проекция всех точек на него будет как можно более рассеянной (то есть иметь наибольшую дисперсию).
- Оказывается, подходит пространство, сумма квадратов расстояния от которого до всех точек минимальна.
- Первая компонента (ось) выбирается так, чтобы дисперсия проекции вдоль нее была максимальна.
- После этого все точки проецируются вдоль первой компоненты и там таким же способом выбирается вторая компонента и так далее.
- Получившиеся KK компонент будут образовывать KK-мерное пространство, проекция точек на которое будет иметь наибольшую дисперсию.
Оказывается, если применить TruncatedSVD к центрированным данным (среднее по каждой координате равно 00), то именно это и получится!
В каком-то смысле PCA — это лучший линейный способ уменьшить размерность пространства.
Плюсы PCA:
- считается относительно быстро
- детерминированность (зависит от реализации, в sklearn не так)
- любая размерность
- полученную модель уменьшения размерности можно применять и к новым точкам (нужно просто спроецировать ее на выделенное KK-мерное пространство)
- визуализация при K=2K = 2 — это честная проекция на какую-то плоскость, легкая интерпретируемость результатов
- при увеличении размерности старые координаты не меняются
- отлично подходит для отбора признаков
Минусы PCA:
- алгоритм слишком простой — он линейный
- некоторые непохожие точки могут спроецироваться в одну и ту же при K=2K = 2
t-SNE
Визуализация метода уменьшения размерности t-SNE.
Это гораздо более сложный нелинейный алгоритм. Он очень крут для визуализации данных, и работает только с переводом в 2D и 3D.
Внутри там происходит что-то физическое — элементы будто разлетаются, причем чем дальше они друг от друга, тем сильнее они друг друга отталкивают.
Плюсы t-SNE:
- отлично визуализирует (2D, 3D) данные
- физически разносит разные точки дальше друг от друга
- сильно разные точки не могут в конце оказаться рядом
Минусы t-SNE:
- недетерминированность, результат меняется при каждом запуске
- координаты ничего не значат сами по себе
- нельзя легко добавить новые данные (т.к. нет явной функции отображения в новое пространство)!
- долго работает
- уменьшает только до 2 и 3 размерности
Применение уменьшения размерности для классификации
Часто предварительное уменьшение размерности помогает лучше решать задачу обучения с учителем (например классификацию). Это помогает меньше переобучаться и позволяет алгоритмам обучаться быстрее (часть данных выкинули).
P.S. При обучении алгоритм уменьшения размерности не должен видеть тестовых данных, это приведет к переобучению!
Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве. Все будет показано на примерах.
Перпендикулярные прямая и плоскость – основные сведения
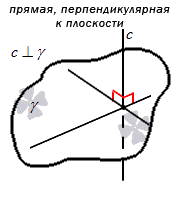
Прямая перпендикулярна к плоскости, когда она перпендикулярна к любой прямой, лежащей в этой плоскости.
Верно то, что и плоскость перпендикулярна к прямой, как и прямая к плоскости.
Перпендикулярность обозначается «⊥». Если в условии задано, что прямая с перпендикулярна плоскости γ, тогда запись имеет вид с⊥γ.
Например, если прямая перпендикулярна к плоскости, тогда возможно провести только одну прямую, благодаря которой две смежных стены комнаты пересекутся. Прямая считается перпендикулярной к плоскости потолка. Канат, расположенный в спортзале рассматривается в качестве отрезка прямой, который перпендикулярен плоскости, в данном случае полу.
При наличии перпендикулярной прямой к плоскости, угол между прямой и плоскостью считается прямым, то есть равен 90 градусов.
Перпендикулярность прямой и плоскости – признак и условия перпендикулярности
Для нахождения выявления перпендикулярности необходимо использовать достаточное условие перпендикулярности прямой и плоскости. Оно гарантирует выполнение перпендикулярности прямой и плоскости. Данное условие считается достаточным и называют признаком перпендикулярности прямой и плоскости.
Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, которые лежат в этой плоскости.
Подробное доказательство приведено в учебнике геометрии 10-11 класса. Теорема применяется для решения задач, где необходимо установить перпендикулярность прямой и плоскости.
При условии параллельности хоть одной из прямых плоскости, считается, что вторая прямая также перпендикулярна к данной плоскости.
Признак перпендикулярности прямой и плоскости рассматривается еще со школы, когда необходимо решить задачи по геометрии. Рассмотрим подробнее еще одно необходимое и достаточное условие, при котором прямая и плоскость будут перпендикулярны.
Для того, чтобы прямая а была перпендикулярна плоскости γ , необходимым и достаточным условием является коллинеарность направляющего вектора прямой а и нормального вектора плоскости γ.
При a→=(ax, ay, az) являющимся вектором прямой a, при n→=(nx, ny, nz) являющимся нормальным вектором плоскости γ для выполнения перпендикулярности нужно, чтобы прямая a и плоскость γ принадлежали выполняемости условия коллинеарности векторов a→=(ax, ay, az) и n→=(nx, ny, nz). Отсюда получаем, что a→=t·n→⇔ax=t·nxay=t·nyaz=t·nz, t является действительным числом.
Данное доказательство основывается на необходимом и достаточном условии перпендикулярности прямой и плоскости, направляющего вектора прямой и нормального вектора плоскости.
Данное условие применимо для доказательства перпендикулярности прямой и плоскости, так как достаточно найти координаты направляющего вектора прямой и координаты нормального вектора в трехмерном пространстве, после чего производить вычисления. Используется для случаев, когда прямая определена уравнением прямой в пространстве, а плоскость уравнением плоскости некоторого вида.
Доказать перпендикулярность заданной прямой x2-1=y-12=z+22-7 с плоскостью x+22+1y-(5+62)z.
Решение
Знаменатели канонических уравнений являются координатами направляющего вектора данной прямой. Отсюда имеем, что a→=(2-1, 2, 2-7) является направляющим вектором прямой x2-1=y-12=z+22-7.
В общем уравнении плоскости коэффициенты перед переменными x, y, z являются координатами нормального вектора данной плоскости. Отсюда следует, что n→=(1, 2(2+1), -(5+62)) — это нормальный вектор плоскости x+22+1y-(5+62)z-4=0
Необходимо произвести проверку выполнимости условия. Получаем, что
2-1=t·12=t·2(2+1)2=t·(-(5+62))⇔t=2-1, тогда векторы a→ и n→ связаны выражением a→=(2-1)·n→.
Это и есть коллинеарность векторов. отсюда следует, что прямая x2-1=y-12=z+22-7 перпендикулярна плоскости x+2(2+1)y-(5+62)z-4=0.
Ответ: прямая и плоскость перпендикулярны.
Определить, перпендикулярны ли прямая y-1=0x+4z-2=0и плоскость x12+z-12=1.
Решение
Чтобы ответить на вопрос перпендикулярности, необходимо, чтобы было выполнено необходимое и достаточное условие, то есть для начала нужно найти вектор заданной прямой и нормальный вектор плоскости.
Из прямой y-1=0x+4z-2=0 видно, что направляющий вектор a→ — это произведение нормальных векторов плоскости y-1=0 и x+4z-2=0.
Отсюда получаем, что a→=i→j→k→010104=4·i→-k→.
Координаты вектора a→=(4, 0, -1).
Уравнение плоскости в отрезках x12+z-12=1 является эквивалентным уравнению плоскости 2x-2z-1=0, нормальный вектор которой равен n→=(2, 0, -2).
Следует произвести проверку на коллинеарность векторов a→=(4, 0, -1) и n→=(2, 0, -2).
Для этого запишем:
4=t·20=t·0-1=t·(-2)⇔t=2t∈R ⇔t∈∅t=12
Отсюда делаем вывод о том, что направляющий вектор прямой не коллинеарен нормальному вектору плоскости. Значит, y-1=0x+4z-2=0 — это прямая, не перпендикулярная к плоскости x12+z-12.
Ответ: прямая и плоскость не перпендикулярны.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта