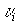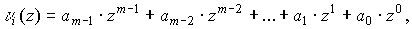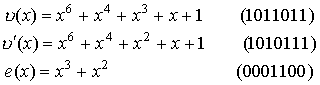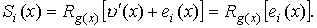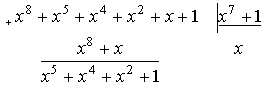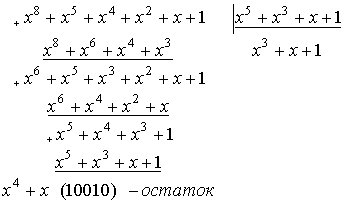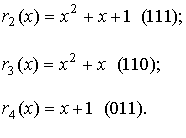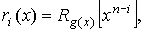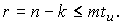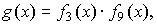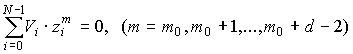Циклические коды исправляющие две ошибки - Исправление ошибок и поиск оптимальных решений проблем

В предыдущем параграфе было дано описание кодов Хэмминга как циклических кодов, порождающие многочлены которых имеют корень в соответствующем расширении основного поля. Описанные коды исправляют одну ошибку. Сейчас мы возвращаемся к исправляющим две ошибки кодам над полем GF (2). Пусть длина кода имеет вид для некоторого и пусть а — примитивный элемент поля Мы рассмотрим те даоичиые коды, для которых а и а? являются корнями порождающих многочленов, и покажем, что такие коды позволяют исправлять две ошибки.

Пусть многочлен наименьшей степени, для которого из являются корнями. Описав процедуру декодирования, позволяющую исправлять все одиночные и двойные ошибки, мы докажем, что минимальное расстояние этого кода равно по меньшей мере 5.

Принятое слово записывается многочленом степени вида

где содержит не более двух ненулевых коэффициентов, поскольку мы рассматриваем случай исправления не более двух ошибок. Таким образом, или или с или Целые числа и маркируют позиции, в которых произошли ошибки. Для маркировки ошибочных позиций мы будем также использовать элементы поля Элемент поля а соответствует компоненте с номером . В этой роли элементы поля называются локаторами. Обозначим — Так как длина кода равна порядку элемента а, то локаторы А, и определяются однозначно. Если произошла только одна ошибка, то положим если ошибок не произошло, то .

Пусть Эти элементы, известные также под названием компонент синдрома, вычисляются непосредственно по принятому слову Так как являются корнями то Предположим, что произошли две ошибки: Но это в точности дает систему двух уравнений относительно двух неизвестных в поле

Если может произойти не более двух ошибок, то величина равна нулю тогда и только тогда, когда не произошло ни одной ошибки. Декодер должен продолжать работу в том случае, когда отлично от нуля. Если выписанная система из двух нелинейных уравнений однозначно разрешима относительно то две ошибки могут быть исправлены, и минимальное расстояние рассматриваемого кода равно по меньшей мере 5.

Прямого очевидного способа решения такой системы нет. Один из методов состоит во введении нового многочлена, определяемого так, чтобы локаторы ошибок были его корнями:

Если мы сумеем найти коэффициенты этого многочлена, то, разложив его на линейные множители, мы сможем найти Но над расширением поля

Таким образом,

если произошли одна или две ошибки. Многочлен в правой части нам известен, поскольку известны Локаторы ошибок являются корнями этого многочлена, а корни любого многочлена над полем определяются однозначно. Следовательно, код исправляет две ошибки.

Указав процедуру декодирования, мы установили, что выбранный многочлен порождает код, исправляющий две произвольные ошибки. Практически можно использовать любую удобную процедуру декодирования, и одной из них является процедура вычисления корней выписанного выше квадратного уравнения в Так как всего имеется возможностей выбора каждого из корней, то это часто делается методом проб и ошибок. Другие схемы декодирования будут рассмотрены в следующих главах.

Рассмотренные в настоящем параграфе коды, исправляющие две ошибки, служат иллюстрацией того, как построить

циклические коды над некоторым полем, используя лежащие в большем поле корни порождающих эти коды многочленов. В гл. 7 будет рассмотрен общий случай такого построения для произвольного поля символов и произвольного числа исправляемых ошибок.

Источник

In coding theory, a cyclic code is a block code, where the circular shifts of each codeword gives another word that belongs to the code. They are error-correcting codes that have algebraic properties that are convenient for efficient error detection and correction.

If 00010111 is a valid codeword, applying a right circular shift gives the string 10001011. If the code is cyclic, then 10001011 is again a valid codeword. In general, applying a right circular shift moves the least significant bit (LSB) to the leftmost position, so that it becomes the most significant bit (MSB); the other positions are shifted by 1 to the right.

Definition[edit]

Let be a linear code over a finite field (also called Galois field) GF(q) of block length . is called a cyclic code if, for every codeword ${displaystyle c=(c_{1},ldots ,c_{n})}$ from , the word ${displaystyle (c_{n},c_{1},ldots ,c_{n-1})}$ in $GF(q)^{n}$ obtained by a cyclic right shift of components is again a codeword. Because one cyclic right shift is equal to n-1 cyclic left shifts, a cyclic code may also be defined via cyclic left shifts. Therefore, the linear code is cyclic precisely when it is invariant under all cyclic shifts.

Cyclic codes have some additional structural constraint on the codes. They are based on Galois fields and because of their structural properties they are very useful for error controls. Their structure is strongly related to Galois fields because of which the encoding and decoding algorithms for cyclic codes are computationally efficient.

Algebraic structure[edit]

Cyclic codes can be linked to ideals in certain rings. Let $R=A[x]/(x^{n}-1)$ be a polynomial ring over the finite field A=GF(q) . Identify the elements of the cyclic code with polynomials in such that
$(c_{0},ldots ,c_{n-1})$ maps to the polynomial
$c_{0}+c_{1}x+cdots +c_{n-1}x^{n-1}$ : thus multiplication by corresponds to a cyclic shift. Then is an ideal in , and hence principal, since is a principal ideal ring. The ideal is generated by the unique monic element in of minimum degree, the generator polynomial .^[1]
This must be a divisor of $x^{n}-1$ . It follows that every cyclic code is a polynomial code.
If the generator polynomial has degree then the rank of the code is n-d .

The idempotent of is a codeword such that $e^{2}=e$ (that is, is an idempotent element of ) and is an identity for the code, that is for every codeword . If and are coprime such a word always exists and is unique;^[2] it is a generator of the code.

An irreducible code is a cyclic code in which the code, as an ideal is irreducible, i.e. is minimal in , so that its check polynomial is an irreducible polynomial.

Examples[edit]

For example, if ${displaystyle A=mathbb {F} _{2}}$ and n=3 , the set of codewords contained in cyclic code generated by is precisely

{displaystyle ((0,0,0),(1,1,0),(0,1,1),(1,0,1))}

It corresponds to the ideal in $mathbb {F} _{2}[x]/(x^{3}-1)$ generated by (1+x) .

The polynomial (1+x) is irreducible in the polynomial ring, and hence the code is an irreducible code.

The idempotent of this code is the polynomial $x+x^{2}$ , corresponding to the codeword .

Trivial examples[edit]

Trivial examples of cyclic codes are $A^{n}$ itself and the code containing only the zero codeword. These correspond to generators and $x^{n}-1$ respectively: these two polynomials must always be factors of $x^{n}-1$ .

Over GF(2) the parity bit code, consisting of all words of even weight, corresponds to generator x+1 . Again over GF(2) this must always be a factor of $x^{n}-1$ .

Quasi-cyclic codes and shortened codes[edit]

Before delving into the details of cyclic codes first we will discuss quasi-cyclic and shortened codes which are closely related to the cyclic codes and they all can be converted into each other.

Definition[edit]

Quasi-cyclic codes:^{[citation needed]}

An (n,k) quasi-cyclic code is a linear block code such that, for some which is coprime to , the polynomial ${displaystyle x^{b}c(x){pmod {x^{n}-1}}}$ is a codeword polynomial whenever c(x) is a codeword polynomial.

Here, codeword polynomial is an element of a linear code whose code words are polynomials that are divisible by a polynomial of shorter length called the generator polynomial. Every codeword polynomial can be expressed in the form , where g(x) is the generator polynomial. Any codeword $(c_{0},..,c_{n-1})$ of a cyclic code can be associated with a codeword polynomial, namely, $sum _{i=0}^{n-1}c_{i}*x^{i}$ . A quasi-cyclic code with equal to is a cyclic code.

Definition[edit]

Shortened codes:

An [n,k] linear code is called a proper shortened cyclic code if it can be obtained by deleting positions from an cyclic code.

In shortened codes information symbols are deleted to obtain a desired blocklength smaller than the design blocklength. The missing information symbols are usually imagined to be at the beginning of the codeword and are considered to be 0. Therefore, − is fixed, and then is decreased which eventually decreases . It is not necessary to delete the starting symbols. Depending on the application sometimes consecutive positions are considered as 0 and are deleted.

All the symbols which are dropped need not be transmitted and at the receiving end can be reinserted. To convert (n,k) cyclic code to shortened code, set symbols to zero and drop them from each codeword. Any cyclic code can be converted to quasi-cyclic codes by dropping every th symbol where is a factor of . If the dropped symbols are not check symbols then this cyclic code is also a shortened code.

Cyclic codes for correcting errors[edit]

Now, we will begin the discussion of cyclic codes explicitly with error detection and correction. Cyclic codes can be used to correct errors, like Hamming codes as cyclic codes can be used for correcting single error. Likewise, they are also used to correct double errors and burst errors. All types of error corrections are covered briefly in the further subsections.

The (7,4) Hamming code has a generator polynomial $g(x)=x^{3}+x+1$ . This polynomial has a zero in Galois extension field GF(8) at the primitive element alpha , and all codewords satisfy . Cyclic codes can also be used to correct double errors over the field GF(2) . Blocklength will be equal to $2^{m}-1$ and primitive elements alpha and $alpha ^{3}$ as zeros in the $GF(2^{m})$ because we are considering the case of two errors here, so each will represent one error.

The received word is a polynomial of degree n-1 given as

where e(x) can have at most two nonzero coefficients corresponding to 2 errors.

We define the Syndrome Polynomial, S(x) as the remainder of polynomial v(x) when divided by the generator polynomial g(x) i.e.

as .

For correcting two errors[edit]

Let the field elements $X_{1}$ and $X_{2}$ be the two error location numbers. If only one error occurs then $X_{2}$ is equal to zero and if none occurs both are zero.

Let $S_{1}={v}(alpha )$ and $S_{3}={v}(alpha ^{3})$ .

These field elements are called «syndromes». Now because g(x) is zero at primitive elements alpha and $alpha ^{3}$ , so we can write $S_{1}=e(alpha )$ and $S_{3}=e(alpha ^{3})$ . If say two errors occur, then

$S_{1}=alpha ^{i}+alpha ^{i'}$ and
$S_{3}=alpha ^{3i}+alpha ^{3i'}$ .

And these two can be considered as two pair of equations in $GF(2^{m})$ with two unknowns and hence we can write

$S_{1}=X_{1}+X_{2}$ and
$S_{3}=(X_{1})^{3}+(X_{2})^{3}$ .

Hence if the two pair of nonlinear equations can be solved cyclic codes can used to correct two errors.

Hamming code[edit]

The Hamming(7,4) code may be written as a cyclic code over GF(2) with generator $1+x+x^{3}$ . In fact, any binary Hamming code of the form Ham(r, 2) is equivalent to a cyclic code,^[3] and any Hamming code of the form Ham(r,q) with r and q-1 relatively prime is also equivalent to a cyclic code.^[4] Given a Hamming code of the form Ham(r,2) with rgeq 3 , the set of even codewords forms a cyclic $[2^{r}-1,2^{r}-r-2,4]$ -code.^[5]

Hamming code for correcting single errors[edit]

A code whose minimum distance is at least 3, have a check matrix all of whose columns are distinct and non zero. If a check matrix for a binary code has rows, then each column is an -bit binary number. There are $2^{m}-1$ possible columns. Therefore, if a check matrix of a binary code with $d_{min}$ at least 3 has rows, then it can only have $2^{m}-1$ columns, not more than that. This defines a $(2^{m}-1,2^{m}-1-m)$ code, called Hamming code.

It is easy to define Hamming codes for large alphabets of size . We need to define one matrix with linearly independent columns. For any word of size there will be columns who are multiples of each other. So, to get linear independence all non zero -tuples with one as a top most non zero element will be chosen as columns. Then two columns will never be linearly dependent because three columns could be linearly dependent with the minimum distance of the code as 3.

So, there are $(q^{m}-1)/(q-1)$ nonzero columns with one as top most non zero element. Therefore, a Hamming code is a $[(q^{m}-1)/(q-1),(q^{m}-1)/(q-1)-m]$ code.

Now, for cyclic codes, Let alpha be primitive element in $GF(q^{m})$ , and let $beta =alpha ^{q-1}$ . Then $beta ^{(q^{m}-1)/(q-1)}=1$ and thus beta is a zero of the polynomial $x^{(q^{m}-1)/(q-1)}-1$ and is a generator polynomial for the cyclic code of block length $n=(q^{m}-1)/(q-1)$ .

But for q=2 , . And the received word is a polynomial of degree n-1 given as

where, e(x)=0 or $x^{i}$ where represents the error locations.

But we can also use $alpha ^{i}$ as an element of $GF(2^{m})$ to index error location. Because , we have $v(alpha )=alpha ^{i}$ and all powers of alpha from to $2^{m}-2$ are distinct. Therefore, we can easily determine error location from $alpha ^{i}$ unless which represents no error. So, a Hamming code is a single error correcting code over GF(2) with $n=2^{m}-1$ and k=n-m .

Cyclic codes for correcting burst errors[edit]

From Hamming distance concept, a code with minimum distance 2t+1 can correct any errors. But in many channels error pattern is not very arbitrary, it occurs within very short segment of the message. Such kind of errors are called burst errors. So, for correcting such errors we will get a more efficient code of higher rate because of the less constraints. Cyclic codes are used for correcting burst error. In fact, cyclic codes can also correct cyclic burst errors along with burst errors. Cyclic burst errors are defined as

A cyclic burst of length is a vector whose nonzero components are among (cyclically) consecutive components, the first and the last of which are nonzero.

In polynomial form cyclic burst of length can be described as $e(x)=x^{i}b(x)mod (x^{n}-1)$ with b(x) as a polynomial of degree t-1 with nonzero coefficient $b_{0}$ . Here b(x) defines the pattern and $x^{i}$ defines the starting point of error. Length of the pattern is given by deg b(x)+1 . The syndrome polynomial is unique for each pattern and is given by

A linear block code that corrects all burst errors of length or less must have at least check symbols. Proof: Because any linear code that can correct burst pattern of length or less cannot have a burst of length or less as a codeword because if it did then a burst of length could change the codeword to burst pattern of length , which also could be obtained by making a burst error of length in all zero codeword. Now, any two vectors that are non zero in the first components must be from different co-sets of an array to avoid their difference being a codeword of bursts of length . Therefore, number of such co-sets are equal to number of such vectors which are $q^{2t}$ . Hence at least $q^{2t}$ co-sets and hence at least check symbol.

This property is also known as Rieger bound and it is similar to the Singleton bound for random error correcting.

Fire codes as cyclic bounds[edit]

In 1959, Philip Fire^[6] presented a construction of cyclic codes generated by a product of a binomial and a primitive polynomial. The binomial has the form $x^{c}+1$ for some positive odd integer .^[7] Fire code is a cyclic burst error correcting code over GF(q) with the generator polynomial

$g(x)=(x^{2t-1}-1)p(x)$

where p(x) is a prime polynomial with degree not smaller than and p(x) does not divide $x^{2t-1}-1$ . Block length of the fire code is the smallest integer such that g(x) divides
$x^{n}-1$ .

A fire code can correct all burst errors of length t or less if no two bursts b(x) and $x^{j}b'(x)$ appear in the same co-set. This can be proved by contradiction. Suppose there are two distinct nonzero bursts b(x) and $x^{j}b'(x)$ of length or less and are in the same co-set of the code. So, their difference is a codeword. As the difference is a multiple of g(x) it is also a multiple of $x^{2t-1}-1$ . Therefore,

$b(x)=x^{j}b'(x)mod (x^{2t-1}-1)$ .

This shows that is a multiple of 2t-1 , So

$b(x)=x^{l(2t-1)}b'(x)$

for some . Now, as l(2t-1) is less than and is less than $q^{m}-1$ so $(x^{l(2t-1)}-1)b(x)$ is a codeword. Therefore,

$(x^{l(2t-1)}-1)b(x)=a(x)(x^{2t-1}-1)p(x)$ .

Since b(x) degree is less than degree of p(x) , p(x) cannot divide b(x) . If is not zero, then p(x) also cannot divide $x^{l(2t-1)}-1$ as is less than $q^{m}-1$ and by definition of , p(x) divides $x^{l(2t-1)}-1$ for no smaller than $q^{m}-1$ . Therefore and equals to zero. That means both that both the bursts are same, contrary to assumption.

Fire codes are the best single burst correcting codes with high rate and they are constructed analytically. They are of very high rate and when and are equal, redundancy is least and is equal to 3t-1 . By using multiple fire codes longer burst errors can also be corrected.

For error detection cyclic codes are widely used and are called t-1 cyclic redundancy codes.

Cyclic codes on Fourier transform[edit]

Applications of Fourier transform are widespread in signal processing. But their applications are not limited to the complex fields only; Fourier transforms also exist in the Galois field GF(q) . Cyclic codes using Fourier transform can be described in a setting closer to the signal processing.

Fourier transform over finite fields[edit]

Fourier transform over finite fields

The discrete Fourier transform of vector $v=v_{0},v_{1},....,v_{n-1}$ is given by a vector $V=V_{0},V_{1},.....,V_{n-1}$ where,

$V_{k}$ = $Sigma _{i=0}^{n-1}e^{-j2pi n^{-1}ik}v_{i}$ where,

where exp() is an th root of unity. Similarly in the finite field th root of unity is element omega of order . Therefore

If $v=(v_{0},v_{1},....,v_{n-1})$ is a vector over , and be an element of of order , then Fourier transform of the vector is the vector $V=(V_{0},V_{1},.....,V_{n-1})$ and components are given by

$V_{j}$ = $Sigma _{i=0}^{n-1}omega ^{ij}v_{i}$ where,

Here is time index, is frequency and is the spectrum. One important difference between Fourier transform in complex field and Galois field is that complex field omega exists for every value of while in Galois field omega exists only if divides q-1 . In case of extension fields, there will be a Fourier transform in the extension field $GF(q^{m})$ if divides $q^{m}-1$ for some .
In Galois field time domain vector is over the field GF(q) but the spectrum may be over the extension field $GF(q^{m})$ .

Spectral description of cyclic codes[edit]

Any codeword of cyclic code of blocklength can be represented by a polynomial c(x) of degree at most n-1 . Its encoder can be written as . Therefore, in frequency domain encoder can be written as $C_{j}=A_{j}G_{j}$ . Here codeword spectrum $C_{j}$ has a value in $GF(q^{m})$ but all the components in the time domain are from GF(q) . As the data spectrum $A_{j}$ is arbitrary, the role of $G_{j}$ is to specify those where $C_{j}$ will be zero.

Thus, cyclic codes can also be defined as

Given a set of spectral indices, $A=(j_{1},....,j_{n-k})$ , whose elements are called check frequencies, the cyclic code is the set of words over GF(q) whose spectrum is zero in the components indexed by $j_{1},...,j_{n-k}$ . Any such spectrum will have components of the form $A_{j}G_{j}$ .

So, cyclic codes are vectors in the field GF(q) and the spectrum given by its inverse fourier transform is over the field $GF(q^{m})$ and are constrained to be zero at certain components. But every spectrum in the field $GF(q^{m})$ and zero at certain components may not have inverse transforms with components in the field GF(q) . Such spectrum can not be used as cyclic codes.

Following are the few bounds on the spectrum of cyclic codes.

BCH bound[edit]

If be a factor of $(q^{m}-1)$ for some . The only vector in $GF(q)^{n}$ of weight d-1 or less that has d-1 consecutive components of its spectrum equal to zero is all-zero vector.

Hartmann-Tzeng bound[edit]

If be a factor of $(q^{m}-1)$ for some , and an integer that is coprime with . The only vector in $GF(q)^{n}$ of weight d-1 or less whose spectral
components $V_{j}$ equal zero for $j=ell _{1}+ell _{2}b(mod n)$ , where $ell _{1}=0,....,d-s-1$ and $ell _{2}=0,....,s-1$ , is the all zero vector.

Roos bound[edit]

If be a factor of $q^{m}-1$ for some and . The only vector in
$GF(q)^{n}$ of weight d-1 or less whose spectral components $V_{j}$ equal to zero for $j=l_{1}+l_{2}b(mod n)$ , where $l_{1}=0,...,d-s-2$ and $l_{2}$ takes at least s+1 values in the range , is the all-zero vector.

Quadratic residue codes[edit]

When the prime is a quadratic residue modulo the prime there is a quadratic residue code which is a cyclic code of length , dimension (p+1)/2 and minimum weight at least over GF(l) .

Generalizations[edit]

A constacyclic code is a linear code with the property that for some constant λ if (c₁,c₂,…,c_n) is a codeword then so is (λc_n,c₁,…,c_n-1). A negacyclic code is a constacyclic code with λ=-1.^[8] A quasi-cyclic code has the property that for some s, any cyclic shift of a codeword by s places is again a codeword.^[9] A double circulant code is a quasi-cyclic code of even length with s=2.^[9] Quasi-twisted codes and multi-twisted codes are further generalizations of constacyclic codes.^[10]^[11]

Notes[edit]

^ Van Lint 1998, p. 76
^ Van Lint 1998, p. 80
^ Hill 1988, pp. 159–160
^ Blahut 2003, Theorem 5.5.1
^ Hill 1988, pp. 162–163
^ P. Fire, E, P. (1959). A class of multiple-error-correcting binary codes for non-independent errors. Sylvania Reconnaissance Systems Laboratory, Mountain View, CA, Rept. RSL-E-2, 1959.
^ Wei Zhou, Shu Lin, Khaled Abdel-Ghaffar. Burst or random error correction based on Fire and BCH codes. ITA 2014: 1-5 2013.
^ Van Lint 1998, p. 75
^ ^a ^b MacWilliams & Sloane 1977, p. 506
^ Aydin, Nuh; Siap, Irfan; K. Ray-Chaudhuri, Dijen (2001). «The Structure of 1-Generator Quasi-Twisted Codes and New Linear Codes». Designs, Codes and Cryptography. 24 (3): 313–326. doi:10.1023/A:1011283523000. S2CID 17376783.
^ Aydin, Nuh; Halilović, Ajdin (2017). «A generalization of quasi-twisted codes: multi-twisted codes». Finite Fields and Their Applications. 45: 96–106. doi:10.1016/j.ffa.2016.12.002. S2CID 7694655.

References[edit]

Blahut, Richard E. (2003), Algebraic Codes for Data Transmission (2nd ed.), Cambridge University Press, ISBN 0-521-55374-1
Hill, Raymond (1988), A First Course In Coding Theory, Oxford University Press, ISBN 0-19-853803-0
MacWilliams, F. J.; Sloane, N. J. A. (1977), The Theory of Error-Correcting Codes, New York: North-Holland Publishing, ISBN 0-444-85011-2
Van Lint, J. H. (1998), Introduction to Coding Theory, Graduate Texts in Mathematics 86 (3rd ed.), Springer Verlag, ISBN 3-540-64133-5

External links[edit]

John Gill’s (Stanford) class notes – Notes #3, October 8, Handout #9, EE 387.
Jonathan Hall’s (MSU) class notes – Chapter 8. Cyclic codes — pp. 100 — 123
David Terr. «Cyclic Code». MathWorld.

This article incorporates material from cyclic code on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Источник

Definition[edit]

Algebraic structure[edit]

An irreducible code is a cyclic code in which the code, as an ideal is irreducible, i.e. is minimal in , so that its check polynomial is an irreducible polynomial.

Examples[edit]

For example, if ${displaystyle A=mathbb {F} _{2}}$ and n=3 , the set of codewords contained in cyclic code generated by is precisely

It corresponds to the ideal in $mathbb {F} _{2}[x]/(x^{3}-1)$ generated by (1+x) .

The polynomial (1+x) is irreducible in the polynomial ring, and hence the code is an irreducible code.

The idempotent of this code is the polynomial $x+x^{2}$ , corresponding to the codeword .

Trivial examples[edit]

Over GF(2) the parity bit code, consisting of all words of even weight, corresponds to generator x+1 . Again over GF(2) this must always be a factor of $x^{n}-1$ .

Quasi-cyclic codes and shortened codes[edit]

Before delving into the details of cyclic codes first we will discuss quasi-cyclic and shortened codes which are closely related to the cyclic codes and they all can be converted into each other.

Definition[edit]

Quasi-cyclic codes:^{[citation needed]}

Definition[edit]

Shortened codes:

An [n,k] linear code is called a proper shortened cyclic code if it can be obtained by deleting positions from an cyclic code.

Cyclic codes for correcting errors[edit]

The received word is a polynomial of degree n-1 given as

where e(x) can have at most two nonzero coefficients corresponding to 2 errors.

We define the Syndrome Polynomial, S(x) as the remainder of polynomial v(x) when divided by the generator polynomial g(x) i.e.

as .

For correcting two errors[edit]

Let the field elements $X_{1}$ and $X_{2}$ be the two error location numbers. If only one error occurs then $X_{2}$ is equal to zero and if none occurs both are zero.

Let $S_{1}={v}(alpha )$ and $S_{3}={v}(alpha ^{3})$ .

$S_{1}=alpha ^{i}+alpha ^{i'}$ and
$S_{3}=alpha ^{3i}+alpha ^{3i'}$ .

And these two can be considered as two pair of equations in $GF(2^{m})$ with two unknowns and hence we can write

$S_{1}=X_{1}+X_{2}$ and
$S_{3}=(X_{1})^{3}+(X_{2})^{3}$ .

Hence if the two pair of nonlinear equations can be solved cyclic codes can used to correct two errors.

Hamming code[edit]

Hamming code for correcting single errors[edit]

So, there are $(q^{m}-1)/(q-1)$ nonzero columns with one as top most non zero element. Therefore, a Hamming code is a $[(q^{m}-1)/(q-1),(q^{m}-1)/(q-1)-m]$ code.

But for q=2 , . And the received word is a polynomial of degree n-1 given as

where, e(x)=0 or $x^{i}$ where represents the error locations.

Cyclic codes for correcting burst errors[edit]

A cyclic burst of length is a vector whose nonzero components are among (cyclically) consecutive components, the first and the last of which are nonzero.

This property is also known as Rieger bound and it is similar to the Singleton bound for random error correcting.

Fire codes as cyclic bounds[edit]

$g(x)=(x^{2t-1}-1)p(x)$

where p(x) is a prime polynomial with degree not smaller than and p(x) does not divide $x^{2t-1}-1$ . Block length of the fire code is the smallest integer such that g(x) divides
$x^{n}-1$ .

$b(x)=x^{j}b'(x)mod (x^{2t-1}-1)$ .

This shows that is a multiple of 2t-1 , So

$b(x)=x^{l(2t-1)}b'(x)$

for some . Now, as l(2t-1) is less than and is less than $q^{m}-1$ so $(x^{l(2t-1)}-1)b(x)$ is a codeword. Therefore,

$(x^{l(2t-1)}-1)b(x)=a(x)(x^{2t-1}-1)p(x)$ .

For error detection cyclic codes are widely used and are called t-1 cyclic redundancy codes.

Cyclic codes on Fourier transform[edit]

Fourier transform over finite fields[edit]

Fourier transform over finite fields

The discrete Fourier transform of vector $v=v_{0},v_{1},....,v_{n-1}$ is given by a vector $V=V_{0},V_{1},.....,V_{n-1}$ where,

$V_{k}$ = $Sigma _{i=0}^{n-1}e^{-j2pi n^{-1}ik}v_{i}$ where,

where exp() is an th root of unity. Similarly in the finite field th root of unity is element omega of order . Therefore

If $v=(v_{0},v_{1},....,v_{n-1})$ is a vector over , and be an element of of order , then Fourier transform of the vector is the vector $V=(V_{0},V_{1},.....,V_{n-1})$ and components are given by

$V_{j}$ = $Sigma _{i=0}^{n-1}omega ^{ij}v_{i}$ where,

Spectral description of cyclic codes[edit]

Thus, cyclic codes can also be defined as

Following are the few bounds on the spectrum of cyclic codes.

BCH bound[edit]

If be a factor of $(q^{m}-1)$ for some . The only vector in $GF(q)^{n}$ of weight d-1 or less that has d-1 consecutive components of its spectrum equal to zero is all-zero vector.

Hartmann-Tzeng bound[edit]

Roos bound[edit]

Quadratic residue codes[edit]

When the prime is a quadratic residue modulo the prime there is a quadratic residue code which is a cyclic code of length , dimension (p+1)/2 and minimum weight at least over GF(l) .

Generalizations[edit]

Notes[edit]

^ Van Lint 1998, p. 76
^ Van Lint 1998, p. 80
^ Hill 1988, pp. 159–160
^ Blahut 2003, Theorem 5.5.1
^ Hill 1988, pp. 162–163
^ P. Fire, E, P. (1959). A class of multiple-error-correcting binary codes for non-independent errors. Sylvania Reconnaissance Systems Laboratory, Mountain View, CA, Rept. RSL-E-2, 1959.
^ Wei Zhou, Shu Lin, Khaled Abdel-Ghaffar. Burst or random error correction based on Fire and BCH codes. ITA 2014: 1-5 2013.
^ Van Lint 1998, p. 75
^ ^a ^b MacWilliams & Sloane 1977, p. 506
^ Aydin, Nuh; Siap, Irfan; K. Ray-Chaudhuri, Dijen (2001). «The Structure of 1-Generator Quasi-Twisted Codes and New Linear Codes». Designs, Codes and Cryptography. 24 (3): 313–326. doi:10.1023/A:1011283523000. S2CID 17376783.
^ Aydin, Nuh; Halilović, Ajdin (2017). «A generalization of quasi-twisted codes: multi-twisted codes». Finite Fields and Their Applications. 45: 96–106. doi:10.1016/j.ffa.2016.12.002. S2CID 7694655.

References[edit]

Blahut, Richard E. (2003), Algebraic Codes for Data Transmission (2nd ed.), Cambridge University Press, ISBN 0-521-55374-1
Hill, Raymond (1988), A First Course In Coding Theory, Oxford University Press, ISBN 0-19-853803-0
MacWilliams, F. J.; Sloane, N. J. A. (1977), The Theory of Error-Correcting Codes, New York: North-Holland Publishing, ISBN 0-444-85011-2
Van Lint, J. H. (1998), Introduction to Coding Theory, Graduate Texts in Mathematics 86 (3rd ed.), Springer Verlag, ISBN 3-540-64133-5

External links[edit]

John Gill’s (Stanford) class notes – Notes #3, October 8, Handout #9, EE 387.
Jonathan Hall’s (MSU) class notes – Chapter 8. Cyclic codes — pp. 100 — 123
David Terr. «Cyclic Code». MathWorld.

This article incorporates material from cyclic code on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Источник

Основной недостаток применения групповых
линейных кодов – сложность кодирующих
и декодирующих устройств, являющихся
устройствами параллельного типа. Переход
к циклическим кодам позволяет упростить
схемную реализацию кодирующих и
декодирующих устройств за счет
многотактных способов обработки
циклических кодов с помощью сдвиговых
регистров. Таким образом, в системах,
использующих циклические коды,
«обменивают» увеличение времени
кодирования и декодирования на упрощение
аппаратуры. Циклическим кодом называют
такой групповой код, который замкнут
относительно циклической перестановки
любой кодовой комбинации этого кода,
т.е. в результате циклической перестановки
любого кодового вектора получается
кодовый вектор, принадлежащий этому же
циклическому коду.

Циклической перестановкой называется
такая перестановка, при которой все
разряды смещаются в сторону старших
разрядов, причем последний разряд
переходит на место первого.

1.2 Построение цк

Циклическим кодом называется циклического
векторное пространство, обладающее
всеми свойствами группового кода, но
замкнутого не только относительно
линейных операций, но и относительно
операции циклического сдвига. В результате
циклического сдвига любого кодового
вектора получается кодовый вектор,
принадлежащий этому же векторному
пространству. В основе циклических
кодов лежит алгебра полиномов по модулю
над
пространственным полем (полем Галуа).

Циклическим сдвигом называется такой
сдвиг, при котором все разряды смещаются
в сторону старших разрядов, причем
последний разряд переходит на место
первого.

Пусть

Тогда после циклического сдвига получим

Математической основой построения
циклических кодов является представление
любого двоичного числа в виде полинома,
содержащего переменную Х, причем двоичные
цифры являются коэффициентами при этой
переменной.

Пример 1

В дальнейшем, если нет особых замечаний,
высшие степени пишем справа. Над такими
полиномами можно производить все
операции согласно законам алгебры.
Однако при всех операциях суммирование
производиться по модулю 2 (без переносов
в старшие разряды в отличие от
арифметического суммирования).

Вычитание, используемое при делении
полиномов, также необходимо осуществлять
по модулю два (mod2), и оно
заменяется эквивалентной операцией
суммирования поmod2.

Пример 2

Циклический код полностью задаётся
так называемым порождающим полиномом
g(x) степениk, гдеk–
число контрольных (избыточных) символов
циклического кода.

Кодовые комбинации циклического кода
строятся так, чтобы соответствующие им
полиномы делились без остатка на g(x).
С другой стороны, циклический код может
быть полностью определен многочленомh(x) степениm, гдеm–
число информационных символов циклического
кода:

(1)

n– число разрядов (длина)
циклического кода (n=m+k):

Полином, соответствующий кодовой
комбинации циклического кода, имеет
вид:

Циклические коды, исправляющие одну
ошибку (),
либо исправляющие одну и обнаруживающие
две ошибки ()
называются циклическими кодами Хемминга.

Для циклических кодов Хемминга имеет
место

Пример 3

Наибольший интерес представляют
систематические циклические коды, так
как они позволяют наиболее просто
реализовать кодирующие и декодирующие
устройства. Условимся в любом
систематическом циклическом коде первые
символов, т.е. коэффициенты привсегда
выбирать в качестве проверочных символов,
а последниеmсимволов,
т.е. коэффициенты при— в качестве информационных символов.

Соседние файлы в папке Теория

#
#
#
#
#
03.07.20181.15 Mб3Теория.mht
#

Источник

4. Циклические коды

4.1 Основные понятия

Циклическим кодом
называется линейный блоковый (n,k)-код, который характеризуется свойством
цикличности, т.е. сдвиг влево на один шаг любого разрешенного кодового слова
дает также разрешенное кодовое слово, принадлежащее этому же коду и у которого,
множество кодовых слов представляется совокупностью многочленов степени (n-1) и
менее, делящихся на некоторый многочлен g(x) степени r = n-k, являющийся
сомножителем двучлена xⁿ+1.
Многочлен g(x) называется
порождающим.
Как следует из определения, в циклическом коде кодовые слова
представляются в виде многочленов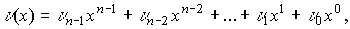

где n — длина кода;

— коэффициенты из поля GF(q).
Если код построен над полем GF(2), то
коэффициенты принимают значения 0 или 1 и код называется двоичным.

Пример. Если кодовое слово циклического кода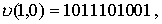

то соответствующий
ему многочлен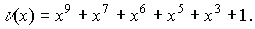
Например, если код
построен над полем GF(q)=GF(2³), которое является расширением GF(2)
по модулю неприводимого многочлена f(z)=z³+z+1, а элементы этого поля
имеют вид, представленный в таблице 3,

Таблица 3

0	000	0	a³	011	Z+1
a⁰	001	1	a⁴	110	Z²+Z
a¹	010	Z	a⁵	111	Z²+Z+1
a²	100	Z²	a⁶	101	Z²+1

то
коэффициенты 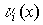принимают значения
элементов этого поля и поэтому они сами отображаются в виде многочленов
следующего вида

где m — степень многочлена, по которому получено расширение поля GF(2);

a_i — коэффициенты, принимающие значение элементов GF(2), т.е. 0 и
1.
Такой код называется q-ным.
Длина циклического кода
называется примитивной и сам код называется примитивным, если его длина
n=q^m-1 над GF(q).
Если длина кода меньше длины примитивного кода,
то код называется укороченным или непримитивным.
Как следует
из определения общее свойство кодовых слов циклического кода — это их делимость
без остатка на некоторый многочлен g(x), называемый порождающим.
Результатом деления двучлена xⁿ+1 на многочлен g(x)
является проверочный многочлен h(x).
При декодировании
циклических кодов используются многочлен ошибок e(x) и синдромный многочлен
S(x).
Многочлен ошибок степени не более (n-1) определяется из выражения

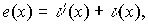
где —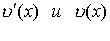
многочлены, отображающие соответственно принятое (с ошибкой) и переданное
кодовые слова.
Ненулевые коэффициенты в е(x) занимают позиции, которые
соответствуют ошибкам.
Пример.

Синдромный многочлен, используемый при декодировании циклического
кода, определяется как остаток от деления принятого кодового слова на
порождающий многочлен, т.е.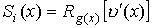

или

Следовательно, синдромный многочлен зависит непосредственно от многочлена
ошибок е(х).Это положение используется при построении таблицы
синдромов, применяемой в процессе декодирования. Эта таблица содержит список
многочленов ошибок (см. первый столбец стандартного расположения кода в разделе
2.4) и список соответствующих синдромов, определяемых из выражения 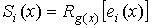(см.
таблицу 4).

Таблица 4

(x)	S(x)
1	R_g(x)[1]
X	R_g(x)[x]
X²	R_g(x)[x2]
·	·
·	·
·	·
X+1	R_g(x)[x+1]
X²+1	R_g(x)[x2+1]
·	·
·	·
·	·

В процессе
декодирования по принятому кодовому слову вычисляется синдром, затем в таблице
находится соответствующий многочлен е(х), суммирование которого с принятым
кодовым словом дает исправленное кодовое слово, т.е.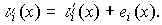

Перечисленные
многочлены 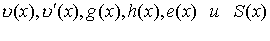можно складывать,
умножать и делить, используя известные правила алгебры, но с приведением
результата по mod 2, а затем по mod xⁿ+1, если степень результата
превышает степень (n-1).
Примеры.

Допустим,
что длина кода n=7, то результат приводим по mod x⁷+1.

При
построении и декодировании циклических кодов в результате деления многочленов
обычно необходимо иметь не частное, а остаток от деления.
Поэтому
рекомендуется более простой способ деления, используя не многочлены, а только
его коэффициенты (вариант 2 в примере).

Пример.: 1.; 2.

4.2 Матричное задание кодов

Циклический
код может быть задан порождающей и проверочной матрицами. Для их построения
достаточно знать порождающий g(x) и проверочный h(x) многочлены.
Для несистематического циклического кода матрицы строятся
циклическим сдвигом порождающего и проверочного многочленов, т.е. путем их
умножения на x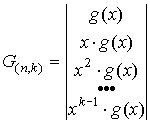
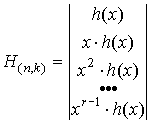
и
При построении
матрицы H_(n,k) старший коэффициент многочлена h(x) располагается
справа.
Пример. Для циклического (7,4)-кода с порождающим многочленом
g(x)=x³+x+1 матрицы G_(n,k) и H_(n,k) имеют вид:

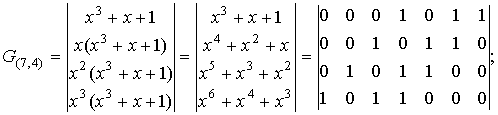
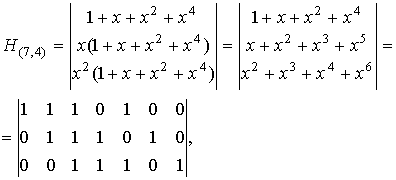
где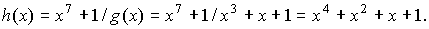
Для систематического циклического кода матрица G_(n,k)
определяется из выражения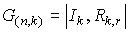

где

I_k — единичная матрица;
R_k,r — прямоугольная
матрица.
Строки матрицы R_k,r определяются из выражений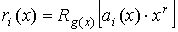
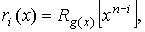
или
где
a_i(x) — значение i-той строки матрицы I_k;
i — номер
строки матрицы R_k,r.
Пример. Матрица G_(n,k) для
(7,4)-кода на основе порождающего многочлена g(x)=x³+x+1, строится в
следующей последовательности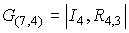

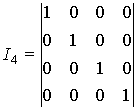
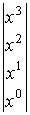
или
Определяется
R_4,3, используя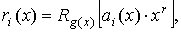
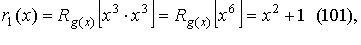
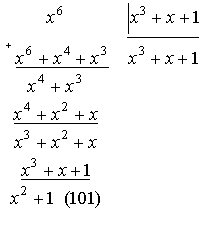
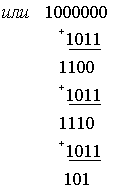
так как

Аналогичным способом
определяется

В результате получаем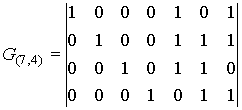
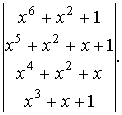
или
Используя выражение

получим тот же результат.
Строки матрицы G_(n,k) можно определить
непосредственно из выражения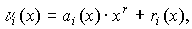
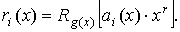
где
Проверочная матрица в систематическом виде строится на основе
матрицы G_(n,k), а именно: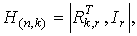

где

I_r — единичная матрица;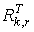
— матрица из
G_(n,k) в транспонированном виде.
Пример. Для (7,4)-кода
матрица H_(n,k) будет иметь вид: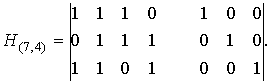

Одна из основных
задач, стоящих перед разработчиками устройств защиты от ошибок при передаче
дискретных сообщений по каналам связи является выбор порождающего многочлена
g(x) для построения циклического кода, обеспечивающего требуемое минимальное
кодовое расстояние для гарантийного обнаружения и исправления t-кратных ошибок.

Существуют специальные таблицы по выбору g(x) в зависимости от предъявляемых
требований к корректирующим возможностям кода. Однако у каждого циклического
кода имеются свои особенности формирования g(x). Поэтому при изучении конкретных
циклических кодов будут рассматриваться соответствующие способы построения g(x).

4.3 Коды БЧХ

Одним из классов
циклических кодов, способных исправлять многократные ошибки, являются коды БЧХ.

Примитивным кодом БЧХ, исправляющим t_u ошибок,
называется код длиной n=q^m-1 над GF(q), для которого элементы 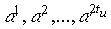являются
корнями порождающего многочлена.
Здесь a —
примитивный элемент GF(q^m).
Порождающий многочлен
определяется из выражения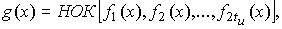
где
f₁(x),f₂(x)…- минимальные многочлены корней g(x).

Число проверочных элементов кода БЧХ удовлетворяет соотношению

Пример. Определить значение порождающего многочлена для построения
примитивного кода БЧХ над GF(2) длины 31, исправляющего двух кратные ошибки
(t_u=2).
Исходя из определения кода БЧХ корнями многочлена g(x)
являются: 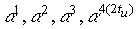, где a — примитивный элемент GF(q^m)=GF(2⁵).

Порождающий многочлен определяется из выражения 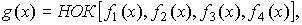где f₁(x),
f₂(x), f₃(x), f₄(x) — минимальные многочлены
корней соответственно .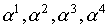
Примечание.
Минимальный многочлен элемента b поля
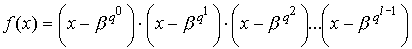
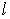
GF(q^m) определяется из выражения , где — наименьшее целое
число, при котором .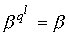
Значения
минимальных многочленов будут следующими: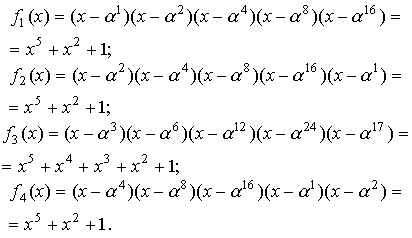

Так как f1(x)=
f2(x)= f4(x), то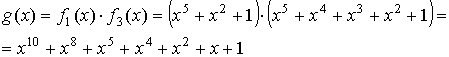

На
практике при определении значений порождающего многочлена пользуются специальной
таблицей минимальных многочленов (см. таблицу 8 приложения), и выражением для
порождающего многочлена 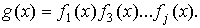При этом работа
осуществляется в следующей последовательности.
По заданной длине кода n и
кратности исправляемых ошибок t_u определяют:
— из выражения
n=2^m-1 значение параметра m, который является максимальной степенью
сомножителей g(x);
— из выражения j=2t_u-1 максимальный порядок
минимального многочлена, входящего в число сомножителей g(x).
— пользуясь
таблицей минимальных многочленов, определяется выражение для g(x) в зависимости
от m и j. Для этого из колонки, соответствующей параметру m, выбираются
многочлены с порядками от 1 до j, которые в результате перемножения дают
значение g(x).
Примечание.
В выражении для g(x) содержаться минимальные
многочлены только для нечетных степеней a, так как
обычно соответствующие им минимальные многочлены четных степеней a имеют аналогичные выражения.
Например, минимальные
многочлены элементов 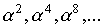соответствуют
минимальному многочлену элемента a¹,
минимальные многочлены элементов 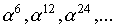соответствуют
минимальному многочлену a³ и т.п.

Пример. Определить значение порождающего многочлена для построения
примитивного кода БЧХ над GF(2) длины 31, обеспечивающего t_u=3.

Определяем значения m и j.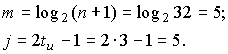

Из таблицы
минимальных многочленов в соответствии с m=5 и j=5 получаем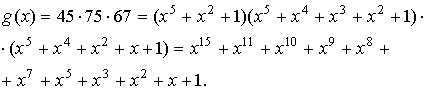

Заданные исходные
данные: n и t_u или k и t_u для построения циклического кода
часто приводят к выбору завышенного значения m и как следствие этого к
неоправданному увеличению длины кода. Такое положение снижает эффективность
полученного кода, так как часть информационных разрядов вообще не используется.

Пример. Требуется построить циклический код, исправляющий двух
кратные ошибки, если длина информационной части кода k=40.
Согласно
выражению для примитивного кода n=2^m-1, ближайшая длина кода равна
63, для которой m=6, а r=mt_u=12. Следовательно, код будет иметь n=63,
k=51. Неиспользованных информационных разрядов будет 11(51-40).
Подобное
несоответствие в ряде случаев можно устранить, применяя непримитивный код БЧХ.

Непримитивным кодом БЧХ, исправляющим t_u ошибок,
называется код длины n над GF(q), для которого элементы 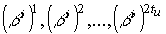являются корнями
порождающего многочлена.
Здесь bⁱ-непримитивный элемент GF(q^m), а
длина кода n равна порядку элемента bⁱ.

Примечание.
Порядком элемента bⁱ
является наименьшее n, для которого .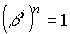
Пример.
Порядок элемента b³ поля GF(2⁶)
равен 21, так как .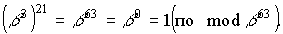
Порождающий многочлен непримитивного кода БЧХ, по аналогии с
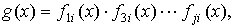
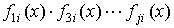
примитивным кодом, определяется из выражения — минимальные многочлены
элементов 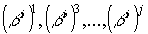поля
GF(q^m), которые являются корнями g(x); i — степень непримитивного
элемента b.
Пример. Определить значение g(x)
для построения непримитивного кода БЧХ над GF(2) длины n=20, исправляющего двух
кратные ошибки.
Из таблицы непримитивных элементов GF(2^m) (см.
таблицу 7 приложения) выбираем поле, элемент b которого
имеет порядок больший, но близкий к заданному n.
Такими являются
GF(2⁶) и b³, порядок которого
n=21.
Так как j=2t_u-1=2(2-1=3, то выражение для g(x) будет иметь
вид

где f₃(x) и f₉(x) — минимальные многочлены элементов
b³ и b⁹
поля GF(2⁶).
Значения этих многочленов следующие: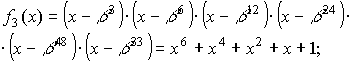

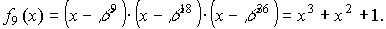
Выражения для
f₃(x) и f₉(x) можно определить из таблицы минимальных
многочленов, используя для этого параметр m выбранного поля GF(2^m) и
порядковые номера сомножителей g(x).
Для рассмотренного примера m=6, а
порядковые номера равны 3 и 9. Поэтому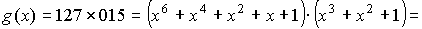
.

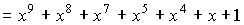
4.4 Способы кодирования

Задача кодирования
заключается в формировании по информационным словам a(x) кодовых слов u(x) циклического (n,k)-кода, который по своей структуре
может быть несистематическим и систематическим.
Формирование
кодовых слов несистематического кода заключается в умножении многочлена a(x),
отображающего информационную последовательность длины k, на порождающий
многочлен, т.е. u(x)=a(x)(g(x). Формирование кодовых
слов систематического кода заключается в преобразовании информационной
последовательности a(x) в соответствии с выражением u(x)=a(x)·x^r+r(x).
Проверочная последовательность r(x) определяется двумя способами:

при использовании «классического» способа кодирования ;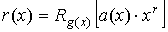
при использовании
способа кодирования, рекомендованного МККТТ ,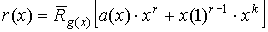
где
x(1)^r-1 — единичный многочлен степени (r-1).
Указанные выше
математические операции выполняют кодеры несистематического и систематического
кодов.

4.5 Способы декодирования с обнаружением ошибок

Процедура декодирования
циклического кода с обнаружением ошибок, по аналогии с процессом кодирования,
использует два способа:
— при кодировании «классическим»
способом декодирование основано на использовании свойства делимости без остатка
кодового многочлена u(x) циклического (n,k)-кода на
порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя
деление принятого кодового слова, описываемого многочленом 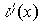на g(x), вычисление и
анализ остатка r(x). Если r(x)=0, то принятое кодовое слово считается
неискаженным. Если r(x)№0, то принятое кодовое слово
стирается и формируется сигнал «ошибка».
— при кодировании
способом МККТТ декодирование основано на свойстве получения определенного
контрольного остатка R₀(x) при делении принятого кодового многочлена
u(x) на порождающий многочлен. Поэтому, если полученный
при делении остаток 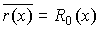, то принятое кодовое
слово считается неискаженным. Если остаток 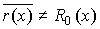, то принятое кодовое
слово стирается и формируется сигнал «ошибка».
Значение контрольного остатка
определяется из выражения .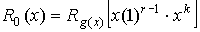

4.6 Способы декодирования с исправлением ошибок
и схемная реализация декодирующих устройств

Декодирование циклического
кода в режиме исправления ошибок можно осуществлять различными способами. Ниже
излагаются два способа, являющиеся наиболее простыми.
В
основу первого способа положено использование таблицы синдромов (декодирования),
в которой каждому многочлену или образцу ошибок e_i(x), соответствует
определенный синдром S_i(x), представляющий остаток от деления
принятого кодового слова 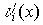и соответствующего ему
e_i(x) на g(x). Процедура декодирования следующая. Принятое кодовое
слово 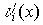делится на g(x),
определяется S_i(x) и соответствующий ему многочлен e_i(x),
а затем 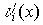суммируется с
e_i(x). В результате получаем исправленное кодовое слово, т.е. .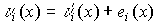

В состав декодера входят: вычислитель
синдрома (ВС), два регистра сдвига RG1 и RG2, постоянное запоминающее устройство
(ПЗУ), котороесодержит 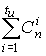слова длины n,
соответствующие многочленам ошибок e_i(x).
Принятое кодовое слово

поступает на вход вычислителя синдрома, где осуществляется деление его на g(x) и
формирование S_i(x), и одновременно — на вход RG2, где
накапливается. Синдром S_i(x) используется в качестве адреса, по
которому из ПЗУ в регистр RG1 записывается e_i(x), соответствующий
синдрому S_i(x). Перечисленные операции завершаются за n тактов. В
течение последующих n тактов происходит поэлементное суммирование содержимого
RG2 и RG1, т.е. операция 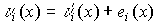, и исправление ошибок.

В основе второго способа исправления ошибок, позволяющего
значительно сократить объем используемых табличных синдромов и существенно
упростить схему декодера, лежат следующие положения:
1. Синдром
S_i(x), соответствующий принятому кодовому слову равен остатку от
деления 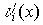на g(x), а также остатку
от деления соответствующего многочлена ошибок ei(x) на g(x), т.е. .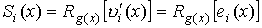
2.
Если S_i(x) соответствует 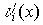и e_i(x), то
x( S_i(x) является синдромом, который соответствует и или .
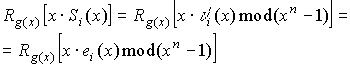
3.
При исправлении ошибок используются синдромы образцов ошибок только с ненулевым
коэффициентом в старшем разряде.
Поэтому при реализации
этого способа множество всех образцов ошибок разбивается на классы
эквивалентности. Каждый класс представляет циклический сдвиг одного образца
ошибок, а синдром этого класса соответствует образцу ошибок с ненулевым старшим
разрядом. Если вычисленный синдром принадлежит одному из классов эквивалентности
образцов исправляемых ошибок, то старший символ кодового слова исправляется.
Затем принятое слово и синдром циклически сдвигается, а процесс нахождения в
предыдущей по старшинству позиции повторяется.
Для исправления ошибок,
принадлежащих данному классу эквивалентности, нужно произвести n циклических
сдвигов.
Простейшим является декодер Меггитта. В состав декодера
входят: вычислитель синдрома, осуществляющий деление кодового слова 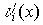на g(x)
и формирование соответствующего синдрома; блок декодеров (ДК), который настроен
на синдромы всех образцов исправляемых ошибок с ненулевыми старшими разрядами;
регистр сдвига RG.
При поступлении на вход схемы кодового слова 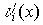его
символы заполняют регистр RG, а в вычислителе формируется соответствующий
синдром S_i(x). Вычисленный синдром сравнивается со всеми табличными
синдромами, заложенными в схему блока ДК, и в случае совпадения с одним из них
на его выходе формируется сигнал, который исправляет ошибочный символ,
находящийся в старшем разряде регистра. После этого содержимое вычислителя и RG
циклически сдвигается на один шаг. Этот сдвиг реализует операции 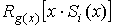и . Если
новый синдром совпадает с одним из табличных синдромов, то это означает, что
произошла ошибка во втором по старшинству символе кодового слова, который,
перейдя в старший разряд RG, исправляется. Затем производится новый циклический
сдвиг на одну позицию и новая проверка на совпадение синдромов. После повторения
этого процесса n раз в RG будет сформировано исправленное кодовое слово.
Введение обратной связи для RG не обязательно, так как в процессе исправления
ошибок символы кодового слова поступают на выход декодера.
Пример. Рассмотрим схему и работу декодера Меггитта
циклического (15,7)-кода, обеспечивающего исправление одиночных и двойных
ошибок, с g(x)=x⁸+ x⁷+ x⁶+ x⁴+1 (см.
рисунок 8).
Блок декодеров настраивается на 15 синдромов, которые
представлены в таблице 5 и соответствуют классам эквивалентности с образцами
ошибок в старшем разряде.

Таблица 5

№	е(х)	S(x)	№	е(х)	S(x)
1	x¹⁴	x⁷+ x⁶+x⁵+ x³	9	x¹⁴+ x⁶
2	x¹⁴+ x¹³	x⁷+ x⁴+x³+ x²	10	x¹⁴+ x⁵	x⁷+ x⁶+x³
3	x¹⁴+ x¹²	x⁷+ x⁶+x⁴+ x	11	x¹⁴+ x⁴	x⁷+ x⁶+x⁵+ x⁴+x³
4	x¹⁴+ x¹¹		12	x¹⁴+ x³	x⁷+ x⁶+x⁵
5	x¹⁴+ x¹⁰		13	x¹⁴+ x²	x⁷+ x⁶+x⁵+ x³+x²
6	x¹⁴+ x⁹		14	x¹⁴+ x¹	x⁷+ x⁶+x⁵+ x³+x
7	x¹⁴+ x⁸		15	x¹⁴+ x⁰	x⁷+ x⁶+x⁵+ x³+0
8	x¹⁴+ x⁷

Допустим, что
ошибки в 3 и 5 разрядах, т.е. им соответствует многочлен ошибки
e(x)=x¹²+x¹⁰.
При поступлении на вход декодера
искаженного кодового слова он заполняет регистр и в вычислителе формируется
синдром .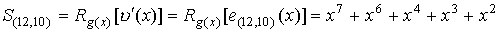
Блок декодеров не
реагирует на этот синдром.
Затем происходит сдвиг кодового слова в RG, а в
BC формируется новый синдром .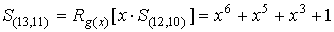
Блок декодеров и в
этом случае не срабатывает.
При следующем сдвиге кодового слова в RG первый
искаженный разряд занимает старшую позицию в RG, а в BC формируется синдром 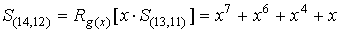, от
которого срабатывает БДК. В результате исправляется первая ошибка.
Следующим
сдвиг приводит к формированию синдрома .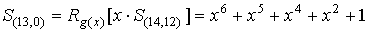
Этот синдром
соответствует многочлену ошибки e(x)=x¹³+x⁰, т.к. первый
искаженный разряд по обратной связи должен занять младшую позицию RG.
На
синдром S_(13,0) блок декодеров не реагирует.
При следующем сдвиге
кодового слова в RG второй искаженный разряд занимает старшую позицию в RG, а в
BC формируется синдром 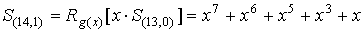, от которого срабатывает
БДК. В результате исправляется вторая ошибка в кодовом слове.

4.7 Коды Рида-Соломона (РС)

Коды РС
являются недвоичными циклическими кодами, символы кодовых слов которых берутся
из конечного поля GF(q). Здесь q степень некоторого простого числа, например
q=2^m.
Допустим, что РС-код построен над GF(8), которое является
расширением поля GF(2) по модулю примитивного многочлена f(z)=z³+z+1.
В этом случае символы кодовых слов кода будут иметь значения, представленные в
таблице 6.

Таблица 6

000	0	0	011	z+1	a³
001	1	a⁰	110	z²+z	a⁴
010	z	a¹	111	z²+z+1	a⁵
100	z²	a²	101	z²+1	a⁶

Кодовые слова РС-кода
отображаются в виде многочленов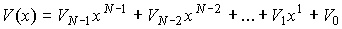
,
где N — длина кода;
V_i — q-ичные коэффициенты (символы кодовых слов), которые могут
принимать любое значение из GF(q).
Эти коэффициенты как это следует из
таблицы, также отображаются многочленами с двоичными коэффициентами 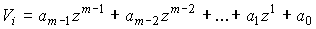. Коды РС являются максимальными, т.к. при длине кода N и
информационной последовательности k они обладают наибольшим кодовым расстоянием
d=N-k+1.
Порождающим многочленом g(x) РС-кода является делитель двучлена
x^N+1 степени меньшей N с коэффициентами из GF(q) при условии, что
элементы 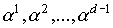этого поля являются
корнями g(x). Здесь 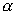— примитивный элемент
GF(q).
На основе этого определения, а также теоремы Безу,
выражение для порождающего многочлена РС-кода будет иметь вид .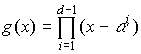

Степень g(x) равна d-1=N-k=R.
В РС-кодах принадлежность кодовых слов
данному коду определяется выполнением d-1 уравнений в соответствии с выражением

(*),
где V_i — символы-коэффициенты из GF(q);
z₀,
z₁… z_N-1 — ненулевые элементы GF(q).
Элементы
z₀, z₁… z_N-1 называются локаторами, т.е.
указывающими на номер позиции символа кодового слова.
Например, указателем i
— позиции является локатор zi или элемент aⁱ
GF(q).
Так как все локаторы должны быть различны и причем ненулевыми, то их
число в GF(q) равно q-1. Следовательно, такое количество символов должно быть в
кодовых словах кода.Поэтому обычно длина РС-кода определяется из
выражения N=q-1.
Пример. Допустим, что длина РС-кода равна N, кодовое
расстояние d=3, то в соответствии с (*) проверочными уравнениями будут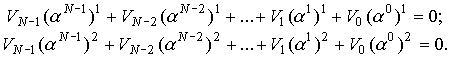

Свойства РС-кодов.

1. Циклический сдвиг кодовых слов, символы которых принимают значение из
GF(q), порождает новые кодовые слова этого же кода.
2. Сумма по mod2 двух и
более кодовых слов дает кодовое слово, принадлежащее этому же коду.
3.
Кодовое расстояние РС-кода определяется не по двоичным элементам, а по q-ичным
символам.
4. В РС-коде, исправляющем t_u ошибок порождающий
многочлен определяется из выражения 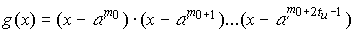. Обычно m₀
принимают равным 1. Однако, с помощью разумного выбора значения m₀,
иногда можно упростить схему кодера.
5. Корректирующие способности РС-кода
определяются его кодовым расстоянием.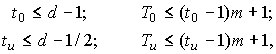

где T₀ и
T_u — длина пакетов, в которых обнаруживаются и исправляются ошибки.

Обнаружение ошибок в кодовых словах состоит в проверке условий ((), т.е.
определении синдрома 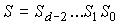, элементы которого
определяются из выражения .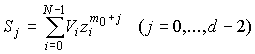
Пример. Требуется сформировать кодовое слово РС-кода над
GF(2³), соответствующее двоичной информационной последовательности
a(1,0)=000000011100101.
Так как m=3, то каждый q-ичный символ кода состоит
из трех двоичных элементов. Поэтому с учетом таблицы 6 a(x)=a³x²+ a²x+a⁶.

Определяем параметры кода.
N=q-1=7; k=5; R=2; d=N-k+1=3;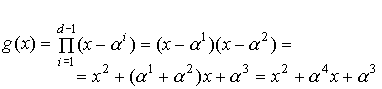
.

Кодовое слово формируется в соответствии с выражением.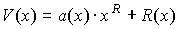
,
где
.

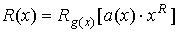
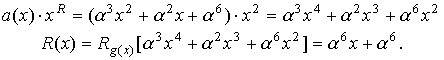
В
результате 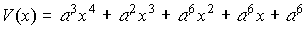или в двоичной форме
V(1,0)=000.000.011.100.101.101.101.