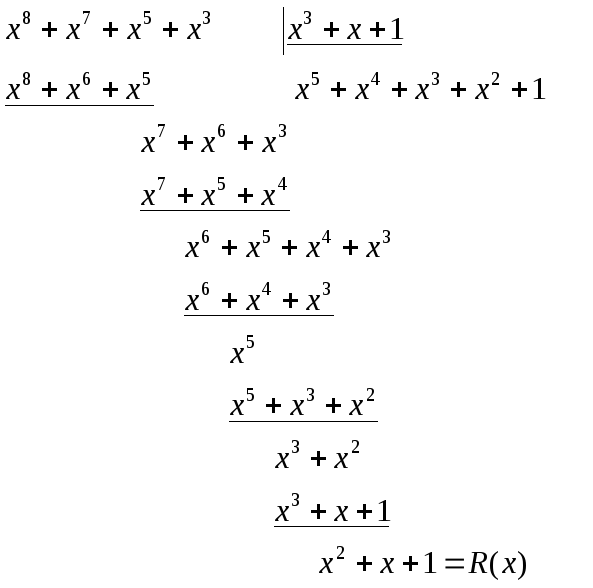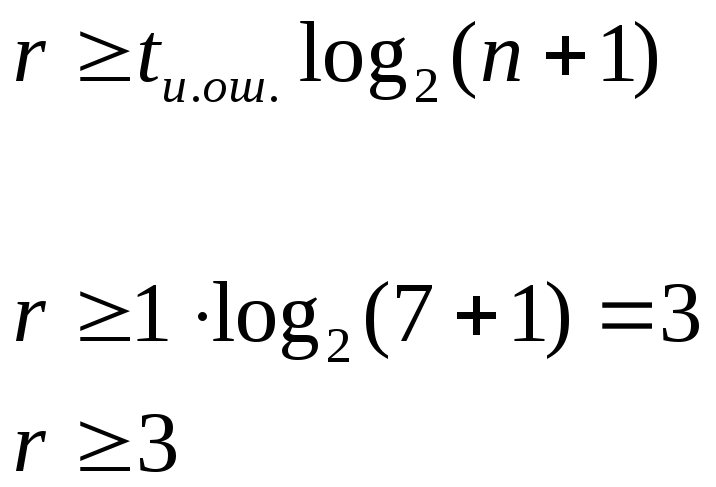Циклический
код
является разновидностью помехоустойчивых
кодов, применяется в технике передачи
дискретных сообщений. Особенности
циклических кодов заключены в двух
свойствах разрешенных кодовых комбинаций:
1. любая
из разрешенных кодовых комбинаций
циклического кода делится по модулю
два без остатка на некоторое, так
называемое «образующее двоичное число»,
определяющее помехоустойчивые свойства
кода, т.е. расстояние d;
2.
циклический сдвиг разрядов разрешенной
кодовой комбинации на один элемент
влево порождает другую разрешенную
кодовую комбинацию.
Например:
01011 и 10110 – две разрешенные кодовые
комбинации некоторого циклического
кода с образующим числом 1011 (d=3).
Поэтому они делятся по модулю два без
остатка на образующее число:
0
1011 10110 1011
0000
01
1011
10
1011
0000
1011
0000
000
000
При
этом d=4
>d=3.
Кроме
того циклический сдвиг на один разряд
влево элементов первой комбинации
порождают вторую комбинацию.
01011 => 10110
Делимость
без остатка разрешенных кодовых
комбинаций на известное образующее
число лежит в основе операций обнаружения
и исправления ошибок при использовании
циклических кодов.
Структурная
схема СПДС, содержит кодер и декодер
циклического кода. Структура разрешенных
кодовых комбинаций циклического кода
состоит из двух частей. В начале комбинации
располагается n-проверочных
разрядов, структура которых определяется
кодерами циклического кода из условия
обеспечения делимости без остатка
формируемой разрешенной кодовой
комбинации на образующее число.
Идея
построения циклического кода (n,k)
сводится к тому, что информационную
часть кодовой комбинации G(x)
нужно преобразовать в комбинацию F(x),
которая без остатка делится на порождающий
полином Р(х) степени r=n-k.
Рассмотрим последовательность операций
построения циклического кода:
1.
Представляем информационную часть
кодовой комбинации в виде полинома
G(x).
Например информационная часть 110101.
Тогда
.
2.
Умножаем G(x)
на одночлен
( старшую степень порождающего полинома
Р(х) ) и получаем.
Пусть
у нас порождающий полином 1011,
тогда
.
3. Делим
на
порождающий полином Р(х), при этом
получаем остаток от деленияR(x).
Добавим
полученный остаток R
(x)
к комбинации
и
получим комбинацию,
которая будет передана в линию. Данная
комбинацияF(x)
делится без остатка на образующий
полином и представляет собой разрешенную
кодовую комбинацию циклического (n,k)
кода. На приеме производится деление
полученной кодовой комбинации на
образующий полином. Если ошибок нет, то
деление пройдет без остатка. Если при
делении получен остаток, то комбинация
принята с ошибками.
При
использовании в циклических кодах
декодирования с исправлением ошибок
остаток от деления может играть роль
синдрома. Нулевой синдром указывает на
то, что принятая комбинация является
разрешенной. Всякому ненулевому синдрому
соответствует определенная конфигурация
ошибок, которая и исправляется.
Построение
кодеров, декодеров.
Пример:
Кодер
строится на основе полинома P(x).
=> 1011
–
веса
При
построении устройства число ячеек
регистров сдвига берется по высшей
степени образующего полинома
=>
3 регистра сдвига; число регистров
задержки берется также по высшей степени
образующего полинома; число сумматоров
по модулю два берется по весовой части
образующего полинома минус единица =>
3-1=2m.
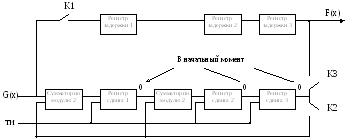
Состояния
регистров (1,2,3
– регистры; m
– сумматоры)
На
вход подается
110101000
Декодер
–
правила построения такие же, как у
кодера, но количество регистров задержки
определяется по высшей степени
информационной комбинации плюс 1
5+1=6
Деление
на образующий полином происходит за 9
тактов. Пока идет деление на образующий
полином К2 разомкнут, а К1 замкнут в
течении 6 тактов пока идет запись
информационных импульсов. После 6 такта
К1 размыкается. После 10 такта К2 замыкается
и формируется сигнал:
1. Если хотя бы в
одной ячейке регистра будет «1», то
значит произошла ошибка. Формируется
сигнал «1» и информация из регистров
сдвигов будет удаляться.
2. Если во всех
ячейках регистров сдвига будут «0», то
формируется сигнал «0» и информация
будет выдана потребителю.
Состояния
регистров
Если хотя бы в одной
ячейке регистра будет «1», то значит
произошла ошибка.
Информация из
регистров сдвигов будет удаляться. Если
во всех ячейках регистров сдвига будут
«0», то формируется сигнал «0» и информация
будет выдана потребителю.
Выбор образующего
полинома.
В
теории циклических кодов показано, что
образующий полином представляет собой
произведение так называемых минимальных
многочленов (),
являющихся простыми сомножителями,
(т.е. делящимися без остатка лишь на себя
и на 1).
Кроме
образующего полинома необходимо найти
и количество проверочных разрядов
r.
=1
если n=7,
то
tи.ош
– число ошибок, исправляемых циклическим
кодом.
После
определения количества проверочных
разрядов
r
вычисление образующего полинома удобно
осуществить, пользуясь таблицей
минимальных многочленов.
Ниже приведена часть такой таблицы.
|
r |
Pr(x) |
Двоичная |
|
2 |
|
111 |
|
3 |
|
1011 1101 |
В частности, если
r=3,
tи.ош=1,
j=2*1-1=1,
образующий полином будет представлять
собой единственный минимальный многочлен
P(x)= x3+x+1
(первая строка, второй столбец таблицы
). Соответственно образующее число равно
1011.
Синдром циклического
кода.
Синдром циклического
кода определяется суммой по модулю 2
принятых проверочных элементов и
элементов проверочной группы,
сформированных из принятых элементов
информационной группы. В циклическом
коде для определения синдрома следует
разделить принятую кодовую комбинацию
на кодовую комбинацию порождающего
полинома. Если все элементы приняты без
ошибок, то остаток от деления R(х)
равен нулю. Если есть ошибки, то остаток
не будет равен нулю. Следовательно,
синдромом циклического кода является
многочлен R(x).
Обнаружение и исправление ошибок
производится только на основе анализа
синдрома. В зависимости от остатка
определяется элемент в котором произошла
ошибка. Для исправления ошибок необходимо
чтобы количество ненулевых остатков
равнялось количеству элементов n
( при исправлении одной ошибки ) или
числу комбинаций из n.
Соседние файлы в папке Будылдина2
- #
11.04.20152.54 Mб24ДКР рисунок Mumarev.vsd
- #
11.04.20152.49 Mб30ДКР рисунок.vsd
- #
- #
- #
- #
Вычисление
синдрома для циклических кодов является
довольно простой процедурой.
Пусть
U(x)
и r(х)
‑
полиномы, соответствующие переданному
кодовому слову и принятой последовательности.
Разделив
r(x)
на g(x),
получим
r(x)
= q(x)
g(x)
+ s(x),
(1.73)
где
— q(x)
— частное от деления, s(x)
— остаток от деления.
Если
r(x)
является кодовым полиномом, то он делится
на g(x)
без остатка, то есть s(x)
= 0.
Следовательно,
s(x)
0
является условием наличия ошибки в
принятой последовательности, то есть
синдромом принятой последовательности.
Синдром
s(x)
имеет в общем случае вид
S(x)
= S0
+ S1
x + … + Sn-
k-1
xn-k-1
. (1.74)
Очевидно,
что схема вычисления синдрома является
схемой деления, подобной схемам
кодирования рис. 1.10 или 1.11 .
При
наличии в принятой последовательности
r
хотя бы одной ошибки вектор синдрома S
будет иметь, по крайней мере, один
нулевой элемент, при этом факт наличия
ошибки легко обнаружить, объединив по
ИЛИ
выходы всех ячеек регистра синдрома.
Покажем,
что синдромный многочлен S(x)
однозначно связан с многочленом ошибки
e(x),
а
значит, с его помощью можно не только
обнаруживать, но и локализовать ошибку
в принятой последовательности.
Пусть
e(x)
= e0
+ e1
x
+ e2
x2
+ … + en-1
x
n-1
(1.75)
— полином
вектора ошибки.
Тогда
полином принятой последовательности
r(x)
= U(x)
+ e(x).
(1.76)
Прибавим
в этом выражении слева и справа U(x),
а также учтем, что
r(x)
= q(x)
g(x) + S(x), U(x) = m(x)
g(x), (1.77)
тогда
,
(1.78)
то
есть синдромный
полином S(x)
есть
остаток от
деления полинома ошибки e(x)
на порождающий полином g(x).
Отсюда следует, что по синдрому S(x)
можно однозначно определить вектор
ошибки e(x), а следовательно,
исправить эту ошибку.
На рис. 1.14 приведена схема синдромного
декодера с исправлением однократной
ошибки для циклического (7,4)-кода.
По своей структуре она подобна схеме,
приведенной на рис. 1.6, с той лишь разницей,
что вычисление синдрома принятой
последовательности производится здесь
не умножением на проверочную матрицу,
а делением на порождающий полином. При
этом она сохраняет и недостаток, присущий
всем синдромным декодерам: необходимость
иметь запоминающее устройство, ставящее
в соответствие множеству возможных
синдромов S множество векторов
ошибок e. Цикличность структуры
кода в этом случае не учитывается.
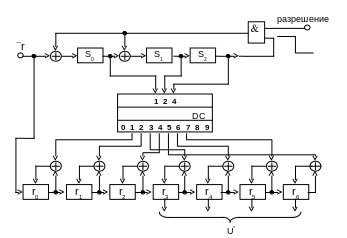
Рис.
1.14
1.3.4. Неалгебраические методы декодирования циклических кодов
Все
методы декодирования линейных блочных
кодов можно разбить на две группы:
алгебраические
и неалгебраические.
В
основе алгебраических методов лежит
решение систем уравнений, задающих
значение и расположение ошибок.
Рассмотренные синдромные декодеры
относятся именно к этой группе методов.
При
неалгебраических методах та же цель
достигается с помощью простых структурных
понятий теории кодирования, позволяющих
находить комбинации ошибок более простым
путем.
Одним
из неалгебраических методов является
декодирование с использованием алгоритма
Меггитта,
пригодного для исправления как одиночных,
так и l-кратных
ошибок (на практике l
3).
При
декодировании в соответствии с алгоритмом
Меггитта также вычисляется синдром
принятой последовательности S(x),
однако используется он иначе, нежели в
рассмотренных ранее синдромных декодерах.
Идея,
лежащая в основе декодера Меггитта,
очень проста и основывается на следующих
свойствах циклических кодов:
—
существует взаимно-однозначное
соответствие между множеством всех
исправляемых ошибок и множеством
синдромов;
—
если S(x)
— синдромный многочлен, соответствующий
многочлену ошибок е(x),
то xS(x)
mod
g(x)
— синдромный многочлен, соответствующий
x
e(x) mod (xn
+ 1).
Равенство
а(x)
= b(x) mod p(x)
читается как “а(x),
сравнимо с b(x)
по модулю р(x)”
и означает, что а(x)
и b(x)
имеют одинаковые остатки от деления на
полином p(x).
Таким
образом, второе
условие
означает, что если
комбинация ошибок циклически сдвинута
на одну позицию вправо, то для получения
нового синдрома нужно сдвинуть содержимое
регистра сдвига с обратными связями,
содержащего S(x),
также на одну позицию вправо.
Следовательно,
основным
элементом декодера Меггитта является
сдвиговый регистр. Структурная схема
декодера Меггитта для циклических кодов
произвольной длины приведена
на рис. 1.15.

Рис.
1.15
Декодер
работает следующим образом. Перед
началом работы содержимое всех разрядов
регистров равно нулю. Принимаемая
последовательность r
в
течение первых n
тактов вводится в буферный регистр и
одновременно с этим в (n—k)-разрядном
сдвиговом регистре с обратными связями
производится ее деление на порождающий
полином g(x).
Через
n
тактов
в буферном регистре оказывается принятое
слово r
,
a в регистре синдрома — остаток от
деления вектора ошибки на порождающий
полином.
Вычисленный
синдром сравнивается со всеми табличными
синдромами, и в случае совпадения с
одним из них старший разряд буферного
регистра исправляется путем прибавления
к его значению единицы.
После
этого синдромный и буферный регистры
один раз циклически сдвигаются. Это
реализует умножение S(x)
на
x
и деление на g(x).
Содержимое ячеек синдромного регистра
теперь равно остатку от деления xS(x)
на g(x)
или синдрому ошибки x
е(x) mod (Хn
+ 1).
Если
новый синдром совпадает с одним их
табличных, то исправляется очередная
ошибка и т.д. Через n
тактов
все позиции будут, таким образом,
исправлены.
Рассмотрим
работу декодера Меггитта для циклического
(7,4)-кода,
исправляющего одиночную ошибку. Схема
декодера изображена на рис. 1.16.

Рис.
1.16
Принцип
работы декодера заключается в том, что
независимо
от того, в какой позиции произошла
ошибка, осуществляется ее сдвиг в
последнюю ячейку буферного регистра с
соответствующим пересчетом синдрома
и ее исправление в этой позиции.
Полином
ошибки в старшем разряде для (7,4)-кода
Хемминга имеет вид е6
(x)
= x6,
соответствующий ему синдромный полином
S6
(x)
= 1 + x3
(
S
= (101)),
детектор ошибки настроен на это значение
синдрома.
Пусть,
например, передана последовательность
U
= (1001011),
ей соответствует кодовый полином U(x)
= 1 + x3
+ x5
+ x6.
Произошла ошибка в третьей позиции е(x)
= x3,
принятый вектор имеет вид r
= (1000011),
его полином r(x)
= 1 + x5
+ x6.
Kогда
принятая последовательность полностью
входит в буферный регистр, в регистре
синдрома оказывается синдром,
соответствующий ошибке е(x)
= x3
S3
= (110).
Поскольку он не совпадает с табличным
для е6,
на выходе детектора ошибок будет 0
и исправления не происходит.
Далее
производятся однократный циклический
сдвиг принятой последовательности в
буферном регистре, однократное деление
синдрома x∙S3
на порождающий полином в регистре с
обратными связями и проверка на совпадение
синдрома с заданным.
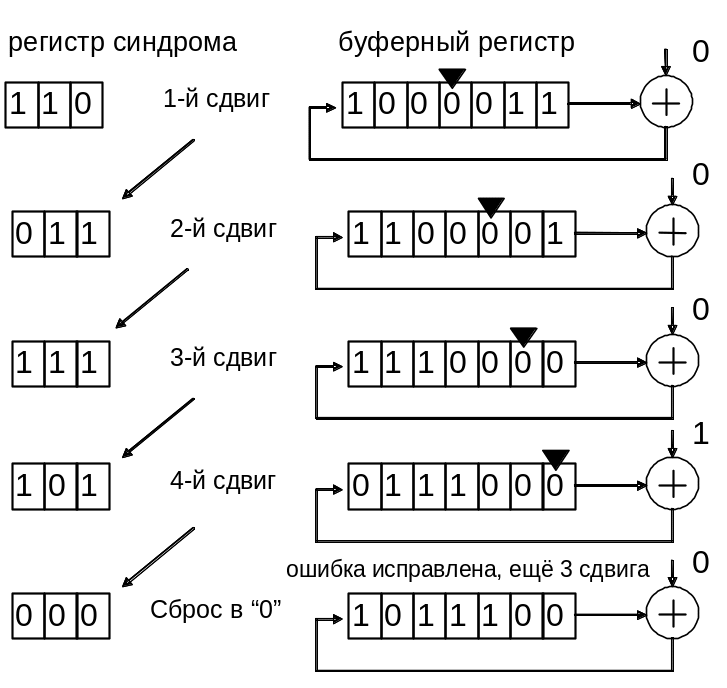
Последовательность
состояний регистров декодера в процессе
декодирования показана на рис. 1.17.
Рис.
1.17
Т
аким
образом, исправление ошибки в декодере
Меггитта осуществляется за 2n
тактов: в течение n
тактов производится ввод принятой
последовательности в буферный регистр,
в течение l
тактов
— исправление ошибки, и еще в течение
n
— l
— восстановление
буферного регистра в исходное состояние
с исправленным словом. Простота декодера
достигается увеличением времени
декодирования.
Следует
отметить, что в связи с успехами в
разработке БИС и устройств памяти в
значительной степени снимается вопрос
о размерах таблиц, связывающих значения
синдрома и вектора ошибки (для синдромных
декодеров) и даже значения кодовых слов
и принятых последовательностей (для
декодера максимального правдоподобия).
Поэтому в перспективе возможно снижение
интереса к кодам, обладающим специальной
структурой, и к методам их декодирования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
10.06.2015684.82 Кб13P4.pdf
- #
- #
- #
- #
Макеты страниц
Синдром циклического кода, как и в любом систематическом коде, определяется суммой по модулю 2, принятых проверочных элементов и элементов проверочной группы, сформированных из принятых элементов информационной группы.
В циклическом коде для определения синдрома следует разделить принятую кодовую комбинацию на кодовую комбинацию производящего полинома Если все элементы приняты без ошибок, остаток 








Многочлен ошибок 














Указанное однозначное соответствие можно использовать для определения места ошибки. Синдром не зависит от переданной кодовой комбинации, но в нем сосредоточена вся информация о наличии ошибок. Обнаружение и исправление ошибок в систематических кодах может производиться только на основе анализа синдрома.
На основании приведенного свойства существует следующий метод определения места ошибки. Сначала определяется остаток 1 (0, 1), соответствующий наличию ошибки в старшем разряде. Если ошибка произошла в следующем разряде (более низком), то такой же остаток получится в произведении принятого многочлена и 
Пример 7.10. Предположим, задан код (11,7) в виде кодовой комбинации 10110111100 Здесь последние четыре разряда проверочные и получены на основе использования производящего многочлена 
Вычисляем 





В данном примере для этого пришлось дописать четыре нуля. Это означает, что ошибка произошла в пятом элементе, т. е. исправленная кодовая комбинация будет иметь вид

In coding theory, a cyclic code is a block code, where the circular shifts of each codeword gives another word that belongs to the code. They are error-correcting codes that have algebraic properties that are convenient for efficient error detection and correction.
If 00010111 is a valid codeword, applying a right circular shift gives the string 10001011. If the code is cyclic, then 10001011 is again a valid codeword. In general, applying a right circular shift moves the least significant bit (LSB) to the leftmost position, so that it becomes the most significant bit (MSB); the other positions are shifted by 1 to the right.
Definition[edit]
Let 









Cyclic codes have some additional structural constraint on the codes. They are based on Galois fields and because of their structural properties they are very useful for error controls. Their structure is strongly related to Galois fields because of which the encoding and decoding algorithms for cyclic codes are computationally efficient.
Algebraic structure[edit]
Cyclic codes can be linked to ideals in certain rings. Let ![R=A[x]/(x^{n}-1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8595f12ff1f64bc73a4e3e03851397cc877af6e2)











This must be a divisor of 
If the generator polynomial 



The idempotent of 









An irreducible code is a cyclic code in which the code, as an ideal is irreducible, i.e. is minimal in 
Examples[edit]
For example, if 


.
It corresponds to the ideal in ![mathbb {F} _{2}[x]/(x^{3}-1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b419295ea611763fd442a22f8f56fe8dc30c023)

The polynomial 
The idempotent of this code is the polynomial 

Trivial examples[edit]
Trivial examples of cyclic codes are 



Over 



Quasi-cyclic codes and shortened codes[edit]
Before delving into the details of cyclic codes first we will discuss quasi-cyclic and shortened codes which are closely related to the cyclic codes and they all can be converted into each other.
Definition[edit]
Quasi-cyclic codes:[citation needed]
An 




Here, codeword polynomial is an element of a linear code whose code words are polynomials that are divisible by a polynomial of shorter length called the generator polynomial. Every codeword polynomial can be expressed in the form 






Definition[edit]
Shortened codes:
An ![[n,k]](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d9e3e5f03db243c10e64608605d156ae1885952)


In shortened codes information symbols are deleted to obtain a desired blocklength smaller than the design blocklength. The missing information symbols are usually imagined to be at the beginning of the codeword and are considered to be 0. Therefore, 



All the symbols which are dropped need not be transmitted and at the receiving end can be reinserted. To convert 





Cyclic codes for correcting errors[edit]
Now, we will begin the discussion of cyclic codes explicitly with error detection and correction. Cyclic codes can be used to correct errors, like Hamming codes as cyclic codes can be used for correcting single error. Likewise, they are also used to correct double errors and burst errors. All types of error corrections are covered briefly in the further subsections.
The (7,4) Hamming code has a generator polynomial 









The received word is a polynomial of degree 

where 
We define the Syndrome Polynomial, 




For correcting two errors[edit]
Let the field elements 


Let 

These field elements are called «syndromes». Now because 






And these two can be considered as two pair of equations in 


Hence if the two pair of nonlinear equations can be solved cyclic codes can used to correct two errors.
Hamming code[edit]
The Hamming(7,4) code may be written as a cyclic code over GF(2) with generator 

![[2^{r}-1,2^{r}-r-2,4]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf755cb5b384b44e604aa2cc03660048b528348)
Hamming code for correcting single errors[edit]
A code whose minimum distance is at least 3, have a check matrix all of whose columns are distinct and non zero. If a check matrix for a binary code has 






It is easy to define Hamming codes for large alphabets of size 



So, there are 
![[(q^{m}-1)/(q-1),(q^{m}-1)/(q-1)-m]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6447e6a6ef3646859efcaa879911eae094aae869)
Now, for cyclic codes, Let 






But for 



where, 


But we can also use 












Cyclic codes for correcting burst errors[edit]
From Hamming distance concept, a code with minimum distance 

A cyclic burst of length 

In polynomial form cyclic burst of length 








A linear block code that corrects all burst errors of length 











This property is also known as Rieger bound and it is similar to the Singleton bound for random error correcting.
Fire codes as cyclic bounds[edit]
In 1959, Philip Fire[6] presented a construction of cyclic codes generated by a product of a binomial and a primitive polynomial. The binomial has the form 



where 







A fire code can correct all burst errors of length t or less if no two bursts 







This shows that 


for some 






Since 















Fire codes are the best single burst correcting codes with high rate and they are constructed analytically. They are of very high rate and when 


For error detection cyclic codes are widely used and are called 
Cyclic codes on Fourier transform[edit]
Applications of Fourier transform are widespread in signal processing. But their applications are not limited to the complex fields only; Fourier transforms also exist in the Galois field 
Fourier transform over finite fields[edit]
Fourier transform over finite fields
The discrete Fourier transform of vector 




where exp(




If 









Here 











In Galois field time domain vector 



Spectral description of cyclic codes[edit]
Any codeword of cyclic code of blocklength 











Thus, cyclic codes can also be defined as
Given a set of spectral indices, 





So, cyclic codes are vectors in the field 



Following are the few bounds on the spectrum of cyclic codes.
BCH bound[edit]
If 





Hartmann-Tzeng bound[edit]
If 







components 



Roos bound[edit]
If 











Quadratic residue codes[edit]
When the prime 





Generalizations[edit]
A constacyclic code is a linear code with the property that for some constant λ if (c1,c2,…,cn) is a codeword then so is (λcn,c1,…,cn-1). A negacyclic code is a constacyclic code with λ=-1.[8] A quasi-cyclic code has the property that for some s, any cyclic shift of a codeword by s places is again a codeword.[9] A double circulant code is a quasi-cyclic code of even length with s=2.[9] Quasi-twisted codes and multi-twisted codes are further generalizations of constacyclic codes.[10][11]
See also[edit]
- Cyclic redundancy check
- BCH code
- Reed–Muller code
- Binary Golay code
- Ternary Golay code
- Eugene Prange
Notes[edit]
- ^ Van Lint 1998, p. 76
- ^ Van Lint 1998, p. 80
- ^ Hill 1988, pp. 159–160
- ^ Blahut 2003, Theorem 5.5.1
- ^ Hill 1988, pp. 162–163
- ^ P. Fire, E, P. (1959). A class of multiple-error-correcting binary codes for non-independent errors. Sylvania Reconnaissance Systems Laboratory, Mountain View, CA, Rept. RSL-E-2, 1959.
- ^ Wei Zhou, Shu Lin, Khaled Abdel-Ghaffar. Burst or random error correction based on Fire and BCH codes. ITA 2014: 1-5 2013.
- ^ Van Lint 1998, p. 75
- ^ a b MacWilliams & Sloane 1977, p. 506
- ^ Aydin, Nuh; Siap, Irfan; K. Ray-Chaudhuri, Dijen (2001). «The Structure of 1-Generator Quasi-Twisted Codes and New Linear Codes». Designs, Codes and Cryptography. 24 (3): 313–326. doi:10.1023/A:1011283523000. S2CID 17376783.
- ^ Aydin, Nuh; Halilović, Ajdin (2017). «A generalization of quasi-twisted codes: multi-twisted codes». Finite Fields and Their Applications. 45: 96–106. doi:10.1016/j.ffa.2016.12.002. S2CID 7694655.
References[edit]
- Blahut, Richard E. (2003), Algebraic Codes for Data Transmission (2nd ed.), Cambridge University Press, ISBN 0-521-55374-1
- Hill, Raymond (1988), A First Course In Coding Theory, Oxford University Press, ISBN 0-19-853803-0
- MacWilliams, F. J.; Sloane, N. J. A. (1977), The Theory of Error-Correcting Codes, New York: North-Holland Publishing, ISBN 0-444-85011-2
- Van Lint, J. H. (1998), Introduction to Coding Theory, Graduate Texts in Mathematics 86 (3rd ed.), Springer Verlag, ISBN 3-540-64133-5
Further reading[edit]
- Ranjan Bose, Information theory, coding and cryptography, ISBN 0-07-048297-7
- Irving S. Reed and Xuemin Chen, Error-Control Coding for Data Networks, Boston: Kluwer Academic Publishers, 1999, ISBN 0-7923-8528-4.
- Scott A. Vanstone, Paul C. Van Oorschot, An introduction to error correcting codes with applications, ISBN 0-7923-9017-2
External links[edit]
- John Gill’s (Stanford) class notes – Notes #3, October 8, Handout #9, EE 387.
- Jonathan Hall’s (MSU) class notes – Chapter 8. Cyclic codes — pp. 100 — 123
- David Terr. «Cyclic Code». MathWorld.
This article incorporates material from cyclic code on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
In coding theory, a cyclic code is a block code, where the circular shifts of each codeword gives another word that belongs to the code. They are error-correcting codes that have algebraic properties that are convenient for efficient error detection and correction.
If 00010111 is a valid codeword, applying a right circular shift gives the string 10001011. If the code is cyclic, then 10001011 is again a valid codeword. In general, applying a right circular shift moves the least significant bit (LSB) to the leftmost position, so that it becomes the most significant bit (MSB); the other positions are shifted by 1 to the right.
Definition[edit]
Let 









Cyclic codes have some additional structural constraint on the codes. They are based on Galois fields and because of their structural properties they are very useful for error controls. Their structure is strongly related to Galois fields because of which the encoding and decoding algorithms for cyclic codes are computationally efficient.
Algebraic structure[edit]
Cyclic codes can be linked to ideals in certain rings. Let ![R=A[x]/(x^{n}-1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8595f12ff1f64bc73a4e3e03851397cc877af6e2)











This must be a divisor of 
If the generator polynomial 



The idempotent of 









An irreducible code is a cyclic code in which the code, as an ideal is irreducible, i.e. is minimal in 
Examples[edit]
For example, if 


.
It corresponds to the ideal in ![mathbb {F} _{2}[x]/(x^{3}-1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b419295ea611763fd442a22f8f56fe8dc30c023)

The polynomial 
The idempotent of this code is the polynomial 

Trivial examples[edit]
Trivial examples of cyclic codes are 



Over 



Quasi-cyclic codes and shortened codes[edit]
Before delving into the details of cyclic codes first we will discuss quasi-cyclic and shortened codes which are closely related to the cyclic codes and they all can be converted into each other.
Definition[edit]
Quasi-cyclic codes:[citation needed]
An 




Here, codeword polynomial is an element of a linear code whose code words are polynomials that are divisible by a polynomial of shorter length called the generator polynomial. Every codeword polynomial can be expressed in the form 






Definition[edit]
Shortened codes:
An ![[n,k]](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d9e3e5f03db243c10e64608605d156ae1885952)


In shortened codes information symbols are deleted to obtain a desired blocklength smaller than the design blocklength. The missing information symbols are usually imagined to be at the beginning of the codeword and are considered to be 0. Therefore, 



All the symbols which are dropped need not be transmitted and at the receiving end can be reinserted. To convert 





Cyclic codes for correcting errors[edit]
Now, we will begin the discussion of cyclic codes explicitly with error detection and correction. Cyclic codes can be used to correct errors, like Hamming codes as cyclic codes can be used for correcting single error. Likewise, they are also used to correct double errors and burst errors. All types of error corrections are covered briefly in the further subsections.
The (7,4) Hamming code has a generator polynomial 









The received word is a polynomial of degree 

where 
We define the Syndrome Polynomial, 




For correcting two errors[edit]
Let the field elements 


Let 

These field elements are called «syndromes». Now because 






And these two can be considered as two pair of equations in 


Hence if the two pair of nonlinear equations can be solved cyclic codes can used to correct two errors.
Hamming code[edit]
The Hamming(7,4) code may be written as a cyclic code over GF(2) with generator 

![[2^{r}-1,2^{r}-r-2,4]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf755cb5b384b44e604aa2cc03660048b528348)
Hamming code for correcting single errors[edit]
A code whose minimum distance is at least 3, have a check matrix all of whose columns are distinct and non zero. If a check matrix for a binary code has 






It is easy to define Hamming codes for large alphabets of size 



So, there are 
![[(q^{m}-1)/(q-1),(q^{m}-1)/(q-1)-m]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6447e6a6ef3646859efcaa879911eae094aae869)
Now, for cyclic codes, Let 






But for 



where, 


But we can also use 












Cyclic codes for correcting burst errors[edit]
From Hamming distance concept, a code with minimum distance 

A cyclic burst of length 

In polynomial form cyclic burst of length 








A linear block code that corrects all burst errors of length 











This property is also known as Rieger bound and it is similar to the Singleton bound for random error correcting.
Fire codes as cyclic bounds[edit]
In 1959, Philip Fire[6] presented a construction of cyclic codes generated by a product of a binomial and a primitive polynomial. The binomial has the form 



where 







A fire code can correct all burst errors of length t or less if no two bursts 







This shows that 


for some 






Since 















Fire codes are the best single burst correcting codes with high rate and they are constructed analytically. They are of very high rate and when 


For error detection cyclic codes are widely used and are called 
Cyclic codes on Fourier transform[edit]
Applications of Fourier transform are widespread in signal processing. But their applications are not limited to the complex fields only; Fourier transforms also exist in the Galois field 
Fourier transform over finite fields[edit]
Fourier transform over finite fields
The discrete Fourier transform of vector 




where exp(




If 









Here 











In Galois field time domain vector 



Spectral description of cyclic codes[edit]
Any codeword of cyclic code of blocklength 











Thus, cyclic codes can also be defined as
Given a set of spectral indices, 





So, cyclic codes are vectors in the field 



Following are the few bounds on the spectrum of cyclic codes.
BCH bound[edit]
If 





Hartmann-Tzeng bound[edit]
If 







components 



Roos bound[edit]
If 











Quadratic residue codes[edit]
When the prime 





Generalizations[edit]
A constacyclic code is a linear code with the property that for some constant λ if (c1,c2,…,cn) is a codeword then so is (λcn,c1,…,cn-1). A negacyclic code is a constacyclic code with λ=-1.[8] A quasi-cyclic code has the property that for some s, any cyclic shift of a codeword by s places is again a codeword.[9] A double circulant code is a quasi-cyclic code of even length with s=2.[9] Quasi-twisted codes and multi-twisted codes are further generalizations of constacyclic codes.[10][11]
See also[edit]
- Cyclic redundancy check
- BCH code
- Reed–Muller code
- Binary Golay code
- Ternary Golay code
- Eugene Prange
Notes[edit]
- ^ Van Lint 1998, p. 76
- ^ Van Lint 1998, p. 80
- ^ Hill 1988, pp. 159–160
- ^ Blahut 2003, Theorem 5.5.1
- ^ Hill 1988, pp. 162–163
- ^ P. Fire, E, P. (1959). A class of multiple-error-correcting binary codes for non-independent errors. Sylvania Reconnaissance Systems Laboratory, Mountain View, CA, Rept. RSL-E-2, 1959.
- ^ Wei Zhou, Shu Lin, Khaled Abdel-Ghaffar. Burst or random error correction based on Fire and BCH codes. ITA 2014: 1-5 2013.
- ^ Van Lint 1998, p. 75
- ^ a b MacWilliams & Sloane 1977, p. 506
- ^ Aydin, Nuh; Siap, Irfan; K. Ray-Chaudhuri, Dijen (2001). «The Structure of 1-Generator Quasi-Twisted Codes and New Linear Codes». Designs, Codes and Cryptography. 24 (3): 313–326. doi:10.1023/A:1011283523000. S2CID 17376783.
- ^ Aydin, Nuh; Halilović, Ajdin (2017). «A generalization of quasi-twisted codes: multi-twisted codes». Finite Fields and Their Applications. 45: 96–106. doi:10.1016/j.ffa.2016.12.002. S2CID 7694655.
References[edit]
- Blahut, Richard E. (2003), Algebraic Codes for Data Transmission (2nd ed.), Cambridge University Press, ISBN 0-521-55374-1
- Hill, Raymond (1988), A First Course In Coding Theory, Oxford University Press, ISBN 0-19-853803-0
- MacWilliams, F. J.; Sloane, N. J. A. (1977), The Theory of Error-Correcting Codes, New York: North-Holland Publishing, ISBN 0-444-85011-2
- Van Lint, J. H. (1998), Introduction to Coding Theory, Graduate Texts in Mathematics 86 (3rd ed.), Springer Verlag, ISBN 3-540-64133-5
Further reading[edit]
- Ranjan Bose, Information theory, coding and cryptography, ISBN 0-07-048297-7
- Irving S. Reed and Xuemin Chen, Error-Control Coding for Data Networks, Boston: Kluwer Academic Publishers, 1999, ISBN 0-7923-8528-4.
- Scott A. Vanstone, Paul C. Van Oorschot, An introduction to error correcting codes with applications, ISBN 0-7923-9017-2
External links[edit]
- John Gill’s (Stanford) class notes – Notes #3, October 8, Handout #9, EE 387.
- Jonathan Hall’s (MSU) class notes – Chapter 8. Cyclic codes — pp. 100 — 123
- David Terr. «Cyclic Code». MathWorld.
This article incorporates material from cyclic code on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.