Dop error gps

From Wikipedia, the free encyclopedia

Dilution of precision (DOP), or geometric dilution of precision (GDOP), is a term used in satellite navigation and geomatics engineering to specify the error propagation as a mathematical effect of navigation satellite geometry on positional measurement precision.

Introduction[edit]

The concept of dilution of precision (DOP) originated with users of the Loran-C navigation system.^[1] The idea of geometric DOP is to state how errors in the measurement will affect the final state estimation. This can be defined as:^[2]

Conceptually you can geometrically imagine errors on a measurement resulting in the term changing. Ideally small changes in the measured data will not result in large changes in output location. The opposite of this ideal is the situation where the solution is very sensitive to measurement errors. The interpretation of this formula is shown in the figure to the right, showing two possible scenarios with acceptable and poor GDOP.

More recently, the term has come into much wider usage with the development and adoption of GPS. Neglecting ionospheric ^[3] and tropospheric^[4] effects, the signal from navigation satellites has a fixed precision. Therefore, the relative satellite-receiver geometry plays a major role in determining the precision of estimated positions and times. Due to the relative geometry of any given satellite to a receiver, the precision in the pseudorange of the satellite translates to a corresponding component in each of the four dimensions of position measured by the receiver (i.e., , , , and ). The precision of multiple satellites in view of a receiver combine according to the relative position of the satellites to determine the level of precision in each dimension of the receiver measurement. When visible navigation satellites are close together in the sky, the geometry is said to be weak and the DOP value is high; when far apart, the geometry is strong and the DOP value is low. Consider two overlapping rings, or annuli, of different centres. If they overlap at right angles, the greatest extent of the overlap is much smaller than if they overlap in near parallel. Thus a low DOP value represents a better positional precision due to the wider angular separation between the satellites used to calculate a unit’s position. Other factors that can increase the effective DOP are obstructions such as nearby mountains or buildings.

DOP can be expressed as a number of separate measurements:

HDOP

Horizontal dilution of precision

VDOP

Vertical dilution of precision

PDOP

Position (3D) dilution of precision

TDOP

Time dilution of precision

GDOP

Geometric dilution of precision

These values follow mathematically from the positions of the usable satellites. Signal receivers allow the display of these positions (skyplot) as well as the DOP values.

The term can also be applied to other location systems that employ several geographical spaced sites. It can occur in electronic-counter-counter-measures (electronic warfare) when computing the location of enemy emitters (radar jammers and radio communications devices). Using such an interferometry technique can provide certain geometric layout where there are degrees of freedom that cannot be accounted for due to inadequate configurations.

The effect of geometry of the satellites on position error is called geometric dilution of precision (GDOP) and it is roughly interpreted as ratio of position error to the range error. Imagine that a square pyramid is formed by lines joining four satellites with the receiver at the tip of the pyramid. The larger the volume of the pyramid, the better (lower) the value of GDOP; the smaller its volume, the worse (higher) the value of GDOP will be. Similarly, the greater the number of satellites, the better the value of GDOP.

Interpretation[edit]

DOP value	Rating[5]	Description
<1	Ideal	Highest possible confidence level to be used for applications demanding the highest possible precision at all times.
1–2	Excellent	At this confidence level, positional measurements are considered accurate enough to meet all but the most sensitive applications.
2–5	Good	Represents a level that marks the minimum appropriate for making accurate decisions. Positional measurements could be used to make reliable in-route navigation suggestions to the user.
5–10	Moderate	Positional measurements could be used for calculations, but the fix quality could still be improved. A more open view of the sky is recommended.
10–20	Fair	Represents a low confidence level. Positional measurements should be discarded or used only to indicate a very rough estimate of the current location.
>20	Poor	At this level, measurements should be discarded.

The DOP factors are functions of the diagonal elements of the covariance matrix of the parameters, expressed either in a global or a local geodetic frame.

Computation[edit]

As a first step in computing DOP, consider the unit vectors from the receiver to satellite i:

where denote the position of the receiver and denote the position of satellite i. Formulate the matrix, A, which (for 4 pseudorange measurement residual equations) is:

The first three elements of each row of A are the components of a unit vector from the receiver to the indicated satellite. The last element of each row refers to the partial derivative of pseudorange w.r.t. receiver’s clock bias.
Formulate the matrix, Q, as the covariance matrix resulting from the least-squares normal matrix:

In general: where is the Jacobian of the sensor measurement residual equations , with respect to the unknowns, ; is the Jacobian of the sensor measurement residual equations with respect to the measured quantities , and is the correlation matrix for noise in the measured quantities. For the preceding case of 4 range measurement residual equations: , , , , , , , and the measurement noises for the different have been assumed to be independent which makes . This formula for Q arises from applying best linear unbiased estimation to a linearized version of the sensor measurement residual equations about the current solution , except in the case of B.L.U.E. is a noise covariance matrix rather than the noise correlation matrix used in DOP, and the reason DOP makes this substitution is to obtain a relative error. When is a noise covariance matrix, is an estimate of the matrix of covariance of noise in the unknowns due to the noise in the measured quantities. It is the estimate obtained by the first-order second moment (F.O.S.M.) uncertainty quantification technique which was state of the art in the 1980s. In order for the F.O.S.M. theory to be strictly applicable, either the input noise distributions need to be Gaussian or the measurement noise standard deviations need to be small relative to rate of change in the output near the solution. In this context, the second criteria is typically the one that is satisfied.

This (i.e. for the 4 time of arrival/range measurement residual equations) computation is in accordance with [6] where the weighting matrix,
happens to simplify down to the identity matrix.

Note that P only simplifies down to the Identity matrix because all the sensor measurement residual equations are time of arrival (pseudo range) equations. In other cases, for example when trying to locate someone broadcasting on an international distress frequency, would not simplify down to the identity matrix and in that case there would be a «frequency DOP» or FDOP component either in addition to or in place of the TDOP component. (Regarding «in place of the TDOP component»: Since the clocks on the legacy International Cospas-Sarsat Programme LEO satellites are much less accurate than GPS clocks, discarding their time measurements would actually increase the geolocation solution accuracy.)

The elements of are designated as:

PDOP, TDOP, and GDOP are given by:^[6]

Notice GDOP is the square root of the trace of the matrix.

The horizontal and vertical dilution of precision,

,

are both dependent on the coordinate system used. To correspond to the local horizon plane and the local vertical in either a north, east, up coordinate system.

EDOP^2   x      x      x
 x     NDOP^2   x      x
 x       x    VDOP^2   x
 x       x      x    TDOP^2

derived DOPs:

See also[edit]

• Circular error probable
• GNSS positioning calculation

References[edit]

Further reading[edit]

• DOP Factors
• manually calculating GDOP
• HDOP AND GPS HORIZONTAL POSITION ERRORS

• Article on DOP and Trimble’s program: Determining Local GPS Satellite Geometry Effects On Position Accuracy.
• Notes & GIF image on manually calculating GDOP: Geographer’s Craft
• GPS Errors & Estimating Your Receiver’s Accuracy: Sam Wormley’s GPS Accuracy Web Page
• GPS Accuracy, Errors & Precision: Radio-Electronics.com

Распространение ошибки с различной топологией

Снижение точности (DOP ), или геометрическое снижение точности (GDOP ) — это термин, используемый в спутниковой навигации и инженерной геоматике для определения распространения ошибки как математическое влияние геометрии навигационного спутника на точность позиционных измерений.

Понимание геометрического снижения точности (GDOP) на простом примере. В A кто-то измерил расстояние до двух ориентиров и нанес их точку как точку пересечения двух окружностей с измеренным радиусом. В B измерения имеют некоторые пределы погрешности, и их истинное местоположение будет находиться где-нибудь в зеленой зоне. В C ошибка измерения такая же, но ошибка в их положении значительно выросла из-за расположения ориентиров. Навигационные спутники с плохой геометрией для геометрического снижения точности (GDOP). Навигационные спутники с хорошей геометрией для снижения геометрической точности (GDOP).

Содержание

• 1 Введение
• 2 Значение значений DOP
• 3 Вычисление значений DOP
• 4 Ссылки
  • 4.1 Примечания
  • 4.2 Общие
• 5 Внешние ссылки

Введение

Концепция снижения точности (DOP) возникла у пользователей навигационной системы Loran-C. Идея геометрического DOP состоит в том, чтобы указать, как ошибки измерения повлияют на окончательную оценку состояния. Это можно определить как:

GDOP = Δ (O utput L ocation) Δ (M измер. D ata) { displaystyle GDOP = { frac { Delta ({ rm {Output Location}})} { Дельта ({ rm {Measured Data}})}}}

Концептуально вы можете геометрически представить ошибки измерения, приводящие к Δ (Измеренное значение D ata) { displaystyle Delta ({ rm { Измерено Data}})}срок меняется. В идеале небольшие изменения в измеренных данных не приведут к большим изменениям в местоположении выхода. Противоположностью этому идеалу является ситуация, когда решение очень чувствительно к ошибкам измерения. Интерпретация этой формулы показана на рисунке справа, где показаны два возможных сценария с приемлемым и плохим GDOP.

В последнее время этот термин стал использоваться гораздо шире с развитием и внедрением GPS. Без учета ионосферных и тропосферных эффектов сигнал с навигационных спутников имеет фиксированную точность. Следовательно, относительная геометрия спутникового приемника играет важную роль в определении точности предполагаемых местоположений и времени. Из-за относительной геометрии любого заданного спутника к приемнику точность в псевдодиапазоне спутника преобразуется в соответствующий компонент в каждом из четырех измерений положения, измеренных приемником (т. Е. x { displaystyle x}, y { displaystyle y}, z { displaystyle z}и t { displaystyle t}). Точность нескольких спутников в поле зрения приемника складывается в соответствии с относительным положением спутников для определения уровня точности в каждом измерении приемника. Когда видимые навигационные спутники находятся близко друг к другу в небе, геометрия считается слабой, а значение DOP высокое; когда они далеко друг от друга, геометрия сильная, а значение DOP низкое. Рассмотрим два перекрывающихся кольца или кольца с разными центрами. Если они перекрываются под прямым углом, наибольшая степень перекрытия намного меньше, чем если бы они перекрывались почти параллельно. Таким образом, низкое значение DOP представляет лучшую точность позиционирования из-за более широкого углового разнесения между спутниками, используемых для расчета местоположения объекта. Другими факторами, которые могут увеличить эффективный DOP, являются препятствия, такие как близлежащие горы или здания.

DOP можно выразить в виде ряда отдельных измерений:

• HDOP — горизонтальное снижение точности
• VDOP — вертикальное снижение точности
• PDOP — положение (3D) снижение точности
• TDOP — уменьшение точности по времени
• GDOP — геометрическое снижение точности

Эти значения математически следуют из положений используемых спутников. Приемники сигналов позволяют отображать эти положения (небесную диаграмму), а также значения DOP.

Этот термин также может применяться к другим системам определения местоположения, которые используют несколько географически разнесенных сайтов. Это может происходить в средствах электронного противодействия (радиоэлектронная борьба) при вычислении местоположения источников излучения противника (глушителей радаров и устройств радиосвязи). Использование такой методики интерферометрии может обеспечить определенную геометрическую схему, в которой есть степени свободы, которые нельзя учесть из-за неадекватных конфигураций.

Влияние геометрии спутников на ошибку определения местоположения называется геометрическим снижением точности (GDOP) и грубо интерпретируется как отношение ошибки местоположения к ошибке дальности. Представьте, что квадратная пирамида образована линиями, соединяющими четыре спутника с приемником на вершине пирамиды. Чем больше объем пирамиды, тем лучше (меньше) значение GDOP; чем меньше его объем, тем хуже (выше) будет значение GDOP. Аналогично, чем больше количество спутников, тем лучше значение GDOP.

Значение значений DOP

Значение DOP	Рейтинг	Описание
1	Идеально	Максимально возможный уровень достоверности для приложений, требующих максимально возможная точность в любое время.
1-2	Отлично	На этом уровне достоверности позиционные измерения считаются достаточно точными, чтобы соответствовать всем приложениям, кроме наиболее чувствительных.
2-5	Хорошо	Представляет уровень, который отмечает минимум, подходящий для принятия точных решений. Позиционные измерения могут использоваться для предоставления пользователю надежных рекомендаций по навигации по маршруту.
5-10	Умеренный	Для расчетов можно использовать позиционные измерения, но качество исправления все же можно улучшить. Рекомендуется более открытый вид на небо.
10-20	Удовлетворительно	Представляет низкий уровень достоверности. Позиционные измерения следует отбросить или использовать только для очень приблизительной оценки текущего местоположения.
>20	Плохо	На этом уровне измерения неточны на целых 300 метров с помощью устройства с точностью до 6 метров (50 DOP × 6 метров), и от них следует отказаться.

Коэффициенты DOP являются функциями диагональных элементов ковариационной матрицы параметров, выраженных в глобальной или локальной геодезической системе координат.

Вычисление значений DOP

В качестве первого шага в вычислении DOP рассмотрим единичные векторы от приемника до спутника i: ((xi — x) R i, (yi — у) р я, (zi — z) р я) { displaystyle left ({ frac {(x_ {i} -x)} {R_ {i}}}, { frac {(y_ {i} — y)} {R_ {i}}}, { frac {(z_ {i} -z)} {R_ {i}}} right)}где R i = (xi — x) 2 + (yi — y) 2 + (zi — z) 2 { displaystyle R_ {i} = { sqrt {(x_ {i} -x) ^ {2} + (y_ {i} -y) ^ {2} + (z_ {i} -z) ^ {2}}}}и где x, y { displaystyle x, y}и z { displaystyle z}обозначают положение получателя, а xi, yi { displaystyle x_ {i}, y_ {i}}и zi { displaystyle z_ {i}}обозначают положение спутника i. Сформулируйте матрицу A, которая (для 4 уравнений невязки измерения дальности):

A = [(x 1 — x) R 1 (y 1 — y) R 1 (z 1 — z) R 1 — 1 ( x 2 — x) R 2 (y 2 — y) R 2 (z 2 — z) R 2 — 1 (x 3 — x) R 3 (y 3 — y) R 3 (z 3 — z) R 3 — 1 (Икс 4 — Икс) R 4 (Y 4 — Y) R 4 (Z 4 — Z) R 4-1] { Displaystyle A = { begin {bmatrix} { frac {(x_ {1} -x))} {R_ {1}}} { frac {(y_ {1} -y)} {R_ {1}}} и { frac {(z_ {1} -z)} {R_ {1}} } — 1 \ { frac {(x_ {2} -x)} {R_ {2}}} { frac {(y_ {2} -y)} {R_ {2}}} { frac {(z_ {2} -z)} {R_ {2}}} — 1 \ { frac {(x_ {3} -x)} {R_ {3}}} { frac {(y_ {3} -y)} {R_ {3}}} { frac {(z_ {3} -z)} {R_ {3}}} — 1 \ { frac {(x_ {4} — x)} {R_ {4}}} { frac {(y_ {4} -y)} {R_ {4}}} и { frac {(z_ {4} -z)} {R_ {4} }} — 1 end {bmatrix}}}

Первые три элемента каждой строки A являются компонентами единичного вектора от приемника до указанного спутника. Если элементы в четвертом столбце — это c, который обозначает скорость света, то коэффициент σ t { displaystyle sigma _ {t}}(временное разбавление) равен всегда 1. Если элементы в четвертом столбце равны -1, то коэффициент σ t { displaystyle sigma _ {t}}рассчитывается правильно. Сформулируйте матрицу Q в виде:

Q = (ATA) — 1 { displaystyle Q = left (A ^ {T} A right) ^ {- 1}}

В общем: Q = (J x T (J d C d J d T) — 1 J x) — 1 { displaystyle Q = (J_ {x} ^ {T} (J_ {d} C_ {d} J_ {d} ^ {T}) ^ {- 1} J_ {x}) ^ {- 1}}где J x { displaystyle J_ {x}}— якобиан остаточные уравнения измерения датчика fi (x _, d _) = 0 { displaystyle f_ {i} ({ underline {x}}, { underline {d}}) = 0}, что касается неизвестных, x _ { displaystyle { underline {x}}}; J d { displaystyle J_ {d}}— это якобиан измерения датчика остаточные уравнения относительно измеренных величин d _ { displaystyle { underline {d}}}и C d { displaystyle C_ {d}}— матрица корреляции шума в измеряемых величинах. Для предыдущего случая четырех уравнений остатка измерения диапазона: x _ = (x, y, z, τ) T { displaystyle { underline {x}} = (x, y, z, tau) ^ { T}}, d _ = (τ 1, τ 2, τ 3, τ 4) T { displaystyle { underline {d}} = ( tau _ {1}, tau _ {2}, тау _ {3}, тау _ {4}) ^ {T}}, τ = ct { displaystyle tau = ct}, τ я = cti { displaystyle tau _ {i} = ct_ {i}}, R i = | τ i — τ | знак равно (τ я — τ) 2 { Displaystyle R_ {я} = | тау _ {я} — тау | = { sqrt {( тау _ {я} — тау) ^ {2}}}}, fi (x _, d _) = (xi — x) 2 + (yi — y) 2 + (zi — z) 2 — (τ я — τ) 2 { displaystyle f_ {i} ({ подчеркивание {x}}, { underline {d}}) = { sqrt {(x_ {i} -x) ^ {2} + (y_ {i} -y) ^ {2} + (z_ {i} -z) ^ {2}}} — { sqrt {( tau _ {i} — tau) ^ {2}}}}, J x = A { displaystyle J_ {x} = A}, J d = — I { displaystyle J_ {d} = — I}и шумы измерения для различных τ i { displaystyle tau _ {i}}считаются независимыми, что составляет C d = I { displaystyle C_ {d} = I}. Эта формула для Q возникает в результате применения наилучшей линейной несмещенной оценки к линеаризованной версии остаточных уравнений измерения датчика относительно текущего решения Δ x _ = — Q ∗ (J x T (J d C d J d T) — 1 f) { displaystyle Delta { underline {x}} = — Q * (J_ {x} ^ {T} (J_ {d} C_ {d} J_ {d} ^ {T})) ^ {- 1} f)}, кроме случая СИНИЙ C d { displaystyle C_ {d}}— это матрица ковариации шума, а не матрица корреляции шума, используемая в DOP, и причина, по которой DOP выполняет эту замену, состоит в том, чтобы получить относительную ошибку. Когда C d { displaystyle C_ {d}}представляет собой ковариационную матрицу шума, Q { displaystyle Q}представляет собой оценку матрицы ковариации шум в неизвестных из-за шума в измеряемых величинах. Это оценка, полученная с помощью метода количественной оценки неопределенности Второй момент первого порядка (F.O.S.M.), который был самым современным в 1980-х годах. Чтобы F.O.S.M. Чтобы теория была строго применимой, либо распределение входного шума должно быть гауссовым, либо стандартные отклонения шума измерения должны быть небольшими по сравнению со скоростью изменения выходного сигнала вблизи решения. В этом контексте обычно удовлетворяется второй критерий.

Это вычисление (т. Е. Для четырех остаточных уравнений измерения диапазона) выполняется в соответствии с матрицей весов, P = (J d C d J d T) — 1 { displaystyle P = (J_ {d} C_ {d} J_ {d} ^ {T}) ^ {- 1}}, был установлен в единичную матрицу.

Элементы Q обозначаются следующим образом:

Q = [σ x 2 σ xy σ xz σ xt σ xy σ y 2 σ yz σ yt σ xz σ yz σ z 2 σ zt σ xt σ yt σ zt σ T 2] { displaystyle Q = { begin {bmatrix} sigma _ {x} ^ {2} sigma _ {xy} sigma _ {xz} sigma _ {xt} \ sigma _ {xy} sigma _ {y} ^ {2} sigma _ {yz} sigma _ {yt} \ sigma _ {xz} sigma _ {yz} sigma _ {z} ^ {2} sigma _ {zt} \ sigma _ {xt} sigma _ {yt} sigma _ {zt} sigma _ {t} ^ {2} end {bmatrix}}}

PDOP, TDOP и GDOP задаются следующим образом:

PDOP = σ x 2 + σ y 2 + σ z 2 TDOP = σ t 2 GDOP = PDOP 2 + TDOP 2 { displaystyle { begin {выровненный} PDOP = { sqrt { sigma _ {x} ^ {2} + sigma _ {y} ^ {2} + sigma _ {z} ^ {2}}} \ TDOP = { sqrt { sigma _ {t} ^ {2}}} \ GDOP = { sqrt {PDOP ^ {2} + TDOP ^ {2}}} \ end {align}}}

в соответствии с Раздел 1.4.9 Принципов спутникового позиционирования. В более общем смысле GDOP — это квадратный корень из следа матрицы Q { displaystyle Q}.

Снижение точности по горизонтали, HDOP = σ x 2 + σ y 2 { displaystyle scriptstyle HDOP = { sqrt { sigma _ {x} ^ {2} + sigma _ { y} ^ {2}}}}, и вертикальное снижение точности, VDOP = σ z 2 { displaystyle scriptstyle VDOP = { sqrt { sigma _ {z} ^ {2}}}}, оба зависят от используемой системы координат. Чтобы соответствовать локальной плоскости горизонта и местной вертикали, x, y и z должны обозначать положения в системе координат север, восток, вниз или в системе координат восток, север, вверх.

Ссылки

Примечания

Общие

Внешние ссылки

• Статья о DOP и программе Trimble: Определение влияния геометрии местного GPS-спутника на положение Точность.
• Примечания GIF изображение при вычислении GDOP вручную: Geographer’s Craft
• Ошибки GPS и оценка точности вашего приемника: Веб-страница «Точность GPS» Сэма Уормли
• Точность GPS, Ошибки и точность: Radio-Electronics.com

Regular maintenance is necessary to maintain

performance. Check the items mentioned be-

low monthly to keep the equipment in good

working order.

Antenna unit

Check for fixing bolts for tightness.

Antenna cable

Check connector for tight-

ness, rust, damage and wa-

ter leaks.

Power cable

Check for tight connection.

Ground terminal

Check for rust and tight connection.

Fuse

The 2A fuse in the power cable protects the

unit from overvoltage and equipment fault. If

the fuse blows, find out the cause before re-

placing the fuse. If the fuse blows after re-

placement, request service.

WARNING

Use only a 2A fuse in the power cable.

Use of different fuses may cause fire.

9-2

9.3 Error Messages

Error messages appear on the display to alert

you to possible trouble.

WARNING

Do not open the display unit cover.

High voltage exists inside.

If the unit is not working properly,

contact your dealer.

GPS error

When GPS signal is suddenly lost and posi-

tion cannot be calculated within one minute

the message shown in Figure 9-5 appears.

GPS No fix

Figure 9-5 GPS error message

This message may appear when there is an

interfering object between the satellite and

GPS receiver (for example, mast) or the an-

tenna cable is disconnected.

DOP error

When PDOP value exceeds 6 in the 3D mode,

or HDOP value exceeds 4 in the 2D mode,

this error occurs and following indication ap-

pears.

DOP Error

Figure 9-6 DOP error message

Анализ ошибок для глобальной системы позиционирования важен для понимания того, как работает GPS, и для того, чтобы знать, какой величины ошибки следует ожидать. GPS вносит поправки на ошибки часов приемника и другие эффекты, но остаются остаточные ошибки, которые не исправляются. Положение приемника GPS вычисляется на основе данных, полученных со спутников. Ошибки зависят от геометрического снижения точности и источников, перечисленных в таблице ниже.

Обзор

Источники ошибок эквивалентного диапазона пользователя (UERE)

Источник	Эффект (м)
Прибытие сигнала C/A	±3
Приход сигнала P(Y)	±0,3
Ионосферные эффекты	±5
Эфемеридные ошибки	±2,5
Ошибки спутниковых часов	±2
Многолучевое искажение	±1
Тропосферные эффекты	±0,5
С/А	±6,7
П(Д)	±6,0

Ошибки эквивалентного диапазона пользователя (UERE) показаны в таблице. Существует также числовая ошибка с расчетным значением,, около 1 метра (3 фута 3 дюйма). Стандартные отклонения,, для грубого/сбора (C/A) и точного кодов также показаны в таблице. Эти стандартные отклонения рассчитываются путем извлечения квадратного корня из суммы квадратов отдельных компонентов (т . е. RSS для квадратов суммы корней). Чтобы получить стандартное отклонение оценки положения приемника, эти ошибки дальности должны быть умножены на соответствующее снижение точности.термины, а затем RSS с числовой ошибкой. Ошибки электроники являются одним из нескольких эффектов снижения точности, описанных в таблице выше. В совокупности автономные гражданские GPS-фиксаторы горизонтального положения обычно имеют точность около 15 метров (50 футов). Эти эффекты также снижают точность более точного кода P(Y). Однако развитие технологий означает, что в настоящее время гражданские GPS-фиксаторы при ясном виде неба в среднем имеют точность около 5 метров (16 футов) по горизонтали.

Термин ошибка эквивалентного диапазона пользователя (UERE) относится к ошибке компонента расстояния от приемника до спутника. Эти ошибки UERE представлены как ошибки ±, что означает, что они являются несмещенными или ошибками с нулевым средним значением. Поэтому эти ошибки UERE используются при вычислении стандартных отклонений. Стандартное отклонение ошибки положения приемника,
, вычисляется путем умножения PDOP (Разбавление Точности Позиции) на
, стандартное отклонение пользовательских эквивалентных ошибок диапазона.
вычисляется путем извлечения квадратного корня из суммы квадратов стандартных отклонений отдельных компонентов.

PDOP вычисляется как функция положения приемника и спутника. Подробное описание того, как рассчитать PDOP, дано в разделе Расчет геометрического снижения точности (GDOP) .

для кода C/A задается:

Стандартное отклонение ошибки в предполагаемом местоположении приемника, опять же для кода C/A:

Диаграмма ошибок слева показывает взаимосвязь указанного положения приемника, истинного положения приемника и пересечения четырех сферических поверхностей.

Измерение времени прихода сигнала

Положение, рассчитанное приемником GPS, требует текущего времени, положения спутника и измеренной задержки принятого сигнала. Точность определения местоположения в первую очередь зависит от положения спутника и задержки сигнала.

Чтобы измерить задержку, приемник сравнивает битовую последовательность, полученную со спутника, с внутренне сгенерированной версией. Сравнивая передний и задний фронты битовых переходов, современная электроника может измерять смещение сигнала с точностью до одного процента от ширины битового импульса., или примерно 10 наносекунд для кода C/A. Поскольку сигналы GPS распространяются со скоростью света , это представляет собой ошибку около 3 метров.

Этот компонент точности позиционирования можно улучшить в 10 раз, используя сигнал P(Y) с более высокой скоростью передачи микросхем. Предполагая тот же один процент точности ширины импульса в битах, высокочастотный сигнал P (Y) дает точность или около 30 см.

Атмосферные эффекты

Несоответствия атмосферных условий влияют на скорость сигналов GPS при их прохождении через атмосферу Земли , особенно через ионосферу. Исправление этих ошибок является серьезной проблемой для повышения точности определения местоположения GPS. Эти эффекты минимальны, когда спутник находится прямо над головой, и становятся сильнее для спутников, находящихся ближе к горизонту , поскольку путь через атмосферу длиннее (см. Воздушная масса ). Как только приблизительное местоположение приемника известно, можно использовать математическую модель для оценки и компенсации этих ошибок.

Ионосферная задержка микроволнового сигнала зависит от его частоты. Он возникает из-за ионизированной атмосферы (см. Общее содержание электронов ). Это явление известно как дисперсия , и его можно рассчитать на основе измерений задержек для двух или более полос частот, что позволяет оценить задержки на других частотах. ^[1] Некоторые военные и дорогие гражданские приемники геодезического класса рассчитывают атмосферную дисперсию по разным задержкам частот L1 и L2 и применяют более точную коррекцию. Это можно сделать в гражданских приемниках без расшифровки сигнала P(Y), передаваемого по L2, отслеживая несущую волну вместо модулированной .код. Чтобы облегчить это на более дешевых приемниках, новый гражданский кодовый сигнал на L2, называемый L2C, был добавлен к спутникам Block IIR-M, который был впервые запущен в 2005 году. Он позволяет напрямую сравнивать сигналы L1 и L2 с использованием кодированных сигналов. сигнал вместо несущей волны.

Эффекты ионосферы обычно изменяются медленно и могут быть усреднены во времени. Их для любой конкретной географической области можно легко рассчитать, сравнив положение, измеренное с помощью GPS, с известным местом съемки. Эта коррекция также действительна для других приемников в том же общем месте. Некоторые системы отправляют эту информацию по радио или другим каналам связи, чтобы позволить приемникам только L1 вносить ионосферные поправки. Ионосферные данные передаются через спутник в спутниковые системы дополнений (SBAS), такие как широкомасштабная система дополнений (WAAS) (доступна в Северной Америке и на Гавайях), EGNOS (Европа и Азия), многофункциональная спутниковая система дополнений (MSAS) ( Япония) иGPS Aided Geo Augmented Navigation (GAGAN) (Индия), которая передает его на частоте GPS с использованием специальной последовательности псевдослучайных шумов (PRN), поэтому требуются только один приемник и антенна.

Влажность также вызывает переменную задержку, что приводит к ошибкам, подобным ионосферной задержке, но происходящим в тропосфере . Этот эффект более локализован, чем ионосферные эффекты, изменяется быстрее и не зависит от частоты. Эти особенности делают точное измерение и компенсацию погрешностей влажности более сложными, чем влияние ионосферы. ^[2]

Атмосферное давление также может изменить задержку приема сигналов из-за присутствия сухих газов в тропосфере (78% N2, 21% O2, 0,9% Ar…). Его влияние изменяется в зависимости от местной температуры и атмосферного давления вполне предсказуемым образом, используя законы идеальных газов. ^[3]

Многолучевые эффекты

На сигналы GPS также могут влиять проблемы с многолучевым распространением , когда радиосигналы отражаются от окружающей местности; здания, стены каньона, твердая почва и т. д. Эти задержанные сигналы вызывают ошибки измерения, которые различаются для каждого типа сигнала GPS из-за его зависимости от длины волны. ^[4]

Разнообразие методов, в первую очередь узкое расстояние между корреляторами, было разработано для уменьшения ошибок многолучевости. При многолучевом распространении с большой задержкой приемник сам может распознать своенравный сигнал и отбросить его. Для устранения многолучевости с более короткой задержкой из-за отражения сигнала от земли можно использовать специализированные антенны (например, антенну с дроссельным кольцом ) для уменьшения мощности сигнала, принимаемого антенной. Отражения с короткой задержкой труднее отфильтровать, потому что они мешают истинному сигналу, вызывая эффекты, почти неотличимые от обычных колебаний атмосферной задержки.

Эффекты многолучевости гораздо менее серьезны в движущихся транспортных средствах. Когда антенна GPS движется, ложные решения, использующие отраженные сигналы, быстро не сходятся, и только прямые сигналы приводят к устойчивым решениям.

Эфемериды и ошибки часов

Хотя эфемеридные данные передаются каждые 30 секунд, сама информация может иметь возраст до двух часов. Изменчивость давления солнечного излучения ^[5] оказывает косвенное влияние на точность GPS из-за влияния на ошибки эфемерид. Если требуется быстрое время до первого определения (TTFF), можно загрузить действительные эфемериды в приемник, и в дополнение к установке времени определение местоположения может быть получено менее чем за десять секунд. Такие эфемеридные данные можно размещать в Интернете, чтобы их можно было загружать в мобильные устройства GPS. ^[6] См. также Assisted GPS .

Атомные часы спутников подвержены шуму и ошибкам дрейфа часов . Навигационное сообщение содержит исправления этих ошибок и оценки точности атомных часов. Однако они основаны на наблюдениях и могут не указывать текущее состояние часов.

Эти проблемы, как правило, очень малы, но могут составлять погрешность в несколько метров (десятков футов). ^[7]

Для очень точного позиционирования (например, в геодезии ) эти эффекты могут быть устранены с помощью дифференциальной GPS : одновременного использования двух и более приемников в нескольких точках съемки . В 1990-х годах, когда приемники были довольно дорогими, были разработаны некоторые методы квазидифференциальной GPS, использующие только один приемник, но повторно занимающие точки измерения. В Техническом университете Вены этот метод был назван qGPS, и было разработано программное обеспечение для постобработки. ^{[ нужна ссылка ]}

Снижение точности

Вычисление геометрического снижения точности

Понятие геометрического ослабления точности было введено в разделе « Источники ошибок и анализ » . Были предоставлены расчеты, чтобы показать, как использовалась PDOP и как она влияла на стандартное отклонение ошибки местоположения приемника.

Когда все видимые спутники GPS находятся в небе близко друг к другу (т. е. небольшое угловое расстояние), значения DOP высокие; когда они далеко друг от друга, значения DOP низкие. Теоретически спутники, расположенные близко друг к другу, не могут предоставить столько информации, сколько спутники, находящиеся далеко друг от друга. Низкие значения DOP представляют лучшую точность позиционирования GPS благодаря более широкому угловому разносу между спутниками, используемому для расчета положения приемника GPS. HDOP, VDOP, PDOP и TDOP — это, соответственно, горизонтальная, вертикальная, позиционная (трехмерная) и временная потеря точности.

Рисунок 3.1 Снижение точности данных GPS Navstar от Береговой охраны США дает графическое представление того, как геометрия влияет на точность. ^[8]

Теперь мы беремся за задачу, как вычислить разбавление членов точности. В качестве первого шага в вычислении DOP рассмотрим единичный вектор от приемника к спутнику i с компонентами,, и где расстояние от приемника до спутника, , дан кем-то:

где и обозначают положение приемника и и обозначают положение спутника i . Эти компоненты x , y и z могут быть компонентами в системе координат север, восток, вниз, системе координат юг, восток, вверх или в любой другой удобной системе. Сформулируйте матрицу A как:

Первые три элемента каждой строки A являются компонентами единичного вектора от приемника до указанного спутника. Элементы в четвертом столбце — c, где c обозначает скорость света. Сформулируйте матрицу, Q , как

Это вычисление соответствует главе 11 Глобальной системы позиционирования Паркинсона и Спилкера, где весовая матрица P была установлена ​​равной единичной матрице. Элементы матрицы Q обозначаются как: ^[9]

Греческое письмоиспользуется довольно часто там, где мы использовали d . Однако элементы матрицы Q не представляют дисперсии и ковариации, как они определены в вероятности и статистике. Вместо этого они являются строго геометрическими терминами. Таким образом, используется d как снижение точности. PDOP, TDOP и GDOP задаются

в соответствии с «Разделом 1.4.9 ПРИНЦИПОВ СПУТНИКОВОГО МЕСТОПОЗИЦИОНИРОВАНИЯ» .

Горизонтальное ослабление точности, , и вертикальное ослабление точности, , оба зависят от используемой системы координат. Чтобы соответствовать локальной плоскости горизонта и местной вертикали, x , y и z должны обозначать положения либо в системе координат Север, Восток, Вниз, либо в системе координат Юг, Восток, Вверх.

Вывод уравнений для расчета

Уравнения для вычисления геометрического разбавления членов точности были описаны в предыдущем разделе. В этом разделе описывается вывод этих уравнений. Используемый здесь метод аналогичен тому, который использовался в «Глобальной системе позиционирования (предварительная версия) Паркинсона и Спайкера».

Рассмотрим вектор ошибки положения,, определяемый как вектор от пересечения четырех поверхностей сферы, соответствующих псевдодальностям, до истинного положения приемника.где жирным шрифтом обозначен вектор и,, иобозначают единичные векторы вдоль осей x, y и z соответственно. Позволятьобозначают временную ошибку, истинное время минус указанное приемником время. Предположим, что среднее значение трех компонентов и равны нулю.

где ,,, и— ошибки в псевдодиапазонах с 1 по 4 соответственно. Это уравнение получено путем линеаризации уравнения Ньютона-Рафсона, связывающего псевдодальности с положением приемника, положением спутников и ошибками часов приемника. Умножая обе части на есть результаты

.

Транспонирование обеих сторон:

.

После умножения матриц в обеих частях уравнения (2) на соответствующие матрицы в уравнении (3) получаются результаты

.

Принимая ожидаемое значение обеих сторон и вынося неслучайные матрицы за пределы оператора ожидания E, мы получаем:

Предполагая, что ошибки псевдодальности некоррелированы и имеют одинаковую дисперсию, ковариационная матрица в правой части может быть выражена как скаляр, умноженный на единичную матрицу. Таким образом

поскольку

Примечание: поскольку

Замена для далее следует

Из уравнения (7) следует, что дисперсии показанного положения приемника и времени равны

и

Оставшиеся члены дисперсии ошибки положения и времени следуют прямым образом.

Выборочная доступность

GPS включает (в настоящее время отключенную) функцию под названием Selective Availability ( SA ), которая добавляет преднамеренные изменяющиеся во времени ошибки до 100 метров (328 футов) к общедоступным навигационным сигналам. Это было сделано для того, чтобы противник не мог использовать гражданские GPS-приемники для наведения высокоточного оружия.

Ошибки SA на самом деле являются псевдослучайными, генерируемыми криптографическим алгоритмом из секретного начального ключа , доступного только для авторизованных пользователей (военных США, их союзников и некоторых других пользователей, в основном правительственных) со специальным военным приемником GPS. Простого обладания приемником недостаточно; ему по-прежнему нужен строго контролируемый ежедневный ключ.

До того, как он был отключен 2 мая 2000 г., типичные ошибки SA составляли около 50 м (164 фута) по горизонтали и около 100 м (328 футов) по вертикали. ^[10] Поскольку SA почти одинаково влияет на каждый приемник GPS в данной области, стационарная станция с точно известным положением может измерить значения ошибки SA и передать их на местные приемники GPS, чтобы они могли скорректировать свои привязки местоположения. Это называется дифференциальной GPS или DGPS . DGPS также исправляет несколько других важных источников ошибок GPS, в частности ионосферную задержку, поэтому он продолжает широко использоваться, даже несмотря на то, что SA был отключен. Неэффективность SA в условиях широкодоступного DGPS была распространенным аргументом в пользу отключения SA, и в конце концов это было сделано по приказу президента Клинтона .в 2000 г. ^[11]

Услуги DGPS широко доступны как из коммерческих, так и из государственных источников. К последним относятся WAAS и сеть морских навигационных маяков LF Береговой охраны США . Точность поправок зависит от расстояния между пользователем и приемником DGPS. По мере увеличения расстояния ошибки на двух участках также не будут коррелировать, что приведет к менее точным дифференциальным поправкам.

Во время войны в Персидском заливе 1990–1991 годов из-за нехватки военных устройств GPS многие военнослужащие и их семьи покупали легкодоступные гражданские устройства. Избирательная доступность значительно препятствовала использованию этих GPS вооруженными силами США на поле боя, поэтому военные приняли решение отключить его на время войны.

В 1990-х FAA начало оказывать давление на военных, чтобы они навсегда отключили SA. Это позволит FAA ежегодно экономить миллионы долларов на обслуживании собственных радионавигационных систем. Количество добавленных ошибок было «обнулено» ^[12] в полночь 1 мая 2000 г. после заявления президента США Билла Клинтона ., предоставляя пользователям доступ к безошибочному сигналу L1. Согласно директиве, индуцированная ошибка SA была изменена, чтобы не добавлять ошибок в общедоступные сигналы (код C/A). Распоряжение Клинтона требовало обнуления SA к 2006 году; это произошло в 2000 году, когда американские военные разработали новую систему, которая дает возможность отказывать в GPS (и других навигационных услугах) враждебным силам в конкретном районе кризиса, не затрагивая остальной мир или их собственные военные системы. ^[12]

19 сентября 2007 г. Министерство обороны США объявило, что будущие спутники GPS III не смогут реализовать SA, ^[13] в конечном итоге сделав эту политику постоянной. ^[14]

Защита от спуфинга

Еще одно ограничение на GPS, антиспуфинг, остается включенным. Это шифрует P-код , чтобы он не мог быть имитирован передатчиком, отправляющим ложную информацию. Немногие гражданские приемники когда-либо использовали P-код, и точность, достижимая с общедоступным кодом C/A, была намного лучше, чем первоначально ожидалось (особенно с DGPS ), настолько, что политика защиты от спуфинга оказывает относительно небольшое влияние на большинство гражданских пользователей. Отключение защиты от спуфинга в первую очередь принесет пользу геодезистам и некоторым ученым, которым нужны чрезвычайно точные координаты для таких экспериментов, как отслеживание движения тектонических плит.

Относительность

Существует ряд источников ошибок из-за релятивистских эффектов ^[15] , которые сделали бы систему бесполезной, если бы ее не исправили. Три релятивистских эффекта — это замедление времени, гравитационный сдвиг частоты и эффекты эксцентриситета. Примеры включают релятивистское замедление времени из-за скорости спутника примерно на 1 часть в 10 ¹⁰ , гравитационное замедление времени, из-за которого спутник движется примерно на 5 частей в 10 ¹⁰ быстрее , чем земные часы, и эффект Саньяка из-за вращения относительно приемников на Земле. Эти темы рассматриваются ниже, по одной за раз.

Специальная и общая теория относительности

Согласно теории относительности , из-за их постоянного движения и высоты относительно земно-центрированной, невращающейся приблизительно инерциальной системы отсчета , на часы на спутниках влияет их скорость. Специальная теория относительности предсказывает, что частота атомных часов, движущихся с орбитальной скоростью GPS, будет идти медленнее, чем у стационарных наземных часов, в несколько раз., или привести к задержке около 7 мкс/день, где орбитальная скорость v = 4 км/с, а c = скорость света. Этот эффект замедления времени был измерен и подтвержден с помощью GPS.

Влияние гравитационного сдвига частоты на GPS из-за общей теории относительности заключается в том, что часы, расположенные ближе к массивному объекту, будут идти медленнее, чем часы, находящиеся дальше. Применительно к GPS приемники находятся намного ближе к Земле, чем спутники, в результате чего часы GPS работают быстрее в 5×10 ⁻¹⁰ раз , или примерно на 45,9 мкс/день. Этот гравитационный сдвиг частоты заметен.

При объединении замедления времени и гравитационного сдвига частоты расхождение составляет около 38 микросекунд в сутки, разница составляет 4,465 части на 10 ¹⁰ . ^[16] Без коррекции в местоположении накапливались бы ошибки порядка 11,4 км/день. ^[17] Эта начальная ошибка псевдодальности корректируется в процессе решения навигационных уравнений . Кроме того, эллиптические, а не идеально круглые орбиты спутников вызывают изменение эффектов замедления времени и гравитационного сдвига частоты со временем. Этот эффект эксцентриситета приводит к тому, что разница в тактовой частоте между спутником GPS и приемником увеличивается или уменьшается в зависимости от высоты спутника.

Чтобы компенсировать несоответствие, стандарт частоты на борту каждого спутника перед запуском получает смещение скорости, что делает его работу немного медленнее, чем желаемая частота на Земле; в частности, на частоте 10,22999999543 МГц вместо 10,23 МГц. ^[18] Поскольку атомные часы на борту спутников GPS точно настроены, это делает систему практическим инженерным приложением научной теории относительности в реальных условиях. ^[19] Размещение атомных часов на искусственных спутниках для проверки общей теории Эйнштейна было предложено Фридвардтом Винтербергом в 1955 году. ^[20]

Расчет замедления времени

Чтобы рассчитать величину дневного замедления времени, испытываемого спутниками GPS относительно Земли, нам необходимо отдельно определить величины, обусловленные специальной теорией относительности (скорость) и общей теорией относительности (гравитация), и сложить их вместе.

Величина, обусловленная скоростью, будет определяться с помощью преобразования Лоренца . Это будет:

Для малых значений v/c с помощью биномиального разложения это приближается к:

Спутники GPS перемещаются на 3874 м/с относительно центра Земли. ^[18] Таким образом, мы определяем:

Эта разница ниже 1 из8,349 × 10 ⁻¹¹ представляет собой долю, на которую часы спутников идут медленнее, чем часы Земли. Затем он умножается на количество наносекунд в сутках:

То есть часы спутников теряют 7 214 наносекунд в день из-за эффектов
специальной теории относительности .

Отметим, что эта скорость3874 м/с измеряется относительно центра Земли, а не ее поверхности, где находятся приемники (и пользователи) GPS. Это связано с тем, что эквипотенциал Земли делает чистое замедление времени равным по всей ее геодезической поверхности. ^[21] То есть комбинация Специальных и Общих эффектов делает чистое замедление времени на экваторе равным замедлению полюсов, которые, в свою очередь, покоятся относительно центра. Следовательно, мы используем центр в качестве точки отсчета для представления всей поверхности.

Величина расширения из-за гравитации будет определяться с помощью уравнения
гравитационного расширения времени :

Для малых значений M/r с помощью биномиального расширения это приближается к:

Нас снова интересует только дробь меньше 1 и разница между Землей и спутниками. Для определения этой разницы возьмем:

Земля имеет радиус 6 357 км (на полюсах), что делает R _земли = 6 357 000 м, а спутники имеют высоту 20 184 км ^[18] , что делает радиус их орбиты R _gps = 26 541 000 м. Подставляя их в приведенное выше уравнение, где M _земля =5,974 × 10 ²⁴ , G =6,674 × 10-11 и с = ^_2,998 × 10 ⁸ (все в единицах СИ ), дает:

Это представляет долю, на которую часы спутников идут быстрее, чем часы Земли. Затем он умножается на количество наносекунд в сутках:

То есть часы спутников отстают на 45 850 наносекунд в день из-за эффектов общей теории относительности . Эти эффекты суммируются, чтобы дать (округленное до 10 нс):

45850 – 7210 = 38640 нс

Следовательно, часы спутников отстают примерно на 38 640 наносекунд в день или 38,6 мкс в день из-за эффектов относительности в целом.

Чтобы компенсировать это усиление, частота часов GPS должна быть уменьшена на долю:

5,307 × 10 ⁻¹⁰ –  8,349 × 10-11 = ^_4,472 × 10–10 ^_

Эта дробь вычитается из 1 и умножается на предварительно настроенную тактовую частоту 10,23 МГц:

(1 –  4,472 × 10 ⁻¹⁰ ) × 10,23 = 10,22999999543

То есть нам нужно замедлить часы с 10,23 МГц до 10,22999999543 МГц, чтобы свести на нет эффекты относительности.

Искажение Саньяка

Обработка наблюдений GPS также должна компенсировать эффект Саньяка . Шкала времени GPS определяется в инерциальной системе, но наблюдения обрабатываются в системе , ориентированной на Землю и привязанной к Земле (совместное вращение), системе, в которой одновременность не определена однозначно. Таким образом, преобразование координат применяется для преобразования из инерциальной системы в систему ECEF. Полученная коррекция времени прохождения сигнала имеет противоположные алгебраические знаки для спутников восточного и западного небесных полушарий. Игнорирование этого эффекта приведет к ошибке восток-запад порядка сотен наносекунд или десятков метров в положении. ^[22]

Естественные источники помех

Поскольку сигналы GPS в наземных приемниках имеют тенденцию быть относительно слабыми, естественные радиосигналы или рассеяние сигналов GPS могут снижать чувствительность приемника, что затрудняет или делает невозможным получение и отслеживание спутниковых сигналов.

Космическая погода ухудшает работу GPS двумя способами: прямыми помехами из-за шума солнечных радиовсплесков в той же полосе частот ^[23] или рассеянием радиосигнала GPS в ионосферных неоднородностях, называемых мерцанием. ^[24] Обе формы деградации следуют 11-летнему солнечному циклу и достигают максимума при максимуме солнечных пятен, хотя они могут произойти в любое время. Солнечные радиовсплески связаны с солнечными вспышками и корональными выбросами массы (КВМ) ^{[25] .}и их воздействие может повлиять на прием на половине Земли, обращенной к Солнцу. Мерцание чаще всего происходит в тропических широтах, где оно является ночным явлением. Реже это происходит в высоких или средних широтах, где магнитные бури могут привести к мерцанию. ^[26] В дополнение к мерцанию магнитные бури могут создавать сильные ионосферные градиенты, которые снижают точность систем SBAS. ^[27]

Искусственные источники помех

В автомобильных GPS-приемниках металлические детали лобовых стекол ^[28] , такие как антиобледенители или тонировочные пленки автомобилей ^[29] , могут действовать как клетка Фарадея , ухудшая качество приема непосредственно внутри автомобиля.

Искусственные EMI (электромагнитные помехи) также могут нарушить или заглушить сигналы GPS. В одном хорошо задокументированном случае было невозможно принимать сигналы GPS во всей гавани Мосс-Лендинг, штат Калифорния, из-за непреднамеренных помех, вызванных неисправными предусилителями телевизионных антенн. ^{[30] [31]} Возможно также преднамеренное заклинивание. Как правило, более сильные сигналы могут создавать помехи для приемников GPS, когда они находятся в пределах радиодиапазона или прямой видимости. В 2002 году в онлайн-журнале Phrack было опубликовано подробное описание того, как построить глушитель ближнего действия GPS L1 C/A . ^[32]

Правительство США сообщило, что такие глушители время от времени использовались во время войны в Афганистане , а американские военные уничтожили шесть глушителей GPS во время войны в Ираке , в том числе один, который был уничтожен с помощью бомбы с GPS-наведением, отметив неэффективность глушителей, использовавшихся при этом. ситуация. ^[33] Блоки помех GPS относительно легко обнаружить и определить местонахождение, что делает их привлекательной мишенью для противорадиолокационных ракет . 7 и 8 июня 2007 г. Министерство обороны Великобритании ^{провело испытания} системы радиопомех в западной части Великобритании ^.

В некоторых странах разрешено использование ретрансляторов GPS для обеспечения приема сигналов GPS внутри помещений и в скрытых местах; в то время как в других странах это запрещено, поскольку повторно передаваемые сигналы могут вызывать многолучевые помехи для других приемников GPS, которые получают данные как со спутников GPS, так и с ретранслятора. В Великобритании Ofcom теперь разрешает использование ретрансляторов GPS/GNSS ^[34] в режиме «облегченного лицензирования».

Из-за возможного наличия как естественных, так и техногенных шумов продолжают разрабатываться многочисленные методы борьбы с помехами. Во-первых, не полагаться на GPS как на единственный источник. По словам Джона Рули, « пилоты ППП должны иметь запасной план на случай неисправности GPS». ^[35] Автономный мониторинг целостности приемника (RAIM) — это функция, включенная в некоторые приемники, предназначенная для предупреждения пользователя в случае обнаружения глушения или другой проблемы. Военные США также с 2004 года развернули свой модуль селективной доступности / защиты от спуфинга (SAASM) в усовершенствованном GPS-приемнике Министерства обороны (DAGR). ^[36]В демонстрационных видеороликах было показано, что DAGR обнаруживает помехи и поддерживает блокировку зашифрованных сигналов GPS во время помех, из-за которых гражданские приемники теряют блокировку.

Смотрите также

• Дополнение GPS

Примечания

Ссылки

• Гревал, Мохиндер С .; Вайль, Лоуренс Рэндольф; Эндрюс, Ангус П. (2001). Системы глобального позиционирования, инерциальная навигация и интеграция . Джон Уайли и сыновья. ISBN 978-0-47135-032-3.
• Паркинсон; Спилкер (1996). Система глобального позиционирования . Американский институт аэронавтики и астрономии. ISBN 978-1-56347-106-3.
• Уэбб, Стивен (2004). Не от мира сего: сталкивающиеся вселенные, браны, струны и прочие дикие идеи современной физики . Спрингер. ISBN 0-387-02930-3. Проверено 16 августа 2013 г. .

Внешние ссылки

• GPS.gov — общедоступный образовательный веб-сайт, созданный правительством США.
• Стандарт производительности GPS SPS — официальная спецификация службы стандартного позиционирования (версия 2008 г.).
• Стандарт производительности GPS SPS — официальная спецификация службы стандартного позиционирования (версия 2001 г.).

Dilution of Precision (DOP) is a term used to specify the error in positional fix provided by a GNSS receiver due to the geometry of the navigational satellites from which signals are received. It is also called geometric dilution of precision (GDOP), where geometry refers to the number of satellites that are visible (for line-of-sight propagation), their altitude and the bearing towards them. DOP is only a value of probability for the geometrical effect on GPS accuracy and is roughly interpreted as the ratio of position error to the range error. The complete calculation of DOP can be complex and is computed from the geometric relationships between the receiver position and the positions of the satellites being used for navigation.

Figure 1 Example of satellites with poor geometry for high DOP values

A GNSS receiver usually requires only four satellite signals to provide a complete positional fix in three dimensions. The accuracy of this fix depends to some degree on the exact positions of the four satellites relative to the receiver. If the four signals acquired come from satellites spread throughout the sky relative to the receiver, then the fix will be highly accurate. But if all four satellites are close to each other within a single quadrant, then the fix will be less accurate. If two or more satellites are aligned and to appear to occupy the same space, then it may be impossible to obtain any fix. Alternatively, the fix obtained may be out to the tune by 150 or even 200 meters. When visible navigation satellites are close together in the sky, the geometry is said to be weak and the DOP value is high; when they are far apart, the geometry is said to be strong and the DOP value is low. Hence, a low DOP value represents a better positional precision due to the wider angular separation between the satellites used to calculate a GNSS receiver unit’s position.

Figure 2 Example of satellites with good geometry for low DOP values

The various interpretations of DOP values are as follows:

DOP Value	Rating	Description
<1	Ideal	Highest possible accuracy to be used for applications demanding the highest possible precision at all times.
1-2	Excellent	At this level of accuracy, positional measurements are considered accurate enough to meet all but the most sensitive applications.
2-5	Good	Represents a level that marks the minimum appropriate for making accurate decisions. Positional measurements could be used to make reliable in-route navigation suggestions to the user.
5-10	Moderate	Positional measurements could be used for calculations, but the fix still needs improvement. More open view of the sky may be recommended.
10-20	Fair	Represents a low level of accuracy. Positional measurements should be discarded or used only to indicate a very rough estimate of the current location.
>20	Poor	At this level, measurements are inaccurate by as much as 300 meters with a 6-meter accurate device (50 DOP × 6 meters) and should be discarded.

DOP can be expressed as several separate measurements with different definitions:

Position (3D) DOP (PDOP): This value describes how many satellites are spread evenly throughout the sky. The more the satellites directly above and the less on the horizon, the lower the PDOP value is.

Horizontal DOP (HDOP): This describes the effect of DOP on the horizontal position value. The more good visible satellites low in the sky, the better the HDOP and the horizontal position (Latitude and Longitude) are.

Vertical DOP (VDOP): This refers to the effect of DOP on the vertical position value. The more good visible low satellites in the sky, the better the VDOP and the vertical position (Altitude) are.

Time DOP (TDOP): This value describes the difference in time values of the satellites and receiver’s internal clocks. The more in sync their clocks are the lesser the TDOP value.

While each of these DOP terms can be individually computed, they are formed from covariances and so are not independent of each other. For example, a high TDOP (time dilution of precision) will cause receiver clock errors which will eventually result in increased position errors. The above DOP components are used because the accuracy of the GPS system varies as satellites move, thus varying the geometry with time.

DOP values have much importance in satellite navigation, geomatics engineering and other location systems that employ several geographical spaced sites. In electronic warfare DOP values of electronic-counter-counter-measures are important when computing the location of enemy emitters (radar jammers and radio communications devices). 

photos, graphics and article by Capt. Gunter Schütze

In the first part of my contribution about GPS, I wrote about the structure, the functionality, technical and physical basics of GPS:

To GPS (Part 1)

In my announced sequel, the second part of GPS, it is primarily about the technical and physical operational and functional limitations to which GPS is subject. These limitations, in part, have serious implications for the accuracy of GPS, and even go as far as limiting the functionality of GPS in its functions or even making it impossible. In doing so, I anticipate that these are errors that occur on a purely technical or physical basis. Much of these errors are taken into account in the configuration of GPS and implemented by means of appropriate correction tools, in GPS, so that unnoticed by the user, these errors are automatically corrected. But not all errors that occur can be solved by these tools. As a result, the GPS partially or temporarily limited in its functionality or temporarily even not effectively usable.

These bugs have nothing to do with SPOOFING/JAMMING. They are based on functional technical and physical causes, without human action. I will write more about spoofing/jamming at the following and last 3rd Part of GPS about artificial human initiated technical effects.

Let us therefore deal with the technical and physical sources of error that influence the function of GPS.

TYPES OF ERRORS

Below are several listed types of error, which of course should be the subject of closer consideration.

The division made by me relies on the corresponding error components.

It can also be distinguished into technical errors (see list under items 1, 3, 4) and natural errors (see item 2).

Priority will be given to errors which are highly relevant to satellite navigation in maritime shipping.

Some, rather untypical for the navigation GNSS errors are addressed only briefly. However, this is necessary as they are intended to help understand why in ports, in canals, in port approaches, GNSS data may be restricted in their accuracy and GNSS receivers limited in their function, until to temporary malfunctions.

Why is it important to know these types of errors?

All listed types of errors affect the operation and accuracy of GNSS. As can be seen, in this case GPS is not mentioned individually. Instead, the term GNSS (Global Navigation Satellite Systems) is used. The background is that all types of errors listed are applicable to all currently existing satellite navigation systems.

In the case of GPS-specific errors, this is of course only referred to GPS and marked.

1. Errors associated with satellites

1.1. Errors in the satellite orbit

1.2. Error in the satellite clock

1.3. Geometry of satellites

1.3.1. DOP values and their differences

1.4. Elevation errors

2. Errors affecting signal propagation

2.1. Basics of atmospheric effects

2.1.1. Ionospheric effects

2.2. Physical basics

2.2.1. The reflection

2.2.2. The refraction

2.3. Ionosphere error

2.4. Troposphere error

2.5. Noise of the receiver

2.6. Multipath transmission (reflection)

3. Recognition errors

3.1. Receiver clock error

3.2. Receiver electronics

3.3. Position of the phase center (refers primarily to the geodesic use)

3.4. Subjective factors

4. Artificial errors

4.1. Premeditated errors

4.2. Unintended Interferences

4.3. Intentional Interferences

4.3.1. Jamming,

4.3.2. Spoofing,

4.3.3. Meaconing

Item 4 with its sub-items is separately described by me in the 3rd part of GPS, due to its complexity and increasing importance in the civil and military use of GNSS

1. Errors associated with satellites

1.1. Errors in the satellite orbit

These errors, also called ephemeris errors, are based on the difference in the predicted satellite position and its actual position.

To calculate the position with GNSS, knowledge of the exact satellite position is required. The satellite positions contained in the GNSS navigation messages are predictions of where the satellite is likely to be located. Deviations between prediction and actual satellite position can have a probability of error of up to 10 meters. For the seafaring this value is relatively insignificant. But this looks in further kinds of use quit different, e.g. in geodesy

Causes of this error are:

The current position of a satellite is calculated from the transmitted ephemeris (precise orbit data) contained in the navigation messages. Ephemeris mathematically describes the predicted orbit of a satellite, which allows a receiver to determine the current position of a satellite in space at a given time. However, there are slight disturbances of the satellite orbit. These disorders can have different causes like:

These disorders can have different causes like:

a) the effect of the gravitational fields of the moon and the sun, whereby in particular the gravitational field of the moon has considerable influence,

b) the radiation pressure exerted by the sun on the satellites,

c) the movements of the satellites are affected by frictional forces from the rest of the atmosphere.

Consequence: the satellites are not exactly on the theoretically calculated orbit, as represented in the graphic for satellite orbit-error above, which in turn affects the position determination.

In order to keep the ephemerides always precise despite the disturbances that occur, the satellite orbits are permanently monitored by the GPS ground segment. As can be seen from the adjacent graphic using the example of GPS.

The data from the observations are used to calculate the orbit data in advance. The newly calculated orbit data is then transmitted to the satellites and updated hourly. To get even more accurate orbit data, the satellites are not only observed by the GPS ground segment, but also by a large number of worldwide distributed observation stations. These observation stations belong to the international GPS Service.

1.2. Clock error in the satellite

In GPS (Part 1), it was explained in the subject time dilation and gravitational dilation that even the slightest time deviation of the clocks in the receivers compared to the time in the clocks of the satellites can cause considerable position errors. However, the use of atomic clocks, because of their higher accuracy, does not protect them from interference. The time in the satellites is determined by the satellite atomic clocks. Nevertheless, there is a time difference between the satellite time and the GPS system time. The reason lies in the effects of dilatation. This happens partly because of the speed of a satellite, because the satellite clock is relatively slower than a non-moving clock on the earth’s surface and partly because of the lower gravity field of the earth in the satellite orbit. As a result, a satellite clock is faster than a resting clock on the earth’s surface (gravitational dilation). The clock error has an influence on the accuracy of the path data (ephemeris error) and thus also on the accuracy of the distance measurement. This is because the ephemeris are assigned to a wrong time.

The deviation of the satellite time from the GPS system time is determined for each satellite in the Main Control Station (MCS) and transmitted to the satellites using the ground transmitter station. The satellites then transmit the time correction parameters in the navigation message (in the so-called sub-frames of the navigation message).

1.3. Geometric Errors of Satellites — Dilution of Position (DOP)

The accuracy of positioning with satellites is highly dependent on the satellite geometry, that is, the distance angles between the satellites. It is called DILUTUON of POSITION (DOP) and stands for the influence of satellite geometry on the measurement accuracy. In other words — DOP — stands for the weakening of the position accuracy and is thus a measure of the satellite constellation-dependent inaccuracy.

The more acute the angles between the satellites observed, the less accurate the position determined. The background to this is that the intersections of the distance lines of corrected distance and pseudo-error removal result in large error areas in comparison to distance angles of > 30 °.

It follows the same principle, which is used in traditional navigation (terrestrial, radio navigation, astronomical) application that angles of <30 ° in their intersections in any case adversely affect the accuracy of positioning, since an accurate intersection assignment is only possible inaccurately , due to long cutting lines. They should therefore not be used.

In the left-hand diagram, this is illustrated by an example with 2 satellites, with a distance angle γ > 30 ° and γ < 30 ° and the associated effects on the position accuracy and the area of the region of the position error.

Angles of γ > 30 ° (90 ° in the example), it can be seen that the dimension of the area of the region of the position error is significantly smaller and thus the position determined is significantly more accurate than with distances of γ < 30 ° (15 ° in the example). Where the area of the position error and thus also the region of the possible determined position increases significantly.

The logical conclusion is that if 4 satellites are used for observation and they are close to each other, i.e. with small distance angles, this means that the accuracy of the position determination is reduced. If the distance angles between these satellites are increased, this means that the accuracy of the position determination is increased. Optimum positioning accuracy is achieved when all 4 satellites are distributed at 120 ° intervals, with one satellite at the zenith of the receiver and the other 3 satellites should have a relatively small elevation above the horizon. However, too low elevation angles also mean a higher influence of atmospheric disturbances.

The last listed satellite constellation would mean that the DOP would take on the minimum value, so there are optimal conditions for determining the position.

From this it can be concluded that the larger the DOP value, the greater the expected inaccuracy in the position. In other words, the DOP value is proportional to the accuracy of the measurement.

Thus, when the DOP value doubles, the error value of the position determination also doubles.

In the specialist literature, it is formulated by the Swiss J. M. Zogg, in his publication «GPS and GNSS: Basics of positioning and navigation with satellites», published in 2015, as follows:

The DOP value «(…) can be interpreted as the reciprocal value of the volume of a tetrahedron formed from satellite and user positions» (p. 92).

When the volume of the tetrahedron reaches its maximum, the DOP value reaches its minimum (see figure above).

An illustrative example of how the DOP changes depending on the satellite constellation. DOP is therefore a variable value that must be considered in relation to the variability of the satellite configuration and is subject to constant change.

1.3.1. DOP values and their differences

DOPis divided into the following values:

a) GDOP: referred to as Geometric DOP. Value Describes the influence of satellite geometry and timekeeping on position in space (3D). For a good position determination, the GDOP value should be <5.

b) PDOP: referred to as Position DOP. The value Describes the influence of the satellite geometry on the 3D position

c) HDOP: referred to as Horizontal DOP. The value describes the influence of the satellite geometry on the position in the plane (2D). Meaning of accuracy values for HDOP: < 4 very good, 4 — 6, good, 6-8, inaccurate, > 8 not usable. The higher the selected satellites in the sky, the worse the HDOP values.

d) VDOP: referred to as Vertical DOP. Value Describes the influence of satellite geometry on altitude (1D). The VDOP values are bad as soon as the satellites are very close to the horizon.

e) TDOP: referred to as Time DOP. The value describes the influence of the satellite geometry on the time measurement

GDOP is the most important DOP value because it represents the error information of the entire system. It results from the position DOP (position error in space) and Time DOP (time offset) and is calculated as follows:

From this it becomes clear that the value GDOP is dependent on the location of the receiver and the time.

If more than 4 satellites on the visible horizon, the receiver selects the 4 satellites that give the best GDOP value and thus have the most favorable satellite constellation.

1.4. Satellite elevation effects on the VDOP

The adjacent graphic shows the influence of satellite elevation on VDOP quality. Again, the smaller the VDOP value, the better the satellite constellation.

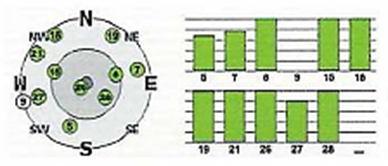
An elevation between (-75 °) — Zenith (90 °) — (+ 75 °) and between 5 ° — 15 ° means less favorable VDOP values, which adversely affect the position determination. Particularly low-altitude satellites are more exposed to atmospheric disturbances because their signals travel a longer distance in the atmosphere, which causes a delay in the signal resulting in larger range finding errors.

Heights between 0 ° — 5 ° result a very large VDOP, which can no longer be used for position determination, since the influence of atmospheric disturbances becomes too great to receive a usable satellite signal for the distance measurement.

Under normal conditions, satellite elevations between 15 ° to 75 ° elevation are the most favorable angles for maritime GNSS receivers to limit rangefinding errors due to atmospheric disturbances. However, it is possible by manual adjustment to change the elevation angle to be used. Likewise, in the GNSS (GPS) configurations, the sub-menus of the receivers display the values for HDOP and VDOP, thus providing information about the quality of the satellite data and thus the accuracy of the distance measurement. Depending on the particular manufacturer of GNSS receivers, they are also referred to as Satellite angle or VDOP. Signal to Noise Ratio (SNR) describes the signal quality and is represented by various diagram shapes (bar graphs, line graphs).

In addition, the data used for the local DGPS beacons can be called up in order to obtain an overview of the signal quality and accuracy of the positioning of DGPS.

RAIM…Receiver Autonomus Integrity Monitoring— technology developed to assess the integrity of global positioning system (GPS) signals in a GPS receiver system. It is of special importance in safety-critical GPS applications, such as in aviation or marine navigation

SNR…Signal to Noise Ratio— Measure of the technical quality of a useful signal, which is superimposed by a noise signal.

For detailed instructions on how to use and the settings of the GPS / GNSS receiver, refer to the Operational Manuals provided by the manufacturers.

2. Errors affecting signal propagation

Since we are dealing at satellite signals as electromagnetic waves, they are also subject to the laws of physics of the propagation of waves. Especially when waves enter media of different densities. This means that the physical principles of refraction and reflection come into play. On the way from the satellite to the receiver, the electromagnetic waves undergo three different media of different ionization and density, which influence the wave direction and the propagation velocity of the wave. Since satellites in GPS at a height of 20200 km have their orbit around the earth, we have to divide into 3 different spheres:

a) Interplanetary space (> 1000 km — ∞)

b) Ionosphere (60 — 1000 km)

i. Exosphere (700 — 1000)

ii. Thermosphere (85-700 km)

iii. Mesosphere (50-85 km)

c) Stratosphere 15-50 km

d) Troposphere 0-15 km

The stratosphere is not considered in the further analysis, as its effects on the satellite signals can be neglected.

In interplanetary space, due to its extremely low gas density, there is an almost unrestricted linear wave propagation with almost no friction losses, since it resembles a vacuum, a space void of air. The propagation speed electromagnetic / light waves takes place there at the speed of light.

That changes with the transition from the interplanetary space to the Ionosphere.

2.1. Basics of atmospheric effects

2.1.1 Ionospheric effects (at a height of 60 — 1000 km)

As the name implies, the ionosphere is an atmospheric layer containing large amounts of ions and free electrons. High-energy hard UV and X-rays of solar radiation cause ionization of the gas molecules.

The ionosphere plays a crucial role in radio communications due to their local layers with their ionization maximum. The ionization of these layers is influenced by the daily and seasonal course of the sun, as well as by the solar cycle (11 years). The ionization depends on the solar radiation intensity and the location. Why the dependence on the place? At the equator we find the strongest ionization during the day, which decreases towards the poles. The background is that in the equatorial region the atmosphere has its greatest extent.

The factors mentioned have a significant influence on the character of the ground and space waves in the different frequency ranges of long / medium and short waves and can reach ranges of up to 1000 km in the best case. With overreach up to 2500 km are possible. The following table shows the structure of the 3 local layers and their sublayers of the ionosphere.

As mentioned, the structure of the ionized D-, E-, and F-layer is strongly dependent on the influence of the daily and seasonal sun-rise and the associated radiation intensity of the sun. How this is pictorially illustrated are shown in the two following graphics.

When the satellite signal enters the denser ionosphere from interplanetary space, two wave phenomena occur. The refraction and reflection of the wave.

2.2. Physical basics of wave propagation

As a short introduction to the understanding of wave propagation a short explanation of reflection and refraction

2.2.1. The Reflection

Reflection in physics means the reflection of waves on surfaces of different density (also called interfaces) depending on the characteristic impedance of the different media or the refractive index of the electromagnetic wave (called the propagation medium)

The energy of electromagnetic radiation is usually only partially reflected at an interface. Also referred to as partial reflection.

The basis of reflection is the law of reflection, which states that if the incident beam, the perpendicular, and the outgoing beam lie on one plane, then the angle of incidence α = the angle of departure α ‘.

The refractive index reflects the ratio of the wavelength of the light and thus the phase velocity in vacuum to another medium. In general it depends on the wavelength. That is, waves of different wavelengths can be reflected to different degrees.

The other part of the energy penetrates the 2nd layer and exits at the back side. Depending on the refractive index n, which is determined as follows

This results in the angle of refraction which results from the law of refraction.

2.2.2. The Refraction

Refractionin physics means changing the propagation direction of waves through a spatial change in the refractive index of the medium which the wave passing through. The change in the refractive index leads to a change in the phase velocity (c) of the shaft. Refraction occurs with any type of waves that propagate in more than one dimension.

The basis of the refraction is the law of refraction by Snellius (Willebrord van Roijen Snell, 1580-1626, Dutch astronomer and mathematician).

It describes the change of direction of the direction of propagation of a plane wave during the transition to another medium. The cause of the change in direction is the change in the material-dependent phase velocity, which enters the refractive law as a refractive index. The most well-known phenomenon described by the law of refraction is the directional deflection of a light beam as it passes through a media boundary. The law is not limited to optical phenomena, but valid for any wave, especially ultrasonic waves.

In all the processes of reflection and refraction, it must be taken into account that this also involves energy losses, which cause the signal in the satellite signal to be reduced.

2.2.2. The Refraction

On the way from the satellite through the interplanetary space, the satellite signal propagates in a straight line and at the speed of light. Upon entry into the ionosphere, i.e. into the denser medium, caused by the ionization of the gases located there, by the sunlight, a part of the wave is reflected at the interface (partial reflection), while the other part of the wave is refracted at the interface and the dense medium passed through. Thereby it results in a propagation delay of the satellite signal, it will be attenuated, it slows down and there is a change in direction of the wave, caused by the change in the wavelength at penetration of the interface. The reduced propagation speed of the satellite signal causes a delay of the signal. This so-called ionospheric delay is frequency-dependent and can be up to 300 ns in the worst case, which would correspond to a position error of about 100 m. Since waves with high frequencies, i.e. in the L band (frequency range 1-2 GHz, λ = 30-15 cm), are exposed to the influences of the ionosphere less, it follows as a logical conclusion to use these for satellite navigation.

It thus becomes apparent that the sun plays a significant role in the effect of the ionospheric error as a deciding factor, which depends on the daily routine, the annual cycle of the sun and the solar cycles (11 years). It must be pointed out that the so-called twilight or night effect in the ionosphere (polarization changes of space waves), which occurs after the sunset (reduction of ionization in the ionosphere), can have effects on satellite signals. The ionosphere error is a frequency dependent error. This distinguishes him from the troposphere. He can be determined by using of two frequencies and eliminated up to 99%.

However, since only one frequency (GPS — L1) is available in the navigation for the public, this error must be reduced by means of geophysical calculation models. The best-known model is the Klobuchar model, named after its developer. It is based on the approximation of the vertical ionospheric transit time delay by a cosine function of the local time during the day and a constant magnitude for the night and compensates for about 50% of the error.

2.4. The Troposphere error

The troposphere as the lowest layer of the earth’s atmosphere from the earth’s surface to about 15 km in height is characterized by the fact that their density decreases with altitude. The main causes of the tropospheric error are satellite elevation angles, temperature, humidity and the density of the gas molecules. It can be put into simple terms: the higher the density and temperature, the lower the humidity in the troposphere and the smaller the satellite elevation angle, the greater the propagation delay of the satellite signal, by attenuation to the propagation velocity of the wave, this means she is reduced, there is thus a time lag of the signal and of course there is also the influence of the refraction and partial reflection of the wave, so the refraction and reflection at the interface. The troposphere is not frequency dependent. The resulting tropospheric error is approximately 5 — 25 m in the distance measurement. Can amount up to approx. 33 m in extreme cases be.

Tropospheric effects vary mainly due to the influence of the elevation angle of the satellites and the temperature of the region in which the receiver is located. Tropospheric models consist of a dry and moist component, whereby the dry component produces approx. 80 — 90% of the tropospheric error and the wet component approx. 10 — 20%, caused by the water vapor in the atmosphere. At an elevation angle of 90 °, the tropospheric error is predictable with an accuracy of up to 1% and in the best case close to 0. The graphic on the left illustrates the influence of satellite elevation, air humidity and air temperature on the tropospheric error. The tropospheric error has its least effects at satellite elevation angles > 15 ° and the greatest effects at angles of < 15 °, which results from the longer distance traveled in the troposphere and the associated time delays due to atmospheric influences. Whereas the dry component is very accurately predictable is this much more difficult with the wet component. Using algorithms installed in the receivers of existing models for dry and humid tropospheric conditions, so-called mapping functions (mapping functions are used to relate troposphere error at a particular elevation with troposphere error in zenith), it is possible the tropospheric error to almost compensate.

2.5. Receiver noise (Signal to Noise Ratio — SNR)

The signal-to-noise ratio is a measure of the technical quality of a useful signal, which is superimposed by a noise signal. It is defined as the ratio of the average power of the useful signal to the average noise power of the interference signal.

The formula is dimensionless

Both, signal and noise power must be measured at the same or equivalent points in a system and within the same system bandwidth.

To be able to extract the information safely from the signal, the useful signal must stand out clearly from the background noise, so the SNR must be sufficiently large. A ratio of more than 1: 1 (more than 0 dB) indicates more signal than noise.

As a characteristic value of a receiver, the SNR characterizes when the receiver can distinguish noise from the signal.

Using the definitions of SNR, signal and noise in decibels, this leads to an important formula for calculating the signal-to-noise ratio in decibels when the signal and noise are also in decibels.

I deliberately did not use the full logarithmic formula derivation because that would go beyond the scope and I can’t assume that in-depth knowledge of this technical area is available to the navigational officers on board. It’s about basic understanding.

The receiver noise is primarily due to technical effects. And is different for the different reception systems:

We differentiate between 2 types of receiver noise:

a) Thermal noise

On the one hand, it can be traced back to receiver components. On the other hand, external conditions are reflected in the vicinity of the reception system.

b) Oscillator noise

It depends on the frequency standard used. A frequency standard is understood to be a frequency-stable oscillator. What atomic clocks are mostly used for today. The derived high-precision frequencies are referred to as normal frequencies.

The noise behavior of both components is also called white noise. The influences of the receiver noise are largely negligible due to the C / A code method used.

The consideration required in geodesy of the fluctuation of the phase center of the receiving antenna as a receiver error, for highly accurate surveying, is not important in maritime shipping

2.6. Multipath transmission / multipath propagation

These error factors only play a subordinate role in shipping on the open sea. They result from the refraction, diffraction, reflection and scattering of the satellite signals. They are interesting on canals, rivers and in port areas due to the physical effects mentioned for satellite signals on buildings, quay walls, steep bank walls, port crane systems.

3. Detection error

3.1. Receiver clock error

The distance between satellite and receiver is approx. 0.07 seconds taking into account the signal speed (speed of light with 299.792.458 m / s). With a required measuring accuracy of less than one meter, it requires watches with a very high accuracy of < 10-9 (ten to the minus 9). This is only possible with high-precision atomic clocks, which of course have their price. Taking into account economic constraints, watches with such accuracy are only installed in satellites. The receivers are equipped with less expensive, more temperature-stabilized atomic clocks, with a precision of 10-5 (10 to the minus 5) to 10-6 (10 to the minus 6). It can be seen that there is a measurement error that needs to be corrected by other means to achieve accuracies of less than one meter. In general, this is possible with algorithms that simulate the receiver clock error. Watch errors can be very diverse. In addition to constant and linear errors, there are also non-linear errors. Since material side measurements on the watch crystals would be very extensive and expensive, this problem must be clarified via software solutions. For this purpose, the clock error of the receiver at the time of determining the position is assumed to be constant. It is the same for all distance measurements. This means that if 4 satellites are measured, the clock error can be calculated as the fourth unknown. However, if other than the receiver clock error, other signal errors due to technical and physical errors at the receiver will occur, the method will fail. Then an increased mathematical effort is required to compensate for these errors.

3.2. Receiver electronics error

Errors in the receiver electronics cover a wide range of technical malfunctions:

Faulty fusess,

Antenna failure, faulty / corroded wire antenna connections and cable connections

Display problems,

Mainboard problems

Interface problems

Data port problems

LAN problems

Random Access Memory (RAM) error

Read-only memory (ROM) error

Ethernet problems (wrong / faulty IP address settings, faulty port settings and Ethernet errors, such as Check sum errors / syntax errors / framing errors etc.)

Failure of electronic components (transistors / circuits / CPU’s / resistors / rectifiers)

It therefore makes sense to use the system intern tests integrated by the manufacturers in the receivers to detect internal errors in advance. In the Operational Manuals of the manufacturers, the necessary instructions and recommendations for action are given.3.3.

3.3. Error in the location of the phase center

This error is not relevant for aboard of ships GNSS receivers.

I want give it in a purely informative way to show that in surveying (geodesy), where high-precision position determinations of up to a few centimeters are used. The phase center of the receiving antennas used must be precisely adjusted, to fulfill the demand in very accurate positions.

3.4. Subjective factors

These are primarily human factors, i.e. incorrect or erroneous operations of the receiver by the user / operator, due to lack of or insufficient knowledge in the handling of the technique.

Especially when incorrectly entering important parameters [e.g. ship size and GNSS antenna positions, GNSS system assignment, elevation mask, RAIM alarm settings, reference date, I / O menu (data output sentence / TX interval / Ethernet — IP address / port) ECDIS synchronization- Configuration, etc.], errors of several hundred meters in the distance determination or malfunctions of the system until to complete breakdown can be triggered.

Final Remarks

As I wrote at the beginning, the ARTIFICIAL ERRORS listed under item 4 are dealt with separately in Part 3 for GPS. The background to this is that this chapter will in future become increasingly important in the mass use of GNSS in a wide variety of application areas.

That requires somewhat more intensive explanations in order to deal more intensively with the sometimes complicated subject matter and at the same time to point out that not everything that is sold to us sensationally in the media as jamming or spoofing, i.e. the targeted disruption by people, institutions, armed forces, governments, have something to do with it in real. Because there are also physical and technical causes for disturbances that can be significantly curbed by new technical solutions. For the user, this 4th chapter in part 3 of GPS should raise awareness, take a closer look at GNSS faults, analyze them with your possibilities, so also take a closer view at the surrounding area and derive correct conclusions.

Of course, this also presupposes that the knowledge gained in GPS Part 1 and Part 2 is applied correctly.

© Copyright December 2019, Capt. Gunter Schütze. Replication or redistribution in whole or in part is expressly prohibited without the prior written consent by Capt. M.Eng. Gunter Schütze

25.11.2021

Источники ошибок GNSS

Приемник GNSS обычно выдает местоположение с номинальной погрешностью менее 15 метров с достоверностью 95 %. На результат влияет ряд шибок.

1. Атмосферные эффекты

Слабый спутниковый сигнал, подвергается воздействию во время своего прохождения через ионосферу и тропосферу. Это искажение выступает наибольшим для сигналов со спутников, расположенных вблизи горизонта.

GPS-графики для пришвартованного судна, показывающие разброс около +/- 15 метров для ряда прошлых позиций. (Функция отслеживания отслеживания) Фото A Knutas 

Ошибки тропосферы вызваны ближайшим к Земле слоем атмосферы, который простирается примерно на 10 км от поверхности. Именно здесь существует «погода». Азот, кислород и водяной пар − это газы, которые могут искажать сигнал. Ошибки уменьшаются за счет компенсационных расчетов, основанных на математической модели тропосферы.

Прохождение сигнала через ионосферу, которая представляет собой слой от 50 до 1000 км, вносит другие ошибки. В этом случае на сигнал влияет присутствие электрически заряженных частиц, что приводит к ошибке синхронизации. Чтобы ограничить размер этой ошибки, так называемая маска высоты, установленная на 10°− 15°, отфильтровывает сигналы со спутников, расположенных близко к горизонту. Военные приемники могут уменьшить размер этого эффекта, используя несколько частот для измерения и моделирования ионосферы. Гражданские приемники смогут использовать дополнительную частоту L5 и затем смогут использовать несколько частот для измерения.

2. Ошибка синхронизации

Ошибка синхронизации возникает, когда часы спутника и приемника не полностью совпадают. Поскольку спутник оснащен несколькими очень точными атомными часами, эта ошибка в первую очередь вызвана приемником. Большую часть этой ошибки можно устранить, подключившись по крайней мере к четырем различным спутникам.

3. Ошибка эфемериды

Станции мониторинга, расположенные по всему экватору, постоянно регистрируют спутниковые сигналы, чтобы рассчитать их орбиты. Орбитальные данные отправляются пользователям, как часть навигационного сообщения, которое включает параметры орбиты, то есть информацию о местоположении спутников. Ошибка в этом источнике называется ошибками траектории орбиты и вносит 3−5 метров в общую величину погрешности.

4. Ошибка мультилучей

Если спутниковые сигналы отражаются от поверхностей таких, как вода, стены или поверхности на борту или трубы, до достижения приемника, то генерируются так называемые «ошибки мультилучей». Отсечение сигналов со спутников, близких к горизонту до >15°, уменьшит размер ошибок мультилучей.

   

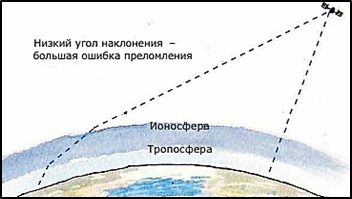
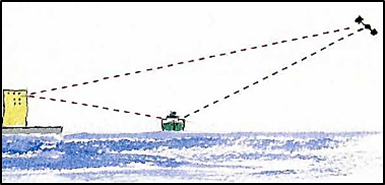
Расположение и доступность спутников

Точность определения положения снижается, когда позиционные линии пересекаются под неблагоприятными углами. Поскольку, спутниковый приемник не отображает никаких линий положения, он показывает, так называемое, значение DOP (размытие точности). Это показатель того, насколько хорошо пересекаются линии координат со спутников.

Хорошее распределение спутников по небу дает низкое значение DOP (1−3), что способствует точному построению карты положения.

Морских навигаторов больше всего интересует HDOP (Горизонтальный DOP). Другие параметры включают: PDOP (Позиционный DOP), который является ошибкой в трехмерном положении и GDOP (Геометрический DOP), который содержит PDOP и ошибку синхронизации.

Фактическая ошибка системы, умноженная на HOOP, генерирует значение позиционной погрешности. HOOP должен быть меньше 4. При загрузке HOOP, изначально велик и уменьшается по мере того, как положение вычисляется с использованием все большего и большего количества спутников. Иногда могут возникать довольно большие неточности, но они, как правило, кратковременны.

Страница в плоттере, на которой показано количество и расположение спутников. В этом случае доступно только пять и три из них находятся рядом друг с другом. Это приводит к неудачному пересечению линий положения. (Az = Азимут)
В этом случае, доступно только несколько спутников и некоторые из них находятся относительно близко друг к другу, тогда HDOP может быть необычно большим. Если ошибка преломления в атмосфере вместе с другими погрешностями составит +/-15 метров, то общее отклонение будет уже 15 х 16 = +/- 240 метров.

Высоты и азимуты на полярной диаграмме, сила сигнала в виде гистограммы 

Информация PDOP с официального сайта. Это показывает, что PDOP может сильно и быстро меняться. PDOP − это описание качества трехмерной позиции. Навигатор больше всего интересует HDOP, который несколько меньше, чем PDOP.

6. Отключение GPS

Солнечные вспышки − это более холодные области, которые кажутся темнее на диске Солнца. Они показывают неравномерное распределение магнитного поля звезды. Их периодичность около 11 лет, с последним максимумом в 2012/13 годах. Процессы на Солнце оказывают влияние на ионосферу Земли и, следовательно, влияют на распространение радиоволн.
На солнечной стороне Земли эффекты солнечных пятен заблокировали приемники GPS от приема спутниковых сигналов 5 и 6 декабря 2006 года. 

7. Вмешательство

Спутниковые приемники чрезвычайно чувствительны, чтобы собирать очень слабые сигналы со спутников. Один из результатов этого, то, что другие источники электромагнитного излучения могут создавать помехи для подлинных сигналов. Обнаружение и отслеживание спутников в этом случае может быть затруднено или даже невозможно.

Некоторыми естественными источниками помех являются: солнечный ветер, магнитные бури, северное сияние, поля излучения, окружающее Землю и метеорологические условия, что сказывается на работе приемника. Физические объекты между спутником и приемником также могут помешать сигналу. Высокая чувствительность приемников, к сожалению, также делает их чувствительными к этим источникам ошибок.

Относительно слабый источник излучения мощностью всего в несколько тысяч ватт, но работающий на частоте GPS, создаст помехи реальному сигналу на большой территории.

В 2001 году GPS-приемники в гавани Мосс-Лэндинг в заливе Монтерей, ощутили помехи в области диаметром около 1000 метров. После их интенсивного поиска, источник был обнаружен на предусилителе телевизионной антенны на лодке.

8. Помехи и подмена

Доступны портативные передатчики, которые намеренно блокируют, глушат или создают помехи сигналам GNSS (глушение). Этот вид оборудования был испытан во время военных маневров. Хотя технически это сложнее, можно обмануть приемник GNSS, генерируя ложные сигналы (подделка).

9. Ошибки приемника

В зависимости от его качества внутренние помехи в приемнике (ошибки программного обеспечения и синхронизации) могут привести к ошибкам в 2 метра и более.

10. Неадекватные сигналы

GPS-приемнику требуется свободной и прямая видимость со спутников. Высокие здания, густая растительность могут в достаточной степени мешать спутниковым сигналам, так, что местоположение может быть не определяться. Так же, на это сильно влияет направление, на котором расположены препятствия. Физические помехи на юге хуже всего, поскольку спутники GPS проходят на максимальной широте 55°. Это обстоятельство серьезно ограничивает количество спутников в северных широтах.

11. Надежность

Существует ряд факторов, влияющих на точность и надежность, которых можно достичь на борту. Спецификация доступности (Надежности обслуживания) указана на уровне 99,996%.

RAIM (Автономный мониторинг целостности приемника) это функция в некоторых приемниках, которая подает сигнал тревоги, когда надежность системы низкая. Функция проверяет сигналы от различных спутников и распознает, когда один из них выдает неожиданное положение. Если это так, то этот спутник удаляется из расчета. Для обнаружения ошибки функции требуется не менее пяти спутников. Если доступно шесть спутников, то программа может не учитывать плохой сигнал.

Надежность системы на судне зависит от того, как была проведена установка и техническое обслуживание, включая модернизацию!

 Старые приемники имеют более низкую производительность

Соседние файлы в папке Лекция№6

• #
• #
• #