|
|
Макеты страниц
Теперь рассмотрим ансамбль случайных СКК, у которых ансамбль внутреннего кода X фиксирован, а символы каждого внешнего кода 

Пусть последовательность слов передается 


Будем исследовать алгоритмы 
Проанализируем алгоритм СКК с независимым декодированием внешними кодами 








Легко заметить, что при использовании алгоритма Чнмп вероятность ошибки ограничена сверху выражением 













Утверждение 6.4. При декодировании с помощью алгоритма 

применять к каждому независимую экспоненту вероятности ошибки. Однако попытаемся действовать по аналогии с алгоритмом 
Рассмотрим сначала экспоненту случайного кодирования. Вероятность ошибки при условии передачи вектора 


где 




Переходим к следующей гртппе событий 





Подставив (6.17) в (6.16) и проведя преобразования, получим

где

Теперь в соответствии с методом получения экспоненты случайного кодирования [24] получим

где 


Подставив (6.20) в (6.19) и проведя необходимые преобразования по аналогии с [24], получим

Используя тот факт, что передача осуществляется по каналу без памяти, получаем

где 



Переходные вероятности в (6.22) можно получить по формулам, аналогичным (6.14):

где 



Положим теперь, что избыточности внешних кодов СКК выбраны таким образом, что выполняется тождество 

или же 

где 





Взяв производную (6.26) по 0 при 


Следует отметить, что, во-первых, 




По аналогии с [24] можно получить выражение экспоненты для ансамбля СКК с выбрасыванием.
Утверждение 6.5. При декодировании по алгоритму 
Рентах 

где 




Кроме того,







Как и в утверждении 6.4, для асимптотики 



Асимптотическая сложность алгоритмов декодирования СКК по максимуму правдоподобия определена формулами 
Утверждение 6.6. Сложность декодирования СКК с ансамблем сигналов X, раскладываемым на цепочку вложенных ансамблей
вектором разбиений 


где 

а при декодировании по максимуму правдоподобия

Рассмотрим для примера двухмерные сигналы ФМ и КАМ. На рис. 6.3 и 6.4 показано разбиение на зоны сигналов 
Для расчета показателей экспонент вероятности ошибки необходимо уметь определять вероятности или плотности вероятностей (см. (6.14) и 






Рис. 6.3 Разбиение на зоны сигналов 
(кликните для просмотра скана)

Для несимметричного канала необходим полный перебор. Величина 
Пусть 








Подставив (6 35) в (6.14) и (6 23), можно оценить соответствующие показатели экспоненты вероятности ошибки декодирования СКК.
На рис. 6.5 и 6.6 показаны зависимости максимально достижимых скоростей передачи от отношения сигнал-шум при ФМ и КАМ соответственно. Кривые на рисунке соответствуют: 1 — пропускной

Рис. 6.6 Максимально достижимые скорости передачи при КАМ
способности ГКБП; 2 — жесткому алгоритму 




Как и следовало ожидать, начиная с 



Рис. 6.7 Зависимость показателя экспоненты ошибочного декодирования СКК от скорости передачи при ФМ

Рис. 6.8 Зависимость показателя экспоненты ошибочного декодирования СКК от скорости передачи при КАМ
Оглавление
- ПРЕДИСЛОВИЕ
- Часть I. Передача дискретных сообщений в каналах без межсимвольной интерференции
- Глава 1. МОДЕЛИ КАНАЛОВ БЕЗ МЕЖСИМВОЛЬНОЙ ИНТЕРФЕРЕНЦИИ
- Глава 2. ВИДЫ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ПО КАНАЛУ БЕЗ МЕЖСИМВОЛЬНОЙ ИНТЕРФЕРЕНЦИИ
- 2.2. СИГНАЛЫ РАЗМЕРНОСТИ ОДИН И ДВА
- 2.3. СИГНАЛЫ РАЗМЕРНОСТИ БОЛЬШЕ ДВУХ
- 2.4. ПОСТРОЕНИЕ ВЛОЖЕННЫХ АНСАМБЛЕЙ СИГНАЛОВ
- 2.5. ПОМЕХОУСТОЙЧИВОСТЬ АНСАМБЛЕЙ СИГНАЛОВ
- Глава 3. ВИДЫ КОРРЕКТИРУЮЩИХ КОДОВ
- 3.2 ЛИНЕЙНЫЕ БЛОЧНЫЕ КОДЫ
- 3.3. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ БЛОЧНЫХ КОДОВ
- 3.4. КАСКАДНЫЕ КОДЫ
- 3.5. ПОТЕНЦИАЛЬНЫЕ СВОЙСТВА КОРРЕКТИРУЮЩИХ КОДОВ
- 3.6. ОЦЕНКИ ПОМЕХОУСТОЙЧИВОСТИ
- Глава 4. СИНТЕЗ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ
- 4.2. ФОРМАЛЬНОЕ ОПИСАНИЕ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ
- 4.3. ПОСТРОЕНИЕ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ
- Глава 5. ДЕКОДИРОВАНИЕ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ
- 5.2. ДЕКОДИРОВАНИЕ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ПО МАКСИМУМУ ПРАВДОПОДОБИЯ
- 5.3. ДЕКОДИРОВАНИЕ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ПО ЕВКЛИДОВУ РАССТОЯНИЮ
- 5.4 ВЕРОЯТНОСТНОЕ МАЖОРИТАРНОЕ ДЕКОДИРОВАНИЕ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ
- Глава 6. АСИМПТОТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИИ
- 6.1. АСИМПТОТИЧЕСКИЕ ЗАВИСИМОСТИ СКОРОСТИ ПЕРЕДАЧИ ОТ КВАДРАТА ЕВКЛИДОВА РАССТОЯНИЯ
- 6.2. ЭКСПОНЕНТА ВЕРОЯТНОСТИ ОШИБКИ РАЗЛИЧНЫХ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ
- Глава 7. ОЦЕНКИ ПОМЕХОУСТОЙЧИВОСТИ И ПЕРСПЕКТИВЫ РЕАЛИЗАЦИИ КОНКРЕТНЫХ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ
- 7.1. СИГНАЛЬНО-КОДОВЫЕ КОНСТРУКЦИИ С ДЕКОДИРОВАНИЕМ ПО МАКСИМУМУ ПРАВДОПОДОБИЯ
- 7.2. СИГНАЛЬНО-КОДОВЫЕ КОНСТРУКЦИИ С ДЕКОДИРОВАНИЕМ ПО ЕВКЛИДОВУ РАССТОЯНИЮ
- 7.3. СИГНАЛЬНО-КОДОВЫЕ КОНСТРУКЦИИ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
- 7.4. ПЕРСПЕКТИВЫ РЕАЛИЗАЦИИ
- Часть II. Передача дискретных сообщений в каналах с межсимвольной интерференцией и и постоянными параметрами
- Глава 8. МОДЕЛЬ КАНАЛА С МЕЖСИМВОЛЬНОЙ ИНТЕРФЕРЕНЦИЕЙ
- 8.1. МОДЕЛЬ КАНАЛА НЕПРЕРЫВНОГО ВРЕМЕНИ
- 8.2. МОДЕЛЬ КАНАЛА ДИСКРЕТНОГО ВРЕМЕНИ
- 8.3 ГАУССОВСКИЙ КАНАЛ С МСИ
- Глава 9. ПРИЕМ СИГНАЛОВ В КАНАЛАХ С МЕЖСИМВОЛЬНОЙ ИНТЕРФЕРЕНЦИЕЙ
- 9.2. ОПТИМАЛЬНЫЙ ПРИЕМ СИГНАЛОВ В КАНАЛАХ С МСИ
- 9.3. ЛИНЕЙНЫЙ МАТРИЧНЫЙ ПРИЕМНИК
- Глава 10. ОПТИМИЗАЦИЯ СИГНАЛОВ ДЛЯ КАНАЛОВ С МСИ
- 10.2. ПРЕОБРАЗОВАНИЕ ГАУССОВСКОГО КАНАЛА С МСИ В СОВОКУПНОСТЬ НЕЗАВИСИМЫХ ГАУССОВСКИХ КАНАЛОВ БЕЗ ПАМЯТИ
- 10.3. ОБЩАЯ СТРУКТУРА СИГНАЛОВ ДЛЯ КАНАЛОВ С МСИ И ИХ ОПТИМАЛЬНЫЙ ПРИЕМ
- 10.4. СИГНАЛЫ ДЛЯ КАНАЛА С МСИ, ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ ПРЕДЫСКАЖЕНИЙ И ОДНОГО АЛФАВИТА КАМ
- 10.5. СИГНАЛЫ ДЛЯ КАНАЛА С МСИ, ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ ПРЕДЫСКАЖЕНИЙ И ПРОИЗВОЛЬНОГО ЧИСЛА АЛФАВИТОВ КАМ
- 10.6. РЕАЛИЗАЦИЯ СИГНАЛОВ ДЛЯ КАНАЛОВ С МСИ ПОСРЕДСТВОМ ЭФФЕКТИВНЫХ МЕТОДОВ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ
- Глава 11. ПОТЕНЦИАЛЬНЫЕ ХАРАКТЕРИСТИКИ КАНАЛОВ С МСИ
- 11.1. ПРОБЛЕМА ПОВЫШЕНИЯ СКОРОСТИ В КАНАЛАХ С МСИ
- 11.2. АНАЛИЗ ПОТЕНЦИАЛЬНЫХ ХАРАКТЕРИСТИК КАНАЛА С МСИ
- Глава 12. СИГНАЛЬНО-КОДОВЫЕ КОНСТРУКЦИИ ДЛЯ ГАУССОВСКИХ КАНАЛОВ С МСИ
- 12.1. СИНТЕЗ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ ГАУССОВСКИХ КАНАЛОВ С МСИ
- 12.2. АНАЛИЗ АСИМПТОТИЧЕСКИХ ХАРАКТЕРИСТИК СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ КАНАЛОВ С МСИ
- 12.3. АНАЛИЗ РЕАЛЬНЫХ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ КАНАЛОВ С МСИ
- Часть III. Передача сообщений в каналах с переменными параметрами и множественным доступом
- 13.1. ПРОБЛЕМА ИДЕНТИФИКАЦИИ КАНАЛА. ТРЕБУЕМАЯ ТОЧНОСТЬ ОЦЕНИВАНИЯ ПАРАМЕТРОВ КАНАЛА
- 13.2. ОЦЕНИВАНИЕ ПАРАМЕТРОВ ЗАРАНЕЕ НЕИЗВЕСТНОГО, НО НЕИЗМЕННОГО ВО ВРЕМЕНИ КАНАЛА
- 13.3. МОДЕЛЬ КАНАЛА С МСИ И ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 13.4. МЕТОДЫ ИДЕНТИФИКАЦИИ КАНАЛА С МСИ И ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ. АДАПТАЦИЯ ПРИЕМНИКА
- 13.5. СИГНАЛЫ И СИГНАЛЬНО-КОДОВЫЕ КОНСТРУКЦИИ ДЛЯ КАНАЛА С МСИ И ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- Глава 14. СИНТЕЗ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ КАНАЛОВ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ И МНОЖЕСТВЕННЫМ ДОСТУПОМ
- 14.1. ПРОБЛЕМА ОРГАНИЗАЦИИ МНОЖЕСТВЕННОГО ДОСТУПА В КАНАЛЕ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 14.2. МОДЕЛЬ СИСТЕМЫ С МНОЖЕСТВЕННЫМ ДОСТУПОМ И ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 14.3. ПРЕДЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ С МНОЖЕСТВЕННЫМ ДОСТУПОМ И ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 14.4. ПОМЕХОУСТОЙЧИВОСТЬ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ СИСТЕМ С МЕДЛЕННЫМИ РЭЛЕЕВСКИМИ ЗАМИРАНИЯМИ
- 14.5. СИНТЕЗ СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ ДЛЯ СИСТЕМ С КОДОВЫМ РАЗДЕЛЕНИЕМ И МНОГОФАЗНОЙ МОДУЛЯЦИЕЙ
- 14.6. СИНТЕЗ СИГНАЛЬНО-КОДОВЫХ конструкции ДЛЯ СИСТЕМ С КОДОВЫМ РАЗДЕЛЕНИЕМ И МНОГОЧАСТОТНОЙ МОДУЛЯЦИЕЙ
- ЗАКЛЮЧЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ
В статистическая проверка гипотез, показатель ошибки процедуры проверки гипотез — это скорость, с которой вероятности Типа I и Типа II экспоненциально убывают с размером выборки, используемой в тесте. Например, если вероятность ошибки P error { displaystyle P _ { mathrm {error}}}



Формально показатель ошибки теста определяется как предельное значение отношения отрицательного логарифма вероятности ошибки к размеру выборки для больших размеров выборки: lim n → ∞ — ln P error n { displaystyle lim _ {n to infty} { frac {- ln P _ { text {error}}} {n}}}
Содержание
- 1 Показатели ошибки при проверке двоичных гипотез
- 1.1 Оптимальная экспонента ошибки для Неймана –Тестирование Пирсона
- 1.2 Оптимальная экспонента ошибки для средней вероятности ошибки при проверке байесовской гипотезы
- 2 Ссылки
Показатели ошибки при проверке двоичной гипотезы
Рассмотрим задачу проверки двоичной гипотезы, в которой наблюдения моделируются как независимые и одинаково распределенные случайные величины по каждой гипотезе. Пусть Y 1, Y 2,…, Y n { displaystyle Y_ {1}, Y_ {2}, ldots, Y_ {n}}






В этом случае есть два возможных события ошибки. Ошибка типа 1, также называемая ложное срабатывание, возникает, когда нулевая гипотеза верна и ошибочно отклоняется. Ошибка типа 2, также называемая ложноотрицательной, возникает, когда альтернативная гипотеза верна, а нулевая гипотеза не отклоняется. Вероятность ошибки типа 1 обозначается P (ошибка ∣ H 0) { displaystyle P ( mathrm {error} mid H_ {0})}

Оптимальный показатель степени ошибки для тестирования Неймана – Пирсона
В шкале Неймана– Версия Пирсона для проверки бинарных гипотез, интересует минимизация вероятности ошибки типа 2 P (error ∣ H 1) { displaystyle P ({ text {error}} mid H_ {1})}





Оптимальная экспонента для средней вероятности ошибки при проверке байесовской гипотезы
В байесовской версии проверки двоичной гипотезы каждый заинтересован в минимизации средней вероятности ошибки при обеих гипотезах, предполагая априорную вероятность появления каждой гипотезы. Пусть π 0 { displaystyle pi _ {0}}




Ссылки
Пусть
имеется некоторый, канал связи, который
описывается условными переходными
вероятностями Р(у | х), х є Хn,
y є Yn,
где X и Y — его входной и выходной алфавиты,
а Xn
и Yn
означают всевозможные последовательности
длины n
из алфавитов X и Y соответственно.
Обозначим через род(V,S)
вероятность ошибочного декодирования
в таком канале при использовании
некоторого кода V, состоящего из М
комбинаций, и алгоритма декодирования
по максимуму правдоподобия, если
передаётся сообщение S, 1 ≤ S ≤ М. Достаточно
общая верхняя граница для род
( V,S) при наилучшем выборе кода V была
получена Р. Галлагером.
Существует
блоковый код V длины n,
состоящий из М комбинаций, для которого
при передаче произвольного сообщения
S, 1 ≤ S ≤ М,
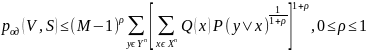
где
P(у
| х) — переходная условная вероятность
для блоков длины n
в заданном канале связи; Q(x) — произвольное
вероятностное распределение на входных
блоках длины n.
Эту
границу можно представить в экспоненциальной
форме, заменив на среднюю по сообщениям
вероятность ошибки
при произвольном наборе вероятностей
этих сообщений.
Для
2СК без памяти с вероятностью ошибки
символа р получается решение в замкнутом
виде

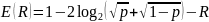
при
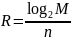
Неравенство
(7.21) позволяет сделать важный вывод, что
при R < С (Е(R)
> 0) вероятность ошибки при выборе
наилучшего кода не только убывает к
нулю при n→∞,
но убывает и как экспонента от n.
Именно поэтому границы подобного типа
называются экспонентами
вероятностей ошибок.
Для
того, чтобы сравнивать коды различной
мощности, воспользуемся понятием
эквивалентной вероятности ошибки рэ.
3) Коды с гарантированным обнаружением и исправлением ошибок
Пусть
задан некоторый блоковый код длины n,
состоящий из М
комбинаций (блоков, слов, векторов)
X1,
Х2
,
•••, ХM.
Будем
всюду считать, что входной X
и выходной Y
алфавиты канала совпадают. В общем
случае канал может иметь память и
задаваться вероятностями p(х|у)
переходов входных блоков х в выходные
у.
Определение
1.
Расстоянием
Хэмминга
ρ(х, х’) между двумя комбинациями х
є Хn
и х’ є
Хn
будем называть число позиций этих
комбинаций, в которых отдельные кодовые
символы х и х’ не совпадают. Очевидно,
что 1≤ ρ (х, х’) ≤ n
для любых х’ ≠ х, и что ρ (х, х) = 0 для
любых х є
Хn.
Определение
2. Образцом ошибки е будем называть
двоичный блок длины n,
который
имеет единицы в тех позициях, в которых
символы переданного х и принятого у
блоков отличаются друг от друга, и нули
— в остальных позициях.
Определение
3. Весом Хэмминга |х| блока (вектора) х
называют число ненулевых символов этих
блоков.
Определение
4. Кратностью
образца ошибки е (или короче — кратностью
ошибки) будем называть его вес Хэмминга
|е|. (По существу это число ошибок, которое
произошло при передаче блока х).
4) Линейные двоичные коды для обнаружения и исправления ошибок. Важные подклассы линейных двоичных кодов.
Определение
1.
Линейным
блочным двоичным кодом длины п
называется любое множество двоичных
последовательностей длины п,
которое содержит чисто нулевую
последовательность, и для каждой пары
последовательностей, принадлежащих
этому множеству, их поразрядная сумма
по mod
2 также является элементом этого
множества.
Пример.
Множество последовательностей длины
5: 00000, 11101, 01010, 10111, образует линейный код,
что проверяется непосредственно.
Поразрядная сумма по mod2
2-й
и 3-ей комбинации даёт 4-ю комбинацию,
сумма 3 и 4 даёт 2-ю, а сумма 2 и 4 даёт 3-ю
комбинацию.
Линейный
код удовлетворяет определению линейного
подпространства V
для пространства V*
всех двоичных последовательностей
длины п.
Из
алгебры известно, что всякое k-мерное
линейное подпространство п-
мерного
пространства, состоящего из конечного
числа (2n)
элементов, содержит базис, т.е.
совокупность k
линейно
независимых элементов, из которых путём
поразрядного суммирования по mod
2 можно образовать любые элементы данного
подпространства, т.е. в данном случае
комбинации линейного кода.
Совокупность
элементов базиса, записанная в виде
линейно независимых строк, образует
k×n
двоичную матрицу G,
которая называется порождающей
матрицей
кода:

Множество
всех кодовых слов, порождённых G,
может быть представлено
как
x
= bG,
где
х — вектор-строка кодовой комбинации
размерности n;
b
—
вектор-строка информационных символов
длины k.
Здесь
выполняется умножение вектора на
матрицу, а все действия осуществлены
по mod
2. В качестве вектора b
можно использовать k
последовательных элементов сообщения,
выдаваемых двоичным источником.
Переход от избыточных кодов общего вида
к линейным кодам практически решает
проблему сложности кодирования.
Действительно, вместо запоминания
М=
2k
комбинаций
длины п,
т.е. п2k
бит в общем случае, нам достаточно
запомнить лишь порождающую матрицу,
состоящую из пк
=
n
log2М
бит. Сама же процедура кодирования
потребует выполнения не более чем
2kn
элементарных операций.
Для
любого линейного кода, заданного
некоторой порождающей матрицей G,
очевидно также следующее свойство:
любые перестановки столбцов и элементарные
преобразования строк, заключающиеся в
их перестановках или в суммировании
друг с другом, не изменяют список весов
данного кода. При помощи таких
преобразований любая (k
х n)
двоичная матрица G
с линейно-независимыми строками может
быть приведена к каноническому
виду
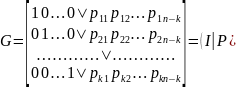
где
{
pij
— некоторые двоичные элементы; Ik
— единичная k
х k
матрица (с единицами на главной
диагонали и нулями в других местах); Р
— матрица k
х (n-k),
состоящая из двоичных элементов; (A
| B)
означает последовательную запись
матриц А и В}.
Тогда
x=(b
| c), (7.49)
где
с = bР.
По
правилу матричного умножения получаем
для с = (c1,
…, cn—k)
cj
= сумм(i
от
1 до
k)(bi
pij
(mod 2)), i=1, 2, …, n-k.
Определение
2. Линейные коды, слова которых представимы
в виде x=b/c,
называются систематическими.
Всякий
линейный код эквивалентен
некоторому
систематическому в смысле сохранения
списка весов, а, следовательно, и
расстояний Хэмминга. Первые k
символов
кодовых слов, совпадающих с символами
источника, называются информационными,
а последние n-k
символов
— проверочными.
Скорость
кода R,
определённая ранее как log2(М/n),
для-линейного
кода будет равна k/n,
т.е. для систематического — отношению
числа информационных символов k
к длине кодового блока n.
Систематические коды с длиной блока
n
и с числом информационных символов k
будем кратко называть (n,
k)-кодами.
Иногда такой код обозначают тремя
параметрами (n,
k,
d),
где d
—
минимальное кодовое расстояние.
В
линейной алгебре существует понятие
ортогонального
пространства
или нуль-пространства для заданного
линейного пространства V.
Это по определению такое множество
V*
векторов х*
длины
n,
для которых (х*,
х) =
0 при любом хє V,
где (, ) означает скалярное произведение
соответствующих векторов (В нашем случае
все операции производятся по mod2).
Доказывается,
что это множество всегда является
линейным пространством, причём если
код V
имеет размерность k,
то код V*
будет иметь размерность n-k,
т.е. содержать 2n—k
комбинаций. Код V*,
совпадающий с ортогональным пространством,
называется дуальным
к коду V.
Он, очевидно, также может быть задан
своей порождающей матрицей G*=H
размерностью (n-k)
х n.
Тогда комбинации исходного кода V
могут быть определены как решения
векторно-матричного уравнения
V
= {х
: хHT
=
0}, (7.51)
где
Т
означает символ транспонирования
матрицы Н,
т.е.
взаимную замену строк и столбцов. Матрица
Н, которая является порождающей для
кода V*,
называется
проверочной
матрицей для исходного кода V.
Матрица Н так же, как и G,
может быть представлена в канонической
форме, причём можно показать, что
Н=(
-PT
| In—k).
Определение
3. Синдромом
по коду V для любого принятого на выходе
канала связи двоичного слова y
длины n
будем называть двоичный вектор-строку
длины n-k:
s = yHT,
где
Н — проверочная матрица кода V.
Оптимальное
декодирование в 2СК без памяти можно
производить, отыскивая слово минимального
веса, синдром которого совпадает с
синдромом, полученным по принятому
слову. Такой алгоритм декодирования
называется синдромным.
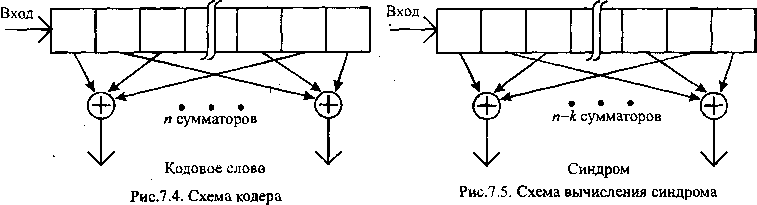
Схемы
кодирования и вычисления синдрома для
произвольного линейного кода приведены
на рисунках:
Элемент
порождающей матрицы pij
определяет характер связи i-й
ячейки регистра с j-м
сумматором: если pij
=
1 — связь есть, если pij
= 0 — связь отсутствует. Кодирование
происходит следующим образом: вектор
b
записывается
в регистр, после чего с выходов сумматоров
считывается вектор с.
Для
кодирования систематического кода
необходимо лишь п-к
сумматоров, связи которых с регистром
задаются матрицей Р. При этом вектор х
образуется
из вектора b
и
выходов п-к
сумматоров (вектора с).
Элемент
проверочной матрицы hij
определяет
характер связи i-й
ячейки
регистра с j-м
сумматором: если hij
=1
— связь есть, если hij
=
0 — связь
отсутствует.
Для вычисления синдрома вектор у
записывается в регистр, после чего с
выходов сумматоров считывается s.
Важные подклассы
линейных двоичных кодов.
Коды
с общей проверкой на чётность.
Это
класс кодов с параметрами (n,
k)
= (k
+ 1, k),
k
=
1, 2, …, когда имеется лишь один проверочный
символ, который образуется как сумма
по mod
2 всех информационных символов. Очевидно,
что минимальное расстояние d
для данных кодов всегда равно 2 и поэтому
они могут гарантированно обнаруживать
лишь одну ошибку. Комбинации данного
кода имеют лишь чётные веса.
Коды
Хэмминга.
Данный
класс кодов имеет параметры (n,
k)
= (2s
-1, 2s
-1-s),
s
— целое. Он определяется проверочной
матрицей Н,
которая
должна содержать все 2s
—
1 ненулевых двоичных векторов. Легко
видеть, что данный класс кодов имеет
при любых s
минимальное кодовое расстояние, равное
3. Это пример совершенного кода,
исправляющего все однократные ошибки
и ничего более. Коды Хэмминга могут
гарантированно обнаруживать ошибки
кратности 1 и 2.
Модифицированный
код Хемминга
(КХМ) способен обнаруживать двойные
ошибки, а так же ошибки нечётной
кратности, плюс к этому – исправлять
одиночные ошибки.
М-последовательности. Это
класс кодов с параметрами (п,
к)
=
(2S
-1,
s),
s
— целое,
которые определяются как дуальные к
кодам Хэмминга той же самой длины. Данный
класс кодов может быть определён также
иначе, как совокупность выходных
последовательностей при различных
начальных заполнениях линейного регистра
длины s
со связями, выбранными так, чтобы период
выходной последовательности оказался
равным 2S
—1.
Поэтому они получили название
последовательностей
максимальной длины
или М-последовательностей.
Все
комбинации данного кода, кроме нулевой,
имеют одинаковый вес 2S
— 1
и, следовательно, для такого кода d
= 2S
— 1.
Коды Хэмминга и М-
последовательности
являются крайними случаями кодов с
малой и большой величиной минимального
кодового расстояния. Они не всегда
удобны для практического использования,
поскольку исправление только однократных
ошибок обычно оказывается недостаточным
для обеспечения высокой верности
передачи, а высокая исправляющая
способность М-последовательностей
покупается за счёт их весьма низкой
кодовой скорости R.
Поэтому необходимо иметь класс кодов
с промежуточными значениями R.
Это может быть достигнуто при переходе
к определённым подклассам циклических
кодов.
Полиномиальные
коды. Циклические коды. Коды Боуза-Чоудхури-
Хоквингема (БЧХ).
Кодовые
слова двоичного линейного кода могут
быть представлены в виде полиномов
x(D)
= x0+xlD
+ x2D2+…+xn
– l
Dn
— l
степени
п-1
от некоторой формальной переменной
D,
причём двоичные коэффициенты хi
задают
символы кодового слова.
Полиномиальный
код определяется как множество
полиномов (кодовых слов) степени п
—1,
получаемых умножением информационного
полинома b(D)
степени k-1
на порождающий полином кода g(D)
степени
п-к:
x(D)
= b(D)g(D).
Уравнение
задаёт процедуру кодирования
полиномиального кода: сообщение
дискретного источника кодируется
примитивным кодом длины к,
символы
примитивного кода становятся коэффициентами
информационного полинома b(D)
= b0+b1D+…+bk
— lD
k
— 1,
последний умножается на порождающий
полином кода g(D)
= go
+glD+…+gn
— kDn
— k,
и после приведения подобных членов
определяются п
коэффициентов полинома x(D),
являющихся символами кодового слова.
Из
уравнения видно, что любой из полиномов
x(D),
соответствующих кодовым словам
полиномиального кода, должен делиться
без остатка на порождающий полином
g(D).
Остаток от деления полинома y(D),
соответствующего принятой из канала
комбинации, на порождающий полином кода
g(D)
называется синдромным
полиномом s(D).
Если синдромный полином равен нулю
(т.е. деление произошло без остатка), то
принятая комбинация является кодовым
словом. В противном случае принятая
комбинация не является кодовым
словом. Таким образом, для полиномиальных
кодов процедура обнаружения ошибок
(вычисление синдрома) состоит в делении
принятой комбинации на порождающий
многочлен.
На
практике находят применение циклические
коды, являющиеся частным случаем
полиномиальных кодов.
Определение
. Линейный двоичный (n,
k)-код
V
называется циклическим кодом, если в
результате циклического сдвига любой
из его комбинаций полученная комбинация
снова принадлежит коду, т.е. Sx
є
V,
если x
є
V.
Теорема.
Для
любого двоичного циклического (п, к)-кода
существует такой многочлен g(D)
степени
r
= n-k
с
двоичными коэффициентами, который делит
без остатка многочлен Dn
+1,
и
при этом любое кодовое слово может быть
представлено как многочлен х(D)
степени n-1
следующего
вида:
x(D)
= g(D)b(D),
где
b(D)
— произвольный
многочлен с двоичными коэффициентами
степени не выше k-
1.
Многочлен
g(D),
о котором идёт речь в данной теореме,
называется порождающим
многочленом
циклического кода.
Циклические
коды значительно упрощают описание
линейного кода, поскольку для них
вместо задания k
х (n—k)
элементов двоичной матрицы Р в
представлении требуется задать (n—k+1)
двоичных коэффициентов многочлена
g(D).
Кроме
того, они упрощают процедуру кодирования
и декодирования для обнаружения
ошибок. Действительно, для осуществления
кодирования достаточно выполнить
перемножение полиномов, что реализуется
с помощью линейного регистра,
содержащего k
ячеек памяти и имеющего обратные
связи, соответствующие многочлену h(D).
Для
обнаружения ошибок достаточно разделить
многочлен, соответствующий принятому
слову y(D),
на порождающий многочлен g(D)
и
проверить, будет ли остаток от деления
равен нулю. Эта процедура также
осуществляется на линейных сдвиговых
регистрах с обратными связями. Однако
более важное преимущество циклических
кодов состоит в том, что они могут быть
сконструированы как коды с некоторым
гарантированным значением минимального
кодового расстояния. Для этого необходимо
определённым образом выбрать порождающий
многочлен кода g(D).
Циклические
коды, которые имеют порождающий многочлен,
заданный своими определёнными
корнями, называются кодами
Боуза-Чоудхури-Хоквингема (кратко
БЧХ-кодами). Однако корни этого многочлена
ищутся не среди вещественных или
комплексных чисел, а как элементы так
называемых конечных полей Галуа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In information theory, the error exponent of a channel code or source code over the block length of the code is the rate at which the error probability decays exponentially with the block length of the code. Formally, it is defined as the limiting ratio of the negative logarithm of the error probability to the block length of the code for large block lengths. For example, if the probability of error 






Error exponent in channel coding[edit]
For time-invariant DMC’s[edit]
The channel coding theorem states that for any ε > 0 and for any rate less than the channel capacity, there is an encoding and decoding scheme that can be used to ensure that the probability of block error is less than ε > 0 for sufficiently long message block X. Also, for any rate greater than the channel capacity, the probability of block error at the receiver goes to one as the block length goes to infinity.
Assuming a channel coding setup as follows: the channel can transmit any of 
Let 







The function 
for 
Since there are a total of M messages, and the entries in the codebook are i.i.d., the probability that 


for any 

Choosing 

Using the independence nature of the elements of the codeword, and the discrete memoryless nature of the channel:
Using the fact that each element of codeword is identically distributed and thus stationary:
Replacing M by 2nR and defining
probability of error becomes
Q and 
Error exponent in source coding[edit]
For time invariant discrete memoryless sources[edit]
The source coding theorem states that for any 







Let 








Thus, as an example of when an error occurs, supposed that the source sequence 




Let 




Let 






and using the fact that 
A simple upper bound for the term on the left can be established as
for some arbitrary real number 





for all possible source strings. Thus, combining everything and introducing some ![rho in [0,1],](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b3530f01a767a0b2ad9364b732d1128ce796ffb)
Where the inequalities follow from a variation on the Union Bound. Finally applying this upper bound to the summation for 
Where the sum can now be taken over all 
Now for simplicity let 



and each of the components of
are independent. Thus, simplifying the above equation yields
The term in the exponent should be maximized over 
Letting 
See also[edit]
- Source coding
- Channel coding
References[edit]
R. Gallager, Information Theory and Reliable Communication, Wiley 1968
From Wikipedia, the free encyclopedia
In information theory, the error exponent of a channel code or source code over the block length of the code is the rate at which the error probability decays exponentially with the block length of the code. Formally, it is defined as the limiting ratio of the negative logarithm of the error probability to the block length of the code for large block lengths. For example, if the probability of error 






Error exponent in channel coding[edit]
For time-invariant DMC’s[edit]
The channel coding theorem states that for any ε > 0 and for any rate less than the channel capacity, there is an encoding and decoding scheme that can be used to ensure that the probability of block error is less than ε > 0 for sufficiently long message block X. Also, for any rate greater than the channel capacity, the probability of block error at the receiver goes to one as the block length goes to infinity.
Assuming a channel coding setup as follows: the channel can transmit any of 
Let 







The function 
for 
Since there are a total of M messages, and the entries in the codebook are i.i.d., the probability that 


for any 

Choosing 

Using the independence nature of the elements of the codeword, and the discrete memoryless nature of the channel:
Using the fact that each element of codeword is identically distributed and thus stationary:
Replacing M by 2nR and defining
probability of error becomes
Q and 
Error exponent in source coding[edit]
For time invariant discrete memoryless sources[edit]
The source coding theorem states that for any 







Let 








Thus, as an example of when an error occurs, supposed that the source sequence 




Let 




Let 






and using the fact that 
A simple upper bound for the term on the left can be established as
for some arbitrary real number 





for all possible source strings. Thus, combining everything and introducing some ![rho in [0,1],](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b3530f01a767a0b2ad9364b732d1128ce796ffb)
Where the inequalities follow from a variation on the Union Bound. Finally applying this upper bound to the summation for 
Where the sum can now be taken over all 
Now for simplicity let 



and each of the components of
are independent. Thus, simplifying the above equation yields
The term in the exponent should be maximized over 
Letting 
See also[edit]
- Source coding
- Channel coding
References[edit]
R. Gallager, Information Theory and Reliable Communication, Wiley 1968
При статистической проверке гипотез показатель ошибки процедуры проверки гипотез — это скорость, с которой вероятности типов I и II экспоненциально убывают с размером выборки, используемой в тесте. Например, если вероятность ошибки теста уменьшается как, где — размер выборки, показатель ошибки равен .
Формально показатель ошибки теста определяется как предельное значение отношения отрицательного логарифма вероятности ошибки в образце размера для больших размеров выборки: . Показатели ошибки для различных проверок гипотез вычисляются с использованием теоремы Санова и других результатов теории больших уклонений .
Показатели ошибки при проверке бинарных гипотез
Рассмотрим задачу проверки бинарной гипотезы, в которой наблюдения моделируются как независимые и одинаково распределенные случайные величины при каждой гипотезе. Обозначим через наблюдения. Позвольте обозначить функцию плотности вероятности каждого наблюдения при нулевой гипотезе и позвольте обозначить функцию плотности вероятности каждого наблюдения при альтернативной гипотезе .
В этом случае возможны два события ошибки . Ошибка типа 1, также называемая ложным срабатыванием, возникает, когда нулевая гипотеза верна и ошибочно отклоняется. Ошибка типа 2, также называемая ложноотрицательной, возникает, когда альтернативная гипотеза верна, а нулевая гипотеза не отклоняется. Обозначается вероятность ошибки 1-го типа и обозначается вероятность ошибки 2-го типа .
Оптимальная экспонента ошибки для тестирования Неймана – Пирсона
В версии проверки бинарных гипотез Неймана – Пирсона каждый заинтересован в минимизации вероятности ошибки типа 2 при условии, что вероятность ошибки типа 1 меньше или равна заранее заданному уровню . В этом случае оптимальной процедурой тестирования является тест отношения правдоподобия . Кроме того, оптимальный тест гарантирует, что вероятность ошибки 2-го типа экспоненциально спадает в размере выборки в соответствии с . Показатель ошибки — это расхождение Кульбака – Лейблера между распределениями вероятностей наблюдений при двух гипотезах. Этот показатель также называют показателем леммы Чернова – Стейна.
Оптимальный показатель ошибки для средней вероятности ошибки при проверке байесовской гипотезы
В байесовской версии проверки бинарных гипотез каждый заинтересован в минимизации средней вероятности ошибки при обеих гипотезах, предполагая априорную вероятность появления каждой гипотезы. Пусть обозначает априорную вероятность гипотезы . В этом случае средняя вероятность ошибки равна . В этой настройке снова оптимальным является тест отношения правдоподобия, и оптимальная ошибка уменьшается, поскольку где представляет информацию Чернова между двумя распределениями, определенными как .
Рекомендации
В предыдущей части мы рассматривали вероятностную постановку задачи машинного обучения, статистические модели, модель регрессии как частный случай и ее обучение методом максимизации правдоподобия.
В данной части рассмотрим метод максимизации правдоподобия в классификации: в чем роль кроссэнтропии, функций сигмоиды и softmax, как кроссэнтропия связана с «расстоянием» между распределениями вероятностей и почему модель регрессии тоже обучается через минимизацию кроссэнтропии. Данная часть содержит много отсылок к формулам и понятиям, введенным в первой части, поэтому рекомендуется читать их последовательно.
В третьей части (статья планируется) перейдем от метода максимизации правдоподобия к байесовскому выводу и его различным приближениям.
Данная серия статей не является введением в машинное обучение и предполагает знакомство читателя с основными понятиями. Задача статей — рассмотреть машинное обучение с точки зрения теории вероятностей, что позволит по новому взглянуть на проблему, понять связь машинного обучения со статистикой и лучше понимать формулы из научных статей. Также на описанном материале строятся более сложные темы, такие как вариационные автокодировщики (Kingma and Welling, 2013), нейробайесовские методы (Müller et al., 2021) и даже некоторые теории сознания (Friston et al., 2022).
Содержание текущей части
-
В первом разделе мы рассмотрим модель классификации, кроссэнтропию и ее связь с методом максимизации правдоподобия, а также ряд несколько фактов про функции softmax и sigmoid.
-
Во втором разделе поговорим о связи минимизации кроссэнтропии с минимизацией расхождения Кульбака-Лейблера, и как минимизация расхождения Кульбака-Лейблера может помочь в более сложных случаях, чем обычная классификация и регрессия.
Звездочкой* отмечены дополнительные разделы, которые не повлияют на понимание дальнейшего материала.
1. Вероятностная модель классификации
1.1. Модель классификации и функция потерь
1.2. Функция softmax в классификации
1.3. Температура softmax и операция hardmax*
1.4. Функция sigmoid в классификации
2. Кроссэнтропия в вероятностных моделях
2.1. Разметка с неуверенностью
2.2. Кроссэнтропия и расхождение Кульбака-Лейблера
2.3. Кроссэнтропия как максимизация правдоподобия*
2.4. Кроссэнтропия в задаче регрессии*
2.5. Кроссэнтропия с точки зрения оптимизации*
1. Вероятностная модель классификации
1.1. Модель классификации и функция потерь
Чтобы задать вероятностную модель, нам нужно определить, в какой форме она будет предсказывать распределение . Если задаче регрессии мы ограничивали распределения
только нормальными распределениями, то в задаче классификации это будет не оптимальным решением, так как классы по сути представляют собой неупорядоченное множество (хотя на них есть порядок, но лишь технически, и он может быть выбран произвольно). В задаче классификации мы можем предсказывать вероятность для каждого класса, и тогда модель будет выдавать столько чисел, сколько есть классов в
.
Пусть мы имеем датасет и предполагаем, что все примеры независимы и взяты и одного и того же распределения (i.i.d., см. предыдущую часть, раздел 3.4). Для обучения модели снова применим метод максимизации правдоподобия, то есть будем искать такие параметры
, которые максимизируют
. В разделе 2.3 мы уже расписывали формулу, которая получается в результате, но ввиду ее важности повторим ее еще раз. Первое равенство ниже следует из i.i.d.-гипотезы, второе по правилам математики:
Таким образом, для максимизации вероятности выборки данных нам нужно минимизировать сумму величин
для всех обучающих примеров .
В модели регрессии эта величина была сведена к квадрату разности предсказания и верного ответа (часть 1, формула 7). Но в задаче классификации на данном этапе считать больше ничего не нужно. Нашей задачей было задать вероятностную модель, определить с ее помощью функцию потерь и таким образом свести обучение к задаче оптимизации, то есть минимизации функции потерь, и мы это уже сделали. Функция потерь (2) называется кроссэнтропией (также перекрестной энтропией, или logloss). Она равна минус логарифму предсказанной вероятности для верного класса .
Категориальная кроссэнтропия
Возьмем произвольный пример и выданные моделью вероятности обозначим за , где
— количество классов. К метке класса (эталонному ответу) применим one-hot кодирование, получив вектор
, в котором лишь один элемент равен единице, а остальные равны нулю. Тогда выражение (2) можно рассчитать таким образом:
Лишь один элемент суммы будет не равен нулю — тот, который соответствует верному классу. Для него первый множитель будет равен единице, а второй будет логарифмом предсказанной вероятности для верного класса, что соответствует выражению (2).
Примечание. На самом деле формула (3) является определением кроссэнтропии, а формула (2) ее частным случаем, когда вырождено и назначает вероятность 1 классу с индексом
. О случае, когда это не так, подробнее поговорим во втором разделе.
Бинарная кроссэнтропия
Если класса всего два, то как правило делают следующим образом: модель выдает лишь одно число от 0 до 1, оно рассматривается как вероятность второго класса, а
рассматривается как вероятность первого класса. Пусть
равно единице, если первый класс верен, иначе равно нулю. Тогда выражение (3) технически можно вычислить следующим образом:
Снова лишь одно слагаемое будет ненулевым, и таким образом мы посчитаем логарифм предсказанной вероятности для верного класса. Формулы (18) и (19) называются категориальной кроссэнтропией (они эквивалентны если для одного из классов), формула (18) называется бинарной кроссэнтропией.
В этом разделе мы рассмотрели обучение модели классификации. Часто в классификации упоминают о функции softmax, но почему-то мы о ней ничего не говорили. Складывается ощущение, что мы что-то упустили. В следующем разделе мы поговорим о роли функции softmax в классификации.
1.2. Функция softmax в классификации
В предыдущем разделе мы определили, что модель классификации должна выдавать вероятности для всех классов. Но модель — это не только формат входных и выходных данных, а еще и внутренняя архитектура. Она может быть совершенно разной: для классификации применяются либо нейронные сети, либо решающие деревья, либо машины опорных векторов и так далее.
Рассмотрим для примера нейронную сеть. Пусть мы имеем классов, и выходной слой нейронной сети выдает
чисел от
до
. Чтобы вектор из
чисел являлся распределением вероятностей, он должен удовлетворять двум ограничениям:
-
Вероятность каждого класса не может быть ниже нуля
-
Сумма вероятностей должна быть равна единице
Для удовлетворения первого ограничения лучше чтобы модель выдавала не вероятности, а их логарифмы: если логарифм некой величины меняется от до
, то сама величина меняется от
до
. Чтобы удовлетворялось второе ограничение, каждую предсказанную вероятность мы можем делить на сумму всех предсказанных вероятностей. Такая операция называется
-нормализацией вектора вероятностей.
Отсюда мы можем вывести формулу для операции softmax. Эта операция принимает на вход набор из чисел от
до
(они называются логитами, англ. logits)
и возвращает распределение вероятностей из
чисел
. Softmax является последовательностью двух операций: взятия экспоненты и
-нормализации:
Таким образом, softmax — это векторная операция, принимающая вектор из произвольных чисел (логитов) и возвращающая вектор вероятностей, удовлетворяющий свойствам 1 и 2. Она применяется как завершающая операция во многих моделях классификации — таким образом мы можем быть уверены, что выданные моделью числа будут именно распределением вероятностей (т. е. удовлетворять свойствам 1 и 2). Существуют и различные альтернативы функции softmax, например sparsemax (Martins and Astudillo, 2016).
Модель, предсказывающая логитов, к которым применяется операция softmax, будет обладать только одним ограничением: она не может предсказывать строго нулевые или строго единичные вероятности. Зато такую модель можно обучать градиентным спуском, так как функция softmax дифференцируема.
Технически иногда функция softmax рассматривается как часть модели, иногда как часть функции потерь. Например, в библиотеке Keras мы можем добавить функцию активации 'softmax' в последний слой сети и использовать функцию потерь CategoricalCrossentropy(), а можем наоборот не добавлять функцию активации в последний слой и использовать функцию потерь CategoricalCrossentropy (from_logits=True), которая включает в себя расчет softmax (и ее производной при обратном проходе). С математической точки зрения разницы между этими двумя способами не будет, но погрешность расчета функции потерь и производной во втором случае будет меньше. В PyTorch мы можем применить LogSoftmax вместе с NLLLoss (negative log-likelihood), а можем вместо этого применить torch.nn.functional.cross_entropy, который включает в себя расчет LogSoftmax.
1.3. Температура softmax и операция hardmax*
У функции softmax (5) есть важное свойство: если ко всем логитам прибавить одну и ту же константу
, то вероятности
никак не изменятся, так как после применения экспоненты константа из слагаемого превратится в множитель, и множители в числителе и знаменателе сократятся. Однако если все логиты
умножить на некую константу
, то тогда вероятности
изменятся: если
, то вероятности
станут ближе друг к другу, что означает меньшую уверенность в предсказании, если же
, то наоборот мы получим большую уверенность в предсказании. Этот дополнительный множитель, если он используется, называется «температурой» softmax.
При тот класс, логит которого был наибольшим, получит вероятность 1, остальные классы — вероятность 0, такую операцию по аналогии часто называют hardmax. Иногда ее упоминают как argmax, потому что hardmax можно считать one-hot кодированием индекса, который возвращает операция argmax.
На этом примере видно то, как употребляются понятия soft и hard в машинном обучении: hard-операции (hardmax, argmax, hard attention, hard labeling, sign) связаны с выбором некоего элемента в множестве, а soft-операции (softmax, soft attention, soft labeling, soft sign) являются их дифференцируемыми аналогами. Например, в softmax можно рассчитать производную каждого выходного элемента по каждому входному. В hardmax или argmax это не имеет смысла: производные всегда будут равны нулю.
Это можно понять даже не прибегая к расчетам, поскольку у дифференцируемости есть очень простая наглядная интерпретация: операция дифференцируема если плавное изменение
приводит к плавному изменению
. Это верно для операции softmax, и благодаря этому мы можем применять градиентный спуск или градиентный бустинг. Но в операции hardmax плавное изменение логитов приводит к тому, что выходные вероятности либо остаются такими же, либо меняются скачкообразно, поэтому (без дополнительных ухищрений) градиентный спуск и градиентный бустинг оказываются неприменимы.
1.4. Функция sigmoid в классификации
Рассмотрим случай бинарной классификации. Представим, что у нас есть 2 класса, и модель выдает 2 логита , из которых с помощью softmax получаем вероятности
, сумма которых равна единице. Но прибавление одной и той же константы к
не меняет вероятности, поэтому иметь две «степени свободы» излишне, и имеет смысл зафиксировать
в значении 0. Теперь меняя
модель будет менять вероятности классов
. Значения
и
, согласно (21), будут связаны следующим образом:
Такая функция носит название сигмоиды:
Примечание. В более широком смысле, сигмоидами называют и другие функции одной переменной, график которых выглядит похожим образом. Для преобразования логита в вероятность вместо можно использовать любую и этих функций, разница между ними не принципиальна. Также сигмоида иногда используется в промежуточных слоях нейронных сетей.
К чему мы в итоге пришли? К тому, что если класса всего два, то иметь два логита в модели не обязательно, достаточно всего одного, к которому применяется сигмоида вместо softmax. Функция потерь при этом становится бинарной кроссэнтропией (4). На самом деле то же рассуждение можно применить и к мультиклассовой классификации: если классов , то достаточно иметь
логитов, но так обычно не делают.
Теперь запишем функцию, обратную сигмоиде. Эта функция преобразует вероятность обратно в логит и называется logit function:
Если — это вероятность второго класса, а
— вероятность первого класса, то выражение
означает то, во сколько раз второй класс вероятнее первого. Это выражение называется odds ratio. Логит является его логарифмом и называется log odds ratio.
Если мы используем в обучении сигмоиду, то модель непосредственно предсказывает логит , то есть логарифм того, во сколько раз второй класс вероятнее первого.
2. Кроссэнтропия в вероятностных моделях
2.1. Разметка с неуверенностью
В выражениях для функции потерь в классификации (2) и регрессии (часть 1, формула 7) мы предполагали наличие для каждого примера эталонного ответа
, к которому модель должна стремиться. Но в более общем случае эталонный ответ
может быть не конкретным значением, а распределением вероятностей на множестве
, так же как и предсказание модели. То есть в разметке датасета значения
указаны с определенной степенью неуверенности: если это классификация, то могут быть указаны вероятности для всех классов, если регрессия — то может быть указана погрешность.
Ситуация, когда разметка датасета содержит некую степень неуверенности, не такая уж редкая. Например, в пусть в задаче классификации эмоций по видеозаписи датасет размечен сразу несколькими людьми-аннотаторами, которые иногда дают разные ответы. Например, одно из видео в датасете может быть размечено как «happiness» 11 аннотаторами и как «sadness» 9 аннотаторами. Оставив только «happiness» мы потеряем часть информации. Вместо этого мы можем оставить обе эмоции, считать их распределением вероятностей: ,
и обучать модель выдавать для данного примера такое же распределение вероятностей.
Благодаря разметке с неуверенностью сохраняется больше информации: есть явно выраженные эмоции, а есть сложно определяемые.
Но с другой стороны для каждого видео есть какая-то истинная эмоция: либо «happiness», либо «sadness» — человек не может испытывать обе эти эмоции одновременно. В теории модель могла бы обучиться определять эмоции точнее, чем человек, и разметка с неуверенностью может помешать модели выучиться точнее человека: если человек дает 50% вероятности обоим классам, и мы используем это как эталонный ответ, то модель будет стремиться к нему, даже если она способна определить эмоцию точнее.
2.2. Кроссэнтропия и расхождение Кульбака-Лейблера
Пусть мы имеем датасет из пар , в котором эталонный ответ
является не конкретным значением признака
, а распределением вероятностей на множестве
. Нам каким-то образом нужно «подогнать» предсказанное распределение
под эталонное распределение
.
Пример 1. Если в задаче классификации в эталонном распределении вероятности классов равны 0.7 и 0.3, то мы хотели бы, чтобы в предсказании они тоже были бы равны 0.7 и 0.3.
Пример 2. Если в задаче регрессии эталонное распределение имеет две моды в значениях 0.5 и 1.5, то нам хотелось бы, чтобы предсказанное распределение вероятностей тоже имело моды в этих точках. Но если мы моделируем
нормальным распределением (как в разделе 2.3 первой части), тогда в нем в любом случае будет только одна мода, и чтобы хоть как-то приблизить предсказание к эталонному ответу, можно расположить моду посередине между точками 0.5 и 1.5 — тогда мат. ожидание ошибки предсказания будет наименьшим.
Как видим, второй пример получился сложнее первого. Если множество непрерывно, то задача приближения предсказанного распределения к эталонному означает задачу сближения функций плотности вероятности.
Такая постановка задачи неоднозначна: сблизить функции можно по-разному, так как «расстояние» между функциями можно определять по-разному. Чаще всего для этого используют расхождение Кульбака-Лейблера (относительную энтропию) — несимметричную метрику сходства между двумя распределениями вероятностей
и
. Расхождение Кульбака-Лейблера можно расписать как сумму в дискретном случае и как интеграл в непрерывном случае.
Дискретный случай (,
— функции вероятности):
Непрерывный случай (,
— функции плотности вероятности):
Пользуясь тем, что , мы можем расписать расхождение Кульбака-Лейблера как разность двух величин. Для дискретного случая:
Первое слагаемое со знаком минус называется энтропией распределения (или дифференциальной энтропией в непрерывном случае) и обозначается как
, а второе слагаемое (включая минус) называется кроссэнтропией
между распределениями
и
. Эти величины можно расписать через мат. ожидание:
В машинном обучении первым аргументом в обычно ставят эталонное распределение, вторым аргументом — предсказанное. Как видно из формулы (9), первое слагаемое не зависит от
, поэтому минимизация
по
равносильно минимизации кроссэнтропии между
и
.
Резюме. Если значения целевого признака в датасете даны как распределения вероятностей, то для обучения модели мы можем минимизировать кроссэнтропию между предсказанными и эталонными распределениями. Мы так уже делали в модели классификации, но там эталонное распределение было вырожденным назначало вероятность 1 одному из классов, поэтому в формуле (3) лишь одно слагаемое было ненулевым. В этом разделе мы рассмотрели более общий случай, когда эталонное распределение невырождено и в (3) может быть много ненулевых слагаемых.
2.3. Кроссэнтропия как максимизация правдоподобия*
Является ли «подгонка» предсказанного распределения под эталонное распределение
применением метода максимизации правдоподобия? Для ответа на этот вопрос нужно понять что такое «правдоподобие» в том случае, когда вместо эталонного ответа мы имеем распределение.
Мы можем сделать таким образом. Пусть для -го примера мы имеем значение
и распределение
. Мысленно сгенерируем из этого примера очень большое (стремящееся к бесконечности) количество примеров (обозначим его
), в которых исходные признаки равны
, а целевой признак взят из распределения
:
Объединение нельзя рассматривать как i.i.d.-выборку, потому что при бесконечном количестве примеров мы имеем лишь
уникальных значений
. Но поскольку мы не моделируем распределение
, это не является проблемой. Поскольку все
независимы:
В итоге при минус логарифм правдоподобия
оказался равен кроссэнтропии между эталонным распределением
и предсказанным моделью распределением
. Отсюда получается, что минимизация кроссэнтропии (или, что эквивалентно, минимизация расхождения Кульбака-Лейблера) максимизирует правдоподобие.
2.4. Кроссэнтропия в задаче регрессии*
Вернемся к случаю регрессии. Если для обучающей пары точно известен ответ
, то его можно представить как распределение вероятностей на
, имеющее лишь одно возможное значение
с вероятностью 1 (такое распределение называют вырожденным, в данном случае его еще называют «эмпирическим»).
Для таких случаев математики придумали специальную функцию, называемую дельта-функцией Дирака . Она равна нулю во всех точках кроме нуля, в нуле равна бесконечности, а ее интеграл равен единице. Например, если мы возьмем функцию плотности вероятности нормального распределения (часть 1, формула 4) с
и устремим
к нулю, то в пределе получим дельта-функцию.
В случае регрессии эмпирическое распределение можно записать как . Попробуем, по аналогии с классификацией, минимизировать кроссэнтропию между эталонным и предсказанным распределениями. Пусть модель выдает для
нормальное распределение
. Распишем кроссэнтропию между эмпирическим и предсказанным распределением:
Обратите внимание, что оба аргумента являются не числами, а функциями от
, и подынтегральное выражение не равно нулю только в одной точке
. С помощью формулы (10) мы пришли к тому, что минимизация кроссэнтропии означает минимизацию
, что эквивалентно максимизации
. Именно это мы и делали в разделе 2. Получается, что модель регрессии тоже обучается с помощью кроссэнтропии, которая по формуле (10) превращается в минимизацию
и далее в минимизацию среднеквадратичного отклонения (часть1, формула 7), если
моделируется нормальным распределением.
Как видим, мы получаем максимально унифицированный и при этом гибкий подход, который можно применять для задания функции потерь в сложных случаях.
Кроссэнтропия с точки зрения оптимизации*
В задаче регрессии мы рассматривали два подхода к выбору функции потерь: первый подход опирается на здравый смысл, наши представления о метрике сходства на множестве и легкость оптимизации. Второй подход опирается на теорию вероятностей и наши представления об условном распределении
, из которого следует формула для функции потерь (статья 1, формулы 5-7).
Теперь вернемся к задаче классификации. Есть ли здесь аналогичные два подхода? Вероятностный подход, который приводит к кроссэнтропии, мы уже рассматривали. Но хороша ли кроссэнтропия с точки зрения оптимизации, или есть более удобная функция потерь? Например, вместо кроссэнтропии мы могли бы минимизировать среднеквадратичную ошибку между предсказанным распределением вероятностей и эталонным распределением вероятностей
, в котором вероятность 1 назначается верному классу:
Смысл такого выражения с точки зрения теории вероятностей не совсем ясен, но видно, что чем ближе предсказание к истине, тем меньше будет функция потерь. А это и есть то свойство, которое требуется от функции потерь.
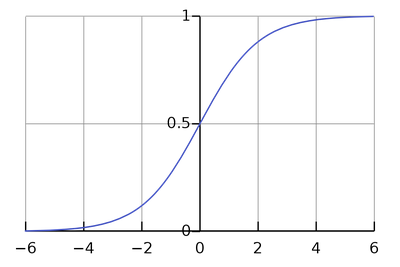
Что же лучше: кроссэнтропия или среднеквадратичная ошибка? Чтобы понять, какая из функций потерь лучше подходит для оптимизации градиентным спуском, давайте рассчитаем градиенты этих функций потерь по логитам (то есть тем значениям, которые выдаются до операции softmax или sigmoid). Пусть классификация является бинарной, верный ответом является второй класс, и модель выдала значение логита, равное . Отсюда вероятность второго класса равна
, где
— операция сигмоиды (6). Рассчитаем производную функции потерь по логиту
.
В случае бинарной кроссэнтропии:
В случае среднеквадратичной ошибки:
При (то есть когда модель выдает уверенный неправильный ответ) при бинарной кроссэнтропии производная стремится к 1, а при среднеквадратичной ошибке производная стремится к нулю. Это означает, что при сочетении сигмоиды и среднеквадратичной ошибки уверенные неправильные ответы практически не корректируются градиентным спуском (градиент близок к нулю), что может негативно сказаться на качестве обучения. Это аргумент в пользу того, чтобы при использовании сигмоиды выбирать бинарную кроссэнтропию, а не среднеквадратичную ошибку.
Хотя, с другой стороны, этот аргумент не окончательный, ведь уверенные неправильные ответы модели могут на самом деле быть выбросами в данных или ошибками разметки, которые модель не должна выучивать. Поэтому, возможно, в некоторых случаях имеет смысл использовать среднеквадратичную ошибку вместо кроссэнтропии.
Конец части 2. Часть 3, посвященная байесовскому выводу, планируется к публикации. Спасибо@ivankomarovи @yorkoза ценные комментарии, которые были учтены при подготовке статьи.



![{ displaystyle C (f_ {0}, f_ {1}) = min _ { lambda in [0, 1]} int (f_ {0} (x)) ^ { lambda} (f_ {1} (x)) ^ {(1- lambda)} , dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93836bc508de0e43dd1d2799f51a9fe4d7b35c24)





![{displaystyle P_{mathrm {error} 1to mathrm {any} }leq M^{rho }sum _{y_{1}^{n}}left(sum _{x_{1}^{n}}Q(x_{1}^{n})[p(y_{1}^{n}mid x_{1}^{n})]^{1-srho }right)left(sum _{x_{2}^{n}}Q(x_{2}^{n})[p(y_{1}^{n}mid x_{2}^{n})]^{s}right)^{rho }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c80e6f8a936e63538f616d5203ef62494cb5c2f)
![{displaystyle P_{mathrm {error} 1to mathrm {any} }leq M^{rho }sum _{y_{1}^{n}}left(sum _{x_{1}^{n}}Q(x_{1}^{n})[p(y_{1}^{n}mid x_{1}^{n})]^{frac {1}{1+rho }}right)^{1+rho }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47e585bc57bb56d410e23c12a6d2b04f75dc1415)
![{displaystyle P_{mathrm {error} 1to mathrm {any} }leq M^{rho }prod _{i=1}^{n}sum _{y_{i}}left(sum _{x_{i}}Q_{i}(x_{i})[p_{i}(y_{i}mid x_{i})]^{frac {1}{1+rho }}right)^{1+rho }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9d6a1c7968f08d5731ea2f63747a9ffdb07ac9e)
![{displaystyle P_{mathrm {error} 1to mathrm {any} }leq M^{rho }left(sum _{y}left(sum _{x}Q(x)[p(ymid x)]^{frac {1}{1+rho }}right)^{1+rho }right)^{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b1c86e37afc9dc15e6007ba4c6257c2de860a66)
![{displaystyle E_{o}(rho ,Q)=-ln left(sum _{y}left(sum _{x}Q(x)[p(ymid x)]^{1/(1+rho )}right)^{1+rho }right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bd7c00e52e92af68e0f30d3ef6ea1e8363ddd3b)

![{displaystyle E_{r}(R)=max _{Q}max _{rho in [0,1]}E_{o}(rho ,Q)-rho R.;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/748bec95dc126d3630cce2d744c88f1df2f64fe7)


![left[P(P(X_{1}^{n}(i'))geq P(X_{1}^{n}(i)))right]leq left({frac {P(X_{1}^{n}(i'))}{P(X_{1}^{n}(i))}}right)^{s},](https://wikimedia.org/api/rest_v1/media/math/render/svg/42d81f364b8577381d1d0c2720eb23b64e1f44b2)






![P(E)leq exp left(-nleft[rho R-ln left(sum _{{x_{i}}}P(x_{i})^{{{frac {1}{1+rho }}}}right)(1+rho )right]right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/92fb3aa7f9ec867c0ae54cb611b5b54671029ff4)
![E_{r}(R)=max _{{rho in [0,1]}}left[rho R-E_{0}(rho )right].,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fec9cb0211c0e4bd31cb9c32342dc8dcec163caf)
![{ displaystyle C (f_ {0}, f_ {1}) = max _ { lambda in [0,1]} left [- ln int (f_ {0} (x)) ^ { лямбда} (f_ {1} (x)) ^ {(1- lambda)} , dx right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64774b98adcee305a496589bab2d5dfcc2a24502)