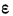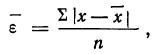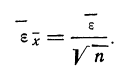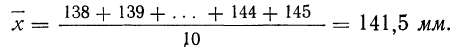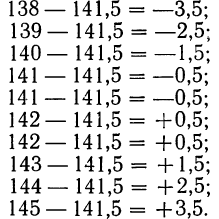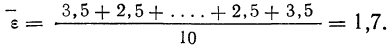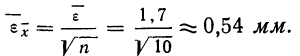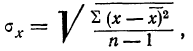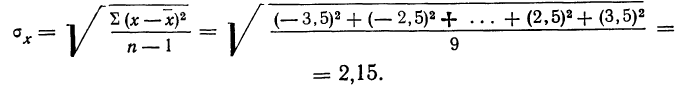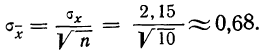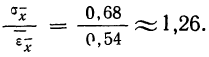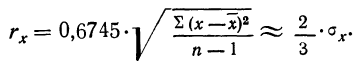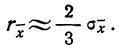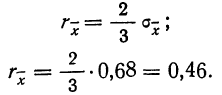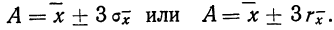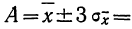Элементы теории ошибок Ошибки как неизбежные погрешности
Слово
«ошибка» в науке не несет в себе привычного
для повседневной жизни негативного
смысла, а означает лишь неизбежную
погрешность, которая свойственна всем
измерениям. Улучшая условия эксперимента,
можно свести к минимуму ошибки, но
избежать их вовсе — невозможно. Поскольку
не удается
избавиться полностью от ошибок, необходимо
научиться правильно оценивать их
величины.
При указании
ошибки, необходимо объяснить способ ее
оценки. Этот
раздел будет посвящен методам расчета
погрешностей.
Систематические погрешности
Систематической
называется погрешность ∆с,
которая не меняется на протяжении серии
измерений. В экспериментальных
исследованиях часто приходится учитывать
влияние главных факторов и пренебрегать
второстепенными. Так в механике иногда
приходится пренебрегать силой трения,
растяжением нитей и их массами, а также
массами вращающихся блоков. Подобные
упрощения приводят к появлению
систематической погрешности, поэтому
экспериментальное значение физической
величины часто отличается от ее истинного
значения. Если увеличить число опытов,
случайная погрешность уменьшится, а
систематическая погрешность останется
неизменной. Ее можно уменьшить, но для
этого необходимо проводить более
детальные исследования (измерять силы
трения, массы нитей), или применять более
сложные математические модели изучаемых
физических явлений, где будет учитываться
влияние факторов, которыми раньше
пренебрегали.
Оценка
систематической погрешности выполняется
на основании методики эксперимента,
точности приборов и контрольных опытов
с помощью более точного оборудования.
Класс точности промышленных измерительных
приборов связан с его систематической
погрешностью. Он выражается в процентах.
Если на шкале измерительного устройства
записан класс 0,5, то это значит, что им
можно выполнять измерения с абсолютной
погрешностью 0,5% от значения измеряемой
физической величины, соответствующего
полной шкале прибора. Класс точности
P,
максимальное значение
шкалы прибора и абсолютная погрешность
связаны
соотношением:
. (1)
Величина абсолютной
погрешности не меняется при переходе
от начала к концу шкалы и равна:
.
(2)
Относительная
погрешность, вычисляемая по формуле:
, (3)
будет
наибольшей у начала шкалы и наименьшей
вблизи ее предельного значения.
Желательно, чтобы показания прибора во
время выполнения опытов были больше
половины максимального показания его
шкалы. Обычно одно деление шкалы
приблизительно равно максимальной
погрешности измерений. Отсчет должен
включать число целых делений и число
десятых долей деления, если это возможно
(например, если стрелка не дрожит). Это
позволит вовремя обнаружить возможные
нестабильности в изучаемых зависимостях.
Случайные погрешности
Случайной
называется погрешность, которая меняется
от опыта к опыту произвольным образом
и может принимать как положительное,
так и отрицательное значение. Если
измерение физической величины выполнено
всего один раз, дать оценку случайной
погрешности нельзя. Получить ее значение
можно только на основании нескольких
измерений. При увеличении их числа
случайная погрешность уменьшается.
Предположим,
удалось выявить все источники
систематической погрешности, и свести
их к минимуму. Тем не менее, источники
случайных отклонений не исчезли.
Например, в случае использования ручного
секундомера, случайной величиной будет
своевременность остановки прибора
рукой человека. Какой бы малой ни была
систематическая погрешность, случайная
ошибка в этом случае останется, причем
для каждого экспериментатора она будет
своя. Разброс времени будет в основном
определяться его реакцией. Иногда она
будет преждевременной, а иногда
замедленной. Известно, что 68% отклонений
при использовании спортивного секундомера
лежит в пределах 0,3с.
Если таймер включается и выключается
с помощью электронных оптических
датчиков, то погрешность может быть
связана с работой электронной схемы,
или с нестабильностью работы фотодиода.
Если выполнить серию измерений, будет
наблюдаться разброс значений, по
которому можно оценить случайную
погрешность.
Пусть
истинное значение величины x
равно
.
Предположим, что величинаx
измеряется бесконечное число раз, тогда
получится совокупность
,
образующая бесконечное множество всех
возможных значений величиныx,
расположенных вокруг истинного значения
,
а для любого интерваламожно рассчитать вероятность попадания
в него случайной величиныx.
Функция, характеризующая вероятность
этого попадания, носит название плотности
вероятности. Обычно при выполнении
эксперимента предполагают, что возможно
влияние множества незначительных
случайных факторов и используют функцию
нормального распределения Гаусса. Она
имеет вид:

Здесь
x
– значение случайной величины, полученное
в единичном измерении,
—
ее истинное значение,— дисперсия значений физической величины,
— ее среднее квадратическое отклонение.
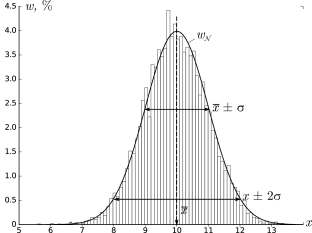
График
функции нормального распределения
изображен на рис. 1. Он симметричен
относительно вертикальной прямой
,
являющейся центром распределения. Его
ширину характеризует величина,
которая называется квадратичным
отклонением от истинного значения
случайной величины или среднеквадратичным
отклонением. Площадь под кривой равняется
единице.
Допустим,
выполнено N
опытов и получены значения величины x:
.
Наилучшим приближением истинного
значения является среднее арифметическое,
рассчитываемое по формуле:

Набор
из N
экспериментальных значений также
называют выборкой, а формулу (5) — формулой
для выборочного среднего. Квадратичное
отклонение от среднего значения случайной
величины рассчитывается на основе
выборки по формуле:

Квадрат
этой величины называется дисперсией
распределения:

Случайные
величины, распределенные по нормальному
закону, различаются значениями параметров
и
,
поэтому полезно выяснить, как эти
параметры влияют на вид нормальной
кривой.
Пусть
не меняется, а меняется только
,
тогда:
-
чем
меньше
,
тем более острым будет максимум, а
кривая вытянута вверх, -
чем
больше
,
тем более пологим будет график, и более
растянутым вдоль оси абсцисс.
Теперь
пусть
остается неизменным, а меняется
.
Форма кривых остается неизменной, но
меняется положение ее центра симметрии
по оси абсцисс.
Рис. 1. График
функции нормального распределения.
Вероятность
получить в единичном измерении значение,
лежащее в некотором интервале
определяется интегралом:
. (8)
Вероятность
того, что результат однократного
измерения будет находиться в пределах
одного среднеквадратичного отклонения
от
,
равна:

Формула
(9) означает, что 68,3%
однократных измерений попадают в
интервал
.
Вероятность попадания результата
окажется в отрезок±2σ,
равна 95,45%, а
вероятность
результата в пределах
±3σ
составляет 99,73%.
Пусть
выполнено N
измерений
величиныx,
имеющей нормальное распределение.
Наилучшей оценкой истинного значения
величины x
будет среднее арифметическое (5).
Погрешность этой оценки называется
стандартным отклонением среднего и
вычисляется по формуле:
. (10)
Величина
также называется стандартной погрешностью.
Значение,
найденное после серии изN
измерений определяется набором
,
но поскольку—
случайные значения, то значениетакже является случайным. Выборочное
среднее (5) будет распределено по
нормальному закону (4), носледует заменить на
(10). Формулы (8) и (9) расчета вероятности
для среднего значенияостаются в силе с учетом замены
на
.
Можно быть уверенным на68,3%,
что истинное значение
лежит в пределах интервала
,
называемого68-процентным
доверительным интервалом. Величина 68%
здесь является коэффициентом доверия
(надежности). Для того, чтобы рассчитать
доверительный интервал с большей
надежностью, необходимо его увеличить,
умножив стандартное отклонение среднего
на коэффициент, который называется
коэффициентом Стьюдента:
. (11)
Интервал
(11) называется α
– процентным
доверительным интервалом. Это значит,
что α процентов
средних значений измеряемой величины,
с учетом случайной погрешности, лежит
в пределах интервала вида (11). Коэффициенты
Стьюдента для заданной надежности и
числа измерений N
записаны в таблице Приложения. Обычно
доверительный интервал рассчитывают
с высокой степенью надежности: например
95% доверительный интервал или 99%
доверительный интервал. C
учетом случайной погрешности результат
записывается в виде:
. (12)
Полная
погрешность измерений определяется
как случайной, так и систематической
погрешностью и рассчитывается по
формуле:
. (13)
Пример.
Измерим при
помощи микрометра диаметр проволоки в
десяти точках, рассчитаем его наилучшее
приближение, 99,7% доверительный интервал
и полную погрешность. Систематическая
погрешность микрометра равна
.
Измерения (в мм) запишем в таблицу:
Таблица
2
|
|
|
|
|
|
|
|
|
|
|
|
0,51 |
0,52 |
0,50 |
0,49 |
0,49 |
0,50 |
0,49 |
0,49 |
0,50 |
0,51 |
Рассчитаем
наилучшее приближение диаметра:
Найдем
стандартное отклонение среднего:
.
Умножим
эту величину на коэффициент Стьюдента
для десяти измерений, равный 2,8 для 98%
доверительного интервала (надежность
0,98) :
.
Тогда
.
Теперь
мы можем написать наилучшую оценку
диаметра проволоки:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений, 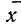
За меру точности соответствия принятой средней арифметической 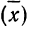
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 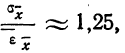
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 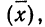
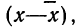
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 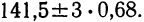
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.
2.1 Случайная величина
Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.
Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].
Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δx] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δx: x∈[x0,x0+δx].
Устремим интервал
δx к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w(x0)=P[x0,x0+δx]δx будет оставаться конечным.
Функцию w(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.
Замечание. В математической литературе распределением часто называют не функцию
w(x), а её интеграл W(x)=∫w(x)𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.
Гистограммы.
Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[kh,(k+1)h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.
σ=1,0, h=0,1, n=104)
Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w(x).
Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.
Свойства распределений.
Из определения функции w(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:
| Px∈[a,b]=∫abw(x)𝑑x. | (2.1) |
Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w(x) по всей области
значений x (то есть суммарная площадь под графиком w(x)) равен единице:
Это соотношение называют условием нормировки.
Среднее и дисперсия.
Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как
Переходя к пределу, получим следующее определение среднего значения
случайной величины:
где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину
| σ2=(x-x¯)2¯=∫(x-x¯)2w𝑑x | (2.3) |
называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.
Доверительный интервал.
Обозначим как P|Δx|<δ вероятность
того, что отклонение от среднего Δx=x-x¯ составит величину,
не превосходящую по модулю значение δ:
| P|Δx|<δ=∫x¯-δx¯+δw(x)𝑑x. | (2.4) |
Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.
2.2 Нормальное распределение
Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).
Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.
Плотность нормального распределения выражается следующей формулой:
| w𝒩(x)=12πσe-(x-x¯)22σ2. | (2.5) |
Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.
Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩(x)).
При значительном отклонении x от среднего величина
w𝒩(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.
Замечание. Точки x=x¯±σ являются точками
перегиба графика w(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w(x¯±σ)/w(x¯)=e-1/2≈0,61
от высоты вершины.
Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.
Вычислим некоторые доверительные вероятности (2.4) для нормально Замечание. Значение интеграла вида ∫e-x2/2𝑑x Вероятность того, что результат отдельного измерения x окажется Вероятность отклонения в пределах x¯±2σ: а в пределах x¯±3σ: Иными словами, при большом числе измерений нормально распределённой Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере Полученные значения доверительных вероятностей используются при означает, что измеренное значение лежит в диапазоне (доверительном Замечание. Хотя нормальный закон распределения встречается на практике довольно Теперь мы можем дать количественный критерий для сравнения двух измеренных Пусть x1 и x2 (x1≠x2) измерены с Допустим, одна из величин известна с существенно большей точностью: Пусть погрешности измерений сравнимы по порядку величины: Замечание. Изложенные здесь соображения применимы, только если x¯ иx-x0σ2=2w(x)σ1=1
Доверительные вероятности.
распределённых случайных величин.
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.
в пределах x¯±σ оказывается равна
P|Δx|<σ=∫x¯-σx¯+σw𝒩𝑑x≈0,68.
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2σ;x¯+2σ],
и лишь 0,27% окажутся за пределами
[x¯-3σ;x¯+3σ].
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись
интервале) x∈[x¯-δx;x¯+δx] с
вероятностью 68%. Таким образом погрешность ±δx считается
равной одному среднеквадратичному отклонению: δx=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δx=2σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.Сравнение результатов измерений.
величин или двух результатов измерения одной и той же величины.
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2σ.
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.
Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.
2.3 Независимые величины
Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:
Обозначим отклонения величин от их средних как Δx=x-x¯ и
Δy=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δx¯=x¯-x¯=0,
Δy¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δx⋅Δy¯
равно произведению средних Δx¯⋅Δy¯
и, следовательно, равно нулю:
| Δx⋅Δy¯=Δx¯⋅Δy¯=0. | (2.6) |
Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:
Найдём дисперсию σz2. В силу независимости имеем
| Δz2¯=Δx2¯+Δy2¯+2Δx⋅Δy¯≈Δx2¯+Δy2¯, |
то есть:
Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.
Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.
Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2x=2σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2x=2σx.
Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.
Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.
Пример. Пусть σy=σx/3,
тогда σz=σx1+19≈1,05σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.
2.4 Погрешность среднего
Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.
Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых
Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать
| σZ=σx12+σx22+…+σxn2=nσx, |
поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем
Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.
Подчеркнём отличия между σx и σ⟨x⟩:
величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;
величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.
2.5 Результирующая погрешность опыта
Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?
Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:
Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δxслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δxсист=x¯-xист=const:
Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:
| σполн2=⟨δxсист2⟩+⟨δxслуч2⟩≤Δсист2+σслуч2. | (2.9) |
Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.
Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:
Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.
Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.
Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:
Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)
d=386±6мкм,εd=1,5%.
Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=162,0м/с,
среднеквадратичное отклонение σv=13,8м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δv, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6м/с
(ε≈4%), так и значение σv≈14м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=163,3м/с,
σv=12,1м/c, σ⟨v⟩=5м/с,
σполн≈11,2м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.
2.6 Обработка косвенных измерений
Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.
2.6.1 Случай одной переменной
Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f(x).
В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:
Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δx=x-x⋆, и пользуясь определением производной,
при условии, что функция y(x) — гладкая
вблизи x≈x⋆, запишем
где f′≡dydx — производная фукнции f(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δy2⟩,
σx2=⟨Δx2⟩), и затем снова извлечём
корень. В результате получим
Пример. Для степенной функции
y=Axn имеем σy=nAxn-1σx, откуда
σyy=nσxx,или εy=nεx,
то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.
Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.
Упражнение. Найдите погрешность логарифма y=lnx, если известны x
и σx.
Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.
2.6.2 Случай многих переменных
Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:
Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:
где символом fx′≡∂f∂x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f(x,y,…):
| σu2=fx′2σx2+fy′2σy2+… | (2.11) |
Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.
Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …
Остановимся на некоторых важных частных случаях формулы
(2.11).
Пример. Для суммы (или разности) u=∑i=1naixi имеем
σu2=∑i=1nai2σxi2.
(2.12)
Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что
σu2u2=α2σx2x2+β2σy2y2+…
или через относительные погрешности
εu2=α2εx2+β2εy2+…
(2.13)
Пример. Вычислим погрешность произведения и частного: u=xy или u=x/y.
Тогда в обоих случаях имеем
εu2=εx2+εy2,
(2.14)
то есть при умножении или делении относительные погрешности складываются
квадратично.
Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу
u=arctgyx.
В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′zx′=-yx2+y2,
uy′=uz′zy′=xx2+y2, и наконец
σu2=y2σx2+x2σy2(x2+y2)2.
Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.
По итогам данного раздела можно дать следующие практические рекомендации.
-
•
Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью. -
•
При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной. -
•
Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.
Справочник /
Лекторий Справочник /
Лекционные и методические материалы по геодезии /
Элементы теории ошибок измерений
Конспект лекции по дисциплине «Элементы теории ошибок измерений»,
pdf
Файл загружается
Благодарим за ожидание, осталось немного.
Конспект лекции по дисциплине «Элементы теории ошибок измерений».
pdf
txt
Конспект лекции по дисциплине «Элементы теории ошибок измерений», текстовый формат
1.5 Элементы теории ошибок измерений
Единицы измерений, применяемые в геодезии
При производстве геодезических измерений находят применение меры
длины, площади, массы, температуры, времени, давления, угловые меры и
др.
В нашей стране линейные измерения производят в метрической системе
мер. За основную единицу измерения длины принят метр. Длина метра была
определена из результатов градусных измерений французскими учеными
Мишеню и Деламбром и в 1799 г. принята условно как 1:40 000 000
Парижского меридиана. На этом основании был изготовлен платиновый жезл
соответствующей длины, получивший название «архивный метр».
В 1875– 1889 гг. из платино-иридиевого сплава был изготовлен 31 жезл,
из которых по международному соглашению Россия получила два эталона за
номерами 11 и 28. Метр-прототип № 28 хранится во Всесоюзном научноисследовательском институте метрологии им. Д.И. Менделеева (ВНИИМ) в
Санкт-Петербурге и является государственным эталоном длины в нашей
стране. Для более надежного хранения установленной длины метра XI
Генеральная конференция по мерам и весам в 1960 г. утвердила новый
стандарт метра как длину, равную 1 650 763,73 длины волны оранжевой
линии спектра излучения в вакууме атома изотопа криптона-86. Этот более
стабильный эталон метра 12 января 1968 г. был утвержден Госстандартом
СССР в качестве нового государственного эталона.
Один метр (м) содержит 10 дециметров (дм), 100 сантиметров (см) или
1000 миллиметров (мм); одна тысячная доля миллиметра, т. е. миллионная
доля метра, называется микрометром (мкм).
Единицей измерения плоских углов является градус, равный 1/90 части
прямого угла; 1° содержит 60′, 1′ – 60″. Значения углов можно выражать
также в радианной мере, представляющей отношение длины
соответствующей дуги к ее радиусу. Следовательно, окружность длиной 2πR
содержит 2π радиан. Отсюда значения радиана ρ в градусах, минутах и
секундах будут равными:
ρ° = 57,3°; ρ’ = 3438′, ρ» =206265″.
Для перевода значения угла из градусной меры в радианную нужно
разделить его на радиан:
В ряде стран (Германия, Франция и др.) при измерении углов применяется
также децимальная (метрическая) система угловых мер. В ней прямой угол
делится на 100 частей, которые называются гонами (ранее их называли
градами). 1 гон равен 0,9 градуса и содержит 100 сантигон (сгон) или 1000
миллигон (мгон). Эта система нашла применение в угломерных кругах
электронных тахеометров.
Единицей измерения площади является квадратный метр; 10000 м2 = 1
гектару (га); 1 000 000 м2 = 100 га = 1 км2.
Единицами измерения времени, массы и температуры являются
соответственно секунда, международный килограмм и градус по шкале
Цельсия.
Единицей измерения атмосферного давления является миллиметр
ртутного столба (мм рт. ст.) или миллибар (мб). 1мб = 0,750 мм рт. ст. За
нормальное давление атмосферы принято давление ртутного столба высотой
760 мм на уровне моря и на географической широте 45° при температуре 0°С.
В некоторых типах приборов для измерения атмосферного давления
(барометр-анероид и микробарометр) в соответствии с Международной
системой единиц (СИ) в качестве единицы измерения принят паскаль (Па); 1
мм рт. ст. = 133,322 Па.
За единицу измерения частоты периодических (модулированных)
электромагнитных колебаний принят герц; 106 герц= 1 мегагерц.
Виды измерений
Результаты измерений разделяют на равноточные и неравноточные.
Под равноточными понимают однородные результаты, полученные в
процессе измерений инструментами одного класса точности при одинаковых
условиях, а неравноточные результаты измерений получают при
несоблюдении условий равноточности.
Измерения различаются на необходимые и избыточные. Число
измерений, требующихся для решения поставленной задачи, называют
необходимыми. Например, при измерении длины линии, чтобы получить
результат, необходимо выполнить одно измерение.
В геодезической практике всегда выполняют некоторое число
избыточных измерений с тем, чтобы обеспечить контроль, повысить
точность и получить сравнительные данные для оценки точности
полученного результата.
Ошибки измерений
В процессе измерений участвуют наблюдатель, приборы и условия
внешней среды, которые постоянно меняются, что и приводит к неизбежным
ошибкам измерений.
Ошибки измерений подразделяют на грубые, систематические и
случайные.
Грубые ошибки возникают из-за промахов и просчетов, связанных с
неисправностью приборов, невнимательностью наблюдателя, резким
ухудшением внешних условий. Теория математической обработки не
рассматривает измерения с грубыми ошибками, такие измерения либо
отбрасываются, либо выполняются заново.
Систематические ошибки обычно имеют одну величину и знак и
могут быть выявлены и учтены путем введения поправок в результате
измерений. Например, при измерении длин линий лентой или рулеткой в
зимнее время необходимо вводить в результаты измерений поправку за
температуру.
Случайные ошибки неустранимы и неизбежны.
Для случайных ошибок установлены следующие свойства:
а) случайные ошибки для данных условий не могут превышать по
абсолютной величине известного предела;
б) малые по абсолютной величине ошибки появляются чаще больших;
в) по знаку положительные ошибки появляются так же часто, как и
равные им по величине отрицательные ошибки;
г) среднее арифметическое из случайных ошибок одной и той же
величины неограниченно стремится к нулю с увеличением числа измерений.
Это свойство можно записать так:
(1)
где ∆ – случайная ошибка; n – число измерений.
Если одна и та же величина равноточно измерена n раз, то за ее
окончательное значение принимают среднее арифметическое, то есть:
Средняя квадратичная ошибка
Чтобы судить о точности измерений, необходимо выбрать критерий
для оценки, причем необходимо, чтобы такой критерий не зависел от знаков
отдельных ошибок и более рельефно отражал бы наличие сравнительно
крупных отдельных ошибок. Таким требованиям удовлетворяет
предложенная Гауссом средняя квадратичная ошибка
(2)
где ∆ – истинная случайная ошибка.
Однако истинные значения величин и истинные ошибки при
ограниченном числе измерений обычно не известны и в практике измерений
получают вероятнейшие значения измеренных величин и вероятнейшие
ошибки V, в связи с чем обычно пользуются для получения средней
квадратической ошибки формулой Бесселя:
Оценка точности топографо-геодезических измерений
Оценка точности геодезических сетей имеет большое теоретическое и
практическое значение. Она выполняется как на стадии проектирования,
когда разрабатывается оптимальный в определенном смысле вариант
построения сети, так и после построения и уравнивания сети.
Оценка точности, выполняемая на заключительном этапе
уравнительных вычислений, дает наиболее достоверные данные о реальной
точности элементов построенной на местности геодезической сети. Они
необходимы для правильного использования геодезических сетей при
решении соответствующих научных и народнохозяйственных задач
геодезическими методами, требующих определения с заданной точностью
длин и азимутов сторон, координат и высот геодезических пунктов.
Особо следует отметить значение оценки точности геодезических сетей
на стадии их проектирования. Благодаря оценке точности представляется
возможность решить задачи, имеющие большое техническое и
экономическое значение: изучить закономерности действия ошибок
измерений при передаче длин и азимутов сторон, координат пунктов в
геодезических сетях разного вида;
установить выгоднейшую форму треугольников в триангуляции и
трилатерации,
обеспечивающих
наиболее
высокую
точность передачи длин сторон, азимутов и координат пунктов;
рассчитать необходимую частоту размещения базисных сторон и
азимутов Лапласа в сети;
определить требуемую точность измерения горизонтальных углов,
длин сторон и азимутов Лапласа в проектируемой сети, а затем на основе
этих данных сделать правильный выбор приборов и методов измерений;
путем моделирования на ЭВМ определить на основе оценки точности
наиболее рациональный вариант построения сети при разном составе
измерений и разном размещении в ней базисных сторон, азимутов, пунктов,
определяемых из наблюдений ИСЗ, и т. п., позволяющий при прочих равных
условиях получить уравненные элементы сети с наивысшей точностью,
достигаемой в массовых работах при наименьших затратах труда, денежных
средств и времени на их производство;
проверить, будет ли достигнута заданная точность определения
уравненных элементов в наиболее слабом месте сети при выбранной схеме и
методах построения сети с учетом намеченного состава и точности
измерений.
Детальность, полнота и точность планово-картографического материала
Планы и карты, полученные в результате различных видов съемок,
имеют неодинаковую детальность и полноту.
Под детальностью понимают степень подобия изображения на плане
всех изгибов и извилин, всех деталей контуров ситуации и рельефа. При
отсутствии детальности говорят, что план (карта) обобщенный. Обобщение
(генерализация) происходит при дешифрировании фотоматериалов или
рисовке рельефа при построении мелкомасштабных карт на основе
крупномасштабных.
Под полнотой понимают степень насыщенности плана объектами
местности, изображение которых на плане необходимо и при данном
масштабе и высоте сечения рельефа возможно.
Детальность и полнота планов зависят от детальности и полноты
абрисов.
Под точностью плана (карты) понимают величину средней
квадратической погрешности mt положения контурной точки на плане
относительно ближайшего пункта главного геодезического обоснования
съемки (контурная точка – точка объекта).
Погрешность положения точки (пункта) mt является двумерной и
определяется формулой
mt
mx2
m 2y ,
где m x и m y – погрешности координат точки (т.е. погрешности положения
точки по осям координат). Если m x m y mk (т.е. точность положения точки
приближенно характеризуется кругом погрешностей, а не эллипсом, что
точнее), тогда
mt mk 2 и mk mt 2 ,
где mk – средняя квадратическая погрешность координат точки.
Точность положения контурных точек на планах
Точность планов разных видов съемок различна, что объясняется
различием приборов и технологических процессов, применяемых на съемках.
Согласно многочисленным исследованиям погрешности положения
точки для теодолитной, мензульной и аэрофотосъемки в масштабе 1:10 000
примерно одинаковы и составляют 4 м, т.е. на плане 0.4 мм. Согласно
Инструкции по топографическим съемкам [7] для масштабов 1:500–1:10 000
средние погрешности в положении на карте четких контуров и предметов
местности относительно ближайших точек планового съемочного
обоснования не должны превышать:
0.5 мм – при создании карт и планов равнинных и холмистых местностей,
6 .
0.7 мм – при создании карт местности с большими уклонами.
Некоторые исследователи замечают, что с укрупнением масштаба
погрешности положения контурных точек на плане увеличиваются. Точность
расплывчатых нечетких контуров, например, болот, достигает 10 м на
местности, а положение контуров почвенных разновидностей – 40 м.
Копии планов обладают меньшей точностью по сравнению с оригиналом.
Наиболее точна ксерокопия и копии, полученные фотомеханическим
способом.
Если
копирование
производится
графическим
или
графомеханическим способами, то для сохранения точности копии на бумаге
строят координатную сетку и все точки (границы, геодезические пункты)
наносят на нее по координатам.
Точность изображения расстояний
Если отдельные точки на плане имеют погрешности, то и расстояния
между ними будут определены с погрешностями. Пусть надо определить
погрешность расстояния S между точкой 1 и точкой 2 с координатами x1, y1 и
x2, y2:
2
2
S 2 x2 x1
y 2 y1 .
Возьмем
полный
дифференциал
этого
выражения
(
dS, dx1 , dy1 , dx2 , dy2 ) и получим при dS ms , dx1 mkx , dy1 mky ,
ms mt , т.е. средняя квадратическая
погрешность расстояния между точками на плане равна средней
квадратической погрешности положения точки.
Средняя квадратическая погрешность определения расстояния между
точками 1 и 2 при помощи измерителя и масштабной линейки ms0 с учетом
mkx
mky
mk ,
mk 2 , что
mt
точности плана получится по формуле
ms0
mt2 mГ2 ,
где mt – средняя квадратическая погрешность расстояний между точками 1 и
2; mГ – графическая погрешность (0.08 – 0.1 мм).
Пример: при mt = 0.4 мм и mГ = 0.1 мм ms0 = 0.41 мм, т.е. точность
измерения расстояний между точками по плану определяется главным
образом точностью плана.
Точность направлений и углов
Точность направления, характеризуемого азимутом (дирекционным
углом) линии между двумя точками на плане (точками 1 и 2), зависит от
погрешностей положения этих точек m x1 , m у1 и m x2 , m x2 .
Тогда дирекционный угол
направления с точки 1 на точку 2
y 2 y1
определим по формуле tg
.
x2 x1
После дифференцирования, переходя к средним квадратическим
погрешностям
mk1 mx1 m y1 , mk2 m x2 m y2 ,
mt1
mk1 2 и mt2
mk2 2
получим
m2
Если же принять mt1
mt2
1
mt21
2
2S
mt , то m
mt22 .
mt
, при этом m
S
выражена в
радианной мере.
Если
m
выразить в минутах, то
m
2
1 2
mt
2 1
mt22
343 8
S
2
и
mt
343 8 , т.е. погрешность дирекционного угла увеличивается с
S
уменьшением расстояния между точками.
Пример: S = 50 мм, mt = 0.4 мм. Тогда m 27 , что представляет
довольно значительную величину.
Погрешность определения направления на плане при помощи
транспортира с учетом точности плана получится равной
m
m
m2
m2
27
2
7
2
27.9 ,
т.е. точность направления между точками по плану определяется главным
образом точностью плана.
Еще большей погрешностью характеризуется точность угла (так как
угол определяется разностью отсчетов на два направления)
y
y2
y y2
arctg 1
arctg 3
;
21
23
x1 x2
x3 x 2
m2
mt2
1
2
S 21
1
2
S 23
cos
;
S 21S 23
m
m ;
при
при
90
m
при
180
m
mt
2 343 8 ;
S
mt
3 343 8 .
S
Точность определения площадей контуров
Погрешности положения контура вызывают погрешность его площади.
Чтобы определить погрешность площади контура в зависимости от
погрешностей положения поворотных точек этого контура, надо представить,
что каждая такая точка определяется на плане независимо от других и ее
положение характеризуется координатами xi и yi со средними
квадратическими погрешностями m xi и m yi .
Зависимость площади контура от координат его поворотных точек
можно представить формулой
2P
n
i 1
xi y i
1
yi
1
.
Для получения зависимости средних квадратических погрешностей
площади от координат точек контура продифференцируем это выражение по
1 n 2 2
mt Di , где
всем переменным xi и yi и после преобразования получим m 2p
8i 1 i
Di – диагонали.
Если участок близок к правильному многоугольнику с n вершинами, то
P sin 360
m p S sin mt n 2 mt
;
2
n
для прямоугольника m p mt P 1 k 2 2k , где k – отношение большей
стороны к меньшей;
для квадрата m p mt P , причем m p м 2 , mt м , P м 2 .
Теперь для выражения m p и P в гектарах на местности и mt в
сантиметрах на плане напишем
mt (см)
m p (га) 1000
M P (га) 10000 .
100
Тогда m p (га) mt (см)
M
P (га) , где M – знаменатель численного
10000
масштаба.
Из анализа формул следует, что погрешности площадей фигур
значительно уменьшаются с увеличением числа точек фигуры и несколько
увеличиваются с увеличением ее вытянутости k.
Для более точного представления о погрешностях определения
площади по плану для фигур, близких по форме к прямоугольнику, с числом
точек n, вытянутостью k и с приблизительно равными расстояниями между
точками по контуру, используют формулу
M
4 0.5n 1 k 1
m p (га) mt (см)
P (га)
.
10000
n
2 k
Особенности расчета точности расстояний, направлений, углов и
площадей на фотоплане
Формулы выведены в предположении, что каждая точка на плане независима
от других (т.е. при наземных съемках они сняты с разных станций, а при
аэрокосмических каждая точка расположена на разных снимках). Если же все
точки (или часть их) сняты с одной станции или расположены на одном
снимке, то их положение не является независимым. Они обладают
корреляционной связью, теснота которой характеризуется коэффициентом
корреляции r (по формуле Неумывакина):
2
m0
,
r
mt
где m0 – средняя квадратическая погрешность положения станции или
положения снимка на фотоплане; mt – средняя квадратическая погрешность
положения каждой точки, mt2 m02 mc2 , (mc – средняя квадратическая
погрешность положения снимаемой точки относительно станции или
положения точки на снимке относительно его положения на фотоплане).
Тогда для учета корреляции во все формулы вводится коэффициент
1 r , тогда
mt
ms mt 1 r ; m
1 r;
S
m
mt
1
2
S 21
1
2
S 23
cos
1 r;
S 21S 23
для площадей многоугольника m p0
mt
1
8
n
1
Di2 1 r ;
1 k2
прямоугольника
m p0 mt P
(1 r ) ;
2k
m p0 mt P (1 r ) ,
квадрата
т.е. корреляционная связь уменьшает среднюю квадратическую погрешность.
В формулах фотограмметрии учитываются еще погрешности из-за
влияния рельефа местности и графическая погрешность (0.1 мм).
Установлено, что большее влияние на погрешность изображения
площади оказывает рельеф, а для малых площадей – погрешности
вычерчивания контуров при дешифрировании.
Точность превышений и уклонов
Превышения и уклоны линий между точками определяют по плану с
горизонталями, изображающими рельеф местности. Точность изображения
рельефа на плане обычно характеризуется средней квадратической
погрешностью высоты точки, лежащей на горизонтали, т.е. средней
квадратической погрешностью положения горизонтали по высоте, которую
можно охарактеризовать по формуле Коппе
mH a btg ,
где а – величина, характеризующая точность определения точки земной
поверхности по высоте; b – величина, характеризующая сдвиг точки в
горизонтальной плоскости вследствие погрешностей определения планового
положения станции и пикетов,
интерполирования,
проведения
горизонталей; – угол наклона.
Среднюю квадратическую погрешность превышения между точками 1
и 2 с высотами H1 и H2: mh mH 2 . Если расстояние между точками мало,
то величины H1 и H2 коррелированы и mh mH 2 1 r .
Средняя квадратическая погрешность уклона, определяемого по
горизонталям плана, можно получить из формул i h S и mi mh S , т.е.
точность определения уклона снижается с уменьшением расстояния.
Следовательно, уклон надо считать по возможно большему расстоянию.
Искажение линий и площадей в проекции Гаусса-Крюгера
Проекция Гаусса-Крюгера равноугольная поперечно-цилиндрическая.
Если план составлен на плоскости в проекции Гаусса–Крюгера, то длины
линий и площади участков, измеренных на плане или вычисленных по
координатам точек, всегда больше соответствующих горизонтальных
проложений этих же линий и площадей на местности, т.е. масштаб
изображений линий в проекции Гаусса-Крюгера всегда крупнее того
масштаба, который принят для составления плана. При этом укрупнение
масштаба тем больше, чем дальше линия или участок расположены от
осевого меридиана зоны.
Известно, что линия, измеренная на местности, при перенесении
(редуцировании) ее на плоскость Гаусса–Крюгера должна быть увеличена в
соответствии с выражением
2
1 y
,
SГ S
S
2 R
где S – горизонтальное проложение линии на местности; y – ордината
(расстояние от осевого меридиана); R – средний радиус кривизны земного
шара ( R 6371 км).
1 y
называют относительным искажением линии.
2 R
Значение ординаты на краю шестиградусной зоны в средних широтах
России 200 км (
53 ), в южных широтах 250 км (
40 ).
При y = 200 км относительное искажение за редуцирование составит
Величину
2
2
200
1
100
1
, при y = 100 км
.
6371
2000
6371
8000
Таким образом, искажением линии в проекции Гаусса-Крюгера можно
пренебречь за исключением краев шестиградусных зон.
Искажение линий вызывает соответственно и искажение площадей
участков. Проекция Гаусса-Крюгера равноугольная (конформная), поэтому
для небольшого участка в несколько тысяч или десятков тысяч гектар его
изображение в проекции Гаусса-Крюгера с площадью PГ можно считать
подобным горизонтальному проложению на местности с площадью P.
Площади P и PГ будут относиться как квадраты сходственных сторон
P
PГ
S2
P
, или
2
PГ
SГ
y2
1 1
2R 2
2
.
y2
Тогда, умножив числитель и знаменатель на 1
2R 2
2
2
и пренебрегая
y
малыми порядка y 4R , получим P PГ PГ
, т.е. относительное
R
искажение площади P в два раза больше относительного искажения линии.
Для небольших площадей поправку можно не учитывать, а для больших
следует учитывать только на краях шестиградусных зон.
Деформация плана и ее учет при планометрических работах
При определении линий и площадей по плану графическим или
механическим способом (при помощи измерителя, планиметра и палеток)
учитывают деформацию бумаги. Величина деформации характеризуется
коэффициентами
деформации,
определяемыми
в
двух
взаимно
перпендикулярных направлениях по формуле
l l
q0 0
,
l0
где l0 – теоретическая (истинная) длина линии в соответствующем масштабе;
l – результат измерения этой же линии на плане.
4000 3980
1
0.005
Пример: l0 4000 м, l 3980 м, q0
.
4000
200
Значения коэффициента деформации различны: 1:400, 1:200, 1:100 и
даже 1:50. Величина его зависит от сорта бумаги, условий хранения плана,
погоды, времени, которое прошло с момента составления плана, и других
условий.
4
4
Бумага, наклеенная на алюминий или высокосортную фанеру,
практически не деформируется, а бумага, наклеенная на полотно,
деформируется сильнее, чем ненаклеенная.
Копии с планшетов деформируются во время печати, в направлении
движения бумага растягивается, а в поперечном направлении – сжимается.
Через некоторое время деформация бумаги, правда, несколько уменьшается,
но все же остается значительной. Особенно сильно деформируется бумага от
свертывания в трубку или складывания.
Если бумага деформируется в двух взаимно перпендикулярных
направлениях одинаково, то учесть ее деформацию нетрудно; при
неравномерной деформации труднее, ведь обычно линии располагаются под
различными углами к линиям координатной сетки.
Для учета деформации бумаги в длины линий, определяемых по плану,
приходится вводить поправки. Если l – результат измерения линии на
деформированном плане, l0 – истинное горизонтальное проложение линии на
местности, q – относительная деформация бумаги (1/200–1/100), то l0 l lq ,
где lq – поправка к длине линии, обусловленная деформацией бумаги. Если
поправка меньше точности масштаба, то ее не вводят в результат измерения
линии на плане. Для площади P на плане истинное значение P0 P 2 Pq .
Требования к оформлению результатов полевых измерений и их
обработке
Все материалы геодезических измерений состоят из полевой
документации, а также документации вычислительных и графических работ.
Многолетний опыт производства геодезических измерений и их обработки
позволил разработать правила ведения этой документации.
Оформление полевых документов. К полевым документам относят
материалы поверок геодезических приборов, журналы измерений и бланки
специальной формы, абрисы, пикетажные журналы. Вся полевая
документация считается действительной только в подлиннике. Она
составляется в единственном экземпляре и в случае утраты может быть
восстановлена лишь повторными измерениями, что практически не всегда
возможно.
Правила ведения полевых журналов сводятся к следующим.
1. Заполнять полевые журналы следует аккуратно, все цифры и буквы
должны быть записаны четко и разборчиво.
2. Исправление цифр и их подчистка, а также написание цифры по цифре
не допускаются.
3. Ошибочные записи отсчетов зачеркиваются одной чертой и справа
указывается «ошибочно» или «описка», а правильные результаты
надписываются сверху.
4. Все записи в журналах ведутся простым карандашом средней
твердости, чернилами или шариковой ручкой; использование для этого
химических или цветных карандашей запрещается.
5. При выполнении каждого вида геодезических съемок записи
результатов измерений делают в соответствующих журналах установленной
формы. До начала работ страницы журналов пронумеровывают и их число
заверяет руководитель работ.
6. В процессе полевых работ страницы с забракованными результатами
измерений зачеркивают по диагонали одной чертой, указывают причину
брака и номер страницы, содержащей результаты повторных измерений.
7. В каждом журнале на заглавном листе заполняют сведения о
геодезическом приборе (марка, номер, средняя квадратическая погрешность
измерения), записывают дату и время наблюдений, метеоусловия (погода,
видимость и т. п.), фамилии исполнителей, приводят необходимые схемы,
формулы и примечания.
8. Журнал должен заполняться таким образом, чтобы другой исполнитель,
не участвующий в полевых работах, мог безошибочно выполнить
последующую обработку результатов измерений. При заполнении полевых
журналов следует придерживаться следующих форм записи:
а) числа в столбцах записываются так, чтобы все цифры соответствующих
разрядов располагались одна под другой без смещения.
Пример:
1175,18
1232,79
234,49, а не 125,15;
б)все результаты измерений, выполненных с одинаковой точностью,
записывают с одинаковым числом знаков после запятой.
Пример:
356,24 и 205,60 м – правильно,
356,24 и 205,6 м – неправильно;
в) значения минут и секунд при угловых измерениях и вычислениях всегда
записывают двузначным числом.
Пример:
127°07′ 05», а не 127°7′ 5′
г) в числовых значениях результатов измерений записывают такое
количество цифр, которое позволяет получить отсчетное устройство
соответствующего средства измерений. Например, если длина линии
измеряется рулеткой с миллиметровыми делениями и отсчитывание
проводится с точностью до 1 мм, то отсчет должен быть записан 27,400 м, а
не 27,4 м. Или если угломерный прибор позволяет отсчитывать только целые
минуты, то отсчет запишется как 47°00′, а не 47° или 47°00’00».
Понятие о правилах геодезических вычислений. К обработке результатов
измерений приступают после проверки всех полевых материалов. При этом
следует придерживаться выработанных практикой правил и приемов,
соблюдение которых облегчает труд вычислителя и позволяет ему
рационально использовать вычислительную технику и вспомогательные
средства.
1. Перед началом обработки результатов геодезических измерений следует
разработать подробную вычислительную схему, в которой указывается
последовательность действий, позволяющая получить искомый результат
наиболее простым и быстрым путем.
2. С учетом объема вычислительных работ выбирать наиболее
оптимальные средства и способы вычислений, требующие наименьших
затрат при обеспечении необходимой точности.
3. Точность результатов вычислений не может быть выше точности
измерений. Поэтому заранее следует задаваться достаточной, но не излишней
точностью вычислительных действий.
4. При вычислениях нельзя пользоваться черновиками, так как
переписывание цифрового материала отнимает много времени и часто
сопровождается ошибками.
5. Для записей результатов вычислений рекомендуется использование
специальных схем, бланков и ведомостей, определяющих порядок расчетов и
обеспечивающих промежуточный и общий контроль.
6. Без контроля вычисление не может считаться законченным. Контроль
можно выполнять, используя другой ход (способ) решения задачи либо
выполняя повторные вычисления другим исполнителем (в «две руки»).
7. Вычисления всегда заканчиваются определением погрешностей и
обязательным их сравнением с допусками, предусматриваемыми
соответствующими инструкциями.
8. Особые требования при вычислительных работах предъявляются к
аккуратности и четкости записи чисел в вычислительных бланках, поскольку
небрежности в записях приводят к ошибкам.
Как и в полевых журналах, при записях столбцов чисел в вычислительных
схемах цифры одинаковых разрядов следует располагать одна под другой.
При этом дробную часть числа отделяют запятой; многоразрядные числа
желательно записывать с интервалами, например:
2 560 129,13. Записи вычислений следует вести только чернилами прямым
вычислительным шрифтом; ошибочные результаты аккуратно перечеркивать
и сверху писать исправленные значения.
При обработке материалов измерений следует знать, с какой точностью
должны быть получены результаты вычислений, чтобы не оперировать с
излишним числом знаков; если окончательный результат вычисления
получается с большим числом знаков, чем это необходимо, то производят
округление чисел.
Округление чисел. Округлить число до n знаков – значит сохранить в нем
первые n значащих цифр.
Значащие цифры числа – это все его цифры от первой слева, отличной от
нуля, до последней записанной цифры справа. При этом нули справа не
считаются значащими цифрами, если они заменяют неизвестные цифры или
поставлены вместо других цифр при округлении данного числа.
Например, число 0,027 имеет две значащие цифры, а число 139,030 –
шесть значащих цифр.
При округлении чисел следует придерживаться следующих правил.
1. Если первая из отбрасываемых цифр (считая слева направо) меньше 5,
то последняя оставляемая цифра сохраняется без изменения.
Например, число 145,873 после округления до пяти значащих цифр будет
145,87.
2. Если первая из отбрасываемых цифр больше 5, то последняя
оставляемая цифра увеличивается на единицу.
Например, число 73,5672 после округления его до четырех значащих цифр
будет 73,57.
3. Если последней цифрой округляемого числа является цифра 5 и она
должна быть отброшена, то предшествующую ей цифру в числе увеличивают
на единицу только в том случае, если она нечетная (правило четной цифры).
Например, числа 45,175 и 81,325 после округления до 0,01 будут
соответственно 45,18 и 81,32.
Действия с приближенными числами. Результаты геодезических
измерений являются числами приближенными. Степень приближения,
характеризующая точность измерения, зависит от способа измерения и
применяемых приборов.
При действиях с приближенными числами необходимо руководствоваться
следующими правилами приближенных вычислений.
1. Чтобы при сложении приближенных чисел получить сумму с п верными
(т. е. заслуживающими доверия) десятичными знаками, следует каждое
слагаемое округлить до л+/-го десятичного знака.
При вычитании, когда уменьшаемое значительно превосходит
вычитаемое, к числу верных знаков разности применяют те же правила, что и
для числа верных знаков суммы.
При сложении или вычитании приближенных чисел в результате (в сумме
или разности) необходимо оставлять столько десятичных знаков, сколько их
дано в числе с наименьшим количеством этих знаков.
Пример:
135,32 + 18,537 + 4,7183 » 135,32 + 18,537 + 4,718 = 158,575 * 158,58;
При умножении двух приближенных чисел, имеющих поровну значащих
цифр, в результате следует сохранять столько значащих цифр, сколько их
было в каждом из сомножителей.
Пример: 72,6 х 32,7 = 2374,02 * 23,7 х 102.
При умножении двух приближенных чисел с разным числом значащих
цифр в результате следует сохранять столько значащих цифр, сколько их
имеется в числе с наименьшим количеством значащих цифр.
Пример: 4,248 х 0,55 = 2,3364 » 2,3.
Для получения произведения с п верными знаками сомножители следует
брать с л -hi или л+2 верными знаками.
2. При делении двух приближенных чисел, имеющих одинаковое число
значащих цифр, в частном следует сохранять столько значащих цифр,
сколько их имеется в каждом из данных.
Пример: 4,347 : 6,173 = 0,704 196 … « 0,7042.
При делении двух приближенных чисел, имеющих различное число
значащих цифр, в частном следует сохранять столько значащих цифр,
сколько их было в числе с меньшим количеством значащих цифр.
Пример: 548,4 : 3,6 = 152,33 » 1,5 х 102.
3. При возведении приближенных чисел в степень в результате следует
оставлять столько значащих цифр, сколько их содержится в основании
степени.
Пример: 12,312 « 151,5; 1,423 « 2,86.
4. При извлечении корня из приближенного числа в результате следует
оставлять столько значащих цифр, сколько их имеется в подкоренном числе.
Пример: V61,3*7,83; ^/229,7«6,214.
5. Если для вычисления искомой величины требуется произвести ряд
разных действий, то в этом случае во всех промежуточных результатах
следует сохранять на одну цифру больше, чем это указано в правилах 1–4,
отбрасывая эту цифру только в окончательном результате.
6. Если некоторые величины, участвующие в вычислении, имеют
десятичных знаков (при сложении и вычитании) или значащих цифр (при
умножении, делении, возведении в степень или извлечении корня) больше,
чем другие, то их предварительно округляют, сохраняя лишь одну цифру
против числа, заданного с наименьшим числом значащих цифр.
Соблюдение данных правил при вычислениях позволяет обеспечить
необходимую точность и повысить производительность вычислительных
работ.
Средства вычислений. При обработке результатов геодезических
измерений широко используются различные средства вычислений: таблицы,
номограммы, логарифмическая (счетная) линейка, микрокалькуляторы,
переносные (notebook) и стационарные компьютеры.
Таблицы. До сих пор в практике используются различные таблицы. Они
содержат численные значения функций, данных с определенной точностью
для последовательно расположенных значений аргументов. Таблицы бывают
общие, или математические (таблицы квадратных и кубических корней,
натуральных значений тригонометрических функций, логарифмов и т. п.)( и
специальные
(таблицы
превышений,
приращений
координат,
тахеометрические таблицы и т. п.). Общие таблицы пригодны для любых
вычислений, а по специальным можно вычислить искомую величину по
одной формуле (например, поправку за наклон, поправку за температуру и
др.).
При
нахождении
значений
тригонометрических
функций
и
логарифмических вычислениях следует пользоваться таблицами с
количеством знаков, обеспечивающих заданную точность. При решении
задач, связанных с отысканием по таблицам величин углов по значениям их
функций, для определения угла следует:
а) по sin а и cos а использовать функцию, меньшую по абсолютному
значению;
б) по tg а и ctg a, sec а и cosec а использовать функцию, большую по
абсолютному значению.
Во всех случаях второе определение будет менее точным, чем первое, и
используется для контроля.
Номограмма представляет собой чертеж, на котором изображена
функциональная зависимость между переменными, входящими в данную
математическую формулу. Номограммы играют роль специальных
приспособлений, позволяющих без вычислений определять численное
значение одной переменной по значениям других переменных. Они могут
использоваться для вычисления величин, содержащих не более трех
значащих цифр.
Логарифмическая линейка используется для приближенных контрольных
подсчетов, а также для расчета поправок, величины которых содержат не
более трех значащих цифр.
Калькуляторы являются одним из самых главных средств при расчетах как
в полевых, так и в камеральных условиях. По количеству производимых
операций калькуляторы подразделяются на следующие типы:
а) простые – с арифметическим объемом операций;
б) инженерные – имеющие встроенные функции (sin, cos, tg, log, In, exp и
др.) и позволяющие производить достаточно сложные расчеты;
в) программируемые – позволяющие производить расчеты без
промежуточных вычислений.
В настоящее время из счетных машин индивидуального пользования
наибольшее
распространение
получили
микрокалькуляторы
типов
«Электроника» и др. Они практически обеспечивают возможность решения
многих геодезических задач без привлечения других вычислительных
средств. Они отличаются малыми габаритами и сравнительно большим
числом производимых математических операций, работают как от
электросети, так и от батарей миниатюрных аккумуляторов, которые при
необходимости могут подзаряжаться, обеспечивая автономную работу
микрокалькулятора в течение нескольких часов. Это позволяет успешно
использовать микрокалькуляторы и в полевых условиях.
Единственным недостатком микрокалькуляторов является их небольшой
объем памяти.
Компьютерная техника является наиболее высокоэффективным средством
обработки геодезических измерений. На современном этапе как
геодезическое, так и землеустроительное производство основано на
применении этих устройств.
Все современные электронные геодезические инструменты имеют
встроенные
калькуляторы
программируемого
типа и
снабжены
электронными накопителями информации. Практически все результаты
измерений хранятся на специальных дискетах в виде файлов или впрямую
передаются на вычислительное устройство – компьютер или ноутбук
(notebook) – переносной компьютер.
Для ввода в дальнейшем обрабатываемой картографической информации
(карт и планов) используются специальные приборы: дигитайзеры,
поточечно фиксирующие графические изображения, и сканеры, передающие
фотографическое изображение объектов.
Камеральная обработка результатов проводится, как правило, в
полуавтоматическом режиме, используя специальное программное
обеспечение. Участие инженера-геодезиста в этом случае сводится к выбору
того или иного шага компьютерной операции.
Для получения искомой (выводной) информации используются принтеры
различных типов (матричные, струйные, лазерные и др.) и плоттеры (или
графопостроители).
Все сложные геодезические вычисления, связанные с решением большого
числа уравнений, выполняются на электронно-вычислительных машинах.
Однако в практической деятельности при выполнении простых вычислений с
небольшим количеством цифр нельзя преуменьшать роли устного счета
(вычислений в «уме»), позволяющего легко и быстро получить
окончательный результат. Для этого нужно научиться устно складывать и
вычитать числа, умножать и делить на такие простые числа, как 2, 3, 4 и 5.
Устным счетом следует также пользоваться при приближенном контроле
вычислений, подставляя в формулы округленные значения исходных данных.
Графические работы. Ценность графических материалов (планов, карт и
профилей), являющихся конечным результатом геодезических съемок, в
значительной мере определяется не только точностью полевых измерений и
правильностью вычислительной их обработки, но и качеством графического
исполнения. Графические работы должны выполняться с помощью
тщательно проверенных чертежных инструментов: линеек, треугольников,
геодезических транспортиров, циркулей-измерителей, остро отточенных
карандашей (Т и ТМ) и т. п. Большое влияние на качество и
производительность чертежных работ оказывает организация рабочего места.
Чертежные работы должны выполняться на листах качественной чертежной
бумаги, закрепленных на ровном столе либо на специальной чертежной
доске. Составленный карандашный оригинал графического документа после
тщательной проверки и корректировки оформляют в туши в соответствии с
установленными условными знаками.
География
Мореходная астрономия
Федеральное агентство морского и речного транспорта РФ
Морской государственный университет
имени адмирала Г.И. Невельского
Кафедра судовождения
А. Н. …
А.Н. Панасенко
Авторы
Социология
Научные исследования
СОДЕРЖАНИЕ
ГЛАВА 1. МЕТОДОЛОГИЯ НАУЧНОГО ПОЗНАНИЯ КАК
ОСНОВА НАУЧНОГО ТВОРЧЕСТВА
1.1. Понятие научного знания
1.2. Методы теоретических и эмпирических…
Теория вероятностей
Основы теории информации
Федеральное агентство морского и речного транспорта
Федеральное государственное образовательное учреждение
высшего профессионального образования
«Морс…
Шевцов А. В.
Авторы
Смотреть все
Поделись лекцией и получи скидку!
Заполни поля, отправь лекцию и мы вышлем тебе скидку-промокод на Автор24
Предмет
Название лекции
Авторы
Описание
Другие Естественные предметы
-
Химия
-
Безопасность жизнедеятельности
-
Нефтегазовое дело
-
Экология
-
Медицина
-
Геология
-
Биология
-
Геодезия
-
География
-
Естествознание
-
Ветеринария
-
Фармация
-
Сельское и рыбное хозяйство
-
Астрономия
-
Землеустройство и кадастр
-
Гидрометеорология
-
Природообустройство и водопользование
-
Почвоведение
-
Хирургия
-
Биотехнология