Error-detecting codes are a sequence of numbers generated by specific procedures for detecting errors in data that has been transmitted over computer networks.
When bits are transmitted over the computer network, they are subject to get corrupted due to interference and network problems. The corrupted bits leads to spurious data being received by the receiver and are called errors.
Error – detecting codes ensures messages to be encoded before they are sent over noisy channels. The encoding is done in a manner so that the decoder at the receiving end can detect whether there are errors in the incoming signal with high probability of success.
Features of Error Detecting Codes
-
Error detecting codes are adopted when backward error correction techniques are used for reliable data transmission. In this method, the receiver sends a feedback message to the sender to inform whether an error-free message has been received or not. If there are errors, then the sender retransmits the message.
-
Error-detecting codes are usually block codes, where the message is divided into fixed-sized blocks of bits, to which redundant bits are added for error detection.
-
Error detection involves checking whether any error has occurred or not. The number of error bits and the type of error does not matter.
Error Detection Techniques
There are three main techniques for detecting errors
Parity Check
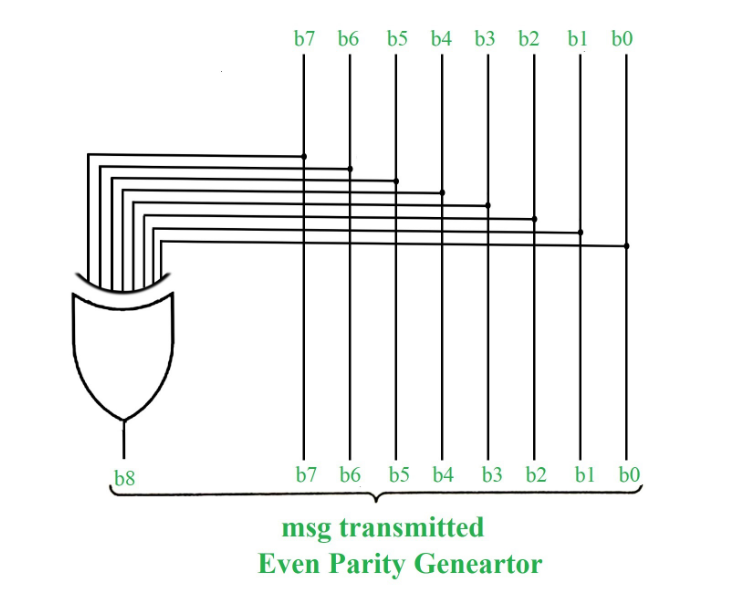
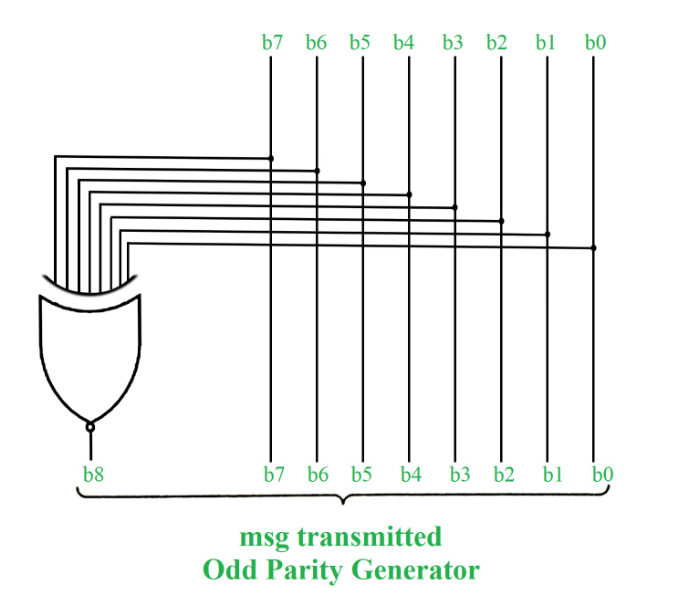
Parity check is done by adding an extra bit, called parity bit to the data to make number of 1s either even in case of even parity, or odd in case of odd parity.
While creating a frame, the sender counts the number of 1s in it and adds the parity bit in following way
-
In case of even parity: If number of 1s is even then parity bit value is 0. If number of 1s is odd then parity bit value is 1.
-
In case of odd parity: If number of 1s is odd then parity bit value is 0. If number of 1s is even then parity bit value is 1.
On receiving a frame, the receiver counts the number of 1s in it. In case of even parity check, if the count of 1s is even, the frame is accepted, otherwise it is rejected. Similar rule is adopted for odd parity check.
Parity check is suitable for single bit error detection only.
Checksum
In this error detection scheme, the following procedure is applied
-
Data is divided into fixed sized frames or segments.
-
The sender adds the segments using 1’s complement arithmetic to get the sum. It then complements the sum to get the checksum and sends it along with the data frames.
-
The receiver adds the incoming segments along with the checksum using 1’s complement arithmetic to get the sum and then complements it.
-
If the result is zero, the received frames are accepted; otherwise they are discarded.
Cyclic Redundancy Check (CRC)
Cyclic Redundancy Check (CRC) involves binary division of the data bits being sent by a predetermined divisor agreed upon by the communicating system. The divisor is generated using polynomials.
-
Here, the sender performs binary division of the data segment by the divisor. It then appends the remainder called CRC bits to the end of data segment. This makes the resulting data unit exactly divisible by the divisor.
-
The receiver divides the incoming data unit by the divisor. If there is no remainder, the data unit is assumed to be correct and is accepted. Otherwise, it is understood that the data is corrupted and is therefore rejected.
To clean up transmission errors introduced by Earth’s atmosphere (left), Goddard scientists applied Reed–Solomon error correction (right), which is commonly used in CDs and DVDs. Typical errors include missing pixels (white) and false signals (black). The white stripe indicates a brief period when transmission was interrupted.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Definitions[edit]
Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.
Error correction is the detection of errors and reconstruction of the original, error-free data.
History[edit]
In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.[5]
The modern development of error correction codes is credited to Richard Hamming in 1947.[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication[7] and was quickly generalized by Marcel J. E. Golay.[8]
Introduction[edit]
All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.
If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Types of error correction[edit]
There are three major types of error correction.[9]
Automatic repeat request[edit]
Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.
Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.
Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.
ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.[10]
For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.
Forward error correction[edit]
Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.[13]
Error-correcting codes are usually distinguished between convolutional codes and block codes:
- Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
- Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.
Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.
The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.
Hybrid schemes[edit]
Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:[10]
- Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
- Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.
The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.
Error detection schemes[edit]
Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).
Minimum distance coding[edit]
A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.
Repetition codes[edit]
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.
A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.[14][15]
Parity bit[edit]
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.
Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.
There are also other bit-grouping techniques.
Checksum[edit]
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy check[edit]
A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.
A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.
The parity bit can be seen as a special-case 1-bit CRC.
Cryptographic hash function[edit]
The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.
Error correction code[edit]
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.
Applications[edit]
Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.
Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.
Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.
Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.
Reliability and inspection engineering also make use of the theory of error-correcting codes.[16]
Internet[edit]
In a typical TCP/IP stack, error control is performed at multiple levels:
- Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
- The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
- The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
- UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
- TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.
Deep-space telecommunications[edit]
The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.
The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.
The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.
The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.
Satellite broadcasting[edit]
The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.
Data storage[edit]
Error detection and correction codes are often used to improve the reliability of data storage media.[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.
Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.
Error-correcting memory[edit]
Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.
Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.[22]
In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.[23][24][25] A few systems[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.
See also[edit]
- Berger code
- Burst error-correcting code
- ECC memory, a type of computer data storage
- Link adaptation
- List of algorithms § Error detection and correction
- List of hash functions
References[edit]
- ^ a b «Masorah». Jewish Encyclopedia.
- ^ Pratico, Gary D.; Pelt, Miles V. Van (2009). Basics of Biblical Hebrew Grammar: Second Edition. Zondervan. ISBN 978-0-310-55882-8.
- ^ Mounce, William D. (2007). Greek for the Rest of Us: Using Greek Tools Without Mastering Biblical Languages. Zondervan. p. 289. ISBN 978-0-310-28289-1.
- ^ Mishneh Torah, Tefillin, Mezuzah, and Sefer Torah, 1:2. Example English translation: Eliyahu Touger. The Rambam’s Mishneh Torah. Moznaim Publishing Corporation.
- ^ Brian M. Fagan (5 December 1996). «Dead Sea Scrolls». The Oxford Companion to Archaeology. Oxford University Press. ISBN 0195076184.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, p. vii, ISBN 0-88385-023-0
- ^ Shannon, C.E. (1948), «A Mathematical Theory of Communication», Bell System Technical Journal, 27 (3): 379–423, doi:10.1002/j.1538-7305.1948.tb01338.x, hdl:10338.dmlcz/101429, PMID 9230594
- ^ Golay, Marcel J. E. (1949), «Notes on Digital Coding», Proc.I.R.E. (I.E.E.E.), 37: 657
- ^ Gupta, Vikas; Verma, Chanderkant (November 2012). «Error Detection and Correction: An Introduction». International Journal of Advanced Research in Computer Science and Software Engineering. 2 (11). S2CID 17499858.
- ^ a b A. J. McAuley, Reliable Broadband Communication Using a Burst Erasure Correcting Code, ACM SIGCOMM, 1990.
- ^ Shah, Pradeep M.; Vyavahare, Prakash D.; Jain, Anjana (September 2015). «Modern error correcting codes for 4G and beyond: Turbo codes and LDPC codes». 2015 Radio and Antenna Days of the Indian Ocean (RADIO): 1–2. doi:10.1109/RADIO.2015.7323369. ISBN 978-9-9903-7339-4. S2CID 28885076. Retrieved 22 May 2022.
- ^ «IEEE SA — IEEE 802.11ac-2013». IEEE Standards Association.
- ^ «Transition to Advanced Format 4K Sector Hard Drives | Seagate US». Seagate.com. Retrieved 22 May 2022.
- ^ Frank van Gerwen. «Numbers (and other mysterious) stations». Archived from the original on 12 July 2017. Retrieved 12 March 2012.
- ^ Gary Cutlack (25 August 2010). «Mysterious Russian ‘Numbers Station’ Changes Broadcast After 20 Years». Gizmodo. Retrieved 12 March 2012.
- ^ Ben-Gal I.; Herer Y.; Raz T. (2003). «Self-correcting inspection procedure under inspection errors» (PDF). IIE Transactions. IIE Transactions on Quality and Reliability, 34(6), pp. 529-540. Archived from the original (PDF) on 2013-10-13. Retrieved 2014-01-10.
- ^ K. Andrews et al., The Development of Turbo and LDPC Codes for Deep-Space Applications, Proceedings of the IEEE, Vol. 95, No. 11, Nov. 2007.
- ^ Huffman, William Cary; Pless, Vera S. (2003). Fundamentals of Error-Correcting Codes. Cambridge University Press. ISBN 978-0-521-78280-7.
- ^ Kurtas, Erozan M.; Vasic, Bane (2018-10-03). Advanced Error Control Techniques for Data Storage Systems. CRC Press. ISBN 978-1-4200-3649-7.[permanent dead link]
- ^ Scott A. Moulton. «My Hard Drive Died». Archived from the original on 2008-02-02.
- ^ Qiao, Zhi; Fu, Song; Chen, Hsing-Bung; Settlemyer, Bradley (2019). «Building Reliable High-Performance Storage Systems: An Empirical and Analytical Study». 2019 IEEE International Conference on Cluster Computing (CLUSTER): 1–10. doi:10.1109/CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite». Tsinghua Space Center, Tsinghua University, Beijing. Archived from the original on 2011-10-02. Retrieved 2009-02-16.
- ^ Jeff Layton. «Error Detection and Correction». Linux Magazine. Retrieved 2014-08-12.
- ^ «EDAC Project». bluesmoke.sourceforge.net. Retrieved 2014-08-12.
- ^ «Documentation/edac.txt». Linux kernel documentation. kernel.org. 2014-06-16. Archived from the original on 2009-09-05. Retrieved 2014-08-12.
Further reading[edit]
- Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
- SoftECC: A System for Software Memory Integrity Checking
- A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
- Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing
External links[edit]
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
- ECC Page — implementations of popular ECC encoding and decoding routines
This article is based on a talk in Chris Budd’s ongoing Gresham
College lecture series. You can see a video of the talk below and there is another article based on the talk here.
We are surrounded by information and are constantly receiving and transmitting it to other people all over the world. With good reason we can call the 21st century the information age. But whenever a message is being sent, be it over the phone, via the internet, or via satellites that orbit the Earth, there is the danger for errors to creep in. Background noise, technical faults, even cosmic rays can corrupt the message and important information may be lost. Rather amazingly, however, there are ways of encoding a message that allow errors to be detected, and even corrected, automatically. Here is how these codes work.
The 15th century scribe, manuscript illuminator, translator and author Jean Miélot at his desk.
Error detecting codes
The need for the detection of errors has been recognised since the earliest scribes copied manuscripts by hand.
It was important to copy these without error, but to check every word would have been too large a task. Instead various checks were used. For example, when copying the Torah the letters, words, and paragraphs were counted, and then checked against the middle paragraph, word and letter of the original document. If they didn’t match, there was a problem.
Modern digital information is encoded as sequences of 0s and 1s. When transmitting binary information a simple check that is often used involves a so-called hash function, which adds a fixed-length tag to a message. The tag allows the receiver to verify the delivered message by re-computing it and comparing it with the one provided in the message.
A simple example of such a tag comes from including a check or parity digit in each block of data. The simplest example of this method is to add up the digits that make up a message and then append a 1 if the sum is odd and a 0 if it is even. So if the original message is 111 then message sent is 1111, and if the original message is 101, then the message sent is 1010. The effect of this is that every message sent should have digits adding up to an even number. On receiving the transmission the receiving computer will add up the digits, and if the sum is not even then it will record an error.
An example of the use of this technology can be found on the bar codes that are used on nearly all mass-produced consumer goods sold. Such consumer products typically use either UPC-A or EAN-13 codes. UPC-A describes a 12-digit sequence, which is broken into four groups. The first digit of the bar code carries some general information about the item: it can either indicate the nationality of the manufacturer, or describe one of a few other categories, such as the ISBN (book identifier) numbers. The next five digits are a manufacturer’s identification. The five digits that follow are a product identification number, assigned by the manufacturer. The last digit is a check digit, allowing a scanner to validate whether the barcode has been read correctly.
Similar check digits are used in the numbers on your credit card, which are usually a sequence of decimal digits. In this case the Luhn algorithm is used (find out more here).
Error correcting codes
Suppose that we have detected an error in a message we have deceived. How can we proceed to find the correct information contained in the message? There are various approaches to this. One is simply to (effectively) panic: to shut the whole system down and not to proceed until the problem has been fixed. The infamous blue screen of death, pictured below and familiar to many computer operators, is an example of this.
Blue Screen of Death on Windows 8.
The rationale behind this approach is that in some (indeed many) cases it is better to do nothing than to do something which you know is wrong. However, all we can do at this point is to start again from scratch, and we lose all information in the process.
A second approach called the automatic repeat request (ARQ), often used on the Internet, is for the message to be repeated if it is thought to contain an error. We do this all the time. For example if you scan in an item at the supermarket and the scanner does not recognise it, then you simply scan it in again.
However, this option is not available to us if we are receiving information from, say, a satellite, a mobile phone or from a CD. In this case if we know that an error has been made in transmission then we have to attempt to correct it. The general idea for achieving correction is to add some extra data to a message, which allows us to recover it even after an error has been made. To do this, the transmitter sends the original data, and attaches a fixed number of check bits using an error correcting code (ECC). The idea behind this is to make the symbols from the different characters in the code as different from each other as possible, so that even if one symbol in the code was corrupted by noise it could still be distinguished from other symbols in the code. Error correcting codes were invented in 1947, at Bell Labs, by the American mathematician Richard Hamming.
Illustration of the U.S./European Ocean Surface Topography Mission (OSTM)/Jason-2 satellite in orbit.
Image: NASA-JPL/Caltech
To understand how error correcting codes work we must define the Hamming distance between two binary strings. Suppose that we have two six-bit strings such as 1 1 1 0 1 0 and 1 0 1 1 1 1. Then the Hamming distance is the number of digits which are different. So in this case the Hamming distance is 3. If one bit in a symbol is changed then it has a Hamming distance of one from its original. This change might be due to the action of noise, which has corrupted the message. If two strings are separated by a large Hamming distance, say 3, then they can still be distinguished even if one bit is changed by noise. The idea of the simplest error correcting codes is to exploit this fact by adding extra digits to a binary symbol, so that the symbols are a large Hamming distance apart.
I will illustrate this with a simple example. The numbers from 0 up to 7, written in binary, are:
000 (0) 001 (1) 010 (2) 011 (3)
100 (4) 101 (5) 110 (6) 111 (7)
(You can read more about binary numbers here, or simply believe me.)
Many of these strings are only one Hamming distance apart. For example a small amount of noise could turn the string for 2 into the string for 3. We now add some extra parity digits (we explain the maths behind these later) to these codes to give the code
000 000 (0) 001 110 (1) 010 011 (2) 011 101 (3)
100 101 (4) 101 011 (5) 110 110 (6) 111 000 (7)
The point of doing this is that each of these codes is a Hamming distance of 3 apart. Suppose that the noise is fairly low and has the effect changing one bit of a symbol. Suppose we take the symbol 101 011 for 5 and this changes to (say) 100 011. This is a Hamming distance of one from the original symbol and a distance of at least two from all of the others. So if we receive 100 011 what we do is to find the nearest symbol on our list to this. This must be the original symbol, and we correct 100 011 to 101 011 to read the symbol without error.
Space flight, Facebook and CDs
All error correcting codes use a similar principle to the one above: receive a string, if it’s not on the list
find the closest string on the list to the one received, correct the string to this one. A lot of mathematical sophistication is used to find codes for more symbols which will work in the presence of higher levels of noise. Basically the challenge is to find symbols which are as different from each other as possible. Alongside the development of a code is that of an efficient decoder, which is used to correct corrupted messages fast and reliably.
Another example of an error correcting code is the Reed-Solomon code invented in 1960. The first commercial application in mass-produced consumer products appeared in 1982, with the CD, where two Reed–Solomon codes are used on each track to give even greater redundancy. This is very useful when having to reconstruct the music on a scratched CD.
Today, Reed–Solomon codes are widely implemented in digital storage devices and digital communication standards (for example digital TV), although they are now being replaced by low-density parity-check (LDPC) codes. Reed–Solomon coding is very widely used in mass storage systems to correct the burst errors associated with media defects. This code can correct up to 2 byte errors per 32-byte block. One significant application of Reed–Solomon coding was to encode the digital pictures sent back by the Voyager space probe, which was launched in 1977 and took the first satellite pictures of Jupiter, Saturn and the far planets.
A major recent user of error correction is on Facebook, which is possibly the largest repository of information in the world. It is estimated that 300 million photos are stored on Facebook every day. This information is stored in vast data banks around the world, mostly on spinning discs. Whilst the individual failure rate of a disc is very low, there are so many discs required to store the information that the chance of one of the discs failing at any one time is high. When this happens the data on the disc is recovered efficiently and quickly by using a Reed-Solomon code, so that Facebook can continue without interruption.
Some mathematics
In this last section we will give some mathematical detail for those who are interested. (If you aren’t interested in the details, you can skip to the next article.) It is far from simple to work out codes which are both efficient and robust, and a whole branch of mathematics, coding theory, has been developed to do it.
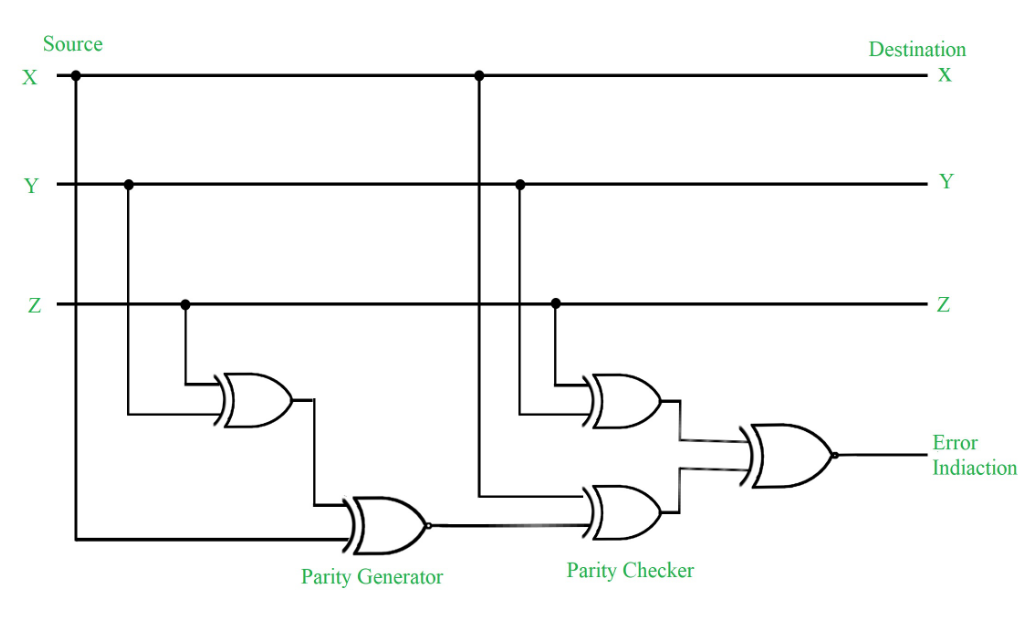
The Hamming (7,4) code is similar to the Hamming code above, only in this case three parity bits are added to a message with four information bits (rather than a message with three information bits , as above). If 
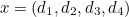
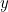
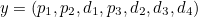
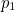
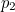
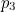
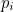
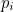
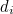
For example, this means that if 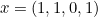
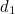
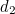
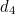
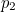
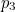
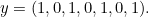
Now suppose that 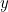
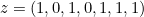
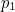
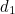
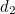
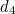
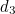
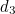
In a more abstract setting
![[ y = G x, ]](https://plus.maths.org/MI/0f3ad8b23b9fbff178e9a0726c0b363d/images/img-0001.png) |
where 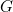

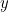
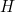
![[ d=Hz ]](https://plus.maths.org/MI/0f3ad8b23b9fbff178e9a0726c0b363d/images/img-0006.png) |
should be the zero vector. If it is not the zero vector, then an error has occurred. The vector 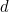
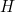
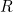
![[ x = R z. ]](https://plus.maths.org/MI/0f3ad8b23b9fbff178e9a0726c0b363d/images/img-0009.png) |
Évariste Galois, drawn from memory by his brother in 1848, sixteen years after his death.
The Reed-Solomon code is more sophisticated in its construction. In the classic implementation of the Reed-Solomon code the original message is mapped to a polynomial with the terms of the message being the coefficients of the polynomial. The transmitted message is then given by evaluating the polynomial at a set of points. As in the Hamming (7,4) code, the Reed-Solomon code is a linear transformation of the original message. Decoding works by finding the best fitting message polynomial. All of the multiplications for the polynomial are performed over mathematical structures called finite fields. The theory behind the construction of these codes uses advanced ideas from the branch of mathematics called Galois theory, which was invented by the French mathematician Évariste Galois
when he was only 19, and at least 150 years before it was used in CD players.
About this article
This article is based on a talk in Budd’s ongoing Gresham
College lecture series. A video of the talk is below and there is another article based on the talk here.
Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.
(Notes for EECS 373, Winter 2005)
Data can be corrupted in transmission or storage by a
variety of undesirable phenomenon, such as radio interference,
electrical noise, power surges, bad spots on disks or tapes,
or scratches or dirt on CD or DVD media.
It is useful to have a way to to detect (and sometimes correct)
such data corruption.
Errors come in several forms.
The most common situation is that a bit in a stream of
data gets flipped (a 0 becomes a 1 or a 1 becomes a 0).
It is also possible for a bit to get deleted,
or for an extra bit to be inserted.
In some situations, burst errors occur,
where several successive bits are affected.
Parity bit
We can detect single errors with a parity bit.
The parity bit is computed as the exclusive-OR (even parity) or
exclusive-NOR (odd parity) of all of the other bits in the word.
Thus, the resulting word with a parity bit will always have an even
(for even parity) or odd (for odd parity) number of 1 bits in it.
If a single bit is flipped in transmission or storage,
the received data will have the wrong parity,
so we will know something bad has happened.
Note that we can’t tell which bit was corrupted
(or if it was just the parity bit that was corrupted).
Double errors go undetected, triple errors get
detected, quadruple errors don’t, etc.
Random garbage has a 50% probability of being accepted as valid.
Overhead is small; if we put a parity bit on each byte,
add 1 bit for each 8, so data transmitted or stored grows
by 12.5%. Larger words reduce the overhead: 16 bit words: 6.25%,
32 bit words: 3.125%, 64 bit words: 1.5625%.
Original data plus correction bits form a codeword.
The codeword, generally larger than the original data,
is used as the representation for that data for transmission
or storage purposes.
An ordered pair notation is often used, (c,d) represents
a codeword of c bits encoding a data word of d bits.
Error correcting codes
What if just detecting errors isn’t enough?
What if we want to find and fix the bad data.
Brute force repetition
Can repeat each bit three times:
00011011 becomes 000 000 000 111 111 000 111 111
Any single bit error can be corrected; just take
a majority vote on each group of three.
Double errors within a group will still corrupt the data.
Overhead is large; 8 bits became 24; 200% increase in data size.
Can extend to correct even more errors;
repeat each bit 5 times to correct up to 2 errors per group,
but even more overhead.
More efficient approaches to single error correction
Just repeating the bits is fairly inefficient.
We could do better if we could have a compact
way to figure out which bit got flipped (if any).
As the number of bits in a word gets large,
things are going to get very complicated very fast.
We need some systematic way to handle things.
Hamming distance
A key issue in designing any error correcting code
is making sure that any two valid codewords
are sufficiently dissimilar so that corruption of
a single bit (or possibly a small number of bits)
does not turn one valid code word into another.
To measure the distance between two codewords, we just
count the number of bits that differ between them.
If we are doing this in hardware or software,
we can just XOR the two codewords and count
the number of 1 bits in the result.
This count is called the Hamming distance
(Hamming, 1950).
The key significance of the hamming distance is that if two
codewords have a Hamming distance of d between them,
then it would take d single bit errors to turn one
of them into the other.
For a set of multiple codewords, the Hamming distance of the
set is the minimum distance between any pair of its members.
Minimum Hamming distance for error detection
To design a code that can detect d single bit errors,
the minimum Hamming distance for the set of codewords
must be d + 1 (or more).
That way, no set of d errors in a single bit
could turn one valid codeword into some other valid codeword.
Minimum Hamming distance for error correction
To design a code that can correct d single bit errors,
a minimum distance of 2d + 1 is required.
That puts the valid codewords so far apart that even after
bit errors in d of the bits, it is still less
than half the distance to another valid codeword,
so the receiver will be able to determine what the
correct starting codeword was.
Pracical Hamming implementation
Here are a few useful references (all PDF format):
- Error Correction with Hamming Codes
- Calculating the Hamming Code
- Applying Hamming Code to blocks of data
Get this book -> Problems on Array: For Interviews and Competitive Programming
In this article, we are going to explore about error detection in computer networks. We will be seeing some standard error detecting codes which help in detecting errors. So let’s get started.
Table of contents:
- Introduction to Error
- TYPES OF ERROR
- ERROR DETECTING CODES
- Simple parity check
- Two dimensional parity check
- Checksum
- Cyclic redundancy check
Introduction to Error
Error as we all know is a situation when message received is not identical as compared to error sent. It is very important to detect the error for proper and perfect transfer of information and message. There are basically two types of errors in computer network which needs to be detected and corrected.
TYPES OF ERROR
SINGLE BIT ERROR:
As the name suggests, in this type of error only one or single bit is changed from 0 to 1 or from 1 to 0. Let’s take an example:
Suppose the message that is to be sent is 000100 and the message received is 001100. So the bit(bolder part) is changed from 0 to 1 as we can see that there is only single bit error.
BURST ERROR:
In this type of error, more than one bits are changed from 0 to 1 or from 1 to 0. Simply we can say that when there is error in multiple bits then it is known as a burst error. Let’s take an example:
Suppose the message that is to be sent is 0100010001000011 and the message received is 0101110101100011. The important thing in this type of error is that we take the length of burst error from first corrupted bit to last corrupted bit. So for this message length of burst error will be 8(bits in bold).
In networking, error detection refers to the techniques used to detect noise or other impairments introduced into data while it is transmitted from sender to receiver. Error detection ensures reliable delivery of data across vulnerable networks. It minimizes the probability or possibility of passing incorrect data frames to the receiver, known as undetected error probability. So if we define error detection in very simple words then it would be like, error detection is nothing but to identify errors in networks. When a message is sent, it may be jumbled by noise or the data may be damaged. To avoid this, we employ error-detecting codes, which are bits of extra data appended to a digital message to assist us detect whether an error occurred during transmission. So there are various error detecting codes or techniques that detect the errors in computer networks. We will explore each of them in brief and see how they detect errors, how they work etc.
ERROR DETECTING CODES
Generally there are four basic error detecting codes in computer networks. They are:
- Simple parity check
- Two dimensional parity check
- Checksum
- Cyclic redundancy check
SIMPLE PARITY CHECK
Simple parity check code is the most basic and easiest error detecting code. In this code, a k-bit data word is changed to an n-bit code word where n = k + 1. There is an extra bit which is known as parity bit which is use to make the number of 1’s(ones) in a code word to be even. Although some implementations specify an odd number of 1s. The minimum Hamming distance for this category is 2, which means that the code is a single-bit error-detecting code and that’s why it is also known as single parity check. It does not correct errors.
WORKING:
In this technique there is an encoder at sender side and a decoder at receiver side. The encoder encodes the message or code word and at first it will check total number of 1’s or number of 0’s in the original message. If there are even number of 1’s in the message then we will add 0 at the end of original message, otherwise we will add 1 at the end to make total number of 1’s as even. This process of making number of 1’s even is known as even parity. The bit to be added at the end is known as parity bit. Now that appended message is sent to receiver.
At the receiver side, decoder decodes the received message and if the transmission was correct there will be no error and the message will be identical at the receiver side as sent by the sender. But if the transmission is incorrect it will detect the error by checking the parity bit.
ADVANTAGES:
- It is very easy to use and implement.
- It can detect single bit errors which help in smaller networks.
- It takes less amount of time in detecting errors as compared to other error detecting codes.
DISADVANTAGES:
- The major issue with this technique is that it can detect only single bit errors.
- If there is error in two bits then it is unable to work properly.
- It does not provide the facility of error correction.
Two dimensional parity check
As we have seen above single parity check is easy but not very beneficial. So two dimensional parity check is an upgraded version of single parity check. Performance can be improved by using this technique, which organizes the block of bits in the form of a table. It can detect as well as correct one or more bit errors.
WORKING:
In this, we will maintain a matrix by putting message in different rows. Then as we have done in single parity check technique, here also we will add a parity bit according to number of 1’s and 0’s. If there are even number of 1’s in the message then we will add 0 at the end of original message, otherwise we will add 1 at the end to make total number of 1’s as even. This process is done for every rows and columns of the matrix. Now in this way, we will generate a new bit(from columns) so now we will sent appended bits and new bit to the receiver. Receiver detects error by checking the parity bit and if there is no problem while transmission then there will be no error otherwise it will detect the error.
ADVANTAGES:
- It will detect and correct one or more bit errors.
- It is more efficient as compared to single parity check.
- The performance of this technique is very good as it is an upgraded version of simple parity check.
DISADVANTAGES:
- In some cases, an only odd number of bit errors can be detected and corrected but even number of errors can only be detected but not corrected.
- This method is unable to detect even no bit error.
CHECKSUM
A checksum is a sequence of numbers and letters used to check data for errors. It is a technique which is used to detect errors in computer networks. The checksum is used in the internet by several protocols although not at the data link layer.
WORKING:
We will see the working and approach of checksum error detection.
CHECKSUM GENERATOR —
Starting with sender side, checksum generator divides code word into smaller units of equal length of p bits. After that they are added to get a new code word using one’s complement method. This result is also of p bits and this is again complemented. The complemented result is called as checksum. The checksum is added at the end of original code word and then that code word generated is transferred to the receiver.
CHECKSUM CHECKER —
Now at receiver side, the data received along with checksum is transmitted to checksum checker. Then these data which is received is divided into equal smaller units and then the final result is complemented. If this answer is zero which means that there is no error, otherwise error can be detected.
ADVANTAGES:
Checksum error detection code or technique helps in detecting errors which have even number of bits or odd number of bits.
DISADVANTAGES:
This code does not detect errors which is present in subunits so it becomes problematic when we transmit information further as it is unable to detect these errors.
CYCLIC REDUNDANCY CHECK
This code is also known as CRC. The cyclic redundancy check (CRC) is a technique used to detect errors in digital data. CRC produces a fixed-length data set based on the build of a file or larger data set. CRC is used in storage devices like hard disks etc. CRC is based on binary division and is also called polynomial code checksum.
WORKING:
In this technique, at sender side (k-1) zeros are appended at the end of original code word. Now this newly generated code word is divided by key that is formed by generator polynomial. Generator polynomial is something like a normal equation like x3+x+1 or x2+1. For x3+x+1 key will be 1011 and for
x2+1 key will 101. Now according to generator polynomial key will be there and we divide appended code word with the key. The division operation used here will be the standard arithmetic division. The remainder obtained after this division is known as CRC remainder. Finding this remainder we will append this remainder in the appended code word which was obtained at the starting.
At receiver side, the newly data generated was transmitted at receiver side and again we will perform the same division as we have done above. If the remainder comes out be zero then there will be no errors otherwise it will detect errors.
ADVANTAGES:
- This is just a simple code and can be produced and implemented in any form of applications.
- It can easily view single bit errors and multiple burst errors.
- CRC is very simple to implement in binary hardware and it is good in detecting errors caused by noise in transmission.
DISADVANTAGES:
- It is not suitable for protecting data.
- In this there is a high possibility of data overflow.
So now we have explored and discussed every aspect of error detection in computer networks. We have seen all the error detection codes their working, advantages and disadvantages. Now i would like to conclude this article with a hope that you all who are reading this article will definitely study this topic.
Thank you.
Happy reading.
Improve Article
Save Article
Improve Article
Save Article
Error Detection Codes :
The binary information is transferred from one location to another location through some communication medium. The external noise can change bits from 1 to 0 or 0 to 1.This changes in values are called errors. For efficient data transfer, there should be an error detection and correction codes. An error detection code is a binary code that detects digital errors during transmission. A famous error detection code is a Parity Bit method.
Parity Bit Method :
A parity bit is an extra bit included in binary message to make total number of 1’s either odd or even. Parity word denotes number of 1’s in a binary string. There are two parity system-even and odd. In even parity system 1 is appended to binary string it there is an odd number of 1’s in string otherwise 0 is appended to make total even number of 1’s.
In odd parity system, 1 is appended to binary string if there is even a number of 1’s to make an odd number of 1’s. The receiver knows that whether sender is an odd parity generator or even parity generator. Suppose if sender is an odd parity generator then there must be an odd number of 1’s in received binary string. If an error occurs to a single bit that is either bit is changed to 1 to 0 or O to 1, received binary bit will have an even number of 1’s which will indicate an error.
The limitation of this method is that only error in a single bit would be identified.
| Message (XYZ) | P(Odd) | P(Even) |
|---|---|---|
| 000 | 1 | 0 |
| 001 | 0 | 1 |
| 010 | 0 | 1 |
| 011 | 1 | 0 |
| 100 | 0 | 1 |
| 101 | 1 | 0 |
| 110 | 1 | 0 |
| 111 | 0 | 1 |
Figure – Error Detection with Odd Parity Bit
Points to Remember :
- In 1’s complement of signed number +0 and -0 has two different representation.
- The range of signed magnitude representation of an 8-bit number in which 1-bit is used as a signed bit as follows -27 to +27.
- Floating point number is said to be normalized if most significant digit of mantissa is one. For example, 6-bit binary number 001101 is normalized because of two leading 0’s.
- Booth algorithm that uses two n bit numbers for multiplication gives results in 2n bits.
- The booth algorithm uses 2’s complement representation of numbers and work for both positive and negative numbers.
- If k-bits are used to represent exponent then bits number = (2k-1) and range of exponent = – (2k-1 -1) to (2k-1).