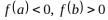Данные пособия являются тестами по численным методам для подготовки к экземенам, проработки численных методов. Подойдет как для студентов ВУЗов, так и для преподователей для организации тестирования в колледжах, ВУЗах.
Тесты по численным методам с ответами вы можете как скачать бесплатно и без регистрации, так и просмотреть ниже. Внимание, правильный ответ везде А!
1)Приближенным числом а называют число, незначительно отличающиеся от
a) точного А
b) неточного А
c) среднего А
d) точного не известного
e) приблизительного А
2) а называется приближенным значением А по недостатку, если
a) а < A
b) a > A
c) a = A
d) a ≥ A
e) a ≤ A
3) а называется приближенным значением числа А по избытку, если
a) a > A
b) a < A
c) a = A
d) a ≥ A
e) a ≤ A
Под ошибкой или погрешностью ∆а приближенного числа а обычно понимается разность между соответствующим точным числом А и данным приближением, т.е.
a) ∆а = А — а
b) ∆а = А + а
c) ∆а = А/а
d) а = ∆а — А
e) А = ∆а + А
7) Если ошибка положительна А>, то
a) ∆a > 0
b) ∆a < 0
c) ∆a = 0
d) ∆a ≤ 0
e) a > a

a) ∆ = ׀∆а׀
b) ∆а = а
c) ∆ = ׀а׀
d) А = ׀∆а׀
e) ∆а = ׀∆в׀
9) Абсолютная погрешность
a) ∆ = ׀А — а׀
b) ∆А = а
c) ∆ = ׀В — а׀
d) а = ׀А + а׀
e) ∆а = ׀А + в׀
10) Предельную абсолютную погрешность вводят если
a) число А не известно
b) число а не известно
c) ∆ не известно
d) А – а не известно
e) не известно В
11) Предельная абсолютная погрешность
a) ∆а
b) ∆в
c) ∆А
d) А
e) А
12) Определить предельную абсолютную погрешность числа а = 3,14, заменяющего число π
a) 0,002
b) 0,001
c) 3,141
d) 0,2
e) 0,003
13) Относительная погрешность
a) σ = ∆/׀А׀
b) σ = ∆
c) σ = ∆/в
d) σ = с/а
e) σ = а – А
14) Погрешность, связанная с самой постановкой математической задачи
a) погрешность задачи
b) погрешность метода
c) остаточная погрешность
d) погрешность действия
e) начальная
15) Погрешности, связанная с наличием бесконечных процессов в математическом анализе
a) остаточная погрешность
b) абсолютная
c) относительная
d) погрешность условия
e) начальная погрешность
16) Погрешности, связанные с наличием в математических формулах, числовых параметров
a) начальном
b) конечной
c) абсолютной
d) относительной
e) остаточной
17) Погрешности, связанные с системой счисления
a) погрешность округления
b) погрешность действий
c) погрешности задач
d) остаточная погрешность
e) относительная погрешность
18) Округлить число π = 3,1415926535… до пяти значащих цифр
a) 3,1416
b) 3,1425
c) 3,142
d) 3,14
e) 0,1415
19) Абсолютная погрешность при округлении числа π до трёх значащих цифр
a) 0,5*10-2
b) 0,5*10-3
c) 0,5*10-4
d) 0,5*10-1
e) 0,5
20) Предельная абсолютная погрешность разности
a) ∆u=∆x1+∆x2
b) ∆u=a+b
c) ∆u=A+b
d) ∆=x1+x2
e) ∆a=b+c
21) Числовой ряд названия сходящимся, если
a) существует предел последовательности его частных сумм
b) можно найти сумму ряда
c) существует последовательность
d) частные суммы равны нулю
e) существует предел разности
24) Найти ln3 c точностью до 10-5
a) 1,09861
b) 1,01
c) 1,098132
d) 1,02
e) 1,3
25) Найти sin 20030I
a) 0,35
b) 0,36
c) 0,2
d) 0,47
e) 0,5
26) Найти tg 400
a) 0,839100
b) 0,84
c) 0,9
d) 1,0
e) 1,2
27) С помощью этого метода число верных цифр примерно удваивается на каждом этапе по сравнению с первоначальным количеством
a) процесс Герона
b) формула Тейлора
c) формула Маклорена
d) метод Крамера
e) процесс Даломбера
Методом половинного деления уточнить корень уравнения х4+2х3-х-1=0
a) 0,867
b) 0,234
c) 0,2
d) 0,43
e) 0,861
31) Используя метод хорд найти положительный корень уравнения х4-0,2х2-0,2х-1,2=0
a) 1,198+0,0020
b) 1,16+0,02
c) 2+0,1
d) 3,98+0,001
e) 4,2+0,0001
32) Вычислить методом Ньютона отрицательный корень уравнения х4-3х2+75х-10000=0
a) −10,261
b) −10,31
c) −5,6
d) −3,2
e) −0,44
33) Используя комбинированный метод вычислить с точностью до 0,005 единственный положительный корень уравнения
a) 1,04478
b) 1,046
c) 2,04802
d) 3,45456
e) 802486
34) Найти действительные корни уравнения х-sinх=0,25
a) 1,17
b) 1,23
c) 2,45
d) 4,8
e) 5,63
35) Определить число положительных и число отрицательных корней уравнения х4-4х+1=0
a) 2 и 0
b) 3 и 2
c) 0 и 4
d) 0 и 1
e) 0 и 4
36) Определить нижнее число и верхнее число перемен знаков в системе 1, 0, 0, -3, 1.
a) 2 и 4
b) 3 и 1
c) 0 и 4
d) 0 и 5
e) 3 и 2
37) Определить состав корней уравнения х4+8х3-12х2+104х-20=0
a) один положительный и один отрицательный
b) нет ни одного корня
c) невозможно найти число корней
d) уравнение не имеет положительных корней
e) два отрицательных корня
38) Две матрицы одного и того же типа, имеющие одинаковое число строк и столбцов, и соответствующие элементы их равны, называют
a) равными
b) одинаковыми
c) разными по рангу
d) схожими
e) транспонированными
39) Укажите свойства суммы матриц А+(В+С)=…
a) (А+В)+С
b) (В+А)*С
c) АВС
d) А+В+С*А
e) А*С+В*С
40) Укажите название матрицы –А=(-1)А
a) противоположная
b) обратная
c) равная
d) матрица не существует
e) транспонированная
41) Заменив в матрице типа m×n строки соответственно столбцами получим
a) транспонированную матрицу
b) равную матрицу
c) среднюю матрицу
d) обратную матрицу
e) квадратную матрицу
42) С какой матрицей совпадает дважды транспонированная матрица
a) с исходной
b) с обратной
c) с нулевой
d) с единичной
e) с квадратной
43) Нахождение обратной матрицы для данной называется
a) обращение данной матрицы
b) транспонированием
c) суммой матриц
d) заменой строк и столбцов
e) произведением матриц
44) Максимальный порядок минора матрицы, отличного от нуля, называют
a) рангом
b) пределом
c) рядом
d) сходимостью
e) определителем
45) Разность между наименьшим из чисел m и n и рангом матрицы называется
a) дефектом
b) пределом
c) рангом
d) определителем
e) разницей
46) Существующие и имеющие важное значение матричные степенные ряды
a) правые и левые
b) средние
c) верхние и нижние
d) высокие
e) дифференцируемые
47) Матричные ряды дают возможность определять
a) трансцендентные функции матрицы
b) миноры матричного ряда
c) сходящиеся ряды
d) геометрические прогрессии
e) каноническую форму ряда
48) Матрица разбитая на клетки, называется клеточной и …
a) блочной
b) равной
c) окаймленной
d) квазидиагональной
e) средней
49) Если элементы квадратной матрицы, стоящие выше (ниже) главной диагонали, равны нулю, то матрицу называют
a) треугольной
b) нулевой
c) диагональной
d) такая матрица не существует
e) единичной
50) Метод, представляющий собой конечные алгоритмы для вычисления корней системы
a) точный метод
b) метод релаксации
c) метод итерации
d) приближенный метод
e) относительный метод
51) Метод позволяющий получить корни системы с заданной точностью путем сходящихся бесконечных процессов
a) итерационный метод
b) точный метод
c) приближенный метод
d) относительный метод
e) метод Зейделя
52) Этот метод является наиболее распространенным приемом решения систем линейных уравнений, алгоритм последовательного исключения неизвестных
a) метод Гаусса
b) метод Крамера
c) метод обратный матриц
d) ведущий метод
e) аналитический метод
53) Целый однородный полином второй степени от n переменных называется
a) квадратичной формой
b) кубической формой
c) прямоугольной формой
d) треугольной формой
e) матричной формой
54) Квадратичная форма называется положительно (отрицательно) определенной, если она принимает положительные (отрицательные) значения, обращаясь в нуль лишь при
a) х1=х2=…=хn=0
b) х1+х2+…+хn=0
c) х1х2…хn=0
d) a+b+c+…=0
e) х1+х2+…+хn=5
55) Простейшая форма этого метода заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения
a) метод ослабления
b) итерационный метод
c) метод обратных матриц
d) ведущий метод
e) метод Гаусса
56) Произведением вектора х=(х1,х2,…,хn) на число k называется вектор
a) kx=(kx1,kx2,…kxn)
b) k=x1+x2+…xn
c) ab=x1+x2+…+xn
d) нельзя вектор умножать на число
e) с=a+b
57) Для векторов x и y естественно определяется линейная комбинация
a) αх+βy
b) αx*βy
c) αx/βy
d) x+y=о
e) (x+y)α=о
58) Любая совокупность n-мерных векторов, рассматриваемая с установленными в ней операциями сложения векторов и умножения вектора на число, не выводящими за пределы этой совокупности называется
a) линейным векторным пространством
b) плоскостью векторов
c) скалярным произведением векторов
d) суммой векторов
e) сходимостью векторного пространства
59) Максимальное число линейно независимых векторов n-мерного пространства Еn в точности равно
a) размерности этого пространства
b) соразмерности векторов
c) сумме линейных векторов
d) совокупности единичных векторов
e) сумме n векторов
60) Название любой совокупности n линейно независимых векторов n-мерного пространства
a) базис
b) орт
c) вектор
d) координата
e) скаляр
61) Как иначе называют метод бисекций?
a) Метод половинного деления
b) Метод хорд
c) Метод пропорциональных частей
d) Метод «начального отрезка»
e) Метод коллокации
62) Методы решения уравнений делятся на:
a) Прямые и итеративные
b) Прямые и косвенные
c) Начальные и конечные
d) Определенные и неопределенные
e) Простые и сложные
63) Кто опубликовал формулу для решения кубического уравнения?
a) Кардано
b) Галуа
c) Абеле
d) Дарбу
e) Фредгольм
64) Основная теорема алгебры:
a) Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k-кратный корень считать за k корней
b) Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
c) Если функция f(x) монотонна на отрезке [α;b], то она интегрируема на этом отрезке
d) Если функция f(x) монотонна на отрезке [α;b], то она дифференцируема на этом отрезке
e) Определитель D=|αij| n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения
65) Отделение корней можно выполнить двумя способами:
a) аналитическим и графическим
b) приближением и отделением
c) аналитическим и систематическим
d) систематическим и графическим
e) приближением последовательным и параллельным
66) Укажите первую теорему Больцано-Коши:
a) Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
b) Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k-кратный корень считать за k корней
c) Если функция f(x) монотонна на отрезке [α;b], то она интегрируема на этом отрезке
d) Если функция f(x) монотонна на отрезке [α;b], то она дифференцируема на этом отрезке
e) Определитель D=|αij| n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения
67) Отделим корни уравнения х3 – 2х – 3=0
a) Единственный корень расположен между √⅔ и ∞
b) Корней нет
c) Один из корней находится на отрезке [1,2]
d) Один из корней находится на отрезке [-1,2]
e) Единственный корень расположен между √⅛ и √⅜
68) При контроле решения алгебраического уравнения может быть полезна:
a) Теорема Виета
b) Теорема Ньютона
c) Теорема Перрона
d) Теорема Штурма
e) Теорема Бюдана-Фурье
69) Итерация iteratio в переводе с латинского:
a) повторение
b) замещение
c) возвращение
d) умножение
e) удаление
70) Укажите рекуррентную формулу метода простой итерации:
a) хn+1=φ(хn)
b) х=φ
c) х=C
d) хn+1=ψ(хn)+φ(хn)
e) хn-1=ψ(хn)-φ(хn)
71) От латинского слова recurrens:
a) возвращающийся
b) меняющийся
c) повторяющийся
d) заменяющийся
e) приближающийся
72) Последовательность, удовлетворяющая условию Коши, называется:
a) фундаментальной последовательностью
b) рекуррентной последовательностью
c) итеративной последовательностью
d) двусторонней последовательностью
e) односторонней последовательностью
Метод хорд-
a) Частный случай метода итераций
b) Частный случай метода коллокации
c) Частный случай метода прогонки
d) Частный случай метода квадратных корней
e) Частный случай метода Гаусса
75) Свойство самоисправляемости:
a) Усиливает надежность метода
b) Не влияет на конечный результат
c) Влияет на конечный результат
d) Не учитывается
e) Считается ошибочным
76) Как иначе называют метод Ньютона?
a) Метод касательных
b) Метод коллокации
c) Метод прогонки
d) Метод итераций
e) Метод хорд
77) Как иначе называют метод хорд?
a) Метод пропорциональных частей
b) Метод касательных
c) Метод коллокации
d) Метод бисекций
e) Метод квадратных корней
78) Метод хорд имеет еще одно имя:
a) Метод пропорциональных частей
b) Метод касательных
c) Метод бисекций
d) Метод коллокации
e) Метод прогонки
79) Что общего у метода хорд и метода итераций?
a) Общая скорость и свойство самоисправляемости
b) Свойство самоисправляемости
c) Общая скорость
d) Легкость при решении
e) Требуется нахождение производной
80) Метод Ньютона-
a) обладает свойством самоисправляемости и имеет высокую скорость сходимости
b) дает большой выигрыш во времени
c) занимает очень много времени
d) предельно прост
e) надежен
81) Методом хорд уточнить корень уравнения х3 – 2х – 3=0, ξ[1;2]; ε=10-3
a) ξ=1.8933±0.0001
b) ξ=0.0001±1
c) ξ=0.0033±0.0001
d) ξ=±1
e) ξ=±3.3
82) Если точка движется равномерно υ(t)=υ=const, то ответ готов:
a) S=υ(T2 — T1)
b) S=0
c) υ= υ0+at
d) υ=s/t
e) S= υ0t+ at2/2
83) Предел суммы S ≈ υ(τ1)∆t1+υ(τ2)∆t2+…+υ(τn)∆tn называется:
a) Определенным интегралом
b) Неопределенным интегралом
c) Рекуррентной формулой
d) Формулой численного дифференцирования
e) Схемой Халецкого
84) Если сила постоянна, ответ дается формулой:
a) A=F(b-
b) A=F(a-
c) F=const
d) A=0
e) F=ma
85) Все методы вычисления интегралов делятся на:
a) Точные и приближенные
b) Прямые и итеративные
c) Прямые и косвенные
d) Аналитические и графические
e) Приближенные и систематические
86) Точный метод вычисления интегралов был предложен:
a) Ньютоном и Лейбницем
b) Ньютоном и Гауссом
c) Гауссом и Стирлингом
d) Вольтерром
e) Гауссом и Крамером
87) Геометрически нижняя сумма Дарбу равна:
a) Площади ступенчатого многоугольника, содержащегося в криволинейной трапеции
b) Площади ступенчатого многоугольника, содержащего внутри себя криволинейную трапецию
c) Площади прямоугольного параллелепипеда
d) Площади ступенчатого шестиугольника
e) Площади ступенчатого прямоугольника
88) Геометрически верхняя сумма Дарбу равна:
a) Площади ступенчатого многоугольника, содержащего внутри себя криволинейную трапецию
b) Площади ступенчатого многоугольника, содержащегося в криволинейной трапеции
c) Площади прямоугольного параллелепипеда
d) Площади ступенчатого шестиугольника
e) Площади ступенчатого прямоугольника
89) Приближенные методы вычисления интегралов можно разделить на 2 группы:
a) аналитические и численные
b) аналитические и графические
c) систематические и численные
d) систематические и случайные
e) приближенные и неприближенные
конец тестов по численным методам, правильный ответ везде А
Численные методы решения инженерных задач
- Зачет/Экзамен
а называется приближенным значением числа А по избытку, если
Выберите один ответ:
- a
- a = A
- a > A
- a ≤ A
- a ≥ A
Абсолютная погрешность при округлении числа π до трёх значащих цифр
Выберите один ответ:
- 0,5
- 0,5*10-1
- 0,5*10-2
- 0,5*10-3
- 0,5*10-4
Абсолютная погрешность это
Выберите один ответ:
- а = ׀А + а׀
- ∆ = ׀А — а׀
- ∆ = ׀В — а׀
- ∆А = а
- ∆а = ׀А + в׀
Вметоде Гаусса линейная система решается
Выберите один ответ:
- в два этапа
- в один этап
- в три этапа
Все методы вычисления интегралов делятся на:
Выберите один ответ:
- Аналитические и графические
- Приближенные и систематические
- Прямые и итеративные
- Прямые и косвенные
- Точные и приближенные
Вычислительный алгоритм должен быть:
Выберите один ответ:
- быть эффективным по времени выполнения и экономичным по требуемым объемам памяти, а также не допускать аварийных остановов
- удовлетворять всем перечисленным выше требованиям
- устойчивым к ошибкам и обеспечивать требуемую точность
Вычислить методом Ньютона отрицательный корень уравнения х4-3х2+75х-10000=0
Выберите один ответ:
- −0,44
- −10,261
- −10,31
- −3,2
- −5,6
Геометрически верхняя сумма Дарбу равна:
Выберите один ответ:
- Площади прямоугольного параллелепипеда
- Площади ступенчатого многоугольника, содержащего внутри себя криволинейную трапецию
- Площади ступенчатого многоугольника, содержащегося в криволинейной трапеции
- Площади ступенчатого прямоугольника
- Площади ступенчатого шестиугольника
Две матрицы одного и того же типа, имеющие одинаковое число строк и столбцов, и соответствующие элементы их равны, называют
Выберите один ответ:
- одинаковыми
- равными
- разными по рангу
- схожими
- транспонированными
Если ошибка положительна А>, то
Выберите один ответ:
- a> a
- ∆a = 0
- ∆a ≤ 0
- ∆a < 0
- ∆a > 0
Если элементы квадратной матрицы, стоящие выше (ниже) главной диагонали, равны нулю, то матрицу называют
Выберите один ответ:
- диагональной
- единичной
- нулевой
- такая матрица не существует
- треугольной
Заменив в матрице типа m×n строки соответственно столбцами получим
Выберите один ответ:
- квадратную матрицу
- обратную матрицу
- равную матрицу
- среднюю матрицу
- транспонированную матрицу
Интерполяционные функции строятся, как правило, в виде
Выберите один ответ:
- линейной комбинации некоторых линейно-независимых элементарных функций
- линейной комбинации некоторых нелинейно-независимых элементарных функций
- нелинейной комбинации некоторых линейно-независимых элементарных функций
Интерполяция – это…
Выберите один ответ:
- Замена одних математических объектов другими, в том или ином смысле близким к исходным.
- Метод решения задач, при котором объекты разного рода объединяются общим понятием.
- Продолжение функции, принадлежащей заданному классу, за пределы ее области определения.
- Способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений
Итерация – это ….
Выберите один ответ:
- Замена одних математических объектов другими, в том или ином смысле близким к исходным
- Повторение. Результат повторного применения какой–либо математической операции
- Продолжение функции, принадлежащей заданному классу, за пределы ее
- Число, изображаемое единицей и 18 нулями
Итерацияiteratio в переводе с латинского:
Выберите один ответ:
- возвращение
- замещение
- повторение
- удаление
- умножение
К методам уточнения корней не относится …
Выберите один ответ:
- Метод аппроксимации
- Метод дихотомии
- Метод касательных
- Метод хорд
Как иначе называют метод бисекций?
Выберите один ответ:
- Метод «начального отрезка»
- Метод коллокации
- Метод половинного деления
- Метод пропорциональных частей
- Метод хорд
Как иначе называют метод Ньютона?
Выберите один ответ:
- Метод итераций
- Метод касательных
- Метод коллокации
- Метод прогонки
- Метод хорд
Как иначе называют метод хорд?
Выберите один ответ:
- Метод бисекций
- Метод касательных
- Метод квадратных корней
- Метод коллокации
- Метод пропорциональных частей
Кто опубликовал формулу для решения кубического уравнения?
Выберите один ответ:
- Абеле
- Галуа
- Дарбу
- Кардано
- Фредгольм
Любая совокупность n-мерных векторов, рассматриваемая с установленными в ней операциями сложения векторов и умножения вектора на число, не выводящими за пределы этой совокупности называется
Выберите один ответ:
- линейным векторным пространством
- плоскостью векторов
- скалярным произведением векторов
- суммой векторов
- сходимостью векторного пространства
Максимальное число линейно независимых векторов n-мерного пространства Еn в точности равно
Выберите один ответ:
- размерности этого пространства
- совокупности единичных векторов
- соразмерности векторов
- сумме n векторов
- сумме линейных векторов
Максимальный порядок минора матрицы, отличного от нуля, называют
Выберите один ответ:
- определителем
- пределом
- рангом
- рядом
- сходимостью
Метод Гаусса–Зейделя относится к
Выберите один ответ:
- итерационным методам
- методам численного интегрирования
- прямым методам
Метод Монте–Карло относится к
Выберите один ответ:
- итерационным методам
- методам численного интегрирования
- прямым методам
Метод позволяющий получить корни системы с заданной точностью путем сходящихся бесконечных процессов
Выберите один ответ:
- итерационный метод
- метод Зейделя
- относительный метод
- приближенный метод
- точный метод
Метод хорд имеет еще одно имя:
Выберите один ответ:
- Метод бисекций
- Метод касательных
- Метод коллокации
- Метод прогонки
- Метод пропорциональных частей
Метод Эйлера решения обыкновенных дифференциальных уравнений является методом
Выберите один ответ:
- второго порядка
- первого порядка
- третьего порядка
Метод, представляющий собой конечные алгоритмы для вычисления корней системы
Выберите один ответ:
- метод итерации
- метод релаксации
- относительный метод
- приближенный метод
- точный метод
Методы Адамса решения обыкновенных дифференциальных уравненийотносятся к
Выберите один ответ:
- многошаговым методам
- одношаговым методам
- прямым методам
МетодLU-факторизации характеризуется такими же оценками нормы матрицы возмущения и относительной ошибки, как:
Выберите один ответ:
- метод Гаусса
- метод Ньютона
- метод Симпсона
Найти действительные корни уравнения х-sin(х)=0,25
Выберите один ответ:
- 1,17
- 1,23
- 2,45
- 4,8
- 5,63
Нахождение обратной матрицы для данной называется
Выберите один ответ:
- заменой строк и столбцов
- обращение данной матрицы
- произведением матриц
- суммой матриц
- транспонированием
Невязка – это…
Выберите один ответ:
- Значение разностей между свободными членами исходной системы и результатами подстановки в уравнения системы найденных значений неизвестных
- Значение разностей между свободными членами исходной системы
- Значение суммы между свободными членами исходной системы и результатами подстановки в уравнения системы найденных значений неизвестных
- Значение суммы результатов подстановки в уравнения системы найденных значений неизвестных
Недостатком интерполяционной формулы Лагранжа является
Выберите один ответ:
- каждое слагаемое зависит от всех узлов интерполяции
- каждое слагаемое не зависит от всех узлов интерполяции
- повышение порядка полинома
неявный метод Адамса четвертого порядка является
Выберите один ответ:
- двухшаговым методом
- одношаговым методом
- трехшаговым методом
Округлить число π = 3,1415926535… до пяти значащих цифр
Выберите один ответ:
- 0,1415
- 3,14
- 3,1416
- 3,142
- 3,1425
Определить предельную абсолютную погрешность числа а = 3,14, заменяющего число π
Выберите один ответ:
- 0,001
- 0,002
- 0,003
- 0,2
- 3,141
Определить состав корней уравнения х4+8х3-12х2+104х-20=0
Выберите один ответ:
- два отрицательных корня
- невозможно найти число корней
- нет ни одного корня
- один положительный и один отрицательный
- уравнение не имеет положительных корней
Определить число положительных и число отрицательных корней уравнения х4-4х+1=0
Выберите один ответ:
- 0 и 1
- 0 и 4
- 0 и 4
- 2 и 0
- 3 и 2
От латинского слова recurrens:
Выберите один ответ:
- возвращающийся
- заменяющийся
- меняющийся
- повторяющийся
- приближающийся
Отделение корней можно выполнить двумя способами:
Выберите один ответ:
- аналитическим и графическим
- аналитическим и систематическим
- приближением и отделением
- приближением последовательным и параллельным
- систематическим и графическим
Относительная погрешность
Выберите один ответ:
- σ = а – А
- σ = с/а
- σ = ∆
- σ = ∆/в
- σ = ∆/׀А׀
Погрешности, связанные с наличиемв математических формулах, числовых параметров
Выберите один ответ:
- абсолютной
- конечной
- начальном
- остаточной
- относительной
Погрешности, связанные с системой счисления
Выберите один ответ:
- остаточная погрешность
- относительная погрешность
- погрешности задач
- погрешность действий
- погрешность округления
Погрешности,связанные с наличием бесконечныхпроцессов вматематическом анализе
Выберите один ответ:
- абсолютная
- начальная погрешность
- остаточная погрешность
- относительная
- погрешность условия
Последовательность, удовлетворяющая условию Коши, называется:
Выберите один ответ:
- двусторонней последовательностью
- итеративной последовательностью
- односторонней последовательностью
- рекуррентной последовательностью
- фундаментальной последовательностью
Предельная абсолютная погрешность разности
Выберите один ответ:
- ∆=x1+x2
- ∆a=b+c
- ∆u=a+b
- ∆u=A+b
- ∆u=∆x1+∆x2
Предельная абсолютная погрешность
Выберите один ответ:
- А
- ∆а
- ∆А
- ∆в
Предельную абсолютную погрешность вводят если
Выберите один ответ:
- А – а не известно
- не известно В
- число а не известно
- число А не известно
- ∆ не известно
При контроле решения алгебраического уравнения может быть полезна:
Выберите один ответ:
- Теорема Бюдана-Фурье
- Теорема Виета
- Теорема Ньютона
- Теорема Перрона
- Теорема Штурма
Приближенные методы вычисления интегралов можно разделить на 2 группы:
Выберите один ответ:
- аналитические и графические
- аналитические и численные
- приближенные и неприближенные
- систематические и случайные
- систематические и численные
Разность между наименьшим из чисел m и n и рангом матрицы называется
Выберите один ответ:
- дефектом
- определителем
- пределом
- разницей
- рангом
С какой матрицей совпадает дважды транспонированная матрица
Выберите один ответ:
- с единичной
- с исходной
- с квадратной
- с нулевой
- с обратной
Свойствосамоисправляемости:
Выберите один ответ:
- Влияет на конечный результат
- Не влияет на конечный результат
- Не учитывается
- Считается ошибочным
- Усиливает надежность метода
Способ арифметизации решения задачи
Выберите один ответ:
- Набор формул решения задачи.
- Способ получения числового результата
- Численный метод
- Численный подход к решению задачи
Точный метод вычисления интегралов был предложен:
Выберите один ответ:
- Вольтерром
- Гауссом и Крамером
- Гауссом и Стирлингом
- Ньютоном и Гауссом
- Ньютоном и Лейбницем
Укажите название матрицы –А=(-1)А
Выберите один ответ:
- матрица не существует
- обратная
- противоположная
- равная
- транспонированная
Укажите первую теорему Больцано-Коши:
Выберите один ответ:
- Если функция f(x) монотонна на отрезке [α;b], то она дифференцируема на этом отрезке
- Если функция f(x) монотонна на отрезке [α;b], то она интегрируема на этом отрезке
- Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
- Определитель D=|αij| n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения
- Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k-кратный корень считать за k корней
Условие устойчивости явных многошаговых методов Адамса накладывает существенные ограничения на величину
Выберите один ответ:
- погрешности интегрирования
- точности интегрирования
- шага интегрирования
Формула трапеций относится к
Выберите один ответ:
- итерационным методам
- методам численного интегрирования
- прямым методам
Целый однородный полином второй степени от n переменных называется
Выберите один ответ:
- квадратичной формой
- кубической формой
- матричной формой
- прямоугольной формой
- треугольной формой
Численный метод “бисекций” предназначен для решения задач:
Выберите один ответ:
- Линейного алгебраического уравнения.
- Нелинейного алгебраического уравнения.
- Системы алгебраических линейных уравнений.
- Системы алгебраических нелинейных уравнений.
Численный метод “Гаусса” предназначен для решения задач:
Выберите один ответ:
- Линейного алгебраического уравнения
- Нелинейного алгебраического уравнения
- Системы алгебраических линейных уравнений
- Системы алгебраических нелинейных уравнений
Численный метод “Зейделя” предназначен для решения задач:
Выберите один ответ:
- Вычисления определенного интеграла.
- Нелинейного алгебраического уравнения.
- Системы алгебраических линейных уравнений.
- Системы алгебраических нелинейных уравнений.
Численный метод “прямоугольников” предназначен для решения задач:
Выберите один ответ:
- Вычисления определенного интеграла
- Нелинейного алгебраического уравнения
- Системы алгебраических линейных уравнений
- Системы алгебраических нелинейных уравнений
Численный метод “Симпсона” предназначен для решения задач:
Выберите один ответ:
- Вычисления определенного интеграла
- Нелинейного алгебраического уравнения
- Системы алгебраических линейных уравнений
- Системы алгебраических нелинейных уравнений
Численный метод итераций определяет решение через нахождение:
Выберите один ответ:
- Координаты пересечения двух графиков
- Координаты пересечения касательной с осью Х
- Координаты пересечения хорды с осью Х
- Координаты средины отрезка где находится корень
Численный метод Ньютона определяет решение через нахождение:
Выберите один ответ:
- Координаты пересечения двух графиков
- Координаты пересечения касательной с осью Х
- Координаты пересечения хорды с осью Х
- Координаты средины отрезка где находится корень
Числовой ряд названия сходящимся, если
Выберите один ответ:
- можно найти сумму ряда
- существует последовательность
- существует предел последовательности его частных сумм
- существует предел разности
- частные суммы равны нулю
Экономичность алгоритма оценивается по требуемым для его реализации объемам
Выберите один ответ:
- быстродействия ЭВМ
- памяти ЭВМ
- скорости ЭВМ
Этот метод является наиболее распространенным приемом решения систем линейных уравнений, алгоритм последовательного исключения неизвестных
Выберите один ответ:
- аналитический метод
- ведущий метод
- метод Гаусса
- метод Крамера
- метод обратный матриц
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Г.Ф. МОРОЗОВА»
ЧИСЛЕННЫЕ МЕТОДЫ
Методические указания для самостоятельной работы студентов,
обучающихся по специальности 09.02.07 Информационные системы и программирование
Воронеж 2019
2
УДК 004.78: 656.13
Оксюта, О. В. Численные методы Электронный ресурс : методические указания для самостоятельной работы студентов, обучающихся по специальности 09.02.07 Информационные системы и программирование / О.В. Оксюта; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж,
2019. – 34 с.
Печатается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № от г.)
Рецензент доцент кафедры информационных технологий моделирования и управления Воронежского государственного университета инженерных технологий А.В. Лемешкин
3
4
Содержание
Рекомендации по распределению времени в процессе работы над заданиями
|
(трудоемкость заданий)………………………………………………………………………………. |
5 |
|
Методические указания по выполнению самостоятельной работы………………. |
5 |
|
Задания для самостоятельной работы …………………………………………………………. |
6 |
|
Критерии оценки выполненного задания…………………………………………………… |
20 |
|
Библиографический список ………………………………………………………………………. |
22 |
5
Рекомендации по распределению времени в процессе работы над заданиями (трудоемкость заданий)
Методические указания предназначены для упорядочивания самостоятельной работы обучающихся в процессе изучения дисциплины «Численные методы» (Тема 1. Источники и классификация погрешностей результата численного решения задачи. Тема 2. Приближенные решения алгебраических и трансцендентных уравнений. Тема 3. Решение систем линейных алгебраических уравнений. Тема 4. Интерполирование и экстраполирование функций. Тема 5. Численное интегрирование. Тема 6. Численное решение обыкновенных дифференциальных уравнений.).
Методические указания по выполнению самостоятельной работы
Методические указания содержат основные требования федерального государственного образовательного стандарта среднего профессионального образования, предъявляемые к знаниям обучающегося, задания в форме тестов для самопроверки и задания, предназначенные для формирования соответствующих практических умений и навыков.
Поскольку основная цель самостоятельной работы по данному разделу — закрепление теоретических знаний, предлагается следующая последовательность действий:
1.Работа с учебником (по каждой теме указаны необходимые для изучения страницы) и конспектом лекции, в результате чего у обучающегося должны сформироваться соответствующие знания и умения (их перечень приводится по каждой теме).
2.Работа в тетради для самостоятельной работы. Для закрепления теоретических знаний обучающийся должен записать в тетрадь определения, которые перечислены в пункте: должен знать.
3.Для самопроверки степени усвоения теоретических положений и выявления пробелов в подготовке обучающийся выполняет предложенное задание.
6
Задания для самостоятельной работы
Тема 1. Источники и классификация погрешностей результата численного решения задачи.
Обучающийся должен:
–знать, понятие приближенного числа; понятия абсолютной и относительной погрешностей; формулы вычисления погрешностей;
–уметь вычислять погрешность результатов арифметических действий. Рекомендуемая литература – 1о, с. 30-38, 1д, с. 158-167, 2д, с.25-45.
Задание для самопроверки
1. Опишите в тетради для самостоятельной работы:
Понятия абсолютной и относительной погрешностей и формулы их вычисления.
2. Выберите один из альтернативных ответов.
2.1. В чем выражается обычно относительная погрешность? а) в процентах (%)
б) в процентах на единицу (%/ед.) в) в штуках (шт)
г) в х (х)
2.2. Приближенным числом «а» называют число, незначительно отличающиеся от
a)точного А
b)неточного А
c)среднего А
d)точного не известного
e)приблизительного А
2.3. Предельная относительная погрешность произведения находится по формуле
а) (xy) x y б) (xy) x y в) (xy) x * y г) (xy) x / y
2.4. «а» называется приближенным значением А по недостатку, если а) а < A
б) a > A в) a = A
г) a ≥ A д) a ≤ A
7
2.5.«а» называется приближенным значением числа А по избытку, если а) a > A
б) a < A в) a = A
г) a ≥ A
д) a ≤ A
2.6.Под ошибкой или погрешностью ∆а приближенного числа «а» обычно понимается разность между соответствующим точным числом А и данным приближением, т.е.
а) ∆а = А – а б) ∆а = А + а в) ∆а = А/а г) а = ∆а – А д) А = ∆а + А
2.7.Если ошибка положительна А>0, то
а) ∆a > 0 б) ∆a < 0 в) ∆a = 0
г) ∆a ≤ 0
д) a > a
2.8.Абсолютная погрешность приближенного числа а) ∆ = ׀∆а׀ б) ∆а = а
в) ∆ = ׀а׀ г) А = ׀∆а׀ д) ∆а = ׀∆в׀
2.9.Абсолютная погрешность
а) ∆ = ׀А – а׀ б) ∆А = а
в) ∆ = ׀В – а׀ г) а = ׀А + а׀ д) ∆а = ׀А + в׀
2.10.Предельную абсолютную погрешность вводят если а) число А не известно б) число «а» не известно в) ∆ не известно г) А – а не известно д) не известно В
2.11.Предельная абсолютная погрешность
а) ∆а б) ∆в в) ∆А г) А
8
д) А
2.12.Погрешность, связанная с самой постановкой математической
задачи а) погрешность задачи
б) погрешность метода в) остаточная погрешность г) погрешность действия д) начальная
2.13.Погрешности, связанные с наличием бесконечных процессов в математическом анализе
а) остаточная погрешность б) абсолютная в) относительная
г) погрешность условия д) начальная погрешность
2.14.Погрешности, связанные с наличием в математических формулах, числовых параметров
а) начальная погрешность б) погрешность условия в) абсолютная г) относительная
д) остаточная погрешность
2.15.Погрешности, связанные с системой счисления
а) погрешность округления б) погрешность действий в) погрешности задач г) остаточная погрешность
д) относительная погрешность 2.16. Предельная абсолютная погрешность разности а) ∆u=∆x1+∆x2
б) ∆u=a+b в) ∆u=A+b г) ∆=x1+x2
д) ∆a=b+c
Тема 2. Приближенные решения алгебраических и трансцендентных уравнений.
Обучающийся должен:
– знать, методы определения корней алгебраических уравнений; алгоритм решения вычислительных задач методом хорд; алгоритм решения вычислительных задач методом касательных; алгоритм для решения
9
вычислительных задач методом половинного деления; определение точности получаемого результата.
– уметь решать алгебраические уравнения приближенными методами (метод хорд и касательных), решать алгебраические уравнения приближенными методами (метод половинного деления и итераций).
Рекомендуемая литература – 1о, с. 38-88; 1д, с. 168-175.
Задание для самопроверки
1.Опишите в тетради для самостоятельной работы:
Основные методы решения алгебраических уравнений.
2.Выберите один из альтернативных ответов.
2.1.В методе бисекции нахождения корней нелинейных уравнений за начальное приближение корня принимают
а) левую границу интервала изоляции корня б) правую границу интервала изоляции корня в) середину интервала изоляции корня г) 1/4 интервала изоляции корня
2.2.Какой из методов определения корней нелинейных уравнений всегда
сходится а) метод хорд
б) метод касательных в) метод бисекции
г) метод простой итерации
2.3.Искомый корень уравнения 
а) функция принимает положительные значения б) функция принимает отрицательные значения
в) функция принимает значения противоположных знаков г) функция стремится к бесконечности
2.4.Число итераций N , требуемое для достижения заданной точности 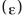
а) касательных б) хорд в) дихотомии
г) простой итерации
2.5.В каком из методов определения корней нелинейных уравнений
итерационный процесс нужно продолжить до достижения условия 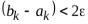
в) простой итерации
10
г) касательных
2.6.Формула 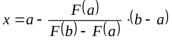
а) хорд б) бисекции
в) простой итерации г) касательных
2.7.Какой из методов нахождения корней нелинейных уравнений не
требует, чтобы функция 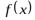
в) простой итерации г) касательных
2.8.При отыскании корня нелинейного уравнения в основе какого метода лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки
а) касательных б) хорд в) бисекции
г) простой итерации
2.9.В каком из методов вычисления корней нелинейных уравнений
уравнение 
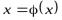
в) простой итерации г) касательных
2.10. По методу Ньютона условием существования решения нелинейного уравнения на отрезке [a, b] является
а) 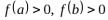

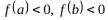
2.11. При решении нелинейного уравнения 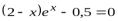
[1,5; 2,5] за начальное приближение корня принято 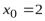
а) парабол б) дихотомии
в) простой итерации г) касательных
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1
Абсолютная
величина разности между точным и приближенным значениями числа называется:
а)
истинной погрешностью
б) абсолютной погрешностью
в) истинной абсолютной погрешностью
г) относительной погрешностью
2
Формула
вычисления истинной абсолютной погрешностью имеет вид:
а)
б)
в)
с)
3
Границей
абсолютной погрешности называется число:
4
Определение
«Отношение границы абсолютной погрешности к модулю самого числа»
относится к:
а) относительной
погрешности
б) границе
относительной погрешности
в) абсолютной
ошибке
г) границе
абсолютной ошибки
5
Формула
относительной погрешности имеет вид:
6
Если
точное число 245,21, а приближенное число 246, то истинной абсолютной погрешностью
будет число:
а) 0,0031
б) 0,081
в) 0,013
г) 0,79
7
Если
абсолютная погрешность числа не превосходит единицы этого разряда, то некоторая
цифра приближённого числа назвается:
а) сомнительной
б) верной
в) абсолютной
г) относительной
8
Если
а=945,673, , то цифра 6
является
а) верной
б) сомнительной
в) абсолютной
г) относительной
9
Если
а=142,5, , то граница
относительной погрешности:
а) 0,03%
б) 0,3%
в) 0,003%
г) 0,0003%
10 Граница
абсолютной погрешности числа а=1348, если равна:
а) 0,539
б) 0,5
в) 0,53
г) 0,54
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1
Если
в матрице число столбцов равно числу строк, то матрица называется:
а) прямоугольной
б) векторной
в) треугольной
г) квадратной
2
Если
в матрице число строк не равно числу столбцов то матрица называется
а) квадратной
б) треугольной
в) векторной
г) прямоугольной
3
Число
строк или столбцов матрицы называется её
а) рангом
б) порядком
в) степенью
г) диагональю
4
Матрица,
у которой все элементы, кроме главной диагонали, равны нулю называется:
а) вектором
б) единичной
в) треугольной
г) диагональной
5
Если
у диагональной матрицы всес элементы главной диагонали равны, то такая матрица
является:
а) скалярной
б) единичной
в) нулевой
г) векторной
6
К
векторам относятся:
а) матрицы-строки
б) диагональные
матрицы
в) единичные
матрицы
г) скалярные
матрицы
7
Операция
замены сnрок и
столбцов матрицы называется:
а) сложением
б) понижением
порядка
в) транспонированием
г) вычитанием
8
Дана
матрица 
дополнением 3 элемента 2 строки является число:
а) 1
б) -1
в) 2
г) -2
9
Дана
матрица
данной матрицы равен:
а) 62
б) 24
в) 86
г) 90
10 Для матриц
несправедливо следующее арифметическое действие:
а) сложение
б) вычитание
в) умножение
г) деление
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1
Для
вычисления определителя матрицы используют:
а) правило
Сарруса
б) правило
Гаусса
в) правило
диагоналей
г) правило
Крамера
2
Для
умножения матриц не справедлив математический закон:
а) Сочетательный
б) Переместительный
в) Распределительный
г) Объединительный
3
Если
для матрицы А существует матрица -А, то она обратная
а) обратная
б) противоположная
в) транспонированная
г) единичная
4
Результатом
сложения матрицы А и противоположной ей матрицы -А — является матрица…
а) обратная
б) единичная
в) нулевая
г) транспонированная
5
При
транспонировании матрицы её определитель:
а) изменяется
б) не
изменяется
в) меняет
знак на противоположный
г) равен 0
6
Определитель
матрицы 
7
Найти
произведение матриц А и В, если 
8
Найти
определитель матрицы С=А*В, если
9
Алгебраическое
дополнение 1 элемента 2 строки матрицы
10 Новый
определитель, который получается из определителя вычеркиванием строки и
столбца, содержащих данный элемент называется:
а) алгебраическое
дополнение
б) минор
в) матрица
г) вектор
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1
Обратимой
называется матрица…
а) вырожденная
б) к которой
можно найти обратную матрицу
в) единичная
г) треугольная
2
Найти
обратную матрицу:
3
Решить
матричное уравнение:
4
Способ
решения СЛАУ, заключающийся составлении матрицы из коэффициентов и вектора из
свободных членов, с последующим нахождением обратной матрицы, является методом
а) Гаусса
б) матричным
в) Крамера
г) Сарруса
5
Дана
матрица 
строки является число:
6. Дана
матрица
данной матрицы равен:
7. Для матриц
несправедливо следующее арифметическое действие:
а) сложение
б) вычитание
в) умножение
г) деление
8. Для
вычисления определителя матрицы используют:
а) правило
Сарруса
б) правило
Гаусса
в) правило
диагоналей
г) правило
Крамера
9. Для
умножения матриц не справедлив математический закон:
а) Сочетательный
б) Переместительный
в) Распределительный
г) Объединительный
10. Если для матрицы А
существует матрица -А, то она обратная
а) обратная
б) противоположная
в) транспонированная
г) единичная
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные
методы
1. Если
абсолютная погрешность числа не превосходит единицы этого разряда, то некоторая
цифра приближённого числа называется:
а) сомнительной
б) верной
в) абсолютной
г) относительной
2. Если
а=945,673, , то цифра 6
является
а) верной
б) сомнительной
в) абсолютной
г) относительной
3. Если
а=142,5, , то граница относительной
погрешности:
а) 0,03%
б) 0,3%
в) 0,003%
г) 0,0003%
4. Граница
абсолютной погрешности числа а=1348, если равна:
а) 0,539
б) 0,5
в) 0,54
г) 0,53
5. Если в
матрице число столбцов равно числу строк, то матрица называется:
а) прямоугольной
б) векторной
в) треугольной
г) квадратной
6. Если в
матрице число строк не равно числу столбцов то матрица называется
а) квадратной
б) треугольной
в) векторной
г) прямоугольной
7. Число
строк или столбцов матрицы называется её
а) рангом
б) порядком
в) степенью
г) диагональю
8. Матрица, у
которой все элементы, кроме главной диагонали, равны нулю называется:
а) вектором
б) единичной
в) треугольной
г) диагональной
9. Если у
диагональной матрицы всес элементы главной диагонали равны, то такая матрица
является:
а) скалярной
б) единичной
в) нулевой
г) векторной
10. К векторам
относятся:
а) матрицы-строки
б) диагональные
матрицы
в) единичные
матрицы
г) скалярные
матрицы
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1)
Приближенным числом а называют число, незначительно отличающиеся
от
а)
точного А
б)
неточного А
в)
среднего А
г)
точного не известного
2)
а называется приближенным значением А по недостатку, если
а)
а < A
б)
a > A
в)
a = A
г)
a ≥ A
3)
а называется приближенным значением числа А по избытку, если
а)
a > A
б)
a < A
в)
a = A
г)
a ≥ A
4)
Под ошибкой или погрешностью ∆а приближенного числа а обычно
понимается разность между соответствующим точным числом А и данным
приближением, т.е.
а)
∆а = А – а
б)
∆а = А + а
в)
∆а = А/а
г)
а = ∆а – А
5)
Если ошибка положительна А>, то
а)
∆a > 0
б)
∆a < 0
в)
∆a = 0
г)
∆a ≤ 0
6)
Абсолютная погрешность приближенного числа
а)
∆ = ׀∆а׀
б)
∆а = а
в)
∆ = ׀а׀
г)
А = ׀∆а׀
7)
Абсолютная погрешность
а)
∆ = ׀А – а׀
б)
∆А = а
в)
∆ = ׀В – а׀
г)
а = ׀А + а׀

Предельную абсолютную погрешность вводят если
а)
число А не известно
б)
число а не известно
в)
∆ не известно
г)
А – а не известно
9)
Предельная абсолютная погрешность
10)
Определить предельную абсолютную погрешность числа а = 3,14,
заменяющего число π
а)
0,002
б)
0,001
в)
3,141
г)
0,2
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1) Относительная
погрешность
а) σ
= ∆/׀А׀
б) σ
= ∆
в) σ
= ∆/в
г)
σ = с/а
2) Погрешность,
связанная с самой постановкой математической задачи
а)
погрешность задачи
б)
погрешность метода
в)
остаточная погрешность
г)
погрешность действия
3) Погрешности,
связанная с наличием бесконечных процессов в математическом анализе
а)
остаточная погрешность
б)
абсолютная
в)
относительная
г)
погрешность условия
4) Погрешности,
связанные с наличием в математических формулах, числовых параметров
а)
начальном
б)
конечной
в)
абсолютной
г)
относительной
5) Погрешности,
связанные с системой счисления
а)
погрешность округления
б)
погрешность действий
в)
погрешности задач
г)
остаточная погрешность
6) Округлить
число π = 3,1415926535… до пяти значащих цифр
а)
3,1416
б)
3,1425
в)
3,142
г)
3,14
7) Абсолютная
погрешность при округлении числа π до трёх значащих цифр
а)
0,5*10-2
б)
0,5*10-3
в)
0,5*10-4
г)
0,5*10-1

абсолютная погрешность разности
а)
∆u=∆x1+∆x2
б)
∆u=a+b
в)
∆u=A+b
г)
∆=x1+x2
9) Числовой
ряд названия сходящимся, если
a)
существует предел последовательности его частных сумм
b)
можно найти сумму ряда
c)
существует последовательность
d)
частные суммы равны нулю
10) С
помощью этого метода число верных цифр примерно удваивается на каждом этапе
по сравнению с первоначальным количеством
a)
процесс Герона
b)
формула Тейлора
c)
формула Маклорена
d)
метод Крамера
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1) Две
матрицы одного и того же типа, имеющие одинаковое число строк и столбцов, и
соответствующие элементы их равны, называю:
а) равными
б) одинаковыми
в) разными по
рангу
г) схожими
2) Для
умножения матриц не справедлив математический закон:
а) Сочетательный
б) Переместительный
в) Распределительный
г) Объединительный
3) Если для
матрицы А существует матрица -А, то она обратная
а) обратная
б) противоположная
в) транспонированная
г) единичная
4) Результатом
сложения матрицы А и противоположной ей матрицы -А — является матрица…
а) обратная
б) единичная
в) нулевая
г) транспонированная
5) При
транспонировании матрицы её определитель:
а) изменяется
б) не
изменяется
в) меняет
знак на противоположный
г) равен 0
6) Определитель
матрицы 
7) Найти
произведение матриц А и В, если 

определитель матрицы С=А*В, если
9)
Заменив в матрице типа m×n строки соответственно столбцами получим:
а)
транспонированную матрицу
б)
равную матрицу
в)
среднюю матрицу
г) обратную
матрицу
10) Новый
определитель, который получается из определителя вычеркиванием строки и
столбца, содержащих данный элемент называется:
а) алгебраическое
дополнение
б) минор
в) матрица
г) вектор
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные методы
1) Укажите
название матрицы –А=(-1)А
а)
противоположная
б)
обратная
в)
равная
г)
матрица не существует
2) Укажите
свойства суммы матриц А+(В+С)=…
а) (А+В)+С
б) (В+А)*С
в) АВС
г) А+В+С*А
3) Решить
матричное уравнение:
4) Способ
решения СЛАУ, заключающийся составлении матрицы из коэффициентов и вектора из
свободных членов, с последующим нахождением обратной матрицы, является методом
а) Гаусса
б) матричным
в) Крамера
г) Сарруса
5) Дана
матрица 
строки является число:
6) Дана
матрица
данной матрицы равен:
7) Для матриц
несправедливо следующее арифметическое действие:
а) сложение
б) вычитание
в) умножение
г) деление

вычисления определителя матрицы используют:
а) правило
Сарруса
б) правило
Гаусса
в) правило
диагоналей
г) правило
Крамера
9) Для
умножения матриц не справедлив математический закон:
а) Сочетательный
б) Переместительный
в) Распределительный
г) Объединительный
10) Если для матрицы А
существует матрица -А, то она обратная
а) обратная
б) противоположная
в) транспонированная
г) единичная
Тестовoе
задание к экзаменационному билету
по
дисциплине ОП.14 Численные
методы
1. Если
абсолютная погрешность числа не превосходит единицы этого разряда, то некоторая
цифра приближённого числа назвается:
а) сомнительной
б) верной
в) абсолютной
г) относительной
2. Если
а=945,673, , то цифра 6
является
а) верной
б) сомнительной
в) абсолютной
г) относительной
3. Если
а=142,5, , то граница
относительной погрешности:
а) 0,03%
б) 0,3%
в) 0,003%
г) 0,0003%
4. Граница
абсолютной погрешности числа а=1348, если равна:
а) 0,539
б) 0,5
в) 0,54
г) 0,53
5. Если в
матрице число столбцов равно числу строк, то матрица называется:
а) прямоугольной
б) векторной
в) треугольной
г) квадратной
6. Если в
матрице число строк не равно числу столбцов то матрица называется
а) квадратной
б) треугольной
в) векторной
г) прямоугольной
7. Число
строк или столбцов матрицы называется её
а) рангом
б) порядком
в) степенью
г) диагональю
8. Матрица, у
которой все элементы, кроме главной диагонали, равны нулю называется:
а) вектором
б) единичной
в) треугольной
г) диагональной
9. Если у
диагональной матрицы всес элементы главной диагонали равны, то такая матрица
является:
а) скалярной
б) единичной
в) нулевой
г) векторной
10. К векторам
относятся:
а) матрицы-строки
б) диагональные
матрицы
в) единичные
матрицы
г) скалярные
матрицы
…
Приближенным числом а называют число, незначительно отличающиеся от
точного А
неточного А
среднего А
точного не известного
приблизительного А
…
а называется приближенным значением А по недостатку, если
a > A
а < A
a = A
a ≥ A
a ≤ A
…
а называется приближенным значением числа А по избытку, если
a < A
a = A
a ≥ A
a ≤ A
a > A
…
Под ошибкой или погрешностью ∆а приближенного числа а обычно понимается разность между соответствующим точным числом А и данным приближением, т.е.
∆а = А — а
∆а = А + а
∆а = А/а
а = ∆а — А
А = ∆а + А
…
Если ошибка положительна А>, то
a > a
∆a ≤ 0
∆a = 0
∆a > 0
∆a < 0
…
Абсолютная погрешность приближенного числа
∆ = ׀∆а׀
∆а = а
∆ = ׀а׀
А = ׀∆а׀
∆а = ׀∆в׀
…
Абсолютная погрешность
∆ = ׀А — а׀
∆А = а
∆ = ׀В — а׀
а = ׀А + а׀
∆а = ׀А + в׀
…
Предельную абсолютную погрешность вводят если
число а не известно
∆ не известно
число А не известно
А – а не известно
не известно В
…
Предельная абсолютная погрешность
а
А
∆А
∆в
∆а
…
Определить предельную абсолютную погрешность числа а = 3,14, заменяющего число π
0,002
0,001
3,141
0,2
0,003
…
Относительная погрешность это
σ = ∆
σ = ∆/׀А׀
σ = ∆/в
σ = с/а
σ = а – А
…
Погрешность, связанная с самой постановкой математической задачи
погрешность метода
остаточная погрешность
погрешность действия
погрешность задачи
начальная погрешность
…
Погрешности, связанная с наличием бесконечных процессов в математическом анализе
остаточная погрешность
абсолютная
относительная
погрешность условия
начальная погрешность
…
Погрешность, связанная с системой счисления это
погрешность действий
погрешность задач
погрешность округления
остаточная погрешность
относительная погрешность
…
Округлить число π = 3,1415926535… до пяти значащих цифр
3,1425
3,142
3,14
3,1416
0,1415
…
Абсолютная погрешность при округлении числа π до трёх значащих цифр
0,5*10-2
0,5*10-3
0,5*10-4
0,5*10-1
0,5
…
Предельная абсолютная погрешность разности
∆u=a+b
∆u=∆x1+∆x2
∆u=A+b
∆=x1+x2
∆a=b+c
…
Числовой ряд называется сходящимся, если
можно найти сумму ряда
существует последовательность
существует предел последовательности его частных сумм
частные суммы равны нулю
существует предел разности
…
Найти ln3 c точностью до 10-5
1,09861
1,01
1,098132
1,02
1,3
…
Найти tg 400
0,84
0,9
0,839100
1,0
1,2
…
Методом половинного деления уточнить корень уравнения х4+2х3-х-1=0
0,234
0,2
0,43
0,867
0,861
…
Используя метод хорд найти положительный корень уравнения х4-0,2х2-0,2х-1,2=0
1,16+0,02
1,198+0,0020
2+0,1
3,98+0,001
4,2+0,0001
…
Вычислить методом Ньютона отрицательный корень уравнения х4-3х2+75х-10000=0
−10,31
-5,6
-3,2
-0,44
−10,261
…
Найти действительные корни уравнения х-sinх=0,25
1,17
1,23
2,45
4,8
5,63
…
Определить число положительных и число отрицательных корней уравнения
х4-4х+1=0
3 и 2
0 и 4
0 и 1
2 и 0
0 и 4
…
Определить нижнее число и верхнее число перемен знаков в системе 1, 0, 0, -3, 1.
3 и 1
0 и 4
2 и 4
0 и 5
3 и 2
…
Две матрицы одного и того же типа, имеющие одинаковое число строк и столбцов, и соответствующие элементы их равны, называют
равными
одинаковыми
разными по рангу
схожими
транспонированными
…
Укажите свойства суммы матриц А+(В+С)=…
(В+А)*С
А+В+С*А
(А+В)+С
А*С+В*С
АВС
…
Укажите название матрицы –А=(-1)А
обратная
равная
матрица не существует
транспонированная
противоположная
…
Заменив в матрице типа m×n строки соответственно столбцами получим
равную матрицу
транспонированную матрицу
среднюю матрицу
обратную матрицу
квадратную матрицу
…
С какой матрицей совпадает дважды транспонированная матрица
с обратной
с нулевой
с единичной
с исходной
с квадратной
…
Нахождение обратной матрицы для данной называется
транспонированием
обращение данной матрицы
суммой матриц
заменой строк и столбцов
произведением матриц
…
Максимальный порядок минора матрицы, отличного от нуля, называют
рангом
пределом
рядом
сходимостью
определителем
…
Если элементы квадратной матрицы, стоящие выше (ниже) главной диагонали, равны нулю, то матрицу называют
нулевой
диагональной
треугольной
такая матрица не существует
единичной
…
Метод, представляющий собой конечные алгоритмы для вычисления корней системы
точный метод
метод релаксации
метод итерации
приближенный метод
относительный метод
…
Этот метод является наиболее распространенным приемом решения систем линейных уравнений, алгоритм последовательного исключения неизвестных
метод Крамера
метод обратный матриц
ведущий метод
метод Гаусса
аналитический метод
…
Как иначе называют метод хорд?
Метод касательных
Метод пропорциональных частей
Метод коллокации
Метод бисекций
Метод квадратных корней
…
Все методы вычисления интегралов делятся на:
Точные и приближенные
Прямые и итеративные
Прямые и косвенные
Аналитические и графические
Приближенные и систематические
…
Точный метод вычисления интегралов был предложен
Ньютоном и Гауссом
Гауссом и Стирлингом
Вольтером
Ньютоном и Лейбницем
Гауссом и Крамером
…
Приближенные методы вычисления интегралов можно разделить на 2 группы
аналитические и графические
аналитические и численные
систематические и численные
систематические и случайные
приближенные и неприближенные
Численные методы решения инженерных задач
- Зачет/Экзамен
а называется приближенным значением числа А по избытку, если
Выберите один ответ:
- a
- a = A
- a > A
- a ≤ A
- a ≥ A
Абсолютная погрешность при округлении числа π до трёх значащих цифр
Выберите один ответ:
- 0,5
- 0,5*10-1
- 0,5*10-2
- 0,5*10-3
- 0,5*10-4
Абсолютная погрешность это
Выберите один ответ:
- а = ׀А + а׀
- ∆ = ׀А — а׀
- ∆ = ׀В — а׀
- ∆А = а
- ∆а = ׀А + в׀
Вметоде Гаусса линейная система решается
Выберите один ответ:
- в два этапа
- в один этап
- в три этапа
Все методы вычисления интегралов делятся на:
Выберите один ответ:
- Аналитические и графические
- Приближенные и систематические
- Прямые и итеративные
- Прямые и косвенные
- Точные и приближенные
Вычислительный алгоритм должен быть:
Выберите один ответ:
- быть эффективным по времени выполнения и экономичным по требуемым объемам памяти, а также не допускать аварийных остановов
- удовлетворять всем перечисленным выше требованиям
- устойчивым к ошибкам и обеспечивать требуемую точность
Вычислить методом Ньютона отрицательный корень уравнения х4-3х2+75х-10000=0
Выберите один ответ:
- −0,44
- −10,261
- −10,31
- −3,2
- −5,6
Геометрически верхняя сумма Дарбу равна:
Выберите один ответ:
- Площади прямоугольного параллелепипеда
- Площади ступенчатого многоугольника, содержащего внутри себя криволинейную трапецию
- Площади ступенчатого многоугольника, содержащегося в криволинейной трапеции
- Площади ступенчатого прямоугольника
- Площади ступенчатого шестиугольника
Две матрицы одного и того же типа, имеющие одинаковое число строк и столбцов, и соответствующие элементы их равны, называют
Выберите один ответ:
- одинаковыми
- равными
- разными по рангу
- схожими
- транспонированными
Если ошибка положительна А>, то
Выберите один ответ:
- a> a
- ∆a = 0
- ∆a ≤ 0
- ∆a < 0
- ∆a > 0
Если элементы квадратной матрицы, стоящие выше (ниже) главной диагонали, равны нулю, то матрицу называют
Выберите один ответ:
- диагональной
- единичной
- нулевой
- такая матрица не существует
- треугольной
Заменив в матрице типа m×n строки соответственно столбцами получим
Выберите один ответ:
- квадратную матрицу
- обратную матрицу
- равную матрицу
- среднюю матрицу
- транспонированную матрицу
Интерполяционные функции строятся, как правило, в виде
Выберите один ответ:
- линейной комбинации некоторых линейно-независимых элементарных функций
- линейной комбинации некоторых нелинейно-независимых элементарных функций
- нелинейной комбинации некоторых линейно-независимых элементарных функций
Интерполяция – это…
Выберите один ответ:
- Замена одних математических объектов другими, в том или ином смысле близким к исходным.
- Метод решения задач, при котором объекты разного рода объединяются общим понятием.
- Продолжение функции, принадлежащей заданному классу, за пределы ее области определения.
- Способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений
Итерация – это ….
Выберите один ответ:
- Замена одних математических объектов другими, в том или ином смысле близким к исходным
- Повторение. Результат повторного применения какой–либо математической операции
- Продолжение функции, принадлежащей заданному классу, за пределы ее
- Число, изображаемое единицей и 18 нулями
Итерацияiteratio в переводе с латинского:
Выберите один ответ:
- возвращение
- замещение
- повторение
- удаление
- умножение
К методам уточнения корней не относится …
Выберите один ответ:
- Метод аппроксимации
- Метод дихотомии
- Метод касательных
- Метод хорд
Как иначе называют метод бисекций?
Выберите один ответ:
- Метод «начального отрезка»
- Метод коллокации
- Метод половинного деления
- Метод пропорциональных частей
- Метод хорд
Как иначе называют метод Ньютона?
Выберите один ответ:
- Метод итераций
- Метод касательных
- Метод коллокации
- Метод прогонки
- Метод хорд
Как иначе называют метод хорд?
Выберите один ответ:
- Метод бисекций
- Метод касательных
- Метод квадратных корней
- Метод коллокации
- Метод пропорциональных частей
Кто опубликовал формулу для решения кубического уравнения?
Выберите один ответ:
- Абеле
- Галуа
- Дарбу
- Кардано
- Фредгольм
Любая совокупность n-мерных векторов, рассматриваемая с установленными в ней операциями сложения векторов и умножения вектора на число, не выводящими за пределы этой совокупности называется
Выберите один ответ:
- линейным векторным пространством
- плоскостью векторов
- скалярным произведением векторов
- суммой векторов
- сходимостью векторного пространства
Максимальное число линейно независимых векторов n-мерного пространства Еn в точности равно
Выберите один ответ:
- размерности этого пространства
- совокупности единичных векторов
- соразмерности векторов
- сумме n векторов
- сумме линейных векторов
Максимальный порядок минора матрицы, отличного от нуля, называют
Выберите один ответ:
- определителем
- пределом
- рангом
- рядом
- сходимостью
Метод Гаусса–Зейделя относится к
Выберите один ответ:
- итерационным методам
- методам численного интегрирования
- прямым методам
Метод Монте–Карло относится к
Выберите один ответ:
- итерационным методам
- методам численного интегрирования
- прямым методам
Метод позволяющий получить корни системы с заданной точностью путем сходящихся бесконечных процессов
Выберите один ответ:
- итерационный метод
- метод Зейделя
- относительный метод
- приближенный метод
- точный метод
Метод хорд имеет еще одно имя:
Выберите один ответ:
- Метод бисекций
- Метод касательных
- Метод коллокации
- Метод прогонки
- Метод пропорциональных частей
Метод Эйлера решения обыкновенных дифференциальных уравнений является методом
Выберите один ответ:
- второго порядка
- первого порядка
- третьего порядка
Метод, представляющий собой конечные алгоритмы для вычисления корней системы
Выберите один ответ:
- метод итерации
- метод релаксации
- относительный метод
- приближенный метод
- точный метод
Методы Адамса решения обыкновенных дифференциальных уравненийотносятся к
Выберите один ответ:
- многошаговым методам
- одношаговым методам
- прямым методам
МетодLU-факторизации характеризуется такими же оценками нормы матрицы возмущения и относительной ошибки, как:
Выберите один ответ:
- метод Гаусса
- метод Ньютона
- метод Симпсона
Найти действительные корни уравнения х-sin(х)=0,25
Выберите один ответ:
- 1,17
- 1,23
- 2,45
- 4,8
- 5,63
Нахождение обратной матрицы для данной называется
Выберите один ответ:
- заменой строк и столбцов
- обращение данной матрицы
- произведением матриц
- суммой матриц
- транспонированием
Невязка – это…
Выберите один ответ:
- Значение разностей между свободными членами исходной системы и результатами подстановки в уравнения системы найденных значений неизвестных
- Значение разностей между свободными членами исходной системы
- Значение суммы между свободными членами исходной системы и результатами подстановки в уравнения системы найденных значений неизвестных
- Значение суммы результатов подстановки в уравнения системы найденных значений неизвестных
Недостатком интерполяционной формулы Лагранжа является
Выберите один ответ:
- каждое слагаемое зависит от всех узлов интерполяции
- каждое слагаемое не зависит от всех узлов интерполяции
- повышение порядка полинома
неявный метод Адамса четвертого порядка является
Выберите один ответ:
- двухшаговым методом
- одношаговым методом
- трехшаговым методом
Округлить число π = 3,1415926535… до пяти значащих цифр
Выберите один ответ:
- 0,1415
- 3,14
- 3,1416
- 3,142
- 3,1425
Определить предельную абсолютную погрешность числа а = 3,14, заменяющего число π
Выберите один ответ:
- 0,001
- 0,002
- 0,003
- 0,2
- 3,141
Определить состав корней уравнения х4+8х3-12х2+104х-20=0
Выберите один ответ:
- два отрицательных корня
- невозможно найти число корней
- нет ни одного корня
- один положительный и один отрицательный
- уравнение не имеет положительных корней
Определить число положительных и число отрицательных корней уравнения х4-4х+1=0
Выберите один ответ:
- 0 и 1
- 0 и 4
- 0 и 4
- 2 и 0
- 3 и 2
От латинского слова recurrens:
Выберите один ответ:
- возвращающийся
- заменяющийся
- меняющийся
- повторяющийся
- приближающийся
Отделение корней можно выполнить двумя способами:
Выберите один ответ:
- аналитическим и графическим
- аналитическим и систематическим
- приближением и отделением
- приближением последовательным и параллельным
- систематическим и графическим
Относительная погрешность
Выберите один ответ:
- σ = а – А
- σ = с/а
- σ = ∆
- σ = ∆/в
- σ = ∆/׀А׀
Погрешности, связанные с наличиемв математических формулах, числовых параметров
Выберите один ответ:
- абсолютной
- конечной
- начальном
- остаточной
- относительной
Погрешности, связанные с системой счисления
Выберите один ответ:
- остаточная погрешность
- относительная погрешность
- погрешности задач
- погрешность действий
- погрешность округления
Погрешности,связанные с наличием бесконечныхпроцессов вматематическом анализе
Выберите один ответ:
- абсолютная
- начальная погрешность
- остаточная погрешность
- относительная
- погрешность условия
Последовательность, удовлетворяющая условию Коши, называется:
Выберите один ответ:
- двусторонней последовательностью
- итеративной последовательностью
- односторонней последовательностью
- рекуррентной последовательностью
- фундаментальной последовательностью
Предельная абсолютная погрешность разности
Выберите один ответ:
- ∆=x1+x2
- ∆a=b+c
- ∆u=a+b
- ∆u=A+b
- ∆u=∆x1+∆x2
Предельная абсолютная погрешность
Выберите один ответ:
- А
- ∆а
- ∆А
- ∆в
Предельную абсолютную погрешность вводят если
Выберите один ответ:
- А – а не известно
- не известно В
- число а не известно
- число А не известно
- ∆ не известно
При контроле решения алгебраического уравнения может быть полезна:
Выберите один ответ:
- Теорема Бюдана-Фурье
- Теорема Виета
- Теорема Ньютона
- Теорема Перрона
- Теорема Штурма
Приближенные методы вычисления интегралов можно разделить на 2 группы:
Выберите один ответ:
- аналитические и графические
- аналитические и численные
- приближенные и неприближенные
- систематические и случайные
- систематические и численные
Разность между наименьшим из чисел m и n и рангом матрицы называется
Выберите один ответ:
- дефектом
- определителем
- пределом
- разницей
- рангом
С какой матрицей совпадает дважды транспонированная матрица
Выберите один ответ:
- с единичной
- с исходной
- с квадратной
- с нулевой
- с обратной
Свойствосамоисправляемости:
Выберите один ответ:
- Влияет на конечный результат
- Не влияет на конечный результат
- Не учитывается
- Считается ошибочным
- Усиливает надежность метода
Способ арифметизации решения задачи
Выберите один ответ:
- Набор формул решения задачи.
- Способ получения числового результата
- Численный метод
- Численный подход к решению задачи
Точный метод вычисления интегралов был предложен:
Выберите один ответ:
- Вольтерром
- Гауссом и Крамером
- Гауссом и Стирлингом
- Ньютоном и Гауссом
- Ньютоном и Лейбницем
Укажите название матрицы –А=(-1)А
Выберите один ответ:
- матрица не существует
- обратная
- противоположная
- равная
- транспонированная
Укажите первую теорему Больцано-Коши:
Выберите один ответ:
- Если функция f(x) монотонна на отрезке [α;b], то она дифференцируема на этом отрезке
- Если функция f(x) монотонна на отрезке [α;b], то она интегрируема на этом отрезке
- Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
- Определитель D=|αij| n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения
- Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k-кратный корень считать за k корней
Условие устойчивости явных многошаговых методов Адамса накладывает существенные ограничения на величину
Выберите один ответ:
- погрешности интегрирования
- точности интегрирования
- шага интегрирования
Формула трапеций относится к
Выберите один ответ:
- итерационным методам
- методам численного интегрирования
- прямым методам
Целый однородный полином второй степени от n переменных называется
Выберите один ответ:
- квадратичной формой
- кубической формой
- матричной формой
- прямоугольной формой
- треугольной формой
Численный метод “бисекций” предназначен для решения задач:
Выберите один ответ:
- Линейного алгебраического уравнения.
- Нелинейного алгебраического уравнения.
- Системы алгебраических линейных уравнений.
- Системы алгебраических нелинейных уравнений.
Численный метод “Гаусса” предназначен для решения задач:
Выберите один ответ:
- Линейного алгебраического уравнения
- Нелинейного алгебраического уравнения
- Системы алгебраических линейных уравнений
- Системы алгебраических нелинейных уравнений
Численный метод “Зейделя” предназначен для решения задач:
Выберите один ответ:
- Вычисления определенного интеграла.
- Нелинейного алгебраического уравнения.
- Системы алгебраических линейных уравнений.
- Системы алгебраических нелинейных уравнений.
Численный метод “прямоугольников” предназначен для решения задач:
Выберите один ответ:
- Вычисления определенного интеграла
- Нелинейного алгебраического уравнения
- Системы алгебраических линейных уравнений
- Системы алгебраических нелинейных уравнений
Численный метод “Симпсона” предназначен для решения задач:
Выберите один ответ:
- Вычисления определенного интеграла
- Нелинейного алгебраического уравнения
- Системы алгебраических линейных уравнений
- Системы алгебраических нелинейных уравнений
Численный метод итераций определяет решение через нахождение:
Выберите один ответ:
- Координаты пересечения двух графиков
- Координаты пересечения касательной с осью Х
- Координаты пересечения хорды с осью Х
- Координаты средины отрезка где находится корень
Численный метод Ньютона определяет решение через нахождение:
Выберите один ответ:
- Координаты пересечения двух графиков
- Координаты пересечения касательной с осью Х
- Координаты пересечения хорды с осью Х
- Координаты средины отрезка где находится корень
Числовой ряд названия сходящимся, если
Выберите один ответ:
- можно найти сумму ряда
- существует последовательность
- существует предел последовательности его частных сумм
- существует предел разности
- частные суммы равны нулю
Экономичность алгоритма оценивается по требуемым для его реализации объемам
Выберите один ответ:
- быстродействия ЭВМ
- памяти ЭВМ
- скорости ЭВМ
Этот метод является наиболее распространенным приемом решения систем линейных уравнений, алгоритм последовательного исключения неизвестных
Выберите один ответ:
- аналитический метод
- ведущий метод
- метод Гаусса
- метод Крамера
- метод обратный матриц
FUZZY GUIDANCE CONTROL FOR A MOBILE ROBOT
W. Gharieb, G. Nagib, in Current Advances in Mechanical Design and Production VII, 2000
3.2 Navigation problem
Fuzzy guidance controller is able to resolve the following navigation problems in unknown environment including fixed obstacles: goal seeking, front obstacle avoidance, right obstacle avoidance and left obstacle avoidance as in Fig. 3.
Fig. 3. Fuzzy guidance control.
Each navigator is a task oriented control algorithm and designed as a separate fuzzy system to compute the recommended steering angle and linear velocity independently. In goal seeking, the distance between the robot position and aim point (d) is used to compute the recommended linear velocity (vr). While the deviation angle (Φ-h) to move towards the aim point is used to determine the recommended steering angle (θr). In obstacle avoidance, the capturing information from sensors determines the recommended steering angle, while the recommended velocity is reduced to half in order to decrease the robot inertia. Finally, the minimum risk criterion detects the applied control to the robot and the final decision will be taken as illustrated in Fig. 3.
In goal seeking, the crisp input to the fuzzy system is the distance (d) to compute the recommended velocity. Input membership functions are triangular in form (VC, CL, SM, ME and LA). They are very close, close, small, medium and large respectively. Output membership functions are singleton (ZE, VS, SM, ME, LA). They are zero, very small, small, medium and large respectively. Fuzzy rules are very simple as:
| If | d | VC | Then | vr | ZE |
| If | d | CL | Then | Vr | VS |
| If | d | SM | Then | Vr | SM |
| If | d | ME | Then | Vr | ME |
| If | d | LA | Then | Vr | LA |
The recommended steering angle θr is computed as function of the deviation angle (ϕ-h). The input membership functions are triangular in form (NL, NS, ZE, PS and PL). They are negative large, negative small, zero, positive small and positive large respectively. The output membership functions are singleton (LH, LF, ZE, RG and RH). They are turn left hard, turn left, turn zero, turn right and turn right hard respectively. The fuzzy rules are:
| If | (ϕ-h) | ZE | Then | θr | ZE |
| If | (ϕ-h) | PS | Then | θr | LF |
| If | (ϕ-h) | PL | Then | θr | LH |
| If | (ϕ-h) | NS | Then | θr | RG |
| If | (ϕ-h) | NL | Then | θr | RH |
In obstacle avoidance, the measured distances RS, LS and FS are fuzzified using membership functions CL, NE and FA. They are Close, Near, and Far respectively. The visual zone for front side is a symmetric 30°.
Right obstacle avoidance rules:
| If | RS | CL | Then | θr | LH |
| If | RS | NE | Then | θr | LF |
| If | RS | FA | Then | θr | ZE |
Left obstacle avoidance rules:
| If | LS | CL | Then | θr | RH |
| If | LS | NE | Then | θr | RG |
| If | LS | FA | Then | θr | ZE |
Front obstacle avoidance rules:
| If | FS | CL | and | RS | FA | Then | θr | RH |
| If | FS | CL | and | LS | FA | Then | θr | LH |
| If | FS | NE | and | RS | FA | Then | θr | RG |
| If | FS | NE | and | LS | FA | Then | θr | LF |
| If | FS | FA | Then | θr | ZE |
When the robot sensors detect the front obstacle only, either right or left steering can be taken. The decision depends on the situation and which is much better to be taken.
In decision making, Each fuzzy system produces its output, then the decision making block has to select the values of recommended variables. The minimum risk criterion aims to avoid the nearest obstacle by computing the minimum distance as follows:
(5)J=Min(LS, RS, FS, d)
The recommended steering angle is selected as:
| If | J=LS | Then | Left obstacle avoidance |
| If | J=RS | Then | Right obstacle avoidance |
| If | J=FS | Then | Front obstacle avoidance |
| If | J=d | Then | Goal seeking |
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080437118500076
Fundamentals of artificial intelligence techniques for apparel management applications
Z.X. Guo, W.K. Wong, in Optimizing Decision Making in the Apparel Supply Chain Using Artificial Intelligence (AI), 2013
2.5.4 Fuzzy logic system
A fuzzy logic system maps crisp inputs into crisp outputs using the theory of fuzzy sets. In a fuzzy logic system, an inference engine works with fuzzy rules.
The engine takes inputs, some of which may be fuzzy, and generates outputs, some of which may be fuzzy. The fuzzy core of the inference engine is bracketed by one step that can convert crisp data into fuzzy data, and another step that does the reverse. Figure 2.10 shows the general procedures involved in a fuzzy logic system as follows.
2.10. The general structure of a fuzzy logic system.
Fuzzification of input data
The first step is to take the crisp input x and determine the degree to which the input belongs to each of the appropriate fuzzy sets.
Fuzzification is the process of mapping crisp input x ∈ U into fuzzy set A ∈ U. This is achieved with three different types of fuzzifier, including singleton fuzzifiers, Gaussian fuzzifiers, and trapezoidal or triangular fuzzifiers. These fuzzifiers map crisp input x into fuzzy set A with different membership functions μA (x) listed below.
Membership function of singleton fuzzifier:
μAx=10ifx=x’otherwise.
Membership function of Gaussian fuzzifier:
μAx=e−x1−x1.a12…e−xn−xn.an12
where {ai, i = 1,…, n} are positive parameters.
Membership function of triangular fuzzifier:
μAx=1−x1−x1’b1…1−xn’−xn’bnifxi−xi’≤bi,i=1,2,…,n0otherwise
where {bi,i = 1,…, n} are positive parameters.
Evaluation of fuzzy rules
After input data are fuzzified and their membership values obtained, the next step involves application of them to the antecedents of fuzzy rules. If a given fuzzy rule has multiple antecedents, a fuzzy operator (AND or OR) is used to obtain a single number that represents the result of antecedent evaluation. This number is then applied to a consequent membership function.
AND is used to evaluate the conjunction of rule antecedents. Typically, fuzzy logic systems utilize the classical fuzzy operation intersection to implement this operation. Consider fuzzy rule 1:
IfxisAANDyisB,thenzisC.
Assume μA(x) = 0.1, μB(y) = 0.6, then we have μC(z) = min[μA(x),μB(y)] = 0.1.
Similarly, OR is used to evaluate the disjunction of rule antecedents, which is implemented by the classical fuzzy operation union in fuzzy logic systems. Consider fuzzy rule 2:
IfxisAORyisB,thenzisC.
Assume μ(x) = 0.1, μB(y) = 0.6, then we have
μCz=maxμAx,μBy=0.6.
Aggregation of outputs of fuzzy rules
Several fuzzy rules often provide fuzzy information about the same variable and different outputs must be combined. Aggregation is the unification of outputs of all fuzzy rules. That is, aggregation takes membership functions of all rules’ consequents and combines them into a single fuzzy set. Fuzzy set operations, such as union and intersection, can be used to implement aggregation.
Defuzzficatwn of the output
The last step in a fuzzy logic system is defuzzification. As the name suggests, defuzzification is the opposite of fuzzification, which produces crisp output y’ for a fuzzy logic system from the aggregated output of fuzzy set B. A number of defuzzifiers have been developed; the most popular is the centroid defuzzifier, which finds a vertical line and divides an aggregated set into two equal portions. Mathematically the center of gravity (COG) can be defined by:
y’=COG=∫abμByydy∫abμBydy.
In addition to centroid defuzzifiers, maximum defuzzifiers and means of maxima defuzzifiers are also commonly used.
- •
-
Maximum Defuzzifier: This defuzzifier chooses y’’ as the point at which associated membership functions achieve their maximum values.
- •
-
Mean of Maxima Defuzzifier: This defuzzifier examines fuzzy set B, determines values for which associated membership functions achieve their maximum values and computes the mean of these values as its output y’
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780857097798500020
Fundamentals of Type-1 Fuzzy Logic Theory
Erdal Kayacan, Mojtaba Ahmadieh Khanesar, in Fuzzy Neural Networks for Real Time Control Applications, 2016
2.3.1.1 Fuzzification
Fuzzification is the process of converting a crisp input value to a fuzzy value that is performed by the use of the information in the knowledge base. Although various types of curves can be seen in literature, Gaussian, triangular, and trapezoidal MFs are the most commonly used in the fuzzification process. These types of MFs can easily be implemented by embedded controllers.
The MFs are defined mathematically with several parameters. In order to fine-tune the performance of a FLC, these parameters, or the shape of the MFs, can be adapted.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128026878000025
Uncertain Input Data Problems and the Worst Scenario Method
Ivan Hlaváěek Dr., … Ivo Babuška Dr., in North-Holland Series in Applied Mathematics and Mechanics, 2004
2.4 On the Origin of Data
We briefly introduced various methods designed to address uncertainties in modeling. One might feel that the methods are or at least may be useful if we face the lack of crisp input data. The feeling might be that in many real life problems data are fairly crisp and that there is almost no need for an extensive uncertainty analysis. On inspection, however, crisp data prove to be less crisp than expected, as illustrated in the following example.
Material properties of a rolled aluminum alloy are dependent on the thickness of the body from which samples are taken. The yield strength and the modulus of elasticity reported in (Wong et al., 1987) and displayed in Table 2.2 correspond to sheet (nominal thickness 5.1 mm) and plate (nominal thickness 10.2 mm) material. The variation in the yield strength is greater than that in the modulus of elasticity.
Table 2.2. Material properties for plate and sheet aluminum
| yield strength [MPa] | modulus of elasticity [GPa] | |
| Plate | 176 | 69.6 |
| Sheet | 214 | 71.7 |
Does the analyst of a structure always know whether this or that piece of alloy comes from a plate, sheet, or different source? Moreover, parameter values respecting the origin of samples are rarely available even in the crisp form of Table 2.2, which does not statistically reflect the diversity of individual measurements. Also, material properties are sensitive to various other factors too, e.g., instantaneous temperature, temperature history, load history, and fatigue.
On top of that, the nature of material response is three-dimensional; nevertheless, sample parameters are measured in one-dimensional arrangements as a rule.
This lack of knowledge will probably be harmless in common linear elasticity problems because the variation of the modulus of elasticity is not significant, especially if compared with the uncertainty in loading. In problems where the yield strength is important, the uncertainty in its value has a more explicit impact.
What are the mines of material data? In mechanical engineering and structural mechanics, design engineers use material handbooks to find input data. Although these sources cover various material parameters, not all useful data are available there and only extensive handbooks contain at least selected basic statistical features of the data (ASM, 1992).
The fact is that we frequently combine the available handbook data with micromechanical arguments. Take assumptions on the character of composite materials made of handbook constituents, for example. The goal is to infer lower and upper bounds of composite material parameters (Torquato, 2002).
Input data are often fully or partially obtained as solutions to inverse problems, i.e., the inputs of a state problem are the outputs of an inverse problem, which itself needs some input data. This embedding makes the uncertainty of inputs more troublesome. It is the context where sensitivity analysis should come into play to determine which input and output data are essential with respect to the goal of computation.
Let us remark that a widely used approach has evolved in the course of fighting with uncertainties in design, analysis, and modeling. Uncertainty is treated by means of engineering rules stipulated and fixed in building, safety, and other codes. They include years of experience and offer more or less step-by-step guidance. They are successfully used in common designs, but less applicable in unusual cases. The question of how far the code-based design is on the safe side usually remains unanswered though the recently introduced information-gap decision theory (Ben-Haim, 2001b) is promising in this respect; see also the Introduction.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0167593104800056
Modeling and control of a quadrotor unmanned aerial vehicle using type-2 fuzzy systems
Ayad Al-Mahturi, … Sreenatha G. Anavatti, in Unmanned Aerial Systems, 2021
2.5 Online fuzzy system identification
In this section, we perform nonlinear identification utilizing the TS fuzzy system. In our approach, we implement the steepest descent algorithm to optimize the antecedent and the consequent parameters of our fuzzy system. The nonlinear system identification scheme is depicted in Fig. 2.4.
Figure 2.4. Online system identification structure, where z indicates a delay operator used in our system.
Figure 2.5. Experimental setup for collecting quadcopter data (Al-Mahturi et al., 2019c).
In the following, we explain the required steps to obtain a dynamic model of a quadcopter drone using a fuzzy system.
- •
-
Fuzzifier: In this stage, the membership degree for every crisp input is calculated as follows:
(2.10)μi=exp(−0.5(xi−ci)2σi2+ε),
where cj and σj denote the center and the width of the Gassian membership function for each input variable xj. Also, ϵ>0 is a small constant to avoid dividing by zero.
- •
-
Firing strength calculation: After calculating the membership degree for each input, we perform the multiplications (the AND operation of the antecedent part). The firing strength is computed using the following equation:
(2.11)fi=∏i=1nμi.
- •
-
Fuzzy output: The first-order TS fuzzy model is given as follows:
(2.12)yˆ(x)=∑j=1Mγj[∏i=1nexp(−0.5(xi−cji)2σji2+ε)σi2+ε]∑j=1M[∏i=1nexp(−0.5(xi−cji)2σji2+ε)σi2+ε],
where n is the number of fuzzy rules; γj is the fuzzy consequent part, which is given as follows:
(2.13)γj=b0+b1x1+…+bjxj,
where bj are fuzzy consequent parameters.
- •
-
Objective function: The objective function of our online system identification is to minimize the prediction error as follows:
(2.14)J(t)=12∑i=1N[yˆ(t)−y(t)]2,
where y and yˆ are the actual output of the plant and the acquired fuzzy model, and N is the length of the experimental flight data.
- •
-
Updating fuzzy parameters: By utilizing the gradient-based learning method, fuzzy parameters can be updated using the backpropagation technique as follows:
(2.15)△cj=−η∂J∂cj=η(y(t)−yˆ(t))bj(t)(x−cj)σj−2,
(2.16)cj(t)=cj(t−1)+△cj(t)+γ(cj(t−1)−cj(t−2)),
(2.17)△σj=−η∂J∂σj=η(y(t)−yˆ(t))bjμj∥x−cj∥2σj−3,
(2.18)σj(t)=σj(t−1)+△σj+γ(σj(t−1)−σj(t−2)),
(2.19)△bj(t)=−η∂J∂bj=η((y(t)−yˆ(t))μj,
(2.20)bj(t)=bj(t−1)+△bj(t)+γ(bj(t−1)−bj(t−2)),
where η∈[0,1] is the learning rate and γ∈[0,1] is the momentum factor.
For collecting the quadcopter data, we used a flamewheel quadcopter UAV. A VICON motion capture system (MCS) was employed to obtain the position and orientation of the quadcopter. Six reflective markers were attached to the drone to enable the VICON system to track position and orientation. Real-time data collected in the Vicon system were transmitted continuously to the drone vehicle at a frequency of 100 Hz using a UDP network protocol. The data were obtained with a sampling rate of 100 Hz.
- •
-
Pitch dynamics: The identified fuzzy model was designed using four Gaussian membership functions to model the pitch dynamics. The oscillation was obtained by applying equal and opposite input signals to the front motors (1 & 4) and rear motors (2 & 3). Fig. 2.6a illustrates the effectiveness of our fuzzy modeling of pitch dynamics with lower error, as shown in Fig. 2.7a (Al-Mahturi et al., 2019c).
Figure 2.6. The identified fuzzy model of a quadcopter drone. Shown are (a) the pitch dynamics, (b) the roll dynamics, (c) the yaw dynamics, and (d) the vertical dynamics (z axis) (Al-Mahturi et al., 2019c).
Figure 2.7. Errors of the identified fuzzy model. Shown are (a) error in the pitch dynamics, (b) error in the roll dynamics, (c) error in the yaw dynamics, and (d) error in the vertical dynamics (z axis) (Al-Mahturi et al., 2019c).
- •
-
Roll dynamics: For collecting roll data, we excited the system by generating an oscillating roll that thoroughly captures the quadcopter dynamics. Following the work in Santoso et al. (2018); Al-Mahturi et al. (2019c), we applied equal and opposite input signals to the right motors (3 & 4) and left motors (1 &2) to stimulate a pure rolling motion. Similarly, we investigated the efficacy of the proposed TS fuzzy model for capturing roll dynamics, where a reasonably good fuzzy identified model was achieved, as shown in Fig. 2.6b with reasonably low prediction error values, as depicted in Fig. 2.7b (Al-Mahturi et al., 2019c).
- •
-
Yaw dynamics: Following a similar manner, to fully excite yaw dynamics, we applied equal and opposite signals to pairs of diagonal motors to generate a yawing moment. A reasonable fuzzy identified model for yaw dynamics is shown in Fig. 2.6c, with a substantially lower prediction error, as illustrated in Fig. 2.7c (Al-Mahturi et al., 2019c).
- •
-
Altitude dynamics: To obtain a dynamic model of the vertical loop, we applied the same thrust to all rotors. Fig. 2.6d shows the effectiveness of our TS fuzzy identified model, with a reasonable magnitude of error values, as depicted in Fig. 2.7d (Al-Mahturi et al., 2019c).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128202760000091
A Neuro-Fuzzy Inference Model for Diabetic Retinopathy Classification
Mohammed Imran, Sarah A. Alsuhaibani, in Intelligent Data Analysis for Biomedical Applications, 2019
7.3.2 Fuzzy Inference System
Fuzzy inference entails the processes of mapping a set of inputs to the output using fuzzy logic. Fuzzy Logic is a multivalued logic that allows an intermediate value to be defined between 0 and 1, which contrasts with the classical Boolean logic where only two values are allowed, either 0 or 1 [29]. FIS is applied in many fields, such as data classification, decision analysis, and expert systems. It is built based on three main components: membership function, fuzzy logic operators, and if–then rules [30].
7.3.2.1 Fuzzy Inference System Architecture
The architecture of FIS involves four steps: Fuzzification, Knowledge Base, Inference Engine, and Defuzzification. Fig. 7.5 illustrates the FIS architecture:
Figure 7.5. FIS architecture.
As shown in the figure, in the fuzzification step the crisp inputs are converted to linguistic variables by using the membership functions which are stored in the knowledge base. The membership function can be of different types, the Triangular function (Eq. (7.5)), Trapezoidal function (Eq. (7.6)), or Gaussian function (Eq. (7.7)).
(7.5)μA(x)={0,x≤ax−am−a,a<x≤mb−xb−m,m<x<b0,x≥b
(7.6)μA(x)={0,(x<a)or(x>b)x−ab−a,a≤x≤b1,b≤x≤cd−xd−c,c≤x≤d
(7.7)μA(x)=e−(x−m)22k2
In the inference engine, the IF–THEN rules stored in the knowledge base are used to compute the fuzzy output from the fuzzy input as illustrated in Fig. 7.6.
Figure 7.6. Inference engine [31].
In the defuzzification step, the fuzzy output is converted to crisp value by using the same membership function used in the fuzzification step. Different defuzzification methods can be used to obtain the crisp value, such as the Centroid of Area, Bisector of Area, Mean of Max, Smallest of Max, and Largest of Max [30].
7.3.2.2 Fuzzy Inference System Types
There are several types of FIS, and the most two types commonly used are the Mamdani Fuzzy model and Sugeno Fuzzy model. The difference between these types comes from the consequents, of their fuzzy rules which make the procedures of their aggregation and defuzzification different as well. A brief description of each type is discussed next.
7.3.2.2.1 Mamdani Fuzzy Model
The Mamdani method is considered the most generally used FIS technique. The method was first introduced by Professor Ebrahim Mamdani in 1975, when he applied a set of fuzzy rules supplied by experienced human operators to build the first fuzzy system to control a steam engine and boiler combination. The process of the Mamdani method is performed in six steps. First, the determination of the needed fuzzy rules. Then, (2) there is the conversion of the crisp inputs to the fuzzy inputs by using the membership function. Then, (3) the fuzzified inputs must be aggregated based on the fuzzy rules. Then, (4) the consequent of the rule is determined by joining the rule strength and (4) the output of the membership function. Next, (5) all the consequents must be combined to get the output distribution. Finally, (6) output distribution is defuzzied [32]. Fig. 7.7 illustrates the Mamdani Fuzzy Inference System.
Figure 7.7. Mamdani fuzzy interface system [33].
7.3.2.2.2 Sugeno Fuzzy Model
This fuzzy method was presented in 1985 by Takagi, Sugeno, and Kang. It is very similar to the Mamdani method except that the consequent of the rule is changed where a mathematical function is used for the input variable instead if fuzzy set [30]. The general format of the rule for the Sugeno fuzzy method is:
IFxisAANDyisBTHENzisf(x,y)
where x, y, and z are linguistic variables; A and B are fuzzy sets; and f(x, y) is the mathematical function.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128155530000070
Fuzzy logic and fuzzy systems
Carlos A. Reyes-García, Alejandro A. Torres-García, in Biosignal Processing and Classification Using Computational Learning and Intelligence, 2022
8.3.2.3 Fuzzy inference mechanism
For each rule in the Sugeno-type FIS, two values must be computed, which are the rule strength wi and the output value zi for the linear function in the rule’s consequent, which depends on the input crisp values for each variable in the rule’s antecedent.
Particularly, the activation strength wi is computed depending on the logic operator/s in the antecedent rule. When the variables are linked with the operator AND, the strength is computed as follows: wi=AndMethod(F1(x),F2(y)), whereas if the variables are linked with an OR operator, the strength is computed as follows: wi=OrMethod(F1(x),F2(y)), where F1(x) and F2(y) are the membership values for the values x and y in the fuzzy sets, called A and B, respectively. The AndMethod could be defined as either the minimum of the operators or their product, whereas the OrMethod could be defined as either the maximum or the probabilistic or (probor). The latter is obtained as follows:
(8.10)probor(F1(x),F2(y))=F1(x)+F2(y)−F1(x)⁎F2(y).
On the other hand, the computing of the output of the rules’ consequent is easy to understand due to it only consisting of evaluating the input crisp values in each rule’s output function. For simplicity, we will call zi the output for the i-th rule in the FIS.
Later on, the system final output is calculated as follows:
(8.11)TSKOutput=∑i=1Nwizi∑i=1Nwi.
We can clearly see in the numerator of Eq. (8.11) that the output level zi of each rule is weighted by the activation strength wi of the rule. Then, all the weighted values are summed, and then divided by the summation of the rules’ activation strengths.
Finally, since the Sugeno model is based on rules with a crisp output as consequent, given by a function instead of a fuzzy set, the model has the advantage of avoiding the time consumption needed for the defuzzification methods in the Mamdani FIS.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128201251000208
Study and comparative analysis of perturb and observe (P&O) and fuzzy logic based PV-MPPT algorithms
Avinash Kumar Pandey, … Sachin Jain, in Applications of AI and IOT in Renewable Energy, 2022
11.3.2 Design of fuzzy logic based maximum power point tracking system
The composition of FL-MPPT utilizes the user experience about the system behavior. As it is given in Fig. 11.6, FLC has three basic stages: fuzzification stage, decision stage, defuzzification stage [13]. In the fuzzification stage, crisp inputs variables are converted to linguistic variables with the help of predefined MFs. These linguistic variables are utilized to make decisions according to the rules set up by the designer. In the third stage, the generated outputs are converted to crisp variables. For FL-MPPT applications, two inputs are utilized to generate one output in order to reach MPP. The input crisp variables can be described as follows:
Figure 11.6. Block diagram of fuzzy logic controller [13].
(11.8)dPpvdVpv=Epv(n)=Ppvn−Ppv(n−1)Vpvn−Vpv(n−1)
(11.9)ΔEpvn=Epvn−Epvn−1
Where Epv (n) is the slope of P-V characteristics for nth, ΔEpv(n) is the change in Epv (n) between the samples nth and (nth-1). Figs. 11.7 and 11.8
Figure 11.7. Input and output membership functions. (A) MFs of first Input Epv(n), (B) MFs of second input ΔEs(n). (C) MFs of output change in duty ratio ΔD.
Figure 11.8. Simulation results of fuzzy logic-maximum power point tracking based photovoltaic system under gradual changing atmospheric conditions. (A) Incident irradiance, (B) Module temperature, (C) photovoltaic power and converter output power, (D) photovoltaic voltage, (E) photovoltaic current photovoltaic, and (F) Duty ratio.
First Input (Epv(n)): This is the first fuzzy logic controller input. Its negative and positive deviations are measured at STC and classified into seven MFs: NMF3, NMF2, NMF1, ZMF, and PMF1, PMF2, and PMF3 as depicted in Fig. 11.9(A). Where α1, α2,… to α9 are the supports of the MFs.
Figure 11.9. Comparative simulation results of fuzzy logic and perturb and observe based photovoltaic-maximum power point tracking algorithms (A) Incident irradiance, (B) Module temperature, (C) photovoltaic module output power, (D) photovoltaic voltage, (E) photovoltaic current and (F) Duty ratio.
Second Input (ΔEpv(n)): This is second fuzzy logic controller input. Its negative and positive values are measured at STC and classified into five MFs: NMF3, NMF1, ZMF, and PMF1, and PMF3s as illustrated in Fig. 11.9(B). Where β1, β2…to β7 are the supports of the MFs. Tables 11.3 and 11.4.
Table 11.3. Nomenclature of membership functions.
| NMF3 | Negative big MF |
| NMF2 | Negative medium MF |
| NMF1 | Negative short MF |
| ZMF | Zero MF |
| PMF1 | Positive short MF |
| PMF2 | Positive medium MF |
| PMF3 | Positive big MF |
Table 11.4. Complete fuzzy rule base.
| Epv(n) | ΔEpv(n) | ||||
|---|---|---|---|---|---|
| NMF3 | NMF1 | ZMF | PMF1 | PMF3 | |
| PMF3 | ZMF | NMF1 | NMF2 | NMF3 | NMF3 |
| PMF2 | PMF1 | ZMF | NMF1 | NMF2 | NMF3 |
| PMF1 | PMF2 | PMF1 | ZMF | NMF1 | NMF3 |
| ZMF | PMF3 | PMF2 | PMF1 | ZMF | NMF3 |
| NMF1 | PMF3 | PMF3 | PMF2 | PMF1 | NMF2 |
| NMF2 | PMF3 | PMF3 | PMF3 | PMF2 | NMF1 |
| NMF3 | PMF3 | PMF3 | PMF3 | PMF3 | ZMF |
Output (ΔD): Defuzzification is the final stage of the FL controller. Here, the defuzzified output ΔD is the fuzzy controller output which is a variable step size control strategy. Therefore, the output ΔD is classified into seven MFs: NMF3, NMF2, NMF1, ZMF, and PMF1, PMF2, and PMF3 as shown in Fig. 8.7(C). In this system “center of gravity” method is used for the defuzzification of the FIS output. Where, γ1, γ2…to γ9 are the supports of the MFs. The output of the FLC is then used to calculate the updated duty ratio according to the following equation.
(11.10)Dk=Dn−1+ΔD
Where D(n) is the duty ratio of “nth” sample D(n-1) is the duty ratio of (nth-1) sample. This updated duty ratio is fed to the pulse width generator to produce a gating signal employed for the converter.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323916998000115
Diagnosis
Diego Galar, Uday Kumar, in eMaintenance, 2017
5.2.2.2.3 Fuzzy Rule-Based Systems
FRBS use fuzzy logic for inference. Fuzzy logic is based on fuzzy set theory in which binary set membership has been extended to include partial membership ranging from 0 to 1 (Zadeh, 1965). Fuzzy sets, in contrast to their crisp counterparts, have gradual transitions between defined sets; this allows the uncertainty associated with these concepts to be modeled directly. After defining each model variable with a series of overlapping fuzzy sets, the mapping of inputs to outputs can be expressed as a set of IF-THEN rules, which can be entirely specified from expert knowledge, or from data. However, unlike NNs, fuzzy models are prone to a rule explosion; that is, as the number of variables or fuzzy sets per variable increases, there is an exponential increase in the number of rules, making it difficult to specify the entire model from expert knowledge alone (Kosko, 1997). Various automated methods for optimizing fuzzy models are now available (Wang, 1994), including NNs and GAs.
The fuzzy sets and rules are called the fuzzy model knowledge base. Crisp inputs to the model are first fuzzified via this knowledge base, and a fuzzy inference engine is used to process the rules in parallel via a fuzzy inference procedure such as max-min or max-product operations (Jang et al., 1997). The fuzzy solution surface resulting from the execution of the rule base is defuzzified to produce the system output(s). Fuzzy IF-THEN rules can also be comprised of functional consequents, usually of a linear or polynomial form, in a formulation referred to as a Takagi–Sugeno–Kang model (Takagi and Sugeno, 1985; Sugeno and Kang, 1988). The crisp inputs are fuzzified according to the fuzzy set definitions, combined via the inference engine, and the functional consequents are weighted by the memberships that result from the execution of the rules. The overall result is a weighted average of the equations, as more than one rule can fire positively during a single pass of the rule base (Abrahart et al., 2008).
Fuzzy logic has found multiple applications, mainly in control theory (see, e.g., Kosko, 1997). FRBSs can be built by interviewing human experts or by processing historical data and forming a data-driven model. The basics of the latter approach and its use in a number of water-related applications can be found in Bárdossy and Duckstein (1995). FRBS have effectively been used for drought assessment (Pesti et al., 1996), prediction of precipitation events (Abebe et al., 2000a), analysis of groundwater model uncertainty (Abebe et al., 2000b), control of water levels in polder areas (Lobbrecht and Solomatine, 1999), and modeling rainfall-discharge dynamics (Vernieuwe et al., 2005).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128111536000051
Process Controllers
William Bolton, in Instrumentation and Control Systems (Third Edition), 2021
5.9.3 Fuzzy Logic Controller
Fuzzy logic has been used to control temperature by the action of varying the on-time of a heater, the system implementing the temperature control consisting of a temperature sensor, a microcontroller and actuator (Figure 5.40). The temperature sensor could be a thermo-transistor such as LM35 (see Section 2.7.6) and the actuator an electric heater. The analogue output of the sensor is converted by the microcontroller ADC input to a digital signal which can be processed by the fuzzy logic program stored in the microcontroller and the output used to operate the heater by switching it off or on according to the output from the fuzzy logic program, the fuzzy rules being:
Figure 5.40. Control system for heater.
IF the error is negative THEN timer switched on for very long period
IF the error is small negative THEN timer switched on for long period
IF the error is zero THEN timer switched on for medium period
IF the error is small positive THEN timer switched on for short period
IF the error is large positive THEN timer switched on very short period
Figure 5.41 shows how the basic components of a feedback control loop can appear when using fuzzy logic control in place of a traditional PID controller for closed-loop control. The input to the fuzzy logic system is ‘crisp’ inputs of the error, and the set of crisp inputs is transformed to the corresponding fuzzy set, probably a triangular membership function, which is then operated on by the fuzzy logic rule. The fuzzy logic controller rules can include rules such as
Figure 5.41. Fuzzy logic controller in feedback control loop.
IF error is zero and change in error is zero THEN output is zero
If error is zero and change in error is positive small THEN output is negative small
If error is zero and change in error is negative small THEN output is positive small
The IF–THEN rule describes the desired relationship between inputs and output to be implemented using fuzzy logic control and so make it possible to design a controller for a system with an unknown transfer function. The fuzzy set output is then defuzzified to give a ‘crisp’ output control signal to the plant. The defuzzification can be obtained by a method such as Mamdani’s inference method.
As an illustration of a fuzzy control system, consider one which might be used for automobile cruise control. Figure 5.42 shows the basic system with fuzzy controller having inputs of the error signals for the velocity and the rate of change of velocity, i.e. acceleration. It is a fuzzy PD control system. The derivative part, i.e. the rate of change of error, is obtained by using backward difference, i.e. the change in error during the last time interval divided by the length of the interval. Possible rules for the controller output for the application of the driving force by the engine are as follows:
Figure 5.42. Illustrative example of a fuzzy logic controller in the feedback loop for an automobile cruise control system.
IF velocity error means too fast and acceleration is negative THEN apply minimum force
IF velocity error means too fast and acceleration is zero THEN apply minimum force
IF velocity error means too fast and acceleration is positive THEN apply minimum force
IF velocity error is zero and acceleration is negative THEN apply normal force.
IF velocity error is zero and acceleration is zero THEN apply normal force.
IF velocity error is zero and acceleration is positive THEN apply normal force
IF velocity error means too slow and acceleration is negative THEN apply maximum force
IF velocity error means too slow and acceleration is zero THEN apply maximum force
IF velocity error means too slow and acceleration is positive THEN apply maximum force
Modern washing machines are quite often programmed to provide the optimum washing conditions using fuzzy logic. The inputs used to provide the facts for the fuzzy control can be the weight of the washing load, the type of fabric being washed and the degree of dirtiness of the load. The outputs can be the amount of detergent, the washing time, water level and temperature. One of the rules might then be something like:
IF amount of dirt is low and fabric type is less sensitive and weight is low THEN wash time is low and spin speed of machine is low and amount of water little and water temperature low
Fuzzy logic can also be used to implement a controller such as the conventional PD, PI or PID. For example, for a PD controller, fuzzification can be used to associate the linguistic terms positive, negative etc. with corresponding input values. Thus a positive error is one where the set value is greater than the feedback value and a negative one where it is less than the feedback value. A positive rate of change of error is where the error is increasing and a negative where the error is decreasing. The control rules might then include:
IF the error is positive and the rate of change of error is positive THEN the controller output is zero.
IF the error is positive and the rate of change of error is negative THEN the controller output is positive.
IF the error is negative and the rate of change of error is positive THEN the controller output is zero.
IF the error negative and the rate of change of error is negative THEN the controller output is zero.
Figure 5.43A illustrates such a PD control system and Figure 5.43B a PI control system.
Figure 5.43. (A) Fuzzy PD control system and (B) fuzzy PI control system.
Fuzzy logic programs, e.g. MATLAB’s Fuzzy Logic Toolbox, can be used to simulate fuzzy logic control systems and analyse the results.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128234716000058