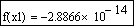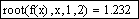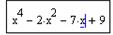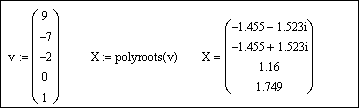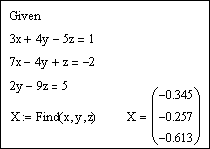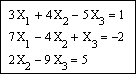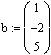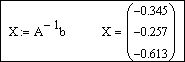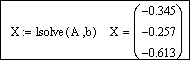|
0 / 0 / 0 Регистрация: 07.12.2018 Сообщений: 5 |
|
|
1 |
|
|
09.12.2018, 16:59. Показов 16182. Ответов 3
Имеется система из 4 уравнений с 4 неизвестными. Миниатюры
__________________
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
09.12.2018, 16:59 |
|
3 |
|
8363 / 6099 / 3234 Регистрация: 14.01.2014 Сообщений: 13,907 |
|
|
09.12.2018, 17:36 |
2 |
|
РешениеНайдите одно отличие Миниатюры
1 |
|
2614 / 2228 / 684 Регистрация: 29.09.2012 Сообщений: 4,578 Записей в блоге: 13 |
|
|
09.12.2018, 17:44 |
3 |
|
Выдаёт ошибку: Нужно максимально упрощать блок. Здесь два уравнения можно вынести за блок, заменив их функциями
0 |
|
0 / 0 / 0 Регистрация: 07.12.2018 Сообщений: 5 |
|
|
09.12.2018, 18:00 [ТС] |
4 |
|
Честно, не нашёл отличий, кроме того, что программа сработала.
0 |
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Find эта переменная не определена
Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
Когда ввожу find, оператор выделяется красным с примечанием переменная не определена. Все переменные вроде как задал. Подскажите пожалуйста в чем проблема?
Заранее спасибо за помощь!
-
Korobov V I
- Сообщения: 1609
- Зарегистрирован: Вт янв 21, 2003 5:12 pm
Re: Find эта переменная не определена
Сообщение Korobov V I » Сб ноя 23, 2013 2:09 pm
nikanto писал(а):Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
Когда ввожу find, оператор выделяется красным с примечанием переменная не определена. Все переменные вроде как задал. Подскажите пожалуйста в чем проблема?
Заранее спасибо за помощь!
1. В девятом уравнении переменная «c» набрана в русской раскладке клавиатуры.
2. Вместо функции Find примените функцию Minerr.
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Re: Find эта переменная не определена
Сообщение nikanto » Сб ноя 23, 2013 7:11 pm
Korobov V I писал(а):1. В девятом уравнении переменная «c» набрана в русской раскладке клавиатуры.
2. Вместо функции Find примените функцию Minerr.
спасибо букву исправил, но minerr не помог. Ничего не происходит =( просто равно появляется и все…
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вс ноя 24, 2013 1:34 am
а у меня после равно прямоугольничек черный. как место для цифры. Ладно, спасибо и на этом
-
Vladimir__
- Сообщения: 1660
- Зарегистрирован: Вс дек 21, 2003 8:52 am
Сообщение Vladimir__ » Вс ноя 24, 2013 2:36 pm
nikanto писал(а):а у меня после равно прямоугольничек черный. как место для цифры. Ладно, спасибо и на этом
А какую версию Mathcad вы используете?
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вс ноя 24, 2013 2:49 pm
Mathcad 14. Еще я попробовал подставить полученные значения в систему и равенство не выполняется. Наверное, я не до конца понимаю способ работы этих операторов. Количество неизвестных равно количеству уравнений. Зачем я задаю в начале приближенные значения? Разве здесь нужны итерации? Хотел избежать решения на листочках и трехэтажных подстановок, но, видимо не удастся =(
-
Vladimir__
- Сообщения: 1660
- Зарегистрирован: Вс дек 21, 2003 8:52 am
Сообщение Vladimir__ » Пн ноя 25, 2013 8:59 am
nikanto писал(а):Mathcad 14. Еще я попробовал подставить полученные значения в систему и равенство не выполняется. Наверное, я не до конца понимаю способ работы этих операторов. Количество неизвестных равно количеству уравнений. Зачем я задаю в начале приближенные значения? Разве здесь нужны итерации? Хотел избежать решения на листочках и трехэтажных подстановок, но, видимо не удастся =(
1. Обновите версию до последнего сервис релиза Mathcad 15 M020.
2. Подробнее про работу функцию «Minerr«:
http://www.exponenta.ru/soft/mathcad/us … 5/15_3.asp
http://www.sistemair.ru/dok/mathcad/text/index5-10.html
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вт ноя 26, 2013 2:12 am
Обновил. Minerr заработал. Только я так и не понял, как получить решение этой системы. То, что в табличке — это не корни.
-
VFO
- Сообщения: 4227
- Зарегистрирован: Ср фев 27, 2002 8:03 pm
Re: Find эта переменная не определена
Сообщение VFO » Вт ноя 26, 2013 8:11 am
[quote=»nikanto»]Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
quote]
А почему вы не используете функцию lsolve
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Re: Find эта переменная не определена
Сообщение nikanto » Ср ноя 27, 2013 11:03 am
VFO писал(а):quote]
А почему вы не используете функцию lsolve
Я до этого не пользовался Mathcad и на поисковый запрос «решение системы уравнений Mathcad» мне попалась функция Find. Хотел заставить комп решить мне уравнения, в итоге сижу решаю на листах, ибо так быстрее =)
Как найти неизвестную переменную в уравнении маткад
Mathcad дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно пятидесяти. В первой части этого раздела описаны процедуры решения систем уравнений. В заключительной части приведены примеры и проведено обсуждение некоторых часто встречающихся ошибок. Результатом решения системы будет численное значение искомого корня. Для символьного решения уравнений необходимо использовать блоки символьного решения уравнений. При символьном решении уравнений искомый корень выражается через другие переменные и константы.
Для решения системы уравнений выполните следующее:
- Задайте начальные приближения для всех неизвестных, входящих в систему уравнений. Mathcad решает уравнения при помощи итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению.
- Напечатайте ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений. При печати слова Given можно использовать любой шрифт, прописные и строчные буквы. Убедитесь, что при этом Вы не находитесь в текстовой области или параграфе.
- Введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями уравнений стоит символ =. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов ,
, и
.
- Введите любое выражение, которое включает функцию Find. При печати слова Find можно использовать шрифт любого размера, произвольный стиль, прописные и строчные буквы.
| Find(z1, z2, z3, . . . ) | Возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных. |
Функция Find возвращает найденное решение следующим образом:
- Если функция Find имеет только один аргумент, то она возвращает решение уравнения, расположенного между ключевым словом Given и функцией Find.
- Если функция Find имеет более одного аргумента, то она возвращает ответ в виде вектора. Например, Find(z1, z2) возвращает вектор, содержащий значения z1 и z2 , являющиеся решением системы уравнений.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называются блоком решения уравнений.
На Рисунке 5 показан рабочий документ, который использует блок решения уравнений для решения одного уравнения с одним неизвестным. Так как имеется только одно уравнение, то только одно уравнение появляется между ключевым словом Given и формулой, включающей функцию Find. Так как уравнение имеет одно неизвестное, то функция Find имеет только один аргумент. Для решения одного уравнения с одним неизвестным можно также использовать функцию root, как показано ниже:
Рисунок 5: Блок решения уравнений для одного уравнения с одним неизвестным.
Между ключевым словом Given и функцией Find в блоке решения уравнений могут появляться выражения строго определенного типа. Ниже приведен список всех выражений, которые могут быть использованы в блоке решения уравнений. Использование других выражений не допускается. Эти выражения часто называются ограничениями. В таблице, приведенной ниже, через x и y обозначены вещественнозначные скалярные выражения, а через z и w обозначены любые скалярные выражения.
| Условие | Как ввести | Описание |
| w = z | [Ctrl] = | Булево равенство возвращает 1, если операнды равны; иначе 0 |
| x > y | > | Больше чем. |
| x |
Следующие выражения недопустимы внутри блока решения уравнений:
- Ограничения со знаком
.
- Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
- Неравенства вида a -15 .
Причиной появления этого сообщения об ошибке может быть следующее:
- Поставленная задача может не иметь решения.
- Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число. Если решение задачи комплексное, то оно не будет найдено, если только в качестве начального приближения не взято также комплексное число. На Рисунке 11 приведен соответствующий пример.
- В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Метод поиска решения, который используется в Mathcad, не позволяет в этом случае построить следующее приближение, которое бы уменьшало невязку. Для поиска искомого решения пробуйте использовать различные начальные приближения или добавьте ограничения на переменные в виде неравенств, чтобы обойти точку локального минимума.
- В процессе поиска решения получена точка, которая не является точкой локального минимума, но из которой метод минимизации не может определить дальнейшее направление движения. Метод преодоления этой проблемы — такой же, как для точки локального минимума: измените начальное приближение или добавьте ограничения в виде неравенств, чтобы миновать нежелательную точку остановки.
- Возможно, поставленная задача не может быть решена с заданной точностью. Если значение встроенной переменной TOL слишком мало, то Mathcad может достигнуть точки, находящейся достаточно близко к решению задачи, но уравнения и ограничения при этом не будут выполнены с точностью, задаваемой переменной TOL. Попробуйте увеличить значение TOL где-нибудь выше блока решения уравнений.
Что делать, когда имеется слишком мало ограничений
Если количество ограничений меньше, чем количество переменных, Mathcad вообще не может выполнить блок решения уравнений. Mathcad помечает в этом случае функцию Find сообщением об ошибке “слишком мало ограничений”.
Задача, аналогичная той, которая приведена на Рисунке 12, называется недоопределенной. Ограничений в ней меньше, чем переменных. Поэтому ограничения не содержат достаточной информации для поиска решения. Поскольку функция Find имеет пять аргументов, Mathcad определяет, что требуется решить два уравнения с пятью неизвестными. Вообще говоря, такая задача обычно имеет бесконечное число решений.
При использовании блока решения уравнений в Mathcad необходимо задать количество уравнений по крайней мере не меньшее, чем число искомых неизвестных. Если зафиксировать значения некоторых переменных, удастся решить уравнения относительно оставшихся переменных. На Рисунке 13 показано, как, зафиксировав часть переменных, решить недоопределенную задачу из Рисунка 12. Поскольку функция Find содержит только два аргумента, z и w, Mathcad определяет переменные x, y и v как имеющие фиксированные значения 10, 50 и 0 соответственно. Блок решения уравнений становится в этом случае корректно определенным, потому что теперь имеются только две неизвестных, z и w, и два уравнения.
Рисунок 12: Функция Find имеет пять аргументов, поэтому Mathcad определяет, что требуется решить два уравнения с пятью неизвестными.
Рисунок 13: Проблема может быть решена, если уменьшить количество аргументов функции Find.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Как найти неизвестную переменную в уравнении маткад
Mathcad для студентов
Mathcad для начинающих
Скачать программы бесплатно
Уравнения с одним неизвестным в Mathcad
Простейший способ найти корень уравнения с одним неизвестным в Mathcad обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение — root (f(x),x) Если уравнение в Mathcad содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.
В случае, если решаемое уравнение в Mathcad представлено полиномом, то все его решения могут быть получены с помощью функции polyroots (v). В качестве аргументов этой функции выступает вектор коэффициентов полинома –v, а результат представляется в виде вектора корней полинома. На листинге представлен пример нахождения корней уравнений с использованием функций root ( ) и polyroots ( ).
Другим способом решения уравнений в Mathcad является применение специального вычислительного блока, начинающегося с ключевого слова given с использованием функций find( ) и minerr ( ).
Блок имеет следующую структуру:
Начальное значение искомой переменной
Выражение с использованием функции find( ) или minerr ( )
Нахождение корней уравнения в Mathcad с использованием блока given…find ( ) в чем – то аналогично использованию функции root ( ). В Mathcad задается начальное значение для искомой переменной, после находится решение, ближайшее к заданному начальному условию. Использовании блока given…minerr ( ) имеет существенные особенности. Решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что ищется не решение системы, а минимальная невязка уравнений. На листинге рассмотрена функция, заведомо не имеющая действительных корней и при использовании блока given…minerr ( ) найдено решение, значение, которое наиболее приближено к оси х, то есть обеспечивает минималь-ную невязку. Значение невязки (ошибки) показывает системная переменная ERR.
Mathcad find переменная не определена
MathCad | ANSYS CFX | MS Office
Поиск по сайту
Выбор языка
Решение уравнений в MathCad
Часто в курсовом проекте, либо в лабораторной работе встает вопрос о решении какого-либо сложного большого уравнения с одним неизвестным. Не всегда хочется тратить 10 — 20 минут на рутинные преобразования в процессе которых, велика вероятность допущения ошибки. Целесообразно воспользоваться математической программой (в данном случае MathCad), которая быстро и правильно сможет дать ответ. Мы рассмотрим пример использования 2-ух способов решения уравнений, причем как в числах так и в символьном виде.
Способ №1: использование вычислительного блока Given — Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем первое слово Given. Это служебное слово. Оно «подключает» определенные программные модули mathcad, необходимые для решения уравнения. Эти модули в своем составе содержат основные численные методы решения: метод бисекции, простой итерации и пр. Далее пишется наше уравнение в любом — явном или неявном виде. Само уравнение набирается с клавиатуры с использованием логического символа «равно». На панельке Boolean (Булева алгебра) он выделен жирным шрифтом (см. рис. 1). 
Далее пишется слово Find(x) (где х — переменная). Это функция, которая и получает ответ. Функцию Find(x) можно присвоить какой-либо переменной и использовать далее в расчетах. Для получения результата, после Find(x) следует поставить символ «→» либо «=» (см. рис. 2). 
В зависимости от сложности уравнения через некоторое время MathCad выведет результат.
Возможности MathCad позволяют определить корень как в численном виде (т. е. результат решения уравнения представляет собой число) так и в символьном (результат — выражение). Для численного определения корня необходимо задать (определить) ВСЕ переменные входящие в уравнение и даже искомую переменную. MathCad воспринимает задание искомой переменной как начальное приближение корня. Крайне важно задаться начальным приближением, поскольку без него корень уравнения невозможно определить в силу особенностей используемых численных методов. Нужно отметить, что некорректное задание начального приближения часто становится причиной получения неверного результата либо его отсутствия вообще. Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
В том случае, если необходимо решить уравнение относительно какой-либо переменной в символьном виде, то нет необходимости задаваться значениями всех входящих в уравнение параметров и начальным приближением переменной. В этом случае достаточно ввести уравнение (также через «жирное равно») и после оператора Find(x) поставить «→». При этом будут работать уже другие функции MathCad, которые заточены под символьное преобразование и упрощение выражений. Результатом решения будет выражение. Стоит отметить, что MathCad сможет записать решение далеко не всякого уравнения. В этом смысле его возможности ограничены.
Для подтверждения и закрепления выше сказанного, Вам предлагается скачать и познакомиться с примерами решения уравнений как в численном так и в символьном виде.
Пример №1. Решение уравнения в MathCad с помощью блока Given Find численно: Скачать
Пример №2. Решение уравнения в MathCad с помощью блока Given Find символьно: Скачать
Способ №2: Применение метода solve:
Этот метод по существу не отличается от выше рассмотренного, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Given и Find. После ввода уравнения на панели Symbolic нажимаем кнопку solve (см. рис. 3), определяем через запятую искомую переменную, жмем «→» и получаем ответ. 
Иногда, то что не получается найти с помощью Given Find получается в solve.
Пример №3. Решение уравнения в MathCad с помощью solve: Скачать
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение 
Решение.
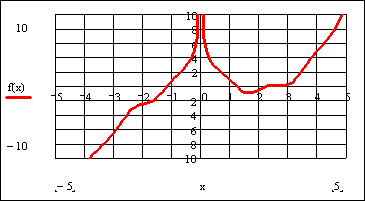
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика 
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение 
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение 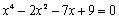
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать 
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить 
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений 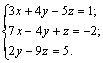
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
программирование mathcad скалярный трехмерный
Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:
— задать начальное приближение
— ввести служебное слово
- — записать уравнение, используя знак боулево равно
- — написать функцию find с неизвестной переменной в качестве параметра
В результате после знака равно выведется найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
В Mathcad можно писать программы двух видов
- 1)в виде скриптов(последовательность команд)
- 2)в виде настоящих программ с входными и выходными параметрами.
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).
Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.
Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).
Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
источники:
http://allmathcad.com/ru/uravneniya-s-odnim-neizvestnym.html
http://web-shpargalka.ru/mathcad-find-peremennaja-ne-opredelena.php
Таблица. Сообщения об ошибках
Ошибка
Перевод
Вероятная причина
Возможные пути устранения
Сообщения об ошибках в численных вычислениях
A «Find» or «Minerr» must be preceded by a matching «Given»
Find или Minerr должны предваряться ключевым словом Given
Эта ошибка выделяет функцию Find или Minerr при их несогласо-
ванности с Given
Каждый вычислите-
льный блок,
который заканчивается функцией Find или Minerr, должен начинаться с ключевого слова Given
All evaluations resulted in either an error or a complex result
Вычисления приводят к ошибке или комплексно-
му результату
Mathcad не может начертить некоторые точки, потому что не существует действительных значений для их нанесения на график
Это сообщение может появиться, если имеется ошибка или все значения комплексные
Arguments in function definitions must be names
Аргументы в определениях функции должны быть именами
Выделенное определение функции содержит неправильный перечень аргументов
В списке аргументов должны быть правильно поименованы переменные, или список имен необходимо отделить запятыми
At least one limit must be infinity
По крайней мере один предел должен быть бесконечным
Когда для интегриро-
вания выбран алгоритм бесконечного предела, то по крайней мере один из пределов интеграла должен быть бесконечным
Тип бесконечности вводится нажатием сочетания клавиш <Ctrl>+<Shift>+<2>.
Для изменения алгоритма, использующего бесконечный предел, или для вычисления какого-либо другого интеграла щелкните на интеграле правой кнопкой мыши и измените алгоритм с помощью контекстного меню
Can only evaluate an n-th order derivative when n=0,1..5.
Можно вычислить n-й порядок производной, только когда п=0,1..5
Порядок производной должен быть одним из следующих чисел: 0, 1, 2,. ..5.
Если Вы хотите посчитать производную более высокого порядка, то делайте это с помощью символьного дифференци-
рования
Can’t evaluate this function when its argument less than or equal to zero
Невозможно вычислить эту функцию, когда ее аргумент меньше или равен нулю
Такое сообщение может касаться XY- или полярных графиков, имеющих логарифмические оси, на которых или пределы, или некоторые из значений, не положительны
Отрицательные числа и ноль не могут быть расположены нигде на логарифмических осях. Смените тип осей графика или постройте его для других значений
Can’t converge to a solution
Не сходится к решению
Численный метод расходится (не может найти решения)
Убедитесь, что операция не применяется к функции в области непосредственной близости точки ее сингулярности (деления на ноль). Попробуйте поменять параметры численного метода (например начальное приближение).
Попробуйте увеличить константу TOL, т. е. осуществить поиск решения с худшей погрешностью.
Попробуйте поменять численный алгоритм, если это возможно (вызвав контекстное меню нажатием на месте ошибки правой кнопки мыши)
Can’t define the same variable more than once in the same expression
Невозможно определить ту же самую переменную более одного раза в одном и том же выражении
Вы пытаетесь вычислить одну и ту же переменную дважды в одном выражении
Пример подобной ошибки: если Вы создаете вектор с левой стороной а := и используете это же имя справа, то получите ошибку
Can’t determine what units the result of this operation should have
Невозможно определить, в каких единицах следует быть результату этой операции
Вы возвели выражение, содержащее единицы измерения, в степень, являющуюся переменной в неких пределах или вектором. В результате невозможно определить размерность результата
Если выражение включает в себя единицы измерений, то можно возводить его только в действительную фиксированную степень
Cant divide by zero
Деление на ноль невозможно
Где-то в программе или внутри численного метода возникло деление на ноль
Найдите место деления на ноль и устраните его
Попробуйте поменять параметры численного метода, константы точности или сам численный алгоритм
Could not find a solution
Невозможно найти решение
Численный метод расходится (не может найти решения)
См. «Can’t converge to a solution»
Can’t find the data file you’re trying to use
Невозможно найти файл, который Вы пытаетесь использовать
Невозможно найти файл данных или другой тип файла, к которому Вы обращаетесь
Удостоверьтесь, что такой файл существует в указанном месте
Can’t have anything with units or dimensions here
Здесь нет ничего в единицах измерений или в размерностях
Это выражение использует единицы измерений где-то, где они не разрешены
Единицы измерений не разрешены:
— в аргументах большинства функций;
— в экспонентах; — в верхних и нижних индексах.
Для того чтобы использовать выражения с единицами измерений, вначале переведите это выражение в UnitsOf (выражение)
Can’t have more than one array in a contour plot
Нельзя иметь более одного массива в контурном графике
Вы вводите более одного массива в местозаполнитель контурного или поверхностного графика
Можно иметь только один массив в данном местозаполнителе, т. к. графики могут выдавать лишь одну поверхность в один момент времени
Can’t perform this operation on the entire array at once. Try using «vectorize» to perform it element by element
Невозможно представить эту операцию в целом массиве сразу. Попытайтесь использовать векторизацию, чтобы представить элемент за элементом
Например, можно увидеть это сообщение при попытке разделить один вектор на другой
Для того чтобы применять функцию или оператор к каждому элементу вектора или матрицы, используйте оператор векторизации
Can’t plot this many points
Невозможно начертить график с таким большим количеством точек
Попытка построения графика с числом точек, превосходящим возможное
Попробуйте сделать число точек меньше, чем 150 000
Can’t put a «:=» inside a solve block
Нельзя помещать «:=» внутрь вычислительного блока
Внутри вычислительного блока не должно быть формулировки присваивания. Он должен содержать только булевы выражения
Используйте панель с булевыми операторами
Can’t raise an expression having units to a complex power
Нельзя возводить в комплексную степень ыражение, имеющее единицы измерений
Это выражение содержит единицы измерений, а Вы возводите его в комплексную степень
Выражение с единицами измерений можно возводить только в действительную степень. Для того чтобы возводить в комплексную степень выражение с единицами измерений, вначале переведите это выражение в UnitsOf (выражение) — единицы измерений будут отменены
Can’t solve a system having this many equations
Невозможно решить систему, имеющую так много уравнений
Mathcad не способен решить систему
См. определение термина «вычислительный блок » (гл. 
Can’t understand something in this data file
Невозможно что-то понять в файле данных
Файл, к которому Вы пытаетесь получить доступ при помощи READ или READ*, имеет дефект
Файл должен быть ASCII-текстом
Все строки файла должны иметь тот же номер значений, что используется в READ*
Если файл имеет требуемый формат, а это сообщение продолжает появляться, попробуйте удалить любую часть текста из файла
Can’t understand the name of this function
Невозможно понять имя этой функции
Такое сообщение может появиться, если в качестве имени функции используется, например, число 6(х)
Выражение должно соответствовать требованиям, предъявляемым в Mathcad к написанию имен функций
Can’t understand the way this range variable is defined
Невозможно понять определение ранжированной переменной
Определение ранжированной переменной неверно
Вводя область определения ранжированной переменной, необходимо использовать один из следующих видов:
Rvar := nl . .n2 Rvar := nl,n2 . .пЗ
Cant understand this number
Невозможно понять это число
Это выражение содержит символ или десятичную точку там, где это непозволительно
Вы увидите эту ошибку, например, если случайно запишете число так: .452.
Cant use a range variable in a solve block
Невозможно использовать ранжированную переменную в вычислительном блоке
Эта ошибка появится, если использовать область определения переменной в неподходящем месте
Придумайте алгоритм, не допускающий применения ранжированной переменной в вычислительном блоке
Cannot evaluate this accurately at one or more of the values you specified
Невозможно точно вычислить одно или более значений
Эта ошибка появляется, если попытаться вычислить функцию для аргумента, находящегося за пределами точной области определения функции
Проверьте область определения функции
Cross product is defined only for vectors having exactly three elements
Векторное произведение определяется только для векторов, имеющих точно три элемента
Векторное произведение определяется только для векторов, имеющих точно три элемента
См. определение векторного произведения (гл. 9)
Can’t evaluate this expression. It may have resulted in an overflow or an infinite loop
Невозможно вычислить это выражение. Это может быть результатом переполнения или бесконечных циклов
Это функциональное определение может содержать слишком много вложенных функций. Или функция может быть константой в бесконечных циклах
Проверьте несколько итераций цикла
Degree of the polynomial must be between 1 and 99.
Степень полинома должна находиться в пределах между 1 и 99
Вектор, пропущенный через функцию поиска корней полинома, должен содержать по крайней мере 2 и не более 99 элементов
Dimensions must be >4
Размерность должна быть >4
Эта матрица должна иметь по крайней мере 4 ряда и 4 столбца
End of file
Коней; файла
Вы пытаетесь прочитать больше значений в файле данных, чем там имеется
Например, если файл данных имеет 10 значений, а записано выражение i : =1…100
xi : =READ* ( file) , то появится это сообщение
End points cannot be the same
Конечные точки не могут быть одинаковы
Это сообщение появляется при некорректном решении дифференциальных уравнений
Конечные точки интервала, на котором будет вычисляться решение, должны быть различны
Equation too large
Уравнение слишком большое
Это выражение слишком сложное для вычисления
Разбейте выражение на два или более простых
Floating point error
Ошибка вычислений с плавающей точкой
Функция вычисляется в точке, в которой это не разрешено
Found a singularity while evaluating this expression. You may be dividing by zero
Найдена сингулярность при вычислении этого выражения. Возможно, Вы делите на ноль
Вычисляется функция или выполняется операция с недопустимым значением
Например, это сообщение возникнет при попытке деления на ноль или обращения сингулярной матрицы; разберитесь, где это происходит
Found a number with a magnitude greater than 1СГ307
Найдено число, превышающее значение 10307
Попробуйте поменять параметры численного алгоритма или сам алгоритм
Illegal context. Press <F1> for help
Недопустимый контекст. Нажмите <F1>, чтобы получить помощь
Часто встречается при синтаксических ошибках
Проверьте синтаксис и порядок расположения формул в документе
Illegal dimensions
Недопустимые размерности
Матрица, на которую Вы ссылаетесь, не имеет достаточно строк или столбцов
Введите имя матрицы с клавиатуры и нажмите знак «=», чтобы проверить число ее строк и столбцов
Integer too large/ Integer too small
Целое число слишком большое/ слишком маленькое
Это число слишком велико/мало для работы с ним
Если Вы работаете со встроенными функциями, то щелкните на имени функции и вызовите подсказку с помощью <F1>
Invalid format
Недопустимый формат
Аргументы этой функции могут быть некорректны
Если Вы работаете со встроенными функциями, то щелкните на имени функции и вызовите подсказку с помощью <F1 >
Live symbolics not available
Символьные вычисления неприменимы
Си. гл. 5
Must be <= 10000
Это значение должно быть <=10000
Must be >= 10л-16
Это значение должно быть >=1<Г16
Must be string
Функция или оператор должен быть строковым аргументом
См. гл. 10
Must be between two lock regions
Должно быть между двумя запертыми областями
См. гл. 16.
Must be function
Этот аргумент должен быть функцией
Must be increasing
Значения вектора должны быть возрастающими
Введите с клавиатуры имя вектора и знак =, чтобы проверить его значения
Must be less than the number of data points
Должен быть меньше, чем число точек данных
Этот аргумент должен быть меньше, чем число точек имеющихся данных
Must be positive
Должен быть положительным
Невозможно вычислить эту функцию, когда ее значения меньше или равны нулю
Это сообщение может касаться построения XY- или полярных графиков с логарифмическими осями. Отрицательные числа или ноль не могут располагаться на логарифмических осях
Must be real
Должно быть действительным
Это значение должно быть действительным. Его мнимая часть должна быть нулем
Примером таких выражений могут служить нижний и верхний индексы, решения дифференциальных уравнений, углы
Must be real scalar
Должно быть действительным скаляром
Это значение не должно быть комплексным или мнимым
Must be real vector
Должно быть действительным вектором
Этот вектор не может иметь комплексные или мнимые элементы. Он должен также быть вектором-столбцом, а не строкой
Must be square
Должна быть квадратной
Эта ошибка выделяет неквадратную матрицу в той операции или функции, в которой ей следует быть квадратной
Например, матрица должна быть квадратной при обращении, возведении ее в степень, или в функциях eigenvals и eigenvec
No solution found
Не найдено решение
Если Вы используете встроенные функции, то щелкните мышью на имени функции и нажмите клавишу <F1>, для того чтобы быть уверенным в корректности использования функции. Однако решение может просто не существовать.
См. также «Can’t converge to a solution»
Not enough memory for this operation
Для этой операции недостаточно памяти
Не хватает памяти, чтобы завершить это вычисление
Попытайтесь освободить немного памяти путем уменьшения массива или матрицы (Mat head тратит около 8 байт памяти на каждый элемент матрицы), или удаления каких-либо больших побитовых отображений, массивов, матриц
Singular matrix
Сингулярная матрица
Эта матрица не может быть ни сингулярной, ни близкой к сингулярности
Матрица называется сингулярной, если ее определитель равен нулю. Матрица близка к сингулярной, если она имеет высокое число обусловленности (см. гл. 9)
The expression to the left of the equal sign cannot be defined
Выражение слева от знака равенства не может быть определено
В левой части находится что-то, что не является допустимым определяемым выражением
В левой части можно разместить одно из следующих определений:
— имя переменной;
— имя переменной с верхним или нижним индексом;
— явный вектор или матрицу;
— имя функции с аргументами: f(x,y)
Любые другие выражение не допустимы
The number of rows and/or columns in these arrays do not match
Число рядов и/или столбцов в этих массивах не согласовано
Попытка произвести матричные или векторные операции над массивами, размеры которых не совпадают
Например, сложение двух матриц разного размера недопустимо. Матричное умножение требует, чтобы число столбцов первой матрицы совпадало с числом строк второй (см, разд. 9. 1)
The units in this expression do not match
Размерности в этом выражении не согласованы
Это сообщение появится, если складываются два элемента разной размерности либо создана матрица, элементы которой имеют разную размерность, либо Вы пытаетесь решить систему уравнений для неизвестных переменных разной размерности
Проверьте использование размерных переменных
There is an extra comma in this expression
В выражении лишняя запятая
Запятые должны использоваться для того, чтобы отделять:
аргументы в функции
первые два элемента области в определении интервала
выражения в графике элементы во входной таблице нижние индексы в матрице
Любые другие применения запятой приводят к ошибке. Например, запись 4,000 неправильная, а запись 4000 — правильная
This expression is incomplete. You must fill in the placeholders
Это выражение неполное. Необходимо добавить содержимое в место-заполнители
Не заполнены указанные местоза-полнители
Необходимо дописать числа или выражения в указанные местозаполнители
This expression is incomplete. You must provide an operator
Это выражение неполное. Необходимо вставить оператор
Не заполнены местозаполнители оператора или пустое пространство между двумя операндами
Это могло произойти при удалении оператора, проверьте правильность ввода выражения
This function has too many arguments
Эта функция имеет слишком много аргументов
Выделенное выражение содержит функцию с числом аргументов большим, нежели требуется
Проверьте правильность применения функции
This function is undefined at one or more of the points you specified
Эта функция не определена для одной или более точек
Попытка вычисления оператора или функции с неподходящими значениями
Например, -3′- выдаст ошибку, 1п(0), т. к. факториал не определен для отрицательного числа, а логарифм для нуля
This function needs more arguments
Этой функции не хватает аргументов
Выделенное выражение содержит функцию с меньшим, нежели требуется, числом аргументов
Для встроенных функций щелкните мышью на имени функции и воспользуйтесь подсказкой <F1>, чтобы проверить правильность числа и типа аргументов; для функции пользователя проверьте ее определение
This operation can only be performed on a function
Эта операция может быть произведена только над функцией
Этот аргумент должен быть функцией
Для встроенных функций щелкните мышью на имени функции и воспользуйтесь подсказкой <F1 >
This operation can only be performed on an array. It can’t be performed on a number
Эта операция может быть произведена только над массивом. Она не может быть произведена над числом
Например, это сообщение появится, если переменная верхнего индекса определена как скаляр. Поскольку переменная верхнего индекса представляет собой столбец матрицы, то ее следует определять как вектор
Для поверхностных или контурных графиков массив данных должен иметь, по крайней мере, два ряда и два столбца
This operation can only be performed on a number or an array
Эта операция может быть произведена только над числом или массивом
Используемая функция или оператор требуют представления в виде константы, матрицы или вектора
This operation can only be performed on a string
Эта операция может быть произведена только над строкой
Используемая функция или оператор требуют представления в виде строки. Например строковые функции обычно требуют по крайней мере одного строкового аргумента
This subscript is too large
Этот нижний индекс слишком велик
Попытка использовать верхний или нижний индекс, который превышает ограничения
This value must be a matrix
Это значение должно быть матрицей
Попытка произвести матричную операцию не над матрицей
This value must be a vector. It can be neither a matrix nor a scalar
Это значение должно быть вектором. Оно не может быть ни матрицей, ни скаляром
Это сообщение маркирует матрицу или скаляр в операциях, которые требуют вектора (одностолбцового массива). Например суммирование элементов вектора
This value must be an integer greater than 1
Это значение должно быть целым числом, превосходящим 1
Это значение должно быть >1
При использовании встроенных функций щелкните мышью на имени функции и нажмите клавишу <F1>
This variable or function is not defined above
Эта переменная или функция не определена выше
Имя неопределенной функции будет помечено красным цветом
Удостоверьтесь, что эта функция или переменнуя определена выше. Это сообщение появится, если переменная некорректно используется в глобальном определении. Эта ошибка часто свидетельствует о том, что другое уравнение выше в документе является ошибкой. В этом случае все выражения, использующие выражение с ошибкой, будут помечены красным цветом
Underflow
Потеря значимости (исчезновение значащих разрядов)
Из-за ограничений, присущих представлению чисел на компьютере, числа, которые слишком малы, не могут быть представлены. Это сообщение появляется, когда выражение включает такое число. Иногда, особенно в сложных вычислениях, промежуточный результат будет слишком мал, и вся разрядная сетка заполнится нулями
Value of subscript or superscript is too big (or too small) for this array
Значение нижнего или верхнего индекса слишком велико (или слишком мало) для этого массива
Это выражение использует нижний или верхний индекс, который относится к несуществующему элементу массива
This is not a scalar. Press <F1 > for help
Это не скаляр. Нажмите клавишу <F1>, чтобы получить помощь
Использован вектор или выражение с интервалами, или какой-то другой тип выражения, где требуется применение скаляра
You have one solve block inside another. Every «Given» must have a matching «Find» or «Min-err».
Один вычислительный блок содержится внутри другого. Каждому ключевому слову Given должно сопоставляться Find или Minerr
Указаны два ключевых слова Given подряд без Find или Minerr посередине. Вычислительный блок не может иметь внутри себя другой вычислительный блок
В качестве альтернативы можно задать функцию в терминах одного вычислительного блока и использовать ее внутри другого вычислительного блока. Во многих случаях это дает тот же самый эффект
You interrupted calculation. To resume, click here and choose «Calculate» from the «Math» menu
Вычисления прерваны. Для того чтобы продолжить, щелкните здесь и выберите пункт Calculate меню Math
Вычисления прерваны нажатием клавиши <Esc>. Для того чтобы пересчитать выделенное уравнение, наведите на него курсор и воспользуйтесь меню Math / Calculate (Математика/ Вычислить)
Сообщение об ошибках в символьных вычислениях
Argument too large (Integer too large in context, Object too large)
Аргумент слишком велик
Обычно это результат вычисления выражения с плавающей точкой со значением большим, чем около 10×10 миллиардов
Discarding large result
Сброс большого результата
Ответ слишком велик для отображения его в отформати-
рованной математической области
Можно разместить ответ в буфере обмена
Expecting array or list
Ожидается массив или список
Операторы в упрощаемом или вычисляемом выражении требуют векторных или матричных операндов
Expression contains non-symbolic operators
Выражение содержит несимвольные операторы
Применена символьная операция к выражению, содержащему местоза-полнители оператора или переменной
Floats not handled
С плавающей запятой не поддерживается
Команда Factor была применена к выражению с десятичным числом
Illegal function syntax
Недопустимый синтаксис функции
Символьный процессор не может интерпретировать выражение, подобное (f)(x)
Invalid arguments
Недопустимые аргументы
Символьный процессор не может выполнить требуемую операцию для данных аргументов
Это сообщение появится, если, например, применить скалярную функцию к массиву без использования оператора векторизации и выбрать команду Symbolics / Simplify (Символика / Упростить)
Invalid range
Недопустимый интервал
Для поиска численного решения уравнения символьный процессор пытается вычислить одну из своих встроенных функций за пределами области ее определения
No answer found; stack limit reached
Ответа не найдено
Символьный процессор достиг предела своих возможностей без вычисления или упрощения, которое затребовал пользователь
No answer found
Ответа не найдено
Символьный процессор не смог найти точного решения уравнения
No closed form found for
Не найдено замкнутой формы для
Символьный процессор не смог найти интеграл или сумму, или произведение в замкнутой форме
Syntax error
Синтаксическая ошибка
Обычно результат применения символьной операции в неподходящих или некорректных выражениях. Символьные вычисления выражений с размерностями также приведут к появлению этого сообщения

 Сообщение было отмечено Nikolay-26 как решение
Сообщение было отмечено Nikolay-26 как решение

 , и
, и 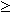 .
.
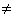 .
.