Floating point error python это

Обработка ошибок увеличивает отказоустойчивость кода, защищая его от потенциальных сбоев, которые могут привести к преждевременному завершению работы.

Прежде чем переходить к обсуждению того, почему обработка исключений так важна, и рассматривать встроенные в Python исключения, важно понять, что есть тонкая грань между понятиями ошибки и исключения.

Ошибку нельзя обработать, а исключения Python обрабатываются при выполнении программы. Ошибка может быть синтаксической, но существует и много видов исключений, которые возникают при выполнении и не останавливают программу сразу же. Ошибка может указывать на критические проблемы, которые приложение и не должно перехватывать, а исключения — состояния, которые стоит попробовать перехватить. Ошибки — вид непроверяемых и невозвратимых ошибок, таких как OutOfMemoryError, которые не стоит пытаться обработать.

Обработка исключений делает код более отказоустойчивым и помогает предотвращать потенциальные проблемы, которые могут привести к преждевременной остановке выполнения. Представьте код, который готов к развертыванию, но все равно прекращает работу из-за исключения. Клиент такой не примет, поэтому стоит заранее обработать конкретные исключения, чтобы избежать неразберихи.

Ошибки могут быть разных видов:

• Синтаксические
• Недостаточно памяти
• Ошибки рекурсии
• Исключения

Разберем их по очереди.

Синтаксические ошибки (SyntaxError)

Синтаксические ошибки часто называют ошибками разбора. Они возникают, когда интерпретатор обнаруживает синтаксическую проблему в коде.

Рассмотрим на примере.

a = 8
b = 10
c = a b

File "", line 3
 c = a b
       ^
SyntaxError: invalid syntax

Стрелка вверху указывает на место, где интерпретатор получил ошибку при попытке исполнения. Знак перед стрелкой указывает на причину проблемы. Для устранения таких фундаментальных ошибок Python будет делать большую часть работы за программиста, выводя название файла и номер строки, где была обнаружена ошибка.

Недостаточно памяти (OutofMemoryError)

Ошибки памяти чаще всего связаны с оперативной памятью компьютера и относятся к структуре данных под названием “Куча” (heap). Если есть крупные объекты (или) ссылки на подобные, то с большой долей вероятности возникнет ошибка OutofMemory. Она может появиться по нескольким причинам:

• Использование 32-битной архитектуры Python (максимальный объем выделенной памяти невысокий, между 2 и 4 ГБ);
• Загрузка файла большого размера;
• Запуск модели машинного обучения/глубокого обучения и много другое;

Обработать ошибку памяти можно с помощью обработки исключений — резервного исключения. Оно используется, когда у интерпретатора заканчивается память и он должен немедленно остановить текущее исполнение. В редких случаях Python вызывает OutofMemoryError, позволяя скрипту каким-то образом перехватить самого себя, остановить ошибку памяти и восстановиться.

Но поскольку Python использует архитектуру управления памятью из языка C (функция malloc()), не факт, что все процессы восстановятся — в некоторых случаях MemoryError приведет к остановке. Следовательно, обрабатывать такие ошибки не рекомендуется, и это не считается хорошей практикой.

Ошибка рекурсии (RecursionError)

Эта ошибка связана со стеком и происходит при вызове функций. Как и предполагает название, ошибка рекурсии возникает, когда внутри друг друга исполняется много методов (один из которых — с бесконечной рекурсией), но это ограничено размером стека.

Все локальные переменные и методы размещаются в стеке. Для каждого вызова метода создается стековый кадр (фрейм), внутрь которого помещаются данные переменной или результат вызова метода. Когда исполнение метода завершается, его элемент удаляется.

Чтобы воспроизвести эту ошибку, определим функцию recursion, которая будет рекурсивной — вызывать сама себя в бесконечном цикле. В результате появится ошибка StackOverflow или ошибка рекурсии, потому что стековый кадр будет заполняться данными метода из каждого вызова, но они не будут освобождаться.

def recursion():
    return recursion()

recursion()

---------------------------------------------------------------------------

RecursionError                            Traceback (most recent call last)

 in 
----> 1 recursion()


 in recursion()
      1 def recursion():
----> 2     return recursion()


... last 1 frames repeated, from the frame below ...


 in recursion()
      1 def recursion():
----> 2     return recursion()


RecursionError: maximum recursion depth exceeded

Ошибка отступа (IndentationError)

Эта ошибка похожа по духу на синтаксическую и является ее подвидом. Тем не менее она возникает только в случае проблем с отступами.

Пример:

for i in range(10):
    print('Привет Мир!')

  File "", line 2
    print('Привет Мир!')
        ^
IndentationError: expected an indented block

Исключения

Даже если синтаксис в инструкции или само выражение верны, они все равно могут вызывать ошибки при исполнении. Исключения Python — это ошибки, обнаруживаемые при исполнении, но не являющиеся критическими. Скоро вы узнаете, как справляться с ними в программах Python. Объект исключения создается при вызове исключения Python. Если скрипт не обрабатывает исключение явно, программа будет остановлена принудительно.

Программы обычно не обрабатывают исключения, что приводит к подобным сообщениям об ошибке:

Ошибка типа (TypeError)

a = 2
b = 'PythonRu'
a + b

---------------------------------------------------------------------------

TypeError                                 Traceback (most recent call last)

 in 
      1 a = 2
      2 b = 'PythonRu'
----> 3 a + b


TypeError: unsupported operand type(s) for +: 'int' and 'str'

Ошибка деления на ноль (ZeroDivisionError)

10 / 0

---------------------------------------------------------------------------

ZeroDivisionError                         Traceback (most recent call last)

 in 
----> 1 10 / 0


ZeroDivisionError: division by zero

Есть разные типы исключений в Python и их тип выводится в сообщении: вверху примеры TypeError и ZeroDivisionError. Обе строки в сообщениях об ошибке представляют собой имена встроенных исключений Python.

Оставшаяся часть строки с ошибкой предлагает подробности о причине ошибки на основе ее типа.

Теперь рассмотрим встроенные исключения Python.

Встроенные исключения

BaseException
 +-- SystemExit
 +-- KeyboardInterrupt
 +-- GeneratorExit
 +-- Exception
      +-- StopIteration
      +-- StopAsyncIteration
      +-- ArithmeticError
      |    +-- FloatingPointError
      |    +-- OverflowError
      |    +-- ZeroDivisionError
      +-- AssertionError
      +-- AttributeError
      +-- BufferError
      +-- EOFError
      +-- ImportError
      |    +-- ModuleNotFoundError
      +-- LookupError
      |    +-- IndexError
      |    +-- KeyError
      +-- MemoryError
      +-- NameError
      |    +-- UnboundLocalError
      +-- OSError
      |    +-- BlockingIOError
      |    +-- ChildProcessError
      |    +-- ConnectionError
      |    |    +-- BrokenPipeError
      |    |    +-- ConnectionAbortedError
      |    |    +-- ConnectionRefusedError
      |    |    +-- ConnectionResetError
      |    +-- FileExistsError
      |    +-- FileNotFoundError
      |    +-- InterruptedError
      |    +-- IsADirectoryError
      |    +-- NotADirectoryError
      |    +-- PermissionError
      |    +-- ProcessLookupError
      |    +-- TimeoutError
      +-- ReferenceError
      +-- RuntimeError
      |    +-- NotImplementedError
      |    +-- RecursionError
      +-- SyntaxError
      |    +-- IndentationError
      |         +-- TabError
      +-- SystemError
      +-- TypeError
      +-- ValueError
      |    +-- UnicodeError
      |         +-- UnicodeDecodeError
      |         +-- UnicodeEncodeError
      |         +-- UnicodeTranslateError
      +-- Warning
           +-- DeprecationWarning
           +-- PendingDeprecationWarning
           +-- RuntimeWarning
           +-- SyntaxWarning
           +-- UserWarning
           +-- FutureWarning
           +-- ImportWarning
           +-- UnicodeWarning
           +-- BytesWarning
           +-- ResourceWarning

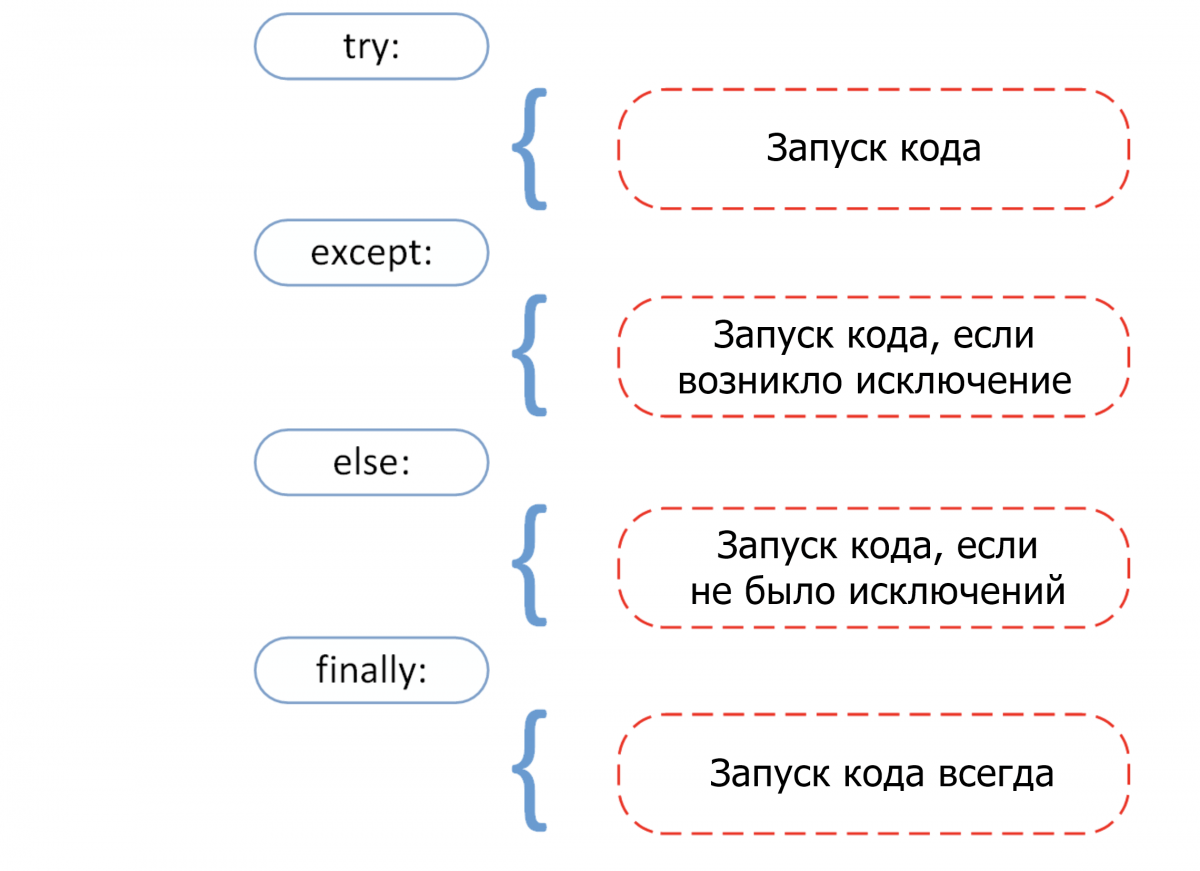
Прежде чем переходить к разбору встроенных исключений быстро вспомним 4 основных компонента обработки исключения, как показано на этой схеме.

• Try: он запускает блок кода, в котором ожидается ошибка.
• Except: здесь определяется тип исключения, который ожидается в блоке try (встроенный или созданный).
• Else: если исключений нет, тогда исполняется этот блок (его можно воспринимать как средство для запуска кода в том случае, если ожидается, что часть кода приведет к исключению).
• Finally: вне зависимости от того, будет ли исключение или нет, этот блок кода исполняется всегда.

В следующем разделе руководства больше узнаете об общих типах исключений и научитесь обрабатывать их с помощью инструмента обработки исключения.

Ошибка прерывания с клавиатуры (KeyboardInterrupt)

Исключение KeyboardInterrupt вызывается при попытке остановить программу с помощью сочетания Ctrl + C или Ctrl + Z в командной строке или ядре в Jupyter Notebook. Иногда это происходит неумышленно и подобная обработка поможет избежать подобных ситуаций.

В примере ниже если запустить ячейку и прервать ядро, программа вызовет исключение KeyboardInterrupt. Теперь обработаем исключение KeyboardInterrupt.

try:
    inp = input()
    print('Нажмите Ctrl+C и прервите Kernel:')
except KeyboardInterrupt:
    print('Исключение KeyboardInterrupt')
else:
    print('Исключений не произошло')

Исключение KeyboardInterrupt

Стандартные ошибки (StandardError)

Рассмотрим некоторые базовые ошибки в программировании.

Арифметические ошибки (ArithmeticError)

• Ошибка деления на ноль (Zero Division);
• Ошибка переполнения (OverFlow);
• Ошибка плавающей точки (Floating Point);

Все перечисленные выше исключения относятся к классу Arithmetic и вызываются при ошибках в арифметических операциях.

Деление на ноль (ZeroDivisionError)

Когда делитель (второй аргумент операции деления) или знаменатель равны нулю, тогда результатом будет ошибка деления на ноль.

try:  
    a = 100 / 0
    print(a)
except ZeroDivisionError:  
    print("Исключение ZeroDivisionError." )
else:  
    print("Успех, нет ошибок!")

Исключение ZeroDivisionError.

Переполнение (OverflowError)

Ошибка переполнение вызывается, когда результат операции выходил за пределы диапазона. Она характерна для целых чисел вне диапазона.

try:  
    import math
    print(math.exp(1000))
except OverflowError:  
    print("Исключение OverFlow.")
else:  
    print("Успех, нет ошибок!")

Исключение OverFlow.

Ошибка утверждения (AssertionError)

Когда инструкция утверждения не верна, вызывается ошибка утверждения.

Рассмотрим пример. Предположим, есть две переменные: a и b. Их нужно сравнить. Чтобы проверить, равны ли они, необходимо использовать ключевое слово assert, что приведет к вызову исключения Assertion в том случае, если выражение будет ложным.

try:  
    a = 100
    b = "PythonRu"
    assert a == b
except AssertionError:  
    print("Исключение AssertionError.")
else:  
    print("Успех, нет ошибок!")

Исключение AssertionError.

Ошибка атрибута (AttributeError)

При попытке сослаться на несуществующий атрибут программа вернет ошибку атрибута. В следующем примере можно увидеть, что у объекта класса Attributes нет атрибута с именем attribute.

class Attributes(obj):
    a = 2
    print(a)

try:
    obj = Attributes()
    print(obj.attribute)
except AttributeError:
    print("Исключение AttributeError.")

2
Исключение AttributeError.

Ошибка импорта (ModuleNotFoundError)

Ошибка импорта вызывается при попытке импортировать несуществующий (или неспособный загрузиться) модуль в стандартном пути или даже при допущенной ошибке в имени.

import nibabel

---------------------------------------------------------------------------

ModuleNotFoundError                       Traceback (most recent call last)

 in 
----> 1 import nibabel


ModuleNotFoundError: No module named 'nibabel'

Ошибка поиска (LookupError)

LockupError выступает базовым классом для исключений, которые происходят, когда key или index используются для связывания или последовательность списка/словаря неверна или не существует.

Здесь есть два вида исключений:

• Ошибка индекса (IndexError);
• Ошибка ключа (KeyError);

Ошибка ключа

Если ключа, к которому нужно получить доступ, не оказывается в словаре, вызывается исключение KeyError.

try:  
    a = {1:'a', 2:'b', 3:'c'}  
    print(a[4])  
except LookupError:  
    print("Исключение KeyError.")
else:  
    print("Успех, нет ошибок!")

Исключение KeyError.

Ошибка индекса

Если пытаться получить доступ к индексу (последовательности) списка, которого не существует в этом списке или находится вне его диапазона, будет вызвана ошибка индекса (IndexError: list index out of range python).

try:
    a = ['a', 'b', 'c']  
    print(a[4])  
except LookupError:  
    print("Исключение IndexError, индекс списка вне диапазона.")
else:  
    print("Успех, нет ошибок!")

Исключение IndexError, индекс списка вне диапазона.

Ошибка памяти (MemoryError)

Как уже упоминалось, ошибка памяти вызывается, когда операции не хватает памяти для выполнения.

Ошибка имени (NameError)

Ошибка имени возникает, когда локальное или глобальное имя не находится.

В следующем примере переменная ans не определена. Результатом будет ошибка NameError.

try:
    print(ans)
except NameError:  
    print("NameError: переменная 'ans' не определена")
else:  
    print("Успех, нет ошибок!")

NameError: переменная 'ans' не определена

Ошибка выполнения (Runtime Error)

Ошибка «NotImplementedError»
Ошибка выполнения служит базовым классом для ошибки NotImplemented. Абстрактные методы определенного пользователем класса вызывают это исключение, когда производные методы перезаписывают оригинальный.

class BaseClass(object):
    """Опередляем класс"""
    def __init__(self):
        super(BaseClass, self).__init__()
    def do_something(self):
	# функция ничего не делает
        raise NotImplementedError(self.__class__.__name__ + '.do_something')

class SubClass(BaseClass):
    """Реализует функцию"""
    def do_something(self):
        # действительно что-то делает
        print(self.__class__.__name__ + ' что-то делает!')

SubClass().do_something()
BaseClass().do_something()

SubClass что-то делает!



---------------------------------------------------------------------------

NotImplementedError                       Traceback (most recent call last)

 in 
     14
     15 SubClass().do_something()
---> 16 BaseClass().do_something()


 in do_something(self)
      5     def do_something(self):
      6         # функция ничего не делает
----> 7         raise NotImplementedError(self.__class__.__name__ + '.do_something')
      8
      9 class SubClass(BaseClass):


NotImplementedError: BaseClass.do_something

Ошибка типа (TypeError)

Ошибка типа вызывается при попытке объединить два несовместимых операнда или объекта.

В примере ниже целое число пытаются добавить к строке, что приводит к ошибке типа.

try:
    a = 5
    b = "PythonRu"
    c = a + b
except TypeError:
    print('Исключение TypeError')
else:
    print('Успех, нет ошибок!')

Исключение TypeError

Ошибка значения (ValueError)

Ошибка значения вызывается, когда встроенная операция или функция получают аргумент с корректным типом, но недопустимым значением.

В этом примере встроенная операция float получат аргумент, представляющий собой последовательность символов (значение), что является недопустимым значением для типа: число с плавающей точкой.

try:
    print(float('PythonRu'))
except ValueError:
    print('ValueError: не удалось преобразовать строку в float: 'PythonRu'')
else:
    print('Успех, нет ошибок!')

ValueError: не удалось преобразовать строку в float: 'PythonRu'

Пользовательские исключения в Python

В Python есть много встроенных исключений для использования в программе. Но иногда нужно создавать собственные со своими сообщениями для конкретных целей.

Это можно сделать, создав новый класс, который будет наследовать из класса Exception в Python.

class UnAcceptedValueError(Exception):   
    def __init__(self, data):    
        self.data = data
    def __str__(self):
        return repr(self.data)

Total_Marks = int(input("Введите общее количество баллов: "))
try:
    Num_of_Sections = int(input("Введите количество разделов: "))
    if(Num_of_Sections < 1):
        raise UnAcceptedValueError("Количество секций не может быть меньше 1")
except UnAcceptedValueError as e:
    print("Полученная ошибка:", e.data)

Введите общее количество баллов: 10
Введите количество разделов: 0
Полученная ошибка: Количество секций не может быть меньше 1

В предыдущем примере если ввести что-либо меньше 1, будет вызвано исключение. Многие стандартные исключения имеют собственные исключения, которые вызываются при возникновении проблем в работе их функций.

Недостатки обработки исключений в Python

У использования исключений есть свои побочные эффекты, как, например, то, что программы с блоками try-except работают медленнее, а количество кода возрастает.

Дальше пример, где модуль Python timeit используется для проверки времени исполнения 2 разных инструкций. В stmt1 для обработки ZeroDivisionError используется try-except, а в stmt2 — if. Затем они выполняются 10000 раз с переменной a=0. Суть в том, чтобы показать разницу во времени исполнения инструкций. Так, stmt1 с обработкой исключений занимает больше времени чем stmt2, который просто проверяет значение и не делает ничего, если условие не выполнено.

Поэтому стоит ограничить использование обработки исключений в Python и применять его в редких случаях. Например, когда вы не уверены, что будет вводом: целое или число с плавающей точкой, или не уверены, существует ли файл, который нужно открыть.

import timeit
setup="a=0"
stmt1 = '''
try:
    b=10/a
except ZeroDivisionError:
    pass'''

stmt2 = '''
if a!=0:
    b=10/a'''

print("time=",timeit.timeit(stmt1,setup,number=10000))
print("time=",timeit.timeit(stmt2,setup,number=10000))

time= 0.003897680000136461
time= 0.0002797570000439009

Выводы!

Как вы могли увидеть, обработка исключений помогает прервать типичный поток программы с помощью специального механизма, который делает код более отказоустойчивым.

Обработка исключений — один из основных факторов, который делает код готовым к развертыванию. Это простая концепция, построенная всего на 4 блоках: try выискивает исключения, а except их обрабатывает.

Очень важно поупражняться в их использовании, чтобы сделать свой код более отказоустойчивым.

As it is known that 1.2 – 1.0 = 0.2 . But when you try to the same in python you will surprised by results:

>>> 1.2 - 1.0

Output:

0.199999999999999996

This can be considered as a bug in Python, but it is not. This has little to do with Python, and much more to do with how the underlying platform handles floating-point numbers. It’s a normal case encountered when handling floating-point numbers internally in a system. It’s a problem caused when the internal representation of floating-point numbers, which uses a fixed number of binary digits to represent a decimal number. It is difficult to represent some decimal number in binary, so in many cases, it leads to small roundoff errors. We know similar cases in decimal math, there are many results that can’t be represented with a fixed number of decimal digits, Example

10 / 3 = 3.33333333.......

In this case, taking 1.2 as an example, the representation of 0.2 in binary is 0.00110011001100110011001100…… and so on. It is difficult to store this infinite decimal number internally. Normally a float object’s value is stored in binary floating-point with a fixed precision (typically 53 bits). So we represent 1.2 internally as,

1.0011001100110011001100110011001100110011001100110011  

Which is exactly equal to :

1.1999999999999999555910790149937383830547332763671875

Still, you thinking why python is not solving this issue, actually it has nothing to do with python. It happens because it is the way the underlying c platform handles floating-point numbers and ultimately with the inaccuracy, we’ll always have been writing down numbers as a string of fixed number of digits. Note that this is in the very nature of binary floating-point: this is not a bug either in Python or C, and it is not a bug in your code either. You’ll see the same kind of behaviors in all languages that support our hardware’s floating-point arithmetic although some languages may not display the difference by default, or in all output modes). We have to consider this behavior when we do care about math problems with needs exact precisions or using it inside conditional statements. Check floating point section in python documentation for more such behaviours.

Today we get started with our in-depth Python Exception Handling series by looking at the FloatingPointError. As with most programming languages, the FloatingPointError in Python indicates that something has gone wrong with a floating point calculation. However, unlike most other languages, Python will not raise a FloatingPointError by default. The ability to do so must be implemented by including the fpectl module when building your local Python environment.

In this article we’ll explore the FloatingPointError by first looking at where it resides in the overall Python Exception Class Hierarchy. We’ll also go over how the fpectl module can be enabled, and how doing so can allow the raising of FloatingPointErrors in your own code. Let’s get to it!

The Technical Rundown

All Python exceptions inherit from the BaseException class, or extend from an inherited class therein. The full exception hierarchy of this error is:

• BaseException
  • Exception
  • ArithmeticError
    • FloatingPointError

Full Code Sample

Below is the full code sample we’ll be using in this article. It can be copied and pasted if you’d like to play with the code yourself and see how everything works.

import fpectl
from gw_utility.logging import Logging

def main():
    Logging.line_separator("FLOATING POINT")
    test_floating_point()

    Logging.line_separator("DIVISION BY ZERO")
    test_division_by_zero()

    Logging.line_separator("FLOATING POINT DIVISION BY ZERO", 60)
    test_floating_point_division_by_zero()

def test_floating_point():
    try:
        Logging.log(round(24.601 / 3.5, 4))
    except FloatingPointError as exception:
        # Output expected FloatingPointErrors.
        Logging.log_exception(exception)
    except Exception as exception:
        # Output expected Exceptions.
        Logging.log_exception(exception, False)

def test_division_by_zero():
    try:
        # Divide by zero.
        Logging.log(24 / 0)
    except FloatingPointError as exception:
        # Output expected FloatingPointErrors.
        Logging.log_exception(exception)
    except Exception as exception:
        # Output expected Exceptions.
        Logging.log_exception(exception, False)

def test_floating_point_division_by_zero():
    try:
        # Divide by floating point zero and round.
        Logging.log(round(24.601 / 0.0, 4))
    except FloatingPointError as exception:
        # Output expected FloatingPointErrors.
        Logging.log_exception(exception)
    except Exception as exception:
        # Output expected Exceptions.
        Logging.log_exception(exception, False)

if __name__ == " __main__":
    main()

import math
import sys
import traceback

class Logging:

    separator_character_default = '-'
    separator_length_default = 40

    @classmethod
    def __output(cls, *args, sep: str=' ', end: str='n', file=None):
        """Prints the passed value(s) to the console.

        :param args: Values to output.
        :param sep: String inserted between values, default a space.
        :param end: String appended after the last value, default a newline.
        :param file: A file-like object (stream); defaults to the current sys.stdout.
        :return: None
        """
        print(*args, sep=sep, end=end, file=file)

    @classmethod
    def line_separator(cls, value: str, length: int=separator_length_default, char: str=separator_character_default):
        """Print a line separator with inserted text centered in the middle.

        :param value: Inserted text to be centered.
        :param length: Total separator length.
        :param char: Separator character.
        """
        output = value

        if len(value) < length:
            # Update length based on insert length, less a space for margin.
            length -= len(value) + 2
            # Halve the length and floor left side.
            left = math.floor(length / 2)
            right = left
            # If odd number, add dropped remainder to right side.
            if length % 2 != 0:
                right += 1

            # Surround insert with separators.
            output = f'{char * left} {value} {char * right}'

        cls.__output(output)

    @classmethod
    def log(cls, *args, sep: str=' ', end: str='n', file=None):
        """Prints the passed value(s) to the console.

        :param args: Values to output.
        :param sep: String inserted between values, default a space.
        :param end: String appended after the last value, default a newline.
        :param file: A file-like object (stream); defaults to the current sys.stdout.
        """
        cls.__output(*args, sep=sep, end=end, file=file)

    @classmethod
    def log_exception(cls, exception: BaseException, expected: bool=True):
        """Prints the passed BaseException to the console, including traceback.

        :param exception: The BaseException to output.
        :param expected: Determines if BaseException was expected.
        """
        output = "[{}] {}: {}".format('EXPECTED' if expected else 'UNEXPECTED', type(exception). __name__ , exception)
        cls.__output(output)
        exc_type, exc_value, exc_traceback = sys.exc_info()
        traceback.print_tb(exc_traceback)

When Should You Use It?

As discussed in the introduction, before a FloatingPointError can even appear you’ll need to make sure your local Python build includes the fpectl module. Since this module is not included with most Python builds by default, you’d likely have had to explicitly build your Python with it if desired. Adding the fpectl module to can be accomplished by using the --with-fpectl flag when compiling Python. Going through the compilation process of Python is well beyond the scope of this article, but once fpectl is an included module, you can start testing the FloatingPointError.

For our example code we’re not doing anything spectacular. In fact, the FloatingPointError is effectively raised in situations where other ArithmeticErrors would normally appear, except that you’re using floating point numbers and the fpectl module is enabled. For example, you might raise a FloatingPointError where you’d normally get a ZeroDivisionError by attempting to divide by zero using a floating point value.

We’ve created a few simple testing methods starting with test_floating_point():

def test_floating_point():
    try:
        Logging.log(round(24.601 / 3.5, 4))
    except FloatingPointError as exception:
        # Output expected FloatingPointErrors.
        Logging.log_exception(exception)
    except Exception as exception:
        # Output expected Exceptions.
        Logging.log_exception(exception, False)

Executing this code works as expected, performing the floating point calculation and rounding the result to four decimal places before outputting the result to our log:

------------ FLOATING POINT ------------
7.0289

Now, let’s step away from using a floating point value and use regular integers while attempting to divide by zero:

def test_division_by_zero():
    try:
        # Divide by zero.
        Logging.log(24 / 0)
    except FloatingPointError as exception:
        # Output expected FloatingPointErrors.
        Logging.log_exception(exception)
    except Exception as exception:
        # Output expected Exceptions.
        Logging.log_exception(exception, False)

This raises an unexpected ZeroDivisionException since, even though fpectl is enabled, we aren’t using a floating point value in our calculation:

----------- DIVISION BY ZERO -----------
[UNEXPECTED] ZeroDivisionError: division by zero
  File "D:/work/Airbrake.io/Exceptions/Python/BaseException/Exception/ArithmeticError/FloatingPointError/main.py", line 30, in test_division_by_zero
    Logging.log(24 / 0)

Finally, let’s try the same division by zero while using floating point values:

def test_floating_point_division_by_zero():
    try:
        # Divide by floating point zero and round.
        Logging.log(round(24.601 / 0.0, 4))
    except FloatingPointError as exception:
        # Output expected FloatingPointErrors.
        Logging.log_exception(exception)
    except Exception as exception:
        # Output expected Exceptions.
        Logging.log_exception(exception, False)

As you might suspect, this raises a FloatingPointError for us:

------------- FLOATING POINT DIVISION BY ZERO --------------
[EXPECTED] FloatingPointError: invalid value encountered in divide
  File "D:/work/Airbrake.io/Exceptions/Python/BaseException/Exception/ArithmeticError/FloatingPointError/main.py", line 42, in test_floating_point_division_by_zero
    Logging.log(round(24.601 / 0.0, 4))

There we have the basics of using FloatingPointErrors. However, before you jump into adding the fpectl module to your Python to distinguish between FloatingPointErrors and normal ArithmeticErrors, there are a number of caveats and cautions to be aware of. The IEEE 754 standard for floating point arithmetic defines a number of universal standards for the formatting, rounding, allowed operations, and exception handling practices of floating point numbers. However, your code must be explicitly told to capture IEEE 754 exceptions in the form of SIGFPE signals generated by the local processor. Consequently, while Python is configured to do so via the fpectl module, many other custom scripts/applications are not.

The other major consideration is that use of the fpectl module is generally discouraged, in large part because it is not thread safe. Thread safe applications (that is, most properly developed Python applications) allow data structures to be safely shared between multiple threads without fear of one thread manipulating or altering some data that another thread is using (or where another thread sees different data). However, using the fpectl module means your floating point data is no longer thread safe, which could cause major issues in multithreaded applications. To be on the safe side, it’s generally recommended that you avoid fpectl and use another form of application logic to check for arithmetic errors.

Airbrake’s robust error monitoring software provides real-time error monitoring and automatic exception reporting for all your development projects. Airbrake’s state of the art web dashboard ensures you receive round-the-clock status updates on your application’s health and error rates. No matter what you’re working on, Airbrake easily integrates with all the most popular languages and frameworks. Plus, Airbrake makes it easy to customize exception parameters, while giving you complete control of the active error filter system, so you only gather the errors that matter most.

Check out Airbrake’s error monitoring software today and see for yourself why so many of the world’s best engineering teams use Airbrake to revolutionize their exception handling practices!

28.12.2019Python, Дизайн компилятора

>>> 1.2 - 1.0

0.199999999999999996

10 / 3 = 3.33333333.......

1.0011001100110011001100110011001100110011001100110011  

1.1999999999999999555910790149937383830547332763671875