В общем случае искомая
физическая величина может быть функцией
не одной, а нескольких измеряемых
величин, то есть: Y=f(X1,X2,…Xn)Каждая из величинX1,X2,…Xn
определяется с соответствующей
погрешностью X1,X2,…Xn.
В этом случае средняя квадратичная
погрешность этой функции будет равна
корню квадратному из суммы квадратов
частных производных функции по всем
независимым переменным, домноженным
на среднеквадратичную погрешность
соответствующей величины (вывод этой
формулы можно посмотреть в приложении
п.6):
|
|
(3) |
В данной формуле каждая
скобка под корнем представляет собой
вклад погрешности соответствующей
величины в погрешность функции. Если
погрешности различных измеряемых
величин определены с одной и той же
доверительной вероятностью, то формулу
можно переписать в следующем виде:
|
|
(4) |
Приведенные формулы
справедливы для любых функциональных
зависимостей, однако, они довольно
громоздки, производить по ним расчеты
бывает достаточно сложно, они требуют
больших затрат времени. В некоторых
случаях бывает удобнее использовать
выражения, преобразованные для частных
случаев функциональной зависимости.
Рассмотрим несколько таких частных
случаев.
Погрешность
алгебраической суммы
Пусть функция имеет
вид:
Y=
,
тогда среднеквадратичная погрешность
такой функции будет определяться:
|
|
(5) |
а выборочная дисперсия:
|
|
(6) |
То есть выборочная
дисперсия алгебраической суммы равна
сумме выборочных дисперсий отдельных
независимых переменных. Обратите
внимание, на то, что в выражение для
выборочной дисперсии функциивсе
слагаемые входятсознаком «+»,независимо от того с каким знаком
соответствующая величина входила в
алгебраическую сумму.
Погрешность
произведения.
Пусть функция имеет
вид:
или
В этих случаях,
воспользовавшись формулой (2)
и, учитывая то, что логарифм произведения
равен сумме логарифмов, получаем
выражение для относительной погрешности
функции:
|
|
(7) |
То есть относительная
погрешность произведения (и частного)
равна корню квадратному из суммы
квадратов относительных погрешностей
всех сомножителей. Также как и в случае
суммы, обратите внимание, на то, что все
слагаемые под корнемберутся со
знаком «+», независимо от того в
числитель или знаменатель выражения
функции они входили.
Производить расчет
по этой формуле обычно гораздо проще,
чем по формуле (3), а
доверительный интервал искомой величины
легко найти:.
Погрешности некоторых
элементарных функций.
-
,
где С=const; -
;
-
;
4. Два способа оценки погрешности при косвенных измерениях.
В случае косвенных
измерений физических величин возможны
два способа вычисления окончательного
результата и погрешности.
Первый способ.
Для каждой измеряемой
физической величины проводят серию
измерений. Эти измерения (прямые)
обрабатывают и находят средние значения
и соответствующие им доверительные
интервалыс одной и той же доверительной вероятностью.
Затем по выражению функциональной
зависимостиY=f(X1,X2,…Xn)
находят среднее значение искомой
физической величины, используя найденные
средние значения всех измеренных величин.
Затем по формулам переноса ошибок
(формула 4 или ее частные случаи)
рассчитывают доверительный интервал
величиныY.
Пример
Задача определить ускорение свободного падения
с помощью математического маятника.
Формула для расчета
,
гдеlдлина маятника,Tпериод его колебаний.
Измерили 5 раз длину
маятника и 5 раз его период. Получили
следующие значения, которые обработали,
как прямые измерения:
|
l(м) |
|
|
|
|
|
1 |
0,965 |
0,0006 |
3,6 |
|
|
2 |
0,966 |
0,0016 |
25,610-7 |
|
|
3 |
0,964 |
-0,0004 |
1,610-7 |
|
|
4 |
0,963 |
-0,0014 |
19,610-7 |
|
|
5 |
0,964 |
-0,0004 |
1,610-7 |
|
|
|
4,822 |
5210-7 |
|
Т(сек) |
Т |
(Т |
=0,000583
|
|
|
1 |
1,970 |
0,0002 |
0,0410-6 |
|
|
2 |
1,969 |
-0,0008 |
0,6410-6 |
|
|
3 |
1,971 |
0,0012 |
1,4410-6 |
|
|
4 |
1,968 |
-0,0018 |
3,2410-6 |
|
|
5 |
1,971 |
0,0012 |
1,4410-6 |
|
|
|
9,849 |
6,810-6 |
Получили:
0,9644и
1,9698.
Затем
рассчитывают
=
=9,812342
и, в
соответствии с формулой (7) рассчитывают
относительную погрешность g:
=
=0,0025400,0025.
Тогда g= gg
=9,812342
0,0025=0,0249
0,025, и окончательный результат,
соответственно:
(9,8120,025)
м/с2 при Р=0,95
Второй способ.
В случаях, когда по
условиям опыта измерения делаются в не
воспроизводимых условиях, значения
функции, Y=f(X1,X2,…Xn)
вычисляют для каждой отдельной серии
измерений{Xi},
а затем полученный ряд значенийYi
, обрабатывают по алгоритму прямых
измерений.
Пример
Пусть поставлена та
же задача определитьg, но при этом
имеется несколько (пять) заведомо
различных маятников. В этом случае
рационально поступить следующим образом.
Для каждого маятника измерить его длину
и период колебаний. По этим значениям
рассчитать величинуg
(для каждого маятника независимо).
Полученные значенияg
обработать, как прямые измерения.
|
№ |
L(м) |
Т(сек) |
g (м/с2) |
|
|
|
1 |
0,965 |
1,970 |
9,816453 |
0,00355 |
0,12603210-4 |
|
2 |
1,222 |
2,222 |
9,771086 |
-0,041817 |
17,4866910-4 |
|
3 |
1,568 |
2,510 |
9,825584 |
0,01268 |
1,6079510-4 |
|
4 |
0,559 |
1,498 |
9,834401 |
0,0215 |
4,6216710-4 |
|
5 |
0,752 |
1,739 |
9,816991 |
0,00409 |
0,16715210-4 |
|
|
49,06452 |
24,009510-4 |
Соседние файлы в папке Matobrabotka
- #
- #
- #
- #
- #
- #
- #
- #
Метод переноса погрешностей
Читайте также:
|
Метод переноса погрешностей применяется в том случае, когда измеренные прямо независимо друг от друга величины x, y, z, …, являющиеся аргументами функции f, образуют выборки {x¢}, {у¢}, {z¢}, … .
Отклонения результатов отдельных наблюдений x¢i, y¢i, z¢i, … от соответствующих истинных значений x0, у0, z0, … включают в себя как случайные, так и систематические составляющие. Случайные Dx, Dy, Dz, … и приборные q(x), q(y), q(z), … погрешности аргументов, определенные для одной и той же доверительной вероятности P0, могут быть объединены в полные погрешности 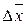



Пусть в опыте получены выборки значений величин x, y, z, … одинакового объема N. Тогда i-е значение функции fi¢ = f(x¢i, y¢i, z¢i), вычисленное при смещенных значениях ее аргументов x¢i = xi + q(x), y¢i = yi + q(y), …, можно представить в виде 


Воспользуемся выражением для полного дифференциала функции нескольких аргументов

Здесь частные производные функции 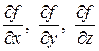
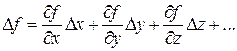
Тогда i-е значение величины fi¢ в окрестности точки 

где 








Рассмотрим вычисление случайной погрешности косвенно определяемой величины f. Для этого вычислим дисперсию ее среднего значения. С учетом (3.2) получим

или

Если аргументы функции случайны и независимы, то их отклонения от средних значений 



где 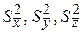


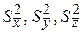

где 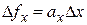


Смещенное среднее значение функции в (3.2), используя выражение (3.1), можно выразить через ее истинное среднее значение

где 





где 
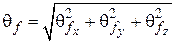
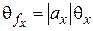



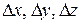


откуда полная погрешность величины f будет определяться как
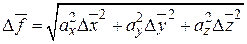
где 
Результат косвенного измерения с учетом погрешности следует записать в виде



где P0 – вероятность определения случайной составляющей погрешности измерения; 
Числовые значения 

Замечание 1.Полученное выражение дляполной погрешностивеличины 



Замечание 2. Если приборные погрешности аргументов функции не являются случайными и независимыми, например, приборная погрешность одного аргумента порождает приборную погрешность другого аргумента, то их необходимо складывать по модулю линейно 

Однако такая ситуация встречается на практике довольно редко. Она, например, может возникнуть в случае влияния работы одного прибора на показания другого. В большинстве же случаев значения аргументов функции измеряются разными приборами, взаимозависимость распределения приборных погрешностей которых ниоткуда не следует. Поэтому верхние границы частных приборных погрешностей аргументов функции будем складывать квадратично.
Замечание 3. Если функция f удобна для логарифмирования, т. е. представляет собой произведение нескольких выражений, формулы для нахождения погрешности могут быть приведены к более удобному виду. Операция логарифмирования, превращает произведение выражений в сумму логарифмов этих выражений, а производная суммы вычисляется значительно проще, чем производная произведения. Например,
ln (axn/(ymtg x)) = ln a + n ln x – m ln у –lntg x.
В таком случае, используя тождество 


где 

Дата добавления: 2015-10-21; просмотров: 731 | Нарушение авторских прав
Читайте в этой же книге: Измерение. Классификация измерений | Классификация погрешностей измерения | Случайное событие. Вероятность | Случайная величина. Генеральная совокупность и выборка | Результат измерения. Доверительный интервал | Нормальное или гауссовское распределение | Выявление грубых погрешностей | Задача регрессии и метод наименьших квадратов | Случай линейной зависимости двух величин | ПРАВИЛА оформления ГРАФИКОВ |
mybiblioteka.su — 2015-2023 год. (0.04 сек.)
Содержание
- Как исправить ошибку #ПЕРЕНОС! в Excel
- Как исправить ошибку #ЗНАЧ! в Excel
- Как исправить ошибку #ПУСТО! в Excel
- Как исправить ошибку #ИМЯ? в Excel
Как исправить ошибку #ПЕРЕНОС! в Excel
Прежде чем рассмотреть ошибку #ПЕРЕНОС! (#SPILL), рассмотрим, что такое перенос. В Excel это означает, что формула возвращает несколько значений (массив), и они автоматически переносятся в соседние ячейки.
Диапазон переноса и значения внутри будут изменяться при обновлении источника данных.
Ошибка #ПЕРЕНОС! возникает, когда формула возвращает несколько значений, но Excel не может вывести один или несколько результатов.
У ошибки может быть множество причин. Поиск решения будет зависеть от используемой версии Excel.
- Веб-версия: наведите мышь на зеленый треугольник в верхнем левом углу ячейки с ошибкой #ПЕРЕНОС!. Появится сообщение с описанием ошибки.
- Десктопная версия: щелкните по ячейке с ошибкой #ПЕРЕНОС!. Нажмите на треугольник, который появится слева от ячейки. Причина ошибки будет указана в верхней части меню справки.
Рассмотрим решения, которые подойдут для наиболее распространенных вариаций этой ошибки.
Диапазон для переноса содержит одну или более ячеек с значениями
Решение: очистить диапазон для переноса.
Диапазон для переноса находится внутри таблицы
Решение 1: преобразовать таблицу в диапазон данных.
Для этого выполните следующие шаги:
- нажмите на любую ячейку в таблице,
- в меню в верхней части окна выберите «Конструктор»,
- выберите команду «Преобразовать в диапазон».
Обратите внимание, что расположение меню и списка команд могут отличаться в зависимости от версии.
Решение 2: переместить формулу за границы таблицы.
Диапазон для переноса содержит объединенные ячейки
Решение: разделить ячейки внутри диапазона.
Как исправить ошибку #ЗНАЧ! в Excel
Ошибка #ЗНАЧ! (#VALUE) возникает в следующих случаях:
- что-то не так с ячейкой (ячейками), на которую ссылается формула,
- что-то не так с самой формулой.
Иногда найти источник проблемы не просто. Ниже — о самых распространенных случаях и как и их исправить.
Математическая формула ссылается на текст
Формулы с математическими операторами могут вычислять только числа. Если одна или несколько ячеек, на которые ссылается формула, содержит текст, формула будет возвращать ошибку.
Решение: использовать вместо формулы (уравнения, составленного пользователем) функцию (формулу, заранее заданную Excel). Функции по умолчанию игнорируют большую часть текстовых значений и производят расчеты лишь с числами.
Например, на примере ниже функция =СУММ(B2,B11) будет игнорировать текст в ячейке B11.
Скриншот: Zapier.com
Стоит помнить, что эта функция не оповещает автоматически о пропусках ячеек, и ее результат может вводить в заблуждение.
Одна или более ячеек содержат пробелы
В этих случаях ячейка выглядит пустой.
Решение: найти и заменить пробелы. Вот как это сделать:
- выделите диапазон ячеек, к которому обращается формула;
- нажмите на иконку с биноклем, нажмите «Найти и выделить»;
- в окне «Найти и заменить» выберите «Заменить»;
- в поле «Найти» вставьте пробелы;
- поле «Заменить на» оставьте пустым;
- нажмите «Заменить все».
Как исправить ошибку #ПУСТО! в Excel
Ошибка #ПУСТО! (#REF) возникает, когда формулы ссылается на ячейку, которая уже не существует. Разберем наиболее распространенные причины возникновения ошибки и как их исправить.
Ячейка, на которую ссылается формула, удалена
Формула использует прямые ссылки на ячейки (каждая ячейка отделена запятой), но одна или несколько ячеек удалены. Это основная причина, почему Excel не рекомендует использовать прямые ссылки на ячейки.
Решение 1: Если ячейки удалены случайно, отмените это действие.
Решение 2: Обновите формулу, чтобы она ссылалась на диапазон ячеек. В этом случае Excel сможет произвести вычисления, даже если одна из ячеек была удалена.
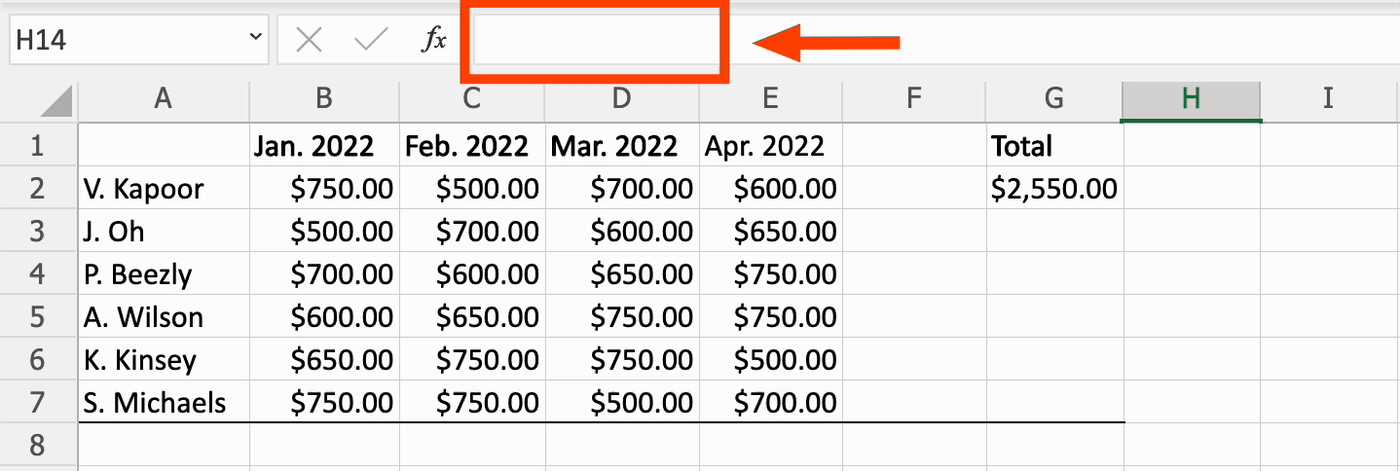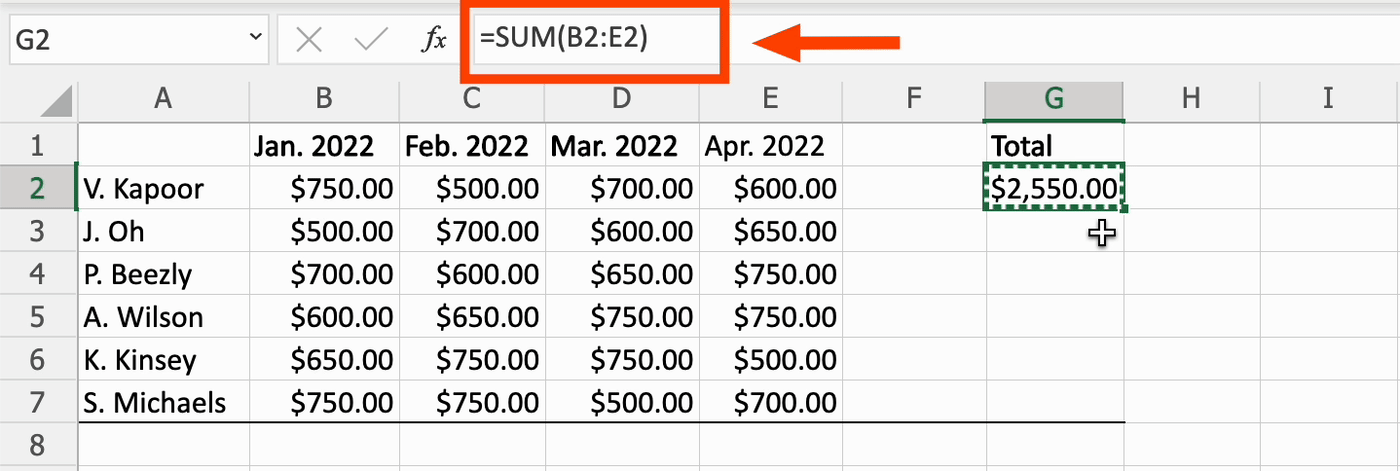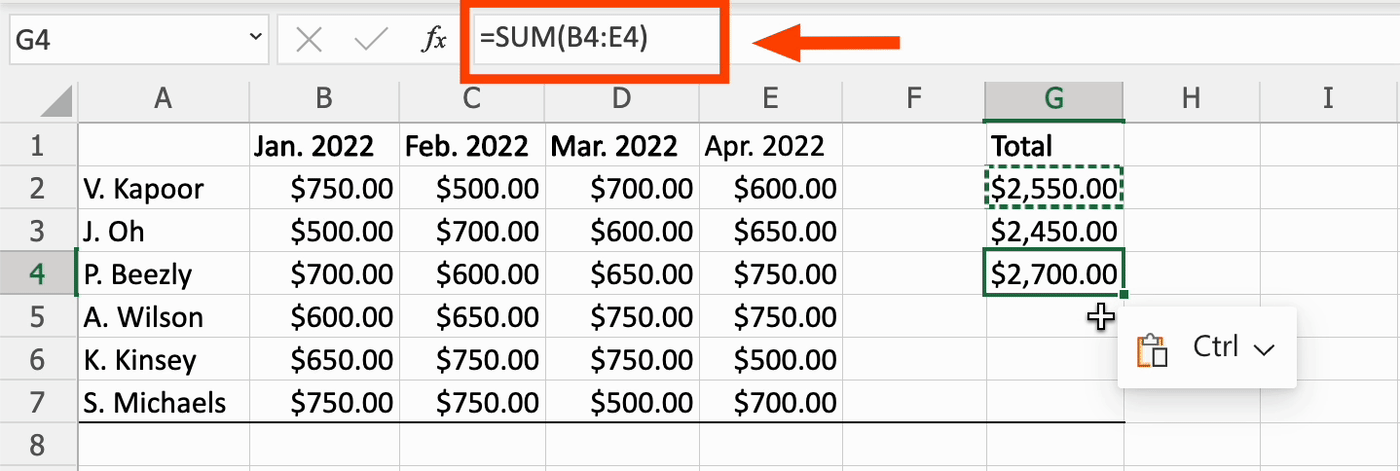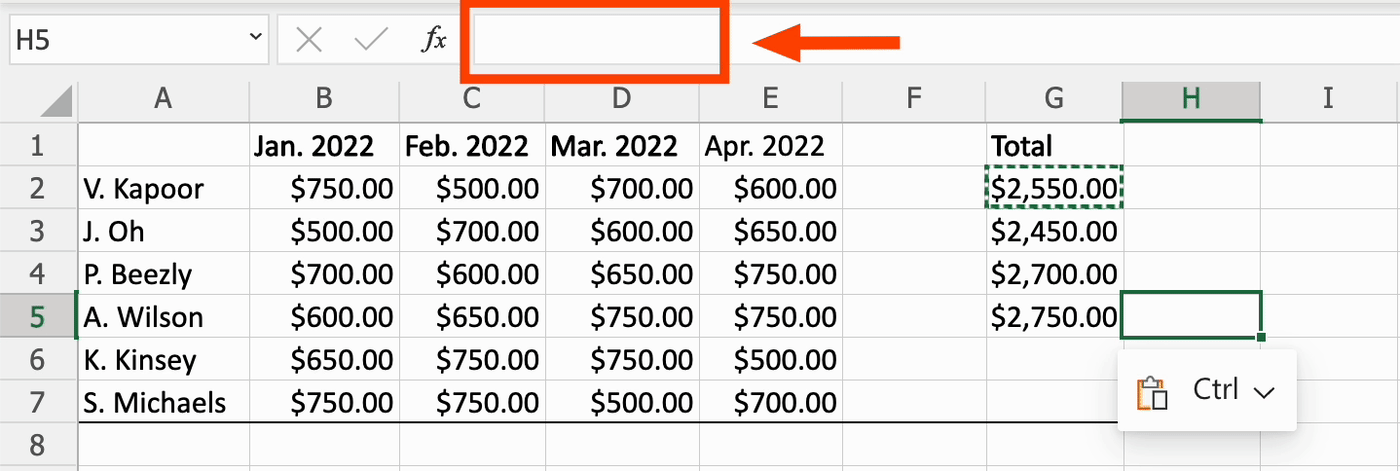
Формула содержит относительные ссылки
Относительная ссылка означает, что используемые данные привязаны к ячейке, в которую вставлена формула. Например, если формулу =СУММ(B2:E2) скопировать из ячейки G2 в G3, Excel предположит, что должен суммировать все ячейки из колонок B-E в ряду 3.
Каждый раз, когда формула с относительными ссылками переносится в другую ячейку, ссылки автоматически меняются. И если установить связь невозможно, происходит ошибка.
Например, если формулу =СУММ(G2:G7) перенести в ячейку I4, Excel предположит, что пользователю требуется сложить шесть ячеек над клеткой I4. В данном случае это невозможно, так как доступны лишь три ячейки.
Решение: обновите формулу, чтобы включить в нее абсолютные значения. Это позволит созранить исходные ссылки, даже если формула будет перенесена. Для этого вставьте символ $ перед каждой буквой, обозначающей столбец, и номером ряда.
Например, формула =СУММ(G2:G7) с абсолютными ссылками будет выглядеть как: =СУММ($G$2:$G$7).
Как исправить ошибку #ИМЯ? в Excel
Ошибка #ИМЯ? (#NAME) возникает, если название формулы неверно написано. Рассмотрим основные решения проблемы.
Название формулы содержит опечатку
Решение: обновить название формулы. Лучший способ избегать опечаток — использовать встроенный редактор формул Excel. Когда пользователь начинает печатать название формулы, программа автоматически предложит список названий, содержащих те же буквы.
Неверное название формулы
Иногда пользователи вводят название несуществующей формулы или формулы, которая называется иначе (например, ПЛЮС вместо реальной функции СУММ). В этом случае формула вернет ошибку #ИМЯ?.
Решение: найти правильное имя формулы и обновить ее.
Вот как это сделать:
- выберите в меню раздел «Формулы»;
- нажмите на «Вставить функцию» в левой части панели инструментов, в открывшемся окне «Вставка функции» просмотрите недавно использовавшиеся функции или полный список всех доступных функций;
- выберите и вставьте нужную функцию;
- в редакторе формул обновите ячейки, к которым будет отсылаться формула (поля зависят от выбранной функции).
Эти советы применимы и к ошибкам в Google Таблицах (за исключением #ПЕРЕНОС!, которая часто отображается как #REF).
Источник.
Фото на обложке: Aihr.com
Подписывайтесь на наш Telegram-канал, чтобы быть в курсе последних новостей и событий!
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel для iPad Excel Web App Excel для iPhone Excel для планшетов с Android Excel для телефонов с Android Еще…Меньше
Ошибки #ПЕРЕНОС! возникают, когда формула возвращает несколько результатов, а Excel не может вернуть результаты в сетку. Дополнительные сведения об этих типах ошибок см. в следующих разделах справки.
Эта ошибка возникает, если диапазон переноса для формулы массива с переносом не является пустым.
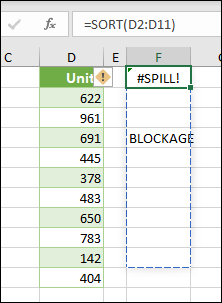
При выборе формулы пунктирная граница будет указывать на намеченный диапазон переноса.
Вы можете щелкнуть плавающий элемент «Ошибка» и выбрать параметр Выделить препятствующие ячейки, чтобы сразу перейти к препятствующим ячейкам. Затем вы можете очистить ошибку, удалив или переместив запись препятствующей ячейки. Как только препятствие будет очищено, формула массива выполнит перенос намеченным образом.
Excel не удалось определить размер массива с переносом, так как он является переменным и меняет размер между этапами вычислений. Например, следующая формула вызывает эту ошибку #ПЕРЕНОС! :
=ПОСЛЕДОВ(СЛУЧМЕЖДУ(1;1000))
Динамическое изменение размера массива может вызвать дополнительные этапы вычислений, чтобы обеспечить полное вычисление таблицы. Если размер массива продолжает изменяться во время этих дополнительных этапов и не стабилизируется, Excel разрешит динамический массив ошибкой #ПЕРЕНОС!.
Это значение ошибки обычно связано с использованием функций СЛЧИС, СЛМАССИВи СЛУЧМЕЖДУ. Другие переменные функции, например СМЕЩ, ДВССЫЛ и СЕГОДНЯ, не возвращают разные значения на каждом этапе вычисления.
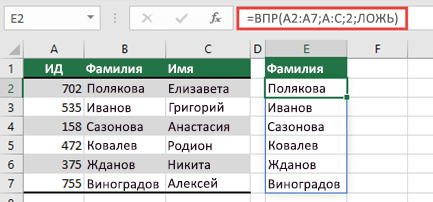
Например, при размещении в ячейке E2 формулы =ВПР(A:A;A:C;2;ЛОЖЬ) (как в примере ниже) ранее выполнялся поиск ИД только в ячейке A2. Однако в динамическом массиве Excel формула вызывает ошибку #ПЕРЕНОС!, так как Excel выполняет поиск во всем столбце, возвращает 1 048 576 результатов и достигает конца сетки Excel.
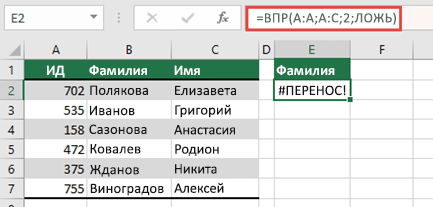
Эту проблему можно устранить 3 простыми способами:
|
# |
Способ |
Формула |
|---|---|---|
|
1 |
Ссылайтесь только на нужные значения поиска. Этот стиль формулы возвращает динамический массив, но не работает с таблицами Excel.
|
=ВПР(A2:A7;A:C;2;ЛОЖЬ) |
|
2 |
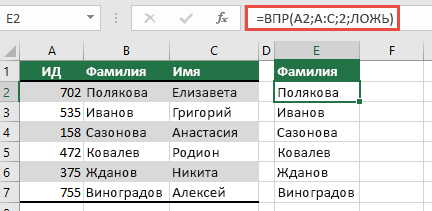
Сошлитесь на значение в той же строке, а затем скопируйте формулу. Этот традиционный стиль формулы работает в таблицах, но не возвращает динамический массив.
|
=ВПР(A2;A:C;2;ЛОЖЬ) |
|
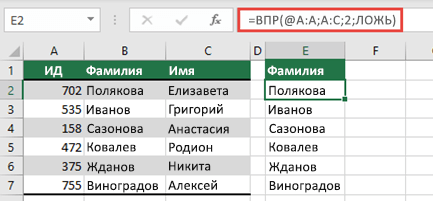
3 |
Создайте в Excel запрос неявного пересечения с помощью оператора @, а затем скопируйте формулу. Этот стиль формулы работает в таблицах, но не возвращает динамический массив.
|
=ВПР(@A:A;A:C;2;ЛОЖЬ) |
Формулы массивов с переносом не поддерживаются в таблицах Excel. Попробуйте переместить формулу из таблицы или преобразовать таблицу в диапазон (нажмите Конструктор таблиц > Инструменты > Преобразовать в диапазон).
Формула массива с переносом, которую вы пытаетесь ввести, привела к нехватке памяти в Excel. Попробуйте сослаться на меньший массив или диапазон.
Формулы массива с переносом не могут выполнять перенос в объединенные ячейки. Отмените объединение ячеек или переместите формулу в другой диапазон, который не пересекается с объединенными ячейками.
При выборе формулы пунктирная граница будет указывать на намеченный диапазон переноса.
Вы можете щелкнуть плавающий элемент «Ошибка» и выбрать параметр Выделить препятствующие ячейки, чтобы сразу перейти к препятствующим ячейкам. Как только объединенные ячейки будут устранены, формула массива выполнит перенос намеченным образом.
Excel не распознает или не может согласовать причину этой ошибки. Убедитесь, что формула содержит все необходимые аргументы для вашего сценария.
Дополнительные сведения

См. также
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Функция ФИЛЬТР
Функция СЛУЧМАССИВ
Функция ПОСЛЕДОВ
Функция СОРТ
Функция СОРТПО
Функция УНИК
Динамические массивы и поведение массива с переносом
Оператор неявного пересечения: @
Нужна дополнительная помощь?
тематическая обработка результатов эксперимента
Работа добавлена на сайт samzan.net: 2015-07-05
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.
Предоплата всего
от 25%
Подписываем
договор
45
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Математическая обработка результатов эксперимента.
Методическое пособие для лабораторного физического практикума
Санкт-Петербург 2009
Печатается по постановлению Ученого совета физического факультета СПбГУ.
Ответственный редактор: В.И. Коротков.
Составители: Е.П. Зароченцева, И.С. Бобкова, Н.А. Малешина.
Рецензент: канд. физ.-мат. наук, ст.н.сотр. Богданов В.Н (СПбГУ)
Математическая обработка результатов эксперимента. Методическое пособие для лабораторного физического практикума. СПбГУ. /Е.П. Зароченцева, И.С. Бобкова, Н.А. Малешина.
Под ред. В.И. Короткова.
СПб., 2009. – 44 с.
Данное пособие содержит рекомендации по обработке результатов измерений полученных при выполнении лабораторных работ в «Лаборатории физического эксперимента» и представляет собой существенно переработанное и дополненное переиздание учебного пособия «Математическая обработка результатов физического эксперимента»/ Составители: В.И. Елфимов, С.И. Стальнова и Ю.Г. Шишкин (Л.: Изд-во ЛГУ, 1989. –33 с.). Предназначено для студентов факультетов: биолого-почвенного, географии и геоэкологии, геологического, медицинского, химического и др.
Ó Е.П. Зароченцева,
И.С. Бобкова,
Н.А. Малешина 2009
Ó Санкт-Петербургский
государственный
университет, 2009.
СОДЕРЖАНИЕ
|
1. Введение. |
5 |
|
2.Погрешности эксперимента, их виды. Возможности оценки |
6 |
|
§ 1. Понятие погрешности |
6 |
|
§ 2. Абсолютная и относительная погрешность |
7 |
|
§ 3. Промахи |
7 |
|
§ 4. Систематические погрешности |
8 |
|
§ 5. Случайные погрешности |
9 |
|
§ 6. Неисключенные систематические погрешности |
9 |
|
3. Элементы теории вероятностей |
10 |
|
4. Распределение Стьюдента |
15 |
|
5. Практические способы расчета случайных погрешностей |
17 |
|
§ 1. Обработка прямых измерений |
17 |
|
§ 2. Обработка косвенных измерений. Функция одной переменной |
18 |
|
§ 3. Обработка косвенных измерений. Функция многих переменных |
19 |
|
§ 4. Два способа оценки погрешностей |
21 |
|
§ 5. Метод наименьших квадратов (МНК) |
23 |
|
§ 6. Некоторые сведения о неравноточных измерениях |
27 |
|
6. Учет погрешности приборов |
28 |
|
7. Вычисления суммарной случайной и систематической погрешности |
30 |
|
8. Некоторые правила приближенных вычислений |
32 |
|
§ 1 Значащие цифры |
32 |
|
§ 2 Верные и сомнительные знаки |
32 |
|
§ 3 Правила округления |
33 |
|
§ 4 Правила записи окончательного результата |
34 |
|
§ 5 Предельная относительная погрешность |
34 |
|
§ 6 Действий с приближенными числами |
35 |
|
9. Правила выполнения отчета по лабораторной работе |
37 |
|
10. Рекомендации по построению графиков |
37 |
|
11. Приложения |
39 |
|
§ 1 Таблица коэффициентов Стьюдента |
39 |
|
§ 2 Распределение Стьюдента |
39 |
|
§ 3 Вычисление среднего арифметического при измерениях высокой точности |
40 |
|
§ 4 Формула среднеквадратичной погрешности (другой вид) |
40 |
|
§ 5 Алгоритм вычисления среднеквадратичного отклонения при прямых измерениях высокой точности |
41 |
|
§ 6 Среднеквадратичная погрешность среднего арифметического вывод |
42 |
|
§ 7 Определение коэффициентов линейной зависимости по МНК вывод |
42 |
|
12. Литература |
44 |
.
1. Введение
В любой экспериментальной науке, мы сталкиваемся с понятием «измерение». А что это значит? Для того чтобы некоторую физическую величину измерить, необходимо, во-первых, наличие меры или эталона данной величины. Во-вторых, должен существовать способ сравнения с эталоном. Например, в качестве эталона длины (единицы измерения длины) принято использовать 1 метр, в качестве эталона массы 1 килограмм. Для измерения длины какого либо объекта мы можем приложить к нему линейку, проградуированную в единицах длины метрах или их долях – сантиметрах, и определить сколько этих единиц укладывается на измеряемой длине. Тем самым мы произведем простейшее измерение.
В общем случае можно сформулировать: измерить физическую величину это означает определить, с помощью измерительного прибора, во сколько раз она отличается от единицы измерения данной характеристики.
Измерения можно разделить на два типа прямые и косвенные. Если измерения проводятся прибором, непосредственно предназначенным для определения данной характеристики, длину измеряют линейкой, температуру термометром, ток амперметром, то такие измерения называют прямыми. Если для определения искомой величины необходимо производить расчеты, то такое измерение будет косвенным. Например, искомая величина объем шара. Измерив диаметр шара с помощью штангенциркуля, полученное значение подставляют в формулу для расчета объема. Измерение объема будет считаться косвенным. На практике часто для определения искомой величины необходимо бывает измерить несколько различных параметров. Например, чтобы определить удельное сопротивление металла, из которого изготовлена проволока, надо измерить длину этой проволоки, ее диаметр и сопротивление. Удельное сопротивление рассчитывается по формуле, в которую входят эти три величины, таким образом, измерение удельного сопротивления тоже будет косвенным.
Следует понимать, что измерения никогда не могут быть абсолютно точными. Причин неточности очень много. Достаточно упомянуть, что прибор или устройство, посредством которого производится измерение, не бывает абсолютно точным. Несовершенство средств измерений может быть связано с их принципом действия, а также с конструктивными и технологическими ограничениями. Это несовершенство определяет одну из важнейших составляющих ошибки, которую называют инструментальной, аппаратурной или приборной. Экспериментатор, который проводит измерения, тоже вносит дополнительную ошибку из-за несовершенства своих органов чувств, например, человеческий глаз не может различить деления меньшие определенной величины и т.п. Кроме того, ошибка в измерениях может быть связана с изменением условий опыта и самого измеряемого объекта, с приближенным характером используемого метода и т. д.
2. Погрешности эксперимента, их виды. Возможности их оценки
§ 1. Понятие погрешности измерения
Любое измерение не является абсолютно точным, то есть измеренное значение некоторой физической величины (xизм) отличается от ее истинного значения (xист). Ошибкой измерения называют отклонение результата полученного на опыте от истинного (xизм xист). Следует отметить, что поскольку истинное значение искомой величины нам неизвестно, то и точную величину ошибки определить невозможно.
Существование ошибок измерений приводит к тому, что при повторении наблюдений в одних и тех же условиях результаты оказываются разными, наблюдается разброс данных. Это указывает на то, что ошибки в отдельных опытах неодинаковы. Как количественно характеризовать ошибку?
На первый взгляд может показаться, что достаточно задать верхнюю границу величины ошибки, то есть такое число x, для которого всегда выполняется условие
|
x xизм xист |
(1) |
Однако оказывается, что определить эту величину как абсолютно надежный предел, который ошибка не может превосходить, невозможно. Поэтому величину x, которую называют погрешностью измерения, задают так, чтобы неравенство (1) выполнялось с некоторой вероятностью Р. Если вероятность равна, например 0.95, то это означает, что при многократном повторении опыта ошибки в 95 случаях из 100 не превысят значения x.
Вероятностный подход применяется и при определении окончательного результата измерения. По данным многократных наблюдений находят наиболее вероятное значение измеряемой величины (обычно это среднее арифметическое ее значение), которое принимается за xизм.
Таким образом, задача обработки всякого измерения состоит из:
- нахождения наиболее вероятного значения измеряемой величины;
- оценки погрешности измерения;
- указания надежности результата, т.е. вероятности с которой истинное значение попадает в данный интервал.
В соответствии с этим результат записывают вместе с погрешностью и вероятностью в виде:
x = xизм x; Р.
Или как неравенство:
; Р,
здесь x погрешность измерения, Р вероятность.
Эту запись надо понимать, как утверждение, что с вероятностью Р истинное значение измеренной величины лежит в интервале от () до (), который называется доверительным интервалом. Вероятность Р, соответственно, называется доверительной вероятностью.
Вероятность обычно задается экспериментатором, в зависимости от условий эксперимента и его значимости она может быть различной. В учебных лабораториях принято выбирать вероятность 0,95; в некоторых случаях 0,9.
§ 2. Абсолютная и относительная погрешности.
Величину x иногда называют абсолютной погрешностью измерения. Знание абсолютной погрешности не всегда удобно для характеристики точности результатов. Например, пусть измерения длины производятся с погрешностью l = 1мм. Если длина предмета несколько метров, такая погрешность незначительна, если же несколько миллиметров, то она весьма существенна. Поэтому вводится понятие относительной погрешности измерений:
|
(2) |
которая указывает, какую часть абсолютная погрешность составляет от самой величины. Обычно выражают в процентах (%).
Причины возникновения погрешностей весьма разнообразны и, в соответствии с этим, на практике известно около 30 различных наименований погрешностей. Классификация погрешностей возможна по различным признакам. Мы будем пользоваться традиционным разделением на три типа – систематические погрешности, случайные и промахи.
§ 3. промахи
промахи — это грубые ошибки, вызванные, например неисправностью прибора, невнимательностью экспериментатора, резким изменением условий опыта и т.п. При обработке результатов измерений промахи следует отбрасывать. Как выделить промах из остальных измерений? Для этого существует специальное правило, оно называется «правило трех сигм», подробнее о нем будет сказано ниже. Опытный экспериментатор в большинстве случаев может выделить промах и, не пользуясь строгим правилом, «на глазок». например, если при многократных измерениях одной величины в большинстве опытов получены близкие ее значения, а одно сильно отличается от остальных, это значение, по-видимому, является промахом.
§ 4. систематические погрешности
систематические погрешности – это погрешности, которые повторяются при одинаковых условиях измерений. Систематические погрешности могут быть связаны с измерительным прибором или с условиями, в которых проводится опыт. Рассмотрим несколько примеров. У прибора может быть неправильно установлено начало отсчета, например стрелка вольтметра при отсутствии напряжения указывает не 0, а 2 деления, тогда (при отсутствии других неисправностей) такой прибор всегда будет показывать значение напряжения на 2 деления больше, чем следует. Эту ошибку легко исключить, введя соответствующую поправку. Другой пример, производя взвешивание на рычажных весах, обладающих большой чувствительностью, нельзя забывать, что на исследуемое тело, помимо силы тяжести, в воздухе действует выталкивающая сила. Зная плотность воздуха, величину этой силы можно оценить, и внести исправления в полученный результат взвешивания. Такого типа систематические погрешности можно оценить и исключить, внеся в результат измерений поправку.
Однако не все систематические погрешности возможно учесть. Как уже было сказано, любой измерительный прибор не является абсолютно точным, его показания включают погрешность, обусловленную его конструктивными особенностями. Обычно в характеристиках прибора указывается его возможная предельная погрешность или класс точности (предельная относительная погрешность). Знание этой погрешности не позволяет, однако, внести поправку в полученный результат, так как не известен ее знак. Она позволяет только оценить интервал, в котором находится измеренный результат. Такую погрешность называют не исключенной систематической погрешностью.
§5. Случайные погрешности
Случайными погрешностями называют непредсказуемые ни по знаку, ни по размеру погрешности, которые определяются совокупностью причин трудно поддающихся анализу, либо недостаточно изученных. Присутствие случайных погрешностей легко обнаруживается при повторных измерениях в виде разброса получаемых результатов. Случайные погрешности устранить нельзя, но их можно оценить и определить границы интервала, в которых заключено значение измеряемой величины.
Как уже было сказано, эти границы определить абсолютно надежно нельзя. Допустим, что получено несколько значений измеряемой величины. Тогда можно предположить, что искомое значение лежит в интервале между максимальным и минимальным из полученных значений, то есть xmin< x <xmax и есть тот интервал, в котором лежит значение искомой величины. Но какова вероятность того, что, сделав еще хотя бы одно измерение, мы не выйдем за пределы определенного таким образом интервала? Какова вероятность того, что вновь полученный результат будет «хуже» или «лучше» предыдущих?
Напрашивается мысль, что мало определить величину интервала, надо еще знать с какой вероятностью искомое значение попадает в этот интервал.
Такую возможность дает теория вероятностей. Случайные погрешности, подобно всем случайным величинам, подчиняются вероятностным законам, а значит, их можно оценить и определить границы интервала, в котором, с достаточно большой вероятностью, заключено значение измеряемой величины.
§6. Неисключенные систематические погрешности
Таким образом, если исключены промахи и внесена поправка на систематическую погрешность, то вклад в окончательную погрешность результата будут вносить случайные погрешности (xсл) и неисключенные систематические (приборные) (xпр).
В случае, когда приборная погрешность существенно больше случайной (xпр>>xсл), принято за окончательную погрешность измерения принимать приборную погрешность. Например, пусть 5 раз с помощью микрометра измерен диаметр проволоки, и все 5 раз получено одно и то же значение, значит случайная погрешность пренебрежимо мала, по сравнению погрешностью измерительного прибора, и за окончательную погрешность надо брать погрешность микрометра.
Если между этими ошибками обратное соотношение xпр<<xсл, то за окончательную погрешность принимают доверительный интервал, обусловленный случайными погрешностями. К примеру, с помощью того же микрометра, цена деления которого 0,01мм, несколько раз измерили толщину некоторого стержня, при этом разброс измерений оказался порядка 0,5 мм. В этом случае приборной погрешностью можно пренебречь.
Однако на практике нередко случается ситуация, когда случайная и приборная погрешности оказываются одного порядка. Тогда общую погрешность вычисляют как композицию этих двух. Подробнее в главе «Вычисление суммарной — случайной и систематической погрешности».
3. Элементы теории вероятностей и математической статистики.
Случайной называется величина, которая в результате опытов может принимать различные заранее неизвестные значения. Конкретное значение хi , появляющееся в результате опыта, называется реализацией случайной величины.
Пусть i= 1,2,. . . , N номера опытов, N их число, а xi – реализации, полученные при повторении опытов. Пусть х0 – истинное значение случайной величины, нам неизвестное.
Обозначим Δxi= x0 — xi абсолютную ошибку i-го измерения, тогда xi= x0 — Δxi. Просуммировав эти равенства по всем i, получим:
или
|
, |
(3) |
где среднее арифметическое всех реализаций. Можно показать, что второе слагаемое в этом выражении стремиться к 0, если N стремиться к бесконечности. Таким образом, среднее арифметическое всех реализаций стремиться к истинному значению случайной величины при стремлении к бесконечности числа измерений. Отсюда можно сделать вывод, что увеличение числа измерений приводит к увеличению точности.
Возможность тех или иных реализаций характеризуют вероятностью их появления. При этом вероятность достоверного события принято считать равной 1, а невозможного – равной 0.
В том случае, когда величины xi могут принимать непрерывный ряд значений, следует говорить не о вероятности конкретного значения xi, а о вероятности попадания результата измерений в некоторый интервал Δxi. Разобьем всю область значений x на одинаковые интервалы шириной Δx каждый.
|
Найдем число реализаций ΔNi, попадающих в каждый i-ый интервал и относительную частоту их появления ΔNi/N Представим результаты графически. По оси абсцисс отложим значение величины x, а относительную частоту ΔNi/N представим высотой полоски, построенной на интервале Δxi как на основании. |
Рис.1 |
Полученный график носит название гистограммы и характеризует распределение данной серии наблюдений. При большом числе измерений на гистограмме проявятся основные статистические закономерности:
- полученные значения измеряемой величины симметрично распределяются относительно некоторого среднего значения ;
- большие отклонения от среднего будут встречаться реже, чем малые.
|
Если увеличивать число измерений и одновременно сужать ширину интервалов Δx, то в пределе при Δx → 0 и N → ∞ ломаная линия, ограничивающая гистограмму сверху, будет стремиться к плавной колоколообразной кривой (рис.2). |
|
|
Рис.2 |
Такая кривая характеризует распределение результатов измерений при бесконечно большом числе наблюдений. Если при построении такой гистограммы по оси ординат откладывать относительную частоту появления реализации, отнесенную к единичному интервалу: ΔNi/(N ·Δx), то получающаяся в пределе кривая будет характеризовать распределение плотности вероятности получения результата хизм=х. Ордината этой кривой – плотность вероятности
|
(4) |
Величина dP(x)=f(x)dx – вероятность того, что результат наблюдения хизм окажется в пределах от результата х до результата х +dx (рис. 2). Площадь под всей кривой f(x) имеет смысл появления хоть какого-нибудь результата наблюдений, то есть вероятности достоверного события, поэтому она равна единице. Это условие нормировки для непрерывной случайной величины.
|
(5) |
Вероятность того, что измеренное значение будет лежать в интервале [x1, x2] определится выражением:
|
(6) |
то есть, равна площади, ограниченной кривой f(x) в этом интервале.
Кривая распределения результатов характеризует гипотетическую совокупность бесконечного числа наблюдений данной величины. Максимум кривой соответствует наиболее вероятному значению х=. Форма кривой зависит от точности измерений. Если точность высокая – большие отклонения встречаются редко, – то кривая имеет вид острого пика. Большая ширина колокола означает наличие больших случайных отклонений, то есть меньшей точности.
Законы теории вероятностей построены как асимптотические при х0 и N. Математическая статистика приближенно использует эти законы при конечных х и N.
Теория вероятностей утверждает, что случайные величины на практике наиболее часто подчиняются, так называемому, закону нормального распределения или закону распределения Гаусса. Плотность распределения определяется выражением:
|
f(x) = exp[] |
(7) |
Как видно из формулы (7) нормальная плотность распределения полностью определяется двумя параметрами теоретическим средним , и величиной 2, которую называют генеральной дисперсией распределения. Значение задает положение максимума, 2 — его ширину. Величина дисперсии характеризует разброс результатов измерений (точность), чем меньше разброс, тем меньше будет 2, на графике это отразится как более узкий и высокий максимум.
Параметр называется теоретическим средне квадратичным отклонением реализаций (или стандартным отклонением). Нетрудно убедиться, что в точках x = ± σ график функции f(x) имеет точки перегиба.
Такая же кривая описывает и распределение ошибок. Достаточно перенести начало координат в точку х= и тогда по оси абсцисс вместо х будут отложены значения ошибок х (отклонений от среднего). График функции f(Δx) изображен на рисунке 3.
Рис.3. Кривые нормального распределения Гаусса для трех значений параметра s.
Функция плотности распределения вероятности позволяет рассчитать теоретическое среднее значение реализаций измеряемой величины, его называют математическим ожиданием х0 случайной величины:
|
(8) |
Величина генеральной дисперсии также может быть вычислена с помощью этой функции:
|
(9) |
Вероятность Р того, что значение случайной величины х, получаемой при одном измерении, окажется внутри заданного интервала (х1 < x < x2) определится выражением:
|
, |
(10) |
Это выражение называют интегралом вероятности. Данное соотношение позволяет решить две задачи – можно задать необходимый интервал и найти соответствующую вероятность; а можно, наоборот, задав требуемую вероятность, найти интервал, в который попадает искомое значение х. На практике чаще пользуются второй возможностью.
Эту вероятность называют доверительной вероятностью, а границы интервала доверительными границами.
Воспользовавшись интегралом (10) можно определить, что вероятности попасть при одном измерении в интервал:
|
x0 — σ< x < x0+σ |
равна |
0,683 (68,3%) |
|
x0 — 2σ< x < x0+2σ |
— |
0,950 (95%) |
|
x0 — 3σ< x < x0+3σ |
— |
0,997 (99,7%) |
Видно, что вероятность того, что результат измерения отличается от среднего больше чем на 3σ, очень мала (0,3%), именно на основании этого факта такие результаты принято считать промахом – «правило трех сигм».
Иногда интеграл вероятности представляют в другом виде. Вводится новая переменная , которая определяется соотношением:
=(х — х0)/ σ, тогда d=dх/ σ и интеграл вероятности (10) принимает вид:
|
(11) |
Доверительные границы тогда будут определяться как Δх =±×σ. Величина задается требуемой вероятностью.
Из сказанного ранее следует, что с вероятностью 68,3% отдельная реализация будет отличаться от х0 (от математического ожидания) не больше, чем на σ; с вероятностью 95% — не больше чем на 2σ, соответственно и т. д.
4. Распределение Стьюдента.
На практике мы никогда не имеем дело с бесконечным числом измерений и не можем, следовательно, определить точно ни значение σ, ни значение х0.
В качестве оценки значения математического ожидания для выборки из n реализаций принято рассматривать их среднее арифметическое значение:
В качестве оценки дисперсии вводится величина выборочной дисперсии и величина выборочного среднеквадратичного отклонения , определяемые:
|
и |
(12) |
Можно показать, что при стремлении n к бесконечности → σ2.
Очевидно, что среднее арифметическое значение всех реализаций отличается от х0 меньше чем отдельное значение. Другими словами дисперсия () и среднеквадратичное отклонение () среднего арифметического меньше чем дисперсия и среднеквадратичное отклонение отдельного измерения. В теории вероятности доказываются следующие соотношения:
|
и = σ2 /n |
(13) |
|
и |
(14) |
Если мы имеем дело с конечным (и обычно не очень большим) числом измерений, то распределение уже не является Гауссовым. Качественно характер распределения подобен нормальному, но описывается другой функцией плотности распределения вероятности и носит название — распределение Стьюдента (псевдоним английского математика В. Госсета).
Распределение Стьюдента, в отличие от Гауссова, не определяется однозначно дисперсией и средним значением реализаций, а зависит еще от числа измерений n. В распределение Стьюдента входит параметр t , называемый коэффициентом Стьюдента, он зависит от двух величин – от числа измерений и от доверительной вероятности, поэтому указывается с двумя индексами: tp,n . Таблица наиболее часто используемых коэффициентов Стьюдента приведена в приложении (§1). Коэффициент Стьюдента связывает среднеквадратичную ошибку среднего арифметического с величиной доверительного интервала.
|
(15) |
Чем больше требуемая вероятность, тем больше коэффициент Стьюдента и, следовательно, больше доверительный интервал. С увеличением числа измерений значение коэффициента Стьюдента убывает.
Окончательный результат представляют в виде:
|
(16) |
Как следует из сказанного, увеличение числа измерений необходимо для увеличения точности результатов. С ростом n среднее арифметическое ближе к истинному значению х0 и доверительный интервал Δх при заданной вероятности Р будет меньше.
Однако не следует забывать о существовании помимо случайных погрешностей еще и неисключенных систематических. Большое число измерений уменьшает только случайную ошибку, но, учитывая наличие систематической погрешности, проводить слишком большое число измерений нерационально.
5. Практические способы расчета случайных погрешностей
Математическая обработка результатов измерений является весьма трудоемким делом, зачастую отнимающим больше времени, чем сами измерения. Она требует внимания и аккуратности. Задача упрощается, если пользоваться соответствующими алгоритмами, которые представляют собой план рациональной последовательности действий при нахождении результата и его погрешности.
§ 1. Обработка прямых измерений (алгоритм прямых измерений).
Пусть искомая величина x измерена n раз, для нахождения и , рекомендуется записать данные в следующую таблицу и производить расчеты в указанном порядке.
Таблица 1
|
№ |
xi |
xi |
(xi -)2 |
|
1 |
x1 |
x1 |
(x1 -)2 |
|
2 |
x2 |
x2 |
(x2 -)2 |
|
3 |
x3 |
x3 |
(x3 -)2 |
|
… |
….. |
…… |
………. |
|
n |
xn |
xn |
(xn -)2 |
- Найти сумму всех xi ()
- Найти =
- Заполнить третий и четвертый столбцы таблицы.
- Сосчитать сумму в четвертом столбце
- Рассчитать среднеквадратичную погрешность среднего арифметического, используя полученную в четвертом столбце сумму.
- Найти в «таблице коэффициентов Стьюдента» tn—1,P для данного числа измерений и выбранной вероятности.
- Определить
- Записать окончательный результат .
Пример. Пять раз измерен диаметр проволоки с помощью микрометра. Получены следующие результаты (столбец 2).
Таблица 2
|
№ |
di, мм |
di,мм |
(di)2, |
|
1 |
3,90 |
0,01 |
1104 |
|
2 |
3,85 |
0,06 |
36104 |
|
3 |
3,88 |
0,03 |
9104 |
|
4 |
3,97 |
0,06 |
36104 |
|
5 |
3,95 |
0,04 |
16104 |
|
19,55 |
98104 |
=19,55 / 5 =3,910 мм
Для доверительной вероятности Р=0,95 и числа измерений n=5, коэффициент Стьюдента =3,2, тогда
=3,20,022= 0,070 мм.
Окончательный результат: = (3,910,07 P=0,95 ) мм.
Относительная погрешность d = (0,07 / 3,91)100% = 1,8%.
Возможны другие способы расчета, смотри приложение §§ 4,5.
§ 2. Обработка косвенных измерений. Функция одной переменной. (Формулы переноса ошибок).
Пусть искомая физическая величина Y является функцией измеряемой величины x.
Y =f(x)
Так как величина x не может быть определена абсолютно точно, то и рассчитанное значение Y будет содержать погрешность. Значение искомой функции следует находить, как функцию среднего арифметического значения измеренной величины , то есть в формулу для ее определения подставить вычисленное среднее значение
Как определить погрешность функции, если известна погрешность аргумента?
Для этого пользуются известным соотношением между дифференциалом функции df(x)и бесконечно малым приращением аргумента dx:
Полагая xdx, а YdY , получаем выражение для погрешности функции:
|
(17) |
где x =tp,n-1 Sx , производная функции при x =.
Иногда оказывается удобнее (проще) вычислить сначала относительную погрешность, а уже зная ее, определить доверительный интервал. Учитывая то, что: легко видеть, что относительную погрешность функции можно вычислить, воспользовавшись следующей формулой:
|
(18) |
§ 3 Обработка косвенных измерений. Функция многих переменных. (Формулы переноса ошибок)
В общем случае искомая физическая величина может быть функцией не одной, а нескольких измеряемых величин, то есть: Y= f(X1, X2,…Xn) Каждая из величин X1, X2,…Xn определяется с соответствующей погрешностью X1, X2,… Xn. В этом случае средняя квадратичная погрешность функции будет равна корню квадратному из суммы квадратов частных производных функции по всем независимым переменным, домноженным на среднеквадратичную погрешность соответствующей величины:
|
(19) |
В данной формуле каждая скобка под корнем представляет собой вклад погрешности соответствующей величины в погрешность функции. Если погрешности различных измеряемых величин определены с одной и той же доверительной вероятностью, то формулу можно переписать в следующем виде:
|
(20) |
Относительная погрешность функции может быть вычислена по формуле:
|
(21) |
Приведенные формулы справедливы для любых функциональных зависимостей, однако, они довольно громоздки, производить по ним расчеты бывает достаточно сложно, они требуют больших затрат времени. В некоторых случаях бывает удобнее использовать выражения, преобразованные для частных случаев функциональной зависимости. Рассмотрим несколько таких частных случаев.
Погрешность алгебраической суммы
Пусть функция имеет вид:
Y = , тогда среднеквадратичная погрешность такой функции будет определяться:
|
(22) |
а выборочная дисперсия:
|
(23) |
То есть выборочная дисперсия алгебраической суммы равна сумме выборочных дисперсий отдельных независимых переменных. Обратите внимание, на то, что в выражение для выборочной дисперсии функции все слагаемые входят со знаком «+», независимо от того, с каким знаком соответствующая величина входила в алгебраическую сумму.
Погрешность произведения.
Пусть функция имеет вид:
или
В этих случаях, воспользовавшись формулой (21) и, учитывая то, что логарифм произведения равен сумме логарифмов, получаем выражение для относительной погрешности функции:
|
(24) |
То есть относительная погрешность произведения (и частного) равна корню квадратному из суммы квадратов относительных погрешностей всех сомножителей. Также как и в случае суммы, обратите внимание, на то, что все слагаемые под корнем берутся со знаком «+», независимо от того в числитель или знаменатель выражения функции они входили.
Производить расчет по этой формуле обычно гораздо проще, чем по формуле (19), а доверительный интервал искомой величины легко найти: .
Погрешности некоторых элементарных функций.
- , где С=const;
- ;
- ;
§ 4. Два способа оценки погрешности при косвенных измерениях.
В случае косвенных измерений физических величин возможны два способа вычисления окончательного результата и погрешности.
Первый способ.
Для каждой измеряемой физической величины проводят серию измерений. Эти измерения (прямые) обрабатывают и находят средние значения и соответствующие им доверительные интервалы с одной и той же доверительной вероятностью. Затем по выражению функциональной зависимости Y= f (X1,X2,…Xn) находят среднее значение искомой физической величины, используя найденные средние значения всех измеренных величин . Затем по формулам переноса ошибок (формула 19 или ее частные случаи) рассчитывают доверительный интервал величины Y.
Пример
Задача определить ускорение свободного падения с помощью математического маятника.
Формула для расчета , где l длина маятника, T период его колебаний.
Измерили 5 раз длину маятника и 5 раз его период. Получили следующие значения, которые обработали, как прямые измерения:
Таблица 3
|
l(м) |
(м) |
0,9644 =0,00051 3,20,00051=0,0016 |
||
|
1 |
0,965 |
0,0006 |
3,6 10-7 |
|
|
2 |
0,966 |
0,0016 |
25,610-7 |
|
|
3 |
0,964 |
-0,0004 |
1,610-7 |
|
|
4 |
0,963 |
-0,0014 |
19,610-7 |
|
|
5 |
0,964 |
-0,0004 |
1,610-7 |
|
|
|
4,822 |
5210-7 |
||
|
Т(сек) |
Т |
(Т)2 |
1,9698 =0,000583 3,2 0,000583 =0,0018660,0019 |
|
|
1 |
1,970 |
0,0002 |
0,0410-6 |
|
|
2 |
1,969 |
-0,0008 |
0,6410-6 |
|
|
3 |
1,971 |
0,0012 |
1,4410-6 |
|
|
4 |
1,968 |
-0,0018 |
3,2410-6 |
|
|
5 |
1,971 |
0,0012 |
1,4410-6 |
|
|
|
9,849 |
6,810-6 |
Получили: 0,9644 и 1,9698.
Затем рассчитывают
и, в соответствии с формулой (7) рассчитывают относительную погрешность g:
.
Тогда g = g g =9,812342 0,0025=0,0249 0,025, и окончательный результат, соответственно: (9,8120,025) м/с2 при Р=0,95
Второй способ.
В случаях, когда по условиям опыта измерения делаются в не воспроизводимых условиях, значения функции, Y= f(X1,X2,…Xn) вычисляют для каждой отдельной серии измерений {Xi}, а затем полученный ряд значений Yi , обрабатывают по алгоритму прямых измерений.
Пример
Пусть поставлена та же задача определить g, но при этом имеется несколько (пять) заведомо различных маятников. В этом случае рационально поступить следующим образом. Для каждого маятника измерить его длину и период колебаний. По этим значениям рассчитать величину g (для каждого маятника независимо). Полученные значения g обработать, как прямые измерения.
Таблица 4
|
№ маятника |
L(м) |
Т(сек) |
g (м/с2) |
||
|
1 |
0,965 |
1,970 |
9,816453 |
0,00355 |
0,12603210-4 |
|
2 |
1,222 |
2,222 |
9,771086 |
-0,041817 |
17,4866910-4 |
|
3 |
1,568 |
2,510 |
9,825584 |
0,01268 |
1,6079510-4 |
|
4 |
0,559 |
1,498 |
9,834401 |
0,0215 |
4,6216710-4 |
|
5 |
0,752 |
1,739 |
9,816991 |
0,00409 |
0,16715210-4 |
|
|
49,06452 |
24,009510-4 |
,
g = 3,20,01096 =0,035
и, соответственно, окончательный результат:
(9,8130,035) м/с2 при Р=0,95
§ 5 Метод наименьших квадратов (МНК).
Помимо двух вышеописанных способов оценки погрешности результата при косвенных измерениях, иногда применяют еще так называемый «метод наименьших квадратов» или сокращенно МНК. Этот метод можно использовать, если известен вид функциональной зависимости между измеряемыми физическими величинами, а требуется определить коэффициенты, входящие в эту функцию. В наших лабораторных работах предлагается применять этот метод для определения параметров линейной зависимости.
Пусть в эксперименте можно измерить ряд значений некоторой величины x и, соответствующие им значения, величины y. И пусть при этом известно, что между ними справедлива зависимость вида: y = ax + b. Как известно, такая зависимость графически представляется прямой линией (рис.4). Однако измеренные значения xi и yi включают в себя погрешность и, в результате, не лягут идеально на прямую линию.
Как по данным экспериментальных наблюдений наилучшим образом найти коэффициенты a и b? Графически эта задача сводится к построению прямой, ближе всего лежащей ко всем экспериментальным токам, так как прямая однозначно задается этими коэффициентами (рис.4.).
|
Для аналитического выражения коэффициентов применяется метод наименьших квадратов. Утверждается, что наилучшей будет та прямая, сумма квадратов расстояний до которой, от всех экспериментальных точек будет минимальной. Расстояние (вдоль оси y) от точки с координатами xi, yi до искомой прямой определяется выражением: (axi +b yi), |
|
|
Рис.4 |
тогда сумма квадратов расстояний будет равна:
Решение задачи на нахождение минимума этого выражения (см. приложение, § 7) приводит к следующим выражениям для коэффициентов a и b.
|
(25) |
|
|
(26) |
Дисперсию отклонения экспериментальных точек от прямой S02 и дисперсию коэффициентов a и b Sa2 и Sb2 можно вычислить по формулам:
|
S02 = |
(27) |
|
(28) |
|
|
Sb2= |
(29) |
Доверительные интервалы для коэффициентов a и b определяются как обычно:
ap = Sa bp = Sb
Если график исследуемой зависимости проходит через начало координат, то есть b =0, формулы 25, 27 и 28 существенно упрощаются. В этом случае коэффициент a и его дисперсию можно рассчитать по следующим формулам:
|
(30) |
|
|
(31) |
|
|
(32) |
Однако следует иметь в виду, что формулы 25-28 включают разности больших величин, мало отличающихся друг от друга, что легко может привести к ошибкам при вычислениях, если их проводить с недостаточным числом значащих цифр. Поэтому все промежуточные вычисления следует выполнять с большим числом значащих цифр, без округления. Если вы проводите вычисления с помощью компьютера, то это условие выполняется. В том случае, если расчеты выполняются «вручную», или с помощью не очень совершенного калькулятора, а результаты измерений имеют более трех верных знаков, то велика вероятность получить неправильный результат вычислений. В этом случае рекомендуется для вычисления коэффициентов a и b, а также доверительных границ их погрешности вместо вышеуказанных формул использовать выражения, преобразованные к другому виду:
|
(33) |
|
|
(34) |
|
|
(35) |
|
|
(36) |
|
|
(37) |
Во всех случаях проведения расчетов по МНК для определения коэффициентов линейной зависимости и их погрешностей необходимо вычислить некоторые суммы. Для этого удобно воспользоваться следующими таблицами – алгоритмами вычислений. Подсчитав суммы в каждом столбце и подставив их в соответствующие формулы, легко определить и значения a, b, a и b
Таблица 5
|
xi |
yi |
xi2 |
yi2 |
xi yi |
|
x1 |
y1 |
x12 |
y12 |
x1 y1 |
|
x2 |
y2 |
x22 |
y22 |
x2 y2 |
|
… |
… |
… |
… |
… |
|
xn |
yn |
xn2 |
yn2 |
xn yn |
|
xi |
yi |
xi2 |
yi2 |
x1 y1 |
Или в случае использования формул 33 -37
Таблица 6
|
xi |
yi |
xi |
(xi )2 |
(xi )yi |
xi2 |
(axi +b yi)2 |
|
x1 |
y1 |
x1 |
(x1 )2 |
(x1 )y1 |
x12 |
(ax1 +b y1)2 |
|
x2 |
y2 |
x2 |
(x2 )2 |
(x2 )y2 |
x22 |
(ax2 +b y2)2 |
|
… |
… |
… |
… |
|||
|
xn |
yn |
xn |
(xn )2 |
(xn )yn |
xn2 |
(axn +b yn)2 |
|
xi |
yi |
(xi ) |
(xi )2 |
(xi )yi |
xi2 |
(axi +b yi)2 |
§6. Некоторые сведения о неравноточных измерениях.
Бывают случаи, когда одну и ту же физическую величину измеряют несколько раз, но не в одинаковых условиях, а с разной степенью точности. Например, определение длины волны спектральной линии по положению дифракционных максимумов разных порядков.
В этом случае в качестве оценки значения искомой величины принимается средне взвешенное ее значение, вычисляемое по формуле:
, (38)
Здесь Рi — вес соответствующей реализации, то есть некоторый коэффициент, зависящий от точности i-того измерения. Подбор этих коэффициентов задача в общем случае не простая. Обычно их выбирают обратно пропорционально квадратам относительных ошибок, соответствующих реализаций. Дисперсия средневзвешенного значения рассчитывается по формуле:
(39)
Пример
Условие образования дифракционного максимума: d sin = k, где k = 0,1,2,… – порядок спектра, d – постоянная решетки, а — угол дифракции. Следовательно, длину волны можно определить, измерив углы для разных k:
Поскольку постоянная решетки известна с большой степенью точности (ее погрешностью можно пренебречь), а порядок спектра – целое число, тогда погрешность длины волны будет определяться только погрешностью определения величины угла. Очевидно, что чем больше угол (больше порядок спектра), тем меньше будет относительная погрешность измерения угла (т.к. абсолютная погрешность прибора одинакова). Воспользовавшись формулой (17), можно получить:
Пусть в процессе измерений получены следующие значения углов:
При k=1 φ1 =1015׳ ctg φ1= 45,8
k=2 φ2 =2030׳ ctg φ2 = 22,9
k=3 φ3 =3042׳ ctg φ3 = 15,5.
Таким образом, относительные ошибки в первом, втором и третьем порядках относятся как 3:2:1. Следовательно, веса следует выбирать: Р1=1, Р2=4, Р3=9. Постоянная решетки d=0,002см.
Получаем:
Тогда средневзвешенное значение будет равно:
Дисперсия среднего взвешенного:
Sλ =2,03нм Δλ= Sλ ×tp,n-1 =2,03×4,3= 8,7нм
Окончательный результат имеет вид λ= (432 ±9) нм
6.Учет погрешности приборов.
Если при измерении какой-либо величины при помощи физического прибора получают одно и то же значение при многократных измерениях, это не значит, что случайные погрешности определения этой величины равны нулю. Из этого факта будет следовать только то, что случайные погрешности при этих измерениях меньше систематических погрешностей, даваемых измерительными приборами, которые могут быть оценены по классу точности прибора. Приборная погрешность может быть указана или на самом приборе, или в его паспорте. В случаях, когда отсутствует паспорт прибора и не указан класс точности, приборную погрешность принято считать равной половине наименьшего деления шкалы прибора (половине цены деления шкалы)
При косвенных измерениях приборная (неисключенная систематическая) погрешность функции будет определяться (см. ф 20) через приборные погрешности аргументов по формуле:
(40)
Здесь Θ – приборная погрешность функции y, Θxi — приборная погрешность величины xi
Пример.
Предположим, что измеряется сопротивление нагрузки путем измерения падения напряжения на ней и тока в цепи. Произведено пять измерений падения напряжения и пять измерений тока, которые дали совершенно одинаковые результаты. Измеренный ток I=5 A, напряжение В
Искомое сопротивление равно .
Так как случайные погрешности не наблюдались, будем оценивать не исключенную систематическую погрешность, обусловленную предельной погрешностью измерительных приборов, используемых в эксперименте (классом точности).
Напряжение измеряется вольтметром, предел измерения которого равен 200 В, а класс точности γкл.т.=1,0. Относительная погрешность напряжения будет определена по формуле и численно равна
тогда предельная абсолютная погрешность напряжения .
Ток в цепи измеряется амперметром, его предел измерения –10 А, класс – 1,0. Относительная погрешность измерения тока
а абсолютная величина предельной погрешности тока =0,1 А
Функция имеет вид , т.е. представляет собой частное двух аргументов. Воспользовавшись формулой 24, получим выражение для вычисления относительной погрешности сопротивления:
Тогда неисключенная систематическая погрешность сопротивления нагрузки
;
Окончательный результат измерения сопротивления будет записан в виде
R = (20,0 ± 0,6) Oм
7. Вычисление суммарной случайной и систематической погрешности.
Если отношение неисключенной систематической погрешности измерения к случайной погрешности удовлетворяет неравенству:
0,8<< 5 (41),
то границы погрешности результата измерений (общие доверительные границы) вычисляют с учетом и случайных и не исключенных систематических погрешностей, рассматриваемых как случайные величины.
При работе в лаборатории рекомендуется использовать следующий вариант расчета:
– оценка суммарного среднеквадратичного отклонения результата измерения.
Θ – приборная (не исключенная систематическая) погрешность результата измерения
– доверительные границы случайной погрешности.
Пример.
Рассмотрим предыдущий пример измерения сопротивления нагрузки путем измерения падения напряжения на ней и тока в цепи.
Пусть были произведены пять измерений напряжения и тока в цепи. И каждый раз были получены различные значения напряжения и тока. Необходимо сопоставить не исключенную систематическую погрешность со случайной погрешностью .
Полученные значения записаны в таблице.
Таблица 7
|
Измеряемая величина |
Результаты измерений |
Средние значения |
||||
|
U В |
100 |
99 |
99 |
101 |
101 |
500/5 = 100 |
|
I А |
5,00 |
4,95 |
4,90 |
5,10 |
5,00 |
24,95/ 5= 4,99 |
По алгоритму прямых измерений вычисляются доверительные границы напряжения и тока для доверительной вероятности P=0,95, а также их средние значения, считая, что погрешности этих величин обусловлены случайными ошибками. Получаем следующие значения:
SI =0,033166 ΔI = 3,2×0,033= 0,11
SU = 0,447 ΔU = 3,2×0,447= 1,43
.
Суммарная средняя квадратичная погрешность сопротивления нагрузки будет определяться по формуле переноса ошибок:
при P=0,95.
Приборная погрешность для такого же примера была рассчитана в предыдущем параграфе:
=0,57/0,51 = 1,1 – следовательно, необходимо учитывать и ту и другую погрешность.
И окончательный результат будет записан в виде
R = (20,0 ± 0,8 Р=0,95) Oм
8.Некоторые правила приближенных вычислений.
Измеряя различные физические величины, мы получаем не точные, а приближенные их значения. Поэтому математическая обработка результатов эксперимента всегда связана с действиями над приближенными числами. Полученный результат, конечно, тоже будет приближенным числом. Задача состоит в том, чтобы, оперируя приближенными числами, получить результат с наибольшей возможной точностью. Точность математической обработки экспериментального материала должна соответствовать точности самих измерений, невозможно получить результат точнее, чем исходные данные. Вычисление с излишним числом значащих цифр, во-первых, создает лишние трудности и занимает больше времени, во-вторых, создает ложное представление о большой точности измерений. Таким образом, вычисления необходимо производить так, чтобы, с одной стороны не потерять достигнутую в эксперименте точность, с другой стороны не тратить лишние силы на ненужную работу.
Напомним некоторые понятия и правила, необходимые при работе с приближенными числами.
§ 1 Значащие цифры в приближенном числе
Значащими цифрами в приближенном числе называются все цифры кроме нулей в начале числа.
Например:
|
Приближенное число |
Количество значащих цифр |
Обратите внимание, на два последние примера. Здесь проявляется одна из особенностей приближенных чисел. В отличие от точных чисел, где нули в конце дробной части можно было бы просто отбросить, эти нули отбрасывать нельзя. |
|
547,3 |
4 |
|
|
0,0041 |
2 |
|
|
0,40005 |
5 |
|
|
0,0040 |
2 |
|
|
1,500 |
4 |
Они означают, что эти разряды известны и равны именно 0. Если вместо числа 1,500 записано 1,5, то это означает, что в этом числе разряд сотых и последующие разряды неизвестны. Если измерена длина предмета с точностью до 1 миллиметра, и она оказалась равной ровно одному метру, то результат следует записать: L=1,000м, запись L=1м будет неверной.
§ 2 Верные знаки в приближенном числе
Если приближенное число записано без указания погрешности, то подразумевается, что значения всех разрядов известны точно – все знаки верные, а погрешность в этом случае не превышает половины единицы последнего десятичного разряда.
Например:
|
Приближенное число |
Число верных знаков |
Погрешность не превышает |
|
1,23 |
3 |
0,005 |
|
4317 |
4 |
0,5 |
|
0,056 |
2 |
0,0005 |
|
8,32104 |
3 |
0,005104 = 50 |
|
1,50 |
3 |
0,005 |
Однако более грамотно записывать приближенные числа с указанием погрешности. Цифры приближенного числа называются верными, если абсолютная погрешность не превосходит половины единицы низшего из этих цифр разряда. Цифры в последующих разрядах называют сомнительными.
Например:
|
Приближенное число |
Число верных знаков |
Сомнительные цифры |
|
47,520,15 |
2 |
0,52 – разряды десятых и сотых |
|
1,054 0,008 |
2 |
0,054 – разряды сотых и тысячных |
|
1454 |
2 |
5 – разряд единиц |
|
1457 |
1 |
45 – разряды единиц и десятков |
|
231,180,45 |
3 |
0,18 – разряды десятых и сотых |
§ 3 Правила округления
При действиях с приближенными числами часто приходится отбрасывать лишние цифры (заведомо неверные) – округлять число. При этом соблюдают следующие правила.
- Отбрасываемая (n+1)-я цифра меньше 5 – оставшаяся n-я цифра не изменяется. Например: 5,7645,76 или 423,1423.
- Отбрасываемая (n+1)-я цифра больше 5 – оставшаяся n-я цифра увеличивается на единицу. Например:15,616 или 189190.
- Отбрасываемая (n+1)-я цифра равна 5, а (n+2)-я отлична от 0 – оставшаяся n-я цифра увеличивается на единицу. Например: 23,52 24 или 0,34530,35.
- Отбрасываемая (n+1)-я цифра равна 5, а (n+2)-я и более мелкие разряды равны 0. В этом случае принято округлять до четной цифры. Если оставшаяся n-я цифра четная – ее сохраняют, если нечетная – ее увеличивают на единицу. Примеры: 13,5014; 275280; 0,54500,54
§ 4 Правила записи окончательного результата
Очень важно уметь правильно записать окончательный результат, не загромождая его лишними, заведомо неверными цифрами, но и не потерять необходимые знаки.
При записи окончательного результата в первую очередь округляют погрешность. Рекомендуемый способ оценки погрешности предполагает ее округление до двух значащих цифр (если первая цифра меньше 5) или одной (если первая цифра больше 5). Погрешность обычно округляют в большую сторону. После этого сам полученный результат округляют до того же разряда, что и погрешность, то есть оставляют в нем два сомнительных знака. Полученное число и его погрешность приводят к одинаковому разрядному множителю и выносят этот множитель за скобки. Обязательно указать размерность.
Например:
|
Получено в результате расчетов |
Следует записать |
|
x=0,0054837 см, x = 0,0002487 см |
x =(5,48 0,25) 10–3 см |
|
x =60540548 Н x = 52487 Н |
x =(60545) 104 Н |
|
x =45,605 Ом x = 0,375 Ом |
x =(45,60 0,38) Ом |
|
x = 1,399821 x = 0,007524 |
x =(1,400 0,008) |
§ 5.Предельная относительная погрешность
Последний верный разряд в приближенном числе связан с абсолютной погрешностью. Относительная погрешность связана с числом верных знаков в нем.
На практике для быстрой оценки погрешности бывает полезно оценить предельную относительную погрешность пр. Она определяется следующим образом. В приближенном числе все цифры, кроме первой значащей заменяются нулями, а абсолютная погрешность полагается равной половине единицы низшего верного разряда. Например, в числе 45738 три цифры верные, тогда пр =(50 / 40000) 100% = 0,12%. Очевидно, что пр.
В процессе промежуточных вычислений часто встает вопрос, какие разряды в числе следует оставлять, а какие, заведомо неверные, можно сразу отбросить, чтобы упростить расчеты. Оценить пр очень легко, а ее знание позволяет предсказать сколько верных знаков должно иметь приближенное число.
Поскольку любое округление вносит систематическую ошибку, то при вычислении окончательного результата приходится производить действия с числом значащих цифр, превышающим на единицу число значащих цифр, полученных при измерениях, чтобы в последующем округлить результат.
§ 6 Действия с приближенными числами.
При сложении и вычитании приближенных чисел абсолютная погрешность суммы не может быть меньше чем абсолютная погрешность наименее точного слагаемого (см. формулы 22 и 23), поэтому сумму (разность) необходимо считать с точностью до того же разряда, что и наименее точное слагаемое.
Примеры:
|
Неправильно |
Правильно |
Почему неправильно |
|
17,55 + 13,45 =31 |
17,55 + 13,45 =31.00 |
В обоих слагаемых известны разряды сотых, этот разряд должен быть и в сумме. |
|
44 11,3 =32,7 |
44 11,3 =33 |
В первом слагаемом неизвестен разряд десятых, невозможно его знать и в результате |
|
12 + 12,25 =24,25 |
12 + 12,25 =24 |
В первом слагаемом неизвестны разряды десятых и сотых, невозможно их знать и в результате |
|
0,571 + 0,429 =1 |
0,571 + 0,429 =1,000 |
В обоих слагаемых известны разряды тысячных, этот разряд должен быть и в сумме |
Однако следует заметить, что в процессе вычислений один лишний разряд необходимо оставлять, чтобы в последующем округлить результат.
Надо иметь в виду, что при вычитании близких друг к другу приближенных чисел с большим числом верных цифр, в результате получается число с меньшим числом верных цифр, т.е. с большей относительной погрешностью. Например: 345,67 – 345, 65 = 0,02. Предельная относительная погрешность уменьшаемого и вычитаемого составляет 0,017%, а для разности она равна 25%. Следует составлять схемы расчетов так, чтобы избегать подобных ситуаций.
При умножении и делении относительная погрешность результата определяется относительными погрешностями исходных чисел (а значит числом верных знаков в них), и, следовательно, не может быть меньше, чем относительная погрешность наименее точного сомножителя. (см. формулу 24). А число значащих цифр в произведении не может быть больше чем в наименее точном сомножителе.
Примеры:
|
Неправильно |
Правильно |
Почему неправильно |
|
1,45 19 =27,55 |
1,45 19 =28 |
Второй сомножитель имеет две значащих цифры, его относительная погрешность около 2%, результат невозможно получить с большей точностью. |
|
625 : 125 =5 |
625 : 125 =5,00 |
В делимом и делителе по три значащих цифры, их относительные погрешности около 0,5% — относительная погрешность результата — порядка 1%. |
|
95 : 27 =3,518 |
95 : 27 =3,6 |
Делитель имеет относительную погрешность около 2%, результат невозможно получить с большей точностью. |
|
1,25 0,800 =1 |
1,25 0,800 =1,00 |
В обоих сомножителях по три значащих цифры, их относительные погрешности около 0,5% — относительная погрешность произведения — порядка 1%. |
При умножении или делении на точное число, относительная погрешность результата равна относительной погрешности приближенного числа, и в результате сохраняют столько же знаков, сколько их было в приближенном числе.
9. Правила выполнения отчета по лабораторной работе
Отчет должен содержать:
- Название и номер работы
- ФИО, факультет и номер группы студента, выполнившего работу.
- Формулы, необходимые для вычисления результата, и обозначения.
- Формулы для расчета погрешности.
- Схему установки и основные характеристики используемых измерительных приборов.
- Значения справочных данных и констант, используемых при расчетах.
- Таблицы наблюдений, в которые должны быть внесены как результаты измерений, непосредственно полученные в процессе работы, так и переведенные в необходимую для расчетов форму.
- Обработку результатов измерений.
- Вычисление результата. (Необходимо показать подстановку).
- Вычисление погрешности.
При подстановке в формулы для вычислений все величины должны быть в одной системе единиц, для расчетов рекомендуется числа представлять в стандартном виде (Например, 0,0000567 = 5,67 • 10 -5)
- Окончательный результат в соответствии с правилами записи окончательного результата.
- Требуемые графики
- Выводы.
10. Рекомендации по построению графиков.
Графики строят на миллиметровой бумаге. По оси абсцисс следует откладывать аргумент, т.е. задаваемую величину, а по оси ординат – функцию, т.е. величину определяемую. На осях указывают обозначения и единицы измерения откладываемой величины.
Начинают построение графика с выбора масштаба, при этом следует руководствоваться следующими несложными правилами:
- Масштаб должен соответствовать (по возможности) точности измерений. Например, если вы измеряли температуру с точностью до 0,1 градуса, то нельзя одному миллиметру на оси температуры придавать значение 1 градус, и нерационально, если 0,1 градуса будет соответствовать 1 см.
- Масштаб должен быть простым. Он должен соответствовать единице измеряемой величины или величине кратной данной единице с множителями 10К, 2 или 5. Например, 1см на графике может соответствовать 0,2 сек, 50 В, 0,001 м, 10 мА и т.д.
- Масштаб должен быть таким, чтобы экспериментальная кривая занимала всю плоскость чертежа, и наклон ее основной части был около 450. Не надо стремиться поместить на графике начало координат. На графике должен помещаться лишь тот интервал значений изучаемых величин, который исследовался в эксперименте.
- Около осей отмечают выбранный масштаб (а не результаты измерений).
- На график наносятся все экспериментальные точки, желательно с указанием погрешности (учитывая, что каждый результат измерения не точка, а интервал). Кривая должна проводиться плавно, указывая тенденцию зависимости. Кривая не должна скрывать опытных точек, так как она представляет лишь толкование эксперимента, а точки – сам результат эксперимента. График должен иметь заголовок
Приложения
§ 1. Таблица коэффициентов Стьюдента
|
n P |
0,70 |
0,80 |
0,90 |
0,95 |
|
2 |
2,1 |
3,1 |
6,3 |
12,7 |
|
3 |
1,3 |
1,9 |
2,9 |
4,3 |
|
4 |
1,3 |
1,6 |
2,4 |
3,2 |
|
5 |
1,2 |
1,5 |
2,1 |
2,8 |
|
6 |
1,2 |
1,5 |
2,0 |
2,6 |
|
7 |
1,1 |
1,4 |
1,9 |
2,4 |
|
8 |
1,1 |
1,4 |
1,9 |
2,4 |
|
9 |
1,1 |
1,4 |
1,9 |
2,3 |
|
10 |
1,1 |
1,4 |
1,9 |
2,3 |
|
11 |
1,1 |
1,4 |
1,8 |
2,2 |
|
12 |
1,1 |
1,4 |
1,8 |
2,2 |
|
13 |
1,1 |
1,4 |
1,8 |
2,2 |
|
14 |
1,1 |
1,4 |
1,8 |
2,2 |
|
15 |
1,1 |
1,3 |
1,8 |
2,2 |
§ 2. Распределение Стьюдента
Распределение Стьюдента (впервые получено английским математиком В. Госсетом в 1908 г, который печатал свои работы под псевдонимом Стьюдент) выражается формулой
где — число измерений, t – коэффициент Стьюдента, Г() –гамма-функция, представляющая обобщенное понятие факториала ( для целых чисел Г(+1)=! Для полуцелых – Г= , Г= /2 и т.д.
Кривые функции имеют такой же вид, как и кривые распределения Гаусса (см. рис.2).
При n→∞ (практически уже при n>20) распределение Стьюдента переходит в нормальное распределение Гаусса с единичной дисперсией (=1).
§ 3. Вычисление среднего арифметического при измерениях высокой точности
Вычисление среднего арифметического
Если выбрать значение близкое к тогда эту формулу можно записать в виде
=
Данная формула оказывается более удобной, чем первая тогда, когда численное значение измеряемых величин имеют несколько значащих цифр. В этом случае приходится находить среднее арифметическое небольших разностей, а не самих больших чисел
§ 4. Расчет среднеквадратичного отклонения (другой вид формулы).
По определению среднее квадратичное отклонение равно (см. формулы 12,13)
Числитель под корнем можно преобразовать:
Следовательно, среднеквадратичную погрешность можно записать в виде:
При использовании этой формулы алгоритм вычисления погрешности при прямых измерениях упрощается.
|
xi |
xi2 |
|
|
x1 |
x12 |
|
|
x2 |
x22 |
|
|
x3 |
x32 |
|
|
….. |
||
|
xn |
xn2 |
|
Однако следует иметь в виду, что в эту формулу входит малая разность, поэтому расчет необходимо производить с большим числом значащих цифр. Если вы проводите вычисления с помощью компьютера, то это условие выполняется. В том случае, если расчеты выполняются «вручную», или с помощью не очень совершенного калькулятора, то надежнее использовать алгоритм, предложенный в главе 5 §1.
§ 5 Алгоритм вычисления среднеквадратичного отклонения при прямых измерениях высокой точности
|
xi |
xi-А |
(xi-А)2 |
|
|
x1 |
x1-А |
(x1-А)2 |
|
|
x2 |
x2-А |
(x2-А)2 |
|
|
….. |
….. |
….. |
|
|
xn |
xn-А |
(xn-А)2 |
|
Здесь А – число близкое к , см § 3.
§ 6 Среднеквадратичная погрешность среднего арифметического
Пусть — результаты отдельных измерений, каждое из которых характеризуется одной и той же дисперсией
Найдем выражение для среднего арифметического:
Т.к. дисперсия суммы равна сумме дисперсий слагаемых, то дисперсия величины
При равноточных измерениях . Следовательно,
и .
Дисперсия среднего арифметического в раз меньше дисперсии отдельного измерения в серии измерений. А среднеквадратичная погрешность среднеквадратичного в раз меньше среднеквадратичного отдельного измерения. Из этого следует важный практический вывод: желая повысить точность измерений в раз, нужно увеличить число измерений в раз.
§ 7 Определение коэффициентов линейной зависимости по МНК вывод.
Пусть в эксперименте измерен ряд значений некоторой величины x и, соответствующие им значения, величины y. Между ними справедлива зависимость вида: y = ax + b.
Тогда сумма квадратов расстояний от экспериментальных точек до прямой будет равна:
Для решения задачи на нахождение минимума этого выражения необходимо приравнять нулю производные от этой суммы по двум неизвестным величинам a и b.
Взяв производные, получаем:
Преобразуем эти уравнения:
Решение системы из двух уравнений с двумя неизвестными приводит к следующим выражениям для коэффициентов a и b.
Литература
- Вентцель Е.С. “Курс теории вероятностей“, М.,Наука, 1976, 464с.
- Агекян Т.А. “Теория вероятностей для астрономов и физиков“, М., Наука, 1974, 264с.
- Гольцман Ф.М. “Физический эксперимент и статистические выводы“, Л., изд. ЛГУ, 1982, 190с.
- Гольцман Ф.М. «Вопросы статистической обработки измерений» СПб, Изд. СПбГУ, 2000г.
- О.Б. Васильев, В.И. Елфимов, С.И. Стальнова, Ю.Г. Шишкин. Математическая обработка результатов физического эксперимента // Изд-во Ленинградского университета, Л-д, 1989, 33 с.
- Соловьев В.А., Яхонтова В.Е. Основы измерительной техники. Руководство к лабораторным работам по физике. Учеб. пособие. Л., 1980.
- Соловьев В.А., Яхонтова В.Е. Руководство к лабораторным работам по физике. Учеб. пособие. Изд. С-Петербургского университета, 1997г., 338 с.
- Зайдель А.Н. «Ошибки измерений физических величин», Ленинград, изд. Наука, 1974г., 108 с
- Дж. Сквайрс Практическая физика. М, Мир, 1971г., 246 с.
- Дж. Тейлор Введение в теорию ошибок, М., Мир, 1985 г., 272 с
Подробнее о способах оценки не исключенной систематической погрешности смотри ниже, главу 6 «Учет погрешности приборов»
О том, как это следует делать см. ниже, главу «Практические способы расчета случайных погрешностей»
Это касается только случайных погрешностей. Поскольку всегда присутствуют и погрешности обусловленные точностью измерительных приборов, то проводить очень большое количество измерений не рационально.
Для нормального распределения среднее значение совпадает с наиболее вероятным, надо отметить, что это справедливо не для любого распределения
Здесь величины X1,X2,…Xn не разные значения одной и той же физической величины, а разные физические величины.
Имеется в виду оценка границ доверительного интервала с указанием доверительной вероятности. При других способах оценки чаще оставляют в погрешности только одну цифру.
ΔNi/N
х
EMBED Equation.DSMT4

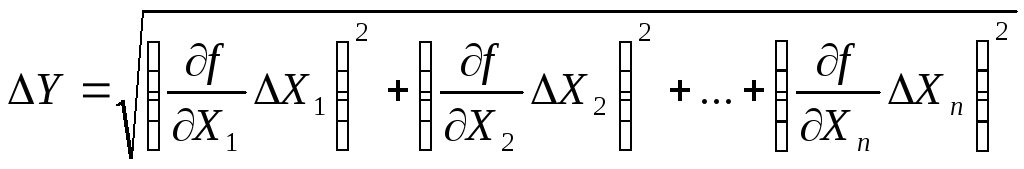
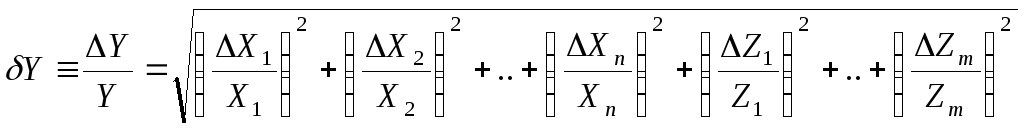
.gif)
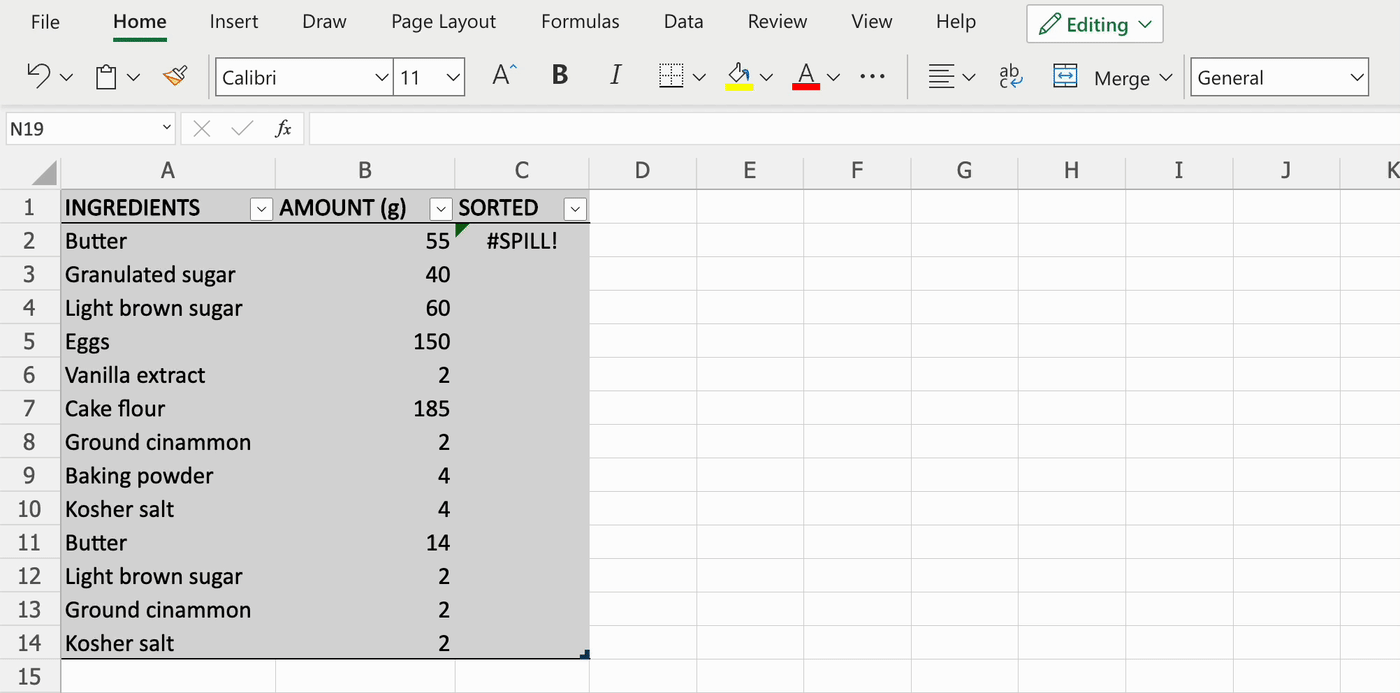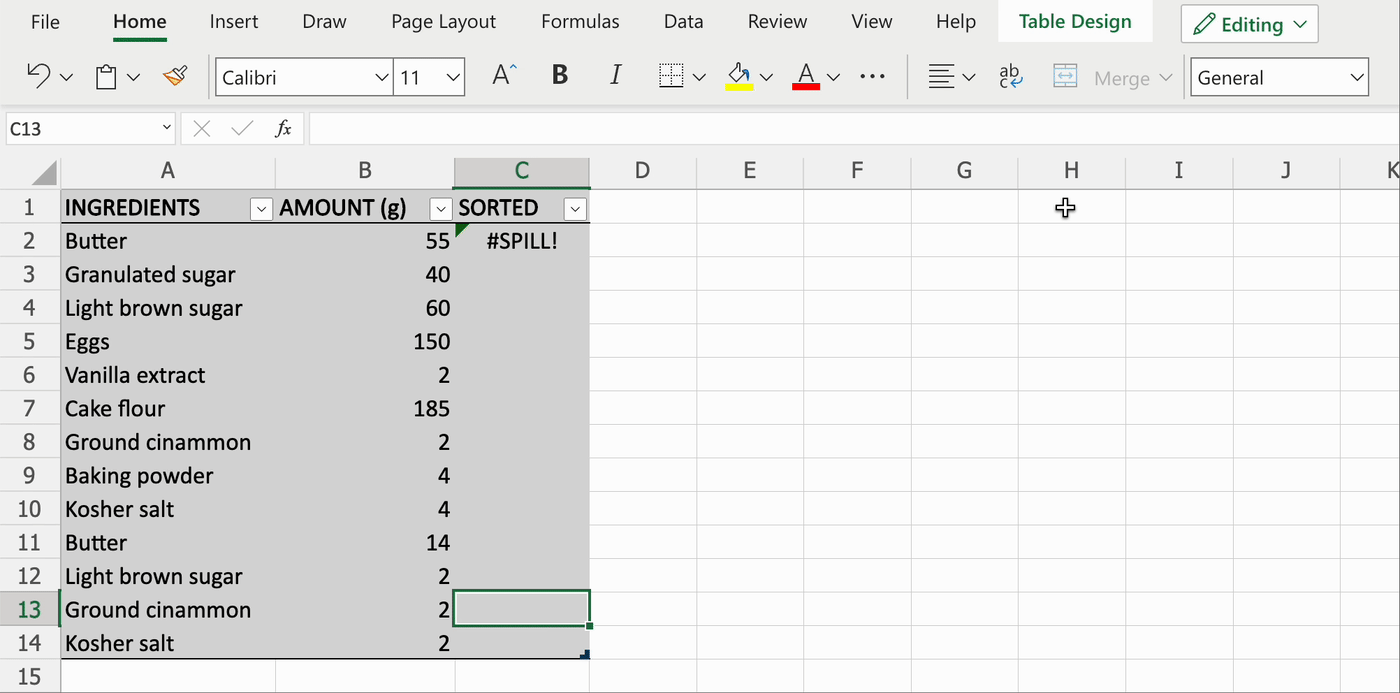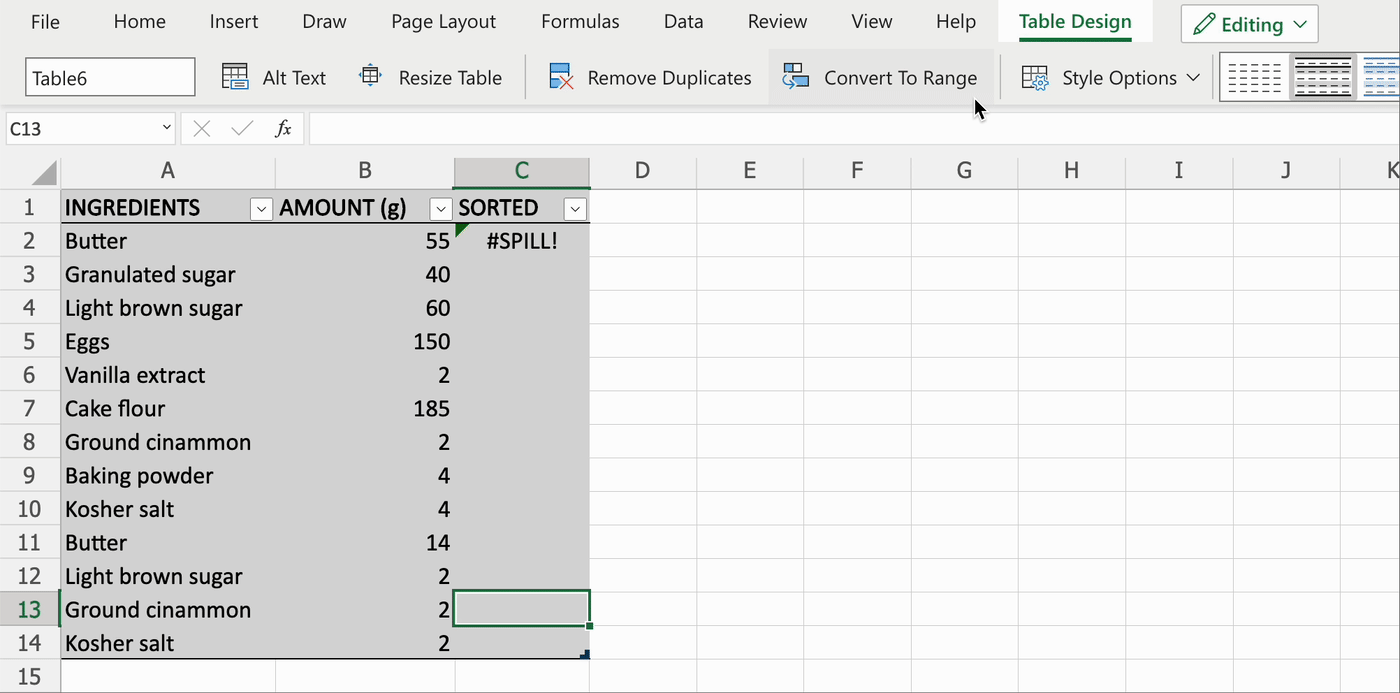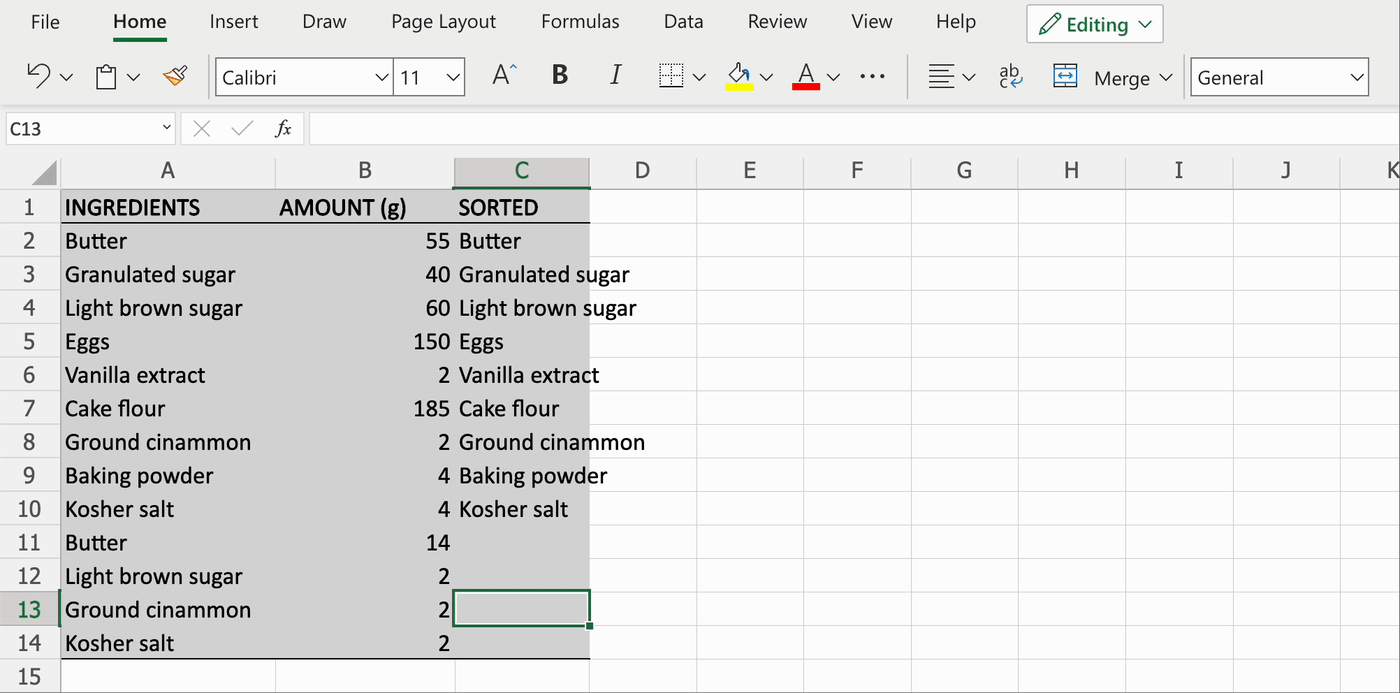
.gif)
.png.700x416_q95.jpg)