|
0 / 0 / 0 Регистрация: 26.11.2011 Сообщений: 3 |
|
|
1 |
|
|
26.11.2011, 21:59. Показов 4252. Ответов 2
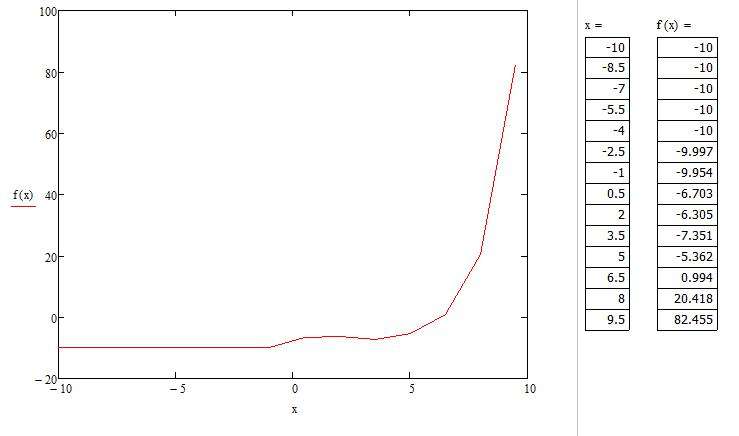
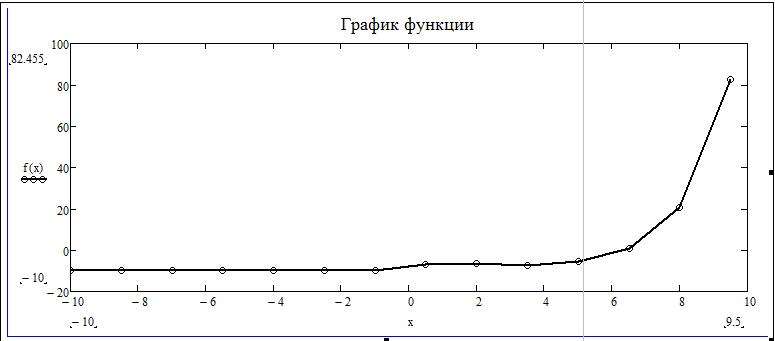
Не могу доделать задание,так как при нахождении коэффициентов уравнения нелинейной регрессии,с помощью функции genfit, все выражение выделяет красным и пишет такую вот ошибку: «: Found a number with a magnitude greater than 10^307 while trying to evaluate this expression». Помогите пожалуйста решить проблему, и доделать это задание
__________________
0 |
|
1 / 1 / 0 Регистрация: 21.11.2011 Сообщений: 22 |
|
|
26.11.2011, 23:33 |
2 |
|
Могу предположить лишь проблему с железом (ПК), либо версией MathCad. У меня 14 на ноуте, где и посмотрел файл. Все решается (см. скрин). Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 26.11.2011 Сообщений: 3 |
|
|
27.11.2011, 18:49 [ТС] |
3 |
|
Спасибо,но у меня вроде все также, маткад 14, и на ноуте и на компе,причем не только у себя пыталась решить,если вас не затруднит скиньте маткадовский файл пожалуйста! Добавлено через 1 час 4 минуты
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
27.11.2011, 18:49 |
|
Помогаю со студенческими работами здесь Ошибки в TextBox, как их избежать? Подскажите, пожалуйста, мои ошибки Подскажите пожалуйста, в чём ошибки? public class Main { public static void main(String args) { Пожалуйста, подскажите, где ошибки Пытаюсь решить задачу: "Найти в целочисленной матрице первый столбец,… Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 3 |
Приложение 4. Сообщения об ошибках
71
Приведенная далее информация об ошибках вычислений выполнена по следующей схеме: текст сообщения об ошибке (перевод сообщения) — вероятная причина ошибки — возможные пути устранения ошибки.
Сообщения об ошибках в численных вычислениях
A «Find» or «Minerr» must be preceded by a matching «Given» (Функциям find или minerr должно предшествовать ключевое слово given). Эта ошибка выделяет функцию find или minerr при их несогласованности с given. Каждый вычислительный блок, который заканчивается функцией find или minerr, должен начинаться с ключевого слова given.
All evaluations resulted in either an error or a complex result (Вычисления приводят к ошибке или к комплексному результату). Mathcad не может начертить некоторые точки, потому что не существует действительных значений для их нанесения на график. Это сообщение может появиться, если имеется ошибка или все значения — комплексные.
Arguments in function definitions must be names (Аргументы в определениях функции должны быть именами). Выделенное определение функции содержит неправильный перечень аргументов. В списке аргументов должны быть правильно поименованы переменные или список имен необходимо отделить запятыми.
All the elements in the vector cannot be the same (Все элементы вектора не могут быть одинаковыми). Если используется встроенная функция, возможно, неправильно указаны ее имя или параметры. Проверьте правильность ввода встроенной функции, установив курсор на имени функции и нажав клавишу F1.
At least one limit must be infinity (По крайней мере один предел должен быть бесконечным). Если для интегрирования выбран алгоритм бесконечного предела, то по крайней мере один из пределов интеграла должен быть бесконечным.
Символ бесконечности вводится нажатием комбинации клавиш Ctrl+Shift+z. Для изменения алгоритма, использующего бесконечный предел, или для вычисления какого-либо другого интеграла щелкните на интеграле правой кнопкой мыши и измените алгоритм с помощью контекстного меню.
Can only evaluate an nth order derivative when n=0, 1..5 (Можно вычислить n-й
порядок производной, только когда n = 0, 1, 2, …, 5). Порядок производной должен быть целым числом от 0 до 5. Если нужно посчитать производную более высокого порядка, сделайте это с помощью символьного дифференцирования.
Can only plot positive values when log axes are used (Только положительные величины могут быть на графике, если используются логарифмические координаты). Двухмерный график в декартовых или полярных координатах строится в логарифмических координатах, в которых не может быть величин отрицательных или равных нулю.
Can’t converge to a solution. Encountered too many integrator steps (Невозможно найти решение. Сделано слишком много шагов интегрирования). Алгоритм решения дифференциального уравнения не позволяет найти решение этого уравнения. Попробуйте изменить начальные или граничные условия. Возможно, решения просто не существует.
Can’t converge to a solution. The integrand may have a singularity or the integral may not be finite (Невозможно найти решение. Подынтегральное выражение может иметь точку сингулярности или интеграл может быть бесконечным). Вычисление интегралов, производных, функций root, find, minerr осуществляется итерационными методами. Вы увидите это сообщение, если после большого числа итераций не получен ответ с требуемой точностью.
Попробуйте изменить значение постоянной TOL. При работе с функциями root, find, minerr попробуйте задавать различные значения начальных приближений.
Can’t define the same variable more than once in the same expression (Невозможно определить ту же самую переменную более одного раза в одном и том же выражении). Вы пытаетесь вычислить одну и ту же переменную дважды в одном выражении. Пример подобной ошибки: если вы создаете вектор с именем a:= и используете это же имя справа, то получите это сообщение.
Can’t determine what units the result of this operation should have (Невозможно определить, в каких единицах должен быть представлен результат операции). Вы возвели выражение, содержащее единицы измерения, в степень, являющуюся переменной или вектором. В итоге невозможно определить размерность результата. Если выражение имеет размерность, то его можно возводить только в действительную фиксированную степень.
Can’t evaluate this expression. It may have resulted in an overflow or an infinite loop
(Невозможно вычислить это выражение. Это может быть результатом переполнения или бесконечным числом циклов). Это выражение может содержать слишком много вложенных функций или функция может быть константой в бесконечных циклах.
Проверьте несколько итераций цикла.
Can’t evaluate this expression because it’s either too complicated or it’s defined in terms of itself (Невозможно вычислить это выражение, потому что оно или слишком сложное,
или определяет само себя). Эта ошибка возникает, если функция определена в 72 терминах самой себя, что ведет к появлению рекурсивной функции, где условие
окончания процесса не определено. Например, f(x) := f(x)+5 ведет к переполнению стека. Необходимо изменить имя функции.
Как правило, имена функций слева и справа должны быть разными, если, конечно, это не рекурсивная функция.
Can’t evaluate this function when its argument is zero (Невозможно вычислить эту функцию, если ее аргумент равен нулю). Функция неопределенна, если аргумент равен нулю. Такое сообщение появляется при вычислении логарифма от нуля. Can’t divide by zero (Деление на ноль невозможно). Где-либо в программе или внутри численного метода возникло деление на ноль. Найдите место деления на ноль и устраните его. Попробуйте поменять параметры численного метода, константы точности или сам численный алгоритм.
Can’t find a solution. Encountered too many iterations (Невозможно найти решение.
Слишком много итераций). Это сообщение появляется при использовании функции polyroot, если степень полинома слишком велика. Попробуйте найти корни полинома символьным методом.
Can’t find a solution to this system of equations (Невозможно найти решение системы уравнений). Попробуйте изменить начальные приближения.
Что делать, если функция find не может найти решение, описано в главе 3.
Can’t find the data file you’re trying to use (Невозможно найти файл, который вы пытаетесь использовать). Удостоверьтесь, что такой файл существует в указанном месте.
Can’t have anything with units or dimensions here (Здесь не должно быть единиц измерений или размерностей). Это выражение использует единицы измерений гделибо, где они не разрешены.
Единицы измерений не разрешены:
варгументах большинства функций;
вэкспонентах;
вверхних и нижних индексах.
Для того чтобы использовать выражения с единицами измерений, вначале переведите это выражение в UnitsOf(выражение).
Can’t have more than one array in a contour plot (Не может быть более одного массива в контурном графике). Вы вводите более одного массива в место ввода контурного или поверхностного графика. Разрешается иметь только один массив в данном месте ввода, так как на контурном графике может быть изображена только одна поверхность.
Can’t plot this many points (Невозможно начертить график с таким большим количеством точек). Попытка построения графика с числом точек, превосходящим возможное. Попробуйте сделать число точек меньшим, чем 150 000.
Can’t perform this operation on the entire array at once. Try using «vectorize» to perform it element by element (Невозможно выполнить эту операцию во всем массиве сразу. Попытайтесь использовать векторизацию, чтобы преобразовать элемент за элементом). Это сообщение можно увидеть, например, при попытке разделить один вектор на другой.
Для того чтобы применить функцию или оператор к каждому элементу вектора или матрицы, используйте оператор векторизации.
Can’t raise an expression having units to a complex power (Нельзя возводить в комплексную степень выражение, имеющее единицы измерения). Выражение с единицами измерения можно возводить только в действительную степень. Для того, чтобы возвести в комплексную степень выражение с единицами измерения, вначале переведите это выражение в UnitsOf(выражение) — единицы измерения будут отменены.
Can’t solve a system having this many equations (Невозможно решить систему,
имеющую так много уравнений). Mathcad может решать системы уравнений, содержащие не больше 200 нелинейных уравнений и не больше 500 линейных.
Can’t understand something in this data file. If this file came from a spreadsheet, make sure you saved it as ASCII text only (Невозможно что-либо понять в этом файле данных. Если этот файл взят из откуда-либо из готовых материалов, убедитесь, что он сохранен в формате ASCII). При считывании файла функцией READPRN файл должен быть записан в формате ASCII.
Все строки в файле должны иметь одинаковое число величин. Строки, не содержащие численных величин, игнорируются. Если файл имеет требуемый формат, а вы видите это сообщение об ошибке, удалите из файла любой текст.
Can’t understand the name of this function. If you’re trying to multiply, use «*»
(Невозможно понять имя этой функции. Если вам нужно умножить, используйте знак умножения). Такое сообщение появляется, если выражение, не являющееся функцией, используется как функция или имя функции записано неверно.
Can’t understand the way this range variable is defined (Невозможно понять определение дискретной (ранжированной) переменной). Неверное определение дискретной переменной.
Дискретная переменная может быть определена двумя способами:
|
var := n1 |
..n2 ; |
|
|
var := n1 |
, n2 ..n3 . |
73 |
Can’t understand this number (Невозможно понять это число). Это выражение содержит символ или десятичную точку там, где это непозволительно. Например, вы увидите этой сообщение об ошибке, если случайно запишете число как .452.
Can’t use a range variable in a solve block (Невозможно использовать дискретную переменную в вычислительном блоке). Эта сообщение об ошибке появляется, если использовать дискретную переменную в неподходящем месте, например, в вычислительном блоке.
Исключите дискретную переменную из вычислительного блока. Попробуйте создать функцию, включающую в себя вычислительный блок.
Cannot evaluate this accurately at one or more of the values you specified (Невозможно точно вычислить выражение в одной или нескольких точках). Эта ошибка указывает, что вы пытаетесь вычислить функцию для аргумента, находящегося за пределами области определения функции.
Cannot perform this operation on a string (Нельзя выполнить эту операцию над строкой). Нельзя выполнить математические операции со строковой переменной. Could not find a solution (Невозможно найти решение). Численный метод расходится (не может найти решения). Возможно, решения не существует. Подробнее об этом написано в главе 3.
Could not find a solution because the root finder failed (Невозможно найти решение.
Сбой при нахождении корней). При решении дифференциального уравнения с граничными условиями функция sbval не может вычислить недостающие начальные условия. Попробуйте изменить начальные приближения.
Cross product is defined only for vectors having exactly three elements (Векторное произведение определяется только для векторов, имеющих ровно три элемента).
Degree of the polynomial must be between 1 and 99 (Степень полинома должна быть от
1 до 99). Вектор коэффициентов полинома, используемый функцией polyroot, должен содержать от 2 до 99 элементов.
Encountered a floating point error (В заданной точке функция не может иметь такого значения).
End of File (Конец файла). Вы пытаетесь функцией READ прочитать больше данных, чем есть в файле.
End points cannot be the same (Конечная и начальная точки не могут быть одинаковыми). При решении дифференциальных уравнений конечные точки интервала интегрирования должны быть разными.
Found a number with a magnitude greater than 10^307 while trying to evaluate this expression (Найдено число, превышающее 10307). Попробуйте поменять параметры численного алгоритма или сам алгоритм.
Found a singularity while evaluating this expression. You may be dividing by zero
(Обнаружена сингулярность при вычислении этого выражения. Возможно деление на ноль). Проверьте численные значения величин в этом выражении.
Illegal context. Press F1 for Help (Недопустимый контекст. Нажмите клавишу F1, чтобы получить помощь). Трудно диагностируемая ошибка. Часто вызывается синтаксическими ошибками при наборе выражений.
При использовании в правой части выражения переменных с индексами или дискретных переменных все индексы и все дискретные переменные обязательно должны появиться и в левой части выражения в качестве индексов или параметров функции.
Illegal dimensions (Недопустимые размеры массива). Массив не имеет столько строк и столбцов, сколько требуется.
Введите имя массива и нажмите клавишу =, чтобы проверить истинные размеры массива.
Invalid expansion point (Невозможно разложить выражение в ряд в окрестности указанной точки). Проверьте правильность использования ключевого слова series при символьном вычислении выражения.
Invalid matrix dimension. The number of rows is less than the number of columns
(Неправильный размер матрицы. Число строк меньше, чем число столбцов). Функция svd требует, чтобы число строк было больше числа столбцов или равно ему.
Live symbolics not available (Символьные вычисления невыполнимы). Это сообщение появляется при использовании символьного знака равенства, если в данной версии Mathcad символьные вычисления отсутствуют.
Loess cannot extrapolate (Функция loess не может экстраполировать выражение). Точки для интерполяции выражения должны лежать между минимальным и максимальным значениями заданных точек.
Matrix is singular. Cannot compute its inverse (Матрица сингулярная. Невозможно вычислить обратную матрицу). Матрица вырожденная или почти вырожденная. Ее определитель равен нулю или число обусловленности очень велико.
Matrix must be positive definite (Матрица должна быть положительно определенной). Это сообщение появляется, когда матричный аргумент функции не является
|
положительно определенным. Матрица является положительно определенной, если |
|||||
|
ее собственные числа действительные и положительные. |
|||||
|
Must be 1 complex matrix or 2 real matrices (Должна быть одна матрица комплексных |
74 |
||||
|
чисел или две матрицы действительных чисел). Это условие необходимо при |
|||||
|
построении графика векторного поля. |
|||||
|
Must be a vector with real elements (Должен быть вектор действительных чисел). |
|||||
|
Вектор не должен иметь мнимых чисел и должен быть столбцом, а не строкой. |
|||||
|
Must be between two lock regions (Курсор должен быть между границами запираемой |
|||||
|
зоны). При создании закрытой области — команда Format |
Area |
Lock |
|||
|
(Формат |
Зона |
Запереть) — необходимо вначале щелкнуть мышью между |
|||
|
границами запираемой зоны. |
|||||
|
Must be less than the number of data points (Аргумент должен быть меньше, чем число |
|||||
|
точек в массиве данных). Для дополнительной информации установите курсор на |
|||||
|
названии встроенной функции и нажмите клавишу F1. |
|||||
|
Must be a real scalar (Должно быть действительным числом). |
|||||
|
Must have more than four rows (Матрица должна иметь больше четырех рядов). |
|||||
|
Must have 1 or 2 columns (Матрица должна иметь один или два столбца). Первый |
|||||
|
матричный аргумент в функциях кубической сплайн-интерполяции должен иметь |
|||||
|
один столбец для одномерной сплайн-интерполяции и два столбца — для |
|||||
|
двухмерной. |
|||||
|
Must have three vectors or one matrix (Должно быть три вектора или одна матрица). |
|||||
|
При построении графика поверхности в поле ввода надо вписать или три вектора, |
|||||
|
разделенных запятыми, или одну матрицу. |
|||||
|
No bitmaps were found in the worksheet (В документе нет графических объектов). Это |
|||||
|
сообщение появляется при выполнении команды Format |
Color |
Optimize Palette. |
|||
|
(Формат |
Цвет |
Оптимизировать палитру). |
Not enough memory for this operation (Для этой операции недостаточно памяти).
Only positive values are allowed here (Здесь можно использовать только положительные величины).
ORIGIN should be an integer whose magnitude is less than 16 million (ORIGIN должно быть целым числом, меньшим 16 млн).
(Rows – 1) must be power of 2 (Матрица должна иметь 2n рядов).
Something is wrong with the solve block used to define this function. It may need a guess value (Что-то неверно в блоке решения. Возможно, необходимо начальное приближение). Такое сообщение появляется при использовании блока решения внутри функции пользователя. Попробуйте оценить непосредственно сам блок решения вне функции пользователя. Вы получите другое более подробное сообщение об ошибке.
String contains the wrong number of characters or the wrong kind of characters (Строка содержит неверное число символов или неверный вид символов). При использовании смешанных программ необходим ввод символов в строке аргументов: I — для целых чисел, B — для бинарных чисел, С — для любого вещественного числа.
The elements in this vector must be in increasing order (Элементы этого вектора должны быть расположены в порядке возрастания). Такое требование предъявляется к вектору аргументов при работе с массивами данных, например, при интерполяции или построении гистограмм.
The expression to the left of the equal sign cannot be defined (Выражение слева от знака равенства не может быть определено). Возможна синтаксическая ошибка. Слева от оператора присваивания могут находиться имена переменных, векторов, матриц и функций (с аргументами в скобках).
The format of this vector is invalid. Press F1 for help (Неверный размер вектора.
Нажмите клавишу F1 для вызова помощи). Некоторые функции требуют в качестве аргумента вектор, созданный другой функцией. Этот вектор имеет специальный формат, создаваемый другой функцией, например cspline, regress и др.
The function values on the two bracket end points must be of opposite signs (Величины функции в двух крайних точках интервала должны быть разного знака). При задании интервала поиска корней функцией root величины функции в двух крайних точках интервала должны быть разного знака. Выбирайте границы интервала поиска корней после построения графика функции.
The number of rows must be a power of 2 (Число элементов вектора должно быть равно 2n). Ошибка возникает при неверном числе данных для волнового преобразования функцией wave.
The number of rows or columns do not match (Число строк и столбцов в этих матрицах не согласовано). Подобное сообщение об ошибке часто появляется при неправильном перемножении матриц. Нажмите клавиши Shift+F1 и щелкните мышью на имени функции, чтобы узнать необходимые размеры матриц.
The unit placeholder can only have real, non-zero scalars put into it (В место ввода размерности при выводе результатов вычислений можно вводить, кроме размерностей, только действительные, не равные нулю скалярные величины).
The units in this expression do not match (Размерности в этом выражении не согласованы). Несогласованные вычисления с размерными и безразмерными величинами. При вычислениях без учета размерностей, видимо, осталась не заданной
какая-либо величина, обозначенная буквами m, s, N и т. д., которые по умолчанию встроены в Mathcad как стандартные размерности длины, времени и силы.
There is an extra comma in this expression (В этом выражении есть лишняя запятая). 75
Проверьте синтаксис. Видимо, запятая использована вместо точки.
There must be more data points than parameters (В массиве данных должно быть больше точек, чем параметров функции). Такое требование предъявляют, например,
функции regress и genfit.
There must be more than three data points (Эта функция требует вектор, содержащий по крайней мере четыре элемента).
This array must have more than one row or column (Этот массив должен иметь больше,
чем одну строку или столбец). Например, при построении графиков поверхности требуется матрица значений. Некоторые функции требуют матричных аргументов.
This expression has a «(» without a matching «)». (В выражении не хватает скобок).
Проверьте выражение.
This expression is incomplete. You must fill in the placeholders (Выражение неполное.
Вы должны заполнить места ввода).
This expression is incomplete. You must provide an operator (Выражение неполное. Вы должны ввести оператор).
This expression is too complicated. Try defining it in smaller pieces (Выражение слишком сложное. Постарайтесь определить его по частям).
This file could not be opened. Make sure it exists (Этот файл не может быть открыт.
Убедитесь, что он существует). При считывании внешнего файла функцией READPRN возможно, что файл имеет статус «только для чтения». Если считываемый файл не находится в том же каталоге, что и файл, используемый Mathcad, необходимо указать полный путь к нему.
This function has too many arguments (Функция имеет слишком много аргументов). Для встроенных функций щелкните мышью на имени функции и нажмите клавишу F1. Проверьте правильность использования функции. Для функции пользователя проверьте определение функции.
This function is undefined at one or more of the points you specified (Функция не определена в одной или нескольких точках). Вы используете оператор или функцию для неприемлемых значений аргумента, например, lg(0) или –3! (факториал отрицательного числа не определен).
This image format is not supported (Этот формат изображения не поддерживается
Mathcad).
This integer is too large (Величина слишком большая для работы с ней). This integer is too small (Величина слишком мала для работы с ней).
This is invalid. If you are using conditional statements in a Mathcad program, make sure all cases are accounted for (Это неверно. Если вы используете условие в Mathcadпрограмме, убедитесь, что все возможные случаи учтены). В условный оператор программирования добавьте еще одно место ввода и впишите еще одно значение с ключевым словом Otherwise (иначе).
This is not a valid interval (Неправильно указан интервал). Начальное значение интервала должно быть меньше конечного.
This is not allowed inside a solve block. For example, definitions are not allowed in a solve block (Это не разрешено внутри вычислительного блока. Например, определения не могут находиться внутри вычислительного блока). Внутри вычислительного блока могут находиться только решаемые уравнения и ограничения к ним.
This list contains too many items (Список содержит слишком много имен). Вы ввели в список слишком много имен, разделенных запятыми. Чаще всего это случается с графиками.
This matrix must be square. It should have the same number of rows as columns (Матрица должна быть квадратной. Число строк должно быть равно числу столбцов).
This must be an integer. The expression you used appears to have a fractional part (Здесь должно быть целое число. Похоже, что выражение содержит дробную часть). Проверьте верхние и нижние индексы. Они должны быть целыми числами. Некоторые функции, такие как identity и submatrix, требуют целочисленных аргументов.
This must be the name of a function or variable (Здесь должно быть имя функции или переменной).
This must be the name of a mapping function (Здесь должно быть имя функции преобразования координат). Такой аргумент требуется функциям CreateMech и CreateSpace.
This operation can only be performed on a function (Эту операцию можно производить только над функцией). Аргумент функции сам должен быть функцией.
This operation can only be performed on an array. It can’t be performed on a number (Эту операцию можно выполнить только над массивом, но не над числом). Например, если вы пишете имя с верхним индексом, то это должен быть вектор.
This operation can only be performed on a number or an array (Эту операцию можно выполнить только над числом или массивом).
This operation can only be performed on a string (Эту операцию можно выполнить только над строкой). Например, строковые функции требуют хотя бы один строковый аргумент.
Как построить график в «Маткаде»? Советы и рекомендации
Mathcad является универсальным инструментом у тех людей, которые плотно связали свою жизнь с вычислениями. «Маткад» способен производить сложные математические расчеты и мгновенно выдавать ответ на экране. Студенты или те, кто в первый раз столкнулся с этой программой, задают множество вопросов, на которые не могут дать ответ самостоятельно. Один из них, затрудняющий дальнейшее обучение: как построить график в «Маткаде»? На самом деле, это не так сложно, как может показаться. Постараемся разобраться также в том, как в «Маткаде» построить график функции, как строить несколько функций, узнаем о некоторых элементах отображение графика на экране.
Быстрый график в Mathcad

Возьмем одну функцию и будем проводить все ниже перечисленные операции с ней. Допустим, имеем следующее техническое задание: построить график функции f(x) = (e^x/(2x-1)^2)-10 на интервале [-10;10], исследовать поведение функции.
Итак, перед тем как построить график в «Маткаде», нужно переписать нашу функцию в математическую среду. После этого просто прикинем возможный график без масштабирования и всего прочего.
Построение дополнительных графиков
Чтобы понять, как построить несколько графиков в «Маткаде», добавим к нашему техническому заданию небольшое дополнение: построить график производной от заданной функции. Единственное, что нам нужно — в поле графика добавить производную по переменной «x».
График, построенный по набору значений
Перед тем как построить график в «Маткаде» по точкам, необходимо создать диапазон значений. Сразу отметим, что график, построенный по точкам, иногда бывает неточным, так как может найтись такая точка, которая не попадет в диапазон значений, но в оригинальном графике в ней происходит разрыв. В этом примере специально будет показан этот случай.
Мы видим, что на графике, построенном по точкам, не отображается та точка, которая осуществляет разрыв на исходном графике. То есть можно сделать вывод о том, что построение по точкам может не учитывать значения функции, которые создают разрыв.
Настройка отображения графика
В этой статье мы уже затрагивали настройки графика. Окно с настройками вызывается двойным нажатием левой кнопкой мыши по графику. В окне форматирования графика есть пять разделов. «Оси X, Y» — содержит информацию про координатные оси, а также отображения вспомогательных элементов. Второй раздел «Трассировка» связан с кривыми линиями построения графика, здесь можно корректировать их толщину, цвет и другое. «Формат числа» отвечает за отображение и расчет единиц. В четвертом разделе можно добавлять подписи. Пятый раздел » По умолчанию» выводит все настройки в стандартную форму.
Почему mathcad не строит график
Почему mathcad не строит график

Может кто с таким сталкивался? Поставила Mathcad 15. Не строит графики поверхности, ну вообщем 3D.
Сообщения об ошибках в Mathcad
Can only evaluate an n-th order derivative when n=0,1..5.
Can’t evaluate this function when its argument less than or equal to zero
Can’t converge to a solution
Can’t define the same variable more than once in the same expression
Can’t determine what units the result of this operation should have
Cant divide by zero
Could not find a solution
См. «Can’t converge to a solution»
Can’t find the data file you’re trying to use
Can’t have anything with units or dimensions here
Can’t have more than one array in a contour plot
Can’t perform this operation on the entire array at once. Try using «vectorize» to perform it element by element
Can’t plot this many points
Can’t understand something in this data file
Can’t understand the name of this function
Can’t understand the way this range variable is defined
Rvar := nl . .n2 Rvar := nl,n2 . .пЗ
Cant understand this number
Cant use a range variable in a solve block
Cannot evaluate this accurately at one or more of the values you specified
Cross product is defined only for vectors having exactly three elements
Can’t evaluate this expression. It may have resulted in an overflow or an infinite loop
Degree of the polynomial must be between 1 and 99.
Dimensions must be >4
End points cannot be the same
Equation too large
Floating point error
Found a singularity while evaluating this expression. You may be dividing by zero
Found a number with a magnitude greater than 1СГ307
Illegal context. Press <F1> for help
Not enough memory for this operation
The expression to the left of the equal sign cannot be defined
The number of rows and/or columns in these arrays do not match
The units in this expression do not match
There is an extra comma in this expression
This expression is incomplete. You must fill in the placeholders
This expression is incomplete. You must provide an operator
This function has too many arguments
This function is undefined at one or more of the points you specified
This function needs more arguments
This operation can only be performed on a function
This operation can only be performed on an array. It can’t be performed on a number
This operation can only be performed on a number or an array
This operation can only be performed on a string
This subscript is too large
This value must be a matrix
This value must be a vector. It can be neither a matrix nor a scalar
This value must be an integer greater than 1
This variable or function is not defined above
Value of subscript or superscript is too big (or too small) for this array
This is not a scalar. Press <F1 > for help
You have one solve block inside another. Every «Given» must have a matching «Find» or «Min-err».
You interrupted calculation. To resume, click here and choose «Calculate» from the «Math» menu
Двумерные графики функций в MathСad
В этом уроке мы рассмотрим типы графиков, которые есть в PTC Mathcad.
Типы графиков
Для изменения типа графика нужно нажать на него и выбрать на вкладке Графики -> Кривые -> Изменить тип. Далее представлены четыре типа графиков, которые можно использовать для функций:
В этом списке вы можете увидеть некоторые типы осей. О них мы поговорим несколько позднее.
Несколько графиков на одних осях
Для добавления кривой на оси разместите курсор мыши на место, где заканчивается обозначение легенды оси Y графика и выберите Графики -> Кривые -> Добавить кривую. Появится дополнительное место для заполнения оси Y.
С помощью этой же команды можно добавлять и другие графики.
Используя вывод нескольких графиков, мы рассмотрим различные варианты вывода, которые доступны в меню Графики -> Стили. Для этого мы пропишем графики, которые будут содержать пять различных прямых линий. В каждой из них будет содержаться 11 точек.
После ввода этих выражений добавьте график XY и после в него четыре легенды для Y. В заполнении для оси Х введите X[i и нажмите [Enter]. Все наши графики будут использовать одну и ту же легенду для оси X. Для последнего места для заполнения оси Y введите y[0,i и нажмите [Enter].
Выше нужно ввести y[1,i , еще выше — y[2,i и дальше по тому же принципу. После вы увидите пять прямых линий, которые будут построены на осях. Каждой из них можно присвоить свое свойство, выбирая его в меню Графики -> Стили.
Ниже вы можете видеть те графики, которые получились. В качестве настроек стиля использовались различные цвета, символы, толщина линии.
Сами метки и присвоенные им значения были исключены в меню Графики -> Оси.
Масштабирование
При построении двух графиков на одной оси, для одного из них может быть выбран не совсем удачный диапазон, когда графики будут перекрываться.
Для исправления этого разделите функцию куба на 5. Такой прием носит имя масштабирование.
Маркеры
Для того чтобы выяснить точные значения по графику, можно пользоваться маркерами из меню Графики -> Маркеры. Стили, которые используются для построения линий маркеров, можно менять так же как и стили графиков.
Кривая «Столбцы»
Поговорим о типе кривой «Столбцы». Воспользуемся таблицей с данными. Перейдем во вкладку Матрицы/таблицы -> Вставить таблицу и в сетке выберем таблицу с 2 столбцами и 10 строчками
Местозаполнители заголовков заполните значениями х и у, а числа заполните так, как изображено на рисунке ниже:
Разместите график XY. Сделайте график визуально более привлекательным, используя перемещение легенды по осям и форматирование значения меток. Для изменения типа графика выберите Графики -> Кривые -> Изменить тип -> Кривая «столбцы».
Таблицу данных при работе с Mathcad удобнее использовать, когда данных не так много. Если данных намного больше, то лучше совместить использование Mathcad с Excel.
Полярный график
Давайте пропишем график спирали, который будет позиционироваться в полярных координатах.
Разместите полярный график с помощью Графики -> Кривые -> Вставить график -> Полярный график. В местозаполнители введите такие данные, как можете видеть на рисунке и нажмите на клавишу [Enter].
Параметрический график
Для построения этого графика окружности нужно использовать параметр t
Графики в логарифмическом масштабе
В науке и технике часто находит применение логарифмический масштаб. В Mathcad Есть возможность построения и такого типа графиков.
Давайте построим график функции y=x 2 , но будем использовать при этом параметр:
Для того, чтобы выполнить ось X в виде логарифмической оси, нужно легенду оси X выделить и нажать Графики -> Оси -> Логарифмический масштаб. Это же выполните и для оси Y. В логарифмическом масштабе функция будет выглядеть как прямая линия.
Резюме
Этот урок научил нас использовать модификации для двухмерных графиков.
- Для изменения типа кривой нужно нажать на легенду по Y и выбрать Графики -> Кривые -> Изменить тип.
- Для добавления кривой нужно разместить курсор на легенду оси Y и выбрать Графики -> Кривые -> Добавить кривую/
- Для изменения внешнего вида лини графиков необходимо выбрать стиль во вкладке Графики -> Стиль, предварительно нажав на необходимую легенду/
- Для масштабирования графика необходимо разделить легенду нужно оси на коэффициент масштабирования.
- Линии маркеров, как вертикальные, так и горизонтальные, можно найти в разделе Графики -> Маркеры. Добавлять можно любое количество маркеров, вплоть до того, что строить из них сетку. Изменение маркеров доступно так же, как и любых других графиков.
- Полярный график размещается так же, как и график XY. Для этого зайдите в Графики -> Кривые -> Вставить график -> Полярный график.
- Изменение масштаба оси на логарифмический доступно с применением команды. Для ее выбора нажмите Графики -> Оси -> Логарифмический масштаб. Выполнять изменения нужно для каждой из осей. При выполнении изменения лишь для одной оси, вы получите логарифмический масштаб.
- Назад
- Вперед
Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.
Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»
Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»
В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»
Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.
Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.
Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.
5.1. Интегрирование
Интегрирование в Mathcad реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярами. Несмотря на то что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным. Если пределы интегрирования имеют размерность (см. разд. «Размерные переменные» гл 4), то она должна быть одной и той же для обоих пределов.
5.1.1. Операторы интегрирования
Интегрирование, дифференцирование, как и множество других математических действий, устроено в Mathcad по принципу «как пишется, так и вводится». Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7> (или символа «&»). Появится символ интеграла с несколькими местозаполнителями (рис. 7.1), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.
Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести -«> (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.

Рис. 7.1. Оператор интегрирования
Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором — в случае успеха, будет найдено точное значение интеграла с помощью символьного процессора Mathcad. Эти два способа иллюстрирует листинг 7.1. Конечно, символьное интегрирование возможно только для небольшого круга несложных подынтегральных функций.
Листинг 7.1. Численное и символьное вычисление определенного интеграла
Подынтегральная функция может зависеть от любого количества переменных. Именно для того чтобы указать, по какой переменной Mathcad следует вычислять интеграл, и нужно вводить ее имя в соответствующий местозаполнитель. Помните, что для численного интегрирования по одной из переменных предварительно следует задать значение остальных переменных, от которых зависит подынтегральная функция и для которых вы намерены вычислить интеграл (листинг 7.2).
Листинг 7.2. Интегрирование функции двух переменных по разным переменным
Оператор интегрирования может использоваться точно так же, как и другие операторы: для определения функций, в циклах и при вычислении ранжированных переменных. Пример присваивания пользовательской функции д(х) значения определенного интеграла и вычисления нескольких ее значений приведен в листинге 7.3.
Листинг 7.3. Использование оператора интегрирования в функции пользователя
5.1.2. Об алгоритмах интегрирования
Результат численного интегрирования — это не точное, а приближенное значение интеграла, определенное с погрешностью, которая зависит от встроенной константы TOL. Чем она меньше, тем с лучшей точностью будет найден интеграл, но и тем больше времени будет затрачено на расчеты. По умолчанию TOL=0.001. Для того чтобы ускорить вычисления, можно установить меньшее значение TOL.
Если скорость расчетов имеет для Вас принципиальное значение, например при многократном вычислении интеграла внутри цикла, проявите осторожность, выбирая значение точности Обязательно поэкспериментируйте на тестовом примере с характерной для Ваших расчетов подынтегральной функцией. Посмотрите, как уменьшение константы TOL сказывается на погрешности интегрирования, вычислив интеграл для разных ее значений и выбрав оптимальное, исходя из соотношения точность / скорость вычислений.
Отдавайте себе отчет в том, что при вводе в редакторе Mathcad оператора численного интегрирования, Вы, фактически, создаете самую настоящую программу. Например, программой является первая строка листинга 7.1, просто большая часть ее скрыта от Вашего взора разработчиками компании MathSoft. В большинстве случаев об этом не приходится специально задумываться, можно полностью положиться на Mathcad. Но иногда может потребоваться умение управлять параметрами этой программы, как мы уже рассмотрели на примере выбора константы TOL. Кроме нее, пользователь имеет возможность выбирать сам алгоритм численного интегрирования. Для этого:
- Щелкните правой кнопкой мыши в любом месте на левой части вычисляемого интеграла.
- В появившемся контекстном меню выберите один из четырех численных алгоритмов (рис. 7.2).

Рис. 7.2. Выбор алгоритма численного интегрирования
Обратите внимание, что, перед тем как один из алгоритмов выбран впервые, как показано на рис. 7.2, флажок проверки в контекстном меню установлен возле пункта AutoSelect (Автоматический выбор). Это означает, что алгоритм определяется Mathcad, исходя из анализа пределов интегрирования и особенностей подынтегральной функции. Как только один из алгоритмов выбран, этот флажок сбрасывается, а избранный алгоритм отмечается точкой.
Разработчиками Mathcad 11 запрограммированы четыре численных метода интегрирования:
- Romberg (Ромберга) — дли большинства функций, не содержащих особенностей;
- Adaptive (Адаптивный) — для функций, быстро меняющихся на интервале интегрирования;
- Infinite Limit (Бесконечный предел) — для интегралов с бесконечными пределами ();
- Singular Endpoint (Сингулярная граница) — для интегралов с сингулярностью на конце. Модифицированный алгоритм Ромберга для функций, не определенных на одном или обоих концах интервала интегрирования.
Старайтесь все-таки оставить выбор численного метода за Mathcad, установив флажок AutoSelect (Автоматический выбор) в контекстном меню. Попробовать другой метод можно, например, чтобы сравнить результаты расчетов в специфических случаях, когда у Вас закрадываются сомнения в их правильности.
Если подынтегральная функция «хорошая», т. е. не меняется на интервале интегрирования слишком быстро и не обращается на нем в бесконечность, то численное решение интеграла не принесет никаких неприятных сюрпризов. Приведем основные идеи итерационного алгоритма Ромберга, который применяется для большинства таких функций.
- Сначала строится несколько интерполирующих полиномов, которые заменяют на интервале интегрирования подынтегральную функцию f(x). В качестве первой итерации полиномы вычисляются по 1,2 и 4 интервалам. Например, первый полином, построенный по 1 интервалу, — это просто прямая линия, проведенная через две граничные точки интервала интегрирования, второй — квадратичная парабола и т. д.
- Интеграл от каждого полинома с известными коэффициентами легко вычисляется аналитически. Таким образом, определяется последовательность интегралов от интерполирующих полиномов: ilf i2, i4,… Например, по правилу трапеций i1=(b-a) (f (a)+f (b) )/2 и т. д.
- Из-за интерполяции по разному числу точек вычисленные интегралы ii, i2,… несколько отличаются друг от друга. Причем, чем больше точек используется для интерполяции, тем интеграл от интерполяционного полинома ближе к искомому интегралу, стремясь к нему в пределе бесконечного числа точек. Поэтому определенным образом осуществляется экстраполяция последовательности ilf i2, I4,… до нулевой ширины элементарного интервала. Результат этой экстраполяции J принимается за приближение к вычисляемому интегралу.
- Осуществляется переход к новой итерации с помощью еще более частого разбиения интервала интегрирования, добавления нового члена последовательности интерполирующих полиномов и вычисления нового (N-ГО) приближения Ромберга JN.
- Чем больше количество точек интерполяции, тем ближе очередное приближение Ромберга к вычисляемому интегралу и, соответственно, тем меньше оно отличается от приближения предыдущей итерации. Как только разница между двумя последними итерациями | JN-j11″11 становится меньше погрешности TOL или меньше TOL-|JN|, итерации прерываются, и JN появляется на экране в качестве результата интегрирования.
Об алгоритме полиномиальной сплайн-интерполяции см .гл. 15.
5.1.3. 0 расходящихся интегралах
Если интеграл расходится (равен бесконечности), то вычислительный процессор Mathcad может выдать сообщение об ошибке, выделив при этом оператор интегрирования, как обычно, красным цветом. Чаще всего ошибка будет иметь тип «Found a number with a magnitude greater than 10^307» (Найдено число, превышающее значение 10307) или «Can’t converge to a solution» (Не сходится к решению), как, например, при попытке вычислить интеграл. Тем не менее, символьный процессор справляется с этим интегралом, совершенно правильно находя его бесконечное значение (листинг 7.4).
Листинг 7.4. Символьное вычисление расходящегося интеграла
Символьный процессор предоставляет замечательные возможности аналитического вычисления интегралов, в том числе зависящих от параметров и неопределенных интегралов, как показано в листингах 7.5 и 7.6. Об этом и о вычислении интегралов с помощью меню Symbolics (Символика), упоминалось в гл. 5.
Листинг 7.5. Символьное вычисление интеграла с переменным пределом
Листинг 7.6. Символьное вычисление неопределенного интеграла
При попытке численного решения задачи из листинга 7.4 методом, отличным от алгоритма вычисления интегралов с бесконечными пределами (Infinite Limit), будет получено неверное решение (листинг 7.7) — вместо бесконечности выдано большое, но конечное число, немного не дотягивающее до численной бесконечности, являющейся для вычислительного процессора просто большим числом 10307 (см. разд. «Встроенные константы» гл. 4). Отметим, что Mathcad в режиме автоматического выбора алгоритма (AutoSelect) предлагает именно алгоритм Infinite Limit.
Листинг 7.7. Плохо выбранный численный алгоритм неверно находит расходящийся интеграл
5.1.4. Кратные интегралы
Для того чтобы вычислить кратный интеграл:
- Введите, как обычно, оператор интегрирования.
- В соответствующих местозаполнителях введите имя первой переменной интегрирования и пределы интегрирования по этой переменной.
- На месте ввода подынтегральной функции введите еще один оператор интегрирования.
- Точно так же введите вторую переменную, пределы интегрирования и подынтегральную функцию (если интеграл двукратный) или следующий оператор интегрирования (если более чем двукратный) и т. д., пока выражение с многократным интегралом не будет введено окончательно.
Пример символьного и численного расчета двукратного интеграла в бесконечных пределах приведен в листинге 7.8. Обратите внимание, что символьный процессор «угадывает» точное значение интеграла pi а вычислительный определяет его приближенно и выдает в виде числа 3.142.
Листинг 7.8. Символьное и численное вычисление кратного интеграла
Аккуратнее вводите в редакторе Mathcad кратные интегралы, если они имеют различные пределы интегрирования по разным переменным. Не перепутайте пределы, относящиеся к разным переменным. Если Вы имеете дело с такого рода задачами, обязательно разберитесь с листингом 7.9, в котором символьный процессор вычисляет двукратный интеграл. В первой строке пределы интегрирования [а, b] относятся к переменной у, а во второй строке — к переменной X.
Листинг 7.9. Символьное вычисление кратных интегралов
5.2. Дифференцирование
С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, от о-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными. Невозможно дифференцирование функций только вблизи точек их сингулярности.
Вычислительный процессор Mathcad обеспечивает превосходную точность численного дифференцирования. Но больше всего пользователь оценит возможности символьного процессора, который позволяет с легкостью осуществить рутинную работу вычисления производных громоздких функций, поскольку, в отличие от всех других операций, символьное дифференцирование выполняется успешно для подавляющего большинства аналитически заданных функций.
В Mathcad 11 для ускорения и повышения точности численного дифференцирования функций, заданных аналитически, автоматически задействуется символьный процессор (см. разд. «Оптимизация вычислений»гл. 3).
5.2.1. Первая производная
Для того чтобы продифференцировать функцию f (х) в некоторой точке:
- Определите точку х, в которой будет вычислена производная, например х:=1.
- Введите оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак <?>.
- В появившихся местозаполнителях (рис. 7.3) введите функцию, зависящую от аргумента х, т. е. f(х), и имя самого аргумента х.
- Введите оператор <=> численного или < -> > символьного вывода для получения ответа.

Рис. 7.3. Оператор дифференцирования
Пример дифференцирования функции f(x)=cos(x)ln(x) приведен в листинге 7.10.
Листинг 7.10. Численное и символьное дифференцирование
Не забывайте предварительно определять точку, в которой производится численное дифференцирование, как это сделано в первой строке листинга 7.10. Иначе будет выдано сообщение об ошибке, показанное на рис. 7.4, гласящее, что переменная или функция, входящая в выражение, ранее не определена. Между тем, символьное дифференцирование не требует обязательного явного задания точки дифференцирования В этом случае вместо значения производной (числа или числового выражения) будет выдана аналитическая зависимость (см. верхнюю часть рис. 7.4).

Рис. 7.4. Ошибка в применении оператора дифференцирования
Конечно, можно, как и при использовании других операторов, предварительно определить функцию в отдельном выражении, а затем посчитать ее производную (см. листинг 7.11); или применить оператор дифференцирования для определения собственных функций пользователя (см. листинг 7.12).
Листинг 7.11. Символьное и численное дифференцирование функции пользователя
Листинг 7.12. Определение функции через оператора дифференцирования
В обоих листингах первой строкой определяется функция f (x)=1/x. Во второй строке листинга 7.11 с помощью символьного процессора находится аналитическое выражение ее производной, а в оставшейся части, подобно листингу 7.10, сначала численно, а затем аналитически определяются значения этой производной в точке х=0.1. В листинге 7.12 через производную от f (х) определяется еще одна пользовательская функция д(х) и затем находится ее конкретное значение в той же точке х=0.1.
Как Вы заметили, оператор дифференцирования, в основном, соответствует его общепринятому математическому обозначению. Однако в некоторых случаях при его вводе следует проявить осторожность. Рассмотрим один показательный пример, приведенный в листинге 7.13. Его первые две строки вычисляют производную sin(x) в точке х=0.5. Последняя строка демонстрирует неправильное применение оператора дифференцирования. Вместо вычисления производной sin(x) в той же точке, как этого можно было ожидать, получено нулевое значение. Это случилось потому, что аргумент функции sin(x) введен не в виде переменной х, а в виде числа. Поэтому Mathcad воспринимает последнюю строку как вычисление сначала значения синуса в точке х=0.5, а затем дифференцирование этого значения (т. е. константы) также в точке х=0.5, в соответствии с требованием первой строки листинга. Поэтому ответ, на самом деле, неудивителен — в какой точке ни дифференцируй константу, результатом будет ноль.
Листинг 7.1З. Приер правильного и неправильного применения дифференцирования
Для численного дифференцирования Mathcad применяет довольно сложный алгоритм, вычисляющий производную с колоссальной точностью до 7-8-го знака после запятой. Этот алгоритм (метод Риддера) описан во встроенной справочной системе Mathcad, доступной через меню Help (Справка). Погрешность дифференцирования не зависит от констант TOL или CTOL, в противоположность большинству остальных численных методов, а определяется непосредственно алгоритмом.
Исключение составляют функции, которые дифференцируются в окрестности сингулярной точки; например для рассмотренной нами функции f (x)=1/x это будут точки вблизи х=о. При попытке найти ее производную при х=о будет выдано сообщение об одной из ошибок деления на ноль «Can’t divide by zero» (Деление на ноль невозможно) или «Found a singularity while evaluating this expression. You may be dividing by zero» (Найдена сингулярность при вычислении этого выражения. Возможно, Вы делите на ноль). Если попробовать численно определить производную очень близко к нулю, например, при х=10-100, то может появиться сообщение об ошибке «Can’t converge to a solution» (Невозможно найти решение). Встретившись с одной из упомянутых ошибок, присмотритесь повнимательнее к дифференцируемой функции и убедитесь, что Вы не имеете дело с точкой сингулярности.
5.2.2. Производные высших порядков
Mathcad позволяет численно определять производные высших порядков, от 0-го до 5-го включительно. Чтобы вычислить производную функции f (х) N-го порядка в точке х, нужно проделать те же самые действия, что и при взятии первой производной (см. разд. 7.2.1), за тем исключением, что вместо оператора производной необходимо применить оператор N-й производной (Nth Derivative). Этот оператор вводится с той же панели Calculus (Вычисления) либо с клавиатуры нажатием клавиш <Ctrl>+<?> и содержит еще два местозаполнителя, в которые следует поместить число N. В полном соответствии с математическим смыслом оператора, определение порядка производной в одном из местозаполнителей приводит к автоматическому появлению того же числа в другом из них.
«Производная» при N=0 по определению равна самой функции, при N=1 получается обычная первая производная. Листинг 7.14 демонстрирует численное и символьное вычисление второй производной. Обратите внимание, что, как и при вычислении обычной производной, необходимо перед оператором дифференцирования присвоить аргументу функции значение, для которого будет вычисляться производная.
Листинг 7.14. Численное и символьное вычисление второй производной
Убедиться в том, что символьный процессор Mathcad в последней строке листинга 7.14 дает тот же результат, что и вычислительный процессор в предыдущей строке, можно, упростив его. Для этого следует выделить полученное последнее выражение и выбрать в меню Symbolics (Символика) пункт Symplify (Упростить). После этого ниже появится еще одна строка с численным результатом выделенного выражения.
Чтобы вычислить производную порядка выше 5-го, следует последовательно применить несколько раз оператор N-й производной, подобно тому как вводились операторы кратного интегрирования (см. разд. 7.1.4). Однако для символьных вычислений этого не потребуется — символьный процессор умеет считать производные порядка выше 5-го. Сказанное иллюстрирует листинг 7.15, в котором сначала численно, а затем символьно вычисляется седьмая производная синуса в точке х=0.1.
Листинг 7.15. Численное и символьное вычисление седьмой производной
Расчет производных высших порядков производится тем же вычислительным методом Риддера, что и расчет первых производных. Причем для первой производной этот метод обеспечивает точность до 7-8 значащих разрядов числа, а при повышении порядка производной на каждую единицу точность падает примерно на один разряд.
Из сказанного ясно, что падение точности при численном расчете высших производных может быть очень существенно. В частности, если попытаться определить девятую производную синуса, подобно идее листинга 7.15, то в качестве результата будет выдан нуль, в то время как истинное значение девятой производной равно cos (0.1).
7.2.3. Частные производные
С помощью обоих процессоров Mathcad можно вычислять производные функций любого количества аргументов. В этом случае, как известно, производные по разным аргументам называются частными. Чтобы вычислить частную производную, необходимо, как обычно, ввести оператор производной с панели Calculus (Вычисления) и в соответствующем местозаполнителе напечатать имя переменной, по которой должно быть осуществлено дифференцирование. Пример приведен в листинге 7.16, в первой строке которого определена функция двух переменных, а в двух следующих строках символьным образом вычислены ее частные производные по обеим переменным — х и у — соответственно. Чтобы определить частную производную численным методом, необходимо предварительно задать значения всех аргументов, что и сделано в следующих двух строках листинга. Последнее выражение в листинге снова (как и в третьей строке) определяет символьно частную производную по у. Но поскольку переменным х и у уже присвоено конкретное значение, то в результате получается число, а не аналитическое выражение.
Листинг 7.16 Символьное и численное вычисление частных производных
Частные производные высших порядков рассчитываются точно так же, как и обычные производные высших порядков (см. разд. 7.2.2). Листинг 7.17 иллюстрирует расчет вторых производных функции из предыдущего примера по переменным х, у и смешанной производной.
Листинг 7.17. Вычисление второй частной производной
Возможно, Вы обратили внимание, что в обоих листингах 7.16 и 7.17 оператор дифференцирования записан в форме частной производной. Подобно тому как существует возможность выбирать вид, например оператора присваивания, можно записывать операторы дифференцирования в виде обычной или частной производной. Запись оператора не влияет на вычисления, а служит лишь более привычной формой представления расчетов. Для того чтобы изменить вид оператора дифференцирования на представление частной производной, следует:
- Вызвать контекстное меню из области оператора дифференцирования нажатием правой кнопки мыши.
- Выбрать в контекстном меню верхний пункт View Derivative As (Показывать производную как).
- В появившемся подменю (рис. 7.5) выбрать пункт Partial Derivative (Частная производная).

Рис. 7.5. Изменение вида оператора дифференцирования
Чтобы вернуть вид производной, принятый по умолчанию, выберите в подменю пункт Default (По умолчанию) либо, для представления ее в обычном виде — Derivative (Производная).
Завершим разговор о частных производных двумя примерами, которые нередко встречаются в вычислительной практике. Программная реализация первого из них, посвященная вычислению градиента функции двух переменных, приведена в листинге 7.18. В качестве примера взята функция f (x,y), определяемая в первой строке листинга, график которой показан в виде линий уровня на рис. 7.6. Как известно, градиент функции f(х,у) является векторной функцией тех же аргументов, что и f (х,у), определенной через ее частные производные, согласно второй строке листинга 7.18. В оставшейся части этого листинга задаются ранжированные переменные и матрицы, необходимые для подготовки графиков функции и ее градиента.
Листинг 7.18. Вычисление градиента
Векторное поле рассчитанного градиента функции f(x,y) показано на рис. 7.7. Как можно убедиться, сравнив рис. 7.6 и 7.7, математический смысл градиента состоит в задании в каждой точке (х,у) направления на плоскости, в котором функция f (х,у) растет наиболее быстро.
До сих пор в данной главе мы рассматривали скалярные функции, к которым, собственно, и можно применять операторы дифференцирования. Часто приходится иметь дело с вычислением производных векторных функций. Например, в различных областях математики (см. разд. «Жесткие системы ОДУ» гл. 11) мы сталкиваемся с проблемой вычисления якобиана (или матрицы Якоби) — матрицы, составленной из частных производных векторной функции по всем ее аргументам. Пример вычисления якобиана векторной функции f (х) векторного аргумента х приведен в листинге 7.19. В нем для определения частных производных якобиана каждый i-й скалярный компонент f (x)i дифференцируется символьным процессором Mathcad.

Рис. 7.6. График линий уровня функции f (х,у) (листинг 7.18)

Рис. 7.7. Векторное поле градиента функции f (х,у) (листинг 7.18)
Тот же самый якобиан можно вычислить и несколько по-другому, если определить функцию не одного векторного, а трех скалярных аргументов f(x,y,z) (листинг 7.20).
Листинг 7.19. Вычисление якобиана векторной фенкции векторного аргумента
Листинг 7.20. Вычисление якобиана векторной функции трех скалярных аргумента
Не забывайте, что для численного определения якобиана необходимо сначала определить точку, в которой он будет рассчитываться, т. е. вектор х в терминах листинга 7.19, или все три переменных х,у, z в обозначениях листинга 7.20.