This simple margin of error (MOE) calculator can be employed to compute the MOE of a survey in accordance with the sample proportion and size, and the desired confidence level.
You can use the calculator to compute the MOE in four simple steps:
- Use the drop-down menu to select the confidence level
- Input the sample size and then the proportion percentage
- If required, provide details of the population size
- Click on the «Calculate» button to generate the outputs.
The Margin of Error in Statistics
The majority of surveys that are conducted for research purposes are based on information that is collected from a sample population as opposed to the full population (a census). As the sample is only representative of the full population, it is likely that some error will occur, not in terms of the calculation, but in terms of the sampling. That is, a sampling error will emerge because the researchers did not include everyone that exists within a given population. The MOE measures the maximum amount by which the sample results may differ from the full population. As most responses to survey questions can be presented in terms of percentages, it makes sense that the MOE is also presented as a percentage.
Margin of Error Formula
The Margin of Error (MOE) Calculator uses the following formulas:
1. MOE = z * √p * (1 — p) / √n
2. MOE (with finite population correction) = z * √p * (1 — p) / √(N — 1) * n / (N — n)
Where:
MOE is the margin of error,
z is the z-score associated with a level of confidence,
p is the sample proportion, expressed as a decimal,
n is the sample size,
N is the population size.
To estimate the sample size, take a look at our sample size calculator.
Margin of Error Calculation Example: A market research agency conducted a survey to identify how many mobile phone users use their devices to access social media. They surveyed 1000 mobile phone users and found that 540 regularly used their devices to access their social media profiles.
Let’s assume that we require a 95% level of confidence; as such, the z-score = 1.96.
The sample population, p, is 540 / 1000 = 0.54. (The sample size, n, was 1000.)
As such, the margin of error in this survey is as follows:
MOE = z * √p * (1 — p) / √n
MOE = 1.96 * √0.54 * (1 — 0.54) / √1000
MOE = 0.977 / 31.623 * 100 = 3.089%
These results indicate that the market research company can conclude with 95% confidence that 54% of mobile phone users use their device to access social media, give or take 3%.
Click here to jump to our Margin of Error Calculator
When essential business decisions are being made based on survey data from market research, you need to know the data you’re using is accurate and reliable.
But can any market research — or any research in general — be 100% accurate? How confident are you that your sample accurately reflects the population size as a whole?
While it’s impossible for survey results to be completely representative all of the time, you can figure out how close you are based on the margin of error built into your survey.
But what exactly is a margin of error, how can you calculate it and how much can or should it impact the level of confidence you have in your survey results?
Keep reading to find out.
Free eBook: 2022 global market research trends report
What is margin of error?
Margin of error is information that’s provided alongside the results of a piece of research, such as a poll, survey, or a scientific study. You’ll recognize it because it’s expressed with a plus and minus sign together, e.g. + or -1%
Researchers use this to provide additional information that helps you interpret their results and to understand how the study was carried out. The figure tells you that the true result may differ from the percentage figure provided, and how much more or less than the stated percentage the reality might be.
Margin of error provides a clearer understanding of what a survey’s estimate of a population characteristic means. A plus or minus 2 percentage points means that if we ask this question using a simple random sample 100 times, 95 of those times it would come out at the estimated value plus or minus 2 points.
The larger your random sample (the more responses you get), the smaller your margin of error will be and the more confidence you’ll have that your sample results are reliable.
Find out how big your sample size should be with our free calculator
When is margin of error used?
Margin of error is used when you have a random or probability sample.
That means the survey respondents have been selected at random from your population as a whole and every population member has a known, non-zero probability of being included.
It’s not appropriate if the sample has been selected in a non-random way, for example when you use an opt-in research panel.
A research panel sample is typically a quota sample, where participants are selected because they have particular characteristics. Additionally, the respondents volunteer for the panel in return for benefits, so they are not randomly selected from the population size at large.
So although it is a popularly known term, it has a specific application in survey research and it won’t always be relevant to your market research data.
Here are a couple of scenarios:
- A sports team has a complete list of everyone who has purchased tickets to their games in the past year. If they randomly select a sample of that population for a survey, they can calculate the margin of error on the percent of people who reported being a fan of the team.
- An organization has a complete list of employees. They poll a simple random sample of these employees on whether they preferred an additional day of leave or a small bonus payment. They can report the margin of error on the percentage preferring each option.
Other kinds of error
Margin of error accounts for the level of confidence you have in your results, and the amount of sampling error you expect based on the size of the sample. But there are other kinds of survey errors that may influence your results too.
These include:
Coverage error
Where your sampling frame doesn’t cover the population you are interested in.
Non-response error
This happens when certain respondents don’t take part in your survey.
Measurement error
This can arise from problems with the questionnaire.
To learn about other sources of error, check out our guide to random and non-random sampling error.
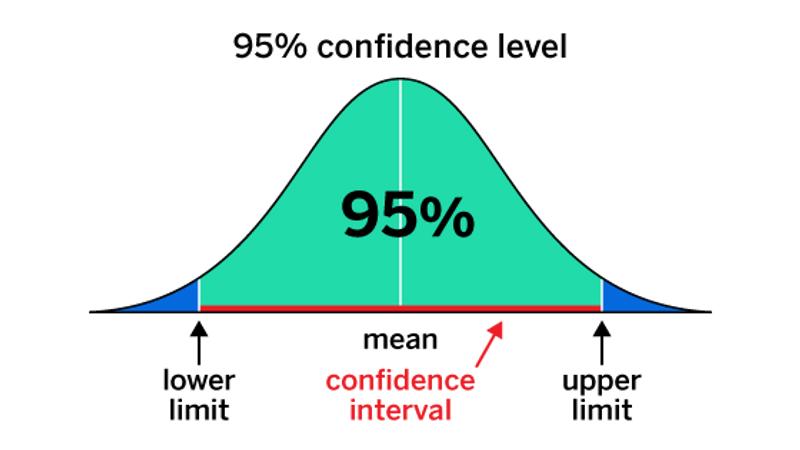
What is a confidence interval?
A confidence interval (CI) is a range of values that include a population value within a degree of confidence.
The values are typically shown in the results as a % value when a population mean sits between a lower and upper limit. Researchers use a CI to measure how accurately the survey sample resembles the overall population.
That’s because it’s almost impossible to find a sample that 100% matches the characteristics of the total population.
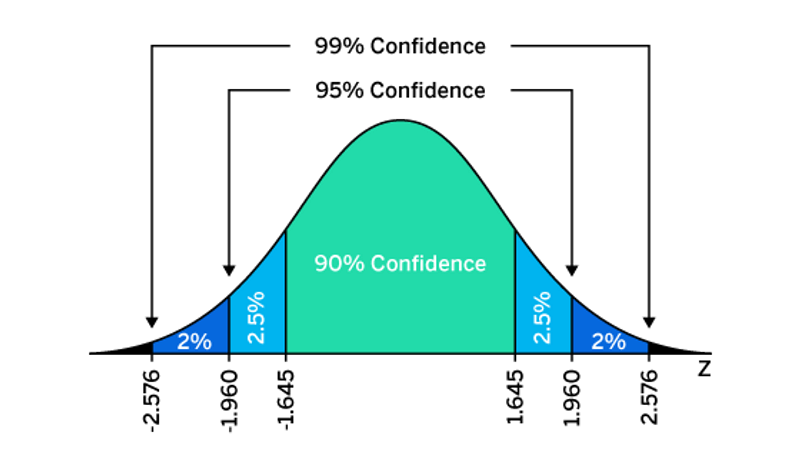
Researchers can choose a CI of any level, but a 95% CI is the most common.
This means researchers can be 95% certain that the results contain the actual mean value of the total population. This can be demonstrated using a normal distribution:
Using the graph above, you can see that if the probability of population mean value is between 1.96 and -1.96 standard deviations (sometimes called the z score), the sample mean is 95% (hence the 95% CI).
This is the most common industry formula for calculating the CI. However, when the costs of an error are extremely high, e.g. a multi-million dollar decision is at stake, the confidence interval should be kept small. This can be done by increasing the sample size.
How do you calculate margin of error?
Margin of Error Calculator
Confidence Interval:
Population Size:
Sample Size:
Margin of Error:
Margin of error is calculated using a formula:
Z * √((p * (1 – p)) / n)
Where
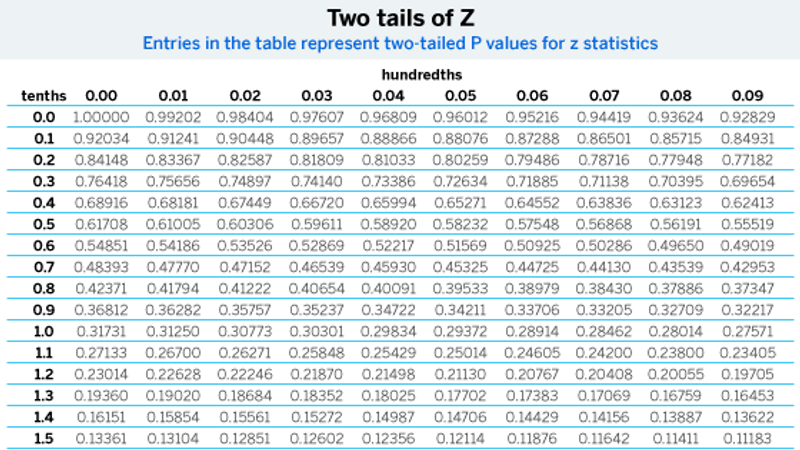
Z* is the Z*-value for your selected confidence level, which you’ll look up in a table of Z scores:
p is the sample proportion
n is the sample size
The sample proportion is the number within the sample that has the characteristic you’re interested in. It’s a decimal number representing a percentage, so while you’re doing the calculation it’s expressed in hundredths. For a 5% sample proportion, it would be 0.05.
The most commonly used confidence level is 95%, so we’ll use that for an example calculation. The Z*-value for a 95% confidence level is 1.96.
We’ll set our sample size at 1000. Next, we’ll follow the process to calculate the margin of error.
How to calculate margin of error with your survey data
- Subtract p from 1. If p is 0.05, then 1-p = 0.95.
- Multiply 1-p by p. So that’s 0.05 x 0.95 – which gives you 0.0475.
- Divide the result (0.0475) by the sample size n. So 0.0475 divided by 1000 = 0.0000475.
- Now we need the square root of that value, which is 0.0068920. This is the standard error.
- Finally, we multiply that number by the Z*-value for our CI, which is 1.96. So 0.0068920 x 1.96 = 0.0134395. That’s a margin of error of just over 1%.
Let’s try it with a real-world example.
Imagine you are a business surveying your current customers. You’ve run a study with a randomly selected sample of 1,000 people from your CRM list. The results tell you that of these 1,000 customers, 52% (520 people) are happy with their latest purchase, but 48% (480 people) are not – yikes. You want to add a margin of error to these results when you report them to your shareholders.
We’ll assume you want a 95% level of confidence, so the z*-value you’re working with is once again 1.96.
The number of customers who are happy with their latest purchase was 520, so that’s the number you’ll use to work out the sample proportion. 520 (p) / 1,000 (n) = 0.52
- 1-p is 0.48
- 0.52 (p) x 0.48 (1-p) = 0.2496
- 0.2496 / 1,000 = 0.0002496
- The square root of 0.0002496 = 0.0157987
- 0.0157987 x 1.96 (the z*-value) = 0.0309654, or in other words, 3.1% (when you round it up).
You can now report with 95% confidence that 52% of your customers were happy with their latest purchase, + or – 3.1%
There are a couple of conditions for using this formula. They are:
- n x p must equal 10 or more
- n x (1-p) must equal 10 or more
Usually, survey research involves quite high numbers of people in a sample, so unless you have a very small sample, or the sample proportion within your sample is very small, there won’t be a problem. If you’re getting numbers below 10 for either of these checks, you may need to increase your sample size.
Determining your sample size
Choosing the right sized sample is a critical part of creating a survey that will give you reliable results, especially when you’re using the data to make critical business decisions.
Determining sample size is based on the number of people you will need to represent the full population. For example, using 2,000 people as a representative sample of the UK workforce.
If you choose a sample that’s too small, you won’t get reliable results. The larger the sample, the smaller the margin of error. Of course, larger sample sizes mean costlier research, so ultimately there’s a trade off.
Determining the size of your sample is a relatively straightforward process:
Calculate margin of error
Your margin for error (also referred to as confidence interval) essentially determines how confident you can be that your sample will represent the same results you’d get if you were able to survey the total population.
If you used the margin of error formula mentioned above — Z * √((p * (1 – p)) / n) — and the associated z score table, you have your own margin of error calculator.
Understanding your confidence level
Your confidence level determines how certain you would be that the actual mean falls within your margin of error — and that if you were to repeat your survey multiple times, you’d still get the same results.
The lower your sample size, the lower your confidence level will be. The higher the sample size, the higher your confidence level.
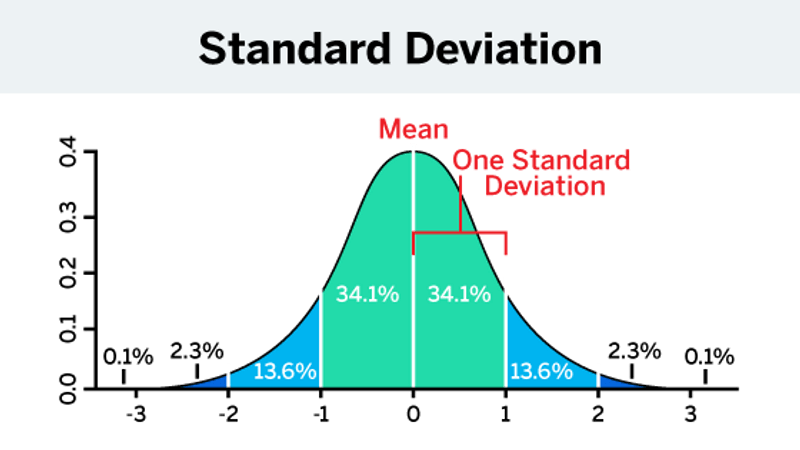
What’s the standard deviation likely to be?
In a population, standard deviation helps you to understand how the completed responses will differ from each other, as well as how they’ll deviate from the mean number.
A low standard deviation means that the values are clustered around the mean number, whereas a high standard deviation means they are spread across a range, with some small and large outlying figures.
What’s the total population size?
Population size is the main factor in determining the sample size you need to get the desired confidence level in your results.
The ‘population’ represents the whole group that you want to understand through your research, while the sample size is the number of people you need to survey to get a representative sample of that whole.
How to reduce the margin of error in your survey results
Reducing your margin of error is an essential part of increasing the reliability of your surveys and ensuring you’re generating better, more accurate results.
There are several ways you can reduce the margin error, some are more practical and will depend on a few variables around your project.
Reduce the variables
It stands to reason the more variables you have in your study the higher the chances that errors will creep into your study.
Reducing the variables in the way you gather your sample or complete your survey can also help to reduce the standard variation, meaning the margin of error will be lower.
Increase the total number in your sample
Often the easiest way to reduce the margin for error is to increase the size of the sample. Having a larger group complete your surveys statistically means you’ll be more likely to generate a representative response for your study and reduce the margin of error.
Use a lower confidence level
A lower confidence level provides you with a more precise margin of error – however you should be wary about this as lowering the confidence level reduces the confidence that your survey will accurately represent the overall population.
Use a single-sided confidence interval
Unlike a two-sided CI, a single-sided interval has a smaller margin of error, because it only shows if one of your parameters is above or below the cut-off value on one side i.e. it will only tell you if the parameter is above or below (it won’t show both).
You can use this method to reduce your margin for error if you’re confident the parameter will fall on one side of the cut-off value.
How Qualtrics can help
No matter the survey, research project or poll, Qualtrics CoreXM has the tools and capabilities you need to derive insight from data — and go from insight to action.
Used by more than 13,000 customers, Qualtrics CoreXM brings your survey, research, and polls into one platform, rather than multiple tools, enabling you to scale your activities, improve data quality, and uncover new opportunities.
With CoreXM, get insights faster through automation, reduce project costs and admin by consolidating your tools, and increase project impact by leveraging best-in-class survey methodologies and tools.
From simple polling and internal feedback surveys for strategy to gleaning customer, product, brand, and market insights, Qualtrics CoreXM empowers every department to carry out and benefit from research.
And if you want to get even more from your research, take advantage of Qualtrics’ Research Services and a network of experienced partners. Through trainer experts, unlock cost and time savings, while benefiting from flexible service options that let you choose how much or how little support you need.
Margin of Error Formula (Table of Contents)
- Margin of Error Formula
- Examples of Margin of Error Formula (With Excel Template)
- Margin of Error Formula Calculator
Margin of Error Formula
In statistic, we calculate the confidence interval to see where the value of the data of sample statistic will fall. The range of values which are below and above the sample statistic in a confidence interval is known as Margin of Error. In other words, it is basically the degree of error in the sample statistic. Higher the margin of error, lesser will the confidence in the results because the degree of deviation in these results is very high. As its name suggests, the margin of error is a range of values above and below the actual results. For example, if we get a response in a survey wherein 70% people have responded “good” and margin of error is 5%, this means that in general, 65% to 75% of the population think that the answer is “good”.
The formula for Margin of Error –
Margin of Error = Z * S / √n
Where:
- Z – Z score
- S – Standard Deviation of a population
- n – Sample Size
Another formula for calculating the margin of error is:
Margin of Error = Z * √((p * (1 – p)) / n)
Where:
- p – Sample Proportion (fraction of sample which is a success)
Now to find the desired z score, you need to know the confidence interval of the sample because the Z score is dependent on that. Below table is given to see the relation of a confidence interval and z score:
| Confidence Interval | Z – Score |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Once you know the confidence interval, you can use the corresponding z value and calculate the margin of error from there.
Examples of Margin of Error Formula (With Excel Template)
Let’s take an example to understand the calculation of Margin of Error in a better manner.
You can download this Margin of Error Template here – Margin of Error Template
Margin of Error Formula – Example #1
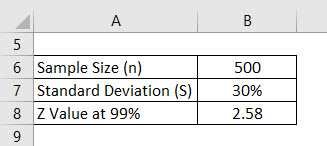
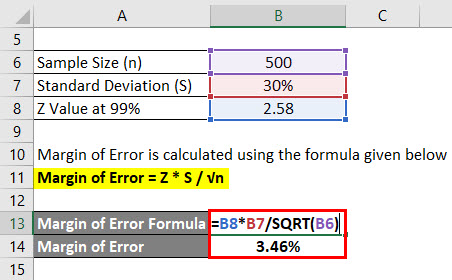
Let’s say we are conducting a survey to see what the grade score which university students are getting is. We have selected 500 students randomly and asked their grade score. The average of that is 2.4 out of 4 and the standard deviation is say 30%. Assume the confidence interval is 99%. Calculate the margin of error.
Solution:
Margin of Error is calculated using the formula given below
Margin of Error = Z * S / √n
- Margin of Error = 2.58 * 30% / √(500)
- Margin of Error = 3.46%
This means that with 99% confidence, the average grade of students is 2.4 plus or minus 3.46%.
Margin of Error Formula – Example #2
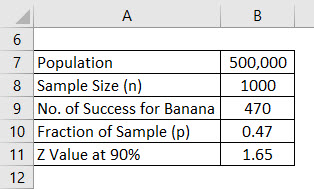
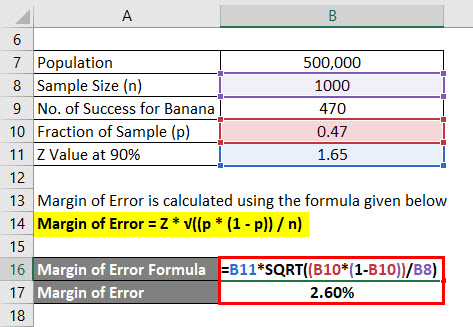
Let say you are launching a new health product in the market but you are confused which flavor will people like. You are confused between banana flavor and vanilla flavor and have decided to conduct a survey. Your population for that is 500,000 which is your target market and out of that you decided to ask the opinion of 1000 people and that will the sample. Assume that a confidence interval is 90%. Calculate the margin of error.
Solution:
Once the survey is done, you came to know that 470 people liked the banana flavor and 530 has asked for vanilla flavor.
Margin of Error is calculated using the formula given below
Margin of Error = Z * √((p * (1 – p)) / n)
- Margin of Error = 1.65 * √((0.47 * (1 – 0.47)) / 1000)
- Margin of Error = 2.60%
So we can say that with 90% confidence that 47% of all people liked banana flavor plus or minus 2.60%.
Explanation
As discussed above, the margin of error helps us understand whether the sample size of your survey is appropriate or not. In case the margin error is too big, it can be the case that our sample size is too small and we need to increase that so that sample results match more closely with population results.
There are some scenarios where the margin of error will not be of much use and will not help us in tracking the error:
- If the questions of the survey are not designed and do not help in getting the required answer
- If the people who are responding to the survey have some bias regarding the product for which the survey is being done, then also, the result not be very accurate
- If the sample chosen itself is the proper representative of the population, in that case also, results will be way off.
Also, one big assumption here is that the population is normally distributed. So if the sample size is too small and the population distribution is not normal, z score cannot be calculated and we will not be able to find the margin of error.
Relevance and Uses of Margin of Error Formula
Whenever we use sample data to find some relevant answer for the population set, there is some uncertainty and chances that the result might deviate from the actual result. The margin of error will tell us that what is the level of deviation is there is the sample output. We need to minimize the margin of error so that our sample results depict the actual story of population data. So lower the margin of error, the better will be the results. The margin of error complements and completes the statistical information which we have. For example, if a survey finds that 48% of the people prefer spending time at home during the weekend, we cannot be so precise and there are some missing elements in that information. When we introduced a margin of error here, say, 5%, then the outcome will be interpreted as 43-53% people liked the idea of being at home during the weekend, which makes complete sense.
Margin of Error Formula Calculator
You can use the following Margin of Error Calculator
| Margin of Error | = |
|
Recommended Articles
This has been a guide to Margin of Error formula. Here we discuss how to calculate the Margin of Error along with practical examples. We also provide a Margin of Error calculator with a downloadable excel template. You may also look at the following articles to learn more –
- Guide To Straight Line Depreciation Formula
- Examples of Doubling Time Formula
- How To Calculate Amortization?
- Formula For Central Limit Theorem