From Wikipedia, the free encyclopedia
The technique for human error-rate prediction (THERP) is a technique used in the field of human reliability assessment (HRA), for the purposes of evaluating the probability of a human error occurring throughout the completion of a specific task. From such analyses measures can then be taken to reduce the likelihood of errors occurring within a system and therefore lead to an improvement in the overall levels of safety. There exist three primary reasons for conducting an HRA: error identification, error quantification and error reduction. As there exist a number of techniques used for such purposes, they can be split into one of two classifications: first-generation techniques and second-generation techniques. First-generation techniques work on the basis of the simple dichotomy of ‘fits/doesn’t fit’ in matching an error situation in context with related error identification and quantification. Second generation techniques are more theory-based in their assessment and quantification of errors. ‘HRA techniques have been utilised for various applications in a range of disciplines and industries including healthcare, engineering, nuclear, transportation and business.
THERP models human error probabilities (HEPs) using a fault-tree approach, in a similar way to an engineering risk assessment, but also accounts for performance shaping factors (PSFs) that may influence these probabilities. The probabilities for the human reliability analysis event tree (HRAET), which is the primary tool for assessment, are nominally calculated from the database developed by the authors Swain and Guttman; local data e.g. from simulators or accident reports may however be used instead. The resultant tree portrays a step by step account of the stages involved in a task, in a logical order. The technique is known as a total methodology [1] as it simultaneously manages a number of different activities including task analysis, error identification, representation in form of HRAET and HEP quantification.
Background[edit]
The technique for human error rate prediction (THERP) is a first generation methodology, which means that its procedures follow the way conventional reliability analysis models a machine.[2] The technique was developed in the Sandia Laboratories for the US Nuclear Regulatory Commission.[3] Its primary author is Swain, who developed the THERP methodology gradually over a lengthy period of time.[1] THERP relies on a large human reliability database that contains HEPs, and is based upon both plant data and expert judgments. The technique was the first approach in HRA to come into broad use and is still widely used in a range of applications even beyond its original nuclear setting.
THERP methodology[edit]
The methodology for the THERP technique is broken down into 5 main stages:
1. Define the system failures of interest
These failures include functions of the system where human error has a greater likelihood of influencing the probability of a fault, and those of interest to the risk assessor; operations in which there may be no interest include those not operationally critical or those for which there already exist safety counter measures.
2. List and analyse the related human operations, and identify human errors that can occur and relevant human error recovery modes
This stage of the process necessitates a comprehensive task and human error analysis. The task analysis lists and sequences the discrete elements and information required by task operators. For each step of the task, possible errors are considered by the analyst and precisely defined. The possible errors are then considered by the analyst, for each task step. Such errors can be broken down into the following categories:
- Errors of omission – leaving out a step of the task or the whole task itself
- Error of commission – this involves several different types of error:
- Errors of selection – error in use of controls or in issuing of commands
- Errors of sequence – required action is carried out in the wrong order
- Errors of timing – task is executed before or after when required
- Errors of quantity – inadequate amount or in excess
The opportunity for error recovery must also be considered as this, if achieved, has the potential to drastically reduce error probability for a task.
The tasks and associated outcomes are input to an HRAET in order to provide a graphical representation of a task’s procedure. The trees’ compatibility with conventional event-tree methodology i.e. including binary decision points at the end of each node, allows it to be evaluated mathematically.
An event tree visually displays all events that occur within a system. It starts off with an initiating event, then branches develop as various consequences of the starting event. These are represented in a number of different paths, each associated with a probability of occurrence. As mentioned previously, the tree works on a binary logic, so each event either succeeds or fails. With the addition of the probabilities for the individual events along each path, i.e., branches, the likelihood of the various outcomes can be found. Below is an example of an event tree that represents a system fire:

Therefore, under the condition that all of a task’s sub-tasks are fully represented within a HRAET, and the failure probability for each sub-task is known, this makes it possible to calculate the final reliability for the task.
3. Estimate the relevant error probabilities
HEPs for each sub-task are entered into the tree; it is necessary for all failure branches to have a probability otherwise the system will fail to provide a final answer. HRAETs provide the function of breaking down the primary operator tasks into finer steps, which are represented in the form of successes and failures. This tree indicates the order in which the events occur and also considers likely failures that may occur at each of the represented branches. The degree to which each high level task is broken down into lower level tasks is dependent on the availability of HEPs for the successive individual branches. The HEPs may be derived from a range of sources such as: the THERP database; simulation data; historical accident data; expert judgement. PSFs should be incorporated into these HEP calculations; the primary source of guidance for this is the THERP handbook. However the analyst must use their own discretion when deciding the extent to which each of the factors applies to the task
4. Estimate the effects of human error on the system failure events
With the completion of the HRA the human contribution to failure can then be assessed in comparison with the results of the overall reliability analysis. This can be completed by inserting the HEPs into the full system’s fault event tree, which allows human factors to be considered within the context of the full system.
5. Recommend changes to the system and recalculate the system failure probabilities
Once the human factor contribution is known, sensitivity analysis can be used to identify how certain risks may be improved in the reduction of HEPs. Error recovery paths may be incorporated into the event tree as this will aid the assessor when considering the possible approaches by which the identified errors can be reduced.
Worked example[edit]
Context[edit]
The following example illustrates how the THERP methodology can be used in practice in the calculation of human error probabilities (HEPs). It is used to determine the HEP for establishing air based ventilation using emergency purge ventilation equipment on in-tank precipitation (ITP) processing tanks 48 and 49 after failure of the nitrogen purge system following a seismic event.
Assumptions[edit]
In order for the final HEP calculation to be valid, the following assumptions require to be fulfilled:
- There exists a seismic event initiator that leads to the establishment of air based ventilation on the ITP processing tanks 48 and 49
- It is assumed that both on and offsite power is unavailable within the context and therefore control actions performed by the operator are done so locally, on the tank top
- The time available for operations personnel to establish air based ventilation by use of the emergency purge ventilation, following the occurrence of the seismic event, is a duration of 3 days
- There is a necessity for an ITP equipment status monitoring procedure to be developed to allow for a consistent method to be adopted for the purposes of evaluating the ITP equipment and component status and selected process parameters for the period of an accident condition
- Assumed response times exist for initial diagnosis of the event and for the placement of emergency purge ventilation equipment on the tank top. The former is 10 hours while the latter is 4 hours.
- The in-tank precipitation process has associated operational safety requirements (OSR) that identify the precise conditions under which the emergency purge ventilation equipment should be hooked up to the riser
- The “tank 48 system” standard operating procedure has certain conditions and actions that must be included within for correct completion to be performed (see file for more details)
- A vital component of the emergency purge ventilation equipment unit is a flow indicator; this is required in the event of the emergency purge ventilation equipment being hooked up incorrectly as it would allow for a recovery action
- The personnel available to perform the necessary tasks all possess the required skills
- Throughout the installation of the emergency purge ventilation equipment, carried out by maintenance personnel, a tank operator must be present to monitor this process.
Method[edit]
An initial task analysis was carried out on the off normal procedure and standard operating procedure. This allowed for the operator to align and then initiate the emergency purge ventilation equipment given the loss of the ventilation system.
Thereafter, each individual task was analyzed from which it was then possible to assign error probabilities and error factors to events that represented operator responses.
- A number of the HEPs were adjusted to take account of various identified performance-shaping factors (PSFs)
- Upon assessment of characteristics of the task and behavior of the crew, recovery probabilities were deciphered. Such probabilities are influenced by such factors as task familiarity, alarms and independent checking
- Once error probabilities were decided upon for the individual tasks, event trees were then constructed from which calculation formulations were derived. The probability of failure was obtained through the multiplication of each of the failure probabilities along the path under consideration.

HRA event tree for align and start emergency purge ventilation equipment on in-tank precipitation tank 48 or 49 after a seismic event
The summation of each of the failure path probabilities provided the total failure path probability (FT)
Results[edit]
- Task A: Diagnosis, HEP 6.0E-4 EF=30
- Task B: Visual inspection performed swiftly, recovery factor HEP=0.001 EF=3
- Task C: Initiate standard operating procedure HEP= .003 EF=3
- Task D: Maintainer hook-up emergency purge ventilation equipment HEP=.003 EF=3
- Task E: Maintainer 2 hook-up emergency purge, recovery factor CHEP=0.5 EF=2
- Task G: Tank operator instructing /verifying hook-up, recovery factor CHEP=0.5 Lower bound = .015 Upper bound = 0.15
- Task H: Read flow indicator, recovery factor CHEP= .15 Lower bound= .04 Upper bound = .5
- Task I: Diagnosis HEP= 1.0E-5 EF=30
- Task J: Analyse LFL using portable LFL analyser, recovery factor CHEP= 0.5 Lower bound = .015 Upper bound =.15
From the various figures and workings, it can be determined that the HEP for establishing air based ventilation using the emergency purge ventilation equipment on In-tank Precipitation processing tanks 48 and 49 after a failure of the nitrogen purge system following a seismic event is 4.2 E-6. This numerical value is judged to be a median value on the lognormal scale. However, this result is only valid given that all the previously stated assumptions are implemented.
Advantages of THERP[edit]
- It is possible to use THERP at all stages of design. Furthermore, THERP is not restricted to the assessment of designs already in place and due to the level of detail in the analysis it can be specifically tailored to the requirements of a particular assessment.[4]
- THERP is compatible with Probabilistic Risk Assessments (PRA); the methodology of the technique means that it can be readily integrated with fault tree reliability methodologies.[4]
- The THERP process is transparent, structured and provides a logical review of the human factors considered in a risk assessment; this allows the results to be examined in a straightforward manner and assumptions to be challenged.[4]
- The technique can be utilized within a wide range of differing human reliability domains and has a high degree of face validity.[4]
- It is a unique methodology in the way that it highlights error recovery and it also quantitatively models a dependency relation between the various actions or errors.
Disadvantages of THERP[edit]
- THERP analysis is very resource intensive, and may require a large amount of effort to produce reliable HEP values. This can be controlled by ensuring an accurate assessment of the level of work required in the analysis of each stage.[4]
- The technique does not lend itself to system improvement. Compared to some other Human Reliability Assessment tools such as HEART, THERP is a relatively unsophisticated tool as the range of PSFs considered is generally low and the underlying psychological causes of errors are not identified.
- With regards to the consistency of the technique, large discrepancies have been found in practice with regards to different analysts assessment of the risk associated with the same tasks. Such discrepancies may have arisen from either the process mapping of the tasks in question or in the estimation of the HEPs associated with each of the tasks through the use of THERP tables compared to, for example, expert judgement or the application of PSFs.[5][6]
- The methodology fails to provide guidance to the assessor in how to model the impact of PSFs and the influence of the situation on the errors being assessed.
- The THERP HRAETs implicitly assume that each sub-task’s HEP is independent from all others i.e. the HRAET does not update itself in the event that an operator takes a suboptimal route through the task path. This is reinforced by the HEP being merely reduced by the chance of recovery from a mistake, rather than by introducing alternative (i.e. suboptimal) “success” routes into the event-tree, which could allow for Bayesian updating of subsequent HEPs.
- THERP is a “first generation” HRA tool, and in common with other such tools has been criticized for not taking adequate account of context.[2]
Other human reliability assessments[edit]
Other Human Reliability Assessments (HRA) have been created by multiple different researchers. They include cognitive reliability and error analysis method (CREAM), technique for human error assessment (THEA), cause based decision tree (CBDT), human error repository and analysis (HERA), standardized plant analysis risk (SPAR), a technique for human error analysis (ATHEANA), human error HAZOP, system for predictive error analysis and reduction (SPEAR), and human error assessment and reduction technique (HEART).[7]
References[edit]
- ^ a b Kirwan, B. (1994) A Guide to Practical Human Reliability Assessment. CRC Press. ISBN 978-0748400522.
- ^ a b Hollnagel, E. (2005) Human reliability assessment in context. Nuclear Engineering and Technology. 37(2). pp. 159-166.
- ^ Swain, A.D. & Guttmann, H.E., Handbook of Human Reliability Analysis with Emphasis on Nuclear Power Plant Applications. 1983, NUREG/CR-1278, USNRC.
- ^ a b c d e Humphreys, P. (1995). Human Reliability Assessor’s Guide. Human Factors in Reliability Group. ISBN 0853564205
- ^ Kirwan, B. (1996) The validation of three human reliability quantification techniques — THERP, HEART, JHEDI: Part I — technique descriptions and validation issues. Applied Ergonomics. 27(6) 359-373. doi.org/10.1016/S0003-6870(96)00044-0
- ^ Kirwan, B. (1997) The validation of three human reliability quantification techniques — THERP, HEART, JHEDI: Part II — Results of validation exercise. Applied Ergonomics. 28(1) 17-25.
- ^ DeMott, D.L. (2014?) «Human Reliability and the Cost of Doing Business». Annual Maintenance and Reliability Symposium
Cognitive functions and human error
Barbara G. Kanki, … Cynthia Null, in Space Safety and Human Performance, 2018
2.2.1 Definition
There are many definitions of human error, though they all have a common feature. Human error is a label given to an action that has negative consequences or fails to achieve the desired outcome. The preface to Behind Human Error (Woods et al., 2010) documents much of the history of the label human error.
[Human] error is merely an out of tolerance action, where the limits of tolerable performance are defined by the system.
(Swain and Guttmann, 1983)
A generic term to encompass all those occasions in which a planned sequence of mental or physical activities fails to achieve its intended outcome, and when these failures cannot be attributed to some chance agency.
(Reason, 1990)
[Human] error means that something has been done which was: not intended by the actor; not desired by a set of rules or an external observer; or that led the task or system outside its acceptable limits.
(Sender and Moray, 1991)
An erroneous action can be defined as an action which fails to produce the expected result and/or which produces an unwanted consequence.
(Hollnagel, 1993)
Either an action that is not intended or desired by the human or a failure on the part of the human to perform a prescribed action within specified limits of accuracy, sequence, or time that fails to produce the expected result and has led or has the potential to lead to an unwanted Consequence.
(NASA, 2008)
When driving a car, changing lanes without signaling may be a violation of the law or of a social norm, but may only be judged as a human error when, after an accident, the failure to signal is deemed a part of the accident event. Likewise, an operator who follows the nominal procedure, as prescribed, can be judged to have made a human error if any steps in the procedure are determined to be inconsistent with a specific unexpected condition, after the accident. For example, if an airline has a policy that the autolanding system is to be used in all cases, the pilot may be considered to have committed a human error if he or she attempted to use the autolanding system in a specific condition that, after the accident, was determined to be beyond the capability of the automation (see discussion of American 1340, Dismukes et al., 2007). There can be a fine line between a mission or operational context in which an action is always correct and the one context where such an action may have detrimental consequences. The sources of successful operation of systems under one set of conditions can be labeled errors after failure occurs (Woods et al., 2010).
There has persisted a view that complex systems would be fine, if not for the erratic behavior of some individuals (Dekker, 2014). The accident proneness of workers has been studied since the 1920s. Arbous and Kerrick (1951) provided a critique of this research. They noted that the researchers studying accident proneness carefully warned of drawing conclusions often due to the paucity of data or inconclusive or contradictory results. In addition, they pointed out the stubbornness with which this notion has been assumed to be true. Rodgers and Blanchard (1993) observe that personality factors have shown little usefulness is predicting accidents, despite the folklore that errors are related to an individual predisposition to make errors or take risks. It is often convenient to blame individuals and ignore the context in which errors are committed. So the question gets asked by those concerned about safety: because individuals are not all the same, can’t we just protect the system with more rules, by telling people to be careful or to put in more effort, and by enforcing compliance? The simple answer is no. Pariès (2011) explains that both automation and proceduralization have been applied in safety critical systems to reduce system uncertainty though processes that reduce variety, diversity, deviation, and instability. The side effect has been to reduce autonomy, creativity, and reactivity of human operators and make systems increasing brittle outside the boundaries of the normal operating envelope.
Years of taking an approach to safety that focused on protecting systems from their operators did not increase safety. Such efforts often have multiple unintended consequences including increasing system complexity, reducing operator(s) flexibility to resolve unexpected failures, and increasing workload (see Chapter 10 for a further discussion).
The “New View” of human error moves the conversation from human errors to human actions. Human behaviors are understood as the product of systematic processes inside the cognitive, operation, and organizational world in which we operate (Woods et al., 2010). According to Reason (1990), errors are seen as consequences, not causes, having their origins in “upstream” systemic factors. The descriptions of how humans succeed, and sometimes fail, often differ only by the outcome. That is, the exact same sequence of events and human actions can have many different results, for a large variety of reasons. Woods, Dekker and others have argued that human errors are the symptoms of deeper system issues—organizational and/or technological. Errors arise while people are pursuing success in an uncertain, resource-constrained world (Dekker, 2014). Hollnagel (2005) argues that human error, as a sought-after signal in accident analysis, is fundamentally inconsistent with understanding that human behavior is primarily a reflection of environmental complexity.
Woods et al. (2010) argue that the designation “human error” is an attribution, not a fact. Social psychologists have attempted to explain how a person makes sense of another person’s behavior and how they make sense of their own behavior by attributing behavior to either characteristics about the person or the context in which the behavior takes place. Behavior attribution theory predicts when interpreting the behavior of others, people will place focus on the characteristics (qualities, intentions) of that person and not focus on the context or environment in which the behavior took place. A person running a red light might be judged as not paying attention, unskilled, irresponsible, or reckless, for example. When making sense of our own behavior, however, attribution theory predicts that the focus becomes the context. A person might attribute their own running of a red light to be a result of the context, for example, responding to a medical emergency in a low-traffic situation. The fundamental attribution error emphasizes personal characteristics and minimizes situational explanations when judging the behavior or others, and conversely emphasizes the situational explanations and minimizes personal characteristics when judging one’s own actions (Harvey and Weary, 1984). A metaanalysis of about 40 years of research demonstrated that the attribution asymmetry has held for negative events (Malle, 2006).
Human error is an after-the-fact designation that is sensitive to hindsight bias. Once the outcome is known, an oversimplified sequence of events often becomes the event model. Hindsight bias is the tendency for people who already know the outcome of an event to believe, falsely, that they would have predicted that outcome (Hawkins and Hastie, 1990). There is a rich scientific literature on hindsight bias (e.g., Blank and Nestler, 2007; Fischhoff, 2007) that informs those that try to understand mishaps and accidents (Woods et al., 2010). Working backward from the outcome can simplify the chain of events, impart knowledge to the actors that they did not and could not have, and exaggerate the obviousness of the consequence of any action or inaction. Thus, the uncertainty faced by the actors in an event is underestimated. Perrow (1999) explains, “But if, as we shall see time and time again, the operator confronted by unexpected and usually mysterious interactions among failures, saying that he or she should have zigged instead of zagged is possible only after the fact” (p. 9). Much has been written on ways to overcome hindsight bias in analysis of mishaps and accidents (Dekker, 2014; Woods et al., 2010).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081018699000029
Human Reliability Analysis
DrEduardo Calixto, in Gas and Oil Reliability Engineering (Second Edition), 2016
5.12.3 Conclusion
Human error during the different asset life cycles, such as design, transportation, commissioning and operation, may affect asset performance and must be avoided. Unfortunately, in many projects human error is not taken into account during RAM analysis based on the assumption of no human error. In fact, human error can be identified in the early asset life cycle design during FMEA as a cause of failure mode. In addition, human error happens also during maintenance activities, which increase the downtime and has an impact on asset performance. Therefore it is good practice to identify human error in different asset life cycle phases, which will affect asset performance during the operational phase. In case of a new asset concept, new equipment, and technology, it is necessary to consider the impact of human error in the asset performance by carrying out human reliability analysis and inputting such information in the RAM analysis to find out the quantitative effect on production efficiency and operational availability and propose mitigate action to avoid them.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128054277000051
Human Reliability Assessment
Yong Bai, Wei-Liang Jin, in Marine Structural Design (Second Edition), 2016
43.3.1 Human Error Quantification
Once the potential human errors have been represented, the next step is to quantify the likelihood of the human errors involved. The human error probability (HEP) is defined as
HEP=NumberoferrorsoccuredNumberofopportunitiesforerrortooccur
In reality, there are very few recorded HEP data, due to the difficulty in estimating the number of opportunities for error in the realistically complex tasks and the unwillingness to publish data on poor performance.
Human error quantification techniques therefore rely on expert judgment or on a combination of data and psychologically based models, which evaluate the effects of major influences on human performance. The major techniques in the field of human error quantification are listed below (Kirwan, 1994).
| APJ | Absolute probability judgment (Seaver and Stillwell, 1983) |
| THERP | Technique used for human error rate prediction (Swain and Guttmann, 1983) |
| SLIM–MAUD | Likelihood of success index method using multiattributed utility decomposition (Embrey et al., 1984) |
| HEART | Human error assessment and reduction technique (Williams, 1986) |
Human error dependence is also an important issue when representing human errors and quantifying their frequencies. For example, the response to the first alarm and the response to the second alarm, it is obvious that if the same operator is involved in both actions, then the errors associated with each of these events are unlikely to be independent. Dependence at this level may be dealt with by the use of conditional probabilities.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080999975000435
Fundamentals of risk management
Gerardo Portela da Ponte Jr, in Risk Management in the Oil and Gas Industry, 2021
2.3.1.4 Principle 4 of protection against human error
Human error is influenced by natural vulnerabilities (unpredictable), human limitations (unavoidable), and the error-inducing environment (designed for). The control of the consequences of human error within the limits of acceptable levels is only possible through a design of human factors that works by limiting the error-inducing environment. Natural vulnerabilities and human limitations are not within the grasp of engineering. To protect against human error is to recognize that human errors are unavoidable and it is up to the human factors design to develop engineering solutions that limit the consequences of these errors to acceptable risk levels.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128235331000101
Human Reliability Analysis
Dr.Eduardo Calixto, in Gas and Oil Reliability Engineering, 2013
5.2 Technique for Human error Rate Prediction
THERP was one of the first probabilistic analyses and was developed by specialists who detected problems in nuclear reactors (1975). But the real effort to develop a human analysis methodology was conducted by Swain when he published the Technique for Human Error Rate Prediction in 1983. The THERP methodology uses a human reliability tree that represents a sequence of probable omission or commission errors with success or human error probability. The following steps are needed to perform THERP analysis:
- •
-
Understand the problem to be assessed
- •
-
Identify the system functions that may be influenced by human error
- •
-
List and analyze the related human tasks
- •
-
Estimate the error probabilities for each task
- •
-
Estimate the final human error probability by tree events
- •
-
Propose recommendations to reduce human error probability
- •
-
Estimate the recommendations effects on human error probability by tree events
As described, the first step is to understand what is being assessed to see if THERP is the best tool for finding the answer. The second step is important for understanding the human error context and how human tasks influence the system or activity being assessed. The third step describes task steps, and in some cases tasks can be summarized. Not all task steps must be considered in analysis because due to difficulties in estimating human error, in some cases it is clear that some task steps do not influence the human error being assessed.
Caution is necessary, but it is important to remember that long tasks are more difficult to analyze, and whenever possible it is best to simplify to understand the human error involved in the problem being assessed to allow for more accurate results. The fourth and more difficult step is to estimate human error probability, which can be done using a data bank, specialist opinion, literature, or a combination of. In this step it must be clear that the main objective is to estimate human error so that the final human error probability is representative of the problem assessed. An example of human error probability values is shown in Figure 5-1.
Figure 5-2 shows that human error probability depends on task duration and activity context. The task duration influences the human error probability, and the shorter the task, the higher the human error probability. The main question to ask when using such data is if it is representative of the case being assessed, and the specialist involved in such analysis must be able to confirm if such data fit well or not. If not, the specialist must propose other values of human error probability when there’s no historical data available. Some human errors are uncommon, and there is often no available reports or data, and in this case it can be estimated by specialist opinion. In newer plants when there has not been enough time to estimate human error, a specialist can also estimate how much human error is expected to occur over the plant life cycle. It is often easier to estimate frequency of occurrence of failure than probability, but it’s not a problem itself, because in this case it’s possible to turn frequency of failure into probability of failure for the time requested by the exponential cumulative density function (CDF) when failure is random, which is represented by:
FIGURE 5-2. Human error probability values.
(Source: Kumamoto, 1996.)
F(t)=∫0tf(x)dx=∫0tλeλt=1−λλeλt=1−eλt
where:
λ = Expected number of human errors per time
T = Time
F(t) = Probability of human error occurring until time t
After estimating human error probability by task it is necessary to calculate the final human error probability for the whole activity and that can be done using THERP event tree. A THERP event tree has two sides where successes and failures are counted. Tasks are represented by letters. The uppercase letters represent failures and the lowercase letters represent successes. On the right side where there are input failure probabilities it is possible also to use successes, but on the left side it is not. An example will be given to illustrate the human reliability event tree diagram.
The THERP methodology can be applied to understanding maintenance human error in exchanging obstructed tubes in heat exchangers because of human failure to close equipment correctly. The performance-shaping factor “workplace environment” was the requirement to quickly perform maintenance to finish it as soon as possible. Figure 5-3 shows the tube and shell heat exchanger, and the following task steps are:
FIGURE 5-3. Tube and shell heat exchanger.
- 1.
-
Check if operator stops equipment (success: a; fail: A)
- 2.
-
Check if lines linked to equipment are depressurized and purged (success: b; fail: B)
- 3.
-
Check if scaffold is safe (success: c; fail: C)
- 4.
-
Isolate equipment lines (success: d; fail: D)
- 5.
-
Open an inspection tube (success: e; fail: E)
- 6.
-
Replace obstructed tubes (success: f; fail: F)
- 7.
-
Close equipment (success: g; fail: G)
All of these steps can shut down equipment if human error succeeds. Such a task sequence can be represented by a THERP event tree as shown in Figure 5-4. Notice that all events are independent.
FIGURE 5-4. THERP event tree.
To calculate human error probability it is necessary to define the probability of failure for each of the seven tasks, because if any of them fail, the maintenance in the heat exchanger will not succeed. Thus, human error probability based on the THERP event tree is described by:
HEP=1−P(Success)
PSuccess=P(a)×P(b)×P(c)×P(d)×P(e)×P(f)×P(g)
HEP=1−P(a)×P(b)×P(c)×P(d)×P(e)×P(f)×P(g)
Thus, based on Figure 5-4 and the probability values, the human error probabilities will be:
P(a)=1−P(A)=1−(0.0005)
P(b)=1−P(B)=1−(0.0005)
P(c)=1−P(C)=1−(0.0005)
P(d)=1−P(D)=1−(0.03)
P(e)=1−P(E)=1−(0.01)
P(f)=1−P(F)=1−(0.1)
P(g)=1−P(G)=1−(0.1)
Human error probability(HEP)=1−P(s)=1−((0.9995)×(0.9995)×(0.9995)×(0.97)×(0.99)×(0.9)×(0.9))=21.63%
Such probability shows that at the end of maintenance, because there was not adequate time to perform the maintenance in the tube and shell heat exchanger, there will be a higher probability of failure in the tasks of replacing the obstructed tube (P(F) = 0.1) and closing the heat exchanger (P(G) = 0.1). Thus, there’s a high probability of chance for human error in such maintenance.
After estimating human error probability it is necessary to assess improvements for reducing human error probability and to estimate the human error probability after recommendations are implemented. When there is enough time to complete the task in the two final tasks (F and G) the probability of failure is reduced from 0.1 to 0.001 and consequently the new human error probability is:
HEP=1−P(s)=1−((0.9995)×(0.9995)×(0.9995)×(0.97)×(0.99)×(0.999)×(0.999))=4.3%
In such maintenance the first four tasks are related to safety. To perform maintenance under safe conditions, such tasks are required, but in many cases those tasks are not conducted properly and checked by maintenance professionals. If accidents occur, in addition to human injuries and equipment damage, maintenance is not completed and a system can be shut down and consequently there will be additional delays in startup. Because of that the first four tasks are considered part of maintenance, and when they are not performed properly, are considered human errors in maintenance.
To better illustrate THERP methodology, a second example of human reliability analysis will be conducted using drilling phases as shown in Figure 5-5. In general, the steps are:
FIGURE 5-5. Drilling phase tasks.
- 1.
-
Drill and condition (success: a; fail: A)
- 2.
-
Circulation (success: b; fail: B)
- 3.
-
Casing (success: c; fail: C)
- 4.
-
Cementation (success: d; fail: D)
In the case of human error, there will be delays on a drilling project or accidents such as a blowout. The event tree can be represented as shown in Figure 5-6. Based on specialist opinion, each event has the probability shown in the following list:
FIGURE 5-6. THERP event tree (drilling phase tasks).
P(a)=1−P(A)=1−(0.01)=0.99
P(b)=1−P(B)=1−(0.02)=0.98
P(c)=1−P(C)=1−(0.01)=0.99
P(d)=1−P(D)=1−(0.005)=0.995
HEP=1−P(s)=1−((0.99)×(0.98)×(0.99)×(0.995))=4.43%
Human error in drilling tasks can result in the tool being stuck. Human failure in circulation can result in kick, and if not controlled, can result in a blowout accident. Human error in a casing task can also result in casing prison. And finally, human error in cementation can cause instability in a well.
Thus, using THERP human reliability methods it is possible to assess human error in task sequences. These drill steps comprise several other tasks in different drill phases that can also be assessed in details when it is necessary. In conclusion, the important points of the THERP methodology are:
- •
-
For simple tasks, using the event tree it is possible to assess sequences of human actions where human error may occur.
- •
-
The THERP method has been widely applied across industries, producing a large pool of experienced analysts and example applications.
- •
-
For complex tasks with many steps it is hard to model an event tree.
- •
-
To calculate human error probability it is necessary to define the human error probability for each task and sometimes this is not easy to do.
- •
-
Such methodology does not consider human performance-shaping factors that cause human error, which is a remarkable characteristic of the first generation of human reliability analysis methodologies.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123919144000058
Human Factors and Human Error
In Lees’ Loss Prevention in the Process Industries (Fourth Edition), 2012
14.10.1.3 Human Error Database (HED)
The Human Error Database (HED), described by Kirwan (1988), is based on the HEP data given in the Rosmussen Report, tempered by expert judgment. In that it derives from that report, it has similarities to THERP, but it is less decompositional and is not dependent on any specific model.
Moreover, a large number of human error data points is collected from a variety of mainly nuclear-power related sources in Computerised Operators Reliability and Error Database or CORE-DATA (Taylor-Adams, 1995; Kirwan et al., 1997). For offshore data, Basra and Kirwan (1998) provided a selection of human error probabilities.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123971890000148
Reliability Modeling Techniques
Dr.David J. Smith, Kenneth G.L. Simpson, in The Safety Critical Systems Handbook (Fifth Edition), 2020
5.4.2 Human Error Rates
Human error rate data for various forms of activity, particularly in operations and maintenance, are needed. In the early 1960s there were attempts, by UKAEA, to develop a database of human error rates and these led to models of human error whereby rates could be estimated by assessing relevant factors such as stress, training, and complexity. These human error probabilities include not only simple failure to carry out a given task, but diagnostic tasks where errors in reasoning, as well as action, are involved. There is not a great deal of data available due to the following problems:
- •
-
Low probabilities require large amounts of experience in order for meaningful statistics to emerge
- •
-
Data collection concentrates on recording the event rather than analyzing the causes.
- •
-
Many large organizations have not been prepared to commit the necessary resources to collect data.
For some time there has been an interest in exploring the underlying reasons, as well as probabilities, of human error. As a result there are currently several models, each developed by separate groups of analysts working in this field. Estimation methods are described in the UKAEA document SRDA-R11, 1995. The better known are HEART (Human Error Assessment and Reduction Technique), THERP (Technique for Human Error Rate Prediction), and TESEO (Empirical Technique to Estimate Operator Errors).
For the earlier overpressure example, failure of the operator to react to a high pressure (3) might be modeled by two of the estimation methods as follows:
“HEART” method
Basic task “Restore system following checks”—error rate = 0.003.
Modifying factors:
| Few independent checks | ×3 | 50% |
| No means of reversing decision | × | 25% |
An algorithm is provided (not in the scope of this book) and thus:
Error probability = 0.003 × [2 × 0.5 + 1] × [7 × 0.25 + 1] = 1.6 × 10−2
“TESEO” method
Basic task “Requires attention” – error rate = 0.01.
-
× 1 for stress
-
× 1 for operator
-
× 2 for emergency
-
× 1 for ergonomic factors
Thus error probability = 0.01 × 1 × 1 × 2 × 1 = 2 × 10−2
The two methods are in fair agreement and thus a figure of 2 × 10−2 might be used for the example.
Figure 5.10 shows a fault tree for the example assuming that the human response is independent of the shutdown system. The fault tree models the failure of the two levels of protection (2) and (3). Typical (credible) probabilities of failure on demand are used for the initiating events. The human error value of 2 × 10−2 could well have been estimated as above.
Figure 5.10. Fault tree involving human error.
Quantifying this tree would show that the overall PFD is 1.4 × 10−4 (incidentally meeting SIL 3 quantitatively).
Looking at the relative contribution of the combinations of initiating events would show that human error is involved in over 80% of the total. Thus, further consideration of human error factors would be called for.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012820258600005X
Risk assessment and management in the context of the seveso II directive
Tony Cox, in Industrial Safety Series, 1998
 Human Factors
Human Factors
- •
-
Human error may occur in: design, construction, start-up, maintenance, management and hands-on operation
- •
-
It is difficult and not very useful to try to quantify human error within a risk analysis, but it should be taken into account in other ways within the Safety Report
- •
-
The “Seveso II” Directive requires that attention be given to the management system for controlling risks
- •
-
The Quantitative Risk Assessment can be thought of as representing the inherent hardware risk, assuming that the human operators are “average” for the industry
- •
-
Any departure from the “average” should be assessed by audit and corrected by management
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0921911098800153
Crew errors in the safety assessment
Duane Kritzinger, in Aircraft System Safety, 2017
10.5.1 Advantages
Human error is an important consideration in complex safety critical systems, because it makes the most significant contribution to overall system risk (Edwards, 1988). The goal of a HF assessment is to make systems successful by enhancing performance, satisfaction and safety. Clearly it is not practical or cost-effective to develop and/or test all possible combinations of conditions that could affect human performance. Nevertheless, a systematic and informed consideration of the human as part of the safety risk management process can provide significant risk reduction, even if all risks are unlikely to be fully alleviated. Explicitly identifying and managing human error risks throughout the product life cycle have the knock-on benefit of improving operational effectiveness.
Error reduction, however, is not the only approach to the problem of error. The second line of attack is directed towards the elimination of disastrous consequences of human error. The design of equipment (including the monitoring/feedback loop to its operators), procedures (e.g. how to deal with the occurrence) and training (e.g. ensure timely intervention) has a major influence on the likelihood and result of human errors.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081008898000106
Human Factors and Human Error
In Lees’ Loss Prevention in the Process Industries (Third Edition), 2005
14.38.1 CCPS Guidelines for Preventing Human Error in Process Safety
The prevention of human error on process plants is addressed in the Guidelines for Preventing Human Error in Process Safety edited by Embrey for the CCPS (1994/17) (the CCPS Human Error Prevention Guidelines).
The Human Error Prevention Guidelines are arranged under the following headings: (1) the role of human error in chemical process safety, (2) understanding human performance and error, (3) factors affecting human performance in the chemical industry, (4) analytical methods for predicting and reducing human error, (5) qualitative and quantitative prediction of human error in risk assessment, (6) data collection and incident analysis methods, (7) case studies and (8) setting up an error reduction program in the plant.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978075067555050102X
These classifications of human interactions can be related to a simple error classification system consisting of three categories (1) slips, (2) non-response, and (3) mistakes. This classification scheme can then be used to qualitatively incorporate human errors in accident scenarios. Table 9.1 provides generic human error probabilities for use in accident scenario [Pg.217]
The development of a generic set of human error probabilities is extremely difficult since there is a strong correlation on the actual person performing the task, the complexity of the task, the time required for task completion, and the training level of the person performing the task. Additionally, a worker may perform any specific task differently depending on the level of alertness due to fatigue or other factors. [Pg.217]
Phase three of a typical HRA begins with developing human error probabilities that can he applied to the selected model. In some cases, a set of nominal human errors can be derived 1mm plant data, however, due to the sparseness and low confidence of these data industry generic information may be used. Chapter 20 of NUREG/CR-1278 includes a typical set of. such data. [Pg.175]
The human error probabilities estimated for a given task can now be modified to reflect the actual performance situation. For example, if the labeling scheme at a particular plant is very poor, the probability should be increased towards an upper bound. If the tagging control system at a plant is particularly good, the probability for certain errors should be decreased toward a lower bound. [Pg.175]
In any given situation, there may be different levels of dependence between an operator s performance on one task and on another because of the characteristics of the tasks theraseb e.s. or because of the manner in which the operator was cued to perform the tasks. Dependence levels between the performances of two (or more) operators also may differ. The analyses should account for dependency in human-error probabilities. In addition, each sequence may have a set of human recovery actions that if successfully performed will terminate or reduce the consequences of the sequence. This information, coupled with a knowledge of the system success criteria leads to the development of human success and failure probabilities which are input to the quantification of the fault iices or event trees. With this last step, the HRA is integrated into the PSA, and Pl. ise 4 is complete. [Pg.175]
List of the generic human error probabilities used to determine a base error rate for each human error considered, and… [Pg.178]
| Table 4.5-11 Sample o/NUCLARR Human Error Probability Data iNUREG/CR-4639f… |  |
The development of the HRA event tree is one of the most critical parts of the quantification of human error probabilities. If the task analysis lists the possible human error events in the order of ihcir potential occurrence, the transfer of this information to the HRA event tree is fadlitutcd. Each potential eiTor and success is represented as a binary branch on the HRA event tiec. with subsequent errors and successes following directly from the immediately preceding ones. Cure should be taken not to omit the errors that are not included in the task analysis table but might affect the probabilities listed in the table. For example, administrative control errors that affect a task being performed may not appear in the task analysis table but must be included in the HRA event tree. [Pg.181]
Human reliability [lata NJUREG/CR-1278 was supplemented by judgment of system analysts and plant personnel. Human error probabilities were developed from NUREG/CR-12 8, human action time windows from system analysis and some recovery limes from analysis of plant specific experience. Data sources were WASH-1400 HEPs,Fullwood and Gilbert assessment ot I S power reactor Bxp., NUREG/ CR -127K. and selected acro ptice li.it.j… [Pg.182]
Voska, K.J. and J.N. O Brien, Human Error Probability Estimation Using Licensee Event Reports, BNL, July 1984. [Pg.470]
V) Reece, W. J. et al., Nuclear Computerized Library for Assessing Reactor Reliability (NUCLARR), Part. 2 Human Error Probability Data (HEP), 1994. [Pg.470]
Chapter 5, Quantitative and Qualitative Prediction of Human Error in Safety Assessments, describes a systematic process for identifying and assessing the risks from human error, together with techniques for quantifying human error probabilities. [Pg.2]
Chapter 4 focuses on techniques which are applied to a new or existing system to optimize human performance or qualitatively predict errors. Chapter 5 shows how these teclmiques are applied to risk assessment, and also describes other techniques for the quantification of human error probabilities. Chapters 6 and 7 provide an overview of techniques for analyzing the underlying causes of incidents and accidents that have already occurred. [Pg.3]
In numerical terms, the probability of each failure state is given by the following expressions (where SP is the success probability and HEP the human error probability at each node) … [Pg.222]
The decomposition approach is used, it is necessary to represent the way in which the various task elements and other possible failures are combined to give the failure probability of the task as a whole. Generally, the most common form of representation is the event tree (see Section 5.7). This is the basis for THERP, which will be described in the next section. Fault trees are only used when discrete human error probabilities are combined with hardware failure probabiliHes in applications such as CPQRA (see Figure 5.2). [Pg.226]
History and Technical Basis. The influence diagram approach (IDA) (also known as the sociotechnical approach to human reliability (STAHR) (see Phillips et al., 1990) is a technique that is used to evaluate human error probabilities as a… [Pg.239]
Quantitative human reliability data collection systems for generating human error probabilities for use in quantitative risk assessment. [Pg.248]
There is considerable interest in developing a database on human error probabilities for use in chemical process quantitative risk assessment (CPQRA). Nevertheless, there have been very few attempts to develop such a database for the CPI compared, for example, with the nuclear industry. Some of the reasons for this are obvious. The nuclear industry is much more highly integrated than the CPI, with a much greater similarity of plant equipment… [Pg.253]
Embrey, D. E., Kirwan, B., Rea, K., Humphreys, P., Rosa, E. A. (1984). SLIM-MAUD. An approach to Assessing Human Error Probabilities Using Structured Expert judgment Vols. I and II. Washington, DC NUREG/CR—3518 US Nuclear Regulatory Commission. [Pg.369]
Human Error Probability The probability that an error will occur during the performance of a particular job or task within a defined time period. Alternative definition The probability that the human operator will fail to provide the required system function within the required time. [Pg.412]
About 1,000 miscellaneous failure rates, event rates, and probabilities. There is some treatment of human error probability… [Pg.30]
After repair, the component is returned to the working state. Minimal cut set analysis is a mathematical technique for developing and providing probability estimates for the combinations of basic component failures and/or human error probabilities, which are necessary and sufficient to result in the occurrence of the top event. [Pg.50]
Human error after maintenance HUM Q = HEPfmc Ts fmc = Corrective maintenance frequency HEP = Human error probability… [Pg.404]
In direct numerical estimation, decision makers are asked to give a numerical estimate of how likely they think the event is to happen. These estimates can be probabilities, odds, log odds, or words (Winterfeldt and Edwards 1986). Winterfeldt and Edwards argue that log odds have certain advantages over the other measures. Gertman and Blackman (1994) note that log odds are normally used in risk assessment for nuclear power applications because human error probabilities (HEPs) vary greatly in value. HEPs between 1 and 0.00001 are typical. [Pg.2191]
SLIM-MAUD (Embrey 1984) implements a related approach in which expert ratings are used to estimate human error probabilities (HEPs) in various environments. The experts first rate a set of tasks in terms of performance-shaping factors (PSFs) that are present. Tasks with known HEPs are used as upper and lower anchor values. The experts also judge the importance of individual PSFs. A subjective likelihood index (SLI) is then calculated for each task in terms of the PSFs. A logarithmic relationship is assumed between the HEP and SLI, allowing calculation of the human error probability for task j (HEPj) from the subjective likelihood index assigned to task j (SLIj). More specifically … [Pg.2192]
After the task is specified, human and machine performance models can be applied to estimate task performance. The MHP and keystroke-level performance model can provide task performance estimates in terms of task completion time. THERP can be used to estimate human error probabilities for each task and task sequence. The ERM approach can be used to estimate performance along any required dimension and to compare required with available resources along any required dimension as long as the human performance data are available. The results of the ERM assessment would identify stress levels on capacities (e.g., resources stressed too long or beyond maximum capacity). These results indicate limiting factors to successful task performance. Limiting factors can be identified at elemental or intermediate performance resource levels. As such, the ERM represents a more comprehensive and internally consistent model than the others. It is more comprehensive in that it can be used to model any performance dimension. It is… [Pg.1317]
Planning errors cause wrong designs and construction flaws and lead to wrong or insufficient instructions in the operating manual. Planning errors stem, for example, from mutual dependencies which have not been identified or sufficiently accounted for as the dependence of human error probabilities on environmental influences or impairment of components due to changes in environmental conditions caused by an accident. [Pg.379]
Author / Affiliation / Email

Article Menu
Font Type:
Arial
Georgia
Verdana
Open AccessArticle
Australian Maritime College (AMC), College of Sciences and Engineering, University of Tasmania, Launceston, TAS 7248, Australia
*
Author to whom correspondence should be addressed.
Received: 25 January 2022
/
Revised: 18 February 2022
/
Accepted: 24 February 2022
/
Published: 27 February 2022
Abstract
:
Liquified natural gas (LNG) as a marine fuel has gained momentum as the maritime industry moves towards a sustainable future. Since unwanted LNG release may lead to severe consequences, performing quantitative risk assessment (QRA) for LNG bunkering operations has become mandatory according to some regulations. Human error is a main contributor to the risks, and the human error probabilities (HEPs) are essential for inclusion in a QRA. However, HEPs data are unavailable in the LNG bunkering industry so far. Therefore, this study attempts to infer HEPs through on-site safety philosophical factors (SPFs). The cognitive reliability and error analysis method (CREAM) was adopted as a basic model and modified to make it suitable for HEP assessment in LNG bunkering. Nine common performance condition (CPC) indicators were identified based on the fuzzy ranking of 23 SPF indicators (SPFIs). A Bayesian network (BN) was built to simulate the occurrence probabilities of different contextual control modes (COCOMs), and a conditional probability table (CPT) for the COCOM node with 19,683 possible combinations in the BN was developed according to the CREAM’s COCOM matrix. The prior probabilities of CPCs were evaluated using the fuzzy set theory (FST) based on data acquired from an online questionnaire survey. The results showed that the prior HEP for LNG bunkering is 0.009841. This value can be updated based on the re-evaluation of on-site SPFIs for a specific LNG bunkering project to capture the dynamics of HEP. The main innovation of this work is realizing the efficient quantification of HEP for LNG bunkering operations by using the proposed fuzzy BN-CREAM model.
1. Introduction
The number of liquified natural gas (LNG) fueled ships is rapidly growing due to LNG being considered as a viable transitional fuel in the maritime industry’s journey towards decarbonization [1,2,3]. LNG is flammable and cryogenic, and unwanted release may lead to severe consequences. Particularly, the safety of LNG bunkering is a key issue of concern to the industry, because bunkering operations have a high likelihood of leakage [4]. Therefore, performing quantitative risk assessment (QRA) for LNG bunkering operations is either mandated or highly recommended for understanding and mitigating the potential risks according to the existing regulations and standards [5]. Human error has become the main contributor to the risks in the maritime industry [6,7], where the combination of human and organizational errors during operations leads to about 65% of all catastrophic accidents [8]. As a result, when performing a QRA for LNG bunkering, the human error probabilities (HEPs) are essential inclusion. The definition of HEP is the opposite of that of the human reliability probability which refers to the probability that a person: (1) correctly performs a system-required activity and (2) performs no extraneous activity that can degrade the system [9].
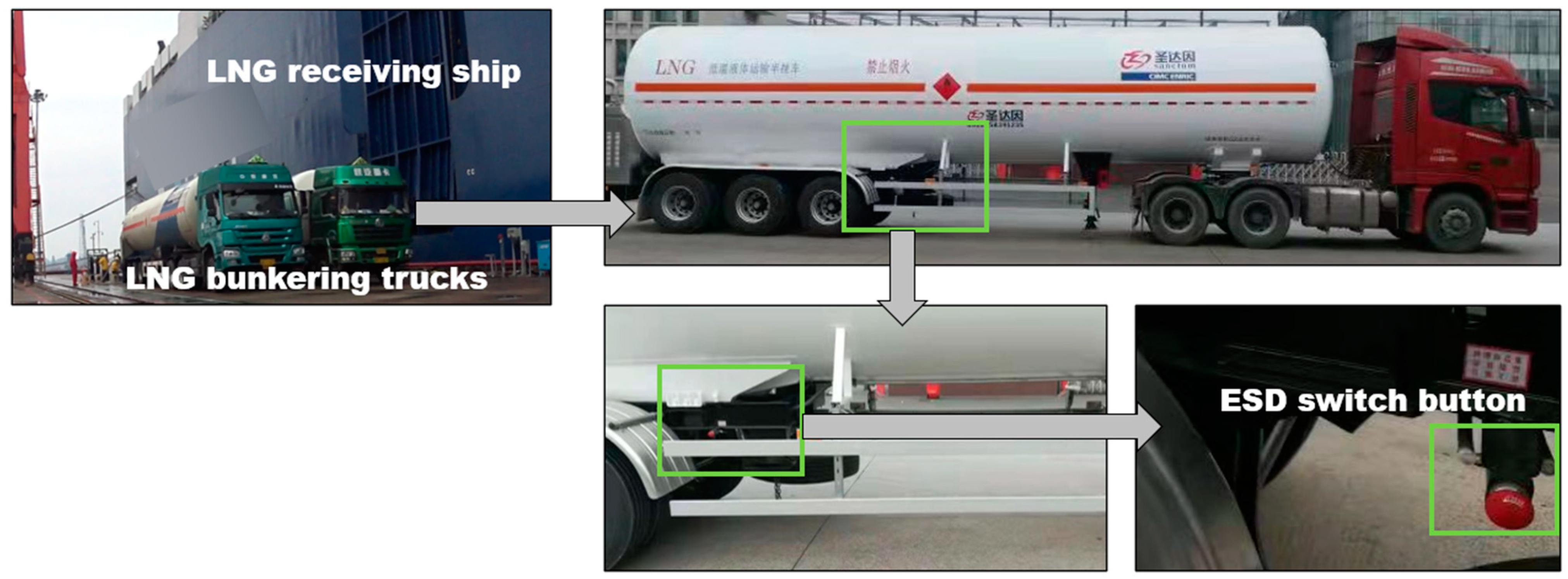
The LNG bunkering consists of the following main steps: preparation, connection (between bunkering side and receiving side), purging, inerting, pre-cooling, LNG transfer, purging, and disconnection. These steps are all involved with human behavior. The complex mechanism that lies behind human behavior leads to human errors. From a Bowtie model-based risk assessment perspective [9], human errors may: (1) contribute to causes of a hazardous event; (2) be the direct triggering events or even sole triggering event for the hazardous event; (3) be related to the safety barriers of potential consequences. For example, Figure 1 shows a truck-to-ship LNG bunkering scenario; as a safety barrier, an operator should press a manual emergency shutdown (ESD) switch button immediately when leakage is observed. Possible human error modes for this operation could comprise: the operator not pressing the switch button, or the operator pressing the button too late. These human error modes lead to different occurrence probabilities of consequences.
Some research studies have been conducted regarding the risks of LNG bunkering. These have mainly focused on the following three aspects: (1) safety zone evaluation [10,11,12,13,14,15,16,17,18,19,20,21,22], (2) risk assessment methodology and practice [23,24,25,26,27], and (3) emergency evacuation assessment [27,28]. Even though these studies have improved our understanding of LNG bunkering safety, none has quantified human errors in LNG bunkering. Stokes et al. have studied the human factor for LNG bunkering [29], and demonstrated qualitatively the importance of human error rather than quantitatively analyzing the HEP. As the LNG bunkering industry is premature, the HEPs are unavailable in existing databases [30,31,32,33]. The International Association of Oil & Gas Producers has suggested the HEPs for rule-based actions by control room personnel after diagnosis of an abnormal event [34]; however, the available data are directly quoted from a report from the nuclear industry [35], and their applicability in the field of LNG bunkering is arguable. As an alternative solution, the HEP can be inferred through human reliability assessment (HRA) methods. Previous studies have reported many HRA approaches which are classified into three generations as summarized in Table 1, and some researchers have comprehensively reviewed these methods [36,37,38]. In recent years, second-generation methods are widely used; third-generation methods are still in the early stages of development since the artificial intelligence and computer-aided simulation techniques are still under development.
The significant human errors occur as a result of a combination of on-site conditions and certain personal psychological factors that trigger error mechanisms in personnel [9]. The psychological factors of operators are complex and difficult to quantify in an LNG bunkering operation. In fact, the negative impact of psychological factors on human performance can be reflected in on-site conditions which can be defined as safety philosophical factors (SPFs). For example, a superior safety culture can ensure that workers have a good mental state during work. Consequently, it is assumed that human errors during LNG bunkering are determined by on-site SPFs.
Further to this background, this research attempts to explore inferring HEP from on-site SFPs of LNG bunkering. Among the second-generation HRA approaches as shown in Table 1, the CREAM (cognitive reliability and error analysis method), which is widely utilized in many industries, is able to infer HEPs through safety factors. Therefore, in this research, the CREAM is employed as a basic method while modified to make it suitable for HEPs inference during LNG bunkering operations.
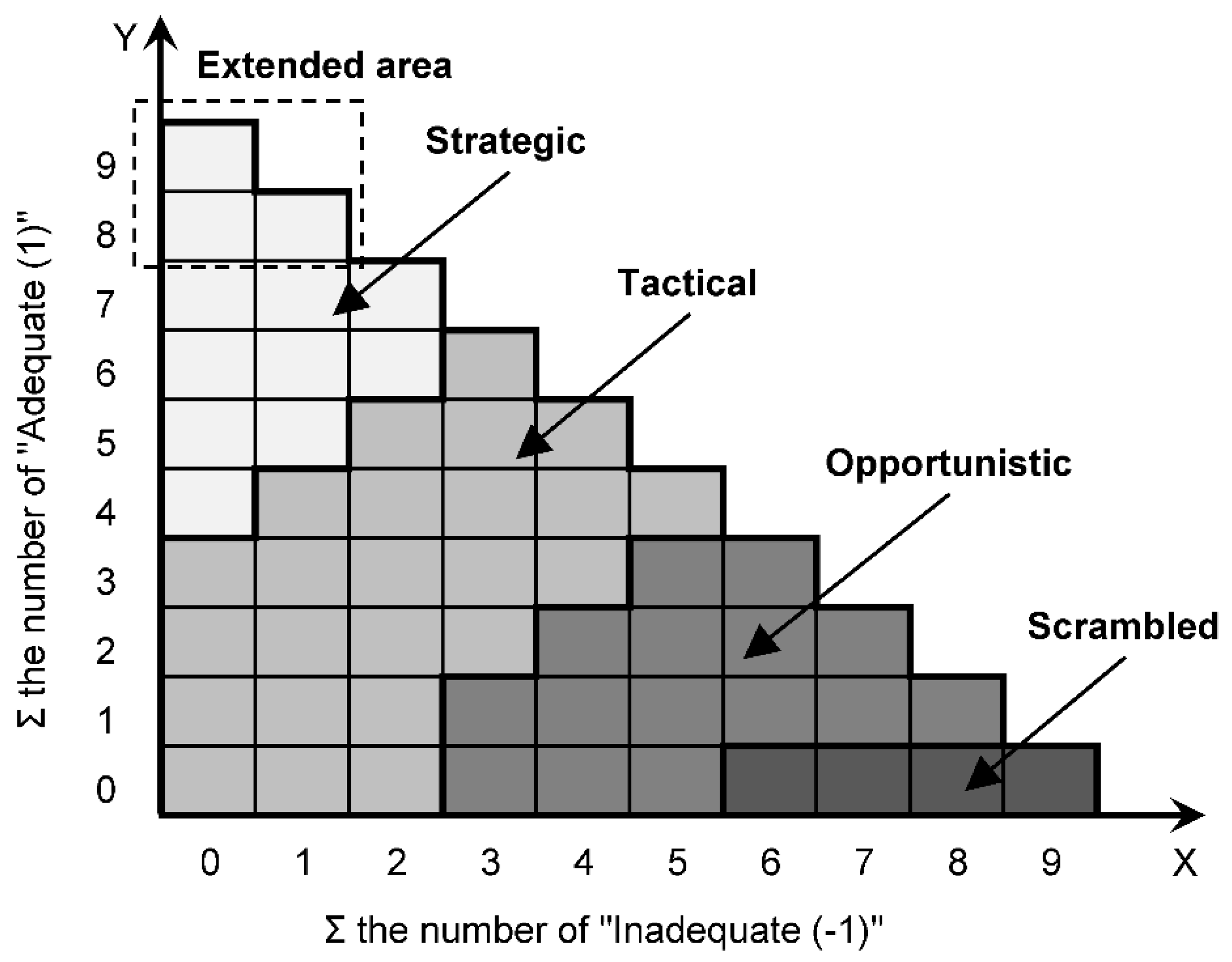
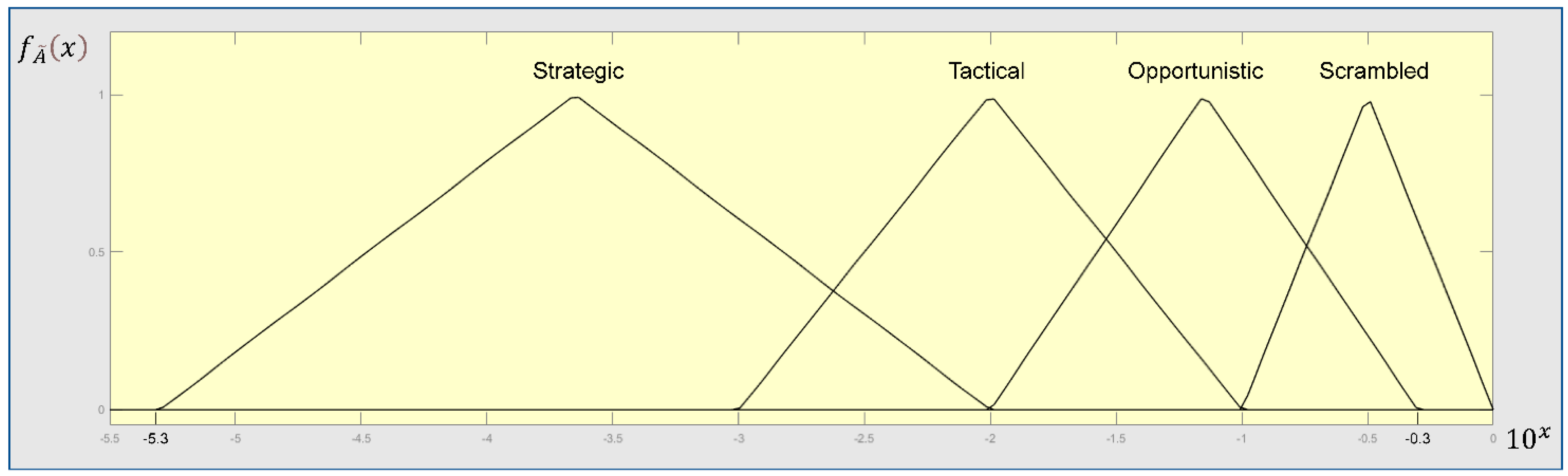
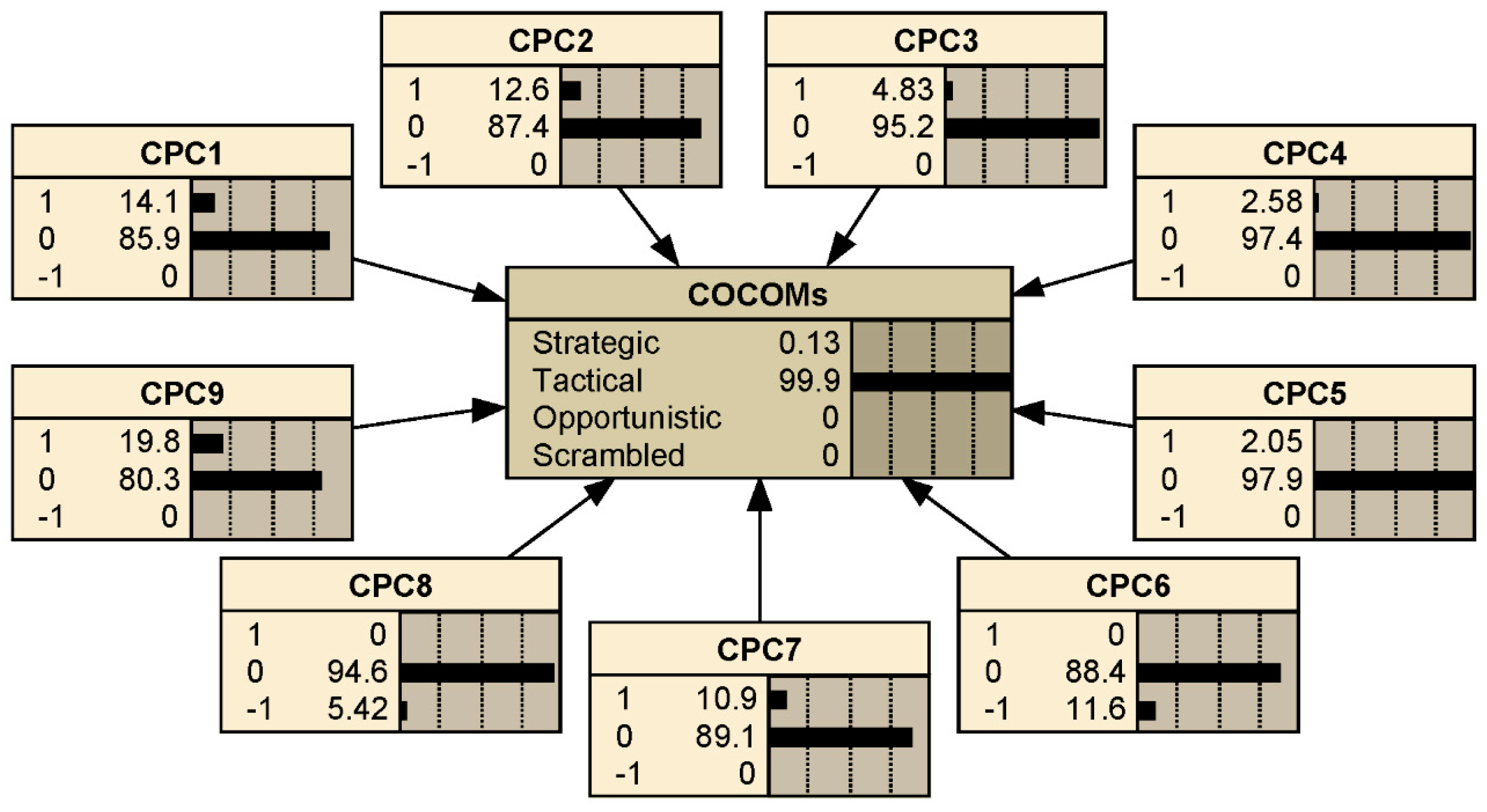
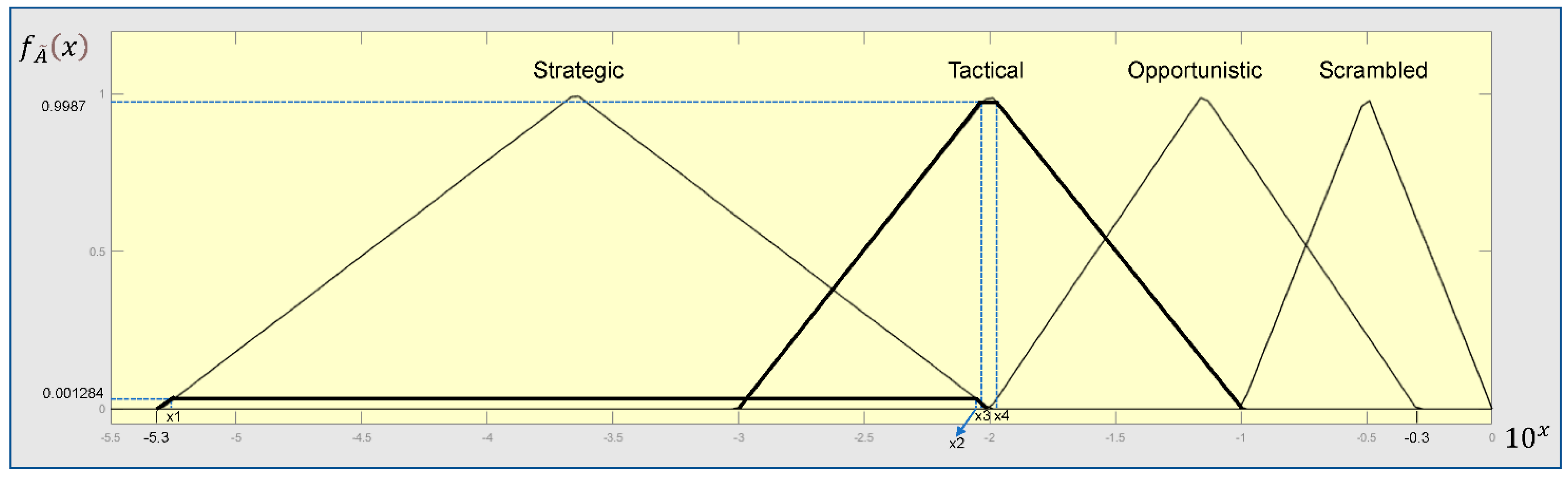
The CREAM was originally developed for the nuclear industry but becomes popular in other industries [41,48,49,50]. A human error has multiple causes, and the original CREAM model uses nine common performance condition (CPC) indicators to determine a specific contextual control mode (COCOM) out of four COCOMs, namely, “Strategic”, “Tactical”,” Opportunistic”, and “Scrambled”. Each CPC is given a score (1,0 or –1) by the analysts, and each COCOM is connected to a HEP interval as described in Table 2. A matrix is used to convert the performance of nine CPCs into a COCOM. The combined CPC score can be derived by counting the number of times where a CPC is expected to have negative effect (–1), no significant effect (0), or positive effect (1). Furthermore, in order to generate a specific crisp HEP, an extended CREAM method should be used [41].
The applications of CREAM have solved HEPs in many studies. However, there is still a major limitation of utilizing CREAM. Experts’ judgments on CPCs are subjective which makes uncertainties in the results of CPCs’ performance higher. Nevertheless, CREAM assigns a human error to a certain COCOM without considering the probabilities of it falling into different COCOMs which increases the uncertainty of the results to a certain extent.
In order to deal with the uncertainty and to capture the conditional independence relationships between the interacting variables, the probabilistic graphical models could be employed. Generally, there are two main probabilistic graphical models, namely, the Bayesian networks (BNs) and the Markov Random Fields. The BNs are directed acyclic graphs with variables representing observable or latent variables of the model. However, the Markov Random Fields are undirected acyclic graphs that might contain cycles, they thus can describe a different set of dependency relationships than their BN counterparts. In this research, a directed acyclic graph is able to establish the causal relationships between the CPCs and the COCOMs; therefore, the BN is employed to calculate the probabilities of COCOMs.
The BN is a powerful method. In addition, the utilization of the fuzzy set theory (FST) can cope with the data shortage in a BN model. In the existing literature, studies have demonstrated that combining BN or fuzzy-BN (FBN) with CREAM can consider the uncertainty of the model and the given information. For example, Yang, Z. et al. established a BN-based CREAM which can provide the instant estimation of HEP given the updated data [51]. Yang, Z.L. et al. proposed a modified BN based CREAM to quantify HEPs in marine engineering by incorporating fuzzy evidential reasoning [52]. Zhou, Q. et al. applied the FBN CREAM model in HRA for a case of tanker shipping [53]. Similarly, Ung. S used a fault tree analysis structure combined with a modified FBN CREAM to analyse the HEPs that trigger oil tanker collisions [54]. Chen, D. et al. conducted an HRA for a submersible diving process based on the CREAM model and BN [55]. Abbasinia, M. et al. used FBN to improve the capabilities of CREAM for determining the COCOMs [56]. Ghasemi, F. et al. used the FBN CREAM model to predict HEP for a road tanker loading operation [57]. Wu, Y. et al. adopted the FBN CREAM to determine the COCOMs and calculate the HEPs in a metallurgical enterprise [49]. These efforts have developed and enhanced the CREAM with computer-aided simulation techniques. However, the proposed methods in the literature cannot be applied directly in the LNG bunkering industry because the CPCs are required to be purpose-defined for LNG bunkering operations. Besides, it is noteworthy that the conditional probability table (CPT) for the COCOM node in the BN has yet to be addressed, because in the existing literature, the dimension of the CPT was reduced to achieve the purpose of simplifying the calculation. For example, the intermediate nodes or assumed rules were used, which violated the principle of the original CREAM model and decreased the accuracy of the results.
With this context, this study attempts to address the following main research questions (RQs) about inferring HEP:
RQ1: How to define CPCs for LNG bunkering?
RQ2: How to build a BN model that fully complies with the original CREAM principle?
RQ3: How to obtain the prior probabilities of CPCs?
As the premise of this research, there are the following basic assumptions:
- (1)
-
All HEPs in a specific LNG bunkering operation are the same. There are two reasons for this. Firstly, the individual differences of operators are ignored due to few on-site operators needed according to practice. Usually, there are less than five on-site operators during LNG bunkering. Secondly, all human operations are stipulated in the LNG bunkering operation manual, and any possible human error is a violation of the procedures in the operation manual. In other words, human error modes are essentially the same.
- (2)
-
The HEP is independent of time. This means that HEP remains the same irrespective of how long the bunking operations last. This is different from the probabilities of failure of technical equipment, which increase with time or deterioration of the equipment. This is equivalent to treating a person as “a new equipment” at all times [9].
The main novelty of this work is an attempt to realize the efficient quantification of HEP for LNG bunkering operations using the fuzzy BN-CREAM model.
The remainder of this article is structured as follows. Section 2 presents the methodology. Section 3 introduces the data collection and analysis. Section 4 presents the results and discussion. Finally, Section 5 outlines the conclusions.
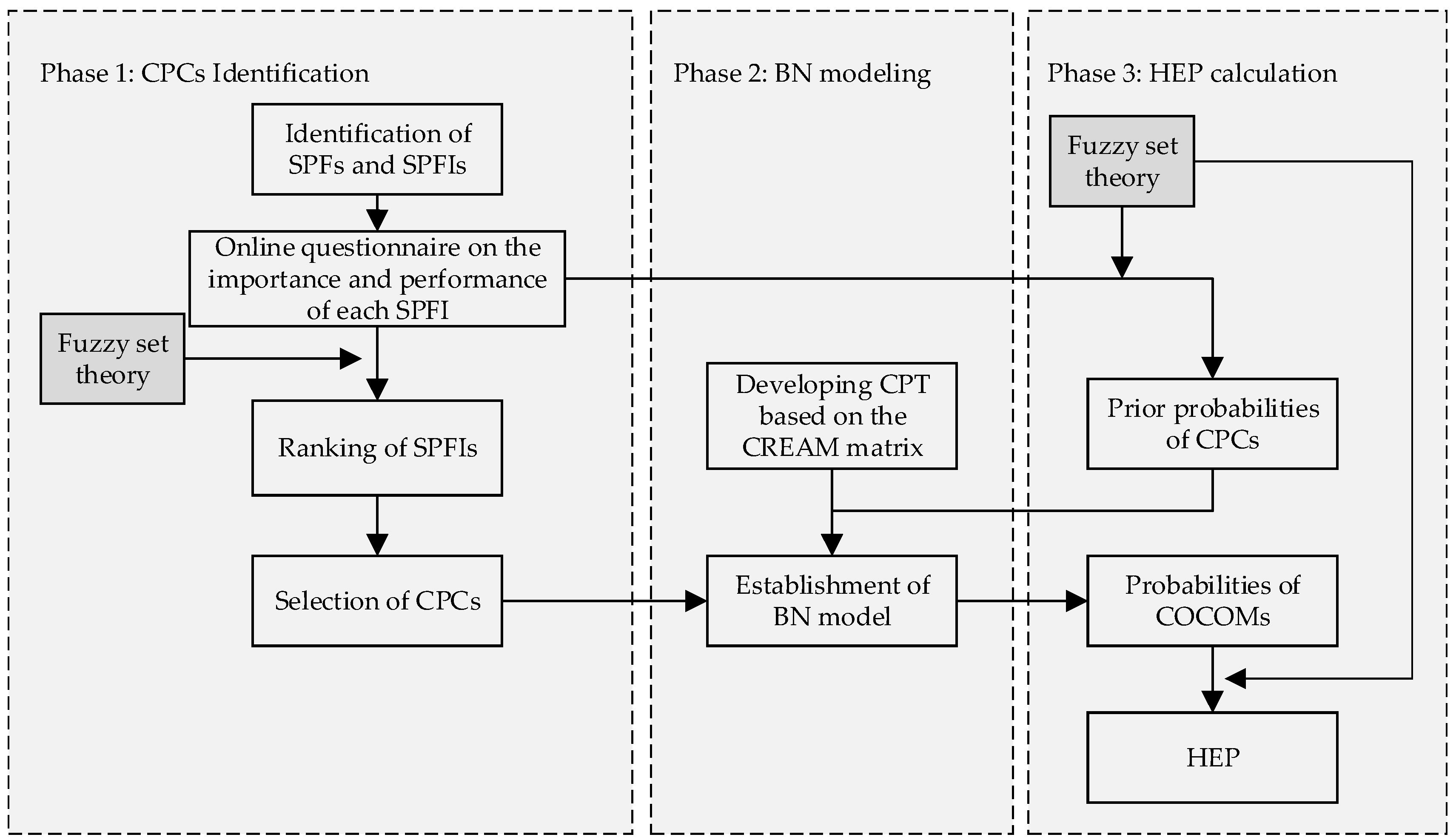
2. Methodology
This section provides a framework of the proposed method for HEP assessment shown in Figure 2. It can be implemented to the project in three phases demonstrated below.
2.1. Identification of the Common Performance Condition Indicators (CPCs)
The original CREAM was developed for the nuclear industry, CPCs are therefore particularly designed for nuclear plants related operations. This paper attempts to use the basic principle of CREAM in the LNG bunkering industry; thus, purpose-defined CPCs should be identified according to the characteristics of LNG bunkering operations. CPCs are environmental factors, personal, or directed to activities that have the potential to affect human performance positively, neutrally or negatively; therefore, identifying CPCs is a key step in this study.
2.1.1. Identifications of the Safety Philosophical Factors (SPFs) and the Safety Philosophical Factors’ Indicators (SPFIs)
Safety philosophical factors (SPFs) influence not only how humans perceive their actions, but also humans’ response to the events. In this study, the safety documents from three LNG bunkering service companies were reviewed. Five safety philosophical factors (SPFs), namely, safety culture (SC), safety management (SM), safety process (SP), safety training (ST), and safety awareness (SA) were identified to encapsulate the human safety performance. Totally, 23 measurable safety philosophical factors’ indicators (SPFIs) are identified. Some environmental factors that might impact safety performance are implicit in some SPFIs, for example, SM5, SP2, and SP4. Table 3 presents five SPFs and the identified 23 SPFIs. The collection of SPFIs is used as a pool for CPCs screening. According to the CREAM model, nine SPFIs are selected to represent nine CPCs. To this end, 23 SPFIs are ranked, and the top nine SPFIs are designated as CPCs. The ranking is based on an online questionnaire survey data and the FST.
2.1.2. Online Questionnaire on Importance and Performance of the Safety Philosophical Factors’ Indicators (SPFIs)
A qualitative online questionnaire survey method is conducted to obtain information for measuring the SPFIs. A survey questionnaire form is developed and made available to potential experts online with the Microsoft Forms tool. The specially designed closed-ended structured questionnaire includes the following sections:
Section A: Demographics information about the experts.
Section B: Likert scale multiple-choice questions.
The gathered demographic information about the experts includes four variables, namely, job affiliation, job professional position, service time, and education level. The information is used to calculate the weights of experts in evaluating the fuzzy numbers (FNs) of SPFIs. In Section B, a seven-point Likert type scale is employed anchored with “Negligible (Very low)” and “Extremely important (Very high)” for the importance of an SPFI to human safety performance. A three-point Likert type scale is also employed with “Adequate”, “Acceptable”, and “Inadequate” options for the current performance of an SPFI which is applied in phase 3, shown in Figure 2, to evaluate the prior probabilities of CPCs. Figure 3 shows an example of questions for the SPFI of “SC1”.
2.1.3. Converting the Experts’ Qualitative Linguistic Expression into Fuzzy Numbers (FNs)
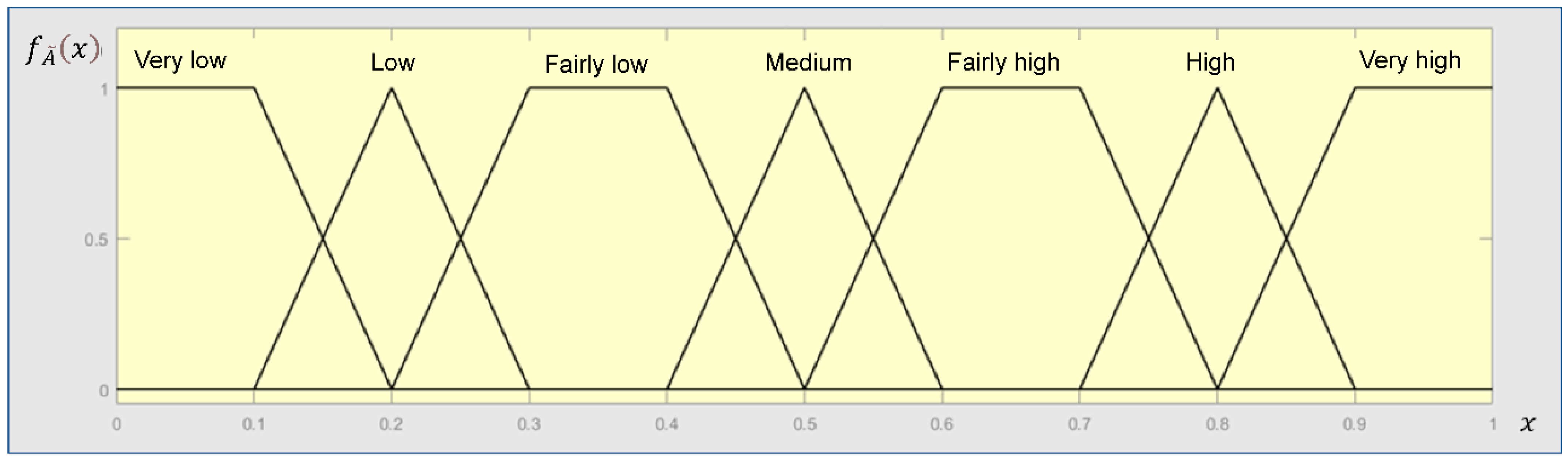
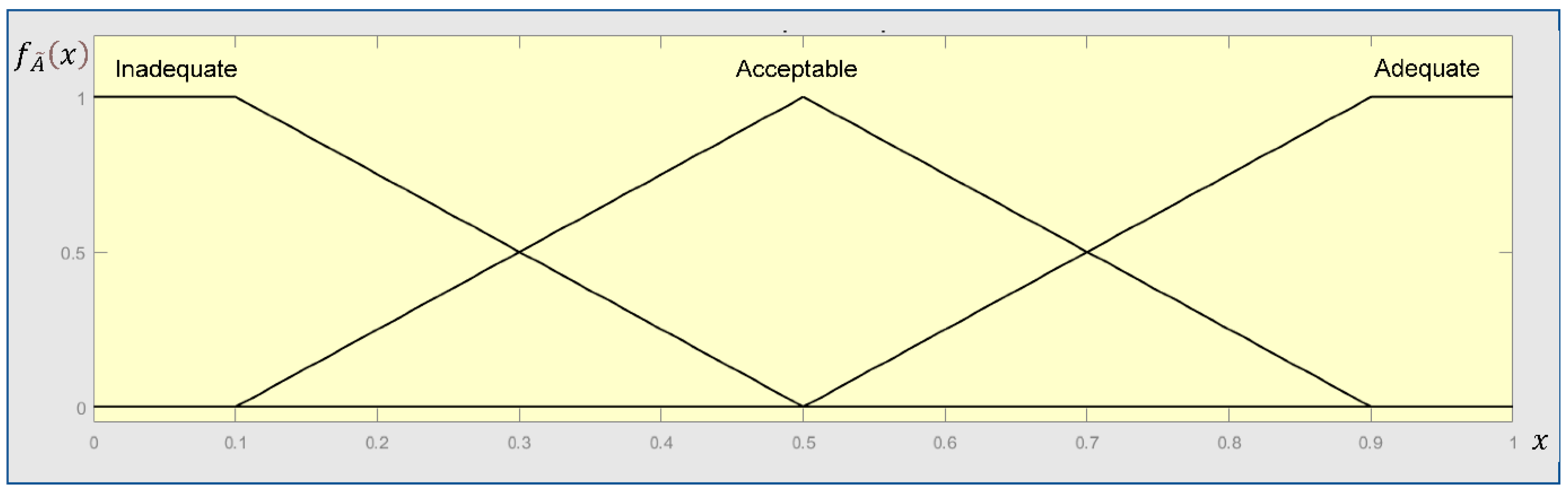
In this step, the qualitative linguistic expressions from experts on the importance of SPFIs are converted into FNs based on the FST [58]. A fuzzy number is a convex fuzzy set, characterized by a given interval of real numbers, each with a grade of membership between 0 and 1. Its membership function is piecewise continuous and satisfies the following conditions:
Let a fuzzy set
A
˜
=
[
a
,
b
,
c
,
d
]
, then the membership function of the fuzzy set,
f
A
˜
(
x
)
,
can be expressed as:
- (1)
-
f
A
˜(
x
)=
0
outside some interval
[
a
,
b]
;
- (2)
-
f
A
˜(
x
)is non-decreasing (monotonic increasing) on
[
a
,
b]
; and non-increasing (monotonic decreasing) on
[
c
,
d]
;
- (3)
-
f
A
˜(
x
)=
1for each
x
∈[
b
,
c]
.
In this study, the trapezoidal fuzzy numbers whose membership functions are defined as Equation (1) are used.
(
x
)
=
{
f
A
˜
L
(
x
)
=
x
−
a
b
−
a
,
a
≤
x
≤
b
1
,
b
≤
x
≤
c
f
A
˜
R
(
x
)
=
d
−
x
d
−
c
,
c
≤
x
≤
d
0
,
o
t
h
e
r
w
i
s
e
(1)
where
f
A
˜
(
x
)
is the membership function of the fuzzy set
A
˜
=
[
a
,
b
,
c
,
d
]
. The
f
A
˜
L
(
x
)
represents the left side of the membership function, and
f
A
˜
R
(
x
)
represents the right side of the membership function.
The conversion scale, which includes seven qualitative linguistic terms, is adopted for estimating the FNs of SPFIs as shown in Figure 4 [59]. This maps an expert’s judgment to a fuzzy set. For example, if an expert’s linguistic expression on the importance of an SPFI is “Medium”, then the fuzzy set is [0.4,0.5,0.5,0.6].
The next step is to aggregate multiple judgements on an SPFI from multiple experts into a single judgement.
2.1.4. Aggregating the Fuzzy Sets into an Integrated Fuzzy Set
Various methods are available in the literature to aggregate experts’ opinions including linear opinion pool [60], max–min Delphi [61], sum-product [62], max–product [63], etc. Among the aforementioned methods, the linear opinion pool is adopted in this study since it is an effective and easy approach [64]. Based on the linear opinion pool method, the aggregated integrated fuzzy set (IFS) can be expressed by Equation (2).
I
F
S
j
=
∑
i
=
1
n
(
W
i
×
E
i
j
)
,
j
=
1
,
2
,
3
…
,
m
(2)
where
I
F
S
j
is the IFS of
j
th SPFI.
W
i
is the weight given to the
i
th expert, and
∑
i
=
1
n
w
i
=
1
;
E
i
j
is the linguistic expression corresponding to fuzzy set obtained from
i
th expert about
j
th SPFI. For example, if the 1st expert’s linguistic expression on the 1st SPFI is “Medium” (see Figure 4), then
E
11
is [0.4, 0.5, 0.5, 0.6];
n
is the total number of experts while
m
is the total number of SPFs.
Each expert’s professional background is different, so his/her judgment contributes differently to the results. This article uses weights for considering the contribution of each expert to the results. The weighting criterion of experts is designed and presented in Table 4. The weights of experts are calculated using the Equation (3) [65].
W
i
=
W
S
i
∑
i
=
1
n
W
S
i
(3)
where
W
S
i
is the weight score of the
i
th expert,
W
S
i
=
P
P
S
i
+
S
T
S
i
+
E
L
S
i
,
P
P
S
i
,
S
T
S
i
, and
E
L
S
i
represent the professional position score, the service time score, and the education level score of the
i
th expert, respectively.
The next step is to convert the aggregated IFS for each SPFI into a fuzzy number (FN), i.e., defuzzification.
2.1.5. Defuzzification
There are many different methods of defuzzification available, including basic defuzzification distributions, bisector of area, center of area, etc. [66,67]. The center of area method which is the most widely used method is adopted in this study. Let a fuzzy set
A
˜
=
[
a
,
b
,
c
,
d
]
, then defuzzification of the trapezoidal fuzzy number
A
˜
is given by Equation (4) [68],
x
¯
0
(
A
˜
)
is obtained as a FN. Equation (5) which is for a single trapezoidal fuzzy number can be derived by Equation (4). According to the ranking of FNs of SPFIs, the top nine SPFIs can be designated as CPCs.
x
¯
0
(
A
˜
)
=
∫
−
∞
+
∞
x
f
A
˜
(
x
)
d
x
∫
−
∞
+
∞
f
A
˜
(
x
)
d
x
=
∫
a
b
x
f
A
˜
L
(
x
)
d
x
+
∫
b
c
x
d
x
+
∫
c
d
x
f
A
˜
R
(
x
)
d
x
∫
a
b
f
A
˜
L
(
x
)
d
x
+
∫
b
c
d
x
+
∫
c
d
f
A
˜
R
(
x
)
d
x
(4)
x
¯
0
(
A
˜
)
=
1
3
×
(
a
+
b
+
c
+
d
−
c
d
−
a
b
c
+
d
−
a
−
b
)
(5)
2.2. BN Modelling
In a BN, the nodes represent variables, arcs represent causal relationships between the linked variables, and their conditional dependencies are represented through the conditional probability tables (CPTs) assigned to the nodes. The joint probability distribution
P
(
U
)
of variables
U
=
{
A
1
,
…
,
A
n
}
included in the BN is expressed by Equation (6).
P
(
U
)
=
∏
i
=
1
n
P
(
A
i
|
P
a
(
A
i
)
)
(6)
where
P
a
(
A
i
)
is the parent set of
A
i
[69].
In the BN, the Bayes theorem is used to update the prior probabilities for events given evidence, thus yielding the posterior probability which is expressed by Equation (7):
P
(
U
|
E
)
=
P
(
U
,
E
)
/
P
(
E
)
(7)
where
P
(
U
|
E
)
represents the posterior probability of the
U
given the evidence
E
;
P
(
U
,
E
)
means the probability of
U
and
E
happening together;
P
(
E
)
represent the occurrence probability of evidence
E
.
The software, Netica, is used to build BN. According to the CREAM model, a BN model is built as shown in Figure 5. Each CPC is represented by a node having three states, namely, 1 (Adequate), 0 (Acceptable), and –1 (Inadequate). A causal arc is directed from each CPC node to the COCOM node which has four states, namely, “Strategic”, “Tactical”, “Opportunistic”, and “Scrambled”. It is assumed that CPCs are independent; therefore, there are no causal arcs among CPC nodes.
Building CPTs is core for a BN. Each CPC has three states, and there are nine CPCs; thus, there are 39=19,683 rows in the CPT of the COCOM node. In practice, it is a challenge to input a CPT with so many rows in the software; therefore, in order to simplify BN, some researchers have attempted to group CPCs into a few intermediate nodes based on some assumptions [49,51,53,56,57], or developed some assumed rules for the CPT of COCOMs node [52,54]. It is argued that these practices increased the uncertainty of the model, because to a certain extent, the formulation of these assumptions and rules is based on the subjective judgments of the researchers, thereby weakening the outcomes of these studies. In this study, the BN model is fully complied with the CREAM matrix without using intermediate nodes or assumed rules. A program based on the Microsoft EXCEL platform is compiled to calculate the CPT of the COCOM node based on Figure 6. The obtained CPT data can then be directly imported into the Netica software. The original CREAM matrix, in which y-axis has 8 values (0–7) is extended to 10, as each CPC has the states of “1”,”0”, and “−1”, as shown in Figure 6. Table 5 shows a part of the CPT, and the original code for the calculation of CPT is attached in Table S1 in the Supplemental Material available online.
2.3. Human Error Probability (HEP) Calculation
This section presents the calculations of prior probabilities of CPCs and HEP.
2.3.1. Prior Probabilities of the Common Performance Condition Indicators (CPCs)
The prior probabilities of CPCs are necessary conditions for solving the probabilities of COCOM node’s states in the BN. The qualitative judgements of experts for the current performance of each CPC can be converted into the prior probability of each CPC through using the FST. As mentioned in Section 2.1.2, a three-point Likert type scale is used to express the current performance of CPCs; therefore, the conversion scale, which includes three qualitative linguistic terms, is adopted for quantifying the prior probability of each CPC as shown in Figure 7. In this model, “Inadequate” represents the negative effect (-1); “Acceptable” represents the no significant effect (0); “Adequate” represents the positive effect (1). The trapezoidal fuzzy numbers’ membership functions are expressed by Equation (8)–(10).
f
A
˜
(
x
)
I
n
a
d
e
q
u
a
t
e
=
{
f
A
˜
L
(
x
)
=
1
,
0
≤
x
≤
0.1
f
A
˜
R
(
x
)
=
0.5
−
x
0.4
,
0.1
≤
x
≤
0.5
0
,
o
t
h
e
r
w
i
s
e
(8)
f
A
˜
(
x
)
A
c
c
e
p
t
a
b
l
e
=
{
f
A
˜
L
(
x
)
=
x
−
0.1
0.4
,
0.1
≤
x
≤
0.5
f
A
˜
R
(
x
)
=
0.9
−
x
0.4
,
0.5
≤
x
≤
0.9
0
,
o
t
h
e
r
w
i
s
e
(9)
f
A
˜
(
x
)
A
d
e
q
u
a
t
e
=
{
f
A
˜
L
(
x
)
=
x
−
0.5
0.4
,
0.5
≤
x
≤
0.9
f
A
˜
R
(
x
)
=
1
,
0.9
≤
x
≤
1
0
,
o
t
h
e
r
w
i
s
e
(10)
The aggregation and defuzzification methods used in this step are the same as what was described in Section 2.1.4 and Section 2.1.5. The FNs of CPCs are designated as the prior probabilities of CPCs. Once the prior probabilities of CPCs are assigned to the associated nodes, the probabilities of COCOM node’s states can be obtained through running the BN model.
2.3.2. Defuzzification of the Fuzzy Sets for COCOMs and HEP Calculation
The fuzzy sets for COCOM node’s states according to Table 2 are shown in Figure 8. The trapezoidal fuzzy numbers’ membership functions are expressed by Equation (11)–(14). Equation (4) is then used to perform the defuzzification process of the trapezoidal fuzzy set
A
˜
, where
f
A
˜
(
x
)
=
f
A
˜
(
x
)
S
t
r
a
t
e
g
i
c
+
f
A
˜
(
x
)
T
a
c
t
i
c
a
l
+
f
A
˜
(
x
)
O
p
p
o
r
t
u
n
i
s
t
i
c
+
f
A
˜
(
x
)
S
c
r
a
m
b
l
e
d
.
Subsequently, HEP can be obtained using Equation (15).
f
A
˜
(
x
)
S
t
r
a
t
e
g
i
c
=
{
f
A
˜
L
(
x
)
=
x
+
5.3
1.65
,
−
5.3
≤
x
≤
−
3.65
f
A
˜
R
(
x
)
=
−
2
−
x
1.65
,
−
3.65
≤
x
≤
−
2
0
,
o
t
h
e
r
w
i
s
e
(11)
f
A
˜
(
x
)
T
a
c
t
i
c
a
l
=
{
f
A
˜
L
(
x
)
=
x
+
3
1
,
−
3
≤
x
≤
−
2
f
A
˜
R
(
x
)
=
−
1
−
x
1
,
−
2
≤
x
≤
−
1
0
,
o
t
h
e
r
w
i
s
e
(12)
f
A
˜
(
x
)
O
p
p
o
r
t
u
n
i
s
t
i
c
=
{
f
A
˜
L
(
x
)
=
x
+
2
0.85
,
−
2
≤
x
≤
−
1.15
f
A
˜
R
(
x
)
=
−
0.3
−
x
0.85
,
−
1.15
≤
x
≤
−
0.3
0
,
o
t
h
e
r
w
i
s
e
(13)
f
A
˜
(
x
)
S
c
r
a
m
b
l
e
d
=
{
f
A
˜
L
(
x
)
=
x
+
1
0.5
,
−
1
≤
x
≤
−
0.5
f
A
˜
R
(
x
)
=
−
x
0.5
,
−
0.5
≤
x
≤
0
0
,
o
t
h
e
r
w
i
s
e
(14)
H
E
P
=
10
x
¯
0
(
A
˜
)
(15)
3. Data Acquisition and Analysis
Data for ranking the SPFIs and analyzing the fuzzy probabilities of CPCs were acquired through an online questionnaire survey. The criterion for the selection of experts was set to have LNG bunkering related knowledge or experience. The ethics application was approved by the University of Tasmania’s Social Sciences Human Research Ethics Committee on 9 February 2021 (Project ID:23903). The online survey was distributed in China, where authors had an extended network of maritime related expertise, and a total of 137 responses were received (14 were from shipping companies; 33 from energy companies; 6 from maritime safety administrations; 6 from port authorities; 20 from classification societies; 20 from ship design companies; 8 from shipyards; 13 from equipment manufacturers; 11 from academia; 6 from other backgrounds). The respondents are 78% Chinese and 22% international companies or institutes. It is believed that acquired data from the diversity of these affiliations ensures better reflection of the actual situation of the LNG bunkering industry.
3.1. Ranking of the Safety Philosophical Factors’ Indicators (SPFIs) and Selection of the Common Performance Condition Indicators (CPCs)
Experts’ weights are obtained by Equation (3) as shown in Table 6. Table 7 presents the selected raw data obtained on the importance of the safety for each SPFI from 137 experts. The FNs of SPFIs are calculated using Equation (2), Equation (3), and Equation (5). Table 8 shows the ranking of top nine SPFIs according to the obtained FNs. The top nine SPFIs are sequentially defined as CPC1 to CPC9.
See Table S2 in the Supplemental Material available online.
See Table S3 in the Supplemental Material available online.
3.2. Prior Probabilities of Common Performance Conditions (CPCs)
The prior probabilities of CPCs are obtained as shown in Table 9 using Equations (2), (3), (5), (8)–(10). The obtained data are then assigned to CPC nodes in the BN model.
See Table S4 in the Supplementary Materials available online.
4. Results and Discussion
This section presents the results and discussion on the probabilities of COCOMs and HEP for five hypothetical cases.
4.1. Results
The probabilities of obtained COCOM node’s states are shown in Figure 9 and Table 10. Figure 10 presents the degrees of fuzzy membership functions of COCOMs, and Table 10 presents the calculation of HEP. The FN is calculated using Equation (4), and HEP = 0.009841 is obtained using Equation (15). This HEP value represents the prior HEP during LNG bunkering operations in the current LNG bunkering industry. These data can also be used in a QRA model. For a specific project, if on-site CPCs are re-evaluated and the posterior probabilities are obtained, then the risk analyst can still use the proposed BN model to update the data in obtaining the posterior HEP.
4.2. Discussion
This sub-section uses five hypothetical cases to discuss the dynamic characteristics of the proposed model. In each case, a specific homogenized probability of CPCs,
P
h
, is assumed. The assumed conditions are Case 1 (
P
h
=
0
), Case 2 (
P
h
=
0.2
), Case 3 (
P
h
=
0.5
), Case 4 (
P
h
=
0.8
), and Case 5 (
P
h
=
1
). These cases reflect the changes of on-site CPCs from low levels to high levels.
Table 11 presents obtained probabilities of CPCs using Equation (8)–(10) for Case 1–5. Gradually increasing the
P
h
value from 0 to 1 means that the safety performance of each CPC is improved gradually. For example, the Case 2 represents the probabilities of “adequate”, “acceptable”, and “inadequate” to be 0, 0.25, and 0.75, respectively, for each CPC. However, the Case 4 represents the probabilities of “adequate”, “acceptable”, and “inadequate” to be 0.75, 0.25, and 0, respectively, for each CPC. From Case 2 to Case 4, the probability of the safety performance of each CPC being “adequate” increases from 0 to 0.75, while the probability of the safety performance being “inadequate” decreases from 0.75 to 0. Table 12 presents the probabilities of COCOMs and HEPs for five cases. Figure 11 shows the relationship between HEP and homogenized probability of CPCs.
It is apparent that as the
P
h
value increases, the value of HEP decreases. When the
P
h
is less than 0.5, the HEP value decreases relatively quickly, and when the
P
h
is greater than 0.5, the HEP value decreases relatively slowly. This trend is related to the intervals of the four states of COCOM, from “Scrambled” to “Strategic”, and the logarithmic interval that each state falls into is gradually widen as shown in Figure 8.
The prior probabilities of CPCs can be updated to obtain the posterior probabilities in the BN model according to the actual safety situation of the LNG bunkering site based on periodic evaluation of SPFIs, such as quarterly or annually. Therefore, the proposed model can be used to conduct a dynamic evaluation of HEP. In fact, most of the current techniques are unable to capture the dynamics of HEP. Dynamic HEP can be used as the input data in the dynamic QRA model so that more accurate dynamic risk profiles of LNG bunkering can be achieved.
5. Conclusions
In this research, the original CREAM model was modified to be adapted to HEP assessment in LNG bunkering operations. Nine CPCs were identified from 23 SPFIs for LNG bunkering operations based on the ranking of FNs as a way of capturing the essential aspects of the situation and the conditions for human behaviors. The BN was employed in the modified CREAM model to consider the uncertainty of a specific task falling into different COCOMs. The CPT for the COCOM node in the BN was coded based on extended COCOMs matrix rather than using intermediate nodes or other assumed rules to reduce the dimension of CPT which decreases the accuracy of the results. Furthermore, sufficient data reflecting the current safety status of the LNG bunkering industry in terms of human factors ensures that the prior probabilities of CPCs are calculated accurately.
This study has the following main findings:
-
The prior HEP of 0.009841 was obtained which represents the current human safety level in the LNG bunkering industry. The analysis process showed the fuzzy BN-CREAM model is efficient in performing the HEP assessment.
-
Five hypothetical case studies demonstrated that an increase in the homogenized probability of CPCs leads to an increase in the human safety level. It can be seen that the CPCs provide insights that may improve the human safety level in an LNG bunkering project.
-
The proposed model can be used to dynamically grasp the changes of HEP. If the reassessments identify the changes in the on-site CPCs, then these changes can be converted into quantitative data, where the input into the model obtains the latest HEP. Furthermore, this dynamic HEP assessment can be an input to a dynamic QRA model to obtain more accurate risk profiles.
To some extent, this study improved the original CREAM from a second-generation HRA to a third generation HRA method which can use computer-aided simulation techniques to evaluate HEPs.
The findings of this research fill a gap in the literature regarding the lack of quantitative HEP data for LNG bunkering operations. However, the generalizability of these results is subject to a limitation. The obtained HEP was based on the current human safety level in the LNG bunkering industry, and real-time variations in human safety levels during LNG bunkering operations may change the result of this study. For example, a large-scale LNG bunkering might take more than 20 h, some CPCs’ safety performances might change during such a time-consuming bunkering operation which generates real-time HEPs. Therefore, further research could be undertaken to explore the methodology for real-time prediction of HEP changes during LNG bunkering based on real-time data variations on site.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/jmse10030333/s1, Table S1: The conditional probability table of the BN model, Table S2: The weights of the experts, Table S3: The experts’ expression on importance of SPFIs, Table S4: The experts’ expression on performance of SPFIs.
Author Contributions
Conceptualization, H.F. and H.E.; methodology, H.F.; validation, H.F., H.E., and S.G.J.; formal analysis, H.F.; resources, H.F. and H.E.; data curation, H.F. and H.E.; writing—original draft preparation, H.F.; writing—review and editing, H.E. and S.G.J.; supervision, H.E. and S.G.J.; project administration, H.F. and H.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to express their gratitude to the experts who participated in the online questionnaire survey.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Ac | Acceptable |
| Ad | Adequate |
| BN | Bayesian network |
| COCOM | Contextual control mode |
| CPC | Common performance condition |
| CPT | Conditional probability table |
| CREAM | The cognitive reliability and error analysis method |
| DN | Defuzzification number |
| E | Engineer |
| ELS | Education level score |
| ESD | Emergency shutdown |
| FN | Fuzzy number |
| FST | Fuzzy set theory |
| HEP | Human error probability |
| HRA | Human reliability assessment |
| IFS | Integrated fuzzy set |
| In | Inadequate |
| JMA | Junior Manager |
| LNG | Liquified natural gas |
| Opp | Opportunistic |
| PPS | Professional position score |
| QRA | Quantitative risk assessment |
| SA | Safety awareness |
| SC | Safety culture |
| Scr | Scrambled |
| SM | Safety management |
| SMA | Senior Manager |
| SP | Safety process |
| SPF | Safety philosophical factor |
| SPFI | Safety philosophical factor’s measurable indicator |
| ST | Safety training |
| Str | Strategic |
| STS | Service time score |
| T | Technician |
| Tac | Tactical |
| W | Worker |
| Symbols | |
|
A |
Fuzzy set |
|
E i |
Linguistic expression corresponding fuzzy set obtained from expert i about indicator j |
|
E S |
Education level score of the i th expert |
|
I S |
Aggregated integrated fuzzy set (IFS) of the
j th SPFI |
|
f A ( |
Membership function of the fuzzy set
A |
|
f A L ( |
Left side of the membership function |
|
f A R ( |
Right side of the membership function |
|
P ( |
Occurrence probability of evidence E |
|
P |
Homogenized probability of CPCs |
|
P ( |
Joint probability distribution of variables
U { A , A } |
|
P ( U ) |
Posterior probability of the variables ( U ) given the evidence ( |
|
P ( U ) |
Probability of U and E happening together |
|
P ( A ) |
Parent set of
A |
|
P S |
Professional position score of the i th expert |
|
S S |
Service time score of the i th expert |
|
W |
Weight given to the i th expert |
|
W S |
Weight score of the i th expert |
|
x 0 ( A ) |
Defuzzification number of the fuzzy set
A |
References
- SGMF. LNG Fueled Ships Database; Society for Gas as a Marine Fuel: London, UK, 2021. [Google Scholar]
- Schuller, O.; Kupferschmid, S.; Hengstler, J.; Whitehouse, S. 2nd Life Cycle GHG Emission Study on the Use of LNG as Marine Fuel; Sphera: Leinfelden-Echterdingen, Germany, 2021. [Google Scholar]
- Park, N.K.; Park, S.K. A study on the estimation of facilities in LNG bunkering terminal by Simulation-Busan port case. J. Mar. Sci. Eng. 2019, 7, 354. [Google Scholar] [CrossRef][Green Version]
- MSC 95/INF.17 Information on Incidents During Bunkering of LNG; IMO: London, UK.
- Fan, H.; Enshaei, H.; Gamini Jayasinghe, S. Safety philosophy and risk analysis methodology for LNG bunkering simultaneous operations (SIMOPs): A literature review. Saf. Sci. 2021, 136, 105150. [Google Scholar] [CrossRef]
- Sánchez-Beaskoetxea, J.; Basterretxea-Iribar, I.; Sotés, I.; Machado, M.d.l.M.M. Human error in marine accidents: Is the crew normally to blame? Marit. Transp. Res. 2021, 2, 100016. [Google Scholar] [CrossRef]
- Islam, R.; Yu, H.; Abbassi, R.; Garaniya, V.; Khan, F. Development of a monograph for human error likelihood assessment in marine operations. Saf. Sci. 2017, 91, 33–39. [Google Scholar] [CrossRef]
- Bai, Y.; Jin, W.-L. Chapter 43—Human Reliability Assessment. In Marine Structural Design, 2nd ed.; Bai, Y., Jin, W.-L., Eds.; Butterworth-Heinemann: Oxford, UK, 2016; pp. 793–802. [Google Scholar]
- Rausand, M. Risk Assessment: Theory, Methods, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Arnet, N.M.L. Establish Probabilistic Safety Distances for LNG Bunkering Operations. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Jeong, B.; Lee, B.S.; Zhou, P.; Ha, S.M. Determination of safety exclusion zone for LNG bunkering at fuel-supplying point. Ocean Eng. 2018, 152, 113–129. [Google Scholar] [CrossRef][Green Version]
- Fan, H.; Zhang, H.; Xu, J. Assessment of the hazard distance of pool fire for LNG bunkering pontoon. Ship Build. China 2013, 54, 186–195. [Google Scholar]
- Park, S.; Jeong, B.; Yoon, J.Y.; Paik, J.K. A study on factors affecting the safety zone in ship-to-ship LNG bunkering. Ships Offshore Struct. 2018, 13, 312–321. [Google Scholar] [CrossRef][Green Version]
- Park, S.I.; Kim, S.K.; Paik, J.K. Safety-zone layout design for a floating LNG-Fueled power plant in bunkering process. Ocean Eng. 2019, 196, 106774. [Google Scholar] [CrossRef]
- Gerbec, M.; Vidmar, P.; Pio, G.; Salzano, E. A comparison of dispersion models for the LNG dispersion at port of Koper, Slovenia. Saf. Sci. 2021, 144, 105467. [Google Scholar] [CrossRef]
- Park, S.-I.; Paik, J.K. A hybrid method for the safety zone design in truck-to-ship LNG bunkering. Ocean Eng. 2021, 243, 110200. [Google Scholar] [CrossRef]
- Lim, B.H.; Ng, E.Y. Model for Cryogenic Flashing LNG Leak. Appl. Sci. 2021, 11, 9312. [Google Scholar] [CrossRef]
- Fan, H.; Cheng, K.; Wu, S. CFD Based Simulation of LNG Release during Bunkering and Cargo Loading/Unloading Simultaneous Operations of a Containership. J. Shipp. Ocean Eng. 2017, 2017, 51–58. [Google Scholar] [CrossRef]
- Jeong, B.; Park, S.; Ha, S.; Lee, J.U. Safety evaluation on LNG bunkering: To enhance practical establishment of safety zone. Ocean Eng. 2020, 216, 107804. [Google Scholar] [CrossRef]
- Jeong, B.; Lee, B.S.; Zhou, P.; Ha, S.M. Evaluation of safety exclusion zone for LNG bunkering station on LNG-fuelled ships. J. Mar. Eng. Technol. 2017, 16, 121–144. [Google Scholar] [CrossRef][Green Version]
- Halford, A.; Robinson, C.; Haynes, D. The safety assessment of LNG marine bunkering. In Proceedings of the Institution of Chemical Engineers Symposium Series, Birmingham, UK, 22–24 May 2019. [Google Scholar]
- Wu, S.; Luo, X.; Fan, H.; Zhang, R. Quantitative risk analysis on refuelling of LNG-fuelled ships with tank trucks. Nat. Gas Ind. 2015, 35, 111–116. [Google Scholar] [CrossRef]
- Iannaccone, T.; Landucci, G.; Scarponi, G.E.; Bonvicini, S.; Cozzani, V. Inherent safety assessment of alternative technologies for LNG ships bunkering. Ocean Eng. 2019, 185, 100–114. [Google Scholar] [CrossRef]
- Iannaccone, T.; Cozzani, V.; Jeong, B.; Zhou, P. Safety analysis of liquefied natural gas bunkering and simultaneous port operations for passenger ships. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Online, 3–7 August 2020. [Google Scholar]
- Wu, J.; Bai, Y.; Zhao, H.; Hu, X.; Cozzani, V. A quantitative LNG risk assessment model based on integrated Bayesian-Catastrophe-EPE method. Saf. Sci. 2021, 137, 105184. [Google Scholar] [CrossRef]
- Vairo, T.; Gualeni, P.; Reverberi, A.P.; Fabiano, B. Resilience Dynamic Assessment Based on Precursor Events: Application to Ship LNG Bunkering Operations. Sustainability 2021, 13, 6836. [Google Scholar] [CrossRef]
- Aneziris, O.; Gerbec, M.; Koromila, I.; Nivolianitou, Z.; Pilo, F.; Salzano, E. Risk assessment for LNG storage and bunkering at ports. In Proceedings of the 30th European Safety and Reliability Conference, ESREL 2020 and 15th Probabilistic Safety Assessment and Management Conference, Venice, Italy, 1–5 November 2020; pp. 597–604. [Google Scholar]
- Kim, I.; Kim, H.; Chang, D.; Jung, D.-H.; Sung, H.G.; Park, S.-K.; Choi, B.C. Emergency evacuation simulation of a floating LNG bunkering terminal considering the interaction between evacuees and CFD data. Saf. Sci. 2021, 140, 105297. [Google Scholar] [CrossRef]
- Stokes, J.; Moon, G.; Bend, R.; Owen, D.; Wingate, K.; Waryas, E. Understanding the human element in LNG bunkering. In Marine Technology and Standards; American Society of Mechanical Engineers: New York, NY, USA, 2018; pp. 105–111. [Google Scholar]
- Uijt de Haag, P.A.M.; Ale, B.J.M.; Post, J.G. T10-1—The ‘Purple Book’: Guideline for Quantitative Risk Assessment in the Netherlands. In Loss Prevention and Safety Promotion in the Process Industries; Pasman, H.J., Fredholm, O., Jacobsson, A., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2001; pp. 1429–1438. [Google Scholar]
- OGP. Risk Assessment Data Directory: Process Release Frequencies; International Association of Oil and Gas Producers, International Association of Oil and Gas Producers: London, UK, 2010. [Google Scholar]
- SINTEF. OREDA Offshore Reliability Data Handbook, 4th ed.; OREDA Participants: Trondheim, Norway, 2002. [Google Scholar]
- HSE. Failure Rate and Event Data for Use Within Risk Assessments; 2012. Available online: https://www.hse.gov.uk/landuseplanning/failure-rates.pdf (accessed on 24 January 2022).
- Risk Assessment Data Directory: Human Factors in QRA; OGP: London, UK, 2010.
- Swain, A.D.; Guttmann, H.E. Handbook of Human Reliability Analysis with Emphasis on Nuclear Power Plant; Sandia National Laboratories: Albuquerque, NM, USA, 1983; 87185 US. [Google Scholar]
- Bell, J.; Holroyd, J. Review of Human Reliability Assessment Methods; Health & Safety Laboratory: Buxton, UK, 2009. [Google Scholar]
- Wu, B.; Yip, T.L.; Yan, X.; Guedes Soares, C. Review of techniques and challenges of human and organizational factors analysis in maritime transportation. Reliab. Eng. Syst. Saf. 2022, 219, 108249. [Google Scholar] [CrossRef]
- Pasquale, V.D.; Iannone, R.; Miranda, S.; Riemma, S. An Overview of Human Reliability Analysis Techniques in Manufacturing Operations. In Operations Management; Schiraldi, M.M., Ed.; IntechOpen: London, UK, 2013. [Google Scholar]
- Kirwan, B. The validation of three human reliability quantification techniques THERP, HEART and JHEDI: Part 1—Technique descriptions and validation issues. Appl. Ergon. 1996, 27, 359–373. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Zheng, W.X.; Kang, R. Human reliability test and identification of HCR model basic parameters for single factor “meta-operation”. Chem. Eng. Trans. 2013, 33, 421–426. [Google Scholar] [CrossRef]
- Hollnagel, E. Chapter 6—CREAM—A Second Generation HRA Method. In Cognitive Reliability and Error Analysis Method (CREAM); Hollnagel, E., Ed.; Elsevier Science Ltd.: Oxford, UK, 1998; pp. 151–190. [Google Scholar]
- Blackman, H.S.; Gertman, D.I.; Boring, R.L. Human error quantification using performance shaping factors in the SPAR-H method. In Proceedings of the Human Factors and Ergonomics Society; 2008; pp. 1733–1737. Available online: https://journals.sagepub.com/doi/abs/10.1177/154193120805202109 (accessed on 24 January 2022).
- Thompson, C.M.; Cooper, S.E.; Kolaczkowski, A.M.; Bley, D.C.; Forester, J.A.; Wreathall, J. Application of ATHEANA: A technique for human error analysis. In Proceedings of the IEEE Conference on Human Factors and Power Plants, Orlando, FL, USA, 8–13 June 1997; pp. 9.13–19.17. [Google Scholar]
- Chang, Y.H.J.; Mosleh, A. Cognitive modeling and dynamic probabilistic simulation of operating crew response to complex system accidents: Part 1: Overview of the IDAC Model. Reliab. Eng. Syst. Saf. 2007, 92, 997–1013. [Google Scholar] [CrossRef]
- Ekanem, N.J.; Mosleh, A.; Shen, S.-H. Phoenix—A model-based Human Reliability Analysis methodology: Qualitative Analysis Procedure. Reliab. Eng. Syst. Saf. 2016, 145, 301–315. [Google Scholar] [CrossRef][Green Version]
- Alvarenga, M.A.B.; Frutuoso e Melo, P.F. A review of the cognitive basis for human reliability analysis. Prog. Nucl. Energy 2019, 117, 103050. [Google Scholar] [CrossRef]
- Parhizkar, T.; Utne, I.B.; Vinnem, J.-E. Human Factor Analysis and Quantification. In Online Probabilistic Risk Assessment of Complex Marine Systems: Principles, Modelling and Applications; Springer International Publishing: Cham, Switzerland, 2022; pp. 75–102. [Google Scholar]
- Akyuz, E.; Celik, M. Application of CREAM human reliability model to cargo loading process of LPG tankers. J. Loss Prev. Process. Ind. 2015, 34, 39–48. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, K.; Wang, R.; Xu, X. Human reliability analysis of hightemperature molten metal operation based on fuzzy CREAM and Bayesian network. PLoS ONE 2021, 16, e0254861. [Google Scholar] [CrossRef]
- Zhang, R.; Tan, H.; Afzal, W. A modified human reliability analysis method for the estimation of human error probability in the offloading operations at oil terminals. Process. Saf. Prog. 2021, 40, 84–92. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J.; Rochdi, M.; Belkacem, O. Bayesian modelling for human error probability analysis in CREAM. In Proceedings of the 2011 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Xi’an, China, 17–19 June 2011; pp. 137–142. [Google Scholar]
- Yang, Z.L.; Bonsall, S.; Wall, A.; Wang, J.; Usman, M. A modified CREAM to human reliability quantification in marine engineering. Ocean Eng. 2013, 58, 293–303. [Google Scholar] [CrossRef]
- Zhou, Q.; Wong, Y.D.; Loh, H.S.; Yuen, K.F. A fuzzy and Bayesian network CREAM model for human reliability analysis—The case of tanker shipping. Saf. Sci. 2018, 105, 149–157. [Google Scholar] [CrossRef]
- Ung, S.-T. Evaluation of human error contribution to oil tanker collision using fault tree analysis and modified fuzzy Bayesian Network based CREAM. Ocean Eng. 2019, 179, 159–172. [Google Scholar] [CrossRef]
- Chen, D.; Fan, Y.; Ye, C.; Zhang, S. Human reliability analysis for manned submersible diving process based on CREAM and Bayesian network. Qual. Reliab. Eng. Int. 2019, 35, 2261–2277. [Google Scholar] [CrossRef]
- Abbasinia, M.; Kalatpour, O.; Motamedzadeh, M.; Soltanian, A.; Mohammadfam, I. Dynamic Human Error Assessment in Emergency Using Fuzzy Bayesian CREAM. J. Res. Health Sci. 2020, 20, e00468. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, F.; Ghasemi, A.; Kalatpour, O. Prediction of human error probability during the hydrocarbon road tanker loading operation using a hybrid technique of fuzzy sets, Bayesian network and CREAM. Int. J. Occup. Saf. Ergon. 2021, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef][Green Version]
- Chen, S.-J.; Hwang, C.-L. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1992; pp. 289–486. [Google Scholar]
- Stone, M. The opinion pool. Ann. Math. Stat. 1961, 1339–1342. [Google Scholar] [CrossRef]
- Ishikawa, A.; Amagasa, M.; Shiga, T.; Tomizawa, G.; Tatsuta, R.; Mieno, H. The max-min Delphi method and fuzzy Delphi method via fuzzy integration. Fuzzy Sets Syst. 1993, 55, 241–253. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Multi-criteria weighted aggregated sum product assessment framework for fuel technology selection using q-rung orthopair fuzzy sets. Sustain. Prod. Consum. 2020, 24, 90–104. [Google Scholar] [CrossRef]
- Cornejo, M.E.; Lobo, D.; Medina, J. On the solvability of bipolar max-product fuzzy relation equations with the standard negation. Fuzzy Sets Syst. 2020. [Google Scholar] [CrossRef]
- Clemen, R.T.; Winkler, R.L. Combining Probability Distributions From Experts in Risk Analysis. Risk Anal. 1999, 19, 187–203. [Google Scholar] [CrossRef]
- Cheliyan, A.S.; Bhattacharyya, S.K. Fuzzy fault tree analysis of oil and gas leakage in subsea production systems. J. Ocean Eng. Sci. 2018, 3, 38–48. [Google Scholar] [CrossRef]
- Leekwijck, W.V.; Kerre, E.E. Defuzzification: Criteria and classification. Fuzzy Sets Syst. 1999, 108, 159–178. [Google Scholar] [CrossRef]
- Patel, A.V.; Mohan, B.M. Some numerical aspects of center of area defuzzification method. Fuzzy Sets Syst. 2002, 132, 401–409. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Yang, J.-B.; Xu, D.-L.; Chin, K.-S. On the centroids of fuzzy numbers. Fuzzy Sets Syst. 2006, 157, 919–926. [Google Scholar] [CrossRef]
- Jensen, F.V. Bayesian Networks and Decision Graphs; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
Figure 1.
A truck-to-ship LNG bunkering scenario.
Figure 1.
A truck-to-ship LNG bunkering scenario.
Figure 2.
The framework of human error probability (HEP) assessment.
Figure 2.
The framework of human error probability (HEP) assessment.
Figure 3.
An example of questions for the safety philosophical factors’ indicator (SPFI) of “SC1”.
Figure 3.
An example of questions for the safety philosophical factors’ indicator (SPFI) of “SC1”.
Figure 4.
The conversion scale including seven qualitative terms.
Figure 4.
The conversion scale including seven qualitative terms.
Figure 5.
The BN model for the CREAM.
Figure 5.
The BN model for the CREAM.
Figure 6.
The relations between the common performance condition indicators (CPCs) and the COCOMs.
Figure 6.
The relations between the common performance condition indicators (CPCs) and the COCOMs.
Figure 7.
The fuzzy membership functions for the common performance condition indicators (CPCs).
Figure 7.
The fuzzy membership functions for the common performance condition indicators (CPCs).
Figure 8.
The fuzzy membership functions for the COCOMs.
Figure 8.
The fuzzy membership functions for the COCOMs.
Figure 9.
The probabilities of the COCOM node’s states.
Figure 9.
The probabilities of the COCOM node’s states.
Figure 10.
The degrees of the fuzzy membership functions of COCOMs (x1 = −5.29788; x2 = −2.0021186; x3 = −2.0013; x4 = −1.9987).
Figure 10.
The degrees of the fuzzy membership functions of COCOMs (x1 = −5.29788; x2 = −2.0021186; x3 = −2.0013; x4 = −1.9987).
Figure 11.
The relationship between the human error probability (HEP) and the homogenized probability of the common performance condition indicators (CPCs).
Figure 11.
The relationship between the human error probability (HEP) and the homogenized probability of the common performance condition indicators (CPCs).
Table 1.
Three generations of human reliability assessment (HRA) approach [39,40,41,42,43,44,45,46,47].
Table 1.
Three generations of human reliability assessment (HRA) approach [39,40,41,42,43,44,45,46,47].
| Generation | Main Characteristics | Representative Approaches |
|---|---|---|
| First | Regarding humans as equipment. Calculating HEP using traditional methods such as the event tree analysis. |
THERP (Technique for Human Error-Rate Prediction). HCR (Human Cognitive Reliability). HEART (Human Error Assessment and Reduction Technique). |
| Second | Considering behavioural science, cognitive science, and psychology. Describing the underlying causes of specific erroneous human actions or context in which human errors occur. Quantifying the HEP based on error-producing conditions or context. |
CREAM (Cognitive Reliability and Error Analysis Method). SPAR-H (Standardized Plant Analysis Risk HRA). ATHEANA (A Technique for Human Event Analysis). |
| Third | Use artificial intelligence and computer-aided simulation techniques to predict HEP. | IDAC (Information-Decision-Action Crew). Phoenix (Phoenix, as the name implies is developed from the ashes of its predecessors in an attempt to address the current issues in the field of HRA). MERMOS (Method d’Evaluation de la Realisation des Missions Operator pout la Surete). Dynamic HRA method. |
Table 2.
The COCOMs and their human error probability (HEP) intervals.
Table 2.
The COCOMs and their human error probability (HEP) intervals.
| COCOM (Contextual Control Mode) | HEP (Human Error Probability) Interval |
|---|---|
| Strategic | (0.000005, 0.01) |
| Tactical | (0.001, 0.1) |
| Opportunistic | (0.01, 0.5) |
| Scrambled | (0.1, 1.0) |
Table 3.
The safety philosophical factors (SPFs) and the safety philosophical factors’ indicators (SPFIs).
Table 3.
The safety philosophical factors (SPFs) and the safety philosophical factors’ indicators (SPFIs).
| SPF | SPFI | Description |
|---|---|---|
| Safety culture (SC) | SC1 | Safety policy is set in the organisation, and its values are shared among members of the organisation. |
| SC2 | The roles and responsibilities for safety are clearly understood. | |
| SC3 | Mistakes are reported without consequences and punishment. | |
| SC4 | Vertical/horizontal safety-related communication is encouraged. (Vertical communication is the transmission of information between different levels of the organizational hierarchy. Horizontal communication is the transmission of information between people, divisions, departments, or units within the same level of organizational hierarchy.) | |
| SC5 | Managers are committed to safety practices. | |
| Safety management (SM) | SM1 | Management encourages employees to voice concerns and safety improvement proposals. |
| SM2 | Employees are involved in setting safety objectives, decision making, and improvement plans. | |
| SM3 | The company has a clear reward and punishment mechanism for employees’ safety practices. | |
| SM4 | Employees are given enough time to carry out their tasks. | |
| SM5 | A positive work environment is provided. | |
| Safety process (SP) | SP1 | Safety audits for the safety management system are well implemented. |
| SP2 | Risk assessment is well conducted in the organisation. | |
| SP3 | Safety checklist related to LNG bunkering simultaneous operations is well developed in the organisation. | |
| SP4 | Emergency plans and procedures are well developed in the organisation. | |
| Safety training (ST) | ST1 | Specialised training and education are periodically offered as part of training program. |
| ST2 | Employees learn lessons from near misses and incident/accidents reports (if applicable). | |
| ST3 | Employees are trained for the company’s safety policy. | |
| ST4 | Learning and contentious safety improvement is part of staff training. | |
| ST5 | Safety training and education are given according to personnel’s level. | |
| Safety awareness (SA) | SA1 | Safety information (i.e., procedures) is commonly demonstrated in the workplace. |
| SA2 | Clear mission statements (e.g., slogans and logos) are commonly demonstrated in the workplace. | |
| SA3 | Supervisors are made responsible to convey safety information to employees. | |
| SA4 | The correct safety signage is implemented. |
Table 4.
The weighting criteria of experts.
Table 4.
The weighting criteria of experts.
| PPS | STS | ELS | |||
|---|---|---|---|---|---|
| Category | Score | Category | Score | Category | Score |
| Senior Manager (SMA) | 5 | ≥ 30 years | 5 | PhD | 5 |
| Junior Manager (JMA) | 4 | 20–29 years | 4 | Master’s | 4 |
| Engineer (E) | 3 | 10-19 years | 3 | Bachelor’s | 3 |
| Technician (T) | 2 | 6-9 years | 2 | Vocational education | 2 |
| Worker (W) | 1 | ≤5 years | 1 | High school | 1 |
Table 5.
A part of the conditional probability table (CPT).
Table 5.
A part of the conditional probability table (CPT).
| Row No. | CPC | COCOM 1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Str | Tac | Opp | Scr | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | 1 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 19,683 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 0 | 0 | 0 | 1 |
Table 6.
Selective information of the experts and the associate weights.
Table 6.
Selective information of the experts and the associate weights.
| Expert | PP | PPS | ST | STS | EL | ELS |
W |
|---|---|---|---|---|---|---|---|
| E1 | JMA | 4 | 10–19 years | 3 | Bachelor | 3 | 0.00657462 |
| E2 | E | 3 | 20–29 years | 4 | Bachelor | 3 | 0.00657462 |
| E3 | E | 3 | 10–19 years | 3 | Master | 4 | 0.00657462 |
| … | … | … | … | … | … | … | … |
| E137 | SMA | 5 | 20–29 years | 4 | Master | 4 | 0.00854701 |
Table 7.
Selective expressions on the importance to the safety of each safety philosophical factors’ indicator (SPFIs).
Table 7.
Selective expressions on the importance to the safety of each safety philosophical factors’ indicator (SPFIs).
| Expert | SPFI | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SC1 | SC2 | SC3 | SC4 | SC5 | SM1 | SM2 | SM3 | SM4 | SM5 | SP1 | SP2 | SP3 | SP4 | ST1 | ST2 | ST3 | ST4 | ST5 | SA1 | SA2 | SA3 | SA4 | |
| E1 | 6 | 6 | 6 | 6 | 6 | 6 | 5 | 7 | 5 | 6 | 6 | 5 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 5 | 6 |
| E2 | 6 | 6 | 6 | 6 | 6 | 6 | 5 | 7 | 7 | 6 | 6 | 7 | 7 | 7 | 7 | 6 | 7 | 6 | 6 | 7 | 7 | 6 | 7 |
| E3 | 6 | 7 | 5 | 7 | 7 | 7 | 7 | 7 | 7 | 6 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 6 | 7 | 7 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| E137 | 7 | 6 | 7 | 7 | 6 | 7 | 6 | 6 | 7 | 6 | 7 | 7 | 7 | 7 | 7 | 7 | 5 | 6 | 3 | 6 | 5 | 6 | 7 |
Table 8.
Top nine ranked safety philosophical factors’ indicator (SPFIs).
Table 8.
Top nine ranked safety philosophical factors’ indicator (SPFIs).
| No. | SPFI | IFS | FN | Ranking | CPC |
|---|---|---|---|---|---|
| 1 | SP4 | (0.7632,0.8632,0.9440,0.9677) | 0.881791 | 1 | CPC1 |
| 2 | SP3 | (0.7503,0.8503,0.9304,0.9586) | 0.869727 | 2 | CPC2 |
| 3 | SC1 | (0.7435,0.8435,0.9259,0.9527) | 0.863768 | 3 | CPC3 |
| 4 | SC2 | (0.7272,0.8272,0.9051,0.9397) | 0.847293 | 4 | CPC4 |
| 5 | ST1 | (0.7286,0.8280,0.8996,0.9393) | 0.846449 | 5 | CPC5 |
| 6 | ST2 | (0.7214,0.8213,0.8881,0.9327) | 0.838476 | 6 | CPC6 |
| 7 | SP1 | (0.7183,0.8183,0.8903,0.9349) | 0.838169 | 7 | CPC7 |
| 8 | SP2 | (0.7160,0.8155,0.8851,0.9303) | 0.834434 | 8 | CPC8 |
| 9 | SA4 | (0.7151,0.8151,0.8827,0.9274) | 0.832728 | 9 | CPC9 |
Table 9.
The prior probabilities of the common performance condition indicators (CPCs).
Table 9.
The prior probabilities of the common performance condition indicators (CPCs).
| CPC | SPFI | Judgement 1 | IFS | FN | Prior Probability | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | … | E137 | Ad (1) | Ac (0) | In (−1) | ||||
| CPC1 | SP4 | Ad | Ac | In | … | Ac | (0.1942,0.5629,0.5962,0.8942) | 0.5565 | 0.14125 | 0.85875 | 0 |
| CPC2 | SP3 | Ad | Ac | Ac | … | Ac | (0.2011,0.5501,0.5913,0.8775) | 0.5504 | 0.126 | 0.874 | 0 |
| CPC3 | SC1 | Ac | Ac | Ac | … | Ac | (0.1593,0.5125,0.5420,0.8709) | 0.5193 | 0.04825 | 0.95175 | 0 |
| CPC4 | SC2 | Ac | Ad | In | … | Ad | (0.1551,0.4988,0.5302,0.8610) | 0.5103 | 0.02575 | 0.97425 | 0 |
| CPC5 | ST1 | Ac | Ac | Ac | … | Ac | (0.1608,0.4934,0.5297,0.8521) | 0.5082 | 0.0205 | 0.9795 | 0 |
| CPC6 | ST2 | Ac | Ac | Ac | … | Ac | (0.1295,0.4130,0.4568,0.7982) | 0.4536 | 0 | 0.884 | 0.116 |
| CPC7 | SP1 | Ac | Ad | Ac | … | Ac | (0.1882,0.5432,0.5793,0.8799) | 0.5436 | 0.109 | 0.891 | 0 |
| CPC8 | SP2 | Ac | Ad | In | … | Ac | (0.1425,0.4497,0.4894,0.8236) | 0.4783 | 0 | 0.94575 | 0.05425 |
| CPC9 | SA4 | Ad | Ac | Ac | … | Ac | (0.2123,0.5944,0.6281,0.9113) | 0.5790 | 0.1975 | 0.8025 | 0 |
Table 10.
The probabilities of the COCOMs and the human error probability (HEP).
Table 10.
The probabilities of the COCOMs and the human error probability (HEP).
| Control Mode | Probability | FN (Fuzzy Number) | HEP (Human Error Probability) |
|---|---|---|---|
| Strategic | 0.001284 | −2.00696 | 0.009841 |
| Tactical | 0.9987 | ||
| Opportunistic | 0 | ||
| Scrambled | 0 |
Table 11.
The probabilities of the common performance condition indicators (CPCs) for five cases.
Table 11.
The probabilities of the common performance condition indicators (CPCs) for five cases.
| CPC | SPFI | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
P |
Probability |
P |
Probability |
P |
Probability |
P |
Probability |
P |
Probability | ||||||||||||
| Ad 1 | Ac 2 | In 3 | Ad | Ac | In | Ad | Ac | In | Ad | Ac | In | Ad | Ac | In | |||||||
| CPC1 | SP4 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC2 | SP3 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC3 | SC1 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC4 | SC2 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC5 | ST1 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC6 | ST2 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC7 | SP1 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC8 | SP2 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
| CPC9 | SA4 | 0 | 0 | 1 | 0 | 0.2 | 0 | 0.25 | 0.75 | 0.5 | 0 | 1 | 0 | 0.8 | 0.75 | 0.25 | 0 | 1 | 1 | 0 | 0 |
Table 12.
The probabilities of the COCOMs and the human error probabilities (HEPs) for five cases.
Table 12.
The probabilities of the COCOMs and the human error probabilities (HEPs) for five cases.
| COCOM | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P 1 | FN | HEP | P | FN | HEP | P | FN | HEP | P | FN | HEP | P | FN | HEP | |
| Strategic | 0 | −0.5 | 0.3162 | 0 | −0.5774 | 0.2646 | 0 | −2 | 0.05 | 0.99 | −2.2883 | 0.005149 | 1 | −3.65 | 0.000224 |
| Tactical | 0 | 0.001343 | 1 | 0.01 | 0 | ||||||||||
| Opportunistic | 0 | 0.1644 | 0 | 0 | 0 | ||||||||||
| Scrambled | 1 | 0.8343 | 0 | 0 | 0 |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
Share and Cite
MDPI and ACS Style
Fan, H.; Enshaei, H.; Jayasinghe, S.G. Human Error Probability Assessment for LNG Bunkering Based on Fuzzy Bayesian Network-CREAM Model. J. Mar. Sci. Eng. 2022, 10, 333.
https://doi.org/10.3390/jmse10030333
AMA Style
Fan H, Enshaei H, Jayasinghe SG. Human Error Probability Assessment for LNG Bunkering Based on Fuzzy Bayesian Network-CREAM Model. Journal of Marine Science and Engineering. 2022; 10(3):333.
https://doi.org/10.3390/jmse10030333
Chicago/Turabian Style
Fan, Hongjun, Hossein Enshaei, and Shantha Gamini Jayasinghe. 2022. «Human Error Probability Assessment for LNG Bunkering Based on Fuzzy Bayesian Network-CREAM Model» Journal of Marine Science and Engineering 10, no. 3: 333.
https://doi.org/10.3390/jmse10030333
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.