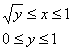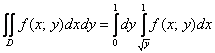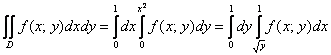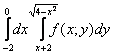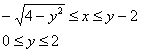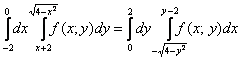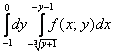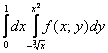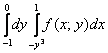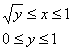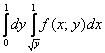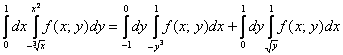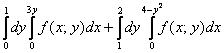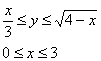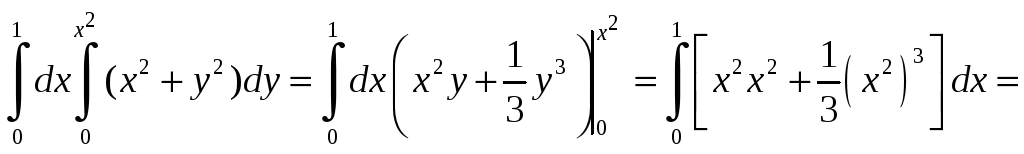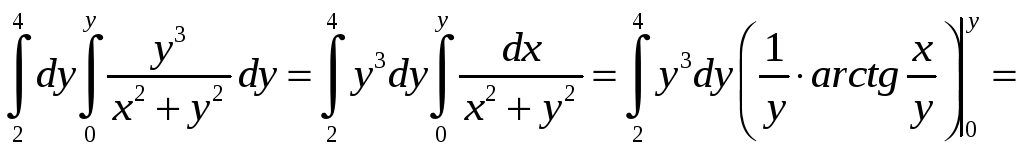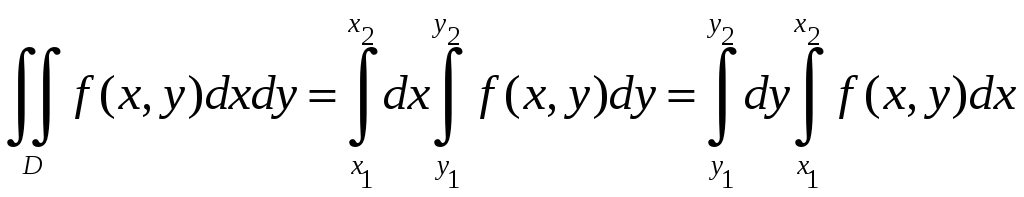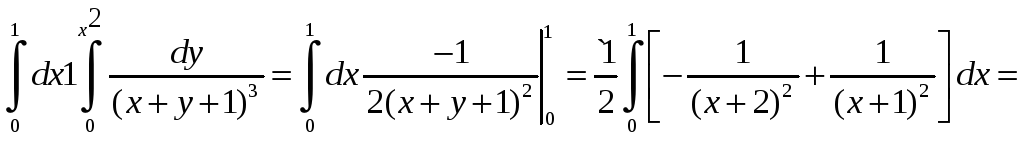Сегодня детально проанализируем алгоритм изменения порядка интегрирования в двойном интеграле. Под изменением порядка интегрирования имеем в виду, что задан двойной интеграл в котором интегрирование проводится сначала по «икс», а дальше полученный результат интегрируют по «игрек». Нужно поменять пределы интегрирования, а возможно и разбить на несколько областей интегрирование, для того, чтобы сначала интегрировать по «игрек», а далее по «иксу». В курсе высшей математики подобные примеры учат решать достаточно длительное время, но не во всех это выходит. Схема изменения порядка интегрирования будет расписана на готовых примерах с красиво выполненными рисунками областей интегрирования. Кто-то может подумать, что рисунки здесь ни к чему, но прочитав статью целиком Вы поймете, что без рисунков Вы не сможете понять как изменяются пределы интегрирования, и как их правильно расставлять.
Пример 3.1 Изменить порядок интегрирования в двойном интеграле:
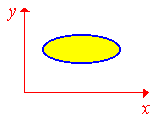
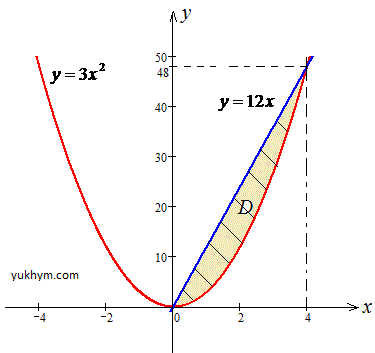
Решение: Построим область интегрирования ограниченую кривыми
0≤x≤4, 3x2≤y≤12x, где
y=3x2 — парабола с вершиной в точке O(0;0) и ветками вверх;
y=12x — прямая, которая проходит через начало координат O(0;0).
График области интегрирования приведен на рисунке.
В этом примере «игрек» изменяется от нижней кривой (параболы) к верхней (прямой), в это время «икс» пробегает значение от 0 до 4.
При изменении порядка интегрирования мы будем пробегать значение от первой кривой по «иксу» (прямой) ко второй (параболы), «игрек» в это время будет проходить значение от 0 ко второй точке пересечения заданных кривых.
Отсюда следует, что для изменения порядка интегрирования нужно найти точки пересечения кривых, дальше для изменения пределов нужно перейти от y(x) к x(y) для этих самых пределов.
Выражаем заданные функции y(x) через переменную y:
y=3x2, отсюда 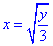
y=12x, отсюда x=y/12.
Найдем точки пересечения:
y=3x2=12x, отсюда
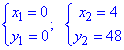
Расставим пределы в заданной области:
D: 0≤y≤48
Выполняем изменение порядка интегрирования
Вот и вся схема перехода от интегрирования по y,x к двойному интегралу по x,y.
Пример 3.2 Изменить порядок интегрирования:
Решение: Запишем область интегрирования для заданного примера
a/2≤x≤a 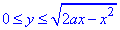
Превратим верхнюю кривую по y к каноническому виду
y=√(2ax-x2), y2=2ax-x2, x2-2ax+a2+y2=a2, (x-a)2+y2=a2 — верхний полукруг с центром в начале координат O(a;0) и радиусом a.
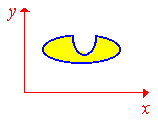
На рисунку наведем область интегрирования
Найдем запись функции через переменную y:
(x-a)^2+y^2=a^2, (x-a)^2 =a^2-y^2,
При изменении порядка интегрирования нашу область необходимо разбить на две подобласти:
D=D1+D2.
Расставим пределы в каждой области:
D1: 0≤y≤a√3/2, a/2≤x≤a;
D2: a√3/2≤y≤a, 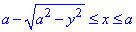
Дальше можем изменить порядок интегрирования
Внимательно пересмотрите фрагмент где область интегрирования разбивается на 2 участка, для чего это делается и от чего зависит.
Многие этого не понимают, поскольку не представляют что делаем, здесь же имеем график из которого видим, что в первой области «икс» изменяется от первой прямой x=a/2 ко второй x=a, во второй области переменная «икс» пробегает значение от полукруга к прямой x=a.
Пример 3.3 Изменить порядок интегрирования:
Решение: Область интегрирования ограничена кривыми
0≤y≤1, 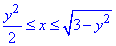
x=√(3-y2), x2=3-y2, x2+y2=(√3)2 — правый полукруг с центром в точке O(0;0) и радиусом R=√3.
Для изменения порядка интегрирования выражаем функции через переменную x:
x=y2/2, y2=2x, y=√(2x);
x2=3-y2, y2=3-x2, y=√(3-x2).
Найдем точки пересечения графиков функций:
параболы с горизонтальной прямой
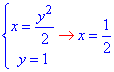
параболы с правой частью полукруга (І четверть)
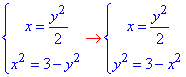
Подставляем y2 из второго уравнения системы уравнений в первое x=1,5-0,5x2;
При решении получим x=1.
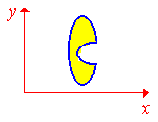
Выполняем построение и разбитие на нужные подобласти интегрирования
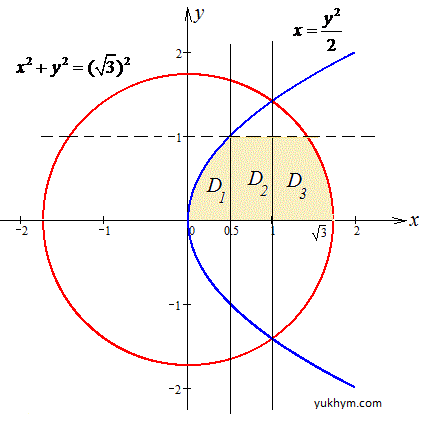
Для изменения порядка интегрирования нашу область разобьем на три подобласти:
D=D1+D2+D3.
Расставим пределы в каждой области:
D1: 0≤x≤0,5, 0≤y≤√(2x);
D2: 0,5≤x≤1, 0≤y≤1;
D3: 1≤x≤√3, 0≤y≤√(3-x2).
Внимательно разберитесь, как это сопоставить с областями на рисунку и почему именно такое разбитие здесь нужно выполнять.
Запишем как изменится интеграл при изменении порядка интегрирования
Думаю приведенных объяснений достаточно, чтобы самостоятельно научиться менять порядок интегрирования.
Пример 3.4 Изменить порядок интегрирования:
Решение: Построим область интегрирования, которая ограничена кривыми
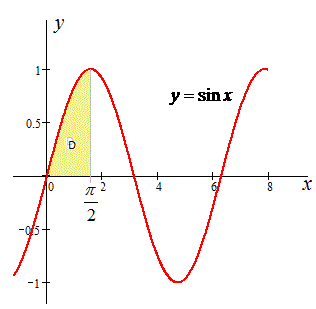
0≤x≤π/2, 0≤y≤sin(x), где y=0 — ось абсцисс;
y=sin(x) — синусоида.
Выражаемый полученные функции через переменную y:
y=sin(x), отсюда x=arcsin(y);
y=0, отсюда x=0.
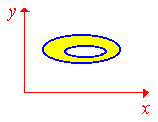
Графику кривых наведем на рисунку
Пределы интегрирования в заданной области поменяются на такие:
D: 0≤y≤1, 0≤x≤arcsin(y).
Записываем двойной интеграл с перечисленными пределами интегрирования
Имеем еще 5 готовых примеров на изменение порядка интегрирования, их Вы можете пересмотреть в следующей статье.
Содержание:
- Рассмотрим двойной интеграл
- Как вычислить двойной интеграл?
Пример 1.
Изменить порядок интегрирования в интеграле:
Решение: В данном интеграле область интегрирования D — правильная область первого типа (рис. 10). По теореме 1 интеграл / записывается в виде двойного интеграла 










Для обоих интегралов переменная х принимает только отрицательные значения. Значит для точек 


Теперь, если рассмотреть область интегрирования D как правильную область второго типа, то согласно теореме 2 интеграл / записывается в виде

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример 2.
Изменить порядок интегрирования в повторном» интеграле.

Решение:
Область интегрирования D ограничена линиями 



Пример 3.
Изменить порядок интегрирования в повторном интеграле

Решение:
Образец выполнения задания в Mathcad:
Зададим подынтегральную функцию и определим границы области интегрирования по пределам повторного интеграла:

Изменим порядок интегрирования. Для этого надо выразить уравнения границ в виде: 

Указание. Для того, чтобы задать уравнения границ в виде: 




Возможно вам будут полезны данные страницы:
Рассмотрим двойной интеграл





Тогда имеет место равенство 

Координаты 


Интеграл
называется двойным интегралом в криволинейных координатах.
Простейшим и важнейшим частным случаем криволинейных координат являются полярные координаты 


a 
При этом имеет место формула замены переменных в двойном интеграле при переходе к полярным координатам 
Расстановка пределов и вычисление двойного интеграла в криволинейных координатах выполняется аналогично случаю прямоугольных координат.
Как вычислить двойной интеграл?

по области D, ограниченной прямыми 
Решение:
Область D — параллелограмм АВСК (рис. 19 а). Хотя подынтегральная функция и область интегрирования просты, вычисление данного интеграла в прямоугольных координатах достаточно громоздко (убедитесь самостоятельно). Заметив, что уравнения прямых можно записать в виде 









Область D изображена на рис. 20 а. Заметим, что расставить пределы интегрирования в исходном интеграле не просто, однако подходящая замена переменных позволяет свести этот интеграл к интегралу по прямоугольнику.
Введем новые переменные при помощи равенств 






Таким образом, исходный интеграл в плоскости 

Граница области G описывается линиями
(так как одна из формул преобразования имеет вид
то линии
в плоскости
соответствует линия
в плоскости
),
(рис. 20 6).
Поэтому область G имеет вид 

Строим круг 






Таким образом, 
Лекции:
- Производная функции заданной неявно
- Методы определенного интегрирования
- Функция распределения
- Рациональные числа
- Матричные уравнения: пример решения
- Найти частные производные
- Уравнения с двумя переменными
- Матрицы
- Расстояние между скрещивающимися прямыми
- Нахождение промежутков возрастания и убывания функции
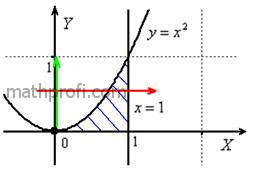
1.2.1. Как изменить порядок обхода области?
Половина задачи решена. Теперь перейдём к повторным интегралам вторым способом.
Для этого нужно найти обратные функции. Смотрим на функции, которыми задается область . Если совсем просто, то перейти к обратным функциям,
это значит – выразить «иксы» через «игреки». Единственной функцией, где есть и «икс» и «игрек», является .
Если , то
, причём:
обратная функция задает
правую ветку параболы;
обратная функция задает
левую ветку параболы.
Нередко возникают сомнения, вот, к примеру, функция определяет левую или правую ветвь параболы? Сомнения развеять
очень просто: возьмите какую-нибудь точку параболы, например, (с правой ветви) и подставьте её координаты в любое уравнение,
например, в то же уравнение :
Получено верное числовое равенство, значит, функция определяет именно правую ветвь параболы, а не левую.
Более того, такую проверку (мысленно или на черновике) желательно проводить всегда – после того, как вы перешли к обратным
функциям. Времени займет всего ничего, а от ошибки убережёт наверняка!
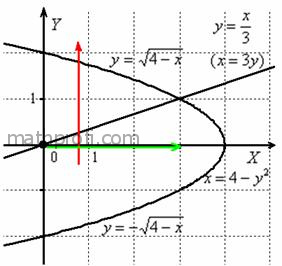
Обойдём область интегрирования вторым способом:
Теперь лазерную указку держим горизонтально, слева от области интегрирования. Луч лазера проходит область
строго слева направо. В данном случае он входит в область через ветвь параболы и выходит из области через прямую, которая задана
уравнением (красная
стрелка). Чтобы просканировать лазером всю область, нужно провести указкой вдоль оси строго снизу вверх от 0 до 1
(зелёная стрелка).
Таким образом:
«икс» изменяется от до
1,
а «игрек» при этом изменяется от 0 до 1.
Запишем порядок обхода области в виде неравенств:
И, следовательно, переход к повторным интегралам таков:
Ответ можно записать следующим образом:
Напоминаю, что окончательный результат вычислений не зависит от того, какой порядок обхода области мы выбрали (поэтому
поставлен знак равенства). Но, до конечного результата ещё далеко, сейчас наша задача – лишь правильно расставить
пределы интегрирования.
Пример 2
Дан двойной интеграл ,
где область ограничена
линиями . Перейти к
повторным интегралам и расставить пределы интегрирования двумя способами.
Это пример для самостоятельного решения. Грамотно постройте чертёж и строго соблюдайте направления обхода
(откуда и куда светить лазерной указкой). Примерный образец чистового оформления задачи в конце книги.
Чаще всего типовое задание встречается немного в другой формулировке:
Пример 3
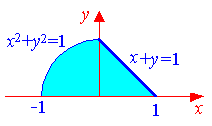
Построить область интегрирования и изменить порядок интегрирования
По условию, дан первый способ обхода области, и решение опять начинается с чертежа. Здесь область не лежит на «блюдечке с
голубой каёмочкой», но построить её не составляет особого труда. Сначала «снимаем» функции с пределов интегрирования: ,
. Функция
, понятно, задаёт прямую, но что задаёт функция
? Давайте её немного преобразуем,
возведя обе части в квадрат:
– окружность с центром
в начале координат радиуса 2. Функция же задаёт верхнюю полуокружность (не забываем, что если есть
сомнения, то всегда можно подставить точку лежащую на верхней или нижней полуокружности).
Смотрим на пределы внешнего интеграла: «икс» изменяется от –2 до 0.
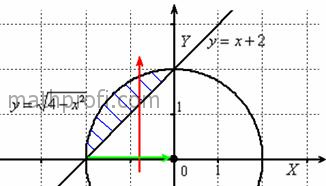
Итак, изобразим на чертеже прямую , полуокружность
и снова посмотрим на исходные повторные интегралы
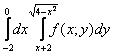
вертикально
снизу через прямую и выходит из области через полуокружность (красная стрелка), при этом лазерную указку нам
нужно переместить слева направо вдоль ось от –2 до 0 (зелёная стрелка). И, исходя из этой
замечательной логики, штрихуем искомую область синим цветом:
Теперь нужно изменить порядок обхода области, для этого перейдем к обратным функциям (выразим «иксы» через
«игреки»): .
Недавно мы преобразовали функцию к уравнению окружности
, и сейчас нам нужно выразить «икс»:
. В результате получаем две обратные функции:
– определяет правую
полуокружность;
– определяет левую
полуокружность.
Опять же, если возникают сомнения, возьмите любую точку окружности и выясните, где лево, а где право.
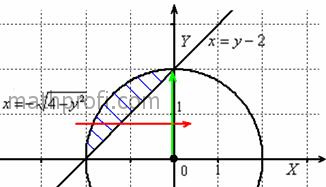
Изменим порядок обхода области. Согласно второму способу обхода, луч лазера входит в область слева через
левую полуокружность и
выходит справа через прямую (красная стрелка). В то же время лазерная указка проводится
вдоль оси ординат снизу вверх от 0 до 2 (зелёная стрелка).
Таким образом, порядок обхода области:
и, в общем-то, можно записать ответ:
Пример 4
Построить область интегрирования и изменить порядок интегрирования
Это пример для самостоятельного решения. Пример не очень сложный, но обратите внимание, что порядок обхода изначально задан
вторым способом! Что делать в подобных случаях? Во-первых, возникает трудность с чертежом, поскольку чертить график обратной
функции наподобие непривычно
даже мне самому. Я рекомендую следующий порядок действий: сначала из получаем «обычную» функцию (выражаем «игрек» через «икс»).
Далее строим график этой «обычной» функции (всегда можно построить хотя бы поточечно). Аналогично поступаем с более простой
линейной функцией: из выражаем
«игрек» и проводим прямую.
Анализируем исходные пределы интегрирования: входим слева в область через и выходим через
. При этом все дела происходят в «игрековой» полосе от –1 до 0.
После того, как вы определили на чертеже область интегрирования, сменить порядок обхода не составит особого труда. Примерный
образец оформления решения в конце книги. Похожий пример будет разобран подробнее чуть позже.
И сейчас внимание! Даже если вы всё отлично поняли, не торопитесь переходить непосредственно к вычислениям
двойного интеграла. Порядок обхода – вещь коварная, и очень важно немного набить руку на данной задаче, тем более, я
ещё не всё рассказал:
Пример 5
Изменить порядок интегрирования
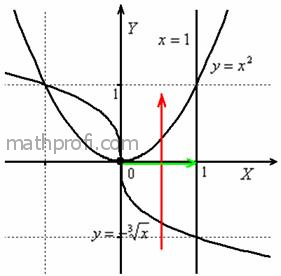
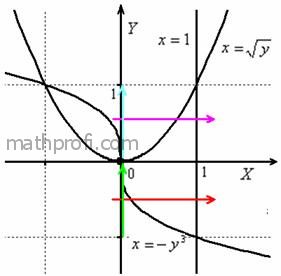
Решение: запишем функции и выполним чертёж. График второй функции представляет собой
кубическую параболу, которая «лежит на боку»:
Порядок обхода области, соответствующий исходным повторным интегралам, обозначен стрелками. Ещё раз посмотрИте на пределы
интегрирования и мысленно просканируйте область лазером!
Также обратите внимание, что в ходе выполнения чертежа у нас прорисовалась еще одна ограниченная фигура (левее оси ). Поэтому следует быть
внимательным при определении области интегрирования – за область можно ошибочно принять не ту фигуру!
Перейдем к обратным функциям:
– нужная нам правая ветвь
параболы;
.
Изменим порядок обхода области. Как вы помните, при втором способе обхода, область нужно сканировать лазерным лучом
горизонтально – слева направо. Но тут наблюдается интересная вещь:
Как поступать в подобных случаях? В таких случаях область интегрирования нужно разделить на две части и для каждой части
составить свои повторные интегралы:
1) Если «игрек» изменяется от –1 до 0 (зеленая стрелка), то луч входит в область через кубическую параболу и выходит через прямую
(красная стрелка). Поэтому
порядок обхода области будет следующим:
И соответствующие повторные интегралы:
2) Если «игрек» изменяется от 0 до 1 (голубая стрелка), то луч входит в область через ветвь параболы и выходит через ту же прямую
(малиновая
стрелка). Следовательно, порядок обхода области будет следующим:
И соответствующие повторные интегралы:
У интегралов (кратных в частности) есть весьма удобное свойство аддитивности, то есть, их можно сложить, что в данном
случае и нужно сделать:
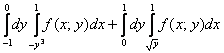
области вторым способом в виде суммы двух интегралов.
Ответ записываем так:
Какой порядок обхода выгоднее? Конечно тот, который был дан в условии задачи – вычислений будет в два раза меньше!
Пример 6
Изменить порядок интегрирования
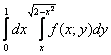
Это пример для самостоятельного решения. В нём присутствуют полуокружности, разборки с которыми были подробно рассмотрены в
Примере 3. Примерный образец оформления решения в конце книги.
А сейчас обещанная задача, когда изначально задан второй способ обхода области:
Пример 7
Изменить порядок интегрирования
Решение: когда порядок обхода задан вторым способом, то перед построением чертежа целесообразно перейти к
«обычным» функциям. В данном примере присутствуют два пациента для преобразования: и
.
С линейной функцией всё просто: .
Да и с функцией тоже
несложно, её график представляет собой параболу, которая «лежит на боку». Выразим «игрек» через «икс»:
и получаем две ветви: и
.
Какую ветку выбрать? Можно провести рассуждения, но проще начертить обе. Даже если вы не сразу понимаете, как они
расположены, всегда можно прибегнуть к поточечному методу построения:
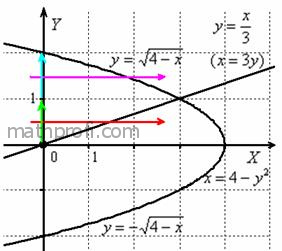
важно выбрать нужную! В выборе искомой фигуры помогут пределы интегрирования исходных повторных
интегралов:
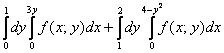
забывайте, что обратная функция задаёт всю параболу.
Стрелочки, которыми обозначен обход фигуры, в точности соответствуют пределам интегрирования интегралов – ОБЯЗАТЕЛЬНО проведите действия с лазерной указкой мысленно!
Довольно быстро вы научитесь без труда определять нужную область.
фигура найдена, заключительная часть решения, в общем-то, элементарна, меняем порядок обхода области (мысленно сканируем
лазером!):
Обратные функции уже найдены, и искомый порядок обхода области таков:
Ответ:
Финальный пример параграфа для самостоятельного решения:
Пример 8
Изменить порядок интегрирования:
Сверяемся с решением и переходим, наконец, непосредственно к вычислению двойного интеграла . Начнём с простейшего случая, когда
функция двух
переменных равна единице: , и это ещё и особый случай:


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
6
ЛЕКЦИЯ 1
Двойные
интегралы. Определение
двойного интеграла и его свойства.
Повторные интегралы. Сведение двойных
интегралов к повторным. Расстановка
пределов интегрирования. Вычисление
двойных интегралов в декартовой системе
координат.
1.
ДВОЙНЫЕ ИНТЕГРАЛЫ
1.1.
Определение двойного интеграла
Двойной интеграл
представляет собой обобщение понятия
определенного интеграла на случай
функции двух переменных. В этом случае
вместо отрезка интегрирования будет
присутствовать какая-то плоская фигура.
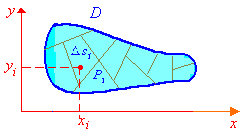
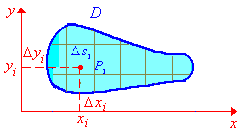
Пусть
D
– некоторая замкнутая ограниченная
область, а f(x,y)
– произвольная функция, определенная
и ограниченная в этой области. Будем
предполагать, что границы области D
состоят из конечного числа кривых,
заданных уравнениями вида y=f(x)
или x=g(y),
где f(x)
и g(y)
– непрерывные функции.
Р
Рис.
1.1
азобьем область D
произвольным образом на n
частей. Площадь i-го
участка обозначим символом si.
На каждом участке произвольно выберем
какую-либо точку Pi,
и пусть она в какой-либо фиксированной
декартовой системе имеет координаты
(xi,yi).
Составим интегральную
сумму для функции
f(x,y)
по области D,
для этого найдем значения функции во
всех точках Pi,
умножим их на площади соответствующих
участков si
и просуммируем все полученные результаты:
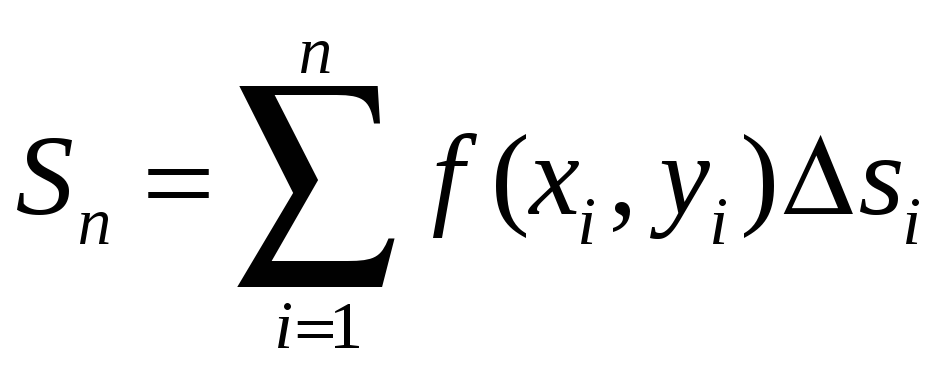
(1.1)
Назовем
диаметром
diam(G)
области G
наибольшее расстояние между граничными
точками этой области.
Двойным
интегралом
функции
f(x,y)
по
области
D
называется
предел, к которому стремится
последовательность интегральных
сумм
(1.1) при
неограниченном увеличении числа
разбиений
n
(при
этом
).
Это
записывают следующим образом
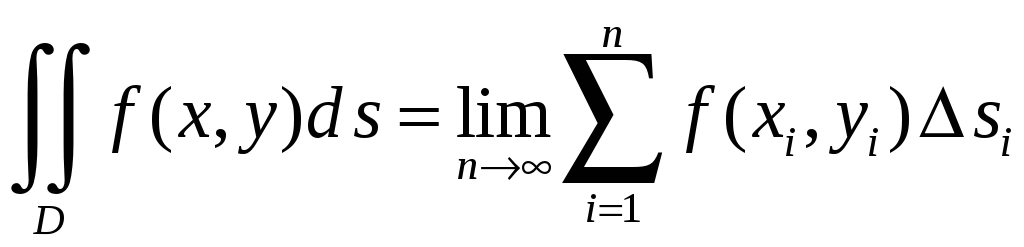
(1.2)
Заметим,
что, вообще говоря, интегральная сумма
для заданной функции и заданной области
интегрирования зависит от способа
разбиения области D
и выбора точек Pi.
Однако если двойной интеграл существует,
то это означает, что предел соответствующих
интегральных сумм уже не зависит от
указанных факторов. Для
того чтобы двойной интеграл существовал
(или, как говорят, чтобы
функция
f(x,y)
была
интегрируемой
в области D),
достаточно чтобы подынтегральная
функция была непрерывной
в заданной области интегрирования.
П
Рис.
1.2
усть функция f(x,y)
интегрируема в области D.
Поскольку предел соответствующих
интегральных сумм для таких функций не
зависит от способа разбиения области
интегрирования, то разбиение можно
производить при помощи вертикальных
и горизонтальных линий. Тогда большинство
участков области D
будет иметь прямоугольный вид, площадь
которых равна si=xiyi.
Поэтому дифференциал площади можно
записать в виде ds=dxdy.
Следовательно, в
декартовой системе координат
двойные
интегралы можно
записывать в виде
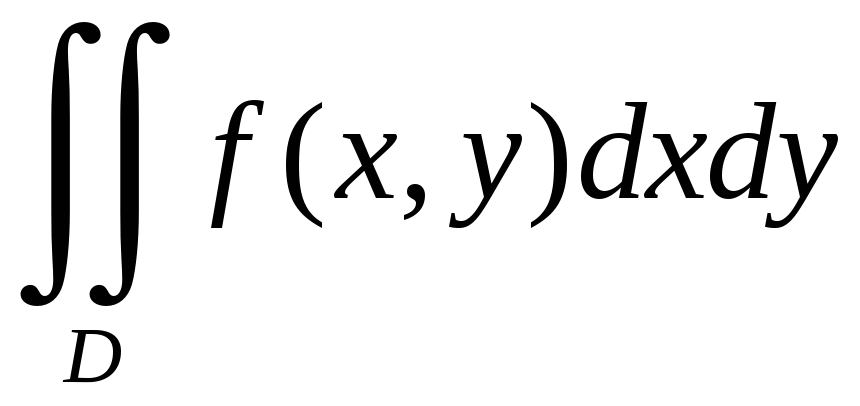
(1.3)
Замечание.
Если
подынтегральная функция
f(x,y)1,
то
двойной интеграл будет равен площади
области интегрирования:
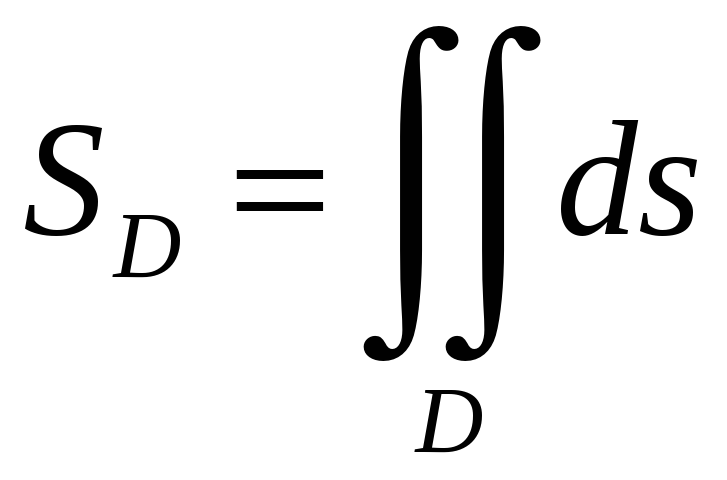
(1.4)
Отметим,
что двойные интегралы обладают такими
же свойствами, что и определенные
интегралы. Отметим некоторые из них.
Свойства
двойных интегралов.
10.
Линейное свойство.
Интеграл от
суммы функций равен сумме интегралов:
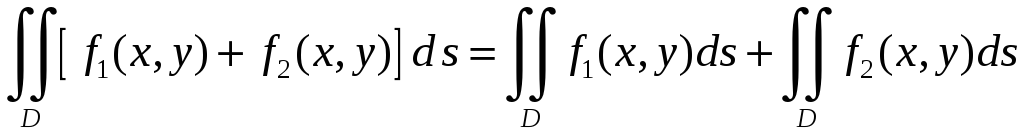
и
постоянный множитель можно выносить
за знак интеграла:

20.
Аддитивное свойство.
Если
область интегрирования D
разбить на две части, то двойной интеграл
будет равен сумме интегралов по каждой
этой части:
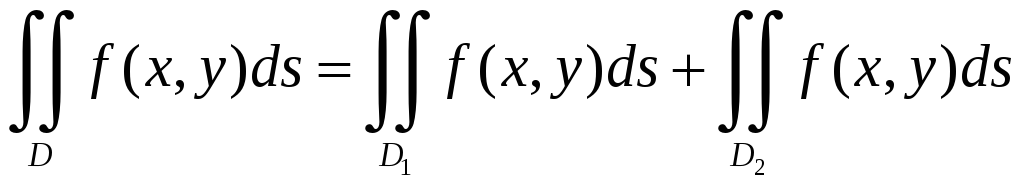
30.
Теорема о среднем.
Если
функция f(x,y)
непрерывна в области D,
то в этой области найдется такая точка
(),
что:
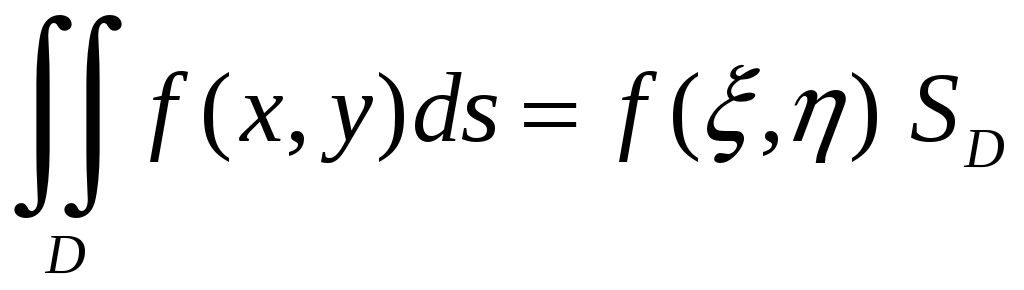
Далее возникает
вопрос: как вычисляются двойные интегралы?
Его можно вычислить приближенно, с этой
целью это разработаны эффективные
методы составления соответствующих
интегральных сумм, которые затем
вычисляются численно при помощи ЭВМ.
При аналитическом вычислении двойных
интегралов их сводят к двум определенным
интегралам.
1.2.
Повторные интегралы
Повторными
интегралами называются интегралы вида
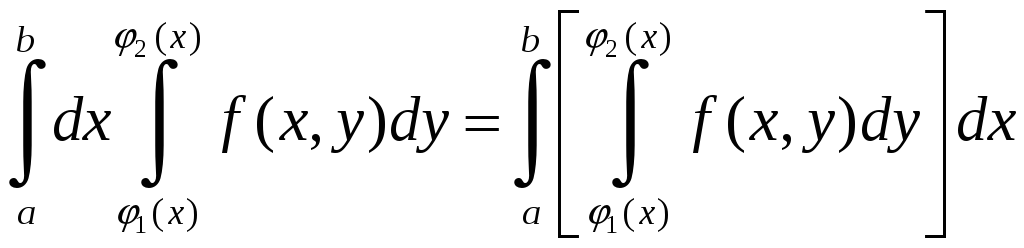
(1.5)
В
этом выражении сначала вычисляется
внутренний интеграл, т.е. производится
сначала интегрирование по переменной
y
(при этом переменная
x
считается постоянной величиной). В
результате интегрирования по y
получится некоторая функция по x:
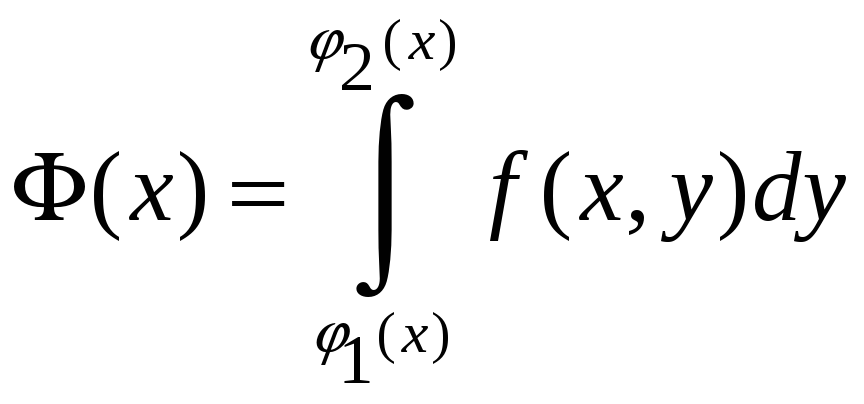
Затем
полученную функцию интегрируют по x:
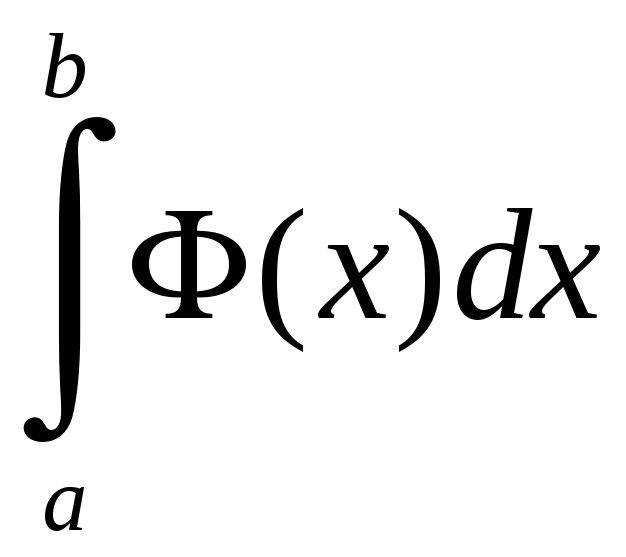
Пример
1.1.
Вычислить интегралы:
а)
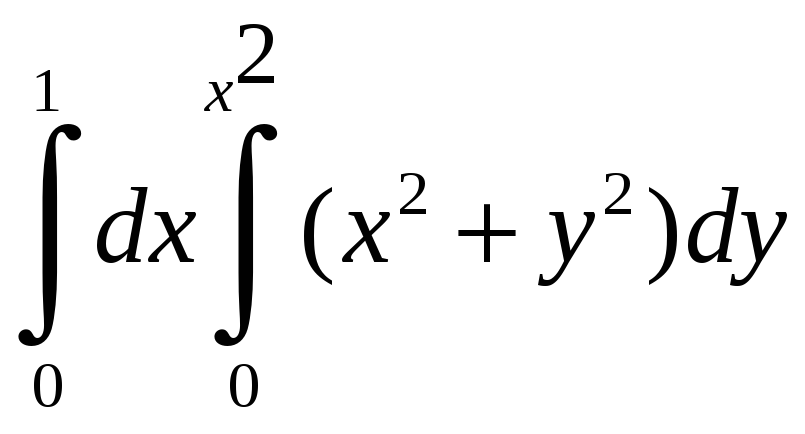
б)
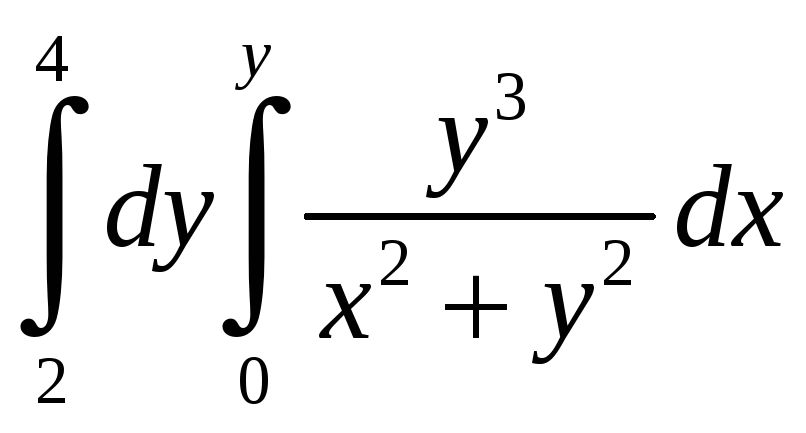
Решение.
а) Произведем интегрирование по y,
считая, что переменная x=const.
После этого вычисляем интеграл по x:
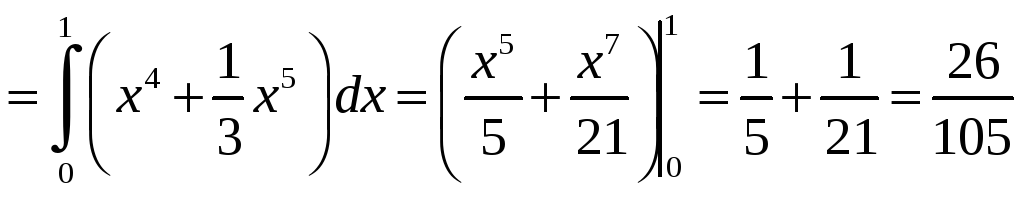
б)
Так как во внутреннем интеграле
интегрирование производится по переменной
x,
то y3
можно вынести во внешний интеграл как
постоянный множитель. Поскольку y2
во внутреннем интеграле считается
постоянной величиной, то этот интеграл
будет табличным. Производя последовательно
интегрирование по y
и x,
получаем
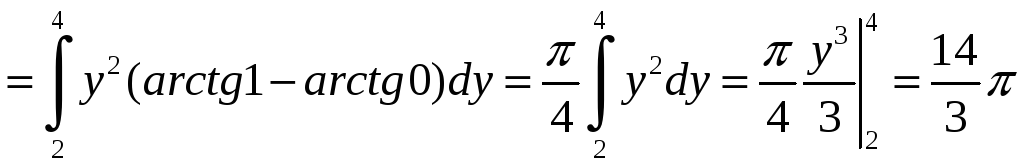
Между
двойными и повторными интегралами
существует взаимосвязь, но сначала
рассмотрим простые и сложные области.
Область называется простой
в каком-либо направлении, если любая
прямая, проведенная в этом направлении,
пересекает границу области не более
чем в двух точках. В декартовой системе
координат обычно рассматривают
направления вдоль осей Ox
и Oy.
Если область является простой в обоих
направлениях, то говорят коротко –
простая область, без выделения направления.
Если область не является простой, то
говорят, что она сложная.
Л
а
б
Рис.
1.4
юбую сложную область можно
представить в виде суммы простых
областей. Соответственно, любой двойной
интеграл можно представить в виде суммы
двойных интегралов по простым областям.
Поэтому в дальнейшем мы будем рассматривать,
в основном, только интегралы по простым
областям.
Теорема.
Если
область интегрирования D
– простая в направлении оси Oy
(см. рис.1.4а), то двойной интеграл можно
записать в виде повторного следующим
образом:
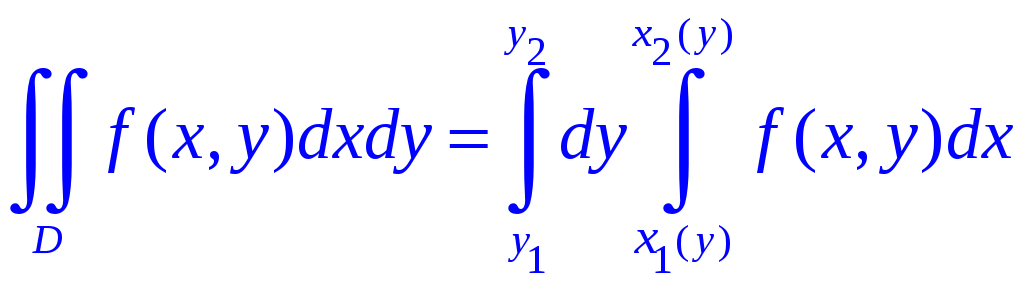
(1.6)
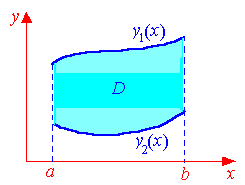
если
область интегрирования D
– простая в направлении оси Ox
(см. рис.1.4б), то двойной интеграл можно
записать в виде повторного следующим
образом:
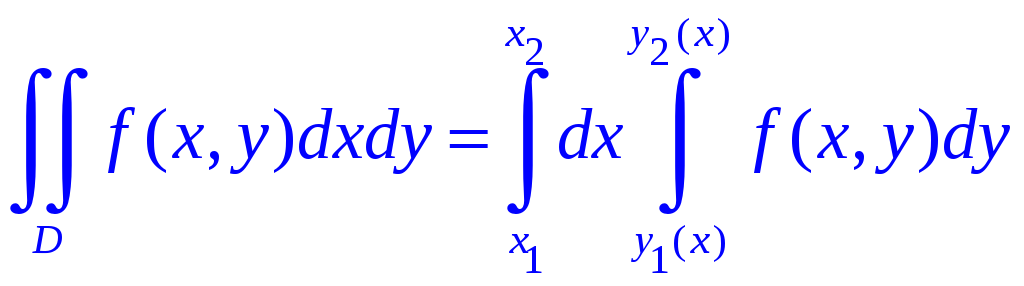
(1.7)
Е
|
простая |
простая |
простая |
сложная |
Рис.
1.3
сли область интегрирования
является правильной в обоих направлениях,
то можно произвольно выбирать вид
повторного интеграла, в зависимости от
простоты интегрирования.
1.3.
РАССТАНОВКА ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ
1.3.1.
Прямоугольная область интегрирования
П
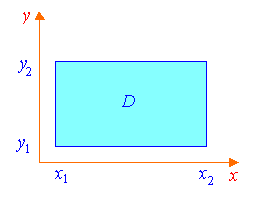
1.5
ри сведении двойных интегралов к
повторным, основная трудность возникает
при расстановке пределов во внутренних
интегралах. Наиболее просто это сделать
для прямоугольных областей (см. рис.
1.5).
Пример
1.2.
Вычислить двойной интеграл
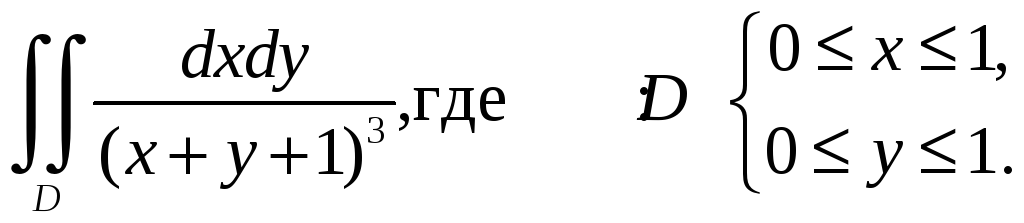
Решение.
Запишем двойной интеграл в виде
повторного:
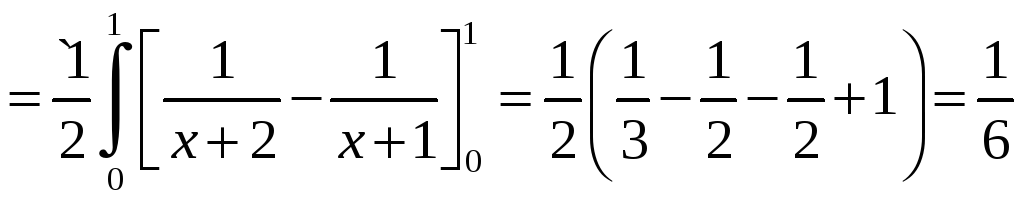
1.3.2.
Произвольная область интегрирования
Для того, чтобы
перейти от двойного интеграла к повторному
следует:
-
построить
область интегрирования; -
расставить
пределы в интегралах, при этом следует
помнить, что пределы внешнего интеграла
должны быть постоянными величинами
(т.е. числами) независимо от того, по
какой переменной вычисляется внешний
интеграл.
Пример
1.3.
Расставить пределы интегрирования в
соответствующих повторных интегралах
для двойного интеграла
,
если а)
б)
Р
1.6
ешение.
а)
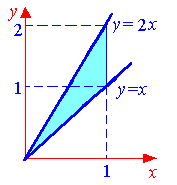
Изобразим область интегрирования D
(см. рис.1.6). Пусть интегрирование во
внешнем интеграле производится по
переменной x,
а во внутреннем – по y.
Расстановку
пределов всегда нужно начинать с внешнего
интеграла, в данном
случае с переменной x.
Из рисунка видно, что x
изменяется от 0 до 1, при
этом значения переменной y
будут изменяться от значений на прямой
y=x
до значений на прямой y=2x.
Таким образом, получаем
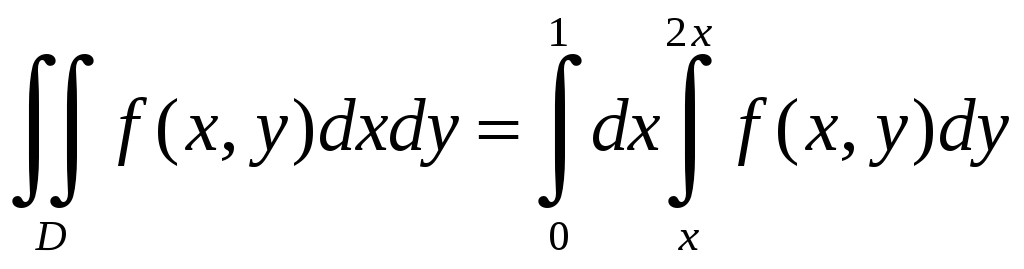
Пусть
теперь интегрирование во внешнем
интеграле производится по y,
а во внутреннем – по x.
В этом случае значения y
будут изменяться от 0 до 2. Однако тогда
верхняя граница изменений значений
переменной x
будет состоять из двух участков x=y/2
и x=1.
Это означает, что область интегрирования
нужно разбить на две части прямой y=1.
Тогда в первой области y
изменяется от 0 до 1, а x
от прямой x=y/2
до прямой x=y.
Во второй области y
изменяется от 1 до 2, а x
– от прямой x=y/2
до прямой x=1.
В результате получим
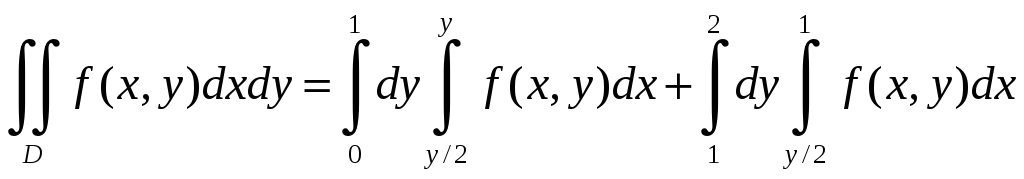
б
Рис.
1.7
) Построим область
интегрирования D
(см. рис.1.7). Пусть во внешнем интеграле
интегрирование производится по x,
а во внутреннем – по y.
В этом случае при изменении x
от –1 до 1 изменения переменной y
сверху будут ограничены двумя линиями:
окружностью и прямой. На отрезке [–1;0]
y
изменяется от y=0
до
;
на отрезке [0;1] переменная y
изменяется от y=0
до y=1–x.
Таким образом,
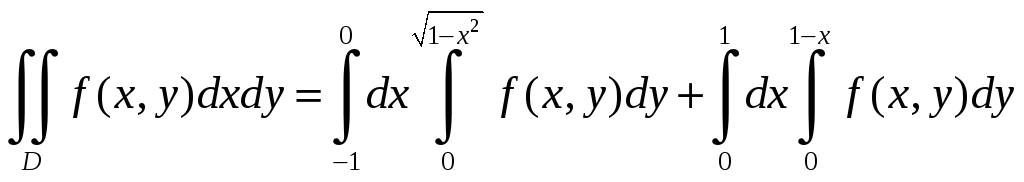
Пусть
теперь во внешнем интеграле интегрирование
производится по y,
а во внутреннем – по x.
В этом случае y
будет изменяться от 0 до 1, а переменная
x
– от дуги окружности
до
прямой x=1–y.
В результате получим
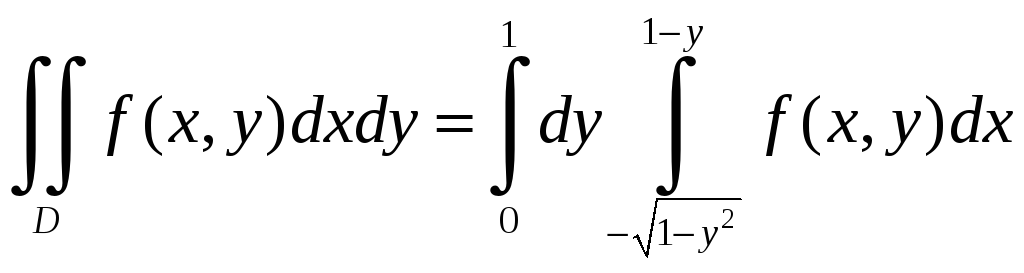
Данные примеры
показывают, как важно правильно выбирать
порядок интегрирования.
Пример
1.4.
Изменить порядок интегрирования
а)
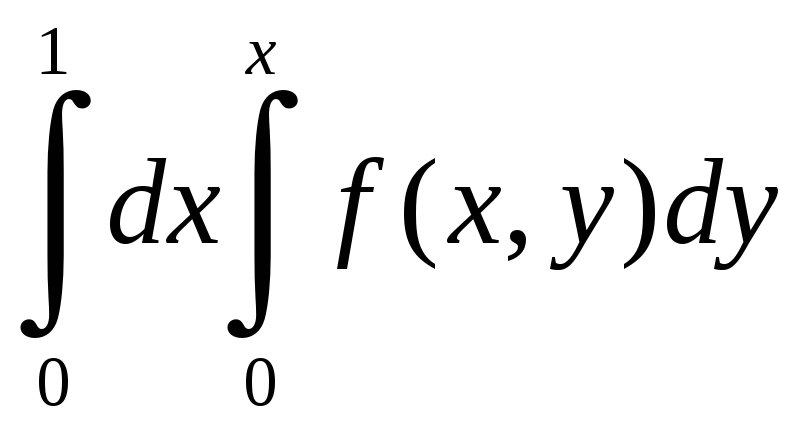
б)
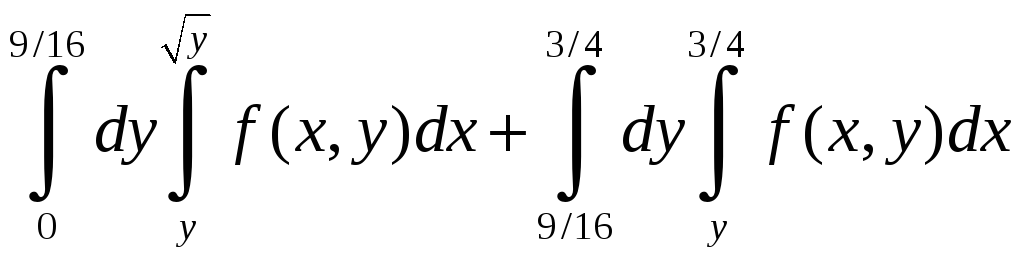
Р
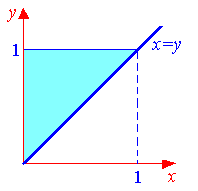
1.8
ешение.
а)
Построим область интегрирования. На
отрезке [0;1] для x
переменная y
изменяется от прямой y=0
до прямой y=x.
В результате получается следующая
область интегрирования (см. рис.1.8). На
основании построенного рисунка,
расставляем пределы интегрирования
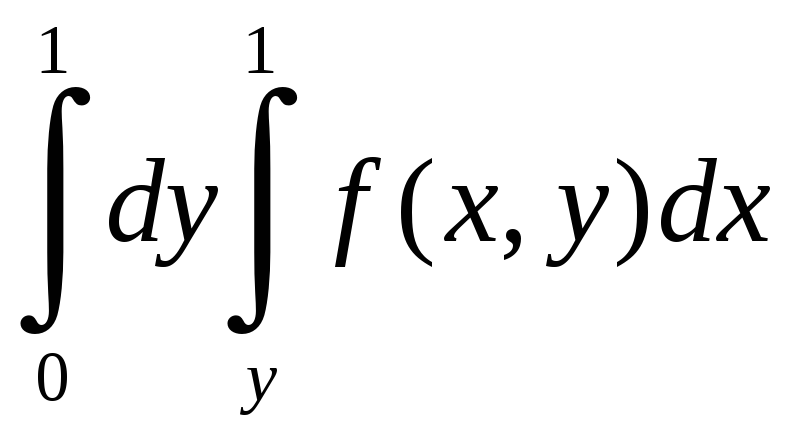
б)
Построим область интегрирования. На
отрезке [0;9/16] для y
переменная x
изменяется от прямой x=y
до параболы
;
на отрезке [9/16;3/4] – от прямой x=y
до прямой x=3/4.
В результате получается следующая
область интегрирования (см. рис.1.9). На
основании построенного рисунка,
расставляем пределы интегрирования,
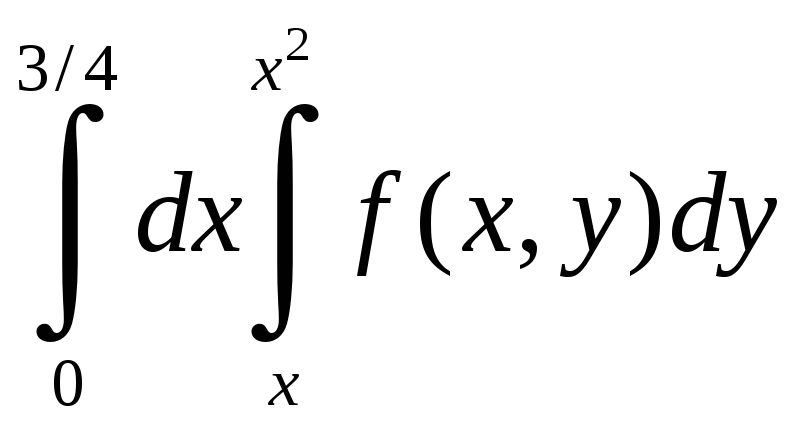
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


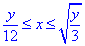
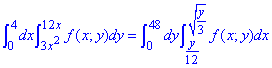
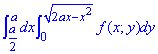
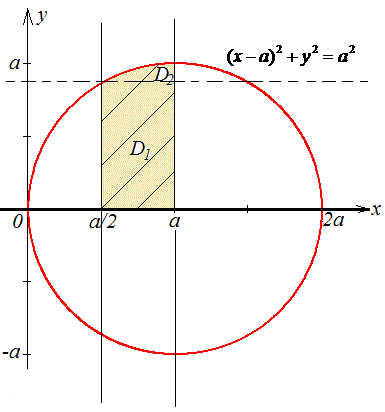
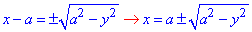
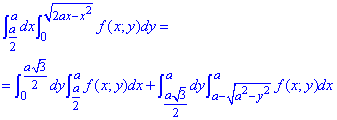
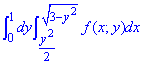
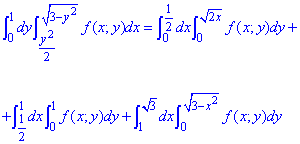
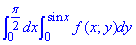
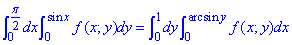







 (так как одна из формул преобразования имеет вид
(так как одна из формул преобразования имеет вид  то линии
то линии  в плоскости
в плоскости  соответствует линия
соответствует линия  в плоскости
в плоскости  ),
),  (рис. 20 6).
(рис. 20 6).