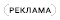Иногда нужно получить определенный фазовый сдвиг ВЧ сигнала. Например, такая задача возникает, когда вы делаете фазированные антенные решетки (ФАР). На УКВ задача решается просто. Берем кабель длиной N×λ с поправкой на коэффициент укорочения кабеля, и получаем фазовый сдвиг N×360°. Но на КВ такой способ не всегда практичен, поскольку λ измеряется десятками метров. Вот о некоторых альтернативных схемах, решающих ту же задачу, далее и пойдет речь.
Важно! У меня возникли небольшие сложности с поиском устоявшихся вариантов перевода для использованных далее терминов. Вся английская терминология верна, однако русская терминология остается под вопросом. Если вы знаете более удачные варианты перевода, прошу поделиться ими в комментариях.
Фазореверсирующий трансформатор
Сдвинуть фазу на 180° можно очень просто. Разрезаем кусок коаксиального кабеля. Жилу левого отрезка припаиваем к экрану правого, а жилу правого отрезка — к экрану левого. Этим мы перевернули сигнал, то есть, сдвинули его на 180°. Но есть нюанс. Мы не можем гарантировать, что экран левого отрезка не имеет контакта с экраном правого. Это зависит от того, кто и в какой задаче использует наше устройство для сдвига фазы. Если контакт есть, то вместо сдвига фазы мы получаем КЗ.
Решение заключается в том, чтобы отрезать путь ВЧ сигналу через внешнюю сторону экрана:
Семь витков RG58 намотано на кольце FT114-43. На входе жила и экран припаяны к BNC-разъему как положено, а на выходе — задом наперед. Такое устройство называется фазореверсирующим трансформатором (phase reversal transformer). Вопреки названию, трансформатора в привычном смысле здесь нет. Принцип действия больше похож на то, как работает балун по току 1:1. Использование отрезка кабеля не нулевой длины приводит к дополнительному фазовому сдвигу. На КВ этот сдвиг будет небольшим.
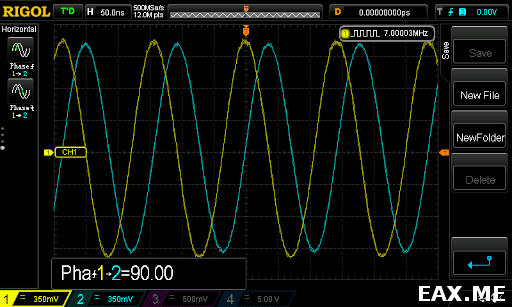
Берем генератор сигналов и осциллограф. Убеждаемся, что все работает:
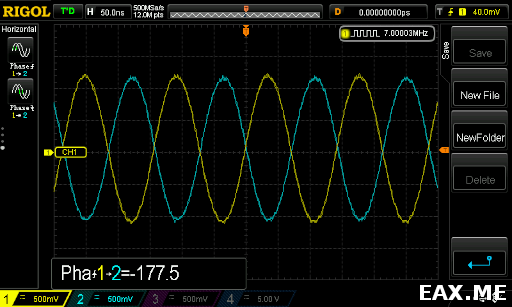
Выход генератора подается на делитель мощности. С первого выхода делителя сигнал идет на первый канал осциллографа, а со второго выхода — на второй канал через DUT. Важно, чтобы кабели по обоим путям были одинаковыми и равной длины. Для согласования импеданса подключение к осциллографу осуществляется через T-образные BNC-коннекторы с нагрузкой 50 Ом. На скриншоте видим фазовый сдвиг 177.5°. Вообще, осциллограф не является самым точным прибором для измерения таких вещей. Его показания скачут где-то на ±3°.
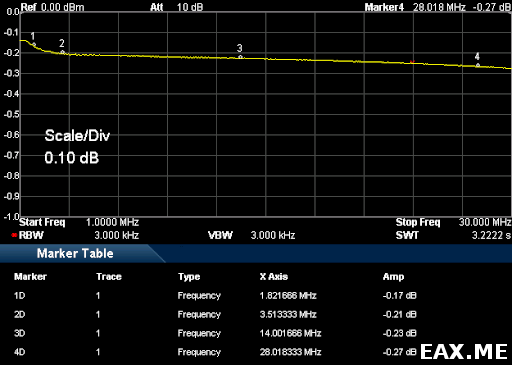
Анализатор спектра показывает вносимые потери порядка 0.25 дБ:
Это довольно много и объясняется использованием недорогого кабеля, который был сильно изогнут. Для минимизации потерь нужно использовать более толстый кабель и ферритовое кольца большего диаметра.
Описание подхода из этого раздела впервые встретилось мне в книге ON4UN’s Low Band DXing, 5th Edition. В этой же книге я нашел отсылку к статье, описывающей гибридный ответвитель. О нем речь пойдет в следующем разделе.
Квадратурный гибридный ответвитель
В качестве следующего устройства рассмотрим гибридный ответвитель со сдвигом фазы 90°, также называемый квадратурным гибридным ответвителем. Часто говорят просто «гибридный ответвитель» (hybrid coupler), так как по контексту понятно, о чем речь.
Описание устройства и формулы для его расчета можно найти в статье «Twisted-Wire Quadrature Hybrid Directional Coupler», написанной Reed Fisher, W2CQH и опубликованной в журнале QST за январь 1978 года. Здесь я не стану пересказывать статью и лишь расскажу о своем опыте изготовления конкретного гибридного ответвителя.
На основе формул из статьи был написан скрипт hybrid-coupler.py. Вы найдете его в этом репозитории на GitHub. Перебирая аргументы скрипта, я остановился на такой схеме:
$ ./hybrid-coupler.py 6300000
L1
IN —+—CCCC—+— OUT1
| |
C1 — C2 —
— —
| |
OUT2 —+—CCCC—+— DUMP
L2
L1 = L2 = L
C1 = C2 = C
C = 252.6269 pF
L = 1.2631 uH
Схема состоит из двух конденсаторов и двух катушек индуктивности. Катушки мотаются бифилярной обмоткой на одном ферритовом кольце. Сигнал подается на порт IN. С портов OUT1 и OUT2 выходит две его копии с уровнем -3 дБ и разностью фаз 90°. Порт DUMP не используется и должен быть нагружен на 50 Ом. Устройство работает на одной частоте, плюс в некоторых ее окрестностях. Номиналы компонентов вычисляются из этой частоты, а также волнового сопротивления портов.
Устройство похоже на делитель/сумматор. В том числе, оно может работать и в обратную сторону, как сумматор. Отличие заключается в фазовом сдвиге между выходами, а также зависимостью от частоты.
Почему выбрана такая странная частота, 6.3 МГц? Дело в том, что большинство имеющихся у меня ферритовых колец имеют высокую магнитную проницаемость. Они обеспечивают индуктивность в 1-2 мкГн, необходимые для работы схемы, буквально в один виток. В качестве исключения в запасах нашлось кольцо FT82-61, имеющее Al = 79 и погрешность ±20%. Четыре витка на таком кольце должны давать примерно:
>>> (79*pow(4,2))/1000
1.264
… 1.264 мкГн, которые позволяют сделать гибридный ответвитель на 6.3 МГц. L1 и L2 я мотал эмалированной проволокой толщиной 0.6 мм простой бифилярной обмоткой, без скручивания. Измеренная индуктивность составила ровно 1.2 мкГн. С парой конденсаторов на 241 пФ мы получим гибридный ответвитель где-то на 6.6 МГц. У меня как раз нашлась пара NP0 конденсаторов по 240 пФ. Это чуть меньше, но я подумал, что разница в 1 пФ не должна все сломать.
Гибридный ответвитель получился таким:
А это вид сверху:
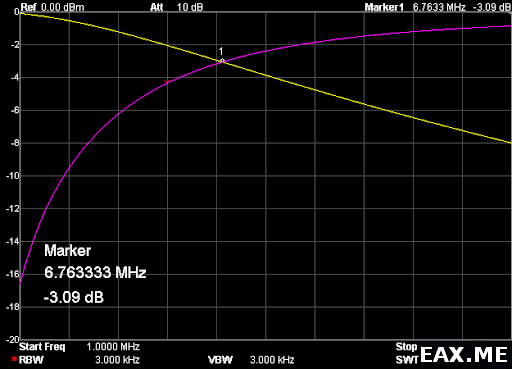
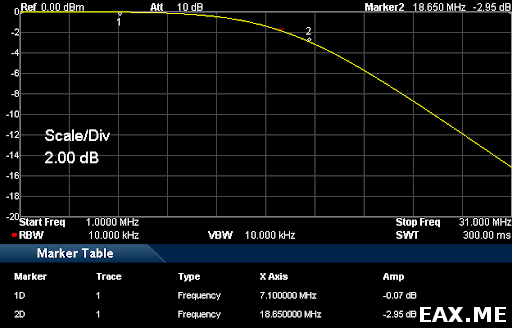
Точка -3 дБ пришлась где-то на 6.76 МГц:
Наконец, проверим фазовый сдвиг при помощи осциллографа:
Как можно видеть, на 7.0-7.2 МГц гибридный ответвитель тоже как-то работает. При этом сигналы на портах OUT1 и OUT2 различаются на 0.3-0.6 дБ.
Устройство было проверено и в режиме сумматора. Все работает. Генерируемые при этом картинки мало отличаются от полученных ранее для самодельного делителя/сумматора. Поэтому здесь я их не привожу.
Сдвиг фазы при помощи LC-цепей
Существует несколько LC-цепей, позволяющих получить произвольный фазовый сдвиг на заданной частоте. Этот вопрос поднимается во многих источниках. Больше всего мне понравилась статья High-Pass Low-Pass Phase Shifters на сайте microwaves101.com. Опять же, пересказывать статью в мои планы не входит. Вместо этого я расскажу об опыте применения ее на практике.
На основе формул из статьи был написан скрипт phase-shifter.py. Как и предыдущий скрипт, вы найдете его на GitHub. При помощи LTspice я убедился, что скрипт генерирует правильные схемы.
Теперь допустим, что я хочу получить фазовый сдвиг 42° на частоте 7.1 МГц. Скрипт предлагает четыре схемы на выбор, из которых мне больше всего приглянулась такая:
$ ./phase-shifter.py 7100000 42
…
Low pass tee:
L1 L2
—CCCC—+—CCCC—
|
——
—— C1
|
V
L1 = L2 = 0.4302 uH
C1 = 299.9872 pF
Катушки на 0.43 мкГн легко намотать, а 300 пФ — это стандартный номинал:
При размещении катушек я старался минимизировать эффект взаимоиндукции.
Фактически, перед нами фильтр нижних частот:
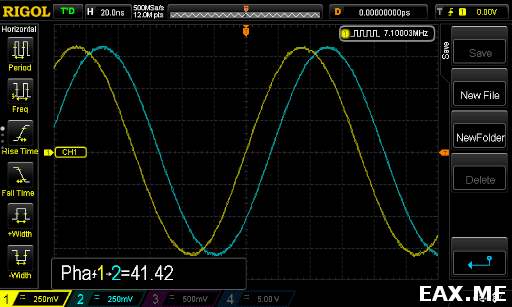
Действительно, 7.1 МГц попадает в полосу пропускания, и на частоте мы видим:
… фазовый сдвиг примерно в 42°. На частоте 1 МГц имеем сдвиг примерно в 5°, а ближе к точке -3 дБ получаем 120°.
Заключение
Список возможных решений не претендует на полноту. Но он покрывает многие реальные случаи. Особенно если не забывать про возможность сдвинуть фазу банально куском кабеля.
А сталкивались ли вы с задачей, где нужно обеспечить фазовый сдвиг сигнала? Если да, то что это была за задача, и как вы ее решали?
Дополнение: См также заметки Получаем сигналы с фазовым сдвигом 90° при помощи двойного D-триггера 74HC74 и Генерация сигналов с фазовым сдвигом при помощи Si5351.
Метки: Беспроводная связь, Любительское радио, Электроника.
Понятие сдвига фазы в аналоговых цепях
Добавлено 19 июня 2020 в 23:11
Рассмотрим, что такое сдвиг фазы, и как это фундаментальное электрическое явление связано с различными конфигурациями схем.
В данной статье рассказывается о сдвиге фазы, о влиянии схемы, вызывающем опережение или отставание напряжения или тока на выходе схемы относительно входа. В частности, нам будет интересно то, как реактивные нагрузки и цепи будут влиять на сдвиг фазы в схеме. Сдвиг фазы может иметь всевозможные последствия, независимо от того, работаете ли вы с генераторами, усилителями, петлями обратной связи, фильтрами и т.п. Например, вы ожидаете, что ваша инвертирующая схема на операционном усилителе будет давать сдвиг фазы на 180°, но вместо этого она возвращает синфазный сигнал и вызывает проблемы с автоколебаниями. Или, например, подключение измерительных щупов для анализа цепи может внести свое влияние. Или, возможно, у вас есть резонансный контур, который используется в петле обратной связи автогенератора, но контур обеспечивает сдвиг фазы только 90°, тогда как вам нужно 180°. Вы должны изменить контур, но как?
Сдвиг фазы для реактивных нагрузок
Частотно-зависимый сдвиг фазы происходит из-за влияния реактивных компонентов: конденсаторов и катушек индуктивности. Это относительная величина, и поэтому она должна быть задана как разность фаз между двумя точками. В данной статье «сдвиг фазы» будет означать разницу по фазе между выходом и входом. Говорят, что конденсатор вызывает отставание напряжения от тока на 90°, в то время как индуктивность вызывает отставание тока от напряжения на 90°. В векторной форме это обозначается +j или -j в индуктивном и емкостном реактивном сопротивлении соответственно. Но емкость и индуктивность в некоторой степени существуют во всех проводниках. Так почему же они не вызывают сдвиги фаз на 90°?
Все наши эффекты сдвига фазы будут моделироваться цепями RC и RL. Все схемы могут быть смоделированы как источник с некоторым внутренним сопротивлением, рассматриваемая схема и нагрузка, следующая за схемой. Внутренний импеданс источника также называется его выходным сопротивлением. Я считаю, что проще всего говорить о входном и выходном импедансе и о каскадах, поэтому позвольте мне перефразировать: все схемы могут быть смоделированы как выход одного каскада с некоторым выходным импедансом, питающий следующий каскад, который нагружен входным импедансом следующего каскада. Это важно, потому что это уменьшает сложность цепей до гораздо более простых RLC-цепей, фильтров и делителей напряжения.
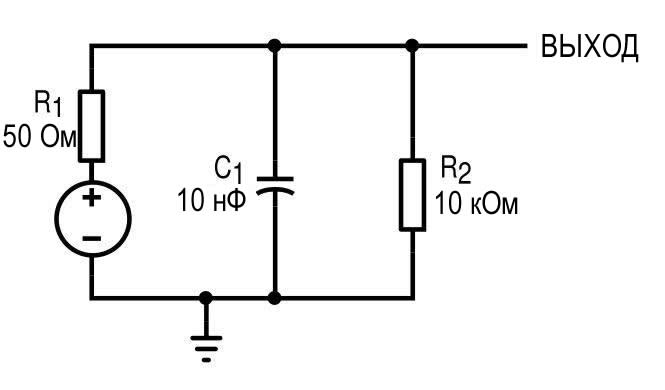
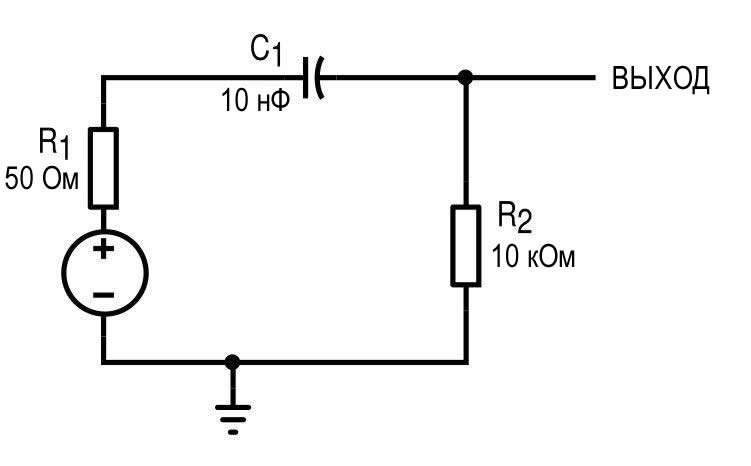
Взгляните на следующую схему.
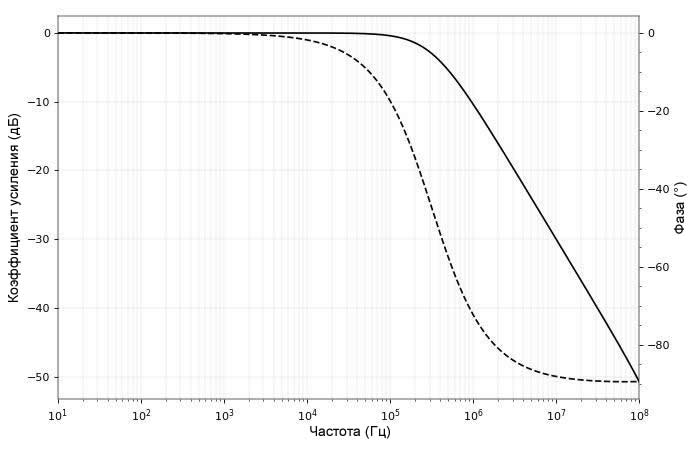
Это будет моделировать некоторую цепь источника (например, усилитель) с выходным сопротивлением 50 Ом, который имеет нагрузку 10 кОм и шунтируется конденсатором 10 нФ. Здесь должно быть понятно, что схема, по сути, является RC-фильтром нижних частот, выполненным из R1 и C1. Из базового анализа цепей мы знаем, что сдвиг фазы напряжения в RC-цепи будет изменяться от 0° до -90°, и моделирование подтверждает это.
Для низких частот фаза выходного сигнала не зависит от конденсатора. Когда мы доберемся до частоты среза (fср) RC-фильтра, фаза падает до -45°. Для частот выше частоты среза фаза приближается к своему асимптотическому значению -90°.
Эта фазо-частотная характеристика моделирует сдвиг фазы, вызванный любым шунтирующим конденсатором. Шунтирующий конденсатор вызовет сдвиг фазы на резистивной нагрузке между 0° и -90°. Конечно, также важно помнить и об ослаблении.
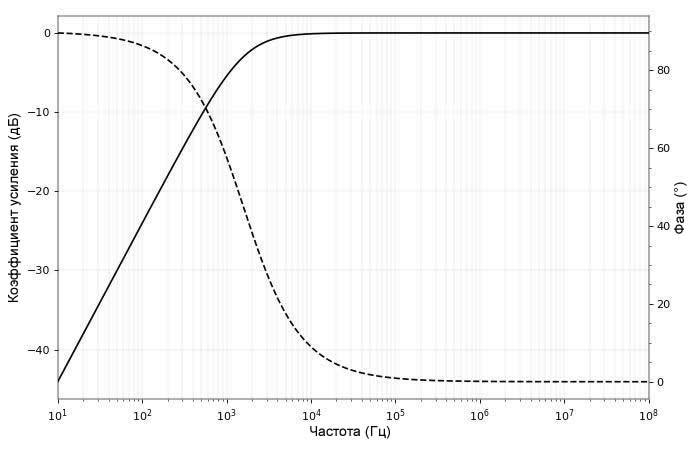
Аналогичный взгляд на последовательный конденсатор (например, конденсатор емкостной связи по переменному току) показывает типовой эффект подобной схемы.
В этом случае сдвиг фазы начинается с +90°, а фильтр является фильтром верхних частот. За пределами частоты среза, в конечном итоге, устанавливается значение 0°. Итак, мы видим, что последовательный конденсатор всегда будет вносить сдвиг фазы между +90° и 0°.
Усилитель с общим эмиттером
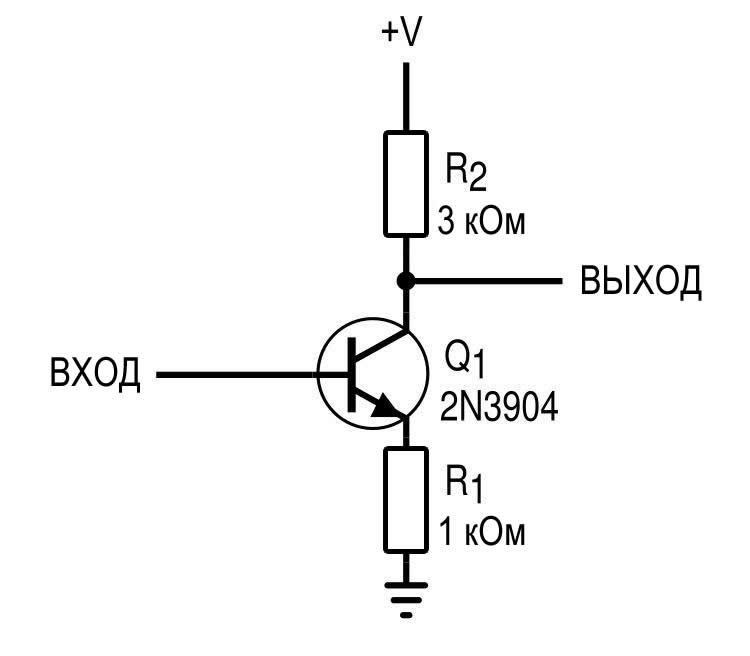
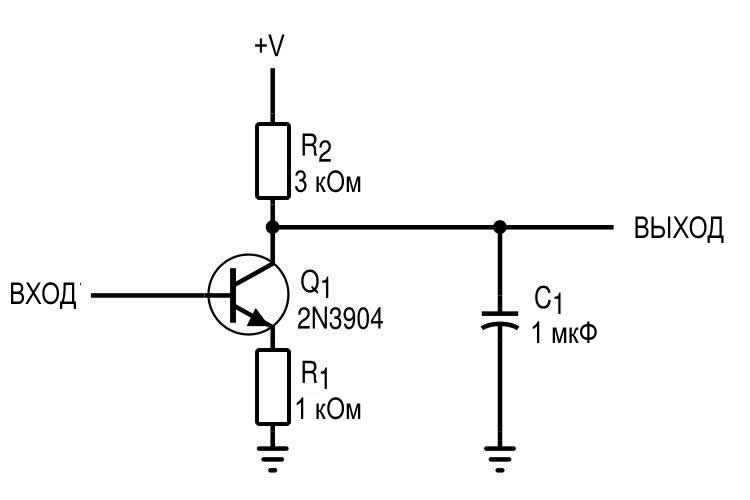
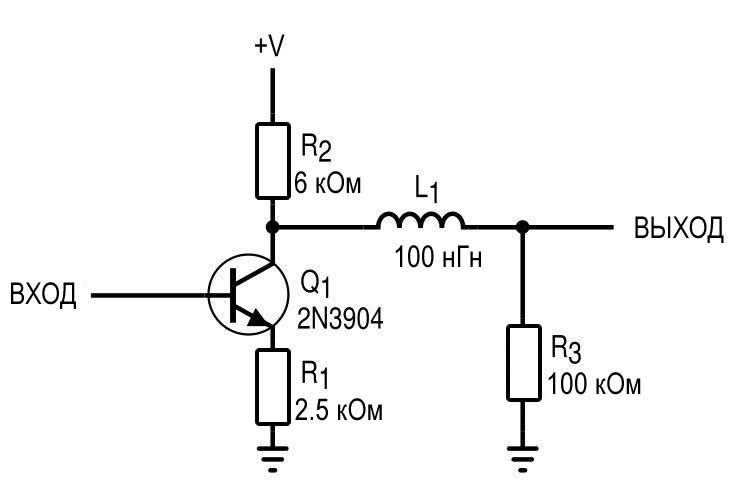
Имея в распоряжении эту информацию, мы можем применить RC-модель к любой цепи, к какой захотим. Например, этот усилитель с общим эмиттером.
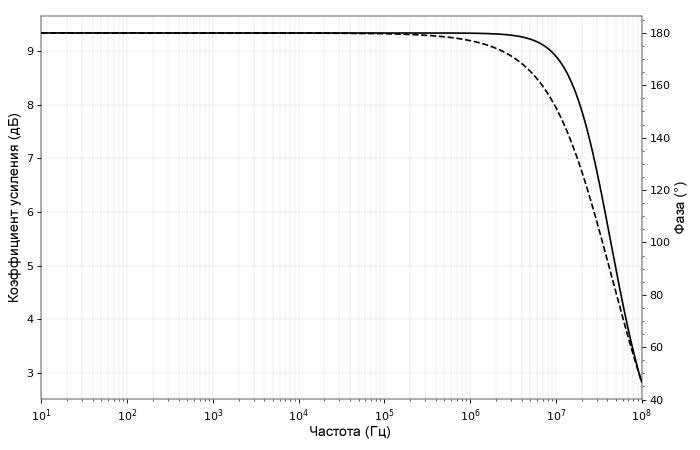
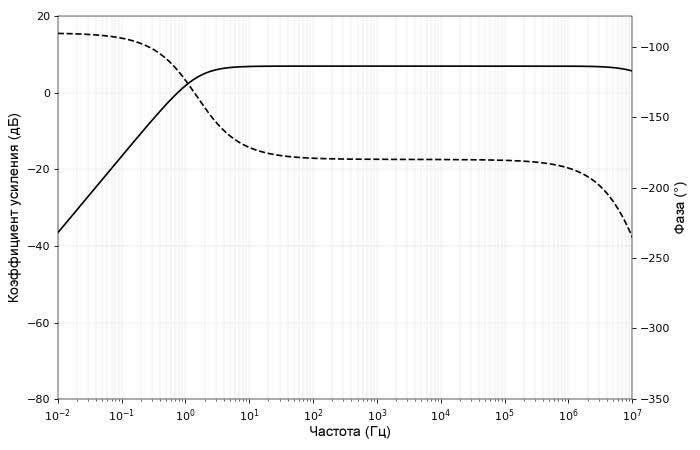
Частотные характеристики данного усилителя будут плоскими примерно до 10 МГц.
Только после примерно 10 МГц мы видим изменения сдвига фазы – ниже 180°, что мы и ожидаем, поскольку схема с общим эмиттером представляет собой инвертирующий усилитель. Выходной импеданс усилителя, пренебрегая эффектом Эрли, равен R2 = 3 кОм, что довольно высоко.
Теперь мы поставили на выходе шунтирующий конденсатор. Что мы можем ожидать от фазы?
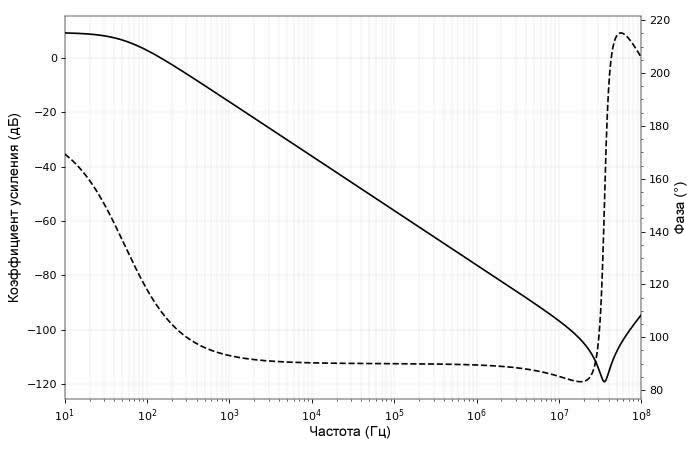
Исходя из нашего опыта, мы ожидаем, что частота среза будет составлять 53 Гц, ниже которой сдвиг фазы должен быть 180° (без влияния конденсатора), и выше которой сдвиг фазы будет равен 180° — 90° = 90° (а также большие потери). Моделирование подтверждает наши подозрения:
Обратите внимание, что это эквивалентно тому, если бы фаза изменялась от -180° до -270°. Теперь мы начинаем понимать, что питание емкостной нагрузки может привести к неожиданным изменениям фазы, что может нанести ущерб усилителю с неожиданной обратной связью.
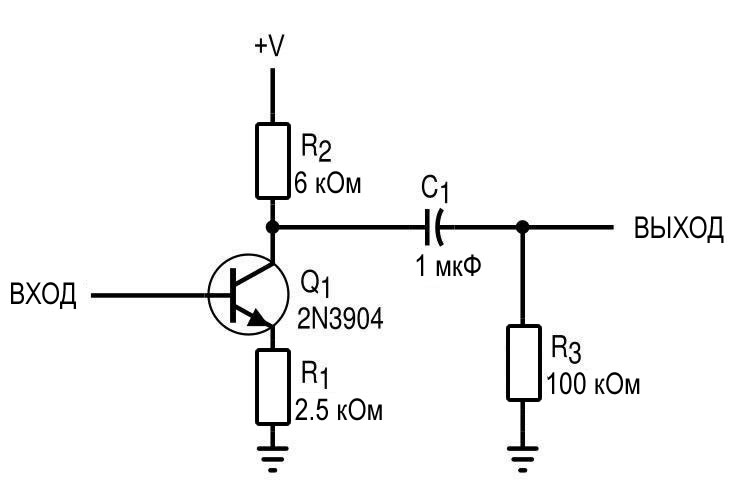
В более распространенном сценарии на выходе используется последовательно включенный конденсатор связи, как показано на следующей схеме.
Я изменил номиналы элементов схемы и добавил резистивную нагрузку 100 кОм. Теперь мы имеем фильтр верхних частот, состоящий из C1 и R3, с частотой среза всего 1,6 Гц. Мы ожидаем, что сдвиг фазы будет равен -90° на частотах ниже 1,6 Гц и -180° на частотах выше частоты среза, что подтверждается моделированием.
Конденсатор связи с таким номиналом подошел бы для сигналов звуковой частоты, поскольку область сдвига фазы -90° (и, следовательно, затухания) значительно ниже 10 Гц.
Конечно, такого рода эффекты не ограничиваются конденсаторами. Индуктивности будут оказывать противоположное влияние: шунтирующие катушки индуктивности вызывают сдвиг фазы от 0° (ниже fср) до +90° (значительно выше fср), в то время как последовательно включенные катушки индуктивности вызывают сдвиг фазы от 0° (выше fср) до -90° (ниже fср) , Однако в этом случае необходимо быть осторожным, чтобы не создавать проблемных замыканий на землю, поскольку катушки индуктивности для постоянного тока будут представлять собой короткое замыкание.
Заключение
Мы заложили основу для понимания сдвига фазы в аналоговых схемах. Рассматривая выход схемы как источник с выходным сопротивлением, мы можем эффективно моделировать влияние реактивных нагрузок на фазу схемы. Таким образом, можно моделировать как пассивные, так и активные схемы, что дает нам полезные инструменты для простого анализа и проектирования. В следующей статье мы проверим эти концепции, применив их к схемам на операционных усилителях и к резонансным контурам.
Теги
Аналоговые цепиЕмкостная связьСдвиг фазыУсилитель
Предполагаемое время на прочтение: 7 минут(ы)
Фазовый сдвиг – что это? А фаза звукового сигнала? Попробуем немного разобраться в этом вопросе. Не факт, что смогу ясно разъяснить этот вопрос, но примерное понятие должно получиться.
Пролог
Музыканты, меломаны, а так же, любители “хай-эндовского” звука, в разговорах между собой, часто используют, вроде бы всем понятные термины – спектр, фаза, частота, меандр, глубина и локализация сцены, и прочие узкозначимые слова. Но зачастую, даже некоторые из “знатоков”, до конца не могут понять, что же это на самом деле такое.
Такие понятия как – “Фазовый сдвиг” очень часто упоминаются при проектировании кроссоверов для акустики. Подробно про кроссоверы мы уже поговорили чуть ранее.
При наличии интернета выяснить тот или иной вопрос не составляет проблем. В отсутствии такового – можно сходить в библиотеку, найти пару реально научных книжек и почитать саму теорию. Но все нынче стали на столько занятые, что даже выуживать информацию из интернета – времени нет. Попробуем найти простое объяснение – что же такое “фазовый сдвиг”?
Что означают эти термины на самом деле? Можно ли “пощупать” их истинное значение? Да, однозначно, можно. Сейчас мы попробуем разобраться в вопросе – “Что такое – фазовый сдвиг?”
Фаза сигнала
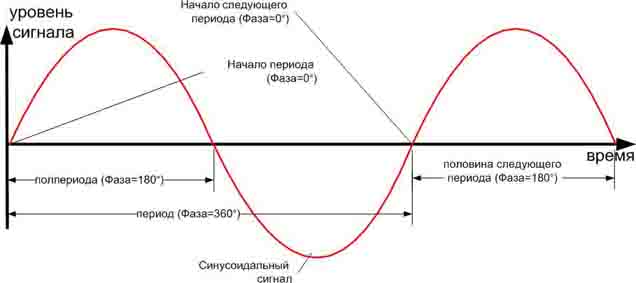
Для начала порассуждаем, что такое – “фаза сигнала”. Фаза сигнала никогда не существует сама по себе. Это виртуальное понятие. Вообще, можно сказать так: Фаза – это уровень сигнала в текущий момент времени, или иначе, – это уровень звукового давления в текущий момент времени в измеряемой точке пространства (к примеру, это место, где находится слушатель).
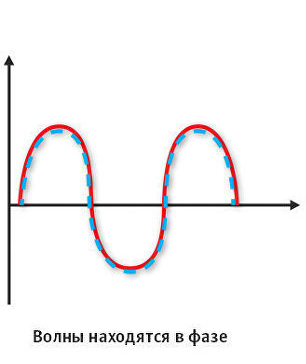
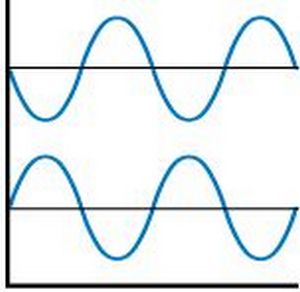
Вот картинка, изображающая звуковые волны в фазе. К примеру, звуковые сигналы двух каналов нашей акустики совпадают. В этом случае, музыка звучит чётко, без каких либо искажений. В музыкальном произведении можно услышать все задействованные инструменты, которые звукорежиссер слышал при записи. Имеется некая область звукового давления, где ощущается “эффект присутствия” – это то, о чем спорят меломаны и аудиофилы. Иными словами – получаем ожидаемый звук и впечатления.
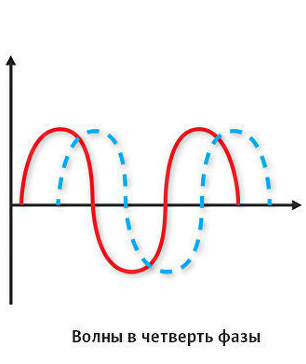
На следующей картинке ниже, фаза смещена на 90 градусов, или на четверть фазы. Этот эффект можно услышать в виде небольшого эха. Это может и не связано с оборудованием самой комнаты. Эффект звуковой задержки с небольшим смещением фазы вносит некую сумятицу в музыку, теряется “картинка”, исполнители “уходят в разные стороны”, появляется ощущение, что находишься в огромном зале с каменными стенами. Звуки становятся не естественными, искаженными.
Далее, мы наблюдаем смещение фаз на 180 градусов. То есть, акустика в этом случае играет в противофазе. Чуть ниже подробно об этом. В данном случае, общая “звуковая картина” на столько становится не понятной, что слушать музыку становится просто не интересно и противно. Звуки становятся “ватные”, многие часты просто могут отсутствовать, хотя они и воспроизводятся колонками. Может сложиться такое впечатление, что слушаешь музыку в завязанной шапке-ушанке.
Далее, немного теории без научных выкладок.
К примеру, слушая, сидя у себя дома, свои акустические системы, мы слышим, как они порождают в районе дивана те или иные переменные звуковые давления. Звуковые волны складываются друг с другом. Эти волны имеют разные частоты и амплитуду. Они то нарастают, то убывают.
Противофаза
А теперь предположим, что давления от обоих колонок (звуковые волны) изменяются одинаково, но имеют противоположную направленность. То есть, одна колонка излучает “плюсовые” волны, а другая колонка – “минусовые”. Это может случиться, когда слушатель, случайно, перепутал клеммы подключения одного из каналов (левый канал например).
Немного проще. Динамики правой колонки играют вперёд, а динамики в левой колонке играют назад, одновременно пытаясь воспроизводить одну и туже частоту. Одна колонка создаёт давление, скажем, 1 Паскаль, а другая – минус 1 Паскаль. Такой эффект называется – противофаза.
Общая громкость звука в том месте, где находится слушатель, теоретически, должна стремится к нулю, но это не означает, что какой либо звук вообще будет не слышно. В этом случае, может сильно поломаться “звуковая сцена”, “картинка” музыкального произведения, а в каком либо месте помещения звук реально будет затухать, но не совсем. Звук станет “смазанным” и исчезнут некоторые частотные составляющие из общего звукового сигнала.
Не будем вдаваться в непростую научную формулировку, приводя формулы. Можно сказать так, что из второй колонки звук доходит к слушателю, но с задержкой по времени (не забываем, что сигнал на колонки подаётся одинаковый!). И задержка в этом случае получается именно 180 градусов. Почему так? Попробуем разобраться на картинке, нагляднее – понятнее.
360 градусов – длина периода сигнала (Фаза), 180 градусов – половина периода сигнала.
Фазовый сдвиг
А теперь, мы дошли до момента, когда можно уже разобрать вопрос – “Что такое – фазовый сдвиг?”
Фаза — это временная связь двух сигналов. И в течении периода колебания меняется от 0 до 360 градусов. Потом опять – от 0 до 360, и так далее. Можно сказать, что это мгновенный уровень сигнала в определенной точке времени внутри периода. Саму фазу мы не слышим, но слышим фазовый сдвиг одного сигнала относительно другого.
Вики про это говорит так: Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Фазовый сдвиг является безмерной величиной и измеряется в градусах или долях периода.
Вывод
Предположим, вы подключили два динамика к выходу усилителя (пусть физически это будут ваши акустические системы). Один динамик как положено – плюс на плюс, минус на минус. А второй, перепутали и он получился подключенным плюс на минус и минус на плюс. Включив усилитель, что мы услышим? Вероятнее всего – жалкое подобие звука. Один динамик будет как-бы гасить сигнал другого своими звуковыми волнами.
На картинках ниже будет нагляднее. Представим, что это мы видим на экране осциллографа, который измеряет сигналы левого и правого каналов вашего усилителя.
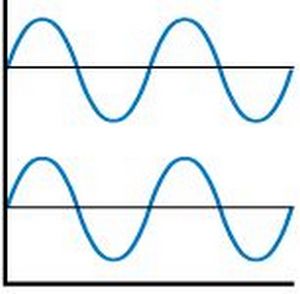
Вторая картинка демонстрирует осциллограмму полного не совпадения. “Горб” левого канала по времени совпадает с “ямой” правого. Чисто по школьной физике – в результате сложения таких колебаний, в идеале, получится ноль. Эти сигналы будут взаимно подавлять друг друга. Сигналы в противофазе.
Фазовый сдвиг подразумевает запаздывание первого сигнала по времени относительно второго.
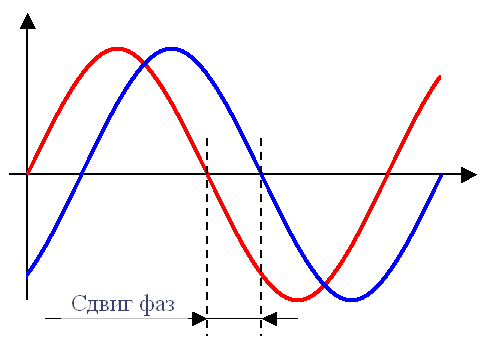
Все эти картинки и рассуждения, о физических свойствах звуковых волн, отдаленно относятся к практике, к реальности. Звуки любого музыкального инструмента нельзя назвать – “одночастотным сигналом” (как осциллограмма на картинках). Частичный сдвиг фаз может ослаблять одни частоты по сравнению с другими. А иногда, усиливать некоторые из них.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
С фазировкой звука я познакомился задолго до анализа искажений динамических головок.
Так уж довелость, что многие люди считают её очень важной, подключение фазировки динамика.
Увы на деле всё оказалось совсем иначе….
Приступим.
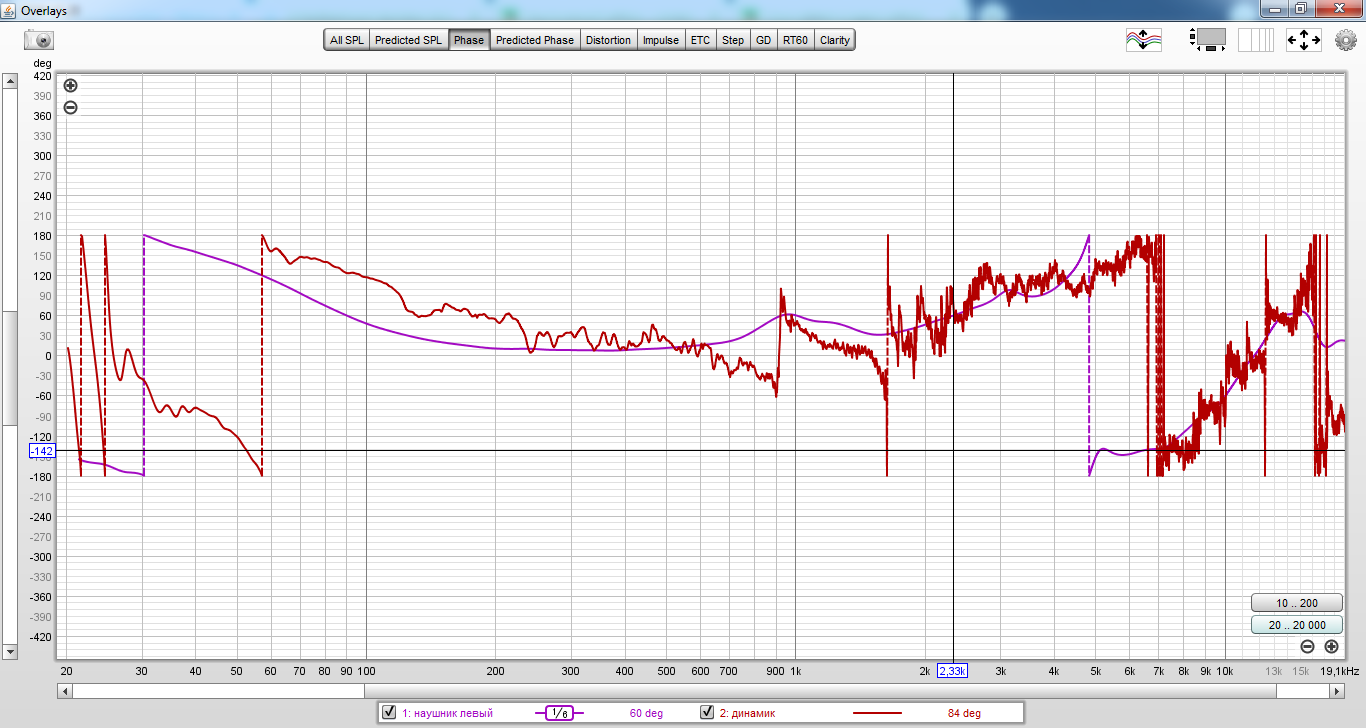
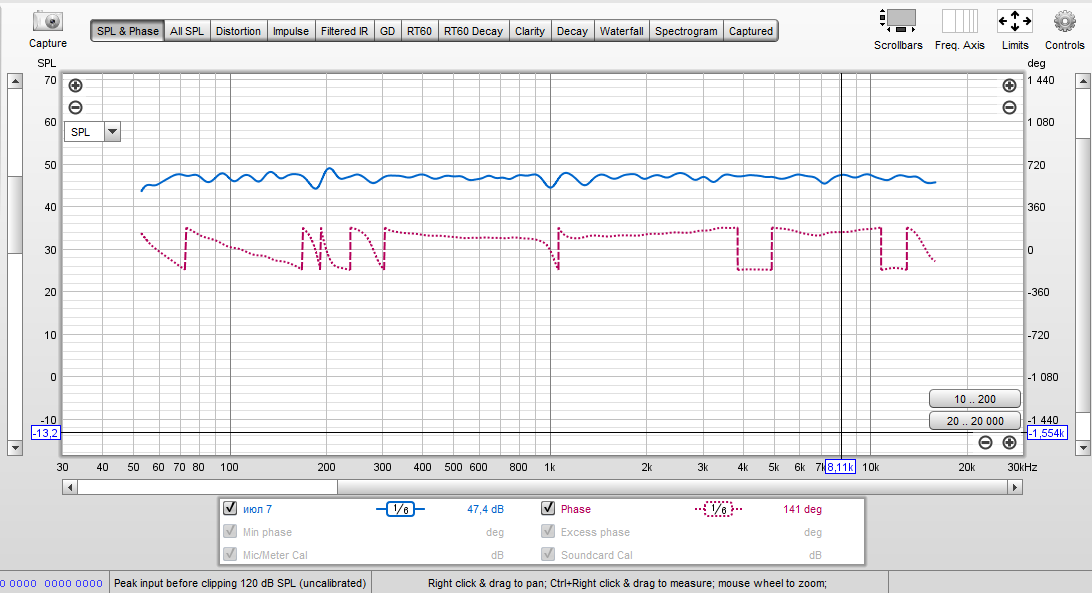
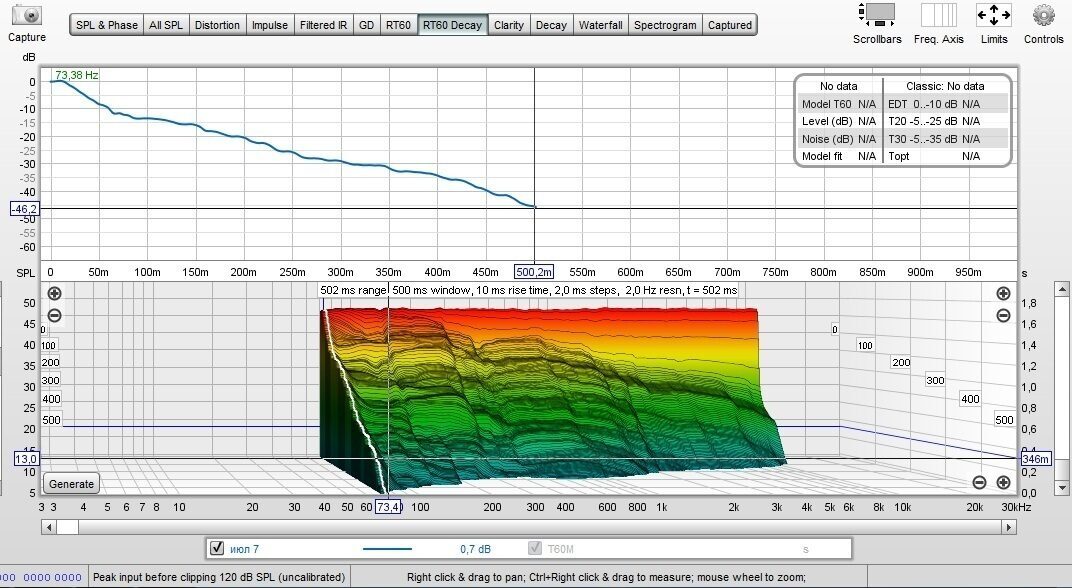
Если посмотреть на данные графики розовым цветом выделена фаза сигнала наушника в мягкой мембране с подключенным в плотную микрофона.
Красным цветом я снял фазу из помещения.
На красном графике видно как фаза имеет очень сильные броски в особенности от ~1,8 kHz, это явление называется интерференция сигнала.
Звуковые волны в помещении переотражаются от стен.
Звуковые же студии специально готовят для исключения эффекта реверберации (но чуть чуть оставляют).
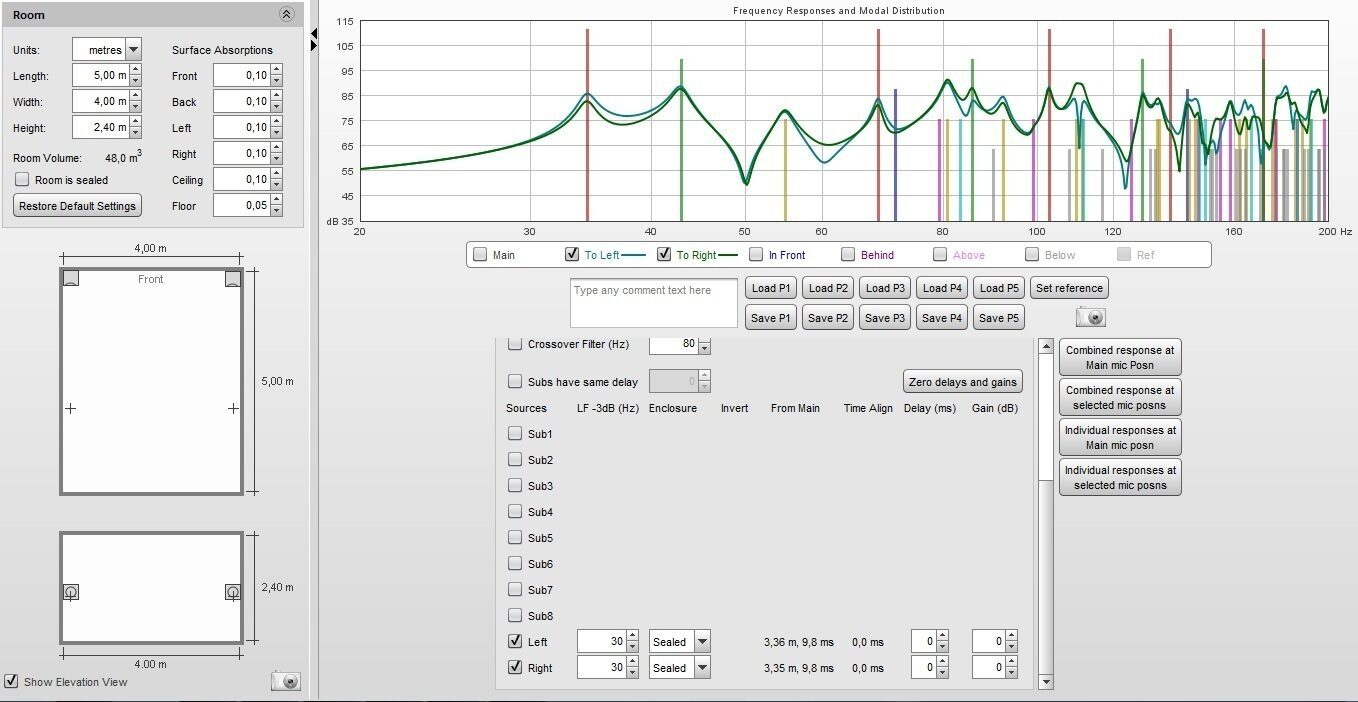
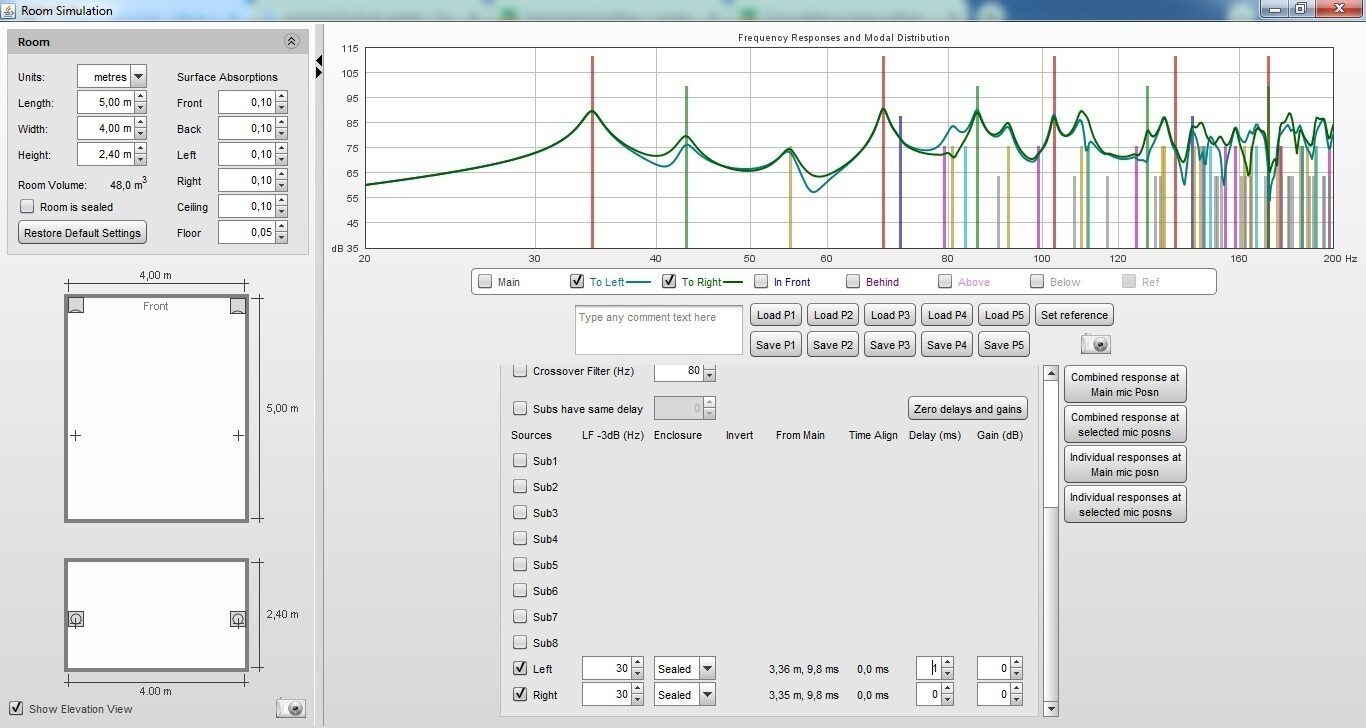
Что я хочу сказать этими словами, если смотреть на графики в подобных помещениях фактически абсолютно до фонаря как вы подключите сигнал к динамику, помещение исказит фазу сигнала с практически прямой линии до уровня картинкой выше.
Единственное условие если у вас стоят рядом на уровне ушей 2 громкоговорителя и вы должны ощущать эффект не только стерео, но и искуственного объемного звука с изменением фазы звуковой карты при различных эффектах кино или игр.
Звуковая карта изменяет фазировку подаваемого сигнала и получается эмуляция 3д эффекта.
При проникновении фазы друг на друга получается эффект активного звукоподавления, на этом принципе работают современные наушники заглушая звук с улицы.
Казалось бы выхода нет, но современное программное обеспечение и звуковые процессоры способны учесть изменение фазы в помещении и выровнять её практически до идеального состояния.
На слух чуда в очередной раз не случается так как человек по своей природе не достаточно проницателен чтоб уловить фазовые искажения.
При данной корекции уже можно говорить о должном стерео эффекте.
К сожалению выравнивание фазы сигнала и эквализация не может изменить эффект реверберации помещения.
Выводы:
При изменении фазировки сигнала кабеля вы не сможете отличить без дополнительных тестов правильную фазу звука.
При наложении звуковых волн в противофазе они ликвидируют друг друга
Изменение при переключении фазы в области низких частот будут, но слышать их будете только за счёт изменения ачх по причине пункта выше.
При добавлении задержек сигнала (расположение акустики на равнозначном расстоянии и получение дополнительного эффекта стерео) будут неминуемо как провалы так и подъемы в области ачх за счёт изменении времени фазы.
На графиках видно отчётливо как изменение фазы ведет к изменению ачх.
Программа использовалась Room Eq Wizard (REW) https://www.roomeqwizard.com/
Plot of one cycle of a sinusoidal function. The phase for each argument value, relative to the start of the cycle, is shown at the bottom, in degrees from 0° to 360° and in radians from 0 to 2π.
In physics and mathematics, the phase of a periodic function 







This convention is especially appropriate for a sinusoidal function, since its value at any argument 

Usually, whole turns are ignored when expressing the phase; so that 






The numeric value of the phase 
The term «phase» is also used when comparing a periodic function 









Mathematical definition[edit]
Let 





Here ![{displaystyle [![,cdot ,]!]!,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8536aff14a69f60ce6d112201324f74f85a061b4)
![{displaystyle [![x]!]=x-leftlfloor xrightrfloor !,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7841bc0e7dc0ad82ff00be9dfa5c3dd4728f0ef6)

This concept can be visualized by imagining a clock with a hand that turns at constant speed, making a full turn every 



The phase concept is most useful when the origin 


The formula above gives the phase as an angle in radians between 0 and 


The phase expressed in degrees (from 0° to 360°, or from −180° to +180°) is defined the same way, except with «360°» in place of «2π».
Consequences[edit]
With any of the above definitions, the phase 

for all
.
The phase is zero at the start of each period; that is
for any integer
.
Moreover, for any given choice of the origin 







In fact, every periodic signal 
where 
0 to 2π, that describes just one cycle of that waveform; and 



Adding and comparing phases[edit]
Since phases are angles, any whole full turns should usually be ignored when performing arithmetic operations on them. That is, the sum and difference of two phases (in degrees) should be computed by the formulas
and
respectively. Thus, for example, the sum of phase angles 190° + 200° is 30° (190 + 200 = 390, minus one full turn), and subtracting 50° from 30° gives a phase of 340° (30 — 50 = −20, plus one full turn).
Similar formulas hold for radians, with 
Phase shift [edit]
Illustration of phase shift. The horizontal axis represents an angle (phase) that is increasing with time.
The difference 





In the clock analogy, each signal is represented by a hand (or pointer) of the same clock, both turning at constant but possibly different speeds. The phase difference is then the angle between the two hands, measured clockwise.
The phase difference is particularly important when two signals are added together by a physical process, such as two periodic sound waves emitted by two sources and recorded together by a microphone. This is usually the case in linear systems, when the superposition principle holds.
For arguments 

For sinusoids[edit]
For sinusoidal signals, when the phase difference 

Conversely, a phase reversal or phase inversion implies a 180-degree phase shift.[2]
When the phase difference 
If the frequencies are different, the phase difference 

For shifted signals[edit]
The phase difference is especially important when comparing a periodic signal 









In this case, the phase shift is simply the argument shift 

If 



Therefore, when two periodic signals have the same frequency, they are always in phase, or always out of phase. Physically, this situation commonly occurs, for many reasons. For example, the two signals may be a periodic soundwave recorded by two microphones at separate locations. Or, conversely, they may be periodic soundwaves created by two separate speakers from the same electrical signal, and recorded by a single microphone. They may be a radio signal that reaches the receiving antenna in a straight line, and a copy of it that was reflected off a large building nearby.
A well-known example of phase difference is the length of shadows seen at different points of Earth. To a first approximation, if 


For sinusoids with same frequency[edit]
For sinusoidal signals (and a few other waveforms, like square or symmetric triangular), a phase shift of 180° is equivalent to a phase shift of 0° with negation of the amplitude. When two signals with these waveforms, same period, and opposite phases are added together, the sum 
The phase shift of the co-sine function relative to the sine function is +90°. It follows that, for two sinusoidal signals 









and
.
Representation of phase comparison.[3]
Left: the real part of a plane wave moving from top to bottom. Right: the same wave after a central section underwent a phase shift, for example, by passing through a glass of different thickness than the other parts.
A real-world example of a sonic phase difference occurs in the warble of a Native American flute. The amplitude of different harmonic components of same long-held note on the flute come into dominance at different points in the phase cycle. The phase difference between the different harmonics can be observed on a spectrogram of the sound of a warbling flute.[4]
Phase comparison[edit]
Phase comparison is a comparison of the phase of two waveforms, usually of the same nominal frequency. In time and frequency, the purpose of a phase comparison is generally to determine the frequency offset (difference between signal cycles) with respect to a reference.[3]
A phase comparison can be made by connecting two signals to a two-channel oscilloscope. The oscilloscope will display two sine signals, as shown in the graphic to the right. In the adjacent image, the top sine signal is the test frequency, and the bottom sine signal represents a signal from the reference.
If the two frequencies were exactly the same, their phase relationship would not change and both would appear to be stationary on the oscilloscope display. Since the two frequencies are not exactly the same, the reference appears to be stationary and the test signal moves. By measuring the rate of motion of the test signal the offset between frequencies can be determined.
Vertical lines have been drawn through the points where each sine signal passes through zero. The bottom of the figure shows bars whose width represents the phase difference between the signals. In this case the phase difference is increasing, indicating that the test signal is lower in frequency than the reference.[3]
Formula for phase of an oscillation or a periodic signal[edit]
The phase of an oscillation or signal refers to a sinusoidal function such as the following:
where 





See also[edit]
- Absolute phase
- AC phase
- In-phase and quadrature components
- Instantaneous phase
- Lissajous curve
- Phase cancellation
- Phase problem
- Phase spectrum
- Phase velocity
- Phasor
- Polarization
- Coherence, the quality of a wave to display a well defined phase relationship in different regions of its domain of definition
- Hilbert Transform, A method of changing phase by 90°
- Reflection phase shift, A phase change that happens when a wave is reflected off of a boundary from fast medium to slow medium
References[edit]
- ^ a b Ballou, Glen (2005). Handbook for sound engineers (3 ed.). Focal Press, Gulf Professional Publishing. p. 1499. ISBN 978-0-240-80758-4.
- ^ «Federal Standard 1037C: Glossary of Telecommunications Terms».
- ^ a b c
Time and Frequency from A to Z (2010-05-12). «Phase». Nist. National Institute of Standards and Technology (NIST). Retrieved 12 June 2016. This content has been copied and pasted from an NIST web page and is in the public domain. - ^ Clint Goss; Barry Higgins (2013). «The Warble». Flutopedia. Retrieved 2013-03-06.
External links[edit]
- «What is a phase?». Prof. Jeffrey Hass. «An Acoustics Primer«, Section 8. Indiana University, 2003. See also: (pages 1 thru 3, 2013)
- Phase angle, phase difference, time delay, and frequency
- ECE 209: Sources of Phase Shift — Discusses the time-domain sources of phase shift in simple linear time-invariant circuits.
- Open Source Physics JavaScript HTML5
- Phase Difference Java Applet
Plot of one cycle of a sinusoidal function. The phase for each argument value, relative to the start of the cycle, is shown at the bottom, in degrees from 0° to 360° and in radians from 0 to 2π.
In physics and mathematics, the phase of a periodic function 







This convention is especially appropriate for a sinusoidal function, since its value at any argument 

Usually, whole turns are ignored when expressing the phase; so that 






The numeric value of the phase 
The term «phase» is also used when comparing a periodic function 









Mathematical definition[edit]
Let 





Here ![{displaystyle [![,cdot ,]!]!,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8536aff14a69f60ce6d112201324f74f85a061b4)
![{displaystyle [![x]!]=x-leftlfloor xrightrfloor !,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7841bc0e7dc0ad82ff00be9dfa5c3dd4728f0ef6)

This concept can be visualized by imagining a clock with a hand that turns at constant speed, making a full turn every 



The phase concept is most useful when the origin 


The formula above gives the phase as an angle in radians between 0 and 


The phase expressed in degrees (from 0° to 360°, or from −180° to +180°) is defined the same way, except with «360°» in place of «2π».
Consequences[edit]
With any of the above definitions, the phase 

for all
.
The phase is zero at the start of each period; that is
for any integer
.
Moreover, for any given choice of the origin 







In fact, every periodic signal 
where 
0 to 2π, that describes just one cycle of that waveform; and 



Adding and comparing phases[edit]
Since phases are angles, any whole full turns should usually be ignored when performing arithmetic operations on them. That is, the sum and difference of two phases (in degrees) should be computed by the formulas
and
respectively. Thus, for example, the sum of phase angles 190° + 200° is 30° (190 + 200 = 390, minus one full turn), and subtracting 50° from 30° gives a phase of 340° (30 — 50 = −20, plus one full turn).
Similar formulas hold for radians, with 
Phase shift [edit]
Illustration of phase shift. The horizontal axis represents an angle (phase) that is increasing with time.
The difference 





In the clock analogy, each signal is represented by a hand (or pointer) of the same clock, both turning at constant but possibly different speeds. The phase difference is then the angle between the two hands, measured clockwise.
The phase difference is particularly important when two signals are added together by a physical process, such as two periodic sound waves emitted by two sources and recorded together by a microphone. This is usually the case in linear systems, when the superposition principle holds.
For arguments 

For sinusoids[edit]
For sinusoidal signals, when the phase difference 

Conversely, a phase reversal or phase inversion implies a 180-degree phase shift.[2]
When the phase difference 
If the frequencies are different, the phase difference 

For shifted signals[edit]
The phase difference is especially important when comparing a periodic signal 









In this case, the phase shift is simply the argument shift 

If 



Therefore, when two periodic signals have the same frequency, they are always in phase, or always out of phase. Physically, this situation commonly occurs, for many reasons. For example, the two signals may be a periodic soundwave recorded by two microphones at separate locations. Or, conversely, they may be periodic soundwaves created by two separate speakers from the same electrical signal, and recorded by a single microphone. They may be a radio signal that reaches the receiving antenna in a straight line, and a copy of it that was reflected off a large building nearby.
A well-known example of phase difference is the length of shadows seen at different points of Earth. To a first approximation, if 


For sinusoids with same frequency[edit]
For sinusoidal signals (and a few other waveforms, like square or symmetric triangular), a phase shift of 180° is equivalent to a phase shift of 0° with negation of the amplitude. When two signals with these waveforms, same period, and opposite phases are added together, the sum 
The phase shift of the co-sine function relative to the sine function is +90°. It follows that, for two sinusoidal signals 









and
.
Representation of phase comparison.[3]
Left: the real part of a plane wave moving from top to bottom. Right: the same wave after a central section underwent a phase shift, for example, by passing through a glass of different thickness than the other parts.
A real-world example of a sonic phase difference occurs in the warble of a Native American flute. The amplitude of different harmonic components of same long-held note on the flute come into dominance at different points in the phase cycle. The phase difference between the different harmonics can be observed on a spectrogram of the sound of a warbling flute.[4]
Phase comparison[edit]
Phase comparison is a comparison of the phase of two waveforms, usually of the same nominal frequency. In time and frequency, the purpose of a phase comparison is generally to determine the frequency offset (difference between signal cycles) with respect to a reference.[3]
A phase comparison can be made by connecting two signals to a two-channel oscilloscope. The oscilloscope will display two sine signals, as shown in the graphic to the right. In the adjacent image, the top sine signal is the test frequency, and the bottom sine signal represents a signal from the reference.
If the two frequencies were exactly the same, their phase relationship would not change and both would appear to be stationary on the oscilloscope display. Since the two frequencies are not exactly the same, the reference appears to be stationary and the test signal moves. By measuring the rate of motion of the test signal the offset between frequencies can be determined.
Vertical lines have been drawn through the points where each sine signal passes through zero. The bottom of the figure shows bars whose width represents the phase difference between the signals. In this case the phase difference is increasing, indicating that the test signal is lower in frequency than the reference.[3]
Formula for phase of an oscillation or a periodic signal[edit]
The phase of an oscillation or signal refers to a sinusoidal function such as the following:
where 





See also[edit]
- Absolute phase
- AC phase
- In-phase and quadrature components
- Instantaneous phase
- Lissajous curve
- Phase cancellation
- Phase problem
- Phase spectrum
- Phase velocity
- Phasor
- Polarization
- Coherence, the quality of a wave to display a well defined phase relationship in different regions of its domain of definition
- Hilbert Transform, A method of changing phase by 90°
- Reflection phase shift, A phase change that happens when a wave is reflected off of a boundary from fast medium to slow medium
References[edit]
- ^ a b Ballou, Glen (2005). Handbook for sound engineers (3 ed.). Focal Press, Gulf Professional Publishing. p. 1499. ISBN 978-0-240-80758-4.
- ^ «Federal Standard 1037C: Glossary of Telecommunications Terms».
- ^ a b c
Time and Frequency from A to Z (2010-05-12). «Phase». Nist. National Institute of Standards and Technology (NIST). Retrieved 12 June 2016. This content has been copied and pasted from an NIST web page and is in the public domain. - ^ Clint Goss; Barry Higgins (2013). «The Warble». Flutopedia. Retrieved 2013-03-06.
External links[edit]
- «What is a phase?». Prof. Jeffrey Hass. «An Acoustics Primer«, Section 8. Indiana University, 2003. See also: (pages 1 thru 3, 2013)
- Phase angle, phase difference, time delay, and frequency
- ECE 209: Sources of Phase Shift — Discusses the time-domain sources of phase shift in simple linear time-invariant circuits.
- Open Source Physics JavaScript HTML5
- Phase Difference Java Applet
Журнал РАДИОЛОЦМАН, август 2014
Einar Abell
EDN
Предлагается простой способ формирования многофазного тактового сигнала, при управлении частотой которого фазовые соотношения остаются практически неизменными.
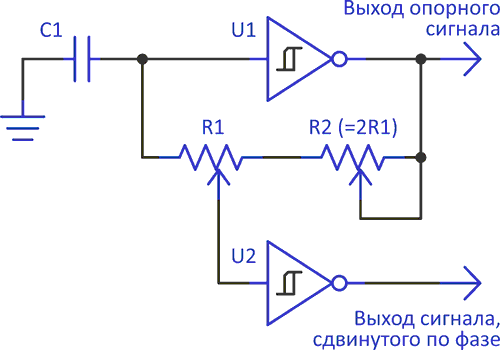
Сдвиг фазы сигнала на втором выходе можно перестраивать практически от нуля до 180°, не затрагивая его частоту. Базовая схема содержит минимальное количество компонентов: один конденсатор, два резистора и два триггера Шмитта (Рисунок 1).
 |
|
| Рисунок 1. | Двухфазный генератор с регулировкой частоты и фазового сдвига. |
Частота является функцией емкости конденсатора C1 и суммы сопротивлений резисторов R1 и R2. Сигнал, опережающий по фазе сигнал на опорном выходе U1, формируется на выходе микросхемы U2, вход которой подключен к движку потенциометра R1. Когда уровень напряжения на выходе U1 высокий, и конденсатор C1 заряжается, напряжение на входе U2 будет больше, чем на входе U1, вследствие чего U2 переключится раньше, чем U1, то есть, опередит U1 по фазе. При низком уровне на выходе U1 напряжение на входе U2 будет ниже, чем на входе U1, и U2 опять будет впереди U1. Чем ближе друг к другу движки потенциометров R1 и R2, тем больше будут различаться фазы на двух выходах.
Входные пороги КМОП триггеров Шмитта не вполне симметричны по отношению к выходу, поэтому два фазовых сдвига не будут одинаковыми. Эта асимметрия особенно заметна при небольшом опережении фазы.
Резистор R1 управляет фазовым сдвигом, а с помощью R2 можно подстраивать частоту. Поскольку регулировка частоты приводит к изменению фазы, частоту надо всегда устанавливать первой, а фазу – последней. На схеме я показал переменные резисторы, но вы можете любой из них, или же оба, заменить постоянными, а также объединить R1 и R2 в один переменный резистор, отказавшись от управления частотой и ограничив диапазон регулировки. Небольшие различия в пороговых напряжениях микросхем U1 и U2 не позволят установить сдвиг фаз нулевым или близким к нулю.
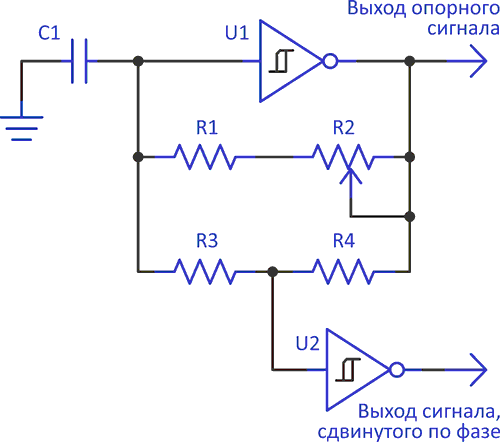
Рисунок 2 демонстрирует способ управления частотой, при котором изменения фазы минимальны. В этой схеме резисторы R1 и R2 задают частоту сигнала, а R3 и R4 – фазу. Сумма сопротивлений резисторов R3 и R4 должна быть равна или больше суммы сопротивлений R1 и R2. Реальный диапазон перестройки частоты, который вам удастся получить, сохранив изменение фазы на приемлемо низком уровне, составит одну декаду или что-то около того. Добиться большего вам не удастся, поскольку схема будет работать плохо из-за фазового сдвига, вносимого входной емкостью U2, влияние которой на более высоких частотах становится весьма значительным.
 |
|
| Рисунок 2. | Генератор с уменьшенной зависимостью частоты от фазы. |
Для простоты я представил только двухфазную схему, но добавив еще какое-то количество резисторов или потенциометров, количество фаз можно увеличить. Так, например, если R3 на Рисунке 2 разделить на две равные части, а сигнал, взятый со средней точки, инвертировать относительно остальных двух фаз, можно получить в результате классическую трехфазную схему. Реализация схемы не ограничивается только КМОП триггерами Шмитта; в ней возможно также использовать генераторы, сделанные на основе компараторов или таймера 556.







![{displaystyle phi (t)=2pi left[!!left[{frac {t-t_{0}}{T}}right]!!right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8667c57b10a88168acb01cf9516d856f5c03426)
![{displaystyle phi (t)=2pi left(left[!!left[{frac {t-t_{0}}{T}}+{frac {1}{2}}right]!!right]-{frac {1}{2}}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dd2752768d013ff1274948be47d3b9b2a060b73)




![{displaystyle 360,left[!!left[{frac {alpha +beta }{360}}right]!!right]quad quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/92b4181dd4ce3b785781bda9f93a9a1015a7df51)
![{displaystyle quad quad 360,left[!!left[{frac {alpha -beta }{360}}right]!!right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2605a5deb796fc44f1fb93adfe219897ecd3ad4b)


![{displaystyle varphi =2pi left[!!left[{frac {tau }{T}}right]!!right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/508adc034e08ef2f58d7d2db68b7a4b715a54548)