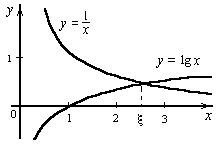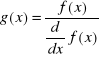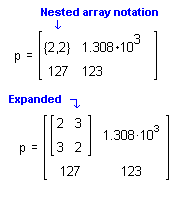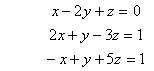— десятичном,
например 12345.6789;
— с порядком,
например 1.234104.
Имеется возможность
изменять формат отображения числа.
Параметры формата, в котором выводятся
числовые значения, можно установить
как для всех областей документа
(глобально) так и для отдельных областей
(локально).
Для глобальной
установки формата необходимо выполнить
следующие действия:
— установить визир
()
на пустом месте документа;
— в меню Формат
(Format) выбрать команду Результат
(Result).
Чтобы установить
формат локально для конкретной области,
в которую осуществляется вывод числового
значения, необходимо:
— установить маркер
ввода справа от оператора вывода (=),
т.е. там, где уже выведен результат или
будет выводиться (при вычислениях в
ручном режиме);
— в меню Формат
(Format) выбрать команду Результат
(Result) или выполнить двойной щелчок левой
кнопкой мыши.
В обоих случаях
на экране появится диалоговое окно
Формат
Результата
(Result Format),
в котором параметры формата будут иметь
вид, установленный в пакете Mathcad
по умолчанию или установленный перед
этим пользователем (рис. 10).
Рис. 10. Диалоговое
окно Формат
Результата
(страница
Формат номера).
Диалоговое окно
имеет четыре страницы с закладками:
-
Формат Номера
(Number Format) – для представления чисел в
различных форматах. -
Параметры экрана
(Display
Options)
– для изменения стиля отображения
массивов, выбора обозначения мнимой
единицы и задания системы счисления. -
Толерантность
(Tolerance)
–для установки порогового значения
округления (в степенях 10) для действительной
и мнимой части числа. Числа, по модулю
меньшие установленного порога,
отображаются
в виде нуля. -
Отображение
размерности (Unit
Display)
– для работы с размерными переменными.
Более подробно
рассмотрим использование страниц с
закладками Формат
Номера и
Параметры
экрана.
Страница Формат
Номера (Number
Format). Здесь можно выбрать формат выводимого
числового результата:
Общий
(General) – числа отображаются в десятичном
представлении или в представлении с
порядком;
Десятичный
(Decimal) — числа отображаются только в
десятичном представлении;
Научный
(Scientific)
— числа отображаются только с порядком;
Инженерный
(Engineering)
— числа
отображаются только с порядком, кратным
3-м;
Дробный
(Fraction)
– число отображается в виде дроби.
В каждом из этих
форматов допускается изменение параметров
представления числа.
При выводе чисел
по умолчанию принят формат
Общий. При
работе с этим форматом можно управлять
количеством отображаемых десятичных
знаков, задавая их количество (от 0 до
15) в поле Число
десятичных мест
(Number of decimal places). В поле Показательный
порог
(Exponential
threshold)
задается порог (от 0 до 15), т.е. показатель
степени 10, после достижения которого,
число отображается с порядком. Опция
Показать
конечные нули позволяет
отображать или скрывать незначащие
нули.
В таблице 1 приведены
примеры вывода числа 123.45678
в формате Общий
с разными значениями показательного
порога и различным количеством десятичных
знаков. Для чисел, отображенных в строках
№ 4 и № 7 был установлен флажок
Показать
конечные нули.
Таблица 1. Примеры
отображения числа 123.45678 в формате Общий.
-
№ п/п
Отображение
числаЧисло
десятичных местПоказательный
порог
1
123.457
3
3
2
123.45678
5
3
3
123.45678
6
3
4
123.456780
6
3
5
1.235102
3
1
6
1.23457102
5
2
7
123.45678000
8
4
Страница Параметры
экрана (Display
Options).
Общий вид этой страницы представлен
на рис. 11.
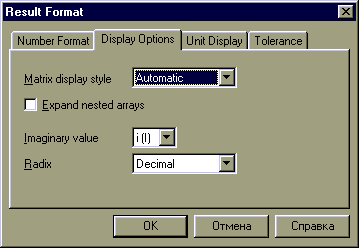
Рис. 11. Диалоговое
окно Формат
Результата
(страница
Параметры экрана).
В пакете Mathcad
существуют два стиля отображения
массивов: в виде матрицы и в виде таблицы
(рис. 12).
Для изменения
стиля отображения массива необходимо
в списке Стиль
отображения (Matrix
display style) выбрать один из предлагаемых
стилей:
— Automatic
( Авто) –стиль выбирается пакетом
Mathcad;
— Matrix
(Матрица);
— Table (Таблица).
Рис. 12. Отображение
массива в виде матрицы (а) и таблицы (б).
На рис. 13 показано
отображение матрицы А,
элементами которой являются вектора
а1,
а2,
а3
и а4.
Вывод матрицы А
приведен в двух вариантах.
а) Вложенные массивы
отображены в свернутой форме. При этом
в фигурных скобках через запятую указаны
количество строк и столбцов в
соответствующих векторах.
б) Вложенные массивы
отображены в развернутой форме. Для
этого установлен флажок
Развернуть
вложенные массивы.
Для записи
комплексных чисел в пакете Mathcad
используется мнимая единица i. По
определению,
.
Можно мнимую единицу выводить не как i
, а как j. Изменение обозначения мнимой
единицы осуществляется в списке Мнимое
значение (Imaginary
Value).
Рис. 13. Отображение
матрицы в свернутом (а) и развернутом
(б) виде.
Результаты
вычислений можно представить не только
в виде десятичного, но и в виде двоичного,
восьмеричного или шестнадцатеричного.
Чтобы задать
систему счисления необходимо выбрать
соответствующий элемент списка Единица
измерения
(Radix):
Decimal
— десятичная;
Binary
— двоичная;
Octal
— восьмеричная;
Hexadecimal
– шестнадцатеричная.
На рис. 14 приведены
примеры вывода числа 12
в различных системах счисления.
Рис. 14. Вывод
числа в различных системах счисления.
ВНИМАНИЕ!
Чтобы
просмотреть число с максимальной
точностью, необходимо установить курсор
ввода в область вывода результата и
нажать клавиши
Ctrl+Shift+N.
При этом в
левой части строки состояния окна
Mathcad будет выведено точное представление
числа.
9. Математические
константы пакета
— символ бесконечности
(машиная бесконечность)
(Ctrl+Shift+<z>,
на панели Матанализ);
— основание
натурального логарифма е (клавиша <е>);
— число
(Ctrl+Shift+<p>, кнопка
панели Арифметика
или Греческий
алфавит);
— i, j — мнимая единица-
(клавишами <1>, <i> или <1>, <j>);
— символ процента
% (клавиша <%>).
Значения
математических констант, действующие
в пакете «по умолчанию»:
10. Системные
переменные пакета.
— TOL – погрешность
численных методов;
— ORIGIN – значение
начального индекса (номера элемента) в
массивах;
— PRNPRECISION — установка
формата данных (количество выводимых
цифр) при выводе
в файл;
—
PRNCOLWIDTH — установка формата (ширины)
столбца при выводе в файл;
—
CWD — строковое
представление пути к текущей рабочей
папке.
Значения системных
переменных, действующие в пакете «по
умолчанию»:
17
Составитель: ст. преп.
Скабалланович Т. И.
Соседние файлы в папке Lr1_Interf_User
- #
- #
Чтобы стать профессиональным пользователем Mathcad, необходимо научиться редактировать выражения.
Подготовка
Mathcad – стабильная программа, и небольшие изменения документа можно провести без предварительной подготовки. Однако, при достаточно больших изменениях (изменение, удаление в буфер обмена, вставка или перемещение больших выражений) лучше выполнить некоторые предупредительные действия:
- Сохраните файл, чтобы можно было вернуть предыдущую версию.
- Нажмите Расчет –> Остановить все расчеты, чтобы расчеты не проводились во время редактирования (индикатор слева внизу из зеленого станет серым, а все расчеты):
После редактирования следует нажать кнопку Автоматический расчет.
Внутри математического выражения
Наберите следующее выражение:
Увеличьте масштаб до 150% с помощью ползунка на панели состояния. Необходимо видеть все операторы, включая светло-серый символ возведения в степень ^.
Вставка
По щелчку мыши до или после элемента выражения появится курсор – мигающая вертикальная синяя линия. Число или символ, который Вы наберете, появится на месте курсора. Щелкните мышью после числа 4 и наберите 7 – и вместо 4 будет число 47:
Как Вы заметили, редактирование выражений похоже на редактирование текста.
Удалите число 7, нажав [Backspace]. Снова щелкните после числа 4 и введите оператор умножения [*]. Появится местозаполнитель, где Вы можете ввести любою константу, переменную или математическое выражение. Введите sin(?). Для ? наберите [a][Ctlr+G]:
Изменение оператора
При щелчке мышью по символу корня он будет мигать синим, а выражение под корнем выделится серым. Нажмите [Delete]. Удалится оператор корня, но не выделенное выражение:
При щелчке по знаку умножения между 2 и a оператор будет мигать синим, а 2 и a подсветятся серым:
Нажатие на [Delete] заменит точку на мигающий символ ?:
При щелчке мышью вне выражения оператор умножения больше не будет виден, хотя он подразумевается:
Оператор возведения в степень не виден, пока Вы не щелкните по выражению
Щелкните по оператору, и основание и показатель степени выделятся серым цветом (здесь это b и 2):
Оператор можно заменить, введя другой оператор. Выделите оператор возведения в степень ^ и наберите [/]:
Попробуйте самостоятельно исправить следующие выражения:
Унарные операции отрицания, факториала и модуля редактируются аналогично. Для удаления оператора нужно щелкнуть по нему и нажать [Delete]:
Чтобы вернуть оператор отрицания, щелкните мышью перед переменной или константой и наберите знак «минус». Для оператора факториала следует поставить курсор за переменной. С оператором модуля несколько сложнее – сначала нужно выделить необходимую переменную протаскиванием указателя мыши. Об этом мы поговорим в следующем разделе.
Выделение протаскиванием указателя мыши
Чтобы выбрать часть выражения, щелкните перед или после выражения и, не отпуская кнопку мыши, протащите указатель. Фон за выделенным выражением станет серым. Выделите часть выражения, как показано на рисунке (без знака корня):
Выделенную часть можно удалять, вырезать, копировать, вставлять как текст. Скопируйте выделенную часть и вставьте в пустую область:
Копирование и вставка выражений полезны для приведения выражения к нужному виду – это мы обсудим в уроке 20.
Выделенную часть можно перепечатать – это один из самых распространенных и полезных способов исправления выражений.
После выделения протаскиванием курсор будет находиться там, где Вы отпустили указатель мыши:
Для вставки некоторых операторов важно, где находится курсор – до или после выделенного выражения. Чтобы подвести выражение под знак факториала, нужно выделить выражение протаскиванием слева направо и набрать [!]. Обратите внимание, что скобки появятся автоматически. Чтобы подвести выражение под знак корня, нужно выделить его справа налево.
Форматирование выражений
Выражения редактируются отдельно от текста, но теми же способами (эта функция доступна только начиная с версии Prime 3.0). Откройте вкладку Форматирование формул, затем нажмите по предыдущему выражению. Вы увидите, что для выражений используется стандартный шрифт: Mathcad UniMath Prime, 11 pt:
Вы можете изменить цвет шрифта и фона выражения. Изменение цвета фона полезно, если нужно выделить выражение.
Вы можете изменить шрифт любого выражения. Использование нового шрифта не изменяет саму переменную, в т.ч. и шрифт Symbol (греческие буквы):
В уроке 10 мы обсудим обозначения. Они изменяют формат, но также изменяют саму переменную. С помощью обозначений можно разделить, например, переменную m для массы и переменную
m
для единицы измерения «метр».
Для изменения шрифта для выражений по умолчанию, щелкните по пустой области, затем настройте шрифт. Если Вы используете шаблон, сделайте это для шаблона. Изменение шрифта по умолчанию не изменит шрифт уже введенных выражений.
Резюме
Для изменения выражения:
- Для больших изменений в документе:
- сохраните файл;
- отключите автоматический расчет.
- Выберите выражение и увеличьте масштаб 150..200%.
- Измените оператор, выделив его щелчком мыши и введя другой оператор.
- Выберите и измените переменную, константу или выражение в два шага:
- щелкните и протащите указатель мыши;
- перепечатайте переменную, константу или выражение.
- При протаскивании указателя мыши слева направо курсор становится в конце выражения, при протаскивании справа налево – в начале.
- Удаление в буфер обмена, копирование и вставка выражений или их частей не отличается от тех же операций для текста. Используйте [Ctrl+C] для копирования, [Ctrl+V] для вставки, [Ctrl+X] для удаления в буфер.
- Не забывайте обратно включать автоматические расчеты.
Математические области форматируются отдельно от текстовых, но теми же способами:
- Чтобы установить шрифт по умолчанию, щелкните по пустой области и настройте необходимый шрифт на вкладке Форматирование формул. Если Вы часто используете шрифт, отличный от предлагаемого Mathcad по умолчанию, используйте шаблоны.
- Вы можете изменить шрифт любого выделенного выражения.
Полный
перечень команд редактирования собран в главном меню Edit (Правка).
Выделение
отдельных элементов текстового или математического блока или всего блока
целиком осуществляется клавишами управления курсором совместно с клавишей Shift
или мышью.
При работе
с текстовыми областями для перемещения в начало строки текстового блока
используется клавиша Home, в конец – End.
Для
удаления отдельных символов в выражениях или тексте используется клавиша Backspace – для удаления символа слева от
курсора, Delete – для удаления символа справа от
курсора.
Копирование
выделенных блоков осуществляется в два этапа:
v v копирование в буфер обмена:
Copy (CTRL+C);
v v вставка в требуемое место
документа: Paste (CTRL+V).
Перемещение
выделенных блоков осуществляется в два этапа:
v v перемещение в буфер обмена:
Cut (CTRL+X);
v v вставка в требуемое место
документа: Paste (CTRL+V).
Для
удаления целого фрагмента используется команда Delete.
Форматирование результатов вычислений
Способ, которым MathCad выводит числа, называется форматом результата. Формат результата может
быть установлен для всего документа (глобальный формат) или для отдельного
результата (локальный формат).
Глобальный формат
устанавливается командой Format — Result. В диалоговом окне, появляющемся после выбора этой команды,
устанавливается:
v
v выводимая
точность числа – Number of Decimal places;
v
v диапазон
показателя степени – Exponential threshold;
v
v точность нуля – Show Trailing Zeros.
Для установки
формата отдельного результата его предварительно необходимо выделить.
Форматирование математических выражений
Математические
выражения имеют сложную структуру. Они содержат переменные, константы,
операторы и специальные знаки. С помощью команды Format — Equation можно назначить для
переменных, надписей, чисел и других символов в математических выражениях
другой шрифт и размер шрифта.
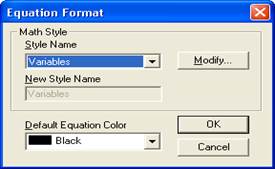
После
выбора данной команды на экране появляется диалоговое окно, показанное на
рис.1.1.
Рисунок 1.1 – Окно форматирования
математических выражений
Рассмотрим
команды данного окна:
v v Style Name — выбор типа
форматируемого объекта: переменная (variables), константа (constants);
v v Default Equation Color — установка цвета
математического выражения;
v v Modify — открыть окно для
настройки параметров шрифта выбранного объекта;
v v для принятия изменений
служит кнопка Ok, для закрытия окна форматирования результата без
внесения изменений — Cancel.
Примечание: новые параметры
форматирования применяются для всех объектов одного типа (например, для всех
переменных) в рамках документа.
Форматирование текста
Команда
Format – Text
используется для установки шрифтов и их параметров. В диалоговом окне,
вызываемом данной командой, можно установить следующие параметры:
v
v
Font – тип
шрифта;
v
v
FontStyle –
начертание шрифта;
v
v
Size – размер
шрифта;
v
v
Effects–
видоизменение шрифта: strikeout(зачеркнутый), underline(подчеркнутый),
subscript(подстрочный),
superscript(надстрочный);
v
v
Color — цвет
текста.
Вставка в документ колонтитулов
При печати
документов нередко требуется внести в заголовок или в нижнюю строку каждой
страницы документа некую служебную информацию или надпись, например имя файла,
номер страницы, дату создания и др. Такие надписи называют колонтитулами. Для
вставки в документ колонтитулов служит команда Format — Headers/Footers.
Команда выводит диалоговое окно, которое содержит две вкладки: Header
(верхний колонтитул) и Footer (нижний колонтитул). Каждая вкладка
содержит:
v v три поля для ввода текста
колонтитула (слева, по центру, справа);
v v командные кнопки для
автоматического занесения в колонтитул следующих данных: Filename (имени
файла), page# (номера страницы), date (текущей даты), time
(текущего времени);
v v кнопка Format дает
возможность выбора подходящего шрифта для текста, вводимого в область
колонтитула.
Примечание:
Колонтитулы
в окне документа не видны. Они видны только в режиме предварительного просмотра
и на печатных
|
1816 / 1030 / 285 Регистрация: 13.02.2012 Сообщений: 3,339 |
|
|
1 |
|
Изменить тип представления результатов19.03.2013, 08:27. Показов 6283. Ответов 9
Подскажите как изменить представление результатов решения системы линейных уравнений, мне нужно чтобы отображение в Find было дробями, а не e в степени ….
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
19.03.2013, 08:27 |
|
Ответы с готовыми решениями: Тип модели представления
Требуется изменить тип файла и изменить шрифт в документе
9 |
|
1816 / 1030 / 285 Регистрация: 13.02.2012 Сообщений: 3,339 |
|
|
19.03.2013, 10:58 [ТС] |
2 |
|
В виде вещественного числа конечно же.
0 |
|
Модератор 5032 / 3863 / 1327 Регистрация: 30.07.2012 Сообщений: 11,439 |
|
|
19.03.2013, 20:19 |
3 |
|
Подскажите как изменить представление результатов решения системы линейных уравнений, мне нужно чтобы отображение в Find было дробями, а не e в степени …. Прикрепите свой ФАЙЛ с решением…
0 |
|
1816 / 1030 / 285 Регистрация: 13.02.2012 Сообщений: 3,339 |
|
|
19.03.2013, 20:28 [ТС] |
4 |
|
Забыл приложить. пожалуйста.
0 |
|
Модератор 5032 / 3863 / 1327 Регистрация: 30.07.2012 Сообщений: 11,439 |
|
|
19.03.2013, 20:48 |
5 |
|
Забыл приложить. пожалуйста. Надеюсь, все прозрачно?
1 |
|
1816 / 1030 / 285 Регистрация: 13.02.2012 Сообщений: 3,339 |
|
|
20.03.2013, 09:35 [ТС] |
6 |
|
Курсор -> на результат (в виде дробей)… Знак =… Уже стояло. Format -> c Fraction на General… Формат/Результат/ Выбрал общий Без изменений
0 |
|
1498 / 1019 / 158 Регистрация: 12.06.2012 Сообщений: 2,079 |
|
|
20.03.2013, 10:13 |
7 |
|
Такой вариант устроит? Миниатюры
0 |
|
1816 / 1030 / 285 Регистрация: 13.02.2012 Сообщений: 3,339 |
|
|
20.03.2013, 10:21 [ТС] |
8 |
|
Не устроит, видимо непонятно объяснил.
0 |
|
1498 / 1019 / 158 Регистрация: 12.06.2012 Сообщений: 2,079 |
|
|
20.03.2013, 11:24 |
9 |
|
Вариант: Миниатюры
1 |
|
1816 / 1030 / 285 Регистрация: 13.02.2012 Сообщений: 3,339 |
|
|
20.03.2013, 11:26 [ТС] |
10 |
|
Vladimir__, Всем пасибы!
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
20.03.2013, 11:26 |
|
10 |
Перед началом работы курсор имеет вид красного крестика. В момент ввода выражения курсор приобретает вид синего уголка, окаймляющего часть вводимого выражения. Ввод начинается с имени переменной, после нее ставится знак присваивания (знак:), а затем само выражение или константа. Имя выражения (та часть, которая левее оператора присваивания) может состоять из латинских, русских, греческих букв и цифр, знаков подчеркивания (_), штриха (`), процента (%), бесконечности?, вводимых с клавиатуры.
Рисунок 2 — Ввод математического выражения
Имена переменных и функций не могут начинаться с цифры, подчеркивания, штриха, процента (%), не могут включать пробелы. Символ бесконечности может быть только первым в имени переменной. Mathcad воспринимает прописные и строчные буквы, а также введенные разными шрифтами как различные.
Редактирование введенных выражений производится следующими способами:
1. ?Курсор перемещается по экрану клавишами со стрелками или левой кнопкой мыши ставится в нужное место экрана.
2. ?Для выделения одного символа синим уголком курсора нужно установить курсор так, чтобы он охватывал этот символ слева или справа.
3. ?Для расширения выделения на часть или выражение целиком удобнее использовать клавиши со стрелками или пробел. Для перехода из оператора на уровень выше можно также использовать пробел. Уголок курсора должен охватывать все выражение или его часть, над которой надо выполнить действие.
4. Для выделения части или всего выражения надо щелкнуть левой кнопкой мыши в начале или в конце выделяемого выражения и переместить курсор до другого края с нажатой левой кнопкой мыши. Можно использовать клавиши Shift+< или Shift+>. Выделенная часть выражения черного цвета. Выделение в Mathcad используется для вырезания или копирования части выражения, изменения шрифта, а также для выполнения некоторых видов символьных вычислений.
5. ?Для выделения объекта или группы (математических, текстовых или графических) надо щелкнуть мышью на свободном месте рабочего листа и протянуть прямоугольник выделения так, чтобы он захватил нужные объекты. Один объект будет выделен синим курсоров, а группа объектов — пунктирной рамкой.
Если надо удалить, вырезать или скопировать выделенную часть выражения, выделенный объект целиком или группу выделенных объектов, используются такие же команды, как и в других приложениях Windows.
Некоторые латинские и греческие буквы зарезервированы в качестве констант. Так, латинская буква е внутри математического выражения является основанием натурального логарифма е = 2,718. Это значение можно отменить, присвоив ей любое другое значение, используя знак локального присваивания:=.
Знак бесконечности ? можно вставить с математической панели Calculus.
Если какой-либо константе или переменной не присвоено никакого значения левее и выше ее на экране, то она будет окрашена в красный цвет, указывая на ошибку. Все переменные и функции должны быть предварительно определены.
Если константы в правой части функции пользователя не заданы непосредственно перед использованием этой функции их значения берутся такими, какие были в последний раз перед этим расчетом.
Для ввода простого текста можно выбрать команду Insert Text Region (Вставить Текстовую область) в главном меню, но удобнее ввести с клавиатуры символ кавычки и далее сам текст. На экране появится текстовая область, в которой можно печатать. Также, сменив латинский шрифт на русский, начать печатать текст в любом месте документа. Как только будет напечатано первое слово, при нажатии пробела эта область автоматически превращается в текстовую.
В Mathcad на точность расчета повлиять нельзя, но можно изменить формат вывода результатов. В Mathcad 11 вычисления совершаются с точностью 12 знаков, а в Mathcad 15 — до 17 знаков.
Основы работы с MathCAD. Математические выражения. Типы данных
Тема: Основы работы с MathCAD. Математические выражения. Типы данных
Правила записи математических выражений. Операторы. Операнды. Глобальные, локальные, системные переменные и константы. Массивы. Функции
MathCAD – это мощная и в то же время простая универсальная среда для решения задач в различных отраслях науки и техники, финансов и экономики, физики и астрономии, математики и статистики… MathCAD остается единственной системой, в которой описание решения математических задач задается с помощью привычных математических формул и знаков. MathCAD позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства научной графики.
Система MathCAD существует в нескольких основных вариантах:
- MathCAD Standard – идеальная система для повседневных технических вычислений. Предназначена для массовой аудитории и широкого использования в учебном процессе;
- MathCAD Professional – промышленный стандарт прикладного использования математики в технических приложениях. Ориентирована на математиков и научных работников, проводящих сложные и трудоемкие расчеты.
- MathCAD Professional Academic – пакет программ для профессионального использования математического аппарата с электронными учебниками и ресурсами.
MathCAD–документ — это чистый лист бумаги, на котором можно размещать блоки трех основных типов: математические выражения, текстовые фрагменты и графические области.
Расположение нетекстовых блоков в документе имеет принципиальное значение – слева направо и сверху вниз.
Математические выражения
К основным элементам математических выражений MathCAD относятся типы данных, операторы, функции и управляющие структуры.
Операторы — элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д.
- действие, которое должно выполняться при наличии тех или иных значений операндов;
- сколько, где и какие операнды должны быть введены в оператор.
Операнд – число или выражение, на которое действует оператор. Например, в выражении 5! + 3 число 3 и выражение 5! – операнды оператора + (плюс), а число 5 операнд оператора факториал (!). После указания операндов операторы становятся исполняемыми по документу блоками.
К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа.
Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в MathCAD представляют собой набор латинских или греческих букв и цифр.
В MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения. Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Options команды Математика Опции.
Рисунок — Математические выражения
Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной.
Если переменной присваивается начальное значение с помощью оператора :=, вызывается нажатием клавиши : (двоеточие) на клавиатуре, такое присваивание называется локальным. До этого присваивания переменная не определена и ее нельзя использовать. Однако с помощью знака (клавиша
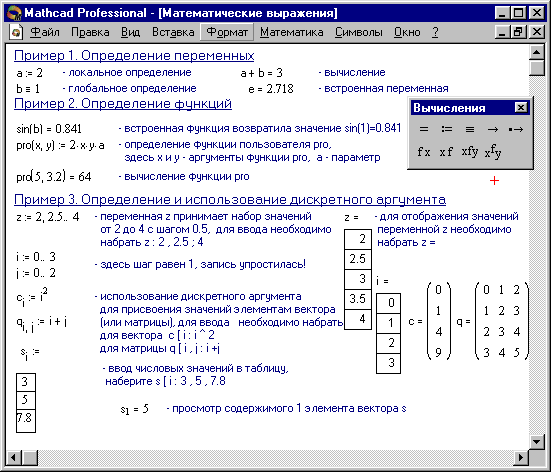
на клавиатуре) можно обеспечить глобальное присваивание (см. Пример 1 Рисунка 1). MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все действия, предписанные локальным оператором присваивания (), а при втором – производятся действия, предписанные локальным оператором присваивания (:=), и отображаются все необходимые результаты вычислений (=).
Существуют также жирный знак равенства = (комбинация клавиш Ctrl + =), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства (комбинация клавиш Ctrl + .).
Дискретные аргументы — особый класс переменных, который в пакете MathCAD зачастую заменяет управляющие структуры, называемые циклами (однако полноценной такая замена не является). Эти переменные имеют ряд фиксированных значений, либо целочисленных (1 способ), либо в виде чисел с определенным шагом, меняющихся от начального значения до конечного (2 способ).
- Name := Nbegin .. Nend,
где Name – имя переменной, Nbegin – ее начальное значение, Nend – конечное значение, .. – символ, указывающий на изменение переменной в заданных пределах (вводится клавишей ;). Если Nbegin < Nend, то шаг переменной будет равен +1, иначе –1.
- Name := Nbegin, (Nbegin + Step) .. Nend
Здесь Step – заданный шаг изменения переменной (он должен быть положительным, если Nbegin < Nend, или отрицательным в обратном случае).
Дискретные аргументы значительно расширяют возможности MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы (Пример 3 Рисунка 1).
Массив — имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов:
- одномерные (векторы);
- двумерные (матрицы).
Порядковый номер элемента, который является его адресом, называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или единицы, в соответствии со значением системной переменной ORIGIN.
Векторы и матрицы можно задавать различными способами:
- с помощью команды Вставка Матрица, или комбинации клавиш Ctrl + M, или щелчком на кнопке панели Матрица, заполнив массив пустых полей для не слишком больших массивов;
- с использованием дискретного аргумента, когда имеется некоторая явная зависимость для вычисления элементов через их индексы (Пример 3 Рисунка 1).
Функция – выражение, согласно которому проводятся некоторые вычисления с аргументами и определяется его числовое значение.
Следует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции (см. Пример 2 Рисунка 1).
Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение.
Функции в пакете MathCAD могут быть встроенные (см. Приложение 3), т. е. заблаговременно введенные разработчиками, и определенные пользователем.
Способы вставки встроенной функции:
- Выбрать пункт меню Вставка Функция.
- Нажать комбинацию клавиш Ctrl + E.
- Щелкнуть на кнопке .
- С помощью какого оператора можно вычислить выражение?
- Чем отличается глобальное и локальное определение переменных? С помощью каких операторов определяются?
- Как изменить формат чисел для всего документа?
- Как изменить формат чисел для отдельного выражения?
- Какие системные (предопределенные) переменные Вам известны? Как узнать их значение? Как изменить их значение?
- Какие виды функций в Mathcad Вам известны?
- Как вставить встроенную функцию в документ Mathcad?
- С помощью каких операторов можно вычислить интегралы, производные, суммы и произведения?
- Как определить дискретные переменные с произвольным шагом? Какой шаг по умолчанию?
- Как определить индексированную переменную?
- Какие виды массивов в Mathcad Вам известны?
- Какая системная переменная определяет нижнюю границу индексации элементов массива?
- Опишите способы создания массивов в Mathcad.
- Как просмотреть содержимое массива, определенного через дискретный аргумент?
Лекция 2
Тема: Построение графиков функций, поверхностей, пространственных кривых и их анимация
Текстовые и графические области. Функции графических построений. Создание анимационных файлов
Текстовые фрагменты
Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов:
- текстовая область предназначена для небольших кусков текста — подписей, комментариев и т. п. Вставляется с помощью команды Вставка Текстовая регион или комбинации клавиш Shift + » (двойная кавычка);
- текстовый абзац применяется в том случае, если необходимо работать с абзацами или страницами. Вставляется с помощью комбинации клавиш Shift + Enter.
Графические области
Графические области делятся на три основных типа — двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим MathCAD на основании обработанных данных.
Для создания декартового графика:
- Установить визир в пустом месте рабочего документа.
- Выбрать команду Вставка График Х-У график, или нажать комбинацию клавиш Shift + @, или щелкнуть кнопку панели Графики. Появится шаблон декартового графика.
- Введите в средней метке под осью Х первую независимую переменную, через запятую – вторую и так до 10, например х1, х2, …
- Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую – вторую и т. д., например у1(х1), у2(х2), …, или соответствующие выражения.
- Щелкните за пределами области графика, что бы начать его построение.
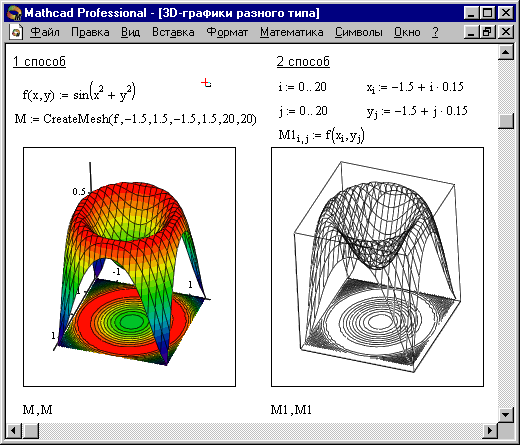
Трехмерные, или 3D-графики, отображают функции двух переменных вида Z(X, Y). При построении трехмерных графиков в ранних версиях MathCAD поверхность нужно было определить математически (Рисунок 2, способ 2). Теперь применяют функцию MathCAD CreateMesh.
CreateMesh(F (или G, или f1, f2, f3), x0, x1, y0, y1, xgrid, ygrid, fmap)
Создает сетку на поверхности, определенной функцией F. x0, x1, y0, y1 – диапазон изменения переменных, xgrid, ygrid – размеры сетки переменных, fmap – функция отображения. Все параметры, за исключением F, — факультативные. Функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от –5 до 5 и с сеткой 2020 точек.
Пример использования функции CreateMesh для построения 3D-графиков приведен на Рисунке 2, способ 1. На Рисунке 2 построена одна и та же поверхность разными способами, с разным форматированием, причем изображены поверхности и под ними те же поверхности в виде контурного графика. Такое построение способно придать рисунку большую наглядность.
Рисунок — Пример построения на одном рисунке двух 3D-графиков разного типа
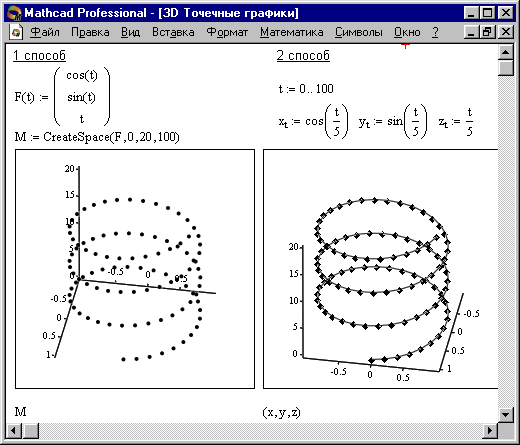
Нередко поверхности и пространственные кривые представляют в виде точек, кружочков или иных фигур. Такой график создается операцией Вставка График 3D Точечный, причем поверхность задается параметрически – с помощью трех матриц (X, Y, Z) (см. Рисунок 3, способ 2), а не одной как в примере на Рисунке 2. Для определения исходных данных для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ 1).
CreateSpace (F , t0, t1, tgrid, fmap) – Возвращает вложенный массив трех векторов, представляющих х-, у-, и zкоординаты пространственной кривой, определенной функцией F. t0 и t1 – диапазон изменения переменной, tgrid – размер сетки переменной, fmap – функция отображения. Все параметры, за исключением F, — факультативные.
Рисунок 3-Построение точечных 3D графиков
Построение пересекающихся фигур
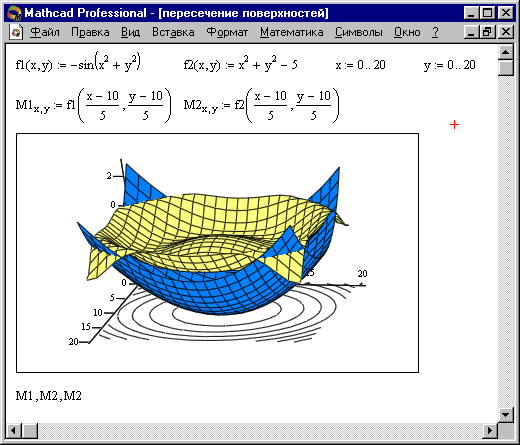
Особый интерес представляет собой возможность построения на одном графике ряда разных фигур или поверхностей с автоматическим учетом их взаимного пересечения. Для этого надо раздельно задать матрицы соответствующих поверхностей и после вывода шаблона 3D-графика перечислить эти матрицы под ним с использованием в качестве разделителя запятой (Рисунок 4).
Рисунок — Построение двух пересекающихся поверхностей и одновременно контурного графика одной из них
Создание анимационного клипа
MathCAD имеет встроенную переменную FRAME, чье единственное назначение — управление анимациями:
- Создайте объект, чей вид зависит от FRAME.
- Убедитесь, что установлен режим автоматического расчета (Математика Автоматическое Вычисление).
- Выберите Вид Анимация для вызова одноименного диалогового окна.
- Заключите в выделяющий пунктирный прямоугольник часть рабочего документа, которую нужно анимировать.
- Установите нижние и верхние границы FRAME (поля От: и До:).
- В поле Скорость введите значение скорости воспроизведения (кадров/сек).
- Выберите Анимация. Сейчас анимация только создается.
- Сохраните анимацию как АVI файл (Сохранить как).
- Воспроизведите сохраненную анимацию Вид Воспроизведение.
- Как вставить текстовую область в документ Mathcad?
- Как построить графики: поверхности; полярный; декартовый?
- Как построить несколько графиков в одной системе координат?
- Как изменить масштаб графика?
- Как определить координату точки на графике?
- Как построить гистограмму?
- Какие функции используются для построения трехмерных графиков?
- Как создать анимацию в Mathcad?
- Какое расширение имеют сохраненные файлы анимаций?
Лекция 3
Тема: Численное и символьное решение уравнений. Корни полинома
Способы решения уравнений. Поиск начального приближения. Графическое решение уравнений. Поиск корней Полина с использованием функции polyroots
Решение уравнений средствами Mathcad
Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Однако такие уравнения могут решаться численными методами с заданной точностью (не более значения заданного системной переменной TOL).
Численное решение нелинейного уравнения
Для простейших уравнений вида f(x) = 0 решение в Mathcad находится с помощью функции root (Рисунок 5).
root( f(х1, x2, …), х1, a, b ) – Возвращает значение х1, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.
f(х1, x2, …) — функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
х1 — — имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
a, b – необязательны, если используются, то должны быть вещественными числами, причем a < b.
Рисунок . Решение уравнений средствами Mathcad
Приближенные значения корней (начальные приближения) могут быть:
- Известны из физического смысла задачи.
- Известны из решения аналогичной задачи при других исходных данных.
- Найдены графическим способом.
Наиболее распространен графический способ определения начальных приближений. Принимая во внимание, что действительные корни уравнения f(x) = 0 — это точки пересечения графика функции f(x) с осью абсцисс, достаточно построить график функции f(x) и отметить точки пересечения f(x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение f(x) = 0 равносильным ему уравнением: ,где функции f1(x) и f2(x) — более простые, чем функция f(x). Тогда, построив графики функций у = f1(x) и у = f2(x), искомые корни получим как абсциссы точек пересечения этих графиков.
Пример. Графически отделить корни уравнения: x lg x = 1. Это уравнение удобно переписать в виде равенства:
Отсюда ясно, что корни уравнения могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = . Построив эти кривые, приближенно найдем единственный корень уравнения или определим его содержащий отрезок [2, 3].
Отсутствие сходимости функции root
Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:
Уравнение не имеет корней.
Корни уравнения расположены далеко от начального приближения.
Выражение имеет локальные max и min между начальным приближением и корнями.
Выражение имеет разрывы между начальными приближениями и корнями.
Выражение имеет комплексный корень, но начальное приближение было вещественным.
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться.
Рекомендации по использованию функции root
Для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида . Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика Параметры… Переменные Допуск сходимости (TOL). .
Для выражения f(x) с известным корнем а нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x) = f(x)/(x a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения f(x) = 0, выбирая различные начальные приближения.
Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их.
Если функция f(x) имеет малый наклон около искомого корня, функция root(f(x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
vnxn + . + v2x2 + v1x + v0,
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.
Возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n + 1. Возвращает вектор длины n, состоящий из корней полинома.
v – вектор, содержащий коэффициенты полинома.
Вектор v удобно создавать использую команду Символы Коэффициенты полинома. Рисунок 6 иллюстрирует определение корней полинома средствами Mathcad.
Рисунок . Определение корней полинома
- Назовите способы нахождения начального приближения.
- Какие функции для решения одного уравнения в MathCAD вы знаете? В чем их отличие?
- Какие аргументы функции root не обязательны?
- В каких случаях MathCAD не может найти корень уравнения?
- Какая системная переменная отвечает за точность вычислений?
- Как изменить точность, с которой функция root ищет корень?
- Как системная переменная TOL влияет на решение уравнения с помощью функции root?
Лекция 4
Тема: Численное и символьное решение систем уравнений. Решение СЛАУ в матричной форме
Функции Find и Miner решения систем уравнений. Функция lsolve для решения матричных уравнений
Решение систем уравнений
MathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.
Для решения системы уравнений необходимо выполнить следующее:
Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов.
Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.
Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, и .
Введите любое выражение, которое включает функцию Find, например: а:= Find(х, у).
Find(z1, z2, . . .) –Возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое–либо выражение, содержащее функцию Find, называют блоком решения уравнений.
Следующие выражения недопустимы внутри блока решения:
Ограничения со знаком .
Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
Неравенства вида a < b < c.
Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find.
Функция, которая завершает блок решения уравнений, может быть использована аналогично любой другой функции. Можно произвести с ней следующие три действия:
Можно вывести найденное решение, напечатав выражение вида:
Определить переменную с помощью функции Find:
a := Find(x) – скаляр,
var := Find(var1, var2,…) – вектор.
Это удобно сделать, если требуется использовать решение системы уравнений в другом месте рабочего документа.
Определить другую функцию с помощью Find
f(a, b, c, …) := Find(x, y, z, …).
Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…, непосредственно входящих в систему уравнений.
Сообщение об ошибке (Решение не найдено) при решении уравнений появляется, когда:
Поставленная задача может не иметь решения.
Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот.
В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Для поиска искомого решения нужно задать различные начальные приближения.
Возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL.
Пример 1 Рисунка 7 иллюстрирует решение системы уравнений в MathCAD.
Рисунок — Решение систем уравнений в MathCAD
Решение матричных уравнений
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn:
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде Ах = b,
Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками – коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы; матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой — искомые неизвестные, называется решением системы.
Если матрица А — неособенная, то есть det A 0 то система (2), или эквивалентное ей матричное уравнение (3), имеет единственное решение. В самом деле, при условии det A 0 существует обратная матрица А-1. Умножая обе части уравнения (3) на матрицу А-1 получим:
Эта формула дает решение матричного уравнения и оно единственно.
Системы линейных уравнений удобно решать с помощью функции lsolve.
lsolve(А, b)–Возвращается вектор решения x такой, что Ах = b.
А — квадратная, не сингулярная матрица.
b — вектор, имеющий столько же рядов, сколько рядов в матрице А.
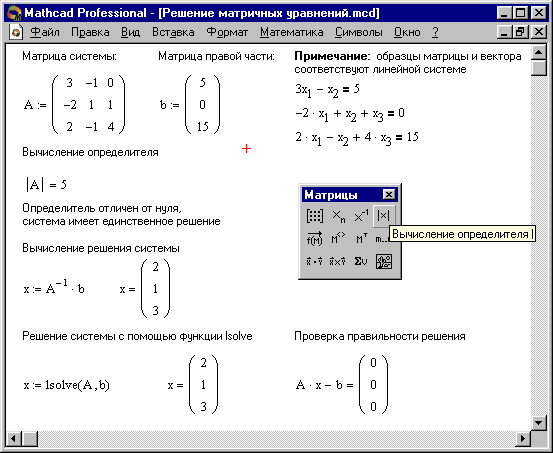
На Рисунке 8 показано решение системы трех линейных уравнений относительно трех неизвестных.
Рисунок . Решение матричных уравнений
Функция Minerr очень похожа на функцию Find (использует тот же алгоритм).
Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и функции Find.
Minerr(z1, z2, . . .)–Возвращает приближенное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
Если Minerr используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.
Символьное решение уравнений
В Mathcad можно быстро и точно найти численное значение корня с помощью функции root. Но имеются некоторые задачи, для которых возможности Mathcad позволяют находить решения в символьном (аналитическом) виде.
Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения:
Если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр. Поэтому вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении.
Если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе или в аналитическом или цифровом виде.
Команда Символы Переменные Вычислить позволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения.
Чтобы решить уравнение символьно необходимо:
Напечатать выражение (для ввода знака равенства используйте комбинацию клавиш [Ctrl]=).
Выделить переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью.
Выбрать пункт меню Символы Переменные Вычислить.
Нет необходимости приравнивать выражение нулю. Если MathCAD не находит знака равенства, он предполагает, что требуется приравнять выражение нулю.
Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующее:
Напечатать ключевое слово Given.
Напечатать уравнения в любом порядке ниже слова Given. Удостоверьтесь, что для ввода знака = используется [Ctrl]=.
Напечатать функцию Find, соответствующую системе уравнений.
Нажать [Ctrl]. (клавиша CTRL, сопровождаемая точкой). Mathcad отобразит символьный знак равенства .
Щелкнуть мышью на функции Find.
Пример 2 Рисунка 7 иллюстрирует символьное решение системы уравнений в MathCAD.
- Назовите функции для решения систем уравнений в MathCAD и особенности их применения.
- Опишите структуру блока решения уравнений.
- Какой знак равенства используется в блоке решения? Какой комбинацией клавиш вставляется в документ?
- Какие выражения не допустимы внутри блока решения уравнения?
- Опишите способы использования функции Find.
- В каких случаях MathCAD не может найти решение системы уравнений?
- Дайте сравнительную характеристику функциям Find и Minerr.
- Какие уравнения называются матричными?
- Как решать матричные уравнения? Назовите способы решения матричных уравнений.
- Как символьно решить уравнение или систему уравнений в MathCAD? Какой знак равенства используется? Какой комбинацией клавиш вставляется в документ?
- Назовите особенности использования символьного решения уравнений.
Лекция 5
Тема: Символьные расчеты в системе MathCAD.
Выполнение операций с выделенными переменными и с выделенными выражениями. Операции с выделенными матрицами. Стиль представления результатов
Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, если такое решение существует в принципе (что бывает далеко не всегда).
Ядро символьного процессора системы MathCAD — несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software, у которой фирма MathSoft (разработчик MathCAD) приобрела лицензию на его применение, благодаря чему MathCAD стала (начиная с версии 3. 0) системой символьной математики. Символьные вычисления выполняются столь же просто (для пользователя), как вычисление квадрата х.
Символьные операции можно выполнять двумя способами:
- Непосредственно в командном режиме (используя операции меню Символы);
- С помощью операторов символьного преобразования (используя палитру инструментов Символы ).
Выделение выражений для символьных вычислений
Чтобы символьные операции выполнялись, процессору необходимо указать, над каким выражением эти операции должны производиться, т. е. надо выделить выражение. Для ряда операций следует не только указать выражение, к которому они относятся, но и наметить переменную, относительно которой выполняется та или иная символьная операция. Само выражение в таком случае не выделяется.
Таким образом, для выполнения операций с символьным процессором нужно выделить объект (целое выражение или его часть) синими сплошными линиями.
Символьные операции разбиты на пять характерных разделов. Первыми идут наиболее часто используемые операции. Они могут выполняться с выражениями, содержащими комплексные числа или имеющими решения в комплексном виде.
Символьные операции
Операции с выделенными выражениями
Если в документе есть выделенное выражение, то с ним можно выполнять различные операции, представленные ниже:
Расчеты — преобразовать выражение с выбором вида преобразований из подменю;
Символические [Shift] F9 – выполнить символьное преобразование выделенного выражения;
С плавающей запятой… – вычислить выделенное выражение в вещественных числах;
Комплексные – выполнить вычисления в комплексном виде;
Упростить — упростить выделенное выражение с выполнением таких операций, как сокращение подобных слагаемых, приведение к общему знаменателю, использование основных тригонометрических тождеств и т д.;
Расширить — раскрыть выражение [например, для (Х + Y) (Х — Y) получаем X 2- Y 2];
Фактор — разложить число или выражение на множители [например, X 2- Y 2 даст (Х + Y) (Х — Y)];
Подобные — собрать слагаемые, подобные выделенному выражению, которое может быть отдельной переменной или функцией со своим аргументом (результатом будет выражение, полиномиальное относительно выбранного выражения);
Коэффициенты Полинома — по заданной переменной найти коэффициенты полинома, аппроксимирующего выражение, в котором эта переменная использована.
Операции с выделенными переменными
Для ряда операций надо знать, относительно какой переменной они выполняются. В этом случае необходимо выделить переменную, установив на ней маркер ввода. После этого становятся доступными следующие операции подменю Переменные:
Вычислить — найти значения выделенной переменной, при которых содержащее ее выражение становится равным нулю;
Замена — заменить указанную переменную содержимым буфера обмена;
Дифференциалы — дифференцировать выражение, содержащее выделенную переменную, по этой переменной (остальные переменные рассматриваются как константы);
Интеграция — интегрировать все выражение, содержащее переменную, по этой переменной;
Разложить на составляющие. — найти несколько членов разложения выражения в ряд Тейлора относительно выделенной переменной;
Преобразование в Частичные Доли — разложить на элементарные дроби выражение, которое рассматривается как рациональная дробь относительно выделенной переменной.
Операции с выделенными матрицами
Операции с выделенными матрицами представлены позицией подменю Матрицы, которая имеет свое подменю со следующими операциями:
Транспонирование — получить транспонированную матрицу;
Инвертирование — создать обратную матрицу;
Определитель — вычислить детерминант (определитель) матрицы.
Результаты символьных операций с матрицами часто оказываются чрезмерно громоздкими и поэтому плохо обозримы.
В позиции Преобразование содержится раздел операций преобразования, создающий подменю со следующими возможностями:
Фурье — выполнить прямое преобразование Фурье относительно выделенной переменной;
Фурье Обратное — выполнить обратное преобразование Фурье относительно выделенной переменной;
Лапласа — выполнить прямое преобразование Лапласа относительно выделенной переменной (результат — функция переменной s);
Лапласа Обратное — выполнить обратное преобразование Лапласа относительно выделенной переменной (результат — функция
Z — выполнить прямое Z-преобразование выражения относительно выделенной переменной (результат — функция переменной z);
Обратное Z — выполнить обратное Z-преобразование относительно выделенной переменной (результат — функция переменной n) .
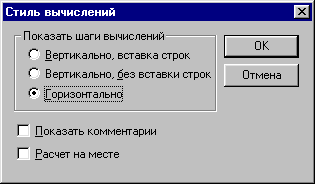
Стиль представления результатов вычислений
На наглядность вычислений влияет стиль представления их результатов. Команда Стиль Вычислений. позволяет задать тот или иной стиль, задать вывод результата символьной операции под основным выражением, рядом с ним или вместо него (Рисунок 9).
Рисунок . Стиль Вычислений
Примеры символьных операций в командном режиме
Большинство символьных операций легко выполняются, так что ниже мы остановимся лишь на некоторых примерах. Символьная операция Расчеты обеспечивает работу с математическими выражениями, содержащими встроенные в систему функции и представленными в различном виде: полиномиальном, дробно-рациональном, в виде сумм и произведений, производных и интегралов и т. д. (Рисунок 10).
Операция расчеты стремится произвести все возможные численные вычисления и представить выражение в наиболее простом виде. Она возможна над матрицами с символьными элементами. Производные и определенные интегралы, символьные значения которых вычисляются, должны быть представлены в своей естественной форме.
Особо следует отметить возможность выполнения численных вычислений с повышенной точностью — 20 знаков после запятой.
Для перехода в такой режим вычислений нужно числовые константы в вычисляемых объектах задавать с обязательным указанием десятичной точки, например 10.0 или 3.0, а не 10 или 3. Этот признак является указанием на проведение вычислений такого типа.
На Рисунке 10 показаны типовые примеры действия операции Расчеты. Здесь слева показаны исходные выражения, подвергаемые символьным преобразованиям, а справа — результат этих преобразований. Операция Расчеты одна из самых мощных, она позволяет в символьном виде вычислять суммы (и произведения) рядов, производные и неопределенные интегралы, выполнять символьные и численные операции с матрицами.
Эта операция содержит подменю. Команда Символические тут наиболее важная. Назначение других команд очевидно: они нужны, если результат требуется получить в форме комплексного или действительного числа. К примеру, если вы хотите вместо числа получить 3.141. используйте команду С плавающей запятой…. В режиме символьных вычислений результат может превосходить машинную бесконечность системы — см. пример на вычисление ехр(1000.0) на Рисунке 10. При этом число точных значащих цифр результата практически не ограничено (или, точнее говоря, зависит от емкости ОЗУ).
Операция Разложить на составляющие. возвращает разложение в ряд Тейлора выражения относительно выделенной переменной с заданным по запросу числом членов ряда n (число определяется по степеням ряда). По умолчанию задано п = 6. В разложении указывается остаточная погрешность разложения. На Рисунке 11 представлено применение этой операции для разложения функции . Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).
Рисунок . Разложение функции в ряд Тейлора
Операторы вычисления пределов функций
Для вычисления пределов функций в систему введен символьный оператор limit. Помимо ввода с наборной панели Матанализ, его в трех формах можно ввести нажатием следующих комбинаций клавиш:
[Ctrl] L — ввод шаблона оператора вычисления предела функции при х, стремящемся к заданному значению,
[Ctrl] A — ввод шаблона вычисления предела функции слева от заданной точки,
[Ctrl] B — ввод шаблона вычисления предела функции справа от заданной точки.
На Рисунке 12 показаны примеры вычисления пределов. При вычислении пределов нужно заполнить шаблоны, входящие в главный шаблон для вычисления пределов, а затем ввести функцию, имя переменной, по которой ищется предел, и значение переменной — аргумента функции.
Для получения результата установите после блока вычисления предела стрелку с острием, направленным вправо. Предел (если он существует) будет вычислен и появится в шаблоне у острия стрелки. Если функция не имеет предела, вместо результата появится надпись Undefine.
5.1 Ввод и редактирование выражений
Перед началом работы курсор имеет вид красного крестика. В момент ввода выражения курсор приобретает вид синего уголка, окаймляющего часть вводимого выражения. Ввод начинается с имени переменной, после нее ставится знак присваивания (знак:), а затем само выражение или константа. Имя выражения (та часть, которая левее оператора присваивания) может состоять из латинских, русских, греческих букв и цифр, знаков подчеркивания (_), штриха (`), процента (%), бесконечности?, вводимых с клавиатуры.
Имена переменных и функций не могут начинаться с цифры, подчеркивания, штриха, процента (%), не могут включать пробелы. Символ бесконечности может быть только первым в имени переменной. Mathcad воспринимает прописные и строчные буквы, а также введенные разными шрифтами как различные.
Редактирование введенных выражений производится следующими способами:
1. ?Курсор перемещается по экрану клавишами со стрелками или левой кнопкой мыши ставится в нужное место экрана.
2. ?Для выделения одного символа синим уголком курсора нужно установить курсор так, чтобы он охватывал этот символ слева или справа.
3. ?Для расширения выделения на часть или выражение целиком удобнее использовать клавиши со стрелками или пробел. Для перехода из оператора на уровень выше можно также использовать пробел. Уголок курсора должен охватывать все выражение или его часть, над которой надо выполнить действие.
4. Для выделения части или всего выражения надо щелкнуть левой кнопкой мыши в начале или в конце выделяемого выражения и переместить курсор до другого края с нажатой левой кнопкой мыши. Можно использовать клавиши Shift+? или Shift+?. Выделенная часть выражения черного цвета. Выделение в Mathcad используется для вырезания или копирования части выражения, изменения шрифта, а также для выполнения некоторых видов символьных вычислений.
5. ?Для выделения объекта или группы (математических, текстовых или графических) надо щелкнуть мышью на свободном месте рабочего листа и протянуть прямоугольник выделения так, чтобы он захватил нужные объекты. Один объект будет выделен синим курсоров, а группа объектов — пунктирной рамкой.
Если надо удалить, вырезать или скопировать выделенную часть выражения, выделенный объект целиком или группу выделенных объектов, используются такие же команды, как и в других приложениях Windows.
Некоторые латинские и греческие буквы зарезервированы в качестве констант. Так, латинская буква е внутри математического выражения является основанием натурального логарифма е = 2,718. Это значение можно отменить, присвоив ей любое другое значение, используя знак локального присваивания:=.
Знак бесконечности ? можно вставить с математической панели Calculus.
Если какой-либо константе или переменной не присвоено никакого значения левее и выше ее на экране, то она будет окрашена в красный цвет, указывая на ошибку. Все переменные и функции должны быть предварительно определены.
Если константы в правой части функции пользователя не заданы непосредственно перед использованием этой функции их значения берутся такими, какие были в последний раз перед этим расчетом.
Для ввода простого текста можно выбрать команду InsertTextRegion (Вставить Текстовую область) в главном меню, но удобнее ввести с клавиатуры символ кавычки и далее сам текст. На экране появится текстовая область, в которой можно печатать. Также, сменив латинский шрифт на русский, начать печатать текст в любом месте документа. Как только будет напечатано первое слово, при нажатии пробела эта область автоматически превращается в текстовую.
В Mathcad на точность расчета повлиять нельзя, но можно изменить формат вывода результатов. В Mathcad 11 вычисления совершаются с точностью 12 знаков, а в Mathcad 15 — до 17 знаков.
1.4 Настройка MathCad для работы
Для настройки параметров вычислений необходимо выбрать команду Options (Параметры) меню Math (Математика). При этом на экране появится диалоговое окно (Свойства), содержащее следующие вкладки:
Built-In Variabls(Встроенные переменные) — позволяет установить значения встроенных системных переменных, влияющих на точность вычислений и параметры некоторых функций системы.
Calculation(Вычисление) — Эта вкладка содержит две опции, задающие режим автоматических вычислений и оптимизации выражений перед вычислением.
Display(Отображение) — Позволяет форматировать вид символов, отображающих основные операторы системы (умножение, деление, локальное и глобальное присваивание и др.)
Unit System(Система единиц) — Позволяет выбрать систему единиц для размерных величин: SI, MKS, CGS, Us и None (не используется ни одна из этих систем).
Dimensions(Размерность) — Позволяет изменить формат размерных величин (на вкладке содержится их перечень). Для этого надо «включить» опциюDisplay Dimensions(Просмотр размерностей)
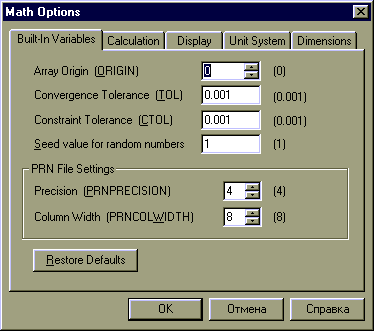
Остановимся подробнее на изучении параметров вкладки Built-In Variabls (Встроенные переменные). Здесь можно изменить значения системных констант и переменных. К ним относятся:
Array Origin (ORIGIN)— Начальное значение для индексов. Например, трехмерный векторvприORIGIN=0(по умолчанию) имеет компонентыv0, v1, v2.
Convergence Tolerance (TOL) — Допустимое отклонение. MathACD использует эту переменную при различных численных расчетах, таких как вычисление определенных интегралов и при решении уравнений с использованием функцийrootиpolyroots. По умолчаниюTOL=10 -3 .
Constraint Tolerance (CTOL)— Задает точность вычислений при использовании блока решений уравнений и систем. Блок начинается со словаGivenи заканчивается словамиFind, Minerrи др. По умолчаниюCTOL=10 -3
Seed value for random numbers— Определяет интервал от0до указанного в поле значения, из которого функцияrnd(x)генерируетxслучайных чисел. Возможность менять этот интервал позволяет получать разные последовательности случайных чисел.
Presision (PRNPRESISION)— Задает точность числовых значений, которые помещаются в файл, создаваемый функциейWRITEPRN
Column Width (PRNCOLWIDTH)— Задает ширину столбца (в символах) при создании файлов с помощью функцииWRITEPRN
Кнопка Restore Defaults(Васстановить по умолчанию) позволяет вернуть стандартно установленные в системе MathCAD параметры вычислений (те, что установлены по умолчанию), если внесенные вами изменения в системные переменные вас не устраивают. Значения переменных по умолчанию указаны справа от полей, предназначенных для ввода.
Форматирование результатов вычислений.
MathCAD представляет результаты вычислений в определенном формате. Этот формат включает в себя, например, число знаков после запятой, Величину, начиная с которой используется экспоненциальное представление чисел, символ i или j для представления мномой единицы и многое другое. Чтобы задать формат представления результатов вычислений надо выбрать команду Result (Результат) меню Format (Формат). В результате на экране появится диалоговое окно Result Format, содержащее несколько вкладок.
1. На вкладке Number format (Формат числа) находятся :
поле Number of decimal places(Число десятичных знаков), в котором задается количество отображаемых знаков после запятой (по умолчанию — 3).
Опция Show trailing zeroz(Показывать конечные нули) -Если установлена эта опция, все числа будут отображаться с тем количеством знаков после запятой, которое указано в полеNumber of decimal places, даже если без этого можно обойтись. В этом случае число5будет иметь вид5.000, а число0—0.000.
Поле Exponential threshold(Порог экспоненты) — Здесь необходимо задать целое числоn. Оно указывает, что чмслаx, для которых справедливы неравенства |x|<10 n и |x|>10 -n+1 , представляются в экспоненциальной форме. Чмслуnможно присваивать знвчения от 0 до 15, по умолчаниюn=3. MathCAD производит вычисления с точностью 15 знаков после запятой.
Опция Show exponents in engeneering format(Показывать экспоненты в инженерном формате) всегда представляет число в экспоненциальном формате, если показатель степени больше 3 или меньше -3,выделяя при этом 3 целых и 3 десятичных разряда. В противном случае число отображается в явном виде, например, число 2233446 при включении опции будет выглядеть как 222.344 10 3 .
Список Format(Формат) — позволяет выбрать формат представления чисел. Выделим среди указанных в списке форматDecimal— при его выборе результат никогда не представляется в экспоненциальной форме. Остальные форматы могут представлять числа в экспоненциальной форме. Более подробно с видами форматов можно познакомиться, нажав кнопкуСправка.
2. На вкладке Tolerance (Допуск) находятся поля Complex threshold (Комплексный порог) и Zero threshold (Нулевой порог).
Целое число n, заданное в поле Complex threshold, указывает, что комплексные числа z, для которых справедливо неравенство |Re(z)/Im(z)|<10 -n , представляются как чисто мнимые. А числа, для которых |Im(z)/Re(z)|<10 -n — как действительные. При вычислениях MathCAD не пренебрегает даже незначительной мнимой. Числу n можно присваивать значения от 0 до 63, по умолчанию n=10.
Целое число n, заданное в поле Zero threshold, указывает, что числа x, для которых справедливо неравенство |x|<10 -n , принимаются равными 0. Числу n можно присваивать значения от 0 до 307, по умолчанию n=15. Для комплексных чисел, у которых |Re(z)|<10 -n , действительная часть принимается равной нулю, то же самое справедливо и для мнимой части. Значение, заданное в поле Zero threshold, действительно для всего документа.
3. Вкладка Display Options содержит следующие поля и опции:
Matrix display style(Стиль отображения матриц) — выпадающий список позаоляет установить отображение матриц в стандартном математическом виде —Matrix, в виде таблицы —Table, либо предоставляет выбрать стиль прелставления матриц системе MathCAD —Automatic.
При этом, если матрица содержит менее 10 строк и столбцов, она представляется в стандартном виде матрицы, в противном случае — в виде таблицы в полосами прокрутки. По умолчанию установлена опция Automatic.
Опция Expand nested arrays (Развернуть вложенные массивы) — позволяет явно вывести элементы матрицы, представляющие, в свою очередь, матрицы.
Поле Imaginary value (Мнимая единица) — позволяет определить символ, который будет использоваться для обозначения мнимой единицы (i или j).
В поле списка Radix (Система) — можно выбрать десятичную, двоичную, восьмеричную или шестнадцатиричную систему счисления.
4. Вкладка Unit display (Отображение единиц измерения) содержит две опции: Format Units (Формат единиц) — включает отображение единиц измерения; Simplify units when possible — включает упрощение единиц измерения (если это возможно).
Окно Result Format можно открыть двойным щелчком на числе, представляющем собой результат вычислений.
Если вы хотите увидеть точное значение некоторого числа, не изменяя его формат, выделите это число и нажмите клавиши [Ctrl+Shift+N]. В строке состояния вы увидите данное число с 15 знаками после запятой.
Если вы хотите применять выполненные установки и в других документах, вам необходимо открыть соответствующий файл шаблона с расширением MCT из папки TEMPLATE и произвести в нем нужные изменения. Кроме того, вы можете сохранить текущий документ как шаблон.
Лабораторная работа №1
Вычислите для каждого значения Х=1,5,7 следующие функции:¶
Рекомендуется использовать операцию векторизации (MathPalette, матричные операции) Измените количество значащих цифр , выводимых на экран после десятичной точки, на 6.
Решите двумя способами (матричным и с помощью функции lsolve) систему линейных уравнений,¶Справку по использованию функцииlsolveнайдите в справочной системе MathCAD.¶
Смените нижнюю границу индексации массивов на 1.Выведете решение системы уравнений из п.2 в виде вектора-столбца и поэлементно.
Скопируйте первую из формул п.1 и замените в ней первое подкоренное выражение в знаменателе на sin(x), а второй операнд в знаменателе — наctg(x/2). Присвойте полученное выражение новой переменнойG(удаливу).
Вставьте в документ текстовую область: «Построение простейшего графика.»
Определите функцию f(x)= sin(x)+cos(x)-1.
Постройте график функции f(x)(воспользуйтесь быстрым построением графиков).



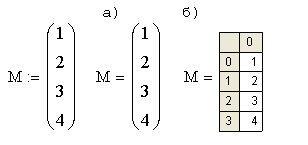


























 Необходимо получить тип элемента и с помощью CType или DirectCast изменить его тип
Необходимо получить тип элемента и с помощью CType или DirectCast изменить его тип