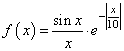Язык Python
- Двумерные графики
- Настройки отображения
- Гистограммы
- Диаграммы рассеяния
- Контурные диаграммы
- Расположение нескольких осей в одном окне
- Резюме
- Источники
Библиотека matplotlib содержит большой набор инструментов для двумерной графики. Она проста в использовании и позволяет получать графики высокого качества. В этом разделе мы рассмотрим наиболее распространенные типы диаграмм и различные настройки их отображения.
Модуль matplotlib.pyplot предоставляет процедурный интерфейс к (объектно-ориентированной) библиотеке matplotlib, который во многом копирует инструменты пакета MATLAB. Инструменты модуля pyplot де-факто являются стандартным способом работы с библиотекой matplotlib, поэтому мы органичимся рассмотрением этого пакета.
Двумерные графики
pyplot.plot
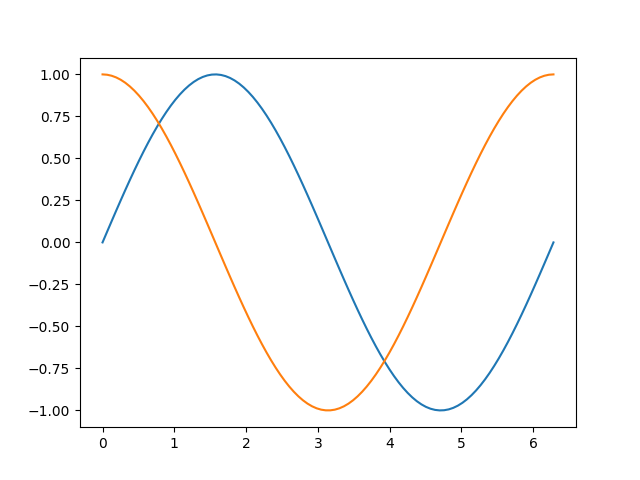
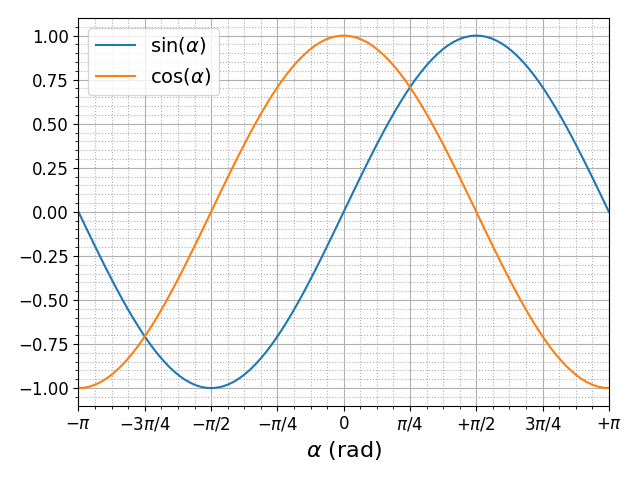
Нарисовать графики функций sin и cos с matplotlib.pyplot можно следующим образом:
import numpy as np import matplotlib.pyplot as plt phi = np.linspace(0, 2.*np.pi, 100) plt.plot(phi, np.sin(phi)) plt.plot(phi, np.cos(phi)) plt.show()
В результате получаем
Мы использовали функцию plot, которой передали два параметра — списки значений по горизонтальной и вертикальной осям. При последовательных вызовах функции plot графики строятся в одних осях, при этом происходит автоматическое переключение цвета.
Строковый параметр
fmt = '[marker][line][color]'
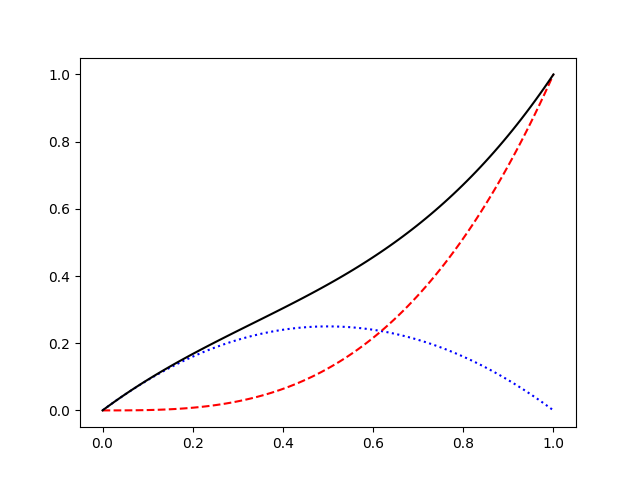
функции plot позволяет задавать тип маркера, тип линии и цвет. Приведем несколько примеров:
x = np.linspace(0, 1, 100) f1 = 0.25 - (x - 0.5)**2 f2 = x**3 plt.plot(x, f1, ':b') # пунктирная синяя линия plt.plot(x, f2, '--r') # штрихованная красная линия plt.plot(x, f1+f2, 'k') # черная непрерывная линия plt.show()
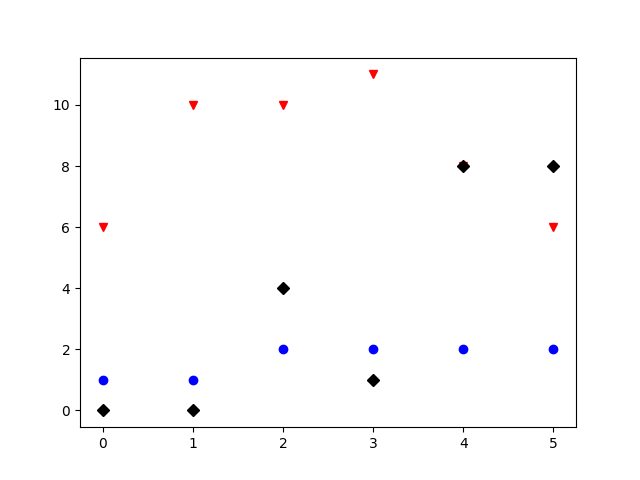
rg = np.random.Generator(np.random.PCG64()) plt.plot(rg.binomial(10, 0.3, 6), 'ob') # синие круги plt.plot(rg.poisson(7, 6), 'vr') # красные треугольники plt.plot(rg.integers(0, 10, 6), 'Dk') # черные ромбы plt.show()
Из последнего примера видно, что если в функцию plot передать только один список y, то он будет использован для значений по вертикальной оси. В качестве значений по горизонтальной оси будет использован range(len(y)).
Более тонкую настройку параметров можно выполнить, передавая различные именованные аргументы, например:
marker:str— тип маркераmarkersize:float— размер маркераlinestyle:str— тип линииlinewidth:float— толщина линииcolor:str— цвет
Полный список доступных параметров можно найти в документации.
pyplot.errorbar
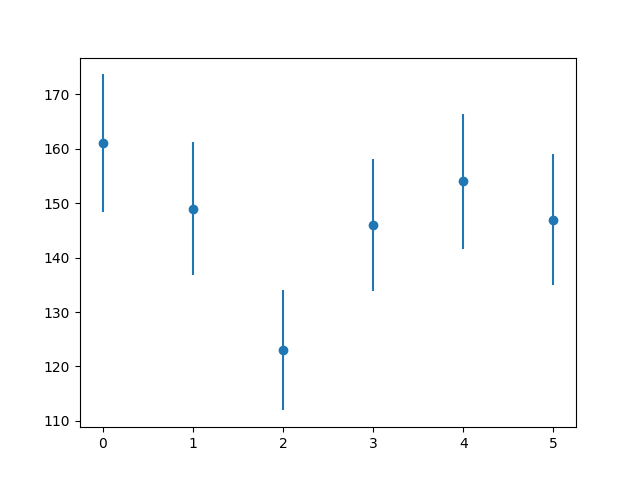
Результаты измерений в физике чаще всего представлены в виде величин с ошибками. Функция plt.errorbar позволяет отображать такие данные:
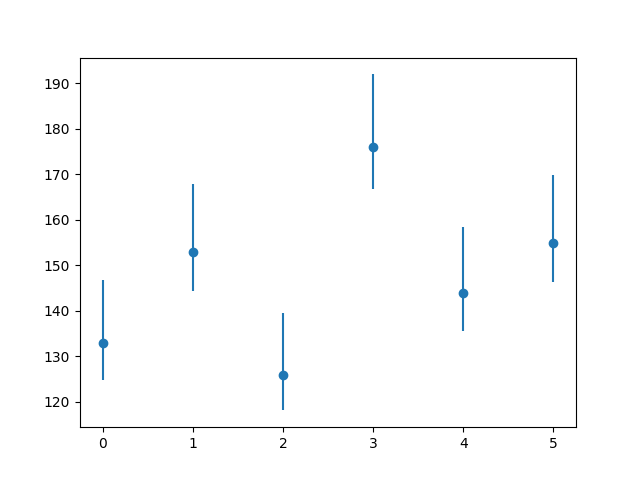
rg = np.random.Generator(np.random.PCG64(5)) x = np.arange(6) y = rg.poisson(149, x.size) plt.errorbar(x, y, yerr=np.sqrt(y), marker='o', linestyle='none') plt.show()
Ошибки можно задавать и для значений по горизонтальной оси:
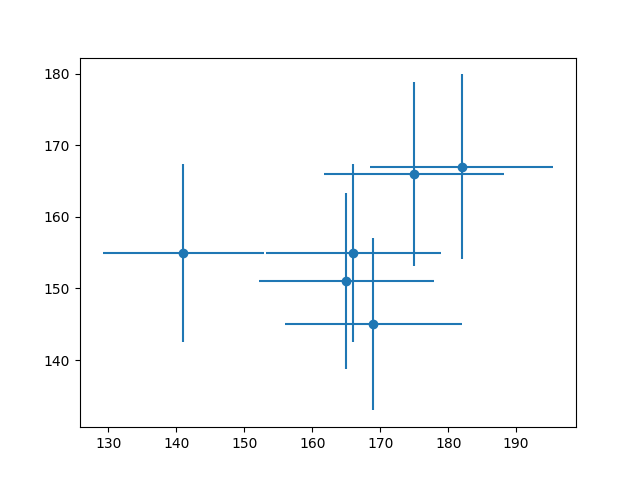
rg = np.random.Generator(np.random.PCG64(5)) N = 6 x = rg.poisson(169, N) y = rg.poisson(149, N) plt.errorbar(x, y, xerr=np.sqrt(x), yerr=np.sqrt(y), marker='o', linestyle='none') plt.show()
Ошибки измерений могут быть асимметричными. Для их отображения в качестве параметра yerr (или xerr) необходимо передать кортеж из двух списков:
rg = np.random.Generator(np.random.PCG64(11)) N = 6 x = np.arange(N) y = rg.poisson(149, N) yerr = [ 0.7*np.sqrt(y), 1.2*np.sqrt(y) ] plt.errorbar(x, y, yerr=yerr, marker='o', linestyle='none') plt.show()
Функция pyplot.errorbar поддерживает настройку отображения графика с помощью параметра fmt и всех именованных параметров, которые доступны в функции pyplot. Кроме того, здесь появляются параметры для настройки отображения линий ошибок («усов»):
ecolor:str— цвет линий ошибокelinewidth:float— ширина линий ошибокcapsize:float— длина «колпачков» на концах линий ошибокcapthick:float— толщина «колпачков» на концах линий ошибок
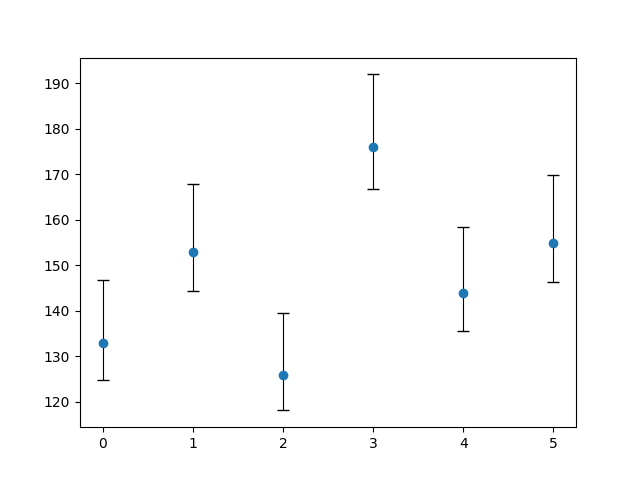
и некоторые другие. Изменим параметры отрисовки данных из предыдущего примера:
# ... plt.errorbar(x, y, yerr=yerr, marker='o', linestyle='none', ecolor='k', elinewidth=0.8, capsize=4, capthick=1) plt.show()
Настройки отображения
Наши графики все еще выглядят довольно наивно. В этой части мы рассмотрим различные настройки, которые позволят достичь качества оформления диаграмм, соответствующего, например, публикациям в рецензируемых журналах.
Диапазон значений осей
Задавать диапазон значений осей в matplotlib можно несколькими способами. Например, так:
pyplot.xlim([0, 200]) # диапазон горизонтальной оси от 0 до 200 pyplot.xlim([0, 1]) # диапазон вертикальной оси от 0 до 1
Размер шрифта
Размер и другие свойства шрифта, который используется в matplotlib по умолчанию, можно изменить с помощью объекта matplotlib.rcParams:
matplotlib.rcParams.update({'font.size': 14})
Объект matplotlib.rcParams хранит множество настроек, изменяя которые, можно управлять поведением по умолчанию. Смотрите подробнее в документации.
Подписи осей
Подписи к осям задаются следующим образом:
plt.xlabel('run number', fontsize=16) plt.ylabel(r'average current ($mu A$)', fontsize=16)
В подписях к осям (и вообще в любом тексте в matplotlib) можно использовать инструменты текстовой разметки TeX, позволяющие отрисовывать различные математические выражения. TeX-выражения должны быть внутри пары символов $, кроме того, их следует помещать в r-строки, чтобы избежать неправильной обработки.
Заголовок
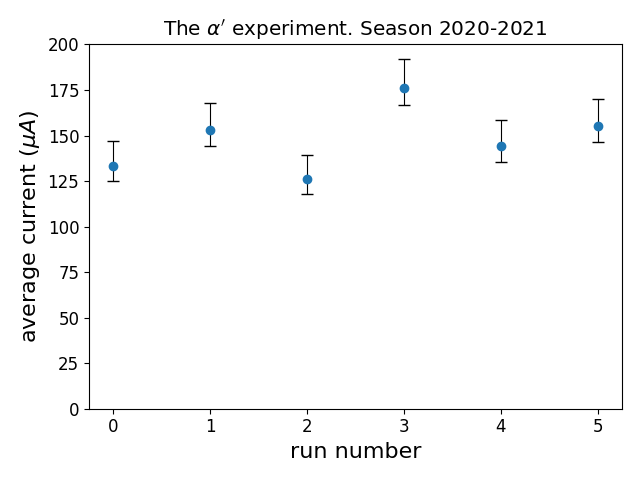
Функция pyplot.title задает заголовок диаграммы. Применим наши новые знания:
import numpy as np import matplotlib.pyplot as plt import matplotlib # задаем размер шрифта matplotlib.rcParams.update({'font.size': 12}) rg = np.random.Generator(np.random.PCG64(11)) x = np.arange(6) y = rg.poisson(149, x.size) yerr = [ 0.7*np.sqrt(y), 1.2*np.sqrt(y) ] plt.errorbar(x, y, yerr=yerr, marker='o', linestyle='none', ecolor='k', elinewidth=0.8, capsize=4, capthick=1) # добавляем подписи к осям и заголовок диаграммы plt.xlabel('run number', fontsize=16) plt.ylabel(r'average current ($mu A$)', fontsize=16) plt.title(r'The $alpha^prime$ experiment. Season 2020-2021') # задаем диапазон значений оси y plt.ylim([0, 200]) # оптимизируем поля и расположение объектов plt.tight_layout() plt.show()
В этом примере мы использовали функцию pyplot.tight_layout, которая автоматически подбирает параметры отображения так, чтобы различные элементы не пересекались.
Легенда
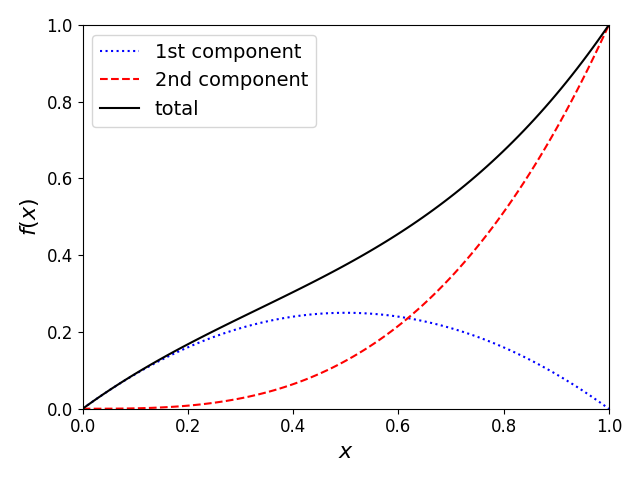
При построении нескольких графиков в одних осях полезно добавлять легенду — пояснения к каждой линии. Следующий пример показывает, как это делается с помощью аргументов label и функции pyplot.legend:
import numpy as np import matplotlib.pyplot as plt import matplotlib matplotlib.rcParams.update({'font.size': 12}) x = np.linspace(0, 1, 100) f1 = 0.25 - (x - 0.5)**2 f2 = x**3 # указываем в аргументе label содержание легенды plt.plot(x, f1, ':b', label='1st component') plt.plot(x, f2, '--r', label='2nd component') plt.plot(x, f1+f2, 'k', label='total') plt.xlabel(r'$x$', fontsize=16) plt.ylabel(r'$f(x)$', fontsize=16) plt.xlim([0, 1]) plt.ylim([0, 1]) # выводим легенду plt.legend(fontsize=14) plt.tight_layout() plt.show()
Функция pyplot.legend старается расположить легенду так, чтобы она не пересекала графики. Аргумент loc позволяет задать расположение легенды вручную. В большинстве случаев расположение по умолчанию получается удачным. Детали и описание других аргументов смотрите в документации.
Сетка
Сетка во многих случаях облегчает анализ графиков. Включить отображение сетки можно с помощью функции pyplot.grid. Аргумент axis этой функции имеет три возможных значения: x, y и both и определяет оси, вдоль которых будут проведены линии сетки. Управлять свойствами линии сетки можно с помощью именованных аргументов, которые мы рассматривали выше при обсуждении функции pyplot.plot.
В matplotlib поддерживается два типа сеток: основная и дополнительная. Выбор типа сетки выполняется с помощью аргумента which, который может принимать три значения: major, minor и both. По умолчанию используется основная сетка.
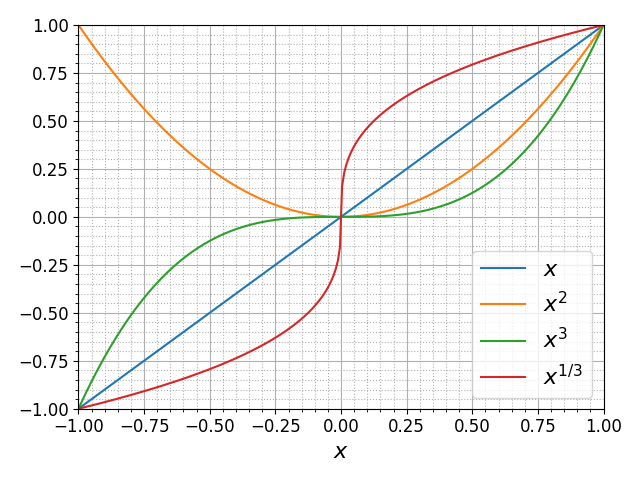
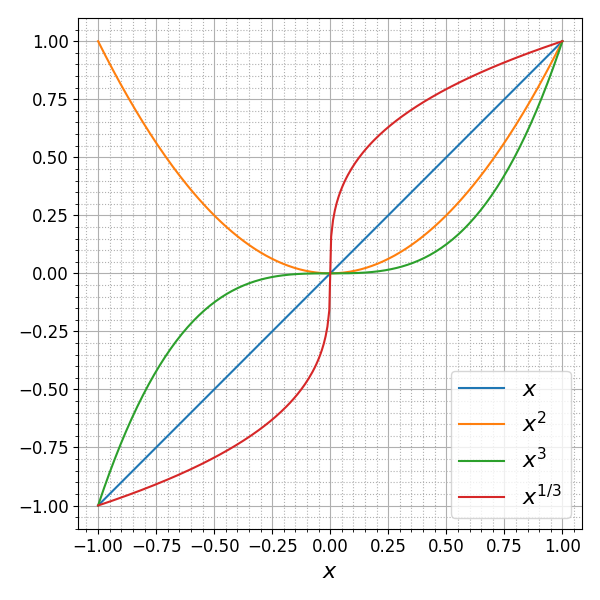
Линии сетки привязаны к отметкам на осях. Чтобы работать с дополнительной сеткой необходимо сначала включить вспомогательные отметки на осях (которые по умолчанию отключены и к которым привязаны линии дополнительной сетки) с помощью функции pyplot.minorticks_on. Приведем пример:
import numpy as np import matplotlib.pyplot as plt import matplotlib matplotlib.rcParams.update({'font.size': 12}) x = np.linspace(-1, 1, 250) plt.plot(x, x, label=r'$x$') plt.plot(x, x**2, label=r'$x^2$') plt.plot(x, x**3, label=r'$x^3$') plt.plot(x, np.cbrt(x), label=r'$x^{1/3}$') plt.legend(fontsize=16) # включаем дополнительные отметки на осях plt.minorticks_on() plt.xlabel(r'$x$', fontsize=16) plt.xlim([-1., 1.]) plt.ylim([-1., 1.]) # включаем основную сетку plt.grid(which='major') # включаем дополнительную сетку plt.grid(which='minor', linestyle=':') plt.tight_layout() plt.show()
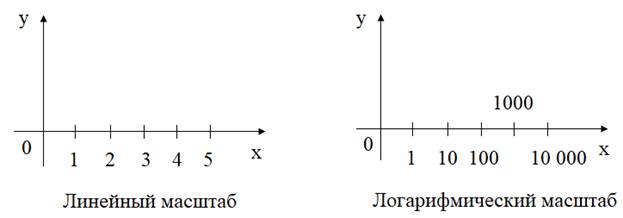
Логарифмический масштаб
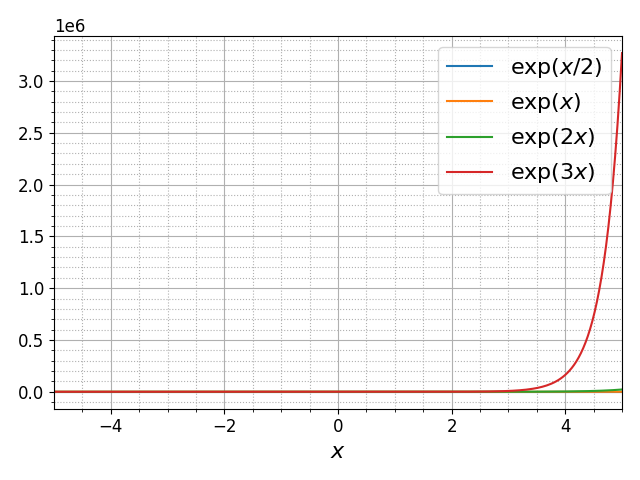
Функции pyplot.semilogy и pyplot.semilogx выполняют переключение между линейным и логарифмическим масштабами осей. В некоторых случаях логарифмический масштаб позволяет отобразить особенности зависимостей, которые не видны в линейном масштабе. Вот так выглядят графики экспоненциальных функций в линейном масштабе:
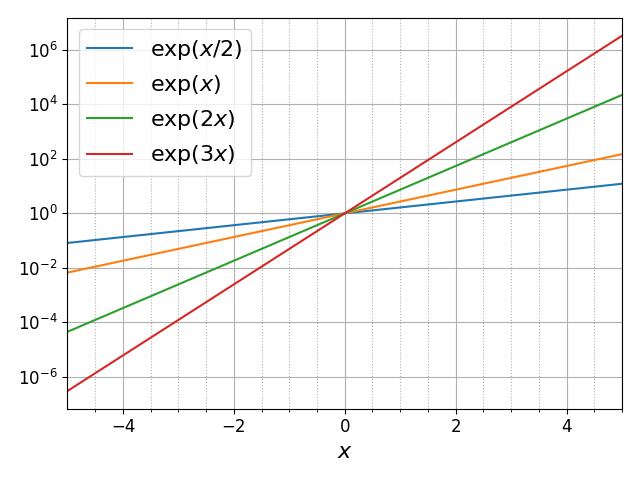
Добавление строки
делает график гораздо более информативным:
Теперь мы видим поведение функций во всем динамическом диапазоне, занимающем 12 порядков.
Произвольные отметки на осях
Вернемся к первому примеру, в котором мы строили графики синуса и косинуса. Сделаем так, чтобы на горизонтальной оси отметки соответствовали различным долям числа pi и имели соответствующие подписи:
Метки на горизонтальной оси были заданы с помощью функции pyplot.xticks:
plt.xticks( np.linspace(-np.pi, np.pi, 9), [r'$-pi$', r'$-3pi/4$', r'$-pi/2$', r'$-pi/4$', r'$0$', r'$pi/4$', r'$+pi/2$', r'$3pi/4$', r'$+pi$'])
Модуль pyplot.ticker содержит более продвинутые инструменты для управления отметками на осях. Подробности смотрите в документации.
Размер изображения
До сих пор мы строили графики в одном окне, размер которого был задан по умолчанию. За кадром matplotlib создавал объект типа Figure, который определяет размер окна и содержит все остальные элементы. Кроме того, автоматически создавался объект типа Axis. Подробнее работа с этими объектами будет рассмотрена ниже. Сейчас же мы рассмотрим функцию pyplot.figure, которая позволяет создавать новые объекты типа Figure и переключаться между уже созданными объектами.
Функция pyplot.figure может принимать множество аргументов. Вот основные:
num:intилиstr— уникальный идентификатор объекта типа. Если задан новый идентификатор, то создается новый объект и он становится активным. В случае, если передан идентификатор уже существующего объекта, то этот объект возвращается и становится активным/media//media/figsize:(float, float)— размер изображения в дюймахdpi:float— разрешение в количестве точек на дюйм
Описание других параметров функции pyplot.figure можно найти в документации. Используем эту функцию и функцию pyplot.axis чтобы улучшить наш пример с построением степенных функций:
Мы добавили две строки по сравнению с прошлой версией:
fig = plt.figure(/media//media/figsize=(6, 6)) # ... plt.axis('equal')
Функция pyplot.axis позволяет задавать некоторые свойства осей. Ее вызов с параметром 'equal' делает одинаковыми масштабы вертикальной и горизонтальной осей, что кажется хорошей идеей в этом примере. Функция pyplot.axis возвращает кортеж из четырех значений xmin, xmax, ymin, ymax, соответствующих границам диапазонов значений осей.
Некоторые другие способы использования функции pyplot.axis:
- Кортеж из четырех
floatзадаст новые границы диапазонов значений осей - Строка
'off'выключит отображение линий и меток осей
Гистограммы
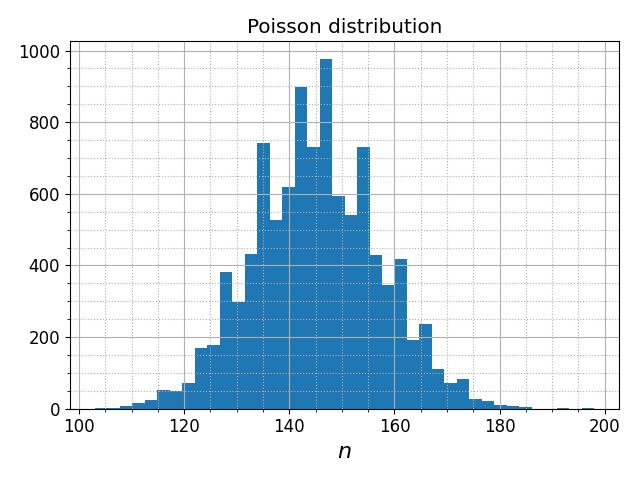
Обратимся теперь к другим типам диаграмм. Функция pyplot.hist строит гистограмму по набору значений:
import numpy as np import matplotlib.pyplot as plt rg = np.random.Generator(np.random.PCG64(5)) data = rg.poisson(145, 10000) plt.hist(data, bins=40) # для краткости мы опускаем код для настройки осей, сетки и т.д.
Аргумент bins задает количество бинов гистограммы. По умолчанию используется значение 10. Если вместо целого числа в аргумент bins передать кортеж значений, то они будут использованы для задания границ бинов. Таким образом можно построить гистограмму с произвольным разбиением.
Некоторые другие аргументы функции pyplot.hist:
range:(float, float)— диапазон значений, в котором строится гистограмма. Значения за пределами заданного диапазона игнорируются.density:bool. При значенииTrueбудет построена гистограмма, соответствующая плотности вероятности, так что площадь гистограммы будет равна единице.weights: списокfloatзначений того же размера, что и набор данных. Определяет вес каждого значения при построении гистограммы.histtype:str. может принимать значения{'bar', 'barstacked', 'step', 'stepfilled'}. Определяет тип отрисовки гистограммы.
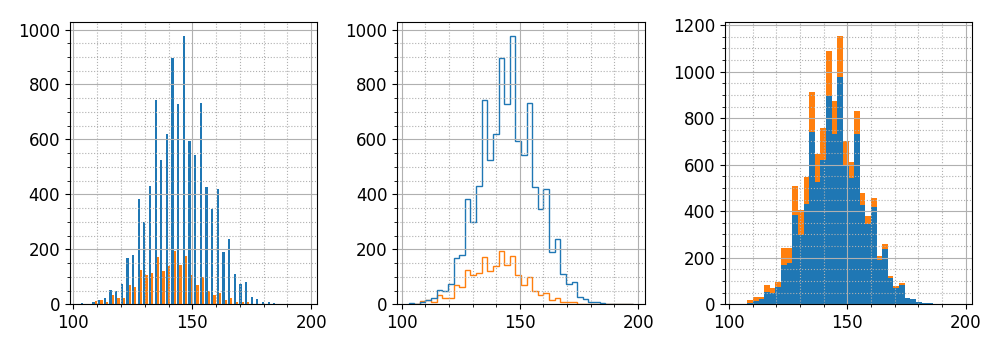
В качестве первого аргумента можно передать кортеж наборов значений. Для каждого из них будет построена гистограмма. Аргумент stacked со значением True позволяет строить сумму гистограмм для кортежа наборов. Покажем несколько примеров:
rg = np.random.Generator(np.random.PCG64(5)) data1 = rg.poisson(145, 10000) data2 = rg.poisson(140, 2000) # левая гистограмма plt.hist([data1, data2], bins=40) # центральная гистограмма plt.hist([data1, data2], bins=40, histtype='step') # правая гистограмма plt.hist([data1, data2], bins=40, stacked=True)
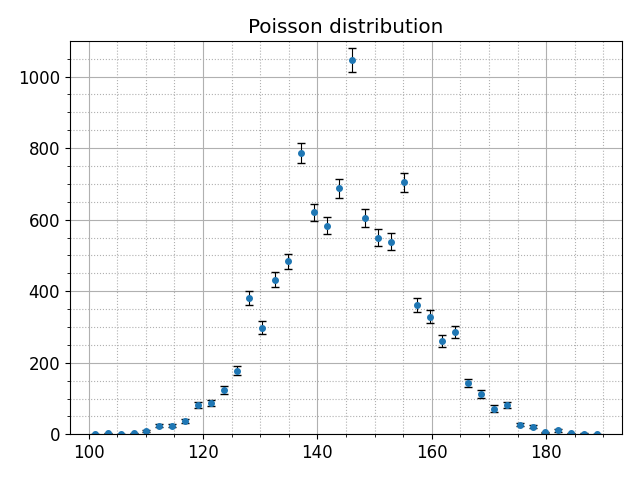
В физике гистограммы часто представляют в виде набора значений с ошибками, предполагая при этом, что количество событий в каждом бине является случайной величиной, подчиняющейся биномиальному распределению. В пределе больших значений флуктуации количества событий в бине могут быть описаны распределением Пуассона, так что характерная величина флуктуации определяется корнем из числа событий. Библиотека matplotlib не имеет инструмента для такого представления данных, однако его легко получить с помощью комбинации numpy.histogram и pyplot.errorbar:
def poisson_hist(data, bins=60, lims=None): """ Гистограмма в виде набора значений с ошибками """ hist, bins = np.histogram(data, bins=bins, range=lims) bins = 0.5 * (bins[1:] + bins[:-1]) return (bins, hist, np.sqrt(hist)) rg = np.random.Generator(np.random.PCG64(5)) data = rg.poisson(145, 10000) x, y, yerr = poisson_hist(data, bins=40, lims=(100, 190)) plt.errorbar(x, y, yerr=yerr, marker='o', markersize=4, linestyle='none', ecolor='k', elinewidth=0.8, capsize=3, capthick=1)
Диаграммы рассеяния
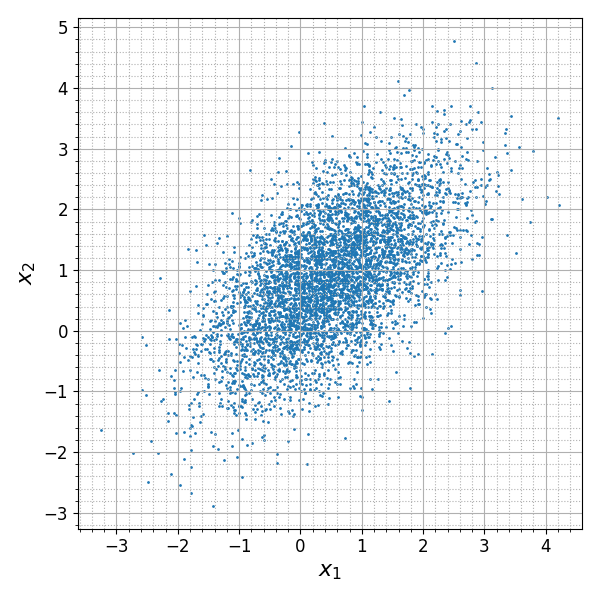
Распределение событий по двум измерениям удобно визуализировать с помощью диаграммы рассеяния:
rg = np.random.Generator(np.random.PCG64(5)) means = (0.5, 0.9) covar = [ [1., 0.6], [0.6, 1.] ] data = rg.multivariate_normal(means, covar, 5000) plt.scatter(data[:,0], data[:,1], marker='o', s=1)
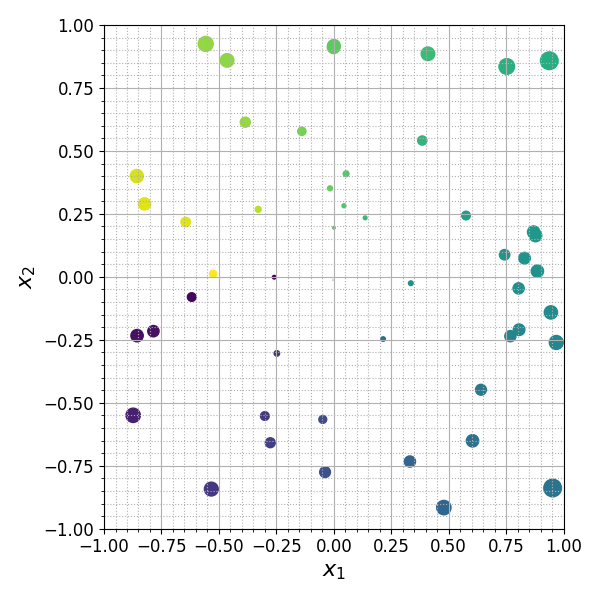
Каждой паре значений в наборе данных соответствует одна точка на диаграмме. Несмотря на свою простоту, диаграмма рассеяния позволяет во многих случаях наглядно представлять двумерные данные. Функция pyplot.scatter позволяет визуализировать и данные более высокой размерности: размер и цвет маркера могут быть заданы для каждой точки отдельно:
rg = np.random.Generator(np.random.PCG64(4)) data = rg.uniform(-1, 1, (50, 2)) col = np.arctan2(data[:, 1], data[:, 0]) size = 100*np.sum(data**2, axis=1) plt.scatter(data[:,0], data[:,1], marker='o', s=size, c=col)
Цветовую палитру можно задать с помощью аргумента cmap. Подробности и описание других аргументов функции pyplot.scatter можно найти в документации.
Контурные диаграммы
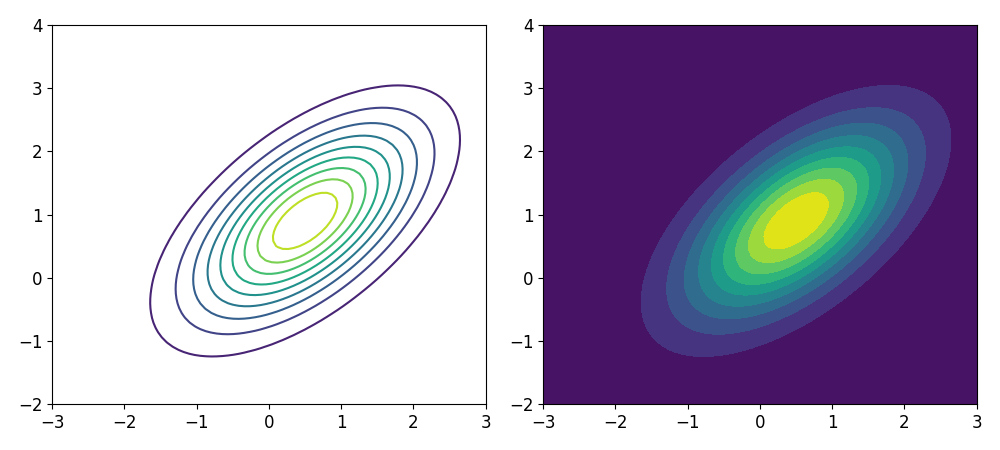
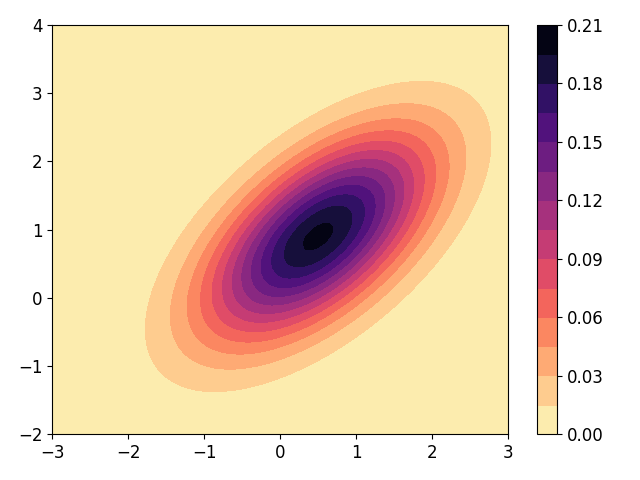
Контурные диаграммы позволяют визуализировать функции двух переменных:
from scipy import stats means = (0.5, 0.9) covar = [ [1., 0.6], [0.6, 1.] ] mvn = stats.multivariate_normal(means, covar) x, y = np.meshgrid( np.linspace(-3, 3, 80), np.linspace(-2, 4, 80) ) data = np.dstack((x, y)) # левая диаграмма — без заливки цветом plt.contour(x, y, mvn.pdf(data), levels=10) # правая диаграмма — с заливкой цветом plt.contourf(x, y, mvn.pdf(data), levels=10)
Аргумент levels задает количество контуров. По умолчанию контуры отрисовываются равномерно между максимальным и минимальным значениями. В аргумент levels также можно передать список уровней, на которых следует провести контуры.
Обратите внимание на использование функций numpy.meshgrid и numpy.dstack в этом примере.
Контурную диаграмму можно дополнить цветовой полосой colorbar, вызвав функцию pyplot.colorbar:
cs = plt.contourf(x, y, mvn.pdf(data), levels=15, cmap=matplotlib.cm.magma_r) cbar = plt.colorbar(cs)
Более подробное описание функций plt.contour и plt.contourf смотрите в документации.
Расположение нескольких осей в одном окне
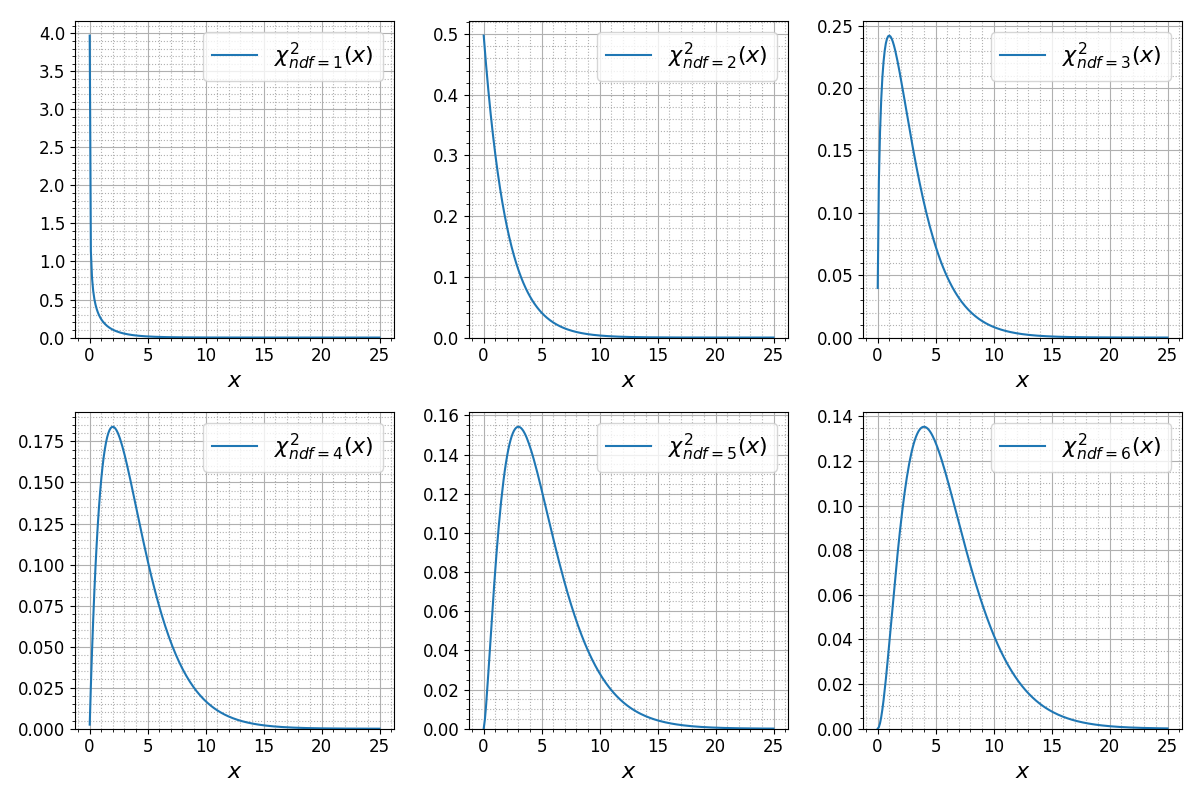
В одном окне (объекте Figure) можно разместить несколько осей (объектов axis.Axis). Функция pyplot.subplots создает объект Figure, содержащий регулярную сетку объектов axis.Axis:
{% raw %}
import numpy as np from scipy import stats import matplotlib.pyplot as plt fig, axes = plt.subplots(ncols=3, nrows=2, /media//media/figsize=(12, 8)) x = np.linspace(0.01, 25, 250) for idx, row in enumerate(axes): for jdx, ax in enumerate(row): ndf = idx * 3 + jdx + 1 y = stats.chi2.pdf(x, ndf) ax.plot(x, y, label=fr'$chi^2_{{ndf={ndf}}}(x)$') ax.set_xlabel(r'$x$', fontsize=16) ax.set_ylim([0, 1.05*y.max()]) ax.minorticks_on() ax.legend(fontsize=16) ax.grid(which='major') ax.grid(which='minor', linestyle=':') fig.tight_layout() plt.show()
{% endraw %}
Количество строк и столбцов, по которым располагаются различные оси, задаются с помощью параметров nrows и ncols, соответственно. Функция pyplot.subplots возвращает объект Figure и двумерный список осей axis.Axis. Обратите внимание на то, что вместо вызовов функций модуля pyplot в этом примере использовались вызовы методов классов Figure и axis.Axis.
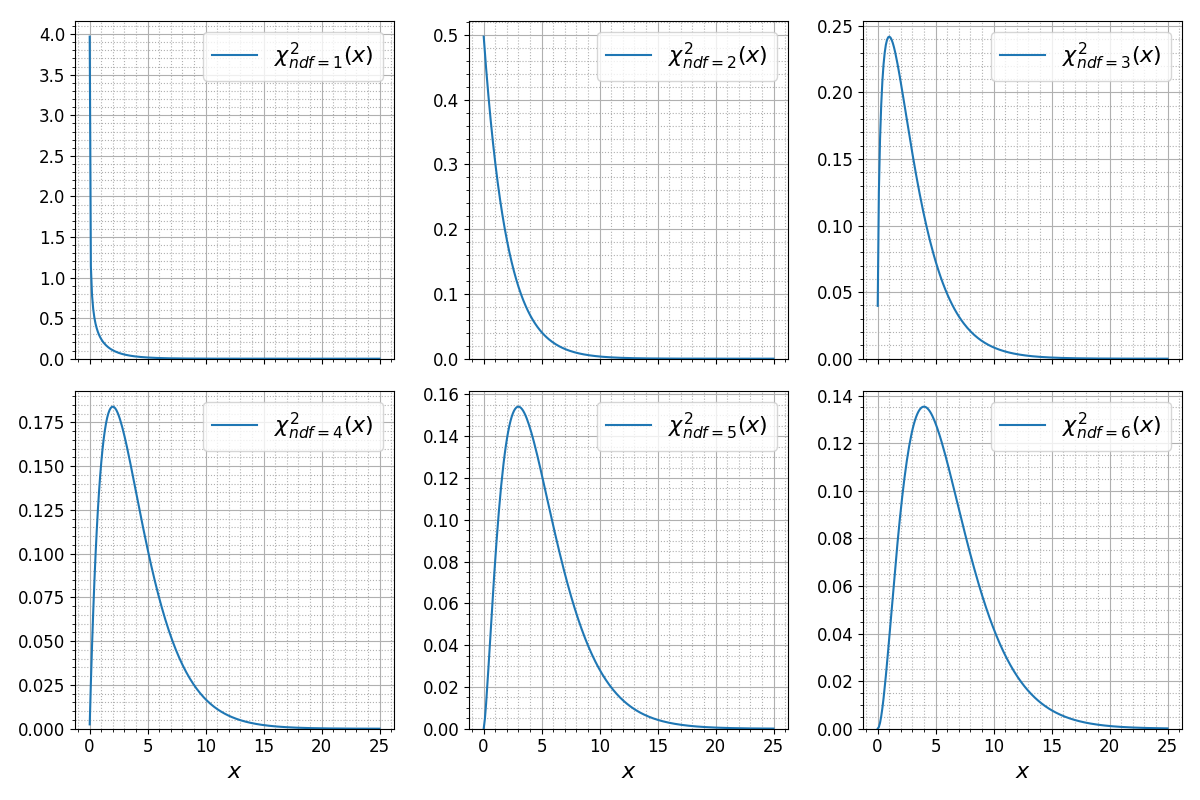
В последнем примере горизонтальная ось во всех графиках имеет один и тот же диапазон. Аргумент sharex функции pyplot.subplots позволяет убрать дублирование отрисовки осей в таких случаях:
fig, axes = plt.subplots(ncols=3, nrows=2, /media//media/figsize=(12, 8), sharex=True) # ... for idx, row in enumerate(axes): for jdx, ax in enumerate(row): # ... if idx: ax.set_xlabel(r'$x$', fontsize=16)
Существует аналогичный параметр sharey для вертикальной оси.
Более гибкие возможности регулярного расположения осей предоставляет функция pyplot.subplot. Мы не будем рассматривать эту функцию и ограничимся лишь ее упоминанием.
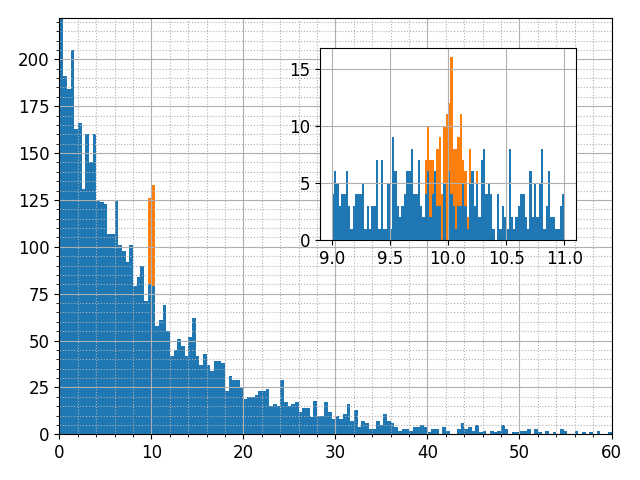
Функция pyplot.axes позволяет добавлять новые оси в текущем окне в произвольном месте:
import numpy as np import matplotlib.pyplot as plt exno = 26 rg = np.random.Generator(np.random.PCG64(5)) x1 = rg.exponential(10, 5000) x2 = rg.normal(10, 0.1, 100) # Строим основную гистограмму plt.hist([x1, x2], bins=150, range=(0, 60), stacked=True) plt.minorticks_on() plt.xlim((0, 60)) plt.grid(which='major') plt.grid(which='minor', linestyle=':') # Строим вторую гистограмму в отдельных осях plt.axes([.5, .5, .4, .4]) plt.hist([x1, x2], bins=100, stacked=True, range=(9, 11)) plt.grid(which='major') plt.tight_layout() # сохраняем диаграмму в файл plt.savefig('histograms.png') plt.show()
В этом примере была использована функция pyplot.savefig, сохраняющая содержимое текущего окна в файл в векторном или растровом формате. Формат задается с помощью аргумента format или автоматически определяется из имени файла (как в примере выше). Набор доступных форматов зависит от окружения, однако в большинстве случаев можно использовать такие форматы как png, jpeg, pdf, svg и eps.
Резюме
Предметом изучения в этом разделе был модуль pyplot библиотеки matplotlib, содержащий инструменты для построения различных диаграмм. Были рассмотрены:
- функции для построения диаграмм
pyplot.plot,pyplot.errorbar.pyplot.hist,pyplot.scatter,pyplot.contourиpyplot.contourf; - средства настройки свойств линий и маркеров;
- средства настройки координатных осей: подписи, размер шрифта, координатная сетка, произвольные метки др.;
- инструмены для расположения нескольких координатных осей в одном окне.
Рассмотренные инструменты далеко не исчерпывают возможности библиотеки matplotlib, однако их должно быть достаточно в большинстве случаев для визуализации данных. Мы рекомендуем заинтересованному читалелю изучить список источников, в которых можно найти много дополнительной информации.
Источники
- matplotlib.pyplot
- Pyplot tutorial
- Colormaps
- Scipy Lecture Notes
|
1 / 1 / 0 Регистрация: 31.01.2020 Сообщений: 148 |
|
|
1 |
|
|
10.02.2020, 14:45. Показов 30715. Ответов 2
Как сделать так, чтобы в на графике 1 оси x по длинне соответствовала 1 оси y? А если можно, то как привести вид графика максимально к тетрадному(стрелки на осях, одинаковый масштаб и т.д.)?
__________________
0 |
|
Рыжий Лис Просто Лис 4832 / 3155 / 991 Регистрация: 17.05.2012 Сообщений: 9,206 Записей в блоге: 9 |
||||
|
10.02.2020, 15:28 |
2 |
|||
|
Вручную задать диапазоны осей:
0 |
|
adena-virgo 0 / 0 / 0 Регистрация: 18.04.2019 Сообщений: 7 |
||||
|
23.09.2021, 15:50 |
3 |
|||
rcParams в ручную задайте для одинакового масштаба по х и у
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
23.09.2021, 15:50 |
|
3 |
- Matplotlib
- Установка пакета и основные возможности
- Функция plot для построения и оформления двумерных графиков
- Отображение нескольких координатных осей в одном окне
- Граничные значения осей и локаторы для расположения меток на них
- Настраиваем формат отображения меток у координатных осей
- Делаем логарифмический масштаб у координатных осей
- Размещаем стандартные текстовые элементы на графике
- Добавляем легенду и рисуем геометрические фигуры на графиках
- Рисуем ступенчатые, стековые, stem и точечные графики
- Рисуем гистограммы, столбчатые и круговые диаграммы
- Показ изображений и цветовых сеток
- Как строить трехмерные графики
- Рисуем линии уровня функциями contour, contourf и tricontour, tricontourf
- Создаем анимацию графиков Классы FuncAnimation и ArtistAnimation
- Главная
- Модули
- Matplotlib
Делаем логарифмический масштаб у координатных осей
До сих пор мы с
вами отображали графики в декартовой системе с линейным шагом изменения
значений. Это довольно частый вариант, который используется в большинстве
случаев. Но бывают функции, которые требуют логарифмического масштаба
(изменения шага) по координатам.
Например, если
сформировать график функции:
Если отобразить
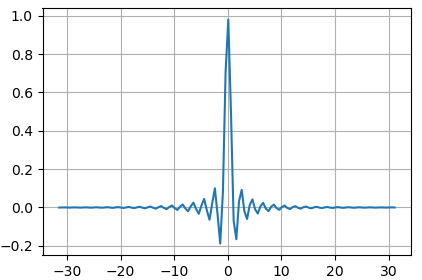
его в линейной системе координат:
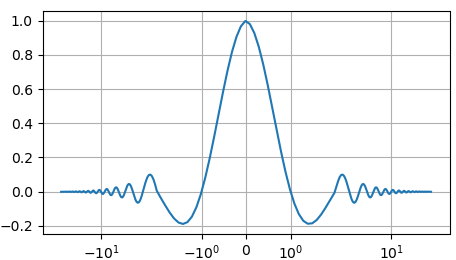
import numpy as np import matplotlib.pyplot as plt fig = plt.figure(figsize=(7, 4)) ax = fig.add_subplot() x = np.arange(-10*np.pi, 10*np.pi, 0.5) ax.plot(x, np.sinc(x) * np.exp( -np.abs(x/10)) ) ax.grid() plt.show()
То мелкие
колебания функции на больших частотах будут не видны:
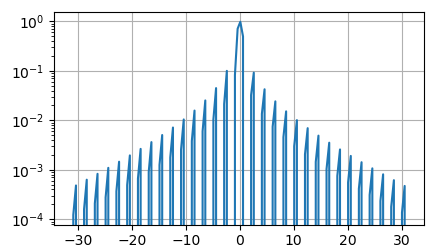
Как раз здесь
может помочь логарифмический масштаб по оси ординат. Для этого достаточно воспользоваться
методом semilogy(), чтобы по оси
Oy откладывался
логарифмический масштаб (логарифм по основанию 10) для графика:
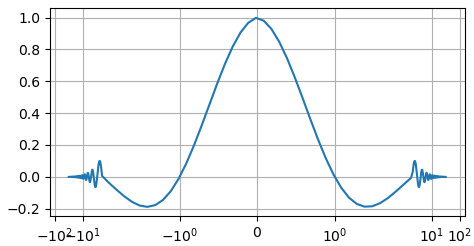
ax.semilogy(x, np.sinc(x) * np.exp( -np.abs(x/10)) )
В результате
получим следующее построение:
Видите, стало
гораздо информативнее и конечному пользователю показывается больше информации о
сигнале.
Аналогично,
можно формировать логарифмический масштаб по оси ординат с помощью метода:
semilogx()
Того же самого
эффекта можно добиться и с помощью прежней функции plot(), только
дополнительно указать логарифмический масштаб по нужной оси. Например, так:
ax.plot(x, np.sinc(x) * np.exp( -np.abs(x/10)) ) ax.set_yscale('log')
Здесь был
использован метод set_yscale() для изменения масштаба со
значения ‘linear’ на значение ‘log’. По аналогии,
можно изменить масштаб и для оси Ox с помощью метода set_xscale():
Вообще, здесь
можно использовать три разных масштаба:
- ‘linear’ – линейный
масштаб (используется по умолчанию); - ‘log’ –
логарифмический масштаб; - ‘symlog’ –
вблизи нуля (в указанных пределах) масштаб линейный, а в остальной области –
логарифмический.
Как я только что
отмечал, логарифмический масштаб формируется по основанию 10. Если нужно
изменить и указать другое основание, то это делается с помощью параметра base:
ax.set_yscale('log', base=5)
Вернемся к
нашему графику. Если на него внимательно посмотреть, то по вертикали
дополнительно отложены небольшие риски. Это восемь промежуточных линейных
значений. Например, между значениями
Откладываются
риски со значениями:
0.9, 0.8, 0.7,
0.6, 0.5, 0.4, 0.3, 0.2
Мы можем
управлять их отображением, указав их значения в виде целых чисел в списке
параметра subs:
ax.set_yscale('log', subs=[2, 9])
Здесь мы указываем
отображать риску со значением 0,2 или 0,02 или 0,002 и т.д. И риску со
значениями 0,9 или 0,09 или 0,009 и т.д.
Рассмотрим далее
возможность использования третьего параметра ‘symlog’. Мы его пропишем для оси Ox в следующем
виде:
x = np.arange(-10*np.pi, 10*np.pi, 0.1) ax.plot(x, np.sinc(x) * np.exp( -np.abs(x/10)) ) ax.set_xscale('symlog', linthresh=2)
Здесь
использован дополнительный параметр linthresh, определяющий
граничное значение [-2; 2], где график следует отображать в линейном масштабе.
А все, что выходит за эти пределы – в логарифмическом. В результате, получим
такое построение:
Дополнительно
линейный масштаб можно растянуть, указав масштаб в дополнительном параметре linscale:
ax.set_xscale('symlog', linthresh=2, linscale=5)
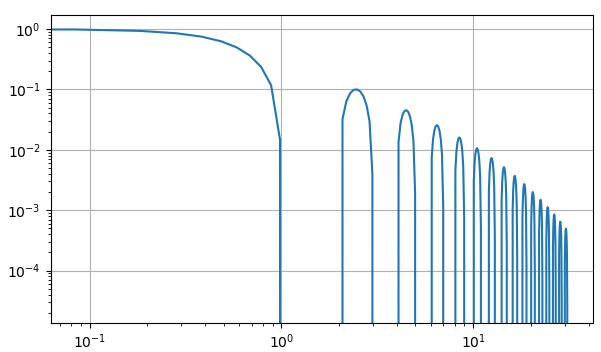
Наконец, если
нам нужно установить логарифмический масштаб по обеим осям, то проще всего для
этого воспользоваться функцией loglog(), вместо функции plot() или semilogx()/semilogy():
ax.loglog(x, np.sinc(x) * np.exp( -np.abs(x/10)) )
Вот так,
достаточно просто можно задавать и управлять логарифмическим масштабом при
отображении графиков в пакете matplotlib.
Видео по теме
- Предыдущая
- Следующая