Как изменить объем тела физика

ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1

Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1 . Определите цену деления мензурки.
2 . Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3 . Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201 ), и снова измерьте объём жидкости.
4 . Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5 . Результаты измерений запишите в таблицу 9 .
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202 ). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.

Таблица 9 .

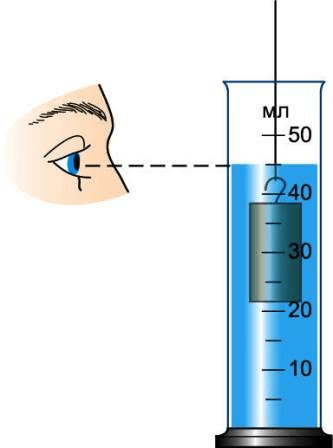
рис. 201

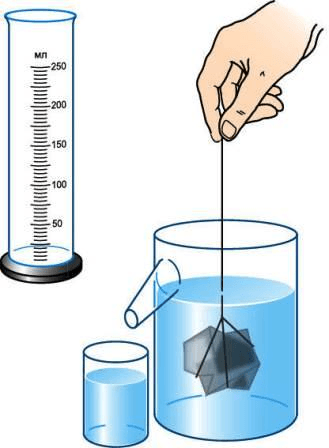
рис. 202

Решение

Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэто­му для измерения объема воспользуемся мензуркой. Тело, полностью погружён­ное в жидкость, вытесняет объём жидкости, кото­рый равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следую­щим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
$V = V_ <2>— V_<1>$ , где $V_<2>$ − объём воды и тела, $V_<1>$ − начальный объём воды в мензурке.

1. Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
   Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
   На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
   Таким образом, цена каждого деления будет равна
   $frac<30 — 20><2>= frac<10><2>$ = 5 мл.
2. В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 $см^<3>$ .
3. Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
   Вычисления.
   $V_ <бр>= 95 — 70 = 25 см^<3>$
   $V_ <ц>= 85 — 65 = 20 см^<3>$
   $V_ <ш>= 75 — 60 = 15 см^<3>$
4. Результаты измерений запишем в таблицу 9 .

№ опыта	Название тела	Начальный объём воды в мензурке $V_<1>, см^<3>$	Объём воды и тела $V_<2>, см^<3>$	Объём тела V, $см^<3>$ $V = V_<2>-V <1>$
1	Брусок	70	95	25
2	Цилиндр	65	85	20
3	Шарик	60	75	15

Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.

Источник

План-конспект и презентация урока по физике в 7 классе на тему «Измерение объема тел».

Выбранный для просмотра документ План-Конспект.docx

в 7 классе в МБОУ Ширинская СШ №4

на тему «Измерение объема тел».

Разработал: Сорокин В.А.______________

слушатель курсов профессиональной переподготовки «Физика: теория и методика преподавания в образовательной организации»

Проверил: Павельева О.Ю._____________

ФИО руководителя практики

Тема урока: «Измерение объема тел».

Дата проведения: 13.08.2020

Тип урока Изучение новой темы и формирование умений и навыков по изученной теме. Технология урока: коллективный способ обучения, работа в малых группах. Цель урока : Научится определять объем тел разных форм, научиться применять полученные навыки при решении качественных задач. Форма урока : Урок-практикум.

повторить материал по теме «Определение цены деления прибора»;

обеспечить усвоение учащимися знаний о физических величинах: масса и объем тел и их единицах измерения;

выработать навыки определения объема тела с помощью измерительного цилиндра (мензурки);

научить, практически использовать полученные знания;

использовать кратные приставки в устном и письменном описании величины (см3 и мл);

знать значение термина объем и единицы его измерения

описывать и обобщать в устной и письменной форме результаты исследования.

формировать умение логически мыслить, сравнивать, самостоятельно делать выводы;

развивать ответственность и самостоятельность при обучении ;

развивать умение работать в группах;

активизировать мышление школьников

способствовать осознанному усвоению материала;

развивать умение проявлять инициативу, активность, самостоятельность, творческий интерес;

развивать аккуратность и внимательность при оформлении работ. Эстетичность при содержании рабочего места;

формировать познавательный интерес к предмету.

Оборудование : измерительный цилиндр; отливной стакан; пустой сосуд; тела правильной и неправильной формы небольшого объема (тела из разных материалов, ручки, кусочки металла, фигурки из пластилина и т.д.); нитки.

Методы: беседа, практическая работа в парах и группах.

I. Организационная часть (3 мин)

На предыдущих уроках мы познакомились с такими физическими величинами как масса и объем. Узнали, что эти величины зависят от агрегатного состояния тела.

Задачи сегодняшнего урока:

научиться определять объем тела правильной геометрической формы с помощью измерительного цилиндра;

научиться определять, объем тела неправильной геометрической формы с помощью отливного стакана и измерительного цилиндра.

II . Актуализация знаний учащихся (5 мин)

На уроках математики, вы уже наверняка рассчитывали объем фигур правильной формы (куб, параллелепипед) по таким параметрам, как длина, ширина, высота.

На предыдущих уроках физики вы изучили такое понятие, как цена деления прибора, и умеете записывать результат прямого измерения с учетом погрешности. Знакомы с правилами заполнения таблицы при сборе данных.

На доске: слева под номерами серия вопросов (общего характера для повторения); справа столбиком ряд цифр, около которых написаны ответы.

Задание: за 5 минут дайте ответы на вопросы, написанные слева, причем ответы нужно выбрать из тех, что написаны справа.

Ниже приведены вопросы и ответы. (тест)

1) Цена деления прибора.

2) Физическая величина.

4) Физическое тело.

6) Природное явление.

Раздел физики.

9) Единица измерения.

7) Стальной шарик

Организационный момент, подготовка к исследованию, техника безопасности на урок.

Проговорить правила безопасности при проведении практической работы.

Получение материала и приборов для измерения. А именно, предложим ученикам самим взять необходимое для эксперимента оборудование со стола учителя.

Определение объема тела правильной формы.

Что такое объём? Как вы уже умеете определять объем тела правильной формы?

Цель выполняемого задания: вспомнить понятие объем, вычислить объем при помощи формулы. V=a×b×c. Работа выполняется в парах. Ответ транслируется на класс от каждой пары.

При помощи ученической линейки определите объем спичечного коробка.

Ответы учеников записываются на доске. Необходимо обратить внимание на правильность выбора единицы измерения длины и объёма.

Если результаты сильно различаются, необходимо задать вопрос из-за чего это могло произойти, а ученики должны сделать предположения.

Вопросы для учащихся после измерения и вычисления:

Какие измерения вы производили для вычисления объёма коробка? (длина, ширина, высота)

Как смогли узнать объем коробка? (Использовали формулу V=a×b×c)

Можно ли использовать эту формулу, если вы хотите узнать объем ручки? (нет, т.к. форма ручки неправильная)

Предложите свой способ, как узнать объем тела, имеющего неправильную форму.

II. Работа в парах. (25 мин.)

Во время выполнения задания необходимо постоянно проводить обратную связь, а именно, проверять работу каждого учащегося и в случае затруднения, задавать вопросы для определения возникшей трудности.

Измерение объёма с помощью измерительного цилиндра

Цель: Определить цену деления измерительного цилиндра, научиться пользоваться им и определять с его помощью объём жидкости, объем тела неправильной формы.

Приборы и материалы: измерительный цилиндр, стакан с водой, другие сосуды, тело.

Порядок выполнения работы

1) Определить цену деления измерительного цилиндра. Ц.д.=_____см3

2) Налить воду в измерительный цилиндр и измерить её объём. V1=______см3

3) Обвязать измеряемое тело ниткой.

4) Опустить тело в воду, удерживая его за нитку, и измерить объем жидкости с телом V2; V2=______см3

5) Посчитать объем помещенного в стакан тела по формуле V = V2 — V1 .

Теперь мы можем приступить к выполнению лабораторной работы «Измерение объема тела», пользуясь инструкцией.

Определение объема тела правильной и неправильной формы :

определите цену деления измерительного стакана.

налейте в измерительный стакан столько воды, чтобы в него можно было поместить тело в и измерить объем воды ещё раз;

опустите тело, объем которого вы хотите измерить, удерживая его за нитку, и снова измерьте объем жидкости в измерительном стакане.

проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.

результаты измерений запишите в таблицу:

Расчет объема тел правильной и неправильной формы

Начальный объем жидкости в мензурке

Объем жидкости и тела V2, см 3

В работе учащиеся учитывают, что 1мл=1 см 3

В процессе выполнения практической работы по «Измерению объема тела» разных форм. Учащиеся получают индивидуальные результаты, характерные только для их пары. Т.к. тела были различны как по форме, так и по составу; объем воды в измерительных стаканах был различен.

Результаты некоторых измерений приведём в таблице №2

Результаты измерений объема тел различной формы

Начальный объем жидкости в мензурке

Объем жидкости и тела V2, см 3

тела правильной формы

тела неправильной формы

Выводы по лабораторной работе : в ходе выполнения работы, мы научились определять объемы тел различной формы с помощью измерительного стакана и вытесненной жидкости. В работе была учтена погрешность измерительного прибора.

Итог урока: (2 мин)

Ребята сдают рабочие листы с выполненной лабораторной работой и использованное в работе оборудование.

Учитель подводит итоги работы на уроке. Домашнее задание

Рефлексия урока. Дает возможность учителю осмыслить прошедший урок.

При измерении получил(а) значение …………………………………………………………

Когда тела имеют правильную форму, то объем можно узнать, если знаешь …………….

Объем небольших тел неправильной формы можно измерить с помощью ……………….

Для этого нужно сначала измерить………………………..……………………….…. затем …………………………………, разница ……………………и есть объем тела.

Домашнее задание: п.22-23 (учебник Пёрышкина)

Задание для детей с повышенной учебной мотивацией.

1.В канистру налито 50 л бензина. Выразите данный объем в дм3 и м3.

2.Рассчитайте количество кирпичей, которое пошло на строительство стены высотой 3,9 м, шириной 70 см и длиной 90 дм, если объем одного кирпича равен 2400 см3.

Список использованной литературы:

1) Учебник «Физика 7 класс» А.В. Пёрышкин.

2) « Физика. 7 класс. Методическое пособие. К учебнику Перышкина А.В. ФГОС.» Н.В. Филонович

3) Методические рекомендации и разработки на сайте infourok . ru

4) «Физика. 7 класс: поурочное планирование.» Пелагейченко Н.Л.

1. Внешние связи урока.

Урок «Измерение объёма тел» изучается в разделе «Взаимодействие тел».

2 . Характеристика триединой цели урока с опорой на характеристику класса.

Этапы урока были выделены четко. Дозировка по времени, отводимая на каждую часть урока, была определена правильно. Основная дидактическая цель и задачи урока реализованы в полном объёме:

Цель урока : Научится определять объем тел разных форм, научиться применять полученные навыки при решении качественных задач.

— образовательные (формирование познавательных УУД)

— воспитательные (формирование коммуникативных и личностных УУД):

— развивающие (формирование регулятивных УУД)

3.Характеристика замысла урока. Характеристика этапов урока.

В ходе проведения урока удалось реализовать поставленную цель и задачи.

В ходе проведения урока удалось реализовать поставленную цель и задачи.

В целях мотивирования детей к учебной деятельности была предложена качественная задача.

Учащиеся с помощью педагога разрабатывали практический план достижения поставленной цели.

Это позволило ученикам сформулировать тему урока и осознать необходимость изучения данной темы.

В ходе реализации построенного проекта ученики проводили экспериментальные работы в группах и предлагали свои выводы. Это способствовало лучшему пониманию изучаемой темы, существенно повысило заинтересованность учащихся в изучении данной темы и явилось дополнительным мотивирующим фактором.

В течение всего урока учитель играл роль советчика, консультировал учащихся на каждом этапе выполнения работы.

Возникшие трудности, ошибки, учащиеся исправляли самостоятельно, самостоятельно поясняя суть затруднений.

Результат урока показал усвоение материала учащимися. В целях актуализации знаний была проведена рефлексия. Для проверки усвоения материала проведён общий опрос с целью определения понимания важности проделанной работы.

В ходе урока использовались знания, полученные на предыдущих уроках, а также на уроках других предметов. Материал для учеников актуален. Для общего развития была продемонстрирована практическая значимость данного вопроса.

Воспитание в процессе урока

В ходе парной работы формировались умения: слушать другого, формулировать собственное мнение, воспринимать чужую точку зрения, рефлексировать, общаться с одноклассниками, стремление добиваться наилучших результатов.

Соблюдение основных принципов дидактики

Современные принципы дидактики обуславливают требования ко всем компонентам учебного процесса – логике, целям и задачам, формированию содержания, выбору форм и методов, стимулированию, планированию и анализу достигнутых результатов.

Деятельность учителя и учащихся была организована правильно. В течение всего урока учащиеся отвечали на вопросы; при изучении нового материала делали выводы, проводили эксперимент; при закреплении материала выполняли тестовое задание, решали качественные задачи.

Выбор методов обучения

При проведении урока соблюдались общие требования к выбору методов обучения. Исходя из специфики учебного материала, выбраны объяснительно иллюстративный, проблемный методы.

Работа учителя на уроке

На уроке был достигнут контакт с классом. На уроке прослушивались ответы учащихся, записывались результаты эксперимента, формулы, единицы измерения и оказывалась помощь и давалась оценка индивидуально каждому ученику.

Работа учащихся на уроке

Класс был активен на всех этапах урока. Виды деятельности менялись: учащиеся отвечали на вопросы, слушали, рассуждали, проводили опыты самостоятельно, формулировали результат проделанной работы.

Гигиенические условия урока

Освещенность классной комнаты была достаточной. Учащиеся сидели с учетом их здоровья, роста и успеваемости. Урок прошел в атмосфере доброжелательности. Была взаимная заинтересованность всех участников процесса.

В ходе проведения урока удалось реализовать поставленные цели. Результат урока показал усвоение материала учащимися. Презентация к уроку легко вписалась в традиционный урок и способствовала лучшему пониманию изучаемой темы, что существенно повысило заинтересованность учащихся в изучении физики и явилось дополнительным мотивирующим фактором.

Материал урока был изложен логично, в доступной форме. На уроке формировались следующие умения: выделять главное, планировать ход своих действий при выполнении практического задания, работать с приборами, анализировать, делать выводы, обобщать, отрабатывать уже имеющие умения и навыки.

В ходе парной работы формировалось умение слушать другого, воспринимать чужую точку зрения, умение рефлексировать, умение культурно общаться с одноклассниками, умение стремление добиваться наилучших результатов.

Урок был выстроен оптимально, соответствовал интересам учащихся, уровню учебной и общей подготовки класса. Адекватна была организация деятельности учащихся обучающим, развивающим и воспитывающим целям урока.

Учащиеся были активны на уроке.

Темп урока был достаточно высоким и соответствовал уровню учащихся данного класса. Интерес к уроку поддерживался на всем его протяжении. При повторении материала учащиеся отвечали на вопросы; при изучении нового материала делали выводы, проводили эксперимент.

В ходе урока использовались знания, полученные на предыдущих уроках, а также жизненный опыт учащихся. Материал для учеников актуален.

Контроль знаний учащихся осуществлялся в начале и конце урока. Формы контроля: устный и письменный.

Домашнее задание задано в конце урока, оно было записано и продиктовано. Проведен детальный инструктаж по его выполнению.

Урок прошел в атмосфере доброжелательности. Была взаимная заинтересованность всех участников процесса.

Повысился интерес к предмету.

Цели урока были достигнуты. Урок был закончен логически верно.

Источник

Содержание:

1. Тепловое расширение твердых и жидких тел
2. Зависимость объёма тел от температуры
3. Линейное расширение твёрдых тел
4. Объёмное расширение твёрдых тел
5. Учёт теплового расширения в технике
6. Терморегулятор
7. Тепловое расширение жидкостей

Тепловое расширение – это изменение размеров и формы тел при изменении температуры. Математически можно высчитать объемный коэффициент расширения, позволяющий спрогнозировать поведение газов и жидкостей в изменяющихся внешних условиях. Чтобы получить такие же результаты для твердых тел, необходимо учитывать коэффициент линейного расширения.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Тепловое расширение твердых и жидких тел

Тепловое расширение (также используется термин «термическое расширение») — это изменение линейных размеров и формы тела при изменении его температуры. Количественно тепловое расширение жидкостей и газов при постоянном давлении характеризуется изобарным коэффициентом расширения (объёмным коэффициентом теплового расширения). Для характеристики теплового расширения твёрдых тел дополнительно вводят коэффициент линейного теплового расширения.

Зависимость объёма тел от температуры

Частицы твёрдого тела занимают друг относительно друга определённые положения, но не остаются в покое, а совершают колебания. При нагревании тела увеличивается средняя скорость движения частиц. Средние расстояния между частицами при этом увеличиваются, поэтому увеличиваются линейные размеры тела, а следовательно, увеличивается и объём тела.

При охлаждении линейные размеры тела сокращаются, и объём его уменьшается.

При нагревании, как известно, тела расширяются, а при охлаждении сжимаются. Качественная сторона этих явлений была уже рассмотрена в начальном курсе физики.

Наша задача теперь — ознакомиться с количественными законами этих явлений.

Линейное расширение твёрдых тел

Твёрдое тело при данной температуре имеет определённую форму и определённые линейные размеры. Увеличение линейных размеров тела при нагревании называется тепловым линейным расширением.

Измерения показывают, что одно и то же тело расширяется при различных температурах по-разному: при высоких температурах обычно сильнее, чем при низких. Но это различие в расширении столь невелико, что при сравнительно небольших изменениях температуры им можно пренебречь и считать, что изменение размеров тела пропорционально изменению температуры.

В начальном курсе физики было установлено, что различные вещества по-разному расширяются при нагревании: одни сильнее, другие слабее; железо, например, расширяется сильнее стекла и слабее меди.

Чтобы количественно характеризовать это важное тепловое свойство тел, введена особая величина, называемая коэффициентом линейного расширения.

Пусть твёрдое тело при температуре 0°С имеет длину  а при температуре t° его длина становится  Значит, при изменении температуры на t° длина тела увеличивается на Предполагая, что увеличение длины при нагревании на каждый градус идёт равномерно, находим, что при нагревании на 1°С вся длина тела увеличилась на каждая единица длины на

 (1)

Величина  (греч. «бэта»), характеризующая тепловое расширение тела, называется коэффициентом линейного расширения.

Формула (1) показывает, что при t = 1°С и = 1 ед. длины величина равна т. е. коэффициент линейного расширения численно равен удлинению, которое получает при нагревании на 1°С стержень, имевший при 0°С длину, равную единице длины.

Из формулы (1) следует, что наименованием коэффициента  является

Формулу (1) можно записать в следующем виде:

Отсюда легко определить длину тела при любой температуре, если известны его начальная длина и коэффициент линейного расширения.

Ниже в таблице приведены коэффициенты линейного расширения некоторых веществ, определённые на опыте.

Объёмное расширение твёрдых тел

При тепловом расширении твёрдого тела с увеличением линейных размеров тела увеличивается и его объём. Аналогично коэффициенту линейного расширения для характеристики объёмного расширения можно ввести коэффициент объёмного расширения. Опыт показывает, что так же, как и в случае линейного расширения, можно без большой ошибки принять, что приращение объёма тела пропорционально повышению температуры.

Обозначив объём тела при 0°С через V₀ , объём при температуре t⁰ через V_t а коэффициент объёмного расширения через  найдём:

  (2)

При V₀ = 1 ед. объёма и t = 1°С величина а равна V_t— V₀, т. е. коэффициент объёмного расширения численно равен приросту объёма тела при нагревании на 1°С, если при 0°С объём был равен единице объёма.

По формуле (2), зная объём тела при температуре 0°С, можно вычислить объём его при любой температуре t°:

Установим соотношение между коэффициентами объёмного и линейного расширения.

Допустим, что имеем кубик, ребро которого при 0° С равно 1 см. При нагревании на 1°С ребро станет равным см, а объём кубика увеличится на см³.

Можно написать следующее равенство:

Но

В этой формуле величины и настолько малы, что ими можно пренебречь и написать:

Коэффициент объёмного расширения твёрдого тела равен утроенному коэффициенту линейного расширения.

Учёт теплового расширения в технике

Из таблицы на странице 124 видно, что коэффициенты расширения твёрдых тел очень малы. Однако самые незначительные, изменения размеров тел при изменении температуры вызывают появление огромных сил.

Опыт показывает, что даже для небольшою удлинения твёрдого тела требуются огромные внешние силы. Так, например, чтобы увеличить длину стального стержня сечением в 1 см² приблизительно на 0,0005 его первоначальной длины, необходимо приложить силу в 1000 кГ. Но такой же величины расширение этого стержня получается при нагревании его на 50°С. Ясно поэтому, что, расширяясь при нагревании (или сжимаясь при охлаждении) на 50°С, стержень будет оказывать давление около 1000  на те тела, которые будут препятствовать его расширению (сжатию).

Огромные силы, возникающие при расширении и сжатии твёрдых тел, учитываются в технике. Так, например, один из концов моста не закрепляют неподвижно, а устанавливают на катках; железнодорожные рельсы не укладывают вплотную, а оставляют между ними просвет; паропроводы подвешивают на крюках, а между отдельными трубами устанавливают компенсаторы, изгибающиеся при удлинении труб паропровода. По этой же причине котёл паровоза закрепляется только на одном конце, другой же его конец может свободно перемещаться.

Огромное значение имеет расширение от нагревания при точных измерениях. В самом деле, если масштабная линейка или калибр, которыми проверяются размеры изготовленной части машины, значительно изменяют свою величину, то необходимой точности при измерении не получится. Для избежания грубых ошибок при измерении или контроле изготовленные изделия заблаговременно приносят в помещение, где производятся измерения, чтобы они успели принять температуру калибров. Самые калибры и измерительные инструменты делают из материала с очень малым коэффициентом расширения. Таким материалом, например, является особая железо-никелевая сталь — инвар, с коэффициентом расширения 0,0000015.

Рис. 132а. Схема устройства металлического термометра.

Как показывает таблица на странице 124, платина и стекло имеют одинаковый коэффициент расширения; поэтому можно вплавлять платину в стекло, причём после охлаждения не происходит ни ослабления связи обоих веществ, ни растрескивания стекла. В электрических лампочках в стекло вплавляется железо-никелевая проволока, имеющая такой же коэффициент расширения, как и стекло. Заслуживает внимания очень малый коэффициент расширения у кварцевого стекла. Такое стекло выдерживает, не лопаясь и не растрескиваясь, неравномерное нагревание или охлаждение. Так, например, в раскалённую докрасна колбочку из кварцевого стекла можно вливать холодную воду, тогда как колба из обычного стекла при таком опыте лопается. Указанная особенность кварцевого стекла является следствием малости его коэффициента теплового расширения.

Терморегулятор

Две одинаковые полоски из разных металлов, например из железа и латуни, склёпанные вместе, образуют так называемую биметаллическую пластинку. При нагревании такие пластинки изгибаются вследствие того, что одна расширяется больше другой. Та из полосок, которая расширяется больше, оказывается всегда с выпуклой стороны. Это свойство биметаллических пластинок широко используется для измерения температуры и её регулирования.

1. Металлический термометр. Этот прибор представляет собой биметаллическую дугу (рис. 132, а), конец которой A прочно закреплён, а конец В свободен. Дуга соединена в В со стрелкой С. При изменении температуры дуга закручивается или раскручивается, двигая соответственно стрелку. Шкала проградуирована по обыкновенному термометру. Если к концу стрелки прикрепить перо, то колебания температуры можно записывать на специальной бумажной ленте. По такому принципу устроен термограф.

2. Термостат. Так называется прибор для установления постоянной температуры.

Рас. 1326. Принцип устройства регулятора температуры с биметаллической пластинкой.

На рисунке 132б изображён принцип устройства одного из типов регуляторов температуры. Биметаллическая дуга С при изменении температуры закручивается или раскручивается. К её свободному концу прикреплена металлическая пластинка М, которая при раскручивании дуги прикасается к контакту К, а при закручивании отходит от него. Если, например, контакт К и пластинка М присоединены к концам электрической цепи АА₁ содержащей нагревательный прибор, то при соприкосновении К и М электрическая цепь замкнётся; прибор начнёт нагревать помещение. Биметаллическая дуга С при нагревании начнёт закручиваться и при определённой температуре отсоединит пластинку М от контакта К цепь разорвётся, нагревание прекратится. При охлаждении дуга С, раскручиваясь, снова заставит включиться  нагревательный прибор: таким образом, температура помещения будет поддерживаться на заданном уровне.

Рис. 132в. Прибор для определения коэффициента расширения жидкостей.

Тепловое расширение жидкостей

В отношении жидкостей имеет смысл говорить лишь об объёмном расширении. У жидкостей оно значительно больше, чем у твёрдых тел. Как показывает опыт, зависимость объёма жидкости от температуры выражается такой же формулой, что и для твёрдых тел.

Если при 0°С жидкость занимает объём V₀, то при температуре t её объём V_t будет:

Для измерения коэффициента расширения жидкости применяется стеклянный сосуд термометрической формы, объём которого известен (рис. 132в). Шарик с трубкой наполняют доверху жидкостью и нагревают весь прибор до определённой температуры; при этом часть жидкости выливается из сосуда. Затем сосуд с жидкостью охлаждают в тающем льду до 0°. При этом жидкость наполнит уже не весь сосуд, и незаполненный объём покажет, на сколько жидкость расширилась при нагревании. Зная коэффициент расширения стекла, можно довольно точно вычислить и коэффициент расширения жидкости.

Коэффициент расширения некоторых жидкостей:

Эфир…………….0,00166 Вода (от 20°С и выше) . . . .0,00020

Спирт……………0,00110 Вода (от 5 до 8°С)…….0,00002

Керосин…………..0,00100 Ртуть…………….0,00018

Расширение воды при нагревании отличается от расширения других жидкостей. Если нагревать воду от 0°С, то можно заметить, что при нагревании до 4°С её объём не увеличивается, а уменьшается. При нагревании же выше 4°С объём воды увеличивается.

Наибольшую плотность, равную 1  вода имеет при 4°С. Изменение плотности воды в зависимости от температуры изображено графически на рисунке 133.

Рис. 133. График изменения плотности воды в зависимости от температуры.

Особенностью расширения воды объясняется то, что вода в прудах и озёрах не промерзает зимой до дна. При охлаждении воды осенью верхние остывшие слои опускаются на дно, а на их место снизу поступают более тёплые слои. Такое перемещение слоёв происходит только до тех пор, пока вода не примет температуру 4°С. При дальнейшем охлаждении верхние слои не опускаются вниз, а, постепенно охлаждаясь, остаются наверху и, наконец, замерзают.

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Масса
7. Взаимодействия тел
8. Механическая энергия
9. Импульс
10. Вращение твердого тела
11. Криволинейное движение тел
12. Колебания
13. Колебания и волны
14. Механические колебания и волны
15. Бегущая волна
16. Стоячие волны
17. Акустика
18. Звук
19. Звук и ультразвук
20. Движение жидкости и газа
21. Молекулярно-кинетическая теория
22. Молекулярно-кинетическая теория строения вещества
23. Молекулярно — кинетическая теория газообразного состояния вещества
24. Теплота и работа
25. Температура и теплота
26. Термодинамические процессы
27. Идеальный газ
28. Уравнение состояния идеального газа
29. Изменение внутренней энергии
30. Переход вещества из жидкого состояния в газообразное и обратно
31. Кипение, свойства паров, критическое состояние вещества
32. Водяной пар в атмосфере
33. Плавление и кристаллизация
34. Тепловое расширение тел
35. Энтропия
36. Процессы перехода из одного агрегатного состояния в другое
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома

Масса, объем и плотность

Масса

Как ни странно, начнем мы с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.

До недавнего времени в Международном бюро мер и весов в Париже хранился цилиндр массой один килограмм. Цилиндр был изготовлен из сплава иридия и платины и служил для всего мира эталоном килограмма. Правда, со временем его масса изменилась, и пришлось придумать новый эталон — электромагнитные весы.

Высота этого цилиндра была приблизительно равна 4 см, но чтобы его поднять, нужно было приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.

В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне.

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.

Откуда берется масса

Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.

Источник: Википедия

Бозон Хиггса невозможно представить — это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.

Объем тела

Масса зависит от двух величин: плотности и объема. Начнем с известной нам из математики величины — с объема.

• Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Уметь соотносить объемы — важный навык. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.

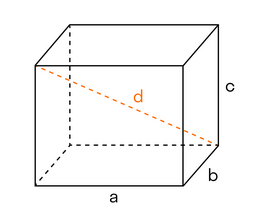
А если вернуться к задачкам, то чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.

Вычисляем объем по формуле:

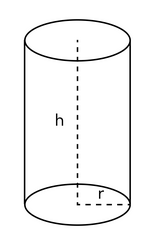
А для цилиндра будет справедлива такая формула:

Плотность вещества

Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объёму.

Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.

Ниже представлены значения плотностей для разных веществ — это поможет при решении задач по физике:

Средняя плотность

В школьном курсе чаще всего говорят о средней плотности тела. Дело в том, что если мы рассмотрим какое-нибудь неоднородное тело, то в одной его части будет, например, большая плотность, а в другой — меньшая.

Если вы когда-то делали ремонт, то знакомы с такой вещью, как цемент. Он состоит из двух веществ: клинкера и гипса. Чтобы найти плотность цемента, нужно его массу разделить на объем.

Инертность

Масса придает телу такое свойство, как инертность. Но не напрямую — у этого есть некая последовательность. Если посмотреть, как строитель толкает тачку или родитель везет ребенка на санках — можно заметить, что и тачка, и санки, изменяют свою скорость только при наличии нескомпенсированного действия — силы, которую прикладывают и строитель, и родитель.

Так как быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела.

Давайте вернемся к нашим строителям и родителям. Если строитель приложит к тачке ту же силу, что и родитель, то ускорение не обязательно будет одинаковым.

Чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело.

• Инертность — это свойство тела сохранять свою скорость постоянной. Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным.

Например, движущийся по дороге автомобиль не может мгновенно остановиться — для уменьшения скорости требуется некоторое время.

Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение. Эту закономерность описывает второй закон Ньютона.

Второй закон Ньютона

Мы уже упоминали его в начале статьи, давайте разберемся подробнее.

В этом законе есть такое понятие, как равнодействующая сила — векторная сумма всех сил, приложенных к телу. Обозначается она так:

.

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина тому — сила.

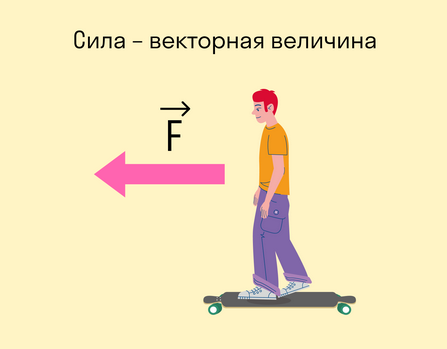
• Сила — это физическая векторная величина, с которой тело воздействует на другое тело.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Первый закон Ньютона

Понятие «инерция» сформулировали отдельно друг от друга Галилео Галилей и Исаак Ньютон:

Варианты формулировки не противоречат друг другу и говорят, по сути, об одном и том же, просто разными словами — выбирайте ту, что вам нравится больше.

Ньютоновская формулировка закона инерции по-другому называется первым законом Ньютона:

Существуют такие системы отсчета, относительно которых тело сохраняет свою скорость постоянной, в том числе равной нулю, если действие на него других сил отсутствует или скомпенсировано.

А вы небось уже подумали, что мы про первый закон Ньютона забыли и сразу перескочили ко второму. Все в порядке — первый тоже на месте.

В этом законе встречается такое словосочетание, как «система отсчета». Оно изучается в самом начале курса физики, но там это понятие читают в контексте «такие системы отсчета». Напрашивается вопрос: какие такие системы отсчета?

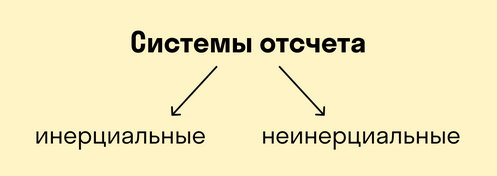
Системы отсчета: инерциальные и неинерциальные

Чтобы описать движение, нам нужны три штуки:

• тело отсчета, относительно которого определяем местоположение других тел;
• система координат: в школьном курсе мы используем прямоугольную декартову систему координат;
• часы, чтобы измерять время.

В совокупности эти три опции образуют систему отсчета:

• Инерциальная система отсчета — система отсчёта, в которой все тела движутся прямолинейно и равномерно, либо покоятся.
• Неинерциальная система отсчета — система отсчёта, движущаяся с ускорением.

Рассмотрим разницу между этими системами отсчета на примере задачи.

Аэростат — летательный аппарат на картиночке ниже — движется равномерно и прямолинейно параллельно горизонтальной дороге, по которой равноускоренно движется автомобиль.

Выберите правильное утверждение:

1. Система отсчёта, связанная с аэростатом, является инерциальной, а система отсчёта, связанная с автомобилем, инерциальной не является.

2. Система отсчёта, связанная с автомобилем, является инерциальной, а система отсчёта, связанная с аэростатом, инерциальной не является.

3. Система отсчёта, связанная с любым из этих тел, является инерциальной.

4. Система отсчёта, связанная с любым из этих тел, не является инерциальной.

Решение:

Система отсчёта, связанная с землёй, инерциальна. Да, планета движется и вращается, но для всех процессов вблизи планеты этим можно пренебречь. Во всех задачах систему отсчета, связанную с землей можно считать инерциальной.

Поскольку система отсчёта, связанная с землёй инерциальна, любая другая система, которая движется относительно земли равномерно и прямолинейно или покоится — по первому закону Ньютона тоже инерциальна.

Движение аэростата удовлетворяет этому условию, так как оно равномерное и прямолинейное, а равноускоренное движение автомобиля — нет. Аэростат — инерциальная система отсчёта, а автомобиль — неинерциальная.

Ответ: 1.

Третий закон Ньютона

Он честно-пречестно последний.

Третий закон Ньютона обобщает огромное количество опытных фактов, которые показывают, что силы — результат взаимодействия тел.

Он формулируется так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще: сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе — можно сказать и так: на каждую силу найдется другая сила 🙈