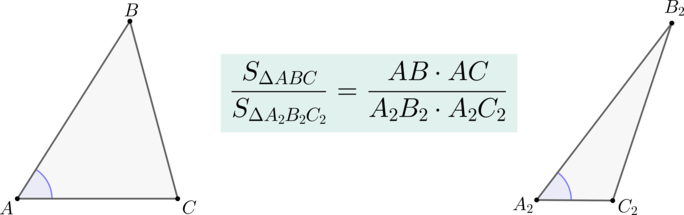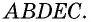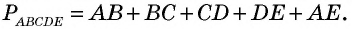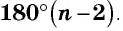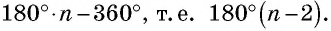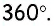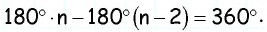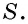[{Large{text{Основные факты о площади}}}]
Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной (1) см, (1) мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см(^2), мм(^2) соответственно.
Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.
Свойства площади
1. Площадь любого многоугольника — величина положительная.
2. Равные многоугольники имеют равные площади.
3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
4. Площадь квадрата со стороной (a) равна (a^2).
[{Large{text{Площадь прямоугольника и параллелограмма}}}]
Теорема: площадь прямоугольника
Площадь прямоугольника со сторонами (a) и (b) равна (S=ab).
Доказательство
Достроим прямоугольник (ABCD) до квадрата со стороной (a+b), как показано на рисунке:
Данный квадрат состоит из прямоугольника (ABCD), еще одного равного ему прямоугольника и двух квадратов со сторонами (a) и (b). Таким образом,
(begin{multline*} S_{a+b}=2S_{text{пр-к}}+S_a+S_b Leftrightarrow
(a+b)^2=2S_{text{пр-к}}+a^2+b^2 Leftrightarrow\
a^2+2ab+b^2=2S_{text{пр-к}}+a^2+b^2 Rightarrow
S_{text{пр-к}}=ab end{multline*})
Определение
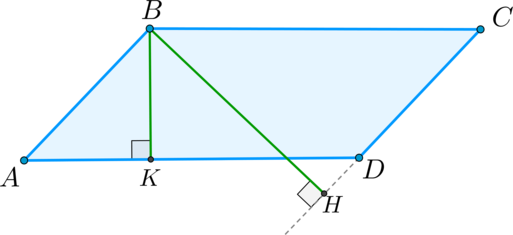
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота (BK) падает на сторону (AD), а высота (BH) — на продолжение стороны (CD):
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры (AB’) и (DC’), как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма (ABCD).
Тогда (AB’C’D) – прямоугольник, следовательно, (S_{AB’C’D}=AB’cdot
AD).
Заметим, что прямоугольные треугольники (ABB’) и (DCC’) равны. Таким образом,
(S_{ABCD}=S_{ABC’D}+S_{DCC’}=S_{ABC’D}+S_{ABB’}=S_{AB’C’D}=AB’cdot
AD.)
[{Large{text{Площадь треугольника}}}]
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
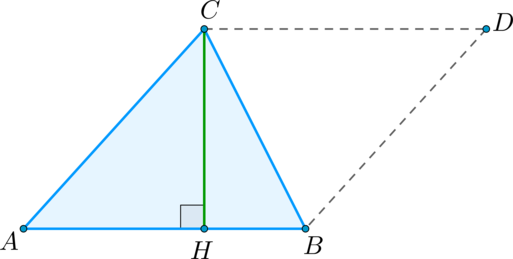
Пусть (S) – площадь треугольника (ABC). Примем сторону (AB) за основание треугольника и проведём высоту (CH). Докажем, что [S = dfrac{1}{2}ABcdot CH.] Достроим треугольник (ABC) до параллелограмма (ABDC) так, как показано на рисунке:
Треугольники (ABC) и (DCB) равны по трем сторонам ((BC) – их общая сторона, (AB = CD) и (AC = BD) как противоположные стороны параллелограмма (ABDC)), поэтому их площади равны. Следовательно, площадь (S) треугольника (ABC) равна половине площади параллелограмма (ABDC), то есть (S = dfrac{1}{2}ABcdot CH).
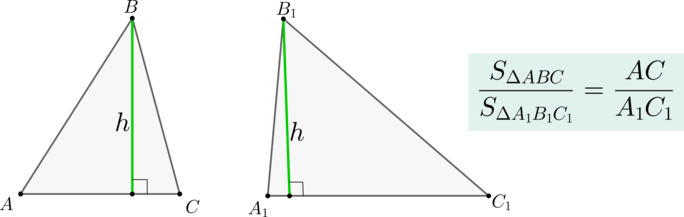
Теорема
Если два треугольника (triangle ABC) и (triangle A_1B_1C_1) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
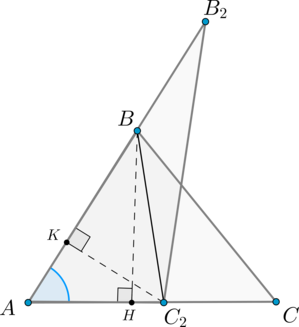
Теорема
Если два треугольника (triangle ABC) и (triangle A_2B_2C_2) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть (angle A=angle A_2). Совместим эти углы так, как показано на рисунке (точка (A) совместилась с точкой (A_2)):
Проведем высоты (BH) и (C_2K).
Треугольники (AB_2C_2) и (ABC_2) имеют одинаковую высоту (C_2K), следовательно: [dfrac{S_{AB_2C_2}}{S_{ABC_2}}=dfrac{AB_2}{AB}]
Треугольники (ABC_2) и (ABC) имеют одинаковую высоту (BH), следовательно: [dfrac{S_{ABC_2}}{S_{ABC}}=dfrac{AC_2}{AC}]
Перемножая последние два равенства, получим: [dfrac{S_{AB_2C_2}}{S_{ABC}}=dfrac{AB_2cdot AC_2}{ABcdot AC} qquad text{ или
} qquad dfrac{S_{A_2B_2C_2}}{S_{ABC}}=dfrac{A_2B_2cdot
A_2C_2}{ABcdot AC}]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть (p) – полупериметр треугольника, (a), (b), (c) – длины его сторон, тогда его площадь равна [S_{triangle}=sqrt{p(p — a)(p —
b)(p — c)}]
[{Large{text{Площадь ромба и трапеции}}}]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
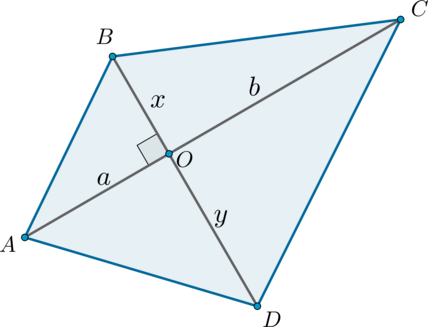
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник (ABCD). Обозначим (AO=a, CO=b, BO=x,
DO=y):
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
(begin{multline*}
S_{ABCD}=frac12ax+frac12xb+frac12by+frac12ay=frac12(ax+xb+by+ay)=\
frac12((a+b)x+(a+b)y)=frac12(a+b)(x+y)end{multline*})
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: [S_{text{ромб}}=dfrac12 d_1cdot d_2]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
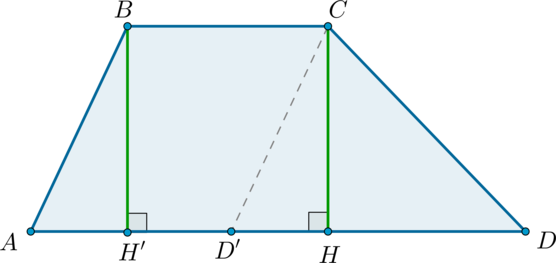
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Рассмотрим трапецию (ABCD) с основаниями (BC) и (AD). Проведем (CD’parallel AB), как показано на рисунке:
Тогда (ABCD’) – параллелограмм.
Проведем также (BH’perp AD, CHperp AD) ((BH’=CH) – высоты трапеции).
Тогда (S_{ABCD’}=BH’cdot AD’=BH’cdot BC, quad S_{CDD’}=dfrac12CHcdot D’D)
Т.к. трапеция состоит из параллелограмма (ABCD’) и треугольника (CDD’), то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
[S_{ABCD}=S_{ABCD’}+S_{CDD’}=BH’cdot BC+dfrac12CHcdot
D’D=dfrac12CHleft(2BC+D’Dright)=] [=dfrac12
CHleft(BC+AD’+D’Dright)=dfrac12 CHleft(BC+ADright)]
Содержание:
Математика, отделяя линию от площади и площадь от тела, утверждает, что реально только тело, а линия и площадь — абстракции.
До настоящего времени в теоремах и задачах рассматривались лишь числовые характеристики отдельных элементов геометрических фигур — длины сторон, градусные меры углов и т. п. В отличие от них площадь характеризует фигуру в целом, т. е. зависит как от ее формы, так и от размеров.
В повседневной жизни человек имеет дело с площадями каждый день — измеряет жилые помещения и приусадебные участки, лесные массивы и сельскохозяйственные угодья и т.д. Вычислением площадей вы занимались и на уроках математики в младших классах. Тем не менее, дать строгое с научной точки зрения определение площади не так просто, и соответствующая математическая теория была создана значительно позже многих известных теорем.
В этой главе мы обобщим сведения о многоугольниках и их площадях. Благодаря этому ваш математический багаж пополнится немалым количеством новых формул, которые необходимо знать и уметь применять. В этой связи дадим вам совет: усвоить какую-либо формулу значительно проще, если понять и запомнить способ ее получения. Более того, откроем вам маленькую профессиональную тайну: иногда даже профессиональные математики не запоминают формулы, а выводят их в уме в случае необходимости. Будет очень здорово, если такую математическую эрудицию удастся приобрести и вам.
Многоугольник и его элементы
Определение многоугольника
Рассмотрим фигуру, которая состоит из отрезков 
В зависимости от количества вершин многоугольник называют треугольником, четырехугольником, пятиугольником и т.д. Многоугольник, который имеет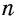 
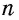
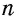
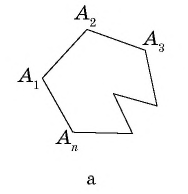
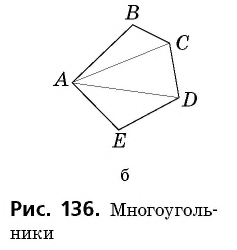
вершин (а следовательно, 
сторон), называют 
-угольником.
Многоугольник обозначают по его вершинам. При этом буквы, которые стоят в названии многоугольника рядом, должны обозначать вершины, которые принадлежат одной стороне (соседние вершины). Например, пятиугольник на рисунке 136, б можно обозначить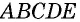 
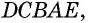
или 
но нельзя обозначать 
Определение
Периметром многоугольника называется сумма длин всех его сторон.
Диагональю многоугольника называется отрезок, соединяющий две несоседние вершины.
Например, на рисунке 136, б отрезки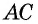 
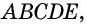
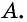
и 
являются диагоналями пятиугольника 
выходящими из вершины 
Периметр этого многоугольника вычисляется по формуле 
Любой многоугольник делит плоскость на две части. Одна из них (на рисунке 136, а она закрашена) является внутренней областью многоугольника. Фигуру, состоящую из многоугольника и его внутренней области, называют плоским многоугольником, или, в некоторых случаях, просто многоугольником. Определение
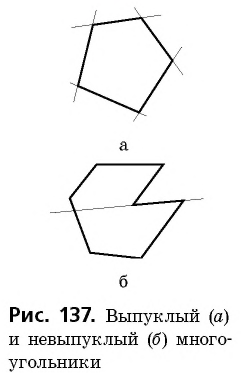
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, которая содержит его сторону.
На рисунке 137, а изображен выпуклый многоугольник, а на рисунке 137, б — невыпуклый. Далее мы будем рассматривать только выпуклые многоугольники.
Рассмотрим выпуклый многоугольник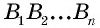 
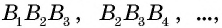
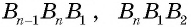
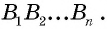
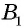
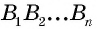
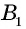
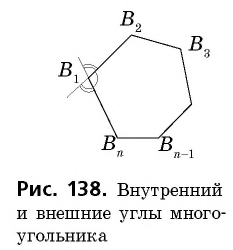
(рис. 138). Углы 
…, 
(на рисунке они закрашены) называют углами (внутренними углами) многоугольника 
В частности, угол данного многоугольника при вершине 
на рисунке обозначен одной дужкой. Углы, смежные с данным внутренним углом, являются внешними углами многоугольника 
при вершине 
(на рисунке они обозначены двумя дужками).
Любой внутренний угол выпуклого многоугольника меньше 
Определение
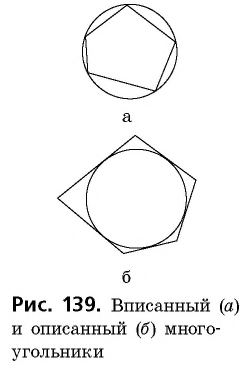
Многоугольник называется вписанным в окружность, если все его вершины лежат на этой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.
На рис. 139, а изображен вписанный многоугольник, а на рис. 139, б — описанный.
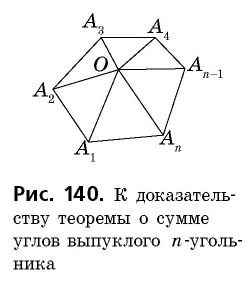
Сумма углов выпуклого многоугольника
Как известно, сумма углов треугольника равна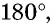 
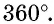
а сумма углов четырехугольника — 
Нетрудно предположить, что сумма углов выпуклого многоугольника должна зависеть от количества его сторон. Эта зависимость выражается следующей теоремой.
Теорема (о сумме углов выпуклого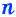 
-угольника)
Сумма углов выпуклого «-угольника равна 
Доказательство:
Пусть дан выпуклый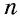 
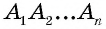
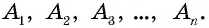
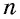
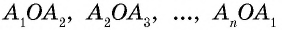
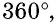
-угольник 
(рис. 140). Обозначим внутри него произвольную точку 
и соединим ее с вершинами 
При этом образуется 
треугольников. Обратим внимание на то, что сумма углов данного многоугольника равна сумме всех углов этих треугольников, кроме углов при вершине 
Поскольку сумма углов 
составляет 
то искомая сумма углов многоугольника равна 
Пример:
Докажите, что сумма внешних углов выпуклого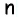 
-угольника, взятых по одному при каждой вершине, равна 
Решение:
Поскольку внешний угол многоугольника по определению является смежным с соответствующим внутренним углом, то сумма этих двух углов равна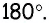 
Таким образом, сумма всех внутренних и внешних углов равна 
Чтобы получить сумму внешних углов, вычтем из этой суммы сумму внутренних углов: 
Понятие площади многоугольника
Понятие площади хорошо известно нам из повседневного опыта: мы измеряем площадь спортивной площадки или садового участка, рассчитываем по площади количество обоев или коврового покрытия для ремонта комнаты и т.д. Попробуем придать представлениям о площади определенную математическую строгость.
Условимся, что под площадью многоугольника мы будем понимать площадь его внутренней области. Как и в случае измерения длин отрезков, измерение площадей основывается на сравнении данной фигуры с фигурой, площадь которой принята за единицу измерения. За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
Например, если за единицу измерения отрезков приняты 1 мм, 1 см или 1 м, то за единицу измерения площади принимают площадь квадрата со стороной 1 мм, 1 см или 1 м. Площадь такого квадрата называется квадратным миллиметром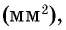 
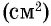
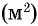
квадратным сантиметром 
или квадратным метром 
соответственно. Из курса математики известны и другие единицы площади: ар (площадь квадрата со стороной 10 м), гектар (площадь квадрата со стороной 100 м) и др.
При выбранной единице измерения площадь каждого многоугольника выражается положительным числом, которое показывает, сколько раз единица измерения площади и ее части укладываются в данном многоугольнике. Обычно площадь обозначается буквой 
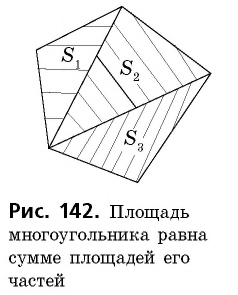
Для определения приближенного значения площади можно использовать палетку — прозрачную пленку с квадратной сеткой (рис. 141).
Наложив палетку на фигуру, площадь этой фигуры определяют обычным подсчетом количества единичных квадратов, которые вместились в данной фигуре. Однако на практике применять такой способ неудобно. Поэтому для определения площади многоугольника обычно измеряют лишь некоторые связанные с ним отрезки, а потом вычисляют площадь по соответствующим формулам. Вывод этих формул основывается на свойствах площадей, которые мы рассмотрим ниже.
Прежде всего заметим, что когда два многоугольника равны, то единица измерения площади и ее части укладываются в каждом из них одинаковое количество раз, т. е. имеет место следующее свойство.
1. Равные многоугольники имеют равные площади.
Далее, пусть многоугольник состоит из нескольких частей — других многоугольников, которые не имеют общих внутренних точек (рис. 142). Если эти части имеют площади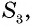 
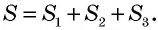
то площадь всего многоугольника равна их сумме: 
В этом заключается второе свойство площадей.
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Третье свойство площадей связано с единицей их измерения.
3. Площадь квадрата со стороной, равной единице длины, равна единице площади.
Три приведенных свойства называют аксиомами площадей. Итак, площадь многоугольника — это положительная величина, численное значение которой удовлетворяет аксиомам площадей.
Из этого, в частности, следует, что каждый многоугольник имеет некоторую площадь, которая однозначно определяется в заданных единицах измерения.
Определение
Две фигуры называются равновеликими, если они имеют равные площади.
Очевидно, что по первой аксиоме площадей любые два равных многоугольника равновеликие. Однако не любые два равновеликих многоугольника равны.
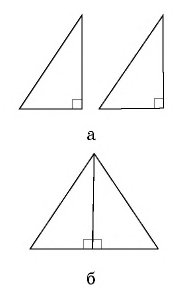
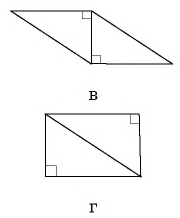
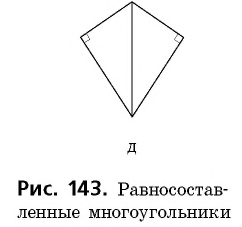
Если рассмотреть два равных прямоугольных треугольника (рис. 143, а), то, прикладывая их равными сторонами друг к другу, можно получить равнобедренный треугольник (рис. 143, б), параллелограмм (рис. 143, в), прямоугольник (рис. 143, г) или четырехугольник с попарно равными соседними сторонами — дельтоид (рис. 143, д). Все эти фигуры равносоставленные, т. е. составлены из одних и тех же многоугольников.
По второй аксиоме площадей все образованные таким способом фигуры имеют равные площади. Следовательно, любые равносоставленные многоугольники являются равновеликими. Интересно, что имеет место и обратное утверждение (теорема Бойяи — Гервина): два равновеликих многоугольника являются равносоставленными (приводим этот факт без доказательства).
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
1)Это прямоугольные треугольники,с любыми сторонами, но прямоугольные.
2)Площадь прямоугольника равна произведению его смежных сторон, или произведению длины на ширину.
3) 1.Равные многоугольники имеют равные площади
2.Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников .
3.Площадь квадрата равна квадрату его стороны
4)Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
5)Много вариантов есть, так как площадь многоугольников может и делиться, и уменьшаться, и увеличиваться.
6)Площадь треугольника равна половине произведения его сторон на синус угла между ними.
7)Площадь прямоугольного треугольника равняется половине произведения катетов. Дан прямоугольный треугольник с катетами a = 8 см, b = 6 см. Также в прямоугольном треугольнике применяется теорема Пифагора. – сумма квадратов двух катетов равняется квадрату гипотенузы.
8)Площадь трапеции равна произведению полусуммы оснований на высоту. Доказательство. Проведя в трапеции ABCD (рис.1) диагональ DB, можно рассматривать ее площадь S как сумму площадей двух треугольников BCD и ADB.
9)Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.
10)Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
11)Отношение площадей треугольников, имеющих равную высоту, равно отношению их оснований.
12)Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
13)1. Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне (S=ah)
2. Если известна сторона ромба (у ромба все стороны равны) и угол между сторонами, то площадь можно найти по следующей формуле(S=a2 sin a)
3. Площадь ромба также равна полупроизведению диагоналей
4. Если известен радиус r окружности, вписанной в ромб и сторона ромба a, то его площадь вычисляется по формуле.
14)Площадь прямоугольного треугольника равняется половине произведения катетов. Дан прямоугольный треугольник с катетами a = 8 см, b = 6 см. Также в прямоугольном треугольнике применяется теорема Пифагора. – сумма квадратов двух катетов равняется квадрату гипотенузы.
15)Если высоты двух треугольников равны, то их площади относятся как основания. И Если высоты двух треугольников равны, то их площади относятся как основания