Improve Article
Save Article
Improve Article
Save Article
Since binary numbers can have only two symbols either 0 or 1 for each position or bit, so it is not possible to add minus or plus symbols in front of a binary number.
We represent negative binary numbers using a minus symbol in front of them. In computer number representation, these numbers can be distinguishable with the help of an extra bit or flag called sign bit or sign flag in the Binary number representation system for signed numbers. This extra bit is called sign bit or sign flag which has a value of sign bit is 0 for positive numbers and 1 for negative binary numbers.
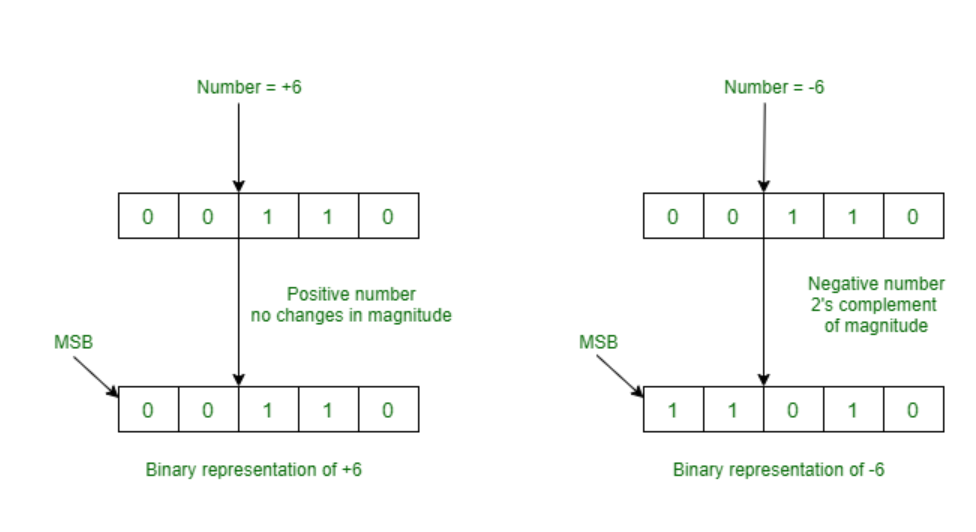
The representation of magnitude of positive numbers is easy and does not need any changes.
The representation of magnitude of negative numbers is changed accordingly to represent it.
Ways to represent magnitudes :
These are: Sign-Magnitude method, 1’s Complement method, and 2’s complement method. These are explained as follows using examples.
- Signed Magnitude Method :
We only add an extra sign bit to recognize negative and positive numbers. Sign bit has 1 for negative number and 0 for positive number.Range of Numbers :
For n bits register, MSB will be sign bit and (n-1) bits will be magnitude. Then,
Negative lowest number that can be stored is -(2(k-1)-1)and positive largest number that can be stored is (2(k-1)-1) .But, this (sign) representation has an ambiguous representation of number 0. It means 0 has two different representation one is -0 (e.g., 1 00000 in six bit register) and second is +0 (e.g., 0 00000 in six bit register).
- 1’s Complement Method :
Please note that MSB is always Sign bit, if it 0, then there are no changes. MSB is always 1 in case of negative numbers. We only take 1’s complement of negative numbers to represent in the computer.Range of Numbers :
For n bits register, negative lowest number that can be stored is -(2(n-1)-1) and positive largest number that can be stored is (2(n-1)-1) .But, this (sign) representation has an ambiguous representation of number 0. It means 0 has two different representations one is -0 (e.g., 1 1111 in five bit register) and second is +0 (e.g., 0 0000 in five bit register).
- 2’s Complement Method :
Please note that MSB is always Sign bit, if it 0, then there are no changes. MSB is always 1 in case of negative numbers. We only take 2’s complement of negative numbers to represent in the computer.Since, there is only one representation of +0 and -0, so this 2’s complement representation is better than sign representation and 1’s complement representation.
Range of Numbers :
For n bits register, negative lowest number that can be stored is -(2(n-1)) and positive largest number that can be stored is (2(n-1)-1) .
Improve Article
Save Article
Improve Article
Save Article
Since binary numbers can have only two symbols either 0 or 1 for each position or bit, so it is not possible to add minus or plus symbols in front of a binary number.
We represent negative binary numbers using a minus symbol in front of them. In computer number representation, these numbers can be distinguishable with the help of an extra bit or flag called sign bit or sign flag in the Binary number representation system for signed numbers. This extra bit is called sign bit or sign flag which has a value of sign bit is 0 for positive numbers and 1 for negative binary numbers.
The representation of magnitude of positive numbers is easy and does not need any changes.
The representation of magnitude of negative numbers is changed accordingly to represent it.
Ways to represent magnitudes :
These are: Sign-Magnitude method, 1’s Complement method, and 2’s complement method. These are explained as follows using examples.
- Signed Magnitude Method :
We only add an extra sign bit to recognize negative and positive numbers. Sign bit has 1 for negative number and 0 for positive number.Range of Numbers :
For n bits register, MSB will be sign bit and (n-1) bits will be magnitude. Then,
Negative lowest number that can be stored is -(2(k-1)-1)and positive largest number that can be stored is (2(k-1)-1) .But, this (sign) representation has an ambiguous representation of number 0. It means 0 has two different representation one is -0 (e.g., 1 00000 in six bit register) and second is +0 (e.g., 0 00000 in six bit register).
- 1’s Complement Method :
Please note that MSB is always Sign bit, if it 0, then there are no changes. MSB is always 1 in case of negative numbers. We only take 1’s complement of negative numbers to represent in the computer.Range of Numbers :
For n bits register, negative lowest number that can be stored is -(2(n-1)-1) and positive largest number that can be stored is (2(n-1)-1) .But, this (sign) representation has an ambiguous representation of number 0. It means 0 has two different representations one is -0 (e.g., 1 1111 in five bit register) and second is +0 (e.g., 0 0000 in five bit register).
- 2’s Complement Method :
Please note that MSB is always Sign bit, if it 0, then there are no changes. MSB is always 1 in case of negative numbers. We only take 2’s complement of negative numbers to represent in the computer.Since, there is only one representation of +0 and -0, so this 2’s complement representation is better than sign representation and 1’s complement representation.
Range of Numbers :
For n bits register, negative lowest number that can be stored is -(2(n-1)) and positive largest number that can be stored is (2(n-1)-1) .
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Операция сложения положительного числа и отрицательного числа, представленного в прямом коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
- Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.
_ 000 0111 000 0101 ------------- 000 0010 - После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -210.
Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Формирование дополнительного кода числа -7.
Прямой код : 1 000 0111
Инверсия : 1 111 1000
Добавление единицы: 1 111 1001 - Операция сложения.
0 000 0101 + 1 111 1001 -------------- 1 111 1110 - Проверка результата путем преобразования к прямому коду.
Дополнительный код: 1 111 1110
Вычитание единицы : 1 111 1101
Инверсия : 1 000 0010 (или -210)
Одним
из способов выполнения операций с
помощью двоичного сумматора, является
замена
операции вычитания операцией суммы с
обратным или дополнительным кодом
отрицательного числа:
А
– В =
А + (-В)обр.
Замена
вычитания сложением ставит проблему
представления отрицательного числа в
цифровом
формате.
Один
метод мы уже рассмотрели. Он использует
прямой код числа
,
где машинное изображениеиспользует 1 (или 11) для обозначения «-».
Итак,
прямой код отрицательного числа есть
код, все цифровые разряды которого
остаются неизменными,
записанными в нормализованной форме,
а в знаковой части числа записывается
«1»(или 11 для модифицированного
кода ).
Например:
N = — 0,101110 то NM
= 1.101110.
Положительное
число в прямом коде не меняет своего
изображения.
Например:
N= 0,110101 то NM=
0.110101
В
прямом коде в числовую сетку автомата
можно записать
,
где n – количество разрядов. А диапазон
чисел,для
прямого кода, лежит в пределах 6.1
– (1
– 2-n)
NM
(1 – 2-n). 6.1
Вторым методом
представления отрицательных чисел есть
представление их в обратном или
дополнительном коде.
7 Коды бинарных чисел
7.1 Обратный код числа
Обратным
кодом числа NM
= 1, a1,
a2,…,
an
называется такое машинное изображение
числа, для которого ai
= 0, если оно равнялось «1» и наоборот,
аi
= 1, если оно равнялось «0».
Иначе, обратным
кодом двоичного числа является инверсное
изображение этого числа, т.е. все разряды
исходного бинарного числа, принимают
обратное значение.
Например:
N = — 0,101110 то No6
= 1,010001.
Обобщая
правила образования обратного кода на
все основания систем счисления можно
считать, что обратный
код отрицательного числа получается
при вычитании из (q-1) цифр по каждому
разряду числа за исключением знаковых
разрядов, которые заменяются значением
(q-1) т. е.
Например:
-0,286357(10)пр=9,713642(10)обр
-0,1010111101(2)пр=1,0101000010(2)обр
Особо обратить
внимание.
Если в знаковом
разряде машинного представления
находится (q-1), то все цифры числа, исключая
знаковый, заменяются вычетом из (q-1)
значения разряда; если в знаковом разряде
находится нуль, то преобразование не
производятся.
Ниже приведены
примеры для различных систем счисления:
7.1.1 Переход от обратного кода к прямому
Переход от обратного
кода к прямому производится по аналогичному
правилу. Из значения (q-1) вычитается
значение по каждому разряду, кроме
знаковых. Для бинарной системы счисления
(просто счастливый случай), можно перейти
к прямому коду простым инвертированием
разрядов обратного кода, кроме разрядов
знаков.
7.2 Дополнительный код числа
Дополнительный
код числа N= – 0,a1a2..an
–такое машинное представление
,
в котором число записывается обратным
кодомс
прибавлением в младшем разряде 1.
Правило перевода
из прямого кода в дополнительный код
следующее:
-если в знаковом
разряде находится (q -1), то все цифры
числа, кроме разрядов знаков, заменяются
вычетами из (q-1) значения разряда, а затем
к цифре последнего младшего разряда
добавляется единица;
-если в знаковом
разряде находится 0 (или 00), то преобразование
цифр не происходит.
Например:
-
9.243476(10)пр
= 9.756523обр. + 0000001 = 9.756524(10)доп -
1.0111000111(2)пр
= 1.1000111000обр. + 0.0000000001 = 1.1000111001(2)доп
-
–0,101110 = 1.101110 =
1.010001 + 0.000001 = 1.010010 -
0.425736пр
= 0.425736доп
Таким образом, для
положительных чисел прямой и дополнительный
код совпадают, для отрицательного числа
они различны. Для положительного числа,
в разряде знака всегда устанавливают
нуль(или 00), а отрицательного (q-1).
Обобщая,
получаем математическую формулу перевода
чисел в дополнительный код.
Отсюда
Nдоп
= q + (-N), т.е. дополнительный
код является математическим дополнением
числа до основания системы счисления.
Пример: 0,275936(10)пр
= 0,275936(10)доп
Пример:
–0,275936(10)пр=10,000000(10)+(–0,275936(10)доп)
= 9,724064(10)доп
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Опорный конспект на тему «Представление отрицательных чисел в памяти ПК»
- Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
- Прямой код
- Дополнительный код
- Прямой, обратный и дополнительный коды двоичного числа
- Прямой код
- Обратный код
- Дополнительный код
- Представление отрицательных чисел в компьютере
- Введение
- Отрицательные числа в дополнительном коде
- Десятичные числа в дополнительном коде
- Перевод числа из прямого кода в дополнительный
- Готовые работы на аналогичную тему
- Достоинства и недостатки
- Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
- Прямой код
- Дополнительный код
Опорный конспект на тему «Представление отрицательных чисел в памяти ПК»
Представление отрицательных чисел в памяти компьютера.
Для хранения чисел в памяти компьютера используется два формата: целочисленный (естественная форма) и с плавающей точкой (нормализованная форма) (точка — разделительный знак для целой и дробной части числа).
Целочисленный формат (формат с фиксированной точкой) используется для представления в компьютере целых ( англ. integer) положительных и отрицательных чисел. Для этого, как правило, используются форматы, кратные байту: 1, 2, 4 байта.
В форме с фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (или точки), отделяющей целую часть от дробной.
Эта форма проста и привычна для большинства пользователей, но имеет небольшой диапазон представления чисел и поэтому не всегда пригодна при вычислениях. Если же в результате какой-либо арифметической операции получается число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, и все дальнейшие вычисления теряют смысл.
Однобайтовое представление применяется только для положительных целых чисел. В этом формате отсутствует знаковый разряд. Наибольшее двоичное число, которое может быть записано при помощи 1 байта, равно 11111111, что в десятичной системе счисления соответствует числу 25510.
Самое большое (по модулю) целое число со знаком, которое может поместиться в 2-байтовом формате, это число 0111111111111111, то есть при помощи подобного кодирования можно представить числа от −32 76810 до 32 76710.
Если число вышло за указанные границы, произойдет переполнение! Поэтому при работе с большими целыми числами под них выделяется больше места, например, 4 байта.
Нормализованная форма представления чисел обеспечивает огромный диапазон их записи и является основной в современных ЭВМ.
Представление целого положительного числа в компьютере
Для представления целого положительного числа в компьютере используется следующее правило:
— число переводится в двоичную систему;
— результат дополняется нулями слева в пределах выбранного формата;
— последний разряд слева является знаковым, в положительном числе он равен 0.
Представление целого отрицательного числа в компьютере
Для представления целого отрицательного числа в компьютере используется следующее правило:
— к полученному коду прибавляется 1.
Обратный код для положительного двоичного числа совпадает с его прямым кодом, а для отрицательного числа нужно во всех разрядах, кроме знакового, нули заменить единицами и наоборот.
Дополнительный код для положительного числа совпадает с его прямым кодом, а для отрицательного числа образуется путем прибавления 1 к обратному коду.
Отрицательное число может быть представлено в виде 2 или 4 байт.
Например, представим число −13510 в 2-байтовом формате:
— 13510 → 10000111 (перевод десятичного числа без знака в двоичный код);
— 0000000010000111(дополнение двоичного числа нулями слева в пределах формата);
— 0000000010000111 → 1111111101111000(перевод в обратный код);
— 1111111101111000 → 1111111101111001 (перевод в дополнительный код).
Представление вещественного (действительного) числа в компьютере
Вещественное число может быть представлено в экспоненциальном виде, например:
1600000010=0,16 ⋅ 10 8
− 0,000015610=−0,156 ⋅ 10 −4
Порядок n указывает, на какое количество позиций и в каком направлении должна сместиться в мантиссе точка (запятая), отделяющая дробную часть от целой. Мантисса, как правило, нормализуется, то есть представляется в виде правильной дроби 0
При представлении в компьютере действительного числа с плавающей точкой тоже используется нормализованная мантисса и целый порядок. И мантисса и порядок представляются в двоичном виде, как это было описано выше.
Для размещения вещественного числа обычно используется 2 или 4 байта.
В 2-байтовом формате представления вещественного числа первый байт и три разряда второго байта выделяются для размещения мантиссы, в остальных разрядах второго байта размещаются порядок числа, знаки числа и порядка.
В 4-байтовом формате представления вещественного числа первые три байта выделяются для размещения мантиссы, в четвертом байте размещаются порядок числа, знаки числа и порядка.
Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.
Источник
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Источник
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Источник
Представление отрицательных чисел в компьютере
Вы будете перенаправлены на Автор24
Представление отрицательных чисел в компьютере — это их выражение в виде дополнительного кода, который является самым применяемым для этих целей.
Введение
Под дополнительным кодом понимается самый используемый метод задания отрицательных целых чисел в компьютерной среде. Этот код даёт возможность использовать операционную процедуру сложения вместо вычитания, что делает данные процедуры равноценными как для чисел, имеющих знак минус, так и для чисел, не имеющих знака.
Такая числовая организация позволяет сильно упростить структурное построение электронных вычислительных машин. В западных версиях обратный код принято обозначать первым дополнением, а дополнительный код обозначать как второе дополнение. Дополнительный код отрицательного числа возможно сформировать путём инверсии его модуля в двоичном коде с последующим добавлением к инвертированному значению единицы. Этот вариант обозначается как второе дополнение. Дополнительный код числа со знаком минус возможно также сформировать, если вычесть это число из нуля. То есть, дополнительный код числа в двоичном коде, может быть сформирован путём добавления единицы к младшему не нулевому разряду первого дополнения этого числа. Второе дополнение числа в двоичном коде формируется как кодовый набор, который получается при вычитании числа из самой большой степени двойки, то есть из два в степени N для второго дополнения числа, состоящего из N двоичных кодов.
Отрицательные числа в дополнительном коде
Десятичные числа в дополнительном коде
Аналогичная методика применяется и для отображения десятичных чисел в электронных вычислительных машинах. Последовательно выполняется замена символа Х на 9 – Х, и результату добавляется единица. К примеру, если применяются числа из четырёх разрядов, то – 2272 нужно заменить на 7728, то есть 7728 + 2272 = 0000, пятый разряд отбрасывается при этом.
Перевод числа из прямого кода в дополнительный
Готовые работы на аналогичную тему
Чтобы преобразовать число из прямого кода в дополнительный, нужно:
Например, необходимо выполнить преобразование отрицательного числа пять, представленного в прямом коде, в формат дополнительного кода. Основным кодом является двоичный код:
Далее необходимо выполнить инверсию числовых разрядов, за исключением знакового, что даёт в результате обратный код числа минус пять:
Осталось прибавить единицу, что даст искомый итоговый дополнительный код:
Достоинства и недостатки
К достоинствам следует отнести:
К недостаткам относятся:
Источник
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Источник