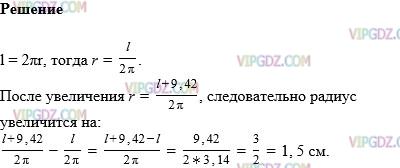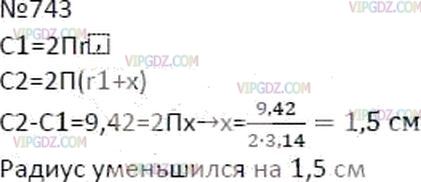Как изменить радиус окружности 3 класс

Математика, 3 класс

Урок №33. Круг. Окружность (центр, радиус, диаметр)

Перечень вопросов, рассматриваемых в теме:

— что такое окружность и круг?

— какие элементы имеет окружность?

— чем отличается круг от окружности?

Глоссарий по теме:

Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра.

Круг – это геометрическая фигура, которая ограничена окружностью.

Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.

Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. с. 94-96.

2. Рудницкая В. Н. Тесты по тматематике:3 класс. М.:Издательство «Экзамен», 2016 с. 48-51.

3. Рудницкая В.Н. Контрольные работы по математике:3 класс. М.: Издательство»Экзамен», 2017, с. 49-54.

4. Рудницкая В. Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 77-79.

Теоретический материал для самостоятельного изучения

С незапамятных времен люди используют в своей жизни круг.

1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).

2. Мы не можем представить свою жизнь без машин: автобус, велосипед, швейная, машинки, самолет, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес.

3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.

4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир .

5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль. 

6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду.

Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.

Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.

Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.

Круг – символ цикличности, повторяемости. Все движется по кругу.

Круг дает ощущение взаимосвязи с Космосом.

Сама природа выбирает эту удобную и компактную форму как шар и круг.

Сравним две фигуры.

На 1 рисунке видим замкнутую кривую линию, на которой находятся точки К и С на одинаковых расстояниях от точки О.Такая замкнутая кривая называется окружностью. Точка О — центр окружности. Все точки, поставленные на окружности, находятся на одинаковом расстоянии от центра!

Есть специальный инструмент, который позволяет чертить окружности – это циркуль.

На рисунке 2 видим геометрическую фигуру, которая ограничена окружностью. Эта фигура называется круг.

Вывод: окружность — граница круга; круг — часть внутри окружности. В таблице указаны отличительные признаки круга и окружности:

Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом.

Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.

Диаметр делит круг на две равные части и все диаметры у окружности равной длины.

Задания тренировочного модуля:

1. Длина радиуса составляет 6 см. Чему равен диаметр окружности?

6см; 12 см; 3см.

Правильный ответ: 12см.

2. Заполните таблицу

Правильный ответ:

Задачи урока:

• Познакомить с определением радиуса окружности, научить находить радиусы на рисунках, чертить их.
• Развивать логическое мышление и познавательную активность в процессе исследовательской деятельности, эмоциональную сферу, речь.
• Формировать умение общаться, работать в группах, самооценку.

Оборудование:

• Аргинская И.И., Ивановская Е.И. Математика: Учебник для 3кл., Самара: Корпорация “Федоров”; Изд. “Учебная литература”, 2006.
• Карточки с окружностями. Карточки для индивидуальной работы. (Приложение 1)
• Циркули, карандаши, линейки.

Ход урока

I. Организационный момент.

Прозвенел уже звонок,
Сядьте тихо и неслышно,
И скорей начнём урок.
Будем мы писать, трудиться,
Ведь заданья нелегки.
Нам, друзья, нельзя лениться,
Так как мы ученики.

II. Устный счет.

1. Индивидуальная работа (задание на карточках)

2. «Головоломка»

– Назови следующие три числа, объясни правило, по которому составлен ряд чисел.

1) 2, 4, 7, 11, 16, 22, … (29, 37, 46)

2) 10, 8, 11, 9, 12, 10, 13, …(11, 14, 12)

3. Выразите:

4. Блиц-турнир. «Какое слово лишнее?»

– Почему?

a) Математика, русский язык, чтение, тетрадь, английский язык, физ-ра.

б) Делимое, делитель, частное, плюс.

в) Стол, стул, диван, тарелка, шкаф.

5. Задачи на смекалку

– Когда об воду можно порезать руку? (когда она превратится в лёд)

– У меня 4 сына. У каждого из них есть родная сестра. Сколько детей у меня? (5)

– Можно ли пустое ведро наполнить три раза подряд, ни разу не выливая из него? (нет)

– Установи порядок: прямоугольник, многоугольник, круг, квадрат, четырехугольник. Что “лишнее”? Почему? (круг – нет углов)

III. Закрепление ранее изученного.

Слайд (Приложение 2)

– На какие две группы можно разделить фигуры? (на круги и окружности)

– Назовите их номера? (круги – 1, 4, 6, 2, окружности – 3, 5, 7)

– Рассмотрим ваши узоры из окружностей, выполненные  дома и вспомним всё то, чему научились на прошлом уроке. (3 ученика у доски)

– Как называется граница круга?

– Чем отличается окружность от круга?

– С помощью какого инструмента вы чертили окружности?

– Вспомните правила безопасной работы с циркулем.

IV. Изучение нового: исследование, наблюдение, вывод.

– Я вас просила вырезать из цветной бумаги круг, приготовьте его для работы. Теперь вместе со мной выполняем следующие действия.

– Согните круг так, чтобы центр оказался на линии сгиба. Сколько половин в круге получилось? (Две)

– Круг разделили на две части и получили две половины.

– Как вы думаете, части получились одинаковые? Равные?

– Они подходят, т.к совмещаются.

– Посмотрим на линию сгиба? Какая она? (Она прямая.)

– Верно, линия сгиба прямая. Есть ли у нее начало и конец? (Есть.)

– А как называется линия, у которой есть начало и конец? (Отрезок)

– Правильно, ребята. Молодцы. Посмотрите, я еще построю несколько отрезков в этом круге. (Учитель делает в круге еще несколько сгибов параллельно диаметру.)

– Чем же интересны эти отрезки? (Они проходят через центр)

Отрезок, который проходит от края круга до другого края через центр, называется – диаметр.

Слайд

– Из всех отрезков, соединяющих два противоположных края круга, диаметр – самый длинный.

– Так сколько диаметров можно провести в окружности? (много)

– А какие они  должны быть все по длине? (одинаковые)

– Еще можно сказать равные.

– Продолжаем работу с нашим кругом .

– Согните ваш круг по диаметру. (Дети складывают.)

– Вы получили полукруг. А теперь сложите полукруг пополам.

– Где оказался центр круга? Покажите его.

– У этой фигуры, которую мы получили, есть свое название.

– Разверните ваш круг. Проведите пальцем от центра круга до его края по сгибу. Этот маленький отрезок называется, словом радиус.

– Сколько радиусов на вашем круге? (4 радиуса)

– Какие по длине все радиусы? Проверьте с помощью циркуля. (Радиусы одинаковые.)

– Чтобы дать верное определение радиуса, мы попробуем выбрать из уже предложенных их детьми. (Учебник стр.74 №140 – объяснить свой выбор)

Слайд

V. Закрепление

1. Задание.

– А теперь мы проверим ваши знания. Я предлагаю вам первое задание.

– Рассмотрите рисунок. Что на нем изображено? (окружность)

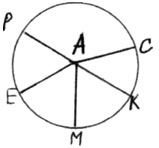
– Кто знает, как называется отрезок AM? (Радиус окружности.)

– Подумайте, есть ли здесь другие радиусы? Если есть, назовите их имена (один ученик пишет на доске ЕА, АР, АС, АК).

– Начертите свою окружность и проведите в ней несколько радиусов.

2. Задание

– Запиши имена линий, которые не являются радиусами. (СЕ, АВ, XУ, ОУ, РЛ)

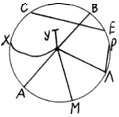
3. Задание

– Начерти окружность, проведи в ней зелёным цветом 3 радиуса, синим столько же отрезков, которые не являются радиусами.

(взаимопроверка и взаимооценка в паре).

– Оценим работу группы (+ хорошо, ошибки исправлены).

4. Задание

– А сейчас я вам предлагаю задание на закономерность Слайд

– В данных окружностях нарисованы радиусы по определённому правилу.

– Пронаблюдайте, по какому правилу нарисованы радиусы?

– Попробуйте догадаться, какой радиус я должна нарисовать в последних окружностях. Если вы внимательно посмотрите на первый ряд, то найдёте отгадку. (по часовой стрелке располагаются радиусы)

Физминутка. (Дежурный ученик проводит упражнения для снятия усталости рук, головы, глаз.)

5. Задание – самостоятельная работа

№ 142 (по рядам: 1 ст. – 1 ряд, 2ст.– 2 ряд, 3ст.– 3 ряд; 3 человека у доски).

VI. Домашнее задание.

№ 141 (1).

7. Итоги урока.

– Что нового узнали на уроке?

– С каким настроением работали?

Тема урока: Радиус окружности.

Содержательная цель урока: Создать условия для формирования у учащихся понятия «радиус окружности».

Деятельностная цель: формирование у учащихся умений реализации новых способов действия (строить окружность, проводить в ней радиус, определять радиус окружности).

Задачи урока:

Предметные: формировать представления о радиусе окружности, формировать умения решать задачи, способствовать совершенствованию вычислительных навыков учащихся.

Личностные УУД: содействовать формированию интереса к изучаемому материалу на уроке.

Метапредметные: способствовать формированию УУД:

Регулятивных – учить принимать учебную задачу и следовать инструкции учителя; выполнять учебные действия в устной и письменной форме.

Познавательных – учить устанавливать причинно-следственные связи внутри математических действий, осуществлять поиск нужной информации, используя материал учебника.

Коммуникативных – формировать коммуникативную компетентность учащихся в общении и сотрудничестве со сверстниками.

Тип урока: урок открытия нового знания.

Оборудование: учебник, индивидуальные карточки для работы в парах, индивидуальные задания для работы в группах, шаблоны «Памятка», мультимедийная презентация к уроку.

Ход урока

1. Организационный момент.

Начнем урок с девиза.

«Маленькие удачи – путь к большой победе. Помогая другим – учимся сами»

— Вы согласным с данным утверждением? (ответы детей) Давайте сегодня отправимся в путь за новыми математическими знаниями и умениями.

Для успешной  работы на уроке давайте вспомним главные правила?

(Правила работы на уроке)

— Если вы работаете в паре со своим соседом, что надо помнить? (ответы детей)

— Если вы работаете в группе?

— Если вы работаете самостоятельно?

(Постепенно на доске вывешиваются опорные слова: «Напарники», «Дружная команда», «Я смогу»).

2. Устный счет  (работа в группах).

Сейчас каждая группа получит вои задания. Внимательно прочитайте их, выполните необходимые вычисления и получите зашифрованные слова.

1, 4 группы:  НАЙТИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ. ЗАПОЛНИТЬ ТАБЛИЦУ.

Ответ: ОКРУЖНОСТЬ

2, 5 группы: НАЙТИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ. ЗАПОЛНИТЬ ТАБЛИЦУ.

Ответ: ОТРЕЗОК

3, 6 группы: НАЙТИ КОРНИ УРАВНЕНИЙ. РАССТАВИТЬ ИХ В ПОРЯДКЕ ВОЗРАСТАНИЯ.

Ответ: РАДИУС

Перед каждым из вас есть «лесенка успеха». Оцените на ней свою работу в группе.

3. Актуализация знаний учащихся. Решение проблемной ситуации.

На экране

окружность                 отрезок              радиус

                                            ?

— Что вы знаете об окружности?

— Что вы можете сказать об отрезке?

— Что такое радиус?  Как взаимосвязаны полученные слова между собой? (ответы детей на основе имеющихся знаний).

— Итак, назовите тему сегодняшнего урока.

Радиус окружности (на доске)

— Какие задачи мы для себя поставим? (дети продолжают предложения)

На доске прикреплены начала задач

Узнать….           Учиться…          Развивать…        Проверить …

4. Работа по теме урока.

— Где мы можем проверить полученное нами открытие? ( В учебнике)

—Сейчас я попрошу вас самостоятельно найти в учебнике страницы, которые помогут нам сегодня на уроке. (Дети ищут в учебнике материал для урока).

Работа по учебнику (стр. 74, № 140)

— Докажите, что здесь изображена окружность.

— Найдите все радиусы данной окружности. Запишите их в тетради (работа в парах, коллективная проверка).

— начертите свою окружность и проведите в ней несколько радиусов. (На доске начерчена окружность, 2-3 ученика выходят к доске и чертят радиус на ней).

— Давайте дадим верное определения радиусу. Проанализируйте с соседом предложенные детьми варианты и найдите правильный (работа в парах, проверка).

На экране правило: Радиус – это отрезок, который соединяет центр окружности с точкой окружности.

5. Физминутка (зрительная) Сейчас потренируем наши глазки (зрительная гимнастика – по цветным кругам, схеме Базарного)

6. Работа по теме урока. Для того чтобы закрепить новые знания выполним 5 пункт № 140 по группам (девочки – выписывают имена радиусов данной окружности,  мальчики имена линий, которые радиусами не являются). Представители каждой группы у доски.

(Взаимопроверка учащимися результатов, самооценка учеников на «лесенке успеха)

— А сейчас давайте поработаем парами. У каждого из вас на столе лежит лист с заданиями. Внимательно прочитайте его и выполните. Чья пара будет готова, дайте сигнал.  

Работа в паре.

(проверка пар по линиям парт, самооценка учеников на «лесенке успеха)

Работа по учебнику (стр. 75, № 141)  Решение задачи: В школьном саду посажены 6 рядов слив по 8 деревьев в каждом ряду и 4 ряда вишен по 9 деревьев в ряду. Каких деревьев в саду больше и на сколько?

(На экране представлены варианты решения этой задачи)

6•8 — 4•9                       8•6 — 9•4                 8•6 + 9•4    

Какое выражение нам необходимо выбрать для решения этой задачи? Почему?

— Ответы детей.

-Запишите самостоятельно в тетради решение и ответ к этой задаче.

(самооценка учеников на «лесенке успеха)

Как вы думаете, сколько обратных задач можно составить к данной? (Варианты детей). Дома я попрошу вас придумать и решить любую обратную задачу.

7. Физминутка (двигательная).

8. Самостоятельная работа Готовы попробовать свои силы? Тогда выполните задания на карточке и разгадайте зашифрованное слово.

Выберите буквы правильных ответов на вопросы. Составьте слово.

1. Радиус – это:

А) линия внутри окружности

О) отрезок, соединяющий центр окружности с точкой окружности

У) отрезок, внутри окружности

2. Значение выражения 352 + 128 =

Б) 780    Д) 450     Т) 480

3. Окружность – это:

У) Круг    Л) Граница круга

4. Площадь прямоугольника со сторонами 5 см и 9см равна:

В) 14 см2      И) 45 см2    О) 45см

5. Значение выражения 900 – 250 =

К) 750    Г) 850    Ч) 650

6. Корень уравнения  9 • х = 63 равен:

Н) 7       Р) 8         М) 4

7. Радиус Земли = 6371 км, радиус Луны = 1737 км, радиус Солнца = 696 тысяч км. Чей радиус больше?

А) Луны     О) Солнца    У) Земли

Зашифрованное слово: ОТЛИЧНО

(самопроверка, самооценка учеников на «лесенке успеха»)

9. Обобщение и закрепление полученных знаний.

— Какую тему на уроке мы сегодня изучили?

— Чтобы полученные знания остались у вас надолго заполним персональные памятки. (Заполнение шаблона, выборочная проверка)

10. Рефлексия.  Оцените свою работу на уроке на итоговой «лесенке успеха».

— Давайте вспомним, какие цели мы перед собой ставили? (беседа с учениками)

11. Итог урока. Урок подошёл к концу. Все работали активно, старались.

12 . Домашнее задание. Учебник, стр. 75, № 141 (п. 3), № 143

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Решение на Упражнение 743 из ГДЗ по Математике за 6 класс: Мерзляк А.Г.

Условие

Решение 1

Решение 2

Поиск в решебнике

Популярные решебники

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. — 2013г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015г.

Радиус и диаметр окружности

Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).

Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.

Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности

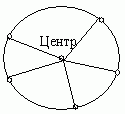
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.

Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.

На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;

Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.

Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.

Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.

Формула радиуса окружности через диаметр:

Формула диаметра окружности через радиус:

Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.

Существует радиус вписанной окружности
и радиус описанной окружности.

Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.

Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.

Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.

Тема: Радиус окружности

Цель:

Цель: сформировать представление о радиусе окружности.

Формирование универсальных учебных действий (УУД) на уроке:

* личностные:

— формирование положительного отношения и интереса к изучению математики;

— оценивание собственной учебной деятельности по критериям определенным совместно с учителем;

* предметные:

— способствовать формированию умения строить окружность нужного радиуса;

— способствовать развитию вычислительных навыков, умений работать с чертёжными инструментами;

* метапредметные

* * регулятивные:

— участвовать в учебном диалоге, аргументировать свою точку зрения;

– сотрудничать с одноклассниками при работе в группе,

** познавательные:

— познакомить учащихся с историей Олимпийских игр, символикой;

— понимать информацию; находить нужную информацию в учебнике;

– определять последовательность действий для решения предметной задачи.

** коммуникативные:

— уметь сотрудничать с товарищами при выполнении заданий в группе: устанавливать очерёдность действий, осуществлять взаимопроверку, обсуждать совместное решение;

Оборудование:

для учителя: видеоролик с песней, презентация, проектор, компьютер, экран, колонки; символы Олимпиады: девиз, кольца; музыкальная физкультминутка; домики из цветной бумаги с числами; смайлики с пояснениями.

для учеников: циркуль, цветная бумага: жёлтая, чёрная, голубая, красная, зелёная, ножницы.

Тип урока: урок открытия новых знаний

Методы: практический, побуждающий диалог, частично-поисковый, деятельностный

Ход урока:

1. Мотивационный этап

Включается видеозапись песни к сочинской Олимпиаде.

Учитель: Почему я включила этот ролик? (Ответы детей)

Учитель: Мы все знаем, что зимние Олимпийские игры 2014 года прошли у нас в России в городе Сочи.

— Как часто проходят Олимпийские игры? (раз в 4 года)

II. Каллиграфическая минутка.

Цель: совершенствование навыков правильного письма цифр

— Откройте тетради, запишите число, классная работа.

— Напишем цифру 4. (слайд 2)

— Назовите родину Олимпийских игр. (Древняя Греция, Олимпия) (слайд 3)

— Кому были посвящены Олимпийские игры? (были посвящены богу Зевсу)

— Участниками Олимпийских игр могли быть только свободные мужчины, коренные греки. Женщинам под страхом смертной казни запрещалось даже находиться на стадионе.

Во время проведения Олимпийских игр прекращались на всей территории Греции все распри и войны. Никто не имел права вступить на олимпийский стадион с оружием.

— Кто знает, сколько длились игры? ( Длились игры 5 дней)

— Запишем цифру 5. (слайд 4)

III. Актуализация знаний.

Цель: повторение пройденного; подготовка к предстоящей работе.

— Первые игры состоялись в 776 году до н.э. Запишите это число.

— Какое задание предложите выполнить с этим числом? (Ответы детей)

— Давайте разложим на сумму разрядных слагаемых. (Один ученик у доски)

776 = 700 + 70 + 6

— Назовите разрядные слагаемые.

— Ниже напишем даты 7. 02. 2014 и 23.02.2014. Кто сможет пояснить, что это за даты?

— Столицей ХХII зимних Олимпийских игр в 2014 году выбран г. Сочи. Период проведения с 7 по 23 февраля 2014 года.

— Какие символы Олимпиады знаете?

— В 1913 году появилась олимпийская символика. К ней относится священный огонь, который по традиции зажигают в Греции. (слайд 5-6)

А также девиз. Какой, вы узнаете, выполнив задание:  по отдельным деталям составьте высказывание одного из знаменитых людей. Для этого цифры в домике нужно перемножить и выполнить действие под домиком. Цифры в значениях выражений будут являться номерами слов.

56

73

88

93

+ 4 + 44 + 1 — 19

1) мускулы,

2) тренировке

3) способности

4) как

5) при

6) растут

7) и

— Проверим:

5 * 6 + 4 = 34 8 * 8 + 1 = 65

9 * 3 + 44 = 71 7 * 3 — 19 = 2

— Какое высказывание получилось?

(Способности, как и мускулы, растут при тренировке. В.А.Обручев, русский писатель)

— Как вы понимаете это высказывание?

— Молодцы. И вы можете хором прочитать девиз – символ Олимпиады — (показываю карточку) “Быстрее, выше, сильнее”.

Время мчится, будто птица,

И, наверно, в добрый час,

В гордой форме олимпийца

Выйдет кто-нибудь из вас.

А чтобы это произошло, нужно что делать? (заниматься спортом)

IV. Физкультминутка

(музыкальная)

V. Проблемная ситуация

Цель: создать проблемную ситуацию с целью выхода на тему.

— А ещё к символам Олимпиады относится 5 переплетённых колец. (слайд 7)

Этот символ мы сегодня с вами построим.

— Олимпийские кольца можно сравнить с какой геометрической фигурой? (окружностью)

— Что такое окружность? (линия, которая является границей круга)

— С помощью какого инструмента мы можем начертить окружность?

— Вспомните технику безопасности при работе с циркулем.

1. Во время работы быть внимательным, не отвлекаться и не отвлекать других;

2. Располагать циркуль на рабочем месте острым концом от себя; не оставлять циркуль в раскрытом виде;

3. Не держать циркуль вверх концами.

— С помощью циркуля в тетради поставьте точку и начертите окружность.

— Посмотрите, какие окружности у вас получились (учитель чертит окружность на доске).

— Почему они разные? (Ответы учеников).

— Сможем мы таким образом вырезать и получить символ Олимпиады — 5 колец? (нет, они разные)

— Что предлагаете?

VI. Сообщение темы и целей урока.

Цель: развитие умений ставить перед собой цели и реализовывать их.

— Прежде, чем изготовить кольца, мы должны узнать, что такое радиус окружности. Значит, какова тема урока? (Тема урока: Радиус окружности)

— Какие цели поставим перед собой? (узнать, что такое радиус и построить олимпийские кольца)

VII. Работа над новой темой.

Цель: получение новых знаний.

1. Работа в тетради.

— Когда мы чертим окружность, то сначала ставим точку. Это точка, которая называется как? (центром окружности) (слайд

— На окружности поставьте пять точек.

— Возьмите линейку и соедините точки с центром.

— Измерьте полученные отрезки.

— Что Вы заметили? (слайд 9)

(Они равны).

— В геометрии отрезок, который соединяет любую точку окружности с центром, называется радиусом и обозначается символом R.

— Начертите окружность радиусом 3 см.

2. Работа с учебником.

— Откройте учебник на странице 74. Прочитайте определения радиуса, которые предложили ребята (про себя).

— Подумайте, кто из друзей предложил верное определение радиуса.

Лера: Радиус — это отрезок, который соединяет две точки окружности.

Олег: Радиус — это линия внутри окружности.

Наташа: Радиус — это отрезок, который соединяет центр окружности с точкой окружности.

Рома: Радиус — это отрезок внутри окружности.

— Почему Лена/ Олег/ Рома дали неверное определение радиуса? Докажите.

3. Работа в группах.

— Приступим к изготовлению олимпийских колец. Разобьёмся на группы по 5 человек. Почему? (5 колец)

— Каждый член группы начертит окружность на одном из цветов бумаги. Какие мы берём цвета? (синий, черный, красный, желтый и зеленый)

— Итак, каждый ученик начертит окружность радиусом 5см и из этого же центра 6 см. Зачем? (чтобы получить кольцо). Вырежьте окружность.

— Как вырежем внутреннюю часть окружности? (Перегнуть пополам и вырезать).

— Как соединим? (разрежем каждое кольцо)

— Что означают 5 колец? (слайд 10) (Пять переплетенных колец – синее, черное, красное, желтое и зеленое, символизируют единство спортсменов пяти континентов)

— Сколько континентов на планете Земля? (6)

— А почему олимпийских колец 5?

А шестой – нежилой,

Там мороз не в меру крут,

В Антарктиде ледяной

Лишь полярники живут.

— А почему разные цвета у колец? Об этом мы узнаем на следующем уроке.

VIII. Итог. Рефлексия.

— А сейчас подведём итог. Какие знания потребовались, чтобы мы смогли сделать символ Олимпийских игр – кольца? (Ответы детей)

— А что такое радиус? ( Это отрезок, соединяющий центр окружности с какой-нибудь ее точкой. Радиусы равны).

— Любой ли отрезок мы можем назвать радиусом окружности?

— Сколько радиусов мы можем провести в одной окружности?

— Что было интересным на уроке?

— Достигли поставленных целей?

— Оцените свою работу на уроке. Для этого начертите окружность радиусом 1 см. Если вы всё поняли по теме и можете помочь другим, дорисуйте лицо такого смайлика.

— Если поняли тему урока, но нужна помощь — дорисуйте лицо такого смайлика.

— А если ничего не поняли — дорисуйте лицо такого смайлика.

1. Домашнее задание

С.74, №155 (3,4), выучить правило, что такое радиус.

7