Как изменить расстояние до недоступной точки

Вернуться к содержанию учебника

Вопросы для повторения к главе 11. Страница 266

Вернуться к содержанию учебника

Обновлено: 09.02.2023

Эту презентацию можно использовать при изучении темы » Применение подобия к доказательству теорем и решению задач. Определение расстояния до недоступной точки».

Предварительный просмотр:

Подписи к слайдам:

И змерение расстояния до недоступной точки

Луч зрения, касающийся обреза козырька (ладони, записной книжки), первоначально направлен на линию противоположного берега. Когда человек поворачивается, то луч зрения, подобно ножке циркуля, как бы описывает окружность, и тогда расстояние до предмета на том берегу равно расстоянию до предмета на этом берегу.

Определение высоты предмета. Задача №2 Своеобразный способ определения высоты дерева — при помощи зеркала . На некотором расстоянии от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку Д, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ЕД), во сколько раз расстояние ВС от зеркала до дерева больше расстояния СД от зеркала до наблюдателя. Почему?

Способ основан на законе отражения света. Вершина А отражается в точке А’ так, что АВ=А’В. Из подобия же треугольников ВСА’ и СЕД следует, что АВ’:ЕД=ВС:СД. В этой пропорции остается лишь заменить А’В равным ему АВ, чтобы обосновать указанное в задаче соотношение . Этот удобный и нехлопотливый способ можно применять во всякую погоду, но не в густом насаждении, а к одиноко стоящему дереву.

По теме: методические разработки, презентации и конспекты

Расстояние между двумя точками. Масштаб.

Урок математики в 5 классе по повторению понятий расстояния между двумя точками, длины пути, масштаба изображения. Урок -путешествие в столицу XXII зимних Олимпийских игр. Для работы на уроке ис.

«Расстояние между двумя точками. Масштаб.»

По данной теме представлен план-конспект урока и две презентации.

Урок . РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ.

Урок-игра. Применение масштаба на практике.

Урок решения задач практического характера с компьютерной поддержкой по тема «Определение расстояния до недоступной точки»

Урок решения задач практического характера с компьютерной поддержкой. 7-й класс. Тема: определение расстояния до недоступной.

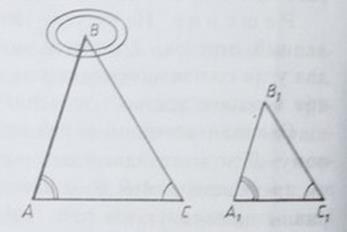
Предположим, что нам нужно найти расстояние от пункта А до недоступного пункта В. Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябии измеряем углы А и С. На листе бумаги строим какой-нибудь треугольник АıВıСı, у которого ∠Аı=∠А, ∠Сı=∠С, и измеряем длины сторон АıВı и АıСı этого треугольника. Так как треугольники АВС и АıВıСı подобны (по первому признаку подобия треугольников), то = , откуда получаем АВ= . Эта формула позволяет по известным расстояниям АС , АıСı и АıВı найти расстояние АВ.

Для упрощения вычислений удобно построить треугольник АıВıСı таким образом, чтобы АıСı:АС=1:1000. Например, если АС=130м, то расстояние АıСı возьмем равным 130мм. В этом случае АВ= * АıВı=1000* АıВı, поэтому, измерив расстояние АıВı в миллиметрах, мы сразу получим расстояние АВ в метрах.
Пример:

Пусть АС=130м, ∠А=73°, ∠С=58°. На бумаге строим треугольник АıВıСı так, чтобы ∠Аı=73°, ∠Сı=58°, АıСı=130мм, и измеряем отрезок АıВı. Он равен 153мм, поэтому искомое расстояние 153м.

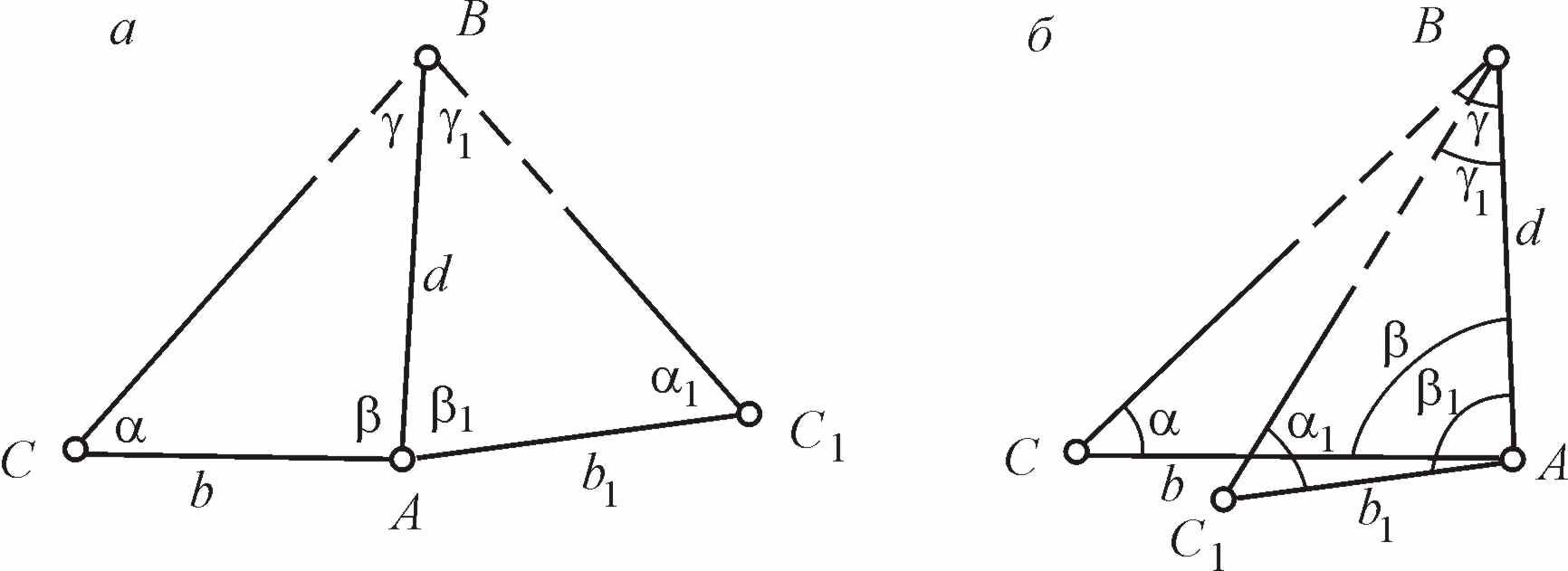
В практике инженерно-геодезических работ часто оказывается невозможным непосредственное измерение расстояний между двумя точками, когда встречается местное препятствие (река, котлован, здание и т. д.). Такие расстояние называют недоступными и определяют косвенным путем. Например, для определения недоступного расстояния d через реку измеряют длину базиса b (рисунок 6.12) и углы α и β. По теореме синусов из треугольника АВС получим

d / sin α = b / sin γ = b / sin(180 0 – α – β) = b / sin α + β) или d = b sin α / sin(α + β).

Для контроля расстояние d определяют еще раз из треугольника АВС₁. При отсутствии недопустимых расхождений из двух результатов принимают среднее арифметическое значение.

Точность определения недоступных расстояний во многом зависит от формы треугольника. Наилучшим считается равносторонний треугольник.

В том случае, когда на линии АВ нет видимости (рисунок 6.13), то для определения недоступного расстояния АВ измеряют длины сторон b₁ и b₂ и угол γ на точке С.

Расстояние d определяют по теореме косинусов:

Наиболее благоприятным считается вариант, когда b₁ = b₂ и угол γ близок к 180 о

sin α = b₂ sin γ / d; sin β = b₁ sin γ / d.

Углы α и β вычисляют для того, чтобы в точках А и В можно было указать направление линии d.

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

Описание презентации по отдельным слайдам:

Выполнил: Пустобоярова А. Учитель: Коряковцева Н.В. 2015г. МБОУ Вятская СОШ Определение расстояния до недоступной точки

Цель: Измерить высоту Воскресенской церкви несколькими способами, и выбрать способ, показывающий наиболее точный результат.

Для этого мне понадобится Рулетка Шест с вращающейся планкой Маленькое зеркало Астролябии

I способ Для определения высоты А1 Воскресенской церкви поставим на некотором А расстоянии от церкви шест АС В С С1 с вращающейся планкой и направим планку на верхнюю точку А1 церкви. Отметим на поверхности земли точку В, в которой прямая АА1 пересекается с поверхностью земли. Прямоугольные треугольники А1С1В и АСВ подобны по первому признаку подобия треугольников (‹С1=‹C=90˚)

Из подобия треугольников следует: А1С1 ВС1 АС ∙ ВС1 _______ = ____ А1С1 = ______ АС ВС , откуда ВС Измерив расстояния ВС1 и ВС и зная длину АС шеста, по полученной формуле определяем высоту А1С1 Воскресенской церкви. ВС1 = 56,3 м 1,6 ∙ 56,3 ВС = 1,5 м А1С1 = __________ ≈60 м АС = 1,6 м 1,5

II Способ Для определения высоты Воскресенской церкви вторым F способом расположим С маленькое зеркало D В на поверхности земли D и встанем на таком расстоянии, чтобы, A зеркало Е смотря в зеркало, отображалась вершина церкви F.

Из подобия треугольников следует: АС АD AC ∙ DE ___ = ____ EF = ______ ЕF DE AD Измерив все необходимые расстояния (АС=161см, ВС=12см, АD=120см, DЕ=30 м), по полученной формуле вычислим высоту Воскресенской церкви. ЕF= 161 ∙ 3000 =4025 см ≈ 41 м 120

Вывод: Итак, я рассмотрела 2 способа измерения высоты Воскресенской церкви. И наиболее точный результат, на мой взгляд, показывает 2 способ.

Цель: Измерить ширину реки Ухтанка

На местности выберем точки А и В и с помощью рулетки измерим длину отрезка АВ. АВ=40м Затем измерим с помощью астролябии углы А и В. С α=‹A=80° d β=‹B=74° А 80˚ 74˚ В Эти данные позволяют 40 м решить треугольник АВС и найти искомое расстояние d=AC

Сначала находим ‹C и sin‹C: ‹C=180°-α-β ‹C=180°-80°-74°=26° sin‹C=0,4384

Затем с помощью теоремы синусов находим d: АС = АВ АС=d; АВ=с; ‹B=β sin‹B sin‹C d= c · sinβ = 40∙0,9613 ≈ 87,7 м sin(α+β) 0,4384

Вывод: Итак, с помощью геометрической теоремы мне удалось найти ширину реки Ухтанка.

Краткое описание документа:

Создание проекта позволяет ученикам использовать свои знания на практике, таким образом знания переходят на новый уровень, кроме того, применение их в нестандартной ситуации закрепляет навыки, позволяет оценить их прочность. На этом уроке ученики применяют знания комплексно (геометрия + алгебра), тренируются в задачах на проценты.

• подготовка к ЕГЭ/ОГЭ и ВПР
• по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

• Курс добавлен 31.01.2022
• Сейчас обучается 35 человек из 22 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

• Для учеников 1-11 классов и дошкольников
• Бесплатные сертификаты учителям и участникам

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 613 288 материалов в базе

Материал подходит для УМК

Глава 7. Подобные треугольники

64. Практические приложения подобия треугольников

• ЗП до 91 000 руб.
• Гибкий график
• Удаленная работа

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

• 21.01.2018 7023
• PPTX 718.5 кбайт
• 77 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Коряковцева Нина Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

• Подготовка к ЕГЭ/ОГЭ и ВПР
• Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Новые курсы: преподавание блогинга и архитектуры, подготовка аспирантов и другие

Время чтения: 16 минут

Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ

Время чтения: 1 минута

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Минтруд предложил упростить направление маткапитала на образование

Время чтения: 1 минута

Время чтения: 2 минуты

ГИА для школьников, находящихся за рубежом, может стать дистанционным

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Читайте также:

  

• Чем отличается свинг от болеро в школе

  

• Какие чувства испытывает владимир дубровский в доме своего отца где хозяйничают приказные кратко

  

• Точка роста в доу что это

  

• Каким было отношение казачества к десанту улагая кратко

  

• Что такое глазомерная съемка кратко

ПРОСТЫЕ СПОСОБЫ ИЗМЕНЕНИЯ ВЫСОТЫ ОБЪЕКТОВ И РАССТОЯНИЯ ДО НЕДСТУПНЫХ ПРЕДМЕТОВ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.

В современном мире мы определяем высоту объектов или расстояние с помощью различных приборов и инструментов (электронные и лазерные высотомеры, рулетки, т.п.). А можно ли измерить высоту предмета, не используя специальные приборы?

Так появилась цель моей работы: изучить методы измерения высоты объектов, применить их на практике.

Глава I.

Объект исследования: высота дерева, высота школы.

Предмет исследования: методы измерения высоты предметов.

Задачи:

изучить интернет ресурсы и литературу по проблеме исследования;

изучить различные методы измерения;

провести практическое исследование по измерению высоты дерева и здания;

найти наиболее точные способы измерения высоты дерева и здания, применимые на практике;

познакомить одноклассников с результатами моего исследования.

провести анкетирование среди учащихся.

Достижение поставленной цели предполагает решение следующих задач:

План работы

1. Продумать способы выполнения эксперимента, для помощи использовать литературу и научно-популярные сайты Интернет.

2. Выбрать несколько способов, доступных для выполнения во время проведения эксперимента.

3. Взять необходимое оборудование.

4. Выполнить эксперимент, производя необходимые расчеты.

5. Оформить результаты работы.

6. Проанализировать результаты и дайте их обоснование.

7. Сделать выводы.

Практическая значимость определяется возможностью использования подручных средств для измерения высоты объектов и расстояния до недоступной точки.

Гипотеза: Предположим, что высоту здания или дерева возможно измерить без специальных приборов.

Глава II.

Измерение высоты объектов

При проведении исследования я познакомился с различными методами измерения высоты предметов, их довольно много, я выбрал наиболее простые и интересные для меня:

Способ по фотографии;

Способ «Воздушный шарик»;

С помощью прямоугольного треугольника;

С помощью шеста (Метод Жюль Верна);

С помощью карандаша;

С помощью тени;

С помощью зеркала

С помощью самодельного высотомера;

С помощью лазерного высотомера.

1.Способ «Фотография»

Высота здания во столько раз больше роста человека, во сколько раз высота дерева на фотографии больше роста человека на фотографии.

Оборудование: фотоаппарат, рулетка, помощник.

Нужно встать рядом со зданием, чтобы на фотографии были видны в полный рост человек и здание.

На фотографии измеряем высоту здания -25,7см, рост человека -4,6см.

Чтобы вычислить высоту здания нужно рост человека -152см умножить на высоту здания на фотографии и полученный результат разделить на рост человека на фотографии:

= = 8,492 м

2. Способ «Воздушный шарик»

Нужно сравнить высоту дерева с длиной нити, которая привязана к воздушному шарику.

Оборудование: воздушный шарик, наполненный гелием, рулетка.

Шарик нужно привязать к нитке и отпускать ее до тех пор, пока шарик не поднимется до верхушки дерева. Затем сделать на нитке отметку, опустить шарик и измерить длину нити.

Получилось примерно 3,56 м.

3. С помощью прямоугольного треугольника

Оборудование: равнобедренный прямоугольный треугольник, рулетка.

В ходе эксперимента получатся два подобных треугольника ABC и A B1C1.

A B1C1 – равнобедренный, значит и ABC тоже равнобедренный ВС = АС, где ВС часть здания равна расстоянию АС от человека до здания. Чтобы найти высоту всего здания нужно к измеренному расстоянию АС прибавить рост человека (до уровня глаз).

Ход работы

1. Держа треугольник вертикально, отойти от школы на такое расстояние, при котором, глядя вдоль гипотенузы, можно увидеть крышу здания.

2. Измерить расстояние от места измерения до школы – 7,27 м.

3. Прибавить к полученному числу свой рост до уровня глаз – 1,32м.

Результат: высота здания – 8,59 м.

4. Метод Жюль Верна: при помощи шеста

При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, который был описан в книге Жюль Верна «Таинственный остров».

Решение: Нужно вбить в землю шест, лечь на землю так, чтобы было видно верхний конец шеста и верхушку измеряемого предмета. Измерить расстояние от шеста до предмета, измерить высоту шеста и расстояние от макушки человека до основания шеста.

Формула: H = (высота шеста · расстояние от макушки человека до предмета) : расстояние от макушки до шеста.

В нашем случае высота дерева получилась:

H = (высота шеста (деревянный метр) 1 м · расстояние от макушки человека до предмета) : расстояние от макушки до шеста = 1м*4,36 м / 1,2 м = 3,57 м.

5. По длине тени, падающей от предмета (Метод Фалеса):

Так как лучи солнца можно считать практически параллельными, то тень от здания во столько же раз длиннее тени человека, во сколько раз здание выше человека.

Так Фалес измерил высоту пирамиды Хеопса.

Чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, — именно следующие два (из которых первое Фалес открыл сам):

1. Что углы при основании равнобедренного треугольника равны, и обратно – что стороны, лежащие против равных углов треугольника, равны между собою;

2. Что сумма углов всякого треугольника равна двум прямым углам.

Только вооружённый этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и следовательно, вершина пирамиды, середина её основания и конец её тени должны обозначить равнобедренный треугольник.

Этим простым способом очень удобно, казалось бы, пользоваться в ясный солнечный день для измерения одиноко стоящих деревьев, тень которых не сливается с тенью соседних. Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в

околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде (по равнобедренному треугольнику) применим не всегда.

Но данный метод применим и к подобным треугольникам.

Здание и человек расположены перпендикулярно к земле, а лучи солнца падают под одинаковыми углами на землю. Образуются подобные треугольники, стороны которых пропорциональны.

1 способ: Тень здания и человека находятся на одной линии.

= = 8,68 м

2 способ. Человек стоит так, что не попадает в тень здания.

Здание и человек расположены перпендикулярно к земле, а лучи солнца падают под одинаковыми углами на землю. Образуются подобные треугольники, стороны которых пропорциональны. Отношение высоты здания к росту человека равно отношению длины тени здания к длине тени человека.

= = 8,69 м

6. Метод измерения высоты предмета с помощью зеркала (лужи).

Этот способ можно удачно применять после дождя, когда на земле появляются лужи.

В моем случае лужу заменяет обычное зеркало, которое я положил между мной и зданием школы. После этого я нашел точку, из которой видно отражение вершины здания. Высота здания будет во столько раз выше меня, во сколько расстояние от него до зеркала больше, чем расстояние от зеркала до меня.

= = 8,63 м

7. Метод измерения высоты предмета с помощью карандаша

Этот способ измерения высоты самый легкий. Так как для него необходим карандаш, помощник, и одно измерение. Решение: Встать от предмета на расстояние, чтобы видеть его

целиком – от основания до верха. У основания установить помощника. Вытянуть перед собой руку с зажатым в кулаке карандашом. Прищурив один глаз, подвести кончик карандаша к вершине предмета. Теперь переместить ноготь большого пальца на карандаше так, чтобы он оказался под основанием предмета. Повернуть кулак на 90 градусов, чтобы карандаш оказался параллельно земле. При этом ноготь оставить в точке основания. Помощник должен отойти от предмета. Когда он достиг точки, на которую указывает острие карандаша, необходимо подать сигнал, чтобы он остановился. Измерить расстояние от предмета до места, где застыл помощник – это высота предмета.

Результат: высота здания – 8,63 м.

8. С помощью высотомера, сделанного своими руками

Высоту можно измерить специальным прибором — высотомером.

Для изготовления данного прибора потребуется:

Плотный белый картон, линейка, ручка, карандаш, ножницы, нитка, грузик, игла.

1. Из белого картона чертим и вырезаем квадрат размером 15х15см.

2. Делим квадрат на два прямоугольника: 5х15 см, 10х15 см.

3. Прямоугольник 10х15 см делим на две части: 5 см и 10 см.

4. На большей части с длиной 10 см, наносим сантиметровые деления и обозначаем их десятичной дробью (0,1;0,2;…).

В точке В иглой делаем отверстие и протаскиваем нитку с грузиком, а затем закрепляем нитку сзади.

Для того, чтобы было удобнее смотреть, отгибаем верхний прямоугольник от основания.

На нём с боков отгибаем два прямоугольника размером 3х5 см и прорезаем два отверстия с разным диаметром: одной поменьше — у глаза, другой побольше – для того, чтобы навести на вершину здания.

Правила в изготовлении и использовании прибора:

Расстояние от измеряемого объекта должно быть точным.

Точно наносить разметку в 1 см.

Эксперимент показал, что метод определения высоты предмета с помощью авторского высотомера является более точным и удобным.

9. С помощью электронных и лазерных высотомеров и дальномеров.

Принцип работы лазерного дальномера (рулетки) довольно простой и основан он на способности твердых тел отражать сигналы различного типа – практически так же работает и масса других подобных приборов. Например, эхолот или металлоискатель – разница между ними заключается только в типе используемого излучения. В случае с дальномером используется сконцентрированный световой поток, именуемый лазерным лучом. Специальный излучатель рулетки выпускает луч, который отражается от твердого тела и возвращается назад – отражение улавливает приемник и на основе задержки во времени между выпущенным и принятым сигналом рассчитывается расстояние. Погрешность при этом, в зависимости от расстояния до цели, может составлять максимум 1мм.

Я измерил высоту школы с помощью лазерного дальномера, результат – 8,54 м.

Изучая методы измерения высоты объектов, мне захотелось самому составить задачи, чтобы по их данным определить высоту недоступных объектов. Представлю вам самые интересные на мой взгляд.

Задача 1. В нашем городе Сызрань есть Кремль. Основан Кремль в 1683 году воеводой Григорием Козловским. Мне стало интересно сравнить точную высоту нашего Кремля с высотой, определенной одним из рассмотренными в проекте методов, а также сравнить с другими. Я стал искать информацию, в каких городах есть Кремли, составил таблицу.

Измерить высоту Сызранского Кремля я решил с помощью своего прибора «высотомера»:

Отходим от кремля на 100 шагов, то есть BC1= 50 м. Измерил показания прибора:

Смотрим через высотомер так, чтобы глядя вдоль линии АВ, через меньшее отверстие в большее, видеть крышу школы D1.

Наклоняясь, грузик пересекает линию EC и образует треугольник BCD, который является подобным к треугольнику BC1D1.

= = 20 м

Для определения высоты школы (D1L ) к найденному значению D1C1 прибавить свой рост (до уровня глаз):

D1L=20+1,32= 21,32 м

Результат получился очень точный, так как настоящая Кремля 21 м.

Также я решил с помощью своего прибора «высотомера» измерить памятник основателю города воеводе Григорию Козловскому. Отходим от памятника на 50 шагов, то есть BC1= 25 м. Измерил показания прибора:

= = 3,75 м

Для определения высоты школы (D1L ) к найденному значению D1C1 прибавить свой рост (до уровня глаз):

D1L=3,75+1,32= 5,07 м

Сама статуя Козловского в высоту около 3 метров, а вместе с гранитным постаментом высота памятника составит порядка 5 метров.

Значит мои измерения точные.

Заключение.

Для выполнения эксперимента «Измерение высоты недоступных предметов при помощи подручных средств» я использовал несколько методов. Получились следующие результаты:

Я рассмотрел такие способы измерения высоты дерева как «Карандаш», «Равнобедренный треугольник», «Шест», «Авторский высотомер», «С помощью лазерного высотомера».

Способы «Фотография» и «Воздушный шарик» были применены к данному дереву и зданию для сравнения результатов измерений и вычислений.

Способы основаны на свойствах подобных треугольников и на определении длины отрезка.

Самый доступный из этих способов — способ «Воздушный шарик». Для этого способа нужна безветренная погода.

Самый экономичный способ — с помощью карандаша, так как требует минимального оборудования. Нужна одна рулетка.

Для способа «Фотография» нужен хороший фотоаппарат, фотограф, фотографии нужно печатать.

Самым сложным в исполнении оказался способ «Тень». Измерения нужно проводить в ясный солнечный день. Было сделано несколько неудачных попыток. Солнце не стоит на месте. Длина тени изменяется быстро.

Способ измерение высоты здания с помощью зеркала оказался немного сложным, так как поймать отражение крыши здания в зеркале сложно.

Самым точным и самым затратным является способ «С помощью лазерного высотомера». Погрешность при этом, в зависимости от расстояния до цели, может составлять максимум 1мм.

Высотомер, сделанный своими руками, является доступным и экономичным способом, и, как показали измерения, результат получается очень точный. Не сложен в изготовлении, удобно носить с собой.

Задачи подобного плана на измерение высоты недоступных предметов при помощи подручных средств встречаются в задачах для подготовки к ОГЭ.

Мое продвижение:

— я научился измерять высоту недоступных предметов при помощи подручных средств;

— самостоятельно выбирать метод, наиболее подходящий для определенных условий, и применять на практике, а также использовать в решении задач ОГЭ;

Выводы:

цель работы достигнута, я узнал много нового и важного методах измерения высоты недоступных предметов при помощи подручных средств.

Анкетирование

После совместной работы я опросил своих одноклассников, понравилось ли им работать с диаграммами, составлять задачи. Предложил им ответить на вопросы анкеты:

1) Знаешь ли ты как можно измерить высоту недоступных предметов при помощи подручных средств?

2) Хотел бы ты научиться измерять высоту недоступных предметов при помощи подручных средств?

3) Интересно ли тебе изготовление и использование высотомера, сделанного своими руками?

По результатам анкетирования, я сделал вывод, что моим одноклассникам интересна тема «Измерение высоты недоступных предметов при помощи подручных средств». На кружке по математике можно продолжить работу по изучению других методов изменения высоты недоступных предметов.

Я буду продолжать работу по данной теме, изучать методы изменения высоты недоступных предметов еще не знаю.

Данный проект может быть использована на уроках математики 5 – 9 классах, во внеурочной деятельности.

Список литературы:

Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняков, И. И. Юдина. Геометрия. М. Просвещение. 2005г. 138с.

И. Баврин. Большой справочник школьника. Математика. М. дрофа. 2006г. 435с.

Сергеев И.Н., Олехник с.Н., Гашков С.Б. Примени математику. – М.: Наука. Гл. ред. физ.-мат. лит.,1989. – 240с.

Ресурсы Интернета.

Просмотров работы: 430

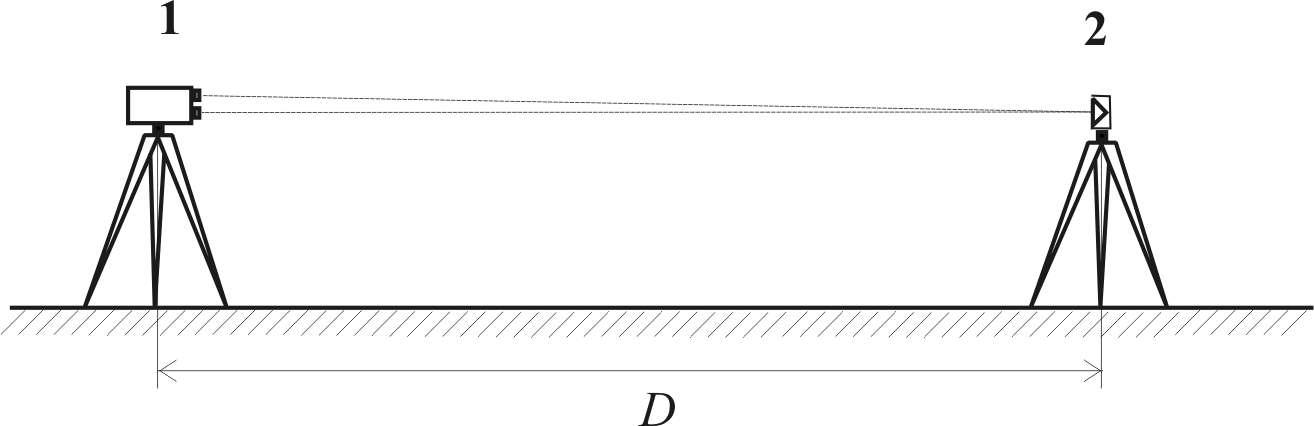
Если препятствие (река, обрыв, здание)
делает расстояние недоступным для
измерения лентой, то его измеряют
косвенным методом.

Так, для определения недоступного
расстояния dизмеряют лентой длину
базисаb(рис. 8.3, а, б) и углыи. ИзABCнаходят

d
= b sin

/ sin (
+ ),

где
учтено, что sin

= sin
(180)
= sin
(
+ ).

Рис. 8.3. Определение
недоступного расстояния

Для
контроля расстояние d
определяют ещё раз из треугольника ABC₁
и при
отсутствии недопустимых расхождений
вычисляют среднее.

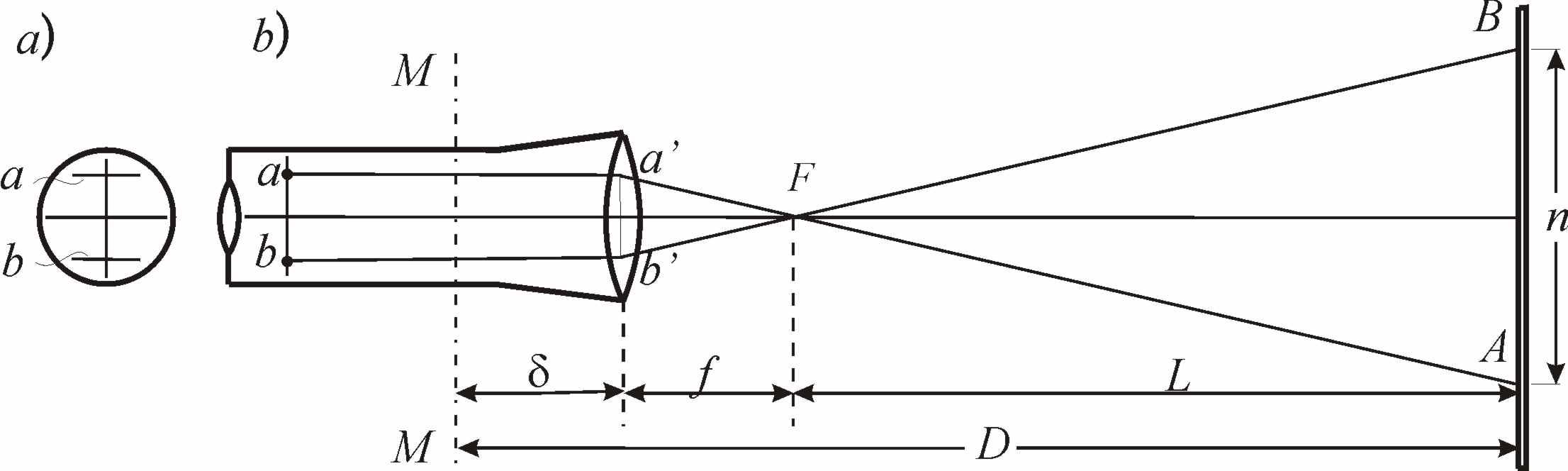
8.3. Нитяный дальномер

Теория
нитяного дальномера.
Зрительные трубы многих геодезических
приборов снабжены нитяным дальномером.
Сетка нитей зрительной трубы, кроме
основных штрихов (вертикальных и
горизонтальных), имеет дальномерные
штрихи a
и b
(рис. 8.4, а).
Расстояние D
от оси вращения прибора MM
(рис. 8.4, б)
до рейки AB
равно

D
= L
+ f
+ 
,

где
L

расстояние от фокуса объектива до рейки;
f

фокусное расстояние; 

расстояние между объективом и осью
вращения прибора.

Лучи,
идущие через дальномерные штрихи сетки
a
и b
параллельно оптической оси, преломляются
объективом, проходят через его фокус F
и проецируют изображения дальномерных
штрихов на точки A
и B,
так что дальномерный отсчёт по рейке
равен n.
Обозначив расстояние между дальномерными
штрихами p,
из подобных треугольников ABF
и abF
находим L = n
f / p. Обозначив
f / p = K
и f + 
= c , получаем

D
= K
n
+ c
,

где
K

коэффициент дальномера и
c 
постоянная дальномера.

Рис. 8.4. Нитяный
дальномер: а) – сетка нитей;б)
– схема определения расстояния

При
изготовлении прибора f
и p
подбирают такими, чтобы K=100,
а постоянная c
была близкой к нулю. Тогда D
= 100 n.

Точность
измерения расстояний нитяным дальномером

1/300.

Определение
горизонтального проложения линии,
измеренной нитяным дальномером.
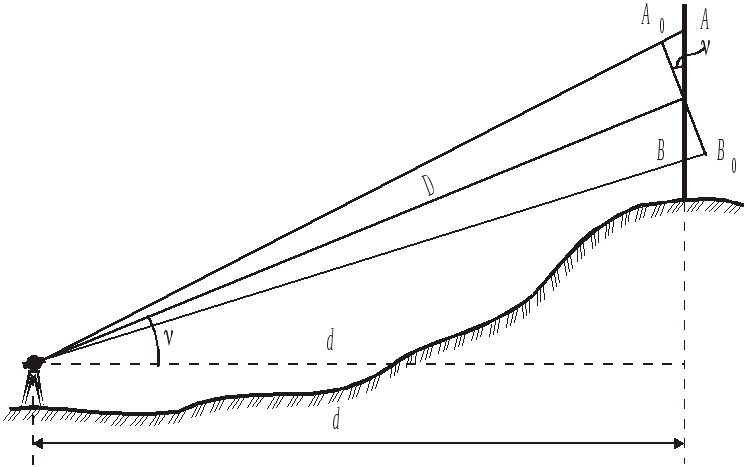
При измерении наклонной линии отсчёт
по рейке это отрезок n
= AB (рис. 8.5).
Если бы рейку наклонить на угол ,
то отсчёт был бы равен n₀
= A₀B₀
= n cos
и наклонное расстояние D=Kn₀+c
= Kncos+c.

Рис.
8.5. Измерение нитяным дальномером
наклонного расстояния

Умножив
наклонное расстояние D
на cos,
получим горизонтальное расстояние d
= K
n
cos²

+ c
cos
.

Прибавив
и отняв с
cos²,
после преобразований получим

d
= (Kn
+ с)
cos²
+ 2c
cos
sin²(2).

Вторым слагаемым по его малости пренебрежем. Получим

d
= (Kn
+ с)
cos²
.

Вычисления
упрощаются, если воспользоваться
составленными с использованием этой
формулы «Тахеометрическими таблицами».

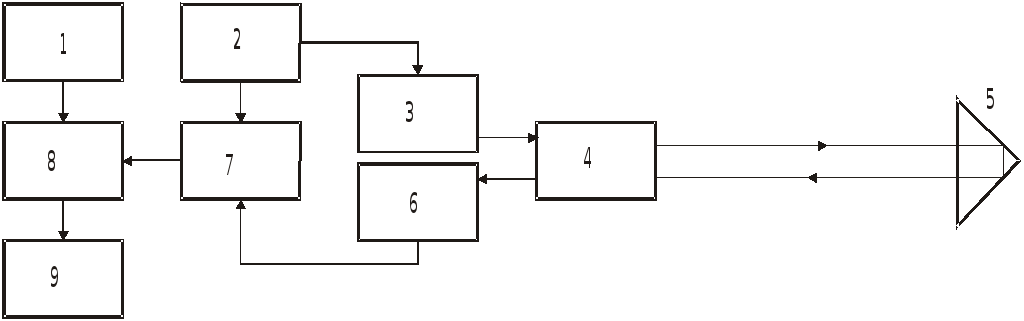
8.4. Светодальномеры, электронные тахеометры

Светодальномер
–
прибор, измеряющий расстояние по времени
прохождения его световым сигналом.

В
комплект светодальномера входят
приёмопередатчик и отражатель.
Приемопередатчик 1 (рис. 8.6) устанавливают
на штативе на одном конце измеряемой
линии, а отражатель 2 на специальной
вешке или тоже на штативе – на другом.

Рис.
8.6. Измерение расстояния
светодальномером

Приёмопередатчик
излучает световой сигнал, принимает
его после возвращения от отражателя,
измеряет время
t, прошедшее
от излучения до приёма, и вычисляет
расстояние

D
= vt/2.

Здесь
v
– скорость света (при средних условиях
v 
299710 км/с).

Время
t
необходимо измерять с высокой точностью.
Так, для точности в расстоянии 1 см время
надо знать с ошибкой не более 10^-10
с. Измерение
времени выполняется фазовым или
импульсным методом.

Рис. 8.7. Схема
импульсного светодальномера

В
импульсном светодальномере (рис. 8.7)
лазерный источник излучения 3 под
воздействием генератора импульсов 2
периодически посылает через объектив
4 световой импульс. Одновременно
переключатель 7 запускает счётчик 8
временных
импульсов, поступающих от высокочастотного
генератора 1. Световой импульс, отразившись
от отражателя 5, поступает на преобразователь
6, который через переключатель 7
останавливает счётчик 8. Число импульсов,
сосчитанное счётчиком 8, пропорционально
прошедшему времени и, следовательно,
измеряемому расстоянию. Для повышения
точности измерения выполняются
многократно и результаты осредняются
процессором 9. Измеренное расстояние
высвечивается на табло.

Измеренное
расстояние исправляют поправками за
атмосферное давление, температуру и
влажность воздуха, влияющие на скорость
света. Для получения горизонтального
проложения вводят поправку за наклон.

Конструктивно
приемопередатчик представляет собой
отдельный прибор, насадку на теодолит
или блок, входящий в состав электронного
тахеометра.

По
их назначению принято различать
светодальномеры для построения
государственных геодезических сетей,
светодальномеры для прикладной геодезии
и маркшейдерии и светодальномеры для
топографических съёмок.

Точность
топографических светодальномеров 2 –
3 см, а применяемых в прикладной геодезии
2 – 3 мм.

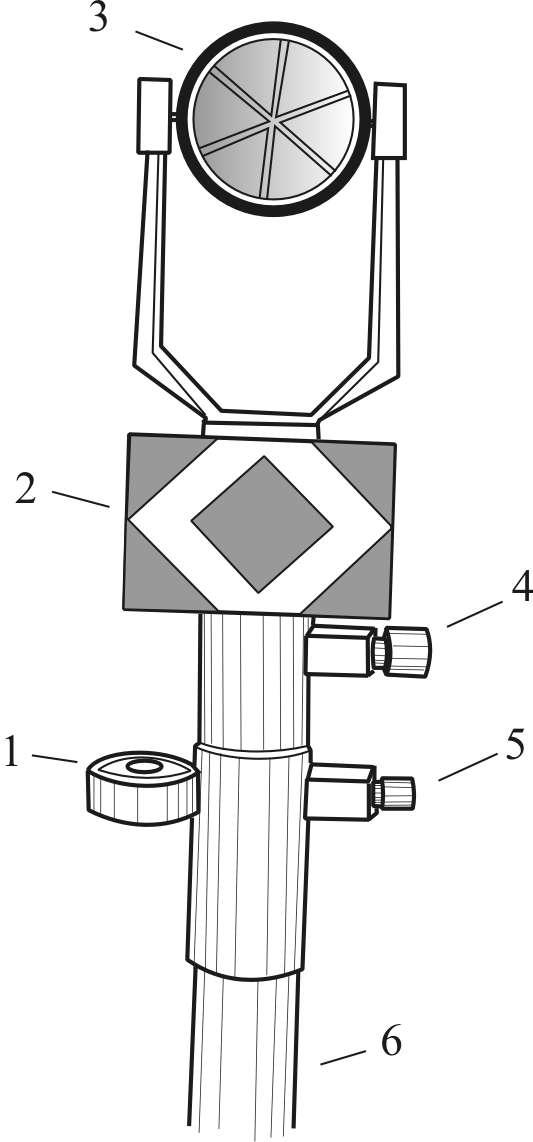
Отражатели
бывают призменные и плёночные. Основным
элементом призменного отражателя (рис.
8.8 б)
является стеклянная трипельпризма
отражающая световые лучи в тех
направлениях, откуда они пришли. Для
увеличения дальности измерений
изготавливают многопризменные отражатели.

Плёночный
отражатель представляет собой отражающую
свет пластиковую плёнку размером 11
см и больше, на которую нанесены штрихи
(например, вертикальный и горизонтальный).
Дальность измерений с пленочными
отражателями меньше, чем с призменным.
Но зато пленочный отражатель можно
закрепить там, где установить призменный
отражатель невозможно, например –
приклеить в нужном месте на сооружение.
Кроме того, пленочные отражатели гораздо
дешевле призменных. При выполнении
угловых измерений центр штрихов на
отражателе служит визирной целью.

Существуют
светодальномеры, использующие диффузное
отражение сигнала от предметов и не
требующие отражателя. Таким дальномером
является «лазерная рулетка» Disto
фирмы Leica (Швейцария). Прибор используют
без штатива, с руки. Световой луч наводят
на нужные объекты и на шкале читают
расстояния до 200 м с точностью 1,5 мм.

Электронные
тахеометры.
Электронным тахеометром (рис. 8.8)
называется прибор, объединяющий в себе
светодальномер, электронный теодолит
и микро-ЭВМ. Светодальномер прибора
измеряет расстояние до отражателя.
Датчики горизонтального и вертикального
кругов электронного теодолита выдают
отсчеты по кругам. Отсчеты расстояния
и углов передаются на индикацию и
регистрацию. Микро-ЭВМ обеспечивает
возможность решения целого ряда
стандартных геодезических задач, для
чего прибор снабжен набором необходимых
прикладных программ. Полученная в
результате измерений и вычислений
информация высвечивается на цифровом
табло, а также регистрируется во
внутренней памяти прибора и на флэш-картах
для последующего ввода в компьютер для
дальнейшей обработки.

Электронный
тахеометр имеет, как правило, две панели
управления, расположенные с обеих сторон
прибора. На панели управления расположены
дисплей и клавиатура для управления
процессом измерений и ввода информации
вручную. Ввод информации и управление
возможны и с дистанционного пульта
управления (контроллера). Тахеометр
может иметь световой указатель створа,
облегчающий установку вехи с отражателем
на линию, по которой направлена труба
прибора.

Рис. 8.8. Электронный
тахеометр: а) – основной прибор;б)однопризменный
отражатель: 1 – уровень; 2 – визирная
марка; 3 – призма; 4, 5 – закрепительные
винты; 6 — штанга.

Программное
обеспечение электронных тахеометров
поддерживает решение достаточно широкого
круга задач. Обычно бывает предусмотрен
ввод и сохранение данных о станции: ее
координат, номера точки, высоты прибора,
имени оператора, даты, времени, сведений
о погоде (ветре, температуре, давлении).
По результатам измерений выполняется
вычисление горизонтальных и вертикальных
углов, дирекционных углов линий,
горизонтальных проложений, превышений,
высот точек, где установлен отражатель,
приращений координат, плоских и
пространственных координат наблюдаемых
точек. Предусмотрена возможность
вычисления координат по результатам
засечек, вычисления расстояния до
недоступной для установки отражателя
точки и координат недоступной точки,
определения высоты недоступного объекта.
Для обеспечения разбивочных работ
служат программы вычисления угла и
расстояния для выноса точки с заданными
координатами. При решении задач
учитывается рефракция световых лучей
в атмосфере.

В
настоящее время на рынке имеется широкий
выбор электронных тахеометров, выпускаемых
разными фирмами, в числе которых Уральский
оптико-механический завод (Россия),
Sokkia
(Япония), Trimble
(США), Leica
(Швейцария) и др. Характеристики приборов
разных марок различаются. Средние
квадратические погрешности измерения
углов тахеометров лежат в пределах от
1
до 6.
Максимальные дальности измерения
расстояний на однопризменный отражатель
различаются от 1600 до 5000 м. При этом,
точность измерений в среднем характеризуется
ошибкой 2 мм + 210^-6
D,
где D
– расстояние. Многие из электронных
тахеометров позволяют измерять расстояния
без отражателя. Дальность таких измерений
меняется в разных приборах в пределах
70 – 350 м.

Использование
электронных тахеометров значительно
повышает производительность труда,
упрощает и сокращает время на обработку
результатов измерений, исключает такие
ошибки исполнителя, которые имеют место
при визуальном взятии отсчетов, при
записи результатов измерений в журналы,
в вычислениях. При работе с электронным
тахеометром отпадает необходимость
иметь калькулятор для выполнения полевых
вычислений.

Светило науки — 7536 ответов — 59701 помощь

Недоступное (неприступное) расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно.

Метод определения недоступного расстояния используется в тех случаях, когда надо измерить наклонное расстояние, горизонтальное проложение и разность высот между начальной точкой и любыми другими точками без перемещения инструмента.
Последняя измеренная точка может быть задана, как начальная для последующих измерений.
Результат измерений может быть выведен как градиент (уклон в %) между двумя точками.
 

Измерение расстояний между точками

Вычисление по введенным координатам

Смена начальной точки

Последняя измеренная точка может быть задана, как начальная для последующих измерений.

1.    Наблюдайте начальную точку и отражатель в соответствии с действиями, описанными в предыдущем разделе. «Измерение расстояний между точками»
2.    После измерения визирных целей нажмите клавишу [СМЕНА], затем клавишу [ДА].
Для отмены измерения нажмите клавишу [НЕТ].

Последняя измеренная точка становится новой начальной точкой.
Выполните процедуру определения недоступного расстояния.