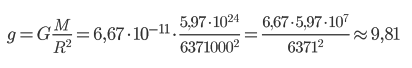Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу с силой, которая прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6,67 · 10−11м3 · кг−1 · с−2
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Ускорение свободного падения
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
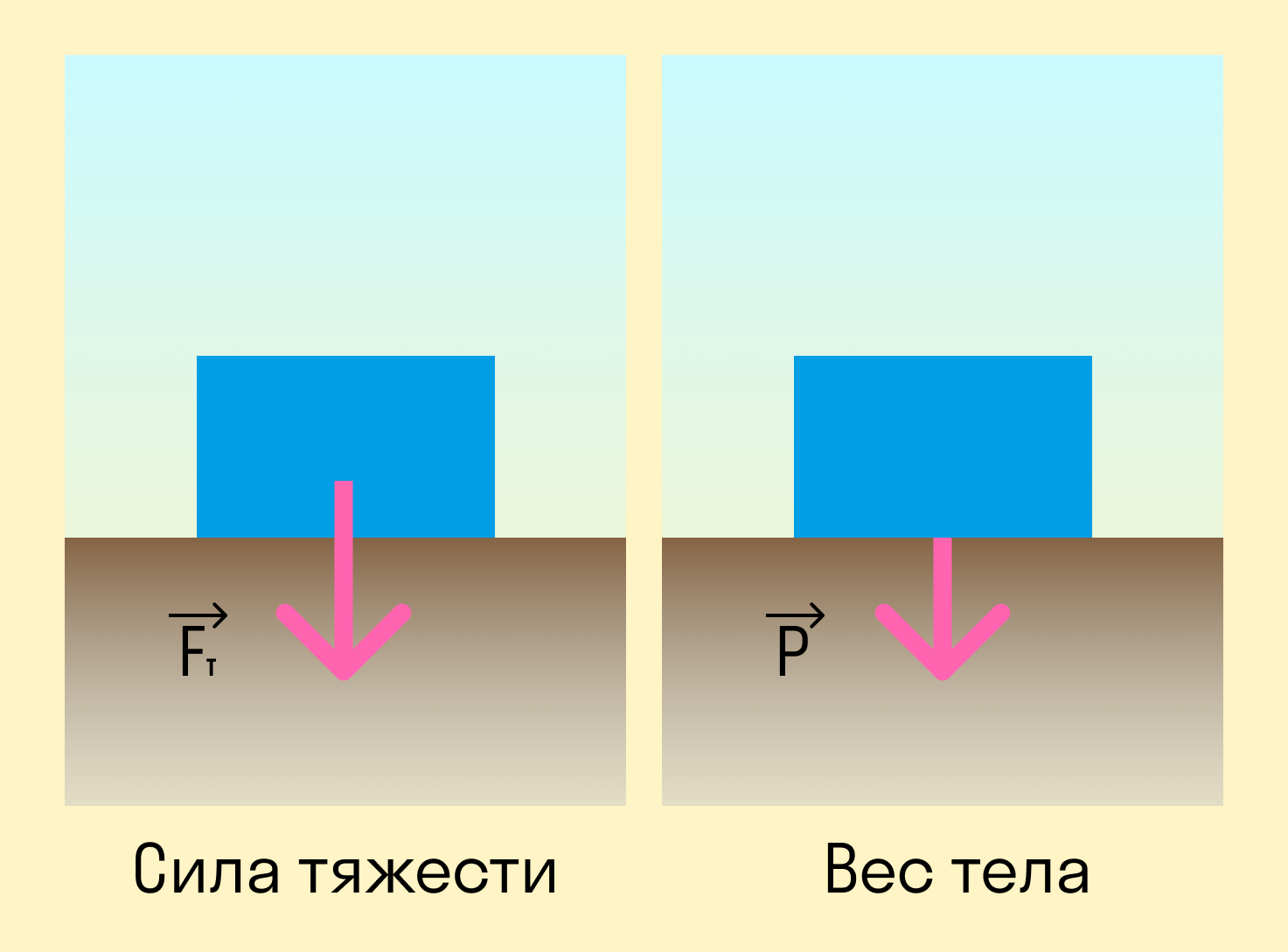
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести
F = mg
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с2, но подробнее об этом чуть позже. 😉
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору или подвес. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу тела левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Формула ускорения свободного падения
g — ускорение свободного падения [м/с2]
M — масса планеты [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6,67 · 10−11м3 · кг−1 · с−2
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Ускорение свободного падения на разных планетах
Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.
Для этого нам понадобятся следующие величины:
- Гравитационная постоянная
G = 6,67 · 10−11м3 · кг−1 · с−2 - Масса Земли
M = 5,97 × 1024 кг - Радиус Земли
R = 6371 км
Подставим значения в формулу:
Есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают то же значение, что мы указали выше: g = 9,81 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 м/с2, в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.
Например, ускорение свободного падения в Алматы меньше, чем в Осло. Значит, если два яблока упадут с одинаковой высоты в этих городах, то к концу падения яблоко в Осло наберет большую скорость, чем яблоко в Алматы.
Но разве это не зависит еще и от массы предмета?
Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

работа №2
Изменение ускорения
свободного падения тел
Цель:
-
Познакомиться
с теоретическим рассмотрением факторов,
влияющих на ускорение свободного
падения; -
Убедиться,
что свободное падение – равноускоренное
движение. Определить ускорение свободного
падения.
Введение
Еще
в древности Аристотелем было высказано
утверждение, будто более тяжёлое тело
падает быстрее лёгкого во столько раз,
во сколько раз оно тяжелее. Это ложное
утверждение принималось за истинное
около двух тысяч лет. Только в 1583 году
Галилей экспериментально показал, что
при отсутствии сил сопротивления (или
когда они пренебрежно малы по сравнению
с весом тела) все тела падают с одинаковым
ускорением. Теоретическое объяснение
этому факту получено Ньютоном почти
сто лет спустя и опубликовано в 1687 году.
Объяснение базируется на открытых
Ньютоном законе всемирного тяготения
и законах динамики.
Закон
всемирного тяготения:
две материальные точки массой m1
и
m2
притягиваются
силой Fm,
прямопропорциональной произведению
их масс, и обратно пропорционально
квадрату расстояния r
между ними:
(1)
где
G
– гравитационная
постоянная, равная 6,67·10-11Нм2/кг2.
Если
тяготеющие тела представляют шарообразное
образование со сферическим симметричным
распределением плотности, то сила
тяготения между ними вычисляется по
(1), но только в этом случае есть расстояние
между центрами шаров.
Силы
притяжения тел Землёй в общем значении
ускорения свободного падения g
превышает 99%. Опытным путём установлено,
что g
в среднем растёт по мере увеличения
широты места: она измеряется от 9,78м/с2
на
экваторе до
9,03 м/с2
на
полюсе. К тому же в пределах одной и той
же широты порой заметно изменяется с
долготой, местами колеблясь около
среднего значения.
Перейдём
к теоретическому численного значения
g.
Ускорение свободного падения – падение
тел без сопротивления – определяется
относительно земли. Поэтому мы выберем
систему отсчёта, жестко связанную с
Землёй. Начало отсчёта поместим в центр
Земли. Для простоты рассуждения положим
сначала, что Земля – шар с сферическим
симметричным распределением плотности,
то есть во всех точках, относящих на
одинаковое расстояние от центра Земли,
плотность одинаковая. Обозначим радиус
Земли через R,
её массу буквой M,
на широте φ
на поверхности Земли возьмём покоящееся
тело массой m.
На тело действует сила тяготения Fm
направленная к центру и равная, согласно
(1)
(2)
Так
как Земля вращается вокруг своей оси,
то связанная с ней система отсчёта
неинерциальная. В неинерциальных
системах отсчёта на тело действует ещё
сила инерции
.
Где а
– ускорение тела, а а*
— ускорение того же тела, но измерено в
неинерциальной системе отсчёта.
На
поверхности Земли на тело в состоянии
покоя, кроме силы тяготения и силы
инерции, действует ещё сила реакции
опоры Q.
Так как под действием всех этих трёх
сил тело покоится, то их сумма равна
нулю:
(3)
Векторная
сумма сил тяготения и сил инерции,
действующей на покоящееся тело, называется
силой тяжести. Наряду с силой тяжести,
вводится вес тела Р,
как сила, с которой тело действует на
опору. По третьему закону Ньютона можно
записать, что P=-Q.
В случае покоящегося тела выполняется
уравнение.
Иными словами, вес покоящегося тела
равен силе тяжести.
Сила
инерции, действующая на покоящееся тело
на поверхности земли, направленно в
радиальном направлении от оси вращения.
В данном случае она называется центробежной
силой инерции. Вычисляется по формуле:
(4)
где
ω=7,3·10-5рад/с,
а
R1
– радиус-вектор,
проведённый от оси вращения до данного
тела.
Если
теперь убрать опору, то есть убрать силу
Q,
то тело под действием силы тяжести, то
есть
,
начнёт свободно падать с ускорением,
определённым по второму закону Ньютона:
(5)
Из
рисунка видно, что векторная суммапо
модулю меньше,
так как угол между силами тупой.
Следовательно, вращение Земли приводит
к уменьшению g.
Правда уменьшение небольшое, составляющее
меньше 0,5%.
В
лабораторной работе изучается падение
стального шарика. При свободном падении
без начальной скорости за время t
шарик опускается на расстояние h,
вычисляемые по формуле:
(6)
Изменив
на опыте t
и
h,
по
(6) находят g.
В
этом и состоит суть метода определения
g.
Работа выполняется на установке.
Она
представляет собой вертикальный стальной
стержень с нанесённой шкалой. Стержень
крепится на стене посредством двух
кронштейнов. На нём установлены два
держателя: верхний и нижний, жестко
закреплённый. К верхнему держателю
крепится электромагнит, удерживающий
шарик, а к нижнему – ловитель с контактной
заслонкой. Время падения шарика от
основания электромагнита до контактной
заслонки отсчитывается по секундомеру.
Пуск секундомера с одновременным
выключением электромагнита производится
переключением тумблера на панели
секундомера. Остановка секундомера
происходит в момент падения шарика на
заслонку, размыкающая цепь электросекундамера
Ход
работы:
1.
Для
того, чтобы убедиться, что падение шарика
это равноускоренное движение установили
электромагнит на разных высотах h.
Каждую следующую высоту мы увеличивали.
При каждой высоте падения определили
три раза t1
– время
падения шарика и вычислили среднее
значение времени. Данные занесли в
таблицу:
|
h, |
0,85 |
0,90 |
0,95 |
1,00 |
1,05 |
1,10 |
||||||||||||
|
t1, |
0,40 |
0,45 |
0,38 |
0,43 |
0,47 |
0,37 |
0,50 |
0,42 |
0,40 |
0,46 |
0,40 |
0,50 |
0,39 |
0,53 |
0,46 |
0,40 |
0,58 |
0,44 |
|
t, |
0,41 |
0,43 |
0,44 |
0,45 |
0,46 |
0,47 |
||||||||||||
|
t2,c |
0,168 |
0,185 |
0,194 |
0,203 |
0,212 |
0,221 |
Затем
построили график зависимости
h
от t2.
Вычислили
по формуле
ускорение свободного падения (где h1
t1
и h2
t2
координаты
двух произвольных точек на линии графика)
получили:
Благодаря
проведённому опыту мы выяснили, что
падение шарика является свободным
падением.
2.
Находим погрешность измерения g.
Но
для
этого
измерим
время падения шарика t1
с высоты 1,8м. Изучая значения внесём
вычисления в таблицу. Вычисляем среднее
время t,
абсолютную Δt
и относительную
Е
погрешность измерения t.
Среднее значение высоты падения h
приняли равным высоте установки
электромагнита, а абсолютную погрешность
Δh=0,01м.
|
t1, |
0,40 |
0,54 |
0,46 |
0,30 |
0,50 |
0,35 |
0,38 |
0,34 |
0,37 |
0,45 |
|
0,409 |
Вычислим
Δg:
Записали
результат:
Вывод:
По результатам опыта мы выяснили, что
ускорение свободного падения всех тел
и при различных условиях одинаково. Это
связано с силой притяжения Земли. На
других планетах сила притяжения будет
иной.
Соседние файлы в папке сборник отчетов
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- 1 Формула для расчета ускорения свободного падения
- 2 Интересные факты
- 3 Ускорение свободного падения у поверхности некоторых небесных тел
- 4 Как вывести формулу ускорения свободного падения
Выберем тело, например, камень. Расположим его не некотором расстоянии от поверхности земли. Расстояние от центра Земли до камня равно ( R = left( r + h right) ), как представлено на рисунке 1.
Рис. 1. Камень (черная точка), притягивается к планете (центральная окружность).
Пусть на камень действует только сила, с которой Земля притягивает его, а других сил нет (нет, например, силы сопротивления воздуха).
Свободное падение – это движение тела под действием только одной силы — силы притяжения.
Из законов Ньютона известно: если на тело действует сила, то тело получает ускорение.
Ускорение свободного падения – это ускорение, с которым движется тело, когда на него действует только сила тяжести.
Формула для расчета ускорения свободного падения
Ускорение свободного падения можно посчитать по формуле:
[ large boxed { g = G cdot frac{M}{left( r + h right)^{2}} }]
( g left( frac{text{м}}{c^{2}} right) ) (метры, деленные на секунду в квадрате) – ускорение свободного падения
( M left( text{кг} right) ) (килограммы) — масса планеты, которая притягивает
( r left( text{м} right) ) (метры) – радиус планеты
( h left( text{м} right) ) (метры) — расстояние от поверхности планеты до тела
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Интересные факты
У разных планет ускорение свободного падения различается.
- чем больше масса планеты (или звезды), тем больше будет ускорение свободного падения рядом с такой планетой (или звездой);
- чем дальше от планеты, тем меньше ускорение свободного падения;
- на полюсах ускорение свободного падения больше, чем на экваторе планеты;
Важно!
Все тела под действием силы тяжести падают с одинаковым ускорением! Это ускорение не зависит от массы тела.
Из житейского опыта мы знаем: чем больше площадь тела, тем больше времени ему нужно, чтобы упасть с какой-либо высоты. При своем падении тело опирается на воздух, поэтому, к примеру, лист бумаги будет падать дольше, чем шарик из пластилина, или гирька.
В безвоздушном пространстве опираться не на что. Поэтому гирька, лист бумаги, птичье перо и пластилиновый шарик, стартовав с одной и той же высоты одновременно, упадут на поверхность планеты тоже одновременно.
Ускорение свободного падения у поверхности некоторых небесных тел
- у поверхности Земли ( g = 9{,}8 left( frac{text{м}}{c^{2}} right) )
- у поверхности Луны ( g = 1{,}68 left( frac{text{м}}{c^{2}} right) )
- у поверхности Марса ( g = 3{,}86 left( frac{text{м}}{c^{2}} right) )
- у поверхности Солнца ( g = 273{,}1 left( frac{text{м}}{c^{2}} right) )
- у поверхности Юпитера ( g = 23{,}95 left( frac{text{м}}{c^{2}} right) )
Как вывести формулу ускорения свободного падения
Рассмотрим камень, находящийся на некотором расстоянии от Земли.
Земля и камень притягиваются, запишем закон притяжения между планетой и камнем
[ F = G cdot frac{mcdot M}{left( r + h right)^{2}} ]
С другой стороны, у камня есть вес, так как на него действует сила тяжести.
[ F_{text{тяж}} = m cdot g ]
Мы можем записать эти уравнения в виде системы.
[ begin{cases} displaystyle F = G cdot frac{mcdot M}{( r + h)^{2}} \ displaystyle F_{text{тяж}} = m cdot g end{cases} ]
Земля и камень притягиваются, благодаря этому на камень действует сила тяжести. На языке математики это запишется так:
[ F = F_{text{тяж}} ]
А если равны левые части уравнений, то будут равны и правые:
[ G cdot frac{mcdot M}{left( r + h right)^{2}} = m cdot g ]
Масса ( m ) камня встречается в обеих частях уравнения. Поделим обе части уравнения на массу камня.
[ G cdot frac{M}{ left( r + h right)^{2}} = g ]
Все)
Вам будет интересно почитать:
Закон всемирного тяготения
Законы Ньютона
Первая космическая скорость
Вторая космическая скорость
Черноуцан А. И. Как зависит g от глубины? //Квант. — 1990. — № 3. — С. 49-52.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Вопрос: Что это — большое, зеленое, живет на глубине трех метров под землей и ест камни? Ответ: Большой Зеленый Камнеед.
Из фольклора МФТИ
Как будет изменяться сила тяготения по мере погружения тела в воображаемую шахту, прорытую сквозь Землю по ее диаметру? Какая сила тяготения действовала бы внутри некоторой «полой» планеты? Можно ли было бы ходить по ее внутренней поверхности? Попытаемся ответить на эти и аналогичные им вопросы. И не для того, конечно, чтобы выработать инструкцию для бурильщиков сверхглубоких скважин или для астронавтов, а чтобы лучше разобраться в законе всемирного тяготения.
Закон всемирного тяготения, открытый Ньютоном, утверждает, что любые две материальные частицы (точечные массы) притягиваются друг к другу с силой, пропорциональной массам этих частиц m1 и m2 и обратно пропорциональной квадрату расстояния r между ними:
(~F = G frac{m_1 m_2}{r^2}) , (1)
где G = 6,67•10-11 Н•м2/кг2 — гравитационная постоянная. В произвольном случае неточечных масс для определения силы тяготения можно воспользоваться широко известным в физике принципом суперпозиции.
Пусть, например, нам нужно рассчитать силу тяготения, действующую на точечную массу m со стороны тела произвольной формы. Мысленно разобьем тело на точечные массы m1, m2, …, mn, вычислим силы, действующие на массу m со стороны всех точечных масс, а затем векторно сложим эти силы. Что же получится в итоге? Сразу бросаются в глаза два факта. Во-первых, сила, действующая на точечную массу m, пропорциональна величине этой массы. Во-вторых, сила существенно зависит от того, какое именно тело взаимодействует с нашей точечной массой — какова его форма и размеры, какой массой оно обладает.
Кто и как действует на массу m в нашем примере? Непосредственно массы m1, …, mn через пустое пространство, их разделяющее? Или существует некоторый «посредник»? По современным представлениям таким материальным посредником является поле тяготения, создаваемое массами m1, …, mn во всем окружающем пространстве. Именно это поле и действует на массу m, в нем находящуюся. Если, например, изменить какую-нибудь из масс или как-то сместить их, то изменится и поле.
Для количественной характеристики поля тяготения в данной точке вводится специальная физическая величина — напряженность гравитационного поля. Определим ее так. Запишем выражение для силы тяготения, действующей на точечную массу m, в виде
(~vec F = m vec g) , или (~vec g = frac{vec F}{m}) , (2)
где (~vec g) (величина, не зависящая от m) и есть напряженность гравитационного поля. Она имеет простой физический смысл: с таким ускорением будет двигаться любая точечная масса, если ее поместить в данную точку поля и освободить. В частном случае, когда точечная масса взаимодействует с Землей, (~vec g) — это известное вам ускорение свободного падения.
От чего и как зависит (~vec g)? Как и сила тяготения, напряженность поля подчиняется принципу суперпозиции :
(~vec g = vec g_1 + vec g_2 + ldots + vec g_n) ,
где (~vec g_1, ldots , vec g_n) — напряженности полей, создаваемых в данной точке пространства отдельными массами m1, …, mn. Из выражений (1) и (2) следует, что любая точечная масса М создает вокруг себя поле, напряженность которого направлена к этой точке и зависит от расстояния r до нее по закону
(~g = G frac{M}{r^2}) . (3)
А какое гравитационное поле создает вокруг себя сферически симметричное тело? Ответ на этот вопрос был известен Ньютону с самого начала — сила притяжения к Земле вычисляется по той же формуле (1), где r — расстояние до центра Земли. Однако Ньютон понимал, что такое утверждение требует доказательства. Потратив очень много времени и сил, он доказал, что сила притяжения к тонкой сфере тел, расположенных вне нее, равна силе притяжения к материальной точке той же массы, расположенной в центре сферы. А поскольку шар можно разбить на тонкие сферы, такой же результат остается в силе и для шара. Переходя на язык поля, скажем, что величина напряженности поля тяготения, создаваемого тонкой сферой (или шаром) радиусом R, на расстоянии r > R от центра задается формулой (3).
Доказательство по принципу суперпозиции является действительно достаточно сложным. Однако его можно обойти. Как это сделать, показано в следующей заметке — «Силовые линии и теорема Гаусса» на примере электрического поля. Попробуйте прочитать эту заметку, всякий раз заменяя слово «заряд» словом «масса», а слова «электрическое поле» словами «поле тяготения». Если вам будет трудно разобраться в деталях, постарайтесь понять хотя бы общий смысл.
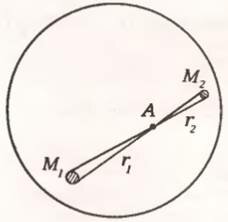
Рис. 1
Выясним теперь, каково поле тяготения внутри тонкой сферы, т. е. при r < R. Оказывается, внутри сферы напряженность поля равна нулю. Для доказательства возьмем произвольную точку, например точку А на рисунке 1, и покажем, что вклады в (~vec g_A) от двух противоположных участков поверхности сферы, отсекаемых узким конусом, взаимно уничтожаются. Действительно, из подобия следует, что линейные размеры выбранных участков относятся как (~frac{r_1}{r_2}), следовательно, отношение их площадей (~frac{S_1}{S_2}), равное отношению масс (~frac{M_1}{M_2}), есть (~frac{r^2_1}{r^2_2}). Тогда из формулы (3) получаем, что создаваемые этими участками в точке А напряженности равны по величине. А поскольку направления их противоположны, они в сумме дают ноль.
Интересный результат, не правда ли? Если бы внутри Земли, скажем, существовала концентрическая пустая полость (как, например, в случае, описанном в научно-фантастическом романе В. А. Обручева «Плутония. Необычайное путешествие в недра земли»), то в этой полости была бы полная невесомость. Оттолкнись чуть-чуть от поверхности и полетишь равномерно и прямолинейно до противоположной стенки. Так что путешествовать по такой Плутонии крайне затруднительно.
Теперь мы можем ответить и на самый первый вопрос — чему равно поле тяготения в шахте, прорытой вдоль диаметра Земли. Для простоты будем считать Землю однородным шаром с радиусом R. Рассмотрим точку на расстоянии r < R от центра Земли. Проведя мысленно сферу радиусом r, разделим Землю на две части — внешнюю и внутреннюю. Как мы уже выяснили, поле, создаваемое в рассматриваемой точке всеми внешними сферическими слоями, равно нулю. Поэтому поле Земли в данной точке совпадает с полем, созданным внутренней частью, т. е. шаром радиусом r. Чтобы использовать формулу (3), надо найти массу Mr этого шара. Очевидно, что отношение массы Mr к массе Mz, всей Земли равно отношению их объемов, т. е. отношению кубов радиусов[~frac{M_r}{M_z} = frac{r^3}{R^3}]. Следовательно,
(~g_r = G frac{M_r}{r^2} = G frac{M_z}{r^2} frac{r^3}{R^3} = g_0 frac{r}{R}) , (4)
где g0 — ускорение свободного падения на поверхности Земли.
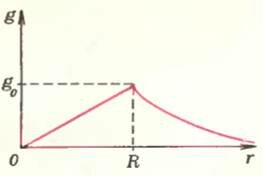
Рис. 2
Итак, мы знаем gr на любых расстояниях от центра Земли, как при r > R, так и при r < R. Эта зависимость изображена графически на рисунке 2. Попробуем использовать полученные результаты для ответа на вопрос, который любили задавать абитуриентам МФТИ в самом конце собеседования: «Что будет с камнем, брошенным в прорытый сквозь Землю колодец?» Ответить на этот вопрос совсем просто, если вы знакомы со свойствами гармонических колебаний. Действительно, раз сила притяжения пропорциональна r, тело будет совершать колебания относительно центра Земли (сопротивление воздуха, естественно, при этом не учитывается). Интересно, что такие же колебания (с таким же периодом) будет совершать и тело в колодце, прорытом наклонно. Существовали даже фантастические проекты межконтинентального пассажирского сообщения по прорытым каналам с помощью вагонов на воздушной подушке (подробнее об этом можно прочитать в книге Я. И. Перельмана «Занимательная физика»).
Рис. 3
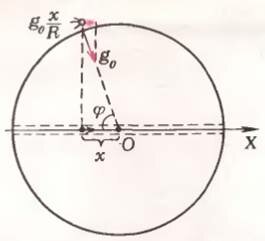
Оказывается, даже не зная ничего о колебаниях, все же можно понять, как будет двигаться камень, брошенный в прорытый колодец. Сравним между собой два движения — камня в колодце и спутника, летящего по околоземной круговой орбите. Точнее, проекции спутника на ось X, проведенную сквозь колодец (рис. 3). Легко убедиться, что проекция ускорения спутника равна (~a_x = g_0 cos varphi = g_0 frac{x}{R}). Но именно с таким ускорением будет двигаться камень на расстоянии x от центра (см. выражение (4)). Значит, и время движения камня сквозь Землю и обратно совпадает с периодом обращения спутника вокруг Земли. Кроме того, легко определить максимальную скорость камня. Очевидно, что она будет равна скорости спутника, т. е. первой космической скорости (~upsilon_1 = sqrt{g_0 R}) ≈ 8 км/с.
А теперь представьте себе выражение лица несчастного абитуриента, когда, изложив все эти тонкие физические соображения, он вдруг слышит в ответ: «Как же так, молодой человек? Такая невнимательность! Вы что, забыли? Камень пролетит в колодце всего три метра, после чего его съест Большой Зеленый Камнеед!»