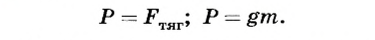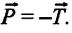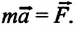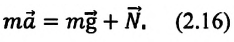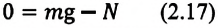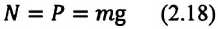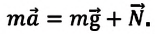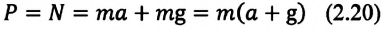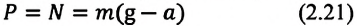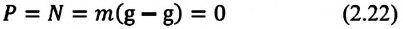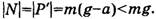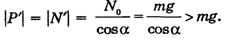Невесомость: что это такое
Невесомость — это состояние, при котором тело не давит на опору или подвес.
Само слово «невесомость» как бы подсказывает нам, что веса здесь быть не должно. При этом непонятно, что с ним тогда происходит. Давайте разбираться.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
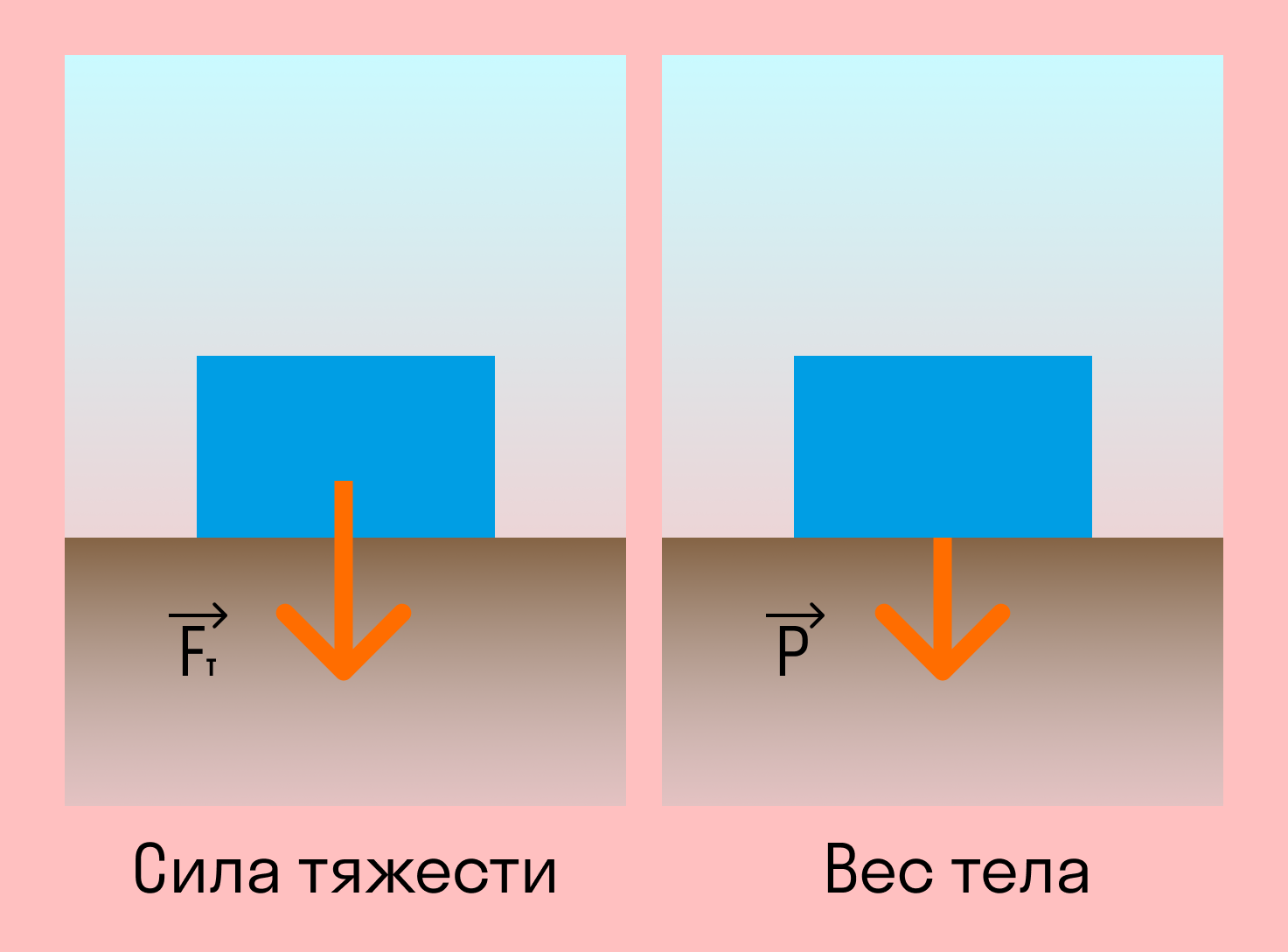
Вес тела
Вес — это сила, с которой тело действует на опору или подвес. Измеряется вес, как и любая другая сила, в Ньютонах.
«Но погодите! Вес же измеряют в килограммах — я вот вешу 50»
Это не совсем верно. В быту мы часто подменяем понятие «масса» понятием «вес» и говорим: вес чемодана — десять килограммам. В физике это два совершенно разных понятия, которые при этом взаимосвязаны.
Если у вас неподалеку есть весы — приглашаем в эксперимент! Один нюанс: наша затея сработает именно с механическими весами, но не с электронными. Поехали!
Шаг 1. Если встать на весы ровно и не двигаться — ваш вес будет высчитываться по формуле:
P = mg
P — вес тела [Н]
m — масса [кг]
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с2
Здесь может возникнуть два возражения:
-
Это же сила тяжести, а не вес. Формула такая же!
-
На весах масса отображается в килограммах. И если я свою массу умножу на ускорение свободного падения, то явно получу число почти в 10 раз больше, чем показывают весы.
Точка приложения силы. Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Весы измеряют силу. Весы работают таким образом, что измеряют вес тела — силу, с которой мы на них действуем, а показывают — массу. Можно сделать вывод, что весы — это динамометр (прибор, измеряющий силу).
Продолжаем эксперимент.
Шаг 2. Теперь пошалим и резко встанем на носочки! Стрелка резко отклонилась влево, а потом вернулась на место. Вы придали себе ускорение, направленное вверх — в то время, как ускорение свободного падения всегда направлено к центру Земли (вниз).
Теперь вес тела вычисляем по формуле:
P = m (g − a)
P — вес тела [Н]
m — масса [кг]
g — ускорение свободного падения [м/с2]
a — ваше ускорение [м/с2]
На планете Земля g = 9,8 м/с2
Шаг 3. Последняя часть эксперимента — резко опуститься на пятки. Теперь вы сильнее давите на весы, потому что придали ускорение, направленное вниз. Стрелка весов отклонится вправо и вернется на место, когда вы придете в состояние покоя.
Формула веса примет вид:
P = m (g + a)
P — вес тела [Н]
m — масса [кг]
g — ускорение свободного падения [м/с2]
a — ваше ускорение [м/с2]
На планете Земля g = 9,8 м/с2
Кстати, если ровно стоять на весах, но взвешиваться в лифте — все будет работать наоборот. Если лифт едет вверх, то он как будто давит весами на человека, стоящего на них, а это как раз ситуация с увеличением веса. А если вниз — весы как будто бы от вас «убегают», чтобы показать меньшее значение.
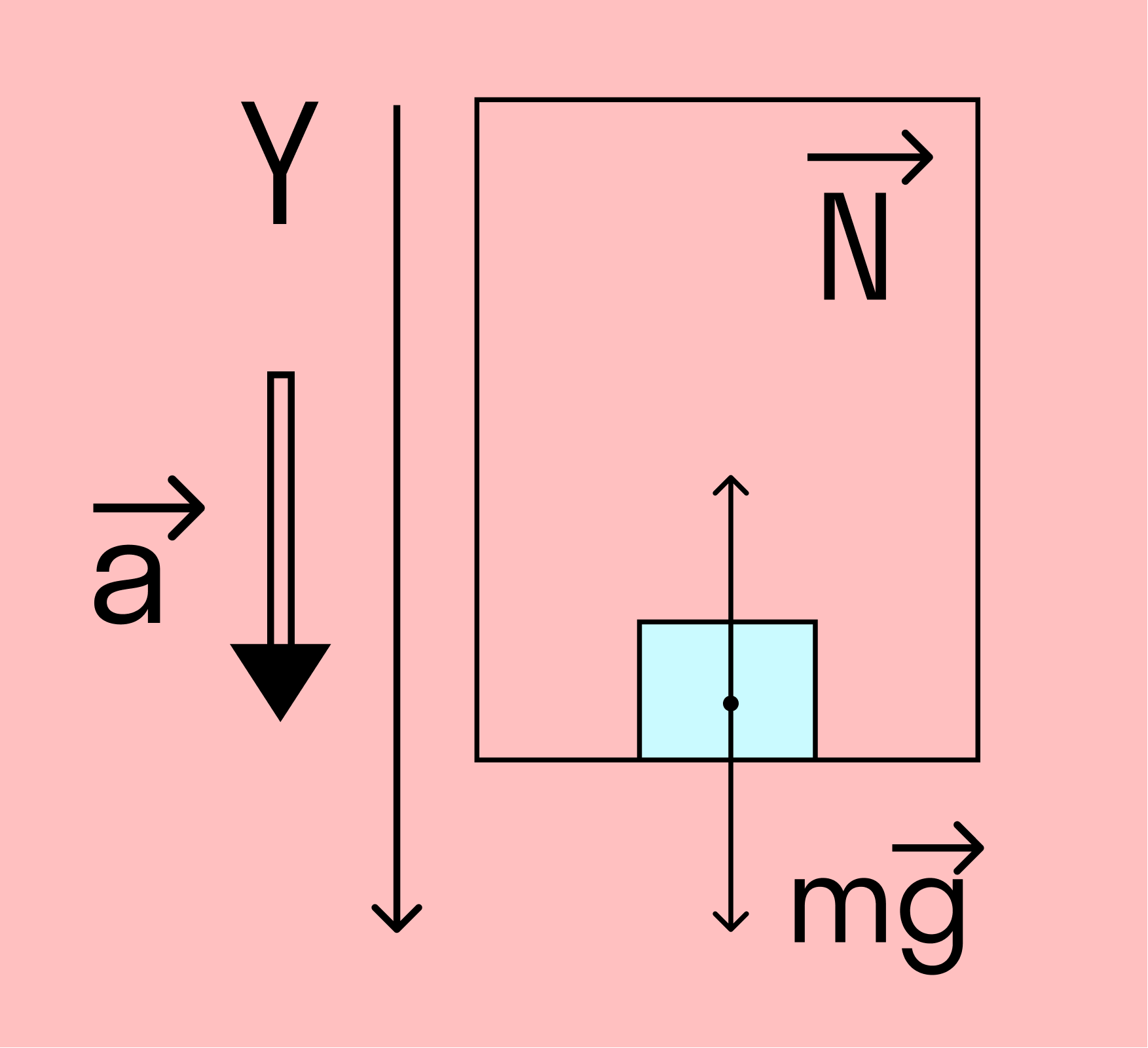
Этот случай мы можем описать через 2 закон Ньютона. Возьмем лифт, который едет вниз. Обозначим силы на рисунке.
N – сила реакции опоры [Н];
mg – сила тяжести [Н];
a – ускорение, с которым движется лифт [м/с2].
N + mg = ma
При проецировании на ось y, направленную вниз, мы получаем:
−N + mg = ma
А теперь нам понадобится третий закон Ньютона — по нему сила реакции опоры равна весу тела:
P = N
−P + mg = ma
P = m (g − a)
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Снова невесомость
Ну что, с весом разобрались. А теперь давайте сделаем так, чтобы его не стало и получилась та самая невесомость.
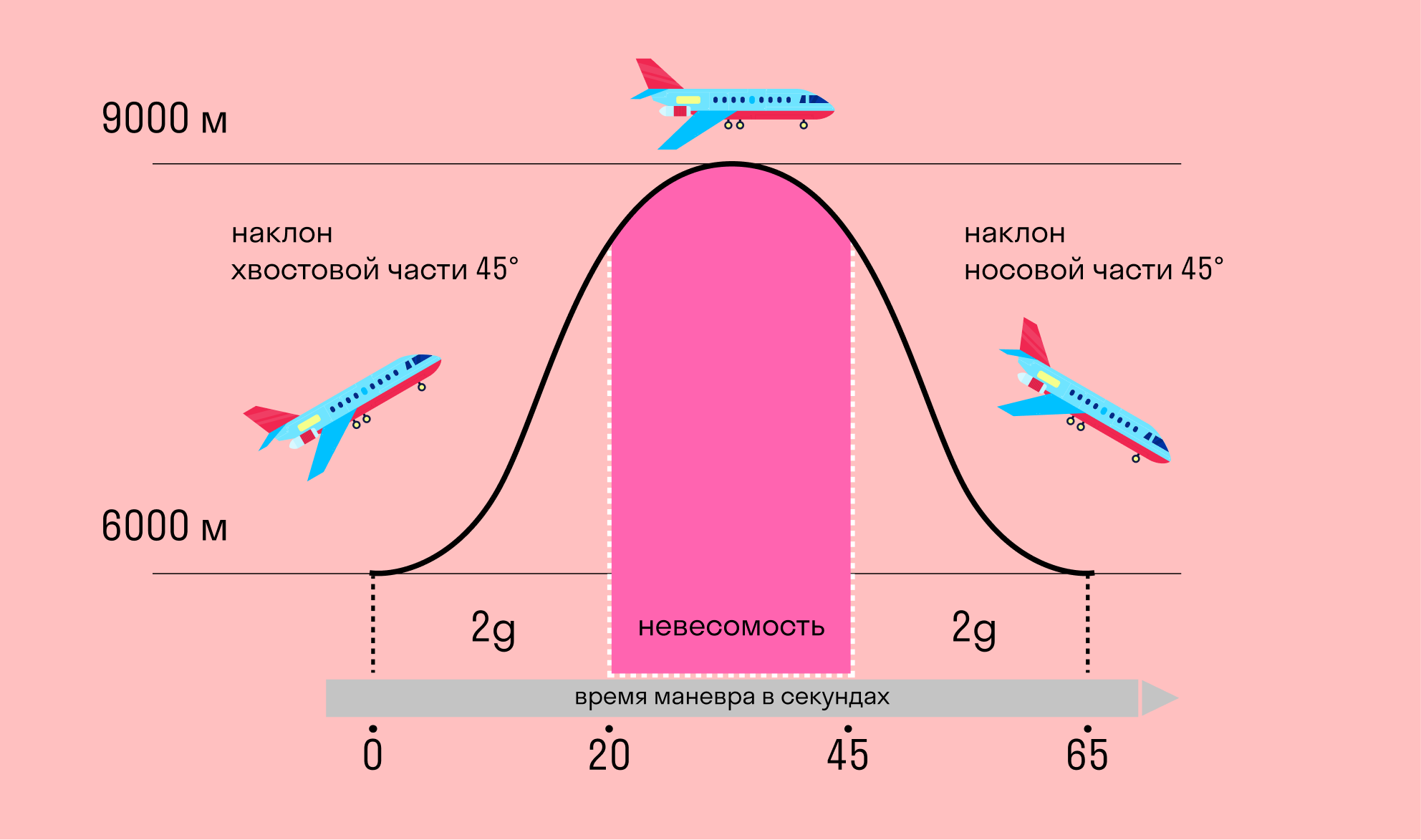
Чтобы привыкнуть к ощущению невесомости в космосе, космонавты тренируется в специальных самолетах-лабораториях:
Он взлетает и начинает просто падать, чтобы ускорение самолета было равно ускорению свободного падения. В этот момент, в формуле веса из g вычитается равное ему значение и получается 0:
P = m (g − a) = m (9,8 − 9,8) = 0
Вот мы и в невесомости!
Так это что же, космонавты испытывают невесомость, потому что падают?
Если они летят вокруг Земли, то да. Как писал Дуглас Адамс в книге «Автоспом по галактике»: «Летать просто. Нужно просто промахнуться мимо Земли».
Когда космический корабль обращается вокруг Земли, он просто пытается на нее упасть, но промахивается. Такой процесс происходит, когда корабль движется с первой космической скоростью, равной 7.9 км/с. Это та скорость, с которой корабль становится искусственным спутником Земли.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это минимальная скорость, с которой должно двигаться тело, чтобы оно могло без затрат дополнительной работы преодолеть влияние поля тяготения Земли, т. е. удалиться на бесконечно большое расстояние от Земли. А тело, которое двигается с третьей космической скоростью, и вовсе вылетит за пределы Солнечной системы. Такие дела. 🙂
Содержание:
Вес тела:
Множество тел на Земле находятся в состоянии покоя относительно ее поверхности. Почему же тела, на которые всегда действует сила тяготения, не изменяют своего положения и скорости под действием этой силы?
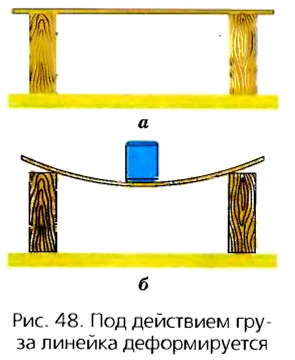
Ответ на этот вопрос найдем при проведении опыта. С этой целью положим линейку на две подставки и поставим на нее груз (рис. 48). Линейка деформируется. Следовательно, груз подействовал на линейку и изменил ее форму, деформировал. А при деформации возникла сила упругости, которая уравновесила силу тяготения, и груз прекратил движение к Земле.
Закрепим в штативе резиновую нить, а к ее концу прикрепим шарик. Если отпустим шарик, то он начнет двигаться вниз и будет растягивать нить до тех пор, пока сила упругости не уравновесит силу тяготения.
В обоих случаях на груз и шарик действовала сила тяготения, поэтому они, в свою очередь, действовали на линейку или резиновую нить.
Что такое вес тела
Силу, с которой тело действует на опору или подвес, называют весом тела.
Вес зависит от механического состояния тела. Если тело неподвижно относительно опоры или подвеса или движется равномерно и прямолинейно, то вес по значению и направлению совпадает с силой тяготения.
Для этого случая можно записать, что
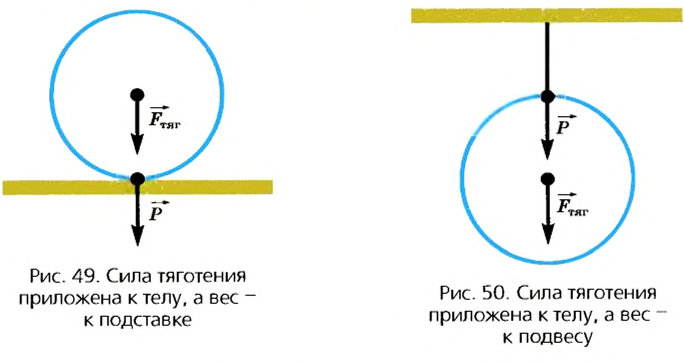
Однако между этими силами есть и существенные различия. Так, они приложены к различным телам. Если сила тяготения приложена к данному телу, то вес приложен к опоре или подвесу (рис. 49, 50).
Отличия проявляются и тогда, когда тело и опора свободно падают под действием силы тяготения. В этом случае вес исчезает и возникает состояние невесомости.
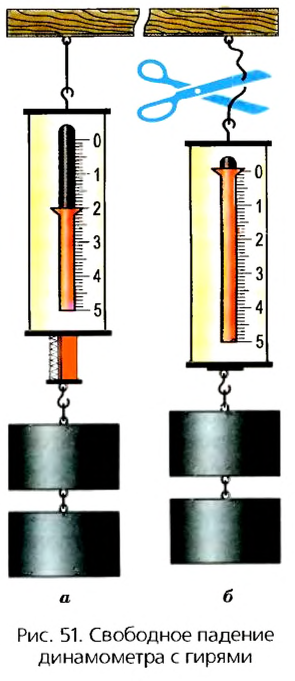
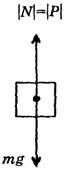
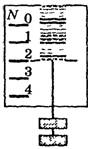
Такую особенность веса можно наблюдать в сравнительно простых опытах. Повесим на нити, закрепленной в штативе, металлический динамометр, к крючку которого прикреплены грузы. Стрелка покажет определенное значение веса грузов. Теперь перережем нить -динамометр с грузом начнет падать. В момент падения стрелка динамометра сместится на деление «ноль» (рис. 51). Таким образом, при свободном падении тела вес тела исчезает, возникает состояние невесомости.
Невесомость ощущают пилоты и космонавты. Если космический корабль движется вокруг Земли, то он все время как бы падает на Землю и все тела в его кабине теряют вес (рис. 52). В таких условиях много обычных явлений происходит своеобразно. Так, вода вне сосуда приобретает шарообразную форму и свободно плавает в пространстве. Брошенный предмет будет двигаться от стенки к стенке прямолинейно, не останавливаясь.
- Заказать решение задач по физике
Вес и невесомость
Вес — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Вес тела обозначается буквой 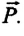
Случай, когда вес тела не меняется
Если тело находится в состоянии покоя или движется прямолинейно равномерно по горизонтальной поверхности, то его вес не изменяется. Почему?
Согласно III закону Ньютона, вес тела действует на опору и равен по модулю и противоположен по направлению силе реакции опоры 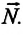
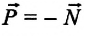
Если тело на подвесе находится в состоянии покоя или вместе с подвесом движется прямолинейно равномерно, то, согласно III закону Ньютона, вес этого тела, действующий на подвес, равен по модулю и направлен противоположно силе натяжения нити 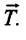
Согласно II закону Ньютона, уравнение движения для тела, находящегося в состоянии покоя или прямолинейного равномерного движения на горизонтальной опоре, записывается в виде:
Принимая во внимание, что результирующая сила равна векторной сумме силы тяжести и силы реакции опоры, уравнение движения примет вид:
Для решения уравнения выбирается ось координат, определяются проекции векторов сил на эту ось и, приняв во внимание знак проекций, записывают их в уравнение. За положительное направление оси 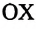
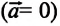
Отсюда видно, что вес тела, находящегося в состоянии покоя или прямолинейного равномерного движения, численно равен модулю силы тяжести:
Случай, когда вес тела меняется
Если тело вместе с опорой (или с подвесом) движется с ускорением 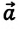
Предположим, что тело вместе с опорой движется вертикально вверх с ускорением 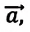
Если направить координатную ось вдоль направления движения (с), получим:
Отсюда видно, что вес тела, движущегося вместе с опорой вертикально вверх с ускорением 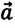
Ясно, что если тело вместе с опорой будет двигаться в направлении действия силы тяжести, то его вес уменьшится:
Случай, когда вес тела равен нулю — невесомость
Если тело движется только под действием гравитационной силы, то есть его ускорение будет равно ускорению свободного падения 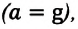
- Закон всемирного тяготения
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Сила упругости в физике и закон Гука
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Вес тела. Невесомость и перегрузка
Вес , как и любая другая сила, в системе СИ измеряется в Ньютонах.
Следы на снегу или на песке свидетельствуют о том, что человек или животное, проходя, давит на снежную или песчаную опору с некоторой силой.
Вес тела во время движения. Состояния невесомости и перегрузки
Вес тела зависит от ускорения, с которым движется тело, а потому может быть различным:
- Если тело покоится или движется равномерно прямолинейно, т.е. ускорение тела равно нулю, вес тела равен силе тяжести.
По второму закону Ньютона:
или в проекции на ось
:
откуда
По третьему закону Ньютона:
- Если тело движется с ускорением, направленным вертикально вверх, вес тела увеличивается. Такое состояние тела называется перегрузкой.
По второму закону Ньютона:
или в проекции на ось
:
откуда
По третьему закону Ньютона:
Перегрузки испытывают космонавты при взлете и на участках торможения космического корабля, летчики при выполнении фигур высшего пилотажа, пассажиры лифта при разгоне или торможении лифта и т.д.
- Если тело движется с ускорением, направленным вертикально вниз, вес тела уменьшается.
По второму закону Ньютона:
или в проекции на ось
:
откуда
По третьему закону Ньютона:
Если ускорение тела в этом случае будет равно ускорению свободного падения, вес тела равен нулю, т.е. тело будет находиться в состоянии невесомости.
Поскольку вес покоящегося тела равен силе тяжести, часто считают, что вес и сила тяжести – это одна и та же сила. Однако это неверно. Во-первых, вес и сила тяжести приложены к разным телам: сила тяжести приложена к телу, а вес – к опоре или подвесу. Во-вторых, вес и сила тяжести имеют различную физическую природу: вес, как правило, является силой упругости, а сила тяжести – это сила гравитационного взаимодействия. Наконец, как было показано выше, вес тела изменяется с изменением ускорения и может быть равен нулю, когда сила тяжести нулю не равна.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Каган И.Е. «Вес тела» (IX класс) // Фiзiка: праблемы выкладання. – 2001. – № 3. – С. 58-74.
Цель урока: изучить вес тела в различных условиях.
Приборы и принадлежности: динамометры демонстрационный и Бакушинского, связка прямоугольных брусков, наклонная плоскость, прямолинейная планка (в качестве подставки), деревянный куб массой 200 г, деревянная полированная доска длиной 1,5 м, метровая линейка, два набора грузов с шестью грузиками в каждом, жестяная банка с водой, штатив с муфтой, шар для демонстрации невесомости, диск с подшипниками на оси, укрепленный на массивной подставке, стакан с водой, прозрачный скотч.
I. Методическое обоснование темы
Тема «Вес тела» является одной из важных и серьезных тем механики, имеет много нюансов, требующих внимания и размышления. Некоторые осложнения связаны с целым рядом расхождений в формулировках и определениях веса тела, а также в описаниях функции весов (особенно рычажных), имеющих место во многих учебниках и пособиях по физике и механике.
Для формирования логического мышления и способности рассуждать учащимся в принципе полезно знать о множестве таких разночтений, но сразу это сделать довольно трудно. Однако для того, чтобы опыты на таком уроке были понятны учащимся, а результаты разбора разных случаев логически доступны, они должны быть предварительно подготовлены по трем вопросам.
1. Что такое вес тела (т.е. нужно определить предмет обсуждения)?
2. Как изобразить вес тела?
3. Что измеряют весы?
1. Прохождение темы имеет смысл начинать с формулировки «веса тела», тем более, что учащиеся с ней сталкиваются уже в VII классе, изучая курс механики либо по учебнику А.В.Перышкина, Н.А.Родиной, либо по учебнику Л.А.Исаченковой, Ю.Д.Лещинского.
Необходимо отметить, что понятие «вес тела» неодинаково формулируется в различных учебниках и пособиях разных лет. Одна из самых популярных и, вероятно, точных формулировок выглядит так: «Вес – это сила, с которой тело действует на опору или подвес под действием притяжения к Земле (или силы тяжести)».
В целом ряде учебников по физике дается чуть-чуть другая формулировка веса: «Вес тела – это сила, с которой тело действует на горизонтальную (!) опору или подвес и т.д.».
А где взять «идеально горизонтальную» опору? Значит, на других, не горизонтальных, опорах вес будет уже другим? Более или менее приближенным? А, может, покоящееся тело сохраняет вес неизменным на любой опоре? И как быть с весом тела, движущегося равномерно прямолинейно?
В некоторых изданиях можно прочесть и другие формулировки веса.
В учебнике «Физика, 9» (авт. Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь, 2000) в § 32 (с. 129) в определении «силы веса» горизонтальная опора не упоминается, но на с. 131 «сила веса» численно приравнивается к нормальной силе реакции, что подтверждается рис. 133 на с. 131. Значит, величина веса зависит от угла наклона плоскости? Каким же будет вес покоящегося тела на вертикальной плоскости? Тем более, что на рис. 133 показана и сила трения.
В учебнике П.Г.Саенко «Физика, 9» (1992), § 25, с. 83 в определении веса «горизонтальная» опора не указывается, но на с. 84 автор все-таки к ней возвращается и, таким образом, себе противоречит.
То же самое можно прочитать в учебнике Ю.А.Селезнева «Основы элементарной физики» (1966, с. 46), где на одной и той же этой странице напечатаны два разных суждения.
Целый ряд авторов, переиздавая свои издания, сами себе противоречат. В одних своих работах они формулируют понятие веса покоящегося тела для любой опоры, в других – для горизонтальной опоры. Таковы учебники физики для 6-7 кл. А.В.Перышкина, Н.А.Родиной, «Методика преподавания физики в 6-7 кл.» под редакцией В.П.Орехова, А.В.Усовой, «Пособие по физике для поступающих в вузы» М.С.Цедрика, Ф.Г.Китуновича, А.С.Микулича, А.М.Качинского, задачники Н.Е.Савченко.
В некоторых изданиях встречаются и другие формулировки веса.
1. В учебнике Б.Б.Буховцева, Ю.Л.Климонтовича, Г.Я.Мякишева «Физика, механика» (1971, § 49) на с. 102 читаем: «…вес тела определяется всей совокупностью действующих на тело сил, а не только силой тяготения (так, вес тела в жидкости или воздухе меньше, чем в вакууме из-за появления выталкивающей силы)». Что же это такое – вес в воздухе, жидкости, вакууме?
2. «Курс физики» (Б.М.Яворский, А.А.Детлаф, Л.Б.Милковская, Г.П.Сергеев, 1965, т. 1), § 6.1, с. 98: «Сила Р,называемая весом тела или силой тяжести, вызывает падение незакрепленного тела к земле».
3. «Повторим физику» (Л.Б.Милковская, 72), § 3.5, с. 73: «Так как тела падают на землю под действием силы тяжести, т.е. своего веса, то P = m∙g».
4. «Законы природы» (Р.Е.Пайернс, 1962), гл. 1, с. 23: «Тот факт, что сила тяготения, действующая на тело, т.е. вес тела, точно пропорциональна его массе или инерции, пока является для нас неожиданным совпадением».
5. «Большой энциклопедический словарь. Физика» (гл. ред. А.М.Прохоров, 1999), с. 70, определяет, что «…вес – это численная величина силы тяжести, действующей на тело, находящееся вблизи земной поверхности».
6. «Физика. Ответы на вопросы для абитуриентов и учащихся 11 кл.» (2000), гл. 2, с. 27 (коллектив авторов), определяет, что «весом тела называют силу нормального давления, действующую на подставку со стороны тела».
7. И даже такие авторы, как Л.Д.Ландау, А.И.Китайгородский в книге «Физика для всех» (1974), с. 9, пишут, что «Вес – это сила, с которой тело притягивается к земле. Эту силу можно измерить пружинными весами».
1. Изображение веса на рисунках
Исходя из имеющихся формулировок веса и третьего закона Ньютона, учащиеся должны понять, что весу тела по модулю равна сила реакции опоры N, и какой она будет, таким будет по величине и вес тела (рис. 1) (m∙g = Fтяжести).
Рис. 1
Учащиеся должны изображать вес тела как силу, приложенную к опоре. Здесь мы имеет несколько вариантов.
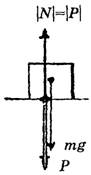
а) Если покоящееся тело – материальная точка, а горизонтальная опора – нет (рис. 2).
Рис. 2
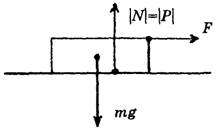
б) Если покоящееся тело и горизонтальная опора – не материальные точки (рис. 3). Элементарные силы реакции действуют на всю опору (рис. 3, а), мы учитываем действие результирующей силы реакции опоры. Следует заметить, что сила реакции опоры N может смещаться, если к телу, например, приложить дополнительную силу F по горизонтали (рис. 3, б).
Рис. 3
а б
Рис. 3
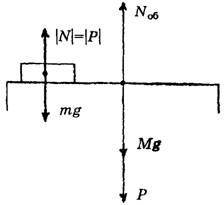
в) Если покоящееся тело и горизонтальная опора – материальные точки (рис. 4). M·g – сила тяжести самой опоры, Р –- вес покоящегося на опоре тела, Nо6 – общая сила реакции нижней опоры. Иногда такие случаи нужно учитывать в задачах.
Рис. 4
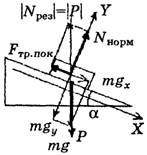
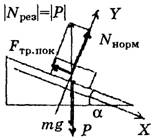
г) Если покоящееся тело – материальная точка, а наклонная опора – не материальная точка (рис. 5, а или 5, б).
а б
Рис. 5
У покоящегося тела на любой опоре вес сохраняется (в инерциональной системе) и численно равен силе тяжести, т.е. |P| = |m∙g| = |Npез|. Результирующая сила реакции N является векторной суммой силы нормальной реакции Nнорм и силы трения покоя Fтр. пок.Вес тела Рприложен к опоре.
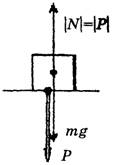
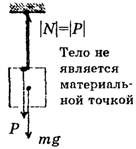
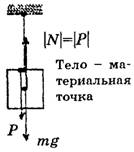
д) Покоящееся тело висит на вертикальном подвесе (рис. 6, а и 6, б).
а б
Рис. 6
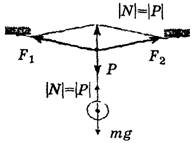
Составляющие F1и F2,образующие при векторном сложении результирующую силу реакции N,численно равную весу Р,сами по себе могут быть по величине больше веса (или одна из них или обе одновременно).
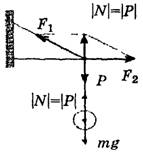
Это бывает на тросах, растянутых под большим углом (рис. 7), или на кронштейнах (рис. 8, а, 8, б).
Рис. 7
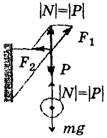
а б
Рис. 8
2. Что измеряют весы?
Многие скажут – «смотря какой конструкции это будут весы».
Обратимся к словарям.
Толковые словари С.И.Ожегова (с. 62) и Д.Н.Ушакова (т. 1, с. 262) утверждают, что весы – это прибор для измерения веса. При этом на с. 64 в первом словаре и т. 1, с. 273 во втором глагол «взвесить» означает – определить вес.
Энциклопедический словарь (1953), т. 1, с. 296, Физический энциклопедический словарь (1960), т. 1, с. 220, Малая Советская Энциклопедия (1958), т. 2, с. 343 (все под редакцией Б.А.Введенского) и Большая Советская Энциклопедия, под редакцией А.М.Прохорова (1971), т. 4, с. 568 указывают, что весы – это прибор для определения массы тела.
Все издания утверждают, что пружинные весы измеряют вес. В то же время многие издания утверждают, что рычажные (равноплечие) весы измеряют массу. Только в учебнике Б.М.Яворского, А.А.Пинского «Основы физики», т. 1, и Г.С.Ландсберга «Элементарный учебник физики», т. 1, указывается, что рычажные весы измеряют вес. Чему должен верить читатель?
Действительно, с пружинными весами все ясно. В их «весовой» функции даже невозможно усомниться.
А на рычажных весах вроде бы очень удобно измерять массу тела. Ведь при балансе чашек (в случае равенства весов тел) мы тут же можем судить о равенстве масс исследуемого тела и уравновешенных гирь.
Кроме того, рычажные весы имеют еще одно неоспоримое удобство. Равновесие чашек с грузами не нарушается, если их перевести на полюс, экватор, с Земли на Луну и т.д. (вес тела при этом меняется, а масса нет!).
Думается, равновесие рычажных весов здесь не нарушается не столько из-за постоянства масс тел, сколько из-за одинаковой кратности изменения весов тел на обеих чашках.
И почему ни одни весы ничего не показывают в состоянии полной невесомости (ведь масса тела остается неизменной и сила тяжести также!)?
Да потому, что в состоянии полной невесомости вес тела равен нулю, вот весы и фиксируют нулевой вес!
А как быть тогда, когда мы на рычажных весах взвешиваем пуховое тело или хлопок (вату)? Ведь это объемное тело, испытывающее ощутимое действие выталкивающей силы воздуха, которая в большинстве случаев незначительная и на гири, стоящие на второй чашке весов, почти не действует. При балансе чашек можно еще говорить о равенстве весов тел на чашках, но именно масса пухового тела при балансе чашек будет обязательно большей, чем совокупная масса гирь. И здесь уже рычажные весы не могут дать точный ответ о массе пухового тела!
А если в состоянии полной невесомости пытаться определить массу тела, то неизбежно нужно будет создать какое-то силовое взаимодействие этого тела с другим телом. Иначе говоря, весы все-таки в принципе созданы для определения силы, и «лишить» их своей весовой функции практически невозможно. Поэтому останавливаемся на точке зрения, что весы любой конструкции измеряют вес, но иногда позволяют оценить и массу. Разговоры о том, что весы градуируются в граммах, килограммах, тоннах и каратах, сути весовой функции весов не меняют.
В интересах доказательства назначения весов для определения массы предлагают даже ввести термин «массометр» («Толковый словарь школьника по физике», 1999, авторы К.К.Гомоюнов, М.Ф.Кесаманлы, Т.Г.Кесаманлы, с 39). Думается, что это не получится. Ведь с древних времен человека интересовала масса как мера тяжести (т.е. проблема веса) гораздо в большей степени, чем масса инертная.
И ссылки на то, что в седьмом классе мы учим детей определять массу на весах, ничего не меняют. Мы видим, какое сложное понятие – «вес тела», и не усложняем жизнь маленьким учащимся. А научить их практически пользоваться весами нужно еще с малых лет.
II. Ход урока
Такое множество формулировок и точек зрения запутывает и дезинформирует учащихся. Тем более, что противоречат друг другу, а иногда и самим себе довольно авторитетные авторы учебных и методических изданий.
К данному уроку учащиеся были подведены проблемно. Они ознакомились с разными формулировками веса, способами изображения веса и различными точками зрения на назначение весов как измерительного прибора (особенно рычажных равноплечих).
Исходя из такой преамбулы, можно более конкретно нацелить урок: на самых простых и доступных опытах убедиться в неизменности веса тела в инерциальных системах и его «изменчивости» в системах неинерциальных, т.е. когда тело будет иметь ускорение.
Предполагается определить вес покоящегося тела на разных опорах, выяснить, меняется ли вес при погружении тела в жидкость, и пронаблюдать, каким будет вес при наличии у тела ускорения.
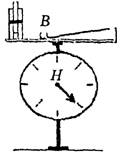
Дополнительно к вышеперечисленному оборудованию были специально изготовлены два небольших приспособления. Из двух фанерок была сбита наклонная плоскость с приступочкой В внизу (рис. 9, а) и сделана связка из трех деревянных брусков (рис. 9, б).
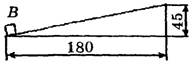
а б
Рис. 9
Средний брусок был несколько поднят, чтобы он не мог касаться опоры при вертикальном положении всей связки.
Первая часть урока. Вес покоящегося тела на различных плоскостях
а) Повторяем формулировку «веса» тела (без слова «горизонтальна»).
б) Устанавливаем стрелку демонстрационного динамометра (пружинных весов) на нуль, на верхнюю подставку динамометра помещаем горизонтальную планку, на которую кладем отдельно связку брусков и наклонную плоскость (как совокупность тел). Связка на планке лежит (рис. 10). Фиксируем показание весов.
Рис. 10
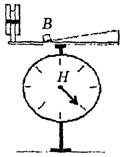
в) Связку брусков кладем на наклонную плоскость (бруски покоятся) (рис. 11). Снова фиксируем показание весов и убеждаемся в его неизменности.
Рис. 11
г) Ничего не меняется в показании весов, если бруски стопорить о приступку В (рис. 12). Приступка В играет роль второй наклонной плоскости, заменяющей силу трения покоя. Как видим, на наклонной плоскости покоящееся тело весит столько же, сколько и на горизонтальной опоре. И это потому, что вес тела численно равен по величине не нормальной реакции тела на наклонной плоскости, а общей реакции, включающей и силу трения покоя и численно равной силе тяжести |m∙g|.
Рис. 12
д) А чему равен вес покоящегося тела на вертикальной плоскости? Если верить некоторым изданиям (например, учебнику «Физика, 9» (2000), авторы Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь, с. 131, рис. 133), утверждающим, что величина веса определяется величиной силы нормальной реакции тела на наклонной плоскости, то на вертикальной плоскости у тела вообще веса не будет, так как при этом Nнорм = 0.
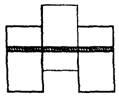
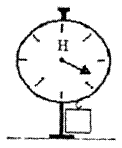
В таком случае наглядно и убедительно используется связка трех брусков. Средний брусок не касается опоры, когда связка стоит (рис. 13).
Рис. 13
Весы показывают совершенно одинаковый вес, стоит связка на двух брусках или на одном, будучи перевернутой (рис. 14). И не имеет абсолютно никакого значения, стоит связка брусков или лежит. Но когда связка лежит, давят на опору все три бруска, а если связка стоит? Весы подтверждают, что на опору все равно давят те же три бруска! Те бруски, которые не касаются опоры в каждом случае, весят или давят на нее благодаря силе трения покоя между вертикальными соприкасающимися стенками брусков.
Рис. 14
Если бы тело, прижатое к вертикальной стенке и покоящееся на ней, не весило, уже давно был бы придуман способ укладки вещевого мешка или другой паковки, которые бы при одинаковом количестве упакованных предметов весили меньше. Но этот фокус не получается! Как бы ни был упакован вещевой мешок или чемодан, все предметы в нем будут весомы. И ни одни весы в мире не покажут уменьшения веса покоящегося тела на наклонной плоскости из-за увеличения угла наклонной плоскости.
Учащимся задаем итоговый вопрос: «Играет ли роль для определения веса покоящегося тела угол наклонной плоскости?» И получаем ответ: «Нет, не играет».
Учащимся было продемонстрировано уменьшение веса тела на наклонной плоскости, когда тело движется вниз практически без трения.
Был поставлен следующий эксперимент.
На рычаге длиной 1 м на одном конце была установлена почти вертикально доска высотой 1,5 м с подвешенным на нити кубом массой 200 г, а на другом – две коробки с грузиками по 1 Н (12 грузиков) (рис. 15).
Рис. 15
Все уравновешивается и балансирует.
Нить пережигается, куб начинает падать, и в это время противоположное плечо рычага с грузиками опускается, что свидетельствует об уменьшении веса тела на наклонной плоскости. Но в это время тело на ней не покоилось, а летело вниз практически без трения.
На первую часть урока уходит 14 минут.
Вторая часть урока. «Вес тела в жидкости или газе»
Во многих изданиях, особенно выпущенных в прежние годы, мы часто сталкиваемся с терминологией «вес тела в воде», «вес тела в воздухе» и др. Например, в «Сборнике вопросов и задач» различных лет (авторы П.А.Знаменский и др.) на с. 52 в задачах № 397 и № 400 – «вес в керосине», «вес в воздухе» – в № 403, «истинный вес хлопка в кипе» – с. 53, № 409.
Был поставлен следующий эксперимент. Взвешиваем на крюке демонстрационного динамометра деревянный куб (рис. 16) и начинаем подводить под него банку с водой. По мере погружения куба в воду стрелка динамометра показывает уменьшение нагрузки на динамометр, создавая иллюзию уменьшения веса. Когда куб начинает плавать в воде, стрелка динамометра устанавливается на нуле. Так что – плавающее тело вообще не имеет веса?
Рис. 16
Снова взвешиваем куб на крюке, снимаем его и взвешиваем банку с водой без куба. Затем в подвешенную на крюк банку с водой кладем плавать куб. И что же? Весы показывают суммарный вес банки с водой и куба.
Это значит, что тело в воде или другой жидкости сохраняет свой вес, т.е. понятия «вес в воде», «вес в воздухе» или «вес в вакууме» и т.д. не имеют смысла.
Есть одно понятие – вес тела, неизменный в инерциальных системах.
Уменьшение показаний динамометра при погружении тела в жидкость связано с появлением еще одной опоры – жидкости, которая «берет на себя» часть веса. То есть вес тела распределяется на две опоры точно так же, как вес рычага, лежащего на двух опорах. В случае плавающего тела жидкость «берет на себя» весь вес тела, вследствие чего динамометр, к которому привязана нить с таким телом, ничего и не показывает.
С помощью учащихся делаем вывод о постоянстве веса тела в инерциальных системах на любой опоре. Выясняем, что вес тела сохраняется у пассажира в равномерно движущемся лифте и у парашютиста, спускающегося равномерно на парашюте.
На эту часть урока уходит еще 12 минут.
Третья часть урока. Вес тела в пеинерциальных системах или вес тела, имеющего ускорение (пока по вертикали)
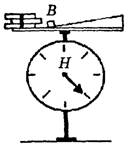
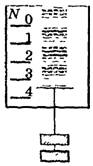
Начинаем с демонстрации подвешенных грузиков на динамометре Бакушинского (рис. 17).
Рис. 17
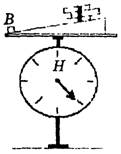
Показываем динамометр с двумя грузиками в состоянии покоя или равномерного прямолинейного движения по вертикали в любую сторону. Динамометр показывает вес, равный 2H = m∙g,т.е. вес тела численно равен силе тяжести. Начинаем поднимать динамометр с грузиками вверх с ускорением. И пока сохраняется ускорение при подъеме, учащиеся ясно видят увеличение растяжения пружины (рис. 18). Объясняем, что увеличение веса – это перегрузка. Напоминаем, что она ощущается в самом начале подъема лифта и в конце его спуска при торможении.
Рис. 18
До этого учащиеся уже решали задачи на расчет силы реакции при подъеме тела вверх с ускорением и знают, что она равна: 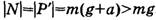
Приводим пример взвешивания с «походом», когда тело швыряют на весы и последние показывают «завышенный» вес. Выясняем, почему нас не устраивает, когда тело швыряют на весы (ведь не только из-за невежливости!), обращаем внимание учащихся на наличие торможения тела. Далее выясняем, чего мы ждем. Учащиеся отвечают, что мы ждем, когда весы уравновесятся и покажут в состоянии покоя вес тела, равный его силе тяжести.
Объясняем, что перегрузка не означает только увеличение воздействия на опору, а предполагает увеличение веса всего, что находится в такой системе. Увеличивается вес всех частей тела человека. Тяжелеет голова, руки, ноги, туловище, сердце, веки глаз, кровь и т.д. Нетренированный человек выдерживает троекратную перегрузку нормально. Особенно большие перегрузки бывают на тренировках космонавтов на больших скоростях (до 11-12 Р0)и при выходе самолета из состояния пикирования. Поясняем всю тяжесть и опасность таких ситуаций.
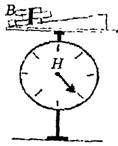
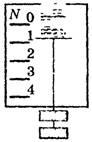
Показываем уменьшение веса при спуске тела с ускорением вниз (рис. 19). Получаем «недогрузку» или частичную невесомость, которая ощущается в начале спуска лифта (пока есть ускорение вниз) или в конце его подъема с торможением. В этом случае
Рис. 19.
Поясняем, что именно тогда, когда ускорение исчезает, сила реакции N будет компенсировать силу тяжести. Только тогда |N| = m∙g = |P0|,т.е. весу тела в состоянии покоя или равномерного прямолинейного движения.
Выясняем с учащимися, что с увеличением ускорения а по вертикали вниз «недогрузка» тела увеличивается, и при ускорении, равном g,вес становится равным нулю, т.е. наступает полная невесомость.
Обязательно обращаем внимание учащихся на то, что полная невесомость бывает только тогда, когда на тело действует одна-единственная сила – сила тяжести и тело находится в свободном падении.
Очень важно отметить, что если не учитывать сопротивление воздуха, полная невесомость имеет место при любых бросках.
Учащимся демонстрируется шар с подсветкой, которая зажигается внутри шара только в состоянии невесомости в любом броске. Шар можно бросать вертикально вверх, под углом к горизонту, горизонтально, ронять или подталкивать отвесно вниз. Шар светится только в полете, а учащиеся подтверждают, что при этом на тело действует только сила тяжести.
Подробно изучить явление полной невесомости на этом уроке невозможно. Эта тема достойна отдельного урока, который проводится после темы «Вес тела».
На эту часть урока уходит 10 минут.
Четвертая часть урока. Перегрузка при наличии ускорения тела по горизонтали
Был поставлен вопрос – каков вес тела при горизонтальном разгоне? Рассуждения проводятся на примере сосуда с водой.
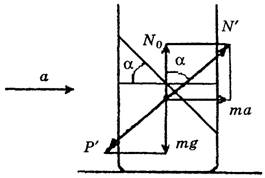
В состоянии инерции (т.е. покоя или равномерного прямолинейного движения) на жидкость действуют сила тяжести m∙g и сила нормальной реакции N0компенсирующие друг друга.
Для того, чтобы сообщить жидкости горизонтальное ускорение а,на нее необходимо подействовать горизонтальной силой т∙а (рис. 20).
Рис. 20
При этом возникает результирующая сила реакции N’,по модулю большая, чем N0(как гипотенуза прямоугольного треугольника). Так как искусственный вес Р’ жидкости по третьему закону Ньютона численно равен силе реакции N’,то и он возрастает, вследствие чего и возникает перегрузка.
Рассчитаем угол α.
и не зависит от массы.
Тогда
Следует обратить внимание учащихся на то, что на рис. 20 точка приложения веса Р’ не должна совпадать с центром масс жидкости.
Опыт с водой или другой не очень вязкой жидкостью очень нагляден из-за наклона свободной поверхности жидкости на угол α и ее «наплыва» на заднюю стенку (рис. 20).
Объясняем учащимся причину появления этого угла наклона. На угол α от вертикали отклоняется линия ответа, по которой направлен вес Р’. Плоскость свободной поверхности жидкости всегда перпендикулярна линии отвеса.
Как и углы с взаимно перпендикулярными сторонами, угол наклона жидкости также равен α. Если ускорение а постоянно, постоянным будет и угол α. При торможении ускорение тела отрицательное и жидкость «наплывает» на переднюю стенку (угол α отрицательный, a tg α – функция нечетная).
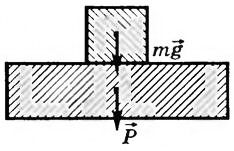
Практически бывает трудно сохранить долго ускорение по горизонтали постоянным. Тогда меняется угол наклона плоскости свободной поверхности жидкости и жидкость начинает плескаться. А если жидкость равномерно вращать? Ведь тогда центростремительное ускорение жидкости а будет постоянным и угол наклона α будет также постоянным. Учащимся демонстрируется установка с гироскопическим колесом (рис. 21). На краю колеса с помощью прозрачного скотча укрепляется стакан с водой. Колесо раскручивается вокруг своей оси и благодаря подшипникам на оси и большой инертности долго сохраняет скорость вращения практически постоянной.
Рис. 21
При большой скорости вращения колеса учащиеся хорошо видят большой угол α наклона плоскости свободной поверхности воды к горизонту.
Постепенно скорость вращение колеса убывает и уменьшается угол a наклона воды.
На эту часть урока уходит 6 минут.
Итак, третья и четвертая части урока были посвящены изучению веса тела, имеющего ускорение. Учащиеся выяснили, что при наличии ускорения вес тела может быть различным – от больших перегрузок до полной невесомости.
Учащимся уместно задать «провокационный» вопрос: «Почему у покоящегося тела на экваторе вес меньший, чем на полюсе?» И находятся ребята, которые подмечают, что на экваторе тело имеет линейную скорость, как следствие этого у него есть центростремительное ускорение, и вес на экваторе должен отличаться от веса на полюсе.
III. Итоги урока
Учащиеся получили полное экспериментальное подтверждение, что:
1) в инерциальных системах отсчета тело, покоящееся или движущееся равномерно прямолинейно, неизменно сохраняет свой вес на любой опоре независимо от того, каков угол наклона опоры, а также жидкая это опора или твердая;
2) в неинерциальных системах отсчета вес тела может изменяться в зависимости от ускорения тела.
Урок вызвал живой интерес у учащихся класса. Они приняли активное участие в обсуждении опытов и их результатов.
На уроке пришлось обратить внимание учащихся на то, что на с. 131 учебника «Физики-9» (авторы Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь) приведен неверный рис. 133. Он был опровергнут экспериментами, проведенными на уроке. Там же имеются ошибки в описании невесомости тела в самолете.
Вес тела
Весом тела называется сила, с которой тело действует на неподвижную относительно него опору или подвес.
Вес тела возникает вследствие его деформации, вызванной действием силы со стороны опоры (силы реакции) или подвеса (силы натяжения) Вес существенно отличается от силы тяжести:
- Это силы разной природы: сила тяжести — гравитационная сила, вес — упругая сила (электромагнитной природы).
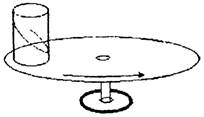
- Они приложены к разным телам: сила тяжести — к телу, вес — к опоре (рис. 2).
-
Рис. 2
-
- Направление веса тела не обязательно совпадает с отвесным направлением.
- Сила тяжести тела в данном месте Земли постоянная и не зависит от характера движения тела; вес зависит от ускорения, с которым движется тело.
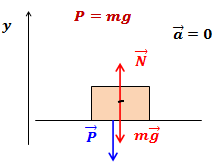
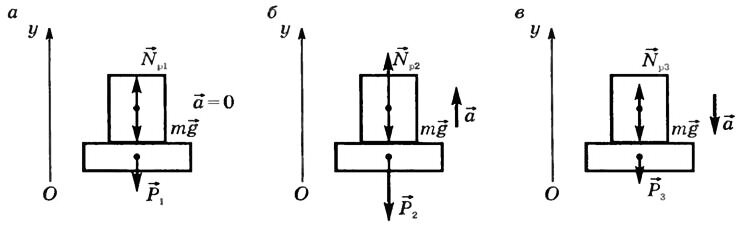
Рассмотрим, как изменяется вес тела, движущегося в вертикальном направлении вместе с опорой (рис. 3 а, б, в). На тело действуют сила тяжести (~vec F_T = m vec g) и сила реакции опоры (~vec N_p).
Рис. 3
Основное уравнение динамики[~m vec a = m vec g + vec N_p]. В проекции на ось Оу:
- а) (~0 = N_{p1} — mg Rightarrow N_{p1} = mg). По третьему закону Ньютона модули сил Np1 = P1. Следовательно, вес тела P1 = mg.
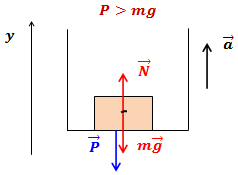
- б) (~ma = N_{p2} — mg Rightarrow N_{p2} = m (a + g)). Значит, (~P_2 = m (a + g) Rightarrow P_2 > mg) (тело испытывает перегрузки).
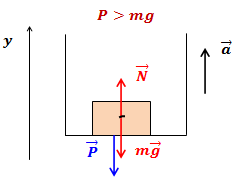
- в) (~-ma = N_{p3} — mg Rightarrow N_{p3} = m (g — a)). Следовательно, вес тела (~P_3 = m (g — a) Rightarrow P_3 < mg). Если a = g, то P = 0.
Таким образом, вес тела при вертикальном движении может быть в общем случае выражен формулой
(~P = m (g pm a).)
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 40-41.