|
0 / 0 / 0 Регистрация: 08.11.2018 Сообщений: 43 |
|
|
1 |
|
Операции с битами. Изменить значение указанного бита произвольного целого числа на противоположное…25.04.2019, 14:26. Показов 12703. Ответов 9
Ребята, буду рад любой помощи. Советы, подсказки, отдельные части кода, ссылки на полезные ресурсы. Мне необходимо написать программу, которая изменяет значение указанного бита произвольного целого числа на противоположное (1 на 0, 0 на 1). Программа должна предоставлять возможность вводить различные целые числа, номер бита n (биты нумеруются справа на левый) и выводить результат как в десятичном, так и в двоичном виде.
__________________
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
25.04.2019, 14:26 |
|
9 |
|
Verevkin Нарушитель 8392 / 4395 / 1010 Регистрация: 12.03.2015 Сообщений: 20,580 |
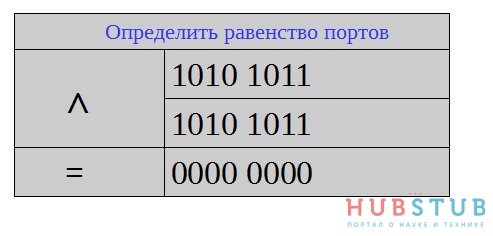
||||
|
25.04.2019, 14:42 |
2 |
|||
|
Ахтунг! Не отлаживал! Писал на заборе!
0 |
|
0 / 0 / 0 Регистрация: 08.11.2018 Сообщений: 43 |
|
|
25.04.2019, 14:54 [ТС] |
3 |
|
Verevkin, спасибо за ответ. Не могли бы вы пройтись по строкам вашей функции с объяснениями?
0 |
|
Нарушитель 8392 / 4395 / 1010 Регистрация: 12.03.2015 Сообщений: 20,580 |
|
|
25.04.2019, 15:00 |
4 |
|
Не могли бы вы пройтись по строкам вашей функции с объяснениями? АХАХАХА, так и знал!
0 |
|
Eanmos 698 / 140 / 57 Регистрация: 20.08.2017 Сообщений: 255 |
||||||||
|
25.04.2019, 15:34 |
5 |
|||||||
|
РешениеДля того, чтобы инвертировать n−ый бит числа можно использовать следующее выражение: A = A XOR (1 << N):
Добавлено через 12 минут Пусть A = 0000 10002 (810), N = 3. Тогда 1 << N = 0000 0001 << 3 = 0000 1000. Далее —
2 |
|
Нарушитель 8392 / 4395 / 1010 Регистрация: 12.03.2015 Сообщений: 20,580 |
|
|
25.04.2019, 16:31 |
6 |
|
Для того, чтобы инвертировать n−ый бит числа можно использовать следующее выражение: A = A XOR (1 << N): И то верно. чот я тормознул. бывает…
0 |
|
0 / 0 / 0 Регистрация: 08.11.2018 Сообщений: 43 |
|
|
25.04.2019, 18:30 [ТС] |
7 |
|
Eanmos, что происходит в 3 строчке кода? Добавлено через 12 минут Добавлено через 30 минут Добавлено через 23 секунды
0 |
|
Eanmos 698 / 140 / 57 Регистрация: 20.08.2017 Сообщений: 255 |
||||
|
25.04.2019, 19:42 |
8 |
|||
|
Можно вот так, например:
1 |
|
0 / 0 / 0 Регистрация: 08.11.2018 Сообщений: 43 |
|
|
25.04.2019, 19:57 [ТС] |
9 |
|
Eanmos, я несколько минут назад доделал уже) Спасибо вам за помощь. Кстати, то, что было непонятным в вашем первом сообщении, стало понятнее после пары часов работы)
0 |
|
Verevkin Нарушитель 8392 / 4395 / 1010 Регистрация: 12.03.2015 Сообщений: 20,580 |
||||
|
25.04.2019, 20:44 |
10 |
|||
|
Verevkin, вы тоже можете помочь в этом. Я был занят. Но свою функцию отдам.
0 |
Битовые операции
Во многих языках программирования допустимы логические операции над битами целых чисел. В отличие от обычных логических операций, результатом выполнения которых является логический тип данных, битовые логические операции просто изменяют целое число согласно определенным правилам. Точнее битовые операции изменяют отдельные биты двоичного представления числа, в результате чего изменяется его десятичное значение.
Например, в языке программирования Паскаль обычные логические операции и логические операции над битами обозначают с помощью одних и тех же ключевых слов: not, and, or, xor. Компилятор определяет, что имелось в виду в зависимости от контекста использования этих слов. Обычные логические операции объединяют два и более простых логических выражения. Например, (a > 0) and (c != b), (c < a) or(not b) и т.п. В свою очередь побитовые логические операции выполняются исключительно над целыми числами (или переменными, которые их содержат). Например, a and b, a or 8, not 247.
Как понять побитовые операции
1. Переведем пару произвольных целых чисел до 256 (один байт) в двоичное представление.
6710 = 0100 00112 11410 = 0111 00102
2. Теперь расположим биты второго числа под соответствующими битами первого и выполним обычные логические операции к цифрам, стоящим в одинаковых разрядах первого и второго числа. Например, если в последнем (младшем) разряде одного числа стоит 1, а другого числа — 0, то логическая операция and вернет 0, а or вернет 1. Операцию not применим только к первому числу.
3. Переведем результат в десятичную систему счисления.
01000010 = 26 + 21 = 64 + 2 = 66 01110011 = 26 + 25 + 24 + 21 + 20 = 64 + 32 + 16 + 2 + 1 = 115 00110001 = 25 + 24 + 20 = 32 + 16 + 1 = 49 10111100 = 27 + 25 + 24 + 23 + 22 = 128 + 32 + 16 + 8 + 4 = 188
4. Итак, в результате побитовых логических операций получилось следующее:
67 and 114 = 66 67 or 114 = 115 67 xor 114 = 49 not 67 = 188
Вот еще один пример выполнения логических операций над битами. Проверьте его правильность самостоятельно.
5 and 6 = 4 5 or 6 = 7 5 xor 6 = 3 not 5 = 250
Зачем нужны побитовые логические операции
Глядя на результат побитовых операций, не сразу можно уловить закономерности в их результате. Поэтому непонятно, зачем нужны такие операции. Однако, они находят свое применение. В байтах не всегда хранятся числа. Байт или ячейка памяти может хранить набор флагов (установлен — сброшен), представляющих собой информацию о состоянии чего-либо. С помощью битовых логических операций можно проверить, какие биты в байте установлены в единицу, можно обнулить биты или, наоборот, установить в единицу. Также существует возможность сменить значения битов на противоположные.
Проверка битов
Проверка битов осуществляется с помощью битовой логической операции and.
Представим, что имеется байт памяти с неизвестным нам содержимым. Известно, что логическая операция and возвращает 1, если только оба операнда содержат 1. Если к неизвестному числу применить побитовое логическое умножение (операцию and) на число 255 (что в двоичном представлении 1111 1111), то в результате мы получим неизвестное число. Обнулятся те единицы двоичного представления числа 255, которые будут умножены на разряды неизвестного числа, содержащие 0. Например, пусть неизвестное число 38 (0010 0110), тогда проверка битов будет выглядеть так:
Другими словами, x and 255 = x.
Обнуление битов
Чтобы обнулить какой-либо бит числа, нужно его логически умножить на 0.
Обратим внимание на следующее:
1111 1110 = 254 = 255 - 1 = 255 - 20 1111 1101 = 253 = 255 - 2 = 255 - 21 1111 1011 = 251 = 255 - 4 = 255 - 22 1111 0111 = 247 = 255 - 8 = 255 - 23 1110 1111 = 239 = 255 - 16 = 255 - 24 1101 1111 = 223 = 255 - 32 = 255 - 25 1011 1111 = 191 = 255 - 64 = 255 - 26 0111 1111 = 127 = 255 - 128 = 255 - 27
Т.е. чтобы обнулить четвертый с конца бит числа x, надо его логически умножить на 247 или на (255 — 23).
Установка битов в единицу
Для установки битов в единицу используется побитовая логическая операция or. Если мы логически сложим двоичное представление числа x с 0000 0000, то получим само число х. Но вот если мы в каком-нибудь бите второго слагаемого напишем единицу, то в результате в этом бите будет стоять единица.
Отметим также, что:
0000 0001 = 20 = 1 0000 0010 = 21 = 2 0000 0100 = 22 = 4 0000 1000 = 23 = 8 0001 0000 = 24 = 16 0010 0000 = 25 = 32 0100 0000 = 26 = 64 1000 0000 = 27 = 128
Поэтому, например, чтобы установить второй по старшинству бит числа x в единицу, надо его логически сложить с 64 (x or 64).
Смена значений битов
Для смены значений битов на противоположные используется битовая операция xor. Чтобы инвертировать определенный бит числа x, в такой же по разряду бит второго числа записывают единицу. Если же требуется инвертировать все биты числа x, то используют побитовую операцию исключающего ИЛИ (xor) с числом 255 (1111 1111).
Операции побитового циклического сдвига
Помимо побитовых логических операций во многих языках программирования предусмотрены битовые операции циклического сдвига влево или вправо. Например, в языке программирования Паскаль эти операции обозначаются shl(сдвиг влево) и shr (сдвиг вправо).
Первым операндом операций сдвига служит целое число, над которым выполняется операция. Во втором операнде указывается, на сколько позиций сдвигаются биты первого числа влево или вправо. Например, 105 shl 3 или 105 shr 4. Число 105 в двоичном представлении имеет вид 0110 1001.
При сдвиге влево теряются старшие биты исходного числа, на их место становятся младшие. Освободившиеся младшие разряды заполняются нулями.
При сдвиге вправо теряются младшие биты исходного числа, на их место становятся старшие. Освободившиеся старшие разряды заполняются нулями, если исходное число было положительным.
Реализуйте метод flipBit, изменяющий значение одного бита заданного целого числа на противоположное.
Договоримся, что биты нумеруются от младшего (индекс 1) к старшему (индекс 32).
public static int flipBit(int value, int bitIndex) {
char[] mass = Integer.toBinaryString(value).toCharArray();
int index = bitIndex%32;
if(mass[index - 1] == '0') mass[index - 1] = '1';
else mass[index - 1] = '0';
return Integer.parseInt(new String(mass), 2);
}
Выдает ошибку:
Failed test #3. Run time error:
Exception in thread «main»
java.lang.ArrayIndexOutOfBoundsException: 30
at
Main.flipBit(Main.java:27)
at Main.main(Main.java:14)
at
Main.main(Main.java:7)
Streletz
11.6k9 золотых знаков27 серебряных знаков39 бронзовых знаков
задан 11 фев 2016 в 1:55
3
Чтобы инвертировать бит на определенной позиции, нужно сдвинуть 1 на желаемое число позиций влево (это будет маска), и затем сделать XOR с исходным числом.
public static long flipBit(int position, long value) {
return value ^ 1 << position;
}
Либо, можно воспользоваться классом BitSet
public static long flipBit(int position, long value) {
BitSet bs = BitSet.valueOf(new long[] { value });
bs.flip(position);
return bs.toLongArray()[0];
}
Биты нумеруются начиная с 0, справа налево.
long value = 10L;
System.out.println(Long.toBinaryString(value)); // 1010
System.out.println(Long.toBinaryString(flipBit(1, value))); // 1000
Дополнительные условия вашей задачи и проверку на допустимые значения добавьте самостоятельно.
ответ дан 11 фев 2016 в 4:10
enzoenzo
4,0591 золотой знак9 серебряных знаков22 бронзовых знака
1
Пошаговый примерчик, где:
a -изменяемое число.
b -номер бита который меняем в изменяемом числе.
public static void main(String[] args) {
int a = 15;
int b = 3;
// т.к. биты нумеруются не с нуля, а с еденеицы;
b--;
// вводим еще одну нулевую переменную, чтобы получить маску с измененным битом в ней.
int c = 0;
System.out.println( " двоичный вид " + c + ": " +Integer.toString(c, 2)); // 0 : 0
// сдвигаем битовую еденицу на нужное значение и получаем маску.
c = 1 << b;
System.out.println( " двоичный вид " + c + ": " +Integer.toString(c, 2)); // 4 : 100
// отобразим битовое значение числа, в котором будем изменять нужный бит.
System.out.println( " двоичный вид " + a + ": " +Integer.toString(a, 2)); // 15 : 1111
// выполняем операцию XOR между маской и изменяемым числом
a = a ^ c;
System.out.println( " двоичный вид " + a + ": " +Integer.toString(a, 2)); // 11 : 1011
}
ответ дан 12 ноя 2019 в 22:50
Начал изучать Java
15.06.2021
09:41
Java
нет комментариев

Пока что все выглядит, как в анекдоте «Два плюс два равно четыре, а теперь решите тригонометрическое уравнение».
Похоже, что курс рассчитан на самостоятельное гугление. Тем не менее комментарии к задачам позволяют найти правильный путь.
Зачем мне Java, не случиться ли с ней тоже самой что с Machine Learning или Django? Надеюсь, что нет. Есть несколько компонентов облачной технологии 1С:Фреш, которые написаны на Java. Также есть 1C:EDT, который написан также на Java. Так что надеюсь, что эти знания не пропадут и будут использоваться на практике.
Понравилась задачка в самом начале:
Реализуйте метод flipBit, изменяющий значение одного бита заданного целого числа на противоположное. Данная задача актуальна, например, при работе с битовыми полями.
Договоримся, что биты нумеруются от младшего (индекс 1) к старшему (индекс 32).
Тут нужно понять что вообще требуется.
Для начала нужно понять, что параметр bitIndex — это индекс места единички в двоичном представлении числа. Т.е. если bitIndex = 1, то смещение должно выглядеть как 0001, если bitIndex = 2, то смещение должно выглядеть как 0010 и так далее. Тут я указал 4 цифры двоичного числа для краткости. Например если bitIndex = 7, то в двоичном виде это будет 1000000. Будем использовать единицу для смещения битов. При этом, если bitIndex = 1, то никакого смещения не требуется, т.к. мы уже находимся там где нужно. Чтобы получить нужное смещение, нужно вычесть из значения bitIndex единицу и для единицы сделать смещение битов влево, используя оператор cмещения — << .
Дальше нужно поменять значение бита у числа. Для этого нужно вспомнить как ведет себя операция XOR.
a b xor 0 0 0 // ничего не происходит с битом 0 1 1 // бит a меняется на противоположный 0 -> 1 1 0 1 // ничего не происходит с битом 1 1 0 // бит a меняется на противоположный 1 -> 0
В результате получим решение:
public static int flipBit(int value, int bitIndex) {
return value ^ (1 << --bitIndex);
}Интереснее будет решение, если расширить выводимую информацию:
public static int flipBit(int value, int bitIndex) {
int result = value ^ (1 << bitIndex - 1);
System.out.println(value + " (" + Integer.toBinaryString(value) + ") и " + bitIndex
+ " (" + Integer.toBinaryString(1 << bitIndex - 1)
+ ") = " + result
+ " (" + Integer.toBinaryString(result) + ")");
return result;
}
Тут становится понятно, что происходит, если поэкспериментировать с параметрами. Изменяется значение одного бита заданного целого числа на противоположное (убрал вывод и добавил пробелов, чтобы было понятнее):
65 (1000001) и 1 (1) = 64 (1000000) 65 (1000001) и 2 (10) = 67 (1000011) 65 (1000001) и 3 (100) = 69 (1000101) 65 (1000001) и 8 (10000000) = 193 (11000001) 65 (1000001) и 7 (1000000) = 1 (1)
На простом примере из первой строки есть число 65 — это 1000001 в двоичном виде. Хотим поменять первый бит на противоположный, получим 1000000 в двоичном виде — это число 64 в десятиричном. И так далее.
Теги: Си битовые операции, побитовые операции, побитовое сложение, побитовое умножение, битовый сдвиг влево, битовый сдвиг вправо
Введение
Язык Си иногда называют макроассемблером за его тягу к железу. Если не использовать оптимизацию, можно даже примерно оценить, в какие конструкции на ассемблере
преобразуется код программы. Простота и минимализм языка (простоту языка не путать с простотой программирования на языке)
привели к тому, что на многих платформах си остаётся единственным высокоуровневым языком программирования. Без обзора побитовых операций, конечно, изучения языка было
бы неполным.
Побитовые операции, как понятно из названия, позволяют оперировать непосредственно с битами. Большое количество примеров использования побитовых операций можно найти, например,
в книге Генри Уоррена «Алгоритмические трюки для программистов». Здесь мы рассмотрим только сами операции и примитивные алгоритмы.
Побитовые И, ИЛИ, НЕ, исключающее ИЛИ
ЗАМЕЧАНИЕ: здесь и далее в примерах используются 8-битные числа для упрощения записи. Всё это верно и для любых других чисел.
Напомню для начала, что логические операции И, ИЛИ, исключающее ИЛИ и НЕ могут быть описаны с помощью таблиц истинности
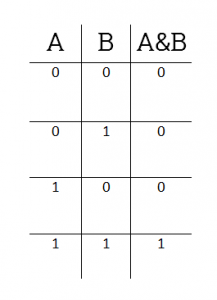
| X | Y | X AND Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
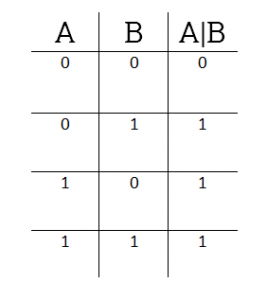
| X | Y | X OR Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
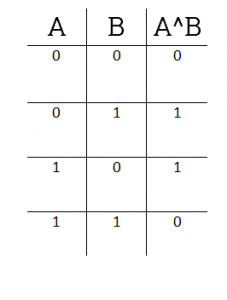
| X | Y | X XOR Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| X | NOT X |
|---|---|
| 0 | 1 |
| 1 | 0 |
В побитовых (bit-wise) операциях значение бита, равное 1, рассматривается как логическая истина, а 0 как ложь. Побитовое И (оператор &) берёт два числа и логически умножает
соответствующие биты. Например, если логически умножить 3 на 8, то получим 0
char a = 3;
char b = 8;
char c = a & b;
printf("%d", c);
Так как в двоичном виде 3 в виде однобайтного целого представляет собой
00000011
а 8
00001000
Первый бит переменной c равен логическому произведению первого бита числа a и первого бита числа b. И так для каждого бита.
00000011
00001000
↓↓↓↓↓↓↓↓
00000000
Соответственно, побитовое произведение чисел 31 и 17 даст 17, так как 31 это
00011111
, а 17 это
00010001
00011111
00010001
↓↓↓↓↓↓↓↓
00010001
Побитовое произведение чисел 35 и 15 равно 3.
00100011
00001111
↓↓↓↓↓↓↓↓
00000011
Аналогично работает операция побитового ИЛИ (оператор |), за исключением того, что она логически суммирует соответствующие биты чисел без переноса.
Например,
char a = 15;
char b = 11;
char c = a | b;
printf("%d", c);
выведет 15, так как 15 это 00001111, а 11 это 00001011
00001111
00001011
↓↓↓↓↓↓↓↓
00001111
Побитовое ИЛИ для чисел 33 и 11 вернёт 43, так как 33 это 00100001, а 11 это 00001011
00100001
00001011
↓↓↓↓↓↓↓↓
00101011
Побитовое отрицание (оператор ~) работает не для отдельного бита, а для всего числа целиком. Оператор инверсии меняет ложь на истину, а истину на ложь, для каждого бита.
Например,
char a = 65;
char b = ~a;
printf("%d", b);
Выведет -66, так как 65 это 01000001, а инверсия даст 10111110
что равно -66. Кстати, вот алгоритм для того, чтобы сделать число отрицательным: для нахождение дополнительного кода числа его надо инвертировать и
прибавить к нему единицу.
char a = 107;
char b = ~a + 1;
printf("a = %d, -a = %d", a, b);
Исключающее ИЛИ (оператор ^) применяет побитово операцию XOR. Например, для чисел
char a = 12;
char b = 85;
char c = a ^ b;
printf("%d", c);
будет выведено 89, так как a равно 00001100, а b равно 01010101. В итоге получим 01011001
Иногда логические операторы && и || путают с операторами & и |. Такие ошибки могут существовать в коде достаточно долго,
потому что такой код в ряде случаев будет работать. Например, для чисел 1 и 0. Но так как в си истиной является любое ненулевое значение,
то побитовое умножение чисел 3 и 4 вернёт 0, хотя логическое умножение должно вернуть истину.
int a = 3;
int b = 4;
printf("a & b = %dn", a & b); //выведет 0
printf("a && b = %dn", a && b);//выведет не 0 (конкретнее, 1)
Операции побитового сдвига
Операций сдвига две – битовый сдвиг влево (оператор <<) и битовый сдвиг вправо (оператор >>). Битовый сдвиг вправо сдвигает биты числа
вправо, дописывая слева нули. Битовый сдвиг влево делает противоположное: сдвигает биты влево, дописывая справа нули. Вышедшие за пределы числа биты отбрасываются.
Например, сдвиг числа 5 влево на 2 позиции
00000101 << 2 == 00010100
Сдвиг числа 19 вправо на 3 позиции
00010011 >> 3 == 00000010
Независимо от архитектуры (big-endian, или little-endian, или middle-endian) числа в двоичном виде представляются слева направо, от более значащего бита к менее значащему.
Побитовый сдвиг принимает два операнда – число, над которым необходимо произвести сдвиг, и число бит, на которое необходимо произвести сдвиг.
int a = 12;
printf("%d << 1 == %dn", a, a << 1);
printf("%d << 2 == %dn", a, a << 2);
printf("%d >> 1 == %dn", a, a >> 1);
printf("%d >> 2 == %dn", a, a >> 2);
Так как сдвиг вправо (>>) дописывает слева нули, то для целых чисел операция равносильна целочисленному делению пополам, а сдвиг влево умножению на 2.
Произвести битовый сдвиг для числа с плавающей точкой без явного приведения типа нельзя. Это вызвано тем, что
для си не определено представление числа с плавающей точкой. Однако можно переместить число типа float в int, затем сдвинуть и вернуть обратно
float b = 10.0f;
float c = (float) (*((unsigned int*)&b) >> 2);
printf("%.3f >> 2 = %.3f", b, c);
Но мы, конечно же, получим не 5.0f, а совершенно другое число.
Особенностью операторов сдвига является то, что они могут по-разному вести себя с числами со знаком и без знака, в зависимости
от компилятора. Действительно, отрицательное число обычно содержит один бит знака. Когда мы будем производить сдвиг влево, он может пропасть, число станет
положительным. Однако, компилятор может сделать так, что сдвиг останется знакопостоянным и будет проходить по другим правилам. То
же самое и для сдвига вправо.
unsigned int ua = 12;
signed int sa = -11;
printf("ua = %d, ua >> 2 = %dn", ua, ua >> 2);
printf("sa = %d, sa >> 2 = %dn", sa, sa >> 2);
printf("(unsigned) sa = %u, sa >> 2 = %un", sa, sa >> 2);
printf("sa = %d, ((unsigned) sa) >> 2 = %d", sa, ((unsigned) sa) >> 2);
В данном случае при первом сдвиге всё работает, как и задумано, потому что число без знака. Во втором случае компилятор VSE2013 оставляет знак. Однако если посмотреть на
представление этого числа, как беззнакового, сдвиг происходит по другим правилам, с сохранением самого левого бита. В последней строчке, если привести число со знаком к
числу без знака, то произойдёт обычный сдвиг, и мы получим в результате положительное число.
Побитовые операторы и операторы сдвига не изменяют значения числа, возвращая новое. Они также как и арифметические операторы, могут входить в состав сложного присваивания
int a = 10; int b = 1; a >>= 3; a ^= (b << 3);
и т.д.
Примеры
1. Напишем функции, которые позволяют определять и изменять определённый бит числа
Для того, чтобы узнать, какой бит (1 или 0) стоит на позиции n, воспользуемся логическим умножением.
Пусть имеется число 9
00001001
Нужно узнать, выставлен ли бит на позиции 3 (начиная с нуля). Для этого умножим его на число, у которого все биты равны нулю, кроме третьего:
00001001 & 00001000 = 00001000
Теперь узнаем значение бита в позиции 6
00001001 & 01000000 = 00000000
Таким образом, если мы получаем ответ, равный нулю, то на искомой позиции находится ноль, иначе единица. Чтобы получить число, состоящее из нулей с одним битом на нужной позиции, сдвинем 1 на нужное число бит влево.
#include <stdio.h>
#include <conio.h>
#include <limits.h>
int checkbit(const int value, const int position) {
int result;
if ((value & (1 << position)) == 0) {
result = 0;
} else {
result = 1;
}
return result;
}
void main() {
int a = 3;
size_t len = sizeof(int) * CHAR_BIT;
size_t i;
for (i = 0; i < len; i++) {
printf("%d", checkbit(a, i));
}
_getch();
}
Заметьте, что в функции условие записано так
(value & (1 << position)) == 0
Потому что без скобок сначала будет вычислено равенство нулю и только потом выполнено умножение.
value & (1 << position) == 0
Функцию можно упростить
int checkbit(const int value, const int position) {
return ((value & (1 << position)) != 0);
}
Функция, которая выставляет бит на n-й позиции в единицу.
Известно, что логическое сложение любого бита с 1 будет равно 1. Так что для установки n-го бита нужно логически сложить число с таким, у которого все биты, кроме нужного,
равны нулю. Как получить такое число, уже рассмотрено.
int setbit(const int value, const int position) {
return (value | (1 << position));
}
Функция, которая устанавливает бит на n-й позиции в ноль.
Для этого нужно, чтобы все биты числа, кроме n-го, не изменились. Умножим число на такое, у которого все биты равны единице, кроме бита под номером n. Например
0001011 & 1110111 = 0000011
Чтобы получить такую маску, сначала создадим число с нулями и одной единицей, а потом инвертируем его.
int unsetbit(const int value, const int position) {
return (value & ~(1 << position));
}
Функция, изменющая значение n-го бита на противоположное.
Для этого воспользуемся функцией исключающего или: применим операцию XOR к числу, которое состоит из одних нулей и одной единицы на месте нужного бита.
int switchbit(const int value, const int position) {
return (value ^ (1 << position));
}
Проверка
#include <stdio.h>
#include <conio.h>
#include <limits.h>
int checkbit(const int value, const int position) {
return ((value & (1 << position)) != 0);
}
int setbit(const int value, const int position) {
return (value | (1 << position));
}
int unsetbit(const int value, const int position) {
return (value & ~(1 << position));
}
int switchbit(const int value, const int position) {
return (value ^ (1 << position));
}
void printbits(int n) {
//CHAR_BIT опеределён в библиотеке limits.h
//и хранит число бит в байте для данной платформы
size_t len = sizeof(int)* CHAR_BIT;
size_t i;
for (i = 0; i < len; i++) {
printf("%d", checkbit(n, i));
}
printf("n");
}
void main() {
int a = 3;
size_t len = sizeof(int) * CHAR_BIT;
size_t i;
printbits(a);
a = setbit(a, 5);
printbits(a);
a = unsetbit(a, 5);
printbits(a);
a = switchbit(a, 11);
printbits(a);
a = switchbit(a, 11);
printbits(a);
_getch();
}
Битовые флаги
Расммотрим синтетический пример. Пусть у нас есть три логические переменные, и нам нужно вывести определённое значение
в зависимости от всех этих переменных сразу. Очевидно, что может быть 23 возможных вариантов. Запишем
это условие в виде ветвления:
#include <stdio.h>
int main() {
unsigned char a, b, c;
a = 1;
b = 0;
c = 0;
if (a) {
if (b) {
if (c) {
printf("true true true");
} else {
printf("true true false");
}
} else {
if (c) {
printf("true false true");
} else {
printf("true false false");
}
}
} else {
if (b) {
if (c) {
printf("false true true");
}
else {
printf("false true false");
}
}
else {
if (c) {
printf("false false true");
}
else {
printf("false false false");
}
}
}
_getch();
return 0;
}
Мы получили 8 ветвей. Пусть теперь нам понадобилось добавить ещё одно условие. Тогда число ветвей удвоится, и программа
станет ещё сложней для понимания и отладки. Перепишем пример.
Если каждое из наших логичесих значений сдвинуть на своё число бит влево и логически сложить, то мы получим свою уникальную
комбинацию бит в зависимоти от значений a, b и c:
#include <stdio.h>
#include <limits.h>
void printbits (int n) {
int i;
for (i = CHAR_BIT - 1; i >= 0; i--) {
printf("%d", (n & (1 << i)) != 0);
}
printf("n");
}
int main() {
unsigned char a, b, c;
unsigned char res;
a = 1; b = 0; c = 0;
res = c | b << 1 | a << 2;
printbits(res);
a = 0; b = 1; c = 1;
res = c | b << 1 | a << 2;
printbits(res);
a = 1; b = 0; c = 1;
res = c | b << 1 | a << 2;
printbits(res);
_getch();
return 0;
}
Используем этот подход к нашей задаче и заменим ветвеление на switch:
#include <stdio.h>
int main() {
unsigned char a, b, c;
unsigned char res;
a = 1;
b = 0;
c = 0;
res = c | b<< 1 | a << 2;
switch (res) {
case 0b00000000:
printf("false false false");
break;
case 0b00000001:
printf("false false true");
break;
case 0b00000010:
printf("false true false");
break;
case 0b00000011:
printf("false true true");
break;
case 0b00000100:
printf("true false false");
break;
case 0b00000101:
printf("true false true");
break;
case 0b00000110:
printf("true true false");
break;
case 0b00000111:
printf("true true true");
break;
}
_getch();
return 0;
}
Этот метод очень часто используется для назначения опций функций в разных языках программирования. Каждый
флаг принимает своё уникальное название, а их совместное значение как логическая сумма всех используемых флагов.
Например, библиотека fcntl:
char *fp = "/home/ec2-user/file.txt"; int flag = O_RDWR | O_CREAT | O_TRUNC | O_APPEND; int fd = open(fp, flag, 0644);
Здесь флаг O_RDWR рaвен
00000000000000000000000000000010
O_CREAT рaвен
00000000000000000000000100000000
O_TRUNC равен
00000000000000000000001000000000
и O_APPEND
00000000000000000000000000001000
Q&A
Всё ещё не понятно? – пиши вопросы на ящик
Об аргументах функции
Для тех кому надо освежить знания оставлю тут памятку, более подробно эти операции будут рассмотрены в статье.
установить нулевой бит
PORTB | = 0x01;
сбростить нулевой бит
PORTB &= ~0x01;
проверить установлен ли бит
if(PORTB & 0x01)
{
}
инвертировать значение нулевого бита
#define LED 0x01
PORTB ^= LED;
Независимо от того какие микроконтроллеры Вы собираетесь программировать, первое что придётся освоить — это битовые операции.
Битовых операций в языке Си всего 6.
& ( AND )
| ( OR )
^ ( XOR )
~ ( NOT )
<<(сдвиг влево)
>>(сдвиг вправо)
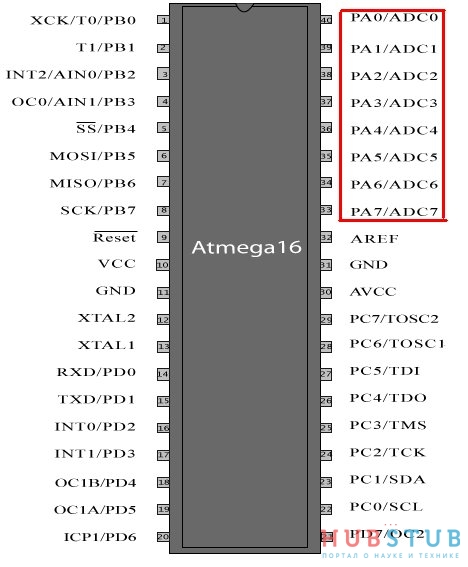
Начнем с того, что выводы микроконтроллера условно разделены на порты, у Atmega16 порт состоит из 8 выводов, у STM32f103 из 16 выводов.
Отмеченные ножки, как раз и составляют порт А.
Побитовое ИЛИ — результат операции равен 1, если один из соответствующих битов равен 1, иначе 0.
Установить в 1 нулевой бит порта B можно следующим образом.
PORTB = 0x01; //шестнадцатеричная запись
или
PORTB = 0b00000001; //двоичная запись
или
PORTB = 1; //десятичная запись
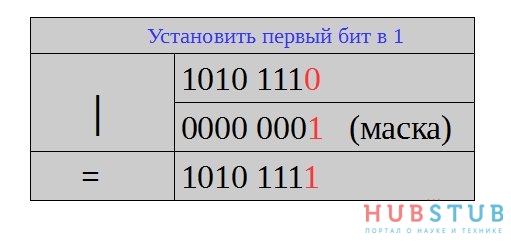
Таким образом, мы установили нулевой бит в 1, а все остальные в 0, то есть мы переопределили все биты порта. А что если мы хотим установить в 1 только нулевой бит и не задеть остальные? В таком случае нужно воспользоваться побитовым ИЛИ.
установить нулевой бит в единицу
PORTB = PORTB | 0x01;
или воспользовавшись составным присваиванием
PORTB | = 0x01;
В результате мы изменили только нулевой бит порта.
Надо отметить, что в микроконтроллерах счёт начинается с нуля, то есть первый бит будет иметь нулевой порядковый номер, а порядковый номер восьмого бита будет 7.
Битовая операция НЕ — изменяет значение бита на противоположное.
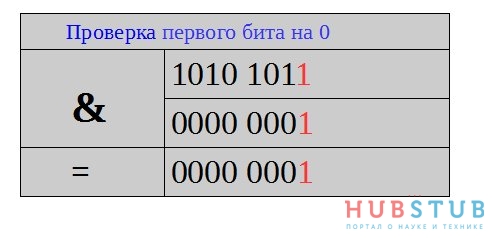
Побитовое И — если соответствующие биты равны 1, результирующий бит равен 1. Если один из соответствующих битов равен 0, то результирующий бит равен 0.
Эта операция совместно с битовым НЕ может использоваться для сброса конкретного бита в ноль.
сростить нулевой бит
PORTB &= 0xFE;
или
PORTB &= ~0x01;
При такой записи, мы выставляем в единицу бит, который хотим обнулить, затем инвертируем получившееся число
Теперь накладываем получившуюся маску
В итоге мы выставили в 0 только первый бит.
Также эту операцию можно использовать для проверки чему равен бит. Например, нам надо проверить чему равен нулевой бит порта B, это можно сделать с помощью следующей конструкции.
if(PORTB & 0x01)Если бит равен единице, выражение в скобках будет правда, иначе — ложь.
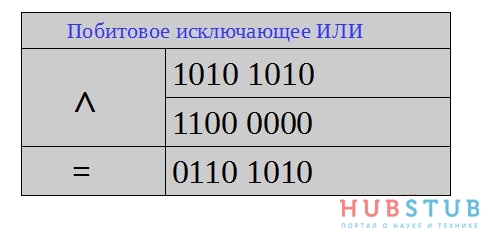
Побитовое исключающее ИЛИ — если сумма соответствующих битов число чётное, результирующий бит 0, иначе 1.
С помощью этой операции можно инвертировать состояние выбранного бита. Например, к нулевому выводу порта подключен светодиод и при выполнении одного и того же фрагмента кода, мы хотим чтобы он погас если горит и наоборот, зажёгся если не горит.
#define LED 0x01
PORTB ^= LED;
Также с помощью этой операции можно определить равенство регистров. Например, мы хотим сравнить в одинаковом ли состоянии находятся порты B и D.
if(PORTB ^ PORTD)Если результат равен нулю, то содержимое регистров равно.
Логический сдвиг влево — все разряды при этом сдвигаются на одну позицию влево, самый левый бит теряется, а в самый правый бит записывается 0.
Операция логического сдвига влево эквивалентна умножению на 2.
0b0000 1011 = 11
0b0001 0110 = 22
Логический сдвиг вправо — все разряды при этом сдвигаются на одну позицию вправо, самый правый бит теряется, а в самый левый бит записывается 0.
Операция логического сдвига влево эквивалентна делению на 2.
0b1000 1011 = 147
0b0100 0101 = 73
Видно, что при делении на 2 результат округляется в меньшую сторону, на этом всё.
В этой статье я расскажу вам о том, как работают битовые операции. С первого взгляда они могут показаться вам чем-то сложным и бесполезным, но на самом деле это совсем не так. В этом я и попытаюсь вас убедить.
Введение
Побитовые операторы проводят операции непосредственно на битах числа, поэтому числа в примерах будут в двоичной системе счисления.
Я расскажу о следующих побитовых операторах:
- | (Побитовое ИЛИ (OR)),
- & (Побитовое И (AND)),
- ^ (Исключающее ИЛИ (XOR)),
- ~ (Побитовое отрицание (NOT)),
- << (Побитовый сдвиг влево),
- >> (Побитовый сдвиг вправо).
Битовые операции изучаются в дискретной математике, а также лежат в основе цифровой техники, так как на них основана логика работы логических вентилей — базовых элементов цифровых схем. В дискретной математике, как и в цифровой технике, для описания их работы используются таблицы истинности. Таблицы истинности, как мне кажется, значительно облегчают понимание битовых операций, поэтому я приведу их в этой статье. Их, тем не менее, почти не используют в объяснениях побитовых операторов высокоуровневых языков программирования.
О битовых операторах вам также необходимо знать:
- Некоторые побитовые операторы похожи на операторы, с которыми вы наверняка знакомы (&&, ||). Это потому, что они на самом деле в чем-то похожи. Тем не менее, путать их ни в коем случае нельзя.
- Большинство битовых операций являются операциями составного присваивания.
Побитовое ИЛИ (OR)
Побитовое ИЛИ действует эквивалентно логическому ИЛИ, но примененному к каждой паре битов двоичного числа. Двоичный разряд результата равен 0 только тогда, когда оба соответствующих бита в равны 0. Во всех других случаях двоичный результат равен 1. То есть, если у нас есть следующая таблица истинности:
38 | 53 будет таким:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A | B | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
В итоге мы получаем 1101112 , или 5510 .
Побитовое И (AND)
Побитовое И — это что-то вроде операции, противоположной побитовому ИЛИ. Двоичный разряд результата равен 1 только тогда, когда оба соответствующих бита операндов равны 1. Другими словами, можно сказать, двоичные разряды получившегося числа — это результат умножения соответствующих битов операнда: 1х1 = 1, 1х0 = 0. Побитовому И соответствует следующая таблица истинности:
Пример работы побитового И на выражении 38 & 53:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A & B | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
Как результат, получаем 1001002 , или 3610 .
С помощью побитового оператора И можно проверить, является ли число четным или нечетным. Для целых чисел, если младший бит равен 1, то число нечетное (основываясь на преобразовании двоичных чисел в десятичные). Зачем это нужно, если можно просто использовать %2? На моем компьютере, например, &1 выполняется на 66% быстрее. Довольно неплохое повышение производительности, скажу я вам.
Исключающее ИЛИ (XOR)
Разница между исключающим ИЛИ и побитовым ИЛИ в том, что для получения 1 только один бит в паре может быть 1:
Например, выражение 138^43 будет равно…
| A | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| A ^ B | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
… 101000012 , или 16010
С помощью ^ можно поменять значения двух переменных (имеющих одинаковый тип данных) без использования временной переменной.
Также с помощью исключающего ИЛИ можно зашифровать текст. Для этого нужно лишь итерировать через все символы, и ^ их с символом-ключом. Для более сложного шифра можно использовать строку символов:
String msg = "This is a message";
char[] message = msg.toCharArray();
String key = ".*)";
String encryptedString = new String();
for(int i = 0; i< message.length; i++){
encryptedString += message[i]^key.toCharArray()[i%key.length()];
}
Исключающее ИЛИ не самый надежный способ шифровки, но его можно сделать частью шифровального алгоритма.
Побитовое отрицание (NOT)
Побитовое отрицание инвертирует все биты операнда. То есть, то что было 1 станет 0, и наоборот.
Вот, например, операция ~52:
| A | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|
| ~A | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Результатом будет 20310
При использовании побитового отрицания знак результата всегда будет противоположен знаку исходного числа (при работе со знаковыми числами). Почему так происходит, узнаете прямо сейчас.
Дополнительный код
Здесь мне стоит рассказать вам немного о способе представления отрицательных целых чисел в ЭВМ, а именно о дополнительном коде (two’s complement). Не вдаваясь в подробности, он нужен для облегчения арифметики двоичных чисел.
Главное, что вам нужно знать о числах, записанных в дополнительном коде — это то, что старший разряд является знаковым. Если он равен 0, то число положительное и совпадает с представлением этого числа в прямом коде, а если 1 — то оно отрицательное. То есть, 10111101 — отрицательное число, а 01000011 — положительное.
Чтобы преобразовать отрицательное число в дополнительный код, нужно инвертировать все биты числа (то есть, по сути, использовать побитовое отрицание) и добавить к результату 1.
Например, если мы имеем 109:
| A | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| ~A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ~A+1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Представленным выше методом мы получаем -109 в дополнительном коде.
Только что было представлено очень упрощенное объяснение дополнительного кода, и я настоятельно советую вам детальнее изучить эту тему.
Побитовый сдвиг влево
Побитовые сдвиги немного отличаются от рассмотренных ранее битовых операций. Побитовый сдвиг влево сдвигает биты своего операнда на N количество битов влево, начиная с младшего бита. Пустые места после сдвига заполняются нулями. Происходит это так:
| A | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|
| A<<2 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Интересной особенностью сдвига влево на N позиций является то, что это эквивалентно умножению числа на 2N. Таким образом, 43<<4 == 43*Math.pow(2,4). Использование сдвига влево вместо Math.pow обеспечит неплохой прирост производительности.
Побитовый сдвиг вправо
Как вы могли догадаться, >> сдвигает биты операнда на обозначенное количество битов вправо.
Если операнд положительный, то пустые места заполняются нулями. Если же изначально мы работаем с отрицательным числом, то все пустые места слева заполняются единицами. Это делается для сохранения знака в соответствии с дополнительным кодом, объясненным ранее.
Так как побитовый сдвиг вправо — это операция, противоположная побитовому сдвигу влево, несложно догадаться, что сдвиг числа вправо на N количество позиций также делит это число на 2N. Опять же, это выполняется намного быстрее обычного деления.
Вывод
Итак, теперь вы знаете больше о битовых операциях и не боитесь их. Могу предположить, что вы не будете использовать >>1 при каждом делении на 2. Тем не менее, битовые операции неплохо иметь в своем арсенале, и теперь вы сможете воспользоваться ими в случае надобности или же ответить на каверзный вопрос на собеседовании.
Источники: «Understanding Bitwise Operators»,
«How to program with Bitwise Operators: The House with 8 Doors»,
«Understand how bitwise operators work».
| layout | title | permalink |
|---|---|---|
|
topic |
Битовые маски. Динамическое программирование по маскам |
topics/bitmasks/ |
Битовые маски
Как известно, числа в памяти компьютера представляются в двоичной системе
счисления в виде последовательности битов. Один бит может иметь значение
$$0$$ или $$1$$. Можно провести аналогию между битами и значениями типа
bool: $$0$$ обозначает false, а $$1$$ —
true. По такой аналогии число (последовательность битов) можно
представить как массив значений bool. Например, тип int
может обозначать массив из $$32$$ значений bool, а long long — из $$64$$.
Чаще всего массивы bool небольшого размера испольуются для обозначения
некоторого подмножества объектов, выбранного из множества. Например, для обозначения
элементов с индексами $$1$$ и $$4$$ (0-индексация), выбранных из множества из пяти
элементов используется массив $${false, true, false, false, true}$$, или
$${0, 1, 0, 0, 1}$$. Его можно представить в виде значения типа int:
$$10010_2$$ (индексация обычно начинается с младших битов числа, записываемых справа).
При интерпретации такого значения как обычного числа, оно будет равно
$$10010_2 = 18_{10}$$. Но при интерпретации его как массива логических значений
(битов), оно будет обозначать $${0, 1, 0, 0, 1}$$. С точки зрения C++ эти два
значения равносильны, и то, является ли значение типа int числом,
или массивом bool, зависит только от контекста, в котором оно
используется.
При использовании значений типа int или long long
как массивов из bool, такие значения называются битовыми
масками.
Операции с битовыми масками
Для работы с масками используются побитовые операции $$and, or, xor$$, и
битовые сдвиги.
Пусть две маски обозначают два множества элементов, и нам нужно получить
маску, содержащую элементы, входящие в оба множества (пересечение
множеств). В новой маске true должны находится только в тех
позициях, где в обеих масках находились true. Несложно заметить,
что такое описание соответствует побитовой операции $$and$$:
int c = a & b; // маска c равна пересечению масок a и b
Другой распространённой операцией является объединение множеств.
При объединении в новой маске true должны находиться в тех
позициях, в которых в хотя бы одной из масок находилось true.
Такое описание соответствует побитовой операции $$or$$:
int c = a | b; // маска c равна объединению масок a и b
Для получения значения индивидуального бита используется комбинация
битового сдвига вправо и операции $$and$$. Сначала нам нужно сдвинуть
биты маски так, чтобы нужный бит оказался самым младшим (находился справа).
Затем нам нужно откинуть все остальные биты маски. Реализуется это следующим
образом:
int bit = (a >> idx) & 1; // bit равен значению idx-го бита в маске a
Для установки значения определённого бита маски в true мы
должны применить к нему операцию $$or true$$. Реализуется это так (ко
всем остальным битам применяется $$or false$$, не имеющая никакого эффекта):
int b = a | (1 << idx); // маска b - копия маски a, в которой idx-ый бит установлен в true
Для изменения значения определённого бита на противоположное, нужно
применить к нему операцию $$xor true$$. Ко всем остальным битам применяется
$$xor false$$, также не имеющая никакого эффекта:
int b = a ^ (1 << idx); // маска b - копия маски a с противоположным значением idx-го бита
Это самые распространённые операции, выполняемые с масками. Существует
множество других, здесь не приведённых, но все они основаны на $$and, or, xor$$,
и сдвигах.
Динамическое программирование по подмножествам
Битовые маски часто используются как параметры для динамического
программирования. Такой вид ДП называется ДП по маскам, или ДП по подмножествам.
Классической задачей на ДП по подмножествам является широко известная
задача о коммивояжёре (англ. TSP — Travelling
Salesman Problem). В общем виде она ставится следующим образом:
Существует $$N$$ городов, между некоторыми из которых есть дороги. Требуется
обойти все города, вернувшись в первый, так, чтобы длина пути была минимальной.
Эта задача является классической NP-полной задачей, и ДП по подмножествам
со сложностью порядка $$O(2^N * N^2)$$ — её оптимальное решение.
Для простоты реализации примем, что города являются точками на геометрической
плоскости, и между каждой парой есть путь, длина которого равна расстоянию между
точками.
Обозначим за $$dp[mask][i]$$ — длину кратчайшего пути, начинающегося
в вершине $$0$$, проходящего через все вершины $$mask$$, и заканчивающегося
в вершине $$i$$ ($$0 in mask; i in mask$$). Начальные
значения ДП можно записать следующим образом:
$$dp[mask][i] = infty \
dp[{0}][0] = 0$$
Запись $${0}$$ обозначает маску, обозначающую множество, состоящее только из
элемента $$0$$.
Формула перехода для ДП выглядит так:
$$dp[mask][i] = min_{substack{j in mask backslash i}} (dp[mask backslash i][j] + dst(j, i))$$
Запись $$mask backslash i$$ обозначает множество $$mask$$ без элемента $$i$$.
Формула перехода обозначает следующее: чтобы попасть в вершину $$i$$, нужно
перейти в неё из какой-либо другой вершины $$j$$, также входящей в $$mask$$. Из
всех таких вершин нужно выбрать такую, что общая длина пути в $$i$$ будет
наименьшей. Общая длина пути рассчитывается как длина пути в $$j$$
($$dp[mask backslash i][j]$$) плюс длина пути из $$j$$ в $$i$$ ($$dst(j, i)$$).
Чтобы найти минимальную длину цикла из всех вершин, нужно перебрать вершину
$$i$$, и выбрать такую, что длина цикла $$0 — ldots — i — 0$$ минимальна. Длина
такого цикла вычисляется по формуле $$dp[mathbb{V}][i] + dst(i, 0)$$:
$$ans = minlimits_{i in mathbb{V}} (dp[mathbb{V}][i] + dst(i, 0))$$
Запись $$mathbb{V}$$ обозначает множество всех вершин.
Может показаться, что порядок пересчёта такого ДП будет достаточно сложным.
На самом деле это не так: заметьте что для пересчета $$dp[mask][i]$$ нам нужно,
чтобы уже был посчитан ответ для маски $$mask backslash i$$. Можно легко доказать,
что в численном выражении $$mask backslash i$$ будет гарантированно меньше $$mask$$,
так как на некоторой позиции в $$mask$$ будет находиться бит $$1$$, а в
$$mask backslash i$$ бит $$0$$. Значит, можно просто пересчитывать ДП в порядке
возрастания значения $$mask$$ в численном выражении.
Реализация решения задачи о коммивояжёре
{% highlight cpp linenos %}
#include <bits/stdc++.h>
using namespace std;
const double INF = 1e9 + 7; //бесконечность
double x[20], y[20]; //координаты городов.
//Заметим, что для N элементов существует 2^N возможных подмножеств (масок)
//значением от 0 до 2^N — 1.
//Можно просто возвести 2 в произвольную степень с помощью битового сдвига:
//2^N = 1 << N
double dp[1 << 20][20];
//Расстояние между городами a и b
double dst(int a, int b) {
double dx = x[a] — x[b], dy = y[a] — y[b];
return sqrt(dx * dx + dy * dy);
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
for (int mask = 0; mask < (1 << n); mask++) {
for (int i = 0; i < n; i++) {
dp[mask][i] = INF;
}
}
dp[1][0] = 0; //Маска 1 содержит только нулевой элемент.
for (int mask = 2; mask < (1 << n); mask++) {
for (int i = 0; i < n; i++) {
if ((mask >> i) & 1) { //Если mask содержит i
int mask_without_i = mask ^ (1 << i);
for (int j = 0; j < n; j++) {
if (j != i && ((mask >> j) & 1)) { //Если j != i и mask содержит j
dp[mask][i] = min(dp[mask][i], dp[mask_without_i][j] + dst(j, i));
}
}
}
}
}
double ans = INF;
int mask_all = (1 << n) - 1; //маска, содержащая все элементы
for (int i = 0; i < n; i++) {
ans = min(ans, dp[mask_all][i] + dst(i, 0));
}
cout << ans << endl;
}
{% endhighlight %}
Двоичная математика, работа с битовой логикой
Наряду с обычными логическими операция над логическими типами Boolean, часто приходится выполнять операции и над отдельными битами, обычно используемыми, как флаги. Для эффективной работы необходимо понимание логических операций.
Паскаль поддерживает следующие логические операции
· AND – логическое И;
· OR — (включающие) логическое ИЛИ;
· XOR — (исключающие) логическое ИЛИ;
· NOT — отрицание или инверсия бита;
· SHL – логический сдвиг влево;
· SHR – логический сдвиг вправо.
Другие логические операции над числами в Паскаль не включены, но доступны через ассемблерные вставки.
Каждый бит может иметь только два состояния ЛОЖЬ (FALSE) или ИСТИНА (TRUE)
Состояние бита можно описывать и другими словами, часть которых пришла из математики, часть из электроники, часть из логики.
Для значения ЛОЖЬ, альтернативные варианты такие – НЕТ, НОЛЬ, ВЫКЛЮЧЕНО, НЕ УСТАНОВЛЕНО, СБРОШЕНО, FALSE, F, 0, — и другие.
Для значения ИСТИНА, альтернативные варианты такие – ДА, ЕДИНИЦА, ВКЛЮЧЕНО, УСТАНОВШЕНО, ВЗВЕДЕНО, TRUE, T, 1, + и другие.
Рассмотрим эти операции по отдельности
AND – логическое И, эта операции выглядит так
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Выражение истинно, когда истинны оба бита. Присказка «И там И там»
OR — (включающие) логическое ИЛИ, эта операции выглядит так
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Выражение истинно, когда истинен хотя бы один бит. Присказка «ИЛИ там ИЛИ там, включая и там и там»
XOR — (исключающие) логическое ИЛИ, эта операции выглядит так
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Выражение истинно, когда истинен только один бит. Присказка «ИЛИ там ИЛИ там, исключая и там и там»
NOT — отрицание или инверсия бита, эта операции применяется только к одному биту, действие простое текущее значение бита изменяется на противоположное
SHL – логический сдвиг влево, операции применяется только к группе битов, одного из целочисленных типов Паскаля, например к байту, слову и т.д.
Сдвиг байта влево на один разряд.
|
Разряды |
B7 |
B6 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
|
До |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
После |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
Сдвиг байта влево на два разряда.
|
Разряды |
B7 |
B6 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
|
До |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
После |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
Байт смещается влево на один или более разрядов, позиции справа замещаются нулями, позиции слева теряются.
SHR – логический сдвиг вправо, операции применяется только к группе битов, одного из целочисленных типов Паскаля, например к байту, слову и т.д.
Сдвиг байта вправо на один разряд.
|
Разряды |
B7 |
B6 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
|
До |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
После |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Сдвиг байта вправо на два разряда.
|
Разряды |
B7 |
B6 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
|
До |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
После |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Байт смещается вправо на один или более разрядов, позиции слева замещаются нулями, позиции справа теряются.
На этом описание операций заканчивается, и переходим к практическим примерам. Но вначале немного слов о нотации
Применяемая нотация при отображении чисел в литературе
Числа в символьной форме принято отображать, так что бы младшие разряды были справа, а строки слева, при этом если используется выравнивание, то оно тоже подчиняется этим правилам.
Нумерация разрядов начинается с нуля в соответствии со степень разряда и описывается формулой K*M^N, где K это коэффициент в диапазоне от 0 до M-1, M это основание числа, а N это степень. Число в степени 0 для всех оснований равно 1.
Посмотрим на примере следующей таблицы для четырех основных оснований.
Для числа 100
|
Основание |
Значение |
Формула |
|
2 |
4 |
1*2^2 + 0*2^1 +0*2^0 |
|
8 |
64 |
1*8^2 + 0*8^1 +0*8^0 |
|
10 |
100 |
1*10^2 + 0*10^1 + 0*2^0 |
|
16 |
256 |
1*16^2 + 0*16^1 + 0*2^0 |
Для числа 123
|
Основание |
Значение |
Формула |
|
2 |
X |
Не допустимая комбинация |
|
8 |
83 |
1*8^2 + 2*8^1 + 3*8^0 |
|
10 |
123 |
1*10^2 + 2*10^1 + 3*10^0 |
|
16 |
291 |
1*16^2 + 2*16^1 + 3*16^0 |
Практические примеры
В начале несколько простых примеров по использованию логических операций, а в заключение будет рассмотрено применение этих приемов для работы с каталогами.
Получение позиции бита или его значения
1 shl N
В данном примере единица сдвигается влево на нужное количество разрядов, и в результате получаем двоичное значение, равное 2^N, где в установлен один единственный бит, соответствующий разряду числа. Этот прием может использоваться с переменной для расчета позиции во время выполнения или во время компиляции, во втором случае код генерироваться не будет, а компилятор просто рассчитает значение и подставит его в программу, не генерируя дополнительного кода. Это удобно для указания номера бита, не представляя его в виде десятичной или шестнадцатеричной константы. Но чаще бывает удобнее использовать именованные константы, поскольку они более информативны, примеры этого будут приведены в конце статьи.
Установка бита
Для установки отдельного бита или группы битов используется операция ИЛИ, использование иллюстрируется ниже приведенным кодом в виде отдельной функции и результатом выполнения в виде таблицы.
function SetBit(Src: Integer; bit: Integer): Integer;
begin
Result := Src or (1 shl Bit);
end;
Здесь происходит следующее:
Сначала мы рассчитываем позицию бита – (1 shl Bit), затем устанавливаем полученный бит и возвращаем результат через предопределенную переменную Result.
Пример использования:
DummyValue := SetBit(DummyValue, 2);
|
Разряды |
B7 |
B6 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
|
До (1) |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
После |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
До (2) |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
После |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Как видим, вне зависимости от начального состояние бита, после выполнения операции бит становится равны единице.
Сброс бита
Для сброса отдельного бита или группы битов используется операция И совместно с инверсной маской, использование иллюстрируется ниже приведенным кодом в виде отдельной функции и результатом выполнения в виде таблицы.
function ResetBit(Src: Integer; bit: Integer): Integer;
begin
Result := Src and not (1 shl Bit);
end;
Здесь происходит следующее:
Сначала мы рассчитываем позицию бита – (1 shl Bit), затем с помощью операции NOT инвертируем полученную маску, устанавливая, не затрагиваемые биты маски в единицу, а затрагиваемый бит в ноль, затем сбрасываем этот бит, а результат возвращаем результат через предопределенную переменную Result.
Пример использования:
DummyValue := ResetBit(DummyValue, 2);
|
Разряды |
B7 |
B6 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
|
До (1) |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
После |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
До (2) |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
После |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Как видим, вне зависимости от начального состояние бита, после выполнения операции бит становится равны нулю.
Переключение бита
Для переключения отдельного бита или группы битов используется операция исключающие ИЛИ, использование иллюстрируется ниже приведенным кодом в виде отдельной функции и результатом выполнения в виде таблицы.
function InvertBit(Src: Integer; bit: Integer): Integer;
begin
Result := Src xor (1 shl Bit);
end;
Здесь происходит следующее:
Сначала мы рассчитываем позицию бита – (1 shl Bit), затем с помощью операции XOR переключаем бит, а результат возвращаем результат через предопределенную переменную Result.
Пример использования:
DummyValue := InvertBit(DummyValue, 2);
|
Разряды |
B7 |
B6 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
|
До (1) |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
После |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
До (2) |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
После |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Как видим, состояние бита B2 изменяется на противоположное.
Проверка бита
Для проверки бита используется операция AND и анализ результата на равенство нулю.
if Value and (1 shl N) <> 0 then ... установлен
if Value and (1 shl N) = 0 then ... не установлен
чаще всего это используется в другой форме, вместо расчета позиции используется именованная константа, например
const
B2 = 4 // B2 (1 shl 2)
Begin
if Value and B2 = B2 then ... установлен
if Value and B2 = 0 then ... не установлен
end;
Это более наглядно, особенно если константе дано более значимое имя, чем B2, например, для проверки готовности передатчика мы можем определить константу с именем TxReady, тогда это будет выглядеть очень красиво.
const
TxReady = 4
Begin
if Value and TxReady then begin
... обработка готовности передатчика
end;
end;
Ну, вот с базисом мы покончили и пора приступить к более полезным и практическим примерам. В качестве примера выберем поиск папок и файлов. Пример был разработан для FAQ конференции fido7.ru.delphi, в дальнейшем был немного модернизирован по замечаниям от Юрия Зотова. Полный пример и остальные статьи из FAQ доступны для загрузки с моего сайта.
procedure ScanDir(StartDir: string; Mask:string; List:TStrings);
var
SearchRec : TSearchRec;
Begin
if Mask = '' then Mask := '*.*';
if StartDir[Length(StartDir)] <> '' then StartDir := StartDir + '';
if FindFirst(StartDir + Mask, faAnyFile, SearchRec) = 0 then
begin
repeat
Application.ProcessMessages;
if (SearchRec.Attr and faDirectory) <> faDirectory
then
List.Add(StartDir + SearchRec.Name)
else if (SearchRec.Name <> '..') and (SearchRec.Name <> '.')
then
begin
List.Add(StartDir + SearchRec.Name + '');
ScanDir(StartDir + SearchRec.Name + '', Mask, List);
end;
until FindNext(SearchRec) <> 0;
FindClose(SearchRec);
end;
end;
Рассмотрим ключевые моменты, относящиеся к данной статье.
if FindFirst(StartDir + Mask, faAnyFile, SearchRec) = 0 then
Здесь является битовой маской, описанной в модуле SysUtils, ее значение равно $3F, она предназначена для включения в поиск специальных файлов и одновременно для изоляции лишних бит из структуры TSearchRec, отдельные биты данной маски описаны как именованные константы.
|
Нименование |
Значение |
Описание |
|
|
FaReadOnly |
$00000001 |
Read-only files |
Файлы с защитой от записи |
|
faHidden |
$00000002 |
Hidden files |
Невидимые файлы |
|
faSysFile |
$00000004 |
System files |
Системные файлы |
|
faVolumeID |
$00000008 |
Volume ID files |
Метка тома |
|
faDirectory |
$00000010 |
Directory files |
Папки |
|
faArchive |
$00000020 |
Archive files |
Архивные файлы (для системы архивации) |
|
faAnyFile |
$0000003F |
Any file |
Все файлы – комбинация выше указанных флагов |
if (SearchRec.Attr and faDirectory) <> faDirectory
здесь мы видим проверку флага faDirectory, работает это следующим образом, сначала изолируются не нужные биты, затем проводится проверка на неравенство нулю, поскольку все остальные биты изолированы, то возможны только два значения, ноль, если флаг не установлен и не ноль установлен, в зависимости от результата выполняется, или часть THEN, или часть ELSE. Других вещей касаемо нашей статьи в примере нет и поэтому рассматривать больше нечего. Прочие логические операции работают с булевыми, а не с битовыми значения.
В заключение статьи можно еще привести примеры использования масок для изоляции битов и выполнения операций над оставшимися битами, возьмем для примера какую ни будь абстрактную комбинацию бит и выполним, что ни будь с ними.
Например, у нас есть такая структура некоторого устройства, и при поступлении данных происходит прерывание, обработка которого поступает в наш обработчик и в другие вместе с кодом состояния, если мы обработали сообщение, то мы должны возвратить значение TRUE, если то FALSE и тогда управление будет передано следующему в цепочке обработчику. Бит TxReady проверять не надо, управление будет поступать, только тогда когда он установлен.
abcccddd – где
a – бит готовности
b – бит разрешения прерывания
ccc – тип операции
ddd – счетчик
function MyHandler(Code: byte): Boolean;
const
TxReady = $80;
IntBit = $40;
TypeMask = $38;
CounterMask = $07;
var
I: Integer;
TypeBits: Byte;
begin
if (Code and Intbit) = Intbit
then
begin
// изллируем биты типа и смещаем вправо для дальнейшей обработки
TypeBits := (Code and TypeMask) shr 3;
Case TypeBits of
0: begin
for I := 1 to (Code and CounterMask) do
begin
считываем N данных, количесво указано в битах CounterMask,
которые мы изолировали и использовали в качестве значения
для окончания цикла.
end;
Result := TRUE; // обрабатали, пусть больше никто не трогает
end;
1: begin
команда 1, что то делаем
Result := TRUE; // обрабатали, пусть больше никто не трогает
end;
2: begin
команда 2, что то делаем
Result := TRUE; // обрабатали, пусть больше никто не трогает
end;
else Result := FALSE; // другие команды не наше дело
end;
end
else
begin
Result := FALSE; // пусть другой обрабатывает
end;
end;
Ошибки при работе с битами
Например, для сложения бит мы можем использовать два варианта или операцию + или операцию OR. Первый вариант является ошибочным.
AnyValue + 2, если бит два установлен, то в результате этой операции произойдет перенос в следующий разряд, а сам бит окажется сброшенным вместо его установки, так можно поступать если только если есть уверенность в результате, то если заранее известно начальное значение. А вот в случае использования варианта AnyValue or 2, такой ошибки не произойдет. Тоже относится к операции вычитания для сброса бита.
faAnyFiles – faDirectory ошибки не даст, а вот AnyFlags – AnyBit может, дать правильный вариант, а может нет. Зато AnyFlags and not AnyBit всегда даст то что замали, использования этой техники будет правильнее и для работы с аттрибутами файлов — faAnyFiles and not faDirectory. В качестве домашнего задания попробуйте выполнить это на бумаге для разных комбинацияй бит.
Еще одна распростаненая ошибка, это логическая при выполнении операций над групами бит. Например неверено выполнять операцию сравнения над следующей конструкцией AnyFlags and 5 <> 0, если истина должна быть при установке обеих бит, надо писать так AnyFlags and 5 = 5, зато если устраивает истина при установке любого из бит, выражение AnyFlags and 5 <> 0 будет верныи.
На этом статья закончена и вы смогли получить начальные сведения по выполнению логических операций с битами, в заключении приведу и таблицу весовых коэффициентов, чтобы было легче рассчитывать константы.
Приложения
Таблица весовых множителей для 32 битного числа
|
Бит |
Dec |
Hex |
Бит |
Dec |
Hex |
Бит |
Dec |
Hex |
Бит |
Dec |
Hex |
|
0 |
1 |
1 |
8 |
256 |
100 |
16 |
65536 |
10000 |
24 |
16777216 |
1000000 |
|
1 |
2 |
2 |
9 |
512 |
200 |
17 |
131072 |
20000 |
25 |
33554432 |
2000000 |
|
2 |
4 |
4 |
10 |
1024 |
400 |
18 |
262144 |
40000 |
26 |
67108864 |
4000000 |
|
3 |
8 |
8 |
11 |
2048 |
800 |
19 |
524288 |
80000 |
27 |
134217728 |
8000000 |
|
4 |
16 |
10 |
12 |
4096 |
1000 |
20 |
1048576 |
100000 |
28 |
268435456 |
10000000 |
|
5 |
32 |
20 |
13 |
8192 |
2000 |
21 |
2097152 |
200000 |
29 |
536870912 |
20000000 |
|
6 |
64 |
40 |
14 |
16384 |
4000 |
22 |
4194304 |
400000 |
30 |
1073741824 |
40000000 |
|
7 |
128 |
80 |
15 |
32768 |
8000 |
23 |
8388608 |
800000 |
31 |
2147483648 |
80000000 |


 Сообщение было отмечено Hellgrove как решение
Сообщение было отмечено Hellgrove как решение