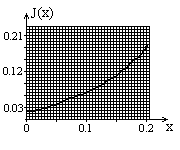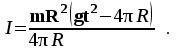Как изменится момент инерции маятника обербека если изменить положение цилиндров на маятнике

Цель работы

Изучение
законов динамики вращательного движения;
теоретическое и экспериментальное
определение момента инерции крестообразного
маятника Обербека; изучение зависимостей
угловой скорости и момента силы от
момента инерции.

Основные
понятия.

Моментом
силы F относительно точки О называется
векторное произведение радиус-вектора
,
проведенного из точки О в точку приложения
силы, на вектор силы
:
.

Моментом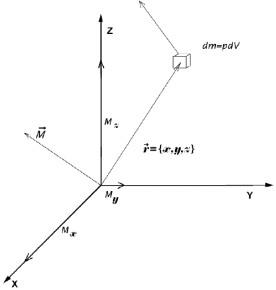
силы относительно оси называется
скалярная величина, равная проекции на
данную ось вектора момента силы
относительно какой-либо точки той же
оси.

Если
рассмотреть отдельную материальную
точку массой dm,
вращающуюся вокруг оси на расстоянии
r,
то ее момент инерции равен J=dmr².
Твердое тело можно мысленно представить
как совокупность большого числа n
материальных точек dm_i
и
просуммировать моменты инерции всех
точек относительно данной оси:

(1)

Если
тело однородно, то dm=dV,
где 
— плотность, dV – элементарный
объем. Тогда момент инерции всего тела
может быть рассчитан по формуле:

(2)

Если
известен момент инерции тела относительно
оси, проходящей через центр инерции
(центр масс) тела J₀,
то можно вычислить момент инерции тела
относительно оси с помощью теоремы
Штейнера:
момент инерции J
относительно произвольной оси вращения
равен сумме моментов инерции J₀
относительно
оси, параллельной данной и проходящей
через центр масс тела, и произведения
массы тела m
на квадрат расстояния a
между
осями:

J=J₀+ma²
(3)

Покажем,
как, пользуясь теоремой Штейнера и
выражением для момента инерции цилиндра,
полученным из (2) после интегрирования
по объему, можно рассчитать момент
инерции крестообразного маятника
Обербека.

Момент
инерции всего маятника относительно
оси вращения равен сумме моментов
инерции четырех стержней с цилиндрическими
грузами на них, момента инерции втулки,
в которой крепятся стержни, и момента
инерции барабана:

J=J_вт+J_б+4(J_ст+J_гр)
(4)

У
втулки и барабана ось вращения проходит
через их центр масс, это цилиндрические
тела, поэтому:

Момент
инерции стержня длиной l_ст,
относительно оси, проходящей через его
конец и перпендикулярный ему

Момент
инерции грузов найдем, считая грузы
материальными точками массой m,
так как их рамеры малы по сравнению с
расстоянием до оси вращения:
J_гр=m_грx²,
где x
–
расстояние от центра груза до оси
вращения. Все части маятника – цилиндры,
поэтому их массы запишутся
,
где =7.810³
кг/м³
– плотность стали, d
– диаметр
цилиндра, l
– его
высота или длина.

(5)

Момент
силы
,
момент инерции J
и угловое
ускорение

связаны основным законом динамики
вращательного движения:
.

Учитывая,
что
,
этот закон можно записать в виде:

(6)

где

— момент
импульса (количества движения) тела.

Методика
эксперимента

Маятник
Обербека состоит из четырех стержней,
расположенных под прямым углом друг к
другу, втулки и барабана, на который
наматывается нить. По стержням могут
перемещаться грузы равной массы, которые
могут быть укреплены в любых точках
стержня.

Маятник
приводится во вращение с помощью груза
m,
подвешенного на шнуре, который наматывается
на барабан. Если груз поднять на некоторую
высоту h,
то он будет опускаться, вращая барабан,
а с ним и весь маятник.

1.
Момент инерции маятника можно определить
из основного закона динамики вращательного
движения
,
где
—
момент
силы, приводящий маятник во вращение,
—
его угловое ускорение. Выразим момент
силы и угловое ускорение через величины,
легко измеряемые на опыте. Момент силы
– это произведение силы на плечо ее
приложения, то есть радиус барабана r_б.
Силой, вращающей маятник, является сила
натяжения шнура. Для определения силы
натяжения шнура рассмотрим силы,
действующие на груз.

Со
стороны Земли действует сила тяжести
mg,
со стороны шнура – сила натяжения F_н.
По второму закону Ньютона
,
где
—
линейное ускорение груза. Спроектируем
на вертикальную ось:

(7)

Ускорение
груза a
найдем из формулы равноускоренного
движения h=at²/2,
где h
– высота, с которой опускается груз, t
– время
движения. Получим a=2h/t².
Окончательно момент силы:

(8)

Угловое
ускорение 
маятника и барабана найдем, связав его
с линейным ускорением груза
a. Так
как шнур плотно намотан на барабан, он
сообщает точкам его поверхности то же
линейное ускорение, которое имеет груз.
Поэтому a=r_б
одновременно
является линейным ускорением груза и
точек поверхности барабана. Тогда:

(9)

Подставив
(10) и (9) в (7), получим
,
откуда

(10)

2.
С помощью маятника Обербека можно
опытным путем получить связь между 
и моментом инерции J.

Меняя
расстояние от грузов на стержнях до оси
вращения, мы тем самым меняем момент
инерции маятника. Поэтому, в соответствии
с основным законом динамики вращательного
движения, если J₁>J₂,
должно получиться ₁<₂.
Угловое ускорение в каждом случае
рассчитывается через время падения
(9). При постоянном моменте силы M:

M=J₁₁=J₂₂.
(11)

.
Установка позволяет определить момент
сил трения, возникающих в трущихся
частях на оси вращения. Груз m,
поднятый на высоту h относительно
нижней точки, сначала опускается до
этой точки, а затем из-за инертности
вращательного движения маятника вновь
поднимается до высоты h₁<h.

Запишем
закон сохранения энергии с учетом сил
трения для одного такого цикла:

mgh=mgh₁+M_Тр,

где

— угол поворота маятника за все время
движения.

Так
как
,
то получим:
.
Отсюда:

(12)

Порядок
выполнения работы

Для
определения момента инерции:

1.
Закрепляем грузы на концах стержней
маятника Обербека и 3 раза измеряем t
– время падения груза с высоты h.

2.
Уменьшаем на одинаковую величину
расстояние от грузов до оси вращения и
повторяем п.1.

x(c)	t1(c)	t2(c)	t3(c)	(c)
0.2	15.5	17	16.5	16.3
0.05	10	11	11	10.6

Для
определения момента сил трения:

1.
Измеряем высоту h
падения
груза относительно нижней точки.

2.
Отпускаем груз и измеряем высоту h₁,
на которую поднимется груз при остановке
маятника.

3.
Повторяем опыт 3 раза и находим среднее
значение
.

h=0.6
м

h1=0.23 м

h1=0.24 м

h1=0.24 м

=0.237 м

Обработка
результатов эксперимента

_стали
=
7,710³
кг/м³;
H =
2,510^-2
м;
a = 2,510^-2
м/c²;
H₀
= 8,310^-2
м;
R = 1,010^-2
м.

1.
По формуле (10) определяем J
для каждого опыта:
J₁=0.057,
J₂=0.068,
J₃=0.064
– при
x=0.2;
J₁=0.024,
J₂=0.028,
J₃=0.028
– при
x=0.05.

Определяем
среднее значение

при каждом положении x:

=0.063
кгм²;

=0.027
кгм².

Строим
график зависимости момента инерции
маятника от положения грузов на стержнях
(x).

2.
По формуле (5) при тех же значениях x
теоретически
рассчитываем и строим зависимость
(x).

x	0,2	0,05
(x)	0,1879	0,0366

3.
По формуле (9) определяем 
и проверяем выполнение соотношения
(11).

J₁₁=2,8510^-2,
J₂₂=2,8810^-2
J₁₁J₂₂

4.
По формуле (12) рассчитываем значение
M_Тр.
M_Тр=1.2510^-2.

Расчет
погрешностей

Абсолютная
погрешность J
измерения
момента инерции рассчитывается по
формуле для косвенных измерений:

Величина
t
определяется как случайная погрешность
прямого измерения.

,

x	t	J
0.2	0.054	0.001
0.05	0.183	0.0014

где
С_N
– коэффициент Стьюдента, t_i
– время,
полученное при i-ом
измерении,
—
среднее время из N
измерений,
—
среднее значение момента инерции.

Погрешность
измерения момента сил трения рассчитывается
по формуле для косвенного измерения:

где
при заданном значении h
величина
h
определяется как приборная погрешность
(половина цены деления измерительной
линейки), а h₁
для N
измерений вычисляется по формуле
Стьюдента:

где

— среднее значение высоты подъема, h_1k
– высота
подъема при k-ом
измерении.

h₁=0.006,
M_Тр=0.002

Проделав все
задания, относящиеся к данной лабораторной
работе и сделав все необходимые
вычисления, мы можем сделать ряд выводов:

• с
  увеличением расстояния между осью
  вращения и положением цилиндров, момент
  инерции маятника J
  увеличивается;

• угловая
  скорость вращения маятника обратно
  пропорционально зависит от величины
  t,
  то есть чем меньше время прохождения
  расстояния h^’
  ,
  тем угловая скорость больше, иначе –
  меньше;

Соседние файлы в папке лабораторная работа

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  24.01.201413.82 Кб65термопара.xls

---

Подборка по базе: 2022_I_Inf_ Сдать отчет ЛБ 2 (Часть 1 + Часть 2).pdf, Форма ежемесячного отчета кафедры.docx, отчёт по воспитательной работе.docx, ! НИР отчёт.docx, Форма отчета классного руководителя за семестр Жунисова 2023.doc, Задачи к практической работе Статистика.docx, Старый отчет Балык.docx, Анализ финансовой отчетности тест.docx, ПП.02 Отчет по производственной практике.docx, Отчет по лабораторной работе 1.docx

---

Пермский национальный исследовательский политехнический университет
Факультет химических технологий, промышленной экологии и биотехнологий

Отчет по лабораторной работе
«Маятник Обербека»

Выполнила студентка группы ХТ2‑20‑1б
Евдокимова Мария Александровна

Пермь, 2020

1. Введение.

Данная лабораторная работа посвящена исследованию вращательного движения, момента инерции c помощью маятника Обербека.

Маятник Обербека – лабораторное устройство, которое особенно актуально при изучении динамики вращательного движения относительно неподвижной оси. На примере работы маятника можно рассмотреть динамические характеристики вращательного движения твердого тела, такие как момент силы, момент инерции. Создателем маятника является немецкий физик Антон Обербек (Anton Oberbeck, 1846-1900). В лабораторной работе проводятся измерения движения маятника, находится его момент инерции, оценивается влияние трения на движение. Установка помогает обучаемым глубже понять основные физические закономерности и приобрести элементарные навыки проведения экспериментов.

Враща́тельное движе́ние — вид механического движения. При вращательном движении материальная точка описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

Моме́нт ине́рции — скалярная физическая величина, мера инерции во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Цель работы: изучение основного закона динамики вращательного движения, определение момента инерции системы грузов.

Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, два круглых груза, груз наборный, нить длиной 55 см с крючком (синяя), измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.

1.1 Краткая теория

Основной закон динамики вращательного движения твердого тела относительно неподвижной оси

(1)

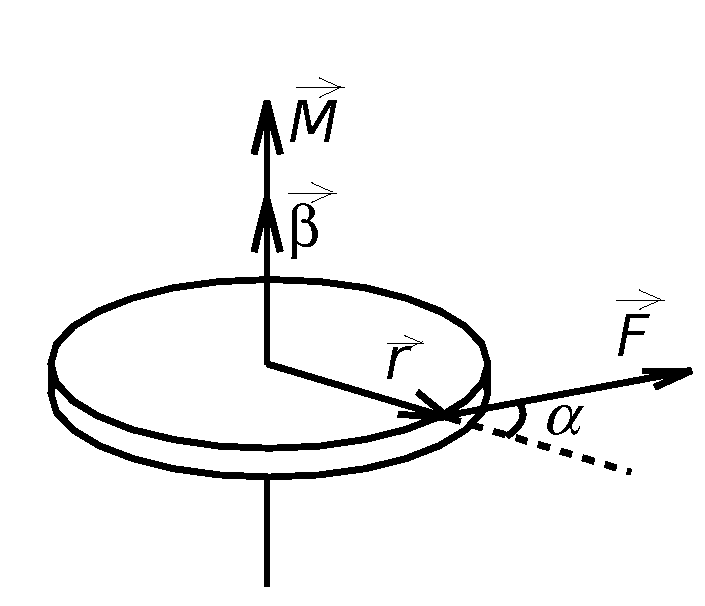
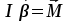
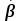
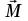
связывает кинематическую характеристику движения – угловое ускорение с динамическими характеристиками – моментом силы и моментом инерции I(рис. 1).

Угловое ускорение характеризует изменение угловой скорости во времени и направлено, как и момент силы, вдоль оси вращения.

Рис. 1. Момент M силы F

. (2)

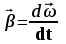
Угловое ускорение связано с касательной составляющей линейного ускорения а_τточки вращающегося тела соотношением

, (3)

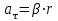
где r –- кратчайшее расстояние от этой точки до оси вращения.

Моментом силы в общем случае называют векторную величину

, (4)

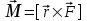
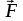
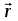
где – сила, лежащая в плоскости, перпендикулярной оси вращения; – вектор, соединяющий точку на оси c точкой приложения силы.

В уравнении (1) 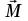– сумма составляющих моментов сил вдоль направления оси вращения.

Момент инерции I характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела. Момент инерции равен сумме произведений элементарных масс Δm_i, на которые мысленно разбито тело, на квадрат их расстояний до оси вращения

I = Σ Δm_ir_{i .} (5)

Выражая Δm_i через плотность тела: Δm_i =ρ ΔV_i,где ΔV_i – элементарный объем тела, и переходя к пределу при ΔV_i → 0, получим

(6)

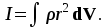
Формула (6) позволяет теоретически найти момент инерции любого тела. Например, момент инерции тонкого однородного стержня длиной l и массой т относительно оси, проходящей перпендикулярно стержню через его центр,

I= т l² / 12 .

Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

Теорема Штейнера устанавливает связь между моментом инерции Iс твердого тела относительно оси, проходящей через центр инерции, и моментом инерции относительно другой оси, параллельной первой

I = Iс + mа² , (7)

где а – расстояние между осями, m – масса тела.

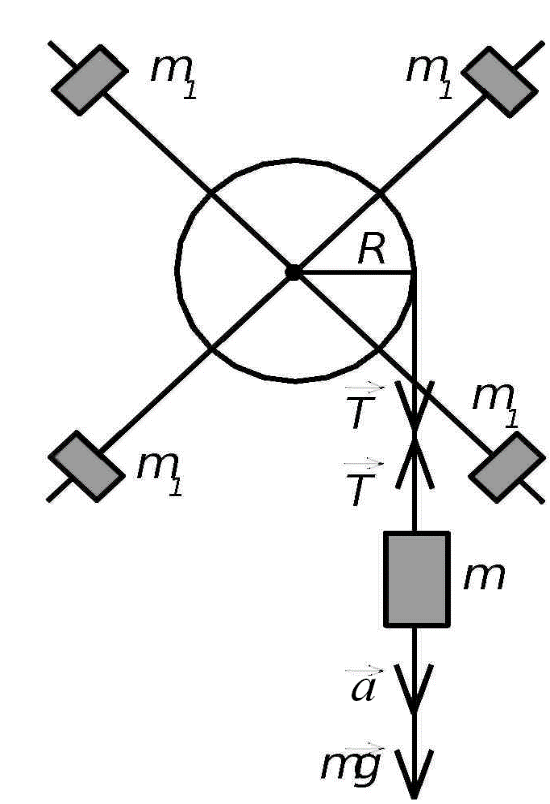
В настоящей работе экспериментально находится момент инерции маятника Обербека (рис.2). Он состоит из блока радиусом R, который может вращаться вокруг неподвижной горизонтальной оси. К блоку прикреплены симметрично относительнооси стержни, на каждом из которых могут свободно перемещаться грузы массами m₁, что дает возможность изменять момент инерции маятника. Грузы m₁ устанавливаются на одинаковом расстоянии от оси, так что центр инерции всей вращающейся части маятника находится на оси вращения.

Рис. 2. Маятник Обербека

К концу нити прикреплен груз массой m. Из закона динамики вращательного движения следует

. (8)

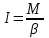
Основной закон динамики вращения (II закон Ньютона для вращательного движения): Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение.

Момент силы М, создающийся силой натяжения нити, исходя из (4)

, (9)

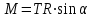
где α – угол между вектором 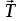и отрезком Rна рис. 2, равный 90°; sin α= 1.

Запишем второй закон Ньютона для поступательного движения груза mв проекции на направление ускорения а,

. (10)

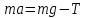
В этой формуле сила натяжения нити T, действующая на груз, по модулю равна силе натяжения нити, действующей на блок в формуле (9) (поэтому они обозначены одинаково). Это справедливо, если массой нити можно пренебречь по сравнению с массой груза т.

Из (9) и (10) получим

. (11)

Т ангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима.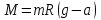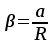

Тогда из (3) следует , (12)

(13)

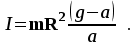
Подставляя (11)и(12)в (8), получим

Из этой формулы следует, что ускорение (а) не зависит от времени, так как все остальные величины в этом уравнении постоянны, значит, движение маятника будет равноускоренным и при нулевой начальной скорости.

(14)

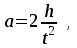
где h – путь, пройденный грузом т за время t.

В данной работе измеряется время одного полного оборота блока, и за это время груз массой m пройдет путь

h=2πR . (15)

Подставив (14) и (15) в (13), получим формулу для вычисления момента инерции маятника

(16)

Момент инерции маятника Обербека будет изменяться при изменении расстояния rот оси вращения маятника до центров грузов массами m₁, перемещаемых вдоль стержней.

Согласно теореме Штейнера (7)

, (17)

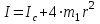
где I_c – момент инерции всей вращающейся части маятника при условии, что центры грузов m₁находились бы на оси вращения.

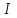
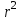
Из (17) следует, что зависимость от – линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.

Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины.

1. Описание экспериментальной установки, её особенности.

1- 9-переключатели

10- стойка

11- блок

12- стержень

13- пластиковый фиксатор

14-два круглых груза

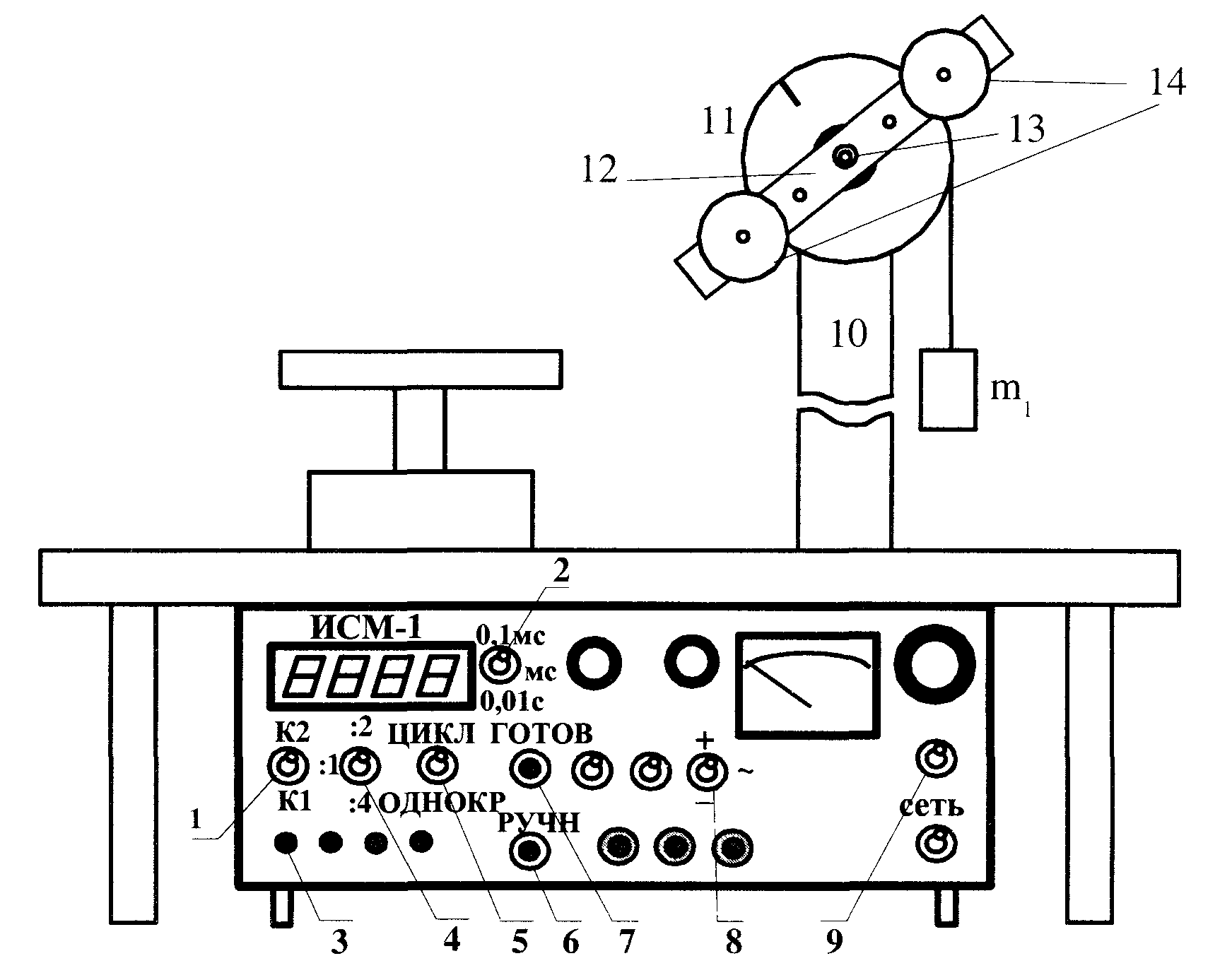
Рис. 2. Маятник Обербека на модуле ЛКМ-3

Маятник Обербека монтируется на блоке 11, закрепленном на стойке 10 модуля ЛКМ-3 (рис. 2). К блоку радиусом 25 мм прикрепляют нить, к концу которой подвешивают наборный груз массой m1 = 100 — 200 г. На ось блока через среднее отверстие надевают стержень 12 и закрепляют его пластиковым фиксатором 13. Вращая стержень накручивают на блок нить и поднимают груз так чтобы он не касался стержня. При опускании груза нить приведет во вращательное движение стержень. После полного раскручивания нити стержень, продолжая вращательное движение, накрутит нить на блок и поднимет груз. При этом вращательное движение прекратится — система перейдет в начальное состояние.

Время опускания и подъема груза (период колебаний маятника Обербека) зависит от многих параметров установки: длины нити, массы груза m1, момента инерции стержня и блока, радиуса блока (от сил трения, толщины и массы нити, которыми мы в данной работе пренебрегаем). Все эти допущения в дальнейшем скажутся на наших результатах.

Конструкция прибора позволяет изменять момент внешних сил и момент инерции системы I. Мо­мент внешних сил изменяется с изменением массы подвешенного к нити груза или при перенесе­нии нити с одного шкива на другой. Момент инерции можно изменять, перемещая грузы m₀ , по стержням крестовины.

Результаты исследования.

Таблица 1

№ п/п	m кг	T	I кг-м2	I-	(I-)2
1		0,901	1,658*10-3	-0,038*10-3	1,444*10-9
2		0,905	1,672*10-3	0,0188*10-3	3,534*10-10
3	0,109	0,890	1,616*10-3	-0,0382*10-3	1,459*10-9
4		0,892	1,624*10-3	-0,0302*10-3	9,120*10-10
5		0,912	1,700*10-3	0,0458*10-3	2,098*10-9
Среднее	—	—	1,6542*10-3	—	—
Сумма	—	—	—	—	5,706*10-9

В таблице 1 представлены результаты серии из пяти экспериментов по определению момента инерции стержня. Все опыты проведены в одинаковых условиях; разброс значений вызван неконтролируемыми факторами и определяется, как случайная погрешность.

Время t поворота отличается. Каждые 5 значений различны. Это может быть связано с тем, что мы могли случайно толкнуть маятник, который бы быстрее или же ,наоборот, медленнее прошел 1 оборот.

Мы провели 5 измерений времени вращения маятника. Рассчитаем момент инерции для каждого измерения (радиус маятника 25 мм):

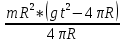
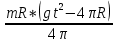
I= = (1)

I₁=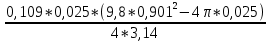 = 1,658*10^-3 кг-м²

I₂=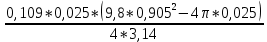 = 1,672*10^-3 кг-м²

I₃=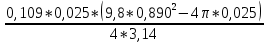 = 1,616*10^-3 кг-м²

I₄=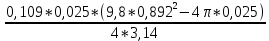 = 1,624*10^-3 кг-м²

I₅=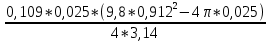 = 1,700*10^-3 кг-м²
Рассчитаем абсолютную и относительную погрешности помощи метода Стьюдента:

2,78 ⋅ 0,05 *10^-3

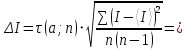
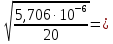
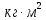
ε _I = (ΔI/ < I >)*100% =(4,696*10^-5/1,654*10^-3)*100%=3%

= 3 % при α = 0,95

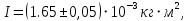
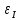
В результате мы получили достаточно точное значение момента инерции с погрешностью 3%. Но так как мы не учитывали массу и толщину нити, которые на практике увеличивали время прохождения полного оборота, То погрешность всё же есть. Также мы не учитывали силы трения в подшипниках оси блока и сопротивление воздуха, которые тоже замедляли время полного оборота.

Измерение момента инерции маятника Обербека в зависимости от положения грузов на стержне.

Таблица 2

№ п/п	т	t с	r м	r2*10-4 м	I *10—3 кг -м2
1		1,101	0,04	16	2,5
2		1,417	0,06	36	4,2
3		1,564	0,08	64	5,1
4	0,109 кг.	1,901	0,1	100	7,6
5		2,156	0,12	144	9,8
6		2,487	0,14	196	13,0
7		2,811	0,16	256	16,7

I= =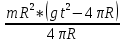

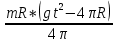
I₁= 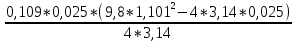= 0,0025 кг-м²

I₂ =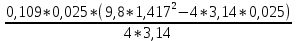 = 0,0042 кг-м²

I₃ =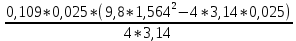 = 0,0051 кг-м²

I₄ =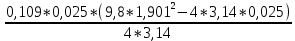 = 0,0076 кг-м²

I₅ =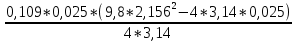 = 0,0098 кг-м²

I₆ =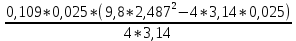 = 0,013 кг-м²

I₇ = 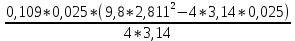= 0,0167 кг-м²

При анализе зависимости значения момента инерции от расстояния между грузами выявилась следующая закономерность: чем больше расстояние между грузами, тем больше момент инерции (Таблица 2).

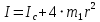
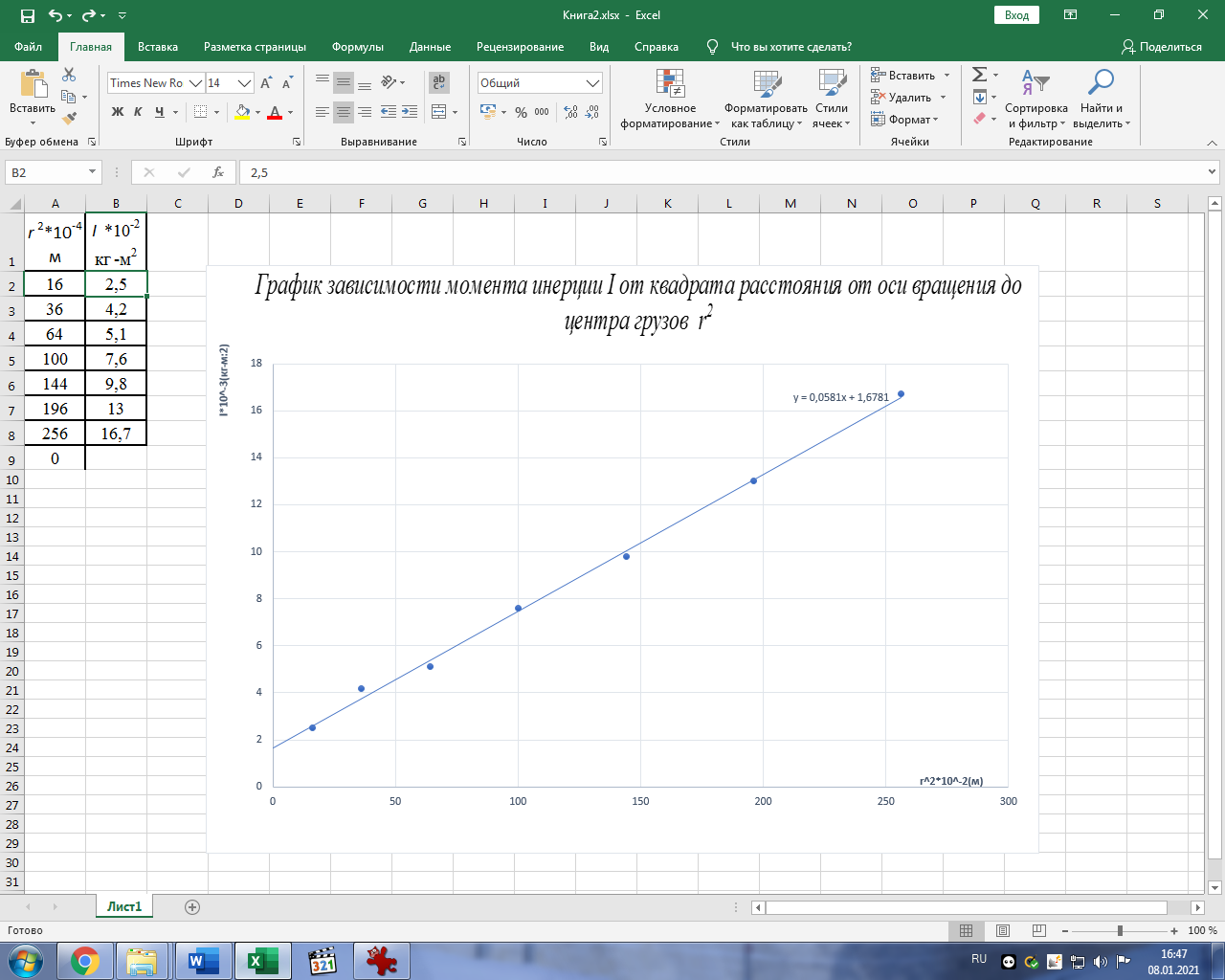
По формуле также можно понять, что момент инерции прямо пропорционален квадрату расстояний.

Построим график зависимости момента инерции Iот квадрата расстояния от оси вращения до центра грузов r².

График зависимости момента инерции I от квадрата расстояния от оси вращения до центра грузов r²

По графику определим момент инерции маятника:

I_C=1,6781 кг∙м²

Это значение входит в пределы доверительного интервала для момента инерции.

1. Анализ результатов.

После проведения опытов и произведения расчётов над полученными результатами, был определён момент инерции с помощью маятника Обербека. При вычислении его расчётным способом не учитывались такие факторы, как сила трения в подшипниках оси блока, сопротивление воздуха, толщина нити, масса нити, впоследствии они дали отклонение в 1,5%. Пренебрежение действия этих сил и является главной причиной систематической погрешности измерения момента инерции.

Результаты вычислений зафиксированы. Пришли к выводу, что при уменьшении радиуса вращения время вращения уменьшается. Построив график прямопропорциональности, заметим чем больше радиус шкива, тем больше момент инерции системы. Все опыты были проведены в одинаковых условиях. Разброс значений вызван неконтролируемыми факторами (случайная погрешность).

При определении зависимости момента инерции от квадрата расстояния от оси вращения до центра грузов получилась линейная зависимость, что указывает на достоверность вычислений.

3.1 Методические погрешности.

1) Сила трения в подшипниках блока замедляет движение блока, вращение перестает быть «свободным». Это влияет на время оборота, и в последствии получатся не полностью достоверные значения с погрешностями.

2) Падение замедляется из-за действия силы трения о воздух.

3) Проскальзывание и нерастяжимость нити также могут привести к погрешности.

1. Заключение.

В результате выполнения данной лабораторной работы , я изучила основной закон динамики вращательного движения, определила момент инерции системы грузов.. Небольшие погрешности обусловлены тем, что присутствует сила упругости, сила трения нити о подшипник, сила трения в блоке, а также инертность блока. Чтобы свести эту погрешность к минимуму, измерения проводились несколько раз с выведением среднего результата.

В ходе выполнения лабораторной работы я определила момент инерции стержня и блока, а также измерила момента инерции маятника Обербека в зависимости от положения грузов на стержне с учётом трения в подшипниках оси блока. Сравнила результаты, полученные в первом и втором опытах.
Литература

1. Методическое пособие. Общая физика, часть 1, механика. Лабораторный практикум. Под общей редакцией профессора Л.Н. Кротова. Издательство Пермского государственного технического университета, 2009. Стр.34-41
2. https://yandex.ru/images/search?text=%D0%BC%D0%B0%D1%8F%D1%82%D0%BD%D0%B8%D0%BA%20%D0%BE%D0%B1%D0%B5%D1%80%D0%B1%D0%B5%D0%BA%D0%B0%20%D0%BD%D0%B0%20%D0%BB%D0%BA%D0%BC%203&from=tabbar&pos=0&img_url=http%3A%2F%2F5fan.ru%2Ffiles%2F2%2F5fan_ru_11906_76f9b372e885658b9710a7fb3b5d5d2e.html_files%2F1.png&rpt=simage

Изучение законов движения на маятнике Обербека

Изучение законов движения на маятнике Обербека

Цель работы: Изучение динамики вращательного движения, оценка влияния трения на точность результатов проведенных измерений.

Оборудование: лабораторная установка (маятник Обербека), набор грузиков, линейка.

Теоретическое введение

Маятник Обербека представляет собой крестовину, состоящую из 4 стержней, прикрепленных ко втулке с осью (см. рис.1).

На стержни надеваются одинаковые грузы массой m1, которые могут быть закреплены на различных расстояниях от оси вращения. Два легких шкива с различными радиусами r1, и r2, насажены на ось вращения маятника. На один из шкивов наматывается нить, к свободному концу которой прикрепляется груз массой m. Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение. Положение груза m отмечается по шкале с делениями. Вся эта система может свободно вращаться вокруг горизонтальной оси. Момент инерции системы можно менять, передвигая грузы m1 вдоль стержней.

Вращение твердого тела постоянной массы вокруг неподвижной оси описывается уравнением моментов:

(1)

Здесь М — момент сил, действующих на тело, I — момент инерции тела, ω — угловая скорость.

Уравнение (1) является прямым следствием второго закона Ньютона, поэтому экспериментальная проверка его является в то же время проверкой основных положений механики. Проверку основного закона динамики для вращающихся тел можно осуществить следующим образом. Оставляя неизменным момент инерции вращающейся части установки (I = const), будем изменять вращающий момент М (изменяя вес груза m). Угловое ускорение при этом будет прямо пропорционально М [см. формулу (1)]. Если же оставить постоянным вращающий момент (M = const) и изменять момент инерции вращающейся системы путем передвижения грузов m1 по стержням крестовины, то угловое ускорение должно быть обратно пропорционально моменту инерции системы. В данной работе для проверки основного закона динамики применены оба указанных метода. Момент сил создается грузом m, привязанным к нити, которая навита на один из шкивов. Если момент сил трения Мтр приложенный к оси маятника, мал по сравнению с моментом М силы натяжения нити (см. рис. 1), то проверка уравнения (1) не представляет труда. Действительно, измеряя время t, в течение которого груз m из состояния покоя опустится на расстояние h, можно легко найти ускорения груза:

(2)

которое связано с угловым ускорением dω/dt соотношением:

(3)

где r — радиус шкива. Если через Т обозначить силу натяжения нити, то

(4)

Силу Т моно найти из уравнения движения груза:

(5)

Легко видеть, что система записанных выше уравнений (1)-(5) полностью решает поставленную задачу. Момент сил трения Мтр обычно оказывается довольно велик и способен существенно исказить результаты опыта.

Уменьшить относительную роль момента сил трения при данной конфигурации установки можно было бы увеличивая массу m. Однако здесь приходится принимать во внимание два обстоятельства:

Увеличение массы m ведет к увеличению давления маятника на ось, что свою очередь вызывает возрастание сил трения. С увеличением m уменьшается время падения t и снижается точность измерения времени.

В дальнейшем вместо (1) мы будем пользоваться более точным уравнением:

(6)

С использованием формул (2)-(6) получаем выражение для момента инерции маятника:

(7)

ВЫПОЛНЕНИЕ РАБОТЫ: В данной работе проводится доказательство того положения, что при постоянном моменте сил, действующем на вращающееся тело, угловое ускорение его dω/dt обратно пропорционально моменту инерции тела I.

ПРИНАДЛЕЖНОСТИ: Маятник Обербека, набор разновесов, секундомер, масштабная линейка, штангенциркуль.

ОПИСАНИЕ ПРИБОРА: Маятник Обербека схематически изображен на рис.1. Основные параметры прибора следующие: радиус шкива г1 = 9,0 мм, радиус шкива r = 17,1 мм, масса одного из стержней крестовины mст = 94 г, длина одного из стержней крестовины lст = 46 см, масса груза m1 = 142 г, высота груза m1 Н = 2,5 см, внешний радиус груза m1 ρ = 1,6 см, вес чашечки Pчаш = (25,75±0,05) г.

В каждом случае установки грузов m на одном из расстояний R от оси маятника необходимо проверять, находятся ли маятник в безразличном равновесии. Прежде, чем начинать эксперимент, рекомендуется несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. На основании этого сделайте вывод о том, находится ли маятник в безразличном равновесии. Увеличивая нагрузку на нить путем добавления на чашечку различных грузов из набора разновесов, найдите минимальное значение массы m0, при котором маятник начинает вращаться. Оцените величину момента сил трения как произведения m, на радиус шкива. Установите грузы m1 в ближнее к оси положение. Положите на чашечку некоторый груз m>m0. С помощью секундомера измерьте время падения груза с заданной высоты h до касания с полом. Повторите опыт не менее пяти раз. Старайтесь при этом выдерживать определенную высоту h и измерять время падения t как можно точнее. Измерьте расстояние R от оси вращения до центра груза m. Результаты измерений занесите в таблицу.

Уравнение поступательного движения для грузов маятника обербека

Справедливость основного уравнения динамики вращательного движения можно проверить на маятнике Обербека, схема которого изображена на рисунке 2.3.

Маятник Обербека состоит из четырех стержней 1, укрепленных на втулке под прямым углом друг к другу. На стержнях закрепляются грузы 2, которые могут быть закреплены на разных расстояниях R от оси вращения. На ось насажен диск 3 радиусом r. Гиря 4, приводящая маятник во вращение, прикреплена к концу нити, которая перекинута через блок 5 и наматывается на диск 3. На основную гирю 4 могут надеваться от одного до четырех дополнительных грузов 6.

Вращение маятника происходит под действием момента М силы натяжения нити и противоположно направленного момента сил трения М_тр. Таким образом, согласно равенству (2.6) уравнение движения маятника имеет вид

(2.7)

. (2.8)

Из равенства (2.8) видно, что если сила трения постоянна (не зависит от скорости), то зависимость величины М от ε является линейной функцией вида . При этом J играет роль углового коэффициента k. Таким образом, экспериментальное исследование взаимосвязи между моментом силы натяжения М и угловым ускорением ε позволяет найти момент инерции маятника J.

Движение гири 4 происходит под действием силы тяжести (где m – масса гири) и силы натяжения нити F. Согласно второму закону Ньютона, уравнение движения гири имеет вид

, (2.9)

где а – ускорение гири, которое можно найти зная время t ее опускания и пройденный путь h. Используя известное уравнение равноускоренного движения, имеем

. (2.10)

Из равенств (2.9) и (2.10) получаем выражение для определения момента сила натяжения

. (2.11)

Учитывая соотношение , связывающее угловое и линейное ускорения для точек окружности диска, из формулы (2.10) находим

. (2.12)

Формулы (2.11) и (2.12) позволяют найти по экспериментальным данным момент силы натяжения М и угловое ускорение ε. Тогда, проведя опыты с гирями различной массы m, можно исследовать зависимость М от ε и построить соответствующий график.

Таким образом, определение момента инерции маятника сводится к определению углового коэффициента найденной из опыта функции коэффициента М (ε), а определение момента силы трения М_тр – к экстраполяции найденной зависимости на ε = 0.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8526 – | 8113 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Изучение законов движения на маятнике Обербека

Цель работы: Изучение динамики вращательного движения, оценка влияния трения на точность результатов проведенных измерений.

Оборудование: лабораторная установка (маятник Обербека), набор грузиков, линейка.

Теоретическое введение

Маятник Обербека представляет собой крестовину, состоящую из 4 стержней, прикрепленных ко втулке с осью (см. рис.1).

На стержни надеваются одинаковые грузы массой m1, которые могут быть закреплены на различных расстояниях от оси вращения. Два легких шкива с различными радиусами r1, и r2, насажены на ось вращения маятника. На один из шкивов наматывается нить, к свободному концу которой прикрепляется груз массой m. Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение. Положение груза m отмечается по шкале с делениями. Вся эта система может свободно вращаться вокруг горизонтальной оси. Момент инерции системы можно менять, передвигая грузы m1 вдоль стержней.

Вращение твердого тела постоянной массы вокруг неподвижной оси описывается уравнением моментов:

(1)

Здесь М – момент сил, действующих на тело, I – момент инерции тела, ω — угловая скорость.

Уравнение (1) является прямым следствием второго закона Ньютона, поэтому экспериментальная проверка его является в то же время проверкой основных положений механики. Проверку основного закона динамики для вращающихся тел можно осуществить следующим образом. Оставляя неизменным момент инерции вращающейся части установки (I = const), будем изменять вращающий момент М (изменяя вес груза m). Угловое ускорение при этом будет прямо пропорционально М [см. формулу (1)]. Если же оставить постоянным вращающий момент (M = const) и изменять момент инерции вращающейся системы путем передвижения грузов m1 по стержням крестовины, то угловое ускорение должно быть обратно пропорционально моменту инерции системы. В данной работе для проверки основного закона динамики применены оба указанных метода. Момент сил создается грузом m, привязанным к нити, которая навита на один из шкивов. Если момент сил трения Мтр приложенный к оси маятника, мал по сравнению с моментом М силы натяжения нити (см. рис. 1), то проверка уравнения (1) не представляет труда. Действительно, измеряя время t, в течение которого груз m из состояния покоя опустится на расстояние h, можно легко найти ускорения груза:

(2)

которое связано с угловым ускорением dω/dt соотношением:

(3)

где r – радиус шкива. Если через Т обозначить силу натяжения нити, то

(4)

Силу Т моно найти из уравнения движения груза:

(5)

Легко видеть, что система записанных выше уравнений (1)-(5) полностью решает поставленную задачу. Момент сил трения Мтр обычно оказывается довольно велик и способен существенно исказить результаты опыта.

Уменьшить относительную роль момента сил трения при данной конфигурации установки можно было бы увеличивая массу m. Однако здесь приходится принимать во внимание два обстоятельства:

Увеличение массы m ведет к увеличению давления маятника на ось, что свою очередь вызывает возрастание сил трения. С увеличением m уменьшается время падения t и снижается точность измерения времени.

В дальнейшем вместо (1) мы будем пользоваться более точным уравнением:

(6)

С использованием формул (2)-(6) получаем выражение для момента инерции маятника:

(7)

ВЫПОЛНЕНИЕ РАБОТЫ: В данной работе проводится доказательство того положения, что при постоянном моменте сил, действующем на вращающееся тело, угловое ускорение его dω/dt обратно пропорционально моменту инерции тела I.

ПРИНАДЛЕЖНОСТИ: Маятник Обербека, набор разновесов, секундомер, масштабная линейка, штангенциркуль.

ОПИСАНИЕ ПРИБОРА: Маятник Обербека схематически изображен на рис.1. Основные параметры прибора следующие: радиус шкива г1 = 9,0 мм, радиус шкива r = 17,1 мм, масса одного из стержней крестовины mст = 94 г, длина одного из стержней крестовины lст = 46 см, масса груза m1 = 142 г, высота груза m1 Н = 2,5 см, внешний радиус груза m1 ρ = 1,6 см, вес чашечки Pчаш = (25,75±0,05) г.

В каждом случае установки грузов m на одном из расстояний R от оси маятника необходимо проверять, находятся ли маятник в безразличном равновесии. Прежде, чем начинать эксперимент, рекомендуется несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. На основании этого сделайте вывод о том, находится ли маятник в безразличном равновесии. Увеличивая нагрузку на нить путем добавления на чашечку различных грузов из набора разновесов, найдите минимальное значение массы m0, при котором маятник начинает вращаться. Оцените величину момента сил трения как произведения m, на радиус шкива. Установите грузы m1 в ближнее к оси положение. Положите на чашечку некоторый груз m>m0. С помощью секундомера измерьте время падения груза с заданной высоты h до касания с полом. Повторите опыт не менее пяти раз. Старайтесь при этом выдерживать определенную высоту h и измерять время падения t как можно точнее. Измерьте расстояние R от оси вращения до центра груза m. Результаты измерений занесите в таблицу.

Лабораторная работа №4

Изучение законов вращательного движения при помощи маятника Обербека.

Выполнил: Курдюков Е.А.

Проверил: Пшеницин В. И.

1. Цель работы: анализ основного уравнения вращательного движения.

2. Основные понятия и закономерности:

Основное уравнение вращательного движения тела относительно неподвижной оси вращения имеет вид:

Где М – сумма проекций на ось вращения моментов всех внешних сил, действующих на тело, ω – его угловая скорость, J – момент инерции тела относительно данной оси. Для однородного твердого тела момент инерции представляет собой постоянную величину. Поэтому уравнение можно записать в виде:

Момент инерции J играет во вращательном движении ту же роль, что и масса m тела в его поступательном движении, момент инерции отражает инертность тела в его вращательном движении. Чем больше J тем труднее заставить вращающееся тело изменить угловую скорость ω.

3. Идея метода измерений и суть предлагаемой методики:

Основное уравнение вращательного движения удобно исследовать с помощью маятника Обербека.

На нити подвешивается груз массы m, натягивающий нить. Если натяжение нити равно Т, то момент сил, действующий на маятник, равен:

Величина Т определяется следующим образом. При вращении маятника, груз начинает опускаться с ускорением а. Уравнение движения опускающегося груза выглядит следующим образом:

Соответственно, момент внешних сил, приложенных к маятнику, равен:

Ускорение а можно вычислить, измерив время τ падения груза с известной высоты h. Падение груза является равноускоренным, поэтому для движения груза справедливо уравнение:

4. Таблицы экспериментальных данных и результаты расчетов.

h	R	m	T	a	ε	M
100		54,2	8.4	0.028	0.93	0.015
100		100.2	5.7	0.061	2.03	0.03
100		146.2	4.5	0.098	3.26	0.04
100		54,2	21.3	0.004	0.25	0.008
100		100.2	11.5	0.015	0.93	0.015
100		146.2	8.9	0.025	1.56	0.02

Расчет плотности материала в СИ:

Вопросы к лабораторной работе:

1.Сформулируйте основной закон динамики вращательного движения.

Ответ: произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси, вокруг которой происходит вращение.

2.дайте определение момента силы, приложенной к телу и момента импульса вращающегося тела. Как направлены векторы этих величин по отношению к оси вращения тела?

Ответ: момент силы – векторная физическая величина, равная произведению радиус-вектора проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения.

Лабораторные работы по физике

ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

Цель работы: 1) изучение кинематических и динамических характеристик вращательного движения;

2) экспериментальное определение момента инерции крестовины маятника Обербека и момента сил трения;

3) проверка справедливости закона сохранения (превращения) энергии механической системы.

Схема экспериментальной установки

1 – ось вращения;

Основным элементом маятника Обербека (рис. 1) является крестовина, способная свободно вращаться вокруг неподвижной горизонтальной оси 1. Крестовина состоит из четырех стержней 2 с грузами-насадками 3, расположенными симметрично относительно оси вращения. С крестовиной жестко скреплен шкив 4 радиусом R. На шкив намотана нить 5, перекинутая через легкий блок 6. К свободному концу нити привязан груз 7, массу которого m можно изменять в процессе опытов. Для измерения высоты h расположения груза над полом служит линейка 8, а для измерения времени его падения – секундомер 9.

Если поднятый на высоту h груз отпустить, то он начнет падать с ускорением , которое определяется вторым законом Ньютона. На груз действуют две силы: сила тяжести и сила натяжения нити (сопротивлением воздуха в данном случае можно пренебречь). Уравнение основного закона динамики:

в проекциях на направление движения груза имеет вид:

Пренебрегая массами нити 5 и блока 6, можно считать, что нить действует на поверхность шкива касательной силой , равной по модулю силе : | | = | | = Fн . Касательная сила создает вращающий момент , по модулю равный произведению модуля силы на ее плечо, т.е. на радиус шкива R: Мн = Fн R. С учетом (1) вращающий момент силы натяжения нити равен

Под действием момента крестовина начинает вращаться с угловым ускорением . При этом на оси вращения возникают, хотя и незначительные, силы трения. Эти силы создают тормозящий момент , направленный противоположно угловому ускорению. С учетом направления моментов сил натяжения и трения алгебраическая запись уравнения основного закона динамики вращательного движения имеет вид

J e = Мн – Мтр , (3)

где J – момент инерции крестовины маятника Обербека относительно оси вращения.

Известно, что момент инерции зависит только от распределения массы тела относительно оси. Для крестовины маятника величина J определяется в основном положением грузов-насадок 3 на стержнях 2. Если их положение в ходе опытов не изменяется, то и момент инерции остается постоянным. Момент сил трения также можно считать практически неизменным. Поэтому зависимость углового ускорения e от момента силы натяжения Мн , согласно уравнению (3), имеет линейный характер. Определив опытным путем значения e при различных Мн и обработав соответствующим образом полученную экспериментальную зависимость e (Мн), с помощью этого уравнения можно найти неизвестные величины J и Мтр . Рассмотрим теперь методику измерения углового ускорения e и момента силы натяжения Мн .

Так как нить 5 практически нерастяжима, все ее точки, включая точки на поверхности шкива, движутся с одинаковым ускорением , равным по модулю ускорению падающего груза : | | = | | = a. Груз падает с высоты h равноускоренно; при этом за время t он проходит путь

Измерив высоту h и время падения груза t, можем найти ускорение

Если известны масса груза т и радиус шкива R, то по формуле (2) можно рассчитать момент силы натяжения нити Мн .

Угловое ускорение вращения шкива, а следовательно, и крестовины и тангенциальное (касательное) ускорение точек на поверхности шкива связаны известным соотношением

Таким образом, зная массу груза т, радиус шкива R и высоту h, с которой падает груз, а также измерив время его падения t, можно экспериментально определить величины e и Мн .

Рассмотрим теперь превращение энергии в вышеописанном опыте. Поднятый на высоту h груз обладает потенциальной энергией

кинетическая энергия системы «груз + крестовина» при этом равна нулю. В момент падения груза на пол его потенциальная энергия обращается в ноль, но за счет ее уменьшения груз приобретает кинетическую энергию

а крестовина – кинетическую энергию вращения

где v – скорость груза в момент падения; w – угловая скорость вращения крестовины к этому моменту.

Итак, начальное значение полной механической энергии рассматриваемой системы равно W0 = Wp , а конечное W = Wk1 + Wk2 . Изменение энергии:

Как известно, изменение полной механической энергии консервативной системы равно нулю, а при наличии неконсервативных сил – их работе. В данной системе действуют неконсервативные силы трения, работа которых равна

где j – угол поворота крестовины за время падения груза. Знак « – » отражает тот факт, что работа сил трения и сопротивления всегда отрицательна (угол между направлениями силы и перемещения равен 180 ° ). Итак, закон сохранения (превращения) энергии в данном случае можно записать как

С учетом соотношений (6)-(9) уравнение (10) примет вид:

Для экспериментальной проверки справедливости уравнения (11) необходимо знать все входящие в него величины. К ним относятся, во-первых, заранее известные ускорение свободного падения g, масса груза т и высота h; во-вторых, определяемые путем обработки экспериментальной зависимости момент инерции крестовины J и момент сил трения Мтр ; в-третьих, кинематические характеристики системы v, w и j . Остановимся на определении последних.

Скорость груза в момент его падения на пол найдем исходя из закономерностей равноускоренного движения:

Такую же по величине скорость имеют и точки на поверхности шкива. Используя связь между линейной и угловой скоростями, получим

Так как линейное расстояние, пройденное точками на поверхности шкива, равно перемещению груза за тот же промежуток времени, угол j (в радианах) может быть рассчитан как

Порядок измерений и обработки результатов

1. Запишите радиус шкива R , выразив его в метрах, в тетрадь (R=17мм).

2. Занесите во второй столбец таблицы 1 значение массы груза т (в кг).

3. Вращая крестовину, намотайте нить на шкив так, чтобы нижняя поверхность груза 7 оказалась на заданной высоте h над полом, запишите значение высоты в тетрадь (значение h задает преподаватель или спишите с экрана монитора).

4. Отпустив крестовину, одновременно включите секундомер, а в момент касания грузом пола – выключите. Запишите время падения в третий столбец таблицы 1.

5. Повторите пп. 3 и 4 с тем же грузом еще два раза. Рассчитайте и занесите в таблицу среднее из трех значений времени t.

6. Увеличивая массу груза согласно рекомендациям, выполните пп. 2-5 еще пять раз.

7. Для каждого из шести проделанных опытов рассчитайте ускорение а по формуле (4), подставляя в нее среднее из трех измеренных значений времени падения t. Величину а (с точностью не менее чем до трех значащих цифр) запишите в четвертый столбец таблицы 1.

8. По формулам (2) и (5) вычислите значения момента силы натяжения нити Мн и углового ускорения e . Результаты занесите в соответствующие столбцы табл. 1.

9. Руководствуясь правилами [1], постройте график зависимости углового ускорения от момента силы натяжения (в данной работе необходимо, чтобы начало координат совпадало с нулевыми значениями откладываемых величин e и Мн). Нанесите на график экспериментально полученные точки.

10. Одним из описанных ниже способов* обработайте линейную экспериментальную зависимость e (Мн) и найдите значения момента инерции крестовины J и момента сил трения Мтр. Запишите эти значения в тетрадь.

11. Для одного из проделанных опытов рассчитайте по формулам (12)-(14) скорость груза v, угловую скорость вращения w и угол поворота j крестовины маятника Обербека в момент падения груза на пол.

12. Вычислите значения левой и правой частей уравнения закона сохранения энергии (11). Сравнив эти значения между собой, сделайте выводы.

Обработка зависимости e (Мн)

Угловое ускорение крестовины e и момент силы натяжения нити Мн связаны уравнением основного закона динамики вращательного движения (3). Зависимость e (Мн) можно представить в виде

где . Таким образом, определив коэффициенты линейной зависимости (15) K и b, легко найти момент инерции J и момент сил трения Мтр :

Обработку экспериментальной зависимости e (Мн) можно провести либо графически, либо методом наименьших квадратов.

Графический способ. По экспериментальным точкам проведите сглаживающую прямую. Из уравнения (3) следует, что угловое ускорение e обращается в нуль при Мн = Мтр . Таким образом, момент сил трения Мтр определяется (с учетом масштаба!) отрезком, отсекаемым проведенной прямой на оси абсцисс (рис. 2).

Величина K в уравнении (15) представляет собой угловой коэффициент прямой, т.е. тангенс угла ее наклона к оси абсцисс. Согласно (16), момент инерции J есть величина, обратная K, – значит, его можно найти как котангенс этого угла. Выбрав на сглаживающей прямой две достаточно удаленные друг от друга точки, рассчитайте значение J как отношение отрезков

причем величины отрезков D Мн и D e должны быть взяты с учетом масштаба графика и выражены в соответствующих единицах измерения: D Мн – в Н × м, а D e – в рад/с2 или в с – 2. Только в этом случае результат будет правильным, и момент инерции будет иметь размерность кг × м2.

Метод наименьших квадратов. (Подробно этот метод рассмотрен в [1]). Изучив данный материал, заполните два последних столбца табл. 1. Найдите суммы значений величин в последних четырех столбцах и занесите их в строку « S = ». Вычислите коэффициенты K и b зависимости (15); результаты расчетов запишите в тетрадь. Для определения момента инерции крестовины J и момента сил трения Мтр воспользуйтесь соотношениями (16). На графике зависимости e (Мн) проведите прямую по двум точкам, координаты которых рассчитайте по найденным значениям коэффициентов. Убедитесь в правильности проведенных расчетов (прямая должна «наилучшим» образом пройти через экспериментальные точки).

Какие величины характеризуют вращательное движение?

Что характеризует момент инерции твердого тела относительно оси вращения? Как он рассчитывается?

Сформулируйте и докажите теорему Штейнера.

Как изменится кинетика опускания гири, если грузы на крестовине передвинуть ближе (дальше) к оси вращения.

Дайте определение момента силы. Какие моменты сил действуют на крестовину маятника Обербека в этой работе.

Запишите математически и сформулируйте главный закон динамики вращательного движения.

Покажите, что в пренебрежении трением, расчетная формула для момента инерции маятника Обербека будет иметь вид:
.

Запишите и поясните закон сохранения (превращения) механической энергии в этой работе.