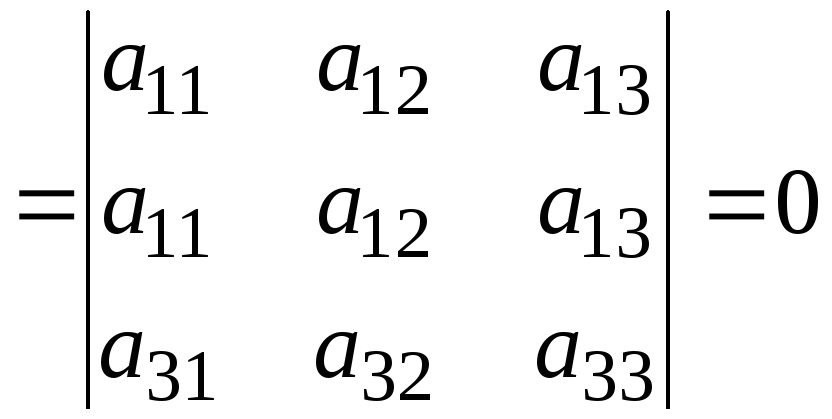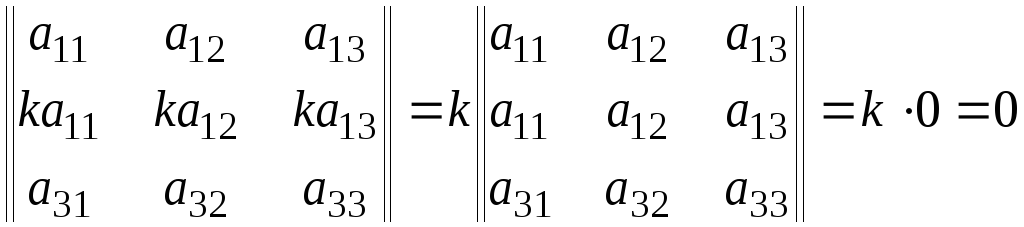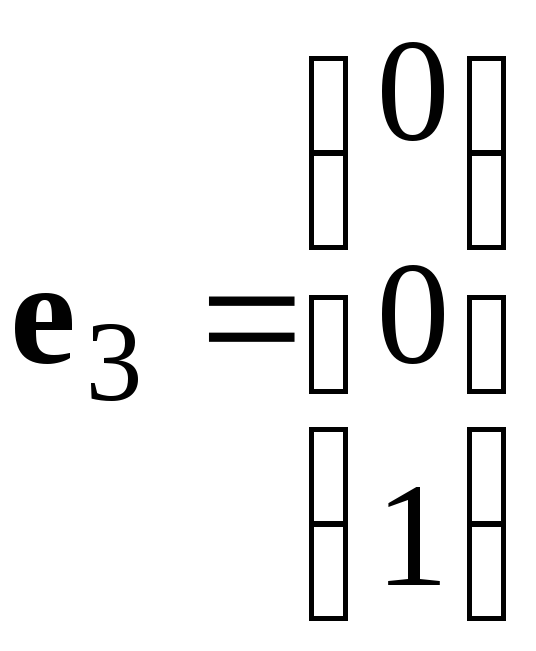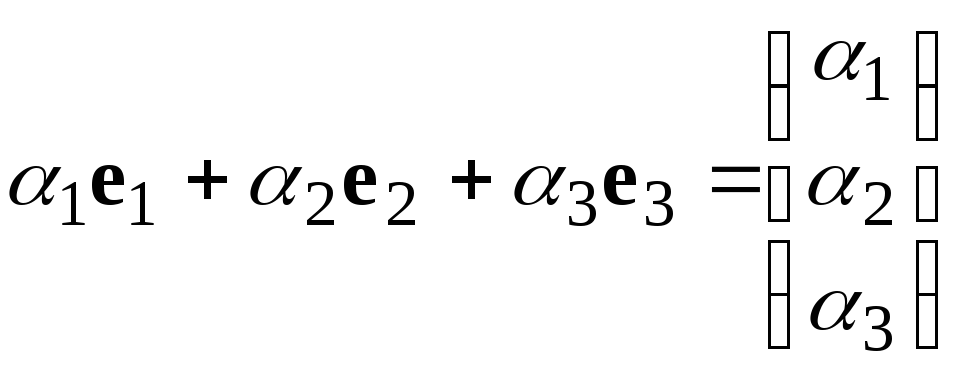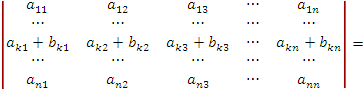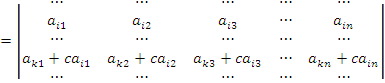Как изменится определитель порядка n если у всех его элементов изменить знак на противоположный

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

Свойства определителя

Все
свойства определителя следуют из
определения определителя и свойств
конечных сумм, приводятся без общих
доказательств с демонстрацией на примере
определителей 2-го и 3-го порядков.

Свойство
1.
Равноправность строк и столбцов.
Определитель не меняет своего значения
при замене всех его строк соответствующими
столбцами

(11.4)

Т.е.

.

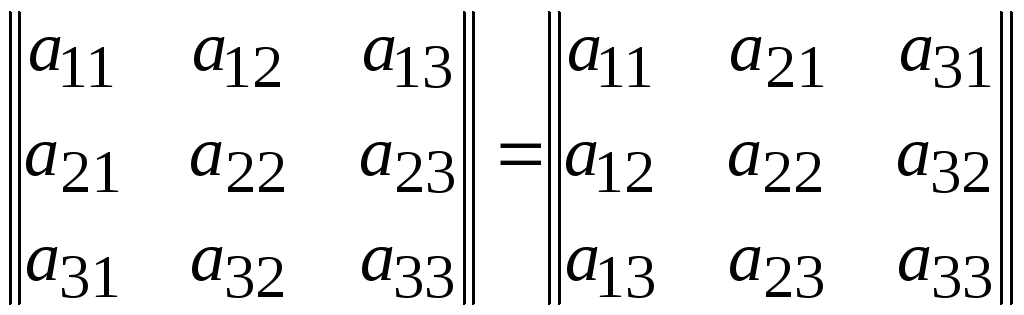
Для
доказательства этого свойства достаточно
вычислить определители в левой и правой
частях равенства и убедиться в равенстве
полученных при этом членов.

В
связи с этим свойством в дальнейшем
вместо слов «строка» или «столбец»
будем говорить просто «ряд», подразумевая
их равноправность.

Свойство
2.
При перестановке двух параллельных
рядов определителя его модуль сохраняет
прежнее значение, а знак меняется на
противоположный

Пример:
.

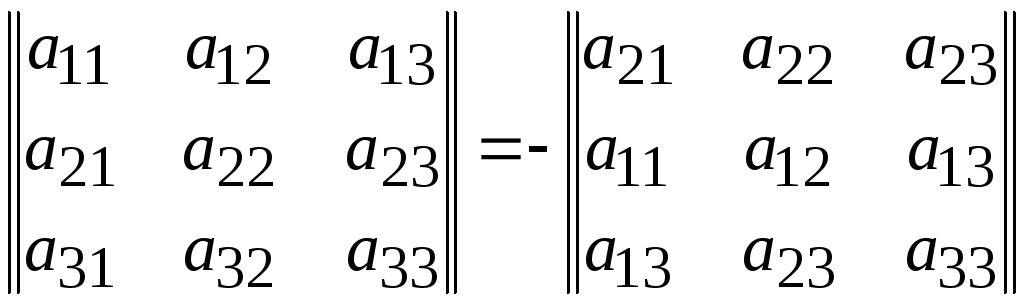
Для
доказательства этого свойства достаточно
вычислить по правилу треугольника
определители, стоящие в правой и левой
частях равенства.

Следствие
1:
Определитель с двумя одинаковыми рядами
равен нулю.

Действительно,
при перестановке двух одинаковых рядов
абсолютное значение определителя не
изменится, а, с другой стороны, в силу
свойства 2 изменит знак на противоположный,
т.е.
,
значит,
следовательно,.

Следствие
2.
Сумма произведений элементов какого
либо ряда на алгебраические дополнения
параллельного ряда равна нулю.

Действительно,
все такие разложения представляют из
себя определители, содержащие два
одинаковых ряда:

Свойство
3. Общий
множитель элементов какого либо ряда
можно выносить за знак определителя.

.

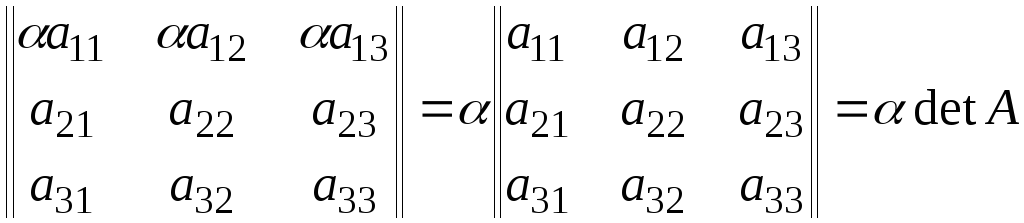
Действительно,
поскольку определитель можно вычислить,
раскладывая его по элементам строки
(столбца), вычислим определитель,
раскладывая его по элементам строки,
умноженной на число
,
тогда каждое слагаемое будет содержать
множитель,
который может быть вынесен за скобку.

Следствие
1.
Если все элементы какого-либо ряда равны
нулю, то определитель равен нулю.

Следствие
2.
Если все элементы какого-либо ряда
определителя пропорциональны
соответствующим элементам параллельного
ряда, то определитель равен нулю.

Действительно,

Свойство
4.
Линейное свойство определителя. Если
в определителе
-го
порядка некоторая-ая
строка представляет собой сумму двух
слагаемых, то определитель может быть
представлен в виде суммы двух определителей.
Первый определитель будет иметь в-ой
строке первые из упомянутых слагаемых
, элементы в остальных строках будут
такими же, как и в исходном определителе,
а второй определитель в-ой
строке будет иметь вторые из упомянутых
слагаемых, а остальные строки будут
совпадать с исходным определителем,
т.е.

.

Это
свойство следует из определения
определителя, если разложить его по
элементам
-ой
строки, а затем воспользоваться
распределительным законом суммы.

Определение.
Элементарными
преобразованиями
матрицы называются следующие
преобразования:

1)
умножение строки (столбца) на число
отличное от нуля;

2)
прибавление к одной строке (столбцу)
другой строки (столбца);

3)
перестановка строк (столбцов).

Свойство
5.
Если к элементам некоторой строки
(столбца) определителя прибавить
соответствующие элементы другой строки
(столбца), умноженные на произвольный
множитель
,
то величина определителя не изменится.

Свойство
6.
Определитель треугольной матрицы равен
произведению диагональных элементов.

=.

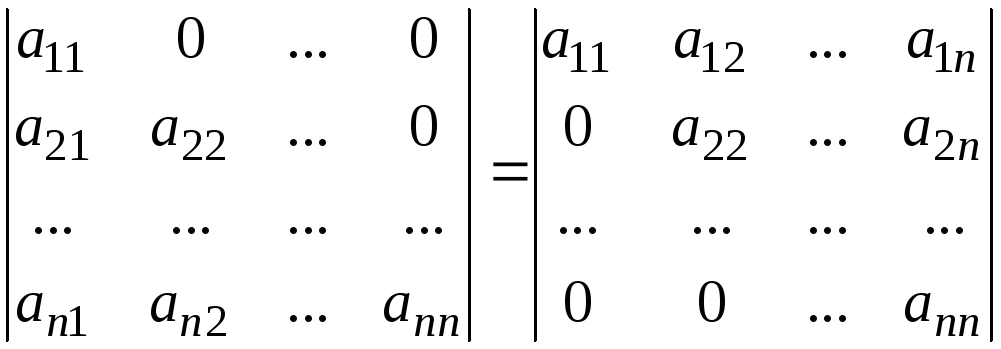
нижний
треугольный верхний треугольный

определитель
определитель

Определение.
Минором
-ого
порядка
матрицы
называется детерминант матрицы порядка,
образованный элементами, стоящими на
пересечении выбранныхстрок и столбцов. Каждая матрица имеет
столько миноров данного порядка,
сколькими способами можно выбрать
номера строк и столбцов. Если матрицаквадратная, то каждому минору
–ого
порядка
сопоставляется дополнительный
минор,
который по определению есть определитель
матрицы порядка (),
составленный из элементов, оставшихся
после вычеркивания
строк
и столбцов.

Лекция 12

Линейные комбинации строк и столбцов.
Базисные строки и столбцы. Линейная
независимость. Ранг матрицы. Вычисление
ранга.

Цель: изучить понятие линейной комбинации
и линейной независимости строк и столбцов
матрицы, методы вычисления ранга и
определения базисного минора.

В
теме «матрицы и действия над ними» мы
ввели понятия матрицы строки и матрицы
столбца,

Определение.
Столбец
назовем линейной комбинацией столбцоводинаковой высоты, если при некоторых
числахимеет место равенство:

(12.1)

Или
в развернутом виде:

.

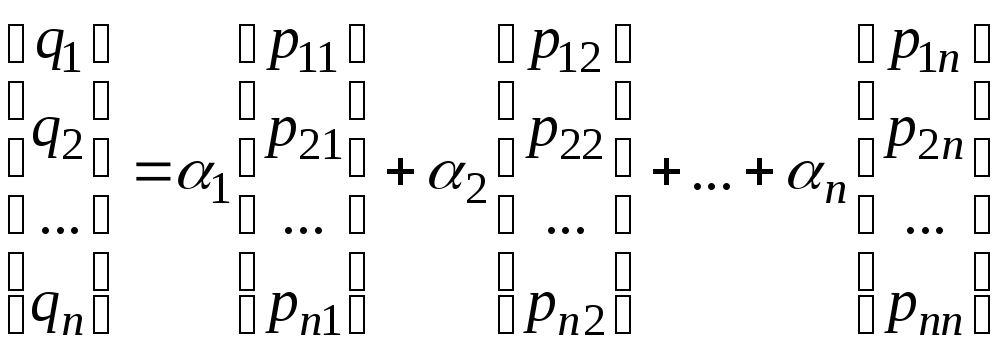
В
силу определения умножения матриц на
число и операции сложения последнее
равенство можно представить в виде
системы равенств, составленных для
каждого элемента:

;

;

…

.

По
аналогии с линейной комбинацией введем
понятие линейной независимости строк
и столбцов матрицы. Пусть
— столбец у которого все элементы равны
нулю.

Определение.
Система из
столбцовназывается линейно независимой, если
из равенстваследует,.
В противном случае, если не все(),
система столбцов линейно зависима.

Все
утверждения записанные для столбцов,
справедливы и для строк матрицы.

Пример:
Столбцы

,

,

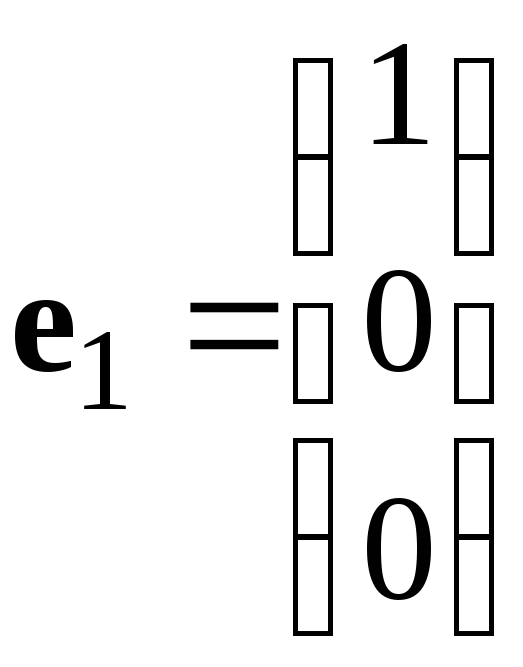
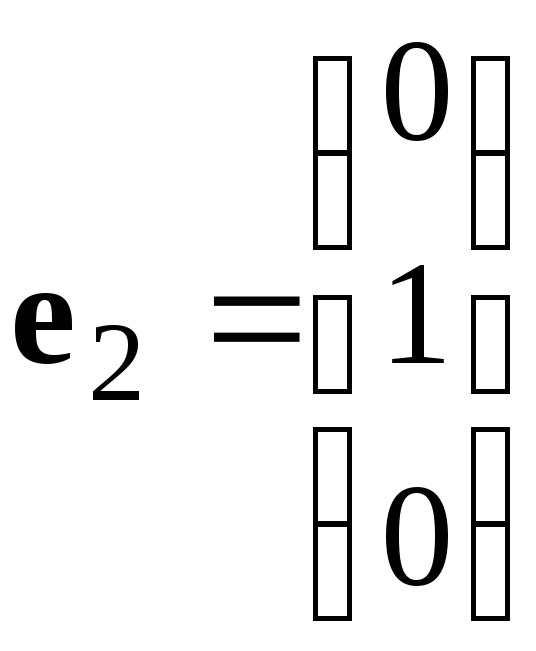
линейно
независимы, т.к. их линейная комбинация

равна
нулевому столбцу, только в случае, когда

,
т.е. является тривиальной.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #

  01.05.201523.47 Mб23Kniga_1.pdf

• #
• #
• #
• #
• #
• #
• #

Некоторые свойства определителей.

Здесь будут изложены те свойства, которые обычно используются для вычисления определителей в стандартном курсе высшей математики. Это вспомогательная тема, к которой будем обращаться из остальных разделов по мере необходимости.

Итак, пусть задана некая квадратная матрица $A_{ntimes n}=left( begin{array} {cccc} a_{11} & a_{12} & ldots & a_{1n} \
a_{21} & a_{22} & ldots & a_{2n} \
ldots & ldots & ldots & ldots \
a_{n1} & a_{n2} & ldots & a_{nn} \
end{array} right)$. Каждая квадратная матрица обладает характеристикой, которая называется определителем (или детерминантом). Я не стану вдаваться здесь в суть этого понятия. Если оно требует пояснений, то прошу отписать об этом на форум, и я коснусь данного вопроса детальнее.

Обозначается определитель матрицы $A$ как $Delta A$, $|A|$ или $det A$. Порядок определителя равен количеству строк (столбцов) в нём.

1. Значение определителя не изменится, если его строки заменить соответствующими столбцами, т.е. $Delta A=Delta A^T$.

   Пример применения этого свойства: показатьскрыть

2. Если поменять местами две строки (столбца) определителя, то знак определителя изменится на противоположный.

   Пример применения этого свойства: показатьскрыть

3. Определитель, у которого все элементы строки (столбца) равны нулю, равен нулю.

   Пример применения этого свойства: показатьскрыть

4. Определитель, у которого все элементы некоей строки (столбца) равны соответствующим элементам иной строки (столбца) равен нулю.

   Пример применения этого свойства: показатьскрыть
5. Если в определителе все элементы одной строки (столбца) пропорциональны соответствующим элементам иной строки (столбца), то такой определитель равен нулю.

   Пример применения этого свойства: показатьскрыть

6. Если все элементы строки (столбца) имеют общий множитель, то этот множитель можно вынести за знак определителя.

   Пример применения этого свойства: показатьскрыть

7. Определитель не изменится, если ко всем элементам некоей строки (столбца) прибавить соответствующие элементы иной строки (столбца), умноженные на произвольное число.

   Пример применения этого свойства: показатьскрыть

8. Если в определителе некая строка (столбец) есть линейная комбинация иных строк (столбцов), то определитель равен нулю.

   Пример применения этого свойства: показатьскрыть

9. Если каждый элемент некоей k-й строки (k-го столбца) определителя равен сумме двух слагаемых, то такой определитель равен сумме определителей, у первого из которых в k-й строке (k-м столбце) стоят первые слагаемые, а у второго определителя в k-й строке (k-м столбце) расположены вторые слагаемые. Иные элементы этих определителей одинаковы.

   Пример применения этого свойства: показатьскрыть

10. Определитель произведения двух квадратных матриц одного порядка равен произведению определителей этих матриц, т.е. $det(Acdot B)=det Acdot det B$. Из этого правила можно получить такую формулу: $det left(A^n right)=left(det A right)^n$.
11. Если матрица $A$ – невырожденная (т.е. её определитель не равен нулю), то $det left(A^{-1}right)=frac{1}{det A}$.

Формулы для вычисления определителей

Для определителей второго и третьего порядков верны такие формулы:

$$
begin{equation}
Delta A=left| begin{array} {cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|=a_{11}cdot a_{22}-a_{12}cdot a_{21}
end{equation}
$$

$$
begin{equation}
begin{aligned}
& Delta A=left| begin{array} {ccc} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} end{array} right|=
a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{21}cdot a_{32}cdot a_{13}-\
& -a_{13}cdot a_{22}cdot a_{31}-a_{12}cdot a_{21}cdot a_{33}-a_{23}cdot a_{32}cdot a_{11}
end{aligned}
end{equation}
$$

Примеры применения формул (1) и (2) есть в теме «Формулы для вычисления определителей второго и третьего порядков. Примеры вычисления определителей».

Определитель матрицы $A_{ntimes n}$ можно разложить по i-й строке, используя следующую формулу:

$$
begin{equation}
Delta A=sumlimits_{j=1}^{n}a_{ij}A_{ij}=a_{i1}A_{i1}+a_{i2}A_{i2}+ldots+a_{in}A_{in}
end{equation}
$$

Аналог данной формулы существует и для столбцов. Формула для разложения определителя по j-му столбцу выглядит следующим образом:

$$
begin{equation}
Delta A=sumlimits_{i=1}^{n}a_{ij}A_{ij}=a_{1j}A_{1j}+a_{2j}A_{2j}+ldots+a_{nj}A_{nj}
end{equation}
$$

Правила, выраженные формулами (3) и (4), подробно проиллюстрированы примерами и пояснены в теме Понижение порядка определителя. Разложение определителя по строке (столбцу).

Укажем еще одну формулу для вычисления определителей верхних треугольных и нижних треугольных матриц (пояснение этих терминов см. в теме «Матрицы. Виды матриц. Основные термины»). Определитель такой матрицы равен произведению элементов, стоящих на главной диагонали. Примеры:

begin{aligned}
&left| begin{array} {cccc} 2 & -2 & 9 & 1 \ 0 & 9 & 8 & 0 \ 0 & 0 & 4 & -7 \ 0 & 0 & 0 & -6 end{array} right|=
2cdot 9cdot 4cdot (-6)=-432.\

&left| begin{array} {cccc} -3 & 0 & 0 & 0 \ -5 & 0 & 0 & 0 \ 8 & 2 & 1 & 0 \ 5 & 4 & 0 & 10 end{array} right|=
-3cdot 0cdot 1 cdot 10=0.
end{aligned}

. Определитель транспонированной матрицы равен определителю исходной матрицы: .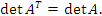

Доказательство. Согласно определению,

             (1)

При транспонировании матрицы A происходит лишь перегруппировка слагаемых в этой сумме.

. Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножееию определителя на это число:

.

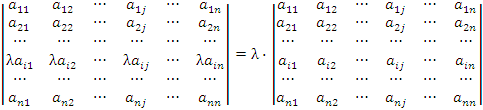
Доказательство. При умножении строки (или столбца) определителя на число λ один из сомножителей в произведении умножается на это число. В результате число λ является общим множителем суммы (1), представляющей собой определение детерминанта матрицы A.

. Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.

Доказательство. По Теореме 1, любая транспозиция изменяет четность перестановки. Следовательно, при перестановке двух строк (столбцов) каждое слагаемое суммы (1) изменяет свой знак на противоположный.

. Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю.

Доказательство. Каждая строка и каждый столбец матрицы A представлены одним из своих элементов в произведении . Следовательно, сумма (1) содержит только нулевые слагаемые.

. Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю.

Доказательство. По Свойству 3, при перестановке двух строк местами определитель изменяет свой знак. С другой стороны, перестановка местами одинаковых строк не изменяет определитель. Следовательно,  det A = –det A, что влечет  det A = 0.

. Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю.

Доказательство. Общий множитель строки можно вынести за знак определителя. Полученный при этом определитель имеет две одинаковых строки. Согласно Свойству 5 такой определитель равен нулю.

. Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:

.

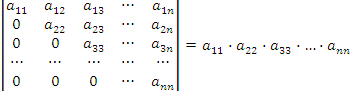
Доказательство. По определению (1), det A представляет собой алгебраическую сумму произведений элементов (с учетом правила выбора знаков), составленных таким образом, чтобы каждая строка и каждый столбец матрицы A были представлены в произведении одним и только одним элементом.

В первом столбце имеется только один ненулевой элемент, а именно a₁₁.

Второй столбец вносит ненулевой вклад в произведение только при выборе элемента a₂₂, поскольку первая строка уже представлена своим элементом.

Аналогично, в третьем столбце выбор может быть остановлен только на элементе a₃₃ и так далее.

Таким образом, сумма (1) содержит только один ненулевой член, который равен произведению элементов, стоящих на главной диагонали.

. Если все элементы k-ой строки (столбца) определителя представлены в виде сумм
 a_k j + b_k j, то определитель можно представить в виде суммы соответствующих определителей:

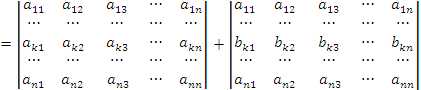
Доказательство. Преобразуем исходный определитель:

. Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и тоже число.

Доказательство. Определитель, стоящий в правой части этого равенства, можно представить в виде суммы двух определителей, один из которых является исходным, а второй имеет две пропорциональные друг другу строки и, следовательно, равен нулю.