Катет равен гипотенузе где ошибка

Геометрический парадокс: катет равен гипотенузе

Мы уже доказали, что прямой угол равен тупому. Теперь докажем, что в прямоугольном треугольнике катет равен гипотенузе

Построим прямоугольный треугольник , угол  равен градусов.
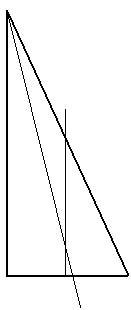
Пусть точка — середина .
Проведем лучи — биссектрису угла , и — серединный перпендикуляр к .
Лучи и пересекаются в точке .

Опустим из точки перпендикуляры на стороны и . Точки и — основания этих перпендикуляров.
Рассмотрим треугольники и .
Они равны, так как оба они — прямоугольные, угол равен углу (по построению), гипотенуза — общая. Следовательно, , .

Рассмотрим треугольники и . Они равны, так как — серединный перпендикуляр к (по построению), то есть медиана и высота треугольника . Следовательно, .

Рассмотрим треугольники и . Они оба — прямоугольные, , (по доказанному),
следовательно, треугольник равен треугольнику , и поэтому .

Попробуйте сами разобраться, где вас обманули. Сделайте аккуратный чертеж. Проверьте каждый пункт «доказательства». Желаем удачи!

---

Условия, в которых репетитор по математике занимается с ребенком, к сожалению, на сегодняшний день далеки от идеальных. Кроме высокой нагрузки и большого объема нематематической информации, сваливающейся на голову ученика репетитора, тормозом движения вперед выступают новые стандарты контроля знаний в лице ЕГЭ и ГИА. Форматы этих экзаменов таковы, что для их успешной сдачи совсем не обязательно иметь представление о внутренней структуре и логике построения предмета. Тотальное шествие ЕГЭ по стране и главенство его над всеми другими формами испытаний оказывает влияние на методику работы как школьных преподавателей — репетиторов по математике, так и профессиональных репетиторов по математике, начиная уже с 8-го класса. Такое впечатление, что математику для того и создали, чтобы с ее помощью сдавать ЕГЭ. И школьный учитель и репетитор вынуждены работать с постоянной оглядкой на заложенные в ЕГЭ и ГИА стандарты, иначе репетитор по математике не сможет отбиться от вопросов такого рода: «Когда же мы будем решать задачи из ЕГЭ?». Как будто задачи не из ЕГЭ — это уже не математика и решать их не надо.

Информация о школьных занятиях, которую я регулярно получаю от своих учеников, а так же данные других репетиторов математики позволяют говорить о первых результатах влияния политики ЕГЭ на содержание уроков в школе: мы получили почти полный отказ преподавателей заниматься формированием умения делать выводы, проверять математические рассуждения и самостоятельно доказывать теоремы. В этом просто нет необходимости. Действительно, зачем этому учить, когда для успешной сдачи ЕГЭ по математике требуется всего лишь умение пользоваться готовыми фактами?

Экзамен по геометрии в классической форме практически полностью упразднен даже в математических классах, а полноценной замены ему нет. Предлагается только письменный экзамен ГИА по геометрии и объединенная ГИА по алгебре и геометрии, для которых не требуется понимание и умение проводить полновесные доказательства. Они просто выпадают из формата экзамена. Живое общение с преподавателем математики, которое во все времена служило главным определителем знаний и умений человека не нашло в лице ГИА и ЕГЭ какую-либо адекватную замену.

Поэтому, из-за низкой мотивации школьных учителей к обучению доказывать теоремы, репетитор по математике часто получает для подготовки к ЕГЭ ученика, со сложившимся представлением о математике как о чрезвычайно сложном и недоступном для понимания предмете, состоящим из большого количества готовых алгоритмов, каждый из которых предназначен для решения какой-то одной задачи. Репетитор по математике в таком случае рассматривается как путеводитель по длинному списку теорем, применяемых в них. Между тем такому важному аспекту, как математическое развитие ученика, внимание практически не уделяется.

Усилия учителей старших классов в основном направлены на разъяснение методов решения узкого набора задач из ЕГЭ, зажатых в рамки классификаций ФИПИ по их типам. Высокая вероятность их появления на реальном ЕГЭ по математике способствует крайне низкому вниманию репетиторов к другим видам задач. Например, обилие задач с2 на кубы заставляет практически забыть про конусы, усеченные пирамиды, цилиндры и шары (особенно вписанные друг в друга). Как следствие, многие навыки чтения стереометрического рисунка ученик просто не получает. Развитие пространственного ощущения тела тоже не происходит. Занятия с репетитором по математике, преследующие часто сугубо прагматические цели родителей сдать ЕГЭ и поступить в ВУЗ, превращаются в однообразные циклы решения пробных и демонстрационных вариантов. Репетитор по математике, как послушный раб своего господина, вынужден выполнять поставленную перед ним задачу, несмотря на то, что математическому развитию такие задания способствуют в наименьшей степени.

А между тем существует огромный спектр заданий и форм работы, который репетитор по математике мог бы с успехом управлять развитием. Одной из таких форм является поиск ошибки в решении или доказательстве.

На страницах сайта «профессиональный репетитор по математике» вы найдете примеры таких заданий, первым из которых будет доказательство того, что катет в прямоугольном треугольнике не меньше, а равен гипотенузе. Я рекомендую репетитору по математике показать ученику софизм сразу после изучения темы «наклонная и перпендикуляр».

Итак, допустим в прямоугольном треугольнике АВС . Проведем ВО — биссектрису угла В и отметим точку D — середину катета АС. Поведем перпендикуляры OD, OE и OF соответственно к сторонам АС, ВС и ВА, как показано на рисунке.
Так как точка О расположена на биссектрисе угла В, то (по гипотенузе и острому углу). Поэтому BF=BE (1).
Далее, ОА=ОС, так как каждая точка перпендикуляра к отрезку СА, проходящего через середину СА, равноудалена от С и от А. Так как OF=OE, то тогда имеем равенство треугольников и поэтому AF=CE (2). Складывая почленно (1) и (2), получим: АВ=СВ, т.е. катет равен гипотенузе.

Это наверняка удивит ученика и в конце урока сработает на поддержание активного внимания. Действительно, в начале урока репетитор по математике доказал, что наклонная больше перпендикуляра, и вдруг такое. Выявленная ошибка (а она в том, что О не лежит внутри треугольника) послужит тем средством, которое научит ребенка критически относится к каждому утверждению, каким бы с виду простым и очевидным оно не казалось. Противоречие сработает словно пружина, подталкивающая ученика к осмыслению происходящего и глубокому осознанию материала.

Колпаков Александр Николаевич, московский репетитор по математике. Профессиональный репетитор в Строгино.

Метки:
Ошибки

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

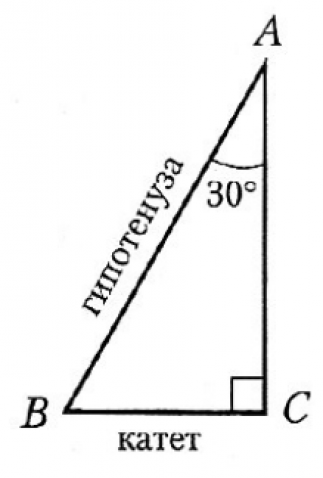
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

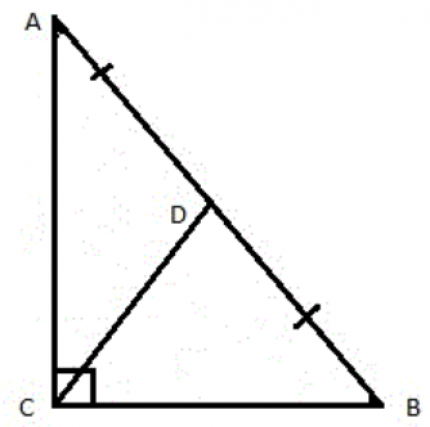
8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Свойства прямоугольного треугольника

• В прямоугольном треугольнике гипотенуза является наибольшей стороной.
• В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

• Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
• Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

1. по катетам;
2. по катету и прилежащему острому углу;
3. по гипотенузе и острому углу;
4. по гипотенузе и катету.

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.

Определить возможность существования треугольника по сторонам

Задача

Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.

Дано: a , b , c – стороны предполагаемого треугольника.

Требуется сравнить длину каждого отрезка-стороны с суммой двух других. Если хотя бы в одном случае отрезок окажется больше суммы двух других, то треугольника с такими сторонами не существует.

Решение

Ниже приведены решения задачи на языке программирования Паскаль двумя способами. В первом случае все стороны проверяются в одном операторе if; во втором случае каждое условие проверяется отдельно, а программа содержит вложенные операторы if-else.

Программа 1 (предпочтительный способ решения):

В языке Паскаль логический оператор and имеет приоритет над операторам >, if проверяется, что каждая из сторон меньше суммы других. Если хотя бы одна будет больше, то все логическое выражение вернет ложь ( false ). В таком случае сработает ветка else .

В данном случае существование треугольника проверяется по-этапно. Если первое условие возвращает ложь, то программа переходит к последнему else. Если же первое условие соблюдено, то поток выполнения программы оказывается у вложенного if. Здесь проверяется уже второе условие. Если оно возвращает ложь, то программа переходит к предпоследнему else. Если и второе логическое выражение возвращает истину (true), то программа идет к третьему условию. При его соблюдении выполняется тело самого вложенного оператора if. При его несоблюдении сработает самое вложенное else.

Несмотря на то, что данная программа кажется длиннее, в определенных ситуациях она может выполняться быстрее, чем первая. Здесь если внешнее if возвращает ложь, то остальные логические выражения вообще не проверяются. В первой программе могут и проверяться (это зависит от особенностей языка программирования).

Добрый день!

Сегодня я попробую «доказать» теорему о том, что все прямоугольные треугольники являются равносторонними. Что вообще можно делать с подобными теоремами? Хорошо бы, например, уметь их опровергать. Помните, в разборе парадокса о двух конвертах мы представили ситуацию, которая удовлетворяет условию задачи, но опровергает предположение о том, что вероятности двух конкретных событий равны? Аналогично можно поступить и с данной теоремой — можно предъявить конкретный прямоугольный треугольник со сторонами разного размера (как на рисунке справа). И это полностью опровергнет всю теорему о равенстве сторон любого прямоугольного треугольника. Да и понятно, что слово «доказать» взято в кавычки, потому что хочется лишь создать иллюзию, что доказательство существует и корректно.

Помните, мы недавно разбирали доказательство того, что все лошади одного цвета? Там было неправильное применение метода математической индукции, приводящее к нелепому выводу. И польза такой задачки состоит в появлении дополнительного самоконтроля — теперь, применяя этот метод, человек будет внимательнее, поэтому будет реже обманывать себя по поводу менее очевидных утверждений.

Когда несколько раз проверяешь все пункты доказательства, убеждаясь, что на каждом шаге всё корректно, но итоговый результат очевидно ошибочный, то приходится копаться в себе всё глубже и глубже — а это очень полезно. Почему мы ищем ошибку? Просто из-за того, что хочется понять, как эта простенькая задачка для шестого класса вдруг обводит умного человека вокруг пальца… Ну а если кого-то не обводит, то данное вступление было не для вас

Итак, сначала вспомним пару признаков равенства прямоугольных треугольников, чтобы было на что ссылаться потом:

1) Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

2) Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники тоже равны.

Для краткости я их здесь доказывать не буду. Отмечу только, что первый признак прямо следует из признака равенства треугольников (по двум сторонам и углу между ними), а второй очевиден из теоремы Пифагора — гипотенузой и одним из катетов жёстко задаётся второй катет (обычно его доказывают иначе, но не в этом суть).

Начнём работать с произвольным прямоугольным треугольником. Возьмём, например, тот, что был на первой картинке. И построим в нём биссектрису из любого острого угла (разделим угол пополам). А из катета, соседнего с другим острым углом, проведём серединный перпендикуляр (перпендикулярную прямую, проходящуюю через его середину). Далее мы построим два отрезка из точки их пересечения — до вершин прямого угла и того острого, который соседствует с данным катетом. На рисунке слева вы можете видеть два зелёных треугольника, равенство которых мы сейчас докажем.

Итак, почему же они равны? Это два треугольника, у которых есть один общий катет (значит он у обоих треугольников имеет одну длину). И второй катет — это половина нижнего отрезка, так как мы на нём строили серединный перпендикуляр. Другими словами, два зелёных треугольника равны по первому признаку — у них попарно совпадают длины катетов. Верно? Тогда идём дальше.

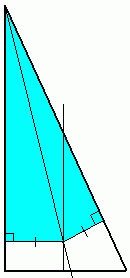
Из той же точки пересечения биссектрисы и серединного перпендикуляра опустим два перпендикуляра — на гипотенузу и на катет. Получаем ещё два прямоугольных треугольника (рисунок справа). На этот раз мы докажем, что эти голубые треугольники равны.

У них есть общая гипотенуза, поэтому можно попробовать применить второй признак (о равенстве гипотенуз и катетов). Поскольку перпендикуляры опускались из точки, лежащей на биссектрисе, то их длины совпадают по свойству биссектрисы (так как это множество точек, равноудаленных от сторон угла) — данное равенство отмечено одинарными штрихами на чертеже. Получается, что выполнено условие — гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника. Это значит, что голубые треугольники тоже равны.

Что это нам даёт? Подождите одну секундочку, осталось совсем чуть-чуть!

Рассмотрим оставшиеся два жёлтых треугольника (на рисунке слева):

Раз зелёные треугольники равны, значит их гипотенузы тоже равны. Но они совпадают с гипотенузами жёлтых треугольников. Это значит, что гипотенузы жёлтых треугольников тоже равны — отметим это на чертеже двойными штрихами.

Ну а раз голубые треугольники равны, то и их катеты равны. Но они совпадают с катетами жёлтых треугольников, поэтому катеты жёлтых треугольников тоже равны (отметим это на чертеже одинарными штрихами).

Выходит, мы опять можем применить второй признак — гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника. Получается, что жёлтые треугольники тоже равны.

В этот момент уже можно говорить «упс»

Если проблема ещё не видна, то предлагаю взглянуть на чертёж справа. На нём отмечены равные стороны жёлтых и голубых треугольников. Хорошо видно, что катет и гипотенуза исходного треугольника состоят из пары одинаковых отрезков. Это значит, что катет и гипотенуза исходного треугольника равны.

Какие это открывает просторы? Огромные! Если один катет равен гипотенузе, то и второй катет тоже равен гипотенузе (по этой же теореме). А это значит, что все прямоугольные треугольники являются равнобедренными — у них равны катеты. А раз оба катета равны гипотенузе, то все прямоугольные треугольники являются равносторонними!

После этого геометрия становится простой и ясной, потому что уж с равносторонними треугольниками мы управимся

Повторюсь: я знаю о существовании прямоугольных треугольников с неодинаковыми сторонами, поэтому не надо опровергать данное доказательство словами «доказана глупость, поэтому в доказательстве ошибка». Интересно именно найти эту ошибку

Приглашаю обсудить сомнительные моменты доказательства в комментариях (но предлагаю сначала найти своё возражение, а не читать сразу чужие). И очень прошу тех, кто раньше сталкивался с этой задачкой, не рассказывать все секреты, чтобы не лишать остальных читателей удовольствия от самостоятельного разбора. Дело в том, что таких красивых задачек очень мало, поэтому будет очень обидно, если человек, желающий с ней разобраться (и получить от этого себе пользу) не успеет сделать это до того, как кто-то всё объяснит.

Хороших вам выходных!